- 1Division MR Physics, Center for Medical Physics and Biomedical Engineering, Medical University Vienna, Vienna, Austria
- 2A.A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Harvard Medical School, Charlestown, MA, United States
- 3Siemens Healthcare GmbH, Erlangen, Germany
Purpose: Many of today's MR coils are still somehow rigid and inflexible in their size and shape as they are intentionally designed to image a specific anatomical region and to fit a wide range of patients. Adaptive coils on the other hand, are intended to follow a one-size-fits-all approach, by fitting different shapes, and sizes. Such coils improve the SNR for a wide range of subjects by an optimal fit to the anatomical region of interest, and in addition allow an increased handling and patient comfort as one MRI receive-coil is maintained instead of multiple.
Material and Methods: To overcome the SNR losses by non-fitting and thus poorly loaded RF coils, we propose a stretchable antenna design. Each loop has the ability to reversibly stretch up to 100% of its original size, to be anatomically adaptive to different shapes and sizes, and therefore make the coil usable for a wide patient population. Besides the mechanical challenge to find a robust but flexible conductive material, various other problems like frequency and matching shifts affect the SNR. Through bench measurements and MR Imaging at 1.5 T, we investigated different stretchable conductor materials, that fit the defined requirements. Finally, a rigid reference coil and an adaptive 6-channel array for knee imaging at 1.5 Tesla were developed to investigate the potential improvement in SNR.
Results: The material tests identified two potentially useful materials: Highly ductile copper and a silver-plated stranded copper wire. Although, the adaptivity causes a frequency shift of the resonance frequency, which entails in variations of the impedance that each coil presents to its connected pre-amplifier, there are strategies to mitigate these effects. The adaptive array prototype made of partly-stretchable loops, showed an improved SNR of up to 100% in 20 mm depth from the phantom surface, and therefore demonstrates the effectiveness of adaptive coils.
Introduction
The past two decades of Magnetic Resonance Imaging (MRI) have seen immense advances in various fields, with a focus toward improved sensitivity, multi-modal imaging and of course reduced scan-time in clinical and research examinations. Acquiring MRI data is still time consuming due to long acquisition times, and therefore prone to motion artifacts. Furthermore, MRI data acquisition is limited in spatial and temporal resolution due to the lack of signal-to-noise ratio (SNR). A simple solution is to apply higher static magnetic field strength (B0) [1] to increase the detectable nuclear magnetization, and thus to achieve higher spatial resolution with sufficient high SNR [2].
While the advancement of gradient coils in strength and slew-rate [1] ensured a speed up in image acquisition, the improvement of sensitivity with higher field strengths or well-crafted detector geometries of MRI probes, have always been critical [3].
Back in 1980, Ackerman et al. demonstrated that an improved SNR could be obtained by placing a small coil on the surface of the sample, close to the region of interest [4]. The use of small surface coils in the regime of sample dominated noise enables large sensitivity improvements, because it provides both, stronger magnetic coupling with the sample and noise reduction due to the smaller volume of tissue being visible for the coil [5].
Many theoretical and experimental works suggested to put a large number of small surface coils as close as possible to the imaging volume to achieve a set of advantageous features like a high filling factor [6–9]. Because of the importance of coil detectors, and the fact that MRI (today) relies on signal detection with receive arrays, the development of such RF antennas is a critical step in gaining SNR, speeding up the acquisition and therefore improving the patient comfort during every MR examination [10–13]. To achieve a high SNR, it is important that at high Qloaded values, the filling factor is very close to η = 1, to gain the maximum SNR. The magnetic field filling factor η is a ratio, for the magnetic energy stored inside a load (e.g., sample, phantom, patient) to the total magnetic energy stored in the coil.
B1 is the value of the RF magnetic field once integrated over the sample and the second time integrated over the total coil volume. As an approximation ηf can also be seen as:
where
is the unloaded Q-value divided by the loaded Q-value of the coil element and P is the input RF power. The introduction of a load decreases the quality factor of the coil and the magnetic field [14]. By bringing the coil closer to the sample, the filling factor is increased and the term in the numerator of the equation for the SNR,
is maximized, which results in an optimized SNR. Many factors determine the SNR available in an MR experiment. In Equation 4 the USignal considers the SNR for a single voxel volume ΔV, with the assumption that the fields of the magnet and the coils are constant over the voxel. The properties of the sample and the coil, contribute to the SNR through the resistance at the coil terminals (Reff) and the sensitivity pattern of the coil. The noise signal UNoise in any MRI experiment is basically thermal noise generated by the receiver coil and the sample scaled to the bandwidth used in detecting the signal [15].
So, by improving the filling factor, the coil resistance RCoil, also called equivalent-series-resistance (ESR), is minimized by making the unloaded Q high, and the sample resistance Rs (through the induced eddy current losses in the conductive sample) can be minimized by choosing the coil size to match the target Field of View (FoV).
Designing a coil array to fit close to the region of interest is quite easily achieved, but to use the same coil with multiple patients that vary in size and shape, is challenging. It requires the coil array to be shape/form adaptive. Mechanical flexibility of the RF array is advantageous as in most cases the shape and size of different body anatomies varies significantly, but most RF coils are rigid and only fit a specific anatomical region and only certain patient sizes. Form-adaptive RF coil arrays improve the electromagnetic coupling between sample and coil, provide a higher filling factor, and therefore, potentially improve the RF receive efficiency, if the mismatch and expected frequency shift is not exceeding the benefits.
Allowing adjustable coil geometries requires equally flexible solutions for mitigating upcoming parasitic effect like increased mutual coupling between elements and frequency shifts. As a result of these shifts in center frequency and the variation in coupling, the source impedance presented to the pre-amplifier changes, which leads to SNR loss. Several approaches to mitigate the effects of coil coupling and frequency shifts, like broad-/wide -band matching [16] have already been more or less implemented in the field. Another approach is to automatically tune and match the coil array [17–20]. Previous work have already shown the feasibility of mechanical adaptation of the receive coil to the body part of interest. A first approach of flexible coils, where a mercury filled tube by Malko et al. [21] was used to form a loop. Other works on adaptive coils include a transmit-receive head array that permits bending to adjust its diameter [22], a sliding mechanism varying the diameter of a conical coil arrangement for wrist imaging [23]. A stretchable coil array for knee imaging at 3T, which utilized braided copper wire mounted on an elastic textile substrate was introduced cite Nordmeyer-Massner et al. [23]. Compared to a standard rigid knee array, the stretchable 8 channel array introduced an overall SNR loss of 20%. Later on on-coil digitization avoiding cabling and increase patient comfort [24] was used with the stretchable copper braid. Further approaches focused on mechanical flexibility, which is offered by several coil designs like screen-printed flexible MRI receive coils [25], or the flexible/rigid PCBs [26, 27]. Ongoing research on coil elements made of coaxial cable looks promising, especially due to the low inter-element coupling [28–30]. Such elements offer a large range in flexibility, potentially enabling wearable coil arrays, but limitations like the dependency of the resonance frequency to the permittivity of the dielectric, and therefore to the diameter of coaxial cable introduce limitations that need to be further investigated.
The present work addresses mechanical and electrical issues of anatomically adaptive coil arrays. In the first part, the concept of partly-stretchable coil arrays is investigated alongside with material tests of conductive materials used as coil elements. In the second part, the performance of a 6-channel adaptive array for 1.5 T is compared with a rigid reference array (Similar to the 15-channel Tx/Rx knee coil array from QED). Both arrays were tested using three different sized knee phantoms, representing various realistic knee sizes. Parts of this work have already been presented at conferences [31, 32].
Materials and Methods
Material Tests
The key challenge in designing anatomically adaptive loops is to find reversibly stretchable coil conductors, which have equal or only slightly worse properties than the used standard (flat) wire with respect to electrical conductivity.
For typical metallic wire, stretching results in irreversible plastic deformation beyond a few percent of elongation. A certain reversibility of a change in length can be achieved by mounting a wire with a certain length reserve (e.g., meandered style) on an elastic material. In addition, this material should be “MR silent,” which means that there is no contribution to the MR signal from this material. To restore the original state after stretching, the wire has to allow enough elasticity and ideally should mechanically behave like a spring. Standard highly conductive materials like copper, silver, gold, aluminum were too pliable for this task. Materials like iron or steel would fulfill the strength requirement, but they are ferromagnetic, and therefore not suitable for MRI. An option in between would be austenitic steel, which is not ferromagnetic and would provide enough strength, but has low conductivity. We developed several mechanical concepts, published in a filed patent [33]. One of the most promising approaches thereof is the partly-stretchable-loop—concept (see Figures 2A,C–F) used in this work.
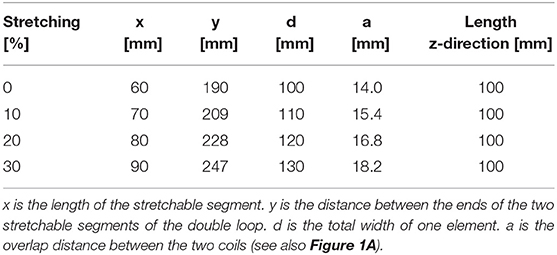
Four different reversibly stretchable materials were investigated (see Table 2) and used for the construction of stretchable double-loops (see Figure 2A). The loops were realized with a stretchable area of length x and a width of 100 mm (z-direction) (see Figure 1A). The stretchable double-loops with loop sizes according to Table 1 were compared to four standard double-loops (see Figure 2B) as reference.
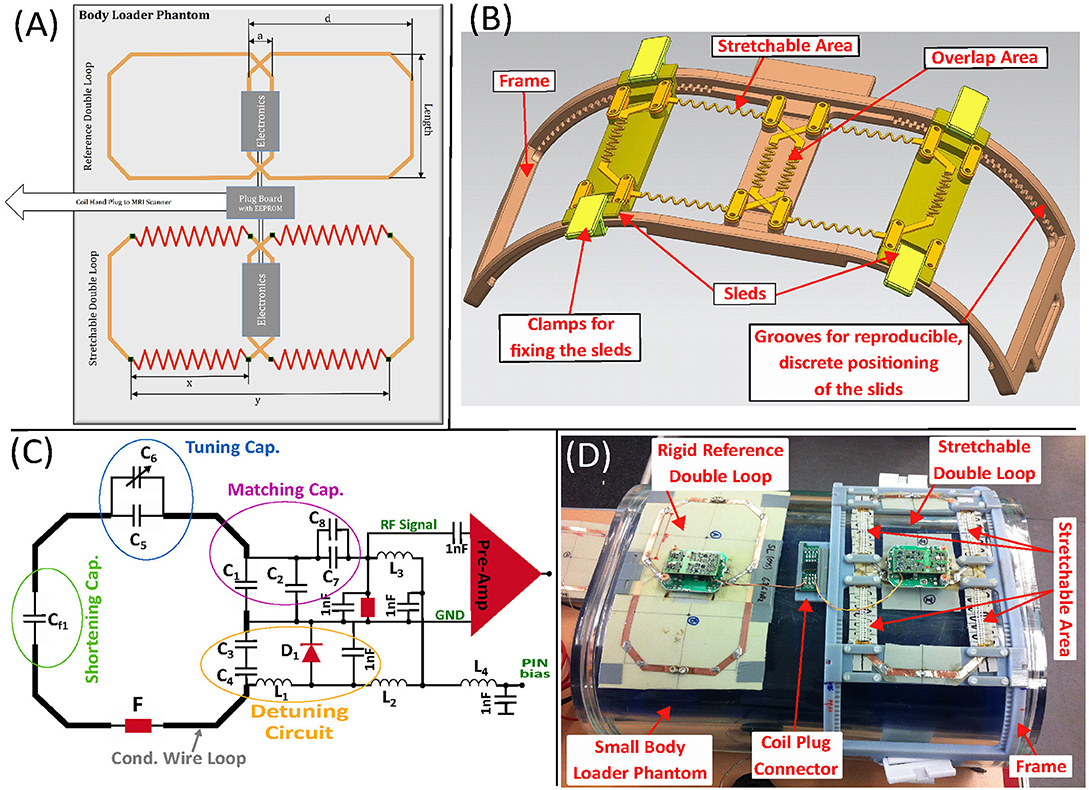
Figure 1. (A) Schematic of the used test-setup for material measurements. The setup allows reproducible testing of different conductive materials used for an adaptive double-loop configuration that can be enlarged/stretched and immediately compared to a rigid reference double-loop. (B) Two rectangular loops with a maximum length (z-direction) of 100 mm can be attached to the frame (brown) and enlarged in x-direction by shifting the sleds (yellow) in 5 mm steps. (C) Simplified RF circuit. (D) Experimental setup with a rigid reference double-loop and a stretchable double-loop mounted on the test-frame, placed on the torso-shaped phantom (see Figure 6) with a main body (blue) filled with per 1,000 mL Bayol-oil and 0.011 g MACROLEX blue and an outer compartment (clear) filled with per 1,000 g H2O dist.: 1.25 g N iSO4x6H2O, 5 g NaCl. The coil plug connector in between the two double-loops serves as connector between the test setup and the MRI scanner and houses the coil code. The test-frame is 3D laser-sintered (StratasysObjetEden500V) using MR-invisible material.

Figure 2. (A) The four investigated stretchable material candidates. A highly reversible flexible special foam padding was used, to support the stretchable materials. The pre-amplifier on the feed boards are already attached. (B) Four differently sized rigid double-loops used as a reference. (C) Stretchable double-loop made of CuBe-Strain springs. (D) Highly ductile copper AP9121R DuPontTMPyralux® flexible laminate. The material is a double-sided, 35 μm copper-clad flexible laminate. (E) Amotape® Conduct Elast. #45756. A 6 mm wide stranded copper wire made of 7 single strands with an area of 0.078 mm2 each. PTFE insulated and connected with 3 elastic threads made of Elastane gimped with PA66 (620dtex + 78/2dtex). (F) Amotape® Conduct Elast. #45792 with same specifications as Amotape® #45756 but with 19 single strands.

Table 2. Materials used for stretchable areas. Amotape® #45756 and Amotape® #45792 provide the stretchability of the stranded wire by three elastic Elastane threads.
The double-loop arrays with rectangular loops were manufactured on FR-4 (fiberglass cloth with a flame-resistant epoxy resin) using the simplified circuitry illustrated in Figure 1C.
The reference loops and the fixed parts of the partly-stretchable loops were made of 6 mm wide adhesive copper tape with a copper thickness of 70 μm. Thin or very narrow copper traces increase the loops resistance thus lowering the Q value, while a wider or thicker copper trace may cause eddy current heating, B1-distortions and/or self-shielding [14]. 16-awg thick tin-plated copper wire bridges were used to overlap at the cross sections of each loop, minimizing capacitance between the two loop traces. Segmenting capacitors were used to provide a homogeneous current distribution over the loop, reduce the E-fields induced into the sample load through voltage splitting between the capacitors, reduce the stray fields caused by the split voltages which influence the load dependence of the resonance frequency and finally reduce capacitive coupling as well as parasitic capacitance between loop and sample. Each loop was tuned to the resonance frequency of 63.6 MHz (1.5T) using a torso-shaped phantom with a main body (blue: per 1,000 mL Bayol-oil and 0.011 g MACROLEX blue) and an outer compartment (clear: per 1,000 g H2O dist.: 1.25 g NiSO4 × 6H2O, 5g NaCl) (see Figure 1D).
The stretchable double-loops were mounted on a 3D laser-sintered (ObjetEden500V, Stratasys, Rechovot, Israel) frame (see Figures 1B,D), which allows the stretching of the loop material in discrete steps of 5 mm in x-direction (the stretching in y-direction is also performed, as the frame is attached to the phantom's surface). The overlap between two loops is constant and provides optimal overlap decoupling for a stretching of 15% (x = 75 mm).
Bench and MRI measurements were performed with 0, 10, 20, and 30% stretching (see Table 1). The stretch area x is fixed to start at 60 mm. The geometrical properties are calculated with Equation 5 and 6, which result from an array design of a 18-channel adaptive knee array with 3 rows of 6 rectangular loop elements (see Table 1 line 1).
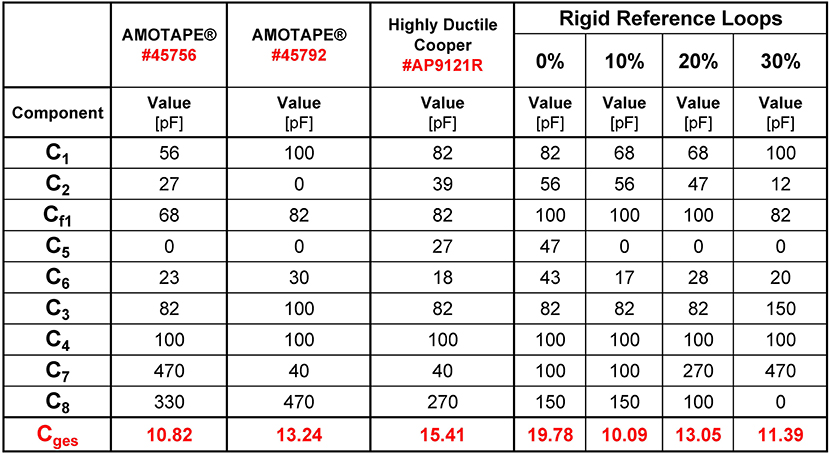
Stretching of the adaptive loops changes the loop's inductance and resistance and is therefore expected to cause a shift in the resonance frequency. Therefore, the partly-stretchable loops were tuned and matched to the Larmor frequency at 1.5 Tesla (63.6 MHz) at the center between the maximum and minimum length of the stretchable areas corresponding to a stretching of 15% with x = 75 mm). The four reference double-loops were individually tuned to and matched. Capacitor values for all built double-loops can be seen in Figure 12.
The inductance of each loop is estimated from the total capacitance and the resonance frequency. The coil resistance is estimated from the measured Q-factor. Q-values for each loop were measured at a distance of 20 mm with an S21 measurement on the network analyzer (E5071C, Keysight Technologies, Santa Rosa, CA, USA) using a double-loop probe with −75 dB decoupling. To estimate the effect of stretching on inter-element coupling, the coupling coefficient k was measured using the two-mode-frequencies method:
with and [34, 35]. The upper frequency and the lower frequency mode are measured on the network analyzer, with an S21 measurement, assuming that the resonant frequencies f 0 are identical for both loops, as well as the capacitance and the inductance values for both loops are the same. The center-to-center distance for rectangular loops to achieve optimal inductive decoupling is 0.9 d [6], but due to the stretching of elements, the decoupling between elements changes. Residual coupling was suppressed by pre-amplifier decoupling. Active detuning using an LC parallel circuit was implemented to detune the loop during transmit, and baluns, reducing common mode currents on the shield of the coaxial cables, were added and tuned to the Larmor frequency.
The experimental setup (see Figure 1D) was placed in the MRI and with every stretchable double-loop configuration and the corresponding reference double-loop noise and signal data was acquired one after another. For every configuration, 2 measurements were performed: per stretched position (4 stretch-points, see Table 1, column 1) signal and noise data was acquired with the reference and the stretchable double loops.
SNR images were generated from signal- and noise datasets, acquired on a Siemens MAGNETOM Aera 1.5 Tesla MRI scanner with software platform Syngo MR E11 (Siemens Healthcare GmbH, Erlangen, Germany). To obtain the SNR images, a standard spin-echo sequence (TE = 15 ms, TR = 300 ms, FoV = 300 mm, TA = 1:20 min, slice thickness = 5 mm, acq. matrix = 256 × 256, voxel = 1.2 × 1.2 mm, bandwidth = 130 Hz/pixel) with a 90° and a 180° RF pulse was applied. For the noise measurement, the RF excitation pulse was set to zero, whereas for the signal measurement the RF excitation was set automatically. The acquired data were exported and then reconstructed offline MATLAB (MATLAB, The Mathworks, Natick, MA, USA).
SNR was calculated using the Sum-of-Squares (SoS) method ideal for high input SNR [36] and the Maximum Available (MA) method [15].
SNRSoS values as calculated in Equation 8, are equal to the SNR for optimal combining with unknown coil sensitivities. The MA method describes optimal coil combination, were sensitivities are known. By multiplying the pixel value in each coil with the complex conjugate of the coil sensitivity for that channel, summing over all channels, and dividing this sum with the sum of the squared coil sensitivity in all channels, an optimal noise decorrelated (noise pre-whitened) combination method is used. Any phase added by the coil itself is removed and the signal is summed up. This method is also known as B1-weighted coil combination [6].
Adaptive Knee Array
Based on the results of the material test, the best performing material was used for further investigation. A preliminary study of the knee geometry (100 mm up/down the knee center) on 25 patients from Europe and U.S.A. showed a diameter range of 102–169 mm for European knees and 110–211 mm for U.S. knees. Standard coils like the 15-channel Tx/Rx knee coil by QED (Quality Electrodynamics, Mayfield village, Ohio, USA) have a limited inner diameter of 173 mm and field of View (FoV) in z-direction of around 200 mm. This diameter limitation makes the knee a good object to demonstrate the performance of a one-size-fits-all adaptive coil array approach.
To investigate the potential SNR improvement, a 6-channel receive-only array for 1.5 Tesla was developed. It consists of 4 adaptive channels (see Figure 3C) and a rigid 2-channel bottom part (see Figure 3B). As reference, a rigid 4-channel reference array (see Figure 3A) with an inner diameter of 180 mm, the size comparable to a single-row of a commercial 15ch knee coil (Quality Electrodynamics, Mayfield, OH, USA) was constructed, which could also be attached to the rigid 2-channel bottom part. The setup is mounted on a baseplate of the 15-channel knee coil, which is attachable to the patient table (see Figure 3A). The four adaptive channels can be attached to three different sized shells with grooves to fit the feed boards, similar to the phantoms (see Figure 4A). Geometrical decoupling was pre-adjusted during construction and is maintained with the bottom part for both arrays.
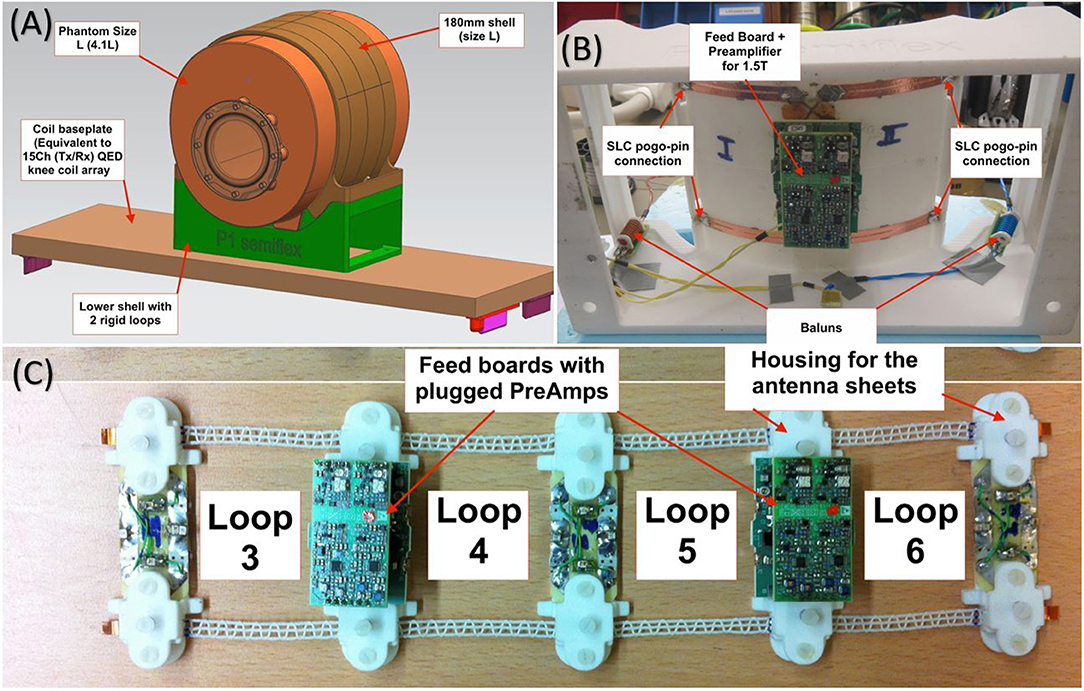
Figure 3. (A) 3D rendering of the reference array mounted on the lower shell with the largest knee Phantom L (4.1 l). (B) The lower shell houses two channels that can be electrically connected to the upper four channels using spring-loaded pins melted into the laser-sintered lower shell. Such pogo-pins (preci-dip SA, Delemont, Switzerland) offer a low resistance military standard connection with high mating cycles and excellent performance at higher frequencies like MRI. The lower shell contains cable traps (blue and yellow) to reduce common mode currents on the shield. (C) 4-channel adaptive array with 4 stretchable elements, were each loop is made of Amotape® #45792, with a stretchable area between the feed-boards of x = 60.1 mm. The 4-channel adaptive array is connected to the 2-channel lower shell for measurements. Together they make the 6-channel adaptive array. The lower shell can be used along with the 4-channel adaptive array or the 4-channel rigid array.
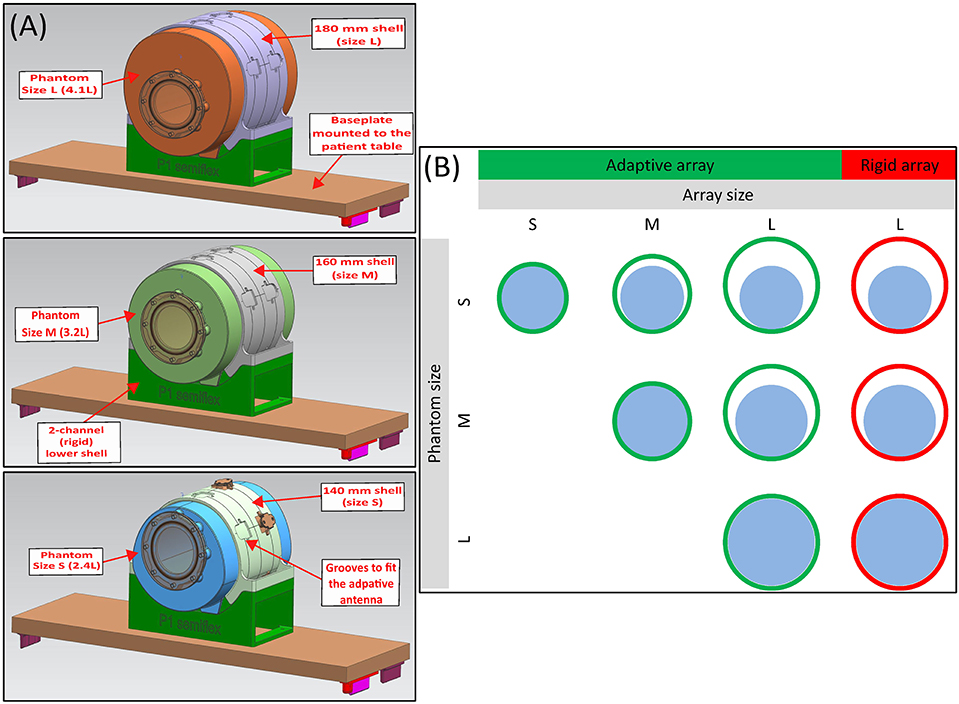
Figure 4. (A) 3D CAD rendering of the adaptive array test setup with 4 stretchable (upper shell) loops and 2 rigid loops in the bottom shell. The adaptive array is evaluated using three differently sized knee phantoms of size L (180 mm diameter, 4.1 l), M (160 mm diameter, 3.2 l), and S (140 mm diameter, 2.4 l). (B) To directly compare the 4-channel adaptive array with the four stretchable loops to the 4-channel reference array (each one connect to the 2-channel lower shell upon each measurement), a shell of size 180 mm is 3D laser sintered and the adaptive loops are mounted on it, while the three differently sized knee phantoms (L, M, S) were imaged.
Three differently sized phantoms with 140 mm (size S, 2.4 l), 160 mm (size M, 3.2 l), and 180 mm (size L, 4.1 l) diameter each filled with per 1,000 g H2O dist.: 1.25 g N iSO4 × 6H2O, 5 g NaCl were used for MR imaging. All housing parts including the three phantoms, were 3D laser sintered using the (ObjetEden500V, Stratasys 500V, Rechovot, Israel). The experimental setup can be seen in Figure 4B.
All loops were tuned and matched to 63.6 MHz and 50 Ω. The adaptive loops were adjusted at a stretching of 13.34%, which equals the diameter of the phantom size M. Decoupling was <18 dB, pre-amplifier decoupling >20 dB, and matching <20 dB. The stretchable areas of the adaptive array were made of 6 mm wide Amotape® Conduct Elast. #45792. The same properties as evaluated during the material test, were measured again for the knee array in the presence of the other loops, while inductively decoupled.
Finally, SNR was measured for the three phantom sizes using the adaptive and the reference array using the same spin-echo sequence as for the material tests. The smallest configuration of the adaptive array was used to acquire signal and noise images of the phantom size S (140 mm). The 2nd configuration was used to image phantoms S and M and the largest configuration was used to image all three knee phantoms (see Figure 4B). The acquired data were exported and reconstructed offline (MATLAB, The Mathworks, Natick, MA, USA).
Results
Material Tests
The goal of the material tests was to identify a suitable material fulfilling the needs of an adaptive coil array. The CuBe2 Strain Springs were found to introduce a too high inductance and were, therefore, not further evaluated.
All tested materials were sufficiently stretchable to cover the envisioned element size. Bench measurement results for the rigid double-loop array and the three stretchable double-loop arrays are summarized in Figure 5 and show the dependence of the following parameters on the amount of stretching: Qloaded (Figure 5A), Qunloaded (Figure 5B), Qratio (Figure 5C), coupling coefficient k (Figure 5D), shift in resonance frequency (Figure 5E), inductive decoupling (Figure 5F), pre-amplifier decoupling (Figure 5G), matching (Figure 5H), coil+sample resistance (loaded) (Figure 5I), and unloaded coil resistance (Figure 5J). All coils showed a shift in resonance frequency of about−125 kHz per mm elongation by stretching (see Figure 5E). Amotape® #45792 showed consistently highest Q-ratio, best inductive and preamplifier decoupling. The loops with Amotape® #45792 showed coupling coefficients and coil resistance values in the unloaded and loaded cases which lie between the values of the other materials. All measured parameters of the stretchable loops were compared to rigid loops with equivalent sizes. Complete measurement data is listed in the Figure 11.
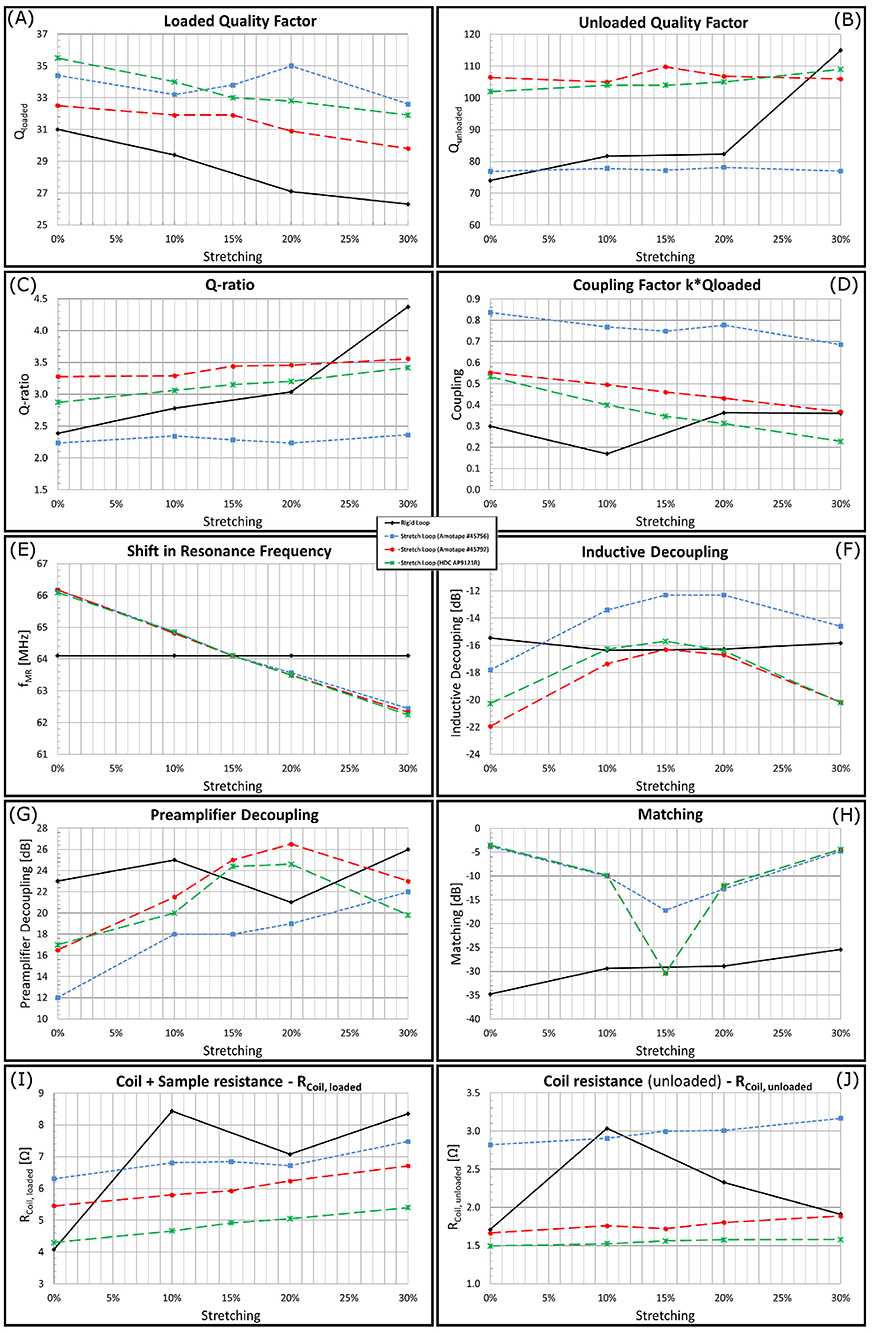
Figure 5. Properties of all tested materials while mounted on the test frame, measured in the laboratory.
The results of SNR measurements in the MR scanner are shown in Figure 6. In most cases and on average, the stretchable loops with Amotape® #45792 showed the least loss in SNR (8/9% in 20/60 mm depth, respectively) as compared to the rigid double coil array.
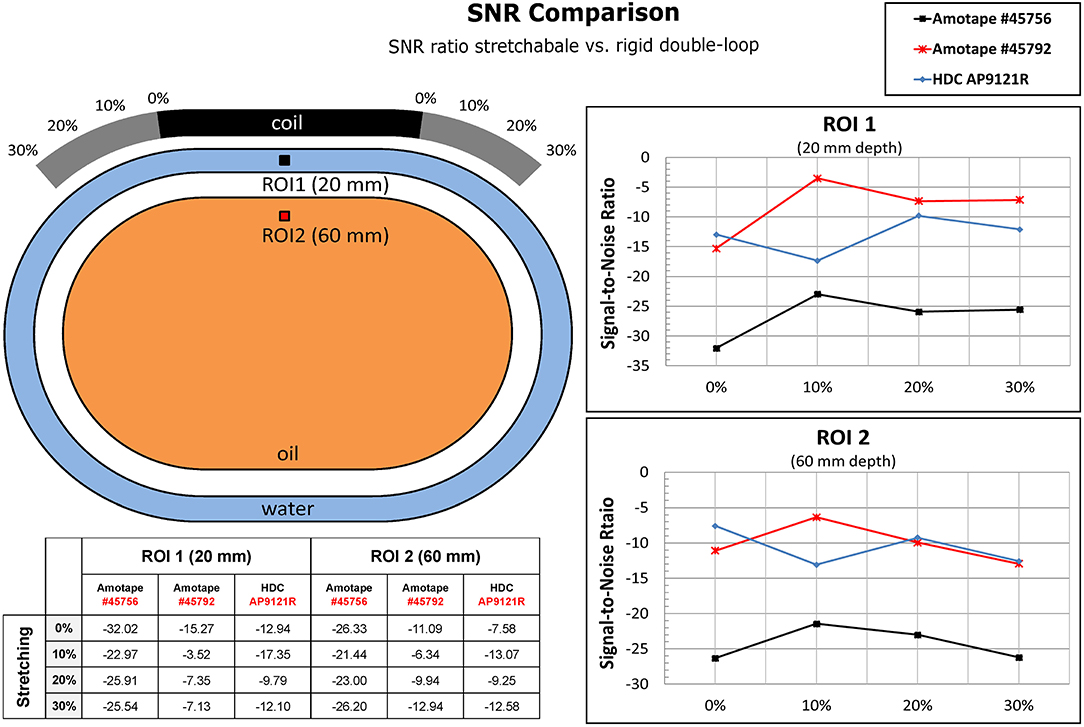
Figure 6. The Signal-to-Noise ratio (SNR) of the three different stretchable materials, compared to each other. The SNR was measured in a region of interest (ROI of 5 × 5 pixel) at 20 and 60 mm depth from the coil. The SNR losses were acquired from the SNR maps, calculated with the maximum available method, the stretchable double loop in the different stretching states compared with the SNR maps of the corresponding reference double loop. The torso-shaped phantom consists of a main body (blue) filled with per 1,000 mL Bayol-oil and 0.011 g MACROLEX blue and an outer compartment (clear) with per 1,000 g H2O dist.: 1.25 g NiSO4 × 6H2O, 5 g NaCl).
Adaptive Knee Array
For the adaptive knee array also Amotape® #45792 was used. The measured shift in resonance frequencies for the 4 stretchable loops within the adaptive array when stretched from a knee diameter of 140 to 180 mm, ranged from 66.39 to 61.23 MHz. This corresponds to a stretching of up to 26.68% from the original array size, the stretchable lengths × change from 60.1 to 91.5 mm. The overall size of an adaptive loop varies between 90.6 × 60 mm (un-stretched) and 122 × 60 mm (fully stretched). This resulted in a frequency shift of 164 kHz per mm elongation, which is comparable to the 128 kHz per mm as measured during the material tests for Amotape® #45792.
Q-ratios for all loops of both the rigid reference and the adaptive knee array were larger than 2, and therefore in sample noise dominance. The unloaded coil resistances RCoil, unloaded of the individual antenna elements for the 180 mm knee phantom ranged from 0.84 to 1.39 Ω (reference array) and from 0.99 to 2.13 Ω (adaptive array). RCoil, loaded for the same phantom size ranged from 2.38 to 3.67 Ω (reference array) and 2.51 to 4.79 Ω (adaptive array).
The coupling factor k*Qloaded between the loops of the reference array ranged from 0.048 to 0.125 and from 0.14 to 1.27 for the adaptive array. For the adaptive array this is higher than expected, which can be explained by the higher number of channels and their closer positioning as compared to the setting with 2 loops during the material tests, i.e., each loop was not only influenced by the direct neighbor, but also by all others.
Inductive decoupling ranged between 16.7 and 26.9 dB for the reference array and between 36.8 and 13.9 dB for the adaptive array. The best decoupling in the adaptive array was achieved at maximum stretching, as expected from the results of the material tests.
(Matching) ranged from −43.0 to −18.1 dB for the reference array. The adaptive array adjusted for the size M phantom was matched between −23.4 and −16.7 dB. At minimum and maximum stretching of the adaptive array loops, matching was completely off between −1.6 to −2.4 dB. Same results were achieved with the pre-amplifier decoupling. The reference array showed reasonable pre-amplifier decoupling values of 22.0 to 29.8 dB, whereas the loops of the adaptive array, from minimal to maximal stretching of the individual elements, ranged from 12.6 to 26.69 dB. Adjusted to the size M phantom, pre-amplifier decoupling for the adaptive array ranged from 19.6 to 26.5 dB, and is comparable to the values of the reference array.
Figure 7 illustrates the SNR images acquired with the reference and the adaptive array using the three different phantom sizes. SNR values were measured in single voxels in the middle transverse slice at three different depths from the surface, relative to the knee phantom size used. In a direct comparison between the adaptive and the reference array using phantom size L, the SNR of the adaptive array was worse at 20 mm below the knee phantoms surface (from the top), compared to the reference array. The SNR values in the center are just slightly worse for the adaptive array. When using smaller phantom sizes, the adaptive array, tuned and matched to phantom size M, achieves equal SNR values at the phantom center and much higher SNR values especially below the surfaces of the phantoms. Noise correlation is not exceeding 0.4 in any configuration of the reference or the adaptive array (see Figure 10).
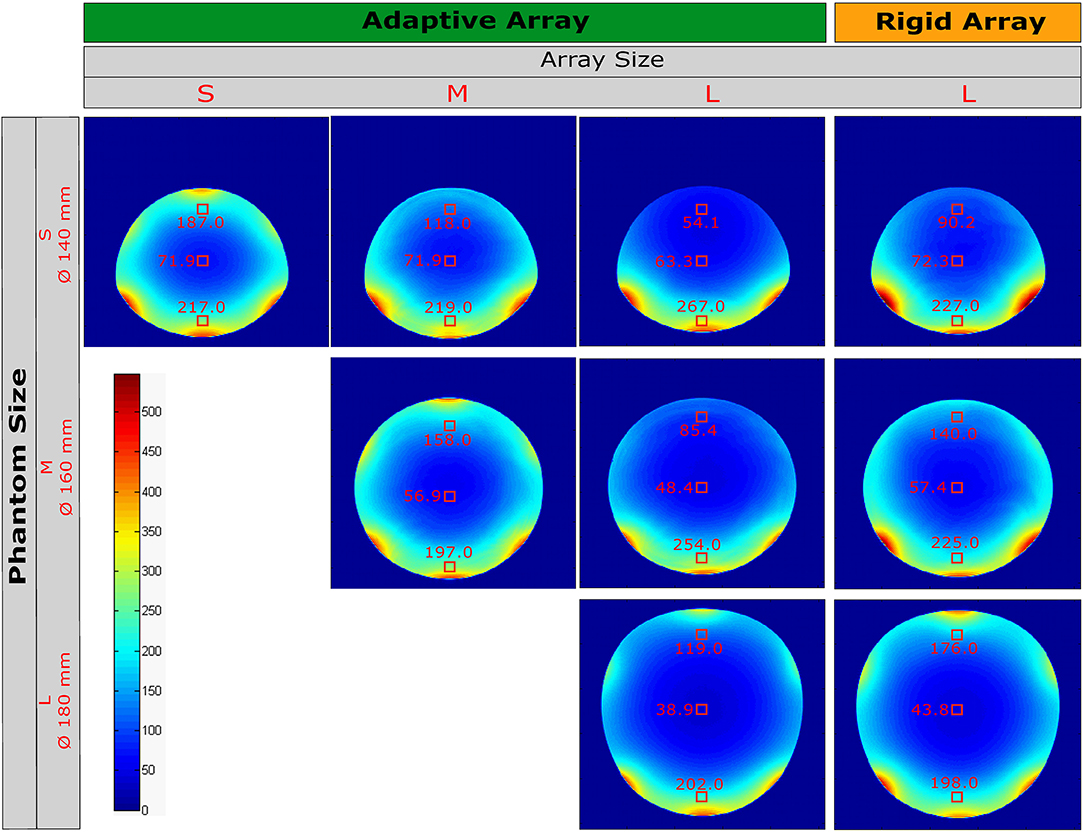
Figure 7. SNR comparison for the adaptive and rigid knee arrays for different phantom sizes. The SNR was measured at three representative points: at the center of each phantom, 25 mm away from the lower shell and 25 mm away from the top of each phantom. The experimental setup is illustrated in Figure 4B.
In Figure 8 one can see the SNR comparison between the arrays using the three different knee phantoms. Comparing at phantom size L, it is evident that the adaptive array stretched to sizes S, M and L (but always tuned and matched for array size M and phantom size M) performs worse (−10 to −40%) than the reference array (tuned and matched for array size L and phantom size L). However, as expected due to the closer fit to the sample, an SNR gain of 29% (array size M, phantom size S), 40% (array size M, phantom size M), or 100% (array size S, phantom size S) was observed in the voxel near the adaptive part of the arrays. SNR in the center of the phantoms was approximately equal to the rigid array, and a consistent 5–10% SNR gain was found for the voxels near the rigid bottom part.
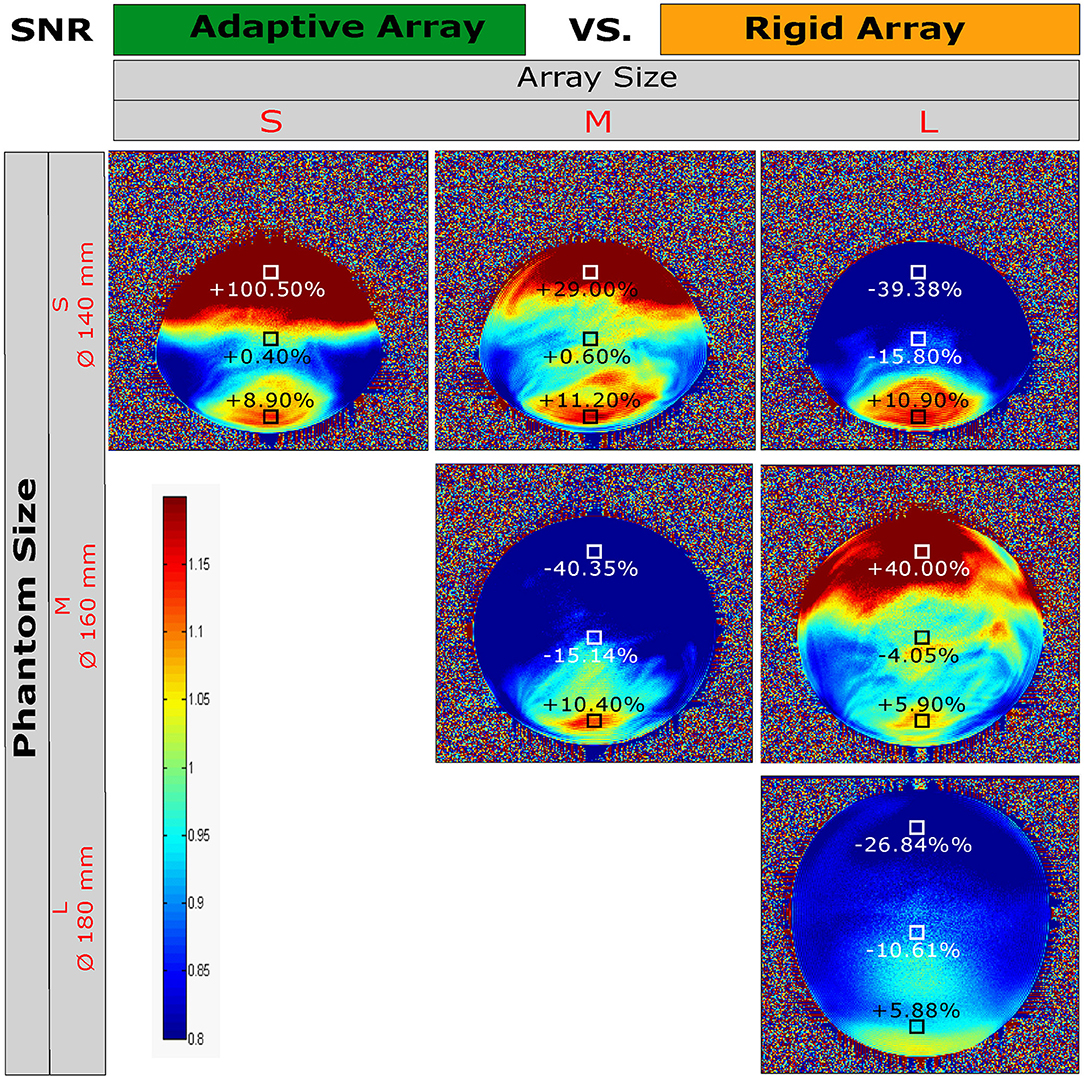
Figure 8. SNR images of the adaptive and the rigid knee array compared to each other using different phantom (knee) sizes. A SNR gain or loss at the ROI is indicated with “+” and “−” symbol and the corresponding percentage value.
Figure 9 shows sagittal in vivo MR images of the knee center using the adaptive array, displayed as uncombined single channel images, and the combined image. The imaged knee had a very small diameter of 100 mm at the center, even smaller than the smallest size configuration of the adaptive array (130 mm), therefore, the optimal fit of the adaptive array was not reached.
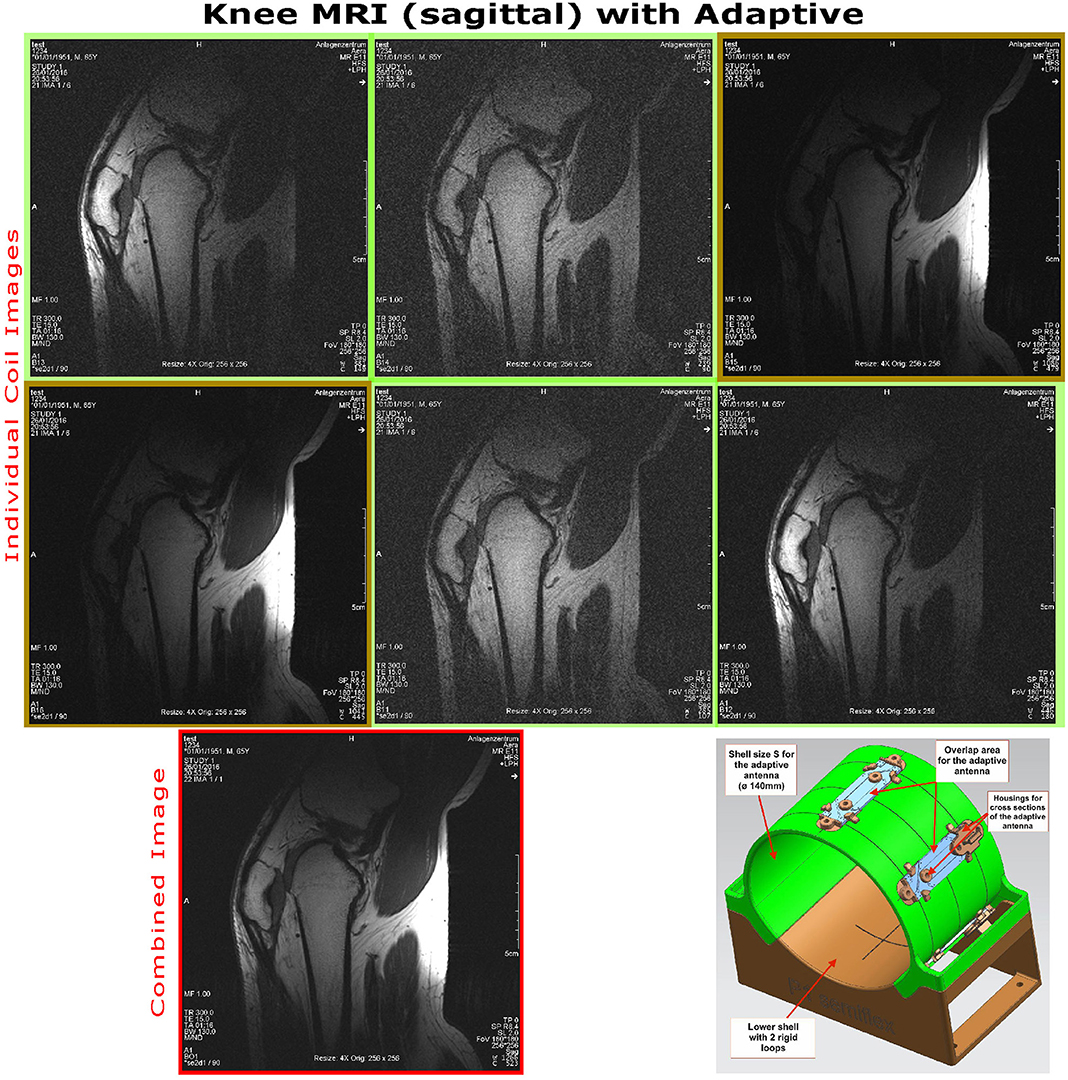
Figure 9. MRI images of the individual channels from the 6ch adaptive array, imaging the right knee of a volunteer. Image 3 (1st row, 3rd column) and 4 (2nd row, 1st column) are from the 2 channels in the lower shell. The image was acquired using a spin-echo sequence in sagittal orientation (TE = 15 ms, TR = 300 ms, FoV = 180 mm, TA = 1:16 min, slice thickness = 2 mm, acq. matrix = 256 × 256, voxel = 1.2 × 1.2mm, bandwidth = 130 Hz/pixel).
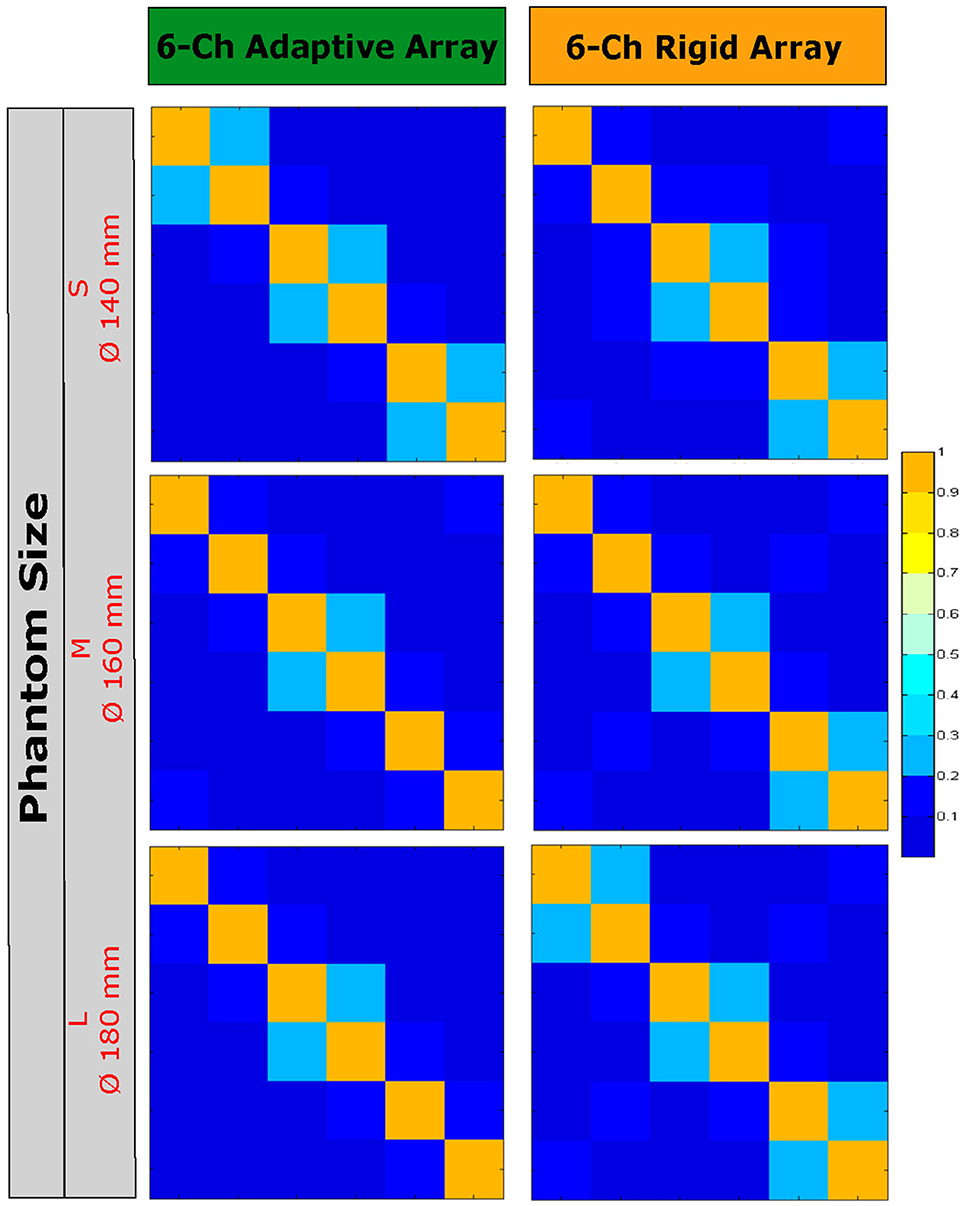
Figure 10. Noise Correlation Images of the adaptive and the rigid knee array on the three different phantoms.
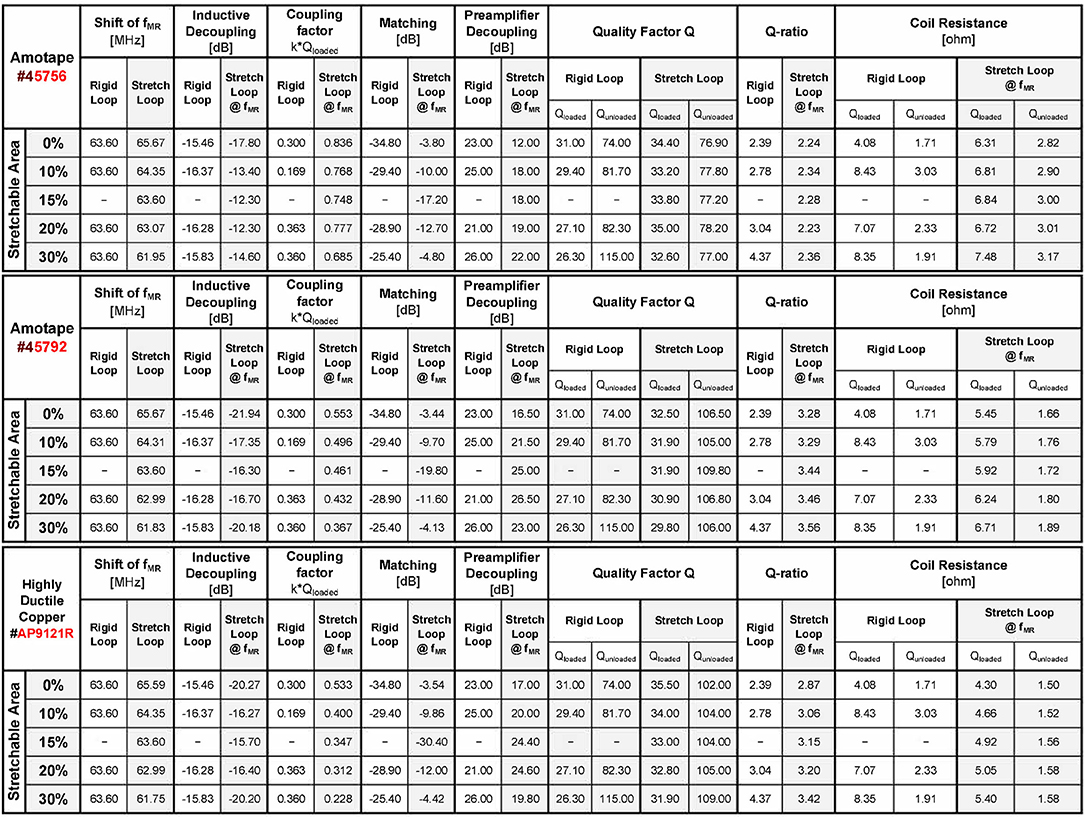
Figure 11. All measured values in the laboratory of each double-loop using the materials described in Table 2 (except CuBe2 strain springs) with the experimental setup described in Figure 1D.
Discussion
An approach for size- and shape-adaptable receive elements using partly-stretchable conductors is presented and its feasibility for in vivo MR imaging is demonstrated. Four different stretchable materials were investigated and a material with 19 strands of meandered conductors on an elastic substrate was identified as the best-performing solution in terms of decoupling and achievable SNR. A similar material with only seven strands showed slightly worse performance due to its higher equivalent series resistance. A solenoidal spring from CuBe2 was excluded from performance tests since it exhibited a too high inductance which would have required impractically low capacitance values to achieve resonance at the Larmor frequency. In direct comparison of the best stretchable double-loops to rigid reference double-loops, the SNR loss is below 10% on average. A 6-channel knee array prototype with two rigid and four stretchable elements was developed and a thorough comparison to geometrically identical rigid standard loop coil arrays was performed. A considerable SNR gain of up to 100% was demonstrated, which shows that the effect of better conformity to the sample outweighs the SNR penalty for stretchable coils. This penalty arises from the facts that the stretchable coils exhibit inherently higher coil losses and can only be optimized in a single state of stretching in terms of resonance frequency, matching, and decoupling. The resulting variation in impedance by stretching affects the optimum noise matching to the preamplifier, thus degrading SNR.
To minimize these effects, the stretchable loops were tuned and matched, and their geometrical overlap optimized in an average stretching configuration. Evidently, a reduction of the stretchable area would lead to lower frequency shift, but would on the other hand limit the range of patient sizes that could be imaged. Additional techniques to compensate for the change of coil characteristics upon stretching would be beneficial, especially at extreme positions of elongation away from the optimized size. Tuning and matching could be restored by automatic tuning and matching techniques. The approach of using varactor-diodes as voltage-controlled tuning elements to match the impedance of the coil elements has been introduced very early [7, 37]. They were also used to design a closed-loop with automatic tuning and matching circuit for a flexible EPR surface resonator [38], or a microcontroller-based automatic tuning technique for MRI [20]. The drawbacks are that the procedure took about 1 min to complete, and involved a physical disconnection of the local coil from the scanner. A later approach [17] for microcontroller-based automatic tuning of electronics, allowed tuning in the scanner in under 1 s, but can only handle frequency shifts up to 10%, yet still, this technique could be a promising candidate for further investigation.
A possible solution to handle the increased inductive coupling introduced due to the frequency shift when stretching the coil, would be achieved by departing from single coil resonances and rather operate in response plateaus between multiple resonance peaks [16]. The advantage of inductive decoupling is its broadband decoupling effect. A mechanical system introducing the required variation of the overlap area between adjacent elements upon the stretching would possibly maintain good decoupling and improve SNR. However, measurements of the coupling coefficient in this work showed that non-ideal decoupling was not a major concern in this case.
Although sample losses were dominant for the investigated stretchable coils (all Qratio > 2), other stretchable materials that might have better conductivity, like carbon nanotubes in rubber-like stretchable support material or silver/gold antenna structures integrated into Polydimethylsiloxane (PDMS), may also be of interest in the development of stretchable coils.
Conclusion
Using array elements with stretchable parts, a viable solution to size- and shape-adaptive coils was demonstrated. Despite a slight SNR loss of 10% in direct comparison to rigid standard loop coils in identical geometrical setup, a considerable SNR gain of up to 100% with an adaptive 6-channel prototype array over a geometrically identical rigid array could be shown in knee phantoms of different sizes. This increase is due to the better form-fitting of the adaptive array to the samples.
This work aims at investigating a novel technology for stretchable and flexible RF coils. To enable the presented methodology for practical application or clinical use, undesirable effects of coil stretching, such as frequency shift, mismatch and imperfect decoupling are yet to be handled.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author Contributions
BG conceptualized the work, did the calculations, created the design which was later fabricated, and sketched further ideas mentioned in the manuscript. Mechanical design was done by SZ. Experiments were designed by BG and SZ and other members of the Local Coil Laboratory at Siemens Healthcare GmbH in Erlangen (Germany). The manuscript was written by BG and co-authored by EL and reviewed by all authors.
Funding
BG had no conflict of interest to declare during the work conducted in 2015 and 2016. The work was partially funded by the National Institute of Health (project # 1U01EB025162-01) and the anniversary fund of the Austrian National Bank (OeNB) (project # 17980) to EL. RR and SZ are employees of Siemens Healthcare GmbH, Erlangen (Germany).
Conflict of Interest
BG and EL declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. RR and SZ declare to be employee of Siemens Healthcare GmbH, Erlangen, Germany.
Acknowledgments
The authors would like to thank the members at the local coil lab in Erlangen as well as their former leader Hubertus Fischer for the support in this research.
References
1. Moser E, Laistler E, Schmitt F, Kontaxis G. Ultra-High Field NMR and MRI - The Role of Magnet Technology to Increase Sensitivity and Specificity. Front Phys. (2017) 5:33. doi: 10.3389/fphy.2017.00033
2. Moser E. Ultra-high field magnetic resonance: why and when? World J Radiol. (2010) 2:37–40. doi: 10.4329/wjr.v2.i1.37
3. Keil B, Wald LL. Massively parallel MRI detector arrays. J Magn Reson. (2013) 229:75–89. doi: 10.1016/j.jmr.2013.02.001
4. Ackerman J, Grove T, Wong G, Gadian D, Radda G. Mapping of metabolites in whole animals by 31P NMR using surface coils. Nat Mag. (1980) 283:167–70. doi: 10.1038/283167a0
5. Kneeland JB, Hyde JS. High-resolution MR imaging with local coils. J Radiol. (1989) 171:1–7. doi: 10.1148/radiology.171.1.2648466
6. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med. (1990) 16:192–225. doi: 10.1002/mrm.1910160203
7. Boskamp E. Improved surface coil imaging in MR: decoupling of the excitation and receiver coils. J Radiol. (1985) 157:449–52. doi: 10.1148/radiology.157.2.4048454
8. Boskamp EB. A new revolution in surface coil technology - the array surface coil. In: Proceedings of the ISMRM 6th Annual Meeting and Exhibition. New York, NY (1987).
9. Wiesinger F, De Zanche N, Pruessmann KP. Approaching ultimate SNR with finite coil arrays. In: Proceedings of the ISMRM 13th Annual Meeting and Exhibition. Miami Beach, FL (2005). p. 672.
10. Hardy CJ, Cline HE, Giaquinto RO, Niendorf T, Grant AK, Sodickson DK. 32-element receiver coil array for cardiac imaging. Magn Reson Med. (2006) 55:1142–9. doi: 10.1002/mrm.20870
11. Wiggins GC, Triantafyllou C, Potthast A, Reykowski A, Nittka M, Wald LL. 32-channel 3 Tesla receive-only phased-array head coil with soccer-ball element geometry. Magn Reson Med. (2006) 56:216–23. doi: 10.1002/mrm.20925
12. Schmitt M, Potthast A, Sosnovik DE, Polimeni JR, Wiggins GC, Triantafyllou C, et al. A 128-channel receive-only cardiac coil for highly accelerated cardiac MRI at 3 Tesla. Magn Reson Med. (2008) 59:1431–9. doi: 10.1002/mrm.21598
13. Wiggins GC, Polimeni JR, Potthast A, Schmitt M, Alagappan V, Wald LL. A 96-channel receive-only head coil for 3 Tesla: design optimization and evaluation. Magn Reson Med. (2009) 62:754–62. doi: 10.1002/mrm.22028
14. Vaughan JT, Griffiths JR. RF Coils for MRI - Encyclopedia of Magnetic Resonance (EMR) Handbooks. Chichester, UK: John Wiley and Sons Ltd. (2012). p. 334–5.
15. Wright SM. Receiver loop arrays. Encyclopedia Magn Reson. (2011) 1–13. doi: 10.1002/9780470034590.emrstm1129
16. Vester M, Biber S, Rehner R, Wiggins GC, Brown R, Sodickson DK. Mitigation of inductive coupling in array coils by wideband port matching. In: Proceedings of the ISMRM 20th Annual Meeting and Exhibition, Vol. 20. Melbourne, VIC (2012). p. 2690.
17. Venook RD, Hargreaves BA, Gold GE, Conolly SM, Scott GC. Automatic tuning of flexible interventional RF receiver coils. Magn Reson Med. (2005) 54:983–93. doi: 10.1002/mrm.20616
18. Sohn SM, Gopinath A, Vaughan JT. Electrically auto-tuned RF coil design. In: Proceedings of the ISMRM 19th Annual Meeting and Exhibition. Montreal, QC (2011). p. 3826.
19. Sohn SM, DelaBarre L, Gopinath A, Vaughan JT. RF coil design with automatic tuning and matching. In: Proceedings of the ISMRM 21th Annual Meeting and Exhibition. Salt Lake City, UT (2013). p. 0731.
20. Rousseau J, Lecouffe P. A new, fully versatile surface coil for MRI. Magn Reson Med. (1990) 8:517–23. doi: 10.1016/0730-725X(90)90061-6
21. Malko JA, McClees EC, Braun IF, Davis PC, Hoffman JC Jr. A flexible Mercury-filled surface coil for MR Imaging. Am J Neuroradiol. (1986) 7:6–247.
22. Adriany G, Van de Moortele PF, Ritter J, Moeller S, Auerbach EJ, Akgun C, et al. A geometrically adjustable 16-channel transmit/receive transmission line array for improved RF efficiency and parallel imaging performance at 7 Tesla. Magn Reson Med. (2008) 59:590–7. doi: 10.1002/mrm.21488
23. Nordmeyer-Massner JA, De Zanche N, Pruessmann KP. Mechanically adjustable coil array for wrist MRI. Magn Reson Med. (2009) 61:429–38. doi: 10.1002/mrm.21868
24. Port A, Reber J, Vogt C, Marjanovic J, Sporrer B, Wu L, et al. Towards wearable MR detection: a stretchable wrist array with on-body digitization. In: Proceedings of the ISMRM 26th Annual Meeting and Exhibition. Paris (2018). p. 17.
25. Corea JR, Flynn AM, Lechene B, Scott G, Reed GD, Shin PJ, et al. Screen-printed flexible MRI receive coils. Nat Commun. (2016) 7:10839. doi: 10.1038/ncomms10839
26. Frass-Kriegl R, de Lara LIN, Pichler M, Sieg J, Moser E, Windischberger C, et al. Flexible 23-channel coil array for high-resolution magnetic resonance imaging at 3 Tesla. PLoS ONE. (2018) 13:e0206963. doi: 10.1371/journal.pone.0206963
27. Hosseinnezhadian S, Frass-Kriegl R, Goluch-Roat S, Pichler M, Sieg J, V'it M, et al. A flexible 12-channel transceiver array of transmission line resonators for 7T MRI. J Magn Reson. (2018) 296:47–59. doi: 10.1016/j.jmr.2018.08.013
28. Zhang B, Sodickson DK, Cloos MA. A high-impedance detector-array glove for magnetic resonance imaging of the hand. Nat Biomed Eng. (2018) 2:570–7. doi: 10.1038/s41551-018-0233-y
29. Ruytenberg T, Webb A, Zivkovic I. Shielded-coaxial-cable coils as receive and transceive array elements for 7T human MRI. Magn Reson Med. (2019) 83:1135–46. doi: 10.1002/mrm.27964
30. Stormont RS, Lindsay SA, Taracila V, Mustafa G, Malik NM, Robb FJL, et al. Systems for a Radio Frequency Coil for MR Imaging US20190277926A1. (2019).
31. Gruber B, Zink S. Anatomically adaptive local coils for MRI imaging–evaluation of stretchable antennas at 1.5T. In: Proceedings of the ISMRM 24th Annual Meeting and Exhibition. Singapore (2016). p.543.
32. Gruber B, Zink S. Anatomically adaptive coils for mr imaging – a 6-channel demonstrator array study at 1.5 Tesla. In: Proceedings of the ISMRM 26th Annual Meeting and Exhibition. Paris. (2018). p. 4289.
33. Gruber B, Jahns K, Zink S. Adaptive MR Local Coil, US2017089991A1, EP3151025A3, CN107064837A. (2019).
34. Hong J-S, Lancaster MJ. Couplings of microstrip square open-loop resonators for cross- coupled planar microwave filters. IEEE Trans Microw Theory Tech. (1996) 44:2099–109. doi: 10.1109/22.543968
35. Vizmuller P. RF Design Guide: Systems, Circuits, and Equations, Series: Artech House Antennas and Propagation Library (Artech Artech House). (1995) p. 296.
36. Larsson EG, Erdogmus D, Yan R, Principe JC, Fitzsimmons J. SNR-optimality of sum-of-squares reconstruction for phased-array magnetic resonance imaging. J Magn Reson. (2003) 163:121–3. doi: 10.1016/S1090-7807(03)00132-0
37. Doornbos J, Grimbergen H, Booijen P, Strake L, Bloem J, Vielvoye G, et al. Application of anatomically shaped surface coils in MRI at 0.5T. Magn Reson Med. (1986) 3:270–81. doi: 10.1002/mrm.1910030210
Keywords: adaptive coils, stretchable loop, meandered conductor, SNR, one-size-fits all
Citation: Gruber B, Rehner R, Laistler E and Zink S (2020) Anatomically Adaptive Coils for MRI—A 6-Channel Array for Knee Imaging at 1.5 Tesla. Front. Phys. 8:80. doi: 10.3389/fphy.2020.00080
Received: 29 November 2019; Accepted: 09 March 2020;
Published: 15 April 2020.
Edited by:
Simo Saarakkala, University of Oulu, FinlandReviewed by:
Ji Chen, University of Houston, United StatesManuel José Freire Rosales, University of Seville, Spain
Copyright © 2020 Gruber, Rehner, Laistler and Zink. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bernhard Gruber, Yi5ncnViZXJAaWVlZS5vcmc=
 Bernhard Gruber
Bernhard Gruber Robert Rehner3
Robert Rehner3 Elmar Laistler
Elmar Laistler