- 1Université Paris-Saclay, CNRS/IN2P3, IJCLab, Orsay, France
- 2Department of Physics, University of Arizona, Tucson, AZ, United States
Ever since quantum field theory was first applied to the derivation of nuclear forces in the mid-twentieth century, the renormalization of pion exchange with realistic couplings has presented a challenge. The implementation of effective field theories (EFTs) in the 1990s promised a solution to this problem but unexpected obstacles were encountered. The response of the nuclear community has been to focus on “chiral potentials” with regulators chosen to produce a good description of data. Meanwhile, a successful EFT without explicit pion exchange—Pionless EFT—has been formulated where renormalization is achieved order by order in a systematic expansion of low-energy nuclear observables. I describe how lessons from Pionless EFT are being applied to the construction of a properly renormalized Chiral EFT.
1. Introduction
In the aftermath of the solution of the “problem of infinities” in Quantum Electrodynamics (QED), an intense quest set in to renormalize nuclear forces, where pion exchange replaced the photon exchange responsible for atomic forces. (For an early example, see reference [1].) It was quickly understood that the only relativistic pion-nucleon coupling that is renormalizable is pseudoscalar [2]. However, pseudoscalar coupling differs from pseudovector coupling by a large nucleon-pair term, which was found to be in conflict with pion phenomenology [3]. For the favored pseudovector coupling, the description of two-nucleon data depended sensitively on the high-momentum (or short-distance) cutoff (see, for example, reference [4]). Efforts moved toward the investigation of various prescriptions for handling short-range effects, including specific cocktails of (usually single-)heavier-meson exchange, form factors with ad hoc shapes, and/or boundary conditions at some finite distance. Nuclear theory acquired an increasingly phenomenological character. Typically, the non-relativistic Schrödinger equation was solved with a two-nucleon (2N) potential including one-pion exchange, some approximation to two-pion exchange, and a more or less arbitrary short-range form, with sufficiently many parameters to fit data to the desired accuracy. The end result was that potentials including quite different physics could produce very good parameterizations of 2N data up to around the pion-production threshold, while typically underpredicting three- and more-nucleon binding by more than 10%. A serious difficulty was to infer a satisfactory form of three-nucleon (3N) forces and, for reactions, 2N currents. Reference [5] recounts some of this history.
In contrast, by the mid-1970s renormalizable quantum field theories had won the day in particle physics, leading to the formulation of Quantum Chromodynamics (QCD) as the theory of strong interactions. Out of the attempts to make predictions for QCD at low energies and to understand how the Standard Model (SM) can arise from a more fundamental theory, the concept of effective field theory (EFT) was born [6]. An EFT comprises all the interactions among relevant degrees of freedom that are allowed by symmetries, including an arbitrary number of fields and derivatives. For predictions, contributions to observables must be ordered according to their expected size. This “power counting” allows for an a priori error estimate from neglected higher-order contributions. At each order in the expansion, only a finite number of “low-energy constants” (LECs)—the interaction strengths—appear. In a consistent power counting, they are sufficient to ensure that any dependence on the regulator can be made arbitrarily small by taking the cutoff large. Thus, EFTs are renormalizable in the modern sense that at each order a finite number of parameters generate results for observables that are independent of details of the arbitrary regularization procedure.
A successful EFT, Chiral Perturbation Theory (ChPT), was developed in the 1980s to handle interactions among pions and one nucleon below the characteristic QCD scale MQCD ~ 1 GeV [7, 8]. Requiring renormalization in a perturbative expansion, a consistent power counting was developed based on “naive dimensional analysis” (NDA) [9]. Taking the typical external momentum in a reaction to be of the order of the pion mass, Q ~ mπ ≪ MQCD, observables are expanded in a series of powers of Q/MQCD times calculable functions of Q/mπ. When Weinberg remarked [10, 11] that ChPT, now generalized as “Chiral EFT” (ChEFT), could be used to derive nuclear forces, he identified an infrared enhancement in nuclear amplitudes by the nucleon mass mN = (MQCD), which can lead to the failure of perturbation theory—a good thing since nuclei are bound states and resonances. He proposed that the ChPT power counting could still be applied to the nuclear potential, defined as the sum of diagrams lacking an explicit enhancement. Then, the Lippmann-Schwinger equation, or equivalently the Schrödinger equation, would be solved with a truncated “chiral potential.”
The potential defined by Weinberg contains pion exchange diagrams where all LECs are fixed, at least in principle, from ChPT. But it also includes shorter-range interactions with LECs that can only be determined in nuclear systems. Implicit in Weinberg's proposal was that the short-range LECs would not contain an implicit enhancement. This would be the case if the solution of the dynamical equation does not generate cutoff dependence beyond that which can be compensated by the LECs already present up to that order according to NDA.
Whether this assumption is true was not immediately clear. NDA says that the potential at leading order (LO) consists of two non-derivative, chirally symmetric contact interactions together with one-pion exchange (OPE). More-pion exchange should come at higher orders together with more-derivative contact interactions. Non-perturbative pion exchange prevents an analytical solution even at the 2N level. The first numerical solution of a chiral potential in the 2N system [12, 13] tested renormalizability of the amplitude: a variation from 0.5 to 1 GeV in the cutoff of a local Gaussian regulator seemed to be compensated by a refitting of the LECs at hand. However, the fitting procedure was cumbersome as an over-complete set of interactions was used and the local regulator mixed different partial waves, limiting the range of cutoffs that could be explored. Since then a large variety of chiral potentials have been developed (for reviews, see for example references [14, 15]). A landmark was a 2N potential [16] that was perceived to match the accuracy of phenomenological potentials (for a recent comparison between chiral 2N potentials and data, see reference [17]). Chiral potentials have become the favorite input to “ab initio” methods, which provide numerically controlled solutions of the Schrödinger equation for multi-nucleon systems.
Unfortunately, pretty early on the first evidence appeared [18] that Weinberg's prescription does not provide amplitudes, and thus observables, that are renormalized order by order. In the 2N 1S0 channel at LO, a semi-analytical argument shows that there remains a logarithmic dependence on the cutoff proportional to the average quark mass. The only way to eliminate it, at least with a momentum- or coordinate-space cutoff, is to include at LO a non-derivative, chirally breaking contact interaction, which according to NDA should appear two orders down the expansion, that is, at next-to-next-to-leading order (N2LO)1. More dramatically, it was later shown [20, 21] that oscillatory cutoff dependence appears at LO in waves where OPE is attractive, singular, and accounted for non-perturbatively. A chirally symmetric LEC is needed for renormalization in each wave, but again NDA assigns those in partial waves beyond S to higher orders. Similar problems afflict processes with external probes [22].
As I describe in section 3, the origin of these problems is the renormalization of attractive singular potentials [23, 24]. NDA might fail because exact solutions of the Schrödinger equation depend on the cutoff differently than perturbative solutions. The LECs needed for the renormalization of the amplitude are enhanced by implicit powers of MQCD.
How to account for this? In response to the renormalization failure of Weinberg's power counting a simpler nuclear EFT [25–27] was developed in the late 1990s. In this “Pionless EFT” pions are integrated out and only contact interactions remain. The effects of loops in the Lippmann-Schwinger equation are much easier to see, including the mN enhancement and a further enhancement of 4π [26, 27] that was not pointed out by Weinberg. The lessons of Pionless EFT for ChEFT are summarized in section 2.
The first attempt to fix power counting using the insights from Pionless EFT was initiated [28, 29] at the same time as the main elements of the power counting of Pionless EFT were being understood. Valid for sufficiently small values of the pion mass and external momenta, this version of ChEFT treats pion exchange in perturbation theory, removing the renormalization problems mentioned above. Unfortunately, in the 2N system at physical pion mass one cannot go in this way to momenta much beyond those of Pionless EFT [30]. The alternative is partly perturbative pions: OPE is iterated only in the low partial waves where it is sufficiently strong, together with the contact interactions whose LECs are necessary for LO renormalization [20]. All subleading pion exchanges, together with the remaining contact interactions, are treated in perturbation theory [31]. This approach is discussed in section 4, including what little has been done to confront it with data.
Section 5 offers the conclusion that this approach solves the renormalization woes of nuclear forces while accounting for the long-range interactions from pion exchange systematically. Although they differ in detail from the field-theoretical renormalization described below, renormalization-group analyses of the Schrödinger equation [22, 32–34] support this picture. How it can meet the accuracy requirements of the nuclear community remains to be seen. My emphasis here is on the internal consistency of ChEFT. I expand on the renormalization issues summarized in reference [35], but I refer the reader to the latter for a more complete review of ChEFT and its relation to other nuclear EFTs.
2. Say What?
As reviewed in reference [35], defining the nuclear potential as the sum of “irreducible” diagrams without the mN infrared (IR) enhancement does indeed ensure that the cutoff-independent parts of pion-exchange diagrams can be ordered according to ChPT power counting. These components of the pion-exchange potentials are in general non-analytic functions of momenta and pion mass that can be calculated in terms of pion-baryon interactions.
The ChPT power counting is designed for processes where the typical external momentum is comparable to the pion mass, Q ~ mπ. A (relativistic) pion propagator scales as Q−2. In contrast, a nucleon is heavy compared to Q and thus non-relativistic. Moreover, energies and three-momenta being comparable, nucleon recoil is suppressed by one power of Q/mN = (Q/MQCD)—that is, the nucleon is static, its propagator scaling as Q−1. Because the Delta-nucleon mass difference is (at physical quark masses) only about twice the pion mass, a Delta propagator scales in the same way. In integrals from the loops that make up the potential one picks poles from the pion propagators, typically resulting in factors of (4π)−2. They combine with factors of the pion decay constant fπ ≃ 92 MeV from the pion-baryon interactions to produce inverse factors of 4πfπ = (MQCD). The power counting explicitly relies on an estimate, NDA [9], of the factors of 4π that distinguish between fπ and the breakdown scale MQCD, which appears in interactions with derivatives and powers of the pion mass. In summary, the ChPT rules (in momentum space) are:
where d, b, and f are the numbers of derivatives/pion masses, pion fields, and baryon fields, respectively, in an interaction.
The expected size of any diagram can be found using the identities and involving the number of loops (L), internal (external) lines I (E), and vertices (Vi) having a set of values d = di, b = bi, and f = fi. In particular,
in terms of the pion-nucleon axial-vector coupling gA ≃ 1.27 and [11]
Because every additional loop (without increase in the number of derivatives/pion masses at vertices) leads to a relative factor , one gets the well-known ordering where p-pion exchange starts at μ = 2(p − 1). Note that the NLO correction vanishes due to parity and time-reversal symmetries [19].
This power counting applies to diagrams that make up the long-range potential. Yet physics, as opposed to metaphysics, is about observables. The meaning of Equation (4) is that it indirectly orders the contributions to amplitudes. For the direct link, we need to consider as well “reducible” diagrams where intermediate states contain only nucleons. One picks poles from the non-relativistic nucleon propagators, for which energies are of the order of recoil—in those diagrams, one cannot approximate nucleons as static. (This of course has nothing to do with relativistic corrections, as sometimes misstated in the literature.) These poles lead not only to an mN enhancement [10, 11], but typically also to different powers of (4π)−1. Experience with Pionless EFT [35, 36], where these are all the loops one needs to deal with, shows that the factors associated with reducible loops are
When one inserts the order-μ potential into a 2N diagram we need one extra reducible loop with two nucleon propagators (compare Figures 1A,B), leading to a relative factor . This amount to an IR enhancement of 4πmN/Q over the factor that arises from Equations (1) and (2). As a consequence, the series in the LO potential fails to converge for Q ~ mNN. This is what makes ChEFT different for A ≥ 2 nucleons compared to ChPT for A ≤ 1.
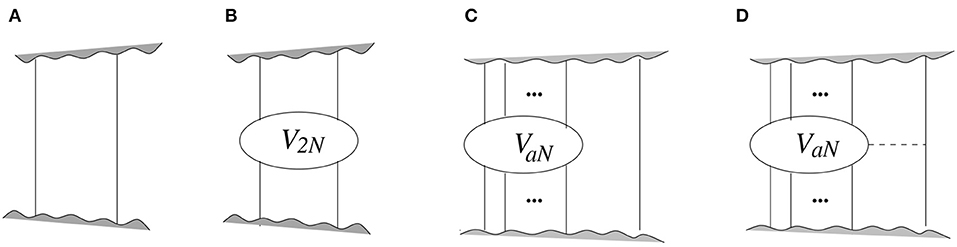
Figure 1. Some diagrams discussed in the text. Inside a diagram, (A) two nucleons (solid lines) propagate; (B) two nucleons interact through the 2N potential (blob); (C) a nucleons interact through the aN potential (blob), while another nucleon propagates; and (D) a + 1 nucleons interact through the (a + 1)N potential formed from the aN potential and the exchange of a pion (dashed line).
The factor of 4π in the IR enhancement had not been recognized before Pionless EFT was developed, but it is important to understand the failure of perturbation theory for pions. The exact solution of the LO potential for Q ~ mNN can give rise to a binding energy per nucleon
This is somewhat larger than observed for light nuclei, indicating a certain amount of fine tuning in the 2N interactions. But it is on the right ballpark for heavier nuclei, so chiral symmetry together with the IR enhancement provides a natural explanation [36] for the shallowness of nuclei compared to MQCD, BA/A ≪ MQCD, long considered a mystery.
The same factor of 4π has implications for the natural size of few-body forces, which were recognized by Friar [37]. To see this, consider connecting a nucleon with OPE to an aN potential to make an (a + 1)N potential, without changing the number of derivatives, pion masses, and loops in the aN potential. (See Figures 1C,D. For example, take the crossed-box two-pion exchange 2N potential and connect one of the intermediate nucleons to the third nucleon.) The additional nucleon propagator inside the aN potential and the additional OPE combine for a factor of . At the same time, at the amplitude level we are adding a reducible loop and one propagator for the extra nucleon, that is, another factor (4π)−1Q3. The contribution of the (a + 1)N potential to the amplitude is, overall, of compared to that of its “parent” aN potential. For Q ~ mNN, the suppression from connecting a nucleon is thus of (Q/MQCD), or one order in the expansion of the potential [37]. In contrast, missing the 4π in the IR enhancement would give an additional , or a suppression of [11, 19, 38, 39]. In either case a hierarchy of many-body forces arises, with perturbative 3N forces coming after the leading 2N forces. Unfortunately, existing calculations do not question the additional suppression of (4π)−1.
Note that when connecting the additional nucleon we might not be able to maintain the number of derivatives or pion masses. In particular, for the leading aN force, this can only be done with an intermediate Delta isobar—for 3N, that is the Fujita-Myiazawa force [40], which has been argued to be important for convergence of the chiral expansion [41]. Keeping this in mind, a contribution to the (connected) aN potential scales as
To estimate the respective contributions to the AN amplitude, one can first consider the LO (μ = 0), 2N potential: to produce a connected diagram, we need at least A − 1 2N interactions linked by A − 2 propagators. Next, one insertion of a subleading aN potential between two LO amplitudes comes with A + a − 2 propagators and A + a loops. Another insertion of the same subleading potential takes a additional propagators and a − 1 additional loops, and so on. The rules (7), (8) imply that an aN potential of index μ gives, at Q ~ mNN,
where
and n is the order in perturbation theory. While ν is the perturbative cost of one insertion of a subleading potential characterized by μ (6) and a, n insertions cost nν as indicated by the power of Q/MQCD in Equation (11). The presence of a − 2 [instead of 2(a − 2)] in ν reflects the suppression by (4π)−1 [instead of (4π)−2] in more-nucleon forces. A sample of pion-range diagrams that contributes at various values of ν is shown in Figure 2 (see reference [35] for more details).
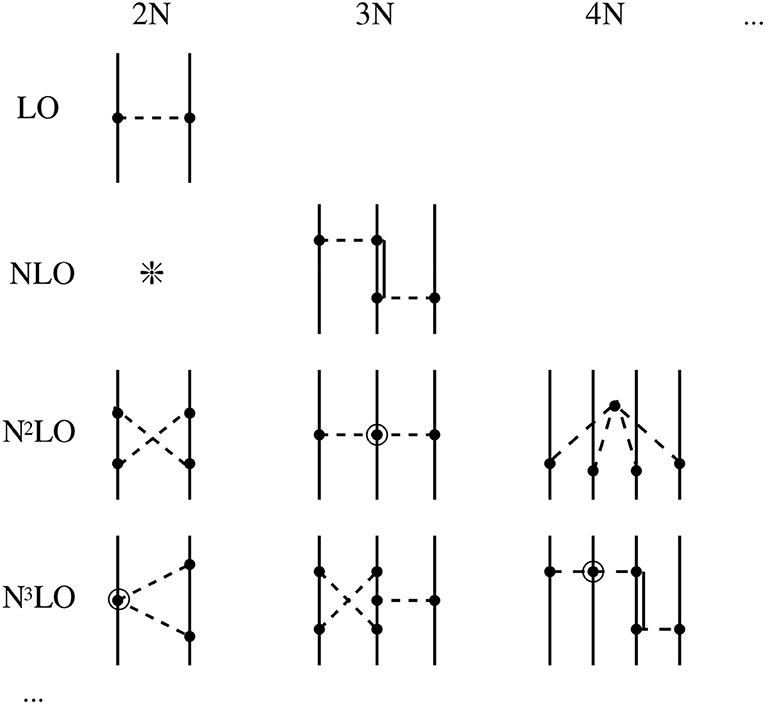
Figure 2. Sample of pion-range diagrams in the aN nuclear potential ordered according to the expected size of their contributions to the amplitude (Equation 12). NνLO denotes relative . A solid (double) line stands for a nucleon (nucleon excitation), while a dashed line, for a pion. A circle (circled circle) represents an interaction with d + f/2 − 2 = 0 (= 1).
The n in Equation (11) encodes the perturbative character of any subleading interaction. A common fallacy is that the mere definition of a potential means that the corresponding dynamical (Lippmann-Schwinger or Schrödinger) equation must be solved exactly. On the contrary, if there is a sense in which a subleading potential can be treated non-perturbatively, then it should also be possible to include it in distorted-wave perturbation theory, where the distortion is caused by the LO potential. If that is not the case, then at least part of that “subleading” potential is not subleading. Such a consistency test is almost completely ignored in the community. The one exception I am aware of is reference [42], where it is shown that this test is not met by most available chiral potentials.
“But surely,” you might be reasoning, “a subleading potential can be treated non-perturbatively.” That is certainly the case for a regular subleading potential, but not necessarily for a singular potential, for which neither the perturbative series nor the exact solution of the dynamical equation are well-defined without (potentially distinct) counterterms. So far I have been glossing over the cutoff dependence that usually arises in loops and is, of course, present in the LECs. A regulator is nothing but a way to split short-range physics between loops and LECs. If we increase a momentum cutoff Λ (or decrease a coordinate cutoff R ~ Λ−1), we account, correctly or incorrectly, for more short-range physics through the loops of the Lippmann-Schwinger equation. As long as Λ ≳ MQCD, we can compensate by changing the LECs present at the same order, without increasing the relative truncation error of (Q/MQCD). The crucial point is that only the combination of the two effects matter, and physics enters through the fitting of as many observables as LECs—observables which are either calculated in the underlying theory (when we speak of “matching” the EFT to the underlying theory) or measured experimentally. This process of renormalization is essential for amplitudes to be free of detailed assumptions about short-range physics, and in general only the sum of all contributions at a given order—loops and LECs ensuring renormalization—can be said to be perturbative or not.
If all we needed was to eliminate the cutoff-dependent parts of pion exchange in the potential, the LECs for the job would be given by NDA, by construction [9]. It is crucial to realize, though, that reducible loops introduce further cutoff dependence, which we need eliminate as well. The potential itself has to depend on the cutoff so that observables do not. The LECs that renormalize this part of the A ≥ 2 problem will not in general satisfy NDA. We examine this aspect of renormalization next.
3. Renormalization of Singular Potentials
The difficulty we face is that EFT potentials are singular and, because of additional derivatives and loops, they get more and more singular as the order of the EFT expansion increases. Singularities are apparent already in the LO (μ = 0, a = 2) pion-range potential, OPE: labeling the two nucleons 1 and 2,
where is the relative position, (τi) is the spin (isospin) Pauli matrix for nucleon i, and
is the spin-tensor operator. While the delta function contributes only to S waves, the tensor potential is non-vanishing for total spin s = 1 and can mix waves with orbital angular momentum l = j ± 1. It is attractive in some uncoupled waves like 3P0 and 3D2, and in one of the eigenchannels of each coupled wave. The regular Yukawa potential is attractive in isovector (isoscalar) channels for s = 0 (s = 1). More-pion exchange leads to more singular terms, p-pion exchange containing for example terms ∝ r−(2p+1) in addition to delta functions and their derivatives.
For Q ~ mNN OPE is expected to be non-perturbative by the argument of the previous section. It has been known for a long time (see e.g., the review [43]) that attractive singular potentials, treated exactly, do not fully determine the solution of the Schrödinger equation [44]. This is a manifestation that renormalization of a singular potential requires contact terms that naturally exist in EFT [23, 24]. In contrast, pion-range corrections to OPE are expected to be perturbative according to the power counting embodied in Equations (11) and (12). From an EFT perspective, additional contact interactions are needed to make these corrections well-defined [31].
The issue I address in this section is how many, and which, contact interactions must be present for the renormalization of specific singular potentials. For simplicity, I consider central potentials; we return to the nuclear potential in section 4.
3.1. Non-perturbative Renormalization
Renormalization is usually discussed at the level of loops in Feynman diagrams for the Lippmann-Schwinger equation in momentum space, but it can also be formulated in terms of the Schrödinger equation in coordinate space. In the latter, which is more familiar to many, renormalization deals with distances on the order of those where the EFT breaks down, which I will call Rund. The fall off of the potential at much larger distances is not important, as it affects instead the near-threshold behavior. For definiteness, let us take a central two-body potential
in the center-of-mass frame, where μ is the reduced mass, α is a constant with mass dimension 2 − n, and n > 0 is an integer. The long-range potential is characterized by an intrinsic distance scale . For n = 2 the action is scale invariant.
In the radial Schrödinger equation the potential is supplemented by the centrifugal barrier with orbital angular momentum l, l(l + 1)/(2μr2). The uncertainty principle implies the kinetic term scales similarly, as 1/(2μr2). For 0 < n < 2 the potential is relatively small at small distances and the corresponding behavior of the wavefunction is determined by l: we find ourselves in the familiar situation where one solution, labeled regular, behaves as rl for small r, while the other, labeled irregular and discarded, as r−(l+1). In contrast, for n = 2 and |α| is sufficiently large, or for n ≥ 3, VL(r) dominates at small distances. If α < 0, the strong repulsion prevents any short-range approach; one can again keep just the regular solution, from which the scattering amplitude can be calculated. But when the potential is attractive, α > 0, observables are sensitive to short-distance physics and renormalization is needed.
To see this in detail, consider first n ≥ 3 at zero energy. For , where VL(r) dominates, the Schrödinger equation becomes an ordinary Bessel equation, and the solution is a combination of spherical Bessel functions. Both solutions are equally irregular as r → 0 [44]. One can write the wavefunction in the l wave at small distances as
where ϕl is a phase that determines the relative importance of the two irregular solutions and is not fixed by the long-range potential VL. This is in strong contrast with the repulsive case, where the solutions are regular and irregular modified Bessel functions, which respectively decrease and increase exponentially as r decreases.
The case n = 2 is borderline singular, the character of the solution depending on the relative size of α and a combination of l(l + 1) with a number (1) coming from the kinetic repulsion. It turns out that the critical value is . For , repulsion wins; one solution is more singular than the other and can again be discarded [45]. For l < lα the situation is similar to n ≥ 3: Equation (16) holds with , where r0 is an arbitrary dimensionful parameter and ϕl = ϕl(r0). This is an example of an anomaly [46, 47] where the scale invariance of the classical system is broken by the renormalization of the quantum system.
Equation (16) is the quantum version of the “fall to the center” in a classical singular potential [45, 48]. The phases ϕl determine the asymptotic behavior of the wavefunction, from which the zero-energy scattering amplitude is extracted. For example, the S-wave scattering length is well-defined for a pure n ≥ 4 potential [48] and given for n = 4 by
If one imposes a particular value on ψl(R) at a chosen distance R—for example, that the wavefunction ψl(R) = 0—the phases are fixed. However, a different value of R leads to different phases. In EFT, this arbitrariness is replaced by the values of LECs. The minimal set of contact interactions is determined by demanding renormalizability.
3.1.1. S Wave
Let us look into the S wave first. Choosing a sharp cutoff in coordinate space at R, we replace the potential (15) by [23]
The depth VS(R) of the spherical well is related to the LEC C0 of a contact interaction,
A solution of the Schrödinger equation for the augmented potential requires the matching of the logarithmic derivatives of outside and regular spherical-well wavefunctions at r = R,
When n = 2 and α ≤ α0, or n = 1, we can solve this equation with VS(R) = 0 if the admixture of the most singular external solution tends to zero as R → 0. Thus the amplitude is renormalized properly without a contact interaction as long as we retain only the least singular wavefunction behavior, the prescription offered in reference [45].
For n = 2 and α > α0, or for n ≥ 3, because the two external solutions differ only by a phase, the contact interaction is necessary. Substituting the wavefunction (16) into Equation (20), yields a transcendental equation linking ϕ0 to VS(R) [23]. Two approximate solutions are
when the right-hand side of Equation (20) is large, and
when it is small, where in both cases m is an integer. Now one can keep the scattering amplitude at zero energy fixed at its experimental value by adjusting , which displays an periodic dependence on a power of the cutoff [23, 24, 49–54]. For n = 2, the dependence is periodic in ln R, characteristic of a limit cycle and a remaining discrete scale invariance. (For discussions of limit cycles, see references [55, 56].) The n ≥ 3 oscillation indicates a generalized limit cycle. The case n = 4 is displayed in Figure 3 [23].
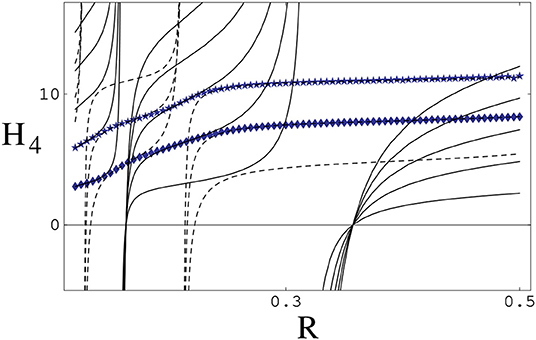
Figure 3. Dependence of for n = 4 on R (in units of r0). Two analytical approximations, Equation (21) (solid lines) and Equation (22) (dashed lines), are shown together with a numerical solution of Equation (20) (bold lines) that interpolates between them. Reprinted figure with permission from reference [23]. Copyright (2001) by the American Physical Society.
Having renormalized zero-energy scattering, an important question is whether the problem is well-defined also at finite energy E ≡ k2/(2μ). That this is the case can be shown [23] with the WKB approximation, which applies to the region where the wavelength is small compared to the characteristic distance over which the potential varies appreciably. For distances where |VL(r)| ≫ E, one recovers Equation (16) for the wavefunction, up to energy-dependent corrections that are determined by Equation (16) itself. In the absence of a short-range interaction, decrease in R would lead to the repeated appearance of low-energy bound states due to the unstoppable growth in attraction, a phenomenon reflected in the never-ending oscillations of the wavefunction [48]. With VS(R) preventing this collapse and ensuring the description of one low-energy datum, bound states can accrete only from negative energies, converging to finite values as R decreases. How many of the bound states are within the region of validity of the EFT depends, of course, on the scales in the problem: the very low-energy spectrum will be affected by the long-distance tail of the potential while states with binding energies are irrelevant for the distances of interest. For n = 2 and α > α0, which is equivalent [57] to the three-boson system with short-range interactions at unitarity, the bound states form a geometric tower (“Efimov states” [58]) that signals the remaining discrete scale invariance stemming from the limit cycle in the contact interaction [59, 60]. While the existence of the tower is a consequence of the symmetry, its position is fixed by the LEC. It is remarkable that it is the proper renormalization of the EFT that underlies the “Efimov physics” intensely explored with cold atoms [61].
A particularly simple example of singular potential is the delta function itself. In this case the external potential vanishes and the external zero-energy wavefunction is replaced by
where a0 determines the ratio between irregular and regular solutions and is nothing but the scattering length. The solution for Equation (20) can be written explicitly,
where m is an integer. It is apparent how a cutoff-dependent C0(R) ∝ R softens the delta function. The scattering length enters in the smaller R2 term. Of course, a similar result is obtained for a momentum cutoff Λ ~ R−1 [27].
A subtlety arises when a regular potential with n = 1 in Equation (15) is present together with the delta function, as is the case for OPE. By itself, the long-range potential needs no regularization; with the delta function, a new cutoff dependence emerges in the irregular solution [24, 62]:
where and R⋆ are length scales that enter the zero-energy scattering amplitude. Instead of Equation (24),
The main difference is the appearance of the ln R with a coefficient ∝ α.
In both these cases, where the outside potential is not singular, it is easy to see that the amplitude at finite energy is well-defined. The energy enters both internal and external wavefunctions as (kr)2 and can only affect the depth of the spherical well by a term of (R0), an effect that disappears as R decreases. The multiple branches in Equations (24) and (26) are a consequence of the fact that a spherical well can have multiple bound states. The zero-energy amplitude is essentially determined by the shallowest state, and we can choose different well depths to place any one state at the desired position. Deeper states have energies ∝ (2μR2)−1 and, again, are beyond the regime of the EFT for R ≲ Rund. Differently from long-range singular potentials, the three-dimensional delta function supports a single bound or virtual state.
3.1.2. Higher Partial Waves
We can now look at higher partial waves. Amplitudes in these waves have additional powers of , where () is the relative incoming (outgoing) nucleon momentum. Just as for k2 in the S wave, in the absence of a long-range potential, dimensional analysis implies that must come together with R2: the no-derivative contact interaction contributes in the small-R limit only to the S wave. For the n = 1 external potential, the l ≥ 1 phase shifts then converge as R → 0. A long-range singular potential of the type (15) contains an intrinsic scale r0 and comes in general with a factor and does not disappear as R → 0. There is a phase ϕl in Equation (16) for every l, which can only be fixed by higher-derivative interactions.
To see this, let us first stick to the potential (18). The k = 0 matching equation that generalizes Equation (20) is
where jl is the spherical Bessel function of the first kind. Using the recurrence relation for Bessel functions,
In the absence of an external potential, the external wavefunction is a combination of the regular jl and the irregular yl, the spherical Bessel function of the second kind. By direct calculation we find that at small R
where al is the l-wave scattering “length” (e.g., volume for l = 1), the zero-energy limit of the ratio of the yl and jl coefficients. Using R0(0) = 1 in Equation (28) gives
which implies, together with Equation (29), that . The argument repeats for l ≥ 2 with different finite pieces, leading to . As anticipated by dimensional analysis, the effect of the non-derivative contact interaction disappears from l ≥ 1 waves as R → 0. A similar argument for a regular outside potential leads to the same conclusion. For the argument with a delta-shell regularization, see reference [63].
In contrast, when the external potential is attractive and singular with n ≥ 3,
Matching in the S wave makes ϕ0 R-independent. Since is approximately cutoff independent as can be seen from either of the two approximate solutions (21) and (22), Equation (28) gives
where Δ1(R ≪ r0) is finite. Comparison with Equation (31) then shows that . Continuing to larger l we find
The phases are thus angular-momentum and energy independent [63] in this limit, but cutoff dependent [48].
What is needed for renormalization is a single contact interaction with a minimum number of derivatives in each wave, with LECs . The interaction is non-local, for example for l = 1,
where is determined so as to keep the phase ϕ1, and thus one P-wave low-energy datum, fixed. The contact interactions are all determined by the underlying interactions, but without additional dynamical assumptions we do not know how they relate to each other. Model independence requires we keep them free.
3.1.3. Implications
Much of the above had been understood without EFT. The use of boundary conditions, for example, goes back at least to the work of Breit [64]. In EFT, a boundary condition corresponds to a specific regulator. At the two-body level, in the S wave we have simply traded the dependence in R by that of VS(R). Renormalization means that, as far as observables are concerned, the regulator choice is irrelevant (within the error of the truncation); only the unobservable cutoff dependence of the LECs depends on the regulator. What matters is that a LEC encodes one parameter. The LO EFT in coordinate space is in the spirit of atomic Quantum-Defect Theory, where the interaction of far-away electrons with an ionic core or molecule is solved for exactly and a few parameters (“defects”) account for short-range interactions [65].
The model independence of the EFT is manifest in the fact that the same two-body contact interactions that renormalize the two-body problem contribute to other processes. For example, the three-boson system was considered in reference [54], where binding energies and the particle-dimer scattering length were calculated. Convergence was observed in a range of cutoffs, with asymptotic values representing model-independent predictions. The role of D and higher waves in these results was, however, not discussed.
The contact interactions can also be seen as providing a self-adjoint extension of the Hamiltonian. As stressed in reference [66], the so-called deficiency index for a singular potential is (∞, ∞), i.e., an infinite number of parameters—the phases ϕl in Equation (16) for all values of l—are needed to determine the self-adjoint extension uniquely. In the EFT this translates into the existence of an infinite number of contact interactions, one with the minimal number of derivatives for each wave (of course, the EFT contains also contact interactions with an arbitrary number of derivatives).
While mathematically the problem looks hopeless, on physical grounds this is clearly a red herring. As remarked in reference [20], increasing l strengthens the centrifugal barrier and shrinks the distances where the attractive n ≥ 3 potential takes over. The distance of closest approach at momentum k can be estimated from the point where the energy is comparable to the centrifugal barrier, or r ≳ [l(l + 1)]1/2k−1. For k ≲ Mund, the breakdown scale, we are only interested in distances . We might then expect that only in waves with l ≲ lcr does a singular potential need to be treated exactly and Equation (16) apply, where [32]
A more precise semi-analytical estimate comes from the investigation of the critical strength α where a Bessel series solution of the Schrödinger equation exhibits a square-root branch point characteristic of non-perturbative behavior. For n = 3 [32], it is described pretty well for large l by the estimates above. For n = 2, consideration of the first two orders in the perturbative expansion suggests lcr = (π|α| − 2)/4 [31]. An attractive singular potential defined with a step function at lcr has a finite deficiency index (lcr, lcr).
The situation is different in the case of n = 1. The potential is larger than both centrifugal barrier and kinetic repulsion for , where n(l) is (1) for l = 0 and grows as l for large l. Balance among these terms leads to bound states of sizes and binding energies . (Taking as an example the Coulomb interaction, where α = 2μαe in terms of the fine-structure constant αe, we get the proper result if we interpret n as the principal quantum number.) These estimates are in any case affected by the long-range tail of the potential, which we are not considering in this section. But at distances Rund ≲ r ≲ r0, we expect lcr ≈ 1: while the S wave might be non-perturbative and perhaps require a short-range potential (26) to generate a bound state at the observed location, higher waves should be perturbative.
3.2. Perturbative Corrections
EFT provides a framework where we can systematically incorporate corrections to the leading interactions, which can be checked with the method developed in reference [67]. We pair subleading long-range interactions with the subleading short-range interactions needed for renormalization order by order. As stressed in reference [68], renormalization at a given order contains clues about the relative importance of higher corrections. Just as a negative power of R indicates at least one missing LEC, so positive powers of R point to the order before at least one new LEC should appear. If the error in an observable not used in the fit of LECs at NiLO (with some integer i) scales as a positive power of the coordinate cutoff, say Rx, then we may expect that corrections appear at Ni+jLO, where j ≤ x is an integer (not necessarily the largest integer). This constraint comes from the demand that the regulator error should not exceed the truncation error when R ≲ Rund. (It does not exclude the presence of a LEC at a lower order than that estimated by the cutoff dependence, corresponding to boundary conditions of the RG equation [22].) We will see examples below.
The next renormalization challenge arises from the more-singular corrections to the long-range potential. An almost automatic reflex is to simply add the correction to the LO potential, as Weinberg prescribed, and solve the Schrödinger equation. For a regular potential, adding a regular correction that is small everywhere can be done in perturbation theory, but it can also be done by solving the Schrödinger equation exactly. For a more-singular correction, however, the perturbing potential will be larger than the LO potential at sufficiently small r. One risks destroying the systematic character of the EFT unless one keeps R relatively large. Whether this risk materializes needs to be checked explicitly. As we will see, renormalization requires distorted-wave perturbation theory around the LO solution [20, 31]. Implications for nuclear interactions are discussed in section 4.1.
3.2.1. Distorted-Wave Perturbation
A pedagogical toy model that nicely illustrates the need for perturbation theory on singular corrections was presented in reference [69]. The model consists of two separable, regular potentials, one of range , the other of range . Because the potentials are separable, exact answers can be found for the effective-range parameters. The potential parameters are fine-tuned so that each potential separately produces a natural scattering length, that is, () in the absence of the short-range (long-range) potential. Next, the short-range potential is expanded in powers of k/mS, creating a series of singular interactions. While for k ~ mL the long-range potential is non-perturbative, the singular corrections should be treated in distorted-wave perturbation theory. Lo and behold, the results up to N2LO obtained with a standard subtraction scheme are found to reproduce the exact results. In contrast, when a truncation of the expanded short-range potential is solved exactly, similar to the “peratization” of Fermi theory [70, 71], one can no longer take a large momentum cutoff. Reference [69] concludes that removing the cutoff dependence is impossible, which is indeed true when one insists on iterating subleading corrections.
The situation is not significantly different for the case of interest in nuclear physics where not only corrections, but also the LO potential is singular. Again, the simplest example is provided by the delta function without external potential, VL(R) = 0 in Equation (18). As discussed above, the energy dependence first affects the matching between internal and external wavefunctions at relative (k2R2). The ratio of irregular and regular solutions, which determines k cot δ0(k) where δ0(k) is the S-wave phase shift, starts at (R). Thus, at LO
which means that the fractional error in δ0 is
For example, the effective range r0 ~ R. This again can be easily obtained with a momentum regulator [27]. In ChEFT, where away from the chiral limit the delta function is accompanied in the singlet S wave by the Yukawa potential, the situation is not substantially different [24]. Aside the (αR ln R) dependence in Equation (26), the argument does not change and Equation (37) still holds with . Despite the presence of pions, the error is still ∝ R. It can be removed in first-order perturbation theory by a two-derivative contact interaction
whose LEC fixes r0 ~ Rund. For R ≲ Rund, this contact interaction is an NLO correction to the LO interaction with LEC C0. This is in fact one of the elements in the power counting in Pionless EFT [35]. Note that, if we were to impose that C2/C0 scaled with as implied by NDA, we would obtain an effective range that scaled the same way, in contrast to what one obtains for typical short-range potentials [27]. Once again, renormalization automatically enforces a general property of short-range interactions.
But what if we solved the Schrödinger equation exactly following Weinberg's prescription? In the simpler case without a long-range potential, it has been shown explicitly [72–74] that this can be done in a renormalized way only if r0 ≲ R, which is arbitrarily small. In other words, the two-derivative contact interaction is non-perturbatively renormalizable only if the theory satisfies a “Wigner bound” [75] r0 ≥ 0. In contrast, when the two-derivative contact interaction is treated in perturbation theory, at second order and higher, which contain loops involving two or more powers of C2, four- and higher-derivative contact interactions appear to guarantee renormalization. When we resum the two-derivative contact interaction we generate diagrams with an arbitrary number of loops, but lack the counterterms to remove the cutoff dependence. A calculator committed to exact solutions might be tempted to eschew renormalization (and thus model independence) and live with a relatively large R. Still, such stubbornness in resumming what needs no resummation might be rewarded by results that are worse than those of the perturbative expansion. An example is provided by a calculation [76] of the S-wave scattering phase shifts for a harmonically trapped unitary system, where the regulator was implemented in the form of a maximum number of shells. One can see explicitly how in first-order perturbation theory the derivatives in Equation (38) give a contribution to the NLO energy which is proportional to the LO energy, apart from a shift in the LO LEC. The result of resumming the NLO interaction is not only cutoff dependent but also gives rise to a larger violation of unitarity than even NLO.
Note that one can introduce an auxiliary “dimeron” field in the EFT Lagrangian [77] whose kinetic term provides an energy-dependent correction to the potential. Exploiting the redundancy of interactions in the enlarged Lagrangian, one can remove the momentum-dependent corrections (38). Renormalization changes with an energy-dependent potential and, in particular, a resummation does not restrict r0. However, unless there is evidence for r0 ≫ Rund, this is still an NLO correction and the resummation does not affect observables up to higher-order terms [27].
Resummation of subleading interactions can lead to an even more paradoxical situation. The problem is that subleading singular potentials are not in general attractive in all the same waves as OPE. If the corrections are iterated together with OPE, the cutoff behavior of the amplitude will change completely: channels that required a counterterm at LO may not require, or even tolerate, one at subleading order [24]. Take a wave where the LO potential is singular with a power n and attractive, thus requiring a counterterm, but the subleading potential is repulsive (strength α′) with a power n′ > n. The exact solution of the Schrödinger equation for the sum of the external potentials is now dominated at short distances by the irregular solution of the subleading potential, which grows exponentially as r decreases. Matching to the short-range potential VS will force a non-vanishing irregular solution, which in turn leads to an exponentially increasing dependence of the fractional phase shift error in R, [24]. The only solution is to remove the LO LEC at subleading order! There is hardly a way to keep the systematic expansion of the EFT.
Another toy model [78] illustrates this paradox. This time the underlying potential consists of a repulsive r−3 component associated with a mass mL together with an attractive r−3 from a heavier mS ≫ mL, as well as less singular terms. Its exact S-wave results are compared to those of a potential consisting of the repulsive r−3 potential plus a delta-function interaction. Parameters are chosen so that the repulsive potential is non-perturbative. Despite the fact that the phase shifts of the repulsive component are well-defined by themselves, reference [78] includes the delta function non-perturbatively, fixing it to reproduce the scattering length of the underlying potential. For the phase shifts are in reasonably good agreement with those of the underlying potential. However, agreement deteriorates as R decreases. Disregarding conceptual differences in renormalization of attractive and repulsive singular potentials [23, 24], reference [78] concludes that cutoff dependence cannot be removed in general, rather than in the particular case of resumming the subleading delta function. In response, reference [79] included the 2n-derivative delta functions, which account for the short-range potential, at N2(n+1)LO in perturbation theory. Calculations up to N8LO show convergence to the exact phase shifts up to at least k ~ 2mL without significant restriction on R. (Reference [80] nevertheless points to some ambiguity in the values of the NLO phase shifts, apparently implying that it is suffcient reason to abandon renormalization.)
Thus the singular nature of the potentials that we want to treat in an EFT expansion of the amplitude requires the use of perturbation theory on corrections, as implied by the power counting of section 2. This in fact ensures small changes in amplitudes after renormalization [31]. But then one might wonder to which extent the singular nature of the LO potential affects the order of the corrections. As we have seen, when the only singular part of the LO potential is a delta function, the first correction comes at NLO. When the outside potential is singular and attractive, the situation is different. For an LO singular attraction, one finds [24] that after fixing the phase ϕ0 the S-wave phase shifts scale as
This means that corrections are expected at (or before) N2LO for n = 2, 3, N3LO for n = 4, 5, etc.. It is unclear why the results reported in reference [54] indicate higher sensitivity to R than given by Equation (39).
Now, the power counting for nuclear interactions in section 2 says that at N2LO there are corrections to the long-range potential with an r−(n+2) singularity. The additional singularity can be removed in first-order perturbation theory by additional contact interactions with two derivatives. This can be shown relatively simply in a toy model where a ±r−4 potential is added to an n = 2 attractive LO potential [31]. The analysis was carried out in momentum space with a sharp cutoff Λ. At N2LO, where the ±r−4 potential is considered as a first-order perturbation, two forms of additional, oscillating cutoff dependence appear: one proportional to Λ2, reflecting the stronger singularity of the perturbing potential, the other proportional to k2. In the S-wave, a two-derivative potential (38) is sufficient, together with an N2LO shift in the C0 of Equation (19), to remove the two additional divergences. This argument can presumably be continued at higher orders and repeated for l ≥ 1 waves by considering interactions of type (34) with two more derivatives. One tentatively concludes that NDA holds in distorted-wave perturbation once it has been corrected at LO.
3.2.2. Simple Perturbation
In partial waves l ≳ lcr where the LO potential is perturbative and particles are free in zeroth approximation, corrections are included in simple perturbation theory. The first task in this case is to quantify the angular-momentum suppression for the long-range potentials so as to establish the orders they come in. The second need is to find the orders the associated contact interactions appear at.
For the μ = 0 long-range potential, rules (7) and (8) indicate that a contact interaction is needed for renormalization at nth order in perturbation theory, where n ≥ 2l + 1. This is consistent with the inference from the residual cutoff dependence of the non-derivative contact interaction. As we saw in section 3.1.2, l-wave scattering “lengths” al are induced through matching at finite R. Just as for the S-wave effective range, they can be made arbitrarily small by taking R → 0. However, the higher power of R, R2l+1, suggests that contact interactions in higher waves enter in perturbation theory at N2l+1LO or lower, another element of Pionless EFT power counting [35].
The increased singularity of subleading potentials asks for counterterms at lower orders in perturbation theory. The first-order perturbative correction due to subleading potentials involving pion loops is renormalized with LECs assigned by NDA. Making further general statements about the order contact interactions are needed is cumbersome without an explicit angular-momentum suppression factor.
If one were to solve the Schrödinger equation exactly in one of these waves, renormalization would require a LEC, which then determines the asymptotic properties of the wavefunction. The tail of the non-perturbative wavefunction can be reproduced with increasing accuracy as the order of perturbation theory increases [23]. Being a series in α, the perturbative expansion cannot reproduce the oscillations found in Equation (16), which are tied to the non-analytic dependence . This is no problem because, by definition of lcr, these oscillations take place at distances smaller than those probed by the EFT. Their effects can be “averaged out” and appear through contact interactions at subleading orders. If one wants to save all the perturbative work by sticking to a non-perturbative solution, one loses some predictive power at LO but, because it is a single LEC (in one wave), this is perhaps acceptable. Alternatively, one could simply not include the LEC if l is sufficiently high for oscillations to happen below R, which might be limited in numerical calculations anyway. In this case R is in the region where perturbation theory works and the result will be relatively insensitive to R. Unnecessary iteration in high waves is thus relatively harmless, other than obscuring the systematic EFT expansion.
4. Renormalization of Chiral EFT
By this point in the manuscript it should be clear how to proceed with ChEFT in the nuclear sector. The power counting of ChPT is based on NDA, which comes from demanding that the EFT expansion be renormalized order by order so as to ensure model independence. In the more general ChEFT we continue to insist on model independence, but now LO is non-perturbative. The results of the previous section apply to pion-exchange potentials, where the spin-isospin factors and the exponential fall-off at large mπr do not substantially affect renormalization. Perhaps not surprisingly in hindsight, NDA is violated.
Since the OPE tensor force is singular and attractive in an infinite number of channels, the first task (section 4.1) is to estimate up to which relative angular momentum l OPE needs to be considered at LO. In sections 4.2 and 4.3 renormalized results for, respectively, two and more nucleons are described.
4.1. Partly Perturbative Pions
The simple power counting of Equations (7) and (8) does not capture factors of l−1, just as it misses other dimensionless factors. More realistically, OPE in the radial Schrödinger equation is an expansion in , where but increases with l depending in general also on the spin s. Once , OPE is perturbative. What do we know about and ?
The bold suggestion was made in references [28, 29] that , so that pion exchange would be amenable to perturbation theory in all waves. The estimate in Equation (5) assumed NDA for the one-nucleon quantities mN = (MQCD), fπ = (MQCD/(4π)), and gA = (1), plus neglected any dimensionless factors. Numerically, MNN ≃ 290 MeV. What if the various spin/isospin factors and other numbers floating around, each of (1), conspire to make OPE more perturbative, so that MNN is effectively comparable to MQCD?
In that case, at LO ChEFT would be formally the same as Pionless EFT [35, 36], where the binding of light nuclei rests on the shoulders of non-derivative 2N and 3N contact interactions [81, 82]. But because pions are explicit, the range of validity of the EFT is enlarged—at least near the chiral limit where integrating out pions becomes a very restrictive condition. An attractive feature of this proposal is that it could potentially explain why Pionless EFT works better than expected, for example for binding energies [35].
This proposal also neatly solves the renormalization issues of the last section. OPE is now an NLO effect of relative (Q/MNN), so no problems associated with its singularity emerge. Being perturbative, it brings NLO cutoff dependence only to S waves. Because at LO the external potential vanishes, Equation (36) requires at NLO one chirally symmetric two-derivative contact interaction in each S wave. Then Q ~ mπ implies the concomitant presence of a chiral-symmetry-breaking non-derivative interaction with LEC proportional to the quark masses, D2. In the background of an LO wavefunction of the type (23), OPE generates an cutoff dependence which can be absorbed in D2. The 2N amplitude is renormalized and in good agreement [28, 29, 83] with the Nijmegen partial-wave analysis (PWA) [84] up to Q ~ mπ.
Alas, calculations at have shown [30, 85] that in the low, spin-triplet partial waves, where the OPE tensor force is attractive, the expansion fails for Q ~ 100 MeV. In partial waves with l = j≫1, where counterterms are needed only at a very large number of loops L ≥ 2l, the breakdown of perturbation theory was estimated in the chiral limit to be at a critical momentum [86]
If we impose pcr ~ MQCD, we get . The radius of convergence of the perturbative series is not as large in waves with l = j ± 1. In both cases the first few orders were found [86] not to be representative of the large-order convergence. For low partial waves counterterms enter already at low orders. When they were assigned arbitrary but natural values, all waves except 3S1-3D1, 3P0, and perhaps 3P1 were found to converge up to pcr ≈ MNN. An example of failure, 3P0, is given in Figure 4 [87], where OPE is NLO, n-iterated OPE NnLO, leading two-pion exchange (TPE) N3LO, and subleading TPE N4LO. The LECs are assumed to be given by NDA instead of being introduced only at the order where they are first needed for renormalization. These signs of the breakdown of perturbative pions are consistent with an expansion in with as indicated by NDA.
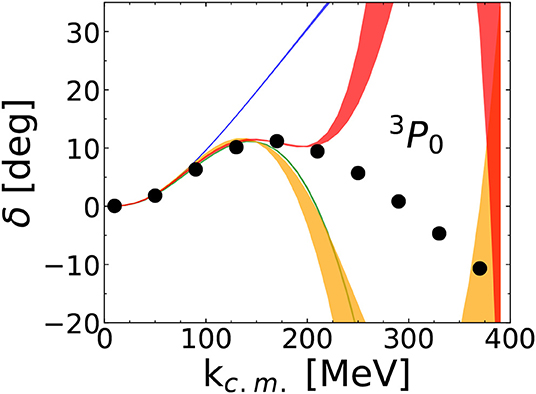
Figure 4. Two-nucleon 3P0 phase shift δ as function of the center-of-mass momentum kc.m.. The NLO (blue), N2LO (green), N3LO (orange), and N4LO (red) bands from a perturbative treatment of pion exchange correspond to cutoff variation from 0.8 to 2.4 GeV. (LO in a perturbative expansion vanishes for this channel.) The empirical phase shifts from the SAID program [88] (solid circles) are shown for comparison. Reprinted figure with permission from reference [87]. Copyright (2019) by the American Physical Society.
It seems inevitable that pions must be treated non-perturbatively in the low partial waves if we want to go beyond Pionless EFT at physical quark masses. Still, based on the general arguments of section 3.1.3 we expect pions to be perturbative for sufficiently high partial waves. The n = 3 tensor force, for which , does not vanish for spin s = 1. Equation (35) with provides an estimate for the critical angular momentum in attractive triplet waves. This conclusion is made firmer by a generalization to the tensor potential of the analysis of the onset of square-root branch points in the Bessel series solution of the Schrödinger equation [32]. Given that the strength of OPE is fixed by MNN, it translates into an upper bound on the critical momentum pcr, including repulsive waves. The results, listed in Table 1, are obtained in the chiral limit; a realistic pion mass could affect the smaller values by factors of (1) but is not expected to be important for the larger values. They indicate that OPE in 3S1-3D1 and 3P0 likely fails to converge already below MNN. In contrast, OPE in high waves, such as F and higher, converges beyond MQCD. The gray zone is the D and P waves other than 3P0. Given the low values of pcr on the scale set by MQCD, one might conclude that . An analysis of spin-triplet phase shifts where OPE and TPE are removed in distorted-wave perturbation [89] supports this conclusion.

Table 1. Estimate of the critical values pcr of the relative momentum in the lowest 2N triplet channels above which the OPE tensor force cannot be treated perturbatively [32].
A different but closely related estimate for comes from the cutoff values where the first bound state crosses threshold in the absence of contact interactions. The very early work on ChEFT and much of its phenomenological improvements, which continue to this day, have used Weinberg's prescription. Unfortunately this prescription assigns to triplet waves a single non-derivative contact interaction at LO, which is incapable to determine more than one phase in a model-independent way. In particular, for a separable regulator the contact interaction contributes only to the S wave. Spurious low-energy bound states can be kept at bay at LO in the 3S1-3D1 coupled channel [62, 90–93], but only in this channel [20, 21]. In triplet waves where OPE is repulsive there is no need for counterterms at LO [20, 94], but without them bound states repeatedly cross threshold in attractive waves and lead to wild variations in the phase shifts at energies within the realm of ChEFT [20, 21, 93, 95]. With a super-Gaussian separable regulator, bound states first emerge at, roughly, Λ ~ 0.5, 1, 2, 4, and 6 GeV in respectively 3S1-3D1, 3P0, 3D2, 3P2-3F2, and 3D3-3G3 channels [20, 93]. Except for 3D3-3G3, this sequence is similar to that of the attractive channels in Table 1. The lowest two channels would display shallow states when Λ ~ MQCD, indicating that OPE is non-perturbative, while the higher waves are less clear—numerical experimentation suggested [20] their effects were not negligible, which can be understood from the results of reference [32].
Perhaps even more seriously, in Weinberg's scheme more-pion exchange and other contact interactions, which should be treated perturbatively, are not. This leads to the pathologies discussed in section 3.2. Indeed, renormalization problems have been reported [21, 96–100] within Weinberg's prescription also for higher-order potentials. These renormalization failures prevent taking a momentum-space cutoff at the breakdown scale MQCD or higher. A “physical cutoff” Λphys ≲ 1 GeV, before 3P0 would develop a bound state [20], is needed, and results are sensitive to the choice of regulator. No wonder then that much effort in phenomenology with chiral potentials has been dedicated to finding the “best” regulator. The limitation to small cutoffs leads to startling dependence on what should be equivalent forms of interactions in the Lagrangian, see for example reference [101].
One concludes that, while it seems well-established that to handle triplet waves beyond MNN pions are non-perturbative in at least 3S1-3D1 and 3P0, there is some uncertainty as to the partial wave up to which this is so. Part of the uncertainty comes from the presence of LECs in lowest orders of the amplitude, which require a closer comparison with data (section 4.2). What is clear is that there is an angular-momentum suppression. The perturbative expressions in reference [86] suggest
apart from an overall suppression of l2. In contrast, the analyses of reference [32] leads to l2 → [l(l + 1)]3/2.
Singlet channels are somewhat simpler, but not devoid of subtleties. Since the tensor force vanishes for s = 0, OPE has n = 1 and . The general argument from section 3.1.3 indicates that only in the S wave should we expect non-perturbative effects, . In higher waves, the OPE potential dominates over kinetic and centrifugal repulsion only at large distances, and there the exponential fall-off of OPE leads to further suppression.
The perturbative convergence of the l ≥ 1 channels was studied in reference [102]. This is particularly easy because the Yukawa potential is well-defined for an arbitrary number of loops. The phase shifts are seen to converge quickly already for 1P1, and faster as l increases. The suppression factor can be estimated from the critical strength needed to generate a zero-energy bound state in the corresponding l wave, shown in Table 2. There are two sequences of channels that alternate because of the factor of −3 in the ratio between isospin singlet and triplet: if we multiply the isosinglet entries in Table 2 the results form a single monotonous sequence. Assuming Q ~ mπ, we find that in each sequence increasing l by 2 roughly suppresses OPE by one order in the expansion, starting with 1P1 at NLO and 1D2 at N2LO. Moreover,
in the isosinglet waves, with a factor 3 larger in isotriplets.

Table 2. Estimate of the critical strength of the Yukawa potential in the lowest 2N singlet channels above which OPE cannot be treated perturbatively [102].
If one insists on the full solution for the Yukawa potential in higher partial waves, there are no renormalization problems [20, 94], as the potential is regular. In the S wave, however, interference with the delta function leads to an unexpected violation of NDA. As first noticed in reference [18] and confirmed many times since—for example, references [62, 96, 103]— cutoff dependence proportional to emerges through the ln R term in Equation (26). Renormalization therefore requires the non-derivative chiral-symmetry-breaking interaction with LEC D2. With Weinberg's prescription, where this LEC is missed at LO, the cutoff dependence can be seen in the 2N system only if quark masses are varied, as one does to match lattice QCD results. From the perspective of phenomenology, the main effect of the absence of the D2 contact interaction is in processes sensitive to its associated pion interactions, which are generated by the way chiral symmetry is broken explicitly in QCD. Regardless of its phenomenological (ir)relevance, this is the simplest example where the renormalization of observables in ChEFT is not guaranteed by NDA.
Clearly, dimensionless factors stemming from spin and isospin make the transition from non-perturbative to perturbative OPE somewhat fuzzy. Moreover, virtually nothing has been done to estimate the angular-momentum suppression for multiple-pion exchange. Multiple-pion exchange is amenable to perturbation theory in all waves, but presumably further suppressed in higher waves. That is sufficient to start comparing with data.
4.2. Two Nucleons
Let us now take a closer look at how a renormalized approach works at the 2N level. I continue to consider Q ~ mπ ~ MNN. Since the OPE tensor force survives in the chiral limit, if we take mπ ≲ MNN we can perform an additional expansion around the chiral limit [62], but such an expansion in mπ/MNN has not been fully explored.
Leading order at the 2N level consists of the exact solution of the Schrödinger equation up to with OPE and the required counterterms, not all of which were accounted for by NDA:
• Two non-derivative, chirally symmetric contact interactions with LECs C0(s), one for each S wave (s = 0, 1). They are needed to renormalize OPE even in the chiral limit, and were anticipated [10, 11] to appear at LO already on the basis of NDA, which estimates C0(s) ~ 4π/(mNMNN).
• A non-derivative, chiral-symmetry-breaking contact interaction with LEC if OPE is treated non-perturbatively in the 1S0 channel. This LEC is on the basis of NDA, and thus N2LO. Renormalization of non-perturbative OPE instead requires [18].
• One chirally symmetric contact interaction with the minimum number of derivatives for each wave where attractive tensor OPE is iterated. The most dramatic effect is in 3P0, where a contact interaction with is needed [20]. NDA would give instead . The two-order enhancement comes from the running of pion exchange, and similar enhancements apply for the LECs in other attractive, singular waves where OPE is non-perturbative.
These counterterms are schematically displayed in Table 3, assuming .

Table 3. Schematic momentum dependence of the lowest-order contact interactions in the 2N system up to D waves, according to references [20, 31, 62, 68, 104, 105].
Results can be found in references [20, 62, 93, 95] for cutoff values as high as 10 GeV in super-Gaussian separable regulators. In comparison with the Nijmegen PWA, one finds:
• In the 3S1-3D1 coupled channels, where Weinberg's prescription is consistent with renormalization, phase shifts come out well with one fitted LEC. Results improve for Λ ≳ MQCD; even the mixing angle, which is somewhat overpredicted with a small Λ ~ 500 MeV, agrees with the Nijmegen PWA to within 1° up to a laboratory energy Elab ≃ 200 MeV for Λ ≳ 4 GeV. When the scattering length is used to fix the LEC, the deuteron binding energy is MeV, which is essentially the same as for lower cutoffs [106].
• For low uncoupled, attractive triplet channels (3P0, 3D2) iterating pions with one fitted LEC works equally well. As an example, Figure 5 [20] shows 3P0, which comes out much better than in Weinberg's prescription with Λ ~ 500 MeV (compare this also with Figure 4 where pions are treated perturbatively). The vanishing of the amplitude beyond Elab ≃ 200 MeV can be described, because attraction from OPE is compensated by the contact interaction. Again, agreement improves with increasing cutoff.
• For low coupled triplet channels (3P2-3F2, 3D3-3G3)—see Figure 5 [20] again for an example—iterated pions with the associated LEC do not improve significantly over Weinberg's prescription with Λ ~ 500 MeV. While 3D3 is much better, changing from repulsion to attraction, 3P2 goes from underprediction to considerable overprediction.
• In triplet channels without free parameters (3P1, 3F3, 3F4-3H4, 3G4) iterated pions tend to work well, whether they are expected to be perturbative or not. In these channels results are the same as in Weinberg's prescription; there is not much change as Λ ≳ MQCD.
• In l ≥ 1 singlet channels (1P1, 1D2, 1F3, 1G4), iterated pions undershoot data except in 1F3. Again results essentially agree with Weinberg's prescription at small Λ ~ 500 MeV.
• In 1S0, the phase shifts resemble those of Pionless EFT, where after the fast rise due to the existence of a virtual state, they remain essentially flat as Elab increases. Weinberg's prescription applies, and renormalization allows us to increase the cutoff beyond MQCD, but agreement with the Nijmegen PWA deteriorates as we do so.
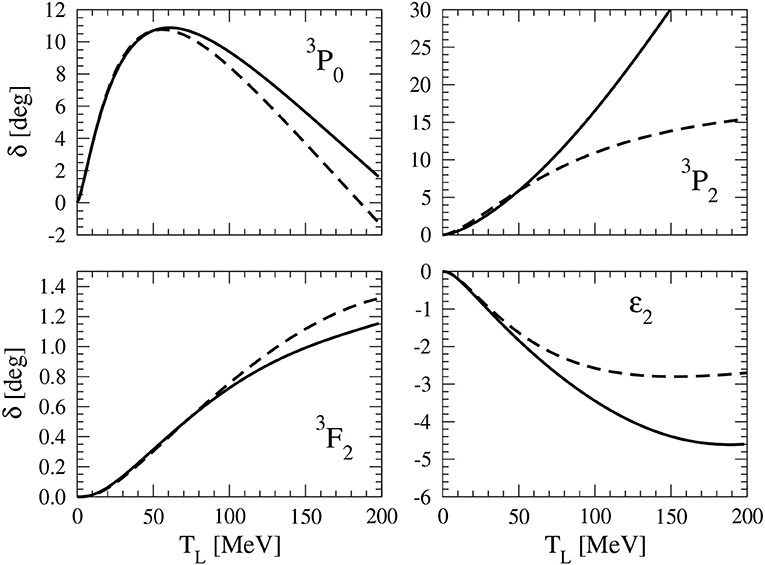
Figure 5. Two-nucleon 3P0 and 3P2-3F2 phase shifts (δ) and mixing angle (ε2) as functions of the laboratory energy TL. The LO results (solid lines) at a cutoff Λ = 3.94 GeV are compared with the Nijmegen PWA [84] (dashed lines). Reprinted figure with permission from reference [20]. Copyright (2005) by the American Physical Society.
Thus, a renormalized approach where the regulator is unimportant gives a qualitative guide to 2N data at LO, which is slightly better than Weinberg's prescription with specific regulators and small momentum-cutoff parameters. It has been shown recently [107] that, with a non-separable regulator, a specific combination of the four possible spin-isospin non-derivative contact interactions that yields only one 3S1-3D1 bound state simultaneously prevents bound states in other channels. While this is not true for an arbitrary regulator, it does allow to extend LO results with Weinberg's prescription to higher cutoff values, in general improving agreement with the Nijmegen PWA. However, results are not clearly better than the renormalized approach, particularly in the 3P0 channel which lacks the repulsion to produce the amplitude zero.
In addition to simple perturbative corrections in higher partial waves, one needs to account in subleading orders for potential corrections via distorted-wave perturbation theory in the lowest partial waves. The residual Λ−1 dependence of the LO amplitude means that at NLO—relative (Q/MQCD)—there is also:
• A two-derivative, chirally symmetric contact interaction with LEC C2(0) in the 1S0 channel. In order to render cutoff effects on the effective range no larger than N2LO, C2(0) ~ C0(0)/(MNNMQCD) [68]. NDA gives instead , or N2LO (confusingly denoted NLO in the nuclear community), which produces a short-range contribution to the effective range smaller than pion's by two powers of the expansion parameter. Yet, only about half of the 1S0 effective range comes from OPE.
The cutoff dependence in other channels is milder, in agreement with the discussion of section 3.2. The NLO interaction is shown in the second line of Table 3. At NLO in the amplitude, the NLO interaction should be included in first order in the distorted-wave expansion.
At higher orders, corrections to the long-range potential enter according to the power counting of section 2. Barring unforeseen renormalization issues, at we need to include LECs with up to μ derivatives more than the LECs appearing at LO [31], except in the 1S0 channel where the Yukawa/delta-function interference takes place. The momentum structures of the LECs up to N3LO are shown in Table 3, again under the assumption . They are:
• In each triplet channel where attractive OPE is iterated at LO (3S1-3D1, 3P0, etc.), a contact interaction with two derivatives more than the contact interaction at LO [104, 105]. While for 3S1-3D1 this coincides with NDA, for other channels NDA would say these contact interactions only appear at N4LO or higher.
• Contact interactions with two derivatives [68] for singlet (1P1) and triplet P waves where OPE is repulsive (3P1). This is the NDA scaling.
• Four- and six-derivative contact interactions in the 1S0 channel at N2LO and N3LO, respectively [68]. Again, NDA would have these contact interactions at N4LO or higher.
Up to N3LO in the amplitude, their contributions are included in first order in the distorted-wave expansion. Meanwhile, the NLO interaction must be included in second and third orders, either by itself or with one N2LO interaction.
The phase shifts have been calculated up to N3LO along these lines in references [68, 104, 105], together with Deltaless TPE:
• In the 3S1-3D1 coupled channels, where LO already yielded very good results at LO, results improve only marginally at N2,3LO.
• In 3P0, which was also relatively well-described at LO, results improve quite a bit around the maximum phase shift at N2LO. Not much improvement, if any, is seen at N3LO. Results from reference [104] are shown in Figure 6, to be compared with LO in Figure 5. Other uncoupled, attractive triplet channels (3D2 etc.) were not calculated.
• The coupled 3P2-3F2 wave with OPE iterated at LO shows no real improvement at N2LO, and only mildly better agreement with the Nijmegen PWA at N3LO. No results are available for higher coupled triplet channels (3D3-3G3 etc.).
• In 3P1, which works well at LO with no free parameter, results deteriorate at N2,3LO. Higher repulsive triplet channels (3F3 etc.) were not considered.
• In 1P1, agreement with the Nijmegen PWA improves at N2,3LO, although results are very sensitive to the pion-nucleon parameters that enter the μ = 3 TPE. Higher singlet partial waves were not studied.
• The 1S0 phase shift improves considerably at NLO but is still not very close to the Nijmegen PWA. N2LO improves further, but the zero of the amplitude is still poorly described.
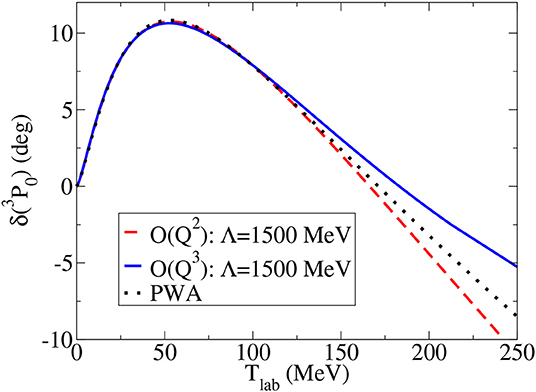
Figure 6. Two-nucleon 3P0 phase shift δ(3P0) as function of the laboratory energy Tlab. The N2LO (red dashed line) and N3LO (blue solid line) results at a cutoff Λ = 1.5 GeV are compared with the Nijmegen PWA [84] (black points). Reprinted figure with permission from reference [104]. Copyright (2011) by the American Physical Society.
Overall, there is some improvement at N2LO but not much at N3LO. This is perhaps an indication that a better description of the pion-nucleon subamplitude with an explicit Delta isobar is needed.
Note that subleading corrections have also been calculated in references [108, 109] with a slightly different accounting of higher orders. For example, TPE is taken to start three orders higher than OPE, which is contrary to the power counting of section 2 and difficult to conciliate with the power counting used in ChPT. Still, results are generically not much different from those described above. A third power-counting variant has been proposed [32] with similar features. It has not been tested in detail, perhaps because no clear prescription is given for handling the LO cutoff dependence in a channel like 3P0 where a counterterm is assigned relative . Reference [67] discusses these alternatives.
The main phenomenological shortcomings of the renormalized approach are 3P1, 3P2 and singlet partial waves. For most of these channels, subsequent work indicates OPE might be perturbative. Equation (42) shows that OPE should be included in 1P1 at NLO, in 1D2 at N2LO, and so on. On the basis of NDA, contact interactions with the minimal number of derivatives are expected at respectively N2LO, N4LO, and so on. Under the assumption that the angular-momentum suppression of TPE is the same as OPE, reference [87] provided evidence that the perturbative expansion converges for singlet waves up to k ≈ 300 MeV and N4LO without explicit Delta isobars. Reference [87] goes further by showing that under NDA for the LECs also triplet waves converge in the same range, except for 3P0 and possibly 3D3. For illustration, results for the 3P2-3F2 coupled channels are shown in Figure 7 [87], which should be compared to Figure 5 where OPE was treated non-perturbatively at LO. The maximum momentum k ≈ 300 MeV seems tied to the absence of an explicit Delta isobar [87] but no similar calculation is available in Deltaful ChEFT. Earlier studies [110–112], which indicated that pions are perturbative in high waves, sometimes included Deltas but did not take into account the IR enhancement in iterated pion exchange. Clearly a more comprehensive study of higher orders with Deltas is needed to confront this renormalized approach with phenomenology.
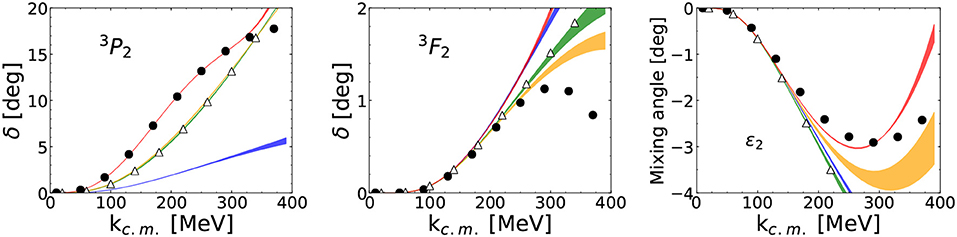
Figure 7. Two-nucleon 3P2-3F2 phase shifts (δ) and mixing angle (ε2) as functions of the center-of-mass momentum kc.m.. The NLO (blue), N2LO (green), N3LO (orange), and N4LO (red) bands from a perturbative treatment of pion exchange correspond to cutoff variation from 0.8 to 4.8 GeV. N2LO results for Λ → ∞ are also shown (triangles) (LO in a perturbative expansion vanishes for these channels.) The empirical phase shifts from the SAID program [88] (solid circles) are shown for comparison. Reprinted figure with permission from reference [87]. Copyright (2019) by the American Physical Society.
The situation is particularly unsatisfactory in the 1S0 channel, where LO—same as in Weinberg's prescription at fixed pion mass—is far off, just as in Pionless EFT [35]. In particular, the Nijmegen PWA displays a zero at a relative low momentum k0 ≃ 340 MeV, which is absent at LO. It is possible that the inclusion of an explicit Delta isobar (separated in mass from the nucleon by ~300 MeV) improves the convergence in this region, as a large part of the central potential moves from N3LO to N2LO. However, the expansion will in any case converge at best very slowly for k ≳ k0, as all subleading orders have to conspire to cancel against LO. Since numerically k0 ~ MNN, only for a fully perturbative-pion approach is this of no concern. Note that also 3S1 and 3P0 have amplitude zeros at relatively low energies, but in both cases they arise at LO from the combination of non-perturbative OPE and contact interactions need for renormalization.
The 1S0 channel is special also for the presence of an unnaturally shallow virtual state that requires a fine-tuning of the short-range interaction. It is the interference between the non-derivative contact interaction and the Yukawa potential that causes a violation of NDA in this channel. It also leads to the piling up of higher-order counterterms seen in Table 3. Given the uniqueness of this channel, it is perhaps not surprising that power counting might require refinement. In reference [113] it was shown that short-range interactions show strong energy dependence. To ameliorate the expansion in 1S0, it was suggested in references [62, 114] that the chirally symmetric two-derivative interaction with LEC C2(0) should be promoted from NLO to LO, following an earlier suggestions for Pionless EFT [115] and ChEFT with purely perturbative pions [116]. To avoid the Wigner bound, this is done through a dibaryon field [77] whose kinetic term is taken to be LO together with its residual mass. This promotion induces promotions at higher orders of the contact interactions with more derivatives. Results of course improve at LO and further at NLO, but not at N2LO, in particular near k0. In reference [117] it was then proposed—similarly to an earlier attempt [118]—that the zero be included at LO by a combination of dibaryon field and contact interaction (or alternatively two dibaryon fields, the kinetic term of one of which is higher order). Again this induces the promotion of contact interactions with more derivatives at higher orders. Phase shifts come out great at LO and essentially on the nose at NLO, even beyond k0 (see Figure 8). Unfortunately these reorganizations of the expansion produce energy-dependent potentials at LO, which complicate few-body calculations.
Figure 8. Two-nucleon 1S0 phase shift δ as function of the laboratory energy Tlab in an expansion that incorporates the amplitude zero at LO. The LO (green) and NLO (blue) bands correspond to cutoff variation from 0.6 to 2 GeV. The results from the Nijm93 potential [119] (black squares) are shown for comparison. Reprinted figure with permission from reference [117]. Copyright (2018) by the American Physical Society.
A further proposed reorganization of ChEFT arises from treating selected relativistic corrections, which are small for the momenta of interest, as LO—see, for example, reference [120]. A modified nucleon propagator ensures less dependence on the regulator, but a 3P0 LEC still has to be promoted compared to NDA, as in the purely non-relativistic context [20]. By resumming higher-order terms into LO whether they are relativistic corrections or not, one can soften the large-momentum behavior of loops and alter the cutoff dependence. This is no different than picking a regulator, which effectively includes an infinite number of higher-derivative interactions. Results then depend on the corresponding cutoff parameter Λ. Renormalization exchanges this dependence for the minimal number of parameters allowed without dynamical assumptions. Achieving cutoff independence with a resummation of a selected interaction merely replaces Λ by the mass parameter characterizing this interaction, call it M′. If is inferred from data, this resummation is justified because the interaction is not of higher order. However, when resumming relativistic corrections : it corresponds to one fixed cutoff value and convergence cannot be used to demote interactions that are needed for renormalization without resummation. As long as no LECs are promoted or demoted, a resummation of higher-order corrections is safe. There is growing interest in the development of a covariant version of ChEFT, which could perhaps be used as input to relativistic formulations of nuclear physics [121, 122].
4.3. More Nucleons
There is not much known about renormalized ChEFT beyond 2N. The power counting of section 2 shows that the 3N force is expected to start at NLO from two-pion exchange when Delta isobars are included explicitly, and at N2LO when they are not. The crucial issue is whether shorter-range interactions are enhanced as in the 2N system. Such an enhancement does take place in Pionless EFT [81] and it has been suggested for ChEFT on phenomenological grounds in reference [123].
In calculations for more than two nucleons in the renormalized approach, one needs to truncate the LO 2N potential for , which is reminiscent of the truncation in total 2N angular momentum typically invoked in solutions of the Faddeev and Faddeev-Yakubovski equations for 3N and 4N systems with phenomenological potentials. As we have seen the optimal values for are uncertain and the l dependence of is not fully determined. Of course, as in the 2N system, subleading orders should be treated in distorted-wave perturbation theory.
Existing calculations are limited to the 3N system and took . At LO [20, 93] and, without explicit Deltas, also at NLO [93], observables converge as the cutoff increases to at least 10 GeV without 3N forces (see Figure 9) [93]. The triton binding energy is MeV and MeV, quite different from results for a low cutoff in Weinberg's prescription, ≃ 11 MeV (≃ 6.5 MeV) at LO (N2LO) [106]. Results were shown not to change significantly when waves beyond lcr = 3 were included. Conversely, if it turns out that , results might change quantitatively, but qualitative statements should stand. In particular, one concludes there is no renormalization justification in ChEFT to take the non-derivative 3N contact interaction as LO. Most likely the same conclusion holds for higher-body forces, but no calculations have been carried out.
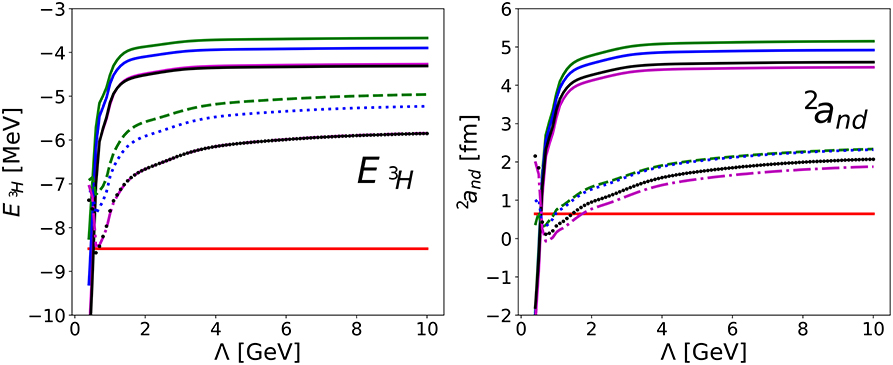
Figure 9. Triton binding energy E3H and doublet neutron-deuteron scattering length 2and as functions of the cutoff Λ. Results at LO (solid lines) and NLO (dashed and dotted lines) for various 2N fitting procedures are compared with experiment (horizontal red lines). Reprinted figure with permission from reference [93]. Copyright (2019) by the American Physical Society.
The tendency for underbinding at LO seen in the deuteron and triton seems to persist for symmetric nuclear matter. In a cutoff-converged Brueckner pair approximation [124], nuclear matter was found to saturate, but with significant underbinding. This is in contrast to Weinberg's prescription, where Deltaless [125] or Deltaful [126] potentials of (1) and do not yield saturation within the EFT domain. Yet higher potentials do lead to saturation with this prescription [125–127]. Although usually presented as a success, the emperor has no clothes: it means that, if nuclear matter is within the regime of ChEFT, interactions that are formally of higher order according to NDA must actually be LO to balance against other LO interactions. Presumably it is the extra repulsion from 3P0 in a renormalized approach that saturates nuclear matter. It is not clear how saturation in Chiral EFT would relate, if it can be related at all, to the proposal of reference [128] where saturation arises from the 3N parameter that appears at LO in Pionless EFT. What is clear is, more EFT calculations beyond the 2N system are sorely needed!
5. Conclusion
The longstanding problem of renormalization of chiral nuclear forces has been solved at the 2N and 3N levels. Perhaps not surprising in hindsight, this solution is a middle ground between Weinberg's original prescription and Kaplan, Savage, and Wise's suggestion of fully perturbative pions. One-pion exchange is iterated in lower waves together with the necessary contact interactions, while all corrections are included in distorted-wave perturbation theory.
That is not to say that the best solution has been found. Issues remain regarding exactly how strong the angular-momentum suppression is and where the non-perturbative/perturbative boundary lies. Whether the ordering of few-body forces holds similar surprises is also unknown. A high-quality fit to 2N data is missing, and there are very few studies of heavier systems. The extent to which Weinberg's phenomenologically successful prescription with a low cutoff can be reproduced remains an open question, although the first step in grounding it on a renormalized approach has been made [42]. Fortunately, there is still plenty to learn.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I thank Manolo Pavón Valderrama for useful discussions and Jaber Balal Habashi for comments on the manuscript. This material was based upon work supported in part by the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under award DE-FG02-04ER41338 and by the European Union Research and Innovation program Horizon 2020 under grant No. 654002.
Footnotes
1. ^A note on notation: It has become usual in the nuclear community to refer to a subleading chiral potential of order n ≥ 2 as “Nn − 1LO,” because with Weinberg's power counting the parity- and time-reversal-invariant potential of order n = 1 vanishes [19]. However, this usage is too provincial to accommodate experience with other observables and power countings in ChEFT or other EFTs. Here, a correction of order n in the expansion is denoted as NnLO, whether it is non-zero or not.
References
1. Watson KM, Lepore JV. Radiative corrections to nuclear forces in the pseudoscalar meson theory. Phys Rev. (1949) 76:1157. doi: 10.1103/PhysRev.76.1157
2. Matthews PT, Salam A. The renormalization of meson theories. Rev Mod Phys. (1951) 23:311. doi: 10.1103/RevModPhys.23.311
4. Gartenhaus S. Two-nucleon potential from the cut-off Yukawa theory. Phys Rev. (1955) 100:900. doi: 10.1103/PhysRev.100.900
5. Machleidt R. Historical perspective and future prospects for nuclear interactions. Int J Mod Phys E. (2017) 26:1730005. doi: 10.1142/S0218301317300053
6. Weinberg S. What is quantum field theory, and what did we think it was? In: Cao T, editor. Conceptual Foundations of Quantum Field Theory. Cambridge: Cambridge University Press (1999). doi: 10.1017/CBO9780511470813.020
7. Weinberg S. Phenomenological Lagrangians. Physica A. (1979) 96:327. doi: 10.1016/0378-4371(79)90223-1
8. Gasser J, Leutwyler H. Chiral perturbation theory to one loop. Ann Phys. (1984) 158:142. doi: 10.1016/0003-4916(84)90242-2
9. Manohar A, Georgi H. Chiral quarks and the nonrelativistic quark model. Nucl Phys B. (1984) 234:189. doi: 10.1016/0550-3213(84)90231-1
10. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett B. (1990) 251:288. doi: 10.1016/0370-2693(90)90938-3
11. Weinberg S. Effective chiral Lagrangians for nucleon pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3. doi: 10.1016/0550-3213(91)90231-L
12. Ordóñez C, Ray L, van Kolck U. Nucleon-nucleon potential from an effective chiral Lagrangian. Phys Rev Lett. (1994) 72:1982. doi: 10.1103/PhysRevLett.72.1982
13. Ordóñez C, Ray L, van Kolck U. The two nucleon potential from chiral Lagrangians. Phys Rev C. (1996) 53:2086. doi: 10.1103/PhysRevC.53.2086
14. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773. doi: 10.1103/RevModPhys.81.1773
15. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1. doi: 10.1016/j.physrep.2011.02.001
16. Entem DR, Machleidt R. Accurate charge dependent nucleon nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001
17. Navarro Pérez R, Ruiz Arriola E. Uncertainty quantification and falsification of chiral nuclear potentials. arXiv. 1907.04032.
18. Kaplan DB, Savage MJ, Wise MB. Nucleon nucleon scattering from effective field theory. Nucl Phys B. (1996) 478:629. doi: 10.1016/0550-3213(96)00357-4
19. Ordóñez C, van Kolck U. Chiral Lagrangians and nuclear forces. Phys Lett B. (1992) 291:459. doi: 10.1016/0370-2693(92)91404-W
20. Nogga A, Timmermans RGE, van Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev C. (2005) 72:054006. doi: 10.1103/PhysRevC.72.054006
21. Pavón Valderrama M, Ruiz Arriola E. Renormalization of NN interaction with chiral two pion exchange potential: non-central phases. Phys Rev C. (2006) 74:064004. doi: 10.1103/PhysRevC.74.064004
22. Pavón Valderrama M, Phillips DR. Power counting of contact-range currents in effective field theory. Phys Rev Lett. (2015) 114:082502. doi: 10.1103/PhysRevLett.114.082502
23. Beane SR, Bedaque PF, Childress L, Kryjevski A, McGuire J, van Kolck U. Singular potentials and limit cycles. Phys Rev A. (2001) 64:042103. doi: 10.1103/PhysRevA.64.042103
24. Pavón Valderrama M, Ruiz Arriola E. Renormalization group analysis of boundary conditions in potential scattering. Ann Phys. (2008) 323:1037. doi: 10.1016/j.aop.2007.08.003
25. Bedaque PF, van Kolck U. Nucleon deuteron scattering from an effective field theory. Phys Lett B. (1998) 428:221. doi: 10.1016/S0370-2693(98)00430-4
26. van Kolck U. Nucleon-nucleon interaction and isospin violation. Lect Notes Phys. (1998) 513:62. doi: 10.1007/BFb0104898
27. van Kolck U. Effective field theory of short-range forces. Nucl Phys A. (1999) 645:273. doi: 10.1016/S0375-9474(98)00612-5
28. Kaplan DB, Savage MJ, Wise MB. A new expansion for nucleon-nucleon interactions. Phys Lett B. (1998) 424:390. doi: 10.1016/S0370-2693(98)00210-X
29. Kaplan DB, Savage MJ, Wise MB. Two nucleon systems from effective field theory. Nucl Phys B. (1998) 534:329. doi: 10.1016/S0550-3213(98)00440-4
30. Fleming S, Mehen T, Stewart IW. NNLO corrections to nucleon-nucleon scattering and perturbative pions. Nucl Phys A. (2000) 677:313. doi: 10.1016/S0375-9474(00)00221-9
31. Long B, van Kolck U. Renormalization of singular potentials and power counting. Ann Phys. (2008) 323:1304. doi: 10.1016/j.aop.2008.01.003
32. Birse MC. Power counting with one-pion exchange. Phys Rev C. (2006) 74:014003. doi: 10.1103/PhysRevC.74.014003
33. Birse MC. The renormalisation group and nuclear forces. Phil Trans R Soc Lond A. (2011) 369:2662. doi: 10.1098/rsta.2010.0381
34. Pavón Valderrama M. Power counting and wilsonian renormalization in nuclear effective field theory. Int J Mod Phys E. (2016) 25:1641007. doi: 10.1142/S021830131641007X
35. Hammer HW, König S, van Kolck U. Nuclear effective field theory: status and perspectives. arXiv. 1906.12122.
36. Bedaque PF, van Kolck U. Effective field theory for few nucleon systems. Ann Rev Nucl Part Sci. (2002) 52:339. doi: 10.1146/annurev.nucl.52.050102.090637
37. Friar JL. Dimensional power counting in nuclei. Few Body Syst. (1997) 22:161. doi: 10.1007/s006010050059
38. Weinberg S. Three body interactions among nucleons and pions. Phys Lett B. (1992) 295:114. doi: 10.1016/0370-2693(92)90099-P
39. van Kolck U. Few nucleon forces from chiral Lagrangians. Phys Rev C. (1994) 49:2932. doi: 10.1103/PhysRevC.49.2932
40. Fujita J, Miyazawa H. Pion theory of three-body forces. Prog Theor Phys. (1957) 17:360. doi: 10.1143/PTP.17.360
41. Pandharipande VR, Phillips DR, van Kolck U. Delta effects in pion-nucleon scattering and the strength of the two-pion-exchange three-nucleon interaction. Phys Rev C. (2005) 71:064002. doi: 10.1103/PhysRevC.71.064002
42. Pavón Valderrama M. Scattering amplitudes versus potentials in nuclear effective field theory: is there a potential compromise? arXiv. 1902.08172.
43. Frank W, Land DJ, Spector RM. Singular potentials. Rev Mod Phys. (1971) 43:36. doi: 10.1103/RevModPhys.43.36
46. Camblong HE, Ordóñez CR. Anomaly in conformal quantum mechanics: from molecular physics to black holes. Phys Rev D. (2003) 68:125013. doi: 10.1103/PhysRevD.68.125013
47. Camblong HE, Ordóñez CR. Renormalization in conformal quantum mechanics. Phys Lett A. (2005) 345:22. doi: 10.1016/j.physleta.2005.06.110
48. Perelomov AM, Popov VS. Collapse onto scattering centre in quantum mechanics. Teor Mat Fiz. (1970) 4:48. doi: 10.1007/BF01246666
49. Bawin M, Coon SA. The singular inverse square potential, limit cycles and selfadjoint extensions. Phys Rev A. (2003) 67:042712. doi: 10.1103/PhysRevA.67.042712
50. Braaten E, Phillips D. The renormalization group limit cycle for the 1/r2 potential. Phys Rev A. (2004) 70:052111. doi: 10.1103/PhysRevA.70.052111
51. Alberg M, Bawin M, Brau F. Renormalization of the singular attractive 1/r4 potential. Phys Rev A. (2005) 71:022108. doi: 10.1103/PhysRevA.71.022108
52. Hammer HW, Swingle BG. On the limit cycle for the 1/r2 potential in momentum space. Ann Phys. (2006) 321:306. doi: 10.1016/j.aop.2005.04.017
53. Bouaziz D, Bawin M. Singular inverse-square potential: renormalization and self-adjoint extensions for medium to weak coupling. Phys Rev A. (2014) 89:022113. doi: 10.1103/PhysRevA.89.022113
54. Odell D, Deltuva A, Bonilla J, Platter L. Renormalization of a finite range inverse cube potential. Phys Rev C. (2019) 100:054001. doi: 10.1103/PhysRevC.100.054001
55. Hammer HW, Platter L. Efimov physics from a renormalization group perspective. Phil Trans R Soc Lond A. (2011) 369:2679. doi: 10.1098/rsta.2011.0001
56. Bulycheva KM, Gorsky AS. Limit cycles in renormalization group dynamics. Phys Usp. (2014) 57:171. doi: 10.3367/UFNe.0184.201402g.0182
57. Efimov VN. Weakly-bound states of 3 resonantly-interacting particles. Sov J Nucl Phys. (1971) 12:589.
58. Efimov V. Energy levels arising form the resonant two-body forces in a three-body system. Phys Lett B. (1970) 33:563. doi: 10.1016/0370-2693(70)90349-7
59. Bedaque PF, Hammer HW, van Kolck U. Renormalization of the three-body system with short range interactions. Phys Rev Lett. (1999) 82:463. doi: 10.1103/PhysRevLett.82.463
60. Bedaque PF, Hammer HW, van Kolck U. The three boson system with short range interactions. Nucl Phys A. (1999) 646:444. doi: 10.1016/S0375-9474(98)00650-2
61. Braaten E, Hammer HW. Universality in few-body systems with large scattering length. Phys Rept. (2006) 428:259. doi: 10.1016/j.physrep.2006.03.001
62. Beane SR, Bedaque PF, Savage MJ, van Kolck U. Towards a perturbative theory of nuclear forces. Nucl Phys A. (2002) 700:377. doi: 10.1016/S0375-9474(01)01324-0
63. Pavón Valderrama M, Ruiz Arriola E. Renormalization of chiral two pion exchange NN interactions with Delta-excitations: correlations in the partial wave expansion. Phys Rev C. (2011) 83:044002. doi: 10.1103/PhysRevC.83.044002
64. Breit G. The scattering of slow neutrons by bound protons. 1. Methods of calculation. Phys Rev. (1947) 71:215. doi: 10.1103/PhysRev.71.215
65. Greene CH, Rau ARP, Fano U. General form of quantum-defect theory. II. Phys Rev A. (1982) 26:2441. doi: 10.1103/PhysRevA.26.2441
66. Behncke H. Some remarks on singular attractive potentials. Nuovo Cim A. (1968) 55:780. doi: 10.1007/BF02819574
67. Grießhammer HW. Assessing theory uncertainties in EFT power countings from residual cutoff dependence. PoS CD. (2016) 15:104. doi: 10.22323/1.253.0104
68. Long B, Yang CJ. Short-range nuclear forces in singlet channels. Phys Rev C. (2012) 86:024001. doi: 10.1103/PhysRevC.86.024001
69. Epelbaum E, Gegelia J. Regularization, renormalization and ‘peratization’ in effective field theory for two nucleons. Eur Phys J A. (2009) 41:341. doi: 10.1140/epja/i2009-10833-3
70. Feinberg G, Pais A. A field theory of weak interactions. I. Phys Rev. (1963) 131:2724. doi: 10.1103/PhysRev.131.2724
71. Feinberg G, Pais A. A field theory of weak interactions. II. Phys Rev. (1964) 133:B477. doi: 10.1103/PhysRev.133.B477
72. Phillips DR, Cohen TD. How short is too short? Constraining contact interactions in nucleon-nucleon scattering. Phys Lett B. (1997) 390:7. doi: 10.1016/S0370-2693(96)01411-6
73. Phillips DR, Beane SR, Cohen TD. Nonperturbative regularization and renormalization: simple examples from nonrelativistic quantum mechanics. Ann Phys. (1998) 263:255. doi: 10.1006/aphy.1997.5771
74. Beane SR, Cohen TD, Phillips DR. The potential of effective field theory in NN scattering. Nucl Phys A. (1998) 632:445. doi: 10.1016/S0375-9474(98)00007-4
75. Wigner EP. Lower limit for the energy derivative of the scattering phase shift. Phys Rev. (1955) 98:145. doi: 10.1103/PhysRev.98.145
76. Stetcu I, Rotureau J, Barrett BR, van Kolck U. An effective field theory approach to two trapped particles. Ann Phys. (2010) 325:1644. doi: 10.1016/j.aop.2010.02.008
77. Kaplan DB. More effective field theory for nonrelativistic scattering. Nucl Phys B. (1997) 494:471. doi: 10.1016/S0550-3213(97)00178-8
78. Epelbaum E, Gasparyan AM, Gegelia J, Meißner UG. How (not) to renormalize integral equations with singular potentials in effective field theory. Eur Phys J A. (2018) 54:186. doi: 10.1140/epja/i2018-12632-1
79. Pavón Valderrama M. Comment on “How (not) to renormalize integral equations with singular potentials in effective field theory”. Eur Phys J A. (2019) 55:55. doi: 10.1140/epja/i2019-12703-9
80. Epelbaum E, Gasparyan AM, Gegelia J, Meißner UG. Reply to Comment on “How (not) to renormalize integral equations with singular potentials in effective field theory”. Eur Phys J A. (2019) 55:56. doi: 10.1140/epja/i2019-12751-1
81. Bedaque PF, Hammer HW, van Kolck U. Effective theory of the triton. Nucl Phys A. (2000) 676:357. doi: 10.1016/S0375-9474(00)00205-0
82. König S, Grießhammer HW, Hammer HW, van Kolck U. Nuclear physics around the unitarity limit. Phys Rev Lett. (2017) 118:202501. doi: 10.1103/PhysRevLett.118.202501
83. Soto J, Tarrús J. Effective field theory with dibaryon degrees of freedom. Phys Rev C. (2008) 78:024003. doi: 10.1103/PhysRevC.78.024003
84. Stoks VGJ, Klomp RAM, Rentmeester MCM, de Swart JJ. Partial wave analysis of all nucleon-nucleon scattering data below 350-MeV. Phys Rev C. (1993) 48:792. doi: 10.1103/PhysRevC.48.792
85. Cohen TD, Hansen JM. The predictive power of effective field theory in NN scattering: 3S1-3D1 mixing at next-to-next-to leading order. nucl-th/9908049.
86. Kaplan DB. On the convergence of nuclear effective field theory with perturbative pions. arXiv. 1905.07485
87. Wu S, Long B. Perturbative NN scattering in chiral effective field theory. Phys Rev C. (2019) 99:024003. doi: 10.1103/PhysRevC.99.024003
88. The SAID Program at the George Washington University. Available online at: http://gwdac.phys.gwu.edu/
89. Birse MC. Deconstructing triplet nucleon-nucleon scattering. Phys Rev C. (2007) 76:034002. doi: 10.1103/PhysRevC.76.034002
90. Frederico T, Timóteo VS, Tomio L. Renormalization of the one pion exchange interaction. Nucl Phys A. (1999) 653:209. doi: 10.1016/S0375-9474(99)00234-1
91. Pavón Valderrama M, Ruiz Arriola E. Renormalization of the deuteron with one pion exchange. Phys Rev C. (2005) 72:054002. doi: 10.1103/PhysRevC.72.054002
92. Yang CJ, Elster C, Phillips DR. Subtractive renormalization of the NN scattering amplitude at leading order in chiral effective theory. Phys Rev C. (2008) 77:014002. doi: 10.1103/PhysRevC.77.014002
93. Song YH, Lazauskas R, van Kolck U. Triton binding energy and neutron-deuteron scattering up to next-to-leading order in chiral effective field theory. Phys Rev C. (2017) 96:024002. doi: 10.1103/PhysRevC.96.024002
94. Eiras D, Soto J. Renormalizing the Lippmann-Schwinger equation for the one pion exchange potential. Eur Phys J A. (2003) 17:89. doi: 10.1140/epja/i2002-10138-1
95. Epelbaum E, Meißner UG. On the renormalization of the one-pion exchange potential and the consistency of Weinberg's power counting. Few Body Syst. (2013) 54:2175. doi: 10.1007/s00601-012-0492-1
96. Pavón Valderrama M, Ruiz Arriola E. Renormalization of NN interaction with chiral two pion exchange potential. central phases and the deuteron. Phys Rev C. (2006) 74:054001. doi: 10.1103/PhysRevC.74.054001
97. Entem DR, Ruiz Arriola E, Pavón Valderrama M, Machleidt R. Renormalization of chiral two-pion exchange NN interactions. Momentum versus coordinate space. Phys Rev C. (2008) 77:044006. doi: 10.1103/PhysRevC.77.044006
98. Yang CJ, Elster C, Phillips DR. Subtractive renormalization of the chiral potentials up to next-to-next-to-leading order in higher NN partial waves. Phys Rev C. (2009) 80:034002. doi: 10.1103/PhysRevC.80.034002
99. Yang CJ, Elster C, Phillips DR. Subtractive renormalization of the NN interaction in chiral effective theory up to next-to-next-to-leading order: S waves. Phys Rev C. (2009) 80:044002. doi: 10.1103/PhysRevC.80.044002
100. Zeoli C, Machleidt R, Entem DR. Infinite-cutoff renormalization of the chiral nucleon-nucleon interaction at N3LO. Few Body Syst. (2013) 54:2191. doi: 10.1007/s00601-012-0481-4
101. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering, and neutron matter. Phys Rev Lett. (2016) 116:062501. doi: 10.1103/PhysRevLett.116.062501
102. Pavón Valderrama M, Sánchez Sánchez M, Yang CJ, Long B, Carbonell J, van Kolck U. Power counting in peripheral partial waves: the singlet channels. Phys Rev C. (2017) 95:054001. doi: 10.1103/PhysRevC.95.054001
103. Pavón Valderrama M, Ruiz Arriola E. Renormalization of singlet NN scattering with one pion exchange and boundary conditions. Phys Lett B. (2004) 580:149. doi: 10.1016/j.physletb.2003.11.037
104. Long B, Yang CJ. Renormalizing chiral nuclear forces: a case study of 3P0. Phys Rev C. (2011) 84:057001. doi: 10.1103/PhysRevC.84.057001
105. Long B, Yang CJ. Renormalizing chiral nuclear forces: triplet channels. Phys Rev C. (2012) 85:034002. doi: 10.1103/PhysRevC.85.034002
106. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys Rev C. (2017) 96:054007. doi: 10.1103/PhysRevC.96.054007
107. Tews I, Huth L, Schwenk A. Large-cutoff behavior of local chiral effective field theory interactions. Phys Rev C. (2018) 98:024001. doi: 10.1103/PhysRevC.98.024001
108. Pavón Valderrama M. Perturbative renormalizability of chiral two pion exchange in nucleon-nucleon scattering. Phys Rev C. (2011) 83:024003. doi: 10.1103/PhysRevC.83.024003
109. Pavón Valderrama M. Perturbative renormalizability of chiral two pion exchange in nucleon-nucleon scattering: P- and D-waves. Phys Rev C. (2011) 84:064002. doi: 10.1103/PhysRevC.84.064002
110. Kaiser N, Brockmann R, Weise W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl Phys A. (1997) 625:758. doi: 10.1016/S0375-9474(97)00586-1
111. Ballot JL, Robilotta MR, da Rocha CA. NN scattering: chiral predictions for asymptotic observables. Phys Rev C. (1998) 57:1574. doi: 10.1103/PhysRevC.57.1574
112. Kaiser N, Gerstendorfer S, Weise W. Peripheral NN scattering: role of delta excitation, correlated two pion and vector meson exchange. Nucl Phys A. (1998) 637:395. doi: 10.1016/S0375-9474(98)00234-6
113. Birse MC. Deconstructing 1S0 nucleon-nucleon scattering. Eur Phys J A. (2010) 46:231. doi: 10.1140/epja/i2010-11034-9
114. Long B. Improved convergence of chiral effective field theory for 1S0 of NN scattering. Phys Rev C. (2013) 88:014002. doi: 10.1103/PhysRevC.88.014002
115. Beane SR, Savage MJ. Rearranging pionless effective field theory. Nucl Phys A. (2001) 694:511. doi: 10.1016/S0375-9474(01)01088-0
116. Ando SI, Hyun CH. Effective range corrections from effective field theory with di-baryon fields and perturbative pions. Phys Rev C. (2012) 86:024002. doi: 10.1103/PhysRevC.86.024002
117. Sánchez Sánchez M, Yang CJ, Long B, van Kolck U. Two-nucleon 1S0 amplitude zero in chiral effective field theory. Phys Rev C. (2018) 97:024001. doi: 10.1103/PhysRevC.97.024001
118. Lutz M. Effective chiral theory of nucleon-nucleon scattering. Nucl Phys A. (2000) 677:241. doi: 10.1016/S0375-9474(00)00206-2
119. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high quality N N potential models. Phys Rev C. (1994) 49:2950. doi: 10.1103/PhysRevC.49.2950
120. Behrendt J, Epelbaum E, Gegelia J, Meißner UG, Nogga A. Two-nucleon scattering in a modified Weinberg approach with a symmetry-preserving regularization. Eur Phys J A. (2016) 52:296. doi: 10.1140/epja/i2016-16296-5
121. Ren XL, Li KW, Geng LS, Long BW, Ring P, Meng J. Leading order relativistic chiral nucleon-nucleon interaction. Chin Phys C. (2018) 42:014103. doi: 10.1088/1674-1137/42/1/014103
122. Ren XL, Li KW, Geng LS, Meng J. Relativistic chiral description of the 1S0 nucleon-nucleon scattering. arXiv. 1712.10083
123. Kievsky A, Viviani M, Gattobigio M, Girlanda L. Implications of Efimov physics for the description of three and four nucleons in chiral effective field theory. Phys Rev C. (2017) 95:024001. doi: 10.1103/PhysRevC.95.024001
124. Machleidt R, Liu P, Entem DR, Ruiz Arriola E. Renormalization of the leading-order chiral nucleon-nucleon interaction and bulk properties of nuclear matter. Phys Rev C. (2010) 81:024001. doi: 10.1103/PhysRevC.81.024001
125. Sammarruca F, Marcucci LE, Coraggio L, Holt JW, Itaco N, Machleidt R. Nuclear and neutron matter equations of state from high-quality potentials up to fifth order of the chiral expansion. arXiv. 1807.06640
126. Ekström A, Hagen G, Morris TD, Papenbrock T, Schwartz PD. Δ isobars and nuclear saturation. Phys Rev C. (2018) 97:024332. doi: 10.1103/PhysRevC.97.024332
127. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys Rev Lett. (2019) 122:042501. doi: 10.1103/PhysRevLett.122.042501
Keywords: effective field theory, renormalization, nuclear physics, singular potentials, pion exchange
Citation: van Kolck U (2020) The Problem of Renormalization of Chiral Nuclear Forces. Front. Phys. 8:79. doi: 10.3389/fphy.2020.00079
Received: 29 October 2019; Accepted: 06 March 2020;
Published: 05 May 2020.
Edited by:
Ruprecht Machleidt, University of Idaho, United StatesReviewed by:
Enrique Ruiz Arriola, University of Granada, SpainDaniel Phillips, Ohio University, United States
Copyright © 2020 van Kolck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: U. van Kolck, dmFua29sY2tAaXBuby5pbjJwMy5mcg==
 U. van Kolck
U. van Kolck