- 1Faculté des Sciences et Techniques, Abdelmalek Essaadi University, Tangier, Morocco
- 2Laboratoire de Physique Fondamentale et Appliquée–Safi, Faculté Polydisciplinaire de Safi, Safi, Morocco
- 3School of Physics and Astronomy, University of Southampton, Southampton, United Kingdom
We perform a comprehensive global analysis in the Minimal Supersymmetric Standard Model (MSSM) as well as in the 2-Higgs Doublet Model (2HDM) of the production and decay mechanisms of charged Higgs bosons (H±) at the Large Hadron Collider (LHC). We start from accounting for the most recent experimental results (SM-like Higgs boson signal strengths and search limits for new Higgs boson states obtained at Run-1 and -2 of the LHC and previous colliders), from (both direct and indirect) searches for supersymmetric particles as well as from flavor observables (from both e+e− factories and hadron colliders). We then present precise predictions for H± cross sections and decay rates in different reference scenarios of the two aforementioned models in terms of the parameter space currently available, specifically, mapped over the customary planes. These include the and hMSSM configurations of the MSSM and the 2HDM Type-I, -II, -X, and -Y for which we also enforce theoretical constraints, such as vacuum stability, perturbativity, and unitarity. We also define specific Benchmark Points (BPs) which are always close to (or coinciding with) the best fits of the theoretical scenarios to experimental data. We finally briefly discuss the ensuing phenomenology for the purpose of aiding future searches for such charged Higgs boson states.
1. Introduction
The Higgs boson discovery of 2012 [1–4] at the CERN Large Hadron Collider (LHC) has led to the confirmation of the Standard Model (SM) as the proper theory of the Electro-Weak (EW) scale. However, there is much evidence that the SM is not appropriate at all scales, rather it should be viewed as an effective low-energy realization of a more complete and fundamental theory on setting beyond the EW regime. Among the many proposals for the latter, one can list theories with some new symmetry, e.g., Supersymmetry (SUSY), or an enlarged particle content (e.g., in the Higgs sector), or both. Following the aforementioned discovery, no new particle has however been seen at the LHC, implying that new physics at the EW scale should be weakly interacting or that strongly interacting particles, if present, should lead to signatures involving soft decay products or in channels with overwhelming (ir)reducible backgrounds. We shall adopt here the first assumption.
Many SM extensions possess in their spectra additional neutral and/or charged Higgs states. Amongst these, SUSY [5] is indeed considered the most appealing one as it addresses several shortcomings of the SM, including the problem of the large hierarchy between the EW and Planck scales as well as the dark matter puzzle. While the search for SUSY was unsuccessful during the first LHC run, the increase in the Center-of-Mass (CM) energy of the machine from 8 to 13 TeV plus the additional luminosity of the second run are improving greatly the sensitivity to the new superparticles which are predicted. While the jury is still out on these, we remind here the reader that SUSY also requires at least two Higgs doublets for a successful EW Symmetry Breaking (EWSB) pattern. For exactly two such fields, yielding the so-called Minimal Supersymmetric Standard Model (MSSM), also having the same gauge group structure of the SM, one obtains four physical Higgs particles, in addition to the discovered SM-like one with the observed mass of 125 GeV. In fact, the same Higgs mass spectrum also belongs to a generic 2-Higgs Doublet Model (2HDM), i.e., one not originating from SUSY. In neither case, though, there exists a precise prediction of the typical masses of the new Higgs states, though we know already that the MSSM allows for one to be lighter than the 125 GeV state in a very small region of parameter space [6], whereas the 2HDM generally does so over a significantly larger expanse of it [7, 8]. Either way, the presence of extra physical Higgs boson states alongside the SM-like one is thus one of the characteristics of Beyond the SM (BSM) physics, whether within SUSY or otherwise. Hence, looking for these additional states in various production and decay channels over a wide range of kinematic regimes is an important part of the physics programme of the multi-purpose LHC experiments, ATLAS, and CMS. Specifically, the discovery of a (singly) charged Higgs boson would point to a likely additional Higgs doublet (or a Higgs field with higher representation, such as triplet). Hence, we concentrate on this Higgs state here.
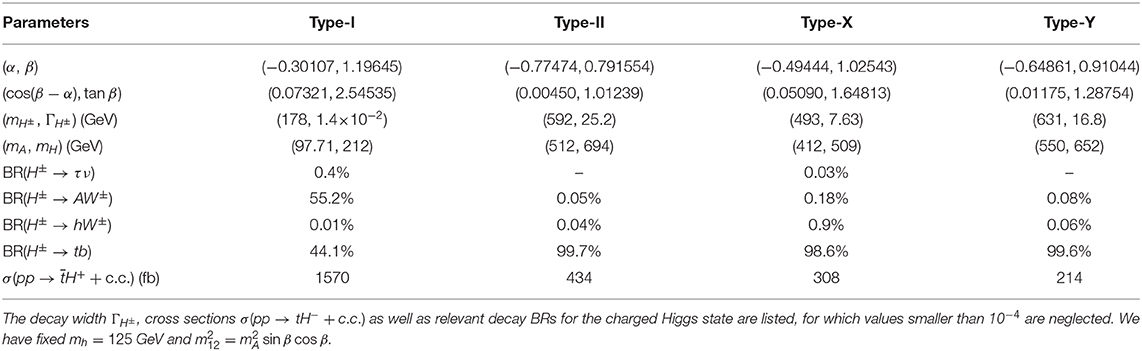
The two Higgs doublet fields pertaining to the MSSM are required to break the EW symmetry and to generate the isospin-up and -down type fermions as well as the W± and Z boson masses [9–11]. The Higgs spectrum herein is given by the following states: two charged H±'s, a CP-odd A and two CP-even Higgses h and H, with mh < mH (conventionally, wherein h is the SM-like Higgs state). The tree-level phenomenology of the Higgs sector of the MSSM is described entirely by two input parameters, one Higgs mass (that can be taken to be that of the CP-odd Higgs state, mA) and the ratio tan β of the Vacuum Expectation Values (VEVs) of the two Higgs doublet fields. Note that one of the most powerful prediction of SUSY is the existence of a light Higgs boson that could be produced at colliders. In the MSSM, at the tree-level, the light CP-even h is predicted to be lighter than the Z boson. However, it is well-known that loop effects could raise the h mass upper bound to 135 GeV for a large soft breaking trilinear parameter, At, and/or a heavy scalar top [12–22]. After the Higgs boson discovery at the LHC, MSSM benchmark scenarios have been refined to match the experimental data and to reveal characteristic features of certain regions of the parameter space [23–25]. Of the many MSSM frameworks presented in literature, we consider in this work the so-called [24] and hMSSM [26–30] ones, which will be described in the coming section. As for the 2HDM, one ought to specify the Yukawa sector, in order to proceed to study phenomenologically its manifestations. While SUSY enforces this in the form of a so-called Type-II, this is only one of four Ultra-Violet (UV) complete realizations of a generic 2HDM, the others been termed Type-I, -X, and -Y. The difference between these four scenarios is the way the fermionic masses are generated. We define as Type-I the model where only one doublet couples to all fermions, Type-II is the scenario where one doublet couples to up-type quarks and the other to down-type quarks and leptons, the Type-X is the model where one doublet couples to all quarks and the other to all leptons while a Type-Y is built such that one doublet couples to up-type quarks and to leptons and the other to down-type quarks. In all such cases, the number of free parameters at tree-level is seven to start with, hence it becomes more cumbersome than in SUSY to map experimental results onto theoretical constraints. Yet, in virtue of the fact that a 2HDM is the simplest realization of a BSM scenario based solely on doublet Higgs fields, its study is vigorously being pursued experimentally.
So far, the non-observation of any Higgs signal events in direct searches above and beyond those of the SM-like Higgs state constrains the parameter space of the underlying physics model. Specifically, in the case of the H± boson, wherein the relevant phenomenological parameters are and tan β in whatever scenario, one can pursue the study of its production and decay modes in a model independent way, which results can a posteriori be translated to exclude the relevant parameter space in a given scenario (whether it be the MSSM, 2HDM, or something else). This recasting is conveniently done on the (mA, tan β) and planes for the MSSM and 2HDM, respectively, so that we will map our findings in the same way.
At hadron colliders, there exists many production modes for charged Higgs bosons which are rather similar in the MSSM and 2HDM. For a light charged Higgs, i.e., with mass , its production comes mainly from top decay. At the LHC, the production of top quark pairs proceeds via Quantum Chromo-Dynamics (QCD) interactions and, when kinematically allowed, one top could decay into a charged Higgs state and a bottom quark in a competition with the SM decay into a W± boson and again a bottom quark. Therefore, the complete H± production mechanism provides the main source of light charged Higgs bosons at the LHC and offers a much more copious signature than any other form of direct production. After crossing the top-bottom threshold, i.e., when , a charged Higgs (pseudo)scalar can be produced through the process gb → tH− [31–34]. In fact, these two mechanisms can be simultaneously captured via the process [35, 36], which again makes it clear that one should expect large H± cross sections induced by QCD interactions also in the heavy H± mass range1.
In the MSSM, and also in a variety of 2HDM Types, light charged Higgs bosons would decay almost exclusively into a (hadronic or leptonic) τ lepton and its associated neutrino for tan β ≳ 1. When the top-bottom channel is kinematically open, then would compete with H± → hW±, HW±, AW± decays as well as various SUSY channels in the MSSM. In the latter, is the dominant channel and the bosonic decays H± → hW±, HW±, AW± (also yielding final states) are subleading. In the 2HDM, if none of these bosonic decays is open, then is the dominant mode. At the LHC Run-1, lighter charged Higgs bosons were probed in the decay channels τν [37, 38], cs [39, 40] and also cb [41]. No excess was observed and model independent limits are set on the following product of Branching Ratios (BRs): BR(t → H+b) × BR(H+ → τν). At Run-2, mainly the decay modes τν [42, 43] and tb [44] are explored in the mass range –1,000 GeV, in the latter mode using multi-jet final states with one electron or muon from the top quark decay. No significant excess above the background-only hypothesis has been observed and upper limits are set on the pp → tbH± production cross section times BR(H± → tb). Several interpretations of these limits have eventually been given in benchmark scenarios of the MSSM, including those mentioned above. Note that current ATLAS and CMS bounds are significantly weakened in the 2HDM once the exotic decay channels into a lighter neutral Higgs, e.g., H± → hW± or H± → AW±, are open. This scenario could also happen in the MSSM if one of the SUSY decay channels of charged Higgs bosons are open (such as into chargino-neutralino pairs). In the 2HDM, the possibility of producing a light charged Higgs boson from top decay with a subsequent step H± → hW± or H± → AW± was studied in Arhrib et al. [45] and it was shown that it can lead to sizable cross sections at low tan β. We stress here that there exist several recent analyses dedicated to 2HDM phenomenology [34, 46, 47] that we consulted. However, unlike Akeroyd et al. [34], Arbey et al. [46], and Bernon et al. [47] only concentrates on neutral Higgs phenomenology and discuss the charged Higgs contribution only to flavor physics observables without singling out the relevant charged Higgs production and decay channels at the LHC, which is indeed one of the aims of this analysis.
In this paper, we analyze the allowed rates by taking into account both theoretical and experiments constraints on the underlying BSM model, the latter including the latest ATLAS and CMS results for SM-Higgs (h) and other Higgs (H, A, H+) searches with the full set of 36.5 fb−1 data collected in the second LHC phase. We will then interpret these results under the proposed scenarios to quantify the magnitude of the available parameter space to be covered by future LHC analyses. In doing so, we will extract several Benchmarks Points (BPs) that could lead to detectable signals, all of which are consistent with the best fit regions in both the MSSM and 2HDM.
The paper is organized as follows. In the second section we review the MSSM and introduce the benchmark scenarios that we will discuss. The 2HDM, with its parameterizations and Yukawa textures, is described in the third section. The fourth section is devoted to a discussion of the theoretical and experimental constraints used in our study. Results and discussions for the MSSM and 2HDM are presented in the fifth section and we finish with our conclusions.
2. The MSSM
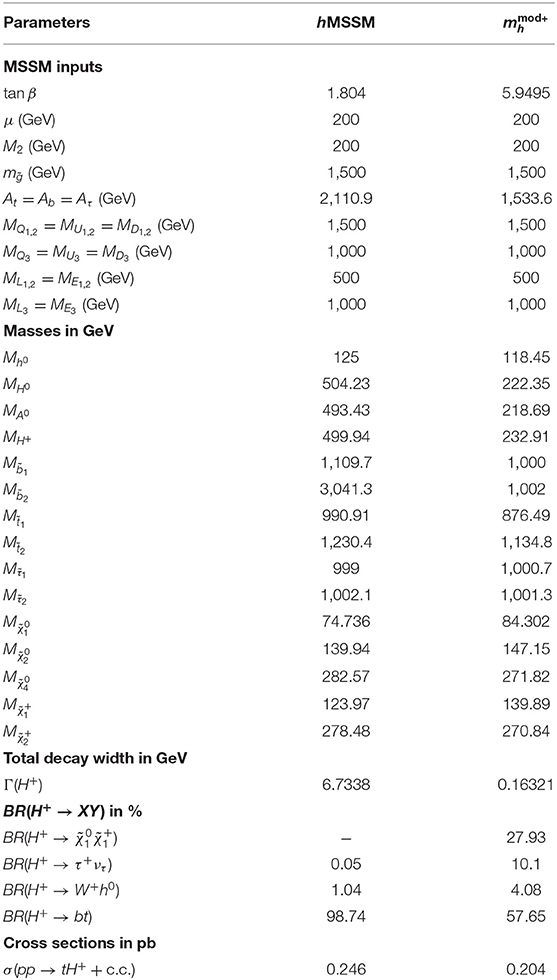
In the MSSM, due to the holomorphy of the superpotential, one introduce two Higgs doublets Φ1, 2 in order to give masses to up-type quarks as well as down-type quarks and leptons, respectively. Both Higgs fields acquire VEVs, denoted by v1, 2. After EWSB takes place, the spectrum of the model contains the aforementioned Higgs states: h, H, A and H±. The MSSM Higgs sector is parameterized at tree-level by tan β = v2/v1, and e.g., the CP-odd mass mA. One of the interesting features of the MSSM is the prediction, at the tree-level, of a light CP-even Higgs h with a mass mh ≤ mZ. However, such tree-level prediction is strongly modified by radiative corrections at one- and two-loop level [12–21]. It has been shown in Degrassi et al. [22], on the one hand, that the loop effects can make the light CP-even mass mh reach a value of 135 GeV and, on the other hand, that the theoretical uncertainties due to unknown high order effects can be of the order of 3 GeV. In fact, these large loop effects are welcome in order to shift the light CP-even Higgs mass to the measured experimental value mh ≈ 125 GeV. Note also that the loop effects will modify not only the tree-level Higgs mass relations but also the Higgs self-couplings and the Higgs coupling to SUSY particles. Therefore, beside the tree-level parameters tan β and mA, the top quark mass and the associated squark masses and their soft SUSY breaking parameters enter through radiative corrections [12–21, 48, 49]. In fact, when trying to push the light CP-even mass from mZ to 125 GeV through loop effects, one needs to introduce a large SUSY scale with large soft trilinear parameter At. Such a large SUSY scale puts automatically the SUSY spectrum at the TeV scale, which is consistent with negative searches for SUSY particles at the LHC.
To compute the masses and couplings of Higgs bosons in a given point of the MSSM parameter space we use the code FeynHiggs [50, 51] for the scenario and the program HDECAY for the hMSSM case [52, 53]. Both codes include the full one-loop and a large part of the dominant two-loop corrections to the neutral Higgs masses. Since the theoretical uncertainty on the Higgs mass calculation in the FeynHiggs code has been estimated to be of the order of 3 GeV, we consider as phenomenologically acceptable the points in the MSSM parameter space where FeynHiggs predicts the existence of a scalar state with mass between 122.5 and 128.5 GeV and with approximately SM-like couplings to gauge bosons and fermions. In addition to the tree-level scalar potential parameters, tan β and mA, when taking into account high order corrections, the MSSM parameters most relevant to the prediction of the masses and production cross sections of the Higgs bosons are: the soft SUSY-breaking masses for the stop and sbottom squarks, which, for simplicity, we assume all equal to a common mass parameter MSUSY, the soft SUSY-breaking gluino mass , the soft SUSY-breaking Higgs-squark-squark couplings At and Ab, the superpotential Higgs(ino)-mass parameter μ and the left-right mixing terms in the stop and sbottom mass matrices (divided by mt and mb)
respectively. Since the (approximate) two-loop calculation of the Higgs masses implemented in FeynHiggs and the Next-to-Leading Order (NLO) calculation of QCD corrections to the production cross section implemented in SusHi [54, 55] employ the same renormalization (on-shell) scheme, the input values of the soft SUSY-breaking parameters can be passed seamlessly from the Higgs mass to the cross section calculations.
In the light of the latest LHC data on the discovered Higgs-like boson, and given the fact that the MSSM contains many independent parameters which makes it a fastidious task to perform a full scan, there have been many studies which lead to several benchmarks that could fit the observed Higgs boson as well as be tested at the future LHC with higher luminosity [24, 26–29]. As intimated already, in this study, we will concentrate on two of these benchmark scenarios: the and hMSSM ones, which we will describe hereafter.
2.1. The Scenario
The scenario is a modification of the time-honored scenario (also called maximal mixing scenario), which was originally defined to give conservative exclusion bounds on tan β in the context of Higgs boson searches at LEP [56]. The scenario was introduced in order to maximize the value of mh by incorporating large radiative correction effects for a large mA >> mZ mass, fixed value of tan β > 8 and large SUSY scale of the order 1 TeV. However, this scenario predicts mh to be much higher than the observed Higgs boson mass, due to the large mixing in the scalar top sector.
Hence, the maximal mixing scenario has been modified, by reducing the amount of scalar top mixing, such that the mass of the lightest Higgs state, mh, is compatible with the mass of the observed Higgs boson within ±3 GeV in a large fraction of the considered parameter space. In fact, modifications of the scenario can be done in two ways depending on the sign of (At − μ cot β)/MSUSY, leading to an and [24]. It has been demonstrated in Carena et al. [24] that when is confronted with LHC data, there is a substantial region in the plane (mA, tan β) with tan β > 7 for which the light CP-even Higgs mass is in a good agreement with the measured one at the LHC, hence our choice of this scenario.
The SUSY input parameters in this scenario are fixed as2
where MSUSY is the aforementioned SUSY mass scale.
2.2. The hMSSM Scenario
In the previous scenario, one need to input tan β, mA and also the other SUSY parameters to get the Higgs and SUSY (mass and coupling) spectrum. Taking into account the theoretical uncertainty of the order 3 GeV on the Higgs mass, which could originate from unknown high order loop effects, a light CP-even Higgs boson with a mass in the range [122, 128] GeV would be an MSSM candidate for the observed Higgs-like particle. However, plenty of points on the (mA, tan β) plane would correspond to one configuration of mh mass. To avoid this situation, the hMSSM benchmark was introduced [26–29]. In this scenario, the light CP-even Higgs state is enforced to be ~125 GeV while setting the SUSY mass scale MSUSY to be rather high (i.e., > 1 TeV) in order to explain the non-observation of any SUSY particle at colliders. The hMSSM setup thus describes the MSSM Higgs sector in terms of just mA and tan β, exactly like for tree-level predictions, given the experimental knowledge of mZ and mh. In this scenario, therefore, the dominant radiative corrections would be fixed by the measured experimental value of mh which in turn fixes the SUSY scale [26–29]. It defines a largely model-independent scenario, because the predictions of the properties of the MSSM Higgs bosons do not depend on the details of the SUSY sector, somewhat unlike the previous case, wherein squark masses are fine-tuned to obtain mh ≈ 125 GeV.
The SUSY input parameters in this scenario are similar to the previous one, Equation (2), except that we take Xt = 2MSUSY = 2 TeV.
2.3. Setup
Both scenarios introduced above are characterized by relatively large values of the ratio Xt/MSUSY, ensuring that the MSSM mass of the SM-like Higgs state falls within the required range without the need for an extremely heavy stop. In addition, the masses of the gluino and first two generation squarks are set to 1.5 TeV, large enough to evade the current ATLAS and CMS limits stemming from SUSY searches [57–61]. We vary the parameters tan β and mA within the following ranges:
The soft trilinear term At is set to be equal to Ab. Due to the smallness of the light quarks masses, the left-right mixing of the first two generation squarks is neglected. The gaugino mass parameters M1, M2 and the soft SUSY-breaking gluino mass are all related through Renormalization Group Equation (RGE) running to some common high scale m1/2 soft term which yields the relations and M1 ≈ 0.5M2. In our analysis, we assume Grand Unified Theory (GUT) relations only between M1 and M2 while M2 and are taken independent from each other. Finally, the soft SUSY-breaking parameters in the slepton sector have a very small impact on the predictions for the Higgs masses and production cross sections, therefore we do not report on them here.
3. The 2HDM
In this section, we define the scalar potential and the Yukawa sector of the general 2HDM. The most general scalar potential which is SU(2)L⊗U(1)Y invariant is given by [62, 63]
The complex (pseudo)scalar doublets Φi (i = 1, 2) can be parameterized as
with v1, 2 ≥ 0 being the VEVs satisfying , with v = 246.22 GeV. Hermiticity of the potential forces λ1, 2, 3, 4 to be real while λ5 and can be complex. In this work we choose to work in a CP-conserving potential where both VEVs are real and so are also λ5 and .
After EWSB, three of the eight degrees of freedom in the Higgs sector of the 2HDM are eaten by the Goldstone bosons (G± and G) to give masses to the longitudinal gauge bosons (W± and Z). The remaining five degrees of freedom become the aforementioned physical Higgs bosons. After using the minimization conditions for the potential together with the W± boson mass requirement, we end up with seven independent parameters which will be taken as
where, as usual, tan β ≡ v2/v1 and β is also the angle that diagonalizes the mass matrices of both the CP-odd and charged Higgs sector while the angle α does so in the CP-even Higgs sector.
The most commonly used versions of a CP-conserving 2HDM are the ones that satisfy a discrete Z2 symmetry (i = 1, 2), that, when extended to the Yukawa sector, guarantees the absence of Flavor Changing Neutral Currents (FCNCs). Such a symmetry would also require , unless we tolerate a soft violation of this by the dimension two term (as we do here).
The Yukawa Lagrangian can then be written as
where and are the left-handed quark doublet and lepton doublet, respectively, the 's (k = 1, 2 and f = u, d, l) denote the 3 × 3 Yukawa matrices and (k = 1, 2). The mass matrices of the quarks and leptons are a linear combination of and , and . Since they cannot be diagonalized simultaneously in general, neutral Higgs Yukawa couplings with flavor violation appear at tree-level and contribute significantly to FCNC processes, such as ΔMK, B, D as well as mediated by neutral Higgs exchanges. To avoid having those large FCNC processes, one known solution is to extend the Z2 symmetry to the Yukawa sector. When doing so, we ended up with the already discussed four possibilities regarding the Higgs bosons couplings to fermions [63].
After EWSB, the Yukawa Lagrangian can be expressed in the mass eigenstate basis as follows [64, 65]:
We give in Table 1 the values of the Yukawa couplings (ϕ = h, H, A), i.e., the Higgs boson interactions normalized to the SM vertices introduced in David et al. [66], in the four 2HDM Types. The couplings of h and H to gauge bosons W±, Z are proportional to sin(β − α) and cos(β − α), respectively. Since these are gauge couplings, they are the same for all Yukawa types. As we are considering the scenario where the lightest neutral Higgs state is the 125 GeV scalar, the SM-like Higgs boson h is recovered when cos(β − α) ≈ 0. As one can see from Table 1, for all 2HDM Types, this is also the limit where the Yukawa couplings of the discovered Higgs boson become SM-like. The limit cos(β − α) ≈ 0 seems to be favored by LHC data, except for the possibility of a wrong sign limit [67, 68], where the couplings to down-type quarks can have a relative sign to the gauge bosons ones, thus oppositely to those of the SM. Our benchmarks will focus on the SM-like limit where indeed cos(β−α) ≈ 0.
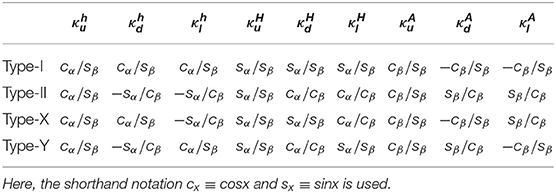
Table 1. Yukawa couplings in terms of the standard κ coefficients, in turn expressed as function of the angles α and β, in the four 2HDM Types.
We end this section by noticing that we have used the public program 2HDMC [69] to evaluate the 2HDM spectrum as well as the decay rates and BRs of all Higgs particles. We have used 2HDMC to also enforce the aforementioned theoretical constraints onto both BSM scenarios considered here.
4. Theoretical and Experimental Constraints
In order to perform a systematic scan over the parameter space of the two MSSM configurations and the four 2HDM Types, we take into account the following theoretical3 and experimental constraints.
4.1. Theoretical Constraints
We list these here as itemized entries.
• Vacuum stability: To ensure that the scalar potential is bounded from below, it is enough to assume that the quartic couplings should satisfy the following relations [70]:
We also impose that the potential has a minimum that is compatible with EWSB. If this minimum is CP-conserving, any other possible charged or CP-violating stationary points will be a saddle point above the minimum [71]. However, there is still the possibility of having two coexisting CP-conserving minima. In order to force the minimum compatible with EWSB, one need to impose the following simple condition [72]:
Writing the minimum conditions as
allows us to express and in terms of the soft Z2 breaking term and the quartic couplings λ1−5.
• Perturbative unitarity: Another important theoretical constraint on the (pseudo)scalar sector of the 2HDM is the perturbative unitarity requirement. We require that the S-wave component of the various (pseudo)scalar scattering amplitudes of Goldstone and Higgs states remains unitary. Such a condition implies a set of constraints that have to be fulfilled and are given by [73, 74]
where
• EW precision observables (EWPOs): The additional neutral and charged (pseudo)scalars, beyond the SM-like Higgs state, contribute to the gauge bosons vacuum polarization through their coupling to gauge bosons. In particular, the universal parameters S, T, and U provide constraints on the mass splitting between the heavy states mH, , and mA in the scenario in which h is identified with the SM-like Higgs state. The general expressions for the parameters S, T, and U in 2HDMs can be found in Kanemura et al. [75]. To derive constraints on the scalar spectrum we consider the following values for S, T, and U:
while using the corresponding covariance matrix given in Baak et al. [76]. The χ2 function is then expressed as
with correlation factor +0.91.
The aforementioned 2HDMC program allows us to check most of the above theoretical constraints, such as perturbative unitarity, boundedness from below of the scalar potential as well as EWPOs (S, T, and U), which are all turned on during the calculation, and can be adapted to the MSSM as well.
4.2. Experimental Constraints
The parameter space of our benchmark scenarios is already partially constrained by the limits obtained from various searches for additional Higgs bosons at the LHC and elsewhere as well as the requirement that one of the neutral scalar states should match the properties of the observed SM-like Higgs boson. We evaluate the former constraints with the code HiggsBounds [77–80] and the latter with the code HiggsSignals [81]. We stress, however, that our study of the existing constraints cannot truly replace a dedicated analysis of the proposed benchmark scenarios by ATLAS and CMS, which alone would be able to combine the results of different searches taking into account all correlations. In this section we briefly summarize the relevant features of HiggsBounds and HiggsSignals used in our study.
4.2.1. Collider Constraints
The code HiggsBounds tests each parameter point for 95% Confidence Level (CL) exclusion from Higgs searches at the LHC as well as LEP and Tevatron. First, the code determines the most sensitive experimental search available, as judged by the expected limit, for each additional Higgs boson in the model. Then, only the selected channels are applied to the model, i.e., the predicted signal rate for the most sensitive search of each additional Higgs boson is compared to the observed upper limit. In the case the prediction exceeds the limit, the parameter point is regarded as excluded. For more details on the procedure, the reader can see Bechtle et al. [80].
Among the searches that are relevant in constraining our scenarios for charged Higgs studies, the version we have used, 5.2.0beta, of HiggsBounds includes the following.
• ATLAS [82] and CMS [83] searches for heavy Higgs bosons decaying to τ+τ− pairs using about 36fb−1 of Run-2 data as well as the CMS results from Run-1 [84].
• Searches at Run-1 and Run-2 by ATLAS [85, 86] and CMS [40, 87] for a heavy scalar decaying to a Z boson pair, H → ZZ.
• Searches at Run-1 and Run-2 by ATLAS [88] and CMS [89, 90] for a heavy scalar decaying to a pair of 125 GeV SM-like Higgs scalars, H → hh.
• Searches at Run-1 by ATLAS [91] and CMS [92] for the 125 GeV scalar decaying to a pair of lighter pseudoscalars, h → AA.
• Searches at Run-1 by ATLAS [93] and CMS [94] for a heavy pseudoscalar decaying to a Z boson and the 125 GeV scalar, A → Zh.
By comparing these results with the predictions of SusHi, FeynHiggs, and 2HDMC for the production cross sections and decay BRs of the additional neutral Higgs bosons, HiggsBounds reconstructs the 95% CL exclusion contours for our benchmark scenarios. In the MSSM and 2HDM Type II, these constraints are typically stronger for large values of tan β, due to an enhancement of the production cross section of the heavier Higgs bosons in bottom-quark annihilation (in that case the most relevant searches are those for the decay to a τ+τ− pair). However, this is not generally true in the other 2HDM Types. HiggsBounds also contains the available constraints from searches for a charged Higgs boson by ATLAS and CMS. Most relevant in our scenarios are the constraints on the production of a light charged Higgs via top quark decay, t → H+b, with subsequent decay H+ → τ+ν [37, 38, 43, 95], as well as top-quark associated H± production, with subsequent decays to the τν [37, 38, 43, 95] and/or tb [38, 44, 96] channels.
In order to estimate the theoretical uncertainty in our determination of the excluded regions, we rely on the uncertainty estimates for the gluon-fusion and bottom-quark annihilation cross sections. The most conservative (i.e., weakest) determination of the exclusion region is obtained by taking simultaneously the lowest values in the uncertainty range for both production processes of each of the heavier Higgs bosons, while the least conservative (i.e., strongest) determination is obtained by taking simultaneously the highest values in the uncertainty range.
With the use of the code HiggsSignals, we test the compatibility of our scenarios with the observed SM-like Higgs signals, by comparing the predictions of SusHi, FeynHiggs, and 2HDMC for the signal strengths of Higgs production and decay in a variety of channels against ATLAS and CMS measurements. The version we have used, 2.2.0beta, of HiggsSignals includes all the combined ATLAS and CMS results from Run-1 of the LHC [97] as well as all the available ATLAS [98–104] and CMS limits from Run-2 [105–113].
4.2.2. DM Constraints
These have naturally been enforced only in the MSSM case, by using the program micrOMEGAs version 5.0.9 [114]4. Such a code calculates the properties of DM in terms of its relic density as well as its direct and indirect detection rates. For the two MSSM scenarios considered here, the DM candidate, i.e., the Lightest Supersymmetric Particle (LSP), is the lightest neutralino. We require that the outcome of the calculation of the relic density should be in agreement with the latest Planck measurement [115].
5. Numerical Results
In this section, we present our findings for the MSSM and 2HDM in turn.
5.1. MSSM Results
In the hMSSM scenario, all superparticles are chosen to be rather heavy so that production and decays of the MSSM Higgs bosons are only mildly affected by their presence due to the decoupling properties of SUSY. In particular, the loop-induced SUSY contributions to the couplings of the light CP-even scalars are small and the heavy Higgs bosons with the masses even up to 2 TeV decay only to SM particles. Therefore, the phenomenology of this scenario at the LHC resembles that of a 2HDM Type-II with MSSM-inspired Higgs couplings and mass relations.
The masses of the third generation squarks and that of the gluino are safely above the current bounds from direct searches at the LHC, as intimated. Specifically, we refer to CMS Collaboration [116, 117], ATLAS Collaboration [118–120], CMS Collaboration [121–123] for the scalar top quarks, CMS Collaboration [116, 117] and ATLAS Collaboration [116, 117, 124–126] for the scalar bottom quarks and CMS Collaboration [117], ATLAS Collaboration [125, 127, 128], and CMS Collaboration [129] for the gluino. The value chosen for Xt is close to the one for which the maximal value of mh is obtained. The scenario is very similar to the hMSSM one except the fact that we take Xt = 2MSUSY = 1 TeV.
In Figure 1 the allowed regions on the (mA, tan β) plane are depicted for various Δχ2, wherein the left and right panel are, respectively, for the hMSSM and scenarios. For the hMSSM and Δχ2 ≤ 12, one can see that mA should be heavier than about 400 GeV. In the case of mA ≈ 400 − 600 GeV, tan β should be in the range [1, 9] while for mA around 1 TeV tan β is in the range [1, 15]. The dashed (solid) line represents the 95% (68%) CL obtained by the HiggsSignals fit and the best fit point is located at mA ≈ 1 TeV and tan β ≈ 2. For the scenario, the situation is quite different. In order to accommodate mh ≈ 125 GeV, one needs tan β>10. Similarly to the left panel, also in the right one the dashed(solid) line represents the 95% (68%) CL obtained by the HiggsSignals fit and the best fit point is located at mA ≈ 1 TeV and tan β ≈ 20. For this scenario and for Δχ2 <12, all tan β ≤ 10 are excluded. Note that after imposing DM constraints onto the best fit analysis, we observe that the best fit points for both the hMSSM and scenarios move to somewhat lighter values of the charged Higgs boson mass. The BPs given in Table 2 account for this effect.
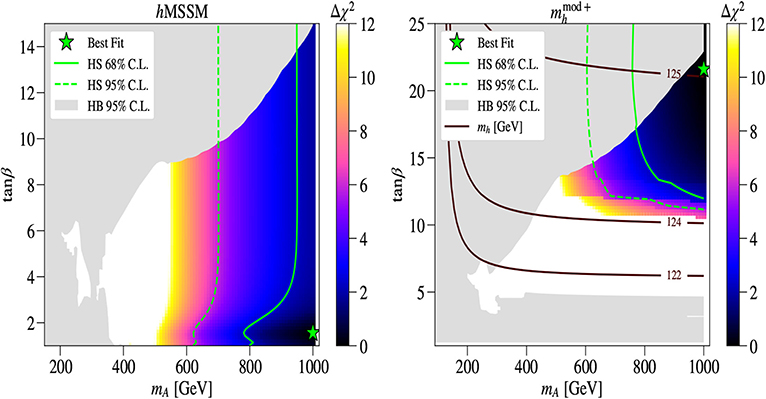
Figure 1. The allowed regions on the (mA, tan β) plane in hMSSM (left) and (right). The cyan lines in the right plot are level curves for the SM-like Higgs mass. By definition, in the hMSSM, mh is fixed at 125 GeV. The best fit points are marked by green stars.
In Figure 2 we present the total width of the charged Higgs boson, again, over the (mA, tan β) plane, for both hMSSM (left) and (right). As one can see from the left panel, the total width for the hMSSM case is largest for tan β ≤ 3, which is when GeV, while for tan β ≥ 5 the width drops to 1–3 GeV. This effect can be attributed to the fact that the total width is fully dominated by , whenever this channel is open, in which the top effect is more pronounced for low tan β. In this case, H+ → τν is subleading and also the decay modes are suppressed. In the case of , since small tan β is not allowed, the total charged Higgs boson width is generally smaller than in the hMSSM case, as a consequence of the fact that is therefore smaller in this scenario. The maximal total width is here obtained for mA ≈ 1 TeV and a large tan β ≈ 20. In the scenario, the decay could have a significant BR, reaching 30%. Hence, the H± is always rather narrow, whichever its mass. In fact, owing to the degeneracy between mA and in the MSSM, as dictated by h data, a remarkable result is that in the minimal SUSY scenario a charged Higgs boson is essentially always heavier than the top quark.
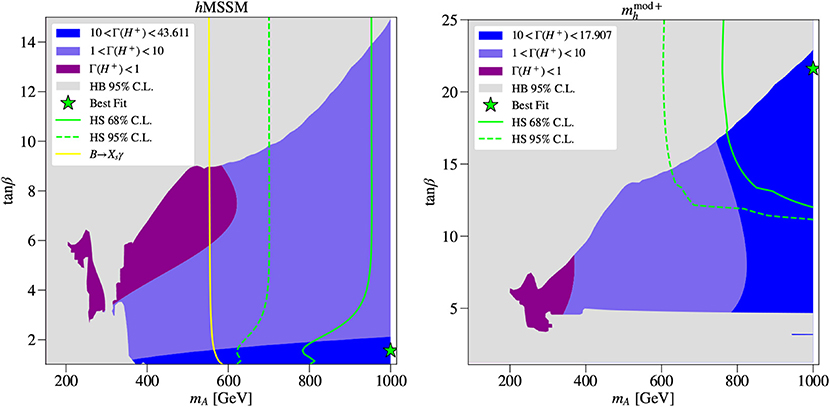
Figure 2. Total charged Higgs boson width (in GeV) mapped on the (mA, tan β) plane in hMSSM (left) and (right). The units of in the legends are intended in GeV. The best fit points are marked by green stars.
In Figure 3 we show the production cross section for single charged Higgs boson production in association with a top quark (as appropriate for the case) times the BR of H+ into a specific final state for both the hMSSM and scenarios using Prospino [130–132]. In fact, as we have seen previously, the total width of the charged Higgs state is rather small in both cases, in relation to the mass, so that one can use the Narrow Width Approximation (NWA) to estimate such a cross section (which we have done here). In the top-left(top-right) panel of Figure 3, we show the size of the cross section of σ(pp → tH− + c.c.) × BR(H± → tb)(σ(pp → tH− + c.c.) × BR(H± → τν)), given in pb.

Figure 3. The σ(pp → tH− + c.c.) × BR(H± → XY) rate (in pb) at =14 TeV in the hMSSM scenario, for XY ≡ tb (top left), XY ≡ τν (top right), XY ≡ AW± (bottom left), and XY ≡ hW± (bottom right). Notice that c.c. channels are included. The best fit points are marked by green stars.
For the hMSSM scenario, one can see that in the tb channel the largest cross section (more than 0.1 pb) is reached for small tan β < 3. There is also a wide region with GeV and tan β < 10 where the cross section is still rather important: between 10−3 and 0.1 pb. As for the τν channel, the cross section is maximized when tan β is in the range [4, 9] and the largest cross section is seen around 10−3 pb. However, amongst the bosonic channels, H± → W±A is hopeless because BR(H± → W±A) is very suppressed while H± → W±h can have a rate that is close to 10−2 pb for small tan β ≈ 1. Note that, for completeness, we have also drawn the exclusion region due to BR, even though we can always assume some kind of flavor violation that takes place in the MSSM and can bring the BR() to a correct value. In terms of σ(pp → tH− + c.c.) × BR(H± → XY) for the scenario, the situation is worse. The best channels are and with the maximum cross section in the allowed region being between 10−3 and 10−2 pb for charged Higgs boson masses in the range 400–600 GeV, as can be seen from Figure 4.
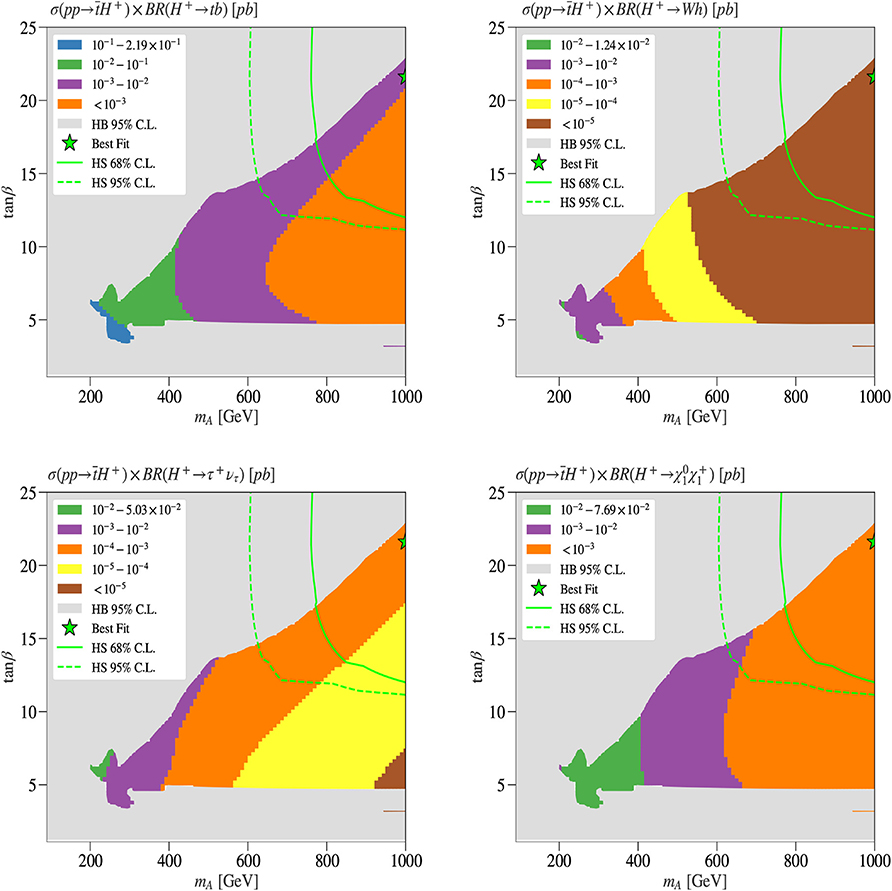
Figure 4. The σ(pp → tH− + c.c.) × BR(H± → XY) rate (in pb) at =14 TeV in the scenario, for XY ≡ tb (top left), XY ≡ W±h (top right), XY ≡ τν (bottom left), and (bottom right). Notice that c.c. channels are included. The best fit points are marked by green stars.
We conclude this section by presenting in Table 2 two BPs, one each for the and hMSSM scenarios, to aid future analyses of Run-2 (and possibly Run-3) data from the LHC. Notice that these BPs do not correspond to the best fit points in these two MSSM configurations, as the latter would yield too small cross sections5, owing to the very large charged Higgs mass involved (of order 1 TeV). Yet, the BPs presented correspond to rather large values of , as dictated by the compatibility tests of the and hMSSM scenarios with current datasets, still giving production and decay rates (in one or more channels) potentially testable in the near future.
5.2. 2HDM Results
We now move on to discuss the 2HDM. In this scenario, we consider h as being again the 125 GeV SM-like Higgs and vary the other six parameters as indicated in Table 3. When performing the scan over the 2HDM parameter space, other than taking into account the usual LHC, Tevatron and LEP bounds (as implemented in HiggsBounds and HiggsSignals) as well as the theoretical ones (as implemented in 2HDMC), we also have to consider flavor observables. In fact, unlike the MSSM, where potentially significant contributions to (especially) B-physics due to the additional Higgs states entering the 2HDM beyond the SM-like one can be canceled by the corresponding sparticle effects (and besides, are generally small because of the rather heavy H, A, and H± masses), the 2HDM has to be tested against a variety of such data. The B-physics observables that we have considered to that effect are listed in Table 4. We have computed the 2HDM predictions for these in all 2HDM Types using our own implementation, which output in fact agrees with the one from SuperIso [137] (when run in 2HDM mode).

Table 4. Experimental results of flavor observables combined by the PDG and/or HFAG collaborations in Amhis et al. [134] and Olive et al. [135].
Based on such constrained scans, we first illustrate in Figure 5, on the (cos(β−α), tan β) plane, the best fit points for the four 2HDM Types. Herein, are also shown the compatibility regions with the observed Higgs signal at the 1σ (green) and 2σ (yellow) level. The details of the best fit points herein (red stars) are given in Table 5 together with the values of the following observables: the total charged Higgs width , σ(pp → tH− + c.c.), BR(H± → τν), BR(H± → tb), BR(H± → AW±), and BR(H± → hW±). Note that in the 2HDM Type-II and -Y, the best fit point is located at a charged Higgs mass around 600 GeV because of the constraints while in the 2HDM Type-I and- X one can fit data with a rather light charged Higgs state.
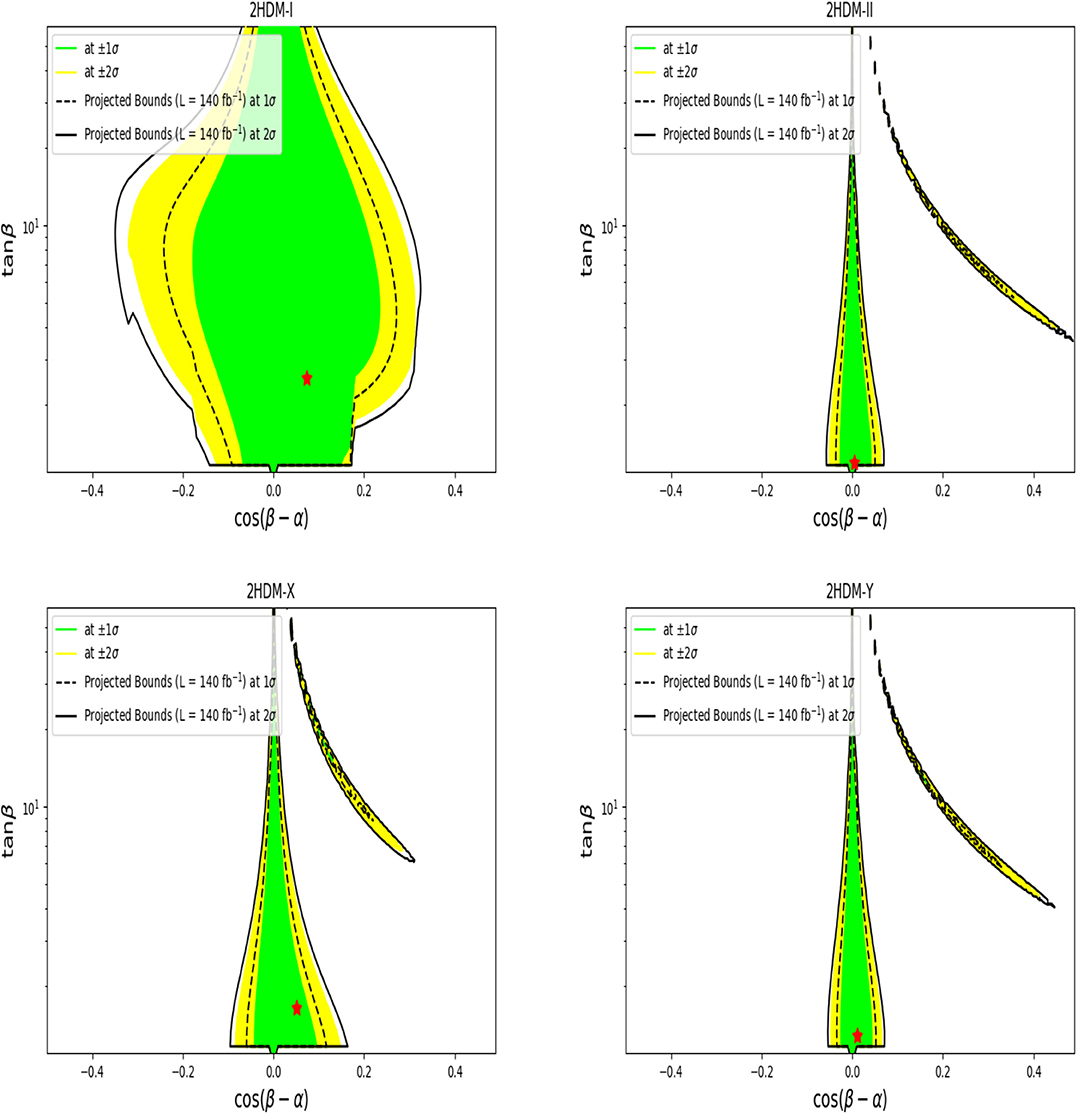
Figure 5. Direct constraints from null heavy Higgs searches at the LHC on the parameter space of the 2HDM Type-I (top left), Type-II (top right), Type-X (bottom left), and Type-Y (bottom right) mapped on the (α, β) plane. The colors indicate compatibility with the observed Higgs signal at 1σ (green), 2σ (yellow) around the best fit points (red stars).
In Figures 6–9, we show (in gray) over the (, tan β) plane the 95% CL exclusion region from the non-observation of the additional Higgs states for 2HDM Type-I(-II)[-X]{-Y}. In all these plots, we also draw (as a solid yellow line) the 95% CL exclusion from together with a solid green line representing the 1σ compatibility with the Higgs signals observed at the LHC. As a green star, we also give the best fit point to these data over the available parameter space for all Types (these are the same as the red stars in the previous figure). It is clear from these plots that, in the 2HDM-I and -X, one can still have relatively light charged Higgs states (of the order 100–200 GeV in mass) that are consistent with all aforementioned data, crucially including B-physics observables. In addition, such light charged Higgs does not affect too much the rate of h → γγ which is strongly dominated by the W± loops while the charged Higgs loops are subleading. In the case of the 2HDM Type-II and -Y, the ) constraint pushes the charged Higgs boson mass to be higher than 580 GeV. (Note that, in the 2HDM Type-II, it is clear that, like for the MSSM case, large tan β is excluded mainly from H, A → τ+τ− as well as from H+ → τν searches at the LHC). However, for 2HDM Type-X, one can see that light charged Higgs states, with ≤ 170 GeV, are excluded for all tan β's and this is due to charged Higgs searches failing to detect H± → τν.
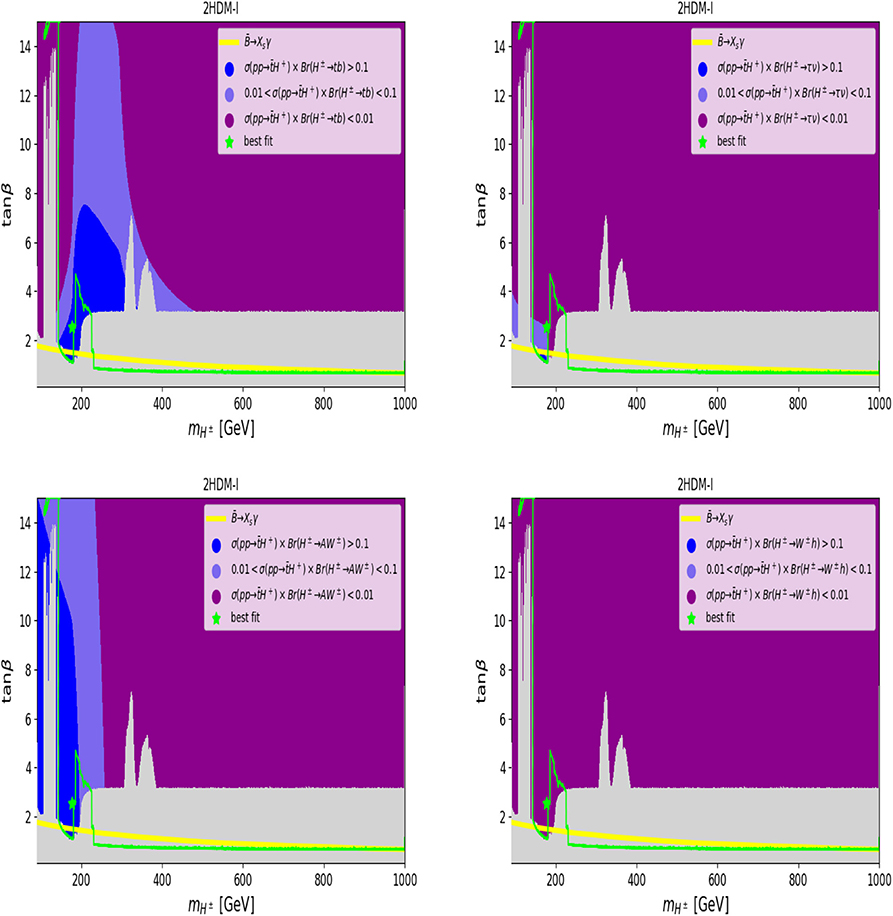
Figure 6. The σ(pp → tH−+c.c.) × BR(H± → XY) rate (in pb) at =14 TeV in the 2HDM Type-I, for XY ≡ tb (top left), XY ≡ τν (top right), XY ≡ AW± (bottom left), and XY ≡ hW± (bottom right). Exclusion bounds at 95% CL from the non-observation of the additional Higgs states are overlaid in gray. The green contour indicates compatibility with the observed Higgs signal at 68% CL and the best fit (benchmark) points are marked by green stars. The solid yellow line contours are the boundary of 95% CL exclusion from measurements. The maximum of the cross section σ(pp → tH−+c.c.) × BR(H± → XY) is 3.1 and 1.83 pb for XY ≡ AW±, tb, respectively.
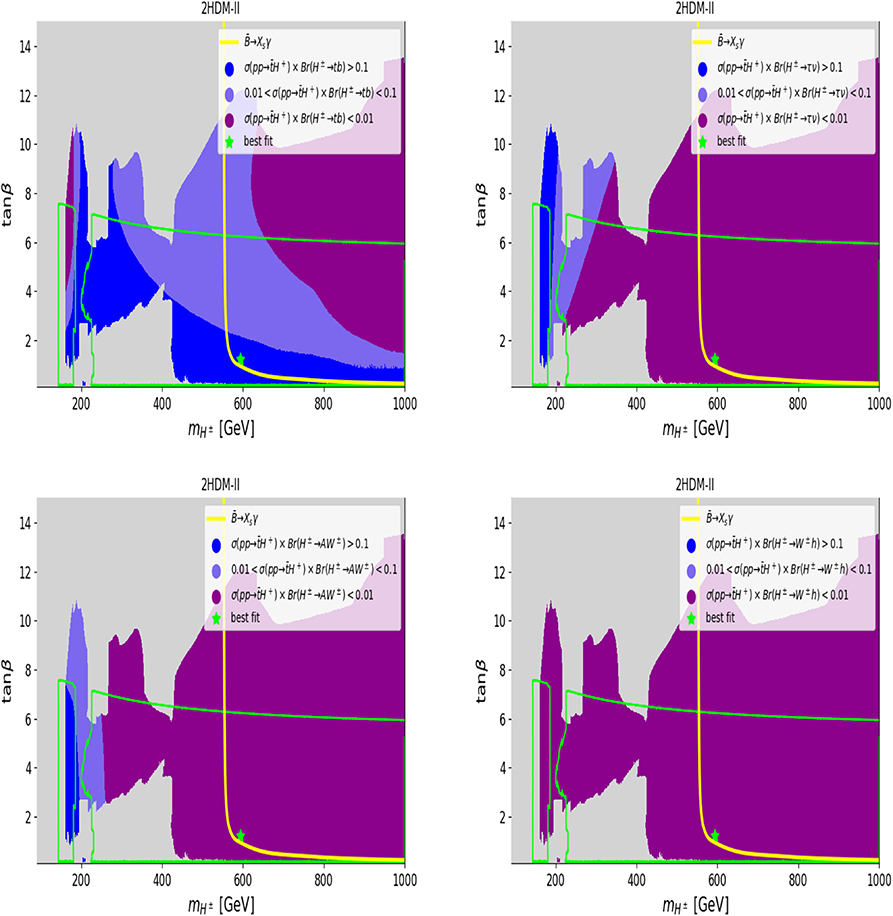
Figure 7. The σ(pp → tH−+c.c.) × BR(H± → XY) rate (in pb) at =14 TeV in the 2HDM Type-II, for XY ≡ tb (top left), XY ≡ τν (top right), XY ≡ AW± (bottom left), and XY ≡ hW± (bottom right). The maximum of the cross section σ(pp → tH−+c.c.) × BR(H± → XY) is 2.3 and 1.38 pb for XY ≡ AW±, tb, respectively. The color coding is the same as in Figure 6.
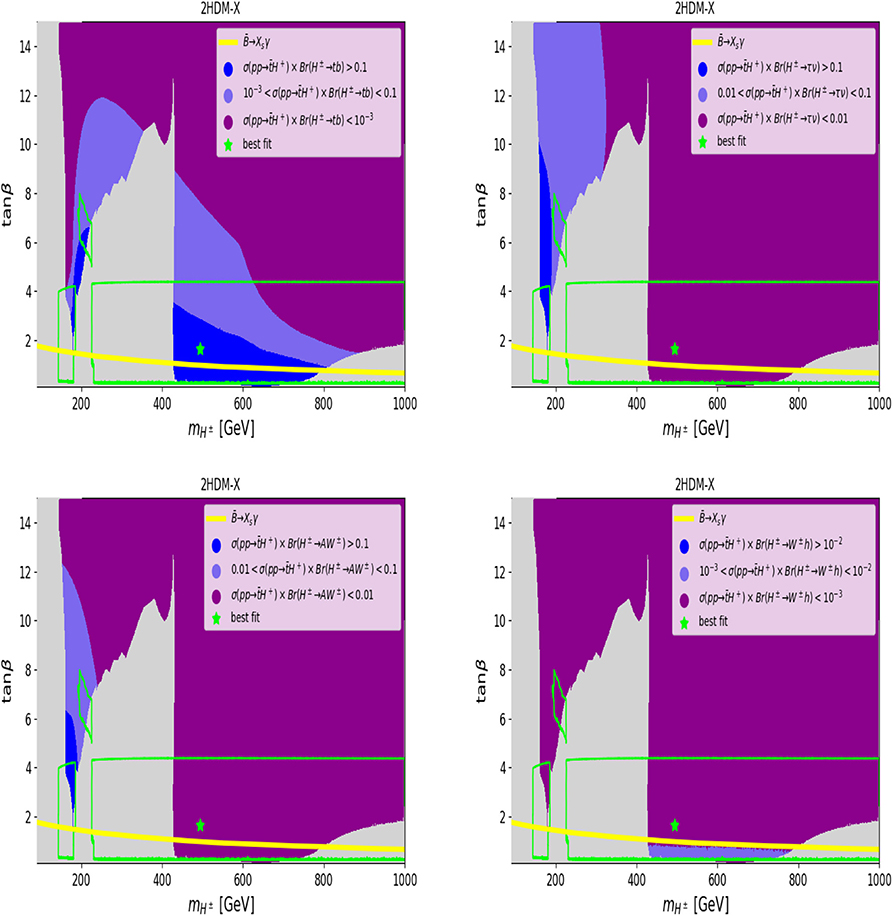
Figure 8. The σ(pp → tH−+c.c.) × BR(H± → XY) rate (in pb) at =14 TeV in the 2HDM Type-X, for XY ≡ tb (top left), XY ≡ τν (top right), XY ≡ AW± (bottom left), and XY ≡ hW± (bottom right). The maximum of the cross section σ(pp → tH−+c.c.) × BR(H± → XY) is 2.3 and 1.23 pb for XY ≡ AW±, tb, respectively. The color coding is the same as in Figure 6.
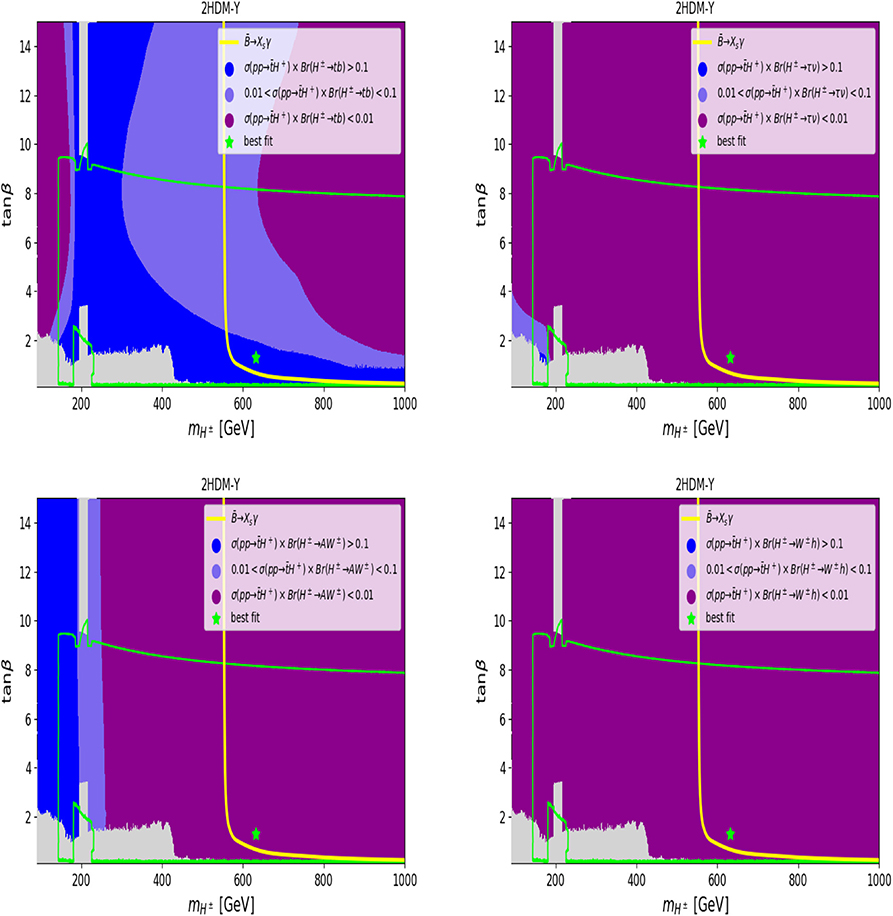
Figure 9. The σ(pp → tH−+c.c.) × BR(H± → XY) rate (in pb) at =14 TeV in the 2HDM Type-Y, for XY ≡ tb (top left), XY ≡ τν (top right), XY ≡ AW± (bottom left), and XY ≡ hW± (bottom right). The maximum of the cross section σ(pp → tH−+c.c.) × BR(H± → XY) is 3.54 and 1.85 pb for XY ≡ AW±, tb, respectively. The color coding is the same as in Figure 6.
We now discuss the size of the charged Higgs production cross section times its BRs in decay channels, such as and hW±. In Figure 6 (top-left panel) we illustrate the values of σ(pp → tH−+c.c.) × BR(H± → tb) (in pb) where we can see that it is possible tohave a production times decay rate in the range 0.01 to 0.2 pb for 1 ≤ tan β ≤ 6 and 180 GeV GeV. This could lead to more than thousands raw signal events for 100 fb−1 luminosity. In the case of H± → τν and H± → hW±, which are suppressed, respectively, by 1/tan β and cos(β−α) ≈ 0, the rate is much smaller than for the tb mode. In contrast, since the coupling H±W∓A is a gauge coupling without any suppression factor, when H± → AW± is open, it may dominate over the H± → tb channel. One can see from Figure 6 (bottom-left panel) that, for 100 GeV GeV and for 1 ≤ tan β ≤ 14, the corresponding rate for σ(pp → tH−+c.c.) × BR(H± → AW±) ≥ 0.01 pb. This could lead to an interesting final state bW+W−A where one W± could decay leptonically, hence offering a clean trigger. The decay H± → hW± is essentially inaccessible, see Figure 6 (bottom-right panel).
In the case of 2HDM Type-II and -Y, as one can see from Figures 7, 9, respectively, there is a wide region over the (, tan β) plane where the rate for σ(pp → tH−+c.c.) × BR(H± → tb) is rather sizable for both moderate ( GeV) and heavy (otherwise) charged Higgs masses (top-left panel). However, if one takes into account the constraint, then is required to be much heavier than 580 GeV (as already discussed), which makes the rate σ(pp → tH− + c.c.) × BR(H± → tb) ≥ 0.1 pb only for tan β < 1.5. All the other channels (in the three remaining panels) have smaller production times decay rates.
The 2HDM Type-X is depicted in Figure 8, wherein the usual production times BR rates are shown. The top-right panel is again for the channel, which exhibits a potentially interesting cross section (≥ 1 fb) in the channel for both a light charged Higgs mass (around 200 GeV) and a heavy one (around 420 GeV). In the case of the τν channel (top-right panel), one can get sizable rates for σ(pp → tH−+c.c.) × BR(H± → τν) for a charged Higgs mass around 200 GeV and tan β ≥ 2.
In all 2HDM Types, we elect the best fit points to also be the BPs amenable to experimental tests by ATLAS and CMS.
6. Conclusions
We have studied charged Higgs boson phenomenology in both the MSSM and 2HDM, the purpose being to define BPs amenable to phenomenological investigation already with the full Run-1 and -2 datasets and certainly accessible with the Run-3 one of the LHC. They have been singled out following the enforcement of the latest theoretical and experimental constraints, so as to be entirely up-to-date. Furthermore, they have been defined with the intent of increasing sensitivity of dedicated (model-dependent) H± searches to some of the most probable parameter space configurations of either scenario. With this in mind, we have listed in two tables their input and output values, the former in terms of the fundamental parameters of the model concerned and the latter in terms of key observables (like, e.g., physical masses and couplings, production cross sections and decay BRs). We have also specified which numerical tools we have used to produce all such an information, including their settings.
For the MSSM we have concentrated on two popular scenarios, i.e., the hMSSM and ones. It was found that the hMSSM case still possesses a rather large available parameter space, here mapped over the (mA, tan β) plane, while the one is instead much more constrained. In terms of the largest production and decay rates, in the hMSSM scenario one finds that the most copious channels, assuming pp → tH− + c.c. production, are via the decay followed by H+ → τν whereas for the scenario the decay modes and offer the largest rates. In both cases, only values are truly admissible by current data.
Within the 2HDM, we have looked at the four standard Yukawa setups, known as Type-I, -II, -X, and -Y. Because of constraints, the profile of a charged Higgs in the 2HDM Type-II and -Y is a rather heavy one, with a mass required to be more than 580 GeV. While this puts an obvious limit to LHC sensitivity owing to a large phase space suppression in production, we have emphasized that channels should be searched for, with intermediate contributions from the AW± and tb modes (including their interference [138]), alongside H± → τν. In the case of the 2HDM Type-I and -X, a much lighter charged Higgs state is still allowed by data, in fact, even with a mass below that of the top quark. While the configuration is best probed by using production and decays into τν, the complementary mass region, i.e., (wherein pp → tH− + c.c. is the production mode), may well be accessible via a combination of and H± → AW± (in Type-I) plus H± → τν (in Type-X).
Data Availability Statement
The datasets analysed in this study can be found in the HiggsBounds repository: https://higgsbounds.hepforge.org.
Author's Note
Since the original submission of this paper, several new experimental analyses have been carried out by ATLAS and CMS using the full Run-2 data sample of ≈ 139 fb−1. Some of these, covering both measurements of the SM-like Higgs Boson and the search for new (pseudo)scalar Higgs states, both charged and neutral, have been captured by the latest versions of HiggsBounds and HiggsSignals, HiggsBounds-5.3.2beta and HiggsSignals-2.2.3beta, respectively. Likewise, further analyses by LHCb of flavor observables have been carried out since and most of these have been captured by the latest version of SuperIso. Hence, we have repeated our scans using all such tools and found negligible differences between our original results and the new ones. Further, we have investigated which ones of the full Run-2 data set analyses were not incorporated in the above codes and found that their ad-hoc application to our analysis did not change our results either.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
AA, RB, and SM were supported by the grant H2020-MSCA-RISE-2014 no. 645722 (NonMinimalHiggs). This work was also supported by the Moroccan Ministry of Higher Education and Scientific Research MESRSFC and CNRST: Project PPR/2015/6. SM was supported in part through the NExT. Institute and the STFC CG ST/L000296/1.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
For the avoidance of doubt, we acknowledge that this paper has already been submitted to a public database as https://arxiv.org/abs/1810.09106.
Footnotes
1. ^For a complete review on charged Higgs production modes, see Akeroyd et al. [34].
2. ^Notice that this configuration is compliant with the theoretical and experimental constraints discussed below, including Dark Matter (DM) ones. So is the case for the hMSSM configuration below.
3. ^Notice that, for the MSSM scenarios considered here, the (dynamically generated) scalar potential is stable in vacuum and does not induce perturbative unitarity violations.
4. ^https://lapth.cnrs.fr/micromegas/
5. ^Probably accessible only at the High-Luminosity LHC [133].
References
1. ATLAS Collaboration. Observation of a new particle in the search for the standard model Higgs Boson with the ATLAS detector at the LHC. Phys Lett B. (2012) 716:1–29. doi: 10.1016/j.physletb.2012.08.020
2. ATLAS Collaboration. Measurements of Higgs Boson production and couplings in Diboson final states with the ATLAS detector at the LHC. Phys Lett B. (2013) 726:88–119. doi: 10.1016/j.physletb.2013.08.010
3. CMS Collaboration. Observation of a New Boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys Lett B. (2012) 716:30. doi: 10.1016/j.physletb.2012.08.021
4. CMS Collaboration. Observation of a New Boson with Mass Near 125 GeV in pp Collisions at = 7 and 8 TeV. JHEP. (2013) 1306:081. doi: 10.1007/JHEP06(2013)081
5. Martin SP. A supersymmetry primer. Adv Ser Direct High Energy Phys. (2010) 21:1. doi: 10.1142/9789812839657_0001
6. Bagnaschi E, Bahl H, Fuchs E, Hahn T, Heinemeyer S, Liebler S, et al. MSSM Higgs Boson searches at the LHC: benchmark scenarios for run 2 and beyond. Eur Phys J C. (2019) 79:617. doi: 10.1140/epjc/s10052-019-7114-8
7. ATLAS Collaboration. Updated coupling measurements of the Higgs Boson with the ATLAS detector using up to 25 fb−1 of proton-proton collision data. In: 49th Rencontres de Moriond on Electroweak Interactions and Unified Theories. La Thuile.
8. CMS Collaboration. Precise determination of the mass of the Higgs Boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV. Eur Phys J C. (2015) 75:212. doi: 10.1140/epjc/s10052-015-3351-7
10. Carena M, Haber HE. Higgs Boson theory and phenomenology. Prog Part Nucl Phys. (2003) 50:63–152. doi: 10.1016/S0146-6410(02)00177-1
11. Djouadi A. The anatomy of electro-weak symmetry breaking. II. The Higgs Bosons in the minimal supersymmetric model. Phys Rept. (2008) 459:1–241. doi: 10.1016/j.physrep.2007.10.005
12. Okada Y, Yamaguchi M, Yanagida T. Upper bound of the lightest Higgs Boson mass in the minimal supersymmetric standard model. Prog Theor Phys. (1991) 85:1. doi: 10.1143/ptp/85.1.1
13. Ellis JR, Ridolfi G, Zwirner F. Radiative corrections to the masses of supersymmetric Higgs Bosons. Phys Lett B. (1991) 257:83.
14. Haber HE, Hempfling R. Can the mass of the lightest Higgs boson of the minimal supersymmetric model be larger than m(Z)? Phys Rev Lett (1991) 66:1815.
15. Carena M, Espinosa JR, Quiros M, Wagner CEM. Analytical expressions for radiatively corrected Higgs masses and couplings in the MSSM. Phys Lett B. (1995) 355:209.
16. Haber HE, Hempfling R, Hoang AH. Approximating the radiatively corrected Higgs mass in the minimal supersymmetric model. Z Phys C. (1997) 75:539.
17. Heinemeyer S, Hollik W, Weiglein G. The Masses of the neutral CP—even Higgs bosons in the MSSM: accurate analysis at the two-loop level. Eur Phys J C. (1999) 9:343.
18. Degrassi G, Slavich P, Zwirner F. On the neutral Higgs boson masses in the MSSM for arbitrary stop mixing. Nucl Phys B. (2001) 611:403. doi: 10.1016/S0550-3213(01)00343-1
19. Brignole A, Degrassi G, Slavich P, Zwirner F. On the two-loop sbottom corrections to the neutral Higgs boson masses in the MSSM. Nucl Phys B. (2002) 643:79. doi: 10.1016/S0550-3213(02)00748-4
20. Brignole A, Degrassi G, Slavich P, Zwirner F. On the O(alpha(t)**2) two-loop corrections to the neutral Higgs boson masses in the MSSM. Nucl Phys B (2002) 631:195. doi: 10.1016/S0550-3213(02)00184-0
21. Harlander RV, Kant P, Mihaila L, Steinhauser M. Higgs boson mass in supersymmetry to three loops. Phys Rev Lett. (2008) 100:191602. doi: 10.1103/PhysRevLett.100.191602
22. Degrassi G, Heinemeyer S, Hollik W, Slavich P, Weiglein G. Towards high precision predictions for the MSSM Higgs sector. Eur Phys J C. (2003) 28:133. doi: 10.1140/epjc/s2003-01152-2
23. Carena M, Heinemeyer S, Wagner CEM, Weiglein G. MSSM Higgs boson searches at the Tevatron and the LHC: impact of different benchmark scenarios. Eur Phys J C. (2006) 45:797. doi: 10.1140/epjc/s2005-02470-y
24. Carena M, Heinemeyer S, Stål O, Wagner CEM, Weiglein G. MSSM Higgs Boson searches at the LHC: benchmark scenarios after the discovery of a Higgs-like particle. Eur Phys J C. (2013) 73:2552. doi: 10.1140/epjc/s10052-013-2552-1
25. Carena M, Heinemeyer S, Wagner CEM, Weiglein G. Suggestions for benchmark scenarios for MSSM Higgs boson searches at Hadron colliders. Eur Phys J C. (2003) 26:601. doi: 10.1140/epjc/s2002-01084-3
26. Djouadi A, Maiani L, Moreau G, Polosa A, Quevillon J, Riquer V. The post-Higgs MSSM scenario: Habemus MSSM? Eur Phys J C. (2013) 73:2650. doi: 10.1140/epjc/s10052-013-2650-0
27. Maiani L, Polosa AD, Riquer V. Probing minimal supersymmetry at the LHC with the Higgs Boson masses. New J Phys. (2012) 14:073029. doi: 10.1088/1367-2630/14/7/073029
28. Maiani L, Polosa AD, Riquer V. Heavier Higgs particles: indications from minimal supersymmetry. Phys Lett B. (2012) 718:465. doi: 10.1016/j.physletb.2012.10.041
29. Djouadi A, Quevillon J. The MSSM Higgs sector at a high MSUSY: reopening the low tan β regime and heavy Higgs searches. JHEP. (2013) 1310:028. doi: 10.1007/JHEP10(2013)028
30. Bagnaschi E, Frensch F, Heinemeyer S, Lee G, Liebler S, Muhlleitner M, et al. Benchmark scenarios for low tan β in the MSSM. LHCHXSWG-2015-002. (2015).
31. Barger VD, Phillips RJN, Roy DP. Heavy charged Higgs signals at the LHC. Phys Lett B. (1994) 324:236.
32. Gunion JF, Haber HE, Paige FE, Tung WK, Willenbrock SSD. Neutral and charged Higgs detection: heavy quark fusion, top quark mass dependence and rare decays. Nucl Phys B. (1987) 294:621.
33. Diaz-Cruz JL, Sampayo OA. Contribution of gluon fusion to the production of charged Higgs at Hadron colliders. Phys Rev D. (1994) 50:6820.
34. Akeroyd AG, Aoki M, Arhrib A, Basso L, Ginzburg IF, Guedes R, et al. Prospects for charged Higgs searches at the LHC. Eur Phys J C. (2017) 77:276. doi: 10.1140/epjc/s10052-017-4829-2
35. Borzumati F, Kneur JL, Polonsky N. Higgs-Strahlung and R-parity violating slepton-Strahlung at Hadron colliders. Phys Rev D. (1999) 60:115011.
36. Guchait M, Moretti S. Improving the discovery potential of charged Higgs bosons at Tevatron run II. JHEP. (2002) 0201:001. doi: 10.1088/1126-6708/2002/01/001
37. ATLAS Collaboration. Search for charged Higgs Bosons decaying via H± → τ±ν in fully hadronic final states using pp collision data at TeV with the ATLAS detector. JHEP. (2015) 1503:088 doi: 10.1007/JHEP03(2015)088
38. CMS Collaboration. Search for a charged Higgs boson in pp collisions at TeV. JHEP. (2015) 1511:018. doi: 10.1007/JHEP11(2015)018
39. ATLAS Collaboration. Search for a light charged Higgs boson in the decay channel in events using pp collisions at = 7 TeV with the ATLAS detector. Eur Phys J C. (2013) 73:2465. doi: 10.1140/epjc/s10052-013-2465-z
40. CMS Collaboration. Search for a light charged Higgs boson decaying to in pp collisions at TeV. JHEP. (2015) 1512:178. doi: 10.1007/JHEP12(2015)178
41. CMS Collaboration. Search for Charged Higgs boson to in lepton+jets channel using top quark pair events.
42. ATLAS Collaboration. Search for charged Higgs bosons produced in association with a top quark and decaying via H± → τν using pp collision data recorded at TeV by the ATLAS detector. Phys Lett B. (2016) 759:555. doi: 10.1016/j.physletb.2016.06.017
43. CMS Collaboration. Search for charged Higgs bosons with the decay channel in the fully hadronic final state at . CMS-PAS-HIG-16-031. (2016).
44. ATLAS Collaboration. Search for charged Higgs bosons in the H± → tb decay channel in pp collisions at TeV using the ATLAS detector. ATLAS-CONF-2016-089. (2016).
45. Arhrib A, Benbrik R, Moretti S. Bosonic decays of charged Higgs Bosons in a 2HDM type-I. Eur Phys J C. (2017) 77:621. doi: 10.1140/epjc/s10052-017-5197-7
46. Arbey A, Mahmoudi F, Stal O, Stefaniak T. Status of the charged Higgs Boson in two Higgs doublet models. Eur Phys J C. (2018) 78:182. doi: 10.1140/epjc/s10052-018-5651-1
47. Bernon J, Gunion JF, Haber HE, Jiang Y, Kraml S. Scrutinizing the alignment limit in two-Higgs-doublet models: mh=125 GeV. Phys Rev D. (2015) 92:075004. doi: 10.1103/PhysRevD.92.075004
48. Heinemeyer S, Hollik W, Weiglein G. QCD corrections to the masses of the neutral CP—even Higgs bosons in the MSSM. Phys Rev D. (1998) 58:091701.
49. Heinemeyer S, Hollik W, Weiglein G. Precise prediction for the mass of the lightest Higgs Boson in the MSSM. Phys Lett B. (1998) 440:296.
50. Heinemeyer S, Hollik W, Weiglein G. FeynHiggs: a program for the calculation of the masses of the neutral CP even Higgs Bosons in the MSSM. Comput Phys Commun. (2000) 124:76. doi: 10.1016/S0010-4655(99)00364-1
51. Hahn T, Heinemeyer S, Hollik W, Rzehak H, Weiglein G. FeynHiggs: a program for the calculation of MSSM Higgs-boson observables—version 2.6.5. Comput Phys Commun. (2009) 180:1426. doi: 10.1016/j.cpc.2009.02.014
52. Djouadi A, Kalinowski J, Spira M. HDECAY: a program for Higgs boson decays in the standard model and its supersymmetric extension. Comput Phys Commun. (1998) 108:56.
53. Djouadi A, Kalinowski J, Muehlleitner M, Spira M. HDECAY: twenty++ years after. Comput Phys Commun. (2019) 238:214. doi: 10.1016/j.cpc.2018.12.010
54. Harlander RV, Liebler S, Mantler H. SusHi: a program for the calculation of Higgs production in gluon fusion and bottom-quark annihilation in the Standard Model and the MSSM. Comput Phys Commun. (2013) 184:1605. doi: 10.1016/j.cpc.2013.02.006
55. Harlander RV, Liebler S, Mantler H. SusHi Bento: beyond NNLO and the heavy-top limit. Comput Phys Commun. (2017) 212:239. doi: 10.1016/j.cpc.2016.10.015
56. Heinemeyer S, Hollik W, Weiglein G. Constraints on tan Beta in the MSSM from the upper bound on the mass of the lightest Higgs Boson. JHEP. (2000) 0006:009. doi: 10.1088/1126-6708/2000/06/009
57. ATLAS Collaboration. Search for strongly produced superpartners in final states with two same sign leptons with the ATLAS detector using 21 fb-1 of proton-proton collisions at sqrt(s) = 8 TeV. ATLAS-CONF-2013-007. (2013).
58. ATLAS Collaboration. Search for new phenomena in final states with large jet multiplicities and missing transverse momentum at =8 TeV proton-proton collisions using the ATLAS experiment. JHEP. (2013) 1310:130. doi: 10.1007/JHEP10(2013)130
59. CMS Collaboration. Search for supersymmetry in hadronic final states with missing transverse energy using the variables αT and b-quark multiplicity in pp collisions at TeV. Eur Phys J C. (2013) 73:2568. doi: 10.1140/epjc/s10052-013-2568-6
60. CMS Collaboration. “Search for new physics in events with same-sign dileptons and jets in pp collisions at = 8 TeV. JHEP. (2014) 1401:163. doi: 10.1007/JHEP01(2014)163
61. CMS Collaboration. Search for new physics in the multijet and missing transverse momentum final state in proton-proton collisions at = 8 TeV. JHEP. (2014) 1406:055. doi: 10.1007/JHEP06(2014)055
62. Gunion JF, Haber HE. The CP conserving two Higgs doublet model: the approach to the decoupling limit. Phys Rev D. (2003) 67:075019. doi: 10.1103/PhysRevD.67.075019
64. Gomez-Bock M, Noriega-Papaqui R. Flavor violating decays of the Higgs Bosons in the THDM-III. J Phys G. (2006) 32:761. doi: 10.1088/0954-3899/32/6/002
65. Arhrib A, Benbrik R, Chen CH, Parry JK, Rahili L, Semlali S, et al. anomaly in type-III 2HDM. arXiv [preprint]. arXiv:1710.05898.
66. David A, Denner A, Duehrssen M, Grazzini M, Grojean C, Passarino G, et al. LHC HXSWG interim recommendations to explore the coupling structure of a Higgs-like particle. arXiv [preprint]. arXiv:1209.0040.
67. Ferreira PM, Gunion JF, Haber HE, Santos R. Probing wrong-sign Yukawa couplings at the LHC and a future linear collider. Phys Rev D. (2014) 89:115003. doi: 10.1103/PhysRevD.89.115003
68. Ferreira PM, Guedes R, Sampaio MOP, Santos R. Wrong sign and symmetric limits and non-decoupling in 2HDMs. JHEP. (2014) 1412:067. doi: 10.1007/JHEP12(2014)067
69. Eriksson D, Rathsman J, Stål O. 2HDMC: two-Higgs-doublet model calculator physics and manual. Comput Phys Commun. (2010) 181:189. doi: 10.1016/j.cpc.2009.09.011
70. Deshpande NG, Ma E. Pattern of symmetry breaking with two Higgs doublets. Phys Rev D. (1978) 18:2574.
71. Ferreira PM, Santos R, Barroso A. Stability of the tree-level vacuum in two Higgs doublet models against charge or CP spontaneous violation. Phys Lett B. (2004) 603:219. doi: 10.1016/j.physletb.2004.10.022
72. Barroso A, Ferreira PM, Ivanov IP, Santos R. Metastability bounds on the two Higgs doublet model. JHEP. (2013) 1306:045. doi: 10.1007/JHEP06(2013)045
73. Akeroyd AG, Arhrib A, Naimi EM. Note on tree-level unitarity in the general two Higgs doublet model. Phys Lett B. (2000) 490:119. doi: 10.1016/S0370-2693(00)00962-X73
74. Kanemura S, Kubota T, Takasugi E. Lee-Quigg-Thacker bounds for Higgs boson masses in a two doublet model. Phys Lett B. (1993) 313:155.
75. Kanemura S, Kikuchi M, Yagyu K. Fingerprinting the extended Higgs sector using one-loop corrected Higgs boson couplings and future precision measurements. Nucl Phys B. (2015) 896:80. doi: 10.1016/j.nuclphysb.2015.04.015
76. Baak M, Cuth J, Haller J, Hoecker A, Kogler R, Moenig K, et al. The global electroweak fit at NNLO and prospects for the LHC and ILC. Eur Phys J C. (2014) 74:3046. doi: 10.1140/epjc/s10052-014-3046-5
77. Bechtle P, Brein O, Heinemeyer S, Weiglein G, Williams KE. HiggsBounds: confronting arbitrary Higgs sectors with exclusion bounds from LEP and the tevatron. Comput Phys Commun. (2010) 181:138. doi: 10.1016/j.cpc.2009.09.003
78. Bechtle P, Brein O, Heinemeyer S, Weiglein G, Williams KE. HiggsBounds 2.0.0: confronting neutral and charged Higgs sector predictions with exclusion bounds from LEP and the tevatron. Comput Phys Commun. (2011) 182:2605. doi: 10.1016/j.cpc.2011.07.015
79. Bechtle P, Brein O, Heinemeyer S, Ståll O, Stefaniak T, Weiglein G, et al. HiggsBounds−4: improved tests of extended Higgs sectors against exclusion bounds from LEP, the tevatron and the LHC. Eur Phys J C. (2014) 74:2693. doi: 10.1140/epjc/s10052-013-2693-2
80. Bechtle P, Heinemeyer S, Stål O, Stefaniak T, Weiglein G. Applying exclusion likelihoods from LHC searches to extended Higgs sectors. Eur Phys J C. (2015) 75:421. doi: 10.1140/epjc/s10052-015-3650-z
81. Bechtle P, Heinemeyer S, Stål O, Stefaniak T, Weiglein G. HiggsSignals: confronting arbitrary Higgs sectors with measurements at the tevatron and the LHC. Eur Phys J C. (2014) 74:2711. doi: 10.1140/epjc/s10052-013-2711-4
82. ATLAS Collaboration. Search for additional heavy neutral Higgs and gauge bosons in the ditau final state produced in 36 fb−1 of pp collisions at = 13 TeV with the ATLAS detector. arXiv [Preprnt]. arXiv:1709.07242.
83. CMS Collaboration. Search for additional neutral MSSM Higgs bosons in the ττ final state in proton-proton collisions at 13 TeV. arXiv [Preprnt]. arXiv:1803.06553.
84. CMS Collaboration. Search for additional neutral Higgs bosons decaying to a pair of tau leptons in pp collisions at = 7 and 8 TeV. CMS-PAS-HIG-14-029. (2015).
85. ATLAS Collaboration. Search for an additional, heavy Higgs boson in the H → ZZ decay channel at in pp collision data with the ATLAS detector. Eur Phys J C. (2016) 76:45. doi: 10.1140/epjc/s10052-015-3820-z
86. ATLAS Collaboration. Search for heavy ZZ resonances in the ℓ+ℓ−ℓ+ℓ− and final states using proton proton collisions at TeV with the ATLAS detector. Eur Phys J C. (2018) 78:293. doi: 10.1140/epjc/s10052-018-5686-3
87. CMS Collaboration. Search for a new scalar resonance decaying to a pair of Z bosons in proton-proton collisions at TeV. JHEP. (2018) 1806:127. doi: 10.1007/JHEP06(2018)127
88. ATLAS Collaboration. Searches for Higgs boson pair production in the hh → bbττ, γγWW*, γγbb, bbbb channels with the ATLAS detector. Phys Rev D. (2015) 92:092004. doi: 10.1103/PhysRevD.92.092004
89. CMS Collaboration. Search for Higgs boson pair production in events with two bottom quarks and two tau leptons in proton proton collisions at = 13 TeV. Phys Lett B. (2018) 778:101. doi: 10.1016/j.physletb.2018.01.001
90. CMS Collaboration. Search for resonant and nonresonant Higgs boson pair production in the final state in proton-proton collisions at TeV. JHEP. (2018) 1801:054. doi: 10.1007/JHEP01(2018)054
91. ATLAS Collaboration. Search for new phenomena in events with at least three photons collected in pp collisions at = 8 TeV with the ATLAS detector. Eur Phys J C. (2016) 76:210. doi: 10.1140/epjc/s10052-016-4034-8
92. CMS Collaboration. Search for light bosons in decays of the 125 GeV Higgs boson in proton-proton collisions at TeV. JHEP. (2017) 1710:076. doi: 10.1007/JHEP10(2017)076
93. ATLAS Collaboration. Search for a CP-odd Higgs boson decaying to Zh in pp collisions at TeV with the ATLAS detector. Phys Lett B. (2015) 744:163. doi: 10.1016/j.physletb.2015.03.054
94. CMS Collaboration. Search for a pseudoscalar boson decaying into a Z Boson and the 125 GeV Higgs Boson in final states. Phys Lett B. (2015) 748:221. doi: 10.1016/j.physletb.2015.07.010
95. ATLAS Collaboration. Search for charged Higgs bosons decaying via in the τ+jets and τ+lepton final states with 36 fb−1 of pp collision data recorded at TeV with the ATLAS experiment. JHEP. (2018) 1809:139. doi: 10.1007/JHEP09(2018)139
96. ATLAS Collaboration. Search for charged Higgs bosons in the H± → tb decay channel in pp collisions at TeV using the ATLAS detector. JHEP. (2016) 1603:127. doi: 10.1007/JHEP03(2016)127
97. ATLAS and CMS Collaborations. Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at and 8 TeV. JHEP. (2016) 1608:045. doi: 10.1007/JHEP08(2016)045
98. ATLAS Collaboration. Measurements of the Higgs boson production cross section via Vector Boson Fusion and associated WH production in the WW* → ℓνℓν decay mode with the ATLAS detector at = 13 TeV. ATLAS-CONF-2016-112. (2016).
99. ATLAS Collaboration. Measurement of gluon fusion and vector boson fusion Higgs boson production cross-sections in the H → WW* → eνμν decay channel in pp collisions at TeV with the ATLAS detector. ATLAS-CONF-2018-004. (2018).
100. ATLAS Collaboration. Evidence for the decay with the ATLAS detector. JHEP. (2017) 1712:024. doi: 10.1007/JHEP12(2017)024
101. ATLAS Collaboration. Measurement of the Higgs boson coupling properties in the H → ZZ* → 4ℓ decay channel at = 13 TeV with the ATLAS detector. JHEP. (2018) 1803:095. doi: 10.1007/JHEP03(2018)095
102. ATLAS Collaboration. Evidence for the associated production of the Higgs boson and a top quark pair with the ATLAS detector. Phys Rev D. (2018) 97:072003. doi: 10.1103/PhysRevD.97.072003
103. ATLAS Collaboration. Search for the standard model Higgs boson produced in association with top quarks and decaying into a pair in pp collisions at = 13 TeV with the ATLAS detector. Phys Rev D. (2018) 97:072016. doi: 10.1103/PhysRevD.97.072016
104. ATLAS Collaboration. Measurements of Higgs boson properties in the diphoton decay channel with 36 fb−1 of pp collision data at TeV with the ATLAS detector. arXiv [Preprint]. arXiv:1803.06553.
105. CMS Collaboration. Measurements of properties of the Higgs boson in the diphoton decay channel with the full 2016 data set. CMS-PAS-HIG-16-040. (2017).
106. CMS Collaboration. Measurements of properties of the Higgs boson decaying into the four-lepton final state in pp collisions at TeV. JHEP. (2017) 1711:047. doi: 10.1007/JHEP11(2017)047
107. CMS Collaboration. Observation of the Higgs boson decay to a pair of τ leptons with the CMS detector. Phys Lett B. (2018) 779:283. doi: 10.1016/j.physletb.2018.02.004
108. CMS Collaboration. Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair. Phys Rev Lett. (2018) 120:071802. doi: 10.1103/PhysRevLett.120.071802
109. CMS Collaboration. Evidence for the Higgs boson decay to a bottom quark antiquark pair. Phys Lett B. (2018) 780:501. doi: 10.1016/j.physletb.2018.02.050
110. CMS Collaboration. Evidence for associated production of a Higgs boson with a top quark pair in final states with electrons, muons, and hadronically decaying τ leptons at TeV. JHEP. (2018) 1808:066. doi: 10.1007/JHEP08(2018)066
111. CMS Collaboration. Search for H production in the all-jet final state in proton-proton collisions at 13 TeV. JHEP. (2018) 1806:101. doi: 10.1007/JHEP06(2018)101
112. CMS Collaboration. Search for H production in the decay channel with leptonic decays in proton-proton collisions at 13 TeV. arXiv [Preprnt]. arXiv:1804.03682.
113. CMS Collaboration. Measurements of properties of the Higgs boson decaying to a W boson pair in pp collisions at 13 TeV. arXiv [Preprnt]. arXiv:1806.05246.
114. Belanger G, Boudjema F, Pukhov A, Semenov A. micrOMEGAs3: a program for calculating dark matter observables. Comput Phys Commun. (2014) 185:960. doi: 10.1016/j.cpc.2013.10.016
115. Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv [Preprnt]. arXiv:1807.06209.
116. CMS Collaboration. Search for new phenomena with the MT2 variable in the all-hadronic final state produced in proton proton collisions at TeV. Eur Phys J C. (2017) 77:710. doi: 10.1140/epjc/s10052-017-5267-x
117. CMS Collaboration. Search for natural and split supersymmetry in proton-proton collisions at TeV in final states with jets and missing transverse momentum. JHEP. (2018) 1805:025. doi: 10.1007/JHEP05(2018)025
118. ATLAS Collaboration. Search for direct top squark pair production in final states with two leptons in TeV pp collisions with the ATLAS detector. Eur Phys J C. (2017) 77:898. doi: 10.1140/epjc/s10052-017-5445-x
119. ATLAS Collaboration. Search for a scalar partner of the top quark in the jets plus missing transverse momentum final state at =13 TeV with the ATLAS detector. JHEP. (2017) 1712:085. doi: 10.1007/JHEP12(2017)085
120. ATLAS Collaboration. Search for top-squark pair production in final states with one lepton, jets, and missing transverse momentum using 36 fb−1 of TeV pp collision data with the ATLAS detector. JHEP. (2018) 1806:108. doi: 10.1007/JHEP06(2018)108
121. CMS Collaboration. Search for top squark pair production in pp collisions at TeV using single lepton events. JHEP. (2017) 1710:019. doi: 10.1007/JHEP10(2017)019
122. CMS Collaboration. Search for direct production of supersymmetric partners of the top quark in the all-jets final state in proton-proton collisions at TeV. JHEP. (2017) 1710:005. doi: 10.1007/JHEP10(2017)005
123. CMS Collaboration. Search for top squarks and dark matter particles in opposite-charge dilepton final states at 13 TeV. Phys Rev D. (2018) 97:032009. doi: 10.1103/PhysRevD.97.032009
124. ATLAS Collaboration. Search for dark matter and other new phenomena in events with an energetic jet and large missing transverse momentum using the ATLAS detector. JHEP. (2018) 1801:126. doi: 10.1007/JHEP01(2018)126
125. ATLAS Collaboration. Search for supersymmetry in final states with two same-sign or three leptons and jets using 36 fb−1 of TeV pp collision data with the ATLAS detector. JHEP. (2017) 1709:084. doi: 10.1007/JHEP09(2017)084
126. ATLAS Collaboration. Search for supersymmetry in events with b-tagged jets and missing transverse momentum in pp collisions at TeV with the ATLAS detector. JHEP. (2017) 1711:195. doi: 10.1007/JHEP11(2017)195
127. ATLAS Collaboration. Search for squarks and gluinos in events with an isolated lepton, jets, and missing transverse momentum at TeV with the ATLAS detector. Phys Rev D. (2017) 96:112010. doi: 10.1103/PhysRevD.96.112010
128. ATLAS Collaboration. Search for squarks and gluinos in final states with jets and missing transverse momentum using 36 fb−1 of TeV pp collision data with the ATLAS detector. Phys Rev D. (2018) 97:112001. doi: 10.1103/PhysRevD.97.112001
129. CMS Collaboration. Search for supersymmetry in multijet events with missing transverse momentum in proton-proton collisions at 13 TeV. Phys Rev D. (2017) 96:032003. doi: 10.1103/PhysRevD.96.032003
130. Dittmaier S, Kramer M, Spira M, Walser M. Charged-Higgs-Boson production at the LHC: NLO supersymmetric QCD corrections. Phys Rev D. (2011) 83:055005. doi: 10.1103/PhysRevD.83.055005
131. Berger EL, Han T, Jiang J, Plehn T. Associated production of a top quark and a charged Higgs Boson. Phys Rev D. (2005) 71:115012. doi: 10.1103/PhysRevD.71.115012
132. Beenakker W, Hopker R, Spira M. PROSPINO: a program for the production of supersymmetric particles in next-to-leading order QCD. arXiv [Preprint]. arXiv: HEP-PH/9611232. (1996).
133. Gianotti F, Mangano ML, Virdee T, Abdullin S, Azuelos G, Ball A, et al. Physics potential and experimental challenges of the LHC luminosity upgrade. Eur Phys J C. (2005) 39:293. doi: 10.1140/epjc/s2004-02061-6
134. Amhis Y, Banerjee S, Ben-Haim E, Blyth S, Bozek A, Bozzi C, et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of summer 2014. arXiv [Preprint]. arXiv:1412.7515.
135. Olive KA, Agashe K, Amsler C, Antonelli M, Arguin JF, Asner DM, et al. Review of particle physics. Chin Phys C. (2014) 38:090001. doi: 10.1088/1674-1137/38/9/090001
137. Mahmoudi F. SuperIso v2.3: a program for calculating flavor physics observables in supersymmetry. Comput Phys Commun. (2009) 180:1579. doi: 10.1016/j.cpc.2009.02.017
Keywords: beyond standard model, Higgs physics, charged Higgs, 2HDM, MSSM, LHC
Citation: Arhrib A, Benbrik R, Harouiz H, Moretti S and Rouchad A (2020) A Guidebook to Hunting Charged Higgs Bosons at the LHC. Front. Phys. 8:39. doi: 10.3389/fphy.2020.00039
Received: 29 March 2019; Accepted: 12 February 2020;
Published: 10 March 2020.
Edited by:
Frank Franz Deppisch, University College London, United KingdomReviewed by:
Athanasios Dedes, University of Ioannina, GreeceYuval Grossman, Cornell University, United States
Copyright © 2020 Arhrib, Benbrik, Harouiz, Moretti and Rouchad. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rachid Benbrik, ci5iZW5icmlrQHVjYS5hYy5tYQ==
 Abdesslam Arhrib
Abdesslam Arhrib Rachid Benbrik
Rachid Benbrik Hicham Harouiz
Hicham Harouiz Stefano Moretti
Stefano Moretti Abdessamad Rouchad
Abdessamad Rouchad