Predictions of New Neutron-Rich Isotopes at N = 126 in the Multinucleon Transfer Reaction 136Xe + 194Ir

Aiming to produce new neutron-rich nuclei at N = 126, the multi-nucleon transfer reactions ¹³⁶Xe+¹⁹⁴Ir, ²⁰⁸Pb are investigated by using the GRAZING model and the three-dimensional time-dependent Hartree-Fock (TDHF) approach. Deexcitation processes of the primary fragments are taken into account in both models. Comparison with the experimental data of ¹³⁶Xe+²⁰⁸Pb at E_c.m. = 450 MeV indicates that the isotopic production cross sections around the entrance channel can be well reproduced by both models. The results of GRAZING indicate that ¹³⁶Xe+¹⁹⁴Ir is a promising candidate for producing new neutron-rich isotones with N = 126. The limitation of using TDHF to investigate multi-nucleon transfer reactions is also discussed.

1. Introduction

Neutron-rich nuclei are of great importance for understanding the astrophysical r-process [1]. For instance, those around the closed neutron shell N = 126 can provide information on the solar r-abundance distribution [2]. The neutron-rich radioactive isotopes can also be used as projectiles for synthesizing super-heavy nuclei which is one of the most interesting challenges in nuclear physics. However, new heavy neutron-rich nuclei out of limits of the present nuclear chart are hardly to be produced via traditional ways, such as fusion reactions with stable beams at low energies or fragmentation of heavy projectile at relativistic energies.

In recent years, theoretical predictions indicate that multi-nucleon transfer (MNT) reactions would be a possible route to produce heavy neutron-rich nuclei far away from the stability line [3, 4]. The experimental results of ¹³⁶Xe + ¹⁹⁸Pt at the incident energy of 8 MeV/nucleon [2] show that the production cross sections of neutron-rich nuclei with N = 126 are orders of magnitude larger than those obtained in fragmentation reaction of ²⁰⁸Pb (1 AGeV) + Be [5]. But in some other experiments of MNT reactions with stable beams such as ⁶⁴Ni + ²⁰⁷Pb [6] and ¹³⁶Xe + ²⁰⁸Pb [7, 8], no new neutron-rich nuclei is detected. Based on the N/Z equilibrium concept, theoretical predictions show that using neutron-rich radioactive beams can remarkably improve the production cross sections of neutron-rich isotopes along N = 126 [9, 10]. However, due to the fact that the experimental intensities of radioactive beams are orders of magnitude lower than stable beams, the advantage of using radioactive beams may be canceled. Opportunities will arise in the near future on the second generation radioactive beam facilities like the European EURISOL [11]. At the present time, to find an optimum stable projectile-target combination are highly appealed.

To describe MNT reactions, many theoretical models are developed. For example, the multidimensional Langevin model shows great success on predicting the isotopic production cross sections, even for those nuclei far away from projectile and target [3, 4, 12]. Semi-classical GRAZING model [13, 14] and the complex Wentzel-Kramers-Brillouin (CWKB) model [15] can well describe transfer process in peripheral collisions. In GRAZING model, the reactants move on classical trajectories in the combined field of Coulomb repulsion and nuclear surface-surface attraction. Surface modes of the colliding nuclei are taken into account. Independent single nucleon transfer between the projectile-like and target-like nuclei during the collision is governed by the quantum coupled equations [13, 14]. Neutron evaporation is considered for the excited primary fragments. The mass, charge, energy, and angular momentum distributions of the products produced in grazing collisions can be obtained. For details of GRAZING model and its applications (see, e.g., [16–19], and references therein). The dinuclear system model can reproduce the experimental data related with quasi-fission or deep-inelastic collisions [10, 20–23]. The improved quantum molecular dynamics (ImQMD) model [24–26] is capable of describing collisions from central to very peripheral regions on a microscopic basis, the widths of isotopic distributions can be reproduced in ImQMD since stochastic two-body collisions are taken into account [27–29]. The time-dependent Hartree-Fock (TDHF) theory shows success in describing few-nucleon transfer process [30–34]. Recently, the stochastic mean-field (SMF) approach beyond TDHF [35] has been proposed to investigate the damped MNT reaction ¹³⁶Xe + ²⁰⁸Pb, the experimental broad mass distribution can be reproduced.

In this work, the GRAZING model and TDHF theory incorporating with GEMINI++¹ [36] are adopted to investigate the production of neutron-rich nuclei in MNT reactions. The TDHF theory [37] is based on the independent particle picture and is a good approximation to the nuclear many-body problem. It is capable of describing low-energy heavy-ion reactions and provides insight on the average behavior of the dynamics. The state-of-art TDHF calculations are performed in a three-dimensional (3D) framework without any symmetry constraints due to the advances in computational power. It has been applied for investigations on various subjects, for instance, collective vibration [38, 39], fusion reaction [40, 41], fission dynamics [42–44], dissipation mechanism [45–48]. Recently, 3D TDHF is applied to MNT reactions [30–33, 49]. Fluctuation and dissipation can not be properly described in TDHF since two-body collisions and internucleon correlations are not included. Thus, widths of the mass or isotopic distributions in MNT reactions at incident energies above the Coulomb barrier are underestimated in TDHF. To consider these effects in TDHF is beyond the scope of this paper and further studied will be carried out in the future.

This paper is outlined as follows. In section 2, the TDHF approach and particle-number projection (PNP) method as well as the numerical details are introduced. In section 3, numerical results of the isotopic production cross sections in both GRAZING and TDHF approach are shown. Dynamical properties of the reactions are also discussed for TDHF. Finally, a summary is drawn in section 4.

2. Brief Introduction to TDHF Approach

In this section, we briefly introduce TDHF formalism, PNP method and the coupling to GEMINI++. Details of the TDHF theory can be found in, e.g., [50, 51], and references therein. In TDHF approach, time evolution for the single-particle states are described by a set of coupled non-linear equations

$\begin{array}{ll}i\hslash {\partial }_t{\psi }_{\alpha }(r,t)=\widehat{h}\left[{\psi }_{\nu }(r,t)\right]{\psi }_{\alpha }(r,t),\alpha ,\nu =1,2,\cdots ,N,& (1)\end{array}$

where ψ_{α, ν}(r, t) is the single-particle state and N is the total number of states. ĥ is the self-consistent mean-field Hamiltonian of single-particle motion and it is always related to Skyrme energy density functional (EDF) which depends on local densities [52]. We underline that there are no adjustable parameters in the TDHF approach. The uncertainty in TDHF calculations may arise from the uncertainty of fundamental nuclear properties, such as the distribution of shape deformation of the reactants in their ground states. This can be obtained by preparing reactants with deformation constraints. The above TDHF equations can be derived from the variation of the action [53]

$\begin{array}{ll}S={\displaystyle \int }\text{d}t\langle \text{Ψ}|i{\partial }_t-\widehat{H}|\text{Ψ}\rangle ,& (2)\end{array}$

where

$\begin{array}{ll}\text{Ψ}=\frac{1}{\sqrt{N!}}\text{det}\{{\psi }_{\alpha }(r,t)\},\alpha =1,2,\cdots ,N,& (3)\end{array}$

is the correlated many-body wave function of the system and is given by a single Slater determinate.

In the present work, the 3D unrestricted TDHF code Sky3D [51] with Skyrme SLy5 parametrization [54] is adopted for both the static and dynamic calculations. The static HF calculations are performed on 32 × 32 × 32 Cartesian grids with 1.0 fm grid spacing in all three directions. In dynamical calculations, the meshes are extended to 70 × 32 × 70 with the same grid spacing in static HF. The projectile and target are initially placed at a separation distance of 24 fm and then boosted with the associated center-of-mass energy E_c.m. and the impact parameter b. The time step △t is set to be 0.2 fm/c and six-order Taylor series expansion is employed. The TDHF simulations are stopped when the separation distance of the primary fragments after collision reaches 30 fm. Since single-particle wave functions are partially exchanged between the projectile-like and target-like nuclei in the collision process, the outgoing states are not the eigenstates of the particle-number operators (Ẑ for protons and $\widehat{N}$ for neutrons) but superpositions of them. One can only get the expectation (mean) values of the charge and mass numbers for each fragment after collision. If one wants to get the distributions of proton or neutron numbers in one of the primary fragments, one should project the many-body states on good particle numbers by introducing the PNP operator [50, 55]

$\begin{array}{ll}{\widehat{P}}_V(N^q)=\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }}\text{d}\varphi e^{i\varphi ({\widehat{N}}_V^q-N^q)},& (4)\end{array}$

where q = n, p labels the nucleon species, and Nⁿ means N neutrons while N^p means Z protons. The subscript V denotes the region of coordinate space encompassing one of the primary fragments, ${\widehat{N}}_V^q=\sum _{\alpha =1}^{N^q}{\Theta }_V(r)$ and Θ_V(r) = 1 if r ∈ subspace V and 0 elsewhere. The integral is performed with an M−point uniform discretion. For convergence, M is set to be 300.

The probability to find N^q particles in subspace V is then obtained accordingly. The cross section of primary fragment with neutron number N and charge number Z at a certain incident energy is

$\begin{array}{ll}\sigma (N,Z)=2\pi {\displaystyle {\int }_0^{b_{\text{max}}}}P(N,Z;b)b\text{d}b,& (5)\end{array}$

where P(N, Z; b) = P(N; b)P(Z; b) represents the probability to find N neutrons and Z protons at the impact parameter b; b_max is a cutoff impact parameter which depends on the incident energy and should be large enough to guarantee that most of the transfer cross sections are included. But it is not necessary to set b_max to be too large, because the transfer probability is extremely small and elastic collision dominates in very peripheral collisions. In this work, we set it to be 10 fm for ¹³⁶Xe+²⁰⁸Pb at E_c.m. = 450 MeV and 13 fm for ¹³⁶Xe+¹⁹⁴Ir at E_c.m. = 720 MeV. b ranges from 0 to b_max with the interval Δb = 1 fm.

Deexcitation of the primary fragments are considered by using the statistical code GEMINI++ with default parameters [36, 56]. All possible sequential binary decay modes, from emission of nucleons and light particles through asymmetric to symmetric fission as well as the γ-emission are included in GEMINI++. The code needs information of a primary fragment including charge and mass number as well as the excitation energies and the angular momentum as the inputs. Detailed calculations of these quantities can be found in Jiang and Wang [34]. The deexcitation of a certain projectile-like fragment (PLF) or target-like fragment (TLF) should be repeated M_trial times due to the statistical nature of GEMINI++. Here M_trial = 1, 000 is used. The number of events in which final fragment with (N_final, Z_final) is counted and denoted as M(N_final, Z_final). Then the final production cross section is given as

$\begin{array}{l}\sigma (N_{\text{final}},Z_{\text{final}})=2\pi {\displaystyle {\int }_0^{b_{\text{max}}}}{\displaystyle \sum _{N⩾N_{\text{final}},Z⩾Z_{\text{final}}}}P(N,Z;b)\\ \times \frac{M(N_{\text{final}},Z_{\text{final}})}{M_{\text{trial}}}b\text{d}b.& (6)\end{array}$

Owing to the intrinsic stochastic nature of the Monte Carlo method employed in GEMINI++, Type A standard uncertainties for the isotopic production cross sections are calculated in the simplest case. The deexcitation process of a certain fragment is performed ten times repeatedly with M_trial = 1, 000 for each time. Average values of σ(N_final, Z_final) and the uncertainties can be obtained straightforwardly. We find the uncertainties are very small. For the sake of simplicity, the deexcitation process is performed only once with M_trial = 1, 000 in this work.

3. Results and Discussions

¹³⁶Xe + ²⁰⁸Pb is a candidate reaction for the production of neutron-rich nuclei at N = 126. The experiment at E_c.m. = 450 MeV was performed at Argonne in 2015 [8]. In Figure 1 we plot the calculated isotopic production cross sections of the PLFs in this reaction. The results of GRAZING are shown as blue solid lines while those of TDHF+GEMINI are presented as black dashed lines. The experimental data are shown for comparison. The production cross sections of the TLFs are also calculated but have already been published in another paper [34]. One can find that for Z = 51 − 53 and Z = 55 − 58, the magnitude of the peak values can be reproduced by TDHF+GEMINI. Whilst those for Z = 52, 53, 55, 56 can be reproduced by GRAZING. For Z = 54, the peak values are overestimated in both models. This is because the results of (quasi)elastic channels are not excluded in our calculations. One can also find that better predictions are obtained for proton pickup channels than stripping channels in both models. As the number of transferred nucleons increases, discrepancies between model predictions and the experimental data get larger. These isotopes far away from the entrance channel may be produced in strongly damped collisions. Such processes can not be well estimated by the two models: two-body collisions are not considered in TDHF [57, 58] while the GRAZING model only takes grazing collisions into account.

FIGURE 1

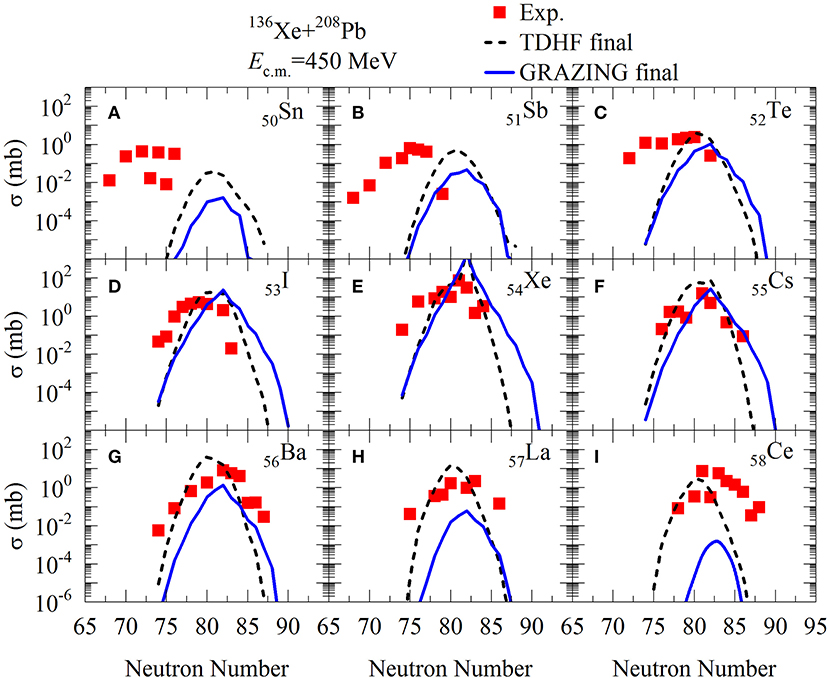
Figure 1. (Color online) Isotopic production cross sections of the PLFs for Z = 50–58 (A–I) in ¹³⁶Xe + ²⁰⁸Pb at E_c.m. = 450 MeV. The results of GRAZING and TDHF+GEMINI are shown as blue solid and black dashed lines, respectively. The experimental data are taken from Barrett et al. [8] and shown as red solid squares.

However, no new neutron-rich nuclei were detected in ¹³⁶Xe + ²⁰⁸Pb. The experiment results of ¹³⁶Xe+¹⁹⁸Pt at E_c.m. = 645 MeV [2] indicate that this reaction is a better candidate to produce neutron-rich nuclei with N = 126. Calculations of this reaction are performed by using both GRAZING and TDHF+GEMINI. Unfortunately, no neutron-rich nuclei with N = 126 is obtained in TDHF+GEMINI. The production cross sections of those nuclei predicted by GRAZING are given in Figure 2. Detailed discussions about the predictions of TDHF on this reaction will be reported elsewhere. At the end of this section, we will show some results of ¹³⁶Xe + ¹⁹⁴Ir given by TDHF+GEMINI and discuss the limits of TDHF approach on investigating MNT reactions when the incident energy is much above the Coulomb barrier. In the following, we concentrate on the predictions of GRAZING on neutron-rich nuclei with N = 126.

FIGURE 2

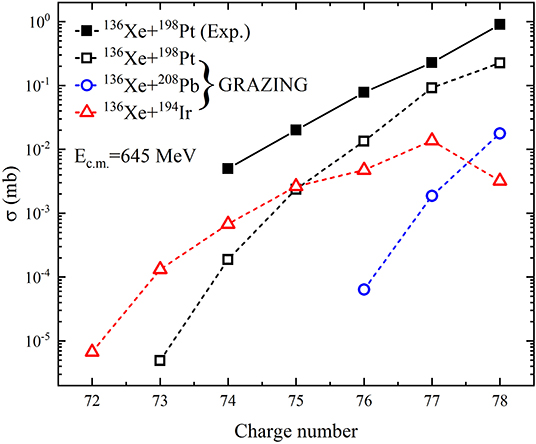
Figure 2. (Color online) Production cross sections of N = 126 isotones predicted by GRAZING in three different systems at E_c.m. = 645 MeV. The results of ¹³⁶Xe + ²⁰⁸Pb, ¹⁹⁸Pt, and ¹⁹⁴Ir are presented as blue open circles, black open squares and red open triangles, respectively. The experimental data of ¹³⁶Xe + ¹⁹⁸Pt are taken from Watanabe et al. [2] and shown as black solid squares. The lines are drawn to guide the eye.

In order to find another optimum projectile-target combination for producing new exotic neutron-rich nuclei with stable reactants, we carry out a systematic study on 15 MNT reactions with projectile around ¹³⁶Xe and target around ¹⁹⁸Pt at various incident energies by using GRAZING. The results indicate that ¹³⁶Xe + ¹⁹⁴Ir is a surrogate reaction to produce neutron-rich nuclei around N = 126. The production cross sections of isotones with N = 126 in ¹³⁶Xe + ¹⁹⁴Ir are compared with those of ¹³⁶Xe + ²⁰⁸Pb and ¹³⁶Xe + ¹⁹⁸Pt. The center-of-mass energy for all the three systems is set to be E_c.m. = 645 MeV (this energy is the same as the experiment of ¹³⁶Xe + ¹⁹⁸Pt [2], and we will show later that it is also an optimum energy for ¹³⁶Xe + ¹⁹⁴Ir). The simulation results are plotted in Figure 2 as open symbols. The experimental data of ¹³⁶Xe + ¹⁹⁸Pt taken from [2] are shown as black solid squares for comparison. One can first see that more N = 126 isotones with charge number Z ⩽ 78 can be produced in both ¹³⁶Xe + ¹⁹⁴Ir and ¹³⁶Xe + ¹⁹⁸Pt rather than ¹³⁶Xe + ²⁰⁸Pb. Particularly, the system ¹³⁶Xe + ¹⁹⁴Ir has huge advantages for producing N = 126 isotones with Z ⩽ 74. Those nuclei are out of the limits of the present nuclear landscape and are of great interest for nuclear and astro-nuclear physics. One can also find that the experimental data are underestimated by GRAZING. This can be understood since only peripheral collisions are treated in GRAZING and those nuclei with large number of nucleon transferred are produced in damped collisions at small impact parameters.

To find an optimum incident energy to produce more neutron-rich nuclei with N = 126 in ¹³⁶Xe + ¹⁹⁴Ir, the production cross sections of N = 126 isotones with Z = 72 − 77 at various incident energies from E_c.m. = 1.07V_B to 1.85V_B (V_B is the Bass barrier [59] and it is around 410 MeV for this reaction) are calculated by using GRAZING. The results are presented in Figure 3. It can be seen that very neutron-rich isotones with Z ⩽ 74 can not be produced if E_lab/A ⩽ 5.5 MeV. The cross sections of all these isotones increase with the increasing incident energy when E_lab/A < 6.5 MeV. However, when E_lab/A is in the range of 7–9 MeV, plateau-like structures are observed for all the curves. This phenomenon indicates that the production cross sections of those nuclei are insensitive to the incident energy if 7 ⩽ E_lab/A ⩽ 9 MeV.

FIGURE 3

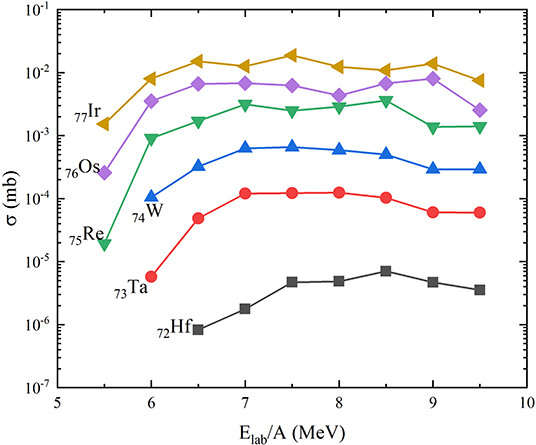
Figure 3. (Color online) Production cross sections of neutron-rich N = 126 isotones with Z = 72 − 77 in ¹³⁶Xe + ¹⁹⁴Ir as a function of the incident energy. The lines are drawn to guide the eye.

In Figure 4 we show the isotopic production cross sections of the TLFs with Z = 72 − 77 in ¹³⁶Xe + ¹⁹⁸Pt and ¹³⁶Xe + ¹⁹⁴Ir at E_c.m. = 645 MeV (E_lab/A ≈ 8 MeV) as black dashed and red solid lines, respectively. It can be found that for nuclei on the proton-rich side, larger production cross sections are obtained in ¹³⁶Xe + ¹⁹⁴Ir. For isotopes with Z = 76 and 77, more neutron-rich ones are produced in ¹³⁶Xe + ¹⁹⁸Pt. Whilst for Z = 75 the two systems give comparable results for isotopes on the neutron-rich side. As Z decreases, the advantage to produce more neutron-rich nuclei arises in ¹³⁶Xe + ¹⁹⁴Ir. Note that the results of Z = 72 in ¹³⁶Xe + ¹⁹⁸Pt are not given by GRAZING. The above results of the two reactions are difficult to be understood through the N/Z equilibrium process because N/Z is around 1.52 for ¹³⁶Xe and ¹⁹⁴Ir while it is about 1.54 for ¹⁹⁸Pt and ²⁰⁸Pb, respectively. It might be related with the Q_gg value effect, where Q_gg is the ground state-to-ground state Q value. Other quantum effect like shell effect might also play a role. Further studies should be carried out to check these discussions.

FIGURE 4

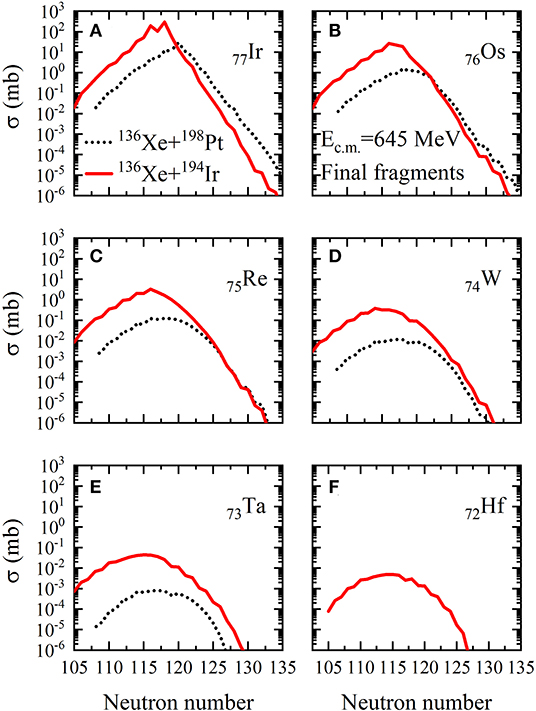
Figure 4. (Color online) Isotopic production cross sections of the TLFs with Z = 72 − 77 (A–F) in ¹³⁶Xe + ¹⁹⁸Pt and ¹³⁶Xe + ¹⁹⁴Ir at E_c.m. = 645 MeV, which are plotted as black dotted and red solid lines, respectively.

Finally, in Figure 5 we show the density contour plots of ¹³⁶Xe + ¹⁹⁴Ir at some special reaction stages in TDHF for two different initial configurations at E_c.m. = 720 MeV (E_lab/A ≈ 9) and b = 6 fm. Isodensities at half the saturation density (ρ₀/2 = 0.08 fm⁻³) is plotted as black solid lines. We should mention that in TDHF the projectile and target are both deformed in their ground states with β₂ = 0.064 and 0.154, respectively. Since the deformation of ¹³⁶Xe is very small, we only take into account the orientation effect of the deformed ¹⁹⁴Ir at the beginning of the dynamical calculations. The two initial configurations are named “tip collision” (the symmetry axis of ¹⁹⁴Ir is set parallel to the bombarding direction: z-axis) and “side collision” (the symmetry axis of ¹⁹⁴Ir is set parallel to x-axis). It can be found that in both configurations, the composite system is strongly elongated before rupture of the neck. The primary fragments produced at the end of the dynamical calculations also have large deformations. Similar results are obtained for TDHF+GEMINI in ¹³⁶Xe + ¹⁹⁸Pt at E_c.m. = 645 MeV. Such large deformation in the exit channel makes the primary fragments have very large excitation energies. This leads to strong evaporation of nucleons in the deexcitation process. So no neutron-rich isotope with N = 126 is observed in TDHF+GEMINI for ¹³⁶Xe + ¹⁹⁴Ir and ¹³⁶Xe + ¹⁹⁸Pt reactions when the incident energy is much larger than the Coulomb barrier. It is well-known that mean-field model such as TDHF is suitable for low-energy reactions, however, the lack of two-body collisions limits the predictive power of TDHF on estimating the yields of MNT reactions when the incident energy is much above the barrier.

FIGURE 5

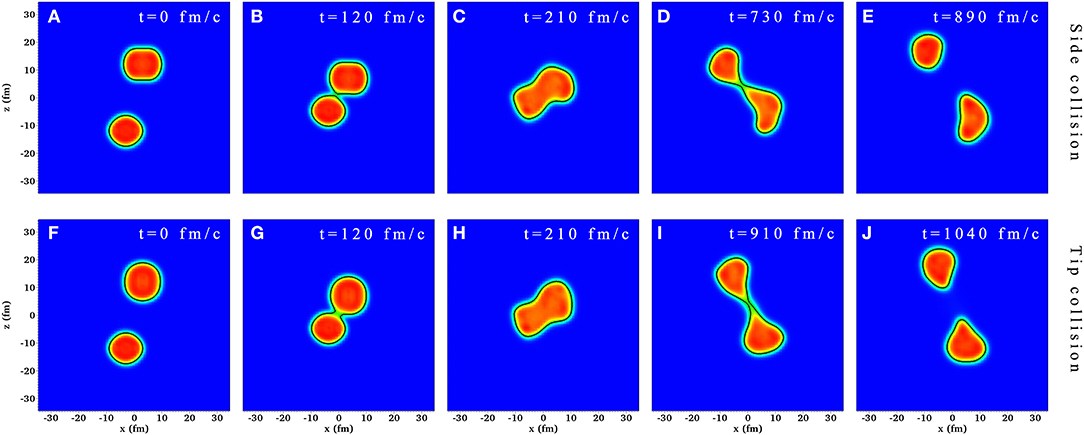
Figure 5. (Color online) Density contour plots of ¹³⁶Xe + ¹⁹⁴Ir for two different configurations (upper panels: “side collision” and lower panels: “tip collision”) at E_c.m. = 720 MeV and b = 6 fm. Five different reaction stages are given: (A,F) the initial stage at t = 0 fm/c, (B,G) the reactants just contact with each other, (C,H) the composite system has the most compact geometric shape, (D,I) the neck is going to rupture and (E,J) the end of the dynamical calculations. The isodensities of 0.08 fm⁻³ are shown as black solid lines.

4. Summary

Employing the semi-classic GRAZING model and the microscopic TDHF approach, we have investigated the MNT reactions of ¹³⁶Xe + ¹⁹⁴Ir, ²⁰⁸Pb. Neutron evaporation is considered in GRAZING while GEMINI++ is coupled with TDHF to deal with the deexcitation process. The calculated production cross sections of the PLFs for ¹³⁶Xe + ²⁰⁸Pb at E_c.m. = 450 MeV are compared with the experimental data. The model predictions can well describe the yields of nuclei near the projectile. The predictions of GRAZING on ¹³⁶Xe + ¹⁹⁴Ir show that this reaction has the advantage to produce more neutron-rich nuclei with N = 126 compared with ¹³⁶Xe + ¹⁹⁸Pt. The latter one has been carried out at GANIL [2] and the results are inspiring. No new neutron-rich isotope is observed for these two reactions at energies much above the barrier in TDHF+GMINI which might be interpreted as the lack of two-body collisions in the mean-field theory. Further investigations on ¹³⁶Xe + ¹⁹⁴Ir by using other theoretical models with two-body collisions included, such as ImQMD, are in progress.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

XJ performed numerical calculations. XJ and NW wrote the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Projects Nos. 11705118, 11647026, and 11475115) and Natural Science Foundation of SZU (grant no. 2016017).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^https://bitbucket.org/arekfu/gemini

References

1. Grawe H, Langanke K, Martínez-Pinedo G. Nuclear structure and astrophysics. Rep Prog Phys. (2007) 70:1525. doi: 10.1088/0034-4885/70/9/R02

CrossRef Full Text | Google Scholar

2. Watanabe YX, Kim YH, Jeong SC, Hirayama Y, Imai N, Ishiyama H, et al. Pathway for the production of neutron-rich isotopes around the N = 126 shell closure. Phys Rev Lett. (2015) 115:172503. doi: 10.1103/PhysRevLett.115.172503

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zagrebaev V, Greiner W. Production of new heavy isotopes in low-energy multinucleon transfer reactions. Phys Rev Lett. (2008) 101:122701. doi: 10.1103/PhysRevLett.101.122701

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Zagrebaev VI, Greiner W. Production of heavy and superheavy neutron-rich nuclei in transfer reactions. Phys Rev C. (2011) 83:044618. doi: 10.1103/PhysRevC.83.044618

CrossRef Full Text | Google Scholar

5. Kurtukian-Nieto T, Benlliure J, Schmidt KH, Audouin L, Becker F, Blank B, et al. Production cross sections of heavy neutron-rich nuclei approaching the nucleosynthesis r-process path around A = 195. Phys Rev C. (2014) 89:024616. doi: 10.1103/PhysRevC.89.024616

CrossRef Full Text | Google Scholar

6. Beliuskina O, Heinz S, Zagrebaev V, Comas V, Heinz C, Hofmann S, et al. On the synthesis of neutron-rich isotopes along the N = 126 shell in multinucleon transfer reactions. Eur Phys J A. (2014) 50:161. doi: 10.1140/epja/i2014-14161-3

CrossRef Full Text | Google Scholar

7. Kozulin EM, Vardaci E, Knyazheva GN, Bogachev AA, Dmitriev SN, Itkis IM, et al. Mass distributions of the system ¹³⁶Xe+²⁰⁸Pb at laboratory energies around the Coulomb barrier: a candidate reaction for the production of neutron-rich nuclei at N = 126. Phys Rev C. (2012) 86:044611. doi: 10.1103/PhysRevC.86.044611

CrossRef Full Text | Google Scholar

8. Barrett JS, Loveland W, Yanez R, Zhu S, Ayangeakaa AD, Carpenter MP, et al. ¹³⁶Xe+²⁰⁸Pb reaction: a test of models of multinucleon transfer reactions. Phys Rev C. (2015) 91:064615. doi: 10.1103/PhysRevC.91.064615

CrossRef Full Text | Google Scholar

9. Loveland W. Synthesis of transactinide nuclei using radioactive beams. Phys Rev C. (2007) 76:014612. doi: 10.1103/PhysRevC.76.014612

CrossRef Full Text | Google Scholar

10. Zhu L, Su J, Xie WJ, Zhang FS. Theoretical study on production of heavy neutron-rich isotopes around the N=126 shell closure in radioactive beam induced transfer reactions. Phys Lett B. (2017) 767:437–42. doi: 10.1016/j.physletb.2017.01.082

CrossRef Full Text | Google Scholar

11. Bonaccorso A, Prete G. EURISOL: an European Isotope Separation On-Line radioactive ion beam facility. J Phys Confer Ser. (2009) 168:012023. doi: 10.1088/1742-6596/168/1/012023

CrossRef Full Text | Google Scholar

12. Karpov AV, Saiko VV. Modeling near-barrier collisions of heavy ions based on a Langevin-type approach. Phys Rev C. (2017) 96:024618. doi: 10.1103/PhysRevC.96.024618

CrossRef Full Text | Google Scholar

13. Winther A. Grazing reactions in collisions between heavy nuclei. Nucl Phys A. (1994) 572:191–235.

Google Scholar

14. Winther A. Dissipation, polarization and fluctuation in grazing heavy-ion collisions and the boundary to the chaotic regime. Nucl Phys A. (1995) 594:203–45.

Google Scholar

15. Corradi L, Stefanini AM, Ackermann D, Beghini S, Montagnoli G, Petrache C, et al. Multinucleon transfer reactions in ³²S+²⁰⁸Pb close to the Coulomb barrier. Phys Rev C. (1994) 49:R2875–9. doi: 10.1103/PhysRevC.49.R2875

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Dasso CH, Pollarolo G, Winther A. Systematics of isotope production with radioactive beams. Phys Rev Lett. (1994) 73:1907–10. doi: 10.1103/PhysRevLett.73.1907

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Corradi L, Pollarolo G, Szilner S. Multinucleon transfer processes in heavy-ion reactions. J Phys G Nucl Part Phys. (2009) 36:113101. doi: 10.1088/0954-3899/36/11/113101

CrossRef Full Text | Google Scholar

18. Montanari D, Corradi L, Szilner S, Pollarolo G, Fioretto E, Montagnoli G, et al. Neutron pair transfer in ⁶⁰Ni+¹¹⁶Sn far below the coulomb barrier. Phys Rev Lett. (2014) 113:052501. doi: 10.1103/PhysRevLett.113.052501

CrossRef Full Text | Google Scholar

19. Wen P, Li C, Zhu L, Lin C, Zhang F. Mechanism of multinucleon transfer reaction based on the GRAZING model and DNS model. J Phys G Nucl Part Phys. (2017) 44:115101. doi: 10.1088/1361-6471/aa8b07

CrossRef Full Text | Google Scholar

20. Penionzhkevich YE, Adamian GG, Antonenko NV. Towards neutron drip line via transfer-type reactions. Physics Lett B. (2005) 621:119–25. doi: 10.1016/j.physletb.2005.05.085

CrossRef Full Text | Google Scholar

21. Adamian GG, Antonenko NV, Lukyanov SM, Penionzhkevich YE. Possibility of production of neutron-rich isotopes in transfer-type reactions at intermediate energies. Phys Rev C. (2008) 78:024613. doi: 10.1103/PhysRevC.78.024613

CrossRef Full Text | Google Scholar

22. Feng ZQ. Production of neutron-rich isotopes around N = 126 in multinucleon transfer reactions. Phys Rev C. (2017) 95:024615. doi: 10.1103/PhysRevC.95.024615

CrossRef Full Text | Google Scholar

23. Guo SQ, Bao XJ, Zhang HF, Li JQ, Wang N. Effect of dynamical deformation on the production distribution in multinucleon transfer reactions. Phys Rev C. (2019) 100:054616. doi: 10.1103/PhysRevC.100.054616

CrossRef Full Text | Google Scholar

24. Wang N, Li Z, Wu X. Improved quantum molecular dynamics model and its applications to fusion reaction near barrier. Phys Rev C. (2002) 65:064608. doi: 10.1103/PhysRevC.65.064608

CrossRef Full Text | Google Scholar

25. Wang N, Li Z, Wu X, Tian J, Zhang Y, Liu M. Further development of the improved quantum molecular dynamics model and its application to fusion reactions near the barrier. Phys Rev C. (2004) 69:034608. doi: 10.1103/PhysRevC.69.034608

CrossRef Full Text | Google Scholar

26. Wang N, Guo L. New neutron-rich isotope production in 154Sm+160Gd. Phys Lett B. (2016) 760:236–41. doi: 10.1016/j.physletb.2016.06.073

CrossRef Full Text | Google Scholar

27. Welsh T, Loveland W, Yanez R, Barrett JS, McCutchan EA, Sonzogni AA, et al. Modeling multi-nucleon transfer in symmetric collisions of massive nuclei. Phys Lett B. (2017) 771:119–24. doi: 10.1016/j.physletb.2017.05.044

CrossRef Full Text | Google Scholar

28. Li C, Wen P, Li J, Zhang G, Li B, Xu X, et al. Production mechanism of new neutron-rich heavy nuclei in the Xe136+198Pt reaction. Phys Lett B. (2018) 776:278–83. doi: 10.1016/j.physletb.2017.11.060

CrossRef Full Text | Google Scholar

29. Desai VV, Loveland W, McCaleb K, Yanez R, Lane G, Hota SS, et al. The ¹³⁶Xe+¹⁹⁸Pt reaction: A test of models of multi-nucleon transfer reactions. Phys Rev C. (2019) 99:044604. doi: 10.1103/PhysRevC.99.044604

CrossRef Full Text | Google Scholar

30. Sekizawa K. Microscopic description of production cross sections including deexcitation effects. Phys Rev C. (2017) 96:014615. doi: 10.1103/PhysRevC.96.014615

CrossRef Full Text | Google Scholar

31. Jiang X, Wang N. Production mechanism of neutron-rich nuclei around N=126 in the multi-nucleon transfer reaction ¹³²Sn + ²⁰⁸Pb. Chinese Phys C. (2018) 42:104105. doi: 10.1088/1674-1137/42/10/104105

CrossRef Full Text | Google Scholar

32. Sekizawa K. TDHF theory and its extensions for the multinucleon transfer reaction: a mini review. Front Phys. (2019) 7:20. doi: 10.3389/fphy.2019.00020

CrossRef Full Text | Google Scholar

33. Wu Z, Guo L. Microscopic studies of production cross sections in multinucleon transfer reaction ⁵⁸Ni+¹²⁴Sn. Phys Rev C. (2019) 100:014612. doi: 10.1103/PhysRevC.100.014612

CrossRef Full Text | Google Scholar

34. Jiang X, Wang N. Probing the production mechanism of neutron-rich nuclei in multinucleon transfer reactions. Phys Rev C. (2020) 101:014604. doi: 10.1103/PhysRevC.101.014604

CrossRef Full Text | Google Scholar

35. Ayik S, Yilmaz B, Yilmaz O, Umar AS. Quantal diffusion approach for multinucleon transfers in Xe + Pb collisions. Phys Rev C. (2019) 100:014609. doi: 10.1103/PhysRevC.100.014609

CrossRef Full Text | Google Scholar

36. Charity RJ. Systematic description of evaporation spectra for light and heavy compound nuclei. Phys Rev C. (2010) 82:014610. doi: 10.1103/PhysRevC.82.014610

CrossRef Full Text | Google Scholar

37. Dirac PAM. Note on exchange phenomena in the Thomas atom. Math Proc Cambridge. (1930) 26:376–85.

Google Scholar

38. Simenel C, Chomaz P. Nonlinear vibrations in nuclei. Phys Rev C. (2003) 68:024302. doi: 10.1103/PhysRevC.68.024302

CrossRef Full Text | Google Scholar

39. Umar AS, Oberacker VE. Time-dependent response calculations of nuclear resonances. Phys Rev C. (2005) 71:034314. doi: 10.1103/PhysRevC.71.034314

CrossRef Full Text | Google Scholar

40. Simenel C, Keser R, Umar AS, Oberacker VE. Microscopic study of 16O+16O fusion. Phys Rev C. (2013) 88:024617. doi: 10.1103/PhysRevC.88.024617

CrossRef Full Text | Google Scholar

41. Jiang X, Maruhn JA, Yan S. Microscopic study of noncentral effects in heavy-ion fusion reactions with spherical nuclei. Phys Rev C. (2014) 90:064618. doi: 10.1103/PhysRevC.90.064618

CrossRef Full Text | Google Scholar

42. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Microscopic description of nuclear fission dynamics. J Phys G Nucl Part Phys. (2010) 37:064037. doi: 10.1088/0954-3899/37/6/064037

CrossRef Full Text | Google Scholar

43. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock: deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610

CrossRef Full Text | Google Scholar

44. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601. doi: 10.1103/PhysRevC.89.031601

CrossRef Full Text | Google Scholar

45. Maruhn JA, Reinhard PG, Stevenson PD, Strayer MR. Spin-excitation mechanisms in Skyrme-force time-dependent Hartree-Fock calculations. Phys Rev C. (2006) 74:027601. doi: 10.1103/PhysRevC.74.027601

CrossRef Full Text | Google Scholar

46. Loebl N, Umar AS, Maruhn JA, Reinhard PG, Stevenson PD, Oberacker VE. Single-particle dissipation in a time-dependent Hartree-Fock approach studied from a phase-space perspective. Phys Rev C. (2012) 86:024608. doi: 10.1103/PhysRevC.86.024608

CrossRef Full Text | Google Scholar

47. Guo L, Simenel C, Shi L, Yu C. The role of tensor force in heavy-ion fusion dynamics. Phys Lett B. (2018) 782:401–5. doi: 10.1016/j.physletb.2018.05.066

CrossRef Full Text | Google Scholar

48. Wen K, Barton MC, Rios A, Stevenson PD. Two-body dissipation effect in nuclear fusion reactions. Phys Rev C. (2018) 98:014603. doi: 10.1103/PhysRevC.98.014603

CrossRef Full Text | Google Scholar

49. Umar AS, Simenel C, Ye W. Transport properties of isospin asymmetric nuclear matter using the time-dependent Hartree-Fock method. Phys Rev C. (2017) 96:024625. doi: 10.1103/PhysRevC.96.024625

CrossRef Full Text | Google Scholar

50. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys. (2003) 75:121–80. doi: 10.1103/RevModPhys.75.121

CrossRef Full Text | Google Scholar

51. Maruhn JA, Reinhard PG, Stevenson PD, Umar AS. The {TDHF} code Sky3D. Comput Phys Commun. (2014) 185:2195–216. doi: 10.1016/j.cpc.2014.04.00

CrossRef Full Text | Google Scholar

52. Vautherin D, Brink DM. Hartree-Fock calculations with Skyrme's interaction. I. Spherical nuclei. Phys Rev C. (1972) 5:626–47. doi: 10.1103/PhysRevC.5.626

CrossRef Full Text | Google Scholar

53. Negele JW. The mean-field theory of nuclear structure and dynamics. Rev Mod Phys. (1982) 54:913–1015. doi: 10.1103/RevModPhys.54.913

CrossRef Full Text | Google Scholar

54. Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl Phys A. (1998) 635:231–56.

Google Scholar

55. Simenel C. Particle transfer reactions with the time-dependent Hartree-Fock theory using a particle number projection technique. Phys Rev Lett. (2010) 105:192701. doi: 10.1103/PhysRevLett.105.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Mancusi D, Charity RJ, Cugnon J. Unified description of fission in fusion and spallation reactions. Phys Rev C. (2010) 82:044610. doi: 10.1103/PhysRevC.82.044610

CrossRef Full Text | Google Scholar

57. Grangé P, Richert J, Wolschin G, Weidenmüller HA. Influence of a collision term on finite-size one-dimensional TDHF. Nucl Phys A. (1981) 356:260–8.

Google Scholar

58. Goeke K, Reinhard PG. Time-Dependent Hartree-Fock and Beyond. Prog Theor Phys Suppl. (1983) 171:33–65.

Google Scholar

59. Bass R. Fusion reactions: successes and limitations of a one-dimensional description. In: von Oertzen W, editor. Deep-Inelastic and Fusion Reactions with Heavy Ions. vol. 117 of Lecture Notes in Physics. Berlin; Heidelberg: Springer (1980). p. 281–93. doi: 10.1007/3-540-09965-4_23

CrossRef Full Text | Google Scholar