- 1Laboratory for Muon Spin Spectroscopy, Paul Scherrer Institute, Villigen, Switzerland
- 2Department of Physics, Tbilisi State University, Tbilisi, Georgia
- 3Department of Chemistry and Biochemistry, University of Bern, Bern, Switzerland
- 4Laboratory for Solid State Physics, ETH Zurich, Zurich, Switzerland
- 5CrystMat Company, Zurich, Switzerland
High quality single crystals of NdFeAsO0.65F0.35 (the superconducting transition temperature Tc ≃ 30.6 K) were studied in zero-field (ZF) and transverse-field (TF) muon-spin rotation/relaxation (μSR) experiments. An upturn in muon-spin depolarization rate at T ≲ 3 K was observed in ZF-μSR measurements and it was associated with the onset of ordering of Nd electronic moments. Measurements of the magnetic field penetration depth (λ) were performed in the TF geometry. By applying the external magnetic field Bex parallel to the crystallographic c-axis (Bex||c) and parallel to the ab-plane (Bex||ab), the temperature dependencies of the in-plane component () and the combination of the in-plane and the out of plane components () of the superfluid density were determined, respectively. The out-of-plane superfluid density component () was further obtained by combining the results of Bex||c and Bex||ab set of experiments. The temperature dependencies of , , and were analyzed within the framework of a self-consistent two-gap model despite of using the traditional α-model. Interband coupling was taken into account, instead of assuming it to be zero as it stated in the α-model. A relatively small value of the interband coupling constant Λ12 ≃ 0.01 was obtained, thus indicating that the energy bands in NdFeAsO0.65F0.35 are only weakly coupled. In spite of their small magnitude, the coupling between the bands leads to the single value of the superconducting transition temperature Tc. The penetration depth anisotropy γλ = λc/λab was found to increase upon cooling, consistent with most of Fe-based superconductors, and their behavior is attributed to the multi-band nature of superconductivity in NdFeAsO0.65F0.35.
1. Introduction
Iron-based superconductors (IBS's) remain a subject of intensive research due to a comparable large value of the transition temperature Tc. It reaches up to 55 K for the RFeAsO1−xFx IBS family (R corresponds to the lanthanides La, Sm, Ce, Nd, Pr, and Gd) [1–5] and approaches Tc ≃ 100 K in a single layer of FeSe on the SrTiO3 substrate [6]. Emergence of superconductivity at such high temperatures raises a puzzling question about the gap symmetry, which can further determine the pairing mechanism for the superconducting state.
The superconductivity in IBS's appears in close proximity to the magnetism offered by d-orbitals of Fe, hence one can expect the unconventional nature of the superconducting state. The electronic band structure calculations manifest that superconductivity in IBS's originates from multiple disconnected Fermi surface sheets derived from Fe d-orbitals, thus reflecting the possibility of a complex nature of the superconducting gap structure [7, 8]. There are already different scenarios proposed for the gap structure in IBS's including two-gap, s-wave, d-wave, isotropic, anisotropic, and surprisingly, p-type wave symmetry of the superconducting order parameter [9–18]. Even after several years of discovery of IBS's, an unified picture of the gap structure is not reached, contradicting the case of cuprate high-temperature superconductors, where almost all superconducting families represent a nodal pairing state [19]. In the context of conflicting results, there is still a need of comprehensive tools to understand the gap symmetry of IBS's. The magnetic penetration depth and its anisotropy carry important information about the low lying quasiparticles and hence can shed light on the gap structure of IBS's.
This paper presents a detailed muon-spin rotation/relaxation (μSR) study of high quality single crystals of NdFeAsO0.65F0.35 grown with high pressure and high temperature cubic anvil technique. Very few investigations were carried out in the direction of exploring the symmetry of the order parameter for NdFeAsO1−xFx (Nd-1111). As an example, a single gap without nodes at the Γ hole pocket was revealed through angle resolved photoemission spectroscopy (ARPES) [20], a nodal type gap structure was concluded through the linear behavior of the lower critical field Bc1 at low temperatures [21]. A multi-band nature of superconductivity seems to be a more generic feature for Nd-1111 as most measurements point toward a two superconducting gaps without nodes as, e.g., magnetic penetration depth measured through Tunnel Diode Resonator (TDR) technique [22], ARPES [23], point contact Andreev reflection spectroscopy [24, 25], conductance [26], and Bc1 measurements [27]. In most cases, however, the analysis of the multiple gap behavior was performed within the framework of a phenomenological α-model [28–37], which assumes zero coupling between the energy bands. In fact, the zero-coupling requires that the temperature dependencies of the energy gaps, as well as the values of the superconducting transition temperatures can not be identical and should vary from one to another energy band. Speaking in a broader way, there is a clear need of different set of data and an analysis which takes in account the coupling between the bands. In the present paper we approach to a so-called self-consistent model [38–41], allowing to analyze the magnetic penetration depth data obtained in the transverse field μSR experiment. Within this model, the energy bands with two different superconducting order parameters were assumed to be coupled and the gap equations were solved self-consistently by considering the presence of the “interband” and “intraband” coupling strengths.
The paper is organized as follows: In section 2 the sample preparation procedure, the results of magnetization measurements and the details of μSR experiments are briefly discussed. The experimental results obtained in zero-field (ZF) and transverse-field (TF) μSR experiments are described in section 3. The subsection 3.1 comprises studies of the magnetic response of NdFeAsO0.65F0.35. The subsection 3.2 describes the results of the field-shift experiments and the measurements of the temperature dependencies of the magnetic field penetration depth. The self-consistent two-gap model and the temperature evolution of the penetration depth anisotropy are presented in section 4. The conclusions follow in section 5.
2. Experimental Techniques
2.1. Sample Preparation
Bulk single crystals of NdFeAsO1−xFx with nominal fluorine content x = 0.35 were synthesized at 3 GPa and ≃ 1, 450°C from NaAs/KAs flux by using the cubic anvil high-pressure and high-temperature technique. The detailed description of the sample preparation procedure is given in reference [42]. The individual crystals obtained after the sample grow had a typical size of ~0.5 × 0.5 × 0.03 mm3.
2.2. Magnetization Measurements
The magnetization measurements were carried out on a Quantum Design MPMS-5 system. Figure 1 shows the temperature variation of the normalized magnetic moment [M(T)/M(T = 5K)] measured simultaneously on about thirty NdFeAsO0.65F0.35 single crystals. These crystals were further used in μSR experiments. The external field Bex = 0.5 mT was applied parallel to the ab plane of the crystals. Measurements were performed in the zero-field cooled (ZFC) mode. A sharp diamagnetic signal is seen across the superconducting transition which confirms the bulk nature of the superconductivity. The superconducting transition temperature Tc ≃ 30.6 K was determined from the cross point of the two lines extrapolated from the high temperature normal state and the low temperature superconducting state, respectively (see Figure 1).
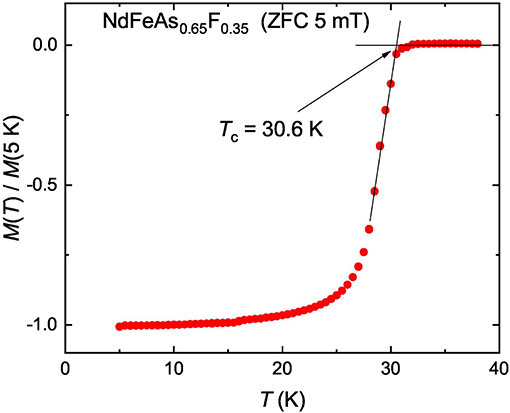
Figure 1. The zero-field cooled magnetization curve [M(T) curve] measured on about thirty NdFeAsO0.65F0.35 single crystals, which were further used in μSR experiments. The external magnetic field Bex = 0.5 mT was applied along the ab-plane of the crystals. The M(T) data were normalized to their M(T = 5K) value.
2.3. Muon-Spin Rotation/Relaxation Experiments
Muon-spin rotation/relaxation (μSR) measurements were carried out in a temperature range of 1.5–50 K at the GPS (General Purpose Surface) (πM3 beam line) and DOLLY (πE1 beam line) spectrometers at the Paul Scherrer Institut (PSI), Villigen, Switzerland. In this technique, 100% spin-polarized muons are implanted uniformly through the sample volume, where they decay with the lifetime of 2.2 μs and the relevant decay positrons are detected successively. Muons act as sensitive magnetic probes. The spin of the muon precesses in the local magnetic field Bμ with a frequency ωμ = γμBμ (γμ is muon gyromagnetic ratio, γμ/2π = 135.53 MHz/T). The detailed description of μSR technique and its applications for studying the superconducting and magnetic samples can be found in references [43–50].
A specific sample holder was designed in order to perform μSR experiments on thin single crystals of NdFeAsO0.65F0.35. A mosaic of about 200 single crystals was sandwiched between two sheets made of several 0.125 nm thick Kapton layers [51]. The first few Kapton layers decelerate the muons from incoming beam and served the role of a degrader. The outgoing muons from the degrader were slow enough to stop inside the thin single crystals. The last few layers were used to stop the muons which still manage to pass through the sample. A schematic picture of the sample holder can be found in the reference [52]. The data were analyzed using the free software package MUSRFIT [53].
3. Experimental Results
3.1. The Magnetic Response of NdFeAsO0.65F0.35: ZF-μSR Experiments
The μSR experiments in zero-field (ZF-μSR) were performed in order to study the magnetic response of the NdFeAsO0.65F0.35 sample. In two sets of experiments the initial muon-spin polarization P(0) was applied parallel to the c-axis and the ab-plane, respectively. Few representative muon-time spectra for P(0)||c and P(0)||ab orientations are shown in Figures 2A,C, respectively.
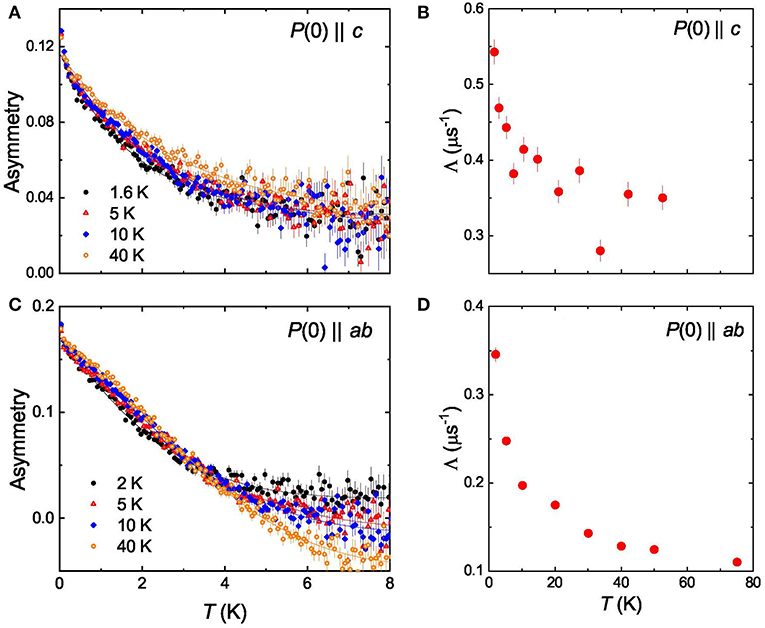
Figure 2. (A) ZF-μSR time-spectra of NdFeAsO0.65F0.35 measured at T = 1.6, 5, 10, and 40 K with the initial muon-spin polarization P(0) applied parallel to the crystallographic c−axis. (B) The temperature evolution of the exponential relaxation rate Λ obtained from the fit of Equation (1) to P(0)||c set of data. (C,D) —the same as in (A,B), but for P(0)||ab set of experiments and T = 2.0, 5, 10, and 40 K.
The experimental data were analyzed by separating the μSR response on the sample (s) and the background (bg) contributions:
Here A0 is the initial asymmetry of the muon-spin ensemble. As (Abg) and Ps(t) [Pbg(t)] are the asymmetry and the time evolution of the muon-spin polarization of the sample (background), respectively. The background contribution accounts for muons missing the sample and/or stopped in Kapton layers [52].
In ZF-μSR experiments the sample contribution was described by assuming the presence of the nuclear and the electronic magnetic moments:
Here the term within the square brackets is the Gaussian Kubo-Toyabe function with the relaxation rate σGKT, which is generally used to describe the nuclear magnetic moment contribution in ZF-μSR experiments (see e.g., references [43–49], and references therein). The exponential term with the relaxation parameter Λ represents the contribution of randomly distributed magnetic impurities and/or disordered magnetic moments [35, 54].
The temperature evolution of the exponential relaxation rate Λ for P(0)||c and P(0)||ab set of experiments are presented in Figures 2B,D. During fits the Gaussian Kubo-Toyabe relaxation σGKT entering Equation (2) was assumed to be dependent on the orientation, but independent on temperature, respectively. From the data presented in Figures 2B,D two important points emerges:
(i) No detectable change in the relaxation rates Λ is observed across the superconducting transition temperature, which rules out the possibility of any spontaneous magnetic field below Tc. This means that the time-reversal symmetry breaking is not an immanent feature of NdFeAsO0.65F0.35 studied here.
(ii) An increase in Λ is seen below 3 K for both orientations, which is probably associated with the onset of ordering of Nd magnetic moments. A similar upturn was seen in measured frequency shift [δf(T)] obtained by means of TDR technique and was explained with the ordering of the local magnetic moments of Nd below 4 K [22]. Further evidence comes form the powder Neutron diffraction experiment, where below ≃ 1.96 K a long range antiferromagnetic order was apparent and it was associated to the combined magnetic ordering of Fe and Nd magnetic moments in the parent compound NdFeAsO [55].
3.2. The Superconducting Response of NdFeAsO0.65F0.35: TF-μSR Experiments
3.2.1. The Homogeneity of the Superconducting State: Field-Shift Experiments
The homogeneity of the superconducting state and the effects of the flux-line lattice (FLL) pinning were probed by performing series of field-shift experiments in the transverse-field (TF) geometry. The measurements were carried out with the external magnetic field Bex applied parallel to the c-axis (Bex||c) and parallel to the ab-plane (Bex||ab), respectively. The sample was initially cooled in Bex ≃ 15 mT to the desired temperature (T ≃ 1.6 K for Bex∥c and T ≃ 5 K for Bex∥ab) where the first muon-time spectra were collected (red curves in Figures 3A,C). Then, by keeping the temperature constant, the field was decreased down to 12 mT and a new “field-shift” data sets were collected (black curves in Figures 3A,C). The corresponding Fast Fourier transform of the TF-μSR time-spectra, which reflects the internal field distribution P(B) inside the sample, are shown in Figures 3B,D.
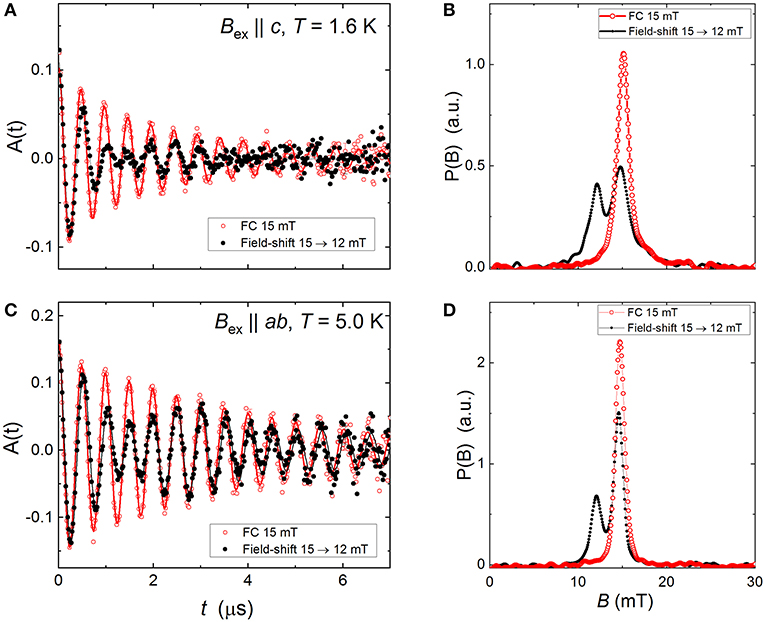
Figure 3. (A) TF-μSR time-spectra of NdFeAsO0.65F0.35 measured at T = 1.6 K with the external field Bex applied parallel to the crystallographic c−axis. The TF-μSR time-spectra denoted by red points correspond to the direct cooling at Bex = 15 mT from T above Tc down to 1.6 K. The black points correspond to time-spectra obtained after a subsequent field decrease to 12 mT without changing temperature. (B) The Fast Fourier transform of the TF-μSR time-spectra presented at (A). (C,D) —the same as in (A,B), but for Bex||ab and at T = 5 K.
The data presented in Figures 3B,D reveal that for both field orientations the main part of the signal, accounting for ~70% of the total signal amplitude, remains unchanged within the experimental accuracy. Only the symmetric sharp peak follows exactly the applied field. It is attributed, therefore, to the residual background signal from muons missing the sample (see also reference [54], where the first μSR field-shift experiments were introduced). The field-shift measurements clearly demonstrate that for both, Bex||c and Bex||ab field orientations, the flux-line lattice in NdFeAsO0.65F0.35 sample is strongly pinned.
The field distribution caused entirely by the flux-line lattice was further obtained by subtracting the symmetric background peak. The corresponding P(B)′s are represented in Figure 4 by blue curves. It is worth noting that, for both field orientation P(B) distributions possess the basic features expected for an arranged flux-line lattice. The cutoff at low fields, the pronounced peak at the intermediate field and the long tail in the high field directions are clearly visible.
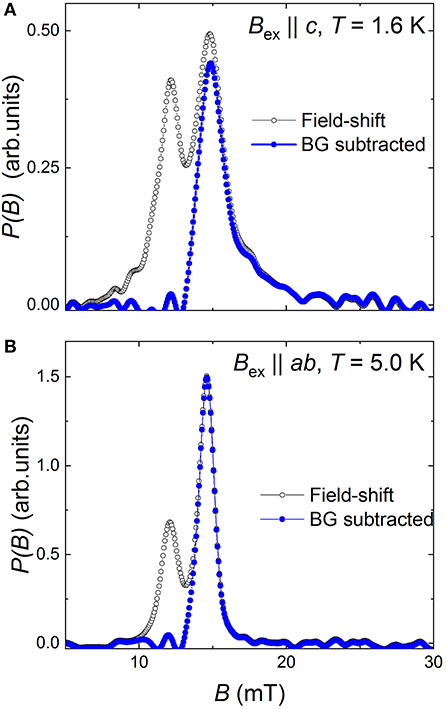
Figure 4. The magnetic field distribution P(B) caused by formation of the flux-line lattice in NdFeAsO0.65F0.35 sample in Bex||c (A) and Bex||ab (B) set of experiments. The blue curves are obtained by subtracting the symmetric background peak (see text for details).
3.2.2. Analysis of Bex||c and Bex||ab Set of TF-μSR Data
The distribution of the internal magnetic fields P(B) in the superconductor in the FLL state is uniquely determined by two characteristic lengths: the magnetic field penetration depth λ and the coherence length ξ. For an isotropic extreme type-II superconductor (λ ≫ ξ) and for fields much smaller than the upper critical field Bc2 (Bex ≪ Bc2) the P(B) is almost independent on ξ and it could be calculated from the spatial variation of the internal magnetic field B(r) (r is the spatial coordinate) [56, 57]. In the present work the magnetic field distribution P(B), measured by means of TF-μSR, was analyzed assuming B(r) is being described within the framework of Ginzburg-Landau approach [56–59].
The spatial distribution of magnetic fields in the mixed state of a type-II superconductor is calculated via the Fourier expansion [56–59]:
Here 〈B〉 is the average magnetic field inside the superconductor, G is the reciprocal vector, r represents the vector coordinate in a plane perpendicular to the applied magnetic field and BG is the Fourier component. Within the Ginzburg-Landau model BG is obtained via [58]:
ϕ0 is the magnetic flux quantum, S = ϕ0/〈B〉 represents the area of the FLL unit cell, b = 〈B〉/Bc2, K1(u) is the modified Bessel function, with u2 = 2ξ2G2(1 + b4)[1 − 2b(1 − b)2]. For the hexagonal FLL, the reciprocal lattice is . m and n are the integer numbers.
The internal field distribution within the “ideal” flux-line lattice was obtained as:
Here dA(B′) is the elementary area of the FLL with a field B′ inside, and the integration is performed over a quarter of the flux-line lattice unit cell [60]. The FLL disorder, the broadening of the TF-μSR line due to the nuclear depolarization and the contribution of the electronic moments were considered by convoluting Pid(B) with Gaussian and Lorentzian functions [34, 35, 57, 61]. Finally, the following depolarization function was fitted to the measured TF-μSR data:
Here ϕ is phase of the muon-spin ensemble, Λ represents the relaxation rate associated with the electronic moment, and σg is associated with the FLL disorder and the nuclear moment contributions, respectively. In our calculations Λ was fixed to the values obtained in ZF-μSR experiments (see section 3.1 and Figure 2).
The results of the fit of Equation (1) with the sample part described by Equation (6) to the Bex||c and B||ab set of data are presented in Figure 5. Note that with the field applied parallel to the c-axis the screening current, flowing around the flux-line cores, remains within the ab-plane. This means that the field distribution P(B) in Bex||c set of experiments is determined by the so-called in-plane component of the magnetic penetration depth λab (Figure 5A). Note that in superconductors with the tetragonal layered crystal structure, as NdFeAsO0.65F0.35, the a- and b- components of the magnetic penetration depth are equal: λa = λb [31]. With the field applied parallel to the a(b)-axis, the screening current flows along the b(a) and c-axes, respectively. Consequently, in Bex||ab set of experiments λab, c is obtained (Figure 5B).
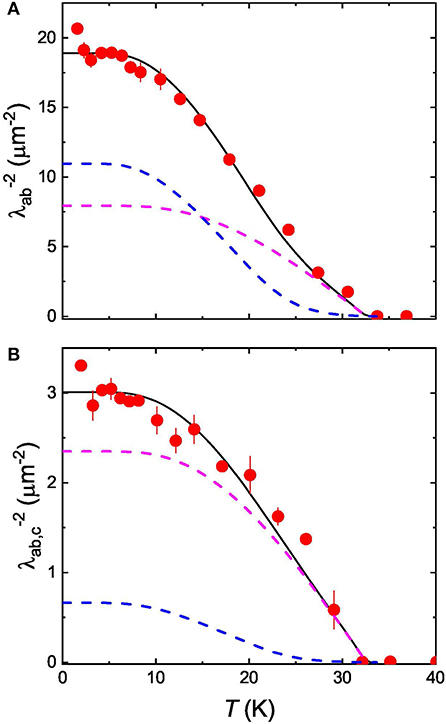
Figure 5. Temperature evolution of the inverse squared magnetic penetration depth of NdFeAsO0.65F0.35: (A) — and (B) —. Black solid lines are theoretical curves obtained by analyzing the data within the self-consistent two-gap model. The dashed pink and blue lines are contributions of the larger (Δ1), and the smaller (Δ2) gaps to the magnetic penetration depth, respectively. See section 4.1 for details.
4. Discussions
4.1. Temperature Dependencies of and
Temperature dependencies of and , as they reported in section 3.2.2, are shown in Figures 5A,B, respectively. Due to a possible influence caused by ordering of Nd magnetic moments (see the discussion in section 3.1 and Figure 2), the data points below 5 K were excluded from consideration.
In order to elucidate the pairing states in NdFeAsO0.65F0.35, the experimental data were analyzed by means of a two-gap model, with both gaps having an s-wave symmetry. Despite of considering a similar BCS type temperature dependence for both the gaps, as in phenomenological α-model [28–33, 35–37], the temperature dependencies of the two gaps (Δ1 and Δ2) were obtained through a self-consistent coupled gap equations [38, 40, 41]:
Here, N1(0) and N2(0) are the partial density of states for each band at the Fermi level. V11 (V22) and V12 (V21) are the intraband and the interband interaction potentials, respectively. ωD1 (ωD2) is the Debye (cut-off) phonon frequency of the band 1 (2).
A simplification of the above expressions can be done by using the notation for the coupling constant Λij = Nj(0)Vij, as is introduced by Kogan et al. [39]. Further simplification is made by assuming a similar Debye frequency for both the bands, i.e., ωD1 = ωD2 = ωD. The gap equation becomes [40, 41]:
The advantage the above mentioned simplifications is that: (i) in the notation of Kogan et al. [39] Λ12 = Λ21 and (ii) the number of the free parameters, which were initially eight in Equation (7), namely: ωD1, ωD2, N1(0), and N2(0), V11, V12, V21, and V22; reduces to four in Equation (8), namely: ωD, Λ11, Λ12, and Λ22 [40, 41].
With the known temperature variation of Δ1(T) and Δ2(T), a rigorous analysis of λ−2 is carried out by separating it into two components [39, 41]:
ω is the weight factor for the larger gap Δ1 and is the superfluid density component of the i−th band. The superfluid density component is related to the superconducting energy gap via the expression [62]:
where is the Fermi distribution function.
For the analysis of the temperature evolution of magnetic penetration depths, the literature value of the Debye frequency, ωD = 37 meV, obtained in Mössbauer experiments [63], was considered. The coupling constants: Λ11, Λ22, and Λ12; the gaps: Δ1(T), Δ2(T) were kept identical during the analysis of and , but the weight factor ω was varied. The common parameters obtained with the analysis of and are: Λ11 ≃ 0.368, Λ22 ≃ 0.315, Λ12 ≃ 0.01, Δ1(0) ≃ 5.2 meV, Δ2(0) ≃ 3.5 meV, and Tc ≃ 33.7 K. The weighting factors (ω) and the zero-temperature values of the inverse squared magnetic penetration depth [λ−2(0)] are 0.42/0.85 and 18.9/3.0 μm−2 for and , respectively.
Contribution of the penetration depths corresponding to the larger gap (Δ1) and the smaller gap (Δ2) are shown in Figures 5A,B by dashed pink and blue lines, respectively. The solid black lines are the theory curves obtained by means of two-gap model as described earlier. The temperature dependencies of the gaps [Δ1(T) and Δ2(T)] and the corresponding superfluid density components [ and ] are presented in Figure 6.
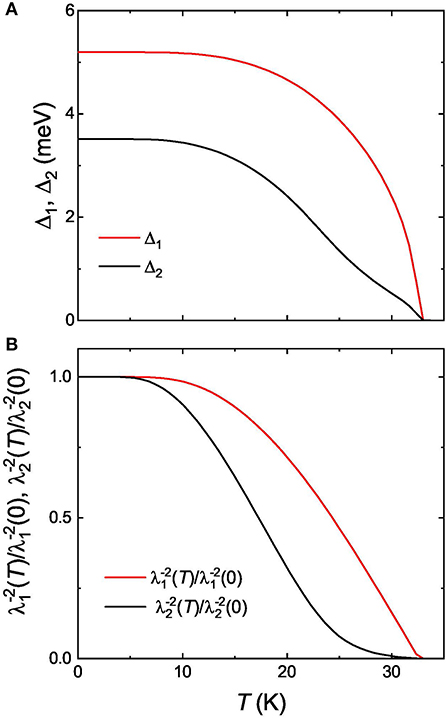
Figure 6. (A) Temperature evolution of the Δ1 and Δ2 superconducting energy gaps obtained within the framework of the self-consistent two-gap model. (B) Temperature evolution of the corresponding superfluid density contributions and . See section 4.1 for details.
From the analysis of the magnetic penetration depths data by means of two-gap model three following important points emerge:
(i) The interband coupling constant Λ12 ≃ 0.01 is relatively small, indicating the fact that the two bands are nearly decoupled. However, the value of Λ12 is significant enough to assign a single Tc for each gap along both the planes.
(ii) The gap to Tc ratio for the bigger gap 2Δ1/kBTc ≃ 3.58 is close to the universal BCS value 3.52. For the lower gap 2Δ2/kBTc = 2.41 is found. This indicates the weak coupling regime for both the gaps.
(iii) The difference in the temperature variation of and arises because of much smaller contribution of larger gap to compared to that to .
4.2. Out of Plane Magnetic Penetration Depth,
This section describes the determination of the out of plane component of the magnetic penetration depth, , and its analysis based on self-consistent two-gap model.
According to the London model, the inverse squared magnetic field penetration depth for the isotropic superconductor is proportional to the superfluid density in terms of (ρs is the superfluid density, ns is the charge carrier concentration and m* is the effective mass of the charge carriers). For an anisotropic superconductor, as NdFeAsO0.65F0.35, the magnetic penetration depth is also anisotropic and is determined by an effective mass tensor [64]:
Here, is the effective mass of charge carrier flowing along i-th principal axis. For a magnetic field applied along i-th principal axis of the effective mass tensor, the effective penetration depth is given as [64]:
By using Equation (12) the out of plane component of the magnetic penetration depth, , was further obtained from and data shown in Figure 5 as:
The resulting dependence of on temperature is shown in Figure 7. The theoretical temperature variation of was also obtained from the theory curves for and , as they are described in Figures 5A,B, and it is represented by solid black line. It is evident that the curve obtained by means of two-gap model replicates the experimental data very well, which indicates that the magnetic penetration depth along c-axis is well-analyzed with two-gap s + s-wave model. For the zero-temperature value of the out-of plane component the value μm−2 is obtained.
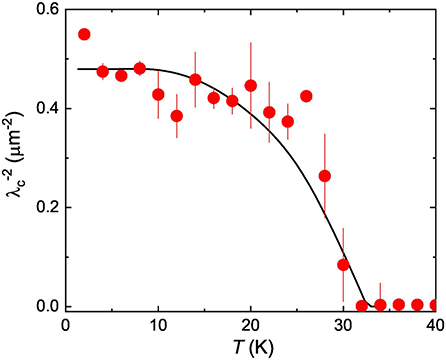
Figure 7. Temperature evolution of the inverse squared out of plane magnetic penetration depth . The solid line is obtained from the theoretical and curves, as they presented in Figure 5, by using Equation (13).
4.3. The Magnetic Penetration Depth Anisotropy, γλ
Figure 8A shows the temperature evolution of the magnetic penetration depth anisotropy obtained with the experimental data presented in Figure 5 and Equation (12):
γλ(T) increases with decreasing temperature from γλ ≃ 1.8 at T = Tc to γλ ≃ 6.3 close to T = 0 K. The theoretical curve obtained within the self-consistent two-band model is represented by the solid black line. The temperature variation of anisotropy is reproduced well with this theoretical curve, which further confirms the multi-band nature of superconductivity in the studied oxypnictide material. It is worth to mention, that and , obtained within the present study, were measured on a mosaic of about 200 NdFeAsO0.65F0.35 single crystalline samples. For such a big number of simultaneously measured crystals a certain misalignment will definitively take place. Consequently, our results put a lower limit on the determination of γλ.
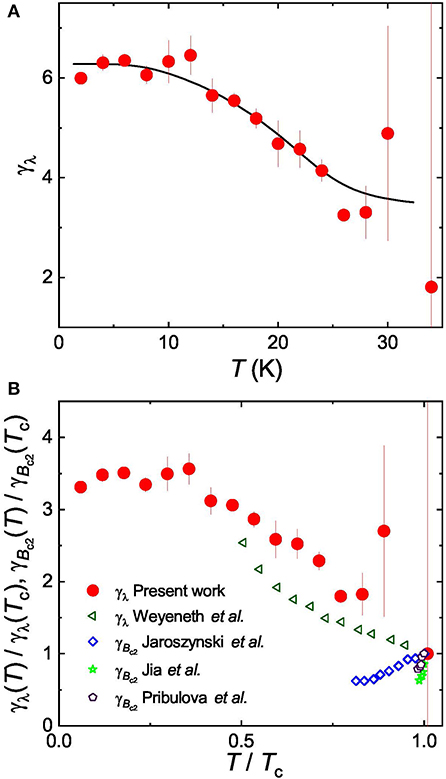
Figure 8. (A) Temperature dependence of the magnetic penetration depth anisotropy, γλ(T) = λc(T)/λab(T). The solid curve is the result of the self-consistent two-gap model. (B) Comparison of γλ(T)/γλ(Tc) (from the present work and reference [65]) with the anisotropy of the upper critical field γBc2(T)/γBc2(Tc) from references [66–68].
Figure 8B compares γλ obtained in the present study with that measured by means of torque magnetometry by Weyeneth et al. [65]. In both cases λλ increases with decreasing T. A similar qualitative behavior of γλ(T) was observed in Sm- and Nd-1111 systems by means of torque magnetometry [65, 69]; in Ba(Fe1−xCox)2As2 by means of TDR [70]; in Ba1−xKxFe2As2 [34], SrFe1.75Co0.25As2 [35], FeSe0.5Te0.5 [71], CaKFe4As4 [37], by means of μSR, etc. In all these works the pronounced temperature dependence of γλ was attributed to the multiple gap nature of superconductivity.
As a further step, γλ is compared with the anisotropy of the upper critical field γBc2 for NdFeAsO1−xFx, as obtained form resistivity [66, 67] and specific heat measurements [68]. According to the phenomenological Ginzburg-Landau theory, these two anisotropies should be equal for a single gap superconductor [62, 72]:
Figure 8B implies that the two anisotropies show opposite trends with temperature and violate the Ginzburg-Landau theory. This situation is reminiscent of well-known two-gap superconductor MgB2, despite the reversed slope for both the anisotropies [73, 74].
5. Conclusions
To conclude, the magnetic and the superconducting properties of NdFeAsO0.65F0.35 single crystalline samples were studied by means of muon-spin rotation/relaxation technique. The results can be summarized as follows:
(i) No changes in the relaxation rate was observed in ZF-μSR spectra across the superconducting transition, thus ruling out the possibility of any spontaneous magnetic field below Tc.
(ii) An upturn in exponential muon-spin depolarization rate at T ≲ 3 K is detected in ZF-μSR measurements. It is most probably associated with the onset of ordering of Nd electronic moments.
(iii) Measurements of the magnetic field penetration depth (λ) were performed in the TF geometry. By applying the external magnetic field Bex parallel to the crystallographic c-axis and parallel to the ab-plane, the temperature dependencies of the in-plane component and the combination of the in-plane and the out of plane components of the superfluid density were determined, respectively. The out-of-plane component was further obtained by combining the results of Bex||c and Bex||ab set of experiments.
(iv) The temperature dependencies of , , and were analyzed within the framework of a self-consistent two-gap model despite of using the traditional α-model. Interband coupling is taken into account instead of assuming it to be zero as is assumed in the α-model. The values of intraband and interband coupling constants were determined to be: Λ11 ≃ 0.368, Λ22 ≃ 0.315, Λ12 ≃ 0.01. A relatively small value of the interband coupling constant Λ12 indicates that the energy bands in NdFeAsO0.65F0.35 are nearly decoupled.
(v) The zero-temperature values of the inverse squared magnetic penetration depth and the superconducting energy gaps were estimated to be: μm−2, μm−2, Δ1(0) ≃ 5.2 meV, and Δ2(0) ≃ 3.5 meV, respectively.
(vi) The magnetic penetration depth anisotropy, γλ = λab/λc increases from γλ ≃ 1.8 at T = Tc to γλ ≃ 6.3 close to T = 0 K, while the upper critical field anisotropy γBc2 demonstrates the opposite temperature behavior. This experimental situation is similar to MgB2, a well-known two-gap superconductor, which further provides a strong evidence for multiple band superconductivity in the studied NdFeAsO0.65F0.35 compound.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
RK conceived the topic, conducted the experiment, analyzed the data, wrote and prepared the manuscript. RG analyzed the data and wrote the manuscript. AM analyzed the data and took part in physics discussions. NZ synthesized the single crystals of NdFeAsO0.65F0.35 and took part in physics discussions. HL and AA revised the manuscript. All authors participated in manuscript review.
Funding
The work of RG was supported by the Swiss National Science Foundation (SNF-Grant No. 200021-175935).
Conflict of Interest
NZ becomes an owner and is employed by the company CRYSTMAT.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was performed at Swiss Muon Source (SμS), Paul Scherrer Institute (PSI, Switzerland). RK, AM, and NZ thank Bertram Batlogg for fruitful discussions on the early stage of this study.
References
1. Ren ZA, Yang J, Lu W, Yi W, Che GC, Dong XL, et al. Superconductivity at 52 K in iron based F doped layered quaternary compound Pr[O1−−xFx]FeAs. Mater Res Innov. (2008) 12:105–6. doi: 10.1179/143307508X333686
2. Yang J, Li ZC, Lu W, Yi W, Shen XL, Ren ZA, et al. Superconductivity at 53.5 K in GdFeAsO1−δ. Supercond Sci Technol. (2008) 21:082001. doi: 10.1088/0953-2048/21/8/082001
3. Ren ZA, Lu W, Yang J, Yi W, Shen XL, Zheng C, et al. Superconductivity at 55 K in iron-based F-doped layered quaternary compound Sm[O1−xFx]FeAs. Chin Phys Lett. (2008) 25:2215–6. doi: 10.1088/0256-307X/25/6/080
4. Chen XH, Wu T, Wu G, Liu RH, Chen H, Fang DF. Superconductivity at 43 K in SmFeAsO1−xFx. Nature. (2008) 453:761–2. doi: 10.1038/nature07045
5. Chen GF, Li Z, Wu D, Li G, Hu WZ, Dong J, et al. Superconductivity at 41 K and its competition with spin-density-wave instability in layered CeO1−xFxFeAs. Phys Rev Lett. (2008) 100:247002. doi: 10.1103/PhysRevLett.100.247002
6. Ge JF, Liu ZL, Liu C, Gao CL, Qian D, Xue QK, et al. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat Mater. (2015) 14:285–9. doi: 10.1038/nmat4153
7. Singh DJ, Du MH. Density functional study of LaFeAsO1−xFx: a low carrier density superconductor near itinerant magnetism. Phys Rev Lett. (2008) 100:237003. doi: 10.1103/PhysRevLett.100.237003
8. Yin ZP, Lebeǵue S, Han MJ, Neal BP, Savrasov SY, Pickett WE. Electron-hole symmetry and magnetic coupling in antiferromagnetic LaFeAsO. Phys Rev Lett. (2008) 101:047001. doi: 10.1103/PhysRevLett.101.047001
9. Daghero D, Tortello M, Gonnelli RS, Stepanov VA, Zhigadlo ND, Karpinski J. Evidence for two-gap nodeless superconductivity in SmFeAsO1−xFx from point-contact Andreev-reflection spectroscopy. Phys Rev B. (2009) 80:060502(R). doi: 10.1103/PhysRevB.80.060502
10. Malone L, Fletcher JD, Serafin A, Carrington A, Zhigadlo ND, Bukowski Z, et al. Magnetic penetration depth of single-crystalline SmFeAsO1−xFy. Phys Rev B. (2009) 79:140501(R). doi: 10.1103/PhysRevB.79.140501
11. Kuzmicheva TE, Kuzmichev SA, Pervakov KS, Pudalov VM, Zhigadlo ND. Evolution of superconducting gaps in Th-substituted Sm1−xThxOFeAs studied by multiple Andreev reflection spectroscopy. Phys Rev B. (2017) 95:094507. doi: 10.1103/PhysRevB.95.094507
12. Matano K, Ren ZA, Dong XL, Sun LL, Zhao ZX, Zheng GQ. Spin-singlet superconductivity with multiple gaps in PrFeAsO0.89F0.11. Eur Phys Lett. (2008) 83:57001. doi: 10.1209/0295-5075/83/57001
13. Kuroki K, Onari S, Arita R, Usui H, Tanaka Y, Kontani H, et al. Unconventional pairing originating from the disconnected fermi surfaces of superconducting LaFeAsO1−xFx. Phys Rev Lett. (2008) 101:087004. doi: 10.1103/PhysRevLett.101.087004
14. Patrick AL, Xiao-Gang W. Spin-triplet p-wave pairing in a three-orbital model for iron pnictide superconductors. Phys Rev B. (2008) 78:144517. doi: 10.1103/PhysRevB.78.144517
15. Evtushinsky DV, Inosov DS, Zabolotnyy VB, Viazovska MS, Khasanov R, Amato A, et al. Momentum-resolved superconducting gap in the bulk of Ba1−xKxFe2As2 from combined ARPES and μSR measurements. New J Phys. (2009) 11:055069. doi: 10.1088/1367-2630/11/5/055069
16. Borisenko SV, Evtushinsky DV, Liu ZH, Morozov I, Kappenberger R, Wurmehl S, et al. Direct observation of spin-orbit coupling in iron-based superconductors. Nat Phys. (2016) 12:311–7. doi: 10.1038/nphys3594
17. Charnukha A, Thirupathaiah S, Zabolotnyy VB, Büchner B, Zhigadlo ND, Batlogg B, et al. Interaction-induced singular fermi surface in a high-temperature oxypnictide superconductor. Sci Rep. (2015) 5:10392. doi: 10.1038/srep10392
18. Khasanov R, Meier WR, Wu Y, Mou D, Bud'ko SL, Eremin I, et al. In-plane magnetic penetration depth of superconducting CaKFe4As4. Phys Rev B. (2018) 97:140503(R). doi: 10.1103/PhysRevB.97.140503
19. Tsuei CC, Kirtley JR. Pairing symmetry in cuprate superconductors. Rev Mod Phys. (2000) 72:969–1016. doi: 10.1103/RevModPhys.72.969
20. Kondo T, Santander-Syro AF, Copie O, Liu C, Tillman ME, Mun ED, et al. Momentum dependence of the superconducting gap in NdFeAsO0.9F0.1 single crystals measured by angle resolved photoemission spectroscopy. Phys Rev Lett. (2008) 101:147003. doi: 10.1103/PhysRevLett.101.147003
21. Wang XL, Dou SX, Ren ZA, Yi W, Li ZC, Zhao ZX, et al. Unconventional superconductivity of NdFeAsO0.82F0.18 indicated by the low temperature dependence of the lower critical field Hc1. J Phys Condens Matter. (2009) 21:205701. doi: 10.1088/0953-8984/21/20/205701
22. Martin C, Tillman ME, Kim H, Tanatar MA, Kim SK, Kreyssig A, et al. Nonexponential london penetration depth of FeAs-based superconducting RFeAsO0.9FP0.1 (R=La, Nd) single crystals. Phys Rev Lett. (2009) 102:247002. doi: 10.1103/PhysRevLett.102.247002
23. Charnukha A, Evtushinsky DV, Matt CE, Xu N, Shi M, Büchner B, et al. High-temperature superconductivity from fine-tuning of Fermi-surface singularities in iron oxypnictides. Sci Rep. (2015) 5:18273. doi: 10.1038/srep18273
24. Samuely P, Szabó P, Pribulová Z, Tillman ME, Bud'ko SL, Canfield PC. Possible two-gap superconductivity in NdFeAsO0.9F0.1 probed by point-contact Andreev-reflection spectroscopy. Supercond Sci Technol. (2009) 22:014003. doi: 10.1088/0953-2048/22/1/014003
25. Kuzmicheva TE, Kuzmichev SA, Zhigadlo ND. Superconducting order parameter and bosonic mode in hydrogen-substituted NdFeAsO0.6H0.36 revealed by multiple-Andreev-reflection spectroscopy. Phys Rev B. (2019) 100:144504. doi: 10.1103/PhysRevB.100.144504
26. Miyakawa N, Minematsu M, Kawashima S, Ogata K, Miyazawa K, Kito H, et al. Probing the superconducting gap from tunneling conductance on NdFeAsO0.7 with Tc = 51 K. J Supercond Nov Mag. (2010) 23:575–8. doi: 10.1007/s10948-010-0689-9
27. Adamski A, Krellner C, Abdel-Hafiez M. Signature of multigap nodeless superconductivity in fluorine-doped NdFeAsO. Phys Rev B. (2018) 96:100503(R). doi: 10.1103/PhysRevB.96.100503
28. Bouquet F, Wang Y, Fisher RA, Hinks DG, Jorgensen JD, Junod A, et al. Phenomenological two-gap model for the specific heat of MgB2. Europhys Lett. (2001) 56:856–62. doi: 10.1209/epl/i2001-00598-7
29. Carrington A, Manzano F. Magnetic penetration depth of MgB2. Phys C. (2003) 385:205–14. doi: 10.1016/S0921-4534(02)02319-5
30. Guritanu V, Goldacker W, Bouquet F, Wang Y, Lortz R, Goll G, et al. Specific heat of Nb3Sn: the case for a second energy gap. Phys Rev B. (2004) 70:184526. doi: 10.1103/PhysRevB.70.184526
31. Prozorov R, Giannetta RW. Magnetic penetration depth in unconventional superconductors. Supercond Sci Technol. (2006) 19:R41–67. doi: 10.1088/0953-2048/19/8/R01
32. Khasanov R, Shengelaya A, Maisuradze A, La Mattina F, Bussmann-Holder A, Keller H, et al. Experimental evidence for two gaps in the high-temperature La1.83Sr0.17CuO4 superconductor. Phys Rev Lett. (2007) 98:057007. doi: 10.1103/PhysRevLett.98.057007
33. Khasanov R, Shengelaya A, Karpinski J, Bussmann-Holder A, Keller H, Müller KA. s-Wave symmetry along the c-axis and s+d in-plane superconductivity in bulk YBa2Cu4O8. J Supercond Nov Magn. (2008) 21:81–5. doi: 10.1007/s10948-007-0302-z
34. Khasanov R, Evtushinsky DV, Amato A, Klauss HH, Luetkens H, Niedermayer Ch, et al. Two-gap superconductivity in Ba1−xKxFe2As2: a complementary study of the magnetic penetration depth by Muon-spin rotation and angle-resolved photoemission. Phys Rev Lett. (2009) 102:187005. doi: 10.1103/PhysRevLett.102.187005
35. Khasanov R, Maisuradze A, Maeter H, Kwadrin A, Luetkens H, Amato A, et al. Superconductivity and field-induced magnetism in SrFe1.75Co0.25As2. Phys Rev Lett. (2009) 103:067010. doi: 10.1103/PhysRevLett.103.067010
36. Khasanov R, Amato A, Biswas PK, Luetkens H, Zhigadlo ND, Batlogg B. SrPt3P: a two-band single-gap superconductor. Phys Rev B. (2014) 90:140507(R). doi: 10.1103/PhysRevB.90.140507
37. Khasanov R, Meier WR, Bud'ko SL, Luetkens H, Canfield PC, Amato A. Anisotropy induced vortex lattice rearrangement in CaKFe4As4. Phys Rev B. (2019) 99:140507(R). doi: 10.1103/PhysRevB.99.140507
38. Bussmann-Holder A, Micnas R, Bishop AR. Enhancements of the superconducting transition temperature within the two-band model. Eur Phys J B. (2004) 37:345–8. doi: 10.1140/epjb/e2004-00065-5
39. Kogan VG, Martin C, Prozorov R. Superfluid density and specific heat within a self-consistent scheme for a two-band superconductor. Phys Rev B. (2009) 80:014507. doi: 10.1103/PhysRevB.80.014507
40. Bussmann-Holder A. Comment on: superfluid density and specific heat within a self-consistent scheme for a two-band superconductor. arXiv:0909.3603.
41. Khasanov R, Bendele M, Amato A, Conder K, Keller H, Klauss HH, et al. Evolution of two-gap behavior of the superconductor FeSe1−x. Phys Rev Lett. (2010) 104:087004. doi: 10.1103/PhysRevLett.104.087004
42. Zhigadlo ND, Weyeneth S, Katrych S, Moll PJW, Rogacki K, Bosma S, et al. High-pressure flux growth, structural, and superconducting properties of LnFeAsO (Ln = Pr, Nd, Sm) single crystals. Phys Rev B. (2012) 86:214509. doi: 10.1103/PhysRevB.86.214509
43. Schenck A. Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State Physics. Bristol: Hilger (1985).
44. Cox SFJ. Implanted muon studies in condensed matter science. J Phys C Solid State Phys. (1987) 20:3187–319. doi: 10.1088/0022-3719/20/22/005
45. Dalmas de Réotier P, Yaouanc A. Muon spin rotation and relaxation in magnetic materials. J Phys Condens Matter. (1997) 9:9113–66. doi: 10.1088/0953-8984/9/43/002
46. Yaouanc A, Dalmas de Réotier P. Muon Spin Rotation, Relaxation and Resonance: Applications to Condensed Matter. Oxford: Oxford University Press (2011).
47. Blundell SJ. Spin-polarized muons in condensed matter physics. Contemp Phys. (1999) 40:175–92. doi: 10.1080/001075199181521
48. Sonier JE, Brewer JH, Kiefl RF. μSR studies of the vortex state in type-II superconductors. Rev Mod Phys. (2000) 72:769–811. doi: 10.1103/RevModPhys.72.769
49. Uemura YJ. Muon spin relaxation studies of unconventional superconductors: first-order behavior and comparable spin-charge energy scales. In: Avella A, Mancini F, editors. Strongly Correlated Systems, Springer Series Solid-State Science, Vol. 180. Berlin; Heidelberg: Springer (2015).
50. Karl R, Burri F, Amato A, Donegà M, Gvasaliya S, Luetkens Hu, et al. Muon spin rotation study of type-I superconductivity: elemental β-Sn. Phys Rev B. (2019) 99:184515. doi: 10.1103/PhysRevB.99.184515
51. Available, online at: https://www.dupont.com/electronic-materials/polyimide-films.html (accessed January 22, 2020).
52. Khasanov R, Zhou H, Amato A, Guguchia Z, Morenzoni E, Dong X, et al. Proximity-induced superconductivity within the insulating (Li0.84Fe0.16)OH layers in (Li0.84Fe0.16)OHFe0.98Se. Phys Rev B. (2016) 93:224512. doi: 10.1103/PhysRevB.93.224512
53. Suter A, Wojek BM. Musrfit: a free platform-independent framework for μSR data analysis. Phys Proc. (2012) 30:69–73. doi: 10.1016/j.phpro.2012.04.042
54. Sonier JE, Kiefl RF, Brewer JH, Bonn DA, Carolan JF, Chow KH, et al. New muon-spin-rotation measurement of the temperature dependence of the magnetic penetration depth in YBa2Cu3O6.95. Phys Rev Lett. (1994) 72:744–7. doi: 10.1103/PhysRevLett.72.744
55. Qiu Y, Bao W, Huang Q, Yildirim T, Simmons JM, Green MA, et al. Crystal structure and antiferromagnetic order in NdFeAsO1−xFx (x=0.0 and 0.2) superconducting compounds from neutron diffraction measurements. Phys Rev Lett. (2008) 101:257002. doi: 10.1103/PhysRevLett.101.257002
56. Brandt EH. Flux distribution and penetration depth measured by muon spin rotation in high-Tc superconductors. Phys Rev B. (1988) 37:2349–52. doi: 10.1103/PhysRevB.37.2349
57. Maisuradze A, Khasanov R, Shengelaya A, Keller H. Comparison of different methods for analyzing μSR line shapes in the vortex state of type-II superconductors. J Phys Condens Matter. (2009) 21:075701. doi: 10.1088/0953-8984/21/7/075701
58. Yaouanc A, Dalmas de Reotier P, Brandt EH. Effect of the vortex core on the magnetic field in hard superconductors. Phys Rev B. (1997) 55:11107–10. doi: 10.1103/PhysRevB.55.11107
59. Clem JR. Simple model for the vortex core in a type II superconductor. J Low Temp Phys. (1975) 18:427–34. doi: 10.1007/BF00116134
60. Laulajainen M, Callaghan FD, Kaiser CV, Sonier JE. Muon spin rotation measurements of the vortex state in vanadium: a comparative analysis using iterative and analytical solutions of the Ginzburg-Landau equations. Phys Rev B. (2006) 74:054511. doi: 10.1103/PhysRevB.74.054511
61. Sonier JE, Poon KF, Luke GM, Kyriakou P, Miller RI, Liang R, et al. Superconductivity and field-induced magnetism in Pr2−xCexCuO4 single crystals. Phys Rev Lett. (2003) 91:147002. doi: 10.1103/PhysRevLett.91.147002
63. Pissas M, Sanakis Y, Psycharis V, Simopoulos A, Devlin E, Ren ZA, et al. A Mössbauer study of the superconducting NdFeAsO0.82F0.18 oxypnictide compound. Supercond Sci Technol. (2008) 21:115015. doi: 10.1088/0953-2048/21/11/115015
64. Thiemann SL, Radović Z, Kogan VG. Field structure of vortex lattices in uniaxial superconductors. Phys Rev B. (1989) 39:11406–12. doi: 10.1103/PhysRevB.39.11406
65. Weyeneth S, Puzniak R, Zhigadlo ND, Katrych S, Bukowski Z, Karpinski J, et al. Evidence for two distinct anisotropies in the oxypnictide superconductors SmFeAsO0.8F0.2 and NdFeAsO0.8F0.2. J Supercond Nov Magn. (2009) 22:347–51. doi: 10.1007/s10948-009-0445-1
66. Jaroszynski J, Hunte F, Balicas L, Jo Y, Raicević I, Gurevich A, et al. Upper critical fields and thermally-activated transport of NdFeAsO0.7F0.3 single crystal. Phys Rev B. (2008) 78:174523. doi: 10.1103/PhysRevB.78.174523
67. Jia Y, Cheng P, Fang L, Luo H, Yang H, Ren C, et al. Critical fields and anisotropy of NdFeAsO0.82F0.18 single crystals. Appl Phys Lett. (2008) 93:032503. doi: 10.1063/1.2963361
68. Pribulova Z, Klein T, Kacmarcik J, Marcenat C, Konczykowski M, Bud'ko SL, et al. Upper and lower critical magnetic fields of superconducting NdFeAsO1−xFx single crystals studied by Hall-probe magnetization and specific heat. Phys Rev B. (2009) 79:020508(R). doi: 10.1103/PhysRevB.79.020508
69. Weyeneth S, Puzniak R, Mosele U, Zhigadlo ND, Katrych S, Bukowski Z, et al. Anisotropy of superconducting single crystal SmFeAsO0.8F0.2 studied by torque magnetometry. J Supercond Nov Magn. (2009) 22:325-9. doi: 10.1007/s10948-008-0413-1
70. Prozorov R, Tanatar MA, Gordon RT, Martin C, Kim H, Kogan VG, et al. Anisotropic London penetration depth and superfluid density in single crystals of iron-based pnictide superconductors. Phys C. (2009) 469:582–9. doi: 10.1016/j.physc.2009.03.012
71. Bendele M, Weyeneth S, Puzniak R, Maisuradze A, Pomjakushina E, Conder K, et al. Anisotropic superconducting properties of single-crystalline FeSe0.5Te0.5. Phys Rev B. (2010) 81:224520. doi: 10.1103/PhysRevB.81.224520
72. Kogan VG. London approach to anisotropic type-II superconductors. Phys Rev B. (1981) 24:1572–5. doi: 10.1103/PhysRevB.24.1572
73. Angst M, Puzniak R, Wisniewski A, Jun J, Kazakov SM, Karpinski J, et al. Temperature and field dependence of the anisotropy of MgB2. Phys Rev Lett. (2002) 88:167004. doi: 10.1103/PhysRevLett.88.167004
Keywords: superconductivity, magnetism, Fe-based superconductors, magnetic penetrations depth, superconducting gap, order parameter
Citation: Gupta R, Maisuradze A, Zhigadlo ND, Luetkens H, Amato A and Khasanov R (2020) Self-Consistent Two-Gap Approach in Studying Multi-Band Superconductivity of NdFeAsO0.65F0.35. Front. Phys. 8:2. doi: 10.3389/fphy.2020.00002
Received: 18 November 2019; Accepted: 06 January 2020;
Published: 30 January 2020.
Edited by:
Dmytro Inosov, Dresden University of Technology, GermanyReviewed by:
Jochen Litterst, Technische Universitat Braunschweig, GermanyRavi Prakash Singh, Indian Institute of Science Education and Research, Bhopal, India
Copyright © 2020 Gupta, Maisuradze, Zhigadlo, Luetkens, Amato and Khasanov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rustem Khasanov, cnVzdGVtLmtoYXNhbm92QHBzaS5jaA==
†ORCID: Rustem Khasanov orcid.org/0000-0002-4768-5524
 Ritu Gupta
Ritu Gupta Alexander Maisuradze1,2
Alexander Maisuradze1,2 Nikolai D. Zhigadlo
Nikolai D. Zhigadlo Rustem Khasanov
Rustem Khasanov