- State Key Laboratory of Electronic Thin Films and Integrated Devices, School of Optoelectronic Science and Engineering, University of Electronic Science and Technology of China, Chengdu, China
Period-doubled dissipative-soliton-resonance (DSR) pulses are numerically investigated in a Yb-doped fiber laser based on non-linear amplifying loop mirror (NALM). In the case of low pump power, stationary dissipative solitons with uniform pulse peak power are obtained in the laser. Further increasing the pump power, the laser operates in the DSR regime, where the phenomenon of period-doubling bifurcations could occur. In a period-doubled state, the pulse peak power returns back to its original one every two cavity roundtrips while the pulse duration remains almost the same. We analyze the effects of cavity parameters on the DSR-pulse features under the dynamic bifurcations. It is found that the saturation power of NALM plays a dominant role in the formation of period-doubled DSR pulses. Our simulation results are conducive to enriching the dynamics of DSR pulses in non-linear systems.
Introduction
Passively mode-locked fiber lasers, as an alternative ultrashort-pulse source, are highly promising for practical usages in material processing, non-linear optics, and optical sensing. To date, numerous pulse shaping mechanisms have been proposed to enable order-of-magnitude increase in the pulse energy. By taking advantage of the anomalous dispersion and Kerr non-linearity of fibers, conventional solitons can be formed in the lasers. Nevertheless, the maximum pulse energy is ultimately limited by the soliton area theorem [1]. By utilizing the dispersion management technique, stretched pulses with the pulse energy reaching to 1-nJ level have been demonstrated in fiber lasers, where the net-cavity dispersion is close to zero [2]. After that, it was shown that normal-dispersion fiber lasers tend to support dissipative solitons (DSs) with unprecedented pulse energy [3]. The formation of DSs requires a composite balance between dispersion and non-linearity as well as gain and loss, and their spectra exhibit steep spectral edges. However, multi-pulsing instabilities are the key obstacle to the further enhancement of pulse energy. In 2008, Chang et al. theoretically predicted a novel localized structure, dissipative soliton resonance (DSR), by solving the well-known master equation [4]. With the increase of pump power, DSR pulses feature a constant pulse peak power and a linearly broadening pulse duration. Over the past decade, DSR phenomena have been manifested in various mode-locked fiber lasers, undoubtedly verifying its superiority for pulse energy scaling [5–19]. In 2009, Wu et al. reported the first observation of DSR pulses in an all-normal dispersion (ANDi) Er-doped fiber laser. The maximum pulse energy as high as 281.2 nJ has been achieved without pulse breaking [5]. Later on, the feasibility of DSR pulses appearing at the anomalous dispersion regime has been confirmed by Li et al. in a long-cavity ring laser. By adjusting the pump power, DSR pulses with the pulse energy of 715 nJ could be obtained [6]. In 2016, Semaan et al. demonstrated the DSR-pulse generation in an Er-Yb double-clad figure-of-eight fiber laser, yielding a recorded 10-μJ pulse directly from the cavity [14]. Most recently, Zheng et al. presented a figure-of-nine Tm-doped fiber laser operating in the DSR regime. The resultant pulse energy could be scaled up to 0.33 mJ with the help of an external amplification [19]. Efforts have also been made to the study of DSR-pulse dynamics [20–25]. In 2013, Komarov et al. numerically investigated the coexistence of DSR pulses in passively mode-locked lasers. It was shown that the number of steady-state pulses depends on the initial conditions, but it does not change with increasing the pump power [20]. Since then several works have shown the generation of multiple DSR pulses in mode-locked fiber lasers with different dispersion regimes [26–29]. In 2019, Wang et al. reported the unusual evolution of DSR pulses in an ANDi figure-of-eight fiber laser, where the shrinkage of pulse duration with the pump power was observed for the first time [30]. Zhao et al. revealed the transformation from DSR to burst-like emission in a Ho-doped mode-locked fiber laser, which is related to the competition between DSR and soliton formation [31]. Therefore, there is a strong motivation to explore the novel features of DSR pulses.
In this paper, we numerically investigate period-doubled DSR pulses in an ANDi Yb-doped fiber laser with non-linear amplifying loop mirror (NALM). At a low pump power, the laser operates in stationary DS state, where the pulse peak power is unchanged for each cavity roundtrip. Period-doubling bifurcations of DSR pulses could be formed in the cavity with further increasing the pump power. In this case, the pulse peak power becomes no longer uniform but alternates between two values. The influence of cavity parameters on the properties of period-doubled DSR pulses is discussed. It is found that the saturation power of NALM is critical for achieving the period-doubling bifurcations of DSR pulses in the laser.
Numerical Model
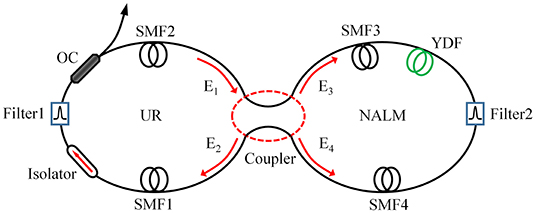
The configuration of our proposed ANDi Yb-doped figure-of-eight fiber laser is displayed in Figure 1. It contains a main unidirectional ring cavity (UR) connected to a NALM by a fused fiber coupler. The main loop is composed of two segments of single-mode fibers (SMFs) with a total length of 2 m, a polarization insensitive isolator (PI-ISO), an output coupler (OC) and a Gaussian-shaped bandpass filter (Filter 1). The spectral bandwidth of Filter 1 is fixed at 9 nm. The PI-ISO ensures the unidirectional pulse propagation while the OC is employed to extract 30% of the intra-cavity pulse energy. The NALM consists of 5-m Yb-doped fiber (YDF), two pieces of SMFs and a spectral filter (Filter 2). In this work, the 3-dB bandwidth of Filter 2 (i.e., BW) is set to 9 nm, the splitting ratio of the central fiber coupler is fixed at 0.9 and the total length of SMFs in the NALM is 2 m. The dispersion and non-linear parameters of the fibers utilized in the laser are β2,YDF = 36 ps2/km, β2,SMF = 23 ps2/km, γYDF = 3 W−1km−1, and γSMF = 1.3 W−1km−1. The NALM performs the role of an artificial saturable absorber allowing mode-locking operation. By adjusting the splitting ratio and loop length of the NALM, its saturable absorption properties can be flexibly controlled, which gives rise to different mode-locked pulse dynamics.
Although the master equation has taken into account the basic terms that govern important physical phenomena occurring in passively mode-locked lasers, a drawback of this averaged model is that the impacts of cavity components on the optical pulses are ignored, which might not accurately describe the real laser systems. In contrast, a pulse tracing technique was utilized to numerically simulate the evolution of mode-locked pulses in our laser. In the simulations, we adopted a more accurate model of NALM rather than using its power-dependent transmission function. As shown in Figure 1, an input field E1 is split into two counter-propagating fields E3 and E4, which can be expressed by
where ρ is the splitting ratio of the central fiber coupler. Then the two fields propagate through the NALM in opposite directions. Pulse propagation in fiber section is described by the scalar non-linear Ginzburg-Landau equation
where E refers to the normalized envelope of the electric field; ß2 and γ represent the dispersion and non-linearity of fiber, respectively; z indicates the propagation distance while t denotes the local time; g is the fiber gain and Ωg describes the gain bandwidth, which is fixed at 30 nm. For the SMF g is equal to zero while for the YDF, the effect of gain saturation is treated as
where g0 denotes the small signal gain and Esat represents the gain saturation energy. In this work, g0 is set to 2 m−1 and Esat is variable. The pulse energy Ep can be expressed by
where TR is the cavity roundtrip time. After they travel around the loop length, the two optical fields return in coincidence to recombine at the coupler. The transmitted field E2 is given by
We utilize the field E2 as an input for the UR cavity. After a roundtrip propagation in the main loop, the final field is employed as a new input for the NALM in the next round of calculation. Eventually, an initial weak pulse could converge into a steady state with proper cavity parameter settings.
Simulation Results and Discussion
In view of the complexity of the simulation model, the split-step Fourier method was adopted to solve it numerically. Figure 2A illustrates the roundtrip-to-roundtrip evolution of output pulses at the position of OC when the pump power Esat is set to 1 nJ. It can be seen that the mode-locked pulse features a Gaussian-shaped temporal profile and its peak power is unchanged for each cavity roundtrip, manifesting that stationary DSs are obtained in the ANDi fiber laser. Further increasing Esat, the DSs transfer to rectangular pulses. Correspondingly, the intensity of pulse spectrum increases while its spectral bandwidth is considerably narrowed. This evolution process is consistent with the theoretical predictions regarding DSR phenomena [32], which indicates that the laser operates in the DSR regime. Figure 2B shows the evolution of DSR pulses with cavity roundtrips at a Esat value of 10 nJ. Surprisingly, the pulse peak power here alternates between two values rather than being clamped at a certain one, exhibiting a phenomenon called period-doubling bifurcations. It should be mentioned that period-doubled mode-locked pulses have been observed in fiber lasers with various net-cavity dispersions, verifying that the period-doubling bifurcation is an intrinsic feature of fiber lasers and its occurrence is independent of the specific pulse-shaping mechanism [33–35]. For the sake of comparison, the temporal profiles and the corresponding spectra of the period-doubled DSR pulses in two adjacent roundtrips are presented in Figures 3A,B. In this case, the pulse peak power alternates between 172 (i.e., the lower peak power PL) and 223 mW (i.e., the upper peak power PH) while the pulse duration remains almost the same. The corresponding spectral intensity takes one of the two alternative values every two consecutive roundtrips while its bandwidth keeps nearly constant. These features are different from those of period-doubled soliton pulses shown in [33–35], as is evident from the numerical results. Figures 4A,B depict the evolution of pulse temporal profiles vs. Esat. The adjacent pulses have the same pulse duration at a certain Esat value. The pulse duration increases linearly with the Esat while both pulses maintain their peak power approximately unchanged, which shows the characteristics of DSR pulses.
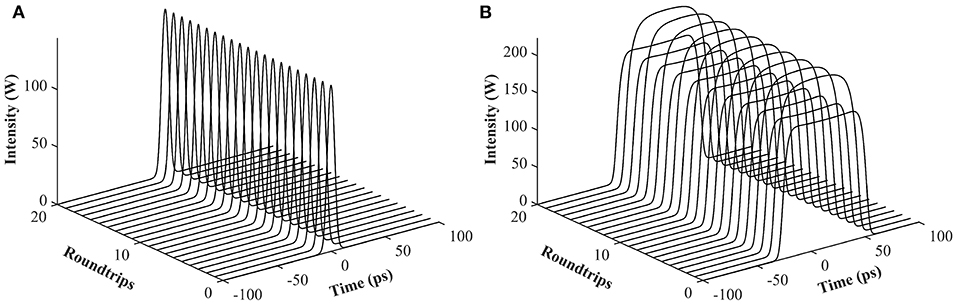
Figure 2. The evolution of output pulses with cavity roundtrips. (A) Three-dimension evolution at a pump Esat of 1 nJ. (B) Three-dimension evolution at a pump Esat of 10 nJ.
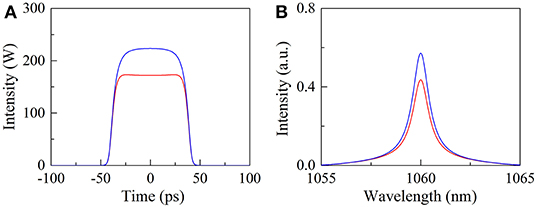
Figure 3. Features of period-doubled DSR pulses. (A) The temporal profiles. (B) The corresponding pulse spectral profiles.
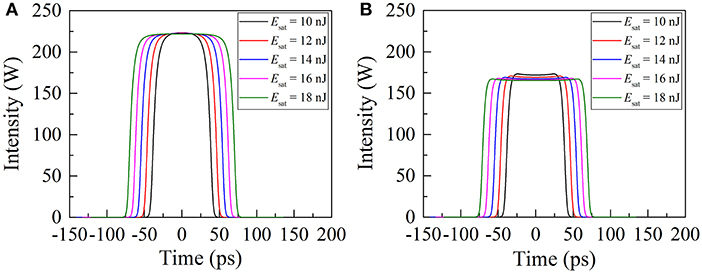
Figure 4. The evolution of pulse temporal profiles as a function of Esat. (A) The pulse profiles with the upper peak power. (B) The pulse profiles with the lower peak power.
The influence of cavity parameters on the properties of DSR pulses under the dynamic bifurcations was analyzed. We first varied the splitting ratio ρ of the central fiber coupler while fixing the other parameters (Esat = 10 nJ, L = 7 m, BW = 9 nm). It was found that the period-doubled DSR pulses could exist in the cavity when ρ is set in the range from 0.9 to 0.93. Figure 5 shows PH and PL as a function of ρ. The dashed blue line depicts the PH values while the dotted red line represents the PL ones. The presence of two separate plots for PH and PL indicates that we are dealing with period-doubled DSR pulses. The solid green line in Figure 5 shows the difference of the PH and PL values. It can be seen that with increasing ρ from 0.9 to 0.93, PH decreases from 223 to 194 mW while PL slightly increases from 172 to 181 mW. In the case of our current parameter settings, their difference moves toward zero once ρ exceeds 0.93, manifesting that period-doubling bifurcations disappear and the laser emits stationary DSR pulses with uniform pulse peak power.
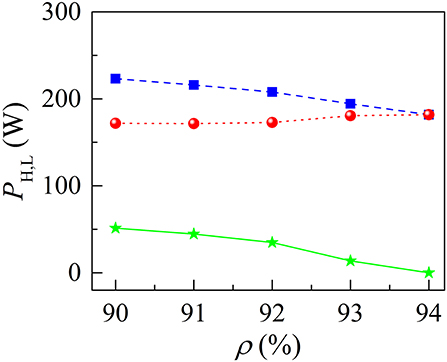
Figure 5. The PH and PL values vs. ρ. Their difference as a function of ρ is shown by the solid green curve.
We further investigated the impact of the loop length L of NALM on period-doubled DSR state. By changing the total length of SMFs in NALM while keeping the other parameters fixed (Esat = 10 nJ, ρ = 0.9, BW = 9 nm), the dependence of PH and PL on L was numerically calculated, as presented in Figure 6. When L increases from 6 to 9 m, PH decreases from 245 to 178 mW while PL reduces from 176 to 161 mW. Their difference equals to zero when L is beyond 9 m, which means that the fiber laser with a long loop is prone to operating in stationary DSR regime. We recall that the power-dependent transmission function of NALM is considered as
where G is the fiber gain and Φ represents the phase difference of the light fields propagating through the two paths in NALM, which can be expressed by
where P is the instantaneous pulse peak power. In general, the input pulse power at which the periodical transmission curve of NALM reaching its first peak is referred to as the saturation power. One can see from Equations (6) and (7) that for a given fiber gain and non-linearity, the saturation power is inversely proportional to product of the splitting ratio and the loop length. Our simulation results confirm that there exists a threshold of saturation power for the occurrence of period-doubling bifurcations in the cavity. When the saturation power is weak, period-doubled DSR state is avoided and the stationary DSR pulses are formed in the laser.
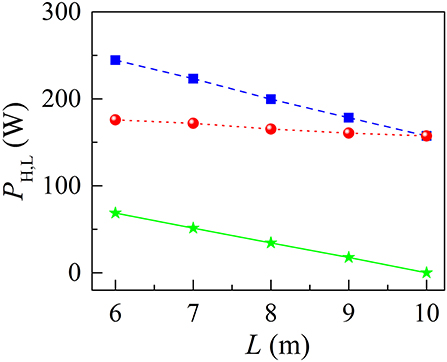
Figure 6. The PH and PL values vs. L. Their difference as a function of L is shown by the solid green curve.
The formation mechanism of period-doubled DSR pulses could be interpreted as follows. Under sufficiently high pump power, the pulse peak power is so strong that it switches the cavity from the positive to the negative feedback regime, namely the transmission of NALM reduces with the pulse peak power. When the pulse peak power is scaled up to a certain level, which depends on the saturation power settings, the dynamic loss encountered by the pulse is same to its effective gain. In this case, the pulse peak power is confined. A further increase in the pump strength results in the expansion of pulse duration instead of its peak power. Eventually, the Gaussian-shaped temporal pulse profile transfers to a rectangular one, and DSR pulses are formed in the laser. On the other hand, the mode-locked fiber laser is essentially a non-linear dynamic system. The appearance of period-doubling phenomenon is a manifestation of the nonlinear cavity effect, which is independent of the specific pulse profile. Under the DSR conditions, larger saturation power will cause the pulse peak power to be confined at a higher level. When the pulse peak power is strong, the strength of nonlinear interaction of DSR pulses with the cavity components becomes intense. To a certain level of the nonlinear interaction, period-doubling bifurcations could appear in the laser [33]. Consequently, the peak power of DSR pulses is no longer uniform but alternates between two values. We note that Peng et al. demonstrated the generation of triple-state DSs via self-parametric-amplification (SPA) effect in a mode-locked fiber laser [36]. A segment of anomalous-dispersion fiber was utilized in their laser cavity to provide negative chirp such that SPA was triggered in the subsequent normal-dispersion gain fiber. Therefore, our proposed ANDi fiber laser excludes the SPA-induced bifurcation.
Additionally, in order to investigate the effect of spectral filtering on the period-doubled DSR state, we altered the bandwidth of filter inserted into the NALM while maintaining the other cavity parameters constant (Esat = 10 nJ, ρ = 0.9, L = 7 m). As illustrated in Figure 7, when the filtering bandwidth is tuned from 8 to 11 nm, PH reduces from 233 to 205 mW whereas PL increases from 164 to 188 mW. When the bandwidth exceeds 11 nm, the difference of PH and PL vanishes and the stationary DSR pulses are formed in the cavity. This means that the reduction of filtering bandwidth could facilitate the period-doubling of DSR pulses. Recently, an emerging technique called dispersive Fourier transform (DFT) has been proposed to investigate the soliton dynamics in mode-locked fiber lasers [37–39]. By virtue of the DFT technique, the single-shot spectra of period-doubled DSR pulses can be measured in our future work, which would be beneficial for further understanding the period-doubling bifurcation.
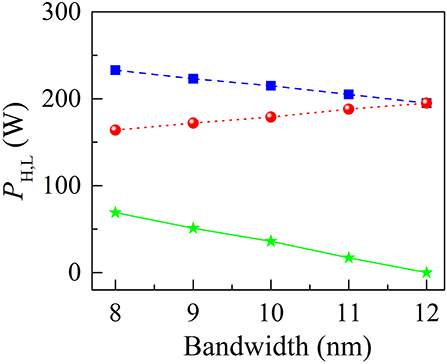
Figure 7. The PH and PL values vs. the filtering bandwidth. Their difference as a function of the bandwidth is shown by the solid green curve.
Conclusion
We have numerically simulated period-doubled DSR pulses in an ANDi Yb-doped fiber laser mode-locked by a NALM. In the case of low pump power, stationary DSs with uniform pulse peak power are achieved. Under sufficiently high pump power, period-doubling bifurcations of DSR pulses could occur in the laser. In this case, the pulse peak power returns back to its original value after two consecutive roundtrips while the pulse duration keeps unchanged. The impact of cavity parameters, including the filtering bandwidth, the splitting ratio and loop length of NALM, on the features of DSR pulses under the dynamic bifurcations has been presented. Theoretical analysis shows that the saturation power of NALM plays a dominant role in the formation of period-doubled DSR pulses.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
WD and HL conceived the idea and developed the numerical model. YLy and CW helped to evaluate and edit the manuscript. YLi supervised the work. All the authors contributed to the analysis and discussion of the results.
Funding
This research was supported by the National Key R&D Program of China (2018YFB2201201) and National Natural Science Foundation of China (NSFC) (61775031, 61435003, 61421002, 61875033).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Nelson LE, Jones DJ, Tamura K, Haus HA, Ippen EP. Ultrashort-pulse fiber ring lasers. Appl Phys B. (1997) 65:277–94. doi: 10.1007/s003400050273
2. Tang DY, Zhao LM. Generation of 47-fs pulses directly from an erbium-doped fiber laser. Opt Lett. (2007) 32:41–3. doi: 10.1364/OL.32.000041
3. Chong A, Renninger WH, Wise FW. All-normal-dispersion femtosecond fiber laser with pulse energy above 20 nJ. Opt Lett. (2007) 32:2408–10. doi: 10.1364/OL.32.002408
4. Chang W, Ankiewicz A, Soto-Crespo JM, Akhmediev N. Dissipative soliton resonances. Phys Rev A. (2008) 78:023830. doi: 10.1103/PhysRevA.78.023830
5. Wu X, Tang DY, Zhang H, Zhao LM. Dissipative soliton resonance in an all-normal-dispersion erbium-doped fiber laser. Opt Express. (2009) 17:5580–4. doi: 10.1364/OE.17.005580
6. Li X, Liu X, Hu X, Wang L, Lu H, Wang Y, et al. Long-cavity passively mode-locked fiber ring laser with high-energy rectangular-shape pulses in anomalous dispersion regime. Opt Lett. (2010) 35:3249–51. doi: 10.1364/OL.35.003249
7. Zhang X, Gu C, Chen G, Sun B, Xu L, Wang A, et al. Square-wave pulse with ultra-wide tuning range in a passively mode-locked fiber laser. Opt Lett. (2012) 37:1334–36. doi: 10.1364/OL.37.001334
8. Liu L, Liao JH, Ning QY, Yu W, Luo AP, Xu SH, et al. Wave-breaking-free pulse in an all-fiber normal-dispersion Yb-doped fiber laser under dissipative soliton resonance condition. Opt Express. (2013) 21:27087–92. doi: 10.1364/OE.21.027087
9. Mei L, Chen G, Xu L, Zhang X, Gu C, Sun B, et al. Width and amplitude tunable square-wave pulse in dual-pump passively mode-locked fiber laser. Opt Lett. (2014) 39:3235–7. doi: 10.1364/OL.39.003235
10. Cheng Z, Li H, Shi H, Ren J, Yang QH, Wang P. Dissipative soliton resonance and reverse saturable absorption in graphene oxide mode-locked all-normal-dispersion Yb-doped fiber laser. Opt Express. (2015) 23:7000–6. doi: 10.1364/OE.23.007000
11. Krzempek K. Dissipative soliton resonances in all-fiber Er-Yb double clad figure-8 laser. Opt Express. (2015) 23:30651–6. doi: 10.1364/OE.23.030651
12. Huang Y, Luo Z, Xiong F, Li Y, Zhong M, Cai Z, et al. Direct generation of 2 W average-power and 232 nJ picosecond pulses from an ultra-simple Yb-doped double-clad fiber laser. Opt Lett. (2015) 40:1097–100. doi: 10.1364/OL.40.001097
13. Krzempek K, Sotor J, Abramski K. Compact all-fiber figure-9 dissipative soliton resonance mode-locked double-clad Er:Yb laser. Opt Lett. (2016) 41:4995–8. doi: 10.1364/OL.41.004995
14. Semaan G, Braham FB, Fourmont J, Salhi M, Bahloul F, Sanchez F. 10 μJ dissipative soliton resonance square pulse in a dual amplifier figure-of-eight double-clad Er:Yb mode-locked fiber laser. Opt. Lett. (2016) 41:4767–70. doi: 10.1364/OL.41.004767
15. Krzempek K, Abramski K. 6.5 μJ pulses from a compact dissipative soliton resonance mode-locked erbium-ytterbium double clad laser. Laser Phys Lett. (2017) 14:015101. doi: 10.1088/1612-202X/14/1/015101
16. Krzempek K, Tomaszewska D, Abramski KM. Dissipative soliton resonance mode-locked all-polarization-maintaining double clad Er:Yb fiber laser. Opt Express. (2017) 25:24853–60. doi: 10.1364/OE.25.024853
17. Du T, Luo Z, Yang R, Huang Y, Ruan Q, Cai Z, et al. 1.2-W average-power, 700-W peak-power, 100-ps dissipative soliton resonance in a compact Er:Yb co-doped double-clad fiber laser. Opt Lett. (2017) 42:462–5. doi: 10.1364/OL.42.000462
18. Du T, Li W, Ruan Q, Wang K, Chen N, Luo Z. 2 μm high-power dissipative soliton resonance in a compact σ-shaped Tm-doped double-clad fiber laser. Appl Phys Express. (2018) 11:052701. doi: 10.7567/APEX.11.052701
19. Zheng Z, Ouyang D, Ren X, Wang J, Pei J, Ruan S. 0.33 mJ, 104.3 W dissipative soliton resonance based on a figure-of-9 double-clad Tm-doped oscillator and an all-fiber MOPA system. Photon Res. (2019) 7:513–7. doi: 10.1364/PRJ.7.000513
20. Komarov A, Amrani F, Dmitriev A, Komarov K, Sanche F. Competition and coexistence of ultrashort pulses in passive mode-locked lasers under dissipative-soliton-resonance conditions. Phys Rev A. (2013) 87:023838. doi: 10.1103/PhysRevA.87.023838
21. Li D, Tang D, Zhao L, Shen D. Mechanism of dissipative-soliton-resonance generation in passively mode-locked all-normal-dispersion fiber lasers. J Lightwave Technol. (2015) 33:3781–7. doi: 10.1109/JLT.2015.2449874
22. Du W, Li H, Li J, Wang P, Zhang S, Liu Y. Mechanism of dissipative-soliton-resonance generation in fiber laser mode-locked by real saturable absorber. Opt Express. (2018) 26:21314–23. doi: 10.1364/OE.26.021314
23. Li D, Shen D, Li L, Tang D, Su L, Zhao L. Internal polarization dynamics of vector dissipative soliton resonance pulses in normal dispersion fiber lasers. Opt Lett. (2018) 43:1222–5. doi: 10.1364/OL.43.001222
24. Du W, Li H, Li J, Wang Z, Wang P, Zhang Z, et al. Polarization dynamics of dissipative-soliton-resonance pulses in passively mode-locked fiber lasers. Opt Express. (2019) 27:8059–68. doi: 10.1364/OE.27.008059
25. Du W, Li H, Li J, Wang Z, Wang P, Zhang Z, et al. Vector nature of dissipative-soliton-resonance pulses in fiber lasers mode-locked by nonlinear polarization rotation technique. IEEE Photonics J. (2019) 11:1502910. doi: 10.1109/JPHOT.2019.2918804
26. Semaan G, Niang A, Salhi M, Sanchez F. Harmonic dissipative soliton resonance square pulses in an anomalous dispersion passively mode-locked fiber ring laser. Laser Phys Lett. (2017) 14:055401. doi: 10.1088/1612-202X/aa6700
27. Lyu Y, Zou X, Shi H, Liu C, Wei C, Li J, et al. Multipulse dynamics under dissipative soliton resonance conditions. Opt. Express. (2017) 25:13286–95. doi: 10.1364/OE.25.013286
28. Lyu Y, Shi H, Wei C, Li H, Li J, Liu Y. Harmonic dissipative soliton resonance pulses in a fiber ring laser at different values of anomalous dispersion. Photon Res. (2017) 5:612–6. doi: 10.1364/PRJ.5.000612
29. Chowdhury SD, Pal A, Chatterjee S, Sen R, Pal M. Multipulse dynamics of dissipative soliton resonance in an all-normal dispersion mode mocked fiber laser. J Light Technol. (2018) 36:5773–9. doi: 10.1109/JLT.2018.2877924
30. Wang Y, Zhao J, Wang S, Shu C, Su L, Tang D, et al. Unusual evolutions of dissipative-soliton-resonance pulses in an all-normal dispersion fiber laser. IEEE Photonics J. (2019) 11:1500509. doi: 10.1109/JPHOT.2019.2895687
31. Zhao J, Zhou J, Li L, Zhao L, Tang D, Shen D, et al. Dissipative soliton resonance and its depression into burst-like emission in a holmium-doped fiber laser with large normal dispersion. Opt Lett. (2019) 44:2414–7. doi: 10.1364/OL.44.002414
32. Chang W, Ankiewicz A, Soto-Crespo JM, Akhmediev N. Dissipative soliton resonances in laser models with parameter management. J Opt Soc Am B. (2008) 25:1972–7. doi: 10.1364/JOSAB.25.001972
33. Zhao LM, Tang DY, Liu AQ. Chaotic dynamics of a passively mode-locked soliton fiber ring laser. Chaos. (2006) 16:013128. doi: 10.1063/1.2173049
34. Zhao LM, Tang DY, Cheng TH, Tam HY, Lu C, Wen SC. Period-doubling of dispersion managed solitons in an Erbium-doped fiber laser at around zero dispersion. Opt Commun. (2007) 278:428–33. doi: 10.1016/j.optcom.2007.06.024
35. Zhao LM, Tang DY, Wu X, Zhang H. Period-doubling of gain-guided solitons in fiber lasers of large net normal dispersion. Opt Commun. (2008) 281:3557–60. doi: 10.1016/j.optcom.2008.02.050
36. Peng J, Zeng H. Triple-state dissipative soliton laser via ultrafast self-parametric amplification. Phys Rev Appl. (2019) 11:044068. doi: 10.1103/PhysRevApplied.11.044068
37. Liu X, Yao X, Cui Y. Real-time observation of the buildup of soliton molecules. Phys Rev Lett. (2018) 121:023905. doi: 10.1103/PhysRevLett.121.023905
38. Liu X, Pang M. Revealing the buildup dynamics of harmonic mode-locking states in ultrafast lasers. Laser Photonics Rev. (2019) 13:1800333. doi: 10.1002/lpor.201800333
Keywords: fiber laser, dissipative soliton resonance, non-linear amplifying loop mirror, period doubling, soliton dynamics
Citation: Du W, Li H, Lyu Y, Wei C and Liu Y (2020) Period Doubling of Dissipative-Soliton-Resonance Pulses in Passively Mode-Locked Fiber Lasers. Front. Phys. 7:253. doi: 10.3389/fphy.2019.00253
Received: 09 November 2019; Accepted: 30 December 2019;
Published: 21 January 2020.
Edited by:
Xueming Liu, Zhejiang University, ChinaReviewed by:
Zhengqian Luo, Xiamen University, ChinaLuming Zhao, Jiangsu Normal University, China
Junsong Peng, East China Normal University, China
Copyright © 2020 Du, Li, Lyu, Wei and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Heping Li, b2VocGxpQHVlc3RjLmVkdS5jbg==
 Wenxiong Du
Wenxiong Du Heping Li
Heping Li Yanjia Lyu
Yanjia Lyu Chen Wei
Chen Wei Yong Liu
Yong Liu