Fractional View Analysis of Third Order Kortewege-De Vries Equations, Using a New Analytical Technique

In the present article, fractional view of third order Kortewege-De Vries equations is presented by a sophisticated analytical technique called Mohand decomposition method. The Caputo fractional derivative operator is used to express fractional derivatives, containing in the targeted problems. Some numerical examples are presented to show the effectiveness of the method for both fractional and integer order problems. From the table, it is investigated that the proposed method has the same rate of convergence as compare to homotopy perturbation transform method. The solution graphs have confirmed the best agreement with the exact solutions of the problems and also revealed that if the sequence of fractional-orders is approaches to integer order, then the fractional order solutions of the problems are converge to an integer order solution. Moreover, the proposed method is straight forward and easy to implement and therefore can be used for other non-linear fractional-order partial differential equations.

1. Introduction

The class of partial differential equations known as Korteweg-De Vries (KDV) equation which play a vital role in the diverse field of physics such as fluid mechanics, signal processing, hydrology, viscoelasticity and fractional kinetics [1, 2]. The KDV equation was first time derived by Korteweg and Vries in 1895. The KDV equation used to model long waves, tides, solitary waves, and wave propagating in a shallow canal. A partial differential Kortewege-De Vries equation of third order is also applied to study the non-linear model of water waves in superficial canal certain namely canal [3], in the time when wave in water was of important concentration in applications in navigational design and also for the awareness of flood and tides [4, 5]. The applications in numerous areas of physics, applied science and other scientific applications, therefore the excessive amount of investigation as a research work has been capitalized in the study of KDV equations [6–10]. We considered the third order time fractional KDV equation in the form [1]

$\begin{array}{ll}\begin{array}{c}\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}+\kappa u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\lambda \frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}+\psi (\chi ,\Im ),0<\gamma \le 1,\end{array}& (1)\end{array}$

with initial source

$\begin{array}{l}u(\chi ,0)=u(\chi ),\end{array}$

where, κ and λ are real numbers.

The KdV equations of fractional order can be applied to examine the influence of the higher-order wave dispersion. The KdV-Burgers equation defines the waves on lower water surfaces. The strength of fractional KdV equation is the non-local property [11–21]. For a higher order Korteweg-de Vries equation, which is a natural extension of the Korteweg-de Vries equation written in a bilinear form, a Bcklund conversion in bilinear forms is provided. For this higher-order equation the Bcklund transition is given in ordinary forms and the inverse scattering scheme [22], Korteweg-de Vries type of equations 3rd order coefficient variable [23] and Solution of the third order Korteweg-De Vries homotopy perturbation approach using elzaki transform [24].

In few decades, integral transform of various types such as Fourier transform, Laplace transform, Hankel transform, Mellin transform, Z-transform, Wavelet transform, Elzaki transform, Kamal transform, Mahgoub transform, Aboodh transform, Mohand transform, Sumudu transform, Hermite transform etc., gained a enormous importance in solving advanced model in the field mathematics, physics and engineering [25–36].

In the current article, we have applied the Mohand transform with decomposition procedure for the analytical treatment of time fractional KDV equation. The Mohand Transform is one of the new integral transform use for the analytical treatment of different physical phenomena are molded by Differential Equations (DEs) of integer order or Fractional Partial Differential Equations (FPDEs). Recently, Kumar and Viswanathan used Mohand transform and solved the mechanics and electrical circuit problems [37]. Aggarwal have Comparatively Studied Mohand and Aboodh transforms for the solution of differential equations. The numerical applications reflect that both the transforms (Mohand and Aboodh transforms) are closely related to each other [38]. Sudhanshu Aggarwal have also discussed the comparative study of Mohand and Laplace transforms, Mohand and Sumudu transforms, Mohand and Mahgoub transforms [39–41]. Sudhanshu Aggarwal have successfully discussed the Mohand transform of Bessels functions of zero, one and two orders, which is very useful for solving many equations in cylindrical or spherical coordinates such as heat equation, wave equation etc. [42]. The exact solution of second kinds of linear Volterra integral equations get by using Mohand transform. It is claimed that Mohand transform take very little time and has no large computational work [43]. Mohand transform have also used the for solution of Abel's integral equation. The obtained results show that Mohand transform is a powerful integral transform for handling Abel's integral equation [44]. The remaining section of the paper are managed as follows. In the second section, we present some related definitions of fractional calculus and basic concepts of Mohand transform. The third section presents the implementation the proposed methodology. The four section represent different models of KDV equation are examined separately and plotted. Finally, we depict our conclusions.

Preliminaries Concepts

In this section, we present some basic necessary definitions and preliminaries concepts related to fractional calculus and Mohand transform.

Definition

Mohand transform first time was define by Mohand and Mahgoub of the function u(ℑ) for ℑ ≥ 0 in the year 2017. The Mohand transform which is represented by M(.) for a function u(τ) is define as [45]

$\begin{array}{ll}M\{u(\Im )\}=R(\upsilon )={\upsilon }^2{\displaystyle {\int }_0^{\infty }u}(\Im )e^{-\upsilon \Im }d\Im , k_1\le \upsilon \le k_2,& (2)\end{array}$

The Mohand transform of a function u(ℑ) is R(υ) then u(ℑ) is called the inverse of R(υ) which is expressed as.

$\begin{array}{ll}{M}^{-1}\{R(\upsilon )\}=u(\Im ),M^{-1}isinverseMohandoperator.& (3)\end{array}$

Definition

Mohand transform for nth derivatives [46]

$\begin{array}{ll}\begin{array}{c}M\{u^n(\Im )\}={\upsilon }^{n}R(\upsilon )-{\upsilon }^{n+1}u(0)-{\upsilon }^n{u}^{\prime }(0)-\cdots -{\upsilon }^2{u}^{n-1}(0),\end{array}& (4)\end{array}$

Definition

Mohand transform for fractional order derivatives [46]

$\begin{array}{ll}R\{u^{\gamma }(\Im )\}={\upsilon }^{\gamma }R(\upsilon )-\underset{k=0}{\overset{n-1}{{{{\displaystyle \sum }}^{\text{}}}^{\text{}}{}^{\text{}}}}\frac{u^k(0)}{{\upsilon }^{k-(\gamma +1)}},0<\gamma \le n,& (5)\end{array}$

Definition

Caputo operator of fractional partial derivative [47]

$\begin{array}{ll}{D}_{\tau }^{\gamma }g(\chi ,\Im )=\{\begin{array}{l}\frac{{\partial }^{n}g(\chi ,\Im )}{\partial {\Im }^n},\gamma =n\in N,\hfill \\ \frac{1}{\Gamma (n-\gamma )}{\int }_0^{\Im }{(\Im -\varphi )}^{n-\gamma -1}{g}^n(\varphi )\partial \varphi ,n-1<\gamma <n\hfill \end{array}& (6)\end{array}$

2. Implementation of Mohand Transform

In this section we have considered the time fractional KDV model in the form

$\begin{array}{l}\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}+\kappa u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\lambda \frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}=\psi (\chi ,\Im ),\\ 0<\gamma \le 1,& (7)\end{array}$

with initial source

$\begin{array}{l}u(\chi ,0)=u(\chi ).\end{array}$

where, κ and λ are real numbers.

Applying Mohand transform [45]

$\begin{array}{l}M\{\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}+\kappa u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\lambda \frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\}\\ =M\{\psi (\chi ,\Im )\},0<\gamma \le 1,& (8)\end{array}$

by using the transform property, we can simplify as

$\begin{array}{l}{\upsilon }^{\gamma }\{R(\upsilon )-\upsilon u(0)\}+M\left\{\kappa u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\lambda \frac{{\partial }^{3}u(x,\tau )}{\partial x^3}\right\}\\ =M\{\psi (x,\tau )\},& (9)\end{array}$

after some evaluation, Equation (8) simplified as

$\begin{array}{l}R(\upsilon )=\upsilon u(0)+\frac{1}{{\upsilon }^{\gamma }}M\left\{-\kappa u(x,\tau )\frac{\partial u(x,\tau )}{\partial x}-\lambda \frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\\ +\frac{1}{{\upsilon }^{\gamma }}M\{\psi (\chi ,\Im )\},& (10)\end{array}$

by applying inverse Mohand transform

$\begin{array}{l}u(\chi ,\Im )=\upsilon u(0)+M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{-\kappa u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }\\ -\lambda \frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\}+\frac{1}{{\upsilon }^{\gamma }}M\{\psi (\chi ,\Im )\}\}.& (11)\end{array}$

Finally we obtain the recursive general relation as

$\begin{array}{l}{u}_0(\chi ,\Im )=u(0)+M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\{\psi (\chi ,\Im )\}\right\}m=0\\ u_{m+1}(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{-\kappa u_m(\chi ,\Im )\frac{\partial u_m(\chi ,\Im )}{\partial \chi }\\ -\lambda \frac{{\partial }^3{u}_m(\chi ,\Im )}{\partial {\chi }^3}\}\},m\ge 0.& (12)\end{array}$

Theorem

Let χ and ${Y}$ be two Banach spaces and $T:\chi \to {Y}$ be a contractive nonlinear operator, such that for all u; u^*∈; χ, ‖T(u)−T(u^*)‖ ≤ K‖u − u^*‖, 0 < K < 1 [48].

Then, in view of Banach contraction theorem, T has a unique fixed point u, such that Tu = u: Let us write the generated series (12), by the Mohand decomposition method as

$\begin{array}{l}{\chi }_m=T({\chi }_{m-1}),{\chi }_{m-1}={\displaystyle \sum _{j=1}^{m-1}{u}_j,j=0,1,2,\cdots }\hfill \end{array}$

and supposed that ${\chi }_0=u_0\in {{S}}_p(u),$ where ${{S}}_p(u)=\left\{u^{*}\in \chi :||u-u^{*}||<p\right\}$ then, we have

$\begin{array}{l}(B_1){\chi }_m\in {{S}}_p(u)\\ (B_2)\underset{m\to \infty }{\lim }{\chi }_n=u.\end{array}$

Proof

(B₁) In view of mathematical induction for m = 1, we have

$\begin{array}{l}\Vert {\chi }_1-u_1\Vert =\Vert T({\chi }_0-T(u))\Vert \le K\Vert u_0-u\Vert .\end{array}$

Let the result is true for m − 1, then

$\begin{array}{l}\Vert {\chi }_{m-1}-u\Vert \le K^{m-1}\Vert u_0-u\Vert .\end{array}$

We have

$\begin{array}{l}\Vert {\chi }_m-u\Vert =\Vert T({\chi }_{m-1}-T(u))\Vert \le K\Vert {\chi }_{m-1}-u\Vert \le K^m\Vert u_0-u\Vert .\end{array}$

Hence, using (B₁), we have

$\begin{array}{l}\Vert {\chi }_m-u\Vert \le K^m\Vert u_0-u\Vert \le K^{m}p<p,\end{array}$

which implies that ${\chi }_m\in {{S}}_p(u)$.

(B₂): Since $||{\chi }_m-u||\le K^m||u_0-u||$ and as a ${\lim }_{m\to \infty }$ K^m = 0.

Therefore; we have ${\lim }_{m\to \infty }||u_n-u||=0\Rightarrow {\lim }_{m\to \infty }$u_n = u.

3. Applications and Discussion

Here, we have implemented the Mohand transform on some time fractional KVD equations.

Example 4.1: Consider the third order time fractional KVD equation [49]

$\begin{array}{ll}\begin{array}{c}\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}+6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}=0,0<\gamma \le 1,\end{array}& (13)\end{array}$

with initial source

$\begin{array}{l}u(\chi ,0)=\chi .\end{array}$

Taking Mohand transform of Equation (12), we get

$\begin{array}{ll}{\upsilon }^{\gamma }\{R(\upsilon )-\upsilon u(0)\}=M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\},& (14)\end{array}$

after some evaluation, Equation (13) is simplified as

$\begin{array}{ll}R(\upsilon )=\upsilon u(0)+\frac{1}{{\upsilon }^{\gamma }}\left\{M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (15)\end{array}$

by applying inverse Mohand transform, we get

$\begin{array}{ll}u(\chi ,\Im )=u(0)+M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (16)\end{array}$

thus, by using recursive scheme of Equation (11), we get

$\begin{array}{ll}{u}_0(\chi ,\Im )=u(0)=\chi ,& (17)\end{array}$

$\begin{array}{l}{u}_{m+1}(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{-6u_m(\chi ,\Im )\frac{\partial u_m(\chi ,\Im )}{\partial \chi }\\ -\frac{{\partial }^3{u}_m(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},m=0,1,\cdots .& (18)\end{array}$

From the recursive formula (17),

for m = 0

$\begin{array}{l}{u}_1(\chi ,\Im )=M^{-1}\text{}\left\{\text{}\frac{1}{{\upsilon }^{\gamma }}M\left\{-6u_0(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_0(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},\\ u_1(\chi ,\Im )=-6\chi \frac{{\Im }^{\gamma }}{\gamma !},& (19)\end{array}$

for m = 1

$\begin{array}{l}{u}_2(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{-6u_0(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }\\ -6u_1(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_1(\chi ,\Im )}{\partial {\chi }^3}\}\},\\ u_2(\chi ,\Im )=72\chi \frac{{\Im }^{2\gamma }}{(2\gamma )!},& (20)\end{array}$

for m = 2

$\begin{array}{l}{u}_3(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{-6u_0(\chi ,\Im )\frac{\partial u_2(\chi ,\Im )}{\partial \chi }\\ -6u_1(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }-6u_2(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi } \\ -\frac{{\partial }^3{u}_2(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_3(\chi ,\Im )=-864\chi \frac{{\Im }^{3\gamma }}{(3\gamma )!}-216\chi (2\gamma )!\frac{{\Im }^{3\gamma }}{(3\gamma )!\gamma !\gamma !},& (21)\end{array}$

Similarly for m = 3, we can get

$\begin{array}{l}{u}_4(\chi ,\Im )=10368\chi \frac{{\Im }^{4\gamma }}{(4\gamma )!}+2592\chi (2\gamma )!\frac{{\Im }^{4\gamma }}{(4\gamma )!\gamma !}\\ +5184\chi (3\gamma )!\frac{{\Im }^{4\gamma }}{(4\gamma )!(2\gamma )!\gamma !},\\ ⋮& (22)\end{array}$

The Mohand transform solution for example 4.1 is

$\begin{array}{l}u(\chi ,\Im )=u_0(\chi ,\Im )+u_1(\chi ,\Im )+u_2(\chi ,\Im )+u_3(\chi ,\Im )\\ +u_4(\chi ,\Im )+\cdots .& (23)\end{array}$

$\begin{array}{l}u(\chi ,\Im )=\chi -6x\frac{{\Im }^{\gamma }}{\gamma !}+72\chi \frac{{\Im }^{2\gamma }}{(2\gamma )!}-864\chi \frac{{\Im }^{3\gamma }}{(3\gamma )!}\\ -216\chi (2\gamma )!\frac{{\Im }^{3\gamma }}{(3\gamma )!\gamma !\gamma !}+10368\chi \frac{{\Im }^{4\gamma }}{(4\gamma )!}\\ +2592\chi (2\gamma )!\frac{{\Im }^{4\gamma }}{(4\gamma )!\gamma !}+5184\chi (3\gamma )!\frac{{\Im }^{4\gamma }}{(4\gamma )!(2\gamma )!\gamma !}+\cdots .& (24)\end{array}$

For particular case γ = 1, the Mohand transform solution become as

$\begin{array}{ll}u(x,\tau )=\chi (1-6\Im +36{\Im }^2-216{\Im }^3+1296{\Im }^4+\cdots ).& (25)\end{array}$

The calculated result provide the exact solution in the close form

$\begin{array}{ll}u(\chi ,\Im )=\frac{\chi }{1+6\Im }.& (26)\end{array}$

Example 4.2: Consider the third order time fractional KVD equation [50]

$\begin{array}{ll}\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}+u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}=0,0<\gamma \le 1,& (27)\end{array}$

with initial source

$\begin{array}{l}u(\chi ,0)=1-\chi .\end{array}$

Taking Mohand transform of Equation (26)

$\begin{array}{ll}{\upsilon }^{\gamma }\{R(\upsilon )-\upsilon u(0)\}=M\left\{-u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\},& (28)\end{array}$

after some evaluation, Equation (27) is simplified as

$\begin{array}{ll}R(\upsilon )=\upsilon u(0)+\frac{1}{{\upsilon }^{\gamma }}\left\{M\left\{-u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (29)\end{array}$

taking inverse Mohand transform of Equation (28)

$\begin{array}{ll}u(\chi ,\Im )=u(0)+M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\left\{-u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (30)\end{array}$

by using the recursive scheme Equation (11), we get

$\begin{array}{ll}{u}_0(\chi ,\Im )=u(0)=1-\chi ,& (31)\end{array}$

$\begin{array}{l}{u}_{m+1}(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{-u_m(\chi ,\Im )\frac{\partial u_m(\chi ,\Im )}{\partial \chi }\\ -\frac{{\partial }^3{u}_m(\chi ,\Im )}{\partial {\chi }^3}\}\},& (32)\end{array}$

From the recursive formula (31),

for m = 0

$\begin{array}{l}{u}_1(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{-u_0(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_0(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_1(\chi ,\Im )=(1-\chi )\frac{{\Im }^{\gamma }}{\gamma !},& (33)\end{array}$

for m = 1

$\begin{array}{l}{u}_2(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{-u_0(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }\\ -u_1(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_1(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_2(\chi ,\Im )=2(1-\chi )\frac{{\Im }^{2\gamma }}{(2\gamma )!},& (34)\end{array}$

for m = 2

$\begin{array}{l}{u}_3(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{-u_0(\chi ,\Im )\frac{\partial u_2(\chi ,\Im )}{\partial \chi }\\ -u_1(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }-u_2(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }\\ -\frac{{\partial }^3{u}_2(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_3(\chi ,\Im )=6(1-\chi )\frac{{\Im }^{3\gamma }}{(3\gamma )!}.\\ ⋮\hfill & (35)\end{array}$

The Mohand transform solution for example 3.2 is

$\begin{array}{ll}u(\chi ,\Im )=u_0(\chi ,\Im )+u_1(\chi ,\Im )+u_2(\chi ,\Im )+u_3(\chi ,\Im )+\mathrm{..}& (36)\end{array}$

$\begin{array}{l}u(\chi ,\Im )=1-\chi +(1-\chi )\frac{{\Im }^{\gamma }}{\gamma !}+2(1-\chi )\frac{{\Im }^{2\gamma }}{(2\gamma )!}\\ +6(1-\chi )\frac{{\Im }^{3\gamma }}{(3\gamma )!}+\cdots .& (37)\end{array}$

For particular case γ = 1, the Mohand transform solution become as

$\begin{array}{ll}u(\chi ,\Im )=1-\chi (1+\Im +{\Im }^2+{\Im }^3+\cdots ).& (38)\end{array}$

The calculated result provide the exact solution in the close form

$\begin{array}{ll}u(\chi ,\Im )=\frac{1-\chi }{1-\Im }.& (39)\end{array}$

Example 4.3 Consider the third order time fractional KVD equation [6]

$\begin{array}{ll}\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}=0,0<\gamma \le 1,& (40)\end{array}$

with initial source

$\begin{array}{l}u(\chi ,0)=6\chi .\end{array}$

Taking Mohand transform of Equation (39)

$\begin{array}{ll}{\upsilon }^{\gamma }\{R(\upsilon )-\upsilon u(0)\}=M\left\{6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\},& (41)\end{array}$

after some evaluation, Equation (40) is simplified as

$\begin{array}{ll}R(\upsilon )=\upsilon u(0)+\frac{1}{{\upsilon }^{\gamma }}\left\{M\left\{6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (42)\end{array}$

by applying inverse Mohand transform, we get

$\begin{array}{ll}u(\chi ,\Im )=u(0)+M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (43)\end{array}$

thus, by using recursive scheme of Equation (11), we get

$\begin{array}{ll}{u}_0(\chi ,\Im )=u(0)=6\chi & (44)\end{array}$

$\begin{array}{l}{u}_{m+1}(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{6u_m(\chi ,\Im )\frac{\partial u_m(\chi ,\Im )}{\partial \chi }\\ -\frac{{\partial }^3{u}_m(\chi ,\Im )}{\partial {\chi }^3}\}\},m=0,1,\cdots .& (45)\end{array}$

From the recursive formula (44),

for m = 0

$\begin{array}{l}{u}_1(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{6u_0(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_0(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_1(\chi ,\Im )=216\chi \frac{{\Im }^{\gamma }}{\gamma !},& (46)\end{array}$

for m = 1

$\begin{array}{l}{u}_2(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{6u_0(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }\\ +6u_1(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_1(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_2(\chi ,\Im )=15552\chi \frac{{\Im }^{2\gamma }}{(2\gamma )!},& (47)\end{array}$

for m = 2

$\begin{array}{l}{u}_3(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\right\{6u_0(\chi ,\Im )\frac{\partial u_2(\chi ,\Im )}{\partial \chi }+6u_1(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }\\ +6u_2(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_2(\chi ,\Im )}{\partial {\chi }^3}\left\}\right\},\\ u_3(\chi ,\Im )=1119744\chi \frac{{\Im }^{3\gamma }}{(3\gamma )!}+279936\chi (2\gamma )!\frac{{\Im }^{3\gamma }}{(3\gamma )!\gamma !\gamma !},\\ ⋮\hfill & (48)\end{array}$

The Mohand transform solution for example 4.3 is

$\begin{array}{ll}u(\chi ,\Im )=u_0(\chi ,\Im )+u_1(\chi ,\Im )+u_2(\chi ,\Im )+u_3(\chi ,\Im )+\cdots .& (49)\end{array}$

$\begin{array}{l}u(\chi ,\Im )=6\chi +216\chi \frac{{\Im }^{\gamma }}{\gamma !}+15552\chi \frac{{\Im }^{2\gamma }}{(2\gamma )!}+\\ 1119744\chi \frac{{\Im }^{3\gamma }}{(3\gamma )!}+279936\chi (2\gamma )!\frac{{\Im }^{3\gamma }}{(3\gamma )!\gamma !\gamma !}+\cdots .& (50)\end{array}$

For particular case γ = 1, the Mohand transform solution become as

$\begin{array}{ll}u(\chi ,\Im )=6\chi (1+36\Im +1296{\Im }^2+46656{\Im }^3+\cdots ).& (51)\end{array}$

The calculated result provide the exact solution in the close form

$\begin{array}{ll}u(\chi ,\Im )=\frac{6\chi }{1-36\Im }.& (52)\end{array}$

Example 4.4 Consider the third order time fractional KVD equation [6]

$\begin{array}{ll}\frac{{\partial }^{\gamma }u(\chi ,\Im )}{\partial {\Im }^{\gamma }}+6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }+\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}=0,0<\gamma \le 1,& (53)\end{array}$

with initial source

$\begin{array}{l}u(\chi ,0)=\frac{6}{{\chi }^2}.\end{array}$

Taking Mohand transform of Equation (52)

$\begin{array}{ll}{\upsilon }^{\gamma }\{R(\upsilon )-\upsilon u(0)\}=M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\},& (54)\end{array}$

after some evaluation, Equation (53) is simplified as

$\begin{array}{ll}R(\upsilon )=\upsilon u(0)+\frac{1}{{\upsilon }^{\gamma }}\left\{M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (55)\end{array}$

by applying inverse Mohand transform, we get

$\begin{array}{ll}u(\chi ,\Im )=u(0)+M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\left\{-6u(\chi ,\Im )\frac{\partial u(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^{3}u(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},& (56)\end{array}$

Thus, by using recursive scheme of Equation (11), we get

$\begin{array}{ll}u0(\chi ,\Im )=u(0)=\frac{6}{{\chi }^2},& (57)\end{array}$

$\begin{array}{l}{u}_{m+1}(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{6u_m(\chi ,\Im )\frac{\partial u_m(\chi ,\Im )}{\partial \chi }\\ -\frac{{\partial }^3{u}_m(\chi ,\Im )}{\partial {\chi }^3}\}\},m=0,1,\cdots .& (58)\end{array}$

From the recursive formula (44),

for m = 0

$\begin{array}{l}{u}_1(\chi ,\Im )=M^{-1}\left\{\frac{1}{{\upsilon }^{\gamma }}M\left\{6u_0(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_0(\chi ,\Im )}{\partial {\chi }^3}\right\}\right\},\\ u_1(\chi ,\Im )=\frac{-288}{{\chi }^5}\frac{{\Im }^{\gamma }}{\gamma !},& (59)\end{array}$

for m = 1

$\begin{array}{l}{u}_2(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{6u_0(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }\\ +6u_1(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }-\frac{{\partial }^3{u}_1(\chi ,\Im )}{\partial {\chi }^3}\}\},\\ u_2(\chi ,\Im )=\frac{12096}{{\chi }^8}\frac{{\Im }^{2\gamma }}{(2\gamma )!},& (60)\end{array}$

for m = 2

$\begin{array}{l}{u}_3(\chi ,\Im )=M^{-1}\{\frac{1}{{\upsilon }^{\gamma }}M\{6u_0(\chi ,\Im )\frac{\partial u_2(\chi ,\Im )}{\partial \chi }\\ +6u_1(\chi ,\Im )\frac{\partial u_1(\chi ,\Im )}{\partial \chi }+6u_2(\chi ,\Im )\frac{\partial u_0(\chi ,\Im )}{\partial \chi }\\ -\frac{{\partial }^3{u}_2(\chi ,\Im )}{\partial {\chi }^3}\}\},\\ u_3(\chi ,\Im )=\frac{4354560}{{\chi }^{11}}\frac{{\Im }^{3\gamma }}{(3\gamma )!}-\frac{2488320}{{\chi }^{11}}(2\gamma )!\frac{{\Im }^{3\gamma }}{(3\gamma )!\gamma !\gamma !},\\ ⋮& (61)\end{array}$

The Mohand transform solution for example 4.3 is

$\begin{array}{ll}u(\chi ,\Im )=u_0(\chi ,\Im )+u_1(\chi ,\Im )+u_2(\chi ,\Im )+u_3(\chi ,\Im )+..& (62)\end{array}$

$\begin{array}{l}u(\chi ,\Im )=\frac{6}{{\chi }^2}-\frac{288}{{\chi }^5}\frac{{\Im }^{\gamma }}{\gamma !}+\frac{12096}{{\chi }^8}\frac{{\Im }^{2\gamma }}{(2\gamma )!}+\frac{4354560}{{\chi }^{11}}\frac{{\Im }^{3\gamma }}{(3\gamma )!}\\ -\frac{2488320}{{\chi }^{11}}(2\gamma )!\frac{{\Im }^{3\gamma }}{(3\gamma )!\gamma !\gamma !}.& (63)\end{array}$

For particular case γ = 1, the Mohand transform solution become as

$\begin{array}{ll}u(\chi ,\Im )=\frac{6}{{\chi }^2}-\frac{288}{{\chi }^5}\Im +\frac{6048}{{\chi }^8}{\Im }^2-\frac{103680}{{\chi }^{11}}{\Im }^3+\cdots .& (64)\end{array}$

The calculated result converge to the exact solution in the close form

$\begin{array}{ll}u(\chi ,\Im )=\frac{6\chi ({\chi }^3-24\Im )}{{({\chi }^3+12\Im )}^2}.& (65)\end{array}$

4. Results and Discussion

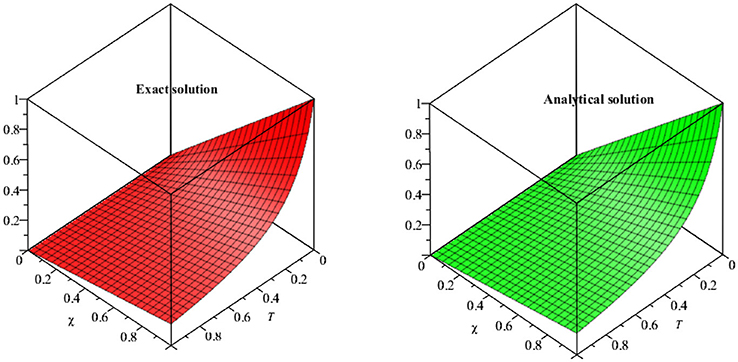
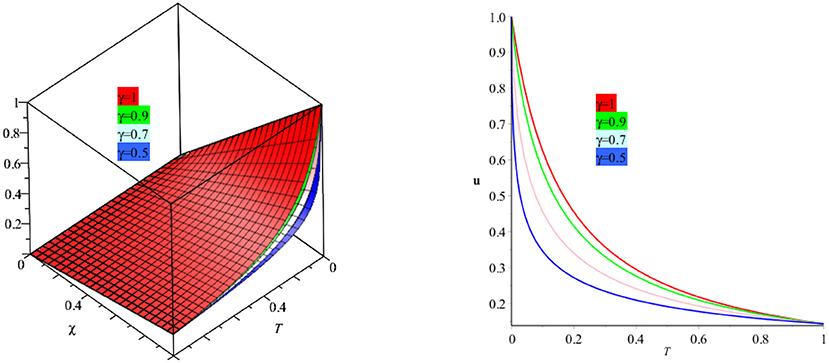
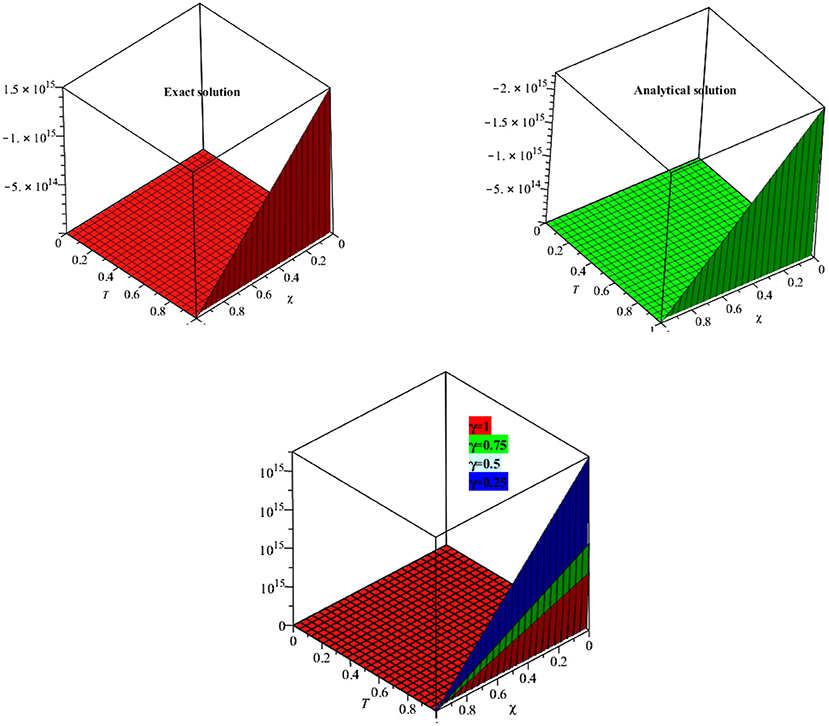
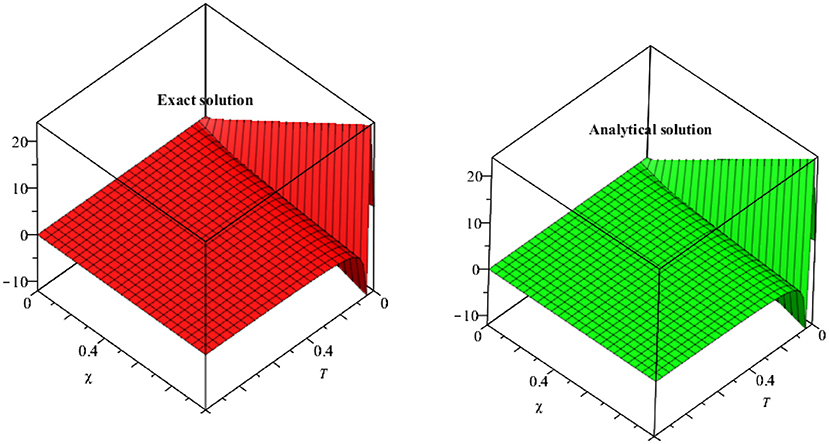
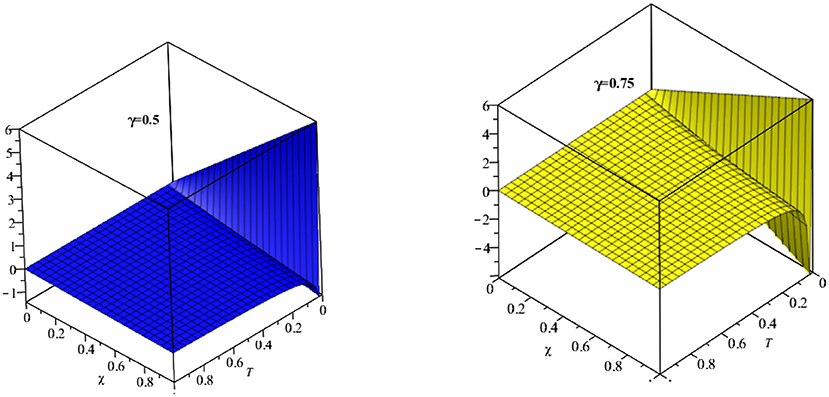
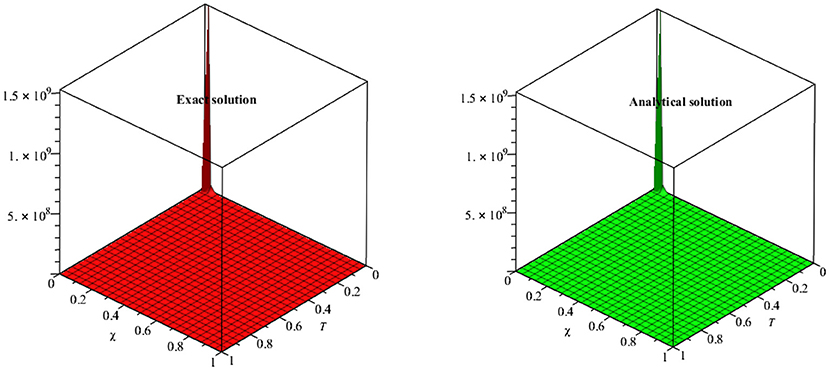
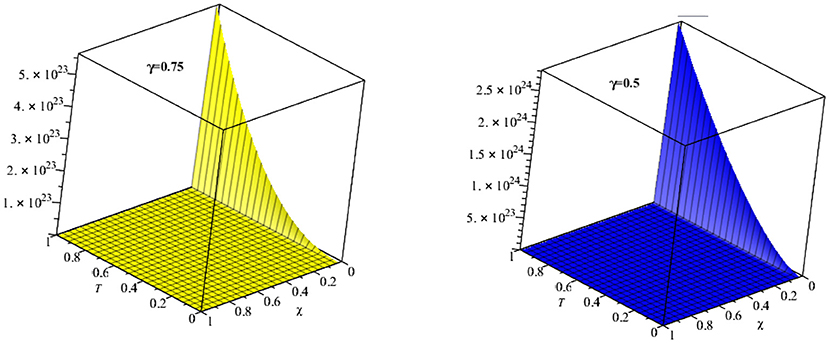
In Figure 1, the exact and analytical solutions of example 4.1 are presented. The solution-graph have confirmed that the obtained results are in good contact with the exact solutions of example 4.1. In Figure 2, the fractional-order solutions are calculated at fractional-order γ = 1, 0.9, 0.7, and 0.5. The solutions graphs are expressed in both two and three dimensions. The convergence phenomena can be observed from Figure 2. The similar implementation and results can be seen in Figures 3–7 for example 4.3 and 4.4 also. In Table 1, the results of MDM are compared with the results of HPTM which provide identical results. It is observed that the proposed method has the sufficient accuracy and rate of convergence to the exact solutions of the problems. It is also investigated that the proposed method provided the simple and straightforward implementation for all examples 1, 2, 3, and 4. These investigations of results have confirmed that the present method can be extended to other fractional-order problems arising in science and engineering.

FIGURE 1

Figure 1. Represents the exact and analytical solution of example 4.1.

FIGURE 2

Figure 2. Represents the solution at different fractional order.

FIGURE 3

Figure 3. Represents the exact and analytical solution of example 4.2.

FIGURE 4

Figure 4. Represents the exact and analytical solution of example 4.3.

FIGURE 5

Figure 5. Represents the solution of example 4.3 at γ = 0.75, γ = 0.5.

FIGURE 6

Figure 6. Represents the exact and analytical solution of example 4.4.

FIGURE 7

Figure 7. Represents the solution of example 4.4 at γ = 0.75, γ = 0.5.

TABLE 1

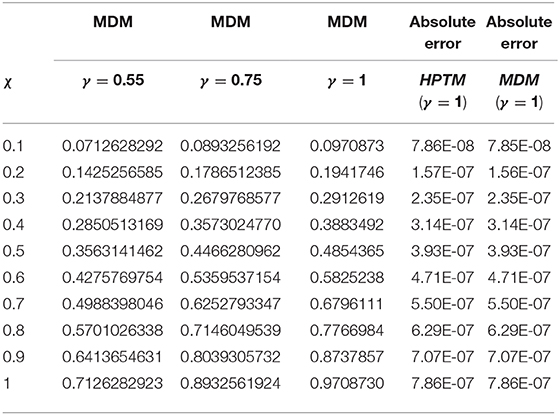
Table 1. Comparison of MDM and HPTM [49] of example 1 at ℑ = 0.5.

5. Conclusion

The proposed method is considered to be one of the pre-eminent and new analytical technique, to solve fractional order partial differential equation. In current research article, the proposed method is applied to solve fractional-order kortewege-De Vries equations. The current method is constructed by using Mohand transformation along with Adomian decomposition method. The new hybrid method is very useful to handle the analytical solutions of fractional-order partial differential equations. To verify, the validity of the suggested method some numerical examples of time fractional third order KdV equations are considered to solve it analytically. The solution graphs have confirmed the validity and reliability of the suggested method toward the solutions of other fractional-order non-linear partial differential equations.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

HK, RS, and UF has the primary contribution to produce this manuscript. PK has provided the financial support to publish this article. DB and MA have provided their expert opinion and writing draft of the paper.

Funding

The research grant for this manuscript was provided by PK, Center of Excellence in Theoretical and Computational Science (TaCS-CoE) and KMUTTFixed Point Research Laboratory, Room SCL 802 Fixed Point Laboratory, Science Laboratory Building, Departments of Mathematics, Faculty of Science, King Mongkut's University of Technology Thonburi (KMUTT), 126 Pracha-Uthit Road, Bang Mod, Thrung Khru, Bangkok 10140, Thailand.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Miura RM, editor. Bäcklund transformations, the inverse scattering method, solitons, and their applications: In: Proceedings of the NSF Research Workshop on Contact Transformations. Nashville, TN: Springer (2006).

Google Scholar

2. Asif M, Ul Haq S, Islam S, Abdullah Alkanhal T, Khan ZA, Khan I, et al. Unsteady flow of fractional fluid between two parallel walls with arbitrary wall shear stress using caputofabrizio derivative. Symmetry. (2019) 11:449. doi: 10.3390/sym11040449

CrossRef Full Text | Google Scholar

3. Whitham GB. Linear and nonlinear waves, Vol. 42. John Wiley & Sons (2011). doi: 10.1002/9781118032954

CrossRef Full Text | Google Scholar

4. Ali F, Murtaza S, Khan I, Sheikh NA, Nisar KS. AtanganaBaleanu fractional model for the flow of Jeffrey nanofluid with diffusion-thermo effects: applications in engine oil. Adv Diff Equat. (2019) 2019:346. doi: 10.1186/s13662-019-2222-1

CrossRef Full Text | Google Scholar

5. Lund LA, Omar Z, Alharbi SO, Khan I, Nisar KS. Numerical investigation of multiple solutions for caputo fractional-order-two dimensional magnetohydrodynamic unsteady flow of generalized viscous fluid over a shrinking sheet using the Adams-type predictor-corrector method. Coatings. (2019) 9:548. doi: 10.3390/coatings9090548

CrossRef Full Text | Google Scholar

6. Kaya D, Aassila M. An application for a generalized KdV equation by the decomposition method. Phys Lett A. (2002) 299:201–6. doi: 10.1016/S0375-9601(02)00652-7

CrossRef Full Text | Google Scholar

7. Drazin PG, Robin SJ. Solitons: An Introduction. Vol. 2. Cambridge: Cambridge University Press (1989).

Google Scholar

8. Saucez P, Vande Wouwer A, Schiesser WE. An adaptive method of lines solution of the Korteweg-de Vries equation. Comput Math Appl. (1998) 35:13–25. doi: 10.1016/S0898-1221(98)00093-5

CrossRef Full Text | Google Scholar

9. Abassy TA, El-Tawil MA, El-Zoheiry H. Exact solutions of some nonlinear partial differential equations using the variational iteration method linked with Laplace transforms and the Pad technique. Comput Math Appl. (2007) 54:940–54. doi: 10.1016/j.camwa.2006.12.067

CrossRef Full Text | Google Scholar

10. Kangalgil F, Ayaz F. Solitary wave solutions for the KdV and mKdV equations by differential transform method. Chaos Solit Fract. (2009) 41:464–72. doi: 10.1016/j.chaos.2008.02.009

CrossRef Full Text | Google Scholar

11. Ganji DD, Mirmohammadsadeghi SE, Safari M. Application fo He's variational iteration method and Adomian's decomposition method to prochhammer-chree equation. Int J Mod Phys B. (2009) 23:435–46. doi: 10.1142/S0217979209049656

CrossRef Full Text | Google Scholar

12. Marin M. On the domain of influence in thermoelasticity of bodies with voids. Arch Math (Brno). (1997) 33:301–8.

Google Scholar

13. Shah R, Khan H, Arif M, Kumam P. Application of Laplace Adomian decomposition method for the analytical solution of third-order dispersive fractional partial differential equations. Entropy. (2019) 21:335. doi: 10.3390/e21040335

CrossRef Full Text | Google Scholar

14. Othman MIA, Marin M. Effect of thermal loading due to laser pulse on thermoelastic porous medium under GN theory. Results Phys. (2017) 7:3863–72. doi: 10.1016/j.rinp.2017.10.012

CrossRef Full Text | Google Scholar

15. Momani S, Odibat Z, Alawneh A. Variational iteration method for solving the space and time fractional KdV equation. Numer Methods Part Diff Equat. (2008) 24:262–71. doi: 10.1002/num.20247

CrossRef Full Text | Google Scholar

16. Wang Q. Homotopy perturbation method for fractional KdV equation. Appl Math Comput. (2007) 190:1795–802. doi: 10.1016/j.amc.2007.02.065

CrossRef Full Text | Google Scholar

17. Wang Q. Homotopy perturbation method for fractional KdV-Burgers equation. Chaos Solit Fract. (2008) 35:843–50. doi: 10.1016/j.chaos.2006.05.074

CrossRef Full Text | Google Scholar

18. Momani S. An explicit and numerical solutions of the fractional KdV equation. Math Comput Simulat. (2005) 70:110–8. doi: 10.1016/j.matcom.2005.05.001

CrossRef Full Text | Google Scholar

19. Song L, Zhang H. Application of homotopy analysis method to fractional KdVBurgersKuramoto equation. Phys Lett A. (2007) 367:88–94. doi: 10.1016/j.physleta.2007.02.083

CrossRef Full Text | Google Scholar

20. Shah R, Khan H, Farooq U, Baleanu D, Kumam P, Arif M. A new analytical technique to solve system of fractional-order partial differential equations. IEEE Access. (2019) 7:150037–50. doi: 10.1109/ACCESS.2019.2946946

CrossRef Full Text | Google Scholar

21. Jeffrey A. Applied Partial Differential Equations: An Introduction. San Diego, CA: Academic Press (2003).

Google Scholar

22. Satsuma J, Kaup DJ. A Bcklund transformation for a higher order Korteweg-de Vries equation. J Phys Soc Jpn. (1977) 43:692–7. doi: 10.1143/JPSJ.43.692

CrossRef Full Text | Google Scholar

23. Grses M, Karasu A. Variable coefficient third order Kortewegde Vries type of equations. J Math Phys. (1995) 36:3485–91. doi: 10.1063/1.530974

CrossRef Full Text | Google Scholar

24. Chavan SS, Panchal MM. Solution of third order Korteweg-De Vries equation by homotopy perturbation method using Elzaki transform. Int J Res Appl Sci Eng Technol. (2014) 2:366–9.

Google Scholar

25. Debnath L, Bhatta D. Integral Transforms and Their Applications. New York, NY: Chapman and Hall/CRC Press (2014).

Google Scholar

26. Mahgoub MAM. The new integral transform “Mahgoub Transform”. Adv Theor Appl Math. (2016) 11:391–8.

Google Scholar

27. Abdelilah K, Hassan S. The new integral transform “Kamal Transform”. Adv Theor Appl Math. (2016) 11:451–8.

Google Scholar

28. Elzaki TM. The new integral transform “Elzaki transform”. Glob J Pure Appl Math. (2011) 7:57–64.

Google Scholar

29. Aboodh KS. The new integral transform “Aboodh Transform”. Glob J Pure Appl Math. (2013) 9:35–43.

Google Scholar

30. Mohand M, Mahgoub A. The new integral transform Mohand Transform. Adv Theor Appl Math. (2017) 12:113–20.

Google Scholar

31. Watugala GK. Sumudu transform: a new integral transform to solve differential equations and control engineering problems. Integr Educ. (1993) 24:35–43. doi: 10.1080/0020739930240105

CrossRef Full Text | Google Scholar

32. Khan H, Shah R, Baleanu D, Kumam P, Arif M. Analytical solution of fractional-order hyperbolic telegraph equation, using natural transform decomposition method. Electronics. (2019) 8:1015. doi: 10.3390/electronics8091015

CrossRef Full Text | Google Scholar

33. Eltayeb H, Klman A. A note on the Sumudu transforms and differential equations. Appl Math Sci. (2010) 4:1089–98.

Google Scholar

34. Aggarwal S, Singh GP. Shehu Transform of Error Function (probability integral). Int J Res Advent Technol. (2019) 7: 54–60. doi: 10.32622/ijrat.76201932

CrossRef Full Text | Google Scholar

35. Shah R, Khan H, Baleanu D, Kumam P, Arif M. A novel method for the analytical solution of fractional ZakharovKuznetsov equations. Adv Diff Equat. (2019) 2019:1–14. doi: 10.1186/s13662-019-2441-5

CrossRef Full Text | Google Scholar

36. Aggarwal S, Gupta AR. Solution of linear Volterra integro-differential equations of second kind using Kamal transform. J Emerg Technol Innovat Res. (2019) 6:741–7.

Google Scholar

37. Kumar PS, Viswanathan A. Applications of Mohand transform to mechanics and electrical circuit problems. Int J Res Adv Technol. (2018) 6:2838–40.

Google Scholar

38. Aggarwal S, Chauhan R. A comparative study of Mohand and Aboodh transforms. Int J Res Adv Technol. (2019) 7:520–9. doi: 10.32622/ijrat.712019107

CrossRef Full Text | Google Scholar

39. Shah R, Khan H, Baleanu D. Fractional WhithamBroerKaup Equations within Modified Analytical Approaches. Axioms. (2019) 8:125. doi: 10.3390/axioms8040125

CrossRef Full Text | Google Scholar

40. Aggarwal S, Sharma SD. A comparative study of Mohand and Sumudu transforms. J Emerg Technol Innovat Res. (2019) 6:145–53.

Google Scholar

41. Aggarwal S. A comparative study of Mohand and Mahgoub transforms. Stat. (2019) 4:1–7.

Google Scholar

42. Aggarwal S, Raman C, Nidhi S. Mohand transform of Bessels functions. Int J Res Adv Technol. (2018) 6:3034–8.

Google Scholar

43. Aggarwal S, Sharma N, Chauhan RṠolution of linear Volterra integral equations of second kind using Mohand transform. Int J Res Adv Technol. (2018) 6:3098–102.

Google Scholar

44. Srivastava HM, Shah R, Khan H, Arif M. Some analytical and numerical investigation of a family of fractional order Helmholtz equations in two space dimensions. Math Methods Appl Sci. (2020) 43:199–212. doi: 10.1002/mma.5846

CrossRef Full Text | Google Scholar

45. Mohand M, Mahgoub A. The new integral transform Mohand Transform. Adv Theor Appl Math. (2017) 12:113–20.

Google Scholar

46. Aggarwal S, Mishra R, Chaudhary A. A comparative study of Mohand and Elzaki transforms. Glob J Eng Sci Res. (2019) 6: 203–13.

Google Scholar

47. Hilfer R, editor. Applications of Fractional Calculus in Physics. Singapore: World Scientific (2000).

Google Scholar

48. Shah K, Khalil H, Ali Khan R. Analytical solutions of fractional order diffusion equations by natural transform method. Iran J Sci Technol Trans A. (2018) 42:1479–90. doi: 10.1007/s40995-016-0136-2

CrossRef Full Text | Google Scholar

49. Eljaily MH, Elzaki TM. Homotopy perturbation transform method for solving korteweg-devries (kdv) equation. Pure Appl Math J. (2015) 4:264–8. doi: 10.11648/j.pamj.20150406.17

CrossRef Full Text | Google Scholar

50. Sedeeg AKH. Homotopy perturbation transform method for solving third order Korteweg De-Vries (KDV) Equation. AJAM. (2016) 4:247–51. doi: 10.11648/j.ajam.20160405.16

CrossRef Full Text | Google Scholar