A New Feature of the Fractional Euler–Lagrange Equations for a Coupled Oscillator Using a Nonsingular Operator Approach

In this new work, the free motion of a coupled oscillator is investigated. First, a fully description of the system under study is formulated by considering its classical Lagrangian, and as a result, the classical Euler–Lagrange equations of motion are constructed. After this point, we extend the classical Lagrangian in fractional sense, and thus, the fractional Euler–Lagrange equations of motion are derived. In this new formulation, we consider a recently introduced fractional operator with Mittag–Leffler non-singular kernel. We also present an efficient numerical method for solving the latter equations in a proper manner. Due to this new powerful technique, we are able to obtain remarkable physical thinks; indeed, we indicate that the complex behavior of many physical systems is realistically demonstrated via the fractional calculus modeling. Finally, we report our numerical findings to verify the theoretical analysis.

1. Introduction

There are two main approaches in the classical mechanics to get the equations of motion for a dynamical system: Newtonian and Lagrangian. However, in the first approach, which is a force-based one, we encounter with some difficulties since all acting forces need to be set up while sometimes they are not clear. The second approach was invented by Joseph Louis Lagrange, a French Mathematician. This approach is considered as a useful technique to find the equations of motion for many kinds of physical processes [1]. During the past decade, the Lagrangian method has been used to solve some interesting systems such as Atwood's machine, coupled and spring pendulums, and many others.

The fractional calculus (FC) is a branch of mathematical analysis, which deals with the non-integer integral and derivative operators. The application of the FC has been extensively expanded in different fields of the basic and engineering sciences [2–9]. Over the past few decades, the classical mechanics has been extended by using the new aspects of the FC. In Riewe [10], the non-conservative Lagrangian systems were studied by Riewe using the concept of the FC. Indeed, the author employed the fractional-order derivatives to define conjugate momenta and formulated the fractional Hamilton equations. In Laskin [11], Laskin studied the path of Lévy flights by using a fractional path integral scheme. In Laskin [12], he also developed the fractional quantum mechanics and proved the hermiticity property of the Hamilton operator in fractional sense. Afterwards, the works by Riewe and Laskin were followed by many scientists and several interesting papers were published in this area [13–19]. According to these studies, the asymptotic behavior of many physical systems was explored by using the fractional Lagrangian (or the fractional Hamiltonian), which leads to the fractional Euler-Lagrange equations (FELEs) [20–22]. However, an important issue here is to solve these equations by an appropriate approximation method [23]. These techniques include the Adams-Bashforth-Moulton scheme [24], variational iteration method [25], Adomian decomposition method [26], and the Grünwald–Letnikov approximation [27].

According to the recent studies in the literature, the complex behavior of physical systems can be represented more precisely by the FC approach. However, some natural phenomena with nonlocal characteristic may not be described properly by the classical fractional derivatives (FDs) due to the appearance of singular kernel in the definition of these operators. Thus, an alternative analytical approach is needed to model and analyze the nonlocal dynamics in a proper manner. To solve this difficulty, a new type of the fractional operator with Mittag-Leffler (ML) kernel (ABC) was developed in Baleanu and Atangana [28] and applied to some practical cases [29]. Indeed, due to the presence of nonsingular kernel, this new definition shows a completely different property compared to the classical FDs, and hence, it can describe the nonlocal dynamics and capture different features of realistic systems more appropriately than the standard FC. Nevertheless, more practical cases should be examined via the ABC operator and some new and efficient numerical methods need to be designed to solve these fractional equations effectively. Motivated by the above discussion, the aim of this paper is to investigate the free motion of a coupled oscillator by using the newly introduced ABC fractional operator with ML kernel. We give a theoretical analysis to formulate the corresponding FELEs. Also, we provide an efficient numerical scheme to solve the aforementioned fractional equations effectively. In accordance with the obtained results, we conclude that a flexible model is provided by using the FC as the fractional order can be varied between 0 and 1. Due to this impressive feature, the new hidden aspects of the coupled oscillator system can be explored, which are not visible in the classic integer manner.

The rest of this paper is organized as follows. In section 2, some preliminary results regarding the fractional operators are given. Section 3 introduces the classical and fractional descriptions of the coupled oscillator. In section 4, an efficient numerical technique is proposed to solve the derived FELEs. In section 5, numerical simulations are presented, and finally, the paper is closed by some conclusions in the last section.

2. Preliminaries

This section gives some definitions and preliminaries regarding the fractional operator with ML kernel (ABC) [28]. For φ ∈ ℍ¹(0, b), the (left) ABC fractional operator of order q ∈ (0, 1) is defined by

$\begin{array}{ll}{}_0{}^{ABC}D{}_t^q\phi (t)=\frac{S(q)}{1-q}{\displaystyle {\int }_0^t{E}_q[-\frac{q}{1-q}{(t-\tau )}^q]}\dot{\phi }(\tau )d\tau ,& (1)\end{array}$

where S(q) denotes a normalization function with S(0) = S(1) = 1 and E_q(t) is the one–parameter ML function. The corresponding right fractional operator of order q ∈ (0, 1) is also expressed as

$\begin{array}{ll}{}_{\mathrm{t}}{}^{ABC}D{}_b^q\phi (t)=-\frac{S(q)}{1-q}{\displaystyle {\int }_t^b{E}_q[-\frac{q}{1-q}{(\tau -t)}^q]}\dot{\phi }(\tau )d\tau .& (2)\end{array}$

The integral operators associated with the definitions (1) and (2) are, respectively, described by

$\begin{array}{ll}{}_0{}^{ABC}I{}_t^q\phi (t)=\frac{1-q}{S(q)}\phi (t)+\frac{q}{S(q)\Gamma (q)}{\displaystyle {\int }_0^t{(t-\tau )}^{q-1}}\phi (\tau )d\tau ,& (3)\end{array}$

$\begin{array}{ll}{}_{\mathrm{t}}{}^{ABC}I{}_b^q\phi (t)=\frac{1-q}{S(q)}\phi (t)+\frac{q}{S(q)\Gamma (q)}{\displaystyle {\int }_t^b{(\tau -t)}^{q-1}\phi (\tau )d\tau .}& (4)\end{array}$

The following useful relations hold between the above–mentioned differential and integral operators

$\begin{array}{ll}{}_0{}^{ABC}I{}_t^q\left[{}_0{}^{ABC}D{}_t^q\phi (t)\right]=\phi (t)-\phi (0),& (5)\end{array}$

$\begin{array}{ll}{}_{\mathrm{t}}{}^{ABC}I{}_b^q\left[{}_{\mathrm{t}}{}^{ABC}D{}_b^q\phi (t)\right]=\phi (t)-\phi (b).& (6)\end{array}$

For more details and discussions, we refer the interested readers to Baleanu and Atangana [28] and Abdeljawad and Baleanu [30].

3. The Classical and Fractional Description

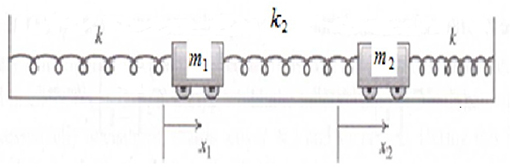
In this section, we consider a coupled oscillator system and provide a fully description of its dynamical equations both in the classical and fractional manner. For this purpose, we consider the physical system shown in Figure 1, which consists of two coupled carts with masses m₁ and m₂ attached to their respective walls by two identical springs (with force constant k) and to each other by another spring (with force constant k₂). It is of interest to mention that in some books this system is known as the diatomic molecules.

FIGURE 1

Figure 1. Two coupled carts with different masses.

Assuming that all springs are massless, we aim to obtain the classical Euler–Lagrange equations (CELEs) for the physical system under consideration. To this end, first we write the instantaneous kinetic and potential energies of the system, respectively, by the formulas

$\begin{array}{ll}{T}_c(t)=\frac{1}{2}{m}_1{ẋ}_1^2(t)+\frac{1}{2}{m}_2{ẋ}_2^2(t),& (7)\end{array}$

$\begin{array}{ll}{U}_c(t)=\frac{1}{2}(k+k_2)x_1^2(t)-k_2{x}_1(t)x_2(t)+\frac{1}{2}(k_2+k)x_2^2(t).& (8)\end{array}$

Then the classical Lagrangian L_c(t) is given in the form

$\begin{array}{l}{L}_c(t)=T_c(t)-U_c(t)=\frac{1}{2}{m}_1{ẋ}_1^2(t)+\frac{1}{2}{m}_2{ẋ}_2^2(t)\\ -\frac{1}{2}(k+k_2)x_1^2(t)+k_2{x}_1(t)x_2(t)-\frac{1}{2}(k_2+k)x_2^2(t).& (9)\end{array}$

Substituting the Lagrangian (9) into the CELEs ($\frac{\partial L_c(t)}{\partial x_i(t)}-\frac{d}{dt}\frac{\partial L_c(t)}{\partial {ẋ}_i(t)}=0$, i = 1, 2), we obtain

$\begin{array}{ll}{m}_1\ddot{x_1}(t)=-(k+k_2)x_1(t)+k_2{x}_2(t),& (10)\end{array}$

$\begin{array}{ll}{m}_2\ddot{x_2}(t)=k_2{x}_1(t)-(k_2+k)x_2(t).& (11)\end{array}$

Now, we aim to derive the classical Hamiltonian equations (CHEs) of motion. For this purpose, first we introduce the following generalized momenta

$\begin{array}{ll}{P}_1(t)=\frac{\partial L_c}{\partial {\dot{x}}_1(t)}=m_1{\dot{x}}_1(t),P_2(t)=\frac{\partial L_c}{\partial {\dot{x}}_2(t)}=m_2{\dot{x}}_2(t).& (12)\end{array}$

Substituting Equations (9) and (12) into the Hamilton function H(t) = ẋ₁(t)P₁(t) + ẋ₂(t)P₂(t) − L_c(t), we provide

$\begin{array}{l}H(t)=\frac{P_1^2(t)}{2m_1}+\frac{P_2^2(t)}{2m_2}+\frac{1}{2}(k+k_2)x_1^2(t)-k_2{x}_1(t)x_2(t)\\ +\frac{1}{2}(k_2+k)x_2^2(t).& (13)\end{array}$

Then the CHEs of motion for the coupled oscillator are obtained from

$\begin{array}{ll}{\dot{x}}_1(t)=\frac{\partial H(t)}{\partial P_1(t)},{\dot{P}}_1(t)=-\frac{\partial H(t)}{\partial x_1(t)},& (14)\end{array}$

$\begin{array}{ll}{\dot{x}}_2(t)=\frac{\partial H(t)}{\partial P_2(t)},{\dot{P}}_2(t)=-\frac{\partial H(t)}{\partial x_2(t)},& (15)\end{array}$

which lead to the same results as the CELEs (10)–(11). Nevertheless, as it was pointed out in Agrawal [31], the theory of the calculus of variations cannot capture many laws of the natural phenomena; for example, the behavior of nonconservative systems cannot be described properly by the dynamical equations achieved in accordance with the traditional energy approach. On the other hand, the FC has overcome this limitation as it can characterize the behavior of many complex physical systems including hereditary properties. Accordingly, in the following, we investigate the fractional Lagrangian for the coupled oscillator in order to expose its new features. To this end, we modify the classical Lagrangian (9) according to the ABC operator defined by Equation (1)

$\begin{array}{l}{L}_f(t)=\frac{1}{2}{m}_1{\left({}_0{}^{ABC}D{}_t^q{x}_1(t)\right)}^2+\frac{1}{2}{m}_2{\left({}_0{}^{ABC}D{}_t^q{x}_2(t)\right)}^2\\ -\frac{1}{2}(k+k_2)x_1^2(t)+k_2{x}_1(t)x_2(t)-\frac{1}{2}(k_2+k)x_2^2(t).& (16)\end{array}$

Substituting L_f(t) from Equation (16) into the formula $\frac{\partial L_f(t)}{\partial x_i(t)}+{}_t{}^{ABC}D{}_b^q\frac{\partial L_f(t)}{\partial {}_0{}^{ABC}D{}_t^q{x}_i(t)}+{}_0{}^{ABC}D{}_t^q\frac{\partial L_f(t)}{{\partial }^{ABC}{}_{t}D{}_b^q{x}_i(t)}=0$, i = 1, 2, yields the following FELEs

$\begin{array}{ll}{}_t{}^{ABC}D{}_b^q{}_0{}^{ABC}D{}_t^q{x}_1(t)-({\omega }_1^2+r{\omega }_2^2)x_1(t)+r{\omega }_2^2{x}_2(t)=0,& (17)\end{array}$

$\begin{array}{ll}{}_t{}^{ABC}D{}_b^q{}_0{}^{ABC}D{}_t^q{x}_2(t)-({\omega }_2^2+\frac{1}{r}{\omega }_1^2)x_2(t)+{\omega }_2^2{x}_1(t)=0,& (18)\end{array}$

where ${\omega }_1=\sqrt{\frac{k}{m_1}}$, ${\omega }_2=\sqrt{\frac{k_2}{m_2}}$, and $r=\frac{m_2}{m_1}$. As can be seen, the FELEs (17)–(18) are reduced to the CELEs (10)–(11) when q goes to 1.

Now, we are going to attain the fractional Hamiltonian equations (FHEs) of motion. To do so, we consider the fractional Hamilton function as follows

$\begin{array}{l}{H}_f(t)=P_{1,1}(t){}_0{}^{ABC}D{}_t^q{x}_1(t)+P_{1,2}(t){}_t{}^{ABC}D{}_b^q{x}_1(t)\\ +P_{2,1}(t){}_0{}^{ABC}D{}_t^q{x}_2(t)+P_{2,2}(t){}_t{}^{ABC}D{}_b^q{x}_2(t)-L_f(t),& (19)\end{array}$

where P_{1, 1}(t), P_{1, 2}(t), P_{2, 1}(t), and P_{2, 2}(t) are the following generalized momenta

$\begin{array}{l}{P}_{1,1}(t)=\frac{\partial L_f(t)}{{\partial }^{AB}{}_0^C{D}_t^q{x}_1(t)}=m_1{{}^{AB}}_0^C{D}_t^q{x}_1(t),\\ P_{1,2}(t)=\frac{\partial L_f(t)}{{\partial }^{AB}{}_t^C{D}_b^q{x}_1(t)}=0,\\ P_{2,1}(t)=\frac{\partial L_f(t)}{{\partial }^{AB}{}_0^C{D}_t^q{x}_2(t)}=m_2{{}^{AB}}_0^C{D}_t^q{x}_2(t),\\ P_{2,2}(t)=\frac{\partial L_f(t)}{{\partial }^{AB}{}_t^C{D}_b^q{x}_2(t)}=0.& (20)\end{array}$

Thus, the fractional Hamilton function is obtained by substituting Equation (16) and (20) into Equation (19)

$\begin{array}{l}{H}_f(t)=\frac{1}{2}{m}_1{\left({}_0{}^{ABC}D{}_t^q{x}_1(t)\right)}^2+\frac{1}{2}{m}_2{\left({}_0{}^{ABC}D{}_t^q{x}_2(t)\right)}^2+\\ \frac{1}{2}(k_1+k_2)x_1^2(t)-k_2{x}_1(t)x_2(t)+\frac{1}{2}(k_1+k_2)x_2^2(t).& (21)\end{array}$

Accordingly, the FHEs of motion are concluded as follows

$\begin{array}{l}\frac{\partial H_f(t)}{\partial x_1(t)}={}_t{}^{ABC}D{}_b^q{P}_{1,1}(t)+{}_0{}^{ABC}D{}_t^q{P}_{1,2}(t)\Rightarrow \\ ({\omega }_1^2+r{\omega }_2^2)x_1(t)-r{\omega }_2^2{x}_2(t)={}_t{}^{ABC}D{}_b^q{}_0{}^{ABC}D{}_t^q{x}_1(t),& (22)\end{array}$

$\begin{array}{l}\frac{\partial H_f(t)}{\partial x_2(t)}={}_t{}^{ABC}D{}_b^q{P}_{2,1}(t)+{}_0{}^{ABC}D{}_t^q{P}_{2,2}(t)\Rightarrow \\ ({\omega }_2^2+\frac{1}{r}{\omega }_1^2)x_2(t)-{\omega }_2^2{x}_1(t)={}_t{}^{ABC}D{}_b^q{}_0{}^{ABC}D{}_t^q{x}_2(t).& (23)\end{array}$

Here, it is notable that the FHEs (22)–(23) are the same as the previously derived FELEs (17)–(18) and reduced to the CELEs (10)–(11) as q → 1.

4. Numerical Method

In this section, we propose an efficient numerical technique to solve the FELEs (17)–(18) [or the FHEs (22)–(23)]. In order to this, we first define the new state variables ${\tilde{x}}_1(t){=}^{AB}{}_0^C{D}_t^q{x}_1(t)$ and ${\tilde{x}}_2(t){=}^{AB}{}_0^C{D}_t^q{x}_2(t)$. Thus, the Equations (17)–(18) are rewritten as

$\begin{array}{ll}\{\begin{array}{l}{}_0{}^{ABC}D{}_t^q{x}_1(t)={\tilde{x}}_1(t),\\ {}_t{}^{ABC}D{}_b^{\alpha }{\tilde{x}}_1=({\omega }_1^2+r{\omega }_2^2)x_1(t)-r{\omega }_2^2{x}_2(t),\\ {}_0{}^{ABC}D{}_t^q{x}_2(t)={\tilde{x}}_2(t),\\ {}_t{}^{ABC}D{}_b^{\alpha }{\tilde{x}}_2=({\omega }_2^2+\frac{1}{r}{\omega }_1^2)x_2(t)-{\omega }_2^2{x}_1(t).\end{array}& (24)\end{array}$

Applying the definition of the left and right integral operators (3) and (4), we derive the following system of fractional integral equations

$\begin{array}{ll}\{\begin{array}{l}{x}_1(t)=x_1(0)+\frac{1-q}{S(q)}{\tilde{x}}_1(t)+\frac{q}{S(q)\Gamma (q)}{\displaystyle {\int }_0^t{(t-\tau )}^{q-1}}{\tilde{x}}_1(\tau )d\tau ,\\ {\tilde{x}}_1(t)={\tilde{x}}_1(b)+\frac{1-q}{S(q)}(({\omega }_1^2+r{\omega }_2^2)x_1(t)-r{\omega }_2^2{x}_2(t))\\ +\frac{q}{S(q)\Gamma (q)}{\displaystyle {\int }_t^b{(\tau -t)}^{q-1}}(({\omega }_1^2+r{\omega }_2^2)x_1(\tau )-r{\omega }_2^2{x}_2(\tau ))d\tau ,\\ x_2(t)=x_2(0)+\frac{1-q}{S(q)}{\tilde{x}}_2(t)+\frac{q}{S(q)\Gamma (q)}{\displaystyle {\int }_t^b{(\tau -t)}^{q-1}}{\tilde{x}}_2(\tau )d\tau ,\\ {\tilde{x}}_2(t)={\tilde{x}}_2(b)+\frac{1-q}{S(q)}(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)x_2(t)-{\omega }_2^2{x}_1(t))\\ +\frac{q}{S(q)\Gamma (q)}{\displaystyle {\int }_t^b{(\tau -t)}^{q-1}}(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)x_2(\tau )-{\omega }_2^2{x}_1(\tau ))d\tau .\end{array}& (25)\end{array}$

Now, we consider a uniform mesh on [0, b] with the time step size $h=\frac{b-0}{N}$ in which N is an arbitrary positive integer. Moreover, we represent the numerical approximation of x_i(t_j) and ${\tilde{x}}_i(t_j)$ by x_{i, j} and ${\tilde{x}}_{i,j}$, respectively, where t_j = 0 + jh (0 ≤ j ≤ N) is the time at node j. Applying the Euler method to discretize the convolution integrals in (25), we derive

$\begin{array}{ll}\left[\begin{array}{c}{x}_{1,1}\\ ⋮\\ x_{1,N}\end{array}\right]=\left[\begin{array}{c}{x}_1(0)\\ ⋮\\ x_1(0)\end{array}\right]+\frac{1-q}{S(q)}\left[\begin{array}{c}{\tilde{x}}_{1,1}\\ ⋮\\ {\tilde{x}}_{1,N}\end{array}\right]+\frac{q}{S(q)}{h}^q{H}_{N,q}\left[\begin{array}{c}{\tilde{x}}_{1,0}\\ ⋮\\ {\tilde{x}}_{1,N-1}\end{array}\right],& (26)\end{array}$

$\begin{array}{l}\left[\begin{array}{c}{\tilde{x}}_{1,0}\\ ⋮\\ {\tilde{x}}_{1,N-1}\end{array}\right]=\left[\begin{array}{c}{\tilde{x}}_1(b)\\ ⋮\\ {\tilde{x}}_1(b)\end{array}\right]+\frac{1-q}{S(q)}(({\omega }_1^2+r{\omega }_2^2)\left[\begin{array}{c}{x}_{1,0}\\ ⋮\\ x_{1,N-1}\end{array}\right]\hfill \\ -r{\omega }_2^2\left[\begin{array}{c}{x}_{2,0}\\ ⋮\\ x_{2,N-1}\end{array}\right])\hfill \\ +\frac{q}{S(q)}{h}^q{H}_{N,q}^T\left(({\omega }_1^2+r{\omega }_2^2)\left[\begin{array}{c}{x}_{1,1}\\ ⋮\\ x_{1,N}\end{array}\right]-r{\omega }_2^2\left[\begin{array}{c}{x}_{2,1}\\ ⋮\\ x_{2,N}\end{array}\right]\right),\hfill & (27)\end{array}$

$\begin{array}{ll}\left[\begin{array}{c}{x}_{2,1}\\ ⋮\\ x_{2,N}\end{array}\right]=\left[\begin{array}{c}{x}_2(0)\\ ⋮\\ x_2(0)\end{array}\right]+\frac{1-q}{S(q)}\left[\begin{array}{c}{\tilde{x}}_{2,1}\\ ⋮\\ {\tilde{x}}_{2,N}\end{array}\right]+\frac{q}{S(q)}{h}^q{H}_{N,q}\left[\begin{array}{c}{\tilde{x}}_{2,0}\\ ⋮\\ {\tilde{x}}_{2,N-1}\end{array}\right],& (28)\end{array}$

$\begin{array}{l}\left[\begin{array}{c}{\tilde{x}}_{2,0}\\ ⋮\\ {\tilde{x}}_{2,N-1}\end{array}\right]=\left[\begin{array}{c}{\tilde{x}}_2(b)\\ ⋮\\ {\tilde{x}}_2(b)\end{array}\right]+\frac{1-q}{S(q)}(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)\left[\begin{array}{c}{x}_{2,0}\\ ⋮\\ x_{2,N-1}\end{array}\right]\hfill \\ -{\omega }_2^2\left[\begin{array}{c}{x}_{1,0}\\ ⋮\\ x_{1,N-1}\end{array}\right])\hfill & (29)\\ +\frac{q}{S(q)}{h}^q{H}_{N,q}^T\left(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)\left[\begin{array}{c}{x}_{2,1}\\ ⋮\\ x_{2,N}\end{array}\right]-{\omega }_2^2\left[\begin{array}{c}{x}_{1,1}\\ ⋮\\ x_{1,N}\end{array}\right]\right),\hfill \end{array}$

where

$\begin{array}{l}{H}_{N,q}=\left[\begin{array}{cccc}{\omega }_{0,q}& 0& \dots & 0\\ {\omega }_{1,q}& \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ {\omega }_{N-1,q}& \dots & {\omega }_{1,q}& {\omega }_{0,q}\end{array}\right],{\omega }_{0,q}=1,\\ {\omega }_{j,q}=(1+\frac{q-1}{j}){\omega }_{j-1,q},j=1,2,\dots ,N-1.& (30)\end{array}$

By defining the augmented matrices A_{N, q} and B_{N, q} such as

$\begin{array}{ll}{A}_{N,q}=\left[\begin{array}{cccc}-\frac{1-q}{q{h}^q}& 0& \cdots & 0\\ & & & ⋮\\ & H_{N,q}& & 0\end{array}\right],B_{N,q}=\left[\begin{array}{cccc}0& & H_{N,q}^T& \\ ⋮& & & \\ 0& \cdots & 0& -\frac{1-q}{q{h}^q}\end{array}\right],& (31)\end{array}$

the system of Equations (26)–(29) is combined in a compact form as follows

$\begin{array}{ll}\{\begin{array}{l}{X}_1-\frac{1-q}{S(q)}{\tilde{X}}_1-\frac{q}{S(q)}{h}^q{A}_{N,q}{\tilde{X}}_1=X_{1,0},\\ {\tilde{X}}_1-\frac{1-q}{S(q)}(({\omega }_1^2+r{\omega }_2^2)X_1-r{\omega }_2^2{X}_2)\\ -\frac{q}{S(q)}{h}^q{B}_{N,q}(({\omega }_1^2+r{\omega }_2^2)X_1-r{\omega }_2^2{X}_2)={\tilde{X}}_{1,b},\\ X_2-\frac{1-q}{S(q)}{\tilde{X}}_2-\frac{q}{S(q)}{h}^q{A}_{N,q}{\tilde{X}}_2=X_{2,0},\\ {\tilde{X}}_2-\frac{1-q}{S(q)}(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)X_2-{\omega }_2^2{X}_1)\\ -\frac{q}{S(q)}{h}^q{B}_{N,q}(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)X_2-{\omega }_2^2{X}_1)={\tilde{X}}_{2,b},\end{array}& (32)\end{array}$

where

$\begin{array}{ll}{X}_i=\left[\begin{array}{c}{x}_{i,0}\\ ⋮\\ x_{i,N}\end{array}\right],{\tilde{X}}_i=\left[\begin{array}{c}{\tilde{x}}_{i,0}\\ ⋮\\ {\tilde{x}}_{i,N}\end{array}\right],X_{i,0}=\left[\begin{array}{c}{x}_{i,0}\\ ⋮\\ x_{i,0}\end{array}\right],& (33)\end{array}$

$\begin{array}{ll}{\tilde{x}}_{i,0}=\left[\begin{array}{c}{\tilde{x}}_i(0)\\ ⋮\\ {\tilde{x}}_i(0)\end{array}\right]X_{i,b}=\left[\begin{array}{c}{x}_i(b)\\ ⋮\\ x_i(b)\end{array}\right],{\tilde{X}}_{i,b}=\left[\begin{array}{c}{\tilde{x}}_i(b)\\ ⋮\\ {\tilde{x}}_i(b)\end{array}\right].& (34)\end{array}$

Rearranging Equation (32), we provide

$\begin{array}{ll}\{\begin{array}{l}{X}_1-C_{N,q}{\tilde{X}}_1=X_{1,0},\\ {\tilde{X}}_1-D_{N,q}(({\omega }_1^2+r{\omega }_2^2)X_1-r{\omega }_2^2{X}_2)={\tilde{X}}_{1,b},\\ X_2-C_{N,q}{\tilde{X}}_2=X_{2,0},\\ {\tilde{X}}_2-D_{N,q}(({\omega }_2^2+\frac{1}{r}{\omega }_1^2)X_2-{\omega }_2^2{X}_1)={\tilde{X}}_{2,b},\end{array}& (35)\end{array}$

where I is the (N + 1) × (N + 1) identity matrix and

$\begin{array}{ll}{C}_{N,q}=\frac{1-q}{S(q)}I+\frac{q}{S(q)}{h}^q{A}_{N,q},D_{N,q}=\frac{1-q}{S(q)}I+\frac{q}{S(q)}{h}^q{B}_{N,q}.& (36)\end{array}$

Finally, we attain the following system of linear algebraic equations

$\begin{array}{l}\left[\begin{array}{cccc}I& -C_{N,q}& 0& 0\\ -({\omega }_1^2+r{\omega }_2^2)D_{N,q}& I& {\omega }_2^2{D}_{N,q}& 0\\ 0& 0& I& -C_{N,q}\\ {\omega }_2^2{D}_{N,q}& 0& -({\omega }_2^2+\frac{1}{r}{\omega }_1^2)D_{N,q}& I\end{array}\right]\\ \left[\begin{array}{l}{X}_1\\ {\tilde{X}}_1\\ X_2\\ {\tilde{X}}_2\end{array}\right]=\left[\begin{array}{l}{X}_{1,0}\\ {\tilde{X}}_{1,b}\\ X_{2,0}\\ {\tilde{X}}_{2,b}\end{array}\right]& (37)\end{array}$

which can be implemented easily by any linear solver. Note that the convergence of the fractional Euler method in the ABC sense was studied by Baleanu et al. [32] and the error bound was also reported. This verifies the validity of all numerical results provided in this paper. For more details on the stability and convergence analysis in this case, the interested reader can refer to Baleanu et al. [32].

5. Simulation Results and Discussion

In this section, we investigate the dynamical behavior of the FELEs of motion for the coupled oscillator expressed by Equations (17)–(18) considering different values of the fractional order q. To this aim, we take into account the following three cases for the physical system under study:

Case 1: A symmetric initial position. In this case, we consider the initial and terminal conditions as x₁(0) = −x₂(0) = 1 and ${\tilde{x}}_1(40)={\tilde{x}}_2(40)=0$, respectively. The other parameters are also assumed to be k = 2, k₂ = 4, m₁ = 3, m₂ = 7, and q = 0.96, 0.965, 0.97, 0.975, 0.98, 0.985, 0.99, 0.995, 0.999. Simulation results for this case are shown in Figures 2, 3 as compared to the solution of the CELEs (10)–(11).

FIGURE 2

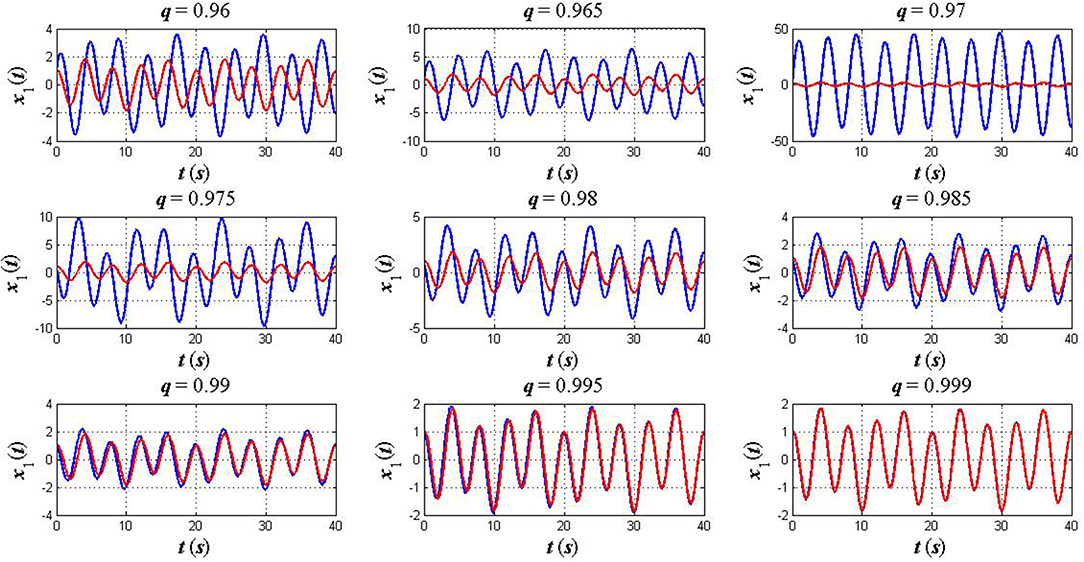
Figure 2. The plots of x₁(t) in the fractional sense (blue) and classical sense (red): a symmetric initial position x₁(0) = −x₂(0) = 1.

FIGURE 3

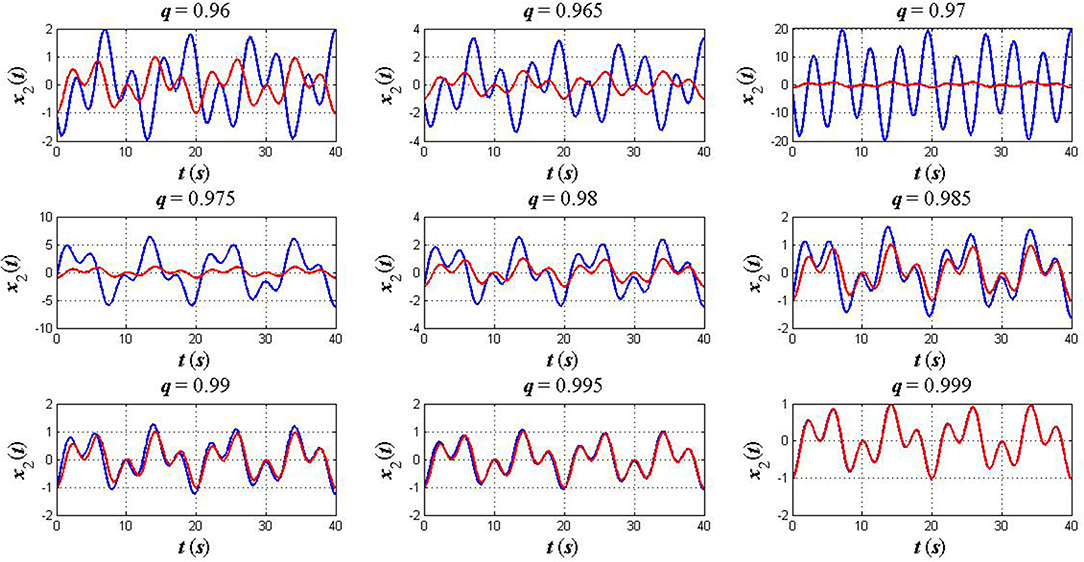
Figure 3. The plots of x₂(t) in the fractional sense (blue) and classical sense (red): a symmetric initial position x₁(0) = −x₂(0) = 1.

Case 2: An anti–symmetric initial position. In this case, we take into account the initial condition as x₁(0) = x₂(0) = 1 while the terminal condition and other parameters take the same values as in the previous case. Simulation and comparative results for this case are depicted in Figures 4, 5.

FIGURE 4

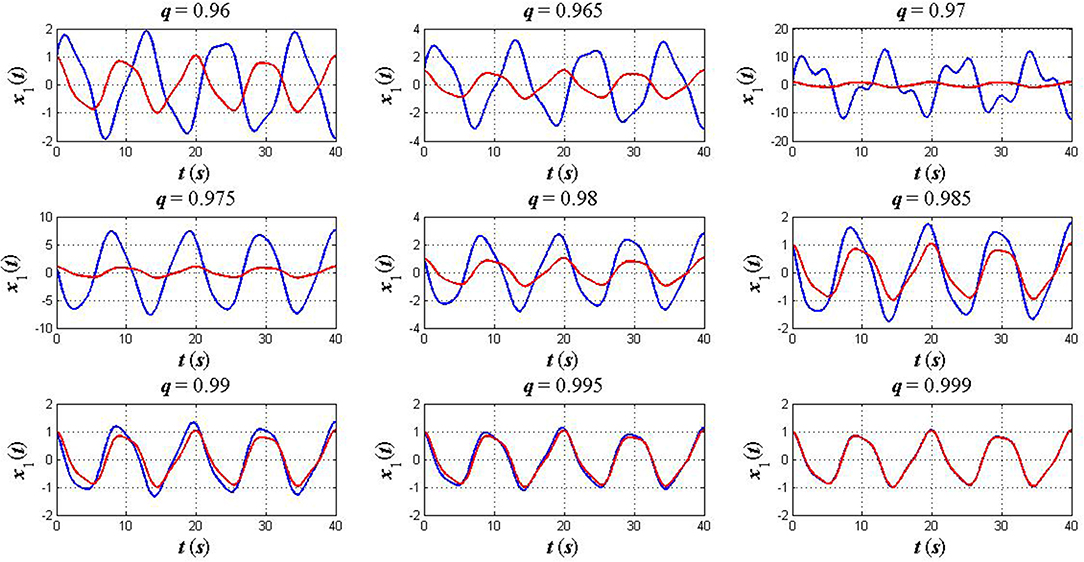
Figure 4. The plots of x₁(t) in the fractional sense (blue) and classical sense (red): an anti–symmetric initial position x₁(0) = x₂(0) = 1.

FIGURE 5

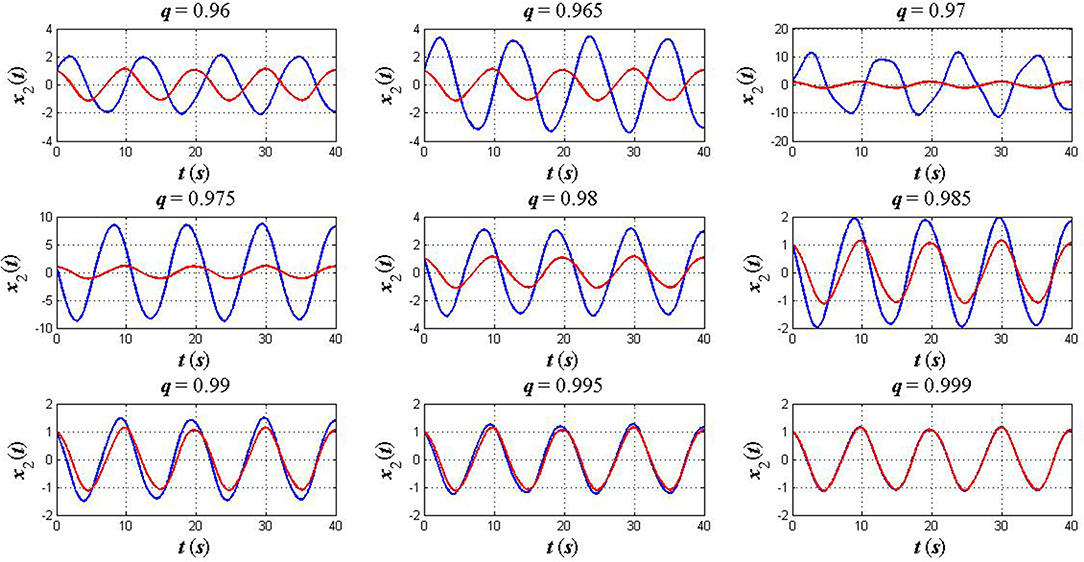
Figure 5. The plots of x₂(t) in the fractional sense (blue) and classical sense (red): an anti–symmetric initial position x₁(0) = x₂(0) = 1.

Case 3: A weak coupled oscillator. Finally, we take into consideration a weak coupled oscillator in which k = 10 and k₂ = 0.1 (k≫k₂). The initial condition is also assumed to be x₁(0) = 1, x₂(0) = 0, and the other parameters remain unchanged as in the previous cases. Simulation results of the Euler–Lagrange equations for both fractional and classical cases are plotted in Figures 6, 7.

FIGURE 6

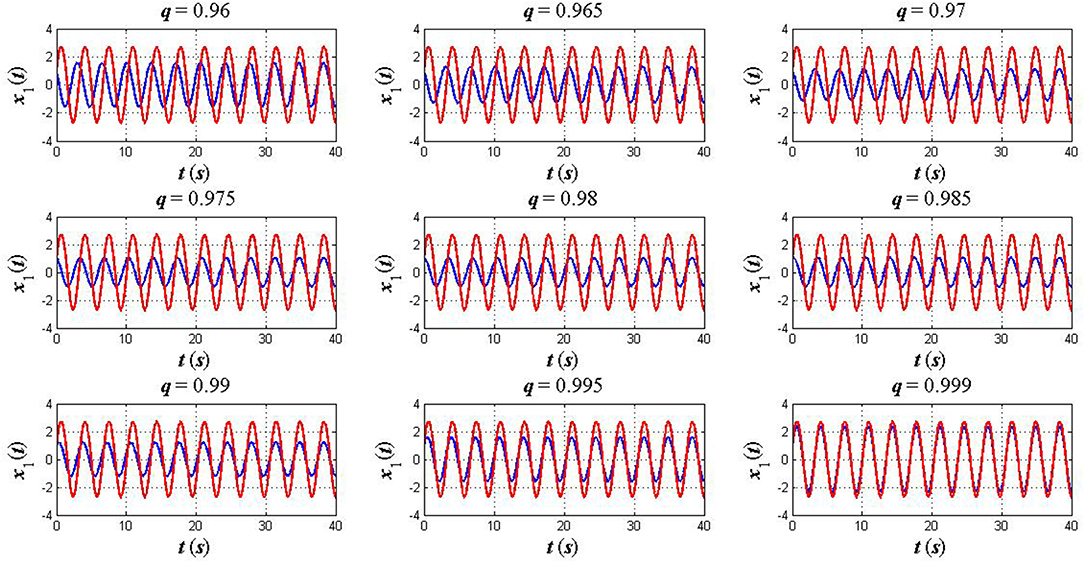
Figure 6. The plots of x₁(t) in the fractional sense (blue) and classical sense (red): a weak coupled oscillator (k ≫ k₂).

FIGURE 7

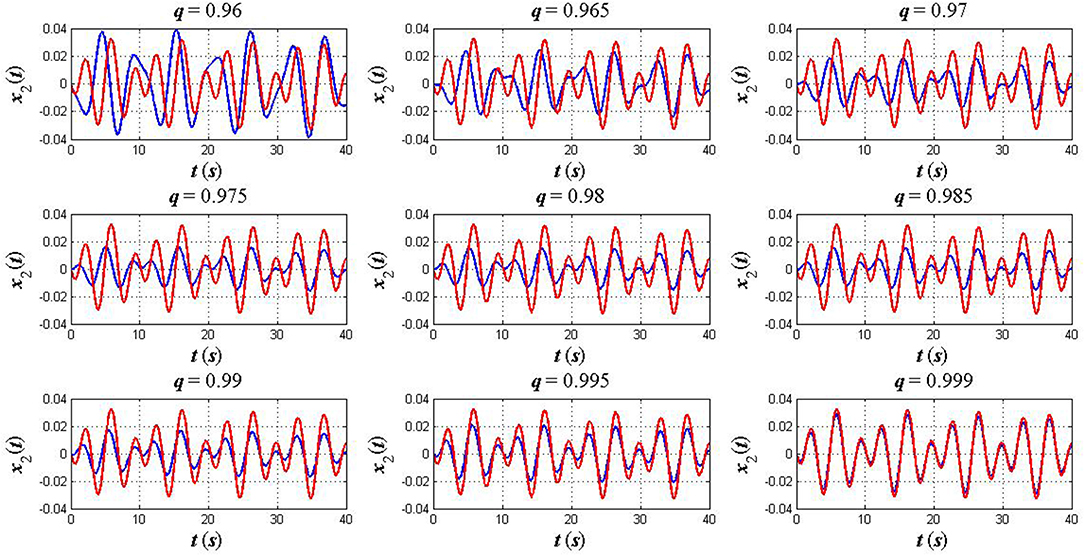
Figure 7. The plots of x₂(t) in the fractional sense (blue) and classical sense (red): a weak coupled oscillator (k ≫ k₂).

As can be seen from Figures 2–7, the numerical solution of the FELEs not only represents different asymptotic behaviors for different values of q but also tends to the solution of the CELEs as q goes to 1. This confirms that the FC provides a flexible model, which is able to extract hidden aspects of the physical system under study while this feature is unavailable when we use the ordinary time–derivatives.

6. Conclusions

This paper studied the concept of the FC to evaluate the equations of motion for a coupled oscillator. In this study, the classical and fractional Lagrangian were established, and then, the FELEs of motion were formulated including the recently introduced ABC operator with ML kernel. In order to solve the aforementioned equations numerically, an efficient approximation method was also suggested, which employed the Euler formula to discretize the convolution integral. Applying this powerful new technique, the FELEs for the considered problem were converted into a system of linear algebraic equations. Simulation results reported in Figures 2–7 indicated that the behavior of the FELEs varied with the fractional order q, and recovered the solution of the CELEs as q → 1. This verifies the advantage of the FC to provide a flexible model capable of extracting hidden aspects of the coupled oscillator system while this property is not available in the presence of ordinary time–derivatives.

Data Availability Statement

All datasets analyzed for this study are included in the article/supplementary material.

Author Contributions

All authors contributed equally to each part of this work. All authors read and approved the final manuscript.

Funding

DB was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK), Grant No: TBAG–117F473.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Greiner W. Classical Mechanics, Systems of Particles and Hamiltonian Dynamics. Berlin; Heidelberg: Springer–Verlag (2010).

Google Scholar

2. Tariboon J, Ntouyas SK, Agarwal P. New concepts of fractional quantum calculus and applications to impulsive fractional q-difference equations. Adv Diff Equat. (2015) 2015:18. doi: 10.1186/s13662-014-0348-8

CrossRef Full Text | Google Scholar

3. Hammouch Z, Mekkaoui T, Agarwal P. Optical solitons for the Calogero-Bogoyavlenskii-Schiff equation in (2 + 1) dimensions with time-fractional conformable derivative. Eur Phys J Plus. (2018) 133:248. doi: 10.1140/epjp/i2018-12096-8

CrossRef Full Text | Google Scholar

4. Saad KM, Iyiola OS, Agarwal P. An effective homotopy analysis method to solve the cubic isothermal auto-catalytic chemical system. AIMS Math. (2018) 3:183–94. doi: 10.3934/Math.2018.1.183

CrossRef Full Text | Google Scholar

5. Turalska M, West BJ. Fractional dynamics of individuals in complex networks. Front Phys. (2018) 6:110. doi: 10.3389/fphy.2018.00110

CrossRef Full Text | Google Scholar

6. Jajarmi A, Hajipour M, Mohammadzadeh E, Baleanu D. A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J Franklin Instit. (2018) 335:3938–67. doi: 10.1016/j.jfranklin.2018.03.012

CrossRef Full Text | Google Scholar

7. Hajipour M, Jajarmi A, Baleanu D, Sun HG. On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun Nonlin Sci Numer Simul. (2019) 69:119–33. doi: 10.1016/j.cnsns.2018.09.004

CrossRef Full Text | Google Scholar

8. Yusuf A, Inc M, Aliyu AI, Baleanu D. Optical solitons possessing beta derivative of the Chen-Lee-Liu equation in optical fiber. Front Phys. (2019) 7:34. doi: 10.3389/fphy.2019.00034

CrossRef Full Text | Google Scholar

9. Morales-Delgado VF, Gómez-Aguilar JF, Saad KM, Khan MA, Agarwal P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: a fractional calculus approach. Phys A. (2019) 523:48–65. doi: 10.1016/j.physa.2019.02.018

CrossRef Full Text | Google Scholar

10. Riewe F. Nonconservative Lagrangian and Hamiltonian mechanics. Phys Rev E. (1996) 53:1890–9. doi: 10.1103/PhysRevE.53.1890

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Laskin N. Fractional quantum mechanics. Phys Rev E. (2000) 62:3135–45. doi: 10.1103/PhysRevE.62.3135

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Laskin N. Fractional quantum mechanics. Phys Rev E. (2002) 66:056108. doi: 10.1103/PhysRevE.66.056108

CrossRef Full Text | Google Scholar

13. Agila A, Baleanu D, Eid R, Irfanoglu B. A freely damped oscillating fractional dynamic system modeled by fractional Euler-Lagrange equations. J Vibrat Control. (2018) 24:1228–38. doi: 10.1177/1077546316685228

CrossRef Full Text | Google Scholar

14. Almeida R, Morgado ML. The Euler-Lagrange and Legendre equations for functionals involving distributed-order fractional derivatives. Appl Math Comput. (2018) 331:394–403. doi: 10.1016/j.amc.2018.03.022

CrossRef Full Text | Google Scholar

15. Baleanu D, Jajarmi A, Asad JH, Blaszczyk T. The motion of a bead sliding on a wire in fractional sense. Acta Phys Polon A. (2017) 131:1561–4. doi: 10.12693/APhysPolA.131.1561

CrossRef Full Text | Google Scholar

16. Baleanu D, Asad JH, Jajarmi A. The fractional model of spring pendulum: new features within different kernels. Proc Roman Acad Ser A. (2018) 19:447–54. Available online at: https://acad.ro/sectii2002/proceedings/doc2018-3/05-Baleanu.pdf

Google Scholar

17. Baleanu D, Asad JH, Jajarmi A. New aspects of the motion of a particle in a circular cavity. Proc Roman Acad Ser A. (2018) 19:361–7. Available online at: https://acad.ro/sectii2002/proceedings/doc2018-2/Art07Baleanu.pdf

Google Scholar

18. Baleanu D, Jajarmi A, Asad JH. Classical and fractional aspects of two coupled pendulums. Roman Rep Phys. (2019) 71:103.

Google Scholar

19. Baleanu D, Sajjadi SS, Jajarmi A, Asad JH. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur Phys J Plus. (2019) 134:181. doi: 10.1140/epjp/i2019-12561-x

CrossRef Full Text | Google Scholar

20. Chung WS. Fractional Newton mechanics with conformable fractional derivative. J Comput Appl Math. (2015) 290:150–8. doi: 10.1016/j.cam.2015.04.049

CrossRef Full Text | Google Scholar

21. Baleanu D, Asad JH, Petras I. Numerical solution of the fractional Euler-Lagrange's equations of a thin elastica model. Nonlin Dyn. (2015) 81:97–102. doi: 10.1007/s11071-015-1975-7

CrossRef Full Text | Google Scholar

22. Agila A, Baleanu D, Eid R, Irfanoglu R. Applications of the extended fractional Euler-Lagrange equations model to freely oscillating dynamical systems. Roman J Phys. (2016) 61:350–9. Available online at: http://www.nipne.ro/rjp/2016_61_3-4/RomJPhys.61.p350.pdf

Google Scholar

23. Guezane-Lakoud A, Khaldi R. Solutions for a nonlinear fractional Euler Lagrange type equation. SeMA J. (2019) 76:195–202. doi: 10.1007/s40324-018-0170-4

CrossRef Full Text | Google Scholar

24. Diethelm K, Ford NJ, Freed AD. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlin Dyn. (2002) 29:3–22. doi: 10.1023/A:1016592219341

CrossRef Full Text | Google Scholar

25. Momani S, Odibat Z, Alawneh A. Variational iteration method for solving the space- and time-fractional KdV equation. Numer Methods Part Differ Equat. (2008) 24:262–71. doi: 10.1002/num.20247

CrossRef Full Text | Google Scholar

26. Prakash A, Verma V. Numerical method for fractional model of Newell-Whitehead-Segel equation. Front Phys. (2019) 7:15. doi: 10.3389/fphy.2019.00015

CrossRef Full Text | Google Scholar

27. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier (2006).

Google Scholar

28. Baleanu D, Atangana A. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci. (2016) 20:763–9. doi: 10.2298/TSCI160111018A

CrossRef Full Text | Google Scholar

29. Tateishi AA, Ribeiro HV, Lenzi EK. The role of fractional time-derivative operators on anomalous diffusion. Front Phys. (2017) 5:52. doi: 10.3389/fphy.2017.00052

CrossRef Full Text | Google Scholar

30. Abdeljawad T, Baleanu D. Integration by parts and its applications of a new nonlocal fractional derivative with Mittag–Leffler nonsingular kernel. J Nonlin Sci Appl. (2017) 10:1098–107. doi: 10.22436/jnsa.010.03.20

CrossRef Full Text | Google Scholar

31. Agrawal OP. Formulation of Euler-Lagrange equations for fractional variational problems. J Math Anal Appl. (2002) 272:368–79. doi: 10.1016/S0022-247X(02)00180-4

CrossRef Full Text | Google Scholar

32. Baleanu D, Jajarmi A, Hajipour M. On the nonlinear dynamical systems within the generalized fractional derivatives with Mittag-Leffler kernel. Nonlin Dyn. (2018) 94:397–414. doi: 10.1007/s11071-018-4367-y

CrossRef Full Text | Google Scholar