Dynamics of Ring Disclinations Driven by Active Nematic Shells

When dispersed in thermotropic nematic liquid crystal oils, surfactant-ladden aqueous droplets often lead to the formation of a equatorial ring disclination in the nearby nematic matrix as a result of a balance between elasticity and interfacial energy. In this experimental work, the aqueous phase contains an extract of cytoskeletal proteins that self-assemble into an active quasi-two-dimensional shell featuring self-sustained periodic flows. The ensuing hydrodynamic coupling drives the surrounding liquid crystal and triggers oscillations in the disclinations. We describe the dynamic modes of the disclinations under different driving conditions, and explore their pathway to collapse under flow conditions.

1. Introduction

Nematic liquid crystals (NLCs) are liquids whose molecules organize with long-range orientational order, which is locally characterized by a director field, $\widehat{n}$ [1]. The latter is typically controlled by means of the boundary conditions on the confinement walls or through the action of electric or magnetic fields. The equilibrium distribution of $\widehat{n}$ is established through the minimization of bulk and interfacial energies compatible with topological constraints dictated by confinement, which may lead to frustrated configurations and the appearance of defects [2]. Although technological applications of these materials are based on their use in defect-free systems, significant current research efforts in Condensed Matter Physics are centered in the preparation and control of tunable defect assemblies, with potential use in the development of metamaterials [3].

A particular case of frustrated geometries in NLCs is obtained by preparing nematic colloidal suspensions [4, 5]. These are systems in which the ordered mesophase, which is typically oriented in a homogeneous fashion by means of the anchoring conditions on bounding plates (far field), is disrupted by the presence of sub-millimeter solid [6–13] or liquid [14–16] inclusions. Realizations include from spherical to more complex geometries such as fractal-like shapes, from sparse to dense colloidal ensembles, from spontaneous to tailored self-assembly [9, 17–20]. Except from the preparation of assemblies of driven colloidal particles [21] or defects [22], or the study of defects formed under flow conditions [23], most research on nematic colloids has focused on stable, equilibrium structures.

Recently, we brought a nematic emulsion out of equilibrium by dispersing aqueous droplets of an active gel in a nematic liquid crystal [24]. The active gel, which is prepared from an in-vitro reconstitution of cytoskeletal proteins develops, under suitable conditions, an active layer with nematic order at the water/oil interface, denoted active nematic (AN) [25, 26]. At the inner side of the spherical droplets, the resulting AN shell exhibits self-sustained flows that are transmitted hydrodynamically into the surrounding nematic matrix. As a result, the ring disclination (Saturn ring, SR) that, in our case, surrounds the dispersed droplets [27–29] is perturbed from its (equilibrium) equatorial position, into different oscillations modes. With the support of numerical simulations, our earlier study revealed a feedback mechanism between the orientation of the SR, determined by the nematic far field, and the spatial arrangement of the AN shell, which led to sustained periodic oscillations of the SR. However, such regimes were not the norm in the experiments, and often driven SR became unstable and collapsed into a dipolar configuration.

In this article, we provide a thorough revision of the different dynamic modes of SR driven by the underlying AN shell, the possible dynamic states, which involve both synchronous and asynchronous oscillations, and the different pathways that lead to the collapse of the SR into a dipolar point-like defect configuration.

The article is structured as follows. After a succinct description of the used materials and employed experimental methods, we describe the main features of the emulsified droplets, including the structure of the underlying AN shell. Then, we describe the observed dynamic modes of the SR, both stable and unstable, and their dependence on control parameters. Finally, we focus on the long term behavior of the dynamic SR.

2. Materials and Methods

2.1. Active Material

The active system we used consisted of an active gel formed by an aqueous suspension of tubulin microtubules, dimeric kinesin molecular motors, and the non-adsorbing depleting agent polyethylene glycol (PEG), which concentrates the microtubules into bundles, hundreds of micrometers long [25]. Precise details of the experimental procedures leading to the preparation of all materials can be found elsewhere [24]. In brief, microtubules were polymerized from tubulin purified from bovine brain (a gift from Brandeis University Biological Materials Facility) in the presence of 0.6 mM of Guanosine-5-[(α, β)-methyleno]triphosphate (GMPCPP), which promotes the formation of short microtubules, 1−2 μm in length, required for the formation of the active material. About 3% of the tubulin is labeled with the fluorophore Alexa-647. Heavy chain kinesin-1 (K401-BCCP-6His) from Drosophila Melanogaster was in-house purified from Escherichia coli that contained the plasmid WC2 from the Gelles Laboratory (Brandeis University, MA, USA). The kinesin was biotinilated and incubated with streptatividin to obtain dimeric clusters, which would act as cross-linkers when mixed with the microtubule suspension. The active mixture was completed with 20 kDa PEG that acted as a depleting agent, Adenosine Triphosphate (ATP) that drove the activity of the gel, anti-bleaching agents, and an enzymatic ATP-regenerating system to maintain a constant activity in the mixture for hours. In order to emulsify the active aqueous suspension in the liquid crystal oil, suitable surfactants were added to the active mixture to ensure a biocompatible water/oil interface and to determine the anchoring conditions for the liquid crystal molecules in contact with the droplets. To promote the desired homeotropic (perpendicular) anchoring, PEGylated phospholipids were used at a concentration 0.2 %w/v.

2.2. Liquid Crystal-Based Emulsions

As dispersing oil phase, we used 4-Cyano-4'-pentylbiphenyl (5CB, Synthon chemicals), which features a nematic phase at room temperature. In order to enhance the homeotropic anchoring on the aqueous droplets surface, about 0.4 w/w% of stearic acid was dissolved in the mesogen. The emulsion was prepared by combining the active gel and the oil in a 1 mL centrifuge tube at a ratio 1:30, and mixed by the action of a vortex stirrer at room temperature.

2.3. Sample Preparation and Characterization

Liquid crystal cells were assembled by gluing two parallel glass plates together with a spacing of 140 μm set by double-sided adhesive tape. The inner side of the plates was treated to promote planar anchoring of the NLC by rubbing a previously spin-coated and baked layer of poly-vinyl alcohol. After the cell is filled by capillarity with the active emulsion, the openings are sealed using UV-curing adhesive. Microscopy observation was performed using a Nikon E400Pol multimode microscope. Fluorescence was used to visualize the AN layer while brightfield was employed to visualized the SR disclinations. The latter is typically preferred to polarized microscopy, which we have occasionally employed, since it results in a more homogeneous appearance of the disclination along all its length. Time-lapse acquisition is performed with an Andor Zyla 4.2 Plus camera controlled with the open-source software ImageJ Micro-Manager [30], which is also employed for further image processing and analysis.

3. Results and Discussion

Dispersed in the mesogenic oil, spherical aqueous droplets promote homeotropic anchoring of the NLC director on their surface due to the employed surfactants (see section 2). This results in a topological mismatch with the homogeneous planar far-field imposed by the boundary conditions on the cell plates. As a result, a ring disclination forms around the droplet's equator, perpendicularly to the NLC far-field direction (Figure 1A). As discussed below, this configuration is metastable [28], and may relax to a less energetic dipolar configuration where the SR collapses as a point-like defect near the North or the South pole of the droplet. Inside the aqueous droplets, the filament bundles formed by fluorescent microtubules crosslinked with kinesin clusters are pushed toward the water/oil interface by the depleting action of PEG. This process is usually studied on a flat interface, leading to the formation of an AN layer a few microns thick, where the filaments are intrinsically prone to buckling instabilities due to internal extensile active stresses. This results in the unbinding of complementary pairs of semi-integer defects, with the +1/2 defects creating flow while the negative counterparts being simply advected [26]. In Figure 1B, some defects present in the observation window of a flat AN, in an independent experiment, are marked. In particular, the tip of +1/2 defects is indicated with a red triangle that points in the direction of the local defect trajectory.

FIGURE 1

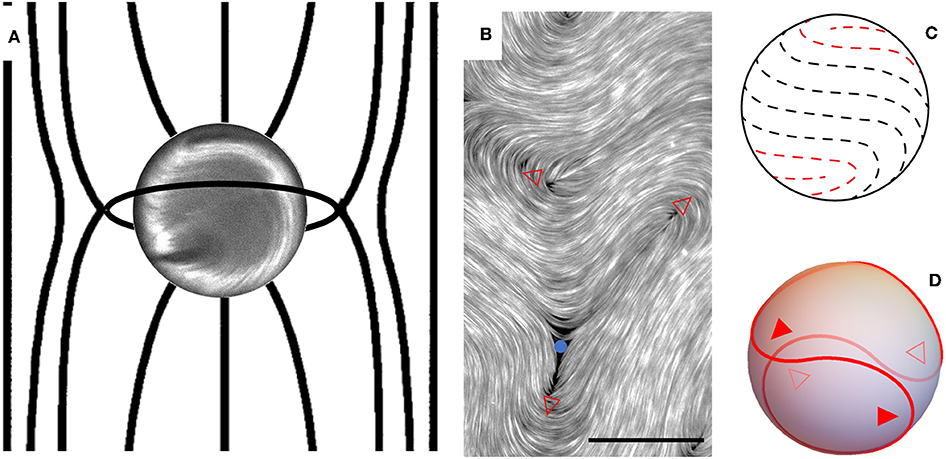
Figure 1. (A) Sketch of the nematic director field lines around a dispersed droplet of aqueous based active material that imposes homeotropic anchoring conditions. The NLC has a homogeneous far field oriented in the vertical direction in this sketch. The confining plates are parallel to the plane of the sketch. The droplet, which is visualized with fluorescence microscopy, has a diameter of 80 μm. The homeotropic anchoring conditions on the droplet surface lead to the formation of a line disclination that wraps around the equator. (B) Structure of an Active Nematic layer forming at a flat water/oil interface, with the core of some positive (red empty triangles) and negative (blue full circles) semi-integer defects being marked. The ruler is 20 μm long. (C) Approximate director field lines of the Active Nematic shell observed in the droplet of (A). In red, the core of the two visible +1/2 defects is sketched. (D) Theoretical rendering of the four +1/2 defects that organize the flows in active shells present in droplets of this size. Solid triangles correspond to visible defects while empty triangles correspond to hidden defects.

The average distance between defects in the AN is characterized by the so-called active length scale [31, 32], which balances the active stresses and the elastic modulus of the filaments [33, 34]. When topology demands the coexistence of a given number of defects, this length scale determines the smallest confinement compatible with the AN. This is important, for instance, in the case of the soft confinement of AN in contact with anisotropic interfaces patterned with disks [35], or in spherical shells [24, 36], which is the relevant case for our purpose.

Wrapping of a two-dimensional nematic on a closed spherical surface requires a net topological charge +2 of the defects present in the director field [37, 38]. In the case of an AN shell, where only semi-integer defects are possible, the simplest conformation compatible with this topological constraint involves four +1/2 defects that will be placed at the vertices of an imaginary rotating tetrahedron in the steady state [36, 39] (Figures 1C,D). Because of the above-mentioned intrinsic active length scale, droplets that are too small cannot accommodate the four defects required for a stable active nematic shell, and droplets that are too large, enable the unbinding of more than four defects, resulting in turbulent-like flow regimes [26, 40]. For the material parameters used in our active preparation, we have found optimal to restrict our studies to droplets with diameters in the range 60–120 μm.

On the other hand, the distance between the disclination and the droplet surface will be instrumental to the coupling between the SR and the underlying active flow, with stronger coupling presumably occurring for SRs that are closer to the droplet. For strong anchoring conditions, this distance is proportional to the droplet size [27, 28], and is determined by the balance between NLC elasticity, represented by an elastic constant K, the radius of curvature of the director field distortions around the droplet, R, and the anchoring strength on the droplet surface, W, through the dimensionless ratio WR/K [1, 2]. For weak anchoring, the homeotropic surface alignment condition will not be satisfied, which results in distortions with small curvature that lead to the disclination stabilizing closer to the surface. In our experiments, W is determined by the nature and concentration of the employed surfactants. In earlier experiments [24], we tested the use of surfactants that led to conical, rather than homeotropic, anchoring, resulting in SR that were closer to the droplet surface and did not exhibit the high energy oscillation modes we report here. In the current study we have restricted to the use phospholipid-based surfactants, which we have found to offer a richer collection of dynamic SR regimes.

Interestingly, we have found a disparity of behaviors in droplets of similar sizes within a single preparation. A possible source for this dispersion is an heterogeneous droplet composition during the emulsification process, which we have assessed by preparing ensembles of droplets of nearly identical size by means of a microfluidic droplet generation device (Figure 2A). We observe disparities in the fluorescence intensity from different droplets, which points to the heterogeneous composition of the encapsulated active aqueous phase. In the example shown in Figure 2A, the continuous phase is a fluorinated oil, which offers better chemical compatibility than the NLC oil with the microfluidic device. For the purpose of the present work, in which we study the behavior of isolated droplets, we have resorted to more traditional emulsification methods, leaving the assembly of lattices of identical active droplets in NLC for future work in which coupling, synchronization, and frustration in driven SR will be explored. In the emulsions prepared by shaking the mixture, droplet sizes feature a broad distribution (Figure 2B), but enough droplets of the suitable size range are obtained for the qualitative study reported here.

FIGURE 2

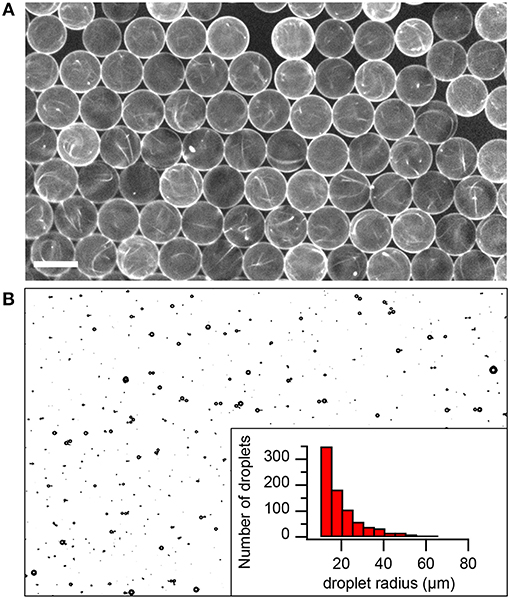
Figure 2. Sources of heterogeneity of the active emulsions. (A) Heterogeneous composition of monodisperse active droplets prepared using microfluidic techniques and dispersed in an isotropic oil. The ruler is 100 μm long. (B) Size distribution of droplets in a typical active nematic emulsion prepared using traditional emulsification techniques. The field of view is 3 mm wide.

In the presence of active stresses, the AN shell develops periodic cortical flows [24, 36]. The latter propagate, through hydrodynamic coupling, both into the aqueous and into the NLC bulk phases. As a result, the SR is set into motion and the steady influx of energy may lead to a wealth of dynamic modes. The presence of the plate walls is likely to affect the flow profile in the NLC. Because of the antagonistic NLC anchoring conditions on the droplets and on the plates, homeotropic and planar, respectively, elastic repulsion prevents the droplets from fully sedimenting on the bottom plate [41]. When the continuous phase is an isotropic oil [25], active droplets self-propel erratically on the supporting surface. Such motion is not observed in our case, presumably due to the elastic repulsion due to the NLC matrix, although the higher viscosity of the NLC will also contribute to hamper such self-propulsion. Moreover, the use of cell gaps much larger than the droplets considered in our study ensures that friction on the complementary plate can also be neglected.

In Figure 3 we display the range of dynamical regimes observed for the activated SR. For each case, a panel with an experimental micrograph and one with a sketch highlighting the main features of the corresponding regime is illustrated. The experimental micrographs are obtained with brightfield and parallel illumination to enhance the ring disclination. The elastic energy in the NLC matrix increases with the length of the SR, and this has an increasing trend from panel A till panel E.

FIGURE 3

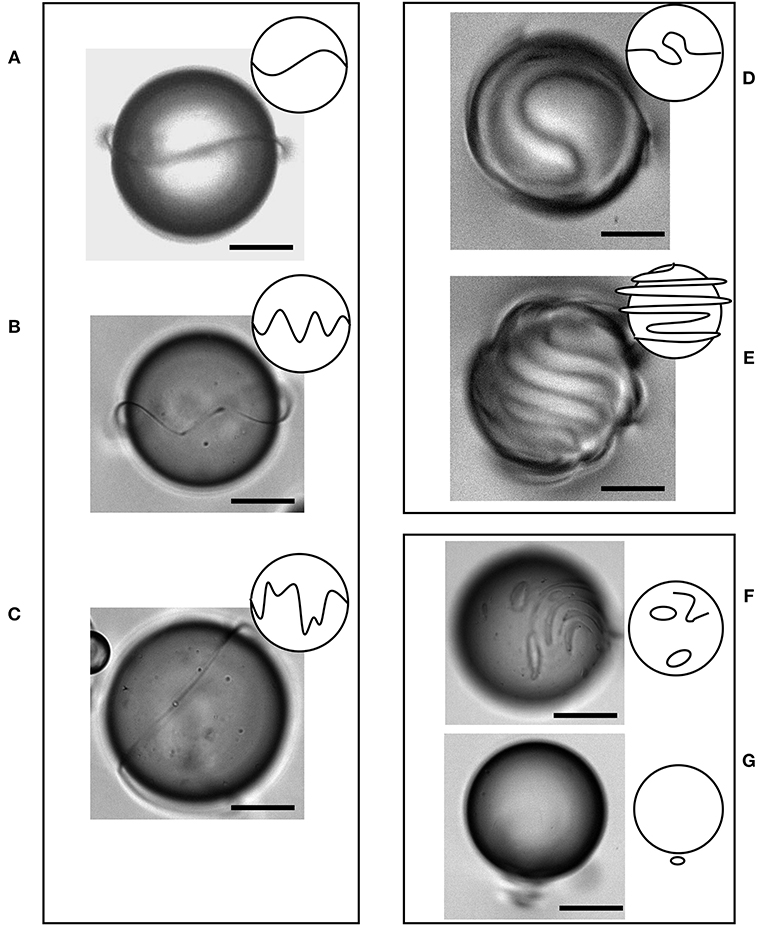
Figure 3. Different dynamic structures of the perturbed Saturn Rings. Sketches on the left and micrographs on the right are included with each case. (A) Single mode (m = 2) synchronous oscillations. (B) Multi-mode synchronous oscillations. (C) Multi-mode asynchronous oscillations. (D) Multi-valued single wrapping of the SR. (E) Multi-valued multiple wrapping of the SR. (F) SR has fragmented into multiple disconnected disclinations and loops. (G) SR has collapsed into a point defect to the South of the droplet. Scale bars, 20 μm.

In Figures 3A–C, we report regimes in which the SR distortion can be considered 1D, in the sense that it can be described by a uni-valued function of the angular coordinate around the droplet's equator. Among these regimes, the first two correspond to synchronized dynamics between the SR and the underlying AN. This dynamics is better put into evidence in the least energetic regime (Figure 3A), where SR oscillations are characterized by a single distortion mode. These distorted SRs lack rotational symmetry, which allows to observe slow degenerate rotations of the dynamic SR about the North-South droplet axis, thus changing the point-of-view, and thus the perception of the oscillating SR and allowing to more clearly assess its oscillation mode (Figure 4). The synchronization between the oscillations of the AN and those of the driven SR are clearly evidenced in fluorescence images. In Figure 5 we show three different fluorescence micrographs that span one half cycle of the SR oscillation. We observe that the SR transits past its equilibrium plane at the same time that the AN is aligned either parallel or perpendicular to this plane, and the SR is farthest from equilibrium when it is being driven by two +1/2 defects moving in antiparallel directions in the underlying AN (Figure 5B). With the help of numerical simulations, we recently demonstrated that this tight coupling between the AN and SR oscillatory dynamics is only possible if a feedback mechanism orients the AN shell with respect to the SR [24].

FIGURE 4

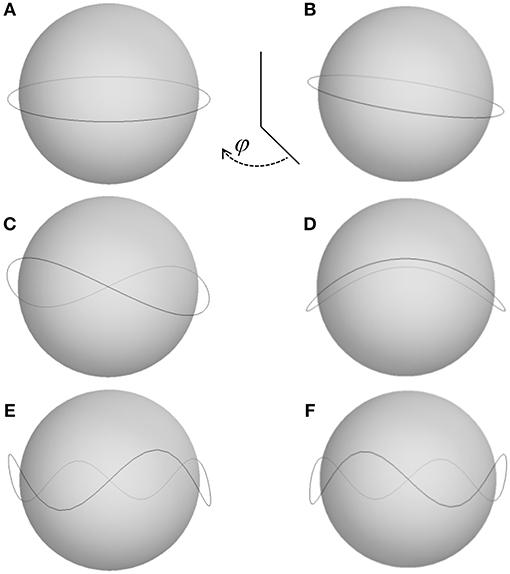
Figure 4. Simulated perception of the Saturn Ring disclination. Different single-mode oscillations are reconstructed at the highest amplitude of deformation for two point-of-view observations, φ. Deformation modes are m = 1 (A,B), m = 2 (C,D), m = 4 (E,F). (B,D,F) correspond to points of view rotated 45° clockwise with respect to (A,C,E), respectively.

FIGURE 5

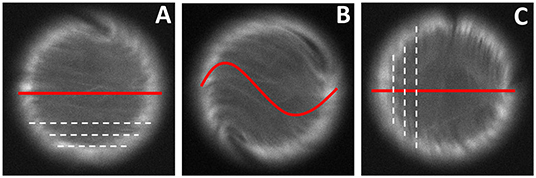
Figure 5. Coordination between the SR and AN orientation during synchronized oscillations. Fluorescence micrographs with three snapshots of the AN oscillation. The SR is sketched as a red line. The dashed lines in (A) and (C) represent the two complementary states of the active shell where filaments are aligned, while panel (B) includes the distorted SR configuration. The droplet has a diameter of 80 μm.

More energetic multi-mode oscillations can also be observed (Figure 3B). On average, such configurations are found by increasing the AN activity, which can be tuned by increasing the ATP concentration. In Figure 6 we compare the dynamics of two droplets that feature synchronous oscillations, found in active nematic emulsions with [ATP] = 140 μM and 1,400 μM, respectively. In the analysis in Figure 6B we find that the oscillations observed in Figure 6A feature a single mode with frequency f ≃ 14 mHz. On the other hand, in Figure 6D we see that the oscillations observed in Figure 6C are multimode, with a leading frequency f ≃ 60 mHz and three of its harmonics present in the spectrum. This change in leading frequency with the corresponding change in ATP concentration is consistent with the results obtained in an earlier detailed analysis performed with flat AN layers, where the inverse of a intrinsic time scale of the system was found to scale linearly with the activity parameter, which is related in a non-linear way with the concentration of ATP [42].

FIGURE 6

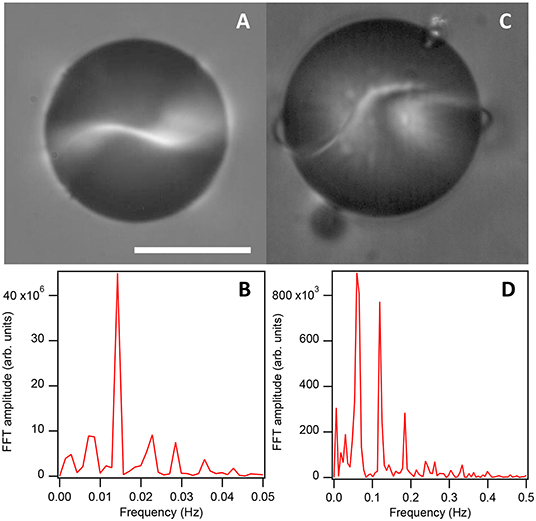
Figure 6. Effect of activity on the SR dynamics. (A) Polarizing micrograph of a single mode oscillating SR driven by an AN shell with [ATP] = 140 μm, and the corresponding power spectrum of the oscillations (B). (C) Polarizing micrograph of a multimode oscillating SR driven by an AN shell with [ATP] = 1,400 μm, and the corresponding power spectrum of the oscillations. (D) Scalebar, 50 μm. See also Video S1.

As the deformations of the SR become more energetic, the synchronization with the underlying AN can be lost (Figure 3C), resulting in severely distorted SRs. This regime is often unstable, and it may either revert back to synchronous oscillations or, more likely, develop into more complex asynchronous modes, where the SR cannot be described by a single-valued function of the spherical azimuthal coordinate (Figures 3D,E), as it can be for the simpler geometries in (Figures 3A–C). In these more complex modes, highly distorted SR may develop large folds but still be wrapped just once around the droplet (Figure 3D), or even be wrapped multiple times around the droplet (Figure 3E). This latter configuration is reminiscent of the multi-wrapping of SR due the helical twist of the director field in cholesteric liquid crystal layers [43], where the equilibrium spacing between consecutive turns is set by the cholesteric pitch. However, these are two very different systems since, in the case of our active nematic emulsions, the spacing between consecutive SR turns is a non-equilibrium feature, and it never reaches a steady state. As seen in Figure 7, the SR progressively increases its length and wraps an increasing number of times around the droplet, until the pitch between neighboring turns of the disclination reaches a limit value. Such configuration is unstable, and the SR can snap and link neighboring turns of the disclination, forming a shrinking fold. Such process is dynamic, and can be repeated numerous times. A possible subsequent outcome is a fragmentation of the SR into disconnected disclination loops (Figure 3F). In equilibrium, these would normally shrink and annihilate but, because of the underlying AN flow, and because of surface impurities, the loops can remain for extended periods of time.

FIGURE 7

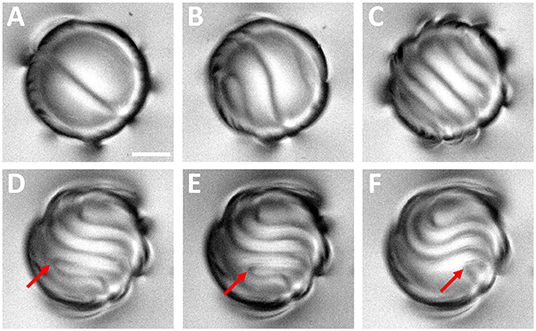
Figure 7. Dynamics of the wrapped SR. (A–C) Progressive increase of the number of turns around the droplet of a SR of increasing length. (D–F) Two neighboring parts of the SR from ajdancent turns snap, and the resulting fold in the disclination shrinks. Red arrow points to the tip of the shrinking fold. Scalebar, 20 μm. See also Video S2.

A SR disclination is not the only distortion compatible with homeotropic anchoring conditions on the droplet surface. Indeed, another possibility is a hyperbolic point defect located near either pole of the droplet (Figure 3G), called hedgehog defect [5]. Upon preparation of the active nematic emulsions, we observe that a similar number of droplets with either type of defects coexist. As the emulsion ages, this distribution changes, and progressively most droplets feature a point-like defect. As a matter of fact, SRs appear less stable and some of them are observed to eventually transit to hedgehog-like defects [28]. The opposite transition, however, is never observed. We explain this phenomenon by the tendency of line disclinations to shrink in order to minimize the elastic energy per unit length associated to director field distortions.

Our experiments show that the kinetics of the collapse of a SR to a point-like defect strongly depends on the dynamic regime of the SR. Synchronous oscillation regimes may never develop into a point defect, while highly-wrapped, asynchronous regimes, which may involve SRs that wrap several times around the droplet, are invariably seen to collapse into a point-like defect. Schematically, we can rationalize this scenario by considering that an energy barrier must be overcome by the SR in order to collapse into a point-like defect. In Figure 8, we have organized the different observed SR configurations in increasing order of elastic energy. As discussed, the equilibrium SR is not the lowest energy level. Below it, we find a sequence of states in which the SR moves from the equatorial position toward a pole, progressively shrinking, i.e., decreasing the NLC elastic energy, until it collapses into a point-like defect. Activated SRs have an average energy above the equilibrium state. Since synchronous oscillation regimes seldom destabilize, their energy levels allow to qualitatively describe a band (shaded in Figure 8) that must be overcome for the SR to evolve into the dipolar defect. Certainly, during their oscillations, SR increase their average energy, which reaches a steady state. Eventually, the fuel of the underlying AN, ATP, encapsulated in the droplet, will run out, and the average energy falls back to the equilibrium value as the SR ceases to oscillate. Two trajectories with stable oscillations in this schematic energy landscape are qualitatively traced in Figure 8. For more energetic configurations, such as for the asynchronous oscillation regime, the energy level may cross the edge of the protected region, and the SR may irreversibly collapse to a point-like defect (red trajectory in Figure 8). Finally, the fact that highly distorted SR regimes are always unstable suggests that their energies invariably reach levels above the stable band, and SRs in these dynamic regimes will evolve into a point-like defect well before activity vanishes due to ATP consumption in the AN shell.

FIGURE 8

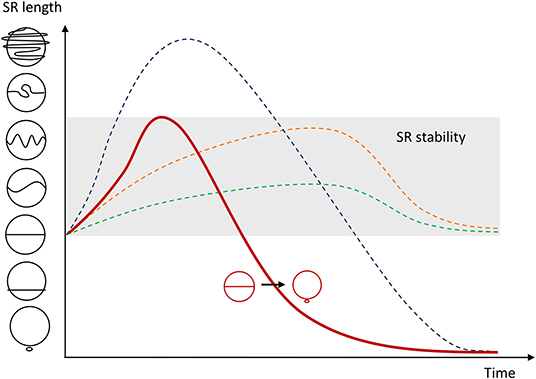
Figure 8. The different dynamic configurations of the system are sketched and ordered in terms of the length of the SR, which determines the elastic energy landscape. The shaded region represents regimes with stable SR oscillations. Solid and dashed lines represent possible pathways in the evolution of the SR, as described in the text. At long times (ATP running out), the SR may either return to its equilibrium conformation or collapse into a dipole.

4. Conclusions

In this manuscript we have described experiments in which Saturn ring disclinations, often encountered in colloids dispersed in nematic liquid crystals, are brought far from equilibrium by the encapsulation of droplets containing an aqueous active suspension of cytoskeletal proteins. Under the used experimental conditions, well-characterized in previous studies, this material condenses as an active nematic shell with periodic self-sustained flows that propagate into the passive nematic phase. As a result, the Saturn ring is set into motion and the steady influx of energy leads to a rich array of dynamic modes. The latter span from simple synchronous oscillations in which the disclination remains close to its equilibrium length, to situations in which the length increases steadily, even wrapping several times around the spherical inclusion. In such cases, the metastable quadrupolar defect might eventually collapse into a dipolar configuration.

The dynamic state of the driven Saturn ring depends on the energy influx received from the underlying active nematic layer. This energy depends on the activity and on the efficiency of the coupling between the active and the passive fluids. While the former can be tuned with the concentration of ATP in the aqueous phase, the latter can be influenced by the nature and concentration of the surfactants that decorate the water/oil interface. We have found, however, that the emulsification process leads to a dispersion in the droplet composition, resulting in a disparity of behaviors.

In this manuscript, we have focused on the dynamics of driven disclinations around individual droplets. Our work should pave the way for the future study of collective effects that should arise when multiple disclinations are linked [44]. This would allow to explore the effects arising from synchronization and topological frustration of knotted driven Saturn ring disclinations.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author Contributions

PG, JI-M, and FS conceived the experiments. PG and JH performed the experiments and analysis of experimental data. JI-M wrote the manuscript with input from all the authors.

Funding

JH, PG, JI-M, and FS acknowledge funding from MINECO (project FIS2016-78507-C2-1-P, AEI/FEDER, EU). PG acknowledges funding from Generalitat de Catalunya through a FI-DGR PhD Fellowship. JH acknowledges funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 674979-NANOTRANS. Brandeis University MRSEC Biosynthesis facility is supported by NSF MRSEC DMR-1420382.

Conflict of Interest

The authors declare that this study received funding from MINECO. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Acknowledgments

The authors are indebted to the Brandeis University MRSEC Biosynthesis facility for providing the tubulin. We thank M. Pons, A. LeRoux, G. Iruela, and B. Martínez-Prat (Universitat de Barcelona) for their assistance in the expression of motor proteins.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00165/full#supplementary-material

Video S1. Oscillating Saturn rings observed between crossed polarizers. ATP concentrations in the encapsulated active material are 140 μM (left) and 1400 μM (right).

Video S2. Dynamics of a wrapped Saturn ring observed without polarizers.

References

1. Oswald P, Pieranski P. Nematic and Cholesteric Liquid Crystals : Concepts and Physical Properties Illustrated by Experiments. The liquid crystals book series. Boca Raton, FL: Taylor & Francis (2005).

Google Scholar

2. Kléman M, Lavrentovich OD. Soft Matter Physics : An Introduction. Partially ordered systems. New York, NY: Springer (2003).

Google Scholar

3. Zheludev NI, Kivshar YS. From metamaterials to metadevices. Nat Mater. (2012) 11:917–24. doi: 10.1038/nmat3431

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Stark H. Physics of colloidal dispersions in nematic liquid crystals. Phys Rep. (2001) 351:387–474. doi: 10.1016/S0370-1573(00)00144-7

CrossRef Full Text | Google Scholar

5. Muševič I. Liquid Crystal Colloids. Soft and Biological Matter. Cham: Springer Nature (2017).

Google Scholar

6. Wood TA, Lintuvuori JS, Schofield AB, Marenduzzo D, Poon WC. A self-quenched defect glass in a colloid-nematic liquid crystal composite. Science. (2011) 334:79–83. doi: 10.1126/science.1209997

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Martinez A, Mireles HC, Smalyukh I. Large-area optoelastic manipulation of colloidal particles in liquid crystals using photoresponsive molecular surface monolayers. Proc Natl Acad Sci USA. (2011) 108:20891–6. doi: 10.1073/pnas.1112849108

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Trivedi RP, Klevets I, Senyuk B, Lee T, Smalyukh I. Reconfigurable interactions and three-dimensional patterning of colloidal particles and defects in lamellar soft media. Proc Natl Acad Sci USA. (2012) 109:4744–9. doi: 10.1073/pnas.1119118109

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Senyuk B, Liu Q, He S, Kamien RD, Kusner RB, Lubensky TC, et al. Topological colloids. Nature. (2013) 493:200–5. doi: 10.1038/nature11710

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Martinez A, Ravnik M, Lucero B, Visvanathan R, Zumer S, Smalyukh I. Mutually tangled colloidal knots and induced defect loops in nematic fields. Nat Mater. (2014) 13:258–63. doi: 10.1038/nmat3840

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Eremin A, Hirankittiwong P, Chattham N, Nadasi H, Stannarius R, Limtrakul J, et al. Optically driven translational and rotational motions of microrod particles in a nematic liquid crystal. Proc Natl Acad Sci USA. (2015) 112:1716–20. doi: 10.1073/pnas.1419850112

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Liu Q, Ackerman PJ, Lubensky TC, Smalyukh I. Biaxial ferromagnetic liquid crystal colloids. Proc Natl Acad Sci USA. (2016) 113:10479–84. doi: 10.1073/pnas.1601235113

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Peng C, Turiv T, Guo Y, Shiyanovskii SV, Wei QH, Lavrentovich OD. Control of colloidal placement by modulated molecular orientation in nematic cells. Sci Adv. (2016) 2:e1600932. doi: 10.1126/sciadv.1600932

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Poulin P, Stark H, Lubensky TC, Weitz DA. Novel colloidal interactions in anisotropic fluids. Science. (1997) 275:1770–3. doi: 10.1126/science.275.5307.1770

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Loudet JC, Barois P, Poulin P. Colloidal ordering from phase separation in a liquid-crystalline continuous phase. Nature. (2000) 407:611–3. doi: 10.1038/35036539

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Yamamoto J, Tanaka H. Transparent nematic phase in a liquid-crystal-based microemulsion. Nature. (2001) 409:321–5. doi: 10.1038/35053035

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Musevic I, Skarabot M, Tkalec U, Ravnik M, Zumer S. Two-dimensional nematic colloidal crystals self-assembled by topological defects. Science. (2006) 313:954–8. doi: 10.1126/science.1129660

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Smalyukh II. Liquid crystal colloids. Annu Rev Condens Matter Phys. (2017) 9:207–26. doi: 10.1146/annurev-conmatphys-033117-054102

CrossRef Full Text | Google Scholar

19. Hashemi SM, Jagodic U, Mozaffari MR, Ejtehadi MR, Musevic I, Ravnik M. Fractal nematic colloids. Nat Commun. (2017) 8:14026. doi: 10.1038/ncomms14026

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Solodkov NV, Shim JU, Jones JC. Self-assembly of fractal liquid crystal colloids. Nat Commun. (2019) 10:198. doi: 10.1038/s41467-018-08210-w

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Hernandez-Navarro S, Tierno P, Farrera JA, Ignes-Mullol J, Sagues F. Reconfigurable swarms of nematic colloids controlled by photoactivated surface patterns. Angew Chem Int Ed Engl. (2014) 53:10696–700. doi: 10.1002/anie.201406136

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li BX, Borshch V, Xiao RL, Paladugu S, Turiv T, Shiyanovskii SV, et al. Electrically driven three-dimensional solitary waves as director bullets in nematic liquid crystals. Nat Commun. (2018) 9:2912. doi: 10.1038/s41467-018-05101-y

CrossRef Full Text | Google Scholar

23. Giomi L, Kos Z, Ravnik M, Sengupta A. Cross-talk between topological defects in different fields revealed by nematic microfluidics. Proc Natl Acad Sci USA. (2017) 114:E5771–7. doi: 10.1073/pnas.1702777114

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Guillamat P, Kos Z, Hardouin J, Ignes-Mullol J, Ravnik M, Sagues F. Active nematic emulsions. Sci Adv. (2018) 4:eaao1470. doi: 10.1126/sciadv.aao1470

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sanchez T, Chen DT, DeCamp SJ, Heymann M, Dogic Z. Spontaneous motion in hierarchically assembled active matter. Nature. (2012) 491:431–4. doi: 10.1038/nature11591

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Doostmohammadi A, Ignes-Mullol J, Yeomans JM, Sagues F. Active nematics. Nat Commun. (2018) 9:3246. doi: 10.1038/s41467-018-05666-8

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kuksenok OV, Ruhwandl RW, Shiyanovskii SV, Terentjev EM. Director structure around a colloid particle suspended in a nematic liquid crystal. Phys Rev E. (1996) 54:5198–203. doi: 10.1103/PhysRevE.54.5198

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gu Y, Abbott N. Observation of saturn-ring defects around solid microspheres in nematic liquid crystals. Phys Rev Lett. (2000) 85:4719–22. doi: 10.1103/PhysRevLett.85.4719

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Stark H. Saturn-ring defects around microspheres suspended in nematic liquid crystals: an analogy between confined geometries and magnetic fields. Phys Rev E. (2002) 66:032701. doi: 10.1103/PhysRevE.66.032701

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Edelstein AD, Tsuchida MA, Amodaj N, Pinkard H, Vale RD, Stuurman N. Advanced methods of microscope control using μManager software. J Biol Methods. (2014) 1:e10. doi: 10.14440/jbm.2014.36

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Giomi L. Geometry and topology of turbulence in active nematics. Phys Rev X. (2015) 5:031003. doi: 10.1103/PhysRevX.5.031003

CrossRef Full Text | Google Scholar

32. Martínez-Prat B, Ignés-Mullol J, Casademunt J, Sagués F. Selection mechanism at the onset of active turbulence. Nat Phys. (2019) 15:362–6. doi: 10.1038/s41567-018-0411-6

CrossRef Full Text | Google Scholar

33. Aditi Simha R, Ramaswamy S. Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys Rev Lett. (2002) 89:058101. doi: 10.1103/PhysRevLett.89.058101

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Voituriez R, Joanny JF, Prost J. Spontaneous flow transition in active polar gels. Europhys Lett. (2005) 70:404–10. doi: 10.1209/epl/i2004-10501-2

CrossRef Full Text | Google Scholar

35. Guillamat P, Ignes-Mullol J, Sagues F. Taming active turbulence with patterned soft interfaces. Nat Commun. (2017) 8:564. doi: 10.1038/s41467-017-00617-1

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Keber FC, Loiseau E, Sanchez T, DeCamp SJ, Giomi L, Bowick MJ, et al. Topology and dynamics of active nematic vesicles. Science. (2014) 345:1135–9. doi: 10.1126/science.1254784

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Lopez-Leon T, Koning V, Devaiah KBS, Vitelli V, Fernandez-Nieves A. Frustrated nematic order in spherical geometries. Nat Phys. (2011) 7:391–4. doi: 10.1038/nphys1920

CrossRef Full Text | Google Scholar

38. Shin H, Bowick M, Xing X. Topological defects in spherical nematics. Phys Rev Lett. (2008) 101:037802. doi: 10.1103/PhysRevLett.101.037802

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Zhang R, Zhou Y, Rahimi M, de Pablo JJ. Dynamic structure of active nematic shells. Nat Commun. (2016) 7:13483. doi: 10.1038/ncomms13483

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Tan AJ, Roberts E, Smith SA, Olvera UA, Arteaga J, Fortini S, et al. Topological chaos in active nematics. Nat Phys. (2019) 15:1033–9. doi: 10.1038/s41567-019-0600-y

CrossRef Full Text | Google Scholar

41. Pishnyak O, Tang S, Kelly J, Shiyanovskii S, Lavrentovich O. Levitation, lift, and bidirectional motion of colloidal particles in an electrically driven nematic liquid crystal. Phys Rev Lett. (2007) 99:127802. doi: 10.1103/PhysRevLett.99.127802

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Guillamat P, Ignes-Mullol J, Sagues F. Control of active liquid crystals with a magnetic field. Proc Natl Acad Sci USA. (2016) 113:5498–502. doi: 10.1073/pnas.1600339113

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Gvozdovskyy I, Jampani VS, Skarabot M, Musevic I. Light-induced rewiring and winding of Saturn ring defects in photosensitive chiral nematic colloids. Eur Phys J E Soft Matter. (2013) 36:97. doi: 10.1140/epje/i2013-13097-8

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Tkalec U, Ravnik M, Copar S, Zumer S, Musevic I. Reconfigurable knots and links in chiral nematic colloids. Science. (2011) 333:62–5. doi: 10.1126/science.1205705

PubMed Abstract | CrossRef Full Text | Google Scholar