Tangled Worldview Model of Opinion Dynamics

We study the joint evolution of worldviews by proposing a model of opinion dynamics, which is inspired in notions from evolutionary ecology. Agents update their opinion on a specific issue based on their propensity to change—asserted by the social neighbors—weighted by their mutual similarity on other issues. Agents are, therefore, more influenced by neighbors with similar worldviews (set of opinions on various issues), resulting in a complex co-evolution of each opinion. Simulations show that the worldview evolution exhibits events of intermittent polarization when the social network is scale-free. This, in turn, triggers extreme crashes and surges in the popularity of various opinions. Using the proposed model, we highlight the role of network structure, bounded rationality of agents, and the role of key influential agents in causing polarization and intermittent reformation of worldviews on scale-free networks.

1. Introduction

1.1. Motivation

Weltanschauung, usually translated from German as “worldview,” is a concept popularized by the philosopher G.W.F. Hegel that refers to the fundamental cognitive orientation of an individual or society; i.e., the set of statements that are assumed consciously or unconsciously about the basic make-up of the world [1, 2]. The worldview and experiences of different individuals affect each other and, interestingly, co-evolve together. In effect, worldviews drive human behavior generating experiences that, in turn, are capable of triggering mutations in the worldview itself. Moreover, interactions between individuals with heterogeneous worldviews can foster significant mutations in their corresponding inclinations. Therefore, human interaction has always been a key driver of worldview evolution.

The evolution of worldviews can exhibit fascinating complexity, as seen for e.g., in the evolution of political preferences. In effect, history shows that political worldviews usually exhibit a life cycle similar to biological organisms: they emerge, maybe become dominant, only for becoming extinct later [3]. However, recent trends in liberal democracies have shown that political worldviews are sometimes capable of reviving after being inactive for a long time [4]. Moreover, opposing worldviews can coexist and even reinforce each other, forming a fragile but persistent balance. This phenomenon, known as political polarization, can lock worldview dynamics until the balance is abruptly disturbed, under events that may be seen very unexpected to external observers [5]. Eminent cases of these “surprising events” include the results of the US presidential election of 2016 and the Brexit referendum in the UK, which suddenly switched the balance in the worldwide political arena.

It is tempting to dismiss abrupt changes in worldviews of societies as rare and inexplicable events, just as the spread of the Black Plague [6] in the 14th century or the Spanish flu [7] of the 20th century. On this point, it is interesting to note how the development of epidemiology changed our views on such subjects by enabling the prediction of sudden spreads of diseases [8]. Similarly, climate catastrophes like cyclones and floods were first considered to be aberrations, but nowadays advances in meteorology have uncovered non-linear dependencies that can be leveraged to understand these phenomena [9]. Similarly, we propose that these sudden transitions in opinions can be regarded as indicators of the non-linear nature of worldviews' dynamics. This paper is an exploration of this rationale.

1.2. State of the Art

As Data-driven studies have been forwarding novel empirical evidence of polarization on online social networks [10, 11], Simulation and mathematical modeling has been useful in studying the dynamics of opinions and polarization (see e.g., [12–18]). These models and their variations have emphasized how homophily and confirmation bias can lead to global polarization. These studies find segregation of like-minded people in 2D space, on which agents interact with their spatial neighbors. However, the role of “space” and how it affects the herding dynamics in causing polarization is not well-understood.

Considering that social media technologies have elevated the reach of individual influence from physical to the internet, modern approaches tend to place agents, not in 2D space but rather connect them via various network topologies. The effect of various topologies was studied in Amblard and Deffuant [19], where they show that agents converge to one opinion above a critical value of connectivity, and this critical value decreases when the number of random links is increased over an initially regular network. Opinion dynamics have also been studied in models where the network structure changes at each time-step [20]. However, existing results suggest that it is difficult to isolate the role of topology in these scenarios due to the constant variations.

From a modeling perspective, opinion dynamic models have evolved from simplistic contagion dynamics [21, 22] to sophisticated decision making agent-based models [14, 23, 24]. Also, while most models focus on the evolution of a single opinion, some body of work has explored the dynamics of collections of opinions. After the early works on cultural segregation reported in Axelrod [12], researchers have used the features of multi-opinion models to study the evolution of social power [25], clustering transitions [26], and convergence with bounded confidence [27].

Most popular opinion dynamics models and consensus algorithms are such that their evolution tends to reach a static steady-state after some time. However, as observed in reality opinions usually don't reach a static equilibrium. Rather they follow a metastable behavior and can exhibit punctuated equilibrium in time. This intermittent behavior is also observed in the “noisy-voter model” [28, 29], where the opinion change is governed by two driving parameters: Herding and Randomness. The model shows weak convergence for very small values of randomness. The added randomness keeps the system away from a static state. Although the model is able to reproduce some significant results, the added randomness acts as an extraneous parameter.

1.3. Contribution and Manuscript Structure

In this article, we study worldview dynamics motivated by the ideas from evolutionary ecology. Worldviews are seen as an encoding of the basic presupposition of a belief system, being analogous to genes that encode biological signatures of specific species. Worldviews—just like species—emerge, dominate, and eventually go extinct. Moreover, just as new species are formed by mutations and interactions of existing species, worldviews emerge out of the cross-cultural exchange. Finally, mass extinctions take place occasionally within ecosystems that eliminate existing species giving way to the emergence of new ones, which is analogous to sudden worldview shifts.

The mentioned properties of evolutionary biology are captured by the well-known Tangled Nature Model [30]. This model, first presented in Christensen et al. [31] as a simple agent-based model of species-species interaction, is successful in showing how interdependent competition and mutations can lead to mass extinctions, which are followed by a chaotic phase of reformation that leads to a new state of meta-stable species. In addition, the Tangled Nature model also exhibits a 1/t decay of the rate of major transitions on the generational time scale [32, 33].

In this work we leverage this model to propose the Tangled Worldview Model of Opinion Dynamics, in which agent's worldview is described by a binary vector and their dynamics is driven on a directed network topology. Here, worldviews are analogous to species in the Tangled Nature Model—which are represented as binary genomes. However, the proposed model exhibits a network-driven dynamics, contrasting to the Tangled Nature model where the dynamics of each individual of the species depends only on the total population of the species and the global population. Whereas in the proposed model the total population of agents is fixed but the dynamics of individual agent depends on its place in the network topology. We use this model to develop our understanding of the role of topology in the formation of opinion's polarization, and also in the occurrence of abrupt global changes. Starting from a few random worldviews, our model shows the metastable evolution of novel worldviews punctuated by sudden abrupt transitions. Depending upon the network topology, these metastable states exhibit polarization or consensus. The present model is developed to analyze the political transitions in the age of social media. Since the model neglect changes that in the external technological and political conditions such as the development of new means of communication or constitutional changes, very long-time behavior of the model is not expected to be directly of relevance in this respect. Nevertheless, in terms of classifying the behavior of the model is it interesting to observe that the model we discuss also show an algebraic decrease of the rate of transitions like 1/t^a, though in our case the value of a is approximately equal to 0.25 while in the Tangled Nature model evolution [33] and of cultural evolution [34], a is about equal to 1.

The proposed model can be understood as an ecological variation of Axelrod's model of cultural segregation [12]. As agents change their opinions driven by the influence of their neighbors and confirmation bias. However, the agents are not directly aiming for “local herding,” rather are trying to maximize their “social fitness.” This allows agents to switch between tribes if a switch increases social fitness. The proposed model also allows for a small non-zero switching probability even if the switch decreases the social fitness. This stochastic switching, inspired by the mutations in the tangled nature model, introduces novel worldviews to the network, which in turn lead to much richer co-evolution.

The main findings reported from this model are the following:

1. Network topologies with just a few cycles do not foster polarization even in the presence of confirmation bias. While multiple cycles act as echo-chambers and reinforce polarization in agents with herding behavior.

2. An important driver of sudden global reformations are changes in opinion of key agents in the social network. These events trigger a cascade of opinion changes on various issues and a brief period of abrupt reformation, which allow new worldviews to emerge.

3. Bounded rational agents self-organize into consensus states on topologies with low cycles. However, on networks with many cycles even highly rational agents self-organize into polarized states.

4. By focusing on the popularity of a particular tagged opinion, the model exhibits noisy voter model-like dynamics (c.f section 1.2).

The rest of the article is structured as follows. First, section 2 introduces our proposed model. Then, section 3 presents our main findings from explorations on the model. Finally, section 4 summarizes our main conclusions and points to future research.

2. The Model

This section introduces our model for worldview dynamics. In the sequel, first section 2.1 introduces some basic definitions, and section 2.2 discusses the switching strategy used by the agents. Then the implementation of this strategy is explained with the help of an example in section 2.3. Finally, in the following section 2.4, the structure of the considered social influence network is discussed along with the algorithm to generate it.

2.1. Model Description

Let us consider a system composed by N social agents, where the internal state of the i-th agent corresponds to the binary vector $(O_1^i,\dots ,O_K^i)$, with $O_j^i\in \left\{0,1\right\}$ for all j = 1…K. This vector represents the agent's worldview: the K entries represent a particular subject/issue and its value (0 or 1) represents the position (for/against) of the agent on that topic. Note that K is the number of considered issues within the worldview.

The social influence that agents have over each other is encoded into a social network. Social influence is generally asymmetric (contrasting with other social interactions like friendships, business etc.) and heterogeneous. Hence we assume that the network of social influences to be represented by the adjacency matrix A_i,j and is weighted by the weights C_i,j ∈ [0, 1] to introduce heterogeneity in the social influence network. This is done to account for the variability of social influence experienced from different kinds of social relationships (friends, acquaintances, co-workers etc.). An algorithm detailing this implementation for the case of directed scale-free influence network is later explained in section 2.4.

Agents interact with each other in this network and change their opinions as a consequence of those interactions. This interaction includes, an agent switching its opinion on a particular issue based on various factors. In our model agents update their worldviews asynchronously. At each time step, one agent is selected randomly, and it selects at random an opinion to update. In the sequel, we consider the major factor that drives their dynamics.

2.1.1. Affinity

This quantity explores the effect of confirmation bias, i.e., the tendency of the agent to favor the opinion of those who agree with pre-existing opinions of the agents on other issues. The affinity between agent i and j, denoted by F_i,j, is a quantification of similarity between the worldviews of any two agents say i and j. There can be many ways to quantify this but for the purpose of this study, we simply take the ratio of the total number of issues with the same opinion to the total number of issues.

$\begin{array}{ll}{F}_{i,j}=\frac{1}{K}{\displaystyle \sum _{n=0}^K}\delta (O_n^i,O_n^j)& (1)\end{array}$

The δ function in the previous equation is defined as follows,

$\delta (O_n^i,O_n^j)=\{\begin{array}{lll}1,\hfill & if\hfill & O_n^i=O_n^j\hfill \\ 0,\hfill & if\hfill & O_n^i\ne O_n^j\hfill \end{array}$

2.1.2. Propensity and Conformity

The propensity to change opinion on issue k by agent i, denoted by P_i,k. In our model this metric is calculated as:

$\begin{array}{ll}{P}_{i,k}=\{\begin{array}{lll}\frac{{\displaystyle {\sum }_{j=0}^N{C}_{j,i}{F}_{j,i}(1-\delta (O_k^i,O_k^j)})}{{\displaystyle {\sum }_{j=0}^N{A}_{j,i}(1-\delta (O_k^i,O_k^j))}},\hfill & if\hfill & {\displaystyle {\sum }_{j=0}^N{A}_{j,i}\ne 0}\hfill \\ 0,\hfill & if\hfill & {\displaystyle {\sum }_{j=0}^N{A}_{j,i}=0}\hfill \end{array}& (2)\end{array}$

This is a measure of average disagreement of agent i, with all those j who influence it (C_j,i ≠ 0), on issue k weighted by the affinity(F_i,j) of their worldviews. In the above equations, 1 − δ(O_i,k, O_j,k) gives the value 1 every time when O_i,k ≠ O_j,k. This in essence quantifies the weighted disagreement. A refers to the adjacency matrix and C refers to the weighted adjacency matrix of the network structure which is mentioned in the previous subsection.

Whereas, conformity (T_i) is the measure of social conformity agent i enjoys with those who are influenced by it. This metric is calculated as follows:

$\begin{array}{ll}{T}_i=\{\begin{array}{lll}\frac{{\displaystyle {\sum }_{j=0}^N{C}_{i,j}{F}_{i,j}}}{{\displaystyle {\sum }_{j=0}^N{A}_{i,i}}},\hfill & if\hfill & {\displaystyle {\sum }_{j=0}^N{A}_{i,j}\ne 0}\hfill \\ 0,\hfill & if\hfill & {\displaystyle {\sum }_{j=0}^N{A}_{i,j}=0}\hfill \end{array}& (3)\end{array}$

Here we quantify conformity as the average influence i has on j (C_i,j) weighted by the Affinity (F_i,j) between i and j.

The propensity is an issue-specific cumulative measure of disagreement that forces an agent to reconsider its opinion on any given issue. However, with any change of opinion the agents may lose/gain social acceptance they enjoy with their followers. Threshold quantifies this effect of social acceptance. The interplay of propensity and conformity decides the switching of any opinion, therefore we define the term “Social Fitness” to explore this interplay in detail in the following section. Both these quantifications are scaled by the number of influencers/followers respectively to accommodate any effect of system size. Both the quantities also take into the account the effect of affinity (confirmation bias) which indirectly extends the dependence of opinion on any issue on opinions on all the issues of the neighbors. Therefore, opinion change is not just guided by the opinion of neighbors on that particular issue but rather on the whole worldview.

2.1.3. Social Fitness

We introduce Social Fitness, a variable denoted by H_i,k, to quantify the net social conformity enjoyed by an agent i on a particular issue k. The social fitness is defined as the difference between the “conformity” and “propensity.” In essence, social fitness is a measure of the difference between the approval of an agent's followers and those who influence it. Agents, therefore, are inclined to change opinion on any given issue in order to maximize social fitness. Therefore, a lower value of social fitness warrants an opinion change on that particular issue.

$\begin{array}{ll}{H}_{i,k}=T_i-P_{i,k}& (4)\end{array}$

2.2. Switching Strategy

At each time step, an agent is selected completely at random and the agent chooses one of the issues at random. The agent then analyses its social fitness on the chosen issue, to consider a change of opinion. The agents follow a probabilistic switching strategy. This strategy also provides a leeway to incorporate the rationality of agents. In the context of the model, a perfectly rational agent will definitely switch on any issue that has a negative value of social fitness. However, bounded rational agents might overestimate or underestimate this value. This error then leads to agents switching on issues they enjoy positive social fitness as well as keep opinions with negative social fitness with some probability. Therefore, the probability s_i,k of agent i switching its opinion on issue k depends upon the social fitness (H_i,k) and the rationality parameter (α) as,

$\begin{array}{ll}{s}_{i,k}=\frac{1}{1+exp({\alpha }_{\text{eff}}{H}_{i,k})}\text{with\hspace{1em}}{\alpha }_{eff}=T_i\alpha & (5)\end{array}$

Here the defined α_eff in Equation (5), is an adaptive rationality parameter which is higher for agents with higher conformity. Whereas, α represents the rationality parameter of the agents or the ability of the agents to process the available information. For very high α, the switching probability essentially becomes a step function about 0, i.e., the agents switch almost certainly even for small negative values of social fitness and rarely for positive values. However, as seen in Figure 1, for lower values of α, the slope of the distribution around “0” becomes less steep. This allows the agent to switch with a finite probability for some positive values of social fitness as well as not switch at times for some small negative values. This inability to optimally process the available information allows for a bounded rational behavior [35] which leads to more variability in the behavior of the agents. The adaptive α_eff accounts for the fact that agents with higher social conformity react more efficiently to social pressure. Mirta et. al. [36] refer to this parameter as a measure of the efficiency of the flow of information among the agents.

FIGURE 1

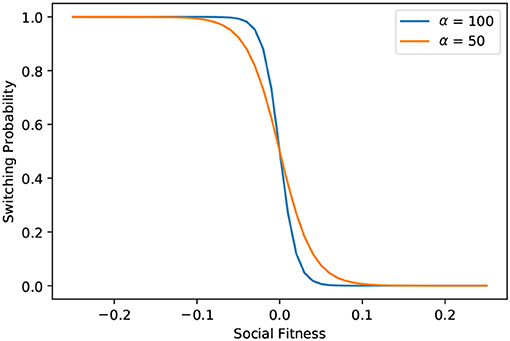
Figure 1. Effect of the rationality parameter (α) on switching probability. It can be observed that for lower α probability of switching decreases for slight negative values of social fitness and subsequently increases for slight positive values of social fitness.

2.3. Example

Let us illustrate how the model works with an example.

At any particular time step, an agent is selected, and the network structure around the agent looks as presented in Figure 2. The agent chooses (randomly) to consider its opinion about issue number 2 (highlighted in the Figure in yellow). As illustrated in Figure 2 agents disagree with the agent on this issue (highlighted in red). For simplicity, we assume that this is the only issue these agents disagree upon.

FIGURE 2

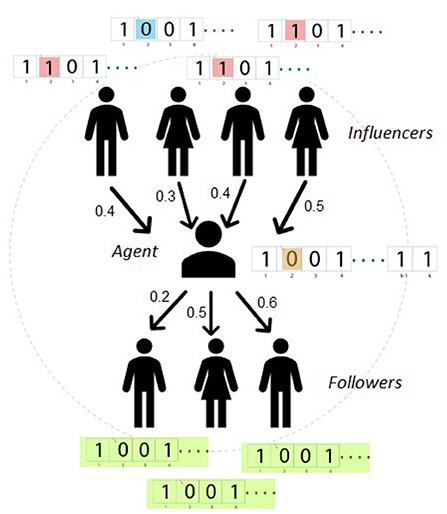
Figure 2. Schematic representation of the model. The agent considers the propensity exerted by the influencers and the conformity enjoyed with the followers, when deciding to switch on issue number 2. Three of the influencers disagree with the agent on issue number 2 (represented by red), while only one agrees (represented by blue). All the followers of the agent (those influenced by the agent) agree with the agent on all given issues (represented in green).

The three disagreeing agents exert social pressure on the agent to change its opinion on this issue. This social pressure corresponds to the propensity, and is calculated according to (2) as:

$\begin{array}{ll}{P}_{i,2}=\frac{0.4\times \frac{K-1}{K}+0.4\times \frac{K-1}{K}+0.5\times \frac{K-1}{K}}{3}.& (6)\end{array}$

For example, if K = 8 then P_i,2 ≈ 0.4,

The agent also enjoys social conformity with those who are influenced by this agent. For simplicity, let us assume that all the three agents agree with the agent under consideration on all issues. Thereby, these agents contribute to the social pressure on the agent to keep its opinion on the issue unchanged. This kind of pressure corresponds to conformity and can be calculated from (3) as,

$\begin{array}{ll}{T}_i=\frac{0.2\times \frac{K}{K}+0.5\times \frac{K}{K}+0.6\times \frac{K}{K}}{3}.& (7)\end{array}$

For K = 8 then T_i,2 ≈ 0.43 Finally, the social fitness of the agent on this issue is H_i,2 = 0.025. Therefore, the switching probability can be calculated as from (5) to be,

$\begin{array}{ll}{s}_{i,2}=\frac{1}{1+exp(\alpha \times T_i{H}_{i,2})}.& (8)\end{array}$

In particular, if α = 100 then the switching probability is s_i,2 ≈ 0.26. Therefore the agent will switch its opinion with a probability of 0.26 and the same procedure is repeated for other agents.

2.4. Network Structure

The diverse set of human interactions drive various emergent consequences, therefore it is imperative to identify the interaction most relevant to the problem at hand to model it mathematically. Literature from social psychology [37–39] asserts the fact that social influence plays a leading role in causing opinion change. Therefore for the purpose of this study, we consider social influence as the primary cause for an agent changing its opinion. In the paragraphs below, we describe the simulated social-influence networks we will be working with. Although there is no clear empirical evidence of what the topology of human social influence networks is like, it is clear that human societies are heterogeneous and hierarchical. Some agents are more competent in certain abilities and hence yield more influence over others. This suggests that the distribution of social influence in social structures follow a Pareto distribution. This assumption is backed by many studies of online social networks [40, 41]. Motivated by this discussion, the network of social influence can be empirically expected to be a directed scale-free network. The following Algorithm 1 describes how such a network is generated for our analysis.

ALGORITHM 1

Algorithm 1: Algorithm for generating the Adjacency matrix for the social influence network

Note that initially, the network has cycles and self-loops only among the first n₀ agents. More cycles are introduced before the final step in the proposed algorithm as node i creates an influence link to random node j(j < i) with some probability c. Now as the node i introduces a “back” link, it may automatically completes an influence cycle. This means that influence on any opinion expressed by agent i travels back to the agent in a loop and reinforces that opinion. In a social context, these influence loops are analogous to echo chambers. A visual representation of how a back link may introduce a cycle is shown in Figure 3. The probability c behaves as a parameter to control the number of such influence cycles.

FIGURE 3

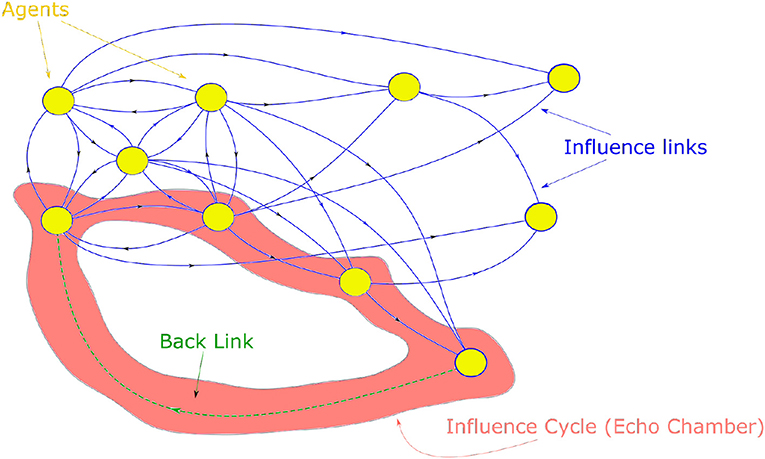
Figure 3. The figure shows a small network of N = 10 nodes. 5 nodes form a completely connected graph. From these nodes, new nodes draw 3 influence link preferentially based on their degree. Finally, when a new node introduces a back-link which close a loop in this network forming an influence cycle (echo chamber).

In order to introduce a certain degree of heterogeneity of social influences as each influence is different from the other, the adjacency matrix (A) is then weighted by weights drawn from a symmetric beta (5,5) distribution between [0,1]. The choice of this distribution is based on the assumption that extreme influences are less likely. The resulting weighted matrix is denoted by C.

3. Results and Analysis

3.1. Method Description

For the purposes of analysis we consider two different sets of systems. For facilitating the visualization of worldview evolution we consider a small system of (N = 100), highly rational (α = 100) agents with a worldview of K = 8 issues. Having demonstrated the worldview dynamics of these agents on a small scale, we then consider a much bigger system of (N = 1, 000), highly rational (α = 100) agents with bigger worldview of K = 10 issues. These systems are still very small as compared to real life social networks with millions of agents discussing thousands of issues. However, since the state space of the grows exponentially with system size, simulating such a system becomes computationally infeasible. We discuss the implications of system size in detail in our conclusions.

The worldviews are initialized completely at random. The agents are updated asynchronously, i.e., at each time step an agent is selected at random and the agent selects an issue at random. Thereafter, the agent updates its opinion on the selected issue as described in the example above. We record the state of the system after every N × K time steps. The state of the system is identified by worldview IDs, i.e., the decimal conversion of the binary string of “K” bits, for each agent. This enables us to study the time evolution of both worldviews and individual opinions. It must be noted that numerically close worldview IDs do not represent similar worldviews. For example, in the case of K = 8, worldview ID 170, is represented in binary as “10101010” and ID 177 is represented as “10110001.” The difference in IDs is just 7 but they disagree on half of the issues. Therefore, worldview IDs must be treated as identifiers. However, this representation is useful in identifying polar opposite worldviews as, the polar opposite of worldview ID w will always be 255 − w.

Simulations start by generating a social network as described in Algorithm 1. First, we obtain an adjacency matrix, A (N × N) and the weighted adjacency matrix C. We simulate the dynamics as discussed in the example in the previous section, on topologies with different back-link probabilities (c).

3.2. Polarization and Cycles

We first explore the effect of the number of cycles on the opinion dynamics for the small system (N = 100, K = 8). Figures 4A–C illustrates the typical behavior for three conditions: c = 0 (No extra back-links), c = 0.2 (A fifth of the agents create a back-link) and c = 0.5 (Half of the agents create a back-link). As discussed before, back link probability (c) controls for the number of cycles in the social influence network.

FIGURE 4

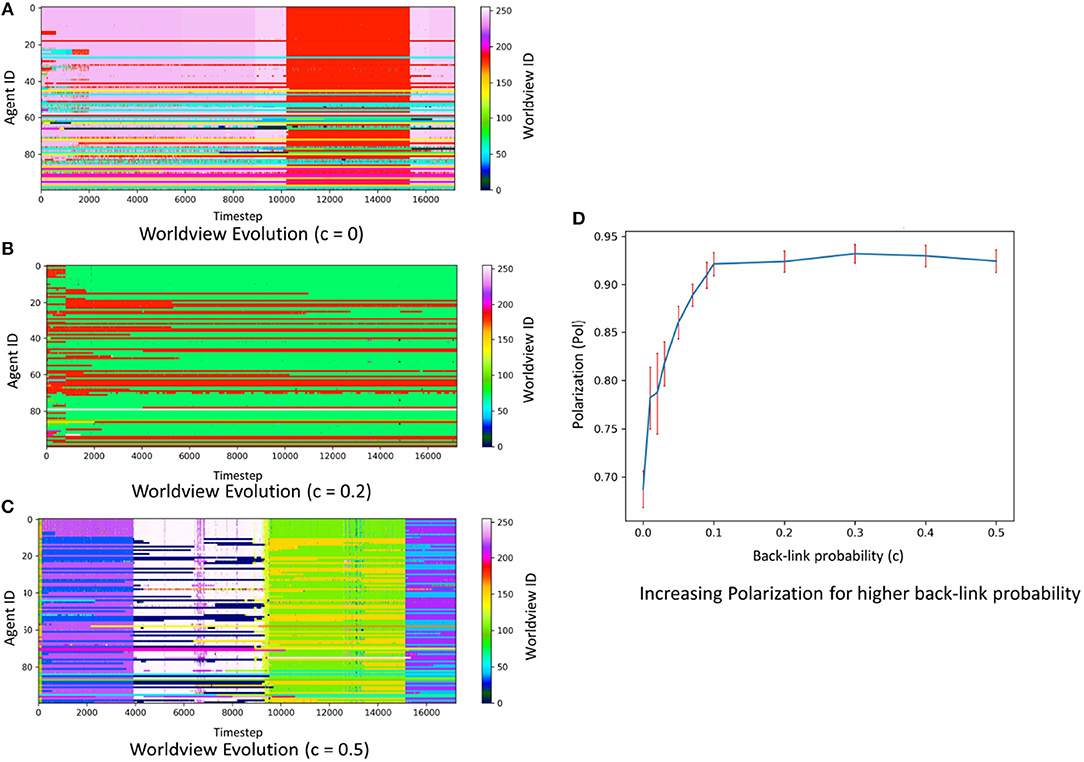
Figure 4. (A–C) Worldview evolution for 100 agents is observed for three different values of back-link probabilities (c = 0, 0.2, 0.5). The horizontal axis of the figure represents the time steps and the vertical axis represents individual agent IDs. The colors at each time-step indicate the Worldview ID of each agent. It is observed that polarization of worldviews increases with more back-links as agents self-organize into opposing worldviews. Some sudden transitions are also observed. (D) The variation of polarization for various values of back-link probability (C) for a system of 1,000 agents and 10 issues. The error bars show the 95% Bootstrap Confidence Intervals for the mean values obtained by 100 simulations for each value of “c.”

In the first case, it can be observed that most of the agents (60%) have the same worldview, and the opposing views are not necessarily the polar opposite of the dominant worldview. For instance, the most popular worldview at T = 8000, in this case, is Worldview ID: 243 (Binary representation: “11110011”) which is adopted by 60 agents. The next most popular worldview is worldview ID: 56 (Binary representation: “00111000”) which is popular among only 11 agents. Also, these two worldviews disagree on some but not all the issues.

However, for c = 0.2, some polarization emerges as a minority of agents hold a worldview which is completely opposite to the majority worldview. For example, in this case at t = 8000, the most popular worldview ID is 72 (Binary Representation: “01001000”) which is popular among 70 out of the 100 agents, however there is a significant minority of 27 agents which follow the worldview ID: 183 (Binary Representation: “10110111”). Here the majority and the minority disagree on all the issues, representing a case of group polarization.

Finally, in the case of c = 0.5, the majority weakens more and almost half of the population follows a worldview, while a significant opposition follows a completely opposing worldview. For example, in this cast at t = 8000, the majority of 57 agents believe in worldview ID 254 (Binary Representation: “11111110”) and the significant minority holds the polar opposite worldview 1 (Binary Representation: “00000001”). This observation suggests that the inclusion of cycles/back-links can indeed lead to this emergent global polarization.

Therefore to measure this it is imperative to discuss a measure of polarization we use to quantify polarization at any given state of the system. Consider the state of the system at any time t is given by n₁:w₁, n₂:w₂...., n_L:w_L, i.e., n_i agents with worldviews w_i for a set of L different worldviews. Now as defined in section 2.1, worldviews are a represented as a binary vector, $w_i=(O_1^i,\dots ,O_K^i)$. We can then define polarization as the euclidean distance of the centroid of existing worldviews from the neutral vector(${N}$) of size K, i.e ${N}=(0.5,0.5,\dots ,0.5)$ as,

$\begin{array}{ll}Pol=\frac{\sqrt{2}-d(C_t,{N})}{\sqrt{2}}\text{Where},C_t=\frac{{\displaystyle {\sum }_{i=1}^L}{n}_i{w}_i}{{\displaystyle {\sum }_{n=1}^L}{n}_i}& (9)\end{array}$

Above, the function $d(C_t,{N})$ gives the Euclidean distance between the centroid of the existing worldviews and the neutral vector. For example, if the system gets into a state where half of the population has an opposite opinion as the other half on all of the issues, then Pol = 1 as the centroid will coincide with the neutral vector. On the other hand, if the system gets into a state where all the agents have the same worldview, Pol = 0, as every possible worldview is at a Euclidean distance of $\sqrt{2}$ from the neutral vector.

Finally we calculate the average polarization for 10⁵ timesteps over 100 simulations for various values of back-link probabilities c, for the large system (N = 1, 000, K = 10). Figure 4D shows a slow but continuous increase of polarization with the back-link probability, confirming the role of cycles in increasing polarization.

A back-link completes an influence cycle and hence creates an echo chamber. When the agents, their influencers and their followers, have the same worldview, the probability of anyone in the echo-chamber to change opinion any issue becomes very small.

In summary, polarization can be said to be the result of agents' trying to minimize propensity (or maximize social fitness). By recalling (Equation 2), agents can do this in two ways: either by coming to the same worldview as all its neighbors (thus there is no disagreement on any issue), or by taking the completely opposite worldview, in which case the fractional similarity of the worldviews goes to zero and consequentially, the propensity.

In the c = 0 case, agents initially get into a polarized state to minimize propensity. But the absence of any cycles (i.e., echo-chambers), eventually a dominant majority is always established. However, as soon as echo chambers are introduced, then agents tend to stay in polarized states. Transitions are triggered by rare changes of opinions by key agents, causing the system to reorganize in a different polarized state.

3.3. Sudden Transitions

Simulations show sudden transitions of worldviews, which can be seen in Figure 4C (3 transitions), and also in Figure 4A (2 transitions). Note that these transitions are rare, as they occur when certain key agents (usually the ones with high influence) change their opinion on a certain issue and thereafter triggering a cascade of opinion changes. After the cascade, the system self-reorganizes in a different meta-stable state, which remains with minor fluctuations until another transition is triggered. This is related to the sigmoidal nature of the switching probability, as agents with very high social conformity and positive social fitness have a small yet non-zero probability of switching their opinion on any issue.

These transitions are a direct parallel from the ecological notions as worldviews, like species, emerge out of individual interactions and thrive during a metastable state, finally, when encountered with a chaotic transition, new worldviews emerge as the old ones go dormant. It must be noted that these sudden transitions are different than just a “minority–majority” switch. These transitions represent a change in the worldview configuration of the entire population, signaling the end of a meta-stable configuration and beginning of a new one. However, within a meta-stable state “minority - majority” switches can happen when a few edge agents decide to switch their worldview entirely in order to increase social fitness.

It is also interesting to note that nature of these transitions show a deviation from that of the Tangled Nature Model. The average rate of big transitions in the Tangled Nature Model shows an 1/t decay in time. Although, the proposed model is designed to capture interactions at a much smaller timescale as compared to that of biological evolution, as observed in Figure 5, the average rate of transitions decay as 1/t^a with small exponent (a ≈ 0.25). Also, the slowly decaying auto-correlation function of average number of transitions attests the non-stationary nature of evolution. It must be noted that the system eventually does relaxes into a steady state, with the transient time proportional to the length of the worldview vector (K).

FIGURE 5

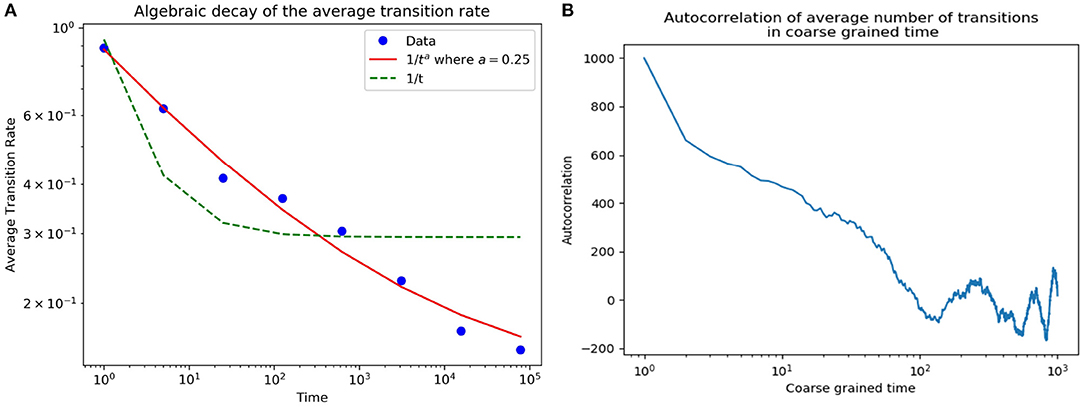
Figure 5. (A) Average transition rate in log binned time decay algebraically with exponent(≈ 0.25, shown in red). This is a slower rate of decay as compared to the 1/t decay in the Tangled nature model (shown in green). (B) Slow decay of the autocorrelations in coarse grained time (time steps of 100) of average number of transitions.

3.4. The Effect of Rationality

To study the role of rationality parameter (α), we calculate the average number of agents following the most popular worldview (i.e., the Mean Cluster Size) for various values of rationality parameter (α) and back-link probability (c). Figure 6A shows the variation of mean cluster size with the rationality parameter for various back-link topologies. It is also observed (Figure 6B) that for c = 0, the mean consensus reaches its maximum (≈700), quickly for a lower value of critical rationality than for c = 0.5. However, for c = 0.5, this transition occurs later, where the consensus quickly rises to the maximum value of half the population after the critical value of rationality. This shows a stark difference in the attained consensus by introduction of more cycles in the network topology. The detailed exploration of the nature of these transitions is part of our future work.

FIGURE 6

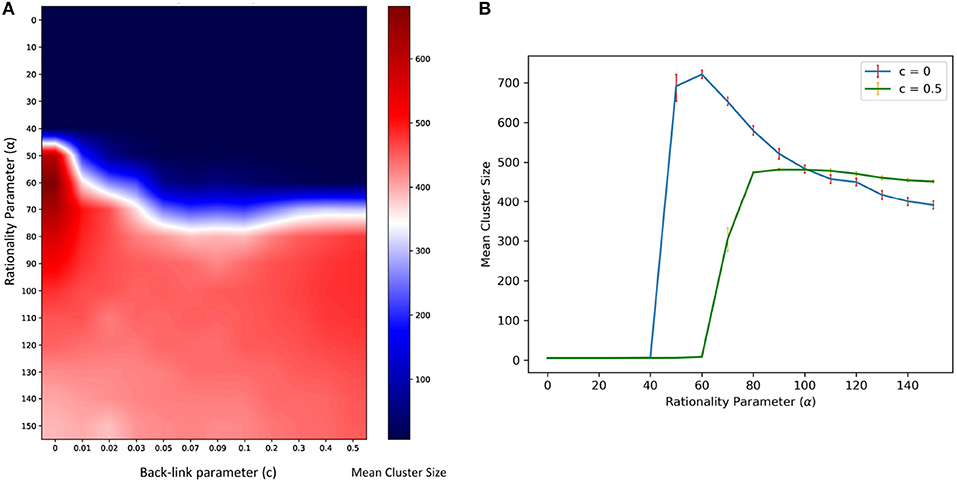
Figure 6. (A) Variation of the average size of the largest consensus group is observed across both Rationality (α) and the back-link parameter. (B) The effect of decreasing the rationality parameter on mean consensus population for 10⁵ time sweeps (100 simulations) for N = 1, 000 and K = 10. Error bars represent the 95% Bootstrap Confidence Intervals.

3.5. Dynamics of Individual Opinions

We now discuss the dynamics of opinions on individual issues. Figure 7 shows the dynamics of a particular opinion on issue “4” in the three discussed values of the cycle parameter (c).

FIGURE 7

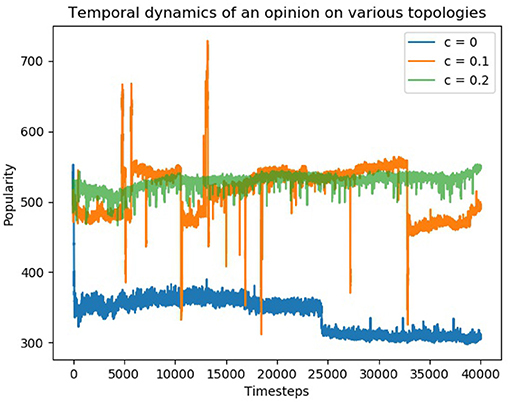
Figure 7. Time evolution of number of agents in favor of issue number 6 (N = 1, 000 and K = 10). Sudden surges are seen during worldview transitions in all the topologies (c = 0, c = 0.1, c = 0.2). However, the variation of opinions is much more variable in c = 0.1 topology.

The dynamics in the case of consensus topologies (c = 0 and c = 0.2) shows that variation in popularity of opinions changes very slightly and sudden surges/crashes happen when there is a sudden transition as discussed in previous sections. However, in the case of c = 0.1, the popularity of opinion shows much more variability as well along with more flash crashes and surges. This volatility can be attributed to the frustration introduced by polarization, as some agents, which are influenced by both poles, tend to switch back and forth.

For certain parameters, this behavior is concurrent with the behavior observed in the noisy voter model [29], which successfully explained the volatility clustering in opinion models. Therefore, the proposed Tangled Worldview Model provides a much more general framework to study different behaviors of opinion dynamics.

4. Conclusion

We proposed a stochastic model for the dynamics and co-evolution of the worldview of agents that participate in a social network. This formalism successfully captures the highly non-trivial macroscopic social phenomenon, including polarization, sudden worldview transitions, and the effect of the rationality of agents. The observed dynamics of opinions shows an intermittent behavior with sudden changes related to worldview transitions.

We discussed the role of network topology in generating and sustaining polarization, given the herding dynamics of the model. It was observed that social influence networks with cycles reinforce and facilitate polarization. Conversely, networks with fewer cycles and more tree-like (hierarchical) structure facilitate consensus. This finding also provides a possible explanation for the tree-like organizational structure observed in most organizations. Such a network structure facilitates the flow of command and propagation of values of the particular organization. This finding also helps in explaining the cultural segregation observed in Axelrod [12] and polarization observed in Deffuant et al. [24] and Hegselmann and Krause [14]. These models considered the social topology to be either an undirected 2D grid or completely connected. Both of these topologies facilitate polarization/segregation as they have multiple cycles. Although local preferential herding driven by homophily is an important driver of polarization, this paper enriches this view by further identifying the role played by the social network topology. The findings of this paper suggest that cycles in social networks restrict the system in reaching complete consensus. However, if these cycles are reduced consensus becomes possible even in the presence of preferential herding behavior like homophily.

It is also observed that sudden transitions in prevailing worldviews are possible even when absolutely no changes in the behavior of the agents, or the network topology are considered. This finding exposes the crucial role of the network topology and the relevance of certain key influential agents in the social structure. In particular, sudden transitions were found to be usually attributed to influential agents that change opinion on a particular issue and consequently trigger a cascade of opinions on all issues. This leads to an abrupt major rearrangement, which relaxes temporally into another meta-stable state. This sort of dynamics could explain the punctuated equilibrium of worldviews, as observed e.g., in real-world politics (For example, Synchronized weakening of liberal democracies and resurgence of nationalism are such transitions observed within the last decade). Therefore, in the age of online social networks and echo chambers, it is imperative to take up the challenges associated with recommendation algorithms and choice architecture (the practice of influencing choice by changing the manner in which options are presented to people [42]. Thaler and Sunstein [42] that can foster more harmonious online and offline social behavior.

There are a couple of limitations of the proposed model that need to be acknowledged, which we plan to address in future work. Firstly, as only one of the human biases is taken into account—namely, confirmation bias, polarization is the only emergent social phenomenon observed among the agents. Human behavioral choices are in general much more complex, which leads to a wider variety of emergent processes. However, due to the effects of non-linearities, a separate study of each of these biases and the macroscopic behavior it generates will underscore the roles of such biases in the overall dynamics. Secondly, polarization is capable of inducing changes in the social network topology. Therefore, in many scenarios, the network of social influence might change and evolve in time. It is therefore important to develop an understanding of the type rules of the temporal evolution of social influence networks that can drive the system into and out of polarized states. Finally, we also plan on corroborating these findings by comparing the prevalence of cycles in twitter retweet networks of polarizing issues and non-polarizing issues. Such a data-driven study will further help in establishing the thesis discussed in this paper for much larger real world networks.

Data Availability Statement

The raw data or the relevant code supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

HR conducted the simulations and analyzed the results. All authors contributed equally to the conceptualization of the model, writing, and approved the final version of the manuscript.

Funding

HR was supported by the Imperial College President's Ph.D. Scholarship. FR was supported by the Ad Astra Chandaria Foundation, and by EUs H2020 research and innovation programme under the Marie Skodowska-Curie grant agreement No. 702981.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Pedro A. M. Mediano for the useful discussions. We also thank Imperial College Research Computing Service, doi: 10.14469/hpc/2232 for the computing facilities.

References

1. Sire JW. The Universe Next Door. Nottingham: InterVarsity Press (1998).

Google Scholar

2. Naugle DK. Worldview: The History of a Concept. Grand Rapids, MI: Eerdmans (2002).

Google Scholar

3. Spengler O. The Decline of the West. London: George Allen and Unwin (1926).

Google Scholar

4. Schwarz G. My Family Has a Nazi Past. I See That Ideology Returning Across Europe. The Guardian. (2018) Available online at: https://www.theguardian.com/commentisfree/2018/apr/18/family-nazi-past-ideology-europe-germany-fascism-far-right (accessed January 15, 2019).

Google Scholar

5. Layman GC, Carsey TM, Horowitz JM. Party polarization in American politics: characteristics, causes, and consequences. Ann Rev Polit Sci. (2006) 9:83–110. doi: 10.1146/annurev.polisci.9.070204.105138

CrossRef Full Text | Google Scholar

6. Horrox R. The Black Death. Manchester: Manchester University Press (2013). Available online at: https://www.manchesterhive.com/view/9781526112712/9781526112712.xml

Google Scholar

7. Trilla A, Trilla G, Daer C. The 1918 “Spanish Flu” in Spain. Clin Infect Dis. (2008) 47:668–73. doi: 10.1086/590567

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Scarpino SV, Allard A, Hbert-Dufresne L. The effect of a prudent adaptive behaviour on disease transmission. Nat Phys. (2016) 12:1042–6. doi: 10.1038/nphys3832

CrossRef Full Text | Google Scholar

9. Bathiany S, Scheffer M, van Nes EH, Williamson MS, Lenton TM. Abrupt climate change in an oscillating World. Sci Rep. (2018) 8:5040. doi: 10.1038/s41598-018-23377-4

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lee JK, Choi J, Kim C, Kim Y. Social media, network heterogeneity, and opinion polarization. J Commun. (2014) 64:702–22. doi: 10.1111/jcom.12077

CrossRef Full Text | Google Scholar

11. Lee FLF. Impact of social media on opinion polarization in varying times. Commun Public. (2016) 1:56–71. doi: 10.1177/2057047315617763

CrossRef Full Text | Google Scholar

12. Axelrod R. The dissemination of culture. J Conflict Resol. (1997) 41:203–26. doi: 10.1177/0022002797041002001

CrossRef Full Text | Google Scholar

13. Starnini M, Frasca M, Baronchelli A. Emergence of metapopulations and echo chambers in mobile agents. Sci Rep. (2016) 6:31834. doi: 10.1038/srep31834

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Soc Simul. (2002) 5. Available online at: http://jasss.soc.surrey.ac.uk/5/3/2.html

Google Scholar

15. Del Vicario M, Scala A, Caldarelli G, Stanley HE, Quattrociocchi W. Modeling confirmation bias and polarization. Sci Rep. (2017) 7:40391. doi: 10.1038/srep40391

CrossRef Full Text | Google Scholar

16. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys. (2009) 81:591–646. doi: 10.1103/RevModPhys.81.591

CrossRef Full Text | Google Scholar

17. Helbing D. Quantitative Sociodynamics. Berlin: Springer (2010).

Google Scholar

18. Lancichinetti A, Fortunato S. Consensus clustering in complex networks. Sci Rep. (2012) 2:336. doi: 10.1038/srep00336

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Amblard F, Deffuant G. The role of network topology on extremism propagation with the relative agreement opinion dynamics. Phys A Stat Mechan Appl. (2004) 343:725–38. doi: 10.1016/S0378-4371(04)00858-1

CrossRef Full Text | Google Scholar

20. Baldassarri D, Bearman P. Dynamics of political polarization. Am Sociol Rev. (2007) 72:784–811. doi: 10.1177/000312240707200507

CrossRef Full Text | Google Scholar

21. Clifford P, Sudbury A. A model for spatial conflict. Biometrika. (1973) 60:581. doi: 10.2307/2335008

CrossRef Full Text | Google Scholar

22. Galam S. Minority opinion spreading in random geometry. Eur Phys J B. (2002) 25:403–6. doi: 10.1140/epjb/e20020045

CrossRef Full Text | Google Scholar

23. Stauffer D. Sociophysics: the Sznajd model and its applications. Comput Phys Commun. (2002) 146:93–8. doi: 10.1016/S0010-4655(02)00439-3

CrossRef Full Text | Google Scholar

24. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst. (2000) 3:87–98. doi: 10.1142/S0219525900000078

CrossRef Full Text | Google Scholar

25. Jia P, MirTabatabaei A, Friedkin NE, Bullo F. Opinion dynamics and the evolution of social power in influence networks. SIAM Rev. (2015) 57:367–97. doi: 10.1137/130913250

CrossRef Full Text | Google Scholar

26. Laguna MF, Abramson G, Zanette DH. Vector opinion dynamics in a model for social influence. Phys A Stat Mechan Appl. (2003) 329:459–72. doi: 10.1016/S0378-4371(03)00628-9

CrossRef Full Text | Google Scholar

27. Alaali A, a Purvis M, Savarimuthu BTR. Vector opinion dynamics: an extended model for consensus in social networks. In: 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology (Sydney, NSW). (2008). p. 394–397.

Google Scholar

28. Granovsky BL, Madras N. The noisy voter model. Stochas Process Appl. (1995) 55:23–43.

Google Scholar

29. Carro A, Toral R, San Miguel M. The noisy voter model on complex networks. Sci Rep. (2016) 6:24775. doi: 10.1038/srep24775

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Jensen HJ. Tangled nature: a model of emergent structure and temporal mode among co-evolving agents. Eur J Phys. (2018) 40:014005. doi: 10.1088/1361-6404/aaee8f

CrossRef Full Text | Google Scholar

31. Christensen K, Di Collobiano SA, Hall M, Jensen HJ. Tangled nature: a model of evolutionary ecology. J Theoret Biol. (2002) 216:73–84. doi: 10.1006/jtbi.2002.2530

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Becker N, Sibani P. Evolution and non-equilibrium physics: a study of the Tangled Nature Model. Europhy Lett. (2014) 105:18005. doi: 10.1209/0295-5075/105/18005

CrossRef Full Text | Google Scholar

33. Anderson PE, Jensen HJ, Oliveira LP, Sibani P. Evolution in complex systems. Complexity. (2004) 10:49–56. doi: 10.1002/cplx.20049

CrossRef Full Text | Google Scholar

34. Nicholson A, Sibani P. Cultural evolution as a nonstationary stochastic process. Complexity. (2016) 21:214–23. doi: 10.1002/cplx.21681

CrossRef Full Text | Google Scholar

35. Ortega DA, Braun PA. Information, Utility and Bounded Rationality. In: Schmidhuber J, Thórisson KR, Looks M, editors. Artificial General Intelligence. Berlin; Heidelberg: Springer Berlin Heidelberg (2011). p. 269–74.

Google Scholar

36. Galesic M, Stein DL. Statistical physics models of belief dynamics: theory and empirical tests. Phys A Statist Mechan Appl. (2019) 519:275–94. doi: 10.1016/j.physa.2018.12.011

CrossRef Full Text | Google Scholar

37. Kelman HC. Compliance, identification, and internalization three processes of attitude change. J Conflict Resol. (1958) 2:51–60.

Google Scholar

38. Moussad M, Kmmer JE, Analytis PP, Neth H. Social influence and the collective dynamics of opinion formation. PLoS ONE. (2013) 8:e078433. doi: 10.1371/journal.pone.0078433

CrossRef Full Text | Google Scholar

39. Chacoma A, Zanette DH. Opinion formation by social influence: from experiments to modeling. PLoS ONE. (2015) 10:e0140406. doi: 10.1371/journal.pone.0140406

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Mislove A, Marcon M, Gummadi KP, Druschel P, Bhattacharjee B. Measurement and analysis of online social networks. In: Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement. IMC '07. New York, NY: ACM (2007). p. 29–42. doi: 10.1145/1298306.1298311

CrossRef Full Text | Google Scholar

41. Anghel M, Toroczkai Z, Bassler KE, Korniss G. Competition-driven network dynamics: emergence of a scale-free leadership structure and collective efficiency. Phys Rev Lett. (2004) 92:058701. doi: 10.1103/PhysRevLett.92.058701

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Thaler RH, Sunstein CR. Nudge. Penguin Books (2009).

PubMed Abstract | Google Scholar