A Continuous Time Bertrand Duopoly Game With Fractional Delay and Conformable Derivative: Modeling, Discretization Process, Hopf Bifurcation, and Chaos

Xin, Baogui; Peng, Wei; Guerrini, Luca

doi:10.3389/fphy.2019.00084

ORIGINAL RESEARCH article

Front. Phys., 04 June 2019

Sec. Statistical and Computational Physics

Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00084

A Continuous Time Bertrand Duopoly Game With Fractional Delay and Conformable Derivative: Modeling, Discretization Process, Hopf Bifurcation, and Chaos

$\nBaogui Xin$ Baogui Xin¹^*

Wei Peng¹

Luca Guerrini²

¹College of Economics and Management, Shandong University of Science and Technology, Qingdao, China
²Department of Management, Polytechnic University of Marche, Ancona, Italy

The purpose of this paper is three-fold. First, we present a discretization process to obtain numerical solutions of a conformable fractional-order system with delays. Second, we extend the classical Bertrand duopoly game with integer delays to that with fractional delays. Third, we extend the game based on ordinary differential derivative to that based on conformable fractional-order derivative. Finally, we analyze the local stability, Hopf bifurcation, and chaos of the proposed game model.

1. Introduction

Bifurcation and chaos [1] are frequent phenomena in various scientific fields including economics. By analyzing bifurcation and chaos, we can reveal its evolutionary mechanism to control proposed systems [2–4]. Delay is another common phenomenon which usually occurs in various economic systems, such as the discrete duopoly game with integer delays [5–13], the monopoly with integer delay and bounded rationality [14, 15], the continuous time Cournot duopoly with integer delays [16, 17], the continuous Bertrand duopoly with integer delay [18, 19]. Naturally, we will consider what the Bertrand duopoly game with fractional delays should be.

As a natural extension of a classical ordinary differential equation, the fractional derivative is a derivative of arbitrary order, real or complex [20–28]. Similarly we also want to extend the integer delay to arbitrary delay, integer or fractional, real or complex. Thus the continuous time Bertrand duopoly game with fractional delay and conformable derivative would have stronger ability to represent complex problems than the corresponding game with integer delay and derivative.In other words, the fractional delay can also be conceived as a kind of conformable fractional delay.

Although researchers proposed various fractional operators, such as Riemann-Liouville, Caputo, and Grunwald-Letnikov [29–33], widely used in many fields including economics, physics, and engineering [34–38], these definitions of operators satisfy two characteristics: one is that they must be non-integer in form, and the other is that they must be non-local in essence. But non-locality is a double-edged sword. It has the advantage of long memory, but it also has the disadvantage of not satisfying the classical differential operator, such as the chain rule. The conformable operator is conceived as a natural extension of the classical differential operator [39–45], whose most important properties hold, such as the chain rule [21, 22, 46]. Certainly, the conformable derivative is only a kind of local definition of fractional derivative and is non-integer in form, but it has no non-locality. In fact, there are two opposing viewpoints about the definitions of fractional derivatives: one is two above-mentioned characteristics must hold simultaneously, but the other is the first characteristic is the key of the fractional derivative. The later opinion means that a derivative is fractional derivative only if the first characteristic holds. We will support the later opinion in this paper. The conformable operator has recently occurred in many scientific fields [23–27, 40, 47–50]. In this paper, we will introduce the conformable fractional-order derivative to the continuous time Bertrand duopoly game with integer delays. Thus we can obtain a conformable Bertrand duopoly game with fractional delay.

After we propose the continuous time Bertrand duopoly game with fractional delay and conformable derivative, we need suitable approaches to obtain its solutions. Though there are several schemes to solve a conformable fractional-order system without any delay [40, 41, 45, 50–72], they are not suitable for conformable system with fractional delays. Mohammadnezhad et al. [73] employed conformable Euler's method to obtain approximation solutions of conformable fractional differential equations. Inspired by the discretization process for other derivatives [74–78], we will present a simple discretization process for a conformable system with fractional delays. Our proposed method well coincides with the conformable Euler method [73]. Using the proposed discretization scheme, we will detect the stability, Hopf bifurcations, and chaotic attractors of the continuous time Bertrand duopoly game with fractional delay and conformable derivative.

The remainder of this paper is organized as follows. In section 2, we show preliminaries of conformable calculus and stability conditions of a discrete system. In section 3, we propose a discretization process for conformable systems with fractional delays. In section 4, we present a continuous time Bertrand duopoly game with fractional delays and conformable derivative. In section 5, we analyze Nash equilibrium points, local stabilities, and Hopf bifurcation in the game model. In section 6, we employ 0-1 test algorithm to detect chaotic attractors. This paper concludes with a summary in section 7.

2. Preliminaries

Definition 1. (See [22])

For a function f : [t₀, ∞) → ℝ, its left conformable fractional derivative starting from t₀ of order α ∈ (0, 1) is defined by

\begin{array}{l} T_{α}^{t_{0}} f (t) = lim_{ε \to 0} \frac{f (t + ε {(t - t_{0})}^{1 - α}) - f (t)}{ε}, & (1) \end{array}

in which the function f is called as α-differentiable.

Definition 2. (See [22])

For a function f : [t₀, ∞) → ℝ, its left conformable fractional integral starting from t₀ of order α ∈ (0, 1) is defined by

\begin{array}{l} I_{α}^{t_{0}} f (t) = \int_{t_{0}}^{t} {(s - t_{0})}^{α - 1} f (s) d s, & (2) \end{array}

where the integral is the usual Riemann improper integral.

Lemma 1. (See [22])

Suppose the derivative order α ∈ (0, 1) and the function f is α-differentiable at a point t₀ > 0, then the left conformable fractional derivative satisfies:

\begin{array}{l} T_{α}^{t_{0}} f (t) = {(t - t_{0})}^{1 - α} \frac{d f (t)}{d t} . & (3) \end{array}

Lemma 2. (Conformable fractional power series expansion) [22] Given an infinitely α−differentiable function f : [0, ∞) → ℝ, α ∈ (0, 1], f has the following conformable fractional power series expansion at a neighborhood of a point t₀:

\begin{array}{l} f (t) = \sum_{n = 0}^{\infty} \frac{{(T_{α}^{t_{0}} f)}^{(n)} (t_{0}) {(t - t_{0})}^{n α}}{α^{n} n!}, t_{0} < t < t_{0} + R^{\frac{1}{α}}, R > 0, \end{array}

where ${(T_{α}^{t_{0}} f)}^{(n)} (t_{0})$ denotes the application of the conformable fractional derivative n times.

Consider the following discrete dynamical system:

\begin{array}{l} X (i + 1) = F (X (i)), i = 1, 2, \cdot\cdot\cdot, n . & (4) \end{array}

where X = (x₁, x₂, ··· , x_n), and F = (f₁, f₂, ··· , f_n) is C² from ℝⁿ to ℝⁿ. Let X^eq be a fixed point of system (4), and λ₁, λ₂, ··· , λ_n be eigenvalues of Jacobian matrix $J (X^{e q}) = \frac{\partial F}{\partial X} |_{X = X^{e q}}$ . Then we can obtain the following characteristic polynomial of J(X^eq)

\begin{array}{l} W (λ) = λ^{n} + w_{1} λ^{n - 1} + w_{2} λ^{n - 2} + \cdot\cdot\cdot + w_{n - 1} λ + w_{n}, & (5) \end{array}

Lemma 3. (See [79]).

(i) If all the eigenvalues λ_i of J(X^eq) have |λ_i| < 1, then the periodic orbit $O_{F}^{+} (X^{e q})$ is attracting.

(ii) If one eigenvalue λ_i0 of J(X^eq) has |λ_i0| > 1, then the periodic orbit $O_{F}^{+} (X^{e q})$ is unstable.

(iii) If all the eigenvalues λ_i of J(X^eq) have |λ_i| > 1, then the periodic orbit $O_{F}^{+} (X^{e q})$ is repelling.

3. Discretization Process of Conformable Fractional Systems With Delays

Theorem 1. (Conformable delay discretization by piecewise constant approximation)

Consider the following conformable fractional-order delay system

\begin{array}{l} T_{α} x (t) = f (x (t - τ)), τ \geq 0, 0 \leq t \leq T, x (0) = x_{0}, & (6) \end{array}

we obtain the following discretization of Equation (6)

\begin{array}{l} \begin{array}{l} x (n + 1) = x (n) + \frac{h^{α}}{α} f (x (n - \frac{τ}{h})), \end{array} & (7) \end{array}

where x_n denotes x_n(t_n), $h = \frac{T}{N} = t_{n + 1} - t_{n}$ , t_n = nh, n = 0, 1, ··· , N.

Proof: By drawing on the discretization process proposed by Raheem and Salman [74], El-Sayed et al. [75], El-Sayed et al. [76], Agarwal et al. [77], and El-Sayed et al. [78], we discretize the fractional-order delay Equation (6) with piecewise constant approximation as follows

\begin{array}{l} \begin{array}{l} T_{α} x (t) = f (x ([\frac{t}{h}] h - τ)), τ \geq 0, 0 \leq t \leq T, x (0) = x_{0}, \end{array} & (8) \end{array}

By using Lemma 1, we rewrite Equation (8) as follows.

\begin{array}{l} {(t - n h)}^{1 - α} \frac{d x (t)}{d t} = f (x (n h - τ)), τ \geq 0, 0 \leq t \leq T, x (0) = x_{0}, \end{array}

which leads to

\begin{array}{l} \frac{d x (t)}{d t} = {(t - n h)}^{α - 1} f (x (n h - τ)), 0 \leq t \leq T, x (0) = x_{0}, & (9) \end{array}

We apply the step method presented in Kartal and Gurcan [59], El-Sayed et al. [76], and El-Sayed et al. [78] for discretizing Equation (9) with piecewise constant approximation as follows

(i) Let n = 0, then t ∈ [0, h), we rewrite Equation (9) as follows

\begin{array}{l} \begin{array}{l} \frac{d x (t)}{d t} = {(t - 0)}^{α - 1} f (x_{0} (0 - τ)), t \in [0, h), \end{array} & (10) \end{array}

and the solution of Equation (10) is given by

\begin{array}{l} x_{1} (t) = x_{0} + \int_{0}^{t} ({(s - 0)}^{α - 1} f (x_{0} (0 - τ))) d s \\ = x_{0} + f (x_{0} (0 - τ)) \int_{0}^{t} s^{α - 1} d s \\ = x_{0} + \frac{t_{α}}{α} f (x_{0} (0 - τ)) . \end{array}

(ii) Let n = 1, then t ∈ [h, 2h), we rewrite Equation (9) as follows

\begin{array}{l} \frac{d x (t)}{d t} = {(t - h)}^{α - 1} f (x_{1} (h - τ)), t \in [h, 2 h), & (11) \end{array}

and the solution of Equation (11) is given by

\begin{array}{l} x_{2} (t) = x_{1} (h) + \int_{h}^{t} ({(s - h)}^{α - 1} f (x_{1} (h - τ))) d s \\ = x_{1} (h) + f (x_{1} (h - τ)) \int_{h}^{t} {(s - h)}^{α - 1} d s \\ = x_{1} (h) + \frac{{(t - h)}^{α}}{α} f (x_{1} (h - τ)) . \end{array}

(iii) By repeating the above process, we obtain the following solution of Equation (9)

\begin{array}{l} x_{n + 1} (t) = x_{n} (n h) + \frac{{(t - n h)}^{α}}{α} f (x_{n} (n h - τ)), t \in [n h, (n + 1) h) . \end{array}

Let t → (n + 1)h, we deduce the the following discretization

\begin{array}{l} x_{n + 1} ((n + 1) h) = x_{n} (n h) + \frac{h^{α}}{α} f (x_{n} (n h - τ)), t \in [n h, (n + 1) h), \end{array}

that is

\begin{array}{l} x_{n + 1} = x_{n} + \frac{h^{α}}{α} f (x_{n} - \frac{τ}{h}) . \end{array}

It is proved.

Remark 1. The presented conformable discretization process is well line with the conformable Euler's method proposed by Mohammadnezhad et al. [73].

Theorem 2. The conformable delay discretization process in Theorem 1 is convergent.

Proof: According to Lemma 2 and the conformable Euler's method [73], we obtain the following conformable fractional power series expansion:

\begin{array}{l} x (t_{n + 1}) = x (t_{n}) + \frac{h^{α}}{α} f (x (t_{n} - \frac{τ}{h})) + \frac{h^{2 α}}{2 α^{2}} T_{2 α} x (t_{n} - \frac{τ}{h} + θ_{n} h) & (12) \end{array}

where 0 < θ_n < 1 and $T_{2 α} x (t) \in C^{0} [0, T]$ .

So the conformable delay discretization process is convergent when step size h is small enough.

4. Modeling

4.1. A Continuous Time Bertrand Duopoly Game With Fractional Delays and Conformable Derivative

Assume that each firm decides on a different product pricing strategy in a duopoly market, in which p_i(t) indicates the i-th firm's price during time period t ∈ Z⁺, q_i(t) represents the i-th firm's supply during time period t ∈ Z⁺, and q_i and p_i satisfies the common linear inverse demand function as follows.

\begin{array}{l} \begin{aligned} p_{i} (t) = a_{i} - q_{i} (t) - b q_{j} (t), i, j = 1, 2, i \neq j, \end{aligned} & (13) \end{array}

where a_i and b are positive constants. a_i denotes the i-th firm's constant reservation price in the product market. b denotes supply margin effects on its price from itself and its rival. Suppose i-th firm's marginal costs is equal to c_i, which is also a positive constant, as follows

\begin{array}{l} \begin{aligned} C_{i} (t) = c_{i} q_{i} (t), i = 1, 2, \end{aligned} & (14) \end{array}

Then the i-th firm's profit is

\begin{array}{l} Π_{i} (p_{i} (t), p_{j} (t)) = p (t) q_{i} (t) - C_{i} (t), i, j = 1, 2, i \neq j . & (15) \end{array}

Thus we can obtain the i−th firm's marginal profit with respect to p_i as follows

\begin{array}{l} \begin{aligned} \frac{\partial Π_{i} (p_{i} (t), p_{j} (t))}{\partial p_{i} (t)} = a_{i} - c_{i} - 2 p_{i} (t) - b p_{j} (t), i, j = 1, 2, i \neq j . \end{aligned} & (16) \end{array}

As we know, the higher a firm's marginal profit is, the greater its price adjustment range is. In other words, the a firm's price growth rate $\frac{\dot{p}}{p}$ is proportional to its marginal profit $\frac{\partial Π}{\partial p}$ . We get the gradient adjustment process of price as follows

\begin{array}{l} \begin{aligned} \dot{p_{i}} (t) = v_{i} p_{i} (t) (a_{i} - c_{i} - 2 p_{i} (t) - b p_{j} (t)), i, j = 1, 2, i \neq j, \end{aligned} & (17) \end{array}

where v_i > 0 represents the i−th firm's price adjustment speed.

Inspired by Matsumoto et al. [15] who regarded the marginal profit as a delayed value, we rewrite Equation (17) with delay τ as follows

\begin{array}{l} \dot{p_{i}} (t) = v_{i} p_{i} (t - τ) (a_{i} - c_{i} - 2 p_{i} (t - τ) - b p_{j} (t - τ)), τ \geq 0, \\ i, j = 1, 2, i \neq j . & (18) \end{array}

We can regard the conformable fractional-order derivative as a natural extension of the integer order form. Thus, we introduce the conformable derivative to Equation (18) and obtain the following Bertrand duopoly game with α_i-order conformable derivative and fractional delay:

\begin{array}{l} T_{α} p_{i} (t) = v_{i} p_{i} (t - τ) (d_{i} - 2 p_{i} (t - τ) - b p_{j} (t - τ)), \\ i, j = 1, 2, i \neq j, & (19) \end{array}

where α ∈ (0, 1], d_i = a_i − c_i, τ ≥ 0 denotes a fractional delay.

Remark 2. When α = 1, Equation (19) degenerates to Equation (18).

Remark 3. When α = 1 and τ = 0, Equation (19) degenerates to Equation (17).

4.2. Discretization Process

According to Theorem 1, we employ piecewise constant approximation to discretize the game model (18) as follows

\begin{array}{l} {\begin{array}{l} p_{1} (n + 1) = p_{1} (n) + \frac{h^{α}}{α} (v_{1} p_{1} (n - \frac{τ}{h}) (a_{1} - c_{1} - 2 p_{1} (n - \frac{τ}{h}) - b p_{2} (n - \frac{τ}{h}))), \\ p_{2} (n + 1) = p_{2} (n) + \frac{h^{α}}{α} (v_{2} p_{2} (n - \frac{τ}{h}) (a_{2} - c_{2} - 2 p_{2} (n - \frac{τ}{h}) - b p_{1} (n - \frac{τ}{h}))) . \end{array} & (20) \end{array}

Remark 4. If τ = mh, and m is integer, then we rewrite the game model (20) as follows

\begin{array}{l} {\begin{array}{l} p_{1} (n + 1) = p_{1} (n) + \frac{h^{α}}{α} (v_{1} p_{1} (n - m) (a_{1} - c_{1} - 2 p_{1} (n - m) - b p_{2} (n - m))), \\ p_{2} (n + 1) = p_{2} (n) + \frac{h^{α}}{α} (v_{2} p_{2} (n - m) (a_{2} - c_{2} - 2 p_{2} (n - m) - b p_{1} (n - m))) . \end{array} & (21) \end{array}

In the following, we only study the case m = 1. Then we rewrite the game model (21) as follows

\begin{array}{l} {\begin{array}{l} p_{1} (n + 1) = p_{1} (n) + \frac{h^{α}}{α} (v_{1} p_{3} (n) (d_{1} - 2 p_{3} (n) - b p_{4} (n))), \\ p_{2} (n + 1) = p_{2} (n) + \frac{h^{α}}{α} (v_{2} p_{4} (n) (d_{2} - 2 p_{4} (n) - b p_{3} (n))), \\ p_{3} (n + 1) = p_{1} (n), \\ p_{4} (n + 1) = p_{2} (n) . \end{array} & (22) \end{array}

5. Local Stability, Hopf Bifurcation, and Chaos

5.1. Local Stability

Fixed points of system (22) satisfy

\begin{array}{l} {\begin{array}{l} p_{1} = p_{1} + \frac{h^{α}}{α} (v_{1} p_{3} (d_{1} - 2 p_{3} - b p_{4})), \\ p_{2} = p_{2} + \frac{h^{α}}{α} (v_{2} p_{4} (d_{2} - 2 p_{4} - b p_{3})), \\ p_{3} = p_{1}, \\ p_{4} = p_{2} . \end{array} & (23) \end{array}

By algebraic computation, we obtain the following fixed points: E₁ = (0, 0, 0, 0), $E_{2} = (0, \frac{d_{2}}{2}, 0, \frac{d_{2}}{2})$ , $E_{3} = (\frac{d_{1}}{2}, 0, \frac{d_{1}}{2}, 0)$ , and E₄ = (p_e1, p_e2, p_e1, p_e2), where $p_{e 1} = \frac{2 d_{1} + b d_{2}}{4 - b^{2}}$ , $p_{e 2} = \frac{2 d_{2} + b d_{1}}{4 - b^{2}}$ . There are some economic information as follows:

(i) At the first fixed point E₁, no firm can gain anything by production if its opponent stops production.

(ii) At the second fixed point E₂, stoping production is the best strategy for firm 1 if $q_{2}^{*} = \frac{d_{2}}{2}$ is the output strategy of firm 2, and vice versa.

(iii) At the third fixed point E₃, stoping production is the best strategy for firm 2 if firm 1 adopts its output strategy $q_{1}^{*} = \frac{d_{1}}{2}$ , and vice versa.

(iv) At the fourth fixed point E₄, firm 1 cannot obtain extra benefit from deviating unilaterally from its equilibrium output strategy $q_{1}^{*} = p_{e 1}$ if firm 2 adopts its equilibrium output strategy $q_{2}^{*} = p_{e 2}$ , and vice versa.

Points E₁, E₂, and E₃ are all bounded equilibria [80]. Thus, we only study the stability of non-bounded equilibrium point E₄.

We obtain the following Jacobian matrix of system (23) evaluated at the fourth fixed point E₄:

\begin{array}{l} J (E_{4}) = (\begin{matrix} 1 & 0 & \frac{2 h^{α} v_{1} (2 d_{1} - b d_{2})}{α (b^{2} - 4)} & \frac{b h^{α} v_{1} (2 d_{1} - b d_{2})}{α (b^{2} - 4)} \\ 0 & 1 & \frac{b h^{α} v_{2} (2 d_{2} - b d_{1})}{α (b^{2} - 4)} & \frac{2 h^{α} v_{2} (2 d_{2} - b d_{1})}{α (b^{2} - 4)} \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}) . & (24) \end{array}

The characteristic equation of Jacobian matrix (24) is

\begin{array}{l} W (λ) = λ^{n} + w_{1} λ^{n - 1} + w_{2} λ^{n - 2} + \cdot\cdot\cdot + w_{n - 1} λ + w_{n} & (25) \end{array}

where

\begin{array}{l} {\begin{aligned} w_{1} = - 2, \\ w_{2} = \frac{((2 d_{1} v_{2} + 2 d_{2} v_{1}) b - 4 d_{1} v_{1} - 4 d_{2} v_{2}) h^{α} + α b^{2} - 4 α}{α b^{2} - 4 α}, \\ w_{3} = \frac{2 h^{α} (2 d_{1} v_{1} + 2 d_{2} v_{2} - b d_{1} v_{2} - b d_{2} v_{1})}{α (b^{2} - 4)}, \\ w_{4} = \frac{h^{2 α} v_{1} v_{2} (2 d_{2} - b d_{1}) (b d_{2} - 2 d_{1})}{α^{2} (b^{2} - 4)} . \end{aligned} \end{array}

According to Jury stability criterion, we directly obtain the following proposition for system (22).

Proposition 1. The fixed point E₄ is locally asymptotically stable if the following stability constraints holds simultaneously: W(1) > 0, W(−1) > 0, |w₄| < 1, $| w_{3} - w_{1} w_{4} | < 1 - w_{4}^{2}$ , |k₁| < k₂, where

\begin{array}{l} {\begin{aligned} W (1) = 1 + w_{1} + w_{2} + w_{3} + w_{4}, \\ W (- 1) = 1 - w_{1} + w_{2} - w_{3} + w_{4}, \\ k_{1} = w_{2} - w_{2} w_{4} - w_{2} w_{4}^{2} + w_{2} w_{4}^{3} - w_{1} w_{3} + w_{1}^{2} w_{4} + w_{3}^{2} w_{4} - w_{1} w_{3} w_{4}^{2}, \\ k_{2} = 1 - 2 w_{4}^{2} + w_{4}^{4} - w_{3}^{2} + 2 w_{1} w_{3} w_{4} - w_{1}^{2} w_{4}^{2} \end{aligned} \end{array}

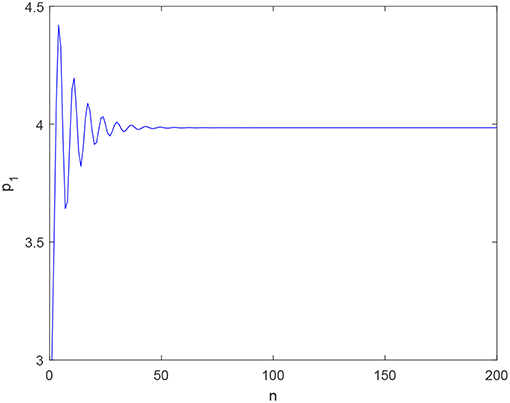
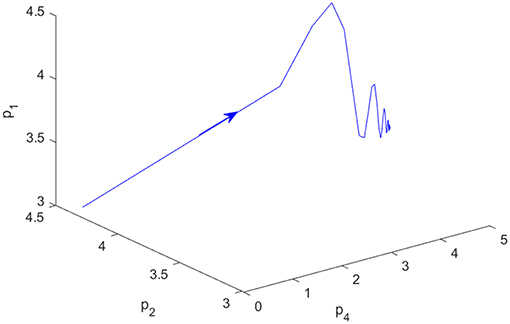
Set h = 0.01, d₁ = 8, d₂ = 6, b = 0.01, v₁ = 0.05, v₂ = 0.01, α = 0.2. We can obtain E₁ = (0, 0, 0, 0), E₂ = (0, 3, 0, 3), E₃ = (4, 0, 4, 0), and E₄ = (3.99, 2.98, 3.99, 2.98). Obviously, Proposition 1 holds, i.e., system (22) is stable, as shown in Figures 1, 2. As time goes on with α = 0.2, Figure 1 demonstrates outputs of firm 1 trend to an invariant value, and Figure 2 demonstrates system (22) convergences to a fixed point. Figures 1, 2 mutually validate the existence of fixed points E₄ in system (22).

FIGURE 1

Figure 1. Evolution of p₁ with α = 0.2.

FIGURE 2

Figure 2. Phase portrait in (p₁, p₂, p₄)-plane with α = 0.2.

5.2. Hopf Bifurcation

According to the explicit criterion of Hopf bifurcation [81], we directly obtain the following theorem:

Theorem 3. In system (22), a Hopf bifurcation occurs at α = α^* if the following conditions (H1)-(H3) hold:

(H1) Eigenvalue assignment $△_{3}^{-} (α^{*}) = 0,$ W(1) > 0, W(−1) > 0, $△_{3}^{+} (α^{*}) > 0,$ $△_{1}^{\pm} (α^{*}) > 0,$

(H2)Transversality condition $\frac{d △_{3}^{-} (α^{*})}{d α} \neq 0,$

(H3) Nonresonance condition cos(2π/m) ≠ ψ or resonance condition cos(2π/m) = ψ, where m = 3, 4, 5, ··· and $ψ = 1 - 0.5 W (1) \frac{△_{1}^{-} (α^{*})}{△_{2}^{+} (α^{*})}$ .

where

\begin{array}{l} △_{3}^{\pm} (α^{*}) = | (\begin{matrix} 1 & w_{1} & w_{2} \\ 0 & 1 & w_{1} \\ 0 & 0 & 1 \end{matrix}) \pm (\begin{matrix} w_{2} & w_{3} & w_{4} \\ w_{3} & w_{4} & 0 \\ w_{4} & 0 & 0 \end{matrix}) |, \end{array}

\begin{array}{l} △_{2}^{\pm} (α^{*}) = | (\begin{matrix} 1 & w_{1} \\ 0 & 1 \end{matrix}) \pm (\begin{matrix} w_{2} & w_{3} \\ w_{3} & w_{4} \end{matrix}) |, △_{1}^{\pm} (α^{*}) = | 1 \pm w_{4} | . \end{array}

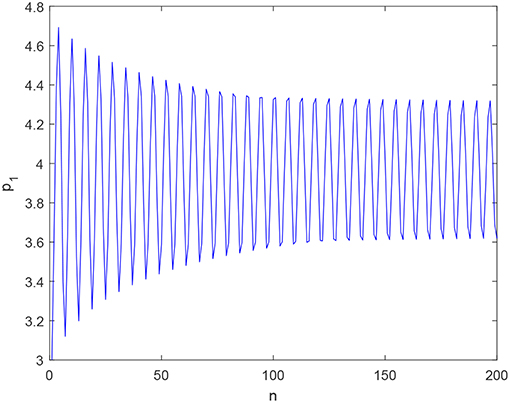
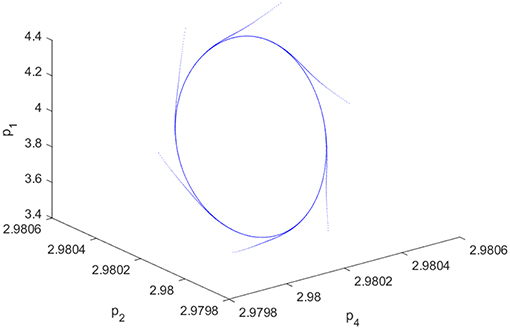
If h = 0.01, d₁ = 8, d₂ = 6, b = 0.01, v₁ = 0.05, v₂ = 0.01, a Hopf bifurcation will occur at α^* = 0.1767. When we adopt a small perturbation Δα = 0.0007, a sufficiently small positive real number, i.e. α = α^* + Δα = 0.176, system (22) has a stable closed invariant curve around the fixed point E₄, as shown in Figures 3, 4. As time goes on with α = 0.1767, Figure 3 demonstrates outputs of firm 1 trend to periodic fluctuation, and Figure 4 demonstrates system (22) convergences to an invariant closed curve. Figures 3, 4 mutually validate the existence of Hopf bifurcation in system (22).

FIGURE 3

Figure 3. Evolution of p₁ with α = 0.176.

FIGURE 4

Figure 4. Phase portrait in (p₁, p₂, p₄)-plane with α = 0.176.

6. 0-1 Test for Chaos

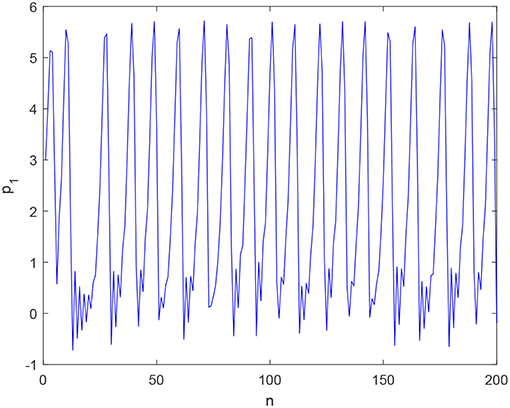
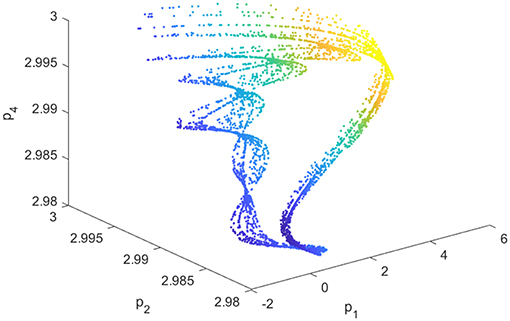
When h = 0.01, d₁ = 8, d₂ = 6, b = 0.01, v₁ = 0.05, v₂ = 0.01, α = 0.2, system (22) is chaotic, as shown in Figures 5, 6. Figure 5 shows that the time series of p₁ irregularly evolutes with time. Figure 6 shows that a chaotic attractor exists in system (22).

FIGURE 5

Figure 5. Evolution of p₁ with α = 0.137.

FIGURE 6

Figure 6. Phase portrait in (p₁, p₂, p₄)-plane with α = 0.137.

Following the 0-1 test algorithm [82–89], we sample 10,000 data points from p₁(n) and set a random number $c \in (\frac{π}{5}, \frac{4 π}{5})$ satisfies (μ(n), ν(n)), as follows

\begin{array}{l} \begin{aligned} μ (n) = \sum_{k = 1}^{n} p_{1} (k) c o s (k c), ν (n) = \sum_{k = 1}^{n} p_{1} (k) s i n (k c) . \end{aligned} & (26) \end{array}

We obtain the 0-1 test value K for chaos as follows:

\begin{array}{l} \begin{aligned} K = median [\frac{cov (ξ, Δ)}{\sqrt{cov (ξ, ξ) cov (Δ, Δ)}}] \end{aligned} & (27) \end{array}

where ξ = (1, 2, 3, …, round(N/10)), Δ = (D_c(1), D_c(2), …, D_c(round(N/10))), the covariance is defined with vectors ξ, Δ of length m by

\begin{array}{l} \begin{aligned} cov (ξ, Δ) = \frac{1}{m} \sum_{k = 1}^{m} [ξ (k) - \frac{1}{m} \sum_{k = 1}^{m} ξ (k)] [Δ (k) - \frac{1}{m} \sum_{k = 1}^{m} Δ (k)], \end{aligned} \end{array}

and

\begin{array}{l} D_{c} (n) = lim_{N \to \infty} \frac{1}{N} \sum_{k = 1}^{N} [{(μ_{c} (k + n) - μ_{c} (k))}^{2} + {(ν_{c} (k + n) - ν_{c} (k))}^{2}] \\ - \frac{1 - cos n c}{1 - cos c} {[lim_{N \to \infty} \frac{1}{N} \sum_{k = 1}^{N} p_{1} (k)]}^{2} \end{array}

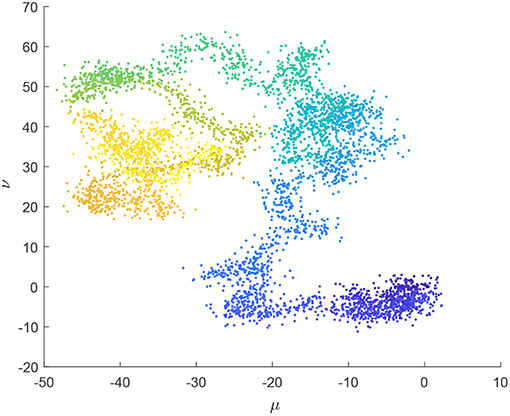
For system (22) with α = 0.137, we obtain K = 0.9977 and plot a phase portrait in (μ, ν)-plane whose trajectories in the (μ, ν)−plane are Brownian-like, which indicate it is chaotic, as shown Figure 7.

FIGURE 7

Figure 7. Phase portrait in (μ, ν)-plane with α = 0.137.

As time goes on with α = 0.137, Figure 5 demonstrates outputs of firm 1 trend to irregular vibration, and Figure 6 demonstrates system (22) has chaotic attractors in (p₁, p₂, p₄)-plane, and Figure 7 demonstrates the motion trajectories of system (22) are Brownian-like in (μ, ν)-plane. Figures 5–7 mutually validate the existence of chaos in system (22).

7. Conclusion

Introducing conformable derivative to a classical continuous Bertrand duopoly game with integer delays, we present a generalized game model with delays, named a continuous time Bertrand duopoly game with fractional delay and conformable derivative. We design a discretization process for conformable systems with fractional delays. Utilizing the proposed discretization process, we obtain a simplified model and get its solutions. At last, we examine the local stability, Hopf bifurcation, and chaos of the game model.

There are some future research directions that deserve our attention. We can apply the modeling approach and discretization process to other scientific researches, such as conformable partial differential equations with delays [90–94], conformable differential games with delays [95]. In addition, we can also develop other discretization methods for conformable system with specific characteristics, such as stochastic, fuzzy, pulse factors.

Data Availability

All datasets generated for this study are included in the manuscript and/or the supplementary files.

Author Contributions

BX and LG: conceptualization. BX, WP, and LG: methodology. BX and WP: software. BX and LG: validation. BX: formal analysis. BX and WP: writing-original draft preparation. BX and LG: writing-review and editing. BX and WP: visualization. BX: supervision, project administration, and funding acquisition.

Funding

This work is supported partly by Natural Science Foundation of Shandong Province (Grant No. ZR2016FM26), National Social Science Foundation of China (Grant No.16FJY008), and National Natural Science Foundation of China (Grant No.11801060).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer ZW declared a shared affiliation, with no collaboration, with the authors BX, WP to the handling editor at time of review.

Acknowledgments

The authors would like to express many thanks to referees for their time and efforts in reviewing this manuscript. Their helpful comments and constructive suggestions greatly improved this manuscript.

References

1. Wei Z, Zhu B, Yang J, Perc M, Slavinec M. Bifurcation analysis of two disc dynamos with viscous friction and multiple time delays. Appl Math Comput. (2019) 347:265–81. doi: 10.1016/j.amc.2018.10.090