- 1Instituto Politécnico Nacional, SEPI ESIME Zacatenco, Mexico City, Mexico
- 2Instituto Politécnico Nacional, Posgrado en Tecnología Avanzada, SEPI-UPIITA, Mexico City, Mexico
The paper is devoted to the spectral properties of one-dimensional Schrödinger operators
with potentials q = q0+qs, where is a regular potential, and is a singular potential with support on a discrete infinite set . We consider the extension of formal operator (1) to an unbounded operator in L2(ℝ) defined by the Schrödinger operator Sq0 with regular potential q0 and interaction conditions at the points of the set . We study the closedness and self-adjointness of . If the set has a periodic structure we give the description of the essential spectrum of operator in terms of limit operators. For periodic potentials q0 we consider the Floquet theory of , and apply the spectral parameter power series method for determining the band-gap structure of the spectrum. We also consider the case when the regular periodic part of the potential is perturbed by a slowly oscillating at infinity term. We show that this perturbation changes the structure of the spectra of periodic operators significantly. This works presents several numerical examples to demonstrate the effectiveness of our approach.
1. Introduction
We consider formal one-dimensional Schrödinger operators
with potentials q = q0 + qs, where is a regular potential and is a singular potential with support on an infinite discrete set . The Schrödinger operator Sq is a far-reaching generalization of the well-known Kronig-Penney Hamiltonian
describing the electron propagation in one-dimensional crystals [1, 2]. There exists an extensive literature devoted to the different spectral problems of one-dimensional Schrödinger operators with singular potentials (see, e.g., [3–9]).
Let be a sequence of points yj ∈ ℝ such that yj < yj+1 for every j ∈ ℤ, ej = (yj, yj+1), j ∈ ℤ, and |ej| = yj+1 − yj, j ∈ ℤ, is the length of ej. We assume that
Let the formal Schrödinger operator (2) have the potential q = q0 + qs, where and
is a singular potential, which is a distribution in with support at . We assume that the functions α(y), β(y) belong to the space with the norm .
Note that the operator Sq coincides with the operator Sq0 on the space . Following the Kurasov paper [9] we consider the extension of to the unbounded operator in L2(ℝ) defined by the Schrödinger operator Sq0 with domain , being
where , , being the Sobolev spaces of the order 2 on the intervals ej, , , and
is a complex 2 × 2-matrix with entries , i, j = 1, 2. For potential (3) the matrix A(y) is of the form
The following results are obtained in the paper:
1. We prove an a priori estimate for the operator Sq0 of the form
This estimate implies that the operator is closed. Moreover, if the potential q0 and the entries of the matrix A (y) are real-valued such that det A (y) = 1 for every , the operator is self-adjoint.
2. Let the set of the singular points of the potential q to have a periodic structure. This means that the set is invariant with respect to the group 𝔾 = ℓℤ, ℓ>0. Let {gm} be a sequence of points of the group 𝔾 tending to ∞. We associate with {gm} the operator-valued sequence . We define the limit operators , which are the limits in some sense of the operator sequences , where Vhu(x) = u(x − h), x ∈ ℝ, h ∈ 𝔾 is the shift operator. Then we give the general description of the essential spectrum in terms of the limit operators.
3. Let every sequence 𝔾 ∋ gm → ∞ have a subsequence 𝔾 ∋ hm → ∞ defining a limit operator . Then we prove that
where is the set of all limit operators of .
4. Periodic structures. Let the potential q0(x), x ∈ ℝ, and the matrix A(y), , be periodic with respect to the group 𝔾 and real-valued. Moreover, we assume that det A (y) = 1 for all . Then is a self-adjoint operator and formula (4) yields
On applying the Floquet transform we obtain that
where is a function defined from a pair of linearly independent solutions φ1, φ2 of the Schrödinger equation Sq0u(x) = λu(x), x∈[0, ℓ), which satisfy the Cauchy conditions φ1(0, λ) = 1, , φ2(0, λ) = 0, , as well as interaction conditions at the points . In the paper we obtain an explicit expression for function D in terms of monodromy matrices associated to the point interactions from the singular potential (3). Entries of monodromy matrices are calculated by means of the SPPS method [10], which allows to consider arbitrary regular potentials q0 satisfying certain smoothness conditions. This approach in turn leads to an effective numerical method for calculating the edges of the spectral bands of Schrödinger operators .
5. Slowly oscillating at infinity perturbations of periodic potentials. We say that a function a ∈ L∞ (ℝ) is slowly oscillating at infinity and belongs to the class SO(ℝ) if
for every compact set K ⊂ ℝ. As above we assume that the set is invariant with respect to the group 𝔾. We apply formula (4) for the investigation of the perturbation of the periodic operators by adding to the potential a slowly oscillating term q1 ∈ SO (ℝ). Let be a periodic operator with respect to the group 𝔾 given by the Schrödinger operator Sq0 with 𝔾-periodic real-valued potential q0 and the 𝔾-periodic real matrices A(y) satisfying det A(y) = 1 for every . We consider the operator , where q1 ∈ SO (ℝ) is a real-valued function. Note that the operator has a band-gap spectrum
The limit operators of the operator are of the form , where . Hence
Applying formula (4) we obtain the essential spectrum of the operator as
where , . Above formula shows that if the oscillation of q1 at infinity is large enough, that is ak+1 − bk < Mq1 − mq1, the gap (bk, ak+1) of the spectrum of periodic operator disappears in . Hence, the slowly oscillating perturbations of the periodic potentials can substantially change the structure of the essential spectrum of .
6. Numerical calculation of the spectra of Schrödinger operator with periodic point interactions. We consider several examples for showing the application of the theory here presented, and calculate approximations of their corresponding spectra.
Notations
We will use the standard notations: C∞ (ℝ) is the space of infinitely differentiable functions on ℝ, is a subspace of C∞(ℝ) of functions with all bounded derivatives on ℝ, is a subspace of C∞(ℝ) consisting of functions with compact support, is the space of distributions under . We denote by Hs(ℝ), s ∈ ℝ, the Sobolev space with the norm
where û(ξ) is the Fourier transform of u(x). If Ω ⊆ ℝ is an open set, then Hs (Ω) is the space of restrictions on Ω of functions on ℝ with the standard norm of restriction.
If exist, we denote the one-sided limits of f at x0 by
and by the (finite) jump of f at x0.
Let X, Y be Banach spaces, then is the space of all bounded linear operators acting from X into Y, and is a subspace of consisting of all compact operators acting from X into Y. If X = Y we simply write and , respectively.
Let A be an unbounded closed operator in a Hilbert space H with domain Dom(A) dense in H. The essential spectrum spessA of operator A is the set of numbers λ ∈ ℂ for which the operator A − λ is not Fredholm as an unbounded operator in H. If A is self-adjoint in H then its discrete spectrum is given by spdisA = spA\spessA, where spA denotes the spectrum of A.
2. One-Dimensional Schrödinger Operators With Point Interactions
In this section we consider one-dimensional Schrödinger operators with potentials involving a countable set of point interactions and investigate some of their functional properties such as closedness, self-adjointness, Fredholmness, as well as their essential spectrum.
2.1. A Self-Adjoint Extension of Schrödinger Operators With a Point Interaction
Let us consider a singular distribution
which represents a point interaction with support at x = 0. By the definitions
and
it follows that the action of qs on the test functions in is defined by
In the study of Schrödinger operators involving point interactions we define a space of discontinuous test functions at x = 0,
where ℝ±: = {x ∈ ℝ: x≷ 0}, and are the spaces of restrictions on of functions in . Continuations of δ- and δ′-distributions on functions in D0(ℝ) are defined as follows
If it follows that and .
Let us consider the formal one-dimensional Schrödinger operator
where q = qs + q0, with as a regular potential, and as a singular potential defined in (5). Note that operator Sq coincides with operator Sq0 on the space . A domain Dom(Sq) of operator Sq as an unbounded operator in L2(ℝ) must consist of functions u∈L2(ℝ) such that . This condition is fulfilled by functions u ∈ D0 (ℝ) satisfying at the origin the following interaction conditions
where matrix A0 satisfies det A0 = 1.
The embedding theorem for Sobolev space implies that if the one-sided limits u(0±), u′(0±) exist, and the jumps [u]0, are well defined. Let be the unbounded operator in L2(ℝ) defined by the Schrödinger operator with domain where
If is a real-valued function, A0 is a real 2 × 2-matrix, and det A0 = 1, then is a self-adjoint operator. We will prove this result in a more general setting in forthcoming Theorem 2. Thus the unbounded operator generated by the Schrödinger operator Sq0 with domain is a self-adjoint extension of formal Schrödinger operator Sq0+qs.
Schrödinger operators involving point interactions of the form have been considered as norm resolvent approximations of certain families of Schrödinger operators with potentials depending on parameters tending to zero. The norm resolvent convergence of such families of operators was established and a class of solvable models that approximate the quantum systems was obtained in the works [11–13].
2.2. Properties of Schrödinger Operators With a Countable Set of Point Interactions
Let be a sequence of real numbers such that yj < yj+1 for every j ∈ ℤ. We denote by ej: = (yj, yj+1), j∈ℤ, the corresponding interval between a pair of adjacent points yj and yj+1. The interval ej has a length |ej|: = yj+1 − yj, such that
We denote
Let us consider the Schrödinger operator Sq defined in (6) with the regular potential , and the singular potential
which is a distribution in with support at . We assume that , where the space consists of all bounded complex-valued functions on the set , which is equipped by the norm . Note that the operator Sq coincides with the Schrödinger operator on the space . Following the ideas of the work [9], the operator Sq defined on is extended to an unbounded operator in L2(ℝ) defined by the Schrödinger operator Sq0 with domain , where is a subspace of H2(Γ) given by
where
are complex 2 × 2-matrices with entries (i, j = 1, 2). In the case of potential (7), the corresponding matrices are of the form
which satisfy det A (y) = 1, for every .
If the conditions:
1. regular potential , and
2. matrices are such that for every
are fulfilled, then the operator Sq0 is bounded from into L2(ℝ). Let us consider the following results for Schrödinger operators involving a countable set of point interactions.
Theorem 1 (An a priori estimate). Let , and conditions (1), (2) be satisfied. Then, there exists a constant C>0 such that for every function the following estimate
holds.
Proof. A priori estimate (8) is proved similarly as in the theory of general boundary-value problems (see, e.g., [14]), but instead of a finite partition of unity we use a countable partition of unity of finite multiplicity. The proof is similar to that of Theorem 3.1 in Rabinovich [15].
Theorem 1 implies the following propositions.
Proposition 1 (Closedness). Let conditions (1), (2) hold. Then, the operator is closed in L2(ℝ).
Proposition 2 (Parameter dependent Schrödinger operators). Let
be a Schrödinger operator acting from into L2(ℝ). We assume that the entries of matrices A(y), , are real-valued, and liminfy → ∞|a12(y)| > 0 or there exists a finite set such that a12(y) = 0 for every . Then, there exists μ0 > 0 such that the operator is invertible for every μ ≥ μ0.
Proof: To prove this proposition we follow the approach of the well-known paper [16] where the authors studied general elliptic boundary-value problems depending on a parameter in bounded domains in ℝn. Similarly to the proof of Theorem 1, here we use a partition of unity and construct local inverses depending on a parameter, and then we form the global inverse operator by sticking these inverses for large values of the parameter. Unlike the paper [16], here we use a countable partition of unity of finite multiplicity, and follow the proof of Proposition 2 in Rabinovich [17].
Theorem 2 (Self-adjointness). Let be real-valued, and let matrices possess real-valued entries . We assume: (i) liminfy → ∞|a12(y)| > 0 or there exists a finite set such that a12(y) = 0 for every ; (ii) det A(y) = 1, for every . Then, the unbounded operator defined by the Schrödinger operator with domain is self-adjoint in L2(ℝ).
Proof: Let . On applying integration by parts twice we obtain
Note that
where we have used the condition det A (y) = 1. Hence, the operators and Sq0 with domain are symmetric operators in L2(ℝ). It follows from Proposition 2 that there exists μ0 > 0 such that is an isomorphism. To prove that with domain is a self-adjoint operator in L2(ℝ) we have to show that . Since is a symmetric operator . Assume that , then . Since is an isomorphism, there exists such that . Since we obtain that . Hence
Therefore, and . Thus, is a self-adjoint operator in L2(ℝ) with domain . Note that the operator of multiplication by is strongly dominated by the operator Sq0 (see, e.g., [18, p. 73]). Hence, with domain is a self-adjoint operator.
2.3. Fredholm Property and Essential Spectrum of Schrödinger Operators With Point Interactions
In this subsection we give the necessary and sufficient conditions of Fredholmness for Schrödinger operators with point interactions in terms of limit operators. We apply these results to the description of the essential spectrum of the corresponding unbounded operators . Through this subsection we assume that the sequence of points where the singular potential qs is supported is periodic with respect to the group 𝔾 = ℓℤ, ℓ > 0. We also assume that matrices are periodic with respect to 𝔾.
Definition 1. A potential is said to be rich if for every sequence g = (gm), 𝔾 ∋ gm → ∞, there exists a subsequence h = (hm), hm → ∞, and a limit function such that for every segment [a, b] ⊂ ℝ
Definition 2. The Schrödinger operator defined by
with a limit function replacing the rich potential q0 is called a limit operator of . The set of all limit operators of Sq0 is denoted by Lim(Sq0).
Let such that 0 ≤ φ(x) ≤ 1, where φ(x) = 1 if , and φ(x) = 0 if |x|≥1. Let φR(x) = φ(x/R), and ψR(x) = 1−φR(x).
Theorem 3. Let be a rich potential, and let matrices be 𝔾-periodic. Then is a Fredholm operator if and only if all limit operators are invertible.
Proof: One can prove that the operator is locally Fredholm, that is for every R > 0 there exist operators such that
where , and since Sq0 is an elliptic operator. Hence, in order to prove that is a Fredholm operator we have to study the local invertibility of Sq0 at infinity, i.e., we have to prove that there exists R0 > 0 and operators such that
Let μ0 > 0 be such that the operator is an isomorphism. We set
It is easy to prove that is locally invertible at infinity if and only if is locally invertible at infinity. For the study of local invertibility at infinity we use the results of the book [19], and the work [20].
Let , and ϕt(x) = ϕ(tx), t∈ℝ. Then it is easy to prove that
that is, belongs to the C*-algebra of so-called band-dominated operators in L2(ℝ) (see, e.g., [20]). We introduce the limit operators of as follows. For 𝔾 ∋ hm → ∞ let Vhmu(x): = u(x−hm) be the corresponding sequence of shift operators. We say that is a limit operator defined by the sequence h = (hm) if
for every . One can see that
Formulas (9), (10) imply that
Moreover, since the potential q0 is rich the operator is rich, that is, every sequence g = (gm) of 𝔾 tending to infinity has a subsequence h = (hm) tending to infinity that defines the limit operator . It follows from the results of Rabinovich et al. [19] and Lindner and Seidel [20] that the operator is locally invertible at infinity if and only if all limit operators are invertible. Since is an isomorphism, this yields the statement of the theorem.
Theorem 3 leads to the following description of the essential spectrum of operator .
Theorem 4. Let be a rich potential, and let the matrices be 𝔾-periodic. Then
where is the limit operator of defined as an unbounded operator in L2(ℝ), generated by the Schrödinger operator with domain .
3. Spectral Analysis of Periodic Schrödinger Operators With Point Interactions
In this section we study the band-gap spectra of periodic Schrödinger operators with point interactions by using the Floquet transform (see e.g., [21]). We also analyze the case when the regular potential q0 is perturbed by a slowly oscillating at infinity term by means of the limit operators method, and provide expressions for the essential spectrum of corresponding Schrödinger operator.
3.1. Periodic Schrödinger Operators With Point Interactions
From now on we will assume that:
1. the sequence of points on which the singular potential qs is supported is periodic with respect to the group 𝔾 = ℓℤ, ℓ>0;
2. the matrices are periodic with respect to the group 𝔾, that is, A(y +g) = A (y) for every g ∈ 𝔾 and . The entries of the matrices are such that det A (y) = 1 for every ; and
3. the potential q0 is a real-valued, piecewise continuous function, periodic with respect to the group 𝔾.
Let Γ0: = [0, ℓ), and 𝔹 = [−π/ℓ, π/ℓ) be the reciprocal unit cell (also known as Brillouin zone) of Γ0. Let be the set of points of discontinuity inside Γ0, which satisfy 0 < y1 < ⋯ < yn < ℓ. We also assume that the finite jumps [q0]yj, not necessarily zero, are well-defined.
From conditions (1–3) and Theorem 3 it follows that the operator with domain is self-adjoint in L2(ℝ). Moreover, the operator Sq0 is invariant with respect to the shifts on the elements of the group 𝔾, that is
for every g ∈ 𝔾. Since VgSq0 = Sq0Vg, and from (11), it yields that , and . In addition, the operator Sq0 is semi-bounded from below, that is
where . This implies that
We introduce the Hilbert space of vector-valued functions with components in , which is equipped by the norm
The Floquet transform is the map defined for functions f that decay sufficiently fast by
where the parameter θ is often called the quasi-momentum. The Floquet transform is an isometry from L2(ℝ) to H, whose inverse is given by
Let us consider the problem
where λ ∈ ℝ is the spectral parameter. The Floquet transform applied to (12) gives a spectral problem depending on the parameter θ ∈ 𝔹, defined by the differential equation
with the interaction conditions at the discontinuity points
and the quasi-periodic conditions
The operator is represented as the orthogonal sum
where
For each θ ∈ 𝔹, the operator defines an unbounded operator in with domain , where
Operators , θ ∈ 𝔹, with domain have discrete spectra
where λj(θ) are continuous functions on 𝔹. Expression (13) implies that
If the image of the Brillouin zone 𝔹 under λj is [aj, bj], aj ≤ bj, j ∈ ℕ, then formula (14) gives
that is, the spectrum of Schrödinger operator with 𝔾-periodic potential q0 involving point interactions has a band-gap structure.
3.2. Spectral Analysis of Periodic Schrödinger Operators With Point Interactions
For each θ ∈ 𝔹 we define the spectral problem
Solutions of this problem are sought in the form
where C1, C2 are arbitrary coefficients, and φ1, φ2 are linearly independent solutions of the Schrödinger equation
satisfying the interaction conditions
as well as the initial conditions
By the Liouville identity, the Wronskian of φ1 and φ2 satisfies
From the quasi-periodic property
we obtain the following system of equations
with C1, C2 as unknowns. System (17) implies that is an eigenvector of the monodromy matrix
associated to the eigenvalue μ: = eiθℓ. In order for system (17) to possess non-trivial solutions its determinant must vanish, that is
This leads to the dispersion equation
where
Equation (18) has solutions of the form μ: = eiθℓ, θ ∈ 𝔹, if and only if |D(λ)| ≤ 1. Hence, the spectrum of is given by
and the edges of the spectral bands of are solutions λedge ∈ ℝ of the equation
3.3. Periodic Potentials Perturbed by Slowly Oscillating at Infinity Terms
A function a ∈ L∞ (ℝ) is slowly oscillating at infinity if the limit
holds for every compact set K ⊂ ℝ. We denote by SO (ℝ) the class of such functions. One can prove (see, e.g., [19, Chap. 3.1]) that all limit functions ah of a ∈ SO (ℝ) defined by the sequence 𝔾 ∋ hm → ∞ are real constants.
Let us consider a Schrödinger operator with a perturbed potential q = q0+q1 consisting of a periodic part satisfying conditions (3), and a real-valued perturbation q1 ∈ SO (ℝ). The result of Theorem 4 can be used for analyzing the essential spectrum of . Note that the spectrum of operator has a band-gap structure according to (15). The limit operators of are of the form , where . Therefore
On considering formula (11) and previous expression we obtain the essential spectrum of perturbed operator , that is
where
Formula (19) implies that some spectral bands of may overlap depending on the intensity of the perturbation q1. Let , l ∈ ℕ, be a gap of , hence if the relation
holds the gap will disappear due to the merging of the adjacent bands. If condition (20) is satisfied for all l ∈ ℕ, all spectral gaps of will disappear resulting a continuous spectrum, that is
4. Dispersion Equation for Periodic Schrödinger Operators With Point Interactions
In this section we determine the function D(λ) from a set of monodromy matrices specified at the points where the singular potential is supported in the fundamental domain Γ0. We also apply the spectral parameter power series method [10] to derive a numerical method for calculating the spectral bands of Schrödinger operators with arbitrary regular potentials q0 satisfying certain smoothness conditions.
4.1. Calculation of Function D(λ) in Terms of Monodromy Matrices
We begin by determining a general solution of the equation
satisfying the interaction conditions
at the points of discontinuity (j = 1, ⋯ , n). By abusing the notation, we set y0≡0, and yn+1≡ℓ. The interval between two adjacent points of discontinuity yj, yj+1 is denoted by ej = (yj, yj+1) (j = 0, ⋯ , n). Let ϕ1, j, ϕ2, j (j = 0, ⋯ , n) be a pair of linearly independent solutions of Equation (21) on the interval ej, which satisfy the Cauchy conditions
From these solutions we define the monodromy matrices
Let uej = u|ej (j = 0, ⋯ , n) be the restriction of solution u of Equation (21) on ej, which can be written as
Hence, on the full interval [0, ℓ), a general solution of Equation (21) is given by the piecewise continuous function
where the coefficients uej(yj) and (j = 1, ⋯ , n) are given in a matrix form by
The restriction uen and its derivative evaluated at x = ℓ gives the matrix relation
By plugging formulas (23) and (24) we obtain the expression
where T: = Mn, n+1AnMn−1, n⋯A2M1, 2A1M0, 1 is a 2 × 2-matrix called the transmission matrix.
Therefore, solutions φ1 and φ2 that fulfill conditions (16) satisfy the matrix equations
thereby the function D(λ) can be written in the form
4.2. Some Solvable Models With Periodic Singular Potentials
If the potential q0 vanishes identically on ℝ it is possible to obtain exact solutions of Equation (21) on the interval ej = (yj, yj+1). One can see that , are solutions of the Schrödinger equation for a free-particle
with energy λ, which satisfy Cauchy conditions (22). In this case, monodromy matrices read
Periodic Potential With Only δ-Distributions
The periodic potential involving only Dirac delta distributions
defines at each singular point the interaction matrix
Let be the Hamiltonian defined by the ℓ-periodic potential qδ(x). In this case , that is, y0 = 0, y1 = ℓ/2, and y2 = ℓ, thereby the transmission matrix reads
hence, the spectrum of Hamiltonian consists of λ ∈ ℝ satisfying
This is the so-called Kronig-Penney model (see [1, 2] and [4, §III.2.3]) that describes the non-relativistic interaction of electrons in a fixed crystal lattice, with ions represented by δ-distributions.
Periodic Potential With Only δ′-Distributions
Consider the periodic singular potential
with the following matrix
defined at the each singular point . Like in the previous case only one point interaction lies inside the fundamental domain Γ0, i.e., . Let be the Hamiltonian defined by the periodic potential . The corresponding transmission matrix is
Hence, the spectrum of Hamiltonian consists of λ ∈ ℝ satisfying
This is the analogous of the Kronig-Penney relation (28), [4, Chap. III.3].
The analysis of problems involving δ′-interactions has gained interest over the years [22–24]. In particular, the spectral analysis of Wannier-Stark Hamiltonians including a countable set of δ′-interactions lead to models for describing high-energy scatterers with vanishing transmission amplitudes as the wave-number k → ∞ (see, e.g., [25–29]).
4.3. Spectral Parameter Power Series Method for the Calculation of Function D(λ)
In previous subsection it was defined a set of monodromy matrices for the points from which a transmission matrix T is defined. This leads to a neat expression for the function D(λ), defined in (25). Given a potential q0 with discontinuities at the points , obtaining solutions ϕ1, j, ϕ2, j (j = 0, ⋯ , n) of Schrödinger equation (21) in the intervals ej (j = 0, ⋯ , n) could be a challenging task. However, it is always possible to apply some numerical method for calculating approximations , of the solutions. Nonetheless, if the potential q0 satisfies certain smoothness conditions it is possible to obtain exact solutions of the equation in the form of power series of the spectral parameter. Here we employ the SPPS method [10, 30] for constructing the entries of transmission matrix T from which we construct function D(λ).
Let u0, j be a particular solution of the equation
such that , where q0, j: = q0|ej (j = 0, ⋯ , n) is the restriction of potential q0 on the interval ej. Then a general solution of (21) on ej (j = 0, ⋯ , n) has the form
where c1, c2 are arbitrary coefficients,
with the functions , defined by the recursive integration
Moreover, series (29) converge uniformly on . From the recursive integration procedure we deduce that solutions u1, j, u2, j satisfy the conditions
We can see that the following solutions
fulfill conditions (22). Hence, the monodromy matrices can be calculated from the matrix expressions
where
In the numerical implementation of the problem, power series (29) should be truncated up to a finite number of terms. Let , be the truncated versions of u1, j, u2, j, respectively, which are given by the sums
From these approximate solutions we construct approximate matrices (j = 0, ⋯ , n), and approximate monodromy matrices as follows
from which we obtain an approximation of the transmission matrix
thereby, function D(λ) is approximated by
Regarding the accuracy of approximate solutions , , a rough estimation of the tail of u1, j is given by (see [10])
where
The corresponding estimation of the tail of u2, j involves the tail of the function . According to these expressions, the error associated to mainly depends on the value of the spectral parameter λ, and on the length of the interval ej. If a number N of terms does not provides the required accuracy, the interval ej can be subdivided, and the resulting initial value problems should be sequentially solved. The particular solution u0, j also influences the accuracy of , . This solution can be obtained by means of numerical techniques, or by the SPPS method itself [10].
Given that the error increases for the large values of λ, a shifting of the spectral parameter (29) can be implemented for reducing the error. More precisely, if u0, j is a solution of the equation
corresponding to λ = λ0, then the series
satisfy equation (21) in the interval ej (j = 0, ⋯ , N).
5. Numerical Examples
In this section we employ the SPPS approach for the calculation of the band edges of the spectral bands of periodic Schrödinger operators with point interactions. For this aim we use the approximate version of the function D(λ) given by (33), and fix N = 200 as the number of terms in the approximate solutions and . This implies calculating finite sets of formal powers and according to recursive integration procedure (30). We employ of Wolfram Mathematica for the numerical study of the spectra of the examples considered in this section. For accurately handling the upper formal powers, even the double-precision floating-point format is not enough, nonetheless Wolfram Mathematica provides the instruction SetPrecision[] for increase the precision of the numbers. In this work we fix the precision of numerical results up to 100 decimal places. For the numerical implementation of our approach we distinguish two main parts, namely, calculating the formal powers, and searching for the zeros of the equation
that define the band edges.
For calculating the formal powers, the integrands are numerically handled by an array of their values at a discrete set of M + 1 points. These values are interpolated by cubic splines with the instruction Interpolation[], and then integrated by the instruction Integrate[]. Here we have segmented each into M = 2, 000 parts. Once formal powers are computed, approximate monodromy matrices are determined from the functions and , which were calculated at the points of Ωj. In turn these matrices lead to the approximate transmission matrix that defines the function according to (33). Calculating the band edges reduces to calculating the polynomial roots of . We use the instruction FindRoot[] to search for numerical solutions of the polynomial equations near the real axis of the complex λ-plane. We prescribe a small tolerance ε>0 such that if the imaginary part of a root λj satisfies |ℑλj| ≤ ε then its real part can be considered as an approximate band edge, that is, .
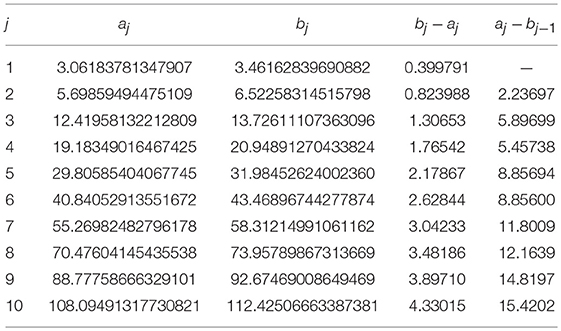
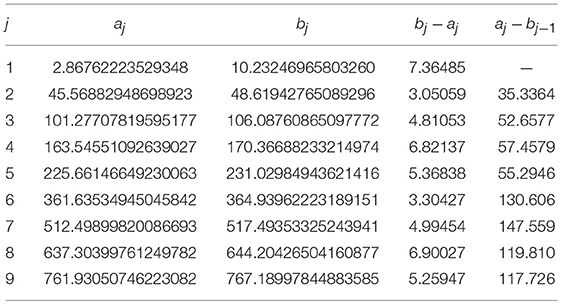
Example 1 (Kronig-Penney model). Let us consider the Kronig-Penney model with the singular potential specified by (26). It was shown that transmission matrix in this case reads T(λ) = M1, 2(λ)AαM0, 1(λ), where matrix Aα is defined in (27). For showing the accuracy of the SPPS approach, in this example we compare the zeros from of the approximate equations and those obtained from the exact Kronig-Penney relation (28), where we take α = 10 and ℓ = 1, see Figure 1. In Table 1 we can see that the results coincide in at least eight decimal places in the least accurate results, and up to fourteen decimal places in the most accurate result. The loss in accuracy is due to the fact that truncated power series with center at λ = 0 depart from exact solutions as |λ| increases. The accuracy of the results can be improved by either increasing the number of subdivisions of the intervals , by increasing the number N of terms of the truncated series, or by means of the shifting of the spectral parameter, in which power series are expanded about another center λ0 ≠ 0, as was explained above.
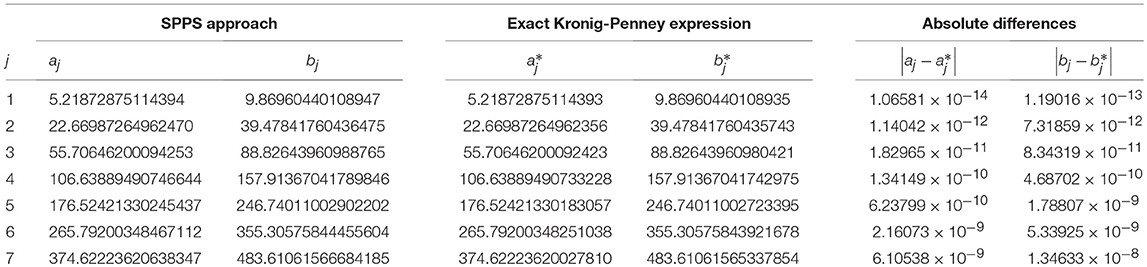
Table 1. Some spectral bands of the Kronig-Penney model calculated from the SPPS approach and the exact expression (28).
Example 2 (Potential without point interactions). Suppose that operator Sq has a potential q consisting on only the regular part q0 defined by
It follows that n = 0, ℓ = 4, and . Operator Sq0 defines an unbounded operator in L2(ℝ) with domain H2(ℝ). The transmission matrix is given by T = M0, 1, where the monodromy matrix
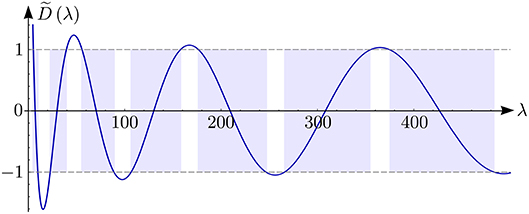
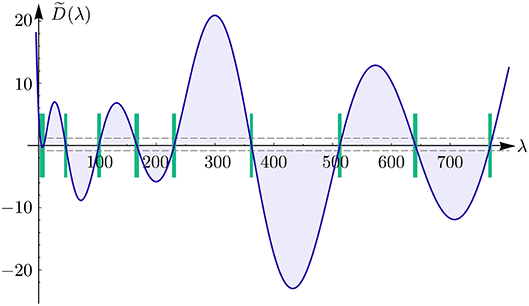
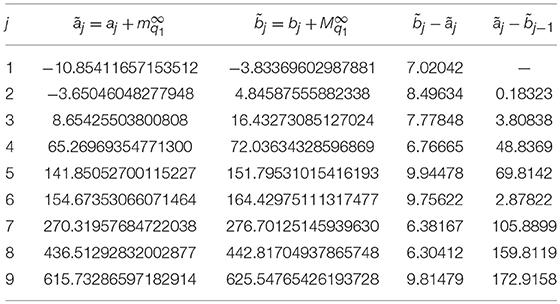
is defined from a pair of solutions ϕ1, ϕ2 of the equation Sq0u = λu, 0 < x < ℓ, satisfying the Cauchy conditions ϕ1(0;λ) = 1, , ϕ2(0;λ) = 0, . In this example the function is approximated by the SPPS approach described in subsection 4.3. In Figure 2 we can see the plot of the approximate function and its intersections with the horizontal lines ±1 that define the spectral bands [aj, bj]. In Table 2 we observe some spectral bands of , whose edges were calculated from the zeros of the equations . The fourth and fifth columns of the table show the widths of the bands and the gaps, respectively. We can see a monotonically increasing of the band widths, while the gaps monotonically decrease. Such a behavior is a characteristic of smooth periodic potentials (see, e.g., [31]) The considered potential q0 is smooth except at a countable set of points of the form xk = kℓ, k ∈ ℤ, nonetheless the potential is continuous at these points.
Example 3 (Potential including δ-interactions). Let the potential q of Schrödinger operator Sq be a π-periodic function defined by
where the regular potential is the piecewise continuous periodic function
It follows that n = 1, ℓ = π, and . The transmission matrix is given by T(λ) = M1, 2(λ)A1M0, 1(λ), where
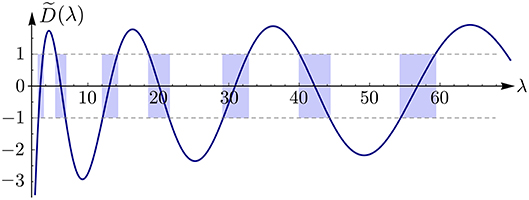
The approximation of function obtained by the SPPS approach is plotted in Figure 3. In Table 3 we observe some spectral bands of , whose edges were calculated from the zeros of the equations . According to the fourth and fifth columns of the table we can see that both the band widths and gaps have a tendency to grow. Moreover, the band-to-gap ratio also has an exponential tendency to grow. This characteristic is shared by operators with singular potentials including point interactions (cf. [25]).
Example 4 (Potential including δ′-interactions). Let us consider a periodic potential q involving δ′-interactions
where the regular potential is defined by
In this example n = 2, ℓ = 1, and . The transmission matrix is given by
where
The approximate function obtained from the SPPS approach is plotted in Figure 4. In this case the spectral bands are indicated by thin vertical strips in the plot. In Table 4 we observe some spectral bands of calculated from the zeros of the equations . The table shows a narrowness of the bands compared with the large gaps, which can be understood on the fact that at the high values of λ the unit cells of the periodic problem get decoupled since δ′-interaction approximates to Neumann conditions [25, 26]. We also observe that the peaks of the plot of are dominated by a straight line with positive slope, which accounts for the increasing gaps of the spectrum. The considered problem has spectral properties that resemble those of Wannier-Stark ladders for a periodic array of δ′-scatterers [26]. These observations agree with the spectra of systems with periodically distributed δ′-distributions (see, e.g., [22, 27, 28]).
Example 5 (Potential including both δ- and δ′-interactions). In this example we consider the following periodic potential
which involves both δ- and δ′-interactions, where the regular potential is given by
In this case n = 2, ℓ = 1, , and the transmission matrix is given by expression (37), where the matrices
On applying the SPPS approach we calculate the approximate function , which is shown in Figure 5. From the zeros of the equations we obtain the spectral bands of , which are shown in Table 5. The spectrum of this operator shares common characteristics with the previous spectra, for instance, the large gap-to-band ratio due to the presence of δ- and δ′-interactions.
Previous examples show the applicability of the SPPS method in the numerical determination of the spectral bands of periodic Schrödinger operators with point interactions. For numerically simulating the influence of a slowly oscillating at infinity potential q1 on the gaps of the essential spectrum of the operators it is necessary to determine the numbers and , and employ formula (19) for calculating the essential spectrum of the perturbed operator.
Example 6 (Perturbed periodic potential). Let , ε ∈ (0, 1), A > 0, x ∈ ℝ. Since q1 ∈ SO (ℝ), it is easy to see that for every sequence ℝ∋ hm → ∞ the limit is a real constant. The limiting values satisfy for every real sequence h = {hm}, hence, and .
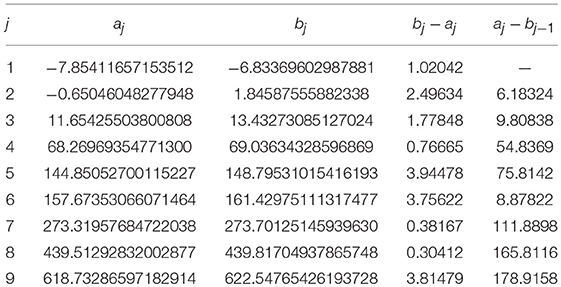
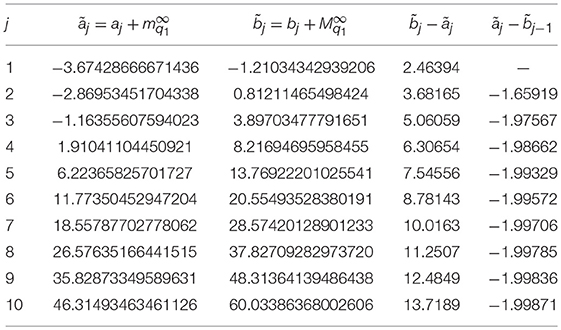
Let us consider the previous Example 2 and suppose that its regular potential q0 defined in (34) is perturbed by the potential q1 ∈ SO (ℝ) with A = 1. In Table 6 we observe the influence of this slowly oscillating function on the spectrum of the unperturbed operator . We observe the broadening of the bands and their corresponding overlapping when the gaps are negative. Since the gaps of the unperturbed problems are monotonically decreasing all the bands will overlap producing a continuous spectrum
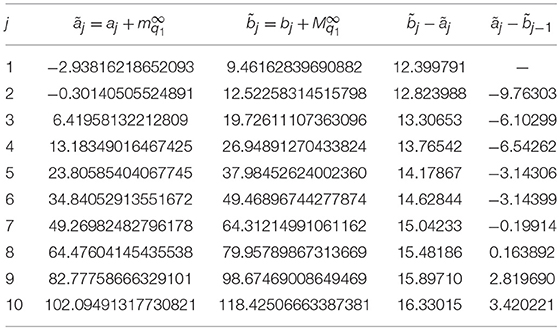
Now, let us consider the previous Example 3, and suppose that its regular potential q0 defined in (35) is perturbed by a more intense perturbation q1∈SO(ℝ) with A = 6. The bands of the resulting perturbed operator are shown in Table 7. In this case the first seven bands of the spectrum overlap, yielding the merged band
From the eighth band, the gaps of the spectrum are open. Hence, in order to close more gaps, it is necessary to increase the intensity of the perturbation.
Finally, on considering the potential (36) from Example 4 and the perturbation q1 ∈ SO (ℝ) with A = 3 we obtain the spectral bands shown in Table 8. In this case, though the bands get broader, none of them overlap with the given perturbation.
6. Conclusions
In this work we have approached one-dimensional Schrödinger operators with point interactions from their corresponding self-adjoint extensions. On assuming that the point interactions are supported on an infinite countable set with a periodic structure we were able to employ the limit operators method for analyzing their essential spectra. If the regular potentials are periodic the Floquet-Bloch theory leads to a formula defining the band-gap spectra of the periodic operators, which is given in terms of a function D(λ). This function is obtained from the monodromy matrices specified at the points where the singular potential is supported. In this work the function D(λ) is determined by the SPPS method, which allows to consider arbitrary regular potentials q0 satisfying certain smoothness conditions, and to derive numerical methods for calculating the band edges of spectra of periodic problems involving point interactions.
We also considered the case when periodic problems are perturbed by slowly oscillating at infinity terms, which can model impurities in the crystals. The perturbed problems are also approached by the limit operators method, which gives a neat formula for their essential spectra. The spectral analysis of perturbed periodic problems relies on a pair of numbers and that depend on the perturbation q1 ∈ SO(ℝ) specified in the problem. These numbers, in general, lead to the broadening (narrowing) of the bands (gaps), which may change significantly the spectra of the operators. The SPPS approach together with the determination of the numbers , give a simpler way for determining the spectra of perturbed periodic problems.
The applicability of the SPPS method and the limit operators method is shown by the numerical examples considered in this work that involved δ- and δ′-interactions as well as a periodic regular potential q0. The accuracy of the results relies on the uniform convergence of power series of the spectral parameter that define the solutions of the involved Schrödinger equations, so that an increasingly number N of terms in the truncated series will reduce the associated errors in the numerical values. Finally, the theory developed in this work can be used for analyzing photonic crystals and electromagnetic waveguides with periodic refractive profiles, as well as quantum problems involving periodic potentials.
Data Availability
All datasets generated and analyzed for this study are included in the manuscript and the supplementary files.
Author Contributions
VR conceived the idea of the paper and developed the theoretical formalism. VB-F performed the analytic calculations, designed the examples, and analyzed the numerical data. VR, VB-F, and LO contributed to the final version of the manuscript.
Funding
VB-F acknowledges CONACyT for support via grant 283133.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Kronig RdeL. The quantum theory of dispersion in metallic conductors. Proc R Soc Lond A. (1929) 124:409–22. doi: 10.1098/rspa.1929.0125
2. Kronig RdeL, Penney WG. Quantum mechanics of electrons in crystal lattices. Proc R Soc Lond A. (1931) 130:499–513. doi: 10.1098/rspa.1931.0019
3. Albeverio S, Kurasov P. Singular Perturbations of Differential Operators. Solvable Schrodinger Type Operators. Cambridge: Cambridge University Press (2000). p. 429.
4. Albeverio S, Gesztesy F, Høegh-Krohn R, Holden H. Solvable Models in Quantum Mechanics. 2nd edn. Providence, RI: AMS Chelsea Publishing (2004). p. 488.
5. Berezin FA, Faddeev LD. A remark on Schrödinger operators with a singular potentials. Soviet Math Dokl. (1961) 2:372–5.
6. Gadella M, Negro J, Nieto L M. Bound states and scattering coefficients of the −aδ(x)+bδ′(x) potential. Phys Lett A. (2009) 373:1310–3. doi: 10.1016/j.physleta.2009.02.025
7. Kostenko AS, Malamud MM. One-dimensional Schrödinger operator with δ-interactions. Funct Anal Appl. (2010) 44:151–5. doi: 10.1007/s10688-010-0019-9
8. Kurasov P. Distribution theory for discontinuous test functions and differential operators with generalized coefficients. J Math Anal Appl. (1996) 201:297–323. doi: 10.1006/jmaa.1996.0256
9. Kurasov P, Larson J. Spectral asymptotics for Schrödinger operators with periodic point interactions. J Math Anal Appl. (2002) 266:127–48. doi: 10.1006/jmaa.2001.7716
10. Kravchenko VV, Porter MR. Spectral parameter power series for Sturm-Liouville problems. Math Meth Appl Sci. (2010) 33:459–68. doi: 10.1002/mma.1205
11. Golovaty Y. 1D Schrödinger operators with short range interactions: two-scale regularization of distributional potentials. Integr Equat Oper Theor. (2013) 75:341–62. doi: 10.1007/s00020-012-2027-z
12. Golovaty YD, Hryniv RO. Norm resolvent convergence of singularly scaled Schrödinger operators and δ′-potentials. Proc R Soc Edinb A. (2013) 143:791–816. doi: 10.1017/S0308210512000194
13. Golovaty Y. Schrödinger operators with singular rank-two perturbations and point interactions. Integr Equat Oper Theor. (2018) 90:57. doi: 10.1007/s00020-018-2482-2
14. Agranovich MS. Elliptic boundary problems. In: Agranovich MS, Egorov YuV, Shubin MA (eds.). Partial Differential Equations IX, Elliptic Boundary Value Problems. Berlin: Springer (1997). p. 1–144.
15. Rabinovich VS. Elliptic differential operators on infinite graphs with general conditions on vertices. Complex Var Ellipt. (2019). (In press) doi: 10.1080/17476933.2019.1575824
16. Agranovich MS, Vishik MI. Elliptic problems with a parameter and parabolic problems of general type. Russ Math Surv. (1964) 19:53. doi: 10.1070/RM1964v019n03ABEH001149
17. Rabinovich VS. Essential spectrum of Schrödinger operators on periodic graphs. Funct Anal Appl. (2018) 52:66–9. (Translated from Funktsional Anal Prilozhen. (2018) 52:80–84.) doi: 10.1007/s10688-018-0210-y
18. Birman MSh, Solomjak MZ. Spectral Theory of Self-Adjoint Operators in Hilbert Space. Dordrecht: Reidel Publishing Company (1987). p. 301.
19. Rabinovich VS, Roch S, Silbermann B. Limit Operators and Their Applications in Operator Theory. Basel: Birkhäuser (2004). p. 392.
20. Lindner M, Seidel M. An affirmative answer to a core issue on limit operators. J Funct Anal. (2014) 267:901–17. doi: 10.1016/j.jfa.2014.03.002
21. Kuchment P. An overview of periodic elliptic operators. Bull Amer Math Soc. (2016) 53:343–414. doi: 10.1090/bull/1528
22. Barseghyan D, Khrabustovskyi A. Gaps in the spectrum of a periodic quantum graph with periodically distributed δ′-type interactions. J Phys A Math Theor. (2015) 48:255201. doi: 10.1088/1751-8113/48/25/255201
23. Cheon T, Shigehara T. Realizing discontinuous wave functions with renormalized short-range potentials. Phys Lett A. (1998) 243:111-6. doi: 10.1016/S0375-9601(98)00188-1
24. Seba P. Some remarks on the δ′-interaction in one dimension. Rep Math Phys. (1986) 24:111–20. doi: 10.1016/0034-4877(86)90045-5
25. Avron JE, Exner P, Last Y. Periodic Schrödinger operators with large gaps and Wannier–Stark ladders. Phys Rev Lett. (1994) 72:896. doi: 10.1103/PhysRevLett.72.896
26. Exner P. The absence of the absolutely continuous spectrum for δ′ Wannier-Stark ladders. J Math Phys. (1995) 36:4561–70. doi: 10.1063/1.530908
27. Exner P, Neidhardt H, Zagrebnov V. Potential approximations to δ′: an inverse Klauder phenomenon with norm-resolvent convergence. Commun Math Phys. (2001) 224:593–612. doi: 10.1007/s002200100567
28. Maioli M, Sacchetti A. Absence of absolutely continuous spectrum for Stark-Bloch operators with strongly singular periodic potentials. J Phys A. (1995) 28:1101. (Erratum (1998) A31:1115. doi: 10.1088/0305-4470/31/3/024)
29. Wannier GH. Wave functions and effective Hamiltonian for Bloch electrons in an electric field. Phys Rev. (1960) 117:432. doi: 10.1103/PhysRev.117.432
30. Kravchenko VV. A representation for solutions of the Sturm–Liouville equation. Complex Var Ellipt. (2008) 53:775–89. doi: 10.1080/17476930802102894
Keywords: periodic Schrödinger operators, limit operators method, spectral parameter power series (SPPS) method, dispersion equation, monodromy matrices, slowly oscillating at infinity perturbation
Citation: Rabinovich VS, Barrera-Figueroa V and Olivera Ramírez L (2019) On the Spectra of One-Dimensional Schrödinger Operators With Singular Potentials. Front. Phys. 7:57. doi: 10.3389/fphy.2019.00057
Received: 26 February 2019; Accepted: 26 March 2019;
Published: 16 April 2019.
Edited by:
Manuel Gadella, University of Valladolid, SpainReviewed by:
Wencai Liu, Texas A&M University, United StatesYuriy Golovaty, Lviv University, Ukraine
Copyright © 2019 Rabinovich, Barrera-Figueroa and Olivera Ramírez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Víctor Barrera-Figueroa, dmJhcnJlcmFmQGlwbi5teA==
 Vladimir S. Rabinovich
Vladimir S. Rabinovich Víctor Barrera-Figueroa
Víctor Barrera-Figueroa Leticia Olivera Ramírez2
Leticia Olivera Ramírez2