Simulated Neutrino Signals of Low and Intermediate Energy Neutrinos on Cd Detectors

Neutrino-nucleus reactions cross sections, obtained for neutrino energies in the range ε_ν ≤ 100–120 MeV (low- and intermediate-energy range), which refer to promising neutrino detection targets of current terrestrial neutrino experiments, are presented and discussed. At first, we evaluated original cross sections for elastic scattering of neutrinos produced from various astrophysical and laboratory neutrino sources with the most abundant Cd isotopes ¹¹²Cd, ¹¹⁴Cd, and ¹¹⁶Cd. These isotopes constitute the main material of the COBRA detector aiming to search for neutrinoless double beta decay events and neutrino-nucleus scattering events at the Gran Sasso laboratory (LNGS). The coherent ν-nucleus reaction channel addressed with emphasis here, dominates the neutral current ν-nucleus scattering, events of which have only recently been observed for a first time in the COHERENT experiment at Oak Ridge. Subsequently, simulated ν-signals expected to be recorded at Cd detectors are derived through the application of modern simulation techniques and employment of reliable neutrino distributions of astrophysical ν-sources (as the solar, supernova, and Earth neutrinos), as well as laboratory neutrinos (like the reactor neutrinos, the neutrinos produced from pion-muon decay at rest and the β-beam neutrinos produced from the acceleration of radioactive isotopes at storage rings as e.g., at CERN).

1. Introduction

In recent interdisciplinary investigations in nuclear, particle and astro-particle physics, the interactions of neutrinos with matter play key role in understanding deeply the underlying physics. Exact measurements and reliable models of neutrino-matter interactions provide unquestionable requirements for unraveling top physics issues as neutrino properties, neutrino oscillations, supernova dynamics, dark matter detection and many others [1–4]. To enable further progress, relevant nuclear model calculations, across a wide energy range and in various nuclear isotopes, may provide significant results [5–7].

Recently, the neutrino-nucleon and neutrino-nucleus cross-section uncertainties have reached a limiting factor in the judgement of neutrino interaction models and in interpreting many neutrino experiments [1–4] and specifically experiments like the COHERENT where recently coherent neutrino nucleus scattering events have been measured for a first time [8–10]. Furthermore, the presence of important nuclear effects impact the interaction cross sections as well as the final nuclear states reached through the scattering process [11–13]. The nuclear effects also affect the rebuilding of the incoming ν-energy spectra of the neutrino sources that are key-role input for the resolution of neutrino detection signals. Understanding neutrino-nucleus scattering processes provides to experimentalists good information to separate the background events from the detection signal [14–20].

The current neutrino physics searches are categorized according to the incident neutrino energy in the scattering process. Thus, the range below about 10 MeV (low-energy, from a nuclear physics viewpoint) is connected to Geo-neutrino and solar neutrino studies [14–19], the neutrino energy range of 10 up to about 100–120 MeV (intermediate energy) covers a set of ν-physics topics in the front of nuclear structure physics and astro-particle physics such as core-collapse supernovae dynamics and dark matter detection [11–13, 21, 22], while the energy range from 0.1–0.2 GeV up to about 10 GeV is related to meson decay neutrino beams such as those employed for long-baseline (high energy) neutrino experiments [23–26].

Due to the fact that neutrinos interact very weakly, they are unique messengers from astrophysical sources (the Earth, the Sun, the supernovae, and other stars) [1, 2, 21] allowing us to investigate deep into the astrophysical objects [21, 27–29]. In the near future, remarkably sensitive detectors as liquid-scintillator detectors, liquid argon time projection chambers and water-Cherenkov detectors would operate aiming to study neutrino physics issues of astrophysical neutrino sources [19, 20, 26] (for higher energy neutrinos, like e.g., those coming from active galactic nuclei, black hole binary stars, etc. operating detectors as IceCube, KM3Net and others are appropriate) [30, 31]. Each detector type has specific advantages (e.g., for supernova neutrinos, a combination of all types may allow for a better investigation of the relevant open issues).

Our present work focuses on the interpretation of various ν signals generated in nuclear detectors of terrestrial neutrino experiments through the investigation of the nuclear response of Cd detector materials to various neutrino energy spectra [3, 4, 26, 32]. We emphasize on signals coming from geo-neutrinos, solar-neutrinos, supernova-neutrinos, reactor-neutrinos, and neutrinos generated from the decay of stopped pions and muons.

The main ingredients to this aim are: (i) The original differential and integrated cross sections of the neutral-current reactions of neutrinos, ^{112, 114, 116}Cd(ν,ν′)^{112, 114, 116}Cd*, and anti-neutrinos, ^{112, 114, 116}Cd${(\tilde{\nu },{\tilde{\nu }}^{\prime })}^{112,114,116}$Cd*, computed for the coherent channel by using a refinement of the quasi particle random phase approximation (QRPA) [11, 13, 32–34]. (ii) Reliable descriptions of the shapes of neutrino energy distributions coming out of numerical simulations of distributions in neutrino-energies ε_ν ≤ 100−120 MeV (for the above mentioned ν-sources). (iii) Modern computational tools [35–39] for the required folding (convolution) procedure in order to simulate the signal expected to be recorded on the Cd detectors CdTe or CdZnTe (the detector media of COBRA experiment) [3, 4, 26] from neutrino sources as the geo-, reactor-, solar-, supernova-, and pion/muon decay neutrinos. We mention that, the response of the Cd isotopes in the particle-bound excitation region, which coincides with the energy range of geo-neutrinos, is rather rich and this is one of the motivations for performing the present calculations. The next generation detectors (LENA, Borexino, SNO+) [19, 20], are expected to give useful answers to several questions of geological importance regarding the precise geo-ν fluxes and abundances of natural radioactive elements (K, U, Th) in the Earth's interior [40–43].

In this work we pay special attention on the coherent elastic neutrino-nucleus scattering (CEvNS) that is a process in which the target nucleus recoils coherently via a combined neutral current exchange width with neutrinos or anti-neutrinos. This process is well predicted by the standard model of the electroweak interactions and has large cross sections (10⁻³⁹cm² in the neutrino-energy region (ε_ν ≤ 50 MeV). This process has very recently been observed in the COHERENT experiment at a 6.7 σ confidence level (CL), by using a low-background CsI[Na] scintillator [8–10]. The detector was exposed to a ν_μ neutrino beam coming from the Spallation Neutron Source (SNS) at Oak Ridge, USA [9]. This facility generates the most intense (pulsed) neutron beam in the world while simultaneously a significant yield of neutrinos is generated when pions (product of proton interactions in the target) decay at rest (prompt neutrinos). In addition, the muons produced from the charged-pion decay generate the known as delayed neutrino beam [10].

Even though many groups world-wide are now studying the difficult low-energy nuclear recoil signature, only a few sources, in specific nuclear reactors and spallation neutron sources yield the required neutrino-energy beams in adequate quantities for such measurements [44–46]. In our present theoretical work, we do not address the improved constraints derived from this dataset on non-standard neutrino interactions with quarks (for a comprehensive discussion on this issue the reader is referred e.g., to Papoulias and Kosmas [47, 48] and references therein). The present article is an extension of our previous calculations performed in Tsakstara and Kosmas [11, 13] and Tsakstara [32] and we used the same but slightly improved nuclear method. The extension refers to the employment of new detector isotopes and the better accuracy of the calculations [11–13, 32].

In the rest of the paper, at first (sections 2 and 3), the main formalism is described and original cross sections calculations are presented. Then (sections 4 and 5), a description of the main characteristics of the low and intermediate energy neutrino sources addressed here are briefly summarized and folded cross sections as well as event rates for neutral current neutrino scattering off the ¹¹²Cd, ¹¹⁴Cd, and ¹¹⁶Cd isotopes are presented and discussed. Finally (section 6), the main conclusions of the present work are extracted.

2. Brief Description of the Formalism

2.1. Angle Differential Coherent ν-Nucleus Cross Section

In the description of the ν-nucleus scattering, the angle differential cross section dσ/dΩ is a useful quantity. For the elastic-scattering of a neutrino with energy ε_ν on a nucleus (A,Z) the angle differential cross section (with respect to the scattering angle ϑ) is defined as Papoulias and Kosmas [47], Engel [49], De Vries et al. [50], and Drukier and Stodolsky [51]

$\begin{array}{ll}\frac{d\sigma }{d\Omega }=\frac{G_F^2}{4{\pi }^2}{\epsilon }_{\nu }^2(1+cos\vartheta )\frac{Q_w^2}{4}{F}{(q^2)}^2& (1)\end{array}$

($G_F=1.1664\times 10^{-5}$ GeV⁻² is the Fermi weak coupling constant). In this definition, the quantity ${F}$(q²) includes the nuclear structure dependence of the cross section as Kosmas et al. [33] and Kosmas [34]

$\begin{array}{ll}F(q^2)=\frac{1}{Q_w}\left[(1-4{\sin }^2{\Theta }_w)Z{F}_Z(q^2)-N{F}_N(q^2)\right]& (2)\end{array}$

where Θ_w denotes the weak mixing angle, known as Weinberg angle which takes the value ${\sin }^2{\Theta }_w\approx 0.2313$. In Equations (1) and (2), Q_w denotes the weak charge of the target nucleus given by

$\begin{array}{ll}{Q}_w=(1-4{sin}^2{\Theta }_w)Z-N.& (3)\end{array}$

The latter expression shows that, the neutron coherence of neutral currents (NC), in the case of neutron rich targets, provides large cross sections. This effect can be exploited in detecting, e.g., earth and sky neutrinos by measuring nuclear recoils. Measurements of these (NC) cross sections may also provide useful information about the neutrino source [21] and yield information about the primary neutrino fluxes, i.e., before flavor conversions in the neutrino sphere of core collapse supernovae.

The sensitivity of the coherent scattering channel to the neutron number in the target nucleus, may provide nuclear structure information through investigation of ν-nucleus scattering and the possibility to search for non-standard neutrino physics by taking advantage of the flavor-blind nature of the process [48, 52].

The ground-state elastic nuclear form factors, $F_Z(q^2)$ for protons and $F_N(q^2)$ for neutrons entering Equation (2), are defined by

$\begin{array}{ll}{F}_k(q^2)=\frac{k}{4\pi }{\displaystyle \int }{j}_0(qr){\rho }_{n,p}(r)r^{2}dr,k=N,Z& (4)\end{array}$

and are normalized as $F_{N,Z}(q^2=0)=1$. In the latter equation, ρ_n,p(r) denote the neutron (n) and proton (p) charge density distributions with j₀(qr) = sin(qr)/(qr) being the zero-order spherical Bessel function (we neglect a small correction from the single-nucleon form factors proportional to $e^{-{(q{b}_N)}^2/6}$ with b_N ≈ 0.8 fm being the nucleon harmonic oscillator size parameter [53]). The proton density ρ_p(r) is often taken from experiment whenever measured charge densities are available [33, 49].

Moreover, assuming that F_N ≈ F_Z, from Equations (1) and (2) (in nuclei with J^π = 0⁺ ground state), one obtains

$\begin{array}{ll}\frac{d\sigma ({\epsilon }_{\nu },\vartheta )}{dcos\vartheta }=\frac{G_F^2}{2\pi }(1+\cos \vartheta ){\epsilon }_{\nu }^2{\left[f_V^{p}Z+f_V^{n}N\right]}^2{F}_Z^2(q^2).& (5)\end{array}$

where $f_V^p$ and $f_V^n$ stand for the polar-vector couplings of the weak neutral current

$\begin{array}{ll}{f}_V^p=\frac{1}{2}-2{sin}^2{\Theta }_W,f_V^n=-\frac{1}{2}.& (6)\end{array}$

Thus, the coherent cross section depends on the square of the ground-state nuclear form factor ${F}$(q²) at momentum transfer q given by

$\begin{array}{ll}q=2{\epsilon }_{\nu }sin(\vartheta /2),& (7)\end{array}$

From Equation (2), we see that, since $f_V^p=(1-4{sin}^2{\Theta }_w)/2\approx 0.0374$ is small, a neutrino scattered elastically on a spin-zero nucleus couples mostly to the neutron distribution, ρ_n(r). A measurement of the cross section for this process would, at some level, provide a determination of the neutron form factor $F_N(q^2)$ [52, 54]. Some authors consider that this would be complementary to parity violating experiments [50, 52] because it would provide additional data, obtained at different energy ranges and with different nuclei that could be used to calibrate nuclear structure calculations [33, 34, 49–51].

In earlier astrophysical estimations of the coherent scattering cross sections within the Standard Model (SM) [51, 55] (also in recent beyond the SM calculations [56, 57]), the approximation $F_N(q^2)\approx F_Z(q^2)\approx 1$ was used for the total coherent cross section σ_tot(ε_ν) written as

$\begin{array}{ll}{\sigma }_{tot}({\epsilon }_{\nu })=\frac{G_F^2}{8\pi }{\left[(1-4{\sin }^2{\Theta }_W)Z-N\right]}^2{\epsilon }_{\nu }^2.& (8)\end{array}$

(we mention that available experimental data for neutron form factors are very limited).

From an experimental point of view, and particularly for the neutrino facilities near spallation sources [45, 58], it is also interesting the expression of the coherent differential cross section as a function of the nuclear recoil energy T_A. This is approximately written as Vergados and Giomataris [58], Vergados et al. [59], Giomataris and Vergados [60], and Vogel and Engel [61]

$\begin{array}{ll}\frac{d\sigma ({\epsilon }_{\nu },T_A)}{d{T}_A}=\frac{G_F^2}{4\pi }{Q}_W^{2}M\left(1-\frac{M{T}_A}{2{\epsilon }_{\nu }^2}\right)F(2M{T}_A^2),& (9)\end{array}$

where M is the nuclear mass and F denotes the ground state elastic form factor of the target nucleus. For the sake of completeness, we note that other expressions, including higher order terms with respect to T_A can be found, see e.g., [9, 10, 58–60]. The contribution, however, of these therms is negligible and thus, higher order terms in Equation (9) does not influence essentially the calculations. Our present coherent differential cross sections are not obtained as functions of the recoil energy but as functions of the scattering angle or the momentum transfer connected through Equation (7).

It should be noted that, the signal on the coherent neutrino-nucleus scattering experiments is significantly different compared to that of the incoherent scattering where the signal could be an outgoing particle or a de-excitation product [32].

The total coherent cross section σ_tot(ε_ν) is obtained by integrating numerically Equation (5) over the angle θ (θ_min = 0 to θ_max = π) or Equation (9) over T_A between

$\begin{array}{l}{T}_A^{min}=\frac{T_A}{2}+\sqrt{\frac{T_A}{2}(M_A+\frac{T_A}{2})},\end{array}$

to $T_A^{max}=\infty$ [47, 61, 62].

Before closing this sections, it is worth mentioning that, in our present calculations of the neutrino-nucleus cross sections part of the cross-section uncertainties are removed by performing realistic nuclear structure calculations for both proton and neutron nuclear form factors (for a recent comprehensive discussion on this issue the reader is referred e.g., to Papoulias and Kosmas [48] where the results coming out of different nuclear models and various approximations are presented and discussed).

3. Original Cross Section Calculations

The neutral-current scattering of low and intermediate energy neutrinos ν_ℓ or anti-neutrinos ${\tilde{\nu }}_{\ell }$ (ℓ = e, μ, τ) off the ^{112, 114, 116}Cd isotopes (with abundances 24.13, 28.8, and 7.5%, respectively, the first two are the most abundant Cd isotopes) are represented by

$\begin{array}{ll}{\nu }_l({\tilde{\nu }}_l){+}^{112,114,116}Cd{\to }^{112,114,116}C{d}^{*}+{\nu }_l^{\prime }({\tilde{\nu }}_l^{\prime }),& (10)\end{array}$

(Cd* denote excited states of Cd-isotopes). We mention that, the above reactions of the Cd-isotopes and also the charged-current (CC) reactions for ℓ = e, play significant role in astrophysical environment by affecting the electron fraction Y_e of the matter and its strong effect on the matter flow [22, 63–66].

In the first step of the present calculations, we evaluate original cross sections for the coherent channel (ground state to ground state transitions) of the reactions of Equation (10) [5, 11, 13, 62, 67, 68]. As can be seen from Equation (5), the original cross section for scattering of neutrinos, ν_l or anti-neutrinos, ${\tilde{\nu }}_l$, are identical (this holds only for the coherent channel). The signal (folded cross section) on the nuclear detector, however, as we will see in sections 4 and 5, could be significantly different. This is due to the flavor dependent energy distributions of the ν-beam reaching the nuclear detector, that enters in the folding procedure.

In this work, the required nuclear ground state wave functions are obtained from mean-field calculations using the successful Woods-Saxon interaction plus the monopole (pairing) interaction of the Bonn C-D potential. The ground state of the studied (even-even) ^{112, 114, 116}Cd isotopes (they have ground state spin $|J_i^{{\pi }_i}\rangle =|0_{gs}^{+}\rangle )$ is computed by solving iteratively the BCS equations [11, 13, 32, 47, 69].

In Table 1, we list the values of the resulting pairing parameters ($g_{pair}^{p,n}$) and the (theoretical) energy gaps (${\Delta }_{p,n}^{th}$) for protons (p) and neutrons (n) determined at the BCS level for the above isotopes. As is well-known, these parameters renormalize the pairing interaction of the Bonn C-D potential in order to fit the theoretical gaps, ${\Delta }_{p,n}^{th}$, to the empirical ones ${\Delta }_{p,n}^{exp}$. The latter are provided through the application of the three point formulas (see Appendix) by using the empirical separation energies (for protons and neutrons, S_{p, n}) of the neighboring nuclear isotopes [13, 32]. The values of the $g_{pair}^{p,n}$ adjust reliably the empirical energy gaps (see Table 1) [11, 13, 32, 69, 70].

TABLE 1

Table 1. Pairing parameters ${g_{pair}}^p$ (for protons), and ${g_{pair}}^n$ (for neutrons) determining the monopole pairing interactions for each of the studied isotopes.

The needed proton and neutron nuclear form factors in the context of QRPA are calculated from the expressions

$\begin{array}{ll}{F}_k(q^2)=\frac{1}{k}{\displaystyle \sum _j}ĵ\langle (n\ell )j\left|j_0(qr)\right|(n\ell )j\rangle {(V_j^k)}^2,k=N,Z& (11)\end{array}$

($V_j^k$ denotes the probability amplitude for proton or neutron occupancies of the single particle (nℓ)j-level). The summation, runs over the 15 active levels of the chosen model space (the same for proton and neutrons) as well as over the fully occupied j-levels for which $V_j^k=1$ (they describe a ⁴⁰Ca closed core). The model space assumed consists of the major harmonic oscillator shells having quantum numbers N = 3, 4, 5 (N = 2n + ℓ).

In Figure 1, the quantities needed for calculating the differential and integrated coherent cross section (see Equations 1, 5) for the neutrino reactions (10) are illustrated. Figures 1A–C, shows the form factors for protons (F_Z) and neutrons (F_N) obtained with our BCS calculations (for the three isotopes ^{112, 114, 116}Cd) and Figure 1D shows the momentum dependence of ${F}$(q²) that enters Equations (1) and (5).

FIGURE 1

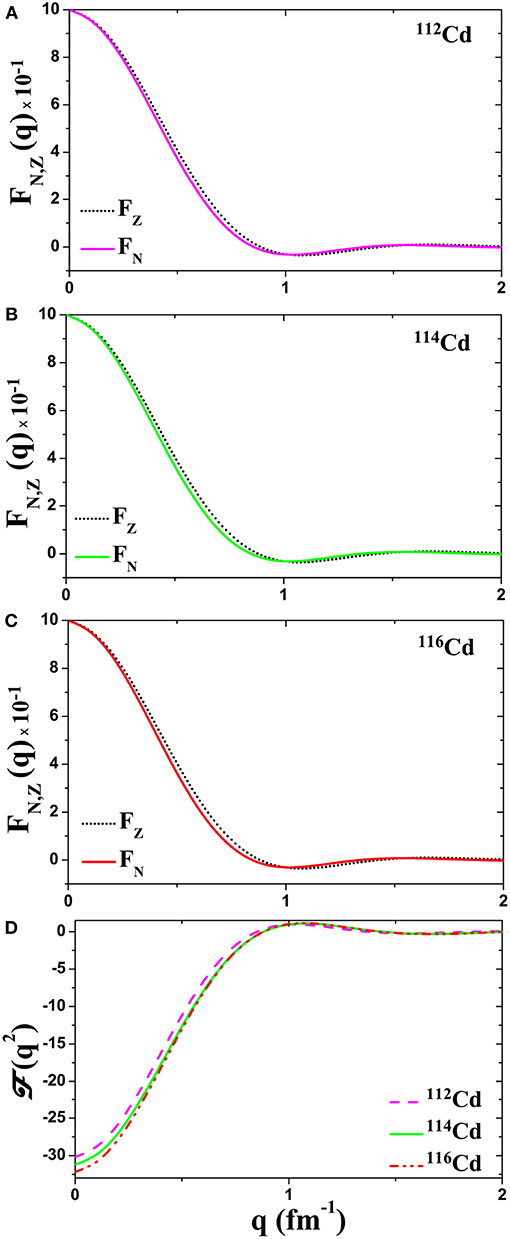
Figure 1. Neutron and proton nuclear form factors $F_{N,Z}(q^2)$ (A) for ¹¹⁴Cd, (B) for ¹¹²Cd, and (C) for ¹¹⁶Cd isotopes. (D) The ground-state elastic nuclear form factor ${F}$(q²) for ^{112, 114, 116}Cd isotopes.

It should be noted that, the corrections due to the nucleon finite size ($e^{-{(q{b}_N)}^2/6}$) and the nuclear center-of-mass motion (e^(qb)2/4A), which enter as an overall q-dependent factor in the F_{N, Z}(q), for the medium heavy Cd-isotopes are negligible and have been ignored. The correction due to the nucleon finite size (the larger of the two) is very well-known, but not essential. For small q the influence is close to zero while at the maximum momentum q it is about 5% [53].

As can be concluded from Figure 1, the above ground state properties of the three Cd isotopes studied are to a large extent similar which means that their nuclear structures are not significantly different (all of them have ground state spin J^π = 0⁺). The differences, are mostly due to the small ratio (ΔN_i/N ≈ 3 − 6%) in their neutron number.

Figure 2 illustrates the total integrated coherent cross sections of ν-^{112, 114, 116}Cd scattering as a function of (i) the momentum transfer q, Figure 2A, and (ii) the incoming neutrino energy ε_ν, Figure 2B. As mentioned before, these original cross sections will be used below for evaluations of flux averaged folded cross sections for various neutrino spectra.

FIGURE 2

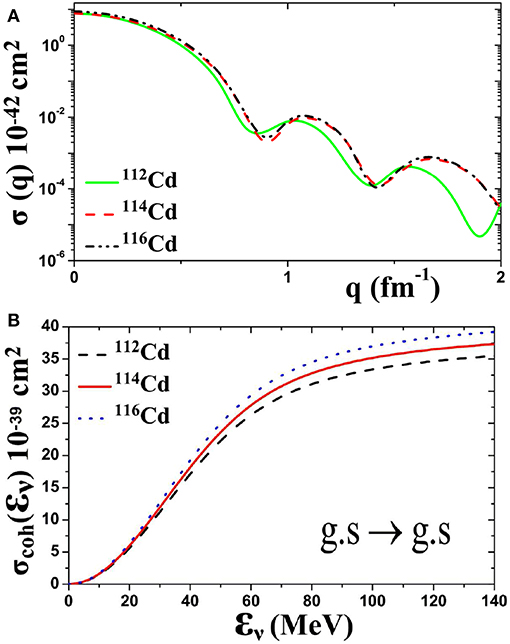
Figure 2. Total cross sections of coherent (ground state to ground state g.s. → g.s.) transitions for the neutral current reactions ^{112, 114, 116}Cd($Cd{({\nu }_l,{{\nu }^{\prime }}_l)}^{112,114,116}$Cd*, l = e, μ, τ, as a function of (A) the momentum transfer q, and (B) the incoming neutrino energy ε_ν.

Before closing this section, it is worth mentioning that, in calculating the nuclear form factors ${F}$(q²), see Figure 1, in the context of the QRPA method, the estimated error at low momentum transfer is very small, while in the momentum range of our interest 0 ≤ q ≤ 2fm⁻¹, it is at maximum 10–15%. On the other hand, the experimental accuracy, for the proton form factors entering Equation (2), usually they come from electron scattering measurements, is of the order of 1% [50]. For neutron form factors, however, the available experimental data are limited and, in general, authors discuss about differences between corresponding proton and neutron nuclear form factors (in medium heavy isotopes like ^{112, 114, 115}Cd) of the order of 4 to 8% [52, 54].

In the next section, we summarize the main features of the ν-energy distributions employed in this work for obtaining folded neutrino-nucleus cross sections for each ν-source.

4. Energy-Spectra of Low-Energy and Intermediate ν-Sources

In this section, we focus on the basic characteristics of the currently interesting astrophysical (solar-, supernova-, geo-neutrino) and laboratory (reactor neutrino and pion/muon decay at rest neutrino) sources, their energy spectra of which will be used in the convolution procedure (see next section) to obtain convoluted cross sections based on our original cross sections.

In general, the ν-beams of the above mentioned neutrino sources have broad energy distributions (sometimes they consist of a mixture of neutrinos and anti-neutrinos) characteristic of the considered source. Some well-known mono-energetic (monochromatic) fluxes are e.g., the one coming out of the charged-pion decay at rest (corresponding to the energy ε_νμ = 29.65 MeV, see Figure 3D. For the non-mono-energetic neutrino fluxes we define the energy distributions η(ε_ν) as

$\begin{array}{ll}\frac{d{N}_{\nu }({\epsilon }_{\nu })}{d{\epsilon }_{\nu }}\equiv \eta ({\epsilon }_{\nu })& (12)\end{array}$

(N_ν represents the number of neutrinos of the beam).

FIGURE 3

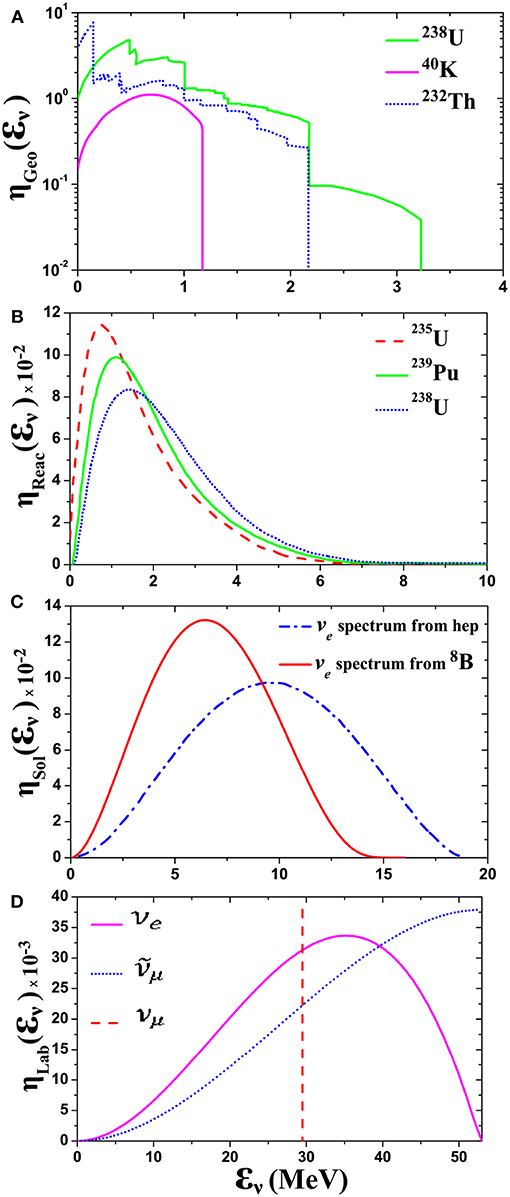
Figure 3. (A) Spectra of the U-Series, Th-Series, and ⁴⁰K Geo-Neutrinos. Neutrinos from ⁴⁰K electron capture are also shown in this figure. (B) Normalized reactor neutrino spectra. (C) Normalized energy spectrum of ⁸B and hep ν_e solar neutrinos. (D) Energy-spectra of ν_e and ${\tilde{\nu }}_{\mu }$ neutrino beams, generated from the muon-decay at rest (see e.g., [71, 72]).

We note that, via these energy spectra η(ε_ν) of the specific neutrino sources, the original ν-nucleus cross sections (of neutral-current reactions) computed with the QRPA method, can be connected with physical observables and signals recorded at the nuclear detectors through the use of the folding (convolution) method described below. The obtained this way folded (convoluted) cross sections represent the simulated nuclear detector response of the ^{112, 114, 116}Cd isotopes, in the energy range of ν-energy distribution of the studied neutrino source.

The main properties of the aforementioned astrophysical and laboratory neutrinos are summarized in the next subsections.

4.1. Geoneutrinos

As it is well-known, the decay of some radioactive isotopes (mainly U, Th, K) in the interior of our planet, makes the Earth a powerful source of low-energy neutrinos in the range ε_ν ≼ 10 MeV [40–43]. Accurate measurements of the flux of these neutrinos [15, 18] are utilized to determine the amount of heat-producing elements in the Earth's mantle. This amount may be compared to that estimated through indirect methods, an information which is important to understand the heat transfer within the Earth. The latter is responsible for earthquakes and volcanoes. The most recent measurements from KamLAND and Borexino [14, 16, 17] are useful to put limits on the parameters of various models describing the structure and evolution of our planet.

The Earth neutrinos (mainly electron anti-neutrinos ${\tilde{\nu }}_e$), are generated through β-decay processes of neutron-rich nuclei like U, Th, and others. These thermonuclear reactions are accompanied by the emission of electrons (e⁻) and release of energy Q_β as [40]

$\begin{array}{ll}(A,Z)\to (A,Z+1)+e^{-}+{\tilde{\nu }}_e+Q_{\beta }.& (13)\end{array}$

A and Z denote the mass and atomic (proton) number, respectively, of the initial (parent) nucleus. Part of the decay energy Q_β is carried away by anti-neutrinos (Q_ν) while the remainder is available for heating (Q_h). Thus, Q_β = Q_ν + Q_h.

In general, the radioactive isotopes of the Earth are classified into three groups: (i) isotopes in the ²³⁸U decay series, (ii) isotopes in ²³²Th decay series, and (iii) ⁴⁰K isotope [40, 41]. Thus, these isotopes are geologically important because they heat (radiogenic heat) the Earth's interior (finally each of them reaches a stable nuclear isotope) via β-decays of all intermediate radioactive isotopes.

Figure 3A, shows the individual anti-neutrino spectra from ⁴⁰K, ²³⁸U series, and ²³²Th series (${\tau }_{1/2}=4.47\times 10^9$ y, ${\tau }_{1/2}=14.0\times 10^9$ y and ${\tau }_{1/2}=1.28\times 10^9$ y, respectively). Essentially, these anti-neutrino (${\tilde{\nu }}_e$) energy spectra come from 82 beta decays in the U series and 70 beta decays in the Th series [40–43, 71, 73].

4.2. Solar Neutrinos

The solar neutrino spectra (mainly ν_e neutrinos) are produced through thermonuclear reactions taking place in the interior of the Sun [74–76]. The shape of the energy distribution (0.1 MeV ≤ ε_ν ≤ 18 MeV) depends on the densities and temperatures in the Sun's environment [75] and the individual process of the reaction chain (p-p neutrinos, ⁷Be neutrinos, ⁸B neutrinos, hep neutrinos, CNO-cycle neutrinos, etc.). In Figure 3C, we show the energy spectra of the important ⁸B [74] and hep [55, 75] neutrino sources predicted by the standard solar model [55]. The ⁸B ν-spectrum, is nearly symmetric, with a peak at 6.4 MeV while the hep spectrum is peaked at 9.6 MeV [55].

The detection of the solar neutrinos (produced either via the pp-chain reactions or via the CNO-cycle processes) by terrestrial experiments (SNO+ [17, 19]), constitutes excellent probes for astrophysics, nuclear physics, and particle physics searches [75, 76]. Besides the huge success of the solar-neutrino experiments the last decades, there are still many unsolved questions related to the metallicity of the Sun's core, the total luminosity in neutrinos, the neutrino oscillations, etc. [14, 16, 17, 19, 20].

4.3. Pion-Muon Decay at Rest Neutrino Energy Distributions

In muon factories (at J-Park, Fermilab, PSI, etc.), from pion and muon decay at rest (DAR), in addition to the monochromatic ν-beam peaked at ε_νμ= 29.65 MeV), ${\tilde{\nu }}_{\mu }$ and ν_e beams (with energy of a few tens of MeV) are created. Such intermediate energy neutrino sources, are also the currently available at high-intensity proton sources, like the SNS at Oak Ridge, the neutrino beam-line produced at Fermilab Booster, the future Project-X facilities at Fermilab, etc. [14, 16, 17, 19, 20].

In the farther future, such high-intensity muon beams would offer a possible site for neutrino experiments related to supernova neutrinos and for neutrino-nucleus cross section measurements in a great number of nuclei [25, 44–46]. In the operating pion-muon decay at rest neutrino sources (in Fermilab, at USA, J-PARC, at Japan, PSI in Switzerland, etc.) and in the neutrino facilities at the Neutron Spallation Source (Oak Ridge, USA), ν_e neutrinos, and ${\tilde{\nu }}_{\mu }$ anti-neutrinos are produced from the decay of muons according to the reaction

$\begin{array}{ll}{\mu }^{+}\to e^{+}+{\nu }_e+{\tilde{\nu }}_{\mu }.& (14)\end{array}$

The decaying muons result from the decay of pions at rest (${\pi }^{+}\to {\mu }^{+}+{\nu }_{\mu }$). Thus, these neutrino beams are not completely pure as, for example, the β-beam neutrinos [23, 25]. The energy-spectra of ν_e and ${\tilde{\nu }}_{\mu }$ neutrinos are fitted with the normalized distributions [71, 72]

$\begin{array}{ll}{\eta }_{{\nu }_e}({\epsilon }_{\nu })=96{\epsilon }_{\nu }^2{M}_{\mu }^{-4}(M_{\mu }-2{\epsilon }_{\nu }),& (15)\end{array}$

$\begin{array}{ll}{\eta }_{{\tilde{\nu }}_{\mu }}({\epsilon }_{\nu })=16{\epsilon }_{\nu }^2{M}_{\mu }^{-4}(3M_{\mu }-4{\epsilon }_{\nu }),& (16)\end{array}$

see Figure 3D, where M_μ = 105.6 MeV, is the muon rest mass. The ${\tilde{\nu }}_{\mu }$ spectrum is peaked at ${\epsilon }_{\nu }^{max}=52.8$ MeV = M_μ/2 while that of ν_e is peaked at ${\epsilon }_{\nu }^{max}=35.2$ MeV = M_μ/3 [7, 72].

Obviously, the analytic expressions of Equations (15) and (16), are convenient for the required integrations in the folding procedure, see below [11, 13, 32, 69]. On the other hand, their energy range and shape roughly resembles that of SN neutrinos.

4.4. Reactor Neutrino Spectra

The fission of very heavy nuclear isotopes ²³⁵U, ²³⁹Pu, and ²³⁸U in the nuclear reactors produces a great number of neutron rich nuclear isotopes. Because these products are unstable, they decay via β-decay emitting anti-neutrinos (${\tilde{\nu }}_e$) [77, 78]. Hence, nuclear reactors, operate as intense ${\tilde{\nu }}_e$ sources for many experiments, giving fluxes of the order of $~10^{13}\tilde{\nu }/$cm² s, at distances ~ 10 m from the reactor core.

The energy spectrum of these anti-neutrinos, characteristic of the β⁻ decay spectrum, is peaked at very low energies ~ 0.3 MeV and covers the energy region below ~ 10 MeV. Figure 3B illustrates the reactor neutrino spectra normalized so as the sum over all data-points to be equal to unity. The adopted fuel composition is 62% ²³⁵U, 30% ²³⁹Pu, and 8% ²³⁸U [77, 79].

Currently operating reactor neutrino experiments, like the TEXONO experiment in Taiwan [80, 81], the MINER experiment at the Nuclear Science Center, Texas A&M University (using neutrinos from the TRIGA reactor) [82], are excellent probes of beyond the standard model neutrino physics searches (electromagnetic ν-properties) and coherent ν-nucleus scattering studies.

4.5. Supernova Neutrino Spectra

Supernovae (SN) play key role in the development of our Universe, indicated e.g., from the fact that modern simulations of galaxies formation cannot reproduce the structure of the galactic disk without considering supernova data. Today, though the physics of core-collapse supernovae is not yet well-understood, investigations of SN neutrinos supply rich information for understanding their dynamics, the mechanism of SN-neutrino emission, etc., and for interpreting the supernova neutrino burst measurements [1, 5, 6]. Multiple physics signatures are expected from a core-collapse explosion in the next supernova observation [21, 42, 43, 46]. The detection of a future galactic supernova will provide invaluable information on the astrophysics of core-collapse explosion while the high statistics of a galactic SN neutrino signal may allow us to unravel the relevant scenarios.

In general, the shape of SN-neutrino energy-distributions is determined by the conditions pertaining during their emission from the collapsing star causing the cooling of the proto-neutron star formed in its center [63, 83–86]. For the energy distribution of SN neutrinos, some authors used available terrestrial neutrino sources with similar energy spectra, like the Neutron Spallation Source neutrinos and the boosted radioactive neutrino beams (beta beam neutrinos), in order to test the response of some ν-detectors to SN neutrinos [44–46]. Recent stellar modeling use analytic expressions that include various effects through a chemical potential parameter in the well-known two-parameter Fermi-Dirac (FD) distribution [87] or through the average ν-energy in the analytically simpler two parameter Power-Law (PL) distribution (see Appendix) [87–89].

Both parametrizations, FD and PL, yield similar distributions characterized by the temperature T or the average ν-energy 〈ε_ν〉 [13, 69, 90–93]. These analytic normalized expressions contain two parameters to include modulation effects due to various corrections required to modify the purely thermal shape initially employed [87, 88, 91]. The two parameter FD distribution includes the known pinching effect through the degeneracy parameter (the chemical potential divided by the neutrino temperature T), n_dg = μ/T which makes the spectrum more narrow compared to the purely thermal shape of temperature T (in MeV) [13]. The two parameter PL distribution of SN-ν energy spectrum [88, 89], contains as parameters the mean neutrino energy 〈ε_ν〉 and the parameter α which adjusts the width w of the distribution [13, 87, 88, 91] (see Appendix).

In Figure 4, some flavor dependent ν-energy spectra (η_SN) emitted by a core-collapse Supernova, needed for our present work, are illustrated. Both FD and PL energy distributions (labeled η_FD and η_PL, respectively) are shown for three different values of the width parameter w = 0.7, w = 0.8, and w = 0.9 (see Appendix) and for five equivalent parametrizations. From the FD distributions (with parameters the temperature T and the width parameter w), we see that, as the temperature grows the maximum of the distribution shifts to larger ν-energy (at the same time the corresponding peak becomes smaller). Also, as the width parameter w grows (keeping the same temperature), both the maximum of the distribution shifts to smaller ε_ν and its peak becomes smaller. Furthermore, the degeneracy parameter shifts the spectrum t o higher energies [13, 91]. In this figure, the PL energy distributions for the corresponding values of mean neutrino energy 〈ε_ν〉, are also illustrated (〈ε_ν〉 reflects the depth of the stars from which the neutrinos are escaping. We see that, as the 〈ε_ν〉 grows, the maximum of the distribution shifts to higher ν-energy ε_ν [88, 91].

FIGURE 4

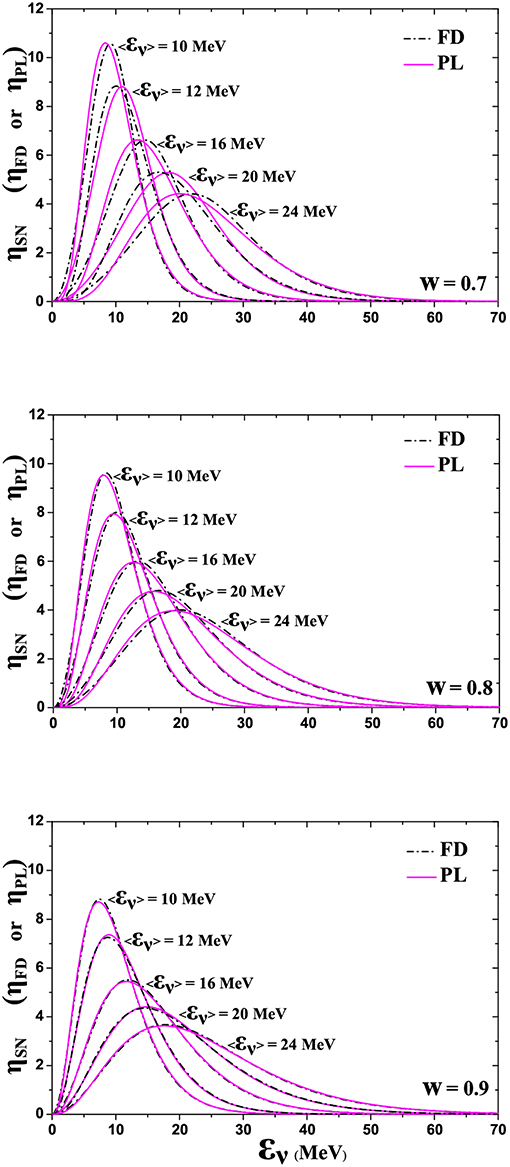
Figure 4. Supernova neutrino energy spectra (η_SN) coming out of the analytic expressions of: (i) the two-parameter Fermi-Dirac distribution (FD) and (ii) the two-parameter Power-law (PL) distribution (see Appendix). The five sets of values of their parameters refer to equivalent distributions (for details see the text).

In Table 2, the corresponding values of parameters for the equivalent FD and PL ν-energy spectra of Figure 4, that have been employed in various SN scenarios are shown (for more details see the Appendix and [13]). It is worth mentioning that, due to neutrino oscillations and other phenomena, at any distance from the source the SN-ν spectra can be different compared to those originally produced at the core of the collapsing star. It is, however, expected that ν-signals with much higher statistics from future galactic SN, may allow us to assess the great number of neutrino mixing scenarios.

TABLE 2

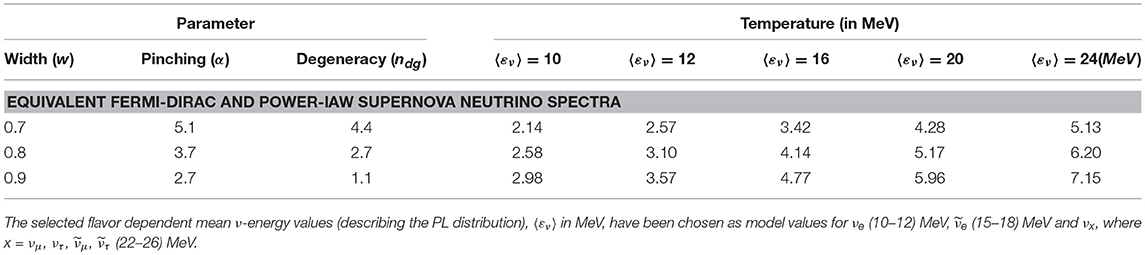
Table 2. Corresponding values of parameters for equivalent Fermi-Dirac (FD) and Power-Law (PL) distributions (SN neutrino energy spectra) of Figure 4.

It is worth mentioning that, the statistics for the SN 1987A were rather poor, just a few dozen ${\tilde{\nu }}_e$ events were received within about 10 s. For the observation of the next core-collapse SN-neutrino burst, however, detectors with huge statistics and remarkably greater flavor sensitivity are in operation or have been planned to operate in the near future [94]. Among those, are the next generation detectors HyperKamiokande, Juno, Dune, etc., which aim at measuring, among others, the diffuse SN neutrino background [95, 96].

5. Simulated Neutrino Signals on Nuclear Detectors

The features of a neutrino-flux that arrives at a neutrino detector are concealed in the nuclear response of the detector-material. In the case of the COBRA detector, the semi-conductor materials CdTe or CdZnTe contain large portion of Cd isotopes [3, 4, 26]. Our aim in this section is to simulate some of these features by calculating convoluted cross sections as discussed in Tsakstara and Kosmas [13] and Tsakstara [32].

The convolution (folding) is carried out with (i) the original cross sections obtained in section 3, and (ii) the low and intermediate energy neutrino spectra of section 4 in order to compute, first, flux averaged total cross sections, 〈σ_tot〉 and, then, corresponding supernova neutrino event rates and fluxes.

5.1. Flux Averaged Cross Sections for Cd Detector Materials

For the coherent channel, which is possible only in neutral current neutrino-nucleus reactions studied in this work, the flux averaged cross section 〈σ_coh〉 is obtained through the folding [6, 11, 13]

$\begin{array}{ll}\langle {\sigma }_{coh}\rangle ={\displaystyle \underset{0}{\overset{\infty }{{\displaystyle \int }}}}{\sigma }_{coh}({\epsilon }_{\nu })\eta ({\epsilon }_{\nu })d{\epsilon }_{\nu }.& (17)\end{array}$

For a CdTe or CdZnTe detector material, the flux averaged cross sections, computed by inserting in Equation (17) the σ_coh(ε_ν) from Figure 2B and the η(ε_ν) from Figures 3, 4, for the isotopes ^{112, 114, 116}Cd, are listed in Tables 3, 4 as described below.

TABLE 3

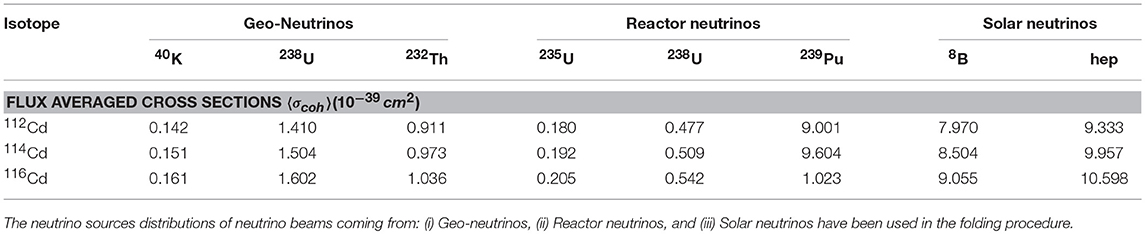
Table 3. Calculated values for the flux averaged coherent cross sections 〈σ_coh〉 (in units 10⁻³⁹ cm²) for ¹¹²Cd, ¹¹⁴Cd, and ¹¹⁶Cd isotopes.

TABLE 4

Table 4. Flux averaged coherent cross sections 〈σ_coh〉, as in Table 3 but now referred to: (i) three different Supernova neutrino spectra determined from the parameters of: (a) Fermi Dirac parametrizations and (b) Power-Law parametrizations, and (ii) the energy spectra of Pion/muon decay at rest (DAR) neutrinos.

In Table 3 we list the flux averaged cross sections evaluated by adopting the neutrino distributions of the geo-neutrinos (see Figure 3A), the reactor neutrinos (see Figure 3B) and the solar neutrinos (see Figure 3C for the ⁸B and the hep solar neutrinos).

In the last two columns of Table 4 we tabulate the 〈σ_coh〉 calculated for the distributions of Equations (15) and (16), i.e., the ν-spectra produced by pion/muon decay at rest (DAR). In the first three columns of this Table, the flux averaged cross sections refer to various supernova neutrino scenarios described by the equivalent FD and PL distributions of Figure 4. The corresponding parameters are listed in Table 2.

In supernova neutrino scenarios, usually average ν-energies between 10 ≤ 〈ε_ν〉 ≤ 12 MeV are employed for the description of ν_e neutrinos, average energies between 15 ≤ 〈ε_ν〉 ≤ 18 MeV for ${\tilde{\nu }}_e$ anti-neutrinos, and average energies between 22 ≤ 〈ε_ν〉 ≤ 26 MeV for ν_x and ${\tilde{\nu }}_x$, with x = μ, τ [87–89, 91].

Due to the dominance of the coherent channel throughout the region of the incoming neutrino energy ε_ν of our present calculations, the flux averaged coherent cross section 〈σ_coh〉 may be even two or three orders of magnitude larger than the total incoherent cross section $\langle {\sigma }_{tot}^{incoh}\rangle$ [11, 13, 69].

5.2. Number of Events in ν-Detectors

The present theoretical results may be connected with current neutrino experiments relying on Cd isotopes as detection materials, and specifically the COBRA experiment at Gran Sasso [3, 4, 26], as follows. By using the flux averaged cross sections 〈σ(ε_ν)〉 of Table 4, for instance those referred to the SN neutrinos of the ^{112, 114, 116}Cd isotopes, we estimate (potentially detectable) neutrino fluxes Φ_ν that should arrive at each detector to create some typical scattering event rates N_ev in the COBRA detector.

In general, the event rate N_ev is related to the flux Φ_ν reaching the nuclear detector with the expression [11, 32, 70]

$\begin{array}{ll}\frac{d{N}_{\nu }}{dt}\equiv N_{ev}=N_{Cd}{\sigma }_{tot}({\epsilon }_{\nu }){\Phi }_{\nu }({\epsilon }_{\nu }).& (18)\end{array}$

We note that, experimentalists use the definition

$\begin{array}{l}{N}_{ev}=ϵN_{Cd}{\sigma }_{tot}({\epsilon }_{\nu }){\Phi }_{\nu }({\epsilon }_{\nu }),\end{array}$

which takes into account the detection efficiency ϵ (usually equal to ϵ ≈ 80–90%) of the specific detector. Here, we assume a COBRA detector of mass m_det=100 kg and two cases of detector materials, i.e., the semiconductors (a) CdZnTe and (b) CdTe [3, 4, 26].

In the first step, we choose three SN neutrino scenarios in which the mean energies are: (i) 〈ε_ν〉 = 12 MeV (corresponding to SN electron neutrinos ν_e), (ii) 〈ε_ν〉 = 16 MeV (corresponding to SN electron anti-neutrinos ${\tilde{\nu }}_e$), and (iii) 〈ε_ν〉 = 24 MeV (corresponding to SN ν_x, ${\tilde{\nu }}_x$, with x = μ, τ (anti)neutrinos of heavy leptons).

Then, based on Equation (18), we perform calculations assuming a total mass 100 kg of CdZnTe as COBRA detector which translates, for example, to approximately m_Cd = 10.6 kg mass of ¹¹⁴Cd isotope or equivalently a number of ¹¹⁴Cd atoms (nuclei) equal to $N_{Cd}\equiv N_{{114}_{Cd}}=94.17N_{Avog}$.

In Equation (18), as total neutrino scattering cross sections, σ_tot(ε_ν) we employ the values of flux averaged cross sections 〈σ_coh〉 of Table 4 obtained through PL distribution for SN neutrino spectra (they refer to the three mean energies chosen above).

Finally, we choose four typical detection rates N_ev as: (a) N_ev=1 event s⁻¹=3.15 × 10⁷ events y⁻¹, (b) N_ev=1 event hr⁻¹=8.76 × 10³ events y⁻¹, (c) N_ev=1 event d⁻¹=3.65 × 10² events y⁻¹, and (d) N_ev= 12 events y⁻¹ and from Equation (18) we compute the corresponding SN ν fluxes Φ_ν.

In a similar way, assuming that the COBRA detector contains 100 kg of the material CdTe, we find 13.5 kg ¹¹⁴Cd or about $N_{Cd}\equiv N_{{114}_{Cd}}=120.11N_{Avog}$ atoms (nuclei) are contained in the second semiconductor material of COBRA detector. By performing similar calculations for the same SN scenarios and the same, as before, set of detection rates N_ev, we find the corresponding fluxes Φ_ν reaching the COBRA CdTe detector.

By performing the steps we followed for ¹¹⁴Cd, for the other two Cd-isotopes, ¹¹²Cd and ¹¹⁶Cd, the resulting neutrino fluxes, for the chosen SN neutrino scenarios are listed in Table 5 (last four columns). Such results are useful for future use of the Cd materials in astrophysical neutrino detection. It should be stressed that, next generation experiments may be effective in the detection of much weaker signals (higher sensitivity, larger detector mass, etc.).

TABLE 5

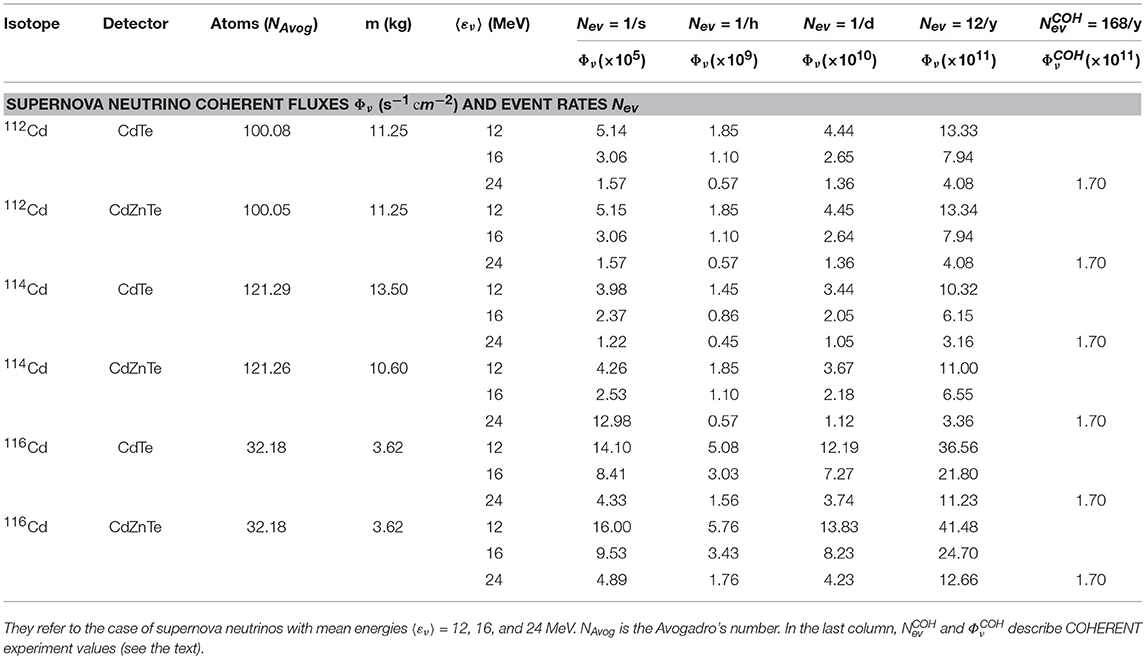
Table 5. Neutrino fluxes Φ_ν(ε_ν) and corresponding event rates N_ev estimated to be recorded on ^{112, 114, 116}Cd isotopes of two detector materials (CdTe and CdZnTe) of the COBRA experiment [3, 4, 26].

The above neutrino fluxes are of the same order with those of the Spallation Neutron Source (SNS) at ORLaND, Oak Ridge [44–46]. We mention that the COHERENT experiment at Oak Ridge, with a 14.57 kg of CsI scintillator detector, by using an SNS ν_μ neutrino flux (coming from π-decay at rest) as high as ${\Phi }_{\nu }^{COH}=1.7\times 10^{11}{\nu }_{\mu }/{\mathrm{\text{c}}m}^2$ s, has measured 142 CEvNS events within a period of 308.1 live days (at a distance of L = 19.3 m from the source) [8]. These results translate to event rate $N_{ev}^{COH}$ = 168/y ν_μ neutrinos.

From the results of Table 5, we may define the ratio N_ev/Φ_ν for the COHERENT experiment (R^COH) and for a special ν_μ neutrino case of the COBRA experiment (R^COB). For a comparison of these two experiments, we choose, for example, the results referred to the ¹¹²Cd isotope of CdTe material of the COBRA detector (sixth line from the beginning of Table 5 refers to ν_μ neutrinos). From these two ratios we find that R = R^COH/R^COB = 98.95/2.94 ≈ 34, which means that, for the chosen SN neutrino scenario, the COBRA detector may observe 12 ν_μ/y only if its mass is equal to m ~ 34 times larger than the assumed above 100 kg, i.e., only if the COBRA detector has a huge total mass m_det = 3.4 t CdTe material (we mention that, in the assumed scenario, the SN ν_μ neutrinos correspond a Temperature T = 24 MeV, see one before last column of Table 5). This example indicates also the corresponding cost for detector improvement so as to be able to record neutrino signals coming from interesting astrophysical sources.

We should finally note that, in this work the detection efficiency ϵ has not been considered (equivalently we assumed ϵ = 1). Also, the neutrino mixing has not been accounted for which means that we assumed the neutrino spectra arrived at the nuclear detector are described by PL distributions (as in stars interior) of the same values of the parameters.

6. Summary and Conclusions

In this work, we present original neutrino-nucleus cross sections obtained with realistic nuclear structure calculations (use of the QRPA method) for scattering of low and intermediate energy neutrinos off the ^{112, 114, 116}Cd isotopes. These Cd-isotopes are contents (with large abundance) of the detector materials of the COBRA detector at Gran Sasso. The neutrino energy assumed covers currently interesting laboratory (reactor, pion/muon decay at rest neutrinos) and Astrophysical (solar, supernova and Earth) neutrino sources. Laboratory neutrino beams are important tools for studying standard and non-standard neutrino physics while astrophysical neutrinos are key particles in investigating the structure and evolution of stars as well to deepen our knowledge on the fundamental neutrino-nucleus interactions.

By utilizing the convolution procedure, we calculated flux averaged cross sections and event rates for the above ν-sources based on specific spectral distributions describing supernova neutrino energy spectra, solar neutrinos, geo-neutrinos and laboratory neutrinos as well as reactor neutrinos and pion-muon-stopped neutrinos. The flux-averaged total coherent cross sections, 〈σ_coh〉, reflect the mean neutrino signals generated in several terrestrial detectors (^{112, 114, 116}Cd) from such ν-sources. Important connection of our present results with current experiments may also be achieved through the evaluation of the neutrino scattering event rates on Cd detectors.

The estimated neutrino fluxes and scattering event rates for Cd-isotopes, contents of the CdTe and CdZnTe materials of the COBRA detector at LNGS, may support this experiment to reach its goal in searching for neutrino observation and detection of rare events (double beta decay, etc.).

Author Contributions

JS and VT: nuclear structure calculations; OK: computation of folding (convolution) procedure.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The present research was financially supported VT and JS by the Department of Informatics Engineering of the Technological Institute of Western Macedonia. Also, OK wishes to acknowledge the support of EPSRC via grand EP/N026136/1 Geometric Mechanics of Solids.

References

1. Ejiri H. Nuclear spin isospin responces for low-energy neutrinos. Phys Rep. (2000) 338:265–351. doi: 10.1016/S0370-1573(00)00044-2

CrossRef Full Text | Google Scholar

2. Ejiri H, Engel J, Kudomi N. Supernova-neutrino studies with ¹⁰⁰Mo. Phys Lett B. (2002) 530:27–32. doi: 10.1016/S0370-2693(02)01349-7

CrossRef Full Text | Google Scholar

3. Zuber K. COBRA-double beta decay searches using CdTe detectors. Phys Lett B. (2001) 519:1–7. doi: 10.1016/S0370-2693(01)01056-5

CrossRef Full Text | Google Scholar

4. Zuber K. Spectroscopy of low energy solar neutrinos using CdTe detectors. Phys Lett B. (2003) 571:148–54. doi: 10.1016/j.physletb.2003.07.070

CrossRef Full Text | Google Scholar

5. Donnelly TW, Peccei RD. Neutral current effects in nuclei. Phys Rep. (1979) 50:185. doi: 10.1016/0370-1573(79)90010-3

CrossRef Full Text | Google Scholar

6. Kosmas TS, Oset E. Charged current neutrino-nucleus reaction cross sections at intermediate energies. Phys Rev C. (1996) 53:1409–15. doi: 10.1103/PhysRevC.53.1409

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Kolbe E, Kosmas TS. Recent highlights on neutrino-nucleus interactions. Springer Trac Mod. Phys. (2000) 163199–225. doi: 10.1007/BFb0109652

CrossRef Full Text | Google Scholar

8. Akimov D, Albert JB, An P, Awe C, Barbeau PS, Becker B, et al. Observation of coherent elastic neutrino-nucleus scattering. Science. (2017) 357:1123–6. doi: 10.1126/science.aao0990

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Scholberg K. Prospects for measuring coherent neutrino-nucleus elastic scattering at a stopped-pion neutrino source. Phys Rev D. (2006) 73:033005. doi: 10.1103/PhysRevD.73.033005

CrossRef Full Text | Google Scholar

10. Scholberg K. Coherent elastic neutrino-nucleus scattering. J Phys Conf Ser. (2015) 606:012010. doi: 10.1088/1742-6596/606/1/012010

CrossRef Full Text | Google Scholar

11. Tsakstara V, Kosmas TS. Low-energy neutral-current neutrino scattering on ^{128, 130}Te isotopes. Phys Rev C. (2011) 83:054612. doi: 10.1103/PhysRevC.83.054612

CrossRef Full Text | Google Scholar

12. Tsakstara V, Kosmas TS, Wambach J. Studying low-energy astrophysical neutrinos with neutrino nucleus cross-section calculations and beta beam neutrino spectra. Prog Part Nucl Phys. (2011) 66:424–9. doi: 10.1016/j.ppnp.2011.01.045

CrossRef Full Text | Google Scholar

13. Tsakstara V, Kosmas TS. Analyzing astrophysical neutrinos through realistic nuclear structure calculations and the convolution procedure. Phys Rev C. (2011) 84:064620. doi: 10.1103/PhysRevC.84.064620

CrossRef Full Text | Google Scholar

14. Abe S, Ebihara T, Enomoto S, Furuno K, Gando Y, Ichimura K, et al. Precision Measurement of Neutrino Oscillation Parameters with KamLAND. Phys Rev Lett. (2008) 100:221803. doi: 10.1103/PhysRevLett.100.221803

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Gando A, Gando Y, Ichimura K, Ikeda H, Inoue K, Kibe Y, et al. Partial radiogenic heat model for Earth revealed by geoneutrino measurements. Nat Geosci. (2011) 4:647–51. doi: 10.1038/ngeo1205

CrossRef Full Text | Google Scholar

16. Bellini G, Benziger J, Bonetti S, Buizza Avanzini M, Caccianiga B, Cadonati L, et al. Observation of geo-neutrinos. Phys Lett B. (2010) 687:299–304. doi: 10.1016/j.physletb.2010.03.051

CrossRef Full Text | Google Scholar

17. Bellini G, Benziger J, Bick D, Bonetti S, Bonfini G, Buizza Avanzini M, et al. Precision measurement of the ⁷Be solar neutrino interaction rate in Borexino. Phys Rev Lett. (2011) 107:141302. doi: 10.1103/PhysRevLett.107.141302

CrossRef Full Text | Google Scholar

18. Bellini G, Benziger J, Bick D, Bonfini G, Bravo D, Buizza Avanzini M, et al. Measurement of geo-neutrinos from 1353 days of Borexino. Phys Lett B. (2013) 722:295–300. doi: 10.1016/j.physletb.2013.04.030

CrossRef Full Text | Google Scholar

19. Zuber K. Status of the double beta experiment COBRA. Prog Part Nucl Phys. (2006) 57:235–40. doi: 10.1016/j.ppnp.2005.12.010

CrossRef Full Text | Google Scholar

20. Wurm M, Beacom JF, Bezrukov LB, Bick D, Blümer J, Choubey S, et al. The next-generation liquid-scintillator neutrino observatory LENA. Astropart Phys. (2012) 35:685–732. doi: 10.1016/j.astropartphys.2012.02.011

CrossRef Full Text | Google Scholar

21. Kolbe E, Langanke K, Martinez-Pinedo G, Vogel P. Neutrino-nucleus reactions and nuclear structure. J Phys G. (2003) 29:2569–96. doi: 10.1088/0954-3899/29/11/010

CrossRef Full Text | Google Scholar

22. Sajjad Athar M, Singh SK. ${\nu }_e({\bar{\nu }}_e){-}^{40}$Ar absorption cross sections for supernova neutrinos. Phys Lett B. (2004) 591:69–75. doi: 10.1016/j.physletb.2004.04.025

CrossRef Full Text

23. Zucchelli P. A novel concept for a ${\bar{\nu }}_e/{\nu }_e$ neutrino factory: the beta-beam. Phys Lett B. (2002) 532:166–72. doi: 10.1016/S0370-2693(02)01576-9

CrossRef Full Text

24. Volpe C. What about a beta beam facility for low-energy neutrinos?. J Phys G. (2004) 30:L1–6. doi: 10.1088/0954-3899/30/7/L01

CrossRef Full Text | Google Scholar

25. Volpe C. Topical review on beta-beams. J Phys G. (2007) 34:R1–44. doi: 10.1088/0954-3899/34/1/R01

CrossRef Full Text

26. Zuber K. The status of the COBRA double-beta-decay experiment. Prog Part Nucl Phys. (2010) 64:267–9. doi: 10.1088/1742-6596/203/1/012070

CrossRef Full Text | Google Scholar

27. Smponias T, Kosmas OT. High energy neutrino emission from astrophysical jets in the galaxy. Adv High Energy Phys. (2015) 2015:921757. doi: 10.1155/2015/921757

CrossRef Full Text | Google Scholar

28. Smponias T, Kosmas OT. Neutrino emission from magnetized microquasar jets. Adv High Energy Phys. (2017) 2017:4962741. doi: 10.1155/2017/4962741

CrossRef Full Text | Google Scholar

29. Kosmas OT. Smponias T. Simulations of gamma-ray emission from magnetized microquasar jets. (2018) Adv High Energy Phys. 2018:9602960. doi: 10.1155/2018/9602960

CrossRef Full Text | Google Scholar

30. Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens M, et al. Search for prompt neutrino emission from gamma-ray bursts with IceCube. Astrophys J Lett. (2015) 805:L5. doi: 10.1088/2041-8205/805/1/L5

CrossRef Full Text | Google Scholar

31. Adrian-Martinez S, Ageron M, Aharonian F, Aiello S, Albert A, Ameli F, et al. Letter of intent for KM3NeT 2.0. J Phys G Nucl Part Phys. (2016) 43:084001. doi: 10.1088/0954-3899/43/8/084001

CrossRef Full Text | Google Scholar

32. Tsakstara V. Convoluted-signals on ¹¹⁴Cd isotope from astrophysical and laboratory neutrino sources. Adv High Energy Phys. (2015) 2015:632131. doi: 10.1155/2015/632131

CrossRef Full Text | Google Scholar

33. Kosmas TS, Vergados JD, Civitarese O, Faessler A. Study of the muon number violating (μ⁻, e⁻ conversion in a nucleus by using quasi-particle RPA. Nucl Phys A. (1994) 570:637–56. doi: 10.1016/0375-9474(94)90077-9

CrossRef Full Text | Google Scholar

34. Kosmas TS. Exotic μ⁻→e⁻ conversion in nuclei: energy moments of the transition strength and average energy of the outgoing e⁻. Nucl Phys A. (2001) 683:443–62. doi: 10.1016/S0375-9474(00)00471-1

CrossRef Full Text | Google Scholar

35. Tsoulos IG, Kosmas OT, Stavrou VN. DiracSolver: a tool for solving the Dirac equation. Comput Phys Commun. (2019) 236:237–43. doi: 10.1016/j.cpc.2018.10.010

CrossRef Full Text | Google Scholar

36. Kosmas O, Leyendecker S. Analysis of higher order phase fitted variational integrators. Adv Comput Math. (2016) 42:605–619. doi: 10.1007/s10444-015-9436-x

CrossRef Full Text | Google Scholar

37. Kosmas O, Leyendecker S. Variational integrators for orbital problems using frequency estimation. Adv Comput Math. (2019) 45:1–219. doi: 10.1007/s10444-018-9603-y

CrossRef Full Text | Google Scholar

38. Kosmas O, Papadopoulos D. Multisymplectic structure of numerical methods derived using non standard finite difference schemes. J Phys Confer Ser. 490:012205. doi: 10.1088/1742-6596/490/1/012205

CrossRef Full Text

39. Kosmas OT. Charged particle in an electromagnetic field using variational integrators. AIP Confer Proc. (2011) 1389:1927. doi: 10.1063/1.3636989

CrossRef Full Text | Google Scholar

40. Vogel P, Beacom JF. Angular distribution of neutron inverse beta decay ${\bar{\nu }}_e+\overrightarrow{p}{e}^{+}+n$. Phys Rev D. (1999) 60:053003. doi: 10.1103/PhysRevD.60.053003

CrossRef Full Text

41. Dye S. Geoneutrinos and the radioactive power of the Earth. Rev Geophys. (2012) 50:3007. doi: 10.1029/2012RG000400

CrossRef Full Text | Google Scholar

42. Fiorentini G, Mantovani E, Ricci B. Neutrinos and energetics of the Earth. Phys Lett B. (2003) 557:139–46. doi: 10.1016/S0370-2693(03)00193-X

CrossRef Full Text | Google Scholar

43. Fiorentini G, Ianni A, Korga G, Lissia M, Mantovani F, Miramonti L, et al. Nuclear physics for geo-neutrino studies. Phys Rev C. (2010) 81:034602. doi: 10.1103/PhysRevC.81.034602

CrossRef Full Text | Google Scholar

44. Avignone FT, Efremenko YV. ORLaND - a neutrino facility at the Spallation Neutron Source. Nucl Phys B. (2000) 87:304–8. doi: 10.1016/S0920-5632(00)00687-3

CrossRef Full Text | Google Scholar

45. Avignone FT, Efremenko YV. Neutrino-nucleus cross-section measurements at intense. pulsed spallation sources. J Phys G. (2003) 29:2615–28. doi: 10.1088/0954-3899/29/11/012

CrossRef Full Text | Google Scholar

46. Burman RL, Louis WC. Neutrino physics at meson factories and spallation neutron sources. J Phys G. (2003) 29:2499–512. doi: 10.1088/0954-3899/29/11/006

CrossRef Full Text | Google Scholar

47. Papoulias DK, Kosmas TS. Nuclear aspects of neutral current non-standard ν-nucleus reactions and the role of the exotic μ⁻→e⁻ transitions experimental limits. Phys Lett B. (2014) 728:482–8. doi: 10.1016/j.physletb.2013.12.028

CrossRef Full Text | Google Scholar

48. Papoulias DK, Kosmas TS. Standard and nonstandard neutrino-nucleus reactions cross sections and event rates to neutrino detection experiments. Adv High Energy Phys. (2015) 215:763648. doi: 10.1155/2015/763648

CrossRef Full Text | Google Scholar

49. Engel J. Nuclear form-factors for the scattering of weakly interacting massive particles. Phys Lett B. (1991) 264:114–9. doi: 10.1016/0370-2693(91)90712-Y

CrossRef Full Text | Google Scholar

50. De Vries H, De Jager CW, De Vries C. Nuclear charge-density-distribution parameters from elastic electron scattering. Atomic Data Nucl Data Tables. (1987) 36:495–536. doi: 10.1016/0092-640X(87)90013-1

CrossRef Full Text | Google Scholar

51. Drukier A, Stodolsky L. Principles and applications of a neutral-current detector for neutrino physics and astronomy. Phys Rev D. (1984) 30:2295–309. doi: 10.1103/PhysRevD.30.2295

CrossRef Full Text | Google Scholar

52. Horowitz CJ, Ahmed Z, Jen C-M, Rakhman A, Souder PA, Dalton MM, et al. Weak charge form factor and radius of ²⁰⁸Pb through parity violation in electron scattering. Phys Rev C. (2012) 85:032501. doi: 10.1103/PhysRevC.85.032501

CrossRef Full Text | Google Scholar

53. Kosmas TS Vergados JD. Nuclear densities with fractional occupation probabilities of the states. Nucl Phys A. (1992) 536:72–86. doi: 10.1016/0375-9474(92)90246-G

CrossRef Full Text | Google Scholar

54. Chiang HC, Oset E, Kosmas TS, Faessler A, Vergados JD. Coherent and incoherent (mu−, e−) conversion in nuclei. Nucl Phys A. (1993) 559:526–42. doi: 10.1016/0375-9474(93)90259-Z

CrossRef Full Text | Google Scholar

55. Bahcall JN. Neutrino Astrophysics. Melbourne, VIC: Cambridge University Press (1989).

Google Scholar

56. Barranco J, Miranda OG, Rashba TI. Probing new physics with coherent neutrino scattering off nuclei. J High Energy Phys. (2005) 05:021. doi: 10.1088/1126-6708/2005/12/021

CrossRef Full Text | Google Scholar

57. Barranco J, Bolanos A, Miranda OG, Rashba TI. Tensorial NSI and Unparticle physics in neutrino scattering. Int J Mod Phys A. (2012) 27:1250147. doi: 10.1142/S0217751X12501473

CrossRef Full Text | Google Scholar

58. Vergados JD, Avignone FT, Giomataris I. Coherent neutral current neutrino-nucleus scattering at a spallation source: a valuable experimental probe. Phys Rev D. (2009) 79:113001. doi: 10.1103/PhysRevD.79.113001

CrossRef Full Text | Google Scholar

59. Vergados JD, Giomataris Y. Dedicated supernova detection by a network of neutral current spherical TPC detectors. Phys Atom Nucl. (2007) 70:140–9. doi: 10.1134/S1063778807010164

CrossRef Full Text | Google Scholar

60. Giomataris Y, Vergados JD. A network of neutral current spherical TPCs for dedicated supernova detection. Phys Lett B. (2006) 634:23–9. doi: 10.1016/j.physletb.2006.01.040

CrossRef Full Text | Google Scholar

61. Vogel P, Engel J. Neutrino electromagnetic form factors. Phys Rev D. (1989) 39:3378–83. doi: 10.1103/PhysRevD.39.3378

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Kolbe E. Differential cross sections for neutrino scattering on ¹²C. Phys Rev C. (1996) 54:1741–8. doi: 10.1103/PhysRevC.54.1741

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Langanke K, Martinez-Pinedo G. Nuclear weak-interaction processes in stars. Rev Mod Phys. (2003) 75:819–62. doi: 10.1103/RevModPhys.75.819

CrossRef Full Text | Google Scholar

64. Juodagalvis A, Langanke K, Martinez-Pinedo G, Hix WR, Dean DJ, Sampaio JM., Neutral-current neutrino-nucleus cross sections for A~50−65 nuclei. Nucl Phys A. (2005) 747:87–108. doi: 10.1016/j.nuclphysa.2004.09.005

CrossRef Full Text | Google Scholar

65. Langanke K. Weak interaction, nuclear physics and supernovae. Acta Phys Polon B. (2008) 39:265–82.

Google Scholar

66. Haxton WC. Nuclear response of water Cherenkov detectors to supernova and solar neutrinos. Phys Rev D. (1987) 36:2283–92. doi: 10.1103/PhysRevD.36.2283

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Donnelly TW, Walecka JD. Semi-leptonic weak and electromagnetic interactions in nuclei with application to ¹⁶O. Phys Lett B. (1972) 41:275–80. doi: 10.1016/0370-2693(72)90577-1

CrossRef Full Text | Google Scholar

68. Donnelly TW, Walecka JD. Elastic magnetic electron scattering and nuclear moments. Nucl Phys A. (1973) 201:81–106. doi: 10.1016/0375-9474(73)90689-1

CrossRef Full Text | Google Scholar

69. Tsakstara V, Kosmas TS. Nuclear responses of ^{64, 66}Zn isotopes to supernova neutrinos. Phys Rev C. (2012) 86:044618. doi: 10.1103/PhysRevC.86.044618

CrossRef Full Text | Google Scholar

70. Balasi KG, Ydrefors E, Kosmas TS. Theoretical study of neutrino scattering off the stable even Mo isotopes at low and intermediate energies. Nucl Phys A. (2011) 868–9:82–98. doi: 10.1016/j.nuclphysa.2011.08.003

CrossRef Full Text | Google Scholar

71. Anderson AJ, Conrad JM, Figueroa-Feliciano E, Ignarra C, Karagiorgi G, Scholberg K, et al. Measuring active-to-sterile neutrino oscillations with neutral current coherent neutrino-nucleus scattering. Phys Rev D. (2012) 86:013004. doi: 10.1103/PhysRevD.86.013004

CrossRef Full Text | Google Scholar

72. Louis WC. Searches for muon-to-electron (anti) neutrino flavor change. Prog Part Nucl Phys. (2009) 63:51–73. doi: 10.1016/j.ppnp.2009.01.002

CrossRef Full Text | Google Scholar

73. de Gouvea A, et al. Working Group Report: Neutrinos (Intensity Frontier Neutrino Working Group). arXiv:1310.4340 [hep-ex] (2013).

74. Bahcall JN, Holstein BR. Solar neutrinos from the decay of 8B. Phys Rev C. (1986) 33:2121–7. doi: 10.1103/PhysRevC.33.2121

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Bahcall JN, Urlich RK. Solar models, neutrino experiments, and helioseismology. Rev Mod Phys. (1988) 60:297–372. doi: 10.1103/RevModPhys.60.297

CrossRef Full Text | Google Scholar

76. Bahcall JN, Basu S, Pinsonneault M, Serenelli AM. Helioseismological implications of recent solar abundance determinations. Astrophys J. (2005) 618:1049–56. doi: 10.1086/426070

CrossRef Full Text | Google Scholar

77. Davis BR, Vogel P, Mann FM, Schenter RE. Reactor antineutrino spectra and their application to antineutrino-induced reactions. Phys Rev C. (1979) 19:2259–66. doi: 10.1103/PhysRevC.19.2259

CrossRef Full Text | Google Scholar

78. Declais Y, de Kerret H, Lefiévre B, Obolensky M, Etenko A, Kozlov Yu, et al. Study of reactor antineutrino interaction with proton at Bugey nuclear power plant. Phys Lett B. (1994) 338:383–9. doi: 10.1016/0370-2693(94)91394-3

CrossRef Full Text | Google Scholar

79. Tengblad O, Aleklett K, Von Dincklage R, Lund E, Nyman G, Rudstam G. Integral $\bar{\nu }$-spectra derived from experimental β-spectra of individual fission products. Nucl Phys A. (1989) 503:136–60. doi: 10.1016/0375-9474(89)90258-3

CrossRef Full Text

80. Kerman S, Sharma V, Deniz M, Wong HT, Chen J-W, Li HB, et al. Coherency in neutrino-nucleus elastic scattering. Phys Rev D. (2016) 93:113006. doi: 10.1103/PhysRevD.93.113006

CrossRef Full Text | Google Scholar

81. Deniz M, Sevda B, Kerman S, Ajjaq A, Singh L, Wong HT, et al. Constraints on scalar-pseudoscalar and tensorial non-standard interaction and tensorial unparticle couplings from neutrino-electron scattering. Phys Rev D. (2017) 95:033008. doi: 10.1103/PhysRevD.95.033008

CrossRef Full Text | Google Scholar

82. Agnolet G, Baker G, Barker D, Beck R, Carroll TJ, Cesar J, et al. Background Studies for the MINER coherent neutrino scattering reactor experiment . Nucl Instrum Methods Phys Res A. (2017) 853:53–60. doi: 10.1016/j.nima.2017.02.024

CrossRef Full Text | Google Scholar

83. Bethe HA. Supernova mechanisms. Rev Mod Phys. (1990) 62:801–66. doi: 10.1103/RevModPhys.62.801

CrossRef Full Text | Google Scholar

84. Fröhlich C, Martínez-Pinedo G, Liebendörfer M, Thielemann FK, Bravo E, Hix WR, et al. Neutrino-induced nucleosynthesis of A>64 nuclei: the vp process. Phys Rev Lett. (2006) 96:142502. doi: 10.1103/PhysRevLett.96.142502

CrossRef Full Text | Google Scholar

85. Janka H-Th, Mueller B. Neutrino-driven type-II supernova explosions and the role of convection. Phys Rep. (1995) 256:135–56.

Google Scholar

86. Janka H-Th, Langanke K, Mareka A, Martinez-Pinedo G, Mullera B. Theory of core-collapse supernovae. Phys Rep. (2007) 442:38–74. doi: 10.1016/j.physrep.2007.02.002

CrossRef Full Text | Google Scholar

87. Janka HT, Hillebrand W. Neutrino emission from type II supernovae – an analysis of the spectra. Astron Astrophys. (1989) 224:49–56.

Google Scholar

88. Keil MT, Raffelt GG, Janka H-T. Monte Carlo study of supernova neutrino spectra formation. Astrophys J. (2003) 590:971–91. doi: 10.1086/375130

CrossRef Full Text | Google Scholar

89. Raffelt GG, Keil MT, Buras R, Janka H-T, Rampp M. Supernova neutrinos: flavor-dependent fluxes and spectra. Proc Neutrino Oscill Origin. (2004) 03:380–7. doi: 10.1142/9789812703101_0044

CrossRef Full Text | Google Scholar

90. Duan H, Fuller GM, Qian Y-Z. Stepwise spectral swapping with three neutrino flavors. Phys Rev D. (2008) 77:085016. doi: 10.1103/PhysRevD.77.085016

CrossRef Full Text | Google Scholar

91. Jachowicz N, McLaughlin GC. Reconstructing supernova-neutrino spectra using low-energy beta beams. Phys Rev Lett. (2006) 96:172301. doi: 10.1103/PhysRevLett.96.172301

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Tsakstara V, Kosmas TS, Divari PC, Sinatkas J. The interpretation of SN?v signals in terrestrial experiments through the folding procedure. AIP Conf Proc. (2009) 1180:140–4. doi: 10.1063/1.3266092

CrossRef Full Text | Google Scholar

93. Tsakstara V, Kosmas TS. Neutrino-nucleus reactions in terrestrial experiments and astrophysics. Prog Part Nucl Phys. (2010) 64:407–10. doi: 10.1016/j.ppnp.2009.12.060

CrossRef Full Text | Google Scholar

94. Scholberg K. Supernova signatures of neutrino mass ordering. J Phys G.(2018) 45:014002. doi: 10.1088/1361-6471/aa97be

CrossRef Full Text | Google Scholar

95. Vissani F, Pagliaroli G. The diffuse supernova neutrino background: expectations and uncertainties derived from SN1987A. Astron Astrophys. (2011) 528:L1. doi: 10.1051/0004-6361/201016109

CrossRef Full Text | Google Scholar

96. Moeller K, Suliga AM, Tamborra I, Denton PB. Measuring the supernova unknowns at the next-generation neutrino telescopes through the diffuse neutrino background. J Cosmol Astropart Phys. (2018) 1805:066. doi: 10.1088/1475-7516/2018/05/066

CrossRef Full Text

97. Bohr A, Mottelson BR. Nuclear Structure. New York, NY: Benjamin (1969).

A. Appendix

A.1. Three-Point Formulas for Empirical Energy Gaps ${\Delta }_{n,p}^{exp}$ of Neutrons and Protons

The empirical energy gaps for neutrons, ${\Delta }_n^{exp}$, and protons, ${\Delta }_n^{exp}$, needed at the BCS level to construct the ground state wave function of the detector nucleus (A, Z), are computed through the respective separation energies for neutrons, S_n or protons, S_p of the isotope (A, Z) and also those of the neighboring nuclear isotopes with N ± 1 neutrons or Z ± 1 protons, respectively, by employing the expressions

$\begin{array}{ll}{\Delta }_n^{exp}=-\frac{1}{4}\left[S_n(N-1,Z)-2S_n(N,Z)+S_n(N+1,Z)\right]& (\text{A}1)\end{array}$

$\begin{array}{ll}{\Delta }_p^{exp}=-\frac{1}{4}\left[S_p(N,Z-1)-2S_p(N,Z)+S_p(N,Z+1)\right]& (\text{A}2)\end{array}$

The above equations are known as the three-point formulas (see, e.g., [69, 97]).

A.2. Normalization of the ν Energy Distributions η(ε_ν) Adopted in This Work

The distributions η(ε_ν) adopted in the present work (see section 4), are considered to be normalized in such a way that

$\begin{array}{ll}{\displaystyle {{\displaystyle \int }}_0^{\infty }}\eta ({\epsilon }_{\nu })d{\epsilon }_{\nu }=1.& (\text{A}3)\end{array}$

For example, in the case of η_νe(ε_ν) of Figure 3D, the normalization gives

$\begin{array}{l}(96/M_{\mu }^4)\left[M_{\mu }{\displaystyle {{\displaystyle \int }}_0^{M_{\mu }/2}}{\epsilon }_{\nu }^{2}d{\epsilon }_{\nu }-2{\displaystyle {{\displaystyle \int }}_0^{M_{\mu }/2}}{\epsilon }_{\nu }^{3}d{\epsilon }_{\nu }\right]=1\end{array}$

where we have used ${\epsilon }_{\nu }^{min}=0$ and ${\epsilon }_{\nu }^{max}=M_{\mu }/2$

A.3. Parametrization of Supernova Neutrino Energy Spectra

The Fermi-Dirac (FD) and Power-law (PL) energy distribution are commonly used in Supernova neutrino parametrizations. Both the FD and PL yield very similar distributions characterized by the temperature T or the average energy 〈ε_ν〉 and the width w of the spectrum is defined as

$\begin{array}{l}w=\sqrt{\langle {\epsilon }_{\nu }^2\rangle -{\langle {\epsilon }_{\nu }\rangle }^2}/w_0\end{array}$

where $w_0={\epsilon }_{\nu }/\sqrt{3}$ is the width of the identical FD and PL distributions [13].

A.3.1. Fermi-Dirac (FD) Energy Distribution

By introducing the degeneracy parameter n_dg (equal to the ratio of the chemical potential μ divided by the neutrino temperature T, i.e., n_dg = μ/T), the Fermi-Dirac energy distribution reads

$\begin{array}{ll}{\eta }_{FD}\left[x,T,n_{dg}\right]=F(n_{dg})\frac{1}{T}\frac{x^2}{1+e^{(x-n_{dg})}},x=\frac{{\epsilon }_{\nu }}{T}.& (\text{A}4)\end{array}$

In this case, the width of the spectrum is reduced compared to the corresponding thermal spectrum (pinching effect). The normalization constant F₂(n_dg) of this distribution depends on the degeneracy parameter n_dg and is given by the relation

$\begin{array}{ll}\frac{1}{F(n_{dg})}\equiv {\displaystyle {\int }_0^{\infty }}\frac{x^2}{e^{x-n_{dg}}+1}dx.& (\text{A}5)\end{array}$

Inserting Equation (A5) into Equation (A4), we take

$\begin{array}{ll}{\eta }_{FD}\left[{\epsilon }_{\nu },T,n_{dg}\right]={\left[{\displaystyle {\int }_0^{\infty }}\frac{x^2}{e^{x-n_{dg}}+1}dx\right]}^{-1}\frac{({\epsilon }_{\nu }^2/T^3)}{1+e^{({\epsilon }_{\nu }/T-n_{dg})}}.& (\text{A}6)\end{array}$

A.3.2. Power-Law Energy Distribution

The SN-neutrino energy spectra can be fitted by using a Power-Law energy distribution of the form [88]

$\begin{array}{ll}{\eta }_{PL}\left[\langle {\epsilon }_{\nu }\rangle ,\alpha \right]=C{\left(\frac{{\epsilon }_{\nu }}{\langle {\epsilon }_{\nu }\rangle }\right)}^{\alpha }{e}^{-(\alpha +1)({\epsilon }_{\nu }/\langle {\epsilon }_{\nu }\rangle )},& (\text{A}7)\end{array}$

where 〈ε_ν〉 is the neutrino mean energy. The parameter α adjusts the width of the spectrum (see text). The normalization factor C, is calculated from the normalization condition

$\begin{array}{ll}C{\displaystyle {\int }_0^{\infty }}{\left(\frac{{\epsilon }_{\nu }}{\langle {\epsilon }_{\nu }\rangle }\right)}^{\alpha }{e}^{-(\alpha +1)({\epsilon }_{\nu }/\langle {\epsilon }_{\nu }\rangle )}d{\epsilon }_{\nu }=1.& (\text{A}8)\end{array}$

From the later equation we find

$\begin{array}{ll}C=\frac{{(\alpha +1)}^{\alpha +1}}{\Gamma (\alpha +1)\langle {\epsilon }_{\nu }\rangle },& (\text{A}9)\end{array}$

therefore, Equation (A7) becomes

$\begin{array}{ll}{\eta }_{PL}\left[\langle {\epsilon }_{\nu }\rangle ,\alpha \right]=\frac{{(\alpha +1)}^{\alpha +1}}{\Gamma (\alpha +1)}\frac{{\epsilon }_{\nu }^{\alpha }}{{\langle {\epsilon }_{\nu }\rangle }^{\alpha +1}}{e}^{-(\alpha +1)({\epsilon }_{\nu }/\langle {\epsilon }_{\nu }\rangle )}.& (\text{A}10)\end{array}$