Light Scalars in Composite Higgs Models

A composite Higgs boson is likely to be accompanied by additional light states generated by the same dynamics. This expectation is substantiated when realizing the composite Higgs mechanism by an underlying gauge theory. We review the dynamics of such objects, which may well be the first sign of compositeness at colliders. We also update our previous analysis of the bounds from LHC searches to the latest results and discuss the projected reach of the High-Luminosity run.

1. Introduction

Models of composite Higgs are a valid option for describing new physics beyond the Standard Model (SM). In this approach, the Higgs sector is replaced by confining dynamics, with the merit of solving the problem of hierarchy, as the only mass scale in the sector is dynamically generated, like in quantum chromo-dynamics (QCD). Furthermore, the breaking of the electroweak (EW) symmetry also arises dynamically, in contrast to the SM where it is merely described by a wrong-sign mass term.

The idea of dynamical EW symmetry breaking is as old as the SM itself [1], however in its first form lacked the presence of a light scalar degree of freedom, the Higgs boson. Later, it was proposed that the Higgs may arise as a pseudo-Nambu Goldstone boson (pNGB) of a global symmetry breaking [2]. This latter class of models saw a revival in the 2000's, following the development of holography in warped extra dimensions [3]. A minimal model of composite pNGB Higgs was thus proposed in Agashe et al. [4], and it has since been extensively studied in the literature (see [5–7], and references therein). The Higgs thus arises as a pNGB from the symmetry breaking pattern SO(5)/SO(4), together with the three Goldstones eaten by the W and Z bosons.

A key ingredient is the concept of partial compositeness [8] for the SM fermions, as a means to generate their masses and the SM flavor structures. The generation of a sizeable top-quark mass is particularly challenging and partial compositeness provides a possible solution by mixing the elementary fermions with a composite operator that has a large scaling dimension. This feature, again, follows from the constructions in warped space [9, 10], where the SM fermions mix with bulk ones. We want to stress here that the main motivation behind the introduction of partial compositeness was to address the mass and flavor problems while avoiding the generic appearance of large flavor changing neutral currents among SM fermions. Only later, inspired by the holographic principle [11], did the role of the composite top partners extended to the role of regulators of the loop divergences of the Higgs mass, by assuming the finiteness of the full one loop expression via sum rules [11, 12]. This, in turn, implies the necessity for light and weakly coupled spin-1/2 resonances [12, 13]. Nevertheless, alternatives to regulate the top loops exist, and the potential generated by such loops can be stabilized by, for instance, the introduction of masses for the underlying fermions [14, 15].

Another approach to composite dynamics, closer in spirit to the origin of the dynamical EW symmetry breaking of Technicolor, consists in defining an underlying theory in terms of gauge and fermion degrees of freedom, that confine at low energies [15]. In this approach, it is not possible to naturally obtain the minimal coset.¹ In turn, once the underlying dynamics is specified, only three kinds of patterns are allowed [19, 20]: SU(N)/Sp(N), SU(N)/SO(N) and SU(N) × SU(N)/SU(N). The minimal model is thus based on SU(4)/Sp(4), which can be obtained with an underlying SU(2) gauge theory [14, 21] and features only 5 pNGBs: the Higgs doublet plus a CP-odd singlet [14, 15]. Other minimal cosets are SU(5)/SO(5) [22] and SU(4) × SU(4)/SU(4) [23].

The inclusion of partial compositeness poses additional constraints in building the model, in primis the fact that many additional underlying fermions are needed, therefore loss of asymptotic freedom follows. In Ferretti and Karateev [24], a systematic construction of underling models, with partial compositeness for the top, was done. The main new ingredient was the sequestering of QCD color charges, which need to be carried by the underlying fermions in order to give color to the spin-1/2 resonances, to a new species of fermions, χ, that transforms under a different representation of the confining group than that of the fermions, ψ, giving rise to the composite Higgs. Thus, no dangerous mixing between the EW symmetry breaking and potential color breaking arises. The spin-1/2 bound states, therefore, arise as “chimera baryons” [25] made of ψψχ or ψχχ, depending on the model. There are few other cases where partial compositeness can be achieved with a single species of fermions: a confining SU(3) gauge symmetry with fermions in the fundamental, à la QCD, as proposed in Vecchi [26]; SU(6) with fermions in the two-index anti-symmetric representation and E₆ with the 27. The QCD colored fermions, in the latter cases, act as “heavy flavors”, in order to avoid light QCD colored pNGBs.

Phenomenologically, the most interesting feature of this class of underlying theories is the fact that global symmetries in the effective low-energy model are determined. In particular, one realizes that a symmetry comprising of QCD is unavoidable. Furthermore, there is always a non-anomalous U(1) charge, acting on both species of fermions, which is broken by (at least) the chiral condensate in the EW (Higgs) sector of the theory. This results in one light pNGB singlet under all the SM gauge symmetries. This state may be the lightest of the pNGB spectra, as it typically does not receive any mass contribution from top and gauge loops [27]. The properties of this state have been studied in Cai et al. [28], Belyaev et al. [29], Belyaev et al. [27], DeGrand et al. [30], and Cacciapaglia et al. [31]. At the LHC, it can be copiously produced via gluon fusion with the coupling to gluons being generated by the Wess-Zumino-Witten anomaly term [32, 33] via the presence of the χ-fermions in the pNGB wave function. Couplings to other pNGBs and tops can also be predicted, once the underlying theory is specified. Furthermore, they can be produced via the decays of the top partner resonances [34]. The fact that the properties of this state can be predicted in terms of the underlying theory, and their potential lightness, is the most attractive feature. As a historical note, they were perfect candidates to explain the WW/WZ resonance at 2 TeV Cai et al. [28] and the γγ resonance at 750 GeV [29] hinted at by the LHC data, which later appeared to have been statistical fluctuations. Other light states comprise of additional EW-charged pNGBs arising from the Higgs sector, and QCD-colored states coming from the condensation of the χ's.

In this work, we will mainly focus on the singlet pNGB associated to the global U(1) symmetry. If both fermion species condense, it is accompanied by a second pseudo-scalar singlet associated to the anomalous U(1) charges. The latter will receive a mass term from the anomaly, in a similar fashion to the η′ in QCD. Nevertheless, it may be relatively light, as expected at large-N_c for instance. We will therefore consider the phenomenology at the LHC to come from the presence of both states. This work follows Belyaev et al. [27] closely, and our main new contribution is the update of the bounds to the latest LHC searches, and the addition of projections at the High-Luminosity-LHC (HL-LHC) run. We will see that the bounds on the compositeness scale derived from the non-discovery of such a state can be much stronger than the typical bounds from electroweak-precision tests. The latter are usually considered the main constraints on models of Composite Higgs. Conversely, they appear to have the best prospects for being discovered at the LHC. The HL-LHC run will be crucial in this case, due to the lightness of such states and the paucity of current searches focusing on the low mass region between 14 and 65 GeV.

Before presenting our results, we should stress that these theories are not full Ultra-Violet (UV) completions of composite Higgs models with partial compositeness. One point is that the number of fermions we can introduce before loosing confinement (asymptotic freedom) is limited, thus one can only have enough to give mass to the top quark in this way. Furthermore, the theory needs to lie outside the conformal Infra-Red (IR) window [35]. It was shown that only 12 models are consistent with these requirements, while having the minimal Higgs cosets [36]. The second point is that the origin of the four-fermion interactions giving rise to the mixing between the SM tops and the composite fermions is not explained. Finally, the consistency of flavor bounds usually requires the theory to enjoy an IR conformal phase right above the condensation scale. This allows to split the scale where the masses of light quarks and leptons are generated from the confinement scale [37, 38], which should not be far from the TeV. In the underlying theory under study, this can be achieved by adding a few additional fermions at a mass close to the condensation scale, such that the theory above this scale is right inside the conformal window. Being just above the lower edge of the conformal window is crucial if one needs the composite fermions to have large anomalous dimensions, as the theory is expected to be strongly interacting around the IR fixed point near the lower edge of the conformal window. A first step toward the construction of truly UV complete theories can be found in Cacciapaglia et al. [39], based on the potential presence of a UV safe fixed point, due to large multiplicities of fermions.

As a final introductory word, we should also mention one main benefit of this approach: once an underlying theory is defined, it can be studied on the lattice. Thus, spectra and various properties of the theory in the strong sector can, in principle, be computed. This includes low-energy constants, which are crucial for the generation of the Higgs misalignment potential and the Higgs boson mass [40]. So far, theories based on confining SU(4) [25, 41] and Sp(4) [42–45] are being studied. For SU(4), preliminary results on the spectra [25] show that the chimera baryons tend to be heavy and beyond the reach of the LHC, while first calculations of the relevant form factors Ayyar et al. (Unpublished) show a suppressed mixing to the top. This would disqualify them as “light” top partners that regulate the Higgs mass loop [12, 13], however they would still play a role in generating the top mass and help with the flavor issue. It should be mentioned however that current lattice results do not yet include a realistic multiplicity of fermions, which may be crucial as the realistic models are close to the conformal window. Finally, we mention the possibility that spin-1/2 resonances may arise as a bound state between a fermion and a scalar, both carrying underlying color charges [46] (see also [17]). The price to pay, in this case, is the presence of fundamental scalars in the theory (unless the underlying scalars arise themselves as bound states of a theory that confines at higher energies or are protected by supersymmetry at high scales).

The paper is organized as follows: in section 2 we recap the main properties of the 12 underlying models. In section 3 we summarize the main properties of the pseudo-scalars associated with the two spontaneously broken U(1) global symmetries and present the updated bounds on the singlet pNGBs in section 4. We offer our conclusions in section 5.

2. Underlying Models for a Composite Higgs With Top Partial Compositeness

In this work we are interested in the underlying models for composite Higgs with top partial compositeness defined in Ferretti and Karateev [24]. These models characterize the underlying dynamics below the condensation scale Λ ≈ 4πf, f being the decay constant of the pNGBs. As such, the need to be outside of the conformal window leaves only 12 models [36], listed in Table 1. They are defined in terms of a confining gauge interaction, that we call hypercolor (HC), and two species of fermions in two different irreducible representations of the HC. The two species of fermions play different roles: the EW charged ψ's generate the Higgs and the EW symmetry breaks upon condensation, and their multiplicity is chosen to match the minimal cosets; the QCD charged χ's consist of a triplet and an anti-triplet of QCD color, thus always amounting to 6 Weyl spinors. We will also assume that both fermions condense and thus the chiral symmetry in each sector is broken. In principle, the χ's may not condense and the 't Hooft anomaly matching condition may lead to the presence of light composite fermions, that may play the role of top partners [47]. However, assuming the persistent mass condition, it is possible to show that chiral symmetry breaking must occur in both cosets [36]: the argument goes that by giving a common mass to one class of fermions at a time, the chimera baryons that saturate the global 't Hooft anomaly would become massive and thus ineffective. The final answer can only be found on the lattice. The phenomenology of two of the models have been studied in detail, M8 in Barnard et al. [48] and M6 in Ferretti [49]. Lattice studies for the two models are also underway based on SU(4)_HC [25] (which also applies to M11), and Sp(4)_HC [44, 45] (which also applies to M5). Note that a study based on a Nambu Jona-Lasinio effective model of M8 can be found in Bizot et al. [50]. As shown in Table 1, the baryons that enter partial compositeness for the top arise either as ψψχ or ψχχ bound states, depending on the representations under HC.

TABLE 1

Table 1. Model details.

It is expected that the lightest states in these models are the pNGBs, that arise from the breaking of the chiral symmetries in the two sectors, while the fermionic and spin-1 resonances are expected to be heavier. The quantum numbers of the pNGBs in the 12 models are listed in Table 2. They can be organized in three classes:

TABLE 2

Table 2. Light pNGBs in each of the 12 models.

A) The ones arising from the EW coset, i.e., the chiral symmetry breaking in the ψ sector, only carry EW quantum numbers. All cosets contain at least one singlet, thus being non-minimal compared to the holographic SO(5)/SO(4) model. The production rate of these states at the LHC is typically very small, as it is due to EW interactions, and thus are very difficult to observe at the LHC. The neutral components may also couple to two gluons via loops of tops, however still give rise to small production rates. The case of the singlet in the SU(4)/Sp(4) coset has been studied in detail in Galloway et al. [14] and Arbey et al. [51], note however that the same considerations apply to singlets in the other cosets. The SU(5)/SO(5) case can be found in Ferretti [49, 52]. Finally, the SU(4)²/SU(4) case is special compared to the other two, as it allows for a stable pNGB that may play the role of Dark Matter [53].

B) The ones arising from the chiral breaking in the χ sector, i.e., QCD coset, always carry QCD charges. A ubiquitous member of this class is a neutral color octet [27, 54]. For all those pNGBs, pair production via QCD interactions can be substantial at the LHC [55] for masses below or around 1 TeV. The phenomenology of the color sextet in the context of model M8 has been studied in Cacciapaglia et al. [54]. After Run-I at the LHC, the bound on their masses can be estimated around the 1 TeV scale. This bound is still compatible with the fact that one-loop self-energy diagrams, involving a gluon, put their masses roughly in that range.

C) The U(1) singlets are ubiquitous to all models. Their phenomenology has been studied in detail in Belyaev et al. [27]. They will be the main focus of this work. While they are singlets under the gauge symmetries of the SM, couplings arise via the topological WZW anomalies, which include coupling to gluons. In this, they differ from the EW cosets, where couplings to gluons can only arise via top loops. We can therefore expect larger production rates for them.

All models in M1-M12 preserve custodial symmetry. Indeed, this requirement is central in their construction and determines the minimum amount of fermionic matter present in each model. For custodial symmetry to be preserved one needs to be able to embed a SU(2)_L × SU(2)_R group into the unbroken group H of the electroweak cosets G/H. This requirement is satisfied by choosing H = SO(N_o) with N_o ≥ 4, H = Sp(2N_p) with N_p ≥ 2 or H = SU(N_u) with N_u ≥ 4. However, the further requirement that there be a Higgs field in the bi-fundamental of SU(2)_L × SU(2)_R, requires to take N_o ≥ 5. Thus, ρ = 1 at tree level in these constructions, as long as the triplet pNGBs (when present), do not acquire a vacuum expectation value.

3. Light U(1) Pseudo-scalars

In this section we summarize the main properties of the two U(1) pseudo-scalars, one of which associated with non-anomalous global symmetry. Most of the results shown in this section can be found in Belyaev et al. [27], where a more detailed analysis can be found. We refer to other results in the literature when necessary. This section can be considered a handbook for anybody who is interested in studying the phenomenology of such states, as we will provide all the relevant couplings and formulas necessary to compute cross-sections and branching ratios.

Following the notation in Belyaev et al. [27], we call two mass eigenstates {a, η′}, with a being the lighter one, which is also closer to the anomaly-free U(1) boson. The masses, which also determine the mixing angle between the two states, receive three contributions: two from the masses of the underlying fermions ψ and χ, and one from the anomalous U(1) combination. Assuming that m_χ ≫ m_ψ, and neglecting the latter, the mixing angle can be determined in terms of the mass eigenvalues. We define the mixing angle α between the mass eigenstates and the pseudo-scalars associated to the U(1)_ψ and U(1)_χ charges. Thus, in the decoupling limit $M_{{\eta }^{\prime }}\gg M_a$, the mixing angle is given by

$\begin{array}{ll}sin\alpha {|}_{dec.}=-1/\sqrt{1+\frac{q_{\psi }^2{N}_{\psi }}{q_{\chi }^2{N}_{\chi }}\frac{f_{\psi }^2}{f_{\chi }^2}},& (1)\end{array}$

where q_ψ and q_χ are the charges of the anomaly-free U(1) (see Table 1), f_{ψ, χ} are the decay constants in the two sectors, and N_{ψ, χ} their multiplicity. Note that only the ratio f_ψ/f_χ is not fixed but depends on the strong dynamics (thus calculable on the lattice [25]). However, we can fix it by applying the Maximal Attractive Channel (MAC) hypothesis [56], see Table 3 in Appendix A. Once this is fixed, all the couplings of the pseudo-scalars to SM states are fixed in terms of the properties of the underlying dynamics, as we will show below.

The relevant effective Lagrangian for both pseudo-scalars, i.e., ϕ = {a, η′}, can be generically parameterized as

$\begin{array}{ll}\begin{array}{c}{{L}}_{\mathrm{\text{eff}}}\supset \frac{1}{2}({\partial }_{\mu }\varphi )({\partial }^{\mu }\varphi )-\frac{1}{2}{m}_{\varphi }^2{\varphi }^2\hfill \\ +\frac{\varphi }{16{\pi }^2{f}_{\psi }}{(g}_s^2{K}_g^{\varphi }{G}_{\mu \nu }^a{\tilde{G}}^{a\mu \nu }\hfill \\ +g^2{K}_W^{\varphi }{W}_{\mu \nu }^i{\tilde{W}}^{i\mu \nu }+g^{\prime 2}{K}_B^{\varphi }{B}_{\mu \nu }{\tilde{B}}^{\mu \nu })\hfill \\ -i{\displaystyle \sum _f}\frac{C_f^{\varphi }{m}_f}{f_{\psi }}\varphi {\bar{\psi }}_f{\gamma }^5{\psi }_f\hfill \\ +\frac{2v}{f_{\psi }^2}{K}_{\varphi h}^{\text{eff}}({\partial }_{\mu }\varphi )({\partial }^{\mu }\varphi )h+\frac{2m_Z}{f_{\psi }}{K}_{hZ}^{\text{eff}}({\partial }_{\mu }\varphi )Z^{\mu }h\hfill \end{array}\hfill & (2)\end{array}$

with ${\tilde{F}}^{\mu \nu }=\frac{1}{2}{ϵ}^{\mu \nu \rho \sigma }{F}^{\rho \sigma }$ for F = {G^a, Wⁱ, B}. Note that we have normalized the couplings with the decay constant in the Higgs sector, f_ψ, which is directly related to the tuning in the misalignment potential as v = f_ψsinθ [27]. We could also have defined a U(1)-singlet decay constant

$\begin{array}{ll}{f}_a=\sqrt{\frac{q_{\psi }^2{N}_{\psi }{f}_{\psi }^2+q_{\chi }^2{N}_{\chi }{f}_{\chi }^2}{q_{\psi }^2+q_{\chi }^2}},& (3)\end{array}$

as in Cacciapaglia et al. [31]. The relation between the two decay constants is given in Table 3.

The Lagrangian in Equation (2) matches with a generic Axion-Like Particle (ALP) Lagrangian [57–59], except that the various coefficients can be computed. The couplings in the last two lines are generated by loops of tops and gauge bosons (dominantly), but differ from the results from a generic ALP Lagrangian [59, 60] due to non-linear couplings of the pNGBs in the composite models [31]. In the following, we shall review how each of the terms in the effective Lagrangian can be calculated. All the numerical coefficients, in the decoupling limit and in the minimal mass splitting limit, are given in Tables 3, 4 in Appendix A. The numbers we provide here assume the MAC relation between the decay constants, as used in Cacciapaglia et al. [31], while the values in Belyaev et al. [27] assume f_ψ = f_χ.

The computability of all the coefficients is one of the main appeals of these models, having an underlying gauge theory construction. For each model that has a fixed gauge group and representation for the underlying fermions, once a discrete choice of the representation of the top partners under the global symmetry is done, the phenomenology of the pseudo-scalars is determined in terms of only three independent continuous parameters (the masses m_ϕ with ϕ = a, η′ and a common decay constant f_ψ). All the couplings and ratios of the decay constants for the various cosets can be computed as shown in Tables 3, 4 in Appendix A. The only assumption we make is that the tops couple dominantly to only one composite operator.

3.1. Couplings to Gauge Bosons

The general couplings of the singlet pseudo-scalars to gauge bosons are almost entirely dictated by the quantum numbers of the underlying dynamics, i.e.,

$\begin{array}{ll}{K}_V^a=c_5\left(\frac{C_V^{\psi }}{\sqrt{N_{\psi }}}cos\alpha +\frac{f_{\psi }}{f_{\chi }}\frac{C_V^{\chi }}{\sqrt{N_{\chi }}}sin\alpha \right),& (4)\end{array}$

with $K_V^{{\eta }^{\prime }}$ obtained from the above expression with the replacement α → α+π/2. In the above expression, $c_5=\sqrt{2}$ for models with SU(5)/SO(5) breaking and 1 otherwise, $C_V^{\psi ,\chi }$ are the anomaly coefficients of the singlets associated with U(1)_{χ, ψ} groups which are fully determined by the SM charges of the underlying fermions². Thus, the only dependence on the mixing angle α remains, which is determined by the masses of the two states. In the Tables in Appendix A we give values in the two limiting cases of minimal mass splitting and decoupling.

One can rewrite the WZW interactions in terms of the physical gauge bosons, i.e.,

$\begin{array}{l}{{L}}_{\text{eff}}\supset \frac{\varphi }{16{\pi }^2{f}_{\psi }}(g_s^2{K}_{gg}^{\varphi }{G}_{\mu \nu }^a{\tilde{G}}^{a\mu \nu }+g^2{K}_{WW}^{\varphi }{W}_{\mu \nu }^{+}{\tilde{W}}^{-\mu \nu }\\ +e^2{K}_{\gamma \gamma }^{\varphi }{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }+\frac{e^2}{s_W^2{c}_W^2}{K}_{ZZ}^{\varphi }{Z}_{\mu \nu }{\tilde{Z}}^{\mu \nu }\\ +\frac{2e^2}{s_W{c}_W}{K}_{Z\gamma }^{\varphi }{F}_{\mu \nu }{\tilde{Z}}^{\mu \nu })& (5)\end{array}$

with

$\begin{array}{ll}\begin{array}{c}{K}_{\gamma \gamma }^{\varphi }=K_W^{\varphi }+K_B^{\varphi },K_{Z\gamma }^{\varphi }=c_W^2{K}_W^{\varphi }-s_W^2{K}_B^{\varphi },\\ K_{ZZ}^{\varphi }=c_W^4{K}_W^{\varphi }+s_W^4{K}_B^{\varphi }.\end{array}& (6)\end{array}$

The couplings of a and η′ to gauge bosons are thus determined purely from the underlying dynamics with one assumption, i.e., the validity of the MAC hypothesis. The only external dependence arises from the masses via the mixing angle α. Table 3 in Appendix A shows the resulting couplings of a and η′ for all 12 underlying models. Typically, in a generic mixing angle, the couplings vary between the two limits shown.

The couplings to two-gauge bosons also receive contributions at loop-level, in particular from top-loops, which are particularly relevant at low masses and can affect the production rate via gluon fusion and the decays. These contributions were fully computed in Belyaev et al. [27], and their effect expressed in terms of the Branching Ratio formulas:

$\begin{array}{l}\Gamma (\varphi \to \text{had})=\frac{{\alpha }_s^2(m_{\varphi })m_{\varphi }^3}{8{\pi }^3{f}_{\psi }^2}\left[1+\frac{83}{4}{\alpha }_s(m_{\varphi })\right]\\ \times {\left|K_{gg}^{\varphi }+C_t^{\varphi }{{C}}_0\left(0,{\tau }_{\varphi /t},0;1\right)\right|}^2& (\mathrm{7a})\end{array}$

$\begin{array}{ll}\Gamma (\varphi \to \gamma \gamma )=\frac{{\alpha }^2{m}_{\varphi }^3}{64{\pi }^3{f}_{\psi }^2}{\left|K_{\gamma \gamma }^{\varphi }+\frac{8}{3}{C}_t^{\varphi }{C}_0\left(0,{\tau }_{\varphi /t},0;1\right)\right|}^2& (\mathrm{7b})\end{array}$

$\begin{array}{l}\Gamma (\varphi \to WW)=\frac{{\alpha }^2{m}_{\varphi }^3{\left(1-4{\tau }_{W/\varphi }\right)}^{3/2}}{32{\pi }^3{f}_{\psi }^2{s}_W^4}\\ \times {\left|K_{WW}^{\varphi }-\frac{3}{2}{C}_t^{\varphi }{C}_{1+2}\left({\tau }_{W/t},{\tau }_{\varphi /t},{\tau }_{W/t};\sqrt{{\tau }_{b/t}}\right)\right|}^2& (\mathrm{7c})\end{array}$

$\begin{array}{l}\Gamma (\varphi \to Z\gamma )=\frac{{\alpha }^2{m}_{\varphi }^3{\left(1-{\tau }_{Z/\varphi }\right)}^3}{32{\pi }^3{f}_{\psi }^2{s}_W^2{c}_W^2}\\ \times {\left|K_{Z\gamma }^{\varphi }+C_t^{\varphi }\left(1-\frac{8}{3}{s}_W^2\right)C_0({\tau }_{Z/f},{\tau }_{\varphi /t},0;1)\right|}^2& (\mathrm{7d})\end{array}$

$\begin{array}{l}\Gamma (\varphi \to ZZ)=\frac{{\alpha }^2{m}_{\varphi }^3{\left(1-4{\tau }_{Z/\varphi }\right)}^{3/2}}{64{\pi }^3{f}_{\psi }^2{s}_W^4{c}_W^4}\\ |K_{ZZ}^{\varphi }+C_t^{\varphi }[s_W^2\left(\frac{8}{3}{s}_W^2-2\right)C_0\left({\tau }_{Z/t},{\tau }_{\varphi /t},{\tau }_{Z/t};1\right)\\ {-\frac{3}{4}{C}_{1+2}\left({\tau }_{Z/t},{\tau }_{\varphi /t},{\tau }_{Z/t};1\right)]|}^2& (7e)\end{array}$

with ${\tau }_{a/b}=m_a^2/m_b^2$ and ${{C}}_i({\tau }_{p_1/t},{\tau }_{p_{1+2}/t},{\tau }_{p_2/t};\sqrt{{\tau }_{f/t}})\equiv m_t^2{\text{C}}_i(p_1^2,{(p_1+p_2)}^2,p_2^2;m_f,m_t,m_t)$ the Passarino-Veltman functions with the normalization given in Package-X [61]. We have used the short-hand notation ${{C}}_{1+2}\equiv {{C}}_1+{{C}}_2$ and analytical expression for some of the simplest loop function can be found in Belyaev et al. [27]. $C_t^{\varphi }$ is the coupling to tops, which is discussed in the following subsection.

3.2. Coupling to Tops, Light Quarks, and Leptons

The coupling to tops only depends on the charges under the two U(1)'s of the composite operators that mix to the left-handed and right-handed tops. If we assume that the two top chiralities mix dominantly to one operator, there are only six possible charges that enter the coupling to tops via the top mass operator:

$\begin{array}{ll}(n_{\psi },n_{\chi })=(\pm 4,2),(0,\pm 2),(\pm 2,0),\mathrm{\text{for}}\psi \psi \chi ,& (8)\end{array}$

$\begin{array}{ll}(n_{\psi },n_{\chi })=(2,\pm 4),(0,\pm 2),(\pm 2,0),\mathrm{\text{for}}\psi \chi \chi ,& (9)\end{array}$

where n_ψ and n_χ are the net numbers of ψ and χ fields, respectively in the two operators coupling to the two top chiralities (see Belyaev et al. [27] for more details). Thus, the $C_t^a$ coefficient reads

$\begin{array}{ll}{C}_t^a=c_5\left(\frac{n_{\psi }}{\sqrt{N_{\psi }}}cos\alpha +\frac{n_{\chi }}{\sqrt{N_{\chi }}}\frac{f_{\psi }}{f_{\chi }}sin\alpha \right).& (10)\end{array}$

Like above, $C_t^{{\eta }^{\prime }}$ is given by α → α + π/2.

For the light quarks and leptons, we will assume, for simplicity, that their mass is coming from a direct coupling to a bilinear of ψ's, i.e., via an effective Yukawa coupling. This corresponds to the top case, but with fixed {n_ψ, n_χ} = {2, 0}.

The coupling to tops above has been computed by writing the effective operators generating the top mass, as in Golterman and Shamir [40] and Golterman and Shamir [62]. However, in Bizot et al. [34] it was noted that computing the coupling of the pseudo-scalars starting from the mixing to the top partners would lead to a different expression, differing by the presence of the mixing angles in the partial compositeness. For the top this has a minor impact on the numerical results, and we therefore chose to remain using the operator case.

3.3. Loop-induced Couplings to the Higgs and to Zh

Models with a pseudo-scalar state generically contain a coupling to Zh [60], which is generated at loop level. In our models, the leading contributions to the effective coupling between the singlet pseudo-scalars, Z and Higgs bosons are given by the diagrams in Figure 1 [31]. Explicit calculation for the coupling $K_{hZ}^{\varphi \mathrm{\text{eff}}}$ defined in Equation (2) gives:

$\begin{array}{l}{K}_{hZ}^{\varphi \text{\hspace{0.05em}eff}}=\frac{3m_t^2}{32{\pi }^{2}v{m}_Z}{C}_t^{\varphi }[2\left({\kappa }_t-{\kappa }_Z\right){{B}}_0\left({\tau }_{\varphi /t}\right)-{\kappa }_t({{B}}_0({\tau }_{h/t})\\ -{{B}}_0({\tau }_{\varphi /t})+(4-{\tau }_{Z/t})C_0({\tau }_{\varphi /t},{\tau }_{h/t},{\tau }_{Z/t};1)\\ +({\tau }_{\varphi /t}+{\tau }_{h/t}-{\tau }_{Z/t})C_1({\tau }_{\varphi /t},{\tau }_{h/t},{\tau }_{Z/t};1))]& (11)\end{array}$

with ${{B}}_0({\tau }_{p/t})\equiv {\text{B}}_0(p^2;m_t,m_t)$, see Belyaev et al. [27] for the analytic expression. In the formula, the κ_t and κ_Z are the corrections to the Higgs coupling to tops and Z, respectively, normalized by the SM value. The loop function B₀ is UV-divergent and we have parameterized it in terms of a cutoff, i.e., $1/ϵ\to -1+ln(16{\pi }^2{f}_{\psi }^2/{\mu }^2)$. Note that the UV-sensitivity is only present in the term proportional to (κ_t − κ_Z), which reflects the non-linearities in the Higgs couplings, a common feature in all composite Higgs models. The partial width for the pseudo-scalar decay gives

$\begin{array}{ll}\Gamma (\varphi \to hZ)=\frac{m_{\varphi }^3}{16\pi f_{\psi }^2}|K_{hZ}^{\varphi \mathrm{\text{eff}}}{|}^2\lambda {(1,{\tau }_{Z/\varphi },{\tau }_{h/\varphi })}^{3/2}& (12)\end{array}$

with λ(x, y, z) the Källén function. For very light pseudo-scalars the decay h → ϕZ is allowed, with a partial width given by the formula above, with the replacement of m_ϕ ↔ m_h.

FIGURE 1

Figure 1. Leading contributions to the decay ϕ → Zh.

At loop level, a coupling hϕ² is also generated. This is relevant for m_ϕ < m_h/2, for which Higgs decays into two pseudo-scalars are open. Explicit calculation of the leading diagrams, shown in Figure 2, gives

$\begin{array}{l}{K}_{\varphi h}^{\text{eff}}=\frac{3{\kappa }_t}{8{\pi }^2}{\left(\frac{C_t^{\varphi }{m}_t}{v}\right)}^2[{{B}}_0({\tau }_{\varphi /t})+2C_0\left({\tau }_{\varphi /t},{\tau }_{h/t},{\tau }_{\varphi /t};1\right)\\ +\frac{1}{1-2{\tau }_{a/h}}\left({{B}}_0({\tau }_{h/t})-{{B}}_0({\tau }_{a/t})\right)].& (13)\end{array}$

FIGURE 2

Figure 2. Leading contributions to the decay h → ϕϕ.

The Higgs decay to two pseudo-scalars is then given by³

$\begin{array}{ll}\Gamma (h\to \varphi \varphi )=\frac{v^2{m}_h^3}{32\pi f_{\psi }^4}|K_{\varphi h}^{\mathrm{\text{eff}}}{|}^2{(1-2{\tau }_{\varphi /h})}^2\sqrt{1-4{\tau }_{\varphi /h}}.& (14)\end{array}$

4. LHC Bounds and High-Luminosity Projections

The presence of the light composite pseudo-scalars can be tested at the LHC via the single production via gluon fusion, which is the dominant production mode, and further decays into a resonant pair of SM states. In this work we include both the effect from the WZW direct coupling to gluons, and the contribution of top and bottom loops. The cross-section calculation is performed at NLO in QCD by use of the HIGLU [63] code. For the tops, as shown above, we have six possible top partner assignment choices: following Belyaev et al. [27] and Cacciapaglia et al. [31], in the numerical results we chose the case {n_ψ, n_χ} = {2, 0}. A discussion of the effect of other choices can be found in Appendix B.

The strategy for applying bounds follows Belyaev et al. [27]. We collected all available searches, looking for resonant final states that may come from the pseudo-scalars, and extract a bound from the production cross section times branching ratio, assuming that the efficiencies of the experimental searches are the same on our model. This is a reasonable assumption, as the searches are mainly sensitive to the resonant nature of the signal, and much less on the possible kinematical differences in the production. Furthermore, we do not attempt to do a statistical combination of various searches, as we cannot take into account correlations of the systematic uncertainties in the experiments. Thus, we simply consider the most constraining search or signal region to extract a bound from for each final state. The final result is shown in Figure 3 for two representative models, M8 and M9. What connects the two is the fact that the global symmetries are the same, thus they can be characterized by the same low energy effective action based on the minimal SU(4)/Sp(4) EW coset and SU(6)/SO(6) QCD coset. However, as shown in the plot, the properties of the two pseudo-scalars are very different, hence leading to very different bounds. Note that we have re-expressed the bound on the cross sections into a bound on the decay constant of the Higgs. This is possible because all the coefficients of the couplings are calculable, as detailed in the previous section.

FIGURE 3

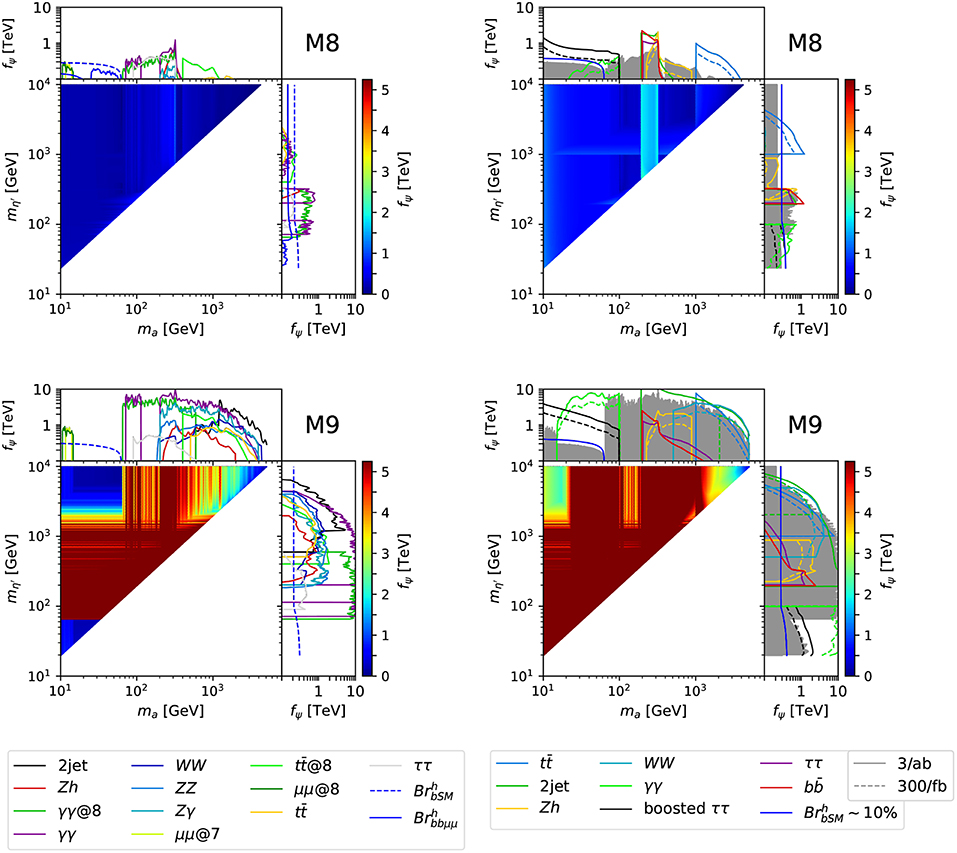
Figure 3. Heat-plots showing the lower bounds on the Higgs decay constant f_ψ in the mass plane of the two pseudo-scalars. The white triangle is not accessible by the masses in each model. The side-bands show the limits from each individual final state. On the left column, we show the current Run-I and Run-II bounds; on the right column, we show the projections at the High-Luminosity LHC run (the solid gray band summarizes the current bounds for comparison). More details in the text. Here we show model M8 (top row) and model M9 (bottom row).

Before commenting on the numerical results, we will list here all the searches we implemented.

i) The $t\bar{t}$ final state is only relevant for large masses and indicated in orange (Run-II at 13 TeV) and green (Run-I at 8 TeV) on the side-bands of the plots. We implemented a fully hadronic Run-II search by CMS [64], and two Run-I searches by CMS [65] (fully reconstructed tops) and ATLAS [66] (semi-leptonic).

ii) Di-jet searches (black line) can tag the di-gluon decay, however they are only sensitive at relatively large masses because of trigger limitations. We implemented Run-II searches by CMS [67, 68] and ATLAS [69].

iii) Di-boson final states, i.e., WW (dark blue line) and ZZ (light blue line), are mostly relevant above ≈160 GeV, when resonant decays are kinematically allowed. Many different final states are searched for at the LHC. We include the following Run-II searches by CMS [70– 77] and ATLAS [78–81].

iv) Di-photon resonances in this model are as important at low mass as at high mass, because they are generated at the same level as the decays to massive gauge bosons. We show in green the results at Run-I at 8 TeV, and in violet the ones at Run-II at 13 TeV. The implemented searches for ATLAS are at Run-I [82] and at Run-II [83]. For CMS, we use the combined Run-I + Run-II results for high mass [84, 85] and low mass [86, 87] ranges.

v) Similarly, γZ resonant search (cyan line) has an impact at high mass. We implemented the Run-II searches from CMS [88, 89] and ATLAS [90].

vi) A new channel we include in this work, which was previously missed in Belyaev et al. [27], is Zh. The limit, shown by the red line, corresponds to the ATLAS search [91]. This channel is always significantly above he threshold, but usually loses significance at the $t\bar{t}$ threshold.

vii) At the LHC, resonant di-tau searches have been performed for invariant masses above 90 GeV. The limit, shown by the gray line, however, typically plays a limited role because the branching ratio in taus is small at such mass values. We implemented the following Run-II searches by CMS [92, 93] and ATLAS [94, 95]. They are typically designed to tag supersymmetric heavy Higgses.

viii) At low mass, the di-muon final state becomes relevant. While the branching ratio is very small, suppressed by the muon mass, the cleanness of the final state makes this channel attractive, as long as it can pass the trigger requirements. The only two applicable bounds are a 7 TeV search (lime green light) at low mass done by CMS [96], which tags the mass range between 10 and 15 GeV thanks to a dedicated trigger, and a 8 TeV search (dark green) done by LHCb [97] in the same mass range.

ix) For masses below m_h/2 ≈ 65 GeV, the decays of the Higgs into two pseudo-scalars starts playing a significant role. We implemented various searches dedicated to this channel, with final states including $b\bar{b}{\mu }^{+}{\mu }^{-}$ (blue line), 4τ's and 4γ's [98– 100], with the two last channels too small to enter in the plots. We also estimated the bound coming from the indirect measurement of undetected decays of the Higgs into new physics, which is currently BR_BSM < 30% [101], shown by the dot-dashed blue line. In our specific models, this is stronger than the direct searches, mainly because at the final states the searches focused on have small branching ratios.

x) Finally, we checked that constraints coming from associated production of the pseudo-scalars with $b\bar{b}$ [102, 103] and $t\bar{t}$ [104] are not competitive with production via Z decays [105] (Z→aγ).

The plots on the left column of Figure 3 show the limit on the Higgs decay constant f_ψ in the plane of the two pseudo-scalar masses and for models M8 and M9. For each point in the m_a–$m_{{\eta }^{\prime }}$ plane we compute independently the bounds on f_ψ coming from the a and η′ resonances and then show the most stringent one. In the two side-bands we show the strongest bound coming from a (top band) and η′ (right band), split into the various channel we considered. One important observation is that the limit often passes the 1 TeV mark. This is significant as typical electroweak precision bounds on this class of models give a lower limit on f around this scale [106–108]. Cases where the limit can be relaxed have been discussed in Contino and Salvarezza [109], Ghosh et al. [110], and Buarque Franzosi et al. (Unpublished). We note, therefore, that searches for these light pseudo-scalars can be the most constraining probe for these class of models. Also note the presence of a poorly constrained region for the 14 < m_a < 65 GeV window of the lightest pseudo-scalar (most evident for M9). This is mainly due to the paucity of direct searches that are significant in this low mass window, the strongest bound being on the new physics Higgs decay rate. Note that the latter will not significantly improve at the end of the HL-LHC [111]. It is therefore crucial to close this gap with searches dedicated to this region, which is present for all models. Note also that the constraints on M8 are always rather mild: this is due to the coupling to gluons, which is particularly low in this specific model. The plots, therefore, show how the constraints are particularly sensitive to the details of the underlying models, as the twin models M8 and M9 dramatically show. For comparison, in Figure 4 we show the bounds for another model, M7, based on the SU(5)/SO(5) coset, which shows an intermediate situation. Similar plots for all the other models are shown in Figures 7–9 in Appendix C. They all show a similar pattern of constraints.

FIGURE 4

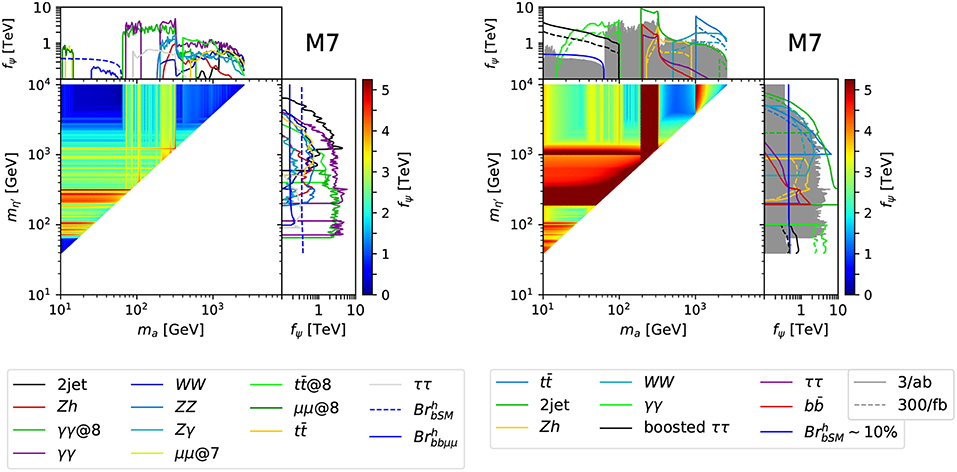
Figure 4. Same as Figure 3, for the model M7, based on the EW coset SU(5)/SO(5).

A new result we show in this paper is the inclusion of projections for the HL-LHC run. First, we would like to attack the low mass window, which is left open after the Run-II searches, as shown in all plots. In this window, the main decay channels are in two jets (either gluons or b quarks), followed by taus. Di-photon final states are also present, however current searches [83, 86, 87] cannot reach this low mass region due to trigger limitations.

In Cacciapaglia et al. [31] we proposed a new search based on the di-tau final state. To be able to pass the trigger requirements, we proposed to aim at the production of a single a that recoils against a high-p_T jet. This also allows to reduce the background level, while the reduction in the cross section still leaves a large signal rate. We analyzed in detail the case of leptonic decays of the two taus into different flavor leptons. Due to the high boost, the angular separation between the two leptons is typically very small. Thus, imposing an upper cut on the angular separation, ΔR_eμ < 1, allows to efficiently reduce the main background, coming from $t\bar{t}$ and Drell-Yan di-tau production. Fakes in this channel should have a limited impact, thus allowing us to derive reliable estimates for the reach. A key ingredient to improve the reach in the case of a small mass below 30−40 GeV is the reduction of the lower cut on the separation angle between the two leptons. The current minimal separation used at the LHC, see Khachatryan et al. [112] for instance, is ΔR_eμ>0.1÷0.2, as such it would lead to a degradation of the sensitivity for low invariant masses where the boost produces very low angles [31]. It would be necessary, therefore, to relax the isolation criteria and remove the minimal separation in order to optimize the reach. Furthermore, due to the low statistics, it is crucial to reduce at the maximum the systematic errors on the lepton reconstructions. For this reason, we focused on the fully leptonic case. The main systematics in boosted di-tau searches [113] come from hadronic tau decays and from the invariant mass reconstruction, which are not required in our study. We optimistically assume, therefore, that systematic uncertainties below the % level can be achieved. In the right plots of Figures 3, 4 and Figures 7–9 in Appendix C, we show the projected reach of this proposed search in black. The plots show that in most models it can effectively cover the low mass open window, with enhanced sensitivity to the low mass end. Note also that we only use the opposite-flavor fully leptonic channel. Nevertheless, semi-leptonic decays may also be used, by implementing advanced techniques, like the “mini-isolation” proposed in Rehermann and Tweedie [114], while tests of fully-hadronic di-tau tagging can be found in Katz et al. [115] and Conte et al. [116].

Another method that would allow to cover the low mass window is extracting indirect bounds from the di-photon differential cross section measurements, as proposed in Mariotti et al. [117]. We added a projection of this bound at High-Luminosity in red. Figure 3 effectively shows the complementarity between the two searches: for M8, the di-tau search gives stronger bounds in the full mass range, while for M9 the di-photon bound is more stringent while di-tau can only compete at the low mass end of the window. In Figure 4 we show another case, M7, where the complementarity between the two methods at the low and high ends of the open mass window is more evident. To complete the High-Luminosity projections, we also include projections for $t\bar{t}$ [118–120] (in blue), di-jet [119, 121, 122] (in green), Zh [123] (in orange), WW [124] (in cyan), ττ [125] (in violet), and $b\bar{b}$ [119, 122] (in red).

The plots on the right side of the Figures 3, 4 and Figures 7–9 in Appendix C show that the High-Luminosity run of the LHC will allow to effectively cover the full parameter space of the pseudo-scalar masses for nearly all models, provided that the searches addressing the low mass window are implemented. This is a last chance situation, as the sensitivity of high-energy future colliders to such low masses will be much lower.

Before concluding the section, we would like to comment on another search that can be potentially useful to cover the low-mass open window, i.e., the LHCb search for dark photons in the di-muon final state [126]. The main strength of this search relies on the cancellation of all systematic uncertainties. A recast of this search in the context of a two Higgs doublet model can be found in Haisch et al. [127]. While the systematics associated to the detector effects are reasonably similar between the pseudo-scalar resonance and the dark photon, the production channel (gluon fusion vs. Drell–Yann) remains different, thus a more detailed determination of the acceptances and systematics is needed for a recast in our case. The results of ongoing work will be presented in a separate publication.

5. Conclusions and Outlook

We have updated the bounds from various experimental searches on two potentially light pseudo-scalar mesons, which arise in models of composite Higgs with top partial compositeness, with an underlying gauge-fermion description. We have provided a handbook containing all the relevant information necessary to study the phenomenology in any of the variations of the 12 possible basic models. In each model, the couplings of the two states can be computed in terms of the properties of the underlying gauge theory and of the two decay constants in the two sectors, one related to the EW symmetry breaking and the other to QCD carrying states.

We found that, in most models, scanning for masses up to 10 TeV, the non-observation of a resonance allows to set a bound on the compositeness scale, that surpasses the typical bound from electroweak precision tests. This result shows how the observation of these states can be a smoking gun for these class of theories, while also carrying precious information on the details of the underlying models. In all cases, there is a poorly constrained region for masses between 10 and 65 GeV, where the “standard” channels relying on Higgs decays or di-muon searches, give very weak bounds in these models.

We thus reviewed two proposals to cover this window: one based on the search for boosted di-tau systems, and the other on indirect bounds from the di-photon differential cross section measurements. At the High-Luminosity LHC, these two strategies would allow to close the gap. In fact, they are complementary in two aspects: the di-tau is more sensitive to small masses while the photon is more sensitive to larger masses; in models where the photon coupling is suppressed, the tau channel is most constraining, and vice versa. Finally, we included the projected sensitivity of Zh, WW, γγ, $t\bar{t}$, $b\bar{b}$, ττ and di-jet searches at High-Luminosity, to push the bounds higher. Our results also show the necessity to keep looking for $t\bar{t}$ resonances down to the mass threshold, as this is the most sensitive channel, in these models, above 350 GeV.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00022/full#supplementary-material

Acknowledgments

We would like to thank Xiabier Cid Vidal, Mike Williams and Martino Borsato for useful feedback on the LHCb dark photon search, and Uli Haisch for discussion on the recast. TF was supported by IBS under the project code IBS-R018-D1. GF is supported in part by a grant from the Wallenberg foundation no. KAW-2017.0100. GC acknowledges partial support from the Institut Franco-Suedois (project Tör), the Labex Lyon Institute of the Origins - LIO (under grant ANR-10-LABX-66 and FRAMA FR3127 Fédération de Recherche André Marie Ampère) and the LIA FKPPL. HS has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No 668679).

Footnotes

1. ^Constructions based on Nambu Jona-Lasinio models with four-fermion interactions [16] or based on Seiberg dualities [17] have been proposed in the literature. See also the attempt in Setford [18].

2. ^See Table 3 in Appendix A of Belyaev et al. [27] for a list of coefficients in all models.

3. ^There is also an additional contribution coming from the diagrams in Figure 2 that is proportional to $p_h^2$. This signals the presence of an effective term of the form ϕ²□h, however, such contribution is always negligible.

References

1. Weinberg S. Implications of dynamical symmetry breaking. Phys Rev. (1976) D13:974–96.

Google Scholar

2. Kaplan DB, Georgi H. SU(2) x U(1) breaking by vacuum misalignment. Phys Lett. (1984) 136B:183–6.

Google Scholar

3. Contino R, Nomura Y, Pomarol A. Higgs as a holographic pseudoGoldstone boson. Nucl Phys. (2003) B671:148–74. doi: 10.1016/j.nuclphysb.2003.08.027

CrossRef Full Text | Google Scholar

4. Agashe K, Contino R, Pomarol A. The minimal composite Higgs model. Nucl Phys. (2005) B719:165–87. doi: 10.1016/j.nuclphysb.2005.04.035

CrossRef Full Text | Google Scholar

5. Contino R. The Higgs as a composite nambu-goldstone boson. In: Physics of the Large and the Small, TASI 09, Proceedings of the Theoretical Advanced Study Institute in Elementary Particle Physics, 1-26 June 2009 Boulder, CO (2011). p. 235–306.

Google Scholar

6. Bellazzini B, Csáki C, Serra J. Composite Higgses. Eur Phys J. (2014) C74:2766. doi: 10.1140/epjc/s10052-014-2766-x

CrossRef Full Text | Google Scholar

7. Panico G, Wulzer A. The composite nambu-goldstone Higgs. Lect Notes Phys. (2016) 913:1–316. doi: 10.1007/978-3-319-22617-0

CrossRef Full Text | Google Scholar

8. Kaplan DB. Flavor at SSC energies: a new mechanism for dynamically generated fermion masses. Nucl Phys. (1991) B365:259–78.

Google Scholar

9. Cacciapaglia G, Csaki C, Galloway J, Marandella G, Terning J, Weiler A. A GIM mechanism from extra dimensions. JHEP. (2008) 04:006. doi: 10.1088/1126-6708/2008/04/006

CrossRef Full Text | Google Scholar

10. Fitzpatrick AL, Perez G, Randall L. Flavor anarchy in a Randall-Sundrum model with 5D minimal flavor violation and a low Kaluza-Klein scale. Phys Rev Lett. (2008) 100:171604. doi: 10.1103/PhysRevLett.100.171604

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Marzocca D, Serone M, Shu J. General composite Higgs models. JHEP. (2012) 08:013. doi: 10.1007/JHEP08(2012)013

CrossRef Full Text | Google Scholar

12. Contino R, Da Rold L, Pomarol A. Light custodians in natural composite Higgs models. Phys Rev. (2007) D75:055014. doi: 10.1103/PhysRevD.75.055014

CrossRef Full Text | Google Scholar

13. Matsedonskyi O, Panico G, Wulzer A. Light top partners for a light composite Higgs. JHEP. (2013) 01:164. doi: 10.1007/JHEP01(2013)164

CrossRef Full Text | Google Scholar

14. Galloway J, Evans JA, Luty MA, Tacchi RA. Minimal conformal technicolor and precision electroweak tests. JHEP. (2010) 10:086. doi: 10.1007/JHEP10(2010)086

CrossRef Full Text | Google Scholar

15. Cacciapaglia G, Sannino F. Fundamental composite (goldstone) Higgs dynamics. JHEP. (2014) 04:111. doi: 10.1007/JHEP04(2014)111

CrossRef Full Text | Google Scholar

16. von Gersdorff G, Pontón E, Rosenfeld R. The dynamical composite Higgs. JHEP. (2015) 06:119. doi: 10.1007/JHEP06(2015)119

CrossRef Full Text | Google Scholar

17. Caracciolo F, Parolini A, Serone M. UV completions of composite Higgs models with partial compositeness. JHEP. (2013) 02:066. doi: 10.1007/JHEP02(2013)066

CrossRef Full Text | Google Scholar

18. Setford J. Composite Higgs models in disguise. JHEP. (2018) 01:092. doi: 10.1007/JHEP01(2018)092

CrossRef Full Text | Google Scholar

19. Witten E. Current algebra, baryons, and quark confinement. Nucl Phys. (1983) B223:433–44.

20. Kosower DA. Symmetry breaking patterns in pseudoreal and real gauge theories. Phys Lett. (1984) 144B:215–6.

Google Scholar

21. Ryttov TA, Sannino F. Ultra minimal technicolor and its dark matter TIMP. Phys Rev. (2008) D78:115010. doi: 10.1103/PhysRevD.78.115010

CrossRef Full Text | Google Scholar

22. Dugan MJ, Georgi H, Kaplan DB. Anatomy of a composite Higgs model. Nucl Phys. (1985) B254:299–326.

Google Scholar

23. Ma T, Cacciapaglia G. Fundamental composite 2HDM: SU(N) with 4 flavours. JHEP. (2016) 03:211. doi: 10.1007/JHEP03(2016)211

CrossRef Full Text | Google Scholar

24. Ferretti G, Karateev D. Fermionic UV completions of composite Higgs models. JHEP. (2014) 03:077. doi: 10.1007/JHEP03(2014)077

CrossRef Full Text | Google Scholar

25. Ayyar V, DeGrand T, Golterman M, Hackett DC, Jay WI, Neil ET, et al. Spectroscopy of SU(4) composite Higgs theory with two distinct fermion representations. Phys Rev D. (2017) 97:074505 doi: 10.1103/PhysRevD.97.074505

CrossRef Full Text | Google Scholar

26. Vecchi L. A dangerous irrelevant UV-completion of the composite Higgs. JHEP. (2017) 02:094. doi: 10.1007/JHEP02(2017)094

CrossRef Full Text | Google Scholar

27. Belyaev A, Cacciapaglia G, Cai H, Ferretti G, Flacke T, Parolini A, et al. Di-boson signatures as standard candles for partial compositeness. JHEP. (2017) 01:094. doi: 10.1007/JHEP01(2017)094

CrossRef Full Text

28. Cai H, Flacke T, Lespinasse M. A composite scalar hint from di-boson resonances? arXiv:1512.04508 (2015).

Google Scholar

29. Belyaev A, Cacciapaglia G, Cai H, Flacke T, Parolini A, Serodio H. Singlets in composite Higgs models in light of the LHC 750 GeV diphoton excess. Phys Rev. (2016) D94:015004. doi: 10.1103/PhysRevD.94.015004

CrossRef Full Text | Google Scholar

30. DeGrand T, Golterman M, Neil ET, Shamir Y. One-loop chiral perturbation theory with two fermion representations. Phys Rev. (2016) D94:025020. doi: 10.1103/PhysRevD.94.025020

CrossRef Full Text | Google Scholar

31. Cacciapaglia G, Ferretti G, Flacke T, Serodio H. Revealing timid pseudo-scalars with taus at the LHC. Eur Phys J. (2018) C78:724. doi: 10.1140/epjc/s10052-018-6183-4

CrossRef Full Text | Google Scholar

32. Wess J, Zumino B. Consequences of anomalous Ward identities. Phys Lett. (1971) 37B:95–97.

Google Scholar

33. Witten E. Global aspects of current algebra. Nucl Phys. (1983) B223:422–32.

Google Scholar

34. Bizot N, Cacciapaglia G, Flacke T. Common exotic decays of top partners. JHEP. (2018) 06:065. doi: 10.1007/JHEP06(2018)065

CrossRef Full Text | Google Scholar

35. Dietrich DD, Sannino F. Conformal window of SU(N) gauge theories with fermions in higher dimensional representations. Phys Rev. (2007) D75:085018. doi: 10.1103/PhysRevD.75.085018

CrossRef Full Text | Google Scholar

36. Ferretti G. Gauge theories of partial compositeness: scenarios for Run-II of the LHC. JHEP. (2016) 06:107. doi: 10.1007/JHEP06(2016)107

CrossRef Full Text | Google Scholar

37. Matsedonskyi O. On Flavour and Naturalness of Composite Higgs Models. JHEP. (2015) 02:154. doi: 10.1007/JHEP02(2015)154

CrossRef Full Text | Google Scholar

38. Cacciapaglia G, Cai H, Flacke T, Lee SJ, Parolini A, Serodio H. Anarchic Yukawas and top partial compositeness: the flavour of a successful marriage. JHEP. (2015) 06:085. doi: 10.1007/JHEP06(2015)085

CrossRef Full Text | Google Scholar

39. Cacciapaglia G, Vatani S, Ma T, Wu Y. Towards a fundamental safe theory of composite Higgs and Dark Matter. arXiv:1812.04005 (2018).

Google Scholar

40. Golterman M, Shamir Y. Top quark induced effective potential in a composite Higgs model. Phys Rev. (2015) D91:094506. doi: 10.1103/PhysRevD.91.094506

CrossRef Full Text | Google Scholar

41. DeGrand TA, Golterman M, Jay WI, Neil ET, Shamir Y, Svetitsky B. Radiative contribution to the effective potential in composite Higgs models from lattice gauge theory. Phys Rev. (2016) D94:054501. doi: 10.1103/PhysRevD.94.054501

CrossRef Full Text | Google Scholar

42. Bennett E, Hong DK, Lee JW, Lin CJD, Lucini B, Piai M, et al. Higgs compositeness in Sp(2N) gauge theories - Resymplecticisation, scale setting and topology. EPJ Web Conf. (2018) 175:08012. doi: 10.1051/epjconf/201817508012

CrossRef Full Text | Google Scholar

43. Bennett E, Hong DK, Lee JW, Lin CJD, Lucini B, Piai M, et al. Higgs compositeness in Sp(2N) gauge theories - Determining the low-energy constants with lattice calculations. EPJ Web Conf. (2018) 175:08011. doi: 10.1051/epjconf/201817508011

CrossRef Full Text | Google Scholar

44. Bennett E, Hong DK, Lee JW, Lin CJD, Lucini B, Piai M, et al. Sp(4) gauge theory on the lattice: towards SU(4)/Sp(4) composite Higgs (and beyond). JHEP. (2018) 03:185. doi: 10.1007/JHEP03(2018)185

CrossRef Full Text | Google Scholar

45. Lee JW, Bennett E, Hong DK, Lin CJD, Lucini B, Piai M, et al. Progress in the Lattice Simulations of Sp(2N) Gauge Theories. PoS. (2018) LATTICE2018:192.

46. Sannino F, Strumia A, Tesi A, Vigiani E. Fundamental partial compositeness. JHEP. (2016) 11:029. doi: 10.1007/JHEP11(2016)029

CrossRef Full Text | Google Scholar

47. Cacciapaglia G, Parolini A. Light 't Hooft top partners. Phys Rev. (2016) D93:071701. doi: 10.1103/PhysRevD.93.071701

CrossRef Full Text | Google Scholar

48. Barnard J, Gherghetta T, Ray TS. UV descriptions of composite Higgs models without elementary scalars. JHEP. (2014) 02:002. doi: 10.1007/JHEP02(2014)002

CrossRef Full Text | Google Scholar

49. Ferretti G. UV Completions of Partial Compositeness: The Case for a SU(4) Gauge Group. JHEP. (2014) 06:142. doi: 10.1007/JHEP06(2014)142

CrossRef Full Text | Google Scholar

50. Bizot N, Frigerio M, Knecht M, Kneur JL. Nonperturbative analysis of the spectrum of meson resonances in an ultraviolet-complete composite-Higgs model. Phys Rev. (2017) D95:075006. doi: 10.1103/PhysRevD.95.075006

CrossRef Full Text | Google Scholar

51. Arbey A, Cacciapaglia G, Cai H, Deandrea A, Le Corre S, Sannino F. Fundamental composite electroweak dynamics: status at the LHC. Phys Rev. (2017) D95:015028. doi: 10.1103/PhysRevD.95.015028

CrossRef Full Text | Google Scholar

52. Agugliaro A, Cacciapaglia G, Deandrea A, De Curtis S. Vacuum misalignment and pattern of scalar masses in the SU(5)/SO(5) composite Higgs model. JHEP. (2019) 2019:89. doi: 10.1007/JHEP02(2019)089

CrossRef Full Text | Google Scholar

53. Wu Y, Ma T, Zhang B, Cacciapaglia G. Composite dark matter and Higgs. JHEP. (2017) 11:058. doi: 10.1007/JHEP11(2017)058

CrossRef Full Text | Google Scholar

54. Cacciapaglia G, Cai H, Deandrea A, Flacke T, Lee SJ, Parolini A. Composite scalars at the LHC: the Higgs, the sextet and the octet. JHEP. (2015) 11:201. doi: 10.1007/JHEP11(2015)201

CrossRef Full Text | Google Scholar

55. Degrande C, Fuks B, Hirschi V, Proudom J, Shao HS. Automated next-to-leading order predictions for new physics at the LHC: the case of colored scalar pair production. Phys Rev. (2015) D91:094005. doi: 10.1103/PhysRevD.91.094005

CrossRef Full Text | Google Scholar

56. Raby S, Dimopoulos S, Susskind L. Tumbling gauge theories. Nucl Phys. (1980) B169:373–83.

Google Scholar

57. Brivio I, Gavela MB, Merlo L, Mimasu K, No JM, del Rey R, et al. ALPs effective field theory and collider signatures. Eur Phys J. (2017) 77:572. doi: 10.1140/epjc/s10052-017-5111-3

CrossRef Full Text | Google Scholar

58. Bellazzini B, Mariotti A, Redigolo D, Sala F, Serra J. R-axion at colliders. Phys Rev Lett. (2017) 119:141804. doi: 10.1103/PhysRevLett.119.141804

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Bauer M, Neubert M, Thamm A. Collider probes of axion-like particles. JHEP. (2017). doi: 10.1007/JHEP12(2017)044

CrossRef Full Text | Google Scholar

60. Bauer M, Neubert M, Thamm A. Analyzing the CP nature of a new scalar particle via S->Zh decay. Phys Rev Lett. (2016) 117:181801. doi: 10.1103/PhysRevLett.117.181801

CrossRef Full Text | Google Scholar

61. Patel HH. Package-X: a Mathematica package for the analytic calculation of one-loop integrals. Comput Phys Commun. (2015) 197:276–90. doi: 10.1016/j.cpc.2015.08.017

CrossRef Full Text | Google Scholar

62. Golterman M, Shamir Y. Effective potential in ultraviolet completions for composite Higgs models. Phys Rev. (2018) D97:095005. doi: 10.1103/PhysRevD.97.095005

CrossRef Full Text | Google Scholar

63. Spira M. HIGLU: A Program for the Calculation of the Total Higgs Production Cross-Section at Hadron Colliders via Gluon Fusion Including QCD Corrections. (1995) DESY T-95-05.

64. CMS collaboration. Search for $\text{t}\overline{\text{t}}$ resonances in highly boosted lepton+jets and fully hadronic final states in proton-proton collisions at $\sqrt{s}=13$ TeV. JHEP. (2017) 07:001. doi: 10.1007/JHEP07(2017)001

CrossRef Full Text

65. CMS collaboration. Search for resonant $t\bar{t}$ production in proton-proton collisions at $\sqrt{s}=$ 8 TeV. Phys Rev. (2016) D93:012001. doi: 10.1103/PhysRevD.93.012001

CrossRef Full Text

66. ATLAS collaboration. A search for $t\overline{t}$ resonances using lepton-plus-jets events in proton-proton collisions at $\sqrt{s}=8$ TeV with the ATLAS detector. JHEP. (2015) 08:148. doi: 10.1007/JHEP08(2015)148

CrossRef Full Text | Google Scholar

67. CMS collaboration. Search for dijet resonances in proton-proton collisions at $\sqrt{s}$ = 13 TeV and constraints on dark matter and other models. Phys Lett. (2017) B769:520–42. doi: 10.1016/j.physletb.2017.02.012

CrossRef Full Text

68. CMS collaboration. Searches for Dijet Resonances in pp Collisions at $\sqrt{s}=13\text{ TeV}$ Using Data Collected in 2016. Geneva: CERN; 2017. CMS-PAS-EXO-16-056. Available online at: https://cds.cern.ch/record/2256873

69. ATLAS collaboration. Search for new phenomena in dijet events using 37 fb⁻¹ of pp collision data collected at $\sqrt{s}=$13 TeV with the ATLAS detector. Phys Rev. (2017) D96:052004. doi: 10.1103/PhysRevD.96.052004

CrossRef Full Text | Google Scholar

70. CMS collaboration. Search for massive resonances decaying into WW, WZ, ZZ, qW, and qZ with dijet final states at $\sqrt{s}=13\text{TeV}$. Phys Rev. (2018) D97:072006. doi: 10.1103/PhysRevD.97.072006

CrossRef Full Text

71. CMS collaboration. Search for massive resonances decaying into WW, WZ or ZZ bosons in proton-proton collisions at $\sqrt{s}=$ 13 TeV. JHEP. (2017) 03:162. doi: 10.1007/JHEP03(2017)162

PubMed Abstract | CrossRef Full Text

72. CMS collaboration. Search for Heavy Resonances Decaying to Pairs of Vector Bosons in the $l\nu q\bar{q}$ Final State With the CMS Detector in Proton-Proton Collisions at $\sqrt{s}=$ 13 TeV. Geneva: CERN; 2017. CMS-PAS-B2G-16-029. Available online at: https://cds.cern.ch/record/2296237.

73. CMS collaboration. Search for New Resonances Decaying to WW/WZ → lνqq. Geneva: CERN; 2016. CMS-PAS-B2G-16-020. Available online at: https://cds.cern.ch/record/2205880.

74. CMS collaboration. Search for a New Scalar Resonance Decaying to a Pair of Z Bosons in Proton-Proton Collisions at $\sqrt{s}$ = 13 TeV. Geneva: CERN; 2017. CMS-PAS-HIG-17-012. Available online at: https://cds.cern.ch/record/2296714.

75. The CMS Collaboration. Search for ZZ resonances in the 212ν final state in proton-proton collisions at 13 TeV. J High Energ Phys. (2018) 2018:3. doi: 10.1007/JHEP03(2018)003

CrossRef Full Text

76. CMS collaboration. Search for New Diboson Resonances in the Dilepton + Jets Final State at $\sqrt{s}=13\text{ TeV}$ With 2016 Data. Geneva: CERN; 2017. CMS-PAS-HIG-16-034. Available online at: https://cds.cern.ch/record/2243295.

77. CMS collaboration. Search for Heavy Resonances Decaying Into a Z Boson and a Vector Boson in the νν $q\bar{q}$ Final State. Geneva: CERN; 2017. CMS-PAS-B2G-17-005. Available online at: https://cds.cern.ch/record/2273910

78. ATLAS collaboration. Search for heavy resonances decaying into WW in the eνμν final state in pp collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. Eur Phys J. (2018) C78:24. doi: 10.1140/epjc/s10052-017-5491-4

CrossRef Full Text

79. ATLAS collaboration. Search for WW/WZ resonance production in lνqq final states in pp collisions at $\sqrt{s}=$ 13 TeV with the ATLAS detector. JHEP. (2018) 03:042. doi: 10.1007/JHEP03(2018)042

CrossRef Full Text

80. ATLAS collaboration. Searches for heavy ZZ and ZW resonances in the llqq and ννqq final states in pp collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. JHEP. (2018) 03:009. doi: 10.1007/JHEP03(2018)009

CrossRef Full Text

81. ATLAS collaboration. Search for heavy ZZ resonances in the l⁺l⁻l⁺l⁻ and $l^{+}{l}^{-}\nu \bar{\nu }$ final states using proton-proton collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. Eur Phys J. (2018) C78:293. doi: 10.1140/epjc/s10052-018-5686-3

CrossRef Full Text

82. ATLAS collaboration. Search for scalar diphoton resonances in the mass range 65−600 GeV with the ATLAS detector in pp collision data at $\sqrt{s}$ = 8 TeV. Phys Rev Lett. (2014) 113:171801. doi: 10.1103/PhysRevLett.113.171801

CrossRef Full Text

83. ATLAS collaboration. Search for new phenomena in high-mass diphoton final states using 37 fb⁻¹ of proton–proton collisions collected at $\sqrt{s}=13$ TeV with the ATLAS detector. Phys Lett. (2017) B775:105–25. doi: 10.1016/j.physletb.2017.10.039

CrossRef Full Text

84. CMS collaboration. Search for high-mass diphoton resonances in proton-proton collisions at 13 TeV and combination with 8 TeV search. Phys Lett. (2017) B767:147–70. doi: 10.1016/j.physletb.2017.01.027

CrossRef Full Text

85. CMS collaboration. Search for resonant production of high-mass photon pairs in proton-proton collisions at $\sqrt{s}$ =8 and 13 TeV. Phys Rev Lett. (2016) 117:051802. doi: 10.1103/PhysRevLett.117.051802

CrossRef Full Text

86. CMS collaboration. Search for New Resonances in the Diphoton Final State in the Mass Range Between 80 and 115 GeV in pp Collisions at $\sqrt{s}=8$ TeV. Geneva: CERN; 2015. CMS-PAS-HIG-14-037. Available online at: https://cds.cern.ch/record/2063739.

87. CMS collaboration. Search for New Resonances in the Diphoton Final State in the Mass Range Between 70 and 110 GeV in pp Collisions at $\sqrt{s}=$ 8 and 13 TeV. Geneva: CERN; 2017. CMS-PAS-HIG-17-013. Available online at: https://cds.cern.ch/record/2285326.

88. CMS collaboration. Search for Zγ resonances using leptonic and hadronic final states in proton-proton collisions at $\sqrt{s}=$ 13 TeV. JHEP. (2018) 09:148. doi: 10.1007/JHEP09(2018)148

CrossRef Full Text

89. CMS collaboration. Search for high-mass Zγ resonances in e⁺e⁻γ and μ⁺μ⁻γ final states in proton-proton collisions at $\sqrt{s}=$ 8 and 13 TeV. JHEP. (2017) 01:076. doi: 10.1007/JHEP01(2017)076

CrossRef Full Text

90. ATLAS collaboration. Searches for the Zγ decay mode of the Higgs boson and for new high-mass resonances in pp collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. JHEP. (2017) 10:112. doi: 10.1007/JHEP10(2017)112

CrossRef Full Text

91. ATLAS collaboration. Search for Heavy Resonances Decaying to a W or Z Boson and a Higgs Boson in Final States With Leptons and b -jets in 36.1 fb ⁻¹ of pp Collision Data at $\sqrt{s}=13$ TeV with the ATLAS Detector. Geneva: CERN; 2017. ATLAS-CONF-2017-055. Available online at: https://cds.cern.ch/record/2273871.

92. CMS collaboration. Search for Additional Neutral MSSM Higgs Bosons in the di-tau Final State in pp Collisions at $\sqrt{s}=13$ TeV. Geneva: CERN; 2017. CMS-PAS-HIG-17-020. Available online at: https://cds.cern.ch/record/2296333.

93. CMS collaboration. Search for heavy resonances decaying to tau lepton pairs in proton-proton collisions at $\sqrt{s}=13$ TeV. JHEP. (2017) 02:048. doi: 10.1007/JHEP02(2017)048

CrossRef Full Text

94. ATLAS collaboration. Search for additional heavy neutral Higgs and gauge bosons in the ditau final state produced in 36 fb⁻¹ of pp collisions at $\sqrt{s}=13$ TeV with the ATLAS detector. JHEP. (2018) 01:055. doi: 10.1007/JHEP01(2018)055

CrossRef Full Text

95. ATLAS collaboration. Search for Minimal Supersymmetric Standard Model Higgs bosons H/A and for a Z′ boson in the ττ final state produced in pp collisions at $\sqrt{s}=13$ TeV with the ATLAS Detector. Eur Phys J. (2016) C76:585. doi: 10.1140/epjc/s10052-016-4400-6

CrossRef Full Text

96. CMS collaboration. Search for a light pseudoscalar Higgs boson in the dimuon decay channel in pp collisions at $\sqrt{s}=7$ TeV. Phys Rev Lett. (2012) 109:121801. doi: 10.1103/PhysRevLett.109.121801

CrossRef Full Text

97. LHCb collaboration. Search for a dimuon resonance in the Υ mass region. JHEP. (2018) 09:147. doi: 10.1007/JHEP09(2018)147

CrossRef Full Text

98. CMS collaboration. Search for light bosons in decays of the 125 GeV Higgs boson in proton-proton collisions at $\sqrt{s}$ = 8 TeV. JHEP. (2017). doi: 10.1007/JHEP10(2017)076

CrossRef Full Text

99. ATLAS collaboration. Search for new phenomena in events with at least three photons collected in pp collisions at $\sqrt{s}$ = 8 TeV with the ATLAS detector. Eur Phys J. (2016) C76:210. doi: 10.1140/epjc/s10052-016-4034-8

CrossRef Full Text

100. ATLAS collaboration. Search for Higgs bosons decaying to aa in the μμττ final state in pp collisions at $\sqrt{s}=$ 8 TeV with the ATLAS experiment. Phys Rev. (2015) D92:052002. doi: 10.1103/PhysRevD.92.052002

CrossRef Full Text

101. ATLAS and CMS collaborations. Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $\sqrt{s}=7$ and 8 TeV. JHEP. (2016) 08:045. doi: 10.1007/JHEP08(2016)045

CrossRef Full Text

102. CMS collaboration. Search for a low-mass pseudoscalar Higgs boson produced in association with a $b\bar{b}$ pair in pp collisions at $\sqrt{s}=$ 8 TeV. Phys Lett. (2016) B758:296–320. doi: 10.1016/j.physletb.2016.05.003

CrossRef Full Text

103. Kozaczuk J, Martin TAW. Extending LHC coverage to light pseudoscalar mediators and coy dark sectors. JHEP. (2015) 04:046. doi: 10.1007/JHEP04(2015)046

CrossRef Full Text | Google Scholar

104. Casolino M, Farooque T, Juste A, Liu T, Spannowsky M. Probing a light CP-odd scalar in di-top-associated production at the LHC. Eur Phys J. (2015) C75:498. doi: 10.1140/epjc/s10052-015-3708-y

CrossRef Full Text | Google Scholar

105. OPAL collaboration. A Measurement of photon radiation in lepton pair events from Z0 decays. Phys Lett. (1991) B273:338–354.

106. Agashe K, Contino R. The Minimal composite Higgs model and electroweak precision tests. Nucl Phys. (2006) B742:59–85. doi: 10.1016/j.nuclphysb.2006.02.011

CrossRef Full Text | Google Scholar

107. Grojean C, Matsedonskyi O, Panico G. Light top partners and precision physics. JHEP. (2013) 10:160. doi: 10.1007/JHEP10(2013)160

CrossRef Full Text | Google Scholar

108. Contino R, Salvarezza M. Dispersion relations for electroweak observables in composite Higgs models. Phys Rev. (2015) D92:115010. doi: 10.1103/PhysRevD.92.115010

CrossRef Full Text | Google Scholar

109. Contino R, Salvarezza M. One-loop effects from spin-1 resonances in Composite Higgs models. JHEP. (2015) 07:065. doi: 10.1007/JHEP07(2015)065

CrossRef Full Text | Google Scholar

110. Ghosh D, Salvarezza M, Senia F. Extending the analysis of electroweak precision constraints in composite higgs models. Nucl Phys. (2017) B914:346–87. doi: 10.1016/j.nuclphysb.2016.11.013

CrossRef Full Text | Google Scholar

111. ATLAS collaboration. Projections for Measurements of Higgs boson Signal Strengths and Coupling Parameters With the ATLAS Detector at a HL-LHC. Geneva: CERN; 2014. ATL-PHYS-PUB-2014-016. Available online at: https://cds.cern.ch/record/1956710.

112. CMS collaboration. Search for Narrow High-Mass Resonances in Proton-Proton Collisions at $\sqrt{s}$ = 8 TeV Decaying to a Z and a Higgs Boson. Phys Lett. (2015) B748:255–77. doi: 10.1016/j.physletb.2015.07.011

CrossRef Full Text

113. CMS collaboration. Search for Heavy Resonances Decaying Into Two Higgs Bosons or Into a Higgs and a Vector Boson in Proton-Proton Collisions at 13 TeV. Geneva: CERN; 2017. CMS-PAS-B2G-17-006. Available online at: http://cds.cern.ch/record/2296716.

114. Rehermann K, Tweedie B. Efficient identification of boosted semileptonic top quarks at the LHC. JHEP. (2011) 03:059. doi: 10.1007/JHEP03(2011)059

CrossRef Full Text | Google Scholar

115. Katz A, Son M, Tweedie B. Ditau-Jet tagging and boosted higgses from a multi-TeV resonance. Phys Rev. (2011) D83:114033. doi: 10.1103/PhysRevD.83.114033

CrossRef Full Text | Google Scholar

116. Conte E, Fuks B, Guo J, Li J, Williams AG. Investigating light NMSSM pseudoscalar states with boosted ditau tagging. JHEP. (2016) 05:100. doi: 10.1007/JHEP05(2016)100

CrossRef Full Text | Google Scholar

117. Mariotti A, Redigolo D, Sala F, Tobioka K. New LHC bound on low-mass diphoton resonances. Phys Lett B 783:13–8 (2017). doi: 10.1016/j.physletb.2018.06.039

CrossRef Full Text | Google Scholar

118. Azzi P, Cristinziani M. Top quark physics at the high luminosity LHC. In: Proceedings, 9th International Workshop on Top Quark Physics (TOP 2016): September 19-23, 2016 (Olomouc) (2017).

Google Scholar

119. Cid Vidal X, D'Onofrio M, Fox PJ, Torre R, Ulmer KA, Aboubrahim A, et al. Beyond the Standard Model Physics at the HL-LHC and HE-LHC. CERN-LPCC-2018-05 (2018).

120. CMS collaboration. Search for Ttbar Resonances at the HL-LHC and HE-LHC with the Phase-2 CMS Detector. Geneva: CERN; 2018. CMS-PAS-FTR-18-009. Available online at: https://cds.cern.ch/record/2649032.

121. ATLAS collaboration. Dijet Resonance Searches With the ATLAS Detector at 14 TeV LHC. Geneva: CERN; 2015. ATL-PHYS-PUB-2015-004. Available online at: https://cds.cern.ch/record/2002136.

122. Chekanov SV, Childers JT, Proudfoot J, Frizzell D, Wang R. Precision searches in dijets at the HL-LHC and HE-LHC. JINST. (2018) 13:P05022. doi: 10.1088/1748-0221/13/05/P05022

CrossRef Full Text | Google Scholar

123. ATLAS collaboration. Beyond Standard Model Higgs Boson Searches at a High-Luminosity LHC with ATLAS. Geneva: CERN; 2013. ATL-PHYS-PUB-2013-016. Available online at: http://cds.cern.ch/record/1611190.

124. ATLAS collaboration. HL-LHC Prospects for Diboson Resonance Searches and Electroweak Vector Boson Scattering in the WW/WZ → ℓνqq final state. Geneva: CERN; 2018. ATL-PHYS-PUB-2018-022. Available online at: http://cds.cern.ch/record/2645269.

125. ATLAS collaboration. Prospects for the Search for Additional Higgs Bosons in the Ditau Final State With the ATLAS Detector at HL-LHC. Geneva: CERN; 2018. ATL-PHYS-PUB-2018-050. Available online at: http://cds.cern.ch/record/2652284.

126. LHCb collaboration. Search for dark photons produced in 13 TeV pp collisions. Phys Rev Lett. (2017) 120:061801. doi: 10.1103/PhysRevLett.120.061801

CrossRef Full Text

127. Haisch U, Kamenik JF, Malinauskas A, Spira M. Collider constraints on light pseudoscalars. JHEP. (2018) 03:178. doi: 10.1007/JHEP03(2018)178

CrossRef Full Text | Google Scholar