- Departamento de Física e Matemática, Universidade Federal de São João del Rei, São João del Rei, Brazil
We study the effects of local and distance interactions in the unidimensional contact process (CP). In the model, each site of a lattice is occupied by an individual, which can be healthy or infected. As in the standard CP, each infected individual spreads the disease to one of its first-neighbors with rate λ, and with unitary rate, it becomes healthy. However, in our model, an infected individual can transmit the disease to an individual at a distance ℓ apart. This step mimics a vector-mediated transmission. We observe the host-host interactions do not alter the critical exponents significantly in comparison to a process with only Lévy-type interactions. Our results confirm, numerically, early field-theoretic predictions.
1. Introduction
The contact process (CP) [1] is a stochastic epidemics model with spatial structure [2]. In the CP, each individual inhabits a site on a d−dimensional lattice and can be in one of two states: healthy or infected. Each infected individual transmits the disease to one of its nearest-neighbors with rate λ, or become healthy with a unitary rate. When the transmission rate λ is varied, the system undergoes a phase transition between disease-free and endemic phases.
Apart from its interest as an elementary spatial model of epidemic spreading, the critical behavior of the CP (and its variations) is interesting in the study of non-equilibrium universality classes. The disease-free state is an absorbing state, a frozen state with no fluctuations [3–7]. Non-equilibrium phase transitions into absorbing states have been a topic of much interest in recent decades. In addition to their connection with epidemics, they appear in a wide variety of problems, such as heterogeneous catalysis [8], interface growth [9], population models, and ecology [10]. Recent experimental realizations in the liquid crystal electroconvection [11], driven suspensions [12], and superconducting vortices [13] have heightened interest in absorbing transitions.
It is expected that absorbing state phase transitions in models with a positive unidimensional order parameter, short-range interactions, and without additional symmetries or quenched disorder belong generically to the universality class of directed percolation (DP)[14, 15]. Including long-range interactions in spreading processes can provide more realistic models, instead of short-range models as the original CP, for example, to model spreading of vector-borne diseases [16]. One of the first approaches was the model proposed by Grassberger [17], based on the original idea presented in Mollison [18]. In his model, the infection probability obeys a Lévy flight decaying as a power-law relation 1/rα+d with the distance r, where d is the spatial dimension of the system and α is a control parameter. Simulational [19, 20] and field-theoretical renormalization group analysis [21] revealed that such anomalous directed percolation presents critical exponents varying continuously with the parameter α.
A generalized version of the unidimensional CP where inactive (healthy) sites can be activated (infected) over long distance was introduced by Ginelli et al. [22, 23], inspired by pinning-depinning transitions in non-equilibrium wetting phenomena. In such model, an active site infects an inactive with rate q/ℓα, where q is the coordination number and ℓ is the distance between both sites. Depending on the value of the control parameter α, the contact process with long-range interactions exhibits a rich phase diagram, with distinct universality classes and discontinuous phase transitions [20, 22–24]. The robustness of these discontinuous phase transitions was studied in Fiore and de Oliveira [25]. More recent studies focused on the effects of quenched disorder [26] and diffusion [27]. Inspired by diseases that can spread via host-host in addition to long-distance spreading, in this work, we examine the effects of an additional local infection in the unidimensional CP with Lévy flights.
The remainder of this paper is organized as follows. In section 2 we introduce the model and methods used in our analysis. In section 3 we present our results. Section 4 is devoted to discussion and conclusions.
2. Model and Methods
To begin, we modify the standard contact process to include long distance infection. An infected host, placed at a site i on the lattice, is signed by a state variable σi = 1. It infects one of its healthy (signed by σj = 0) nearest-neighbors with rate λh, or become healthy with rate μ = 1. In addition, the infected host can infect a healthy individual located at some distance, with rate λv. Here, λv and λh are the control parameters that govern the epidemic spreading. Each flight is described by using a Lévy distribution [28], which is characterized by an exponent α. These events are schematically represented in Figure 1. Note that the evolution occurs in two independent steps, one concerning direct host-host infection, and the other, vector-mediated infection, related to the flights.
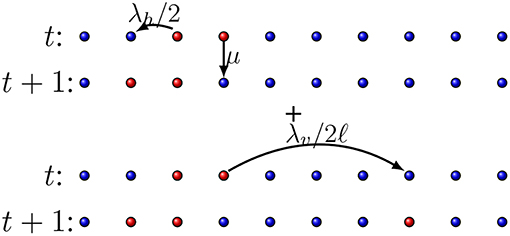
Figure 1. Transition rates for the model. Red circles represent infected and the blue ones represent the healthy individuals. (Top) Local infection (An infected individual transmites the disease to one of its first neighbors with rate λh/2, or become healthy with rate μ.). (Bottom) Long-distance infection (An infected individual transmites the disease to another individual with rate λv/2ℓ, where ℓ is the distance between the individuals).
This model can be interpreted as a prototypical model for diseases which can spread via vectors which can transmit the pathogen over long distances, and also by direct host-host contact. Since the CP is a spatial lattice model, it is in a core of models used in Ecology to investigate criticality in process determined by the local structure (configuration of trees) [29]. In nature, it is possible to occur long-range infections, as, for example in orchards where flying parasites contaminate the trees almost instantaneously in a widespread manner if the timescale of the flights of the parasites is much shorter than the mesoscopic timescale of the epidemic process itself [30]. We should remark, however that our model is not suitable for modeling the spreading of human diseases such as the Zika virus, which is transmitted by mosquitoes, and by parental or sexual contact [31–33]. The length of intrinsic and extrinsic incubation periods of human vector-mediated diseases can be up to 2 weeks, and it is an essential factor that determines the transmission dynamics. In addition, differently from trees, the human contact network is not a lattice, but instead a complex network, which also affects drastically the epidemic spreading [34–36]. Both factors should be introduced in the model in a future work, if one intends modeling such diseases.
In the simulation scheme, each step is divided in two events: (i) local, where an infected individual infects one of its neighbors (chosen at random) with probability q = λh/(1 + λh) or it becomes healthy with probability ν = 1/(1 + λh); (ii) long-range, where an individual is infected with probability , or nothing happens with probability . To improve efficiency, we maintain a list of infected individuals, and time is updated as Δt = 1/Ninf at each iteration (here Ninf is the number of infected individuals).
The implementation of the vector flies consider a Lévy-distributed random variables. The strategy to obtain such random flies is based on a non-linear transformation of Gaussian random variables [37]. This strategy is based on the following recipe: (i) First, a random variable V distributed homogeneously on (−π/2, π/2) is generated. (ii) Second, an exponential variable W with unity mean is generated. (iii) Finally, we compute the random variable ℓ [38], following
where α is a control parameter of the length of the flies (this results in random flies with probability distribution function of length decaying as ℓ−(1 + α)) [38].
We have done dynamical and stationary simulations. The dynamical simulations follow the system stochastic evolution from spreading (where the system is initialized with a “seed”, i.e., only one site is infected at t = 0), and initial decay studies (here the system evolves from a full infected lattice). On the other hand, in the stationary simulations, we are interested in the (long-time) time independent behavior. Stationary analysis nearby the critical point of systems with transitions into absorbing states are hard to be done due to strong finite size effects. This is consequence of that, in conventional simulations, small systems quickly become trapped in the absorbing state (in this case, we can say of a quasistationary state (since the only true stationary state is the absorbing one). In order to circumvent such difficulties, we employ a simulation method that yields quasistationary (QS) properties directly [39, 40]. The method is based in maintaining, and gradually updating, a list of M configurations visited during the evolution; when a transition to the absorbing state is imminent, the system is instead placed in one of the saved configurations. Otherwise, the evolution is exactly that of a conventional simulation. This procedure results in an unbiased sampling of the quasistationary distribution of the process, and improve the statistics.
3. Results and Discussion
In order to analyze the dynamical scaling of the model at criticality, we employed initial decay simulations in a unidimensional lattice of L sites (with periodic boundary conditions). The initial decay studies use an initial configuration with all sites occupied. The order parameter is the density of active sites, i.e., the fraction of infected individuals. At the critical point, one expects to observe a power-law behavior of the density
until it saturates at its QS value. The larger the system size, the longer the period of power-law decay, and the more precise the resulting estimate for the critical exponent δ. In the initial decay studies, we have used systems with size up to L = 108, and averages are taken over up to 106 runs.
From the spreading simulations, we observe there is a critical value of (λh,λv) above which the activity survives, while for values below such critical point, the system becomes trapped in the absorbing state. The phase diagram obtained in the λh × λv plane is plotted in Figure 2. As expected, the absorbing phase is larger when α increases, since small values of α favor the epidemic spreading.
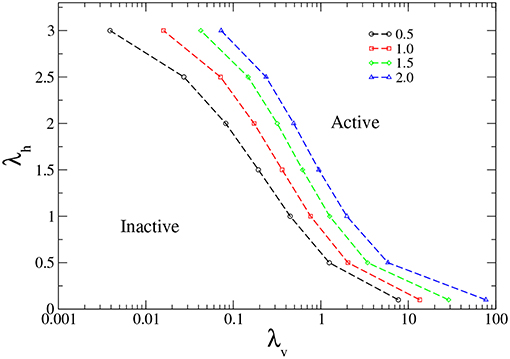
Figure 2. Phase diagram in the λv × λh plane, showing the inactive and active phases, for α = 0.5, 1.0, 1.5, and 2.0 (from left to right).
In Figure 3, we show the critical decay of the density of active sites, for distinct values of λh and α = 1.5. In all cases, we observe a power law decay at criticality. Analysis from the data obtained yields the values of the critical exponent (δ) reported in Table 1. The inset in Figure 3 shows that ρ/tδ converges to a constant value, therefore confirming the accuracy of the exponents obtained. We note the transient behavior is longer for larger values of λh. Also, the increase of λh alters only slightly the value of the exponent δ. Figure 4 shows the evolution of the average density of infected sites for distinct values of α. Increasing α, we observe a slower decay, as expected, since in such case, the flights are short-ranged. Increasing α, the results become close to the original CP, with the critical exponent δ converging to the DP value, δ = 0.159, as shown in Table 1.
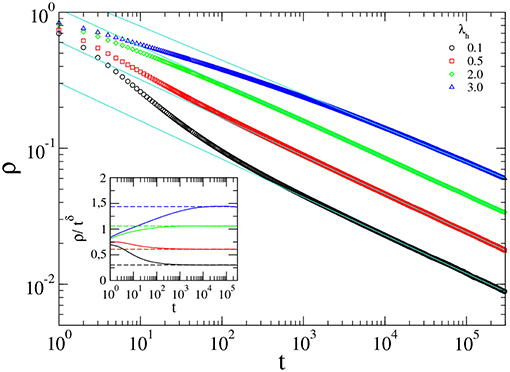
Figure 3. Decay of ρ from an initial configuration with all sites infected for distinct values of λh, for α = 1.5. The straight lines are linear regressions from the data. The inset shows that ρ/tδ converges to constant values in all cases, confirming the accuracy of the regressions.
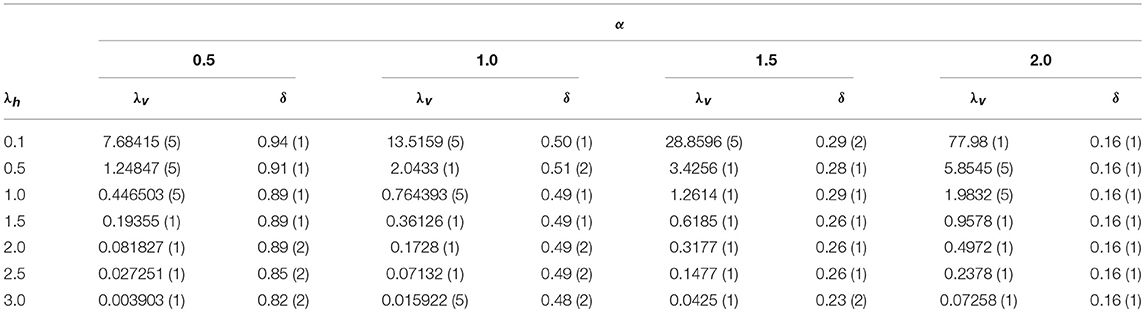
Table 1. Critical values of the control parameter, , and critical exponent δ as a function of λh for α = 0.5, 1.0, 1.5, and 2.0.
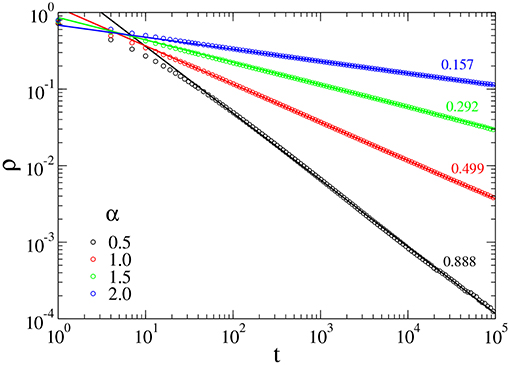
Figure 4. Decay of the density of infected sites ρ from an initial configuration with all sites infected for distinct values of α, with λh = 1.0. The straight lines are linear regressions from the data.
From the data in Table 1, we observe that higher values of α recover the DP critical behavior, which presents δ = 0.15947 [3]. On the other hand, decreasing the value of α, the exponent δ approaches the mean-field value δ = 1. The critical exponent δ varies continuously between these limits. We observe that the effects of λh are more pronounced for lower values of α, since the exponent δ varies from 0.95 to 0.82 when α = 0.5. We note, however, that α = 0.5 is a crossover point, where the dynamical behavior is often plagued by huge corrections to scaling. Otherwise, for higher values of α the exponent does not alter significantly. Finally, in comparison with the results for the CP with only Lévy-type infection (i.e, with λh = 0.0) [19], we observe the non-universal critical exponents are closer the DP values (for the same value of α) when the host-host infection is introduced. For example, in [19] it was found δ = 0.21 for α = 2.0 and δ = 0.94 for α = 0.5, in contrast to δ = 0.16 and δ = 0.82, respectively, in the present work with λh = 3.0.
Now, we turn to the static, long-time behavior, represented by the quasi-stationary state. In the QS simulations, we have used system sizes ranging from L = 102 to L = 105. Each simulation ran until t = 108, and averages were taken over 103 runs. We used a list of size M = 2, 000. At the critical point, the finite-size theory [3] implies the quasistationary order parameter ρqs decays with the system size as a power law
In Figure 5, we show the QS density of infected sites (ρqs) as a function of the system size L, for α = 1.5. We observe that at criticality, ρqs scales as a power law with exponent ratio β/ν⊥ = 0.45, 0.42, 0.42, 0.43, 0.42, 0.41, and 0.44 for λh = 0.1, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0, respectively. Hence, we can conclude that the exponent β/ν⊥ is independent of λh.
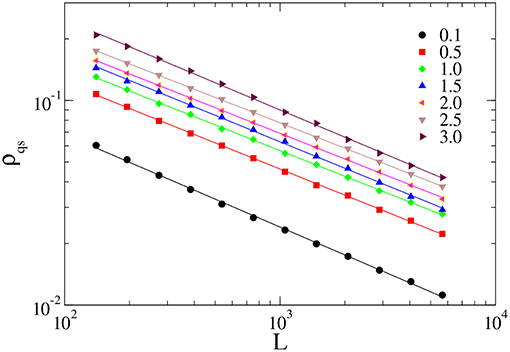
Figure 5. Finite size scaling of the QS density ρqs, for α = 1.0 and λh = 0.1, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0.
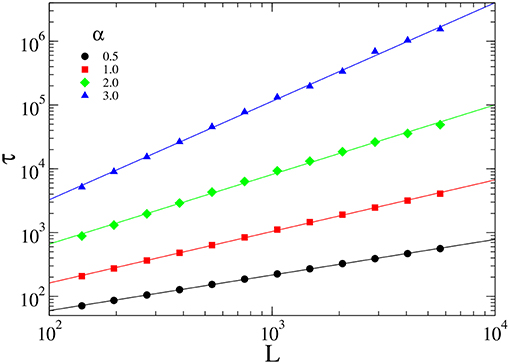
In Figure 6, we evaluate the behavior of the lifetime τ of the QS state at the criticality, which is expected to scale as
with z = ν∥/ν⊥ (here, we evaluate the lifetime as the time between two consecutive visits to the absorbing state). Analysis from the data yields z = 0.84, 0.83, 0.83, 0.80, 0.82, 0.84, and 0.83 for λh = 0.1, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0, respectively. Therefore, this exponent also is not affected by the host-host interaction. Results of the QS simulations for distinct values of α are reported in Table 2. We observe that in all cases the critical exponents obtained from the QS simulations are not significantly affected by the host-host infection.
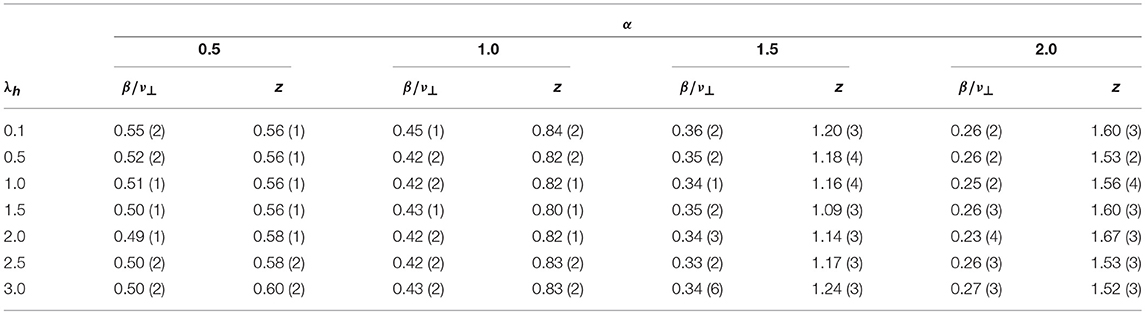
Table 2. Critical values of the control parameter, , and critical exponent δ as a function of λh for α = 0.5, 1.0, 1.5 and 2.0.
In resume, we conclude that the introduction of a local host-host interaction in epidemics with Lévy-type long-range interactions does not affect the long-time critical behavior. On the other hand, we observe an anomalous spreading observed for the dynamical critical exponent for α = 0.5.
4. Conclusions
We have proposed a variation of the contact process that includes both local (host-host) and long-distance (vector-mediated) interactions. We observe the host-host interactions does not alter the static and dynamical critical exponents significantly in comparison to a process with only Lévy-type interactions. Our results are in agreement with early field-theoretic results [30], which revealed that the relative strength of short-and long-range interactions do not affect the critical behavior. Our results also show an anomalous spreading, with the dynamical exponent varying continuously with the host-host infection rate, when α = 0.5. However, we should remark that at this crossover point, the dynamical behavior is affected by huge corrections to scaling, and we cannot discard that this difference could vanish for sufficient long times (note that the static simulations show the same set of exponents for all values of α). Finally, in the limit in which the host-host infection vanishes, our model reduces to the anomalous contact process proposed in [19], and our results in this limit confirm the critical behavior obtained previously in the literature.
A promising extension of the present work includes the study of the model under the influence of temporal disorder [41, 42], that could, for example, affect only the vector-mediated infection, reflecting seasonal variations [16]. Another critical issue is the effect of local interaction in the robustness of the discontinuous phase transition exhibited by some classes of long-range models [22, 23, 43].
Data Availability
All datasets generated for this study are included in the manuscript and/or the supplementary files.
Author Contributions
SA and MdO conceived the study. PS and SA performed the simulations. PS, SA, and MdO analyzed the data and wrote the paper. All authors reviewed the manuscript.
Funding
This work was partially supported by Brazilian agencies CNPq and FAPEMIG.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Harris TE. Contact interactions on a lattice. Ann Probab. (1974) 2:969. doi: 10.1214/aop/1176996493
3. Marro J, Dickman R. Nonequilibrium Phase Transitions in Lattice Models. Cambridge:Cambridge University Press (1999).
4. Henkel M, Hinrichsen H, Lubeck S. Non-Equilibrium Phase Transitions Volume I: Absorbing Phase Transitions. Dordrecht: Springer-Verlag (2008).
5. Ódor G. Universality In Nonequilibrium Lattice Systems: Theoretical Foundations. Singapore: World Scientific (2007).
6. Hinrichsen H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv Phys. (2000) 49:815. doi: 10.1080/00018730050198152
7. Ódor G. Universality classes in nonequilibrium lattice systems. Rev Mod Phys (2004) 76:663. doi: 10.1103/RevModPhys.76.663
8. Ziff RM, Gulari E, Barshad Y. Kinetic phase transitions in an irreversible surface-reaction model. Phys Rev Lett. (1986) 56:2553.10033028
10. de Oliveira MM, Santos RV, Dickman R. Symbiotic two-species contact process. Phys Rev E (2012) 86:011121. doi: 10.1103/PhysRevE.86.011121
11. Takeuchi KA, Kuroda M, Chaté H, Sano M. Directed percolation criticality in turbulent liquid crystals. Phys Rev Lett. (2007) 99:234503. doi: 10.1103/PhysRevLett.99.234503
12. Corté L, Chaikin PM, Gollub JP, Pine DJ. Random organization in periodically driven systems. Nat Phys. (2008) 4:420. doi: 10.1038/nphys891
13. Okuma S, Tsugawa Y, and Motohashi A. Transition from reversible to irreversible flow: absorbing and depinning transitions in a sheared-vortex system. Phys Rev B (2011) 83:012503. doi: 10.1103/PhysRevB.83.012503
14. Janssen HK. On the nonequilibrium phase transition in reaction-diffusion systems with an absorbing stationary state. Z Phys B (1981) 42:151.
16. Botari T, Alves SG, Leonel ED. Explaining the high number of infected people by dengue in Rio de Janeiro in 2008 using a susceptible-infective-recovered model. Phys Rev E (2011) 83:037101. doi: 10.1103/PhysRevE.83.037101
17. Grassberger P. “Spreading of epidemic processes leading to fractal structures” In: Fractals in Physics. Pietronero L, Tosatti E editors. Amsterdam: Elsevier (1986).
18. Mollison D. Spatial contact models for ecological and epidemic spread. J R Stat Soc Ser B Methodol (1977) 39:283.
20. Hinrichsen H. Non-equilibrium phase transitions with long-range interactions. J Stat Mech Theor Exp. (2007) 2007:P07006. doi: 10.1088/1742-5468/2007/07/P07006
21. Janssen HK, Oerding K, van Wijland F, Hilhorst HJ. Lévy-flight spreading of epidemic processes leading to percolating clusters, Eur Phys J B (1999) 7:137. doi: 10.1007/s100510050596
22. Ginelli F, Hinrichsen H, Livi R, Mukamel D, Politi A. Directed percolation with long-range interactions: modeling nonequilibrium wetting. Phys Rev E (2005) 71:026121. doi: 10.1103/PhysRevE.71.026121
23. FGinelli F, Hinrichsen H, Livi R, Mukamel D, Torcini A. Contact processes with long range interactions. J Stat Mech Theor Exp. (2006) 2006:P08008. doi: 10.1088/1742-5468/2006/08/P08008
24. Fiore CE de Oliveira MJ. Contact process with long-range interactions: a study in the ensemble of constant particle number. Phys Rev E (2007) 76:041103. doi: 10.1103/PhysRevE.76.041103
25. Fiore CE de Oliveira MJ. Robustness of first order phase transitions in one-dimensional long-range contact processes. Phys Rev E (2013) 87:042101. doi: 10.1103/PhysRevE.87.042101
26. Juhász R, Kovács IA, Iglói F. Long-range epidemic spreading in a random environment. Phys Rev E (2015) 91:032815. doi: 10.1103/PhysRevE.91.032815
27. Pedro TB, Figueiredo W, Ferreira AL. Mean-field theory for the long-range contact process with diffusion. Phys Rev E (2015) 92:032131. doi: 10.1103/PhysRevE.92.032131
28. Montroll EW, West BJ. Fluctuation Phenomena. Montroll EW, Lebowitz JL editors. Amsterdam: North-Holland (1979).
29. Pascual M, Guichard F. Criticality and disturbance in spatial ecological systems. Trends Ecol Evol. (2005) 20:88. doi: 10.1016/j.tree.2004.11.012
30. Janssen H-K, Stenull O. Field theory of directed percolation with long-range spreading. Phys Rev E (2008) 78:061117. doi: 10.1103/PhysRevE.78.061117
31. D'Ortenzio E, Matheron S, Yazdanpanah Y, de Lamballerie X, Hubert B, Piorkowski G, et al. Evidence of sexual transmission of zika virus. N Engl J Med. (2016) 374:2195. doi: 10.1056/NEJMc1604449
32. Coelho FC, Durovni B, Saraceni V, Lemos C, Codeco CT, Camargo S, et al. Higher incidence of zika in adult women than adult men in rio de janeiro suggests a significant contribution of sexual transmission from men to women. Int J Infect Dis. (2016) 51:128. doi: 10.1016/j.ijid.2016.08.023
33. Towers S, Brauer F, Castillo-Chavez C, Falconar AKI, Mubayi A, Romero-Vivas CME. Estimate of the reproduction number of the 2015 zika virus outbreak in Barranquilla, Colombia, and estimation of the relative role of sexual transmission. Epidemics (2016) 17:50. doi: 10.1016/j.epidem.2016.10.003
34. Moore C, Newman MEJ. Epidemics and percolation in small-world networks. Phys Rev E (2000) 61:5678. doi: 10.1103/PhysRevE.61.5678
35. Parshani R, Carmi S, Havlin S. Epidemic threshold for the susceptible-infectious-susceptible model on random networks. Phys Rev Lett. (2010) 104:258701. doi: 10.1103/PhysRevLett.104.258701
36. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks, Rev Mod Phys. (2015) 87:925. doi: 10.1103/RevModPhys.87.925
37. Janicki A, Weron A. Computer simulation of attractors in stochastic models with α-stable noise. Math Comput Simul. (1995) 39:9. doi: 10.1016/0378-4754(95)00132-H
38. Klafter J, Sokolov M. First Steps in Random Walks. New York, NY: Oxford University Press (2011).
39. de Oliveira MM, Dickman R. How to simulate the quasistationary state. Phys Rev E (2005) 71:016129. doi: 10.1103/PhysRevE.71.016129
40. Dickman R, de Oliveira MM. Quasi-stationary simulation: the subcritical contact process. Braz J Phys. (2006) 36:685. doi: 10.1590/S0103-97332006000500020
41. de Oliveira MM, Fiore CE. Temporal disorder does not forbid discontinuous absorbing phase transitions in low-dimensional systems. Phys Rev E (2016) 94:052138. doi: 10.1103/PhysRevE.94.052138
42. Solano CMD, de Oliveira MM, Fiore CE. Comparing the influence of distinct kinds of temporal disorder in a low-dimensional absorbing transition model. Phys Rev E (2016) 94:042123. doi: 10.1103/PhysRevE.94.042123
Keywords: contact process, Lévy-flights, absorbing state, non-equilibrium phase transitions, critical phenomena
Citation: Silveira PR, de Oliveira MM and Alves SG (2019) Local vs. Long-Range Infection in Unidimensional Epidemics. Front. Phys. 7:17. doi: 10.3389/fphy.2019.00017
Received: 30 November 2018; Accepted: 28 January 2019;
Published: 04 March 2019.
Edited by:
Francisco Welington Lima, Federal University of Piauí, BrazilReviewed by:
Krzysztof Malarz, AGH University of Science and Technology, PolandLin Wang, Institut Pasteur, France
Copyright © 2019 Silveira, de Oliveira and Alves. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marcelo M. de Oliveira, bW1kZW9saXZlaXJhQHVmc2ouZWR1LmJy
 Priscila R. Silveira
Priscila R. Silveira Marcelo M. de Oliveira
Marcelo M. de Oliveira Sidiney G. Alves
Sidiney G. Alves