Possibilities of Future Double Beta Decay Experiments to Investigate Inverted and Normal Ordering Region of Neutrino Mass

An overview of modern experiments on the search for neutrinoless double decay is presented. The obtained limits on the effective mass of the Majorana neutrino 〈m_ν〉 are discussed taking into account the uncertainties in the value of the nuclear matrix elements (NMEs) and the value of the axial-vector constant g_A. Predictions for the values of 〈m_ν〉 from the results of oscillation experiments and modern cosmological data are presented. The possibilities of the next generation experiments with sensitivity to 〈m_ν〉 at the level of ~ 10–50 meV (studying mainly the inverted ordering (IO) region) are discussed. The prospects for studying the normal ordering (NO) region are discussed too. It is shown that the possibilities of studying the NO depend on the mass of the lightest neutrino m₀. In the limiting case of small mass (m₀ ≤ 0.1 meV), the values of 〈m_ν〉 ≈ 1–4 meV are predicted, which makes the study of this region inaccessible by the next generation experiments. But there is an allowed region of m₀ (7–30 meV) in the framework of NO, where the predicted values for 〈m_ν〉 could be ~ 10–30 meV and that is quite achievable for the next generation experiments. The possibility to rich in the future sensitivity to 〈m_ν〉 at the level of ~ 1–10 meV is also discussed.

1. Introduction

The interest in neutrinoless double decay increased significantly after the discovery of neutrino oscillations in experiments with atmospheric, solar, reactor, and accelerator neutrinos (see, for example, discussions in [1–3]). This is due to the fact that the very existence of neutrino oscillations indicates that the neutrino has a non-zero mass. However, oscillation experiments are not sensitive to the nature of the neutrino mass (Dirac or Majorana) and do not provide information on the absolute scale of neutrino masses. Registration of neutrinoless double beta decay will clarify many fundamental aspects of neutrino physics (see, for example, discussions in [4–6]):

(i)   lepton number non-conservation;

(ii)  neutrino nature: whether the neutrino is a Dirac or a Majorana particle;

(iii) absolute neutrino mass scale;

(iv)  the type of neutrino mass ordering (normal or inverted);

(v)  CP violation in the lepton sector (measurement of the Majorana CP-violating phases).

This process assumes a simple form, namely

$\begin{array}{rc}(A,Z)\to (A,Z+2)+2e^{-}.& (1)\end{array}$

The discovery of this process is of fundamental interest, since it is practically the only way to establish the Majorana nature of neutrino. The Majorana nature of the neutrino would have interesting implications in many extensions of the Standard Model. For example the seesaw mechanism requires the existence of a Majorana neutrino to explain the lightness of neutrino masses [7–10]. A Majorana neutrino would also provide a natural explanation for the lepton number violation, and for the leptogenesis process which may explain the observed matter-antimatter asymmetry of the Universe [11].

The standard underlying mechanism behind neutrinoless double-beta decay is the exchange of a light Majorana neutrino. In this case, the half-life time of the decay can be presented as

$\begin{array}{rc}{\left[T_{1/2}(0\nu )\right]}^{-1}=G_{0\nu }{g}_A^4\mid M_{0\nu }{\mid }^2{\left|\frac{\langle m_{\nu }\rangle }{m_e}\right|}^2,& (2)\end{array}$

where G_0ν is the phase space factor, which contains the kinematic information about the final state particles, and is exactly calculable to the precision of the input parameters [12, 13], g_A is the axial-vector coupling constant¹, ∣M_0ν∣ is the nuclear matrix element, m_e is the mass of the electron, and 〈m_ν〉 is the effective Majorana mass of the electron neutrino, which is defined as 〈m_ν〉 = $\mid \sum _i{U}_{ei}^2{m}_i\mid$ where m_i are the neutrino mass eigenstates and U_ei are the elements of the neutrino mixing Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix.

In contrast to two-neutrino decay (this decay has been detected—see review [18], for example), neutrinoless double beta decay has not yet been observed. The best limits on 〈m_ν〉 are obtained for ¹³⁶Xe, ⁷⁶Ge, ¹³⁰Te, ¹⁰⁰Mo, and ⁸²Se (see section 3). The assemblage of sensitive experiments for different nuclei permits one to increase the reliability of the limit on 〈m_ν〉. Present conservative limit can be set as 0.23 eV at 90% C.L. (using conservative value from the KamLAND-Zen experiment). But one has to take into account that, in fact, this value could be in ~ 1.5–2 times greater because of the possible quenching of g_A (see recent discussions in [17]).

The main goal of next generation experiments is to investigate the IO region of neutrino mass (〈m_ν〉 ≈ (14–50) meV). If one will not see the decay in this region then it will be necessary to investigate region with 〈m_ν〉 < 14 meV.

2. Predictions on 〈M_ν〉 From Neutrino Oscillation and Cosmological Data

Using the data of oscillatory experiments, one can obtain predictions for possible values of 〈m_ν〉. Usually a so-called “lobster” (“crab”) plot is constructed, which shows the possible values of 〈m_ν〉, depending on the type of ordering and the mass of the lightest neutrino m₀, which is unknown (see, for example, recent papers [6, 19, 20]). The cosmological constraints on Σm_ν are used to limit the possible values of m₀. In Figure 1, predictions on the effective Majorana neutrino mass are plotted as function of the lightest neutrino mass m₀. The 2σ and 3σ values of neutrino oscillation parameters are taken into account [21]. The PLANCK collaboration in a recent publication gives a limit of Σm_ν < 0.12 eV [22], using the new CMB data with different large scale structure observations. This leads to a limitation on m₀ < 30 and < 16 meV for normal and inverted ordering, respectively. Taking into account PLANCK's limit, different regions of possible values of 〈m_ν〉 are obtained depending on the type of ordering:

1) 〈m_ν〉 ≈ 14–50 meV for all values of m₀ in the IO case.

2) In the NO case the situation is more complicated. The 〈m_ν〉 can take values from practically 0 to 30 meV. And it has to be stressed that there is an allowed region of m₀ = 7–30 meV, where the 〈m_ν〉 could be ~ 10–30 meV and that is quite achievable for the next generation experiments. At m₀ = 10–30 meV, the NO and IO regions partially overlap and it will be difficult to uniquely determine the type of ordering. And only at m₀ < 10 meV it will be possible to reliably distinguish between the NO and IO. At m₀ = 1–10 meV, a strong decrease in the values of 〈m_ν〉 is possible for certain values of the Majorana phases (nevertheless, the probability of almost total nullification 〈m_ν〉 is sufficiently small [20]). At values of m₀ ≤ 0.1 meV the 〈m_ν〉 ≈ 1–4 meV (the so-called “limiting” case).

FIGURE 1

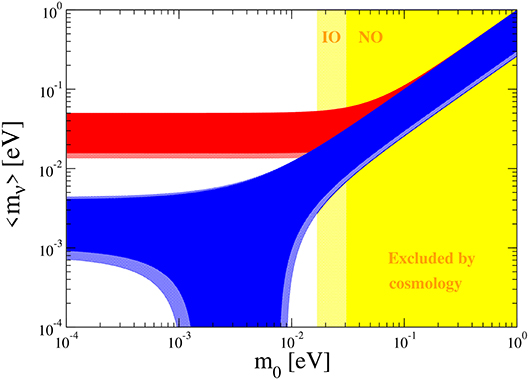
Figure 1. Predictions on 〈m_ν〉 from neutrino oscillations vs. the lightest neutrino mass m₀ in the two cases of normal (the blue region) and inverted (the red region) spectra. The 2σ and 3σ values of neutrino oscillation parameters are considered [21]. The excluded region by cosmological data (Σm_ν < 0.12 eV) m₀ is presented in yellow (>30 meV for the NO and >16 meV for the IO).

A global analysis of all available data was carried out in de Salas et al.[20] and it was shown that the NO is more preferable (at 3.5σ level). It was also demonstrated that Σm_ν ≥ 0.06 eV for the NO case, and Σm_ν ≥ 0.1 eV for the IO. Nevertheless, the question of the order of the neutrino masses is not yet fully clarified and experiments on a double beta decay can contribute to its solution. A limit on 〈m_ν〉 below 14 meV could be used to rule out the IO scheme, assuming that neutrinos are Majorana fermion. On the other hand a positive detection of 0νββ decay in the range that corresponds to 〈m_ν〉 > 14 meV would not give sufficient information to determine the mass ordering without an independent determination of m₀. Finally, in the context of three neutrino mixing, neutrinoless double beta decay experiments alone will be able to determine the neutrino mass ordering only ruling out the inverted scheme, that is to say if the ordering is normal and m₀ ≤ 10 meV.

It is hoped that in a few years the value of Σm_ν could be determined from cosmology (see, for example, discussions in [20, 23]). This will help make a reliable conclusion about the type of ordering (for example, if the measured value will be less than 0.1 eV, it will mean that the NO is realized) and obtain information on the value of m₀. And this, in turn, will improve the predictions for a possible range of 〈m_ν〉. For examlpe, in Penedo and Petcov [19] it was demonstrated that if the sum of neutrino masses is found to satisfy Σm_ν > 0.10 eV, then for NO case 〈m_ν〉 > 5 meV for any values of the Majorana phases.

3. Present Status and Current Experiments

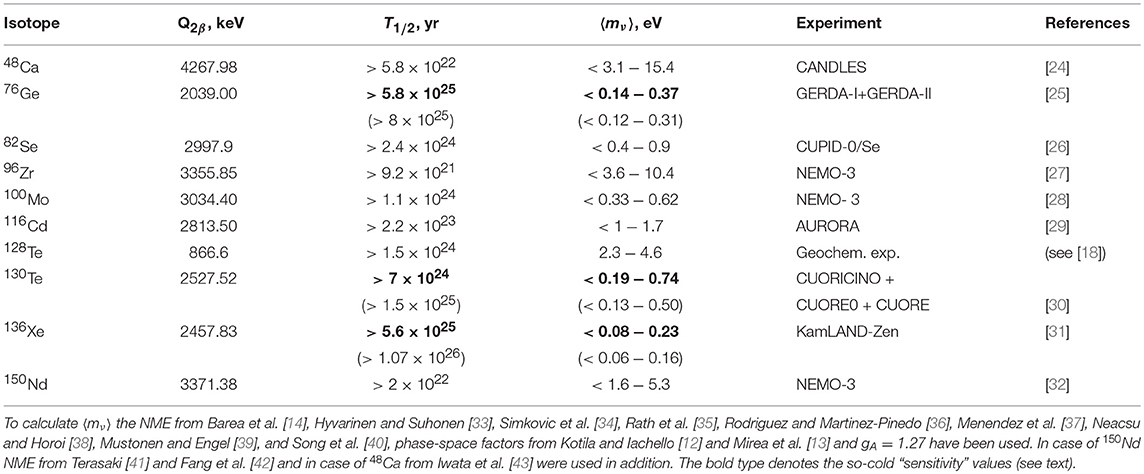
Table 1 shows the best results for today on search for 0νββ decay for the most interesting nucleus-candidates for this process. Limits on the values of T_1/2 and 〈m_ν〉 are given. To calculate 〈m_ν〉 the NMEs from recent works [14, 33–43] and the value g_A = 1.27 have been used. One can see that the best modern experiments have reached a sensitivity of ~ 10²⁵–10²⁶ years for the half-life and ~ 0.1–0.3 eV for the 〈m_ν〉. The spread in the values of the neutrino mass in each case is related to the currently existing uncertainties in the calculations of NMEs. Uncertainty in the values of NMEs is a factor of ~ 2–3. As already noted, quenching of g_A in the nucleus is possible and, as a result, the limits on the neutrino mass could be ~ 1.5–2 times weaker. Table 1 shows that the most stringent limits on the effective mass of Majorana neutrino are obtained in experiments with ¹³⁶Xe, ⁷⁶Ge, ¹³⁰Te, ¹⁰⁰Mo, and ⁸²Se. For some nuclei, Table 1 lists two limit values for T_1/2 and 〈m_ν〉. This is due to the fact that in some cases (¹³⁶Xe, ¹³⁰Te, and ⁷⁶Ge) a large background fluctuation leads to too “optimistic” limits, substantially exceeding the “sensitivity” of the experiments. Therefore, the values of the “sensitivity” of the experiments are also given in the Table 1. I believe that these values are although more conservative, but the most reliable. With this in mind, the conservative limit on 〈m_ν〉 from modern double beta decay experiments is 0.23 eV (90% C.L.).

TABLE 1

Table 1. Best present limits on 0νββ decay (at 90% C.L.).

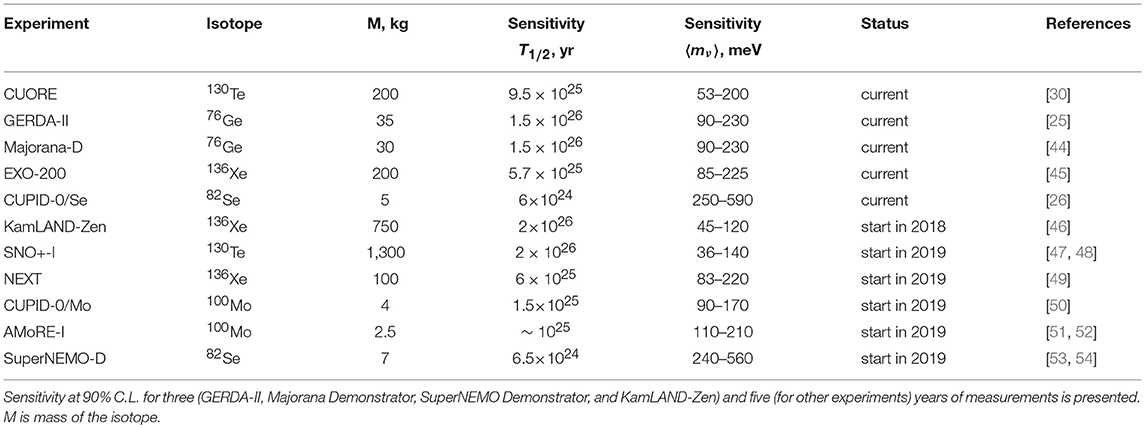
Table 2 shows the best current and planned to start in 2018-2019 modern experiments that will determine the situation in the neutrinoless double beta decay in the coming years. It is seen that in the best of these experiments sensitivity to the 〈m_ν〉 ~ 0.04–0.2 eV will be achieved, which, apparently, will not be enough for verification of the IO region (because to observe the effect, it is necessary to see the signal at least at 3σ level; therefore, even the most sensitive experiments with the most favorable values of NMEs will not be able to register the decay).

TABLE 2

Table 2. Best current and planned to start in 2018-2019 modern experiments.

4. Possibilities of Future Double Beta Decay Experiments to Investigate IO Region of Neutrino Mass

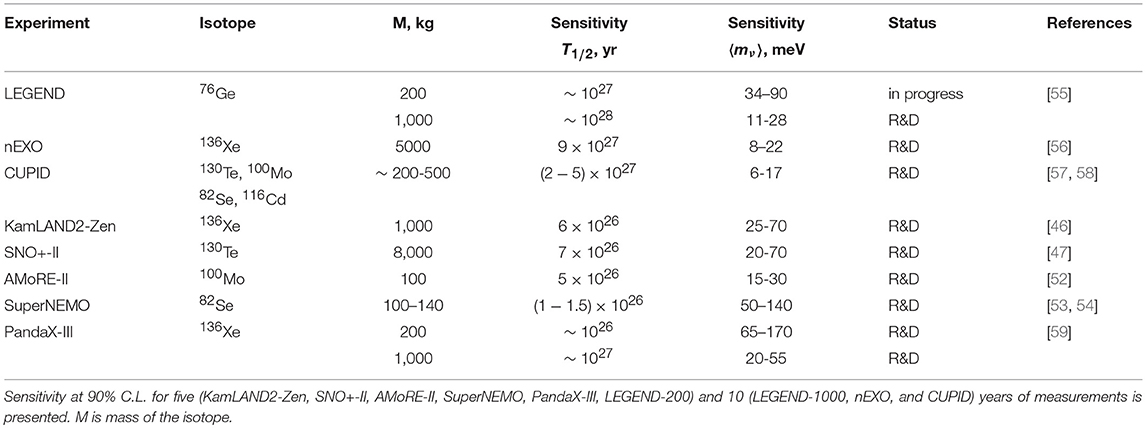
Table 3 shows the most promising planned experiments, which will be realized in ~ 5–15 years. To test the IO region of neutrino masses, it is necessary to achieve sensitivity to 〈m_ν〉 at the level of ~ 14–50 meV. Practically all experiments listed in Table 3 have a chance to register a 0νββ decay, but only CUPID, nEXO, and LEGEND-1000 overlap quite well the range of 〈m_ν〉 associated with the IO. Thus, if the IO is actually realized in nature and the neutrino is Majorana particle, then it is likely that the neutrinoless double beta decay will be registered in the experiment in ~ 5–15 years. And the CUPID, nEXO, and LEGEND-1000 experiments have the greatest chances to see the effect. But even these, the most sensitive experiments, do not guarantee the observation of the effect. At unfavorable values of NMEs and g_A, the sensitivity of these experiments will be insufficient to completely cover the entire range of possible values of 〈m_ν〉 for the IO. And one has to remember that in order to observe the effect it is necessary to have at least 3σ confidence level [in Table 3, the sensitivity is indicated at 90% C.L. (1.6σ)].

TABLE 3

Table 3. Main most developed and promising projects for next generation experiments.

5. Possibilities of Future Double Beta Decay Experiments to Investigate NO Region of Neutrino Mass

In the NO case, the following possible ranges of 〈m_ν〉 can be distinguished:

1) 10–30 meV. In this case, 0νββ decay could be detected in the next generation experiments (see Table 3). But, for this area of mass, it will be difficult to distinguish the NO from IO. In this case additional information about m₀ is required.

2) 3–10 meV. In this case, detectors containing ~ 1–10 tons of ββ isotope are required. And it is possible (in principle) to investigate this region of 〈m_ν〉 in the future (sensitivity to T_1/2 on the level of ~ 10²⁸−10²⁹ yr will be needed).

3) 1–3 meV. In this case, detectors containing ~ 10–100 tons of ββ isotope are required. It will be very difficult (if possible) to investigate this region of 〈m_ν〉 in the future (sensitivity to T_1/2 on the level of ~ 10²⁹−10³⁰ yr will be needed).

4) < 1 meV. This area is not available for observation in foreseeable future.

The possibility of studying 0νββ decay with sensitivity to neutrino mass on the level of ~ 1–5 meV has been analyzed in Barabash [60]. It was shown that the 3–5 meV region can be studied by detectors containing ~ 10 tons of ββ isotope. Moreover, the detectors should have a sufficiently high efficiency (~ 100%), good energy resolution (FWHM <1–2%), and low level of background in the investigated region (~ 10⁻⁶−10⁻⁷ c/kev × kg × yr). In addition, the cost of an isotope becomes important and can seriously limit the feasibility of such experiments [60]. It was noted in Barabash [60] that ¹³⁶Xe, ¹³⁰Te, ⁸²Se, ¹⁰⁰Mo, and ⁷⁶Ge are most promising isotopes, and the most suitable experimental techniques are low-temperature scintillation bolometers, gas Xe TPC, and HPGe semiconductor detectors.

Summarizing all of the above, one can conclude that if we are dealing with the NO and 〈m_ν〉 = 10–30 meV, then 0νββ decay could be registered in next-generation experiments (~ 5–15 years from now). To study the range of 〈m_ν〉 < 10 meV, new, more sensitive experiments with the mass of the investigated isotope ~ 1–10 tons (〈m_ν〉 = 3–10 meV) or ~ 10–100 tons (〈m_ν〉 = 1–3 meV) are required. In more detail, such possible experiments are discussed in Barabash [60].

6. Conclusion

Thus, we can conclude that the present conservative limit on 〈m_ν〉 from double beta decay experiments is 0.23 eV (90% C.L.). Within the next 3–5 years, the sensitivity of modern experiments will be brought to ~ 0.04–0.2 eV. To study the IO region (0.014–0.05 eV), new generation experiments will be realized, which will achieve the required sensitivity in ~ 5–15 years. If we are dealing with NO, then everything depends on the value of 〈m_ν〉 that is realized in nature. If 〈m_ν〉 = 10–30 meV, then this lies in the sensitivity region of the next generation experiments and 0νββ decay could be registered. If 〈m_ν〉 = 3–10 meV, new, more sensitive experiments with ~ 1–10 tons of ββ isotope are required (and it seems possible). For 〈m_ν〉 = 1–3 meV experiments with of ~ 10–100 tons of the isotope are required and it will be very difficult (if possible) to reach needed sensitivity in this case. If, however, 〈m_ν〉 ≤ 1 meV, then apparently 0νββ decay will not be registered in the foreseeable future².

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported by Russian Science Foundation (grant No. 18-12-00003). And I want to thank Prof. F. Simkovic and V. Umatov for help in preparing the figure.

Footnotes

1. ^Usually the value g_A = 1.27 is used (the free neutron decay value). In nuclear matter, however, the value of g_A could be quenched. In 2ν decay case effect of quenching could be quite strong [6, 14–17]. In case of 0ν decay it can be a factor of ~ 1.2–1.5 (see discussion in [17]). This question is still under discussion and there is no final answer up to now.

2. ^In this article, we proceed from the assumption that we are dealing with an 0νββ decay, going through the exchange of light Majorana neutrinos. This mechanism is the most popular at the moment. Nevertheless, it should be emphasized that, in principle, other mechanisms are possible (right-handed currents, supersymmetry, heavy neutrinos, doubly charged Higgs bosons, etc.)—see, for example, discussions in Vergados et al. [6], Engel et al. [61], and Avignone et al. [62]. Therefore, if the 0νββ decay will be detected, then, first of all, it will be necessary to verify that we are dealing with a mechanism associated with a light neutrino. And only after that it will be possible to make a reliable conclusion about the value of 〈m_ν〉. It is not excluded that several mechanisms will contribute to the 0νββ transition at the same time. In this case, it will be difficult to determine the true value of 〈m_ν〉. On the other hand, the presence of other decay mechanisms allows us to hope for the registration of 0νββ decay even at very low value of 〈m_ν〉.

References

1. Mohapatra RN, Smirnov AY. Neutrino mass and new physics. Annu Rev Nucl Part Sci. (2006) 56:569–628. doi: 10.1146/annurev.nucl.56.080805.140534

CrossRef Full Text | Google Scholar

2. Bilenky SM. Neutrino in standard model and beyond. Phys Part Nucl. (2015) 46:475–96. doi: 10.1134/S1063779615040024

CrossRef Full Text | Google Scholar

3. de Salas PF, Forerob DV, Ternes CA, Tórtola M, Valle JWF. Status of neutrino oscillations 2018: first hint for normal mass ordering and improved CP sensitivity. Phys Lett B (2018) 782:633–40. doi: 10.1016/j.physletb.2018.06.019

CrossRef Full Text | Google Scholar

4. Pascoli S, Petcov ST, Schwetz T. The absolute neutrino mass scale, neutrino mass spectrum, Majorana CP-violation and neutrinoless double-beta decay. Nucl Phys B (2006) 734:24–49. doi: 10.1016/j.nuclphysb.2005.11.003

CrossRef Full Text | Google Scholar

5. Bilenky SM, Giunti C. Neutrinoless double-beta decay: a probe of physics beyond the Standard Mode. Int J Mod Phys A (2015) 30:1530001. doi: 10.1142/S0217751X1530001X

CrossRef Full Text | Google Scholar

6. Vergados JD, Ejiri H, Simkovic F. Neutrinoless double beta decay and neutrino mass. Int J Mod Phys E (2016) 25:163007. doi: 10.1142/S0218301316300071

CrossRef Full Text | Google Scholar

7. Minkowski P. μ → eγ at a rate of one out of 10⁹ muon decays? Phys Lett B (1977) 67:421–8. doi: 10.1016/0370-2693(77)90435-X

CrossRef Full Text | Google Scholar

8. Yanagida T. Horizontal symmetry and masses of neutrinos. Prog Theor Phys. (1980) 64:1103–5. doi: 10.1143/PTP.64.1103

CrossRef Full Text | Google Scholar

9. Gell-Mann M, Ramond P, Slansky R. Supergravity. In: van Nieuwenhuizen F, Freedman D, editors. Proceedings of the Supergravity Stony Brook Workshop. New York, NY: North Holland Publishing Co (1979). p. 315.

Google Scholar

10. Mohapatra RN, Senjanovic G. Neutrino mass and spontaneous parity nonconservation. Phys Rev Lett. (1980) 44:912–5. doi: 10.1103/PhysRevLett.44.912

CrossRef Full Text | Google Scholar

11. Fukugita M, Yanagida T. Barygenesis without grand unification. Phys Lett B (1986) 174:45–7. doi: 10.1016/0370-2693(86)91126-3

CrossRef Full Text | Google Scholar

12. Kotila J, Iachello F. Phase space factors for double-β decay. Phys Rev C (2012) 85:034316. doi: 10.1103/PhysRevC.85.034316

CrossRef Full Text | Google Scholar

13. Mirea M, Pahomi T, Stoica S. (2015). Values of the phase space factors involved in double beta decay. Romanian Rep Phys. (2015) 67:872–89. doi: 10.1063/1.4934913

CrossRef Full Text | Google Scholar

14. Barea J, Kotila J, Iachello F. 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys Rev C (2015) 91:034304. doi: 10.1103/PhysRevC.91.034304

CrossRef Full Text | Google Scholar

15. Pirinen P, Suhonen J. Systematic approach to β and 2νββ decays of mass A = 100–136 nuclei. Phys Rev C (2015) 91:054309. doi: 10.1103/PhysRevC.91.054309

CrossRef Full Text | Google Scholar

16. Kostensalo J, Haaranen M, Suhonen J. Electron spectra in forbidden β decays and the quenching of the weak axial-vector coupling constant g_A. Phys Rev C (2017) 95:044313. doi: 10.1103/PhysRevC.95.044313

CrossRef Full Text | Google Scholar

17. Suhonen J. Impact of the quenching of g_A on the sensitivity of 0νββ experiments. Phys Rev C (2017) 96:055501. doi: 10.1103/PhysRevC.96.055501

CrossRef Full Text | Google Scholar

18. Barabash AS. Average and recommended half-life values for two-neutrino double beta decay. Nucl Phys A (2015) 935:52–64. doi: 10.1016/j.nuclphysa.2015.01.001

CrossRef Full Text | Google Scholar

19. Penedo JT, Petcov ST. The 10⁻³ eV frontier in neutrinoless double beta decay. Phys Lett B (2018) 786:410–7. doi: 10.1016/j.physletb.2018.09.059

CrossRef Full Text | Google Scholar

20. de Salas PF, Gariazzo S, Mena O, Ternes CA, Tórtola M. Neutrino mass ordering from oscillations and beyond: 2018 status and future prospects. Front Astron Space Sci. (2018) 5:00036. doi: 10.3389/fspas.2018.00036

CrossRef Full Text | Google Scholar

21. Capozzi F, Di Valentino E, Lisi E, Marrone A, Melchiorri A, Palazzo A. Global constraints on absolute neutrino masses and their ordering. Phys Rev D (2017) 95:096014. doi: 10.1103/PhysRevD.95.096014

CrossRef Full Text | Google Scholar

22. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. arXiv:1807.06209 [astro-ph.CO].

23. Brinckmann T, Hooper DC, Archidiacono M, Lesgourgues J, Sprenger T. The promising future of a robust cosmological neutrino mass measurement. arXiv:1808.05955 [astro-ph.CO].

24. Umehara S. Neutrino-less double beta decay of ⁴⁸Ca studied by CaF₂ (Eu) scintillators. Phys Rev C (2008) 78:058501. doi: 10.1103/PhysRevC.78.058501

CrossRef Full Text | Google Scholar

25. Agostini M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, Bauer C, et al. Improved limit on neutrinoless double-β decay of ⁷⁶Ge from GERDA Phase II. Phys Rev Lett. (2018) 120:132503. doi: 10.1103/PhysRevLett.120.132503

CrossRef Full Text | Google Scholar

26. Azzolini O, Barrera MT, Beeman JW, Bellini F, Beretta M, Biassoni M, et al. First result on the neutrinoless double beta decay of ⁸²Se with CUPID-0. Phys Rev Lett. (2018) 120:232502. doi: 10.1103/PhysRevLett.120.232502

CrossRef Full Text | Google Scholar

27. NEMO-3 Collaboration, Argyriades J, Arnold R, Augier C, Baker J, Barabash AS, et al. Measurement of the two neutrino double beta decay half-life of Zr-96 with the NEMO-3 detector. Nucl Phys A (2010) 847:168–79. doi: 10.1016/j.nuclphysa.2010.07.009

CrossRef Full Text | Google Scholar

28. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Results of the search for neutrinoless double-β decay in ¹⁰⁰Mo with the NEMO-3 experiment. Phys Rev D (2015) 92:072011. doi: 10.1103/PhysRevD.92.072011

CrossRef Full Text | Google Scholar

29. Barabash AS, Belli P, Bernabei R, Cappella F, Caracciolo V, Cerulli R, et al. Final results of the Aurora experiment to study 2β decay of ¹¹⁶Cd with enriched ¹¹⁶CdWO₄ crystal scintillators. Phys Rev D (2018) 98:092007. doi: 10.1103/PhysRevD.98.092007

CrossRef Full Text | Google Scholar

30. Alduino C, Alfonso K, Andreotti E, Arnaboldi C, Avignone FT, Azzolini O, et al. First results from CUORE: a search for lepton number violation via 0νββ decay of ¹³⁰Te. Phys Rev Lett. (2018) 120:132501. doi: 10.1103/PhysRevLett.120.132501

CrossRef Full Text | Google Scholar

31. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for Majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.082503

CrossRef Full Text | Google Scholar

32. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Measurement of the 2νββ decay half-life of ¹⁵⁰Nd and a search for 0νββ decay processes with the full exposure from the NEMO-3 detector. Phys Rev D (2016) 94:072003. doi: 10.1103/PhysRevD.94.072003

CrossRef Full Text | Google Scholar

33. Hyvarinen J, Suhonen J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys Rev C (2015) 91:024613. doi: 10.1103/PhysRevC.91.024613

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Simkovic F, Rodin V, Faessler A, Vogel P. 0νββ and 2νββ nuclear matrix elements, QRPA, and isospin symmetry restoration. Phys Rev C (2013) 87:045501. doi: 10.1103/PhysRevC.87.045501

CrossRef Full Text | Google Scholar

35. Rath PK, Chandra R, Chaturvedi K, Lohani P, Raina PK, Hirsch JG. Neutrinoless ββ decay transition matrix elements within mechanisms involving light Majorana neutrinos, classical Majorons and sterile neutrinos. Phys Rev C (2013) 88:064322. doi: 10.1103/PhysRevC.88.064322

CrossRef Full Text | Google Scholar

36. Rodriguez TR, Martinez-Pinedo G. Energy density functional study of nuclear matrix elements for neutrinoless ββ decay. Phys Rev Lett. (2010) 105:252503. doi: 10.1103/PhysRevLett.105.252503

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Menendez J, Poves A, Caurier E, Nowacki F. Disassembling the nuclear matrix elements of the neutrinoless ββ decay. Nucl Phys A (2009) 818:139–51. doi: 10.1016/j.nuclphysa.2008.12.005

CrossRef Full Text | Google Scholar

38. Neacsu A, Horoi M. Shell model studies of the ¹³⁰Te neutrinoless double-β decay Phys Rev C (2015) 91:024309. doi: 10.1103/PhysRevC.91.024309

CrossRef Full Text | Google Scholar

39. Mustonen M, Engel J. Large-scale calculations of the double-β decay of ⁷⁶Ge, ¹³⁰Te, ¹³⁶Xe, and ¹⁵⁰Nd in the deformed self-consistent Skyrme quasiparticle random-phase approximation. Phys Rev C (2013)87:064302. doi: 10.1103/PhysRevC.87.064302

CrossRef Full Text | Google Scholar

40. Song LS, Yao JM, Ring P, Meng J. Nuclear matrix element of neutrinoless double-β decay: Relativity and short-range correlations. Phys Rev C (2017) 95:024305. doi: 10.1103/PhysRevC.95.024305

CrossRef Full Text | Google Scholar

41. Terasaki J. Many-body correlations of quasiparticle random-phase approximation in nuclear matrix elements of neutrinoless double-β decay. Phys Rev C (2015) 91:034318. doi: 10.1103/PhysRevC.91.034318

CrossRef Full Text | Google Scholar

42. Fang D-L, Faessler A, Simkovic F. Partial restoration of isospin symmetry for neutrinoless double β decay in the deformed nuclear system of ¹⁵⁰Nd. Phys Rev C (2015) 92:044301. doi: 10.1103/PhysRevC.92.044301

CrossRef Full Text | Google Scholar

43. Iwata Y, Shimizu N, Otsuka T, Utsuno Y, Menéndez J, Honma M, et al. Large-scale shell-model analysis of the neutrinoless ββ decay of ⁴⁸Ca. Phys Rev Lett. (2016) 116:112502. doi: 10.1103/PhysRevLett.116.112502

CrossRef Full Text | Google Scholar

44. Aalseth CE, Abgrall N, Aguayo E, Alvis SI, Amman M, Arnquist IJ, et al. Search for neutrinoless double-β decay in ⁷⁶Ge with the majorana demonstrator. Phys Rev Lett. (2018) 120:132502. doi: 10.1103/PhysRevLett.120.132502

CrossRef Full Text | Google Scholar

45. Albert JB, Anton G, Badhrees I, Barbeau PS, Bayerlein R, Beck D, et al. Search for neutrinoless double-beta decay with the upgraded EXO-200 detector. Phys Rev Lett. (2018) 120:072701. doi: 10.1103/PhysRevD.97.072007

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Shirai J. KamLAND-Zen. In: Proceedings of XVII International Workshop on Neutrino Telescopes. Venezia (2018) p. 027. doi: 10.22323/1.307.0027

CrossRef Full Text | Google Scholar

47. Andringa S, Arushanova E, Asahi S, Askins M, Auty DJ, Back AR, et al. Current status and future prospects of the SNO+ experiment. Adv High Energy Phys. (2016) 2016: 6194250. doi: 10.1155/2016/6194250

CrossRef Full Text | Google Scholar

48. Fischer V. Search for neutrinoless double-beta decay with SNO+. arXiv:1809.05986 [physics.ins-det].

49. Martin-Albo J, Muñoz Vidal J, Ferrario P, Nebot-Guinot M, Gómez-Cadenas JJ, Álvarez V, et al. Sensitivity of NEXT-100 to neutrinoless double beta decay. J High Energy Phys. (2016) 5:159. doi: 10.1007/JHEP05(2016)159

CrossRef Full Text | Google Scholar

50. Poda DV. ¹⁰⁰Mo-enriched Li₂MoO₄ scintillating bolometers for 0νββ decay search: from LUMINEU to CUPID-0/Mo projects. AIP Conf Proc. (2017) 1894:020017. doi: 10.1063/1.5007642

CrossRef Full Text | Google Scholar

51. Yoon YS. Status of the AMoRE experiment to search for neutrinoless double beta decay of Mo-100. In: PoS (ICRC2017). Busan (2018) 1056. doi: 10.22323/1.301.1056

CrossRef Full Text | Google Scholar

52. Kim SC. The Status of the AMoRE experiment. In: Proceedings Neutrino 2018 – XXVIII International Conference Physics and Astrophysics. Heidelberg: Zenodo (2018).

Google Scholar

53. Barabash AS, Basharina-Freshville A, Blot S, Bongrand M, Bourgeois Ch, Breton D, et al. Calorimeter development for the SuperNEMO double beta decay experiment. Nucl Instrum Methods A (2017) 868:98–108. doi: 10.1016/j.nima.2017.06.044

CrossRef Full Text | Google Scholar

54. Cascella M, On behalf of the SuperNEMO collaboration. Construction and commissioning of the SuperNEMO detector tracker. Nucl Instrum Methods A (2016) 824:507–9. doi: 10.1016/j.nima.2015.11.083

CrossRef Full Text | Google Scholar

55. Abgrall N, Abramov A, Abrosimov N, Abt I, Agostini M, Agartioglu M, et al. The large enriched germanium experiment for neutrinoless double beta decay (LEGEND). AIP Conf Proc (2017) 1894:02027. doi: 10.1063/1.5007652

CrossRef Full Text | Google Scholar

56. Albert JB, Anton G, Arnquist IJ, Badhrees I, Barbeau P, Beck D, et al. Sensitivity and discovery potential of the proposed nEXO experiment to neutrinoless double-β decay. Phys Rev C (2018) 97:065503. doi: 10.1088/1748-0221/13/01/P0

CrossRef Full Text | Google Scholar

57. Wang G, Chang CL, Yefremenko V, Ding J, Novosad V, Bucci C, et al. CUPID: CUORE (Cryogenic Underground Observatory for Rare Events) Upgrade with Particle IDentification. arXiv:1504.03599 [physics.ins-det].

58. Wang G, Chang CL, Yefremenko V, Ding J, Novosad V, Bucci C, et al. R&D towards CUPID (CUORE Upgrade with Particle IDentification). arXiv:1504.03612 [physics.ins-det].

59. Chen X, Fu CB, Galan J, Giboni K, Giuliani F, Gu LH, et al. PandaX-III: Searching for neutrinoless double beta decay with high pressure ¹³⁶Xe gas time projection chambers. Sci China Phys Mech Astron. (2017) 60:061011. doi: 10.1007/s11433-017-9028-0

CrossRef Full Text | Google Scholar

60. Barabash AS. Main features of detectors and isotopes to investigate double beta decay with increased sensitivity. Int J Mod Phys A (2018) 33:1843001. doi: 10.1142/S0217751X18430017

CrossRef Full Text | Google Scholar

61. Engel J, Menendez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep Prog Phys. (2017) 80:046301. doi: 10.1088/1361-6633/aa5bc5

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Avignone FT, Elliott SR, Engel J. Double beta decay, Majorana neutrinos, and neutrino mass. Rev Mod Phys. (2008) 80:481–516. doi: 10.1103/RevModPhys.80.481

CrossRef Full Text | Google Scholar