
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 13 November 2018
Sec. Low-Temperature Plasma Physics
Volume 6 - 2018 | https://doi.org/10.3389/fphy.2018.00128
This article is part of the Research Topic Adaptive Kinetic-Fluid Models for Plasma Simulations on Modern Computer Systems View all 9 articles
Owing to their ability to model the physics of low-pressure plasmas away from thermodynamical equilibrium, particle-in-cell (PIC) techniques have become one of the tools of choice to simulate the operation of many plasma devices. This trend is reinforced by the growing access to parallel computing resources which enables tackling problems that were previously intractable with PIC techniques. However, accurate modeling of these plasmas often depends critically on the detailed description of a variety of physical phenomena ranging from microscopic to macroscopic scale and from electrons' to neutral particles' timescale. Among those are coupling phenomena between charged particles and neutrals. We illustrate here how the implementation of simplified models for scattering kinematics, neutrals dynamics and particle-wall interaction can affect simulation results. Until the full breadth of these effects can be captured in models, these results underline the importance of using extensive parametric scans to assess the importance of these effects.
Low-pressure gas discharges and plasma sources are used in a great variety of applications [1, 2], such as space propulsion [3, 4], neutral beam injection [5] and plasma separation [6–8]. To optimize these devices and expand the range of application of low-pressure plasmas, numerical modeling capabilities are highly desirable. Yet, experimental results indicate that such plasmas are often far from thermal equilibrium [2]. Furthermore, the mean free path of charge particles in low-pressure discharges is often comparable to, if not greater than, the vacuum vessel dimensions. Under such conditions standard fluid models do not hold [9, 10] and fluid simulation tools can not fully capture the physics at play. In these plasma regimes, kinetic modeling tools such as particle-in-cell (PIC) techniques [11–13] and Vlasov's codes [14, 15] are required for high-fidelity simulations. Kinetic modeling however comes at a significantly larger computing cost which sets an upper limit to the plasma density and plasma volume one can model. This in turn limits the applicability of PIC techniques for whole device simulations. Yet, owing to the expansion of parallel computing, PIC techniques are increasingly used to model a large range of low-pressure plasma sources [16–19].
PIC methods solve numerically Vlasov's equation which describes a fully ionized and collisionless plasma. PIC techniques [11, 13] consists in following the dynamics of a very large number of macro-particles, up to 1013 [20], interacting with the self-generated electromagnetic (EM) fields (and also possibly superimposed externally applied fields).In the explicit PIC implementations that are used in most PIC simulations, macro-particles are pushed at each time-step by solving Lorentz equation using the EM fields at the beginning of the step. Fields are then updated by solving Maxwell's equations, or Poisson's equation in electrostatic (ES) PIC, using the new macro-particle positions and velocities. These methods are particularly suitable for parallelization and have been shown to scale very well up to millions of computing cores [20].
Yet, since plasma sources and laboratory plasmas are neither fully ionized or collisionless, they can not be modeled by standard PIC methods alone. Additional models are indeed required alongside the PIC scheme to handle neutral dynamics and also neutral interaction with charged particles in partially ionized plasmas. For dense plasmas, Coulomb collisions can also be important and require their own dedicated models. Furthermore, laboratory plasmas are inherently of finite volume. Physical boundaries are therefore facing the plasma. PIC schemes hence need to be modified to adequately model the interaction of charged and neutral particles with the walls. Implementation within PIC techniques of detailed models for each of these phenomena is key to ensure that simulation results do reproduce the physics at play in actual devices. On the other hand, modeling of these phenomena leads to additional computational cost and can have a detrimental effect on parallelization performances. Efficient implementation of these models is made even more challenging by the fact that these effects occur on vastly different timescales, ranging from electron to neutral timescale (10−10 to 10−4 s).
In this paper, we review how the modeling of a few specific physical phenomena can play, under some conditions, an important role on PIC simulation results, and offer insights into implementation strategies with an eye to parallelization performances. In section 2, the role played by neutrals dynamics and neutrals interaction with charged particles in low-pressure discharges is highlighted, and possible modeling options are discussed. In section 3, the physics of particle-wall interaction and its importance on the properties of low-pressure plasmas is reviewed. In section 4, the main findings are summarized. Not that this paper is not aimed at covering all aspects of particle-in-cell methods, but rather at underlining the importance that the choice of certain simplifications in physical models can have on simulation results. For an in-depth and detailed description of particle-in-cell methods, the reader is referred to the many excellent reviews available [see 11, 13, 21, 22].
Over the years, the interplay between charged particles and neutral particles has been shown to lead to a variety of phenomena across a wide range of plasma parameters. In magnetically confined fusion plasmas, neutrals play an important role on edge physics [23] and plasma confinement [24, 25]. In high-density plasma sources, neutral depletion [26] can be the cause of enhanced plasma transport [27], oscillations [28] and neutral-heating [29]. Neutrals can also control transport and separation capabilities in rotating plasmas [30]. In astrophysical plasmas, neutrals can lead to instabilities in interplanetary space [31, 32], contribute to the tail structure of comets [33] and modify the properties of planetary atmospheres [34, 35]. The interaction between charged particles and neutrals has also been proposed to explain the formation of the solar system [36, 37] through the critical ionization velocity phenomena [38].
Particular attention must therefore be taken when handling collisions to ensure that simulation results reproduce accurately the coupling mechanisms between charged particles and neutrals. In PIC models, collisions between charged particles and neutrals are typically handled through the addition of a Monte-Carlo collision (MCC) module [39–41]. Between each iteration of the PIC cycle, the MCC module computes the probability
for each charged particle in the simulation to undergo a collision of kind k during the time increment Δt. Here vr = |v − vn| is the relative velocity, x and v are respectively the position and the velocity of the charged particle, vn and nn are respectively the neutral velocity and density, and
is the cross-section for the kth collisional process, with χ the angle of rotation of the velocity after collision. For ionization processes, the angle differential cross-section is itself the result of the integration of a doubly differential cross section which contains information about the energy partitioning between the scattered particle and the secondary electron. Note that in practice, a null-collisions technique [42] is implemented to speed-up the Monte-Carlo collision step.
Equations (1, 2) show that two conditions need to be satisfied to ensure an accurate description of collisions between charged particles and neutrals. First, the differential cross-section assumed in the numerical model must be adequate to ensure a physical determination of post-collision velocities. This point is illustrated in section 2.2. Second, the accurate prediction of collisions is conditioned by an accurate modeling of the distribution functions of neutral particles. This point is addressed in section 2.3. These two conditions also highlight the multi-scale nature of charged particle - neutral collision. Electrons evolve and collide with neutrals on the fastest timescales (100 ps or less for cm−3), while neutral dynamics is much slower (100 μs or more for Tn = 300 K).
A useful parameter to discuss the effects of collisions between charged particles and neutrals is the ionization fraction ι = ni/(nn + ni), where ni and nn are the ion and neutral density, respectively. For low ionization fraction, say ι ≤ 10−3, the effects of charged particles on neutrals can be neglected to first order. This is for example the case in radio-frequency (RF) capacitive discharges, where 10−6 ≤ ι ≤ 10−4 [43]. In this regime, collisions may have a strong influence on the electron energy distribution function [44], but the distribution function of neutral particles is not modified by charged particles. Eq. (1) can then be simplified by assuming a uniform and steady-state density nn of neutrals with a maxwellian distribution of temperature Tn. In this regime, proper handling of collisions then hinges only on the information about scattering kinematics contained in the cross-section.
Further simplifications can be made for electron - neutral collisions. Indeed, since Te≫Tn and me≪mn, one finds vn≪ve, with ve the typical velocity of an electron. The electron velocity ve can then be substituted in lieu of the relative velocity vr to recast the differential cross-section as σk(ϵ, χ). Here is the kinetic energy of an electron.
While experimental data clearly shows [see 45 and references therein] that the angular scattering of electrons rapidly becomes forward as the incident kinetic increases (ϵ ≥ 20 eV), it is common in the literature to see studies in which electron-neutral scattering kinematics is treated as isotropic. Different possible explanations can be brought forward to explain this choice. First, experimental differential cross sections σ(ϵ, χ) are not as broadly available as integrated cross sections σ(ϵ). This is because measuring σ(ϵ, χ) is much more demanding than measuring σ(ϵ). Isotropic treatment can hence be used by default. Second, compared to an isotropic treatment, implementing an anisotropic treatment in a Monte Carlo collision (MCC) module requires generating one additional random number and doing one additional table look-up (interpolation) per collision event. This essentially doubles the computing cost of the collision treatment. While collisions typically only make for a small fraction of the total computing cost of PIC-MCC simulations of gas discharges, this additional computing cost can be canceled by treating electron-neutral collisions as isotropic scattering events. A legitimate question to ask is therefore whether this simplification can affect simulation results.
For elastic collisions, results from Janssen et al. [46] suggest that using an isotropic model instead of an anisotropic model does not lead to significant differences, even at higher energies. Note though that, in order to obtain this agreement, it is essential for the momentum transfer cross-section
to be held constant across the isotropic and anisotropic models. In other words, the collision frequency has to be scaled up when modeling elastic collisions as anisotropic (forward) compared to the isotropic case to preserve momentum transfer. However, isotropic modeling of elastic collision may not be accurate in nearly collisionless regimes. To illustrate this last point, consider an electron packet initially directed along propagating in a low-pressure neutral background for different energies ϵb. A measure of the isotropy of this electron packet is the angle ϑ95 which is defined as
with (ϑ, ϕ) the velocity space coordinates (0 ≤ ϕ ≤ 2π the azimuth and −π/2 ≤ ϑ ≤ π/2 the inclination) and f the normalized electron packet distribution function. The time evolution of ϑ95 obtained both for isotropic and anisotropic elastic collisions is plotted in Figure 1 for ϵb = 5, 50 and 500 eV. Anisotropic scattering is assumed to follow the empirical angular distribution cross-section suggested by Surendra et al. [47]. Results after a few collisions (tνc ≥ 2, with νc the momentum-transfer collision frequency) confirm minimal deviation between isotropic and anisotropic models when maintaining constant, in agreement with Janssen et al. [46]. On the other hand, results for tνc ~ 0.07 and ϵb = 500 eV show that ϑ95 is over 50% larger when assuming isotropic collisions. This over-prediction of fast electron deflection could have implications in certain low-pressure discharges with nearly collisionless trapped electrons, such as hollow cathodes [48] and wire plasma sources [49].
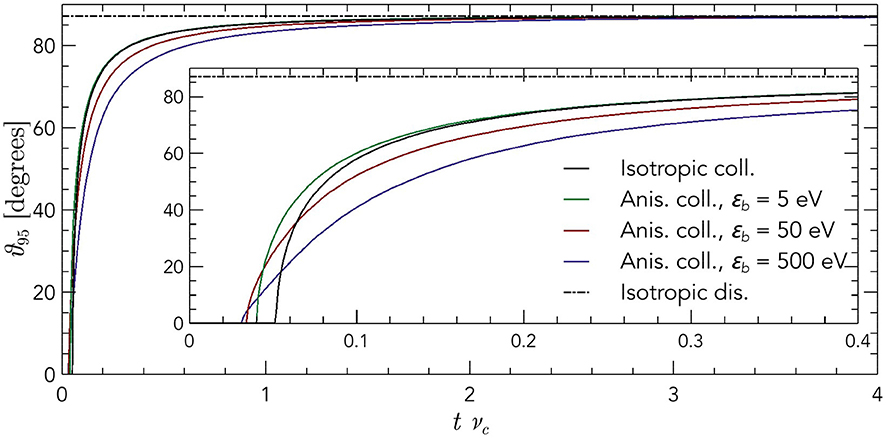
Figure 1. Time evolution of the divergence of an initially directed electron packet propagating in a background gas for different beam energies ϵb and elastic collision models. ϑ95 is defined in Equation (4). Both isotropic and anisotropic models converge toward an isotropic distribution after a few collisions. However, for tνc ≤ 0.2, with νc the momentum-transfer collision frequency, the isotropic model is observed to over-predict electron deflection in the high energy cases.
For inelastic collisions, anisotropic modeling is required at higher kinetic energy (ϵ ≥ 20 eV). For instance, Surendra et al. showed that isotropic scattering leads to a large over-prediction of the ionization rate in a DC glow discharge [47]. Besides DC discharges, the effects of anisotropy may generally be important in discharges featuring high-energy electrons, such as runaway electrons in atmospheric pressure discharges [45, 50] and electron beams formed by sheaths in DC biased RF discharges [51].
Another feature of electron-neutral scattering often neglected in plasma modeling is how kinetic energy is partitioned between scattered and secondary electrons in electron impact ionization processes. This information is described by the doubly differential cross-section for ionization σion(ϵp, ϵs, χ) [52, 53], which is related to the total ionization cross section σion(ϵp) through
where ϵiz is the ionization energy and ϵs and ϵp are the kinetic energy of secondary and scattered electrons, respectively. Data suggest that the post-collision kinetic energy ϵp − ϵiz is randomly distributed between the scattered and secondary electrons at low-energy (≤ 50 eV), but increasingly passed preferentially onto the scattered electron as ϵp increases [52]. Not accounting for this high-energy behavior leads to underestimating the high-energy electron population. Specifically, Tzeng and Kunhardt showed how the choice of a particular energy partitioning model affects the electron energy distribution function (EEDF) [54]. Since the energy partitioning increasingly deviates from random distribution as ϵp increases, the accurate description of these effects is, similarly to angular scattering effects, expected to become important in plasmas featuring high-energy electrons.
An important difference between ion-neutral and electron-neutral collisions lies in the fact that the ion speed vi may be comparable to neutral speed vn. For this reason, the collision kinematics must be considered in the center-of-mass frame.
Transposing methods used for modeling neutral-neutral collisions, ion-neutral collisions are often treated as hard spheres collisions in the literature, that is to say that ion-neutral scattering is assumed isotropic [see 21]. However, experimental measurements [55] and analytic derivations [56, 57] indicate that elastic scattering in symmetric systems is not isotropic. On the contrary, these findings suggest that the angular differential cross-section can be approximated by
where the first term on the right-hand-side corresponds to the mostly small angle momentum-exchange scattering and the second term on the right-hand-side corresponds to the mostly large angle charge-exchange scattering [58]. Here, α > 1, β > 1, A > 0 and B > 0 are function of the incident ion kinetic energy ϵ. However, care must be taken to ensure that, no matter what the chosen form for σ(ϵ, χ) is, simulations reproduce swarm data [see [59–62]] in regimes for which the local field approximation is valid.
Failing to account for anisotropic scattering thus leads to an overestimation of ions scattered at intermediate angles, and an underestimation of ions scattered at small and large angles. The influence of these effects on the properties of a xenon ion beam propagating in a rarefied gas was highlighted by Giuliano and Boyd [63]. Wang et al. further showed that the choice of a particular differential cross-section for ion-neutral elastic collisions affects the ion distribution function in a helium discharge at intermediate pressure [64]. These results suggest that particular attention should be given to these phenomena, especially for devices where ion dynamics plays a key role such as plasma thrusters [65] and ion sources [66, 67]. Another motivation for capturing these effects lies in the role of fast neutral particles on secondary emission at the walls, as discussed in section 3.
For a subset of species and processes, differential cross sections have been experimentally determined and compiled in the literature [see 68–72]. When this information is available, the influence of anisotropy on simulation results can be directly assessed by comparing results obtained with and without anisotropic handling. In the many cases where experimental data for differential cross sections is not available, or limited to a range of energies and angles, it is sometimes possible to make use of computed cross sections. For instance, differential elastic scattering cross sections calculated using the relativistic Dirac partial-wave method for elements up to 96 amu [73]. As a last recourse, different analytical models with varying accuracy have been proposed (see [46] for a discussion of these models).
Irrespective of whether differential cross section are obtained experimentally, numerically or analytically, it is critical to ensure proper normalization of the differential cross section when comparing isotropic and anisotropic models. For example, the momentum transfer cross-section should be conserved across models for elastic electron neutral collisions. Furthermore, parametric scans are highly advisable since cross-section data can vary between studies. Ideally, one would compare the different differential cross section data sets available and run simulation cases reflecting the uncertainty of the scattering data.
Up to this point, the effects of charged particles on the neutral distribution function have been neglected on the ground that the ionization fraction is small in many plasma devices. This allowed us to consider a steady-state maxwellian distribution function for neutrals when modeling collisions.
However, certain low-pressure gas discharges feature much larger ionization fractions, with for example in electron cyclotron resonance (ECR) sources [43] and helicon sources [74] operating in the mTorr range. For such conditions, coupling mechanisms with charged particles have been shown to modify both the neutral density, for example in the form of neutral depletion [26], and the neutral temperature [29]. Accurate modeling of these effects hence requires accounting for the spatial and temporal evolution of the neutral distribution function together with those of charged particles.
Even at lower ionization fractions (ι ~ 10−2), the distribution function of neutrals may be affected by charged particles under some conditions. For instance, neutral depletion has also been predicted [18] in the negative ion source prototype developed for the Neutral Beam Injector (NBI) of the International Thermonuclear Experimental Reactor (ITER) and of the Demonstration power station (DEMO) [5, 75, 76]. For a given background pressure, the plasma density growth with input power is in this case observed to saturate as the neutral population begins being depleted, at which point further increase in input power leads to an increase of the electron temperature Te. This variation in Te then affects the potential drop across the sheath and hence the kinetic energy of ions impacting the walls. This in turn modifies the energy distribution of neutrals formed by ion recombination at the wall. Although depletion occurs in this case for a plasma density about an hundred times smaller than the neutral density, accounting for neutral dynamics is essential to capture these effects. Furthermore, the role of neutral-wall interaction on the neutral dynamics underlines the importance of wall effects discussed in Sec. 3.
Yet another configuration where neutrals modeling may be called for are devices featuring a neutral flow. For instance, the neutral density in plasma thrusters [77, 78] and ion sources [67] typically varies by two order of magnitude or more between the gas injection region and the beam propagation region. In such configurations, neutral flow properties have to be modeled a priori if charged particles are assumed to not affect neutrals, or concurrently if they are. An example of the latter is plasmas where charged particles are expected to impart momentum to neutrals [79].
Various numerical models have been proposed and implemented to capture the dynamics of neutrals concurrently with a particle-in-cell scheme for charged particles. These models can be split into two groups depending on whether or not neutrals can be described as a continuous medium. Introducing the Knudsen number Kn, defined as the ratio of the neutral mean-free-path to the characteristic length of the system, continuous media and rarefied gas correspond to Kn ≤ 1 and Kn ≥ 1, respectively. In either regime, a suite of models exists, ranging from fast but very simplified models to computationally intensive rigorous models handling the full multi-scale nature of the problem.
In regimes where neutrals can be treated as a continuous medium, i. e Kn ≤ 1, the simplest option consists in assuming a constant neutral velocity. The neutral density map is then obtained by solving a continuity equation [80]. For configurations where neutral - wall interaction is expected to play a role, Barral et al. [81] proposed to supplement the continuity equation with a momentum equation in which an adjustable coefficient is used to model the diffusion of neutrals at the wall. Although this method is arbitrary and lacks scientific background, it has proven useful to investigate certain properties of plasma thrusters [see 77, 78]. In coupled models, fluid and PIC-MCC numerical schemes are concurrently advanced in time. The neutral density computed by the fluid model at a given time-step is used as input for the MCC module, while the predictions of the MCC module at a given time-step are used to derive the collision rates needed in the neutrals' continuity and momentum equations.
In gas discharges and low-temperature plasmas, the Knudsen number is often larger than 1. In this regime, Navier-Stokes equations can be inaccurate and one has to turn to kinetic methods such as Direct Simulation Monte Carlo (DSMC) method [41, 82]. A significant challenge in coupling DSMC models with PIC models lies is the very large computational cost of advancing concurrently in time charged particles and neutrals. Serikov et al. [83] suggested that, by using a specific weighted Monte-Carlo scheme to couple these models, PIC and DSMC and their different timescales can be treated separately. However, this choice leads to additional constraints with respect to acceptable particle weights and time-steps. This scheme is also limited to the modeling of quasi-stationary plasmas. To address these limitations and guarantee self-consistent results, one has to simulate both charged particles and neutrals through the entire range of timescales, from electron's to neutral's [84]. In allowing for longer time-steps, implicit methods can in principle relax the constraints on the time dynamics to be simulated, but at the expense of a more complex and computationally expensive field update [85].
Even in the absence of “sub-cycling” scheme such as the one proposed by Serikov et al. [83], particular care is needed when choosing the weight of neutrals and charged species macro-particles, i. e., the number of physical particles that a macro-particle represents. Indeed, performing collisions between macro-particles requires a large number of particles per cell to obtain good statistics since pairs are randomly selected within a given cell. As discussed next, this can become an issue depending on the parallelization strategy implemented, namely particle decomposition or domain decomposition. Furthermore, the different weights for neutral and charged species macro-particles have to be accounted for in the MCC module. Different strategies, including variable weights, rejection methods and accumulation, have been suggested with their own advantages and inconvenients [see 86–88].
Domain decomposition (DD) is generally considered the most advantageous parallelization option for PIC methods [89]. In this approach, each MPI (Message Passing Interface) thread operates on a subset of the whole domain called a subdomain. DD is often supplemented by particle decomposition where OpenMP (Open Multi-Processing) threads are attached to a given MPI thread. OpenMP threads then have access to the whole sub-domain and share an equal amount of particles. This hybrid approach is appealing since it alleviates the load balancing issues which arise in pure DD implementations when density gradients form.
On the other hand, particles of a given OpenMP process can be located anywhere in the subdomain. This means that the number of macro-particles in a given cell and in a given OpenMP thread can be limited, which degrades the collision description. Note that this issue is also found with pure particle decomposition strategies. One option to address this shortcoming and improve the resolution is to use a “sorting” algorithm which, within each subdomain, groups in memory particles that are close together in physical space [90]. Indeed, by running this “sorting” algorithm regularly, the probability to find both incident and target macro-particle in the same cell increases significantly, which is advantageous both for Monte-Carlo and DSMC algorithms [41, 82]. A side benefit of particles sorting is that it limits the access to computer memory and, as a consequence, speed up the calculation of both particle trajectories and source terms. This result is illustrated in Figure 2, which shows a speed up by a factor 5 when sorting particles in 3D. Details about this numerical model can be found in Fubiani et al. [18].
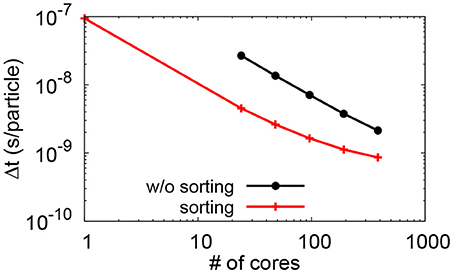
Figure 2. Particle pusher computation time per macroparticle (per time-step) as a function of the number of computing cores, with (red solid line) and without (black) particle sorting. Simulations use 20 particles-per-cell, 1 MPI thread per socket and a 256 × 96 × 96 3D grid, and are run on 24 cores Intel Xeon processors (E5-2697 v4, 46M cache, 2.3 GHz), with 2 sockets per node for a total of 48 cores per node. The number of OpenMP threads is 24.
Since laboratory plasmas are inherently of finite spatial extension, some fraction of particles in the plasma necessarily interact with the walls. This includes both charged and neutral particles. In certain configurations, these wall effects have been shown to govern the plasma dynamics. For instance, secondary electron emission resulting from ion impact at the cathode is essential to the maintenance of a DC discharge [91]. Accurate simulation of laboratory plasmas hence requires appropriate numerical models to describe the interaction of particles with the wall. However, the description of these phenomena in PIC models is made particularly challenging by the range of scale-lengths and time-scales involved.
The physics of electron emission from electron impact on materials is complex. Depending on its properties (energy and angle of incidence) and on the target (material and surface condition), an incident electron can be lost, elastically or inelastically backscattered, or can induce the emission of one or multiple secondary electrons [92, 93]. Furthermore, the emission of an electron upon impact of an incident electron at the wall is not only characterized by a scalar probability, but also by energy and angular distributions for backscattered and emitted electrons. Yet, often in the literature, electron emission is much simplified and assumed to follow a constant probability for re-emission (independent of the incident electron's energy and angle), with electrons re-emitted at a given (low) temperature [see 94, 95].
The electron emission coefficient δ is defined as the number of emitted electrons per incident electron. The typical evolution of δ with incident energy ϵ observed in experiments is illustrated in Figure 3. At low energy, the emission coefficient increases with ϵ and δ = 1 for an electron energy ϵI of a few tens of eV. The secondary emission coefficient reaches a maximum δmax for an electron energy ϵmax of a few hundreds of eV [96]. Experimental measurements indicate that ϵI, δmax and ϵmax are function of the material and surface condition [97]. For modeling purposes, empirical analytical models for δ(ϵ) can be derived from this set of experimental measurements. In low-temperature plasma simulations, an often used model is Vaughan's model [98], which fits well experimental results at high electron energy when δ approaches δmax. This model has for example been incorporated in a modified version of the XPDC1 code [9] and used to study RF discharges [99, 100] and Hall thruster [101–104]. In RF discharges, Horvath et al. have shown the importance of electron emission on sheath dynamics. In particular, they highlighted how the predicted plasma density can be strongly affected by the electron emission model for large discharge voltage [100]. In Hall thrusters, secondary electron emission from the walls can play a significant role on the electron transport perpendicular to the magnetic field [102]. Recently, another analytical model has been proposed [105] to better fit the electron emission near the first cross-over energy (ϵ ~ ϵI) where multipactor effects can be important, which may be useful to simulate undesirable RF discharges on satellites. Yet, a limitation of Vaughan's model remains its inability to properly account for secondary emission from low-energy incident electrons since it assumes zero emission below a threshold incident electron energy. Scholtz and al. [93] proposed a fix to address this limitation, but at the cost of a degraded accuracy in a different energy range.
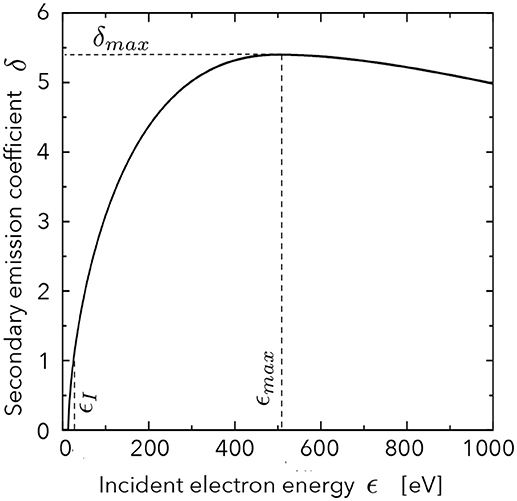
Figure 3. Schematic representation of the electron emission coefficient δ as a function of the incident electron energy ϵ. ϵI and ϵmax are defined as the electron energy for which δ = 1 and δ = δmax, respectively.
A refined model addressing these issues is that of Furman and Pivi (FP) [106]. Indeed, while it is still obtained by fitting experimental data, FP's model captures separately the three components of electron emission (true-secondaries, elastically and inelastically backscattered) as well as the energy distribution of emitted electrons. Comparison with Vaughan's model highlighted the importance of emission from low-energy electrons in the simulation of multipactor effects [107]. Another advantage of FP's model is that it captures the energy distribution of emitted electrons, which can affect the plasma parameters since it contributes to the electron energy balance in the discharge. A limit of FP's model is its large number of parameters (about 45), which limits in turn its applicability. Nevertheless, while input parameters have thus far only been determined for a few materials (copper and stainless-steel), recent experimental measurements obtained for additional materials [108] may be used to extend FP's model. In addition, parameters for metals may also be derived from a simple and validated analytical model [109].
Finally, electron emission from the wall is generally assumed to be isotropic. This assumption is justified for secondary electrons emitted from the target since the properties of the emitted electron have no relation with the incident electron. On the other hand, this justification does not hold true for elastically backscattered electrons. On the contrary, detailed modeling based on Monte Carlo simulations reveal that the angular distribution of elastically backscattered electrons is strongly dependent of the angular distribution of incident electrons. As shown in Figure 4, the angular distribution presents two lobes of emission, one in the incident direction and the other specular to the incident direction [110]. To our knowledge, this property has not yet been included in low-temperature plasma numerical models.
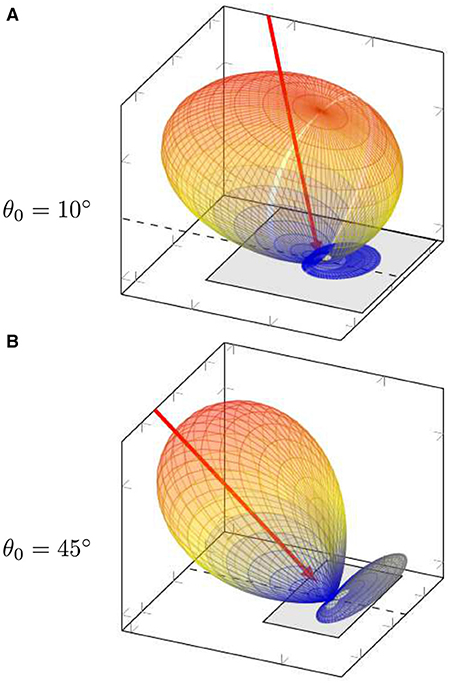
Figure 4. Elastic backscattering lobes for an electron beam (red arrow) of energy E0 = 40 eV incident on an aluminum surface at two different angles (A) and (B) . Adapted from Villemant et al. [110] with permission of the copyright holder.
In summary, while existing models describing secondary electron emission by electron impact capture many important facets of this phenomenon (detailed emission process, energy distribution of secondary electrons), new features such as anisotropic emission continue to be uncovered. Consequently, it remains presumptuous to use these models for predictive simulations. Nevertheless, when compared with simpler models or use parametrically, these models can provide valuable insights into the effects of secondary emission.
Similarly to the physics of electron impact at the wall discussed in the previous paragraph, the physics of heavy particle impact at the wall is intricate and can have a significant impact on the plasma properties.
Electron emission by heavy particle impact stems from two contributions, namely kinetic and potential emission. Potential emission occurs when a charged particle (ion) impact a surface with a kinetic energy ϵ greater than twice the work function of the target material W. Potential emission decreases with W and is relatively independent of ϵ [111]. On the other hand, kinetic emission depends strongly on the energy of the incident heavy particle (ion or neutral), and becomes comparable or larger than potential emission when the incident energy reaches a fraction of a keV. As a result, the secondary emission coefficient γ, defined as the number of emitted electrons per incident ion, is relatively constant for ϵ ≤ 500 eV and increases with ϵ past this energy. Here again, empirical models based on experimental data fits have been derived (see [112]), but their use is limited to heavy particle - target pairs for which detailed experimental measurements are available. Even when data is available, the experimental observation that surface conditions, such as roughness and pollution, can have a strong effect on emission [113, 114] questions the validity of these models to describe experiments since surface conditions are intrinsically hard to determined. The influence of electron secondary emission by heavy particle impact can nevertheless be assessed in numerical simulations through parametric scans, as shown for example by Daksha et al. in capacitively coupled plasmas [115].
Besides the electron emission coefficient, another parameter of importance in the description of heavy particle - wall interaction is the thermal accommodation coefficient α. This coefficient relates the energy of the heavy particle leaving the wall to both the energy of the incident heavy particle and the wall temperature. This coefficient varies from α = 0 when a heavy particle is backscattered off the surface with its incident energy to α = 1 when the heavy particle looses its kinetic energy and leaves with an energy corresponding to the surface temperature. Accurate quantification of this coefficient in numerical models is important since it may, under some conditions, affect simulation results. Such dependence has for example been observed by Fubiani et al. [18] when modeling the operation of the BATMAN ion source [75]. In this source, changing α from 0.5 to 1 has been predicted to lead to a decrease of the hydrogen atom temperature by a factor of 5 and an increase of the neutral hydrogen density by a factor of 2. As seen in Figure 5, the neutral hydrogen temperature scales nearly linearly with α over the 0.5−1 range. Unfortunately, the limited experimental data available combined with a strong dependence of α on surface conditions makes the determination of this coefficient challenging. This cast doubts on the ability of numerical methods to reproduce accurately experimental results from first principles, especially in light of the important role of the neutrals dynamics underlined in section 2. As a baseline for a parametric scan, one can consider that the incoming particle only interacts with the atoms of the wall (i. e., a clean surface), in which case the accommodation coefficient may be estimated numerically. A database for various materials and incident particle masses has been derived using the TRIM code [116].
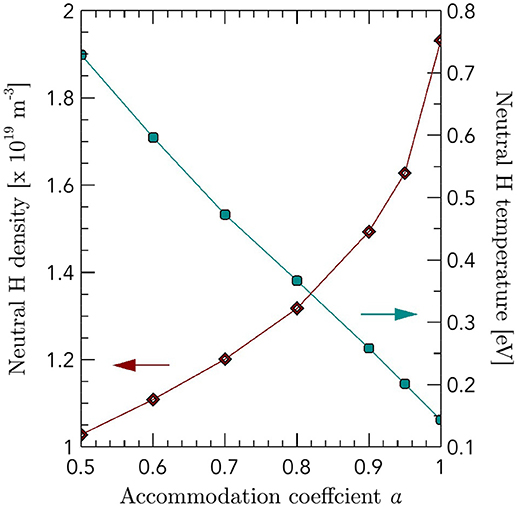
Figure 5. Influence of the thermal accommodation coefficient α on the neutral hydrogen density and temperature in the BATMAN source. See Fubiani et al. [18] for details about the numerical model.
In light of the high complexity of particle - wall interaction phenomena and the limited experimental data available to date to support models, it seems presumptuous to expect numerical simulations to predict, or even fully capture, these effects. The difficulty of accurately describing these phenomena is made even more acute in PIC codes by the various scale-lengths (atomic spacing to surface roughness of a few μm) and time-scales (electron time-scale for backscattering to neutral time-scale for accommodation) involved.
Despite these shortcomings, there are important benefits in implementing wall physics models in PIC codes. First, it allows assessing the relative importance of the various processes at play. Second, parametric scans within a range of realistic experimental values can be used to refine the analysis and examine the influence of idealized experimental conditions on plasma parameters. Practically, since the impact of charged particles at the wall can lead to the emission of neutrals and reciprocally, modeling wall physics in PIC codes requires dealing with the interaction (creation, removal) of macro-particles with different weights. This situation can be handled similarly to collisions in volume between macro-particles with different weights, as discussed in section 2.4.
In low-pressure plasma PIC modeling, the numerical integration of particle trajectories is typically responsible for most of the computing time. As a result, the implementation of particle-wall models should generally have minimal effects on the overall performances. In particular, the implementation of wall models is not expected to modify the pros and cons of the different parallelization strategies discussed in section 2.4.
Yet, for configurations where wall effects dominates bulk effects, or configurations with large particle fluxes to the walls, wall effects handling may in principle lead to load unbalance between subdomains with walls and subdomains without walls. One option to alleviate this limitation is to choose a domain decomposition scheme such that the number of boundary cells is, as much as possible, equally distributed over the subdomains. However, the associated benefits might be offset by a greater number of particles crossing from one subdomain to another at each time-step. Another option for such rare cases might be to use a particle decomposition strategy.
Particle-in-cell (PIC) techniques, coupled with Monte-Carlo Collision (MCC) modules, are increasingly used to simulate a variety of low-pressure plasmas. However, and besides proper implementation, the ability of PIC-MCC techniques to reproduce and simulate accurately these plasmas hinges upon the description of various phenomena. A particular challenge here lies in the fact that these phenomena cover a wide range of timescales and scale-lengths. In this paper, we discuss more specifically the importance of both neutral dynamics and wall physics.
Properties of low-pressure plasmas are often strongly affected by collisions between charged-particles and neutrals. Accounting for these effects in numerical models requires both a detailed description of the kinematics of charged particle—neutral collisions and a proper description of the neutrals distribution function fn. This is made difficult by the fact that electron—neutral collisions have to be modeled on electron timescales while fn evolves on the much slower neutral particle timescale. One important feature in charged particle—neutral collision is the anisotropy of these processes, in particular for energetic particles. Failure to account for this property may, under some conditions, affect simulation results and lead to inaccurate or even unphysical results.
Many low-pressure laboratory plasmas are also strongly affected by the walls. This makes capturing in numerical models the detailed interaction of electrons, ions and neutrals with the wall a requirement. However, describing these phenomena is particularly challenging since they cover various scale-lengths (atomic spacing to surface roughness of a few μm) and time-scales (electron time-scale for backscattering to neutral time-scale for accommodation). Special care must therefore be taken to ensure that all potentially important processes are accounted for.
Unfortunately, while models for particles scattering and wall physics continue to be refined and the experimental database supporting these models grows, it remains ill-fated to assume that implementing these models as is in a PIC-MCC code ensures simulation results accuracy. Until global models describing reliably these complex phenomena become available, the recommended approach to build confidence in simulation results is to start from well established simplified models, and from there to include an additional effect and rely on parametric scans around realistic experimental conditions to quantify the importance of this effect.
Although the detailed scattering physics and wall physics may only be of limited importance in many low-pressure discharges, it should be emphasized that they could play a significant role in some. While, as intended in this paper, some generic guidelines can be put forward to identify conditions where these effects can be important, it most certainly does not cover all cases. This makes it even more important to assess the importance of these effects in numerical simulations.
All three authors RG, GF, and LG have contributed to the bibliographic survey, to the analysis and discussion of the results and to the writing of the manuscript.
Part of this work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement No 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. Support from CEA and from the French Fédération de Recherche sur la Fusion Magnétique is acknowledged.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors would like to thank Gerjan Hagelaar (Laplace) and Pierre Sarrailh and M. Marc Villemant (Onera) for constructive discussions.
1. Charles C. Grand challenges in low-temperature plasma physics. Front Phys. (2014) 2:39. doi: 10.3389/fphy.2014.00039
2. Adamovich I, Baalrud SD, Bogaerts A, Bruggeman PJ, Cappelli M, Colombo V, et al. The 2017 plasma roadmap: low temperature plasma science and technology. J Phys D Appl Phys. (2017) 50:323001. doi: 10.1088/1361-6463/aa76f5
3. Garrigues L, Coche P. Electric propulsion: comparisons between different concepts. Plasma Phys Control Fusion (2011) 53:124011. doi: 10.1088/0741-3335/53/12/124011
4. Mazouffre S. Electric propulsion for satellites and spacecraft: established technologies and novel approaches. Plasma Sour Sci Technol. (2016) 25:033002. doi: 10.1088/0963-0252/25/3/033002
5. Hemsworth RS, Boilson D, Blatchford P, Palma MD, Chitarin G, de Esch HPL, et al. Overview of the design of the ITER heating neutral beam injectors. New J Phys. (2017) 19:025005. doi: 10.1088/1367-2630/19/2/025005
6. Dolgolenko DA, Muromkin YA. Separation of mixtures of chemical elements in plasma. Phys Usp. (2017) 60:994. doi: 10.3367/UFNe.2016.12.038016
7. Gueroult R, Rax JM, Zweben S, Fisch NJ. Harnessing mass differential confinement effects in magnetized rotating plasmas to address new separation needs. Plasma Phys Control Fusion (2018) 60:014018. doi: 10.1088/1361-6587/aa8be5
8. Gueroult R, Rax JM, Fisch NJ. Opportunities for plasma separation techniques in rare earth elements recycling. J Clean Prod. (2018) 182:1060–9. doi: 10.1016/j.jclepro.2018.02.066
9. Kim HC, Iza F, Yang SS, Radmilović-Radjenović M, Lee JK. Particle and fluid simulations of low-temperature plasma discharges: benchmarks and kinetic effects. J Phys D Appl Phys. (2005) 38:R283–301. doi: 10.1088/0022-3727/38/19/r01
10. Alves LL, Bogaerts A, Guerra V, Turner MM. Foundations of modelling of nonequilibrium low-temperature plasmas. Plasma Sour Sci Technol. (2018) 27:023002. doi: 10.1088/1361-6595/aaa86d
11. Birdsall CK, Langdon AB. Plasma Physics via Computer Simulation. New York, NY: McGraw-Hill (1985).
13. Birdsall CK. Particle-in-cell charged-particle simulations, plus monte carlo collisions with neutral atoms, PIC-MCC. IEEE Trans Plasma Sci. (1991) 19:65–85. doi: 10.1109/27.106800
14. Filbet F, Sonnendrücker E, Bertrand P. Conservative numerical schemes for the vlasov equation. J Comput Phys. (2001) 172:166–187. doi: 10.1006/jcph.2001.6818
15. Degond P, Deluzet F, Navoret L, Sun AB, Vignal MH. Asymptotic-preserving particle-in-cell method for the vlasov–poisson system near quasineutrality. J Comput Phys. (2010) 229:5630–52. doi: 10.1016/j.jcp.2010.04.001
16. Boeuf JP, Chaudhury B. Rotating instability in low-temperature magnetized plasmas. Phys Rev Lett. (2013) 111:155005. doi: 10.1103/physrevlett.111.155005
17. Brenning N, Lundin D, Minea T, Costin C, Vitelaru C. Spokes and charged particle transport in HiPIMS magnetrons. J Phys D Appl Phys. (2013) 46:084005. doi: 10.1088/0022-3727/46/8/084005
18. Fubiani G, Garrigues L, Hagelaar G, Kohen N, Boeuf JP. Modeling of plasma transport and negative ion extraction in a magnetized radio-frequency plasma source. New J Phys. (2017) 19:015002. doi: 10.1088/1367-2630/19/1/015002
19. Boeuf JP, Garrigues L. ExB Electron Drift Instability in Hall thrusters: particle-in-cell simulations vs. theory. To Appear Phys Plasmas. (2018) 25:061204. doi: 10.1063/1.5017033
20. Fonseca RA, Vieira J, Fiuza F, Davidson A, Tsung FS, Mori WB, et al. Exploiting multi-scale parallelism for large scale numerical modelling of laser wakefield accelerators. Plasma Phys Control Fusion (2013) 55:124011. doi: 10.1088/0741-3335/55/12/124011
21. Verboncoeur JP. Particle simulation of plasmas: review and advances. Plasma Phys Control Fusion (2005) 47:A231. doi: 10.1088/0741-3335/47/5A/017
22. Lapenta G. Particle simulations of space weather. J Comput Phys. (2012) 231:795–821. doi: 10.1016/j.jcp.2011.03.035
23. Stangeby P, McCracken G. Plasma boundary phenomena in tokamaks. Nucl Fusion (1990) 30:1225–379. doi: 10.1088/0029-5515/30/7/005
24. Carreras BA, Owen LW, Maingi R, Mioduszewski PK, Carlstrom TN, Groebner RJ. Effect of edge neutrals on the low-to-high confinement transition threshold in the DIII-D tokamak. Phys Plasmas (1998) 5:2623–36. doi: 10.1063/1.872949
25. Boivin RL, Goetz JA, Hubbard AE, Hughes JW, Hutchinson IH, Irby JH, et al. Effects of neutral particles on edge dynamics in Alcator C-Mod plasmas. Phys Plasmas (2000) 7:1919–26. doi: 10.1063/1.874016
26. Gilland J, Breun R, Hershkowitz N. Neutral pumping in a helicon discharge. Plasma Sour Sci Technol. (1998) 7:416–22. doi: 10.1088/0963-0252/7/3/020
27. Fruchtman A, Makrinich G, Chabert P, Rax JM. Enhanced plasma transport due to neutral depletion. Phys Rev Lett. (2005) 95:115002. doi: 10.1103/PhysRevLett.95.115002
28. Degeling AW, Sheridan TE, Boswell RW. Model for relaxation oscillations in a helicon discharge. Phys Plasmas (1999) 6:1641–8. doi: 10.1063/1.873419
29. Liard L, Raimbault JL, Rax JM, Chabert P. Plasma transport under neutral gas depletion conditions. J Phys D Appl Phys. (2007) 40:5192–5. doi: 10.1088/0022-3727/40/17/026
30. Ochs IE, Gueroult R, Fisch NJ, Zweben SJ. Collisional considerations in axial-collection plasma mass filters. Phys Plasmas (2017) 24:043503. doi: 10.1063/1.4978949
31. Wu CS, Davidson RC. Electromagnetic instabilities produced by neutral-particle ionization in interplanetary space. J. Geophys. Res. (1972) 77:5399–406. doi: 10.1029/ja077i028p05399
32. Hartle RE, Wu CS. Effects of electrostatic instabilities on planetary and interstellar ions in the solar wind. J Geophys Res. (1973) 78:5802–7. doi: 10.1029/ja078i025p05802
33. Kubo H, Kawashima N, Itoh T. Interaction of plasma streams with a neutral gas cloud. Plasma Phys. (1971) 13:131–40. doi: 10.1088/0032-1028/13/2/004
34. Eviatar A. Plasma-neutral interaction processes in the magnetosphere of saturn. Adv Space Res. (1992) 12:367–75. doi: 10.1016/0273-1177(92)90412-q
35. Tokar RL. The interaction of the atmosphere of enceladus with saturn's plasma. Science (2006) 311:1409–12. doi: 10.1126/science.1121061
37. Alfvén H. Collision between a nonionized gas and a magnetized plasma. Rev Mod Phys. (1960) 32:710–3.
38. Brenning N. Review of the CIV phenomenon. Space Sci Rev. (1992) 59:209–314. doi: 10.1007/BF00242088
39. Boswell RW, Morey IJ. Self-consistent simulation of a parallel-plate rf discharge. Appl Phys Lett. (1988) 52:21–3. doi: 10.1063/1.99327
40. Vahedi V, Surendra M. A monte carlo collision model for the particle-in-cell method: applications to argon and oxygen discharges. Comput Phys Commun. (1995) 87:179–98. doi: 10.1016/0010-4655(94)00171-W
41. Nanbu K. Probability theory of electron-molecule, ion-molecule, molecule-molecule, and coulomb collisions for particle modeling of materials processing plasmas and cases. IEEE Trans Plasma Sci. (2000) 28:971–90. doi: 10.1109/27.887765
42. Skullerud HR. The stochastic computer simulation of ion motion in a gas subjected to a constant electric field. J Phys D Appl Phys. (1968) 1:1567–8. doi: 10.1088/0022-3727/1/11/423
43. Roth JR. Industrial Plasma Engineering: Volume 2 - Applications to Nonthermal Plasma Processing. Bristol: CRC Press (2001).
44. Capitelli M, Celiberto R, Gorse C, Winkler R, Wilhelm J. Electron energy distribution functions in radio-frequency collision dominated nitrogen discharges. J Phys D Appl Phys. (1988) 21:691–699. doi: 10.1088/0022-3727/21/5/005
45. Moss GD, Pasko VP, Liu N, Veronis G. Monte carlo model for analysis of thermal runaway electrons in streamer tips in transient luminous events and streamer zones of lightning leaders. J Geophys Res. (2006) 111:A02307. doi: 10.1029/2005ja011350
46. Janssen JFJ, Pitchford LC, Hagelaar GJM, van Dijk J. Evaluation of angular scattering models for electron-neutral collisions in monte carlo simulations. Plasma Sour Sci Technol. (2016) 25:055026. doi: 10.1088/0963-0252/25/5/055026
47. Surendra M, Graves DB, Jellum GM. Self-consistent model of a direct-current glow discharge: treatment of fast electrons. Phys Rev A (1990) 41:1112–25. doi: 10.1103/physreva.41.1112
48. Kolobov VI, Tsendin LD. Analytic model of the hollow cathode effect. Plasma Sour Sci Technol. (1995) 4:551–60. doi: 10.1088/0963-0252/4/4/006
49. Gueroult R, Elias PQ, Packan D, Bonnet J, Rax JM. Particle in cell modelling of the observed modes of a dc wire discharge. J Phys D Appl Phys. (2010) 43:365204. doi: 10.1088/0022-3727/43/36/365204
50. Chanrion O, Bonaventura Z, Bourdon A, Neubert T. Influence of the angular scattering of electrons on the runaway threshold in air. Plasma Phys Control Fusion (2016) 58:044001. doi: 10.1088/0741-3335/58/4/044001
51. Khrabrov AV, Kaganovich ID, Ventzek PLG, Ranjan A, Chen L. Structure of the velocity distribution of sheath-accelerated secondary electrons in an asymmetric RF-dc discharge. Plasma Sour Sci Technol. (2015) 24:054003. doi: 10.1088/0963-0252/24/5/054003
52. Opal CB, Peterson WK, Beaty EC. Measurements of secondary-electron spectra produced by electron impact ionization of a number of simple gases. J Chem Phys. (1971) 55:4100–6. doi: 10.1063/1.1676707
53. Yoshida S, Phelps AV, Pitchford LC. Effect of electrons produced by ionization on calculated electron-energy distributions. Phys Rev A (1983) 27:2858. doi: 10.1103/PhysRevA.27.2858
54. Tzeng Y, Kunhardt EE. Effect of energy partition in ionizing collisions on the electron-velocity distribution. Phys Rev A (1986) 34:2148–57. doi: 10.1103/physreva.34.2148
55. Chiu YH, Dressler RA, Levandier DJ, Houchins C, Ng CY. Large-angle xenon ion scattering in xe-propelled electrostatic thrusters: differential cross sections. J Phys D Appl Phys. (2008) 41:165503. doi: 10.1088/0022-3727/41/16/165503
56. Boyd ID, Dressler RA. Far field modeling of the plasma plume of a hall thruster. J Appl Phys. (2002) 92:1764–74. doi: 10.1063/1.1492014
57. Mikellides IG, Katz I, Kuharski RA, Mandell MJ. Elastic scattering of ions in electrostatic thruster plumes. J Propul Power (2005) 21:111–8. doi: 10.2514/1.5046
58. Scharfe MK, Koo J, Azarnia G. DSMC implementation of experimentally-based xe++ xe differential cross sections for electric propulsion modeling. 27th International Symposium on Rarefied Gas Dynamics (AIP), (2011) 1333: 1085. doi: 10.1063/1.3562789
59. Ellis H, Pai R, McDaniel E, Mason E, Viehland L. Transport properties of gaseous ions over a wide energy range. At Data Nucl Data Tables (1976) 17:177–210. doi: 10.1016/0092-640x(76)90001-2
60. Ellis H, McDaniel E, Albritton D, Viehland L, Lin S, Mason E. Transport properties of gaseous ions over a wide energy range. part II. At Data Nucl Data Tables (1978) 22:179–217. doi: 10.1016/0092-640x(78)90014-1
61. Ellis H, Thackston M, McDaniel E, Mason E. Transport properties of gaseous ions over a wide energy range. part III. At Data Nucl Data Tables (1984) 31:113–51. doi: 10.1016/0092-640x(84)90018-4
62. Viehland L, Mason E. Transport properties of gaseous ions over a wide energy range, IV. At Data Nucl Data Tables (1995) 60:37–95. doi: 10.1006/adnd.1995.1004
63. Giuliano PN, Boyd ID. Particle simulation of collision dynamics for ion beam injection into a rarefied gas. Phys Plasmas (2013) 20:033505. doi: 10.1063/1.4794954
64. Wang H, Sukhomlinov VS, Kaganovich ID, Mustafaev AS. Simulations of ion velocity distribution functions taking into account both elastic and charge exchange collisions. Plasma Sour Sci Technol. (2017) 26:024001. doi: 10.1088/1361-6595/26/2/024001
65. Boyd ID. Review of hall thruster plume modeling. J Spacecr Rockets (2001) 38:381–7. doi: 10.2514/2.3695
66. Gueroult R, Elias PQ, Packan D, Rax JM. A narrow-band, variable energy ion source derived from a wire plasma source. Plasma Sour Sci Technol. (2011) 20:045006. doi: 10.1088/0963-0252/20/4/045006
67. Gueroult R, Elias PQ, Packan D, Rax JM. Numerical modelling of the properties of an ion beam extracted from a low-pressure wire discharge. J Phys D Appl Phys. (2012) 45:245203. doi: 10.1088/0022-3727/45/24/245203
68. Brunger MJ, Buckman SJ. Electron-molecule scattering cross-sections. I. Experimental techniques and data for diatomic molecules. Phys Rep. (2002) 357:215–458. doi: 10.1016/s0370-1573(01)00032-1
69. Hoshino M, Kato H, Makochekanwa C, Buckman S, J Brunger M, Cho H, et al. Elastic Differential Cross Sctions for Electron Collisions with Polyatomic Molecules, Vol. 101. Research Report NIFS-DATA-101, Toki (2008).
70. Yoon JS, Song MY, Kato H, Hoshino M, Tanaka H, Brunger MJ, et al. Elastic cross sections for electron collisions with molecules relevant to plasma processing. J Phys Chem Ref Data (2010) 39:033106. doi: 10.1063/1.3475647
71. [Dataset]. ANU Database. Available online at: http://www.lxcat.net (Accessed Aug 28, 2018).
72. [Dataset]. Christophorou Database. Available online at: http://www.lxcat.net (Accessed Aug 28, 2018).
73. Powell CJ, Jablonski A, Salvat F, Lee AY. NIST Electron Elastic-Scattering Cross-Section Database, version 4.0. Tech. Rep. (2016).
74. Chen FF. Helicon discharges and sources: a review. Plasma Sour Sci Technol. (2015) 24:014001. doi: 10.1088/0963-0252/24/1/014001
75. Speth E, Falter H, Franzen P, Fantz U, Bandyopadhyay M, Christ S, et al. Overview of the RF source development programme at IPP garching. Nucl Fusion (2006) 46:S220. doi: 10.1088/0029-5515/46/6/S03
76. Fantz U, Hopf C, Wünderlich D, Friedl R, Fröschle M, Heinemann B, et al. Towards powerful negative ion beams at the test facility ELISE for the ITER and DEMO NBI systems. Nucl Fusion (2017) 57:116007. doi: 10.1088/1741-4326/aa778b
77. Adam JC, Héron A, Laval G. Study of stationary plasma thrusters using two-dimensional fully kinetic simulations. Phys Plasmas (2004) 11:295–305. doi: 10.1063/1.1632904
78. Coche P, Garrigues L. A two-dimensional (azimuthal-axial) particle-in-cell model of a hall thruster. Phys Plasmas (2014) 21:023503. doi: 10.1063/1.4864625
79. Brackbill J, Cambier JL, Gimelshein NE, Gimelshein SF. Numerical analysis of neutral entrainment effect on field-reversed configuration thruster efficiency. J Propul Power (2014) 30:1450–8. doi: 10.2514/1.b35260
80. Boeuf JP, Garrigues L. Low frequency oscillations in a stationary plasma thruster. J Appl Phys. (1998) 84:3541–54. doi: 10.1063/1.368529
81. Barral S, Makowski K, Peradzyński Z, Gascon N, Dudeck M. Wall material effects in stationary plasma thrusters. II. near-wall and in-wall conductivity. Phys Plasmas (2003) 10:4137–52. doi: 10.1063/1.1611881
82. Bird GA. Molecular Gas Dynamics and the Direct Simulation of Gas Flows, 2 Edn. Oxford: Oxford University Press (1994).
83. Serikov V, Kawamoto S, Nanbu K. Particle-in-cell plus direct simulation monte carlo (PIC-DSMC) approach for self-consistent plasma-gas simulations. IEEE Trans Plasma Sci. (1999) 27:1389–98. doi: 10.1109/27.799817
84. Munz CD, Auweter-Kurtz M, Fasoulas S, Mirza A, Ortwein P, Pfeiffer M, et al. Coupled particle-in-cell and direct simulation monte carlo method for simulating reactive plasma flows. Comptes Rendus Mécanique (2014) 342:662–70. doi: 10.1016/j.crme.2014.07.005
85. Mattei S, Nishida K, Onai M, Lettry J, Tran M, Hatayama A. A fully-implicit particle-in-cell monte carlo collision code for the simulation of inductively coupled plasmas. J Comput Phys. (2017) 350:891–906. doi: 10.1016/j.jcp.2017.09.015
86. Boyd ID. Conservative species weighting scheme for the direct simulation monte carlo method. J Thermophys Heat Trans. (1996) 10:579–85. doi: 10.2514/3.832
87. Gimelshein SF, Levin DA, Collins RJ. Modeling of glow radiation in the rarefied flow about an orbiting spacecraft. J. Thermophys Heat Transfer (2000) 14:471–9. doi: 10.2514/2.6569
88. Sarrailh P, Garrigues L, Hagelaar GJM, Boeuf JP, Sandolache G, Rowe S. Sheath expansion and plasma dynamics in the presence of electrode evaporation: application to a vacuum circuit breaker. J Appl Phys. (2009) 106:053305. doi: 10.1063/1.3204969
89. Derouillat J, Beck A, Pérez F, Vinci T, Chiaramello M, Grassi A, et al. Smilei : a collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput Phys Commun. (2018) 222:351–73. doi: 10.1016/j.cpc.2017.09.024
90. Bowers K. Accelerating a particle-in-cell simulation using a hybrid counting sort. J Comput Phys. (2001) 173:393–411. doi: 10.1006/jcph.2001.6851
91. Lieberman MA, Lichtenberg AJ. Principles of Plasma Discharge for Materials Processing. New York, NY: John Wiley & Sons (1994).
92. Bruining H. Physics and Applications of Electron Secondary Emission. New York, NY: McGraw Hill (1954).
93. Scholtz JJ, Dijkkamp D, Schmitz RWA. Secondary electron emission properties. Philips J Res. (1996) 50:375–89. doi: 10.1016/S0165-5817(97)84681-5
94. Revel A. Modélisation des plasmas magnétisés. Application à l'injection de neutres pour ITER et au magnétron en régime impulsionnel haute puissance. Ph.D. thesis, Université Paris Sud (2015).
95. Revel A, Minea T, Tsikata S. Pseudo-3d PIC modeling of drift-induced spatial inhomogeneities in planar magnetron plasmas. Phys Plasmas (2016) 23:100701. doi: 10.1063/1.4964480
96. Spangenberg K. Vacuum Tubes. Electrical and Electronic Engineering Series. New York, NY: Mc-Graw Hill (1948).
97. Bruining H, de Boer J. Secondary electron emission: part i. secondary electron emission of metals. Physica (1938) 5:17–30. doi: 10.1016/S0031-8914(38)80103-8
98. Vaughan J. A new formula for secondary emission yield. IEEE Trans Electron Dev. (1989) 36:1963–7. doi: 10.1109/16.34278
99. Radmilović-Radjenović M, Lee JK. Modeling of breakdown behavior in radio-frequency argon discharges with improved secondary emission model. Phys Plasmas (2005) 12:063501. doi: 10.1063/1.1922267
100. Horváth B, Daksha M, Korolov I, Derzsi A, Schulze J. The role of electron induced secondary electron emission from SiO2 surfaces in capacitively coupled radio frequency plasmas operated at low pressures. Plasma Sour Sci Technol. (2017) 26:124001. doi: 10.1088/1361-6595/aa963d
101. Sydorenko D. Particle-in-Cell Simulations of Electron Dynamics in Low Pressure Discharges With Magnetic Fields. Ph.D. thesis, University of Saskatchewan, Saskatoon, SK (2006).
102. Kaganovich ID, Raitses Y, Sydorenko D, Smolyakov A. Kinetic effects in a hall thruster discharge. Phys Plasmas (2007) 14:057104. doi: 10.1063/1.2709865
103. Héron A, Adam JC. Anomalous conductivity in hall thrusters: Effects of the non-linear coupling of the electron-cyclotron drift instability with secondary electron emission of the walls. Phys Plasmas (2013) 20:082313. doi: 10.1063/1.4818796
104. Croes V, Tavant A, Lucken R, Lafleur T, Bourdon A, Chabert P. Study of electron transport in a hall effect thruster with 2d r−θ particle-in-cell simulations. Proceedings of the 35th International Electric Propulsion Conference. Atlanta, GA (2017).
105. Fil N, Belhaj M, Hillairet J, Puech J. Multipactor threshold sensitivity to total electron emission yield in small gap waveguide structure and TEEY models accuracy. Phys Plasmas (2016) 23:123118. doi: 10.1063/1.4972571
106. Furman MA, Pivi MTF. Probabilistic model for the simulation of secondary electron emission. Phys Rev Spec Top Accel Beams (2002) 5:124404. doi: 10.1103/PhysRevSTAB.5.124404
107. Rice SA, Verboncoeur JP. A comparison of multipactor predictions using two popular secondary electron models. IEEE Trans Plasma Sci. (2014) 42:1484–7. doi: 10.1109/tps.2014.2321118
108. Villemant M, Sarrailh P, Belhaj M, Garrigues L, Boniface C. Experimental investigation about energy balance of electron emission from materials under electron impacts at low energy: application to silver, graphite and SiO2. J Phys D Appl Phys. (2017) 50:485204. doi: 10.1088/1361-6463/aa91af
109. Chung MS, Everhart TE. Simple calculation of energy distribution of low-energy secondary electrons emitted from metals under electron bombardment. J Appl Phys. (1974) 45:707–9. doi: 10.1063/1.1663306
110. Villemant M, Sarrailh P, Belhaj M, Inguimbert C, Garrigues L, Boniface C. Electron emission model for hall thruster plasma modelling. Proceedings of the 35th International Electric Propulsion Conference. Atlanta, GA (2017).
111. Kaminsky M. Atomic and Ionic Impact Phenomena on Metal Surfaces. Berlin: Springer-Verlag (1965).
112. Phelps AV, Petrovic ZL. Cold-cathode discharges and breakdown in argon: surface and gas phase production of secondary electrons. Plasma Sources Sci Technol. (1999) 8:R21–44. doi: 10.1088/0963-0252/8/3/201
113. Brunnee C. Uber die ionenreflexion und sekundarelektronenemission beim auftreffen von alkaliionen auf reine molybdan-oberflachen. Zeitschrift fur Physik A Hadrons and Nuclei (1957) 147:161–83. doi: 10.1007/BF01336930
114. Waters PM. Kinetic ejection of electrons from tungsten by cesium and lithium ions. Phys Rev. (1958) 111:1053–61. doi: 10.1103/PhysRev.111.1053
115. Daksha M, Derzsi A, Wilczek S, Trieschmann J, Mussenbrock T, Awakowicz P, et al. The effect of realistic heavy particle induced secondary electron emission coefficients on the electron power absorption dynamics in single- and dual-frequency capacitively coupled plasmas. Plasma Sour Sci Technol. (2017) 26:085006. doi: 10.1088/1361-6595/aa7c88
116. [Dataset]. Eirene Database. Available online at: http://www.eirene.de/html/surface_data.html
Keywords: particle-in-cell, parallel implementation, wall interaction, neutral dynamics, differential cross-section
Citation: Gueroult R, Fubiani G and Garrigues L (2018) Pitfalls in Modeling Walls and Neutrals Physics in Gas Discharges Using Parallel Particle-in-Cell Monte Carlo Collision Algorithms. Front. Phys. 6:128. doi: 10.3389/fphy.2018.00128
Received: 27 April 2018; Accepted: 23 October 2018;
Published: 13 November 2018.
Edited by:
Fabrice Deluzet, UMR5219 Institut de Mathématiques de Toulouse (IMT), FranceReviewed by:
Gian Luca Delzanno, Los Alamos National Laboratory (DOE), United StatesCopyright © 2018 Gueroult, Fubiani and Garrigues. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Renaud Gueroult, cmVuYXVkLmd1ZXJvdWx0QGxhcGxhY2UudW5pdi10bHNlLmZy
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.