
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 20 August 2018
Sec. Nuclear Physics
Volume 6 - 2018 | https://doi.org/10.3389/fphy.2018.00090
Predictions are presented for proton skins based on isospin-asymmetric equations of state derived microscopically from high-precision chiral few-nucleon interactions. Moreover, the relation between the neutron skin of a nucleus and the difference between the proton radii of the corresponding mirror nuclei is investigated.
It is well known that the available information on neutron radii and neutron skins is scarce and carry considerable uncertainty, see, for instance, Sammarruca [1] and references therein for a summary of empirical constraints, particularly on the skin of 208Pb, obtained from a variety of measurements [2–6]. Although future experiments [7]1 are planned which may be able to probe the weak charge density in 208Pb and 48Ca, the identification of other “observables” whose knowledge may give complementary information on neutron skins would be most welcome.
Naturally, the possibility of obtaining reliable values for neutron or proton skins is hindered by similar limitations, as both proton and neutron radii must be known to extract either skin. And while charge densities, particularly for stable isotopes, have been measured with great accuracy, the same cannot be said for the weak charge density.
An issue of current interest is whether information on the neutron skin can be obtained through the knowledge of proton radii alone, specifically those of mirror pairs. In particular, the difference between the charge radii of mirror nuclei in relation to the slope of the symmetry energy, and, in turn, to the neutron skin, was investigated in Brown [8]. As done in the past by the same author [9], correlations between neutron skins and the slope of the symmetry energy are deduced using large sets of phenomenological interactions, such as the numerous parametrizations of the Skyrme interactions. In Brown [8], using similar methods and 48 Skyrme functionals, a proportionality relation was found between the difference in the charge radii of mirror nuclei and the slope of the symmetry energy. This was echoed in Yang and Piekarewicz [10] using a set of relativistic energy density functionals.
Although analyses based on phenomenological interactions are a useful tool to explore sensitivities and interdependences among nuclear properties, microscopic predictions are more insightful being linked to realistic two- and few-nucleon forces. The microscopic aspect of this work is in the equations of state (EoS), which is obtained from self-consistent Brueckner-Hartree-Fock calculations employing high-precision chiral few-nucleon forces [11]. The purpose of the study is twofold. First, I present proton skin predictions and observe general patterns within isotopic chains, comparing with data when available. Second, I wish to explore, based on microscopic EoS as opposed to phenomenological ones, the relation between the neutron skin of a nucleus, on the one hand, and the difference between the proton radii of the mirror pair with the same mass, on the other. To avoid confusion, it is important to underline that this analysis will not be done by varying parameters in a family of models (not an option in this approach). Instead, the predicted relation between the quantities defined above will be investigated for a variety of (realistic) mirror pairs. We will pay particular attention to proton radii of mirror nuclei specifically in the mass range A≈48−54. At this time, the determination of proton radii of neutron-deficient isotopes such as for instance, the “mirror” of Fe is an enormous experimental challenge, which may be met in the future at radioactive beam facilities. The microscopic equations of state are then used in the volume term of a liquid-drop energy functional. This makes the treatment of the volume term distinct from the one of a fully phenomenological study. Hopefully this will provide useful information to complement present and future analyses.
This paper is organized as follows. In the next section, I give a short review of the theoretical tools and the calculation of the neutron and proton skins. I then proceed to proton skin predictions (section 3) and, more specifically, those of some mirror pairs in selected mass ranges (section 4). A brief summary and conclusions are contained in section 5.
Chiral EFT is generally recognized as the most fundamental approach to construct nuclear two- and many-body forces in a systematic and essentially model-independent manner [11, 12]. Nucleon-nucleon (NN) potentials have been constructed from leading order (LO, or zeroth order) to N3LO (fourth order) [11–18], with the latter describing NN data at the high precision level. Nucleon-nucleon chiral potentials at N4LO are also available [19, 20].
A large number of applications of chiral NN potentials (usually up to N3LO) together with chiral three-nucleon forces (3NF) (generally just at N2LO) have been conducted. A fairly extensive, although not exhaustive list is given in Coraggio et al. [21], Hagen et al. [22], Hagen et al. [23], Barrett et al. [24], Hergert et al. [25], Hagen et al. [26], Somà et al. [27], Hebeler et al. [28], Hagen et al. [29], Carlson et al. [30], Hergert et al. [31], Simonis et al. [32], Morris et al. [33], Gezerlis et al. [34] Binder et al. [35] where structure of light- and medium-mass nuclei are addressed, and in Hebeler and Schwenk [36], Hebeler et al. [37], Baardsen et al. [38], Hagen et al. [39], Coraggio et al. [40], Coraggio et al. [41], Sammarruca et al. [42], Drischler et al. [43], Tews et al. [44], Holt et al. [45], where infinite matter at zero temperature is addressed.
The microscopic EoS of symmetric nuclear matter and pure neutron matter applied here were derived in Sammarruca et al. [42]. The derivation is based on high-precision chiral NN potentials at next-to-next-to-next-to-leading order (N3LO) of chiral perturbation theory [11, 17]. The leading 3NF, which is treated as an effective density-dependent force [46, 47], is included.
The various chiral EFT-based EoS can differ from one another. Differences may be due, for instance, to the choice of the (local or non-local) regulator function, the value of the cutoff parameter, the quality of the fit of the few-nucleon forces. Ideally, and this is the most fundamental point of chiral EFT, predictions of a given “observable” should be model independent, within truncation error. Of course the choice of the many-body method for the nuclear/neutron matter calculations can also bring about differences. We discussed some of those in Sammarruca et al. [42] and determined the impact of using a nonperturbative approach beyond particle-particle correlations to be about ± 1 MeV around saturation density for nuclear matter and much smaller in neutron matter.
In this section we summarize briefly how we connect the EoS of infinite matter to properties of finite nuclei [48]. Within the spirit of a liquid droplet model, the energy of a nucleus is written in terms of a volume, a surface, and a Coulomb term as
In the above equation, ρ is the total nucleon density, given by ρn+ρp, with ρn and ρp the neutron and proton densities, respectively, whereas α is the neutron asymmetry parameter, α = (ρn−ρp)/ρ. e(ρ, α) is the microscopic energy per particle in isospin-asymmetric nuclear matter, written as
with esym(ρ) the symmetry energy. The density functions for protons and neutrons are obtained by minimizing the value of the energy, Equation (1), with respect to the paramaters of Thomas-Fermi distributions,
with i = n, p. The radius and the diffuseness, ai and ci, respectively, are extracted by minimization of the energy while ρ0i is obtained by normalizing the proton(neutron) distribution to Z(N). The neutron and proton skins are defined as
and
respectively, where Rn and Rp are the r.m.s. radii of the neutron and proton density distributions,
and T = N or Z. I find that the two-parameter Thomas-Fermi distribution is a reasonable choice for the mass range to be considered. Other choices for the nuclear density functions can be made of course (harmonic oscillator, gaussian, three-parameter Fermi function, folded Yukawa, etc…). When averaging over various possibilities, and particularly when taking differences between r.m.s. radii, such differences may increase the uncertainty but are unlikely to alter the substance of the present study in a significant way.
Note that the above method, although simple, has the advantage of allowing for a very direct connection between the EoS and the properties of finite nuclei. Some comments are in place concerning the semi-classical nature of the functional, particularly the classical treatment of the Coulomb term. The evaluation of averaged properties, such as r.m.s. radii, should not be very sensitive to the detailed orbital (quantum) structure of the nucleus. In support of such statement, we note that the same approach was used in Alonso and Sammarruca [48] in conjunction with meson-theoretic potentials and found to yield realistic predictions for binding energies and charge radii. The general validity of the method, when combined with a realistic EoS, was further tested in Sammarruca and Nosyk [49]. For instance, for the well-studied isospin-symmetric nucleus 40Ca we reported values of 8.333 ± 0.200 MeV and 3.504 ± 0.077 fm for the binding energy per nucleon and the charge radius, respectively, to be compared with the experimental values of 8.55 MeV and 3.48 fm. Note that the ab initio calculation of Hagen et al. [29] reports a value of 3.49(3) fm for the charge radius.
The constant f0 in the (phenomenological) surface term is obtained from fits to β-stable nuclei and determined to be about 60–70 MeV fm5 [50]. How this uncertainty impacts the corresponding predictions was discussed in Sammarruca [1] and will be taken into account in the present calculations.
In Table 1, proton skin predictions are displayed for some isotopic chains. The EoS used for these predictions is based upon N3LO two-nucleon forces (2NF) plus the leading 3NF. The estimated theoretical errors include uncertainties due to variations of the cutoff in the range 450–500 MeV as well as an error (added in quadrature) to account for the uncertainty originating from the method we use to calculate the skins [1]. The latter error is in the order of ± 0.01 fm, and this value is applied across the board.
As a general feature, the proton skins can be quite large. In fact, the neutron skins of the corresponding (neutron-rich) mirror nuclei are smaller. This fact is demonstrated in Table 2, where I show, for the most neutron-deficient isotope in each chain, the proton skin together with the neutron skin of the corresponding mirror nucleus.
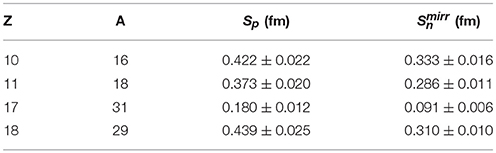
Table 2. Predicted proton skins, Sp, for the given Z and A and neutron skins, , of the corresponding mirror nuclei.
Some data on proton skins can be found in Suzuki et al. [51], Suzuki et al. [52], Ozawa et al. [53], Audi and Wapstra [54]. In Suzuki et al. [52], the existence of neutron and proton skins in β-unstable neutron- or proton-rich Na and Mg isotopes is discussed based on measurements of the interaction cross sections of these isotopes incident on a carbon target around 950A MeV. In Ozawa et al. [53], proton skin thickness for isotopes 32−40Ar were deduced from the interaction cross sections of 31−40Ar and 31−37Cl on carbon targets. The obtained matter radii were combined with measured charge radii for Argon isotopes to obtain skin thicknesses.
In Figure 1, predictions are shown for the proton skins of Argon isotopes in comparison with data deduced from experiments as described in Ozawa et al. [53]. Keeping in mind the large experimental errors, the trend of the empirical information is described reasonably well by the predictions, where the proton skin decreases essentially monotonically with increasing number of neutrons in a given isotopic chain.
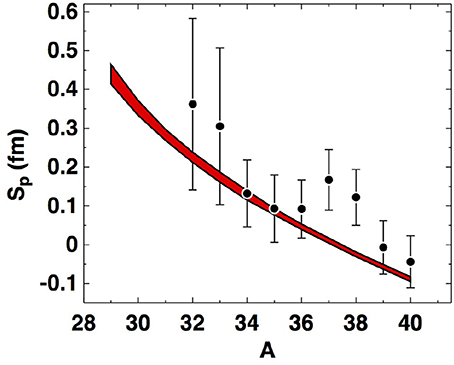
Figure 1. (Color online) Predicted proton skins of Argon isotopes as a function of the mass number, A. The data points are from Ozawa et al. [53].
Assuming perfect charge symmetry, one has, in mirror nuclei,
a relation which has been verified to be exactly satisfied when Coulomb contributions and other charge-dependent effects are turned off. Applying the definition of the neutron skin,
one can then immediately conclude from Equation (7) that
Namely, the neutron skin of nucleus (Z, N) would be equal to the difference between the proton radii of the mirror pair in the presence of perfect charge symmetry. If charge radii could be measured accurately for mirror pairs in the desired mass range, then the neutron skin of the (Z, N) nucleus could be obtained from Equation (9) after theoretical considerations to account for charge effects. Thus, this could be an alternative, although perhaps equally challenging from the experimental side, to the anticipated parity-violating experiments [8].
With the predictions displayed in Table 3, I now move to a specific range within medium mass nuclei, namely A≈48−54. This choice can be motivated by the vicinity to 48Ca, whose neutron skin has already been and is likely to be in the future the object of several investigations, both theoretical and experimental. At the same time, the need to consider mirror pairs limits the spectrum of realistic possibilities.
With Tables 4–6, the relation between neutron skins and ΔRp as defined in Equation (9) is addressed. Table 4 displays the neutron skin of the neutron-rich isotones from Table 3 in relation to ΔRp, with and without Coulomb effects. (Note that the latter case will not be addressed again and is shown here only for numerical verification, since the two items appearing in parentheses in Table 4 are expected to be exactly equal to each other on grounds of elementary nuclear physics).
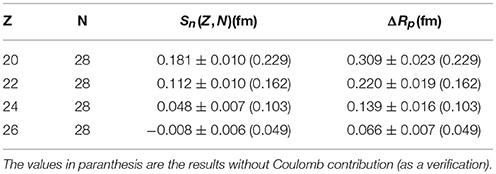
Table 4. Relation between the neutron skin of nucleus (Z, N), Sn(Z, N), and ΔRp of the corresponding mirror pair for the isotone chain N = 28.
Larger ΔRp implies larger neutron skin, as one might reasonably expect unless Coulomb effects were to reverse the relation in Equation (9). Note, though, that quantitatively speaking Coulomb effects are significant.
Next the relation between ΔRp and Sn(Z, N) for other chains will be explored. In particular, I wish to investigate if and how such relation differs, quantitatively, among chains with different masses. For that purpose, I consider in Tables 5, 6 two isotopic chains, one of them in a mass range considerably different than the one studied in Table 4. A visual representation of Tables 4–6 is provided in Figures 2–4.
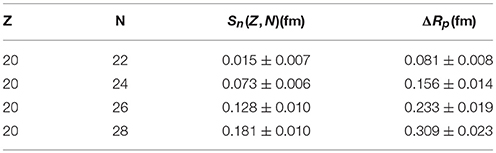
Table 5. Relation between the neutron skin of nucleus (Z, N), Sn(Z, N), and ΔRp for the isotope chain Z = 20.
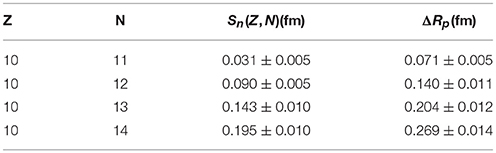
Table 6. Relation between the neutron skin of nucleus (Z, N), Sn(Z, N), and ΔRp for the isotope chain Z = 10.
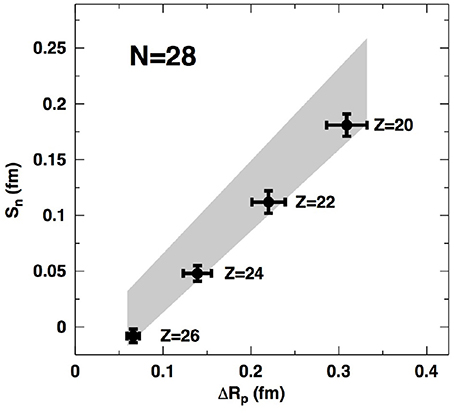
Figure 2. Graphical representation of Table 4. The gray band signifies Equations (10-11).
The first observation is that, for similar values of ΔRp, the corresponding values of Sn(Z, N) are approximately the same, regardless Z and N. Also, in all three cases the relation is clearly linear. It is important to stress again that the results shown in Figures 2–4 are fundamentally distinct from the correlations discussed in Brown [8]. The latter are obtained varying the parameters of Skyrme models (each model constrained to produce a chosen value of the neutron skin in 208Pb) for a fixed mirror pair. Here, the question being explored is to which extent these microscopic EoS (applied in Equation 1), yield, within theoretical uncertainties, a unique relation between Sn and ΔRp.
The parameters of the predicted linear relation,
based upon the three cases shown in Figures 2–4, can be summarized as
By means of Equations (10, 11), a measurement of ΔRp can then be promptly related to the neutron skin of the neutron-rich nucleus in the mirror pair.
As pointed out earlier, perfect charge symmetry imposes equality between the neutron skin and ΔRp for mirror pairs. Under more realistic conditions (that is, in the presence of Coulomb effects), Equations (10, 11) give a small negative value of Sn(Z, N) in the limit of ΔRp = Rp(N, Z)−Rp(Z, N) → 0. This makes sense in the light of Coulomb effects, since, under these conditions, one would have
But, for the same level of asymmetry, namely |N−Z|, the proton r.m.s. radius should be larger than the neutron's one due to Coulomb repulsion, as we observed in section 3, rendering the right-hand side of Equation (12) negative. Also, the two proton radii, as well as the difference between them, become larger in the presence of Coulomb repulsion, whereas the neutron skin becomes smaller (due to the increase in the proton radius). Therefore, Equation (9) suggests that appropriate modifications to account for Coulomb effects should include a slope which is less than unity. These considerations should be nucleus independent, thus the relation is potentially global.
Predictions based on microscopic few-nucleon forces do, of course, differ from one another. Although EFT should, in principle, be a model-independent approach, even EFT-based predictions can differ between them, depending, for instance, on the details of the input forces (e.g., cutoff) and the chosen many-body method. Moreover, the predicted relations between two quantities or observables are not necessarily located on one of the Skyrme models correlations. Here, I suggest that analyses such as the present one, combined with other predictions based on modern few-nucleon forces, are a useful way to provide a global relation between the “observables” being studied (as well as their relation to the density dependence of the symmetry energy), accompanied by a meaningful theoretical uncertainty.
Microscopic predictions of the EoS for isospin-asymmetric nuclear matter have been applied in a liquid-drop inspired density functional to obtain proton and neutron skins of selected chains of nuclei. The calculations of the EoS are based on high-precision chiral forces. A semi-classical density functional with an empirical surface term and Thomas-Fermi density distributions are employed to establish the connection with finite nuclei.
First, proton skin predictions have been presented for a few isotopic chains to observe some of their general features, particularly in comparison with neutron skins. It is found that they are generally large, larger than neutron skins for comparable values of proton-neutron asymmetry. The predictions reported here compare reasonably well with available empirical information, see Figure 1. The data in Figure 1 cover a range of N from 14 to 22, containing the magic number N = 20 (corresponding to A = 38). Enhancement of the proton skin is seen already at the non-magic value N = 19 (corresponding to A = 37), thus it is not entirely clear whether the pattern of the data in that mass range is due to shell effects. If so, the predictions would be expected to follow the data only on the average, as they do, since the liquid-drop functional is semi-classical.
The focus then moves on to mirror nuclei in a specific mass range (A≈ 48–54). At this point the opportunity arose to make some comments about and highlight differences with recent studies [8, 10] which have addressed those nuclei. More specifically, in Brown [8] 48 models are constructed so as to predict different skins of 208Pb within a chosen range. In this way, correlations are determined between the neutron skin and ΔRp for a particular mirror pair. In this paper, a single EoS (within its chiral uncertainty) calculated from few-nucleon forces in a parameter-free way, is applied to a family of mirror pairs to determine a relation between the two observables.
Using the predictions based on microscopic EoS and their uncertainties, a correlation is proposed between the skin of a neutron-rich nucleus and the difference between the proton radii of the corresponding mirror pair. I discussed the meaning and significance of such correlation in contrast to those characteristic of phenomenological interactions. Given the ab initio nature of the EoS, one is in the position of exploring, for instance, the contribution of 3NF to the predictions, the impact of higher chiral orders, the order-by-order pattern of the chiral perturbation series, and, generally, future improvements in the EoS.
I conclude by highlighting the importance of taking into account fully microscopic predictions as a guide toward the planning of future measurements. This work is a step in that direction.
The author confirms being the sole contributor of this work and approved it for publication.
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-FG02-03ER41270.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. ^ Hall A Collaboration, http://hallaweb.jlab.org.
1. Sammarruca F. Investigation of constraints on few-neutron forces in neutron matter by empirical information on the neutron skin of 48Ca and 208Pb. Phys Rev C (2016) 94:054317. doi: 10.1103/PhysRevC.94.054317
2. Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, et al. Constraints on the symmetry energy from experiments and theory. Phys Rev C (2012) 86:015803. doi: 10.1103/PhysRevC.86.015803
3. García-Recio C, Nieves J, Oset E. Neutron distributions from pionic atoms. Nucl Phys A (1992) 547:473–87.
4. Trzcińska A, Jastrzebski J, Lubinski P, Hartmann FJ, Schmidt R, von Egidy T, et al. Neutron density distribution deduced from anti-protonic atoms. Phys Rev Lett. (2001) 87:082501. doi: 10.1103/PhysRevLett.87.082501
5. Friedman E. Neutron skins of 208Pb and 48Ca from pionic probes. Nucl Phys A (2012) 896:46–52. doi: 10.1016/j.nuclphysa.2012.09.007
7. Abrahamyan S, Ahmed Z, Albataineh H, Aniol K, Armstrong DS, Armstrong W. et al Measurement of the neutron radius of 208Pb through parity-violation in electron scattering. Phys Rev Lett. (2012) 108:112502. doi: 10.1103/PhysRevLett.108.112502
8. Brown BA. Mirror charge radii and the neutron equation of state. Phys Rev Lett. (2017) 119:122502. doi: 10.1103/PhysRevLett.119.122502
9. Alex Brown B. Neutron radii in nuclei and the neutron equation of state. Phys Rev Lett. (2000) 85:5296–9. doi: 10.1103/PhysRevLett.85.5296
10. Yang J, Piekarewicz J. Difference in proton radii of mirror nuclei as a possible surrogate for the neutron skin. Phys Rev C (2018) 97:014314. doi: 10.1103/PhysRevC.97.014314
11. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001
12. Epelbaum E, Hammer H-W, Meissner U-G. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773
13. Epelbaum E, Krebs H, Meissner U-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-leading order. Eur Phys J. (2015) A51:53. doi: 10.1140/epja/i2015-15053-8
14. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev C (2016) 94:054007. doi: 10.1103/PhysRevC.94.054007
15. Piarulli M, Girlanda L, Schiavilla R, Navarro Pérez R, Amaro JE, Ruiz Arriola E. Minimally nonlocal potentials with chiral two-pion exchange including Δ resonances. Phys Rev C (2015) 91:024003. doi: 10.1103/PhysRevC.91.024003
16. Marji E, Canul A, MacPherson Q, Winzer R, Zeoli C, Entem DR, et al. Non-perturbative renormalization of the chiral nucleon-nucleon interaction up to next-to-next-to-leading order. Phys Rev C (2013) 88:054002. doi: 10.1103/PhysRevC.88.054002
17. Entem DR, Machleidt R. Accurate charge dependent nucleon nucleon potential at fourth order of chiral perturbation theory. Phys Rev C (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001
18. Epelbaum E, Glökle W, Meissner U-G. The two-nucleon system at next-to-next-to-leading order. Nucl Phys A (2005) 747:362–424. doi: 10.1016/j.nuclphysa.2004.09.107
19. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004
20. Epelbaum E, Krebs H, Meissner U-G. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301
21. Coraggio L, Covello A, Gargano A, Itaco N, Kuo TTS. Effective shell-model hamiltonians from realistic nucleon-nucleon potentials within a perturbative approach. Ann Phys. (2012) 327:2125–51. doi: 10.1016/j.aop.2012.04.013
22. Hagen H, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Continuum effects and three-nucleon forces in neutron-rich oxygen isotopes. Phys Rev Lett. (2012) 108:242501. doi: 10.1103/PhysRevLett.108.242501
23. Hagen H, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Evolution of shell structure in neutron-rich calcium isotopes. Phys Rev Lett. (2012) 109:032502. doi: 10.1103/PhysRevLett.109.032502
24. Barrett B R, Navratil P, Vary J P. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131–81. doi: 10.1016/j.ppnp.2012.10.003
25. Hergert H, Bogner SK, Binder S, Calci A, Langhammer J, Roth R, et al. In-medium similarity renormalization group with chiral two- plus three-nucleon interactions. Phys Rev C (2013) 87:034307. doi: 10.1103/PhysRevC.87.034307
26. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rept Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302
27. Somà V, Cipollone A, Barbieri C, Navratil P, Duget T. Chiral two- and three-nucleon forces along medium-mass isotope chains. Phys Rev C (2014) 89:061301. doi: 10.1103/PhysRevC.89.061301
28. Hebeler K, Holt JD, Menéndez J, Schwenk A. Nuclear forces and their impact on neutron-rich nuclei and neutron-rich matter. Ann Rev Nucl Part Sci. (2015) 65:457–84. doi: 10.1146/annurev-nucl-102313-025446
29. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W. Neutron and weak-charge distributions of the 48Ca nucleus. Nature Phys. (2015) 12:186–90. doi: 10.1038/nphys3529
30. Carlson J, Gandolfi S, Pederiva F, Pieper S C, Schiavilla R, Schmidt K E, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067. doi: 10.1103/RevModPhys.87.1067
31. Hergert H, Bogner S K, Morris TD, Schwenk A, Tsukiyama K. The in-medium similarity renormalization group: a novel Ab initio method for nuclei. Phys Rep. (2016) 621:165–222. doi: 10.1016/j.physrep.2015.12.007
32. Simonis J, Stroberg S R, Hebeler K, Holt J D, Schwenk A. Saturation with chiral interactions and consequences for finite nuclei. Phys Rev C (2017) 96:014303. doi: 10.1103/PhysRevC.96.014303
33. Morris TD, Simonis J, Stroberg SR, Stumpf C, Hagen G, Holt JD, et al. Structure of the lightest Tin isotopes. Phys Rev Lett. (2018) 120:152503. doi: 10.1103/PhysRevLett.120.152503
34. Gezerlis A, Tews I, Epelbaum E, Gandolfi S, Hebeler K, Nogga A, et al. Quantum monte carlo calculations with chiral effective field theory interactions. Phys Rev Lett. (2013) 111:032501. doi: 10.1103/PhysRevLett.111.032501
35. Binder S, Calci A, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, et al. Few-nucleon systems with state-of-the-art chiral nucleon-nucleon forces. Phys Rev C (2016) 93:044002. doi: 10.1103/PhysRevC.93.044002
36. Hebeler K, Schwenk A. Chiral three-nucleon forces and neutron matter. Phys Rev C (2010) 82:014314. doi: 10.1103/PhysRevC.82.014314
37. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C (2011) 83:031301. doi: 10.1103/PhysRevC.83.031301
38. Baardsen G, Ekström A, Hagen G, Hjorth-Jensen M. Coupled-cluster studies of infinite nuclear matter. Phys Rev C (2013) 88:054312. doi: 10.1103/PhysRevC.88.054312
39. Hagen G, Papenbrock T, Ekström A, Wendt KA, Baardsen G, Gandolfi S, et al. Coupled-cluster calculations of nucleonic matter. Phys Rev C (2014) 89:014319. doi: 10.1103/PhysRevC.89.014319
40. Coraggio L, Holt JW, Itaco N, Machleidt R, Sammarruca F. Reduced regulator dependence of neutron-matter predictions with perturbative chiral interactions. Phys Rev C (2013) 87:014322. doi: 10.1103/PhysRevC.87.014322
41. Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE, Sammarruca F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys Rev C (2014) 89:044321. doi: 10.1103/PhysRevC.89.044321
42. Sammarruca F, Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE. Toward order-by-order calculations of the nuclear and neutron matter equations of state in chiral effective field theory. Phys Rev C (2015) 91:054311. doi: 10.1103/PhysRevC.91.054311
43. Drischler C, Carbone A, Hebeler K, Schwenk A. Neutron matter from chiral two- and three-nucleon calculations up to N3LO. Phys Rev C (2016) 94:054307. doi: 10.1103/PhysRevC.94.054307
44. Tews I, Gandolfi S, Gezerlis A, Schwenk A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys Rev C (2016) 93:024305. doi: 10.1103/PhysRevC.93.024305
45. Holt JW, Kaiser N. Equation of state of nuclear and neutron matter at third-order in perturbation theory from chiral effective field theory. Phys Rev C (2017) 95:034326. doi: 10.1103/PhysRevC.95.034326
46. Holt JW, Kaiser N, Weise W. Chiral three-nucleon interaction and the C-14 dating beta decay. Phys Rev C (2009) 79:054331. doi: 10.1103/PhysRevC.79.054331
47. Holt JW, Kaiser N, Weise W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys Rev C (2010) 81:024002. doi: 10.1103/PhysRevC.81.024002
48. Alonso D, Sammarruca F. Neutron densities and the equation of state for neutron rich matter. Phys Rev C (2003) 68:054305. doi: 10.1103/PhysRevC.68.054305
49. Sammarruca F, Nosyk Y. Impact of the neutron matter equation of state on neutron skins and neutron drip lines in chiral effective field theory. Phys Rev C (2016) 94:044311. doi: 10.1103/PhysRevC.94.044311
50. Oyamatsu K, Iida K, Koura H. Neutron drip line and the equation of state of nuclear matter. Phys Rev C (2010) 82:027301. doi: 10.1103/PhysRevC.82.027301
51. Suzuki T, Geissel H, Bochkarev O, Chulkov L, Golovkov M, Hirata D, et al. Neutron skin of Na isotopes studied via their interaction cross sections. Phys Rev Lett. (1995) 75:3241–4.
52. Suzuki T, Geissel H, Bochkarev O, Chulkov L, Golovkov M, Fukunishi N, et al. Nuclear radii of Na and Mg isotopes. Nucl Phys A (1998) 630:661–77.
53. Ozawa A, Baumann T, Chulkov L, Cortina D, Datta U, Fernandez J, et al. Measurements of the interaction cross section for Ar and Cl isotopes. Nucl Phys A (2002) 709:60–72. doi: 10.1016/S0375-9474(02)01071-0
Keywords: neutron skin, proton skin, equation of state, chiral interactions, neutron-rich nuclei
Citation: Sammarruca F (2018) Proton Skins, Neutron Skins, and Proton Radii of Mirror Nuclei. Front. Phys. 6:90. doi: 10.3389/fphy.2018.00090
Received: 23 May 2018; Accepted: 26 July 2018;
Published: 20 August 2018.
Edited by:
Isaac Vidana, Istituto Nazionale di Fisica Nucleare (INFN), ItalyReviewed by:
Artur Polls, University of Barcelona, SpainCopyright © 2018 Sammarruca. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesca Sammarruca, ZnNhbW1hcnJAdWlkYWhvLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.