Noise, Information and Fitness in Changing Environments

In this paper we discuss recent results regarding the question of adaptation to changing environments in intermediate timescales and the quantification of the amount of information a cell needs about its environment, connecting the theoretical approaches with relevant experimental results. We first show how advances in the study of noise in genetic circuits can inform a detailed description of intracellular information flow and allow for simplified descriptions of the phenotypic state of a cell. We then present the different types of strategies that cells can use to respond to changing environments, and what a quantitative description of this process implies about the long term fitness of the population. We present an early approach connecting the transmission of information to the average fitness, and then move on to a full model of the process. This model is then simplified to obtain analytical results for a few cases. We present the necessary notation but avoid technical detail as much as possible, as our goal is to emphasize the biological interpretation and significance of the mathematical results. We focus on how carefully constructed models can answer the long-standing objection to the use of information theory in biology based on decision-theoretic considerations of the difference between the amount of information and its fitness value.

Introduction

It has long been recognized that information about the environment is crucial for survival of all living things, and that a connection exists between long term environment and genotype and short term environment and phenotype. It has even been proposed that information storage and transmission is the fundamental feature of evolution [1]. Since evolution occurs via progressive changes in the genome, some information about the history of the environments the ancestors have faced must be stored in the genetic sequence [2]. On shorter timescales, a given genotype can result in different phenotypes through interactions with the environment and intracellular stochasticity. This can range from gene expression changes in bacteria in response to changes in the surrounding media, to the extreme differences in form and function between specialized cells in mammals. It follows that the phenotype of a cell has information about the current environment and/or the surrounding environment during development. Since selection happens at the level of phenotype, these two levels of information transmission and storage must be connected to the process of evolution. It therefore seems useful to quantify this flow of information in biological systems, which might allow for predictive calculations in a similar way to how optimizing the flow of mass and energy has advanced ecology [3].

Early attempts to use the formal definition of information [4] in biology ran into the following problem: every bit of information is in principle equally valuable in abstract communication channels, but for an organism some bits are more valuable than others. If there is a 50/50 chance that a predator is behind a bush, knowing for sure is a very useful bit, whereas knowing whether its left or right molar is bigger is a less useful bit. Since the meaning of each bit is irrelevant for the engineering problem of information transmission, many biologists thought that the amount of information was irrelevant and the important quantity was its decision-theoretic value [5]: the expected fitness given some particular information minus the expected fitness without it. In the predator-behind-bush example, presumably the best strategy (for the prey) under uncertainty is to leave the bush alone, incurring in a fitness cost in terms of lost food. With full information, half of the time the prey knows that the predator is not there and it can get the food and half of the time it has to run away, so on average he gets half of the food. In this case the value of the information on whether the predator is there or not is the fitness gain of half a bush worth of food, which is not in units of information. Unfortunately, quantifying this in principle would require an intimate knowledge of the fitness function and the dependence of phenotype on environmental cues. Furthermore, such calculations require knowing the fitness value of the wrong combinations of phenotype and environment, which are not easy to observe. For example, determining the value for a type of bird of knowing when the seasons come would require determining how it would do if it didn't migrate. For evolutionary timescales, this would mean knowing the maximum fitness it could have if it eventually adapted to not migrating. The fundamental difference between the information-theory approach and the decision-theory approach is one of the issues answered by the research reviewed here.

For the case of unicellular organisms, it is easier to both define and measure such quantities in laboratory settings. The possible environments for evolution can be defined experimentally [6], short term fitness is directly measurable from competition experiments [7], behavior can be controlled through genetic manipulation [8], and evolution experiments can be performed in human timescales [9]. A more tractable subset of the general problem of information flow in biology is then the quantifying of both the amount and fitness value of the information that a population has about a particular set of environments, and how it would evolve for intermediate timescales.

This question is related to another important problem in biology: how do cells adjust their expression pattern (phenotype) to respond to changing environments? It certainly involves the biochemical mechanisms through which a cell senses the environment and alters gene expression, but the question goes far beyond mechanistic responses. For example, it has been shown that under certain conditions it might be better for a cell not to try to determine precisely what environment it is facing but randomly switch between possible responses [10, 11]. This could be done blindly, but more generally, the response to external signals is increasingly found to be a combination of deterministic and stochastic parts that can result in changing distributions of phenotypes, in what is known as a conditional, distributed or bet-hedging strategy [12]. This is equivalent to mixed strategies in game theory [13]. The possible strategies are sketched in Figure 1: assuming only three possible states of the environment and phenotype, matched by color, the distribution of phenotypes in the population for different environments is given by the bar graphs. In perfect sensing, the response is deterministic and simply changes to the appropriate state after some delay. In a purely stochastic strategy (blind switching), the cells are not measuring the environment and have a constant distribution. This means that for any change in environment some cells will already be in the new correct state but also that in any environment a sizable fraction is in the wrong states. For simplicity the figure ignores the important fact that growth differences would bias the distribution to the correct state, as will be shown in Figure 2, making it look like the distributions for conditional switching. In a conditional switching strategy, cells transition between states but with transition probabilities that depend on a measure of the environment, resulting in distributions that are biased toward the correct state but nevertheless always have some cells in the wrong state. These cells are in a sense a “hedge,” or insurance in case the environment changes and the delay in changing accordingly is costly.

FIGURE 1

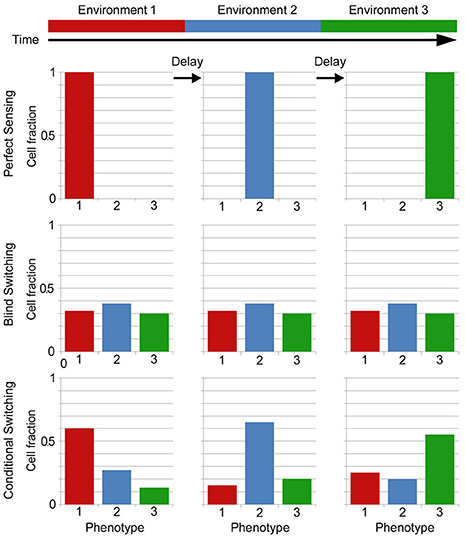
Figure 1. Sketch of phenotype distributions corresponding to different strategies for adapting to fluctuating environments. In this example there are three possible environmental and corresponding phenotypic states. In perfect sensing, cells measure the environment and all change to the correct state. In blind stochastic switching, cells just try to maintain a distribution (which doesn't have to be uniform) regardless of environment. Here we don't show the important effect that growth differences would have, biasing the distribution to the correct state. In conditional stochastic switching, cells switch between states but with rates that depend on information from the environment and can bias it to the correct one even discounting growth effects.

Given the inevitable stochasticity in intracellular processes [15], the cases where the response appears deterministic imply a noise reduction system [16, 17], whereas in many cases this variability is amplified and converted into a distribution of phenotypes [18]. A medically important example of this switching strategy is the phenomenon of bacterial persistence [19], where a very small fraction of a population switches on a timescale of hours in and out of a non-growing or slow-growing state that confers it tolerance against many antibiotics and other attacks. If the rest of the population is killed and the insult withdrawn, these cells can restore the population, but it is important to note that this new population is still susceptible to the insult, as opposed to the case where a genetic mutation confers resistance to the resulting population. The amount of cells in this persistent state does depend on the environment, but it is not simply a deterministic response to it, since a phenotype distribution including a persistent fraction is present before the insult [20]. This exemplifies the type of adaptation that will be discussed here.

Information in an Evolutionary Context

A discussion on whether evolution can be profitably studied as an optimization process (illustrated by the discussions between Maynard-Smith [21] and Gould and Lewontin [22]) has raged on for 40 years between philosophers of biology. There are valuable arguments about the difficulty of defining an objective function (instantaneous individual fitness, inclusive fitness, long term population growth, evolutionary stability?), and other important points that remain under active research. Similarly, the use of information theory in biology has a long history of ardent proponents [1, 23] and detractors [24, 25].

However, a large group of researchers has simply sidestepped the discussion by profitably using optimization and information theory in various fields, from sequence analysis [26] to neural coding [27]. In particular, the recent availability of sequence data has allowed the direct comparison of information theoretic limits with actual observed distributions of sequences in particular contexts [28, 29]. It has even been proposed that information processing constitutes a driver to increasing organismal complexity [30]. Adami [31] has written a very readable account of the use of information concepts in evolutionary biology. Another field where information theory has found great success is neuroscience, where it is nowadays an essential tool; a good review is given by Dimitrov et al. [32]. Such breadth of fields using information theory has led to competing definitions of information for different situations, including mutual information [4], directed information [33], Fisher information [34], and others. While each has advantages, we focus on mutual information, which has important theoretic advantages [35] although directed information will make an appearance later on. It is also important to note that while we focus on prokaryotic gene expression noise for simplicity, phenotypic differences depends not only on gene expression but also on protein states [36] and localization [37] and on epigenetic markers such as methylation [38]. The approaches worked out here will still hold for these other mechanisms, although the details of the calculations of noise and information will vary; see for example Cheong et al. [39], Thomas and Eckford, [40], or Micali and Endres et al. [41]. We also leave aside the long term relation between sequence and selection, although it underlies the assumptions of near optimality.

The Role of Noise

What has changed in the meantime is our knowledge of noise and dynamics in intracellular circuits and our experimental tools to probe them. We have an ever growing collection of data and models which provides examples for many types of circuits in different organisms [42]. We have a rough description of the processes that lead to cell specialization in many multicellular organisms [43, 44]. We have detailed models and measurements of the way stochasticity arises in intracellular circuits [15, 17] and how it can result in phenotypic variability [45, 46]. Experimentally, we have measurements at the single molecule level of mRNAs and proteins [47, 48], single cell transcription data [49, 50], and automated ways to observe populations [6] and single cells [51] in changing environments over long periods. We also have the tools of synthetic biology to probe and manipulate circuits [52, 53], and the methods of experimental evolution [9] and competition [7] in unicellular populations. This detailed knowledge of the noise allows us to compute directly the information content of various biochemical processes. In the next section we will see the example of a single gene, but many other examples have been worked out.

An objection showing up as late as 1997 to the use of information theory in biology was that biology was not stochastic enough [54]. The underlying argument is that if signaling happens through molecules, their numbers are so high that interactions are essentially nonrandom processes. Quantitatively, one could expect that a typical signaling protein with numbers of the order of 10000 would have fluctuations of the order of $\sqrt{10000}=100$, resulting in a relative noise (coefficient of variation) of 1%, and making a probabilistic description unnecessary. This is misleading not only because there are many relevant situations where the number of signaling molecules can be <1 [55], but also because we now know that the most relevant noise in protein level does not come from the fluctuations in the number of proteins itself but in that of the mRNAs that produce it [11], the binding and unbinding of transcription factors that control it [56], and the fluctuations transmitted from other parts of the cell [57, 58]. This means that noise in genetic circuits is large and ubiquitous, and that a detailed description of their dynamics should include its probabilistic aspects.

We have also learned about the effect of feedbacks in genetic circuits, where they can be used to reduce fluctuations or amplify them [59, 60], and can generate metastable states and multimodal distributions [59]. These in turn correspond to different phenotypic states, and in some cases we know how the distribution of states is determined and how to manipulate it [61]. So we now have mechanistic knowledge, in a few cases, of how phenotypic diversity is generated and maintained. Conversely, since those states are in general maintained by the dynamics of noisy genetic circuits, they are susceptible to error and any memory contained within them is limited and imperfect [62]. Therefore if we are interested in how cells adapt to changing environments, we need to know how much information a cell can actually store about the environmental history and how much information can actually be transmitted from the environment to intracellular circuits in the presence of noise.

Information Content of Gene Expression

Tkačik et al. [63] utilize analytical, approximate models of noise in gene expression to determine the channel capacity of a gene, which is the maximum rate of information transmission for a single gene under various conditions. In particular, they look at transcription factor binding and unbinding and the intrinsic noise of gene expression and show that the capacity of a single regulatory element is 1 bit under typical conditions and that under reasonable but more restrictive assumptions it can increase to around 3 bits. This has important implications for biology: the first point validates the use of Boolean networks, a popular approximation to genetic networks, in many cases. The second illustrates that although protein levels are usually on the order of thousands, the reliable transmission of more than a few levels is limited by the stochasticity in the system and parameters need to be carefully tuned to achieve it. In the particular case of the design of synthetic circuits, the need for proper impedance matching has already been noted [64], but the results of Tkačik et al. show that the stochastic effects also need to be properly tuned.

Following their notation, we look at a single gene controlled by a single transcription factor. Let g be the level of expression of the gene (in a simple case, the protein number) and c the amount of transcription factor. c corresponds to the input signal, which can have a distribution p_TF (c). If gene expression were deterministic, there would exist a function g* (c) that directly mapped input level to expression. Since gene expression is stochastic, this situation is described through p (g|c), the conditional probability of observing expression g given input c. Later we will explicitly incorporate the time dependence. With these definitions, we can look at information theory quantities such as the mutual information between the input and output distributions. Using p (g, c) = p (g|c) p_TF (c) and $p_g(g)=\sum _{c}p(g|c)p_{TF}(c)$ the mutual information would be

$\begin{array}{l}I(g,c)={\displaystyle \sum _{g,c}}p(g,c){log}_2\left(\frac{p(g,c)}{p_g(g)p_{TF}(c)}\right)\\ ={\displaystyle \sum _{g,c}}p(g|c)p_{TF}(c){log}_2\left(\frac{p(g|c)}{p_g(g)}\right)& (1)\end{array}$

where the logarithm is in base 2 to obtain units of bits, and we have used g and c for both the random variables and their distribution to simplify the notation. Here we can see more precisely what we meant by “tuning the stochastic effects: ”if the gene expression is to respond with many distinguishable levels, the distribution of transcription factors cannot be arbitrary. For example, a gene with a step response curve could pass no information if the corresponding transcription factor distribution was zero on one side of the threshold. More realistically, a gene with a sigmoidal response curve could transmit more information if the corresponding transcription factor had a distribution proportional to the slope of the response curve than if it had a bimodal distribution.

This approach seems to imply that the system is maximizing the amount of information transmitted. A simple example to the contrary is the case of a binary output, where the cell only needs to precisely transmit the information of whether a certain threshold has been crossed and respond by fully turning on a gene. In this case, the information lost far from the threshold is irrelevant, and a bimodal distribution of inputs would be best. It is important to distinguish two possible issues: one is that not all information might be relevant, and the other is that the evolutionary value (or decision-theory value) of information is not the same as the amount of relevant information. The issue of how much information is actually useful for prediction has been largely solved by the “information bottleneck” method proposed by Tishby et al. [65], where they show how to determine the amount of relevant information a variable has for any particular prediction goal. In the present discussion, what the goal is needs to be quantified using the fitness. We will later return to this point to show how to account for the fitness value of the transmitted information. But first, we need to determine what exactly we mean by fitness for the cases of interest.

Sensing vs. Guessing as a Strategy

Real environments are a mix of predictable and stochastic characteristics. Cells have different ways of managing their phenotypes/strategies to adapt, including systems that allow the prediction of the reliable parts such as circadian clocks, sensing mechanisms such as chemotaxis, and bet-hedging strategies such as the phenomenon of bacterial persistence explained above. While the possibility of bet-hedging as a strategy had been analyzed before [11, 66, 67], it is in the work of Kussell and Leibler [68] that we find a framework that captures the full range of possibilities. An idealized extreme would be to have perfect sensing, where the cell would respond to an environment s (described in general by a vector) with the gene expression pattern g that gives the highest fitness f (g, s) in that environment, g* (s). Perfect sensing is impossible, but even imperfect sensing has a metabolic cost, which must increase with the accuracy of sensing. For example, the noise of ligands binding and unbinding from their receptors can be ameliorated by averaging over more receptors, but those cost energy to produce and recycle. Additionally, there is an unavoidable delay between measurement and response, which in principle can be reduced but again at a metabolic cost [69]. So even in the case of direct sensing there is a tradeoff between the fitness cost of responding late and sometimes wrongly and the fitness cost of increased metabolic load. Note that this description implies that the quantity to be optimized is not the instantaneous fitness f (g, s) but the long term average growth for a sequence of environments.

At the other extreme the idealized case is that of a completely stochastic response: a population that generates large phenotypic variability so as to cover the different possible environments. It can be easily implemented by a positive feedback tuned to amplify noise to produce broad or multimodal distributions of expression [59]. This strategy has some advantages: since the possible state of the environment is given by multiple variables, some of which are continuous, there are infinite possible environments. It then becomes impossible to have sensors for every case, and unfeasible even to have enough to precisely determine the set that would correspond to each possible phenotypic state. Another important effect is that if the switching is slow compared to the environment, a bigger fraction than determined by switching alone will be in the correct state simply because they grow faster. But since there is a fraction of the population that will always have suboptimal fitness, this strategy would seem in principle to be inferior to (imperfect) sensing. By explicitly taking into account the cost of sensing and the disadvantages of delay in a simplified situation, Kussell and Leibler show the range of cases where pure stochasticity surpasses sensing as a strategy. One situation in particular gives the advantage to bet-hedging: cases where there are states of the environment that are rare but rapidly lethal for the wrong phenotype, such as for bacteria in the presence of antibiotics. In this situation, preemptively having a small fraction of the population in a state that can survive in the presence of antibiotics can be advantageous even if those cells are at a big disadvantage in other environments.

The general case is one where the system responds stochastically, but with the probabilities of transition between phenotypic states influenced by what is sensed of the environment. This is the case, for example, in bacterial persistence. While Kussell and Leibler mentioned it as a conjecture, we know now that the rates of transition into and out of the persistent state depend on the media: the probability of going into the persistent state increases if the cell is stressed [70] (for example, by antibiotics) and the probability of coming out increases in rich media. It is important to note that this does not imply that persistence occurs only as a response to stress; it was shown by Balaban et al. that cells enter the persistent state before the stress is applied [20]. It is the probability of going into the persistence state that changes.

Clear experimental evidence for the viability of the stochastic switching strategy comes from the experiments of Acar et al. [14]. They engineered two strains of S. cerevisiae to stochastically switch the gal operon on and off at different rates, but with the URA3 gene under its control. This gene was used because it allows for both positive and negative selection: when the media contains no uracil, cells that express URA3 have an advantage, but when the media contains both uracil and 5-fluoroorotic acid (5-FOA), this small molecule is transformed by the URA3 protein into a toxic compound that gives a disadvantage to the cells that express it but no disadvantage to those that do not. By comparing the growth rates of the strains in media that alternated with different rates between media without uracil and media with uracil and 5-FOA, they found that the strain with fast switching had a faster average growth rate than the slow switching strain in fast switching-media and vice versa.

This experiment is very illustrative for the present discussion for various reasons. If we ignore the time dependence, the slow switchers and fast switchers are simply bet-hedging with different distributions, as can be seen in Figure 2A. In nonselective media there are cells with very different levels of gene expression, and the two clear peaks in the distributions represent the two possible states. Figure 2B shows the distributions of expression after 4 days in media without uracil (environment S₁) and Figure 2C shows the distributions of expression after 4 days in media with uracil and 5-FOA (environment S₂). Although they have no direct sensing of the two environments, the fact that only the correct phenotype can grow results in very skewed distributions in selective media. Note that in both cases the fast switchers have a larger fraction that is not in the correct state (the red tails), and this results in slower growth after some time in either environment but also on an initial advantage after a media change (Figures 2D,E). This happens because the fraction of cells in the wrong state after a long time in an environment is also the fraction of cells that are already in the correct state when the environment changes. However, in repeatedly changing environments the winner depends on the speed of change. If the environment changes every 40 min, the fast switchers have a long term advantage because in the time it takes the slow switchers to switch, the fraction of the fast switchers that was “wrong” has been already growing (Figure 2F). If the environment changes every 100 min the slow switchers have the advantage because they spend longer in the situation where they have the advantage (Figure 2G). While the differences are small for the cases shown, they are amplified exponentially and result in measurable differences in average growth rate. This shows that the instantaneous fitness f (g, s) is not necessarily what is optimized by evolution, but perhaps its long term average over the population is [71–73]. This can be visualized as the red and blue shaded areas in Figures 2F,G representing the cumulative growth advantage of each strain. For rapidly changing environments the total of the red areas is larger than the blue, and conversely for the slowly changing environments.

FIGURE 2

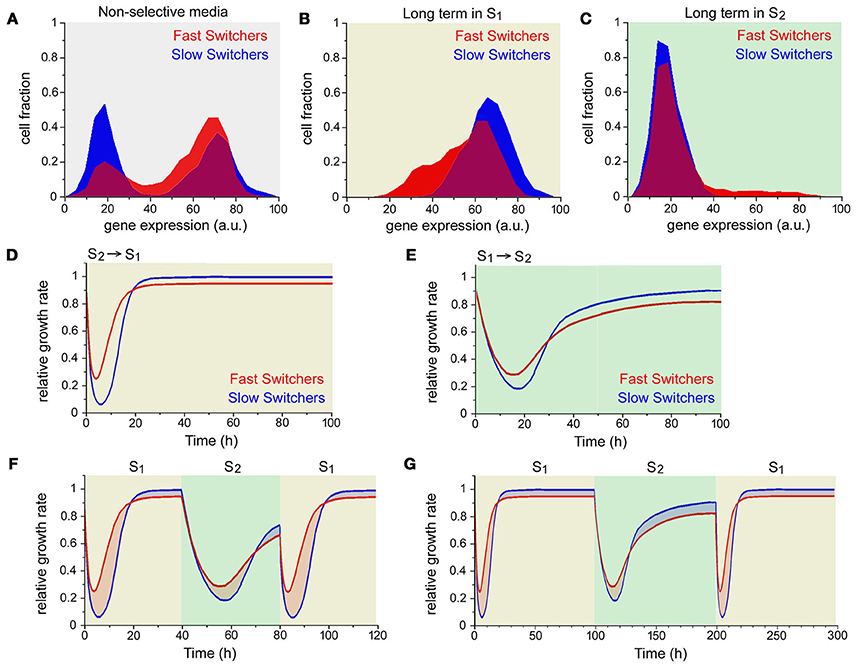
Figure 2. Long term growth in a bet-hedging strategy. (A) Long term distribution of phenotypes (gene expression) for the slow switchers (blue) and fast switchers (red) in nonselective medium. Cells have mostly either high (ON) or low (OFF) expression. (B) In media without uracil (environment S1), only cells that are ON can grow, but the distributions are wide because cells are still switching. The distribution of fast switchers is wider because of a faster stream of cells switching off, resulting in a larger fraction of cells in the wrong state (red tail). (C) Conversely, in media with uracil and 5-FOA (environment S2) only OFF cells can grow, but the distribution is still wider for the fast switchers. (D) When changing from a long time (4 days) in S2 to S1, cells have low growth until the ON fraction grows. After some time, the slow switchers grow faster, because of the different fractions in the ON state shown in (B). (E) When changing from a long time (4 days) in S1 to S2 cells have low growth until the OFF fraction grows. Again after some time, the slow switchers grow faster. (F) If media are alternated every 40 min, this results in longer periods where the fast switchers grow faster than the slow switchers, leading to higher average growth. The total advantage can be visualized by the areas shaded in red vs. the areas shaded in blue. Intuitively, if the time is short the initial advantage of the fast switchers exceeds the eventual advantage of the slow switchers. (G) The opposite happens if the period is changed to 100 min. Adapted from Acar et al. [14].

Since this system was artificial in its construction and the possible states of the environment, it approached the idealized limit of bet-hedging. However, the media was changed periodically rather than randomly. In natural cases of adaptation to a periodically switching environment cells can adapt over evolutionary timescales by developing a matching internal clock, but one that is not completely independent of the environment so that it can be entrained to avoid phase drift [74, 75]. However, it is easy to see that if the environments were changed randomly with average times close to those used in the periodic cases the main effect would still hold: cells that switched with rates matching the environment would have an advantage over those that switch with the wrong rates. Their system thus illustrates a question that will be answered more generally later: if the cells will adopt a distribution of phenotypes without measuring the environment, how do they choose the distribution of phenotypes that maximizes their fitness?

Optimization of Average Fitness Under Information Constraints

In the context just explained of a finite set of possible environments and a set of possible phenotypes, but taking into account the stochasticity mentioned before, it is possible to properly define one of our original questions: given the full fitness f (g, s) for all possible states of gene expression and environment, what is the best possible p (g|s)? The ideal g* (s) can be directly obtained from f, but since the cell cannot measure s nor maintain g with infinite precision the most it could do is optimize the conditional distribution p (g|s). But why not simply make it as narrow a peak as possible around g* (s)? Notice that the metabolic costs mentioned before would in principle go into the state g, but that makes the question somewhat tautological. We must be clear about the timescales and genes under study; as Maynard-Smith noted, we cannot be sure that the optimum has been achieved and what the physical limitations involved are in general, but optimization is a useful heuristic for a limited system. In this case, this means limiting the timescale of study to changing levels of gene expression and perhaps protein affinities rather than the evolution of an entirely different sensing system, and the genes to a particular set directly involved with the response to a particular characteristic of the medium. The disadvantage of this approach is that metabolic costs are hidden in the fitness function; perhaps they can be taken into account by explicitly including the energy needed for a particular sensing and expression control system. This would be a strong simplification, which would only make sense if the way the fitness function was computed in the first place was through a balance of energies.

Taylor et al. [76] solve this problem by using the information concepts explained before. They group the factors that would incur a metabolic cost into the mutual information between g and s, and propose that the optimization be done maximizing the average fitness for a given mutual information, or conversely minimizing the mutual information needed to achieve a given level of fitness. In this view,

$\begin{array}{ll}I(g,s)={\displaystyle \sum _{g,s}}p(g|s)p(s)log\left(\frac{p(g|s)}{p_g(g)}\right)& (2)\end{array}$

and

$\langle f\left(g,s\right)\rangle ={\displaystyle \sum _{g,s}p\left(g,s\right)f\left(g,s\right)}={\displaystyle \sum _{s}p(s)}{\displaystyle \sum _{g}p\left(g|s\right)f\left(g,s\right)}(3)$

where for simplicity we omit the vectorial notation. The last expression has a clear biological interpretation: averaging over the possible states of the environment (externally determined), then for each particular environmental state averaging over the possible responses of the cell to that environment (determined by the genes under study) of the fitness function (determined by the relevant biochemistry). These definitions are illustrated schematically in Figure 3. The fitness function f(g, s) for a one dimensional environmental state s and phenotypic state g can be represented as a heat-map (Figure 3A). The ideal phenotype g*(s) would be the maximum of this function for each possible value of s (Figure 3B). Even in a fixed environment s₁, noise in the sensing systems and in gene expression prevents the cells form knowing $g^{*}(s_1)$ precisely and maintaining a particular level of expression, resulting in a distribution of expression p(g|s₁) (Figure 3C, in gray), in principle centered on $g^{*}(s_1)$. Note that the shaded area in the heat map represents the average fitness for a single cell or the total fitness for a population with the given distribution of expression. The distribution of expression is in general not symmetric, nor is the slope of f(g, s₁) around $g^{*}(s_1)$. If the population is optimizing the total fitness, but is constrained by the noise, it could in principle still shift the shape and position of the distribution within some constrains. For different values of s the optimal shape of the distribution would be different, as shown in Figure 3D. This can be further complicated by the fact that the environments the cell encounters also have a distribution p(s), shown in Figure 3E in black. Note that the resulting distribution of phenotypes p(g), shown in Figure 3E in gray, is not simply the projection of p(s) through the function g*(s). As the colors in Figure 3D show, it is more costly in fitness terms to deviate from the optimal value around $g^{*}(s_2)$ than around $g^{*}(s_1).$ This means that the resulting optimal distribution will depend on the entire range of f(g, s). The colored area in Figure 3E corresponds to the support of p(g, s) = p(g|s)p(s), and 〈f(g, s)〉 would correspond of the sum of the fitness values in this area weighted by p(g, s).

FIGURE 3

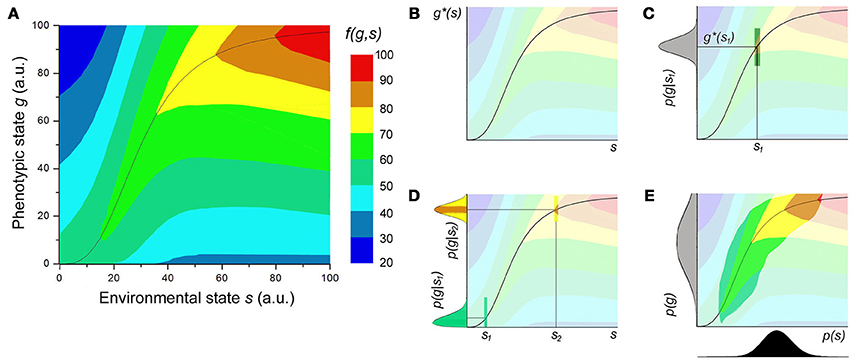
Figure 3. Graphical representation of the definitions. (A) Height map of a possible fitness function f (g,s) (as percentage of the maximum) of one dimensional environmental state and phenotypic state in arbitrary units. Inspired by Taylor et al.'s analysis [76] of Dekel and Alon's data [77]. (B) The function g* (s) is given by the phenotypic state with the highest fitness for each environmental state. (C) Because of intracellular stochasticity, even a fixed known environment can result in a distribution of phenotypes, given by p (g|s) (gray). The mean would not need to lie exactly on g* (s) because f (g,s) can drop off asymmetrically, and evolution would optimize <f (g,s)> (colored rectangle). (D) The shape of the distribution of phenotypes can change for different reasons: The noise in the distribution tends to increase with increasing mean for statistical reasons, but the pressure to reduce the width can vary (in this case, increase) with the curvature of f (g,s). This is represented by the colors indicating the fitness within the distribution. (E) If the environment also has a distribution, p (s) (black), the convolution of all p (g|s) with p (s) gives the total distribution of phenotypes, p (g). Note that this doesn't mean that p (g,s) is just the multiplication of probabilities, but it's shape will be determined in part by f (g,s). In this case 〈f(g, s)〉 corresponds to the height in the colored region, integrated with weight p (g,s).

The problem is thus reduced to an optimization under constrains which can in principle be solved through variational calculus. Intriguingly, when posed in this form the problem has a formal solution reminiscent of a familiar result from statistical mechanics:

$\begin{array}{ll}p(g|s)=\frac{p(g)}{Z(s)}{e}^{\lambda f(g,s)}& (4)\end{array}$

where Z(s) is the normalization for each environment and λ is the Lagrange multiplier for the condition of fixed average fitness. Since $p(g)=\sum _{s}p(g|s)p(s)$, this expression is an implicit solution. This problem has been solved as one of rate distortion functions in the field of communications [78]. However, this still requires an explicit form for the fitness function, which is difficult to obtain even for single variables for the gene and the environment.

There is one case where the fitness, functionally defined as the growth rate in a bacterial culture, has been determined experimentally. Dekel and Alon [77] manipulated the lac system of E. coli so that they could externally induce the expression independently of the lactose in the media. They then tested the growth rate at multiple combinations of gene expression and media, and thus from their data the fitness function f(g, s) can be obtained [76] in terms of the particular g (expression of the lac operon) and s (lactose concentration in the medium). It should be noted that this is not the long term limit for changing media as described before but simply the growth rate in a particular environment. Additionally, from their fitness they obtain the optimal expression g* (s) and show that over relatively short times of about 400 generations in a constant medium cells adjust their average expression to this level.

A Full Model of Adaptation

A difference between the approaches explained so far is that in one case the input is an intracellular signal c and in the other the conditioning variable is the actual state of the environment s. In reality a cell cannot optimize p(g|s) since it must work with its perception of the environment, so at least for the timescales of interest it can only optimize p(g|c), where c is a variable that correlates imperfectly with the environment. What c is depends on the particular case, and depends mostly on what we define as the system of interest. For example, in the case of chemotaxis in E. coli the environmental signal of interest s is the local concentration of a given small molecule, but the only information the cell has access to is the occupancy level of receptors for that molecule. While clearly correlated, these two quantities are not the same. Furthermore the expression of those receptors is under control of the cell, so c could vary from cell to cell in the same environment s. All of this needs to be included in a full model.

The effect of delays and memory, or more precisely, the fact that the current state of the cell can depend on previous states of itself and the environment should also be included. Their importance was shown experimentally by Lambert and Kussell [79], who measured the growth rates of E. coli in media that switched periodically between lactose and glucose as the carbon source, and confirmed that the growth rate even after changing media depended on what the cell had been exposed to before, in some cases almost a generation earlier.

A model incorporating all of these aspects is constructed by Rivoire and Leibler [73]. We present it in a hybrid of their notation and the one we have been using so far. Let p(s_t|s_t−1) be the probability of finding the environment in state s_t at time t given that it was in state s_t−1in the previous time. The discretization of the time works in general, but the underlying assumption here is that the environment is Markovian. Let π(g_t|g_t−1, c_t) be the conditional probability we had been calling p(g|c). This notation allows for the possibility of memory and avoids confusion with other probabilities. This is the part that will be optimized, and it is strongly constrained by any details known about the circuits controlling the expression of the relevant genes, including their stochasticity. Let q(c_t|g_t−1, s_t) be the probability of having c_t as the internal variable given that the state of the environment is s_t and the previous state of the cell was g_t−1.This allows for each cell to receive different information from the environment and have different internal representations of it; in the example of chemotaxis, g_t−1 would include the amount of surface receptors present. Finally, the fitness f (g_t, s_t) is interpreted as the expected number of descendants in the next generation given expression g_t in environment s_t. This is a stochastic process in itself. In this notation, a very general model of adaptation to changing environments can be constructed as shown in Figure 4A. The objective function for optimization would be the asymptotic growth rate of the total population size [71], ${\Lambda }_{p,f,q}(\pi )=\frac{1}{t}\langle \text{log}\left|N_t\right|\rangle$. This corresponds to the Lyapunov exponent in dynamics. Biologically, it can be understood as the growth rate of all cells in the population averaged over different time histories of the environment, for times that are long compared to the average time spent in a particular environment. It is a delicate definition, since the average depends on the statistics of the environmental states, but for reasonable conditions it can be shown to exist. Care should be taken when using it in more general cases, as when taking mutations explicitly into account. With this definition, the optimal strategy is simply the conditional probability $\widehat{\pi }(g_t|g_{t-1},c_t)=argmax{\Lambda }_{p,f,q}(\pi )$, which is the part that the cell can control.

FIGURE 4

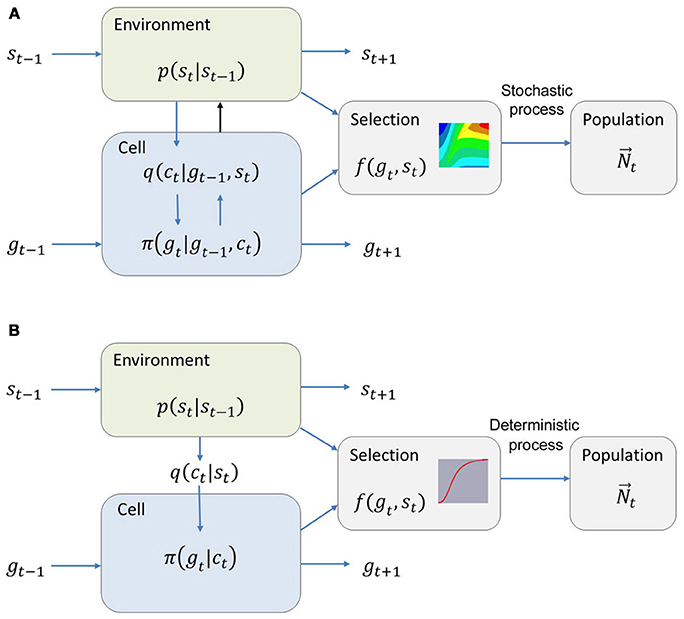
Figure 4. Schema of the models for a cell's response to changing environments. (A) Full model as described in the text. Note the black arrow, which represents the possibility that the cells will change their environment. (B) In the simplified system, all cells receive the same information from the environment, independently of their state. Cells have no memory, the instantaneous fitness is a multiplication factor rather than a probability and it is 0 except for one phenotypic state per environment. Based on Rivoire and Leibler [73].

Note that despite its generality this model does not include the possibility of the environment depending on the actions of the cells. This is an important omission, as it excludes for example a normal growth curve where the media changes with cell activity as well as cases like chemotaxis, where changing the local environment is the function of the circuit. This point is exemplified in the famous evolution experiments of Lenski and Travisano [9] where a population cell is evolved over thousands of generations in media that changes daily through depletion by the population and subsequent reinoculation in fresh media. As shown in detail in similar experiments by Oxman et al. [80], shorter lag times appear earlier than faster growth rates, because it doesn't help to be able to grow faster if in the meantime a competing mutant has depleted the media. This kind of effect could not be predicted by the present model.

Analytic Solution for a Simplified Model

The full model cannot be solved in general, but Rivoire and Leibler follow a very meticulous procedure of starting with multiple simplifying conditions to obtain a simple analytical result and then exploring the consequences of successively lifting some of those conditions. The main insights from a simplified model were obtained previously by Donaldson-Matasci et al. [72], in an engaging article where they emphasize the parallels with the use of information theory in ecology. We present them in the context of the full model because it makes the conditions and limitations of the simple model clearer.

The first condition is that the stochasticity in reproduction is ignored, so that f (g_t, s_t) is simply the number of descendants in the next generation for a cell of phenotype g_t. This greatly simplifies the definition of the long term growth rate of the population, which will determine the objective function of the optimization, but explicitly excludes the possibility of extinction. The second simplifying condition is that cells have no memory, π(g_t|g_t−1, c_t) = π(g_t|c_t). This excludes the long term maintenance of subpopulations as in the case of persistence or differentiation. The third simplifying condition is that the information that can be obtained from the environment is the same for all cells, q(c_t|g_t−1, s_t) = q(c_t|s_t). This excludes the possibility of cells controlling their sensing mechanisms through feedback as in chemotaxis. The fourth simplifying condition is that there is the same number of possible states for the environment and the cell, with only one phenotypic state per environment where cells can grow, f(g_t, s_t) = 0 except for a single pair (g_t, s_t) per environment. We call s_g the environment corresponding to a given phenotype in these pairs. While clearly non-biological, this last condition is necessary for obtaining simple analytical solutions and could in principle be lifted at the expense of cumbersome calculations without changing many of the insights from the paper. Note also that using a discrete, small number of phenotypic states is justified by the results of section Information Content of Gene Expression. The system described by all of these conditions is a much simpler one, summarized in Figure 4B.

Our initial questions can be fully answered in this simplified model: the best strategy in this case is given simply by Bayesian inference. If the only information a cell population had about the environment was the steady state distribution p(s), the best strategy would be proportional betting [81]: to assign the phenotypic states proportionally to the probability of the corresponding environmental state, ${\widehat{\pi }}_0(g)=p(s)$. A classic example is betting on horse races: if you know the probability of winning for each horse and assuming proportional payoffs, you might consider betting all on the horse with the best chance. That would maximize your expected payoff for a single game. But if you want to play many times, that strategy would result almost certainly in you losing everything after a few races. A better long term strategy would be to bet a bit on the other horses to ensure that you can't lose all in a single game. But you would not bet equal amounts on all horses; if the odds are fair the amount should be proportional to the chance each horse has of winning. This intuition was formalized by Kelly [81], who showed that not only is proportional betting the optimal strategy even for unfair odds but that using it your money would grow exponentially with a rate limited by the amount of information you have about the horses.

When a signal c_t is present, the cells can estimate better the current state of the environment, and the best guess for each state is given by a Bayesian estimate, giving rise to conditional proportional betting,

$\begin{array}{ll}\widehat{\pi }(g|c)=\frac{p(s_g)q(c|s_g)}{q(c)}& (5)\end{array}$

where $q(c)=\sum _{s}q(c|s)p(s)$. As the authors point out, this problem has close equivalents in finance and other areas. In the horse race example, this would be equivalent to knowing that the probabilities of each horse winning depend on the jockeys, so you would adjust your bets every race depending on the current jockeys. In both cases mentioned, the cells need to have knowledge of the steady state distributions. If that information can be genetically encoded, the optimization of the long term growth rate insures that evolution would select the mutants with the encoded distribution closest to reality. It is in this sense that evolution can be thought of as the long term process of encoding information about external conditions in the DNA.

The second question, about the value of information, can also be directly answered here: since those two strategies correspond to the best possible outcomes with and without information about the environment, the difference in the objective function is the value of the information acquired. In this case

$\begin{array}{ll}{\Lambda }_{p,f,q}(\widehat{\pi })-{\Lambda }_{p,f,0}({\widehat{\pi }}_0)=I(c,s),& (6)\end{array}$

the mutual information. While this is valid only for an oversimplified model, it is remarkable that the issue mentioned in the introduction about the difference between the amount of information and the value of information completely disappears: they are in this case the same.

In the paper, Rivoire and Leibler obtain various corrections for this result, usually as bounds, when the simplifying assumptions are relaxed, moving back toward the full model. Two points in particular are worth mentioning here: the first is that allowing cells to have memory changes the relevant quantity from the mutual information to the directed information. The second point is that while the calculations presented here compare optimal strategies under different amounts of information, the formalism permits the calculation of the cost of using a suboptimal strategy π. This is important because as mentioned before, there's no guarantee that the population has attained optimality, and for evolutionary experiments it would be useful to predict the changes in growth rate as the cells change their strategy to adapt to a new medium. Remarkably, this cost can be expressed as another information theoretical quantity, the relative entropy or Kullback-Leibler divergence [82]:

$\begin{array}{l}{\Lambda }_{p,f,q}(\widehat{\pi }){-\Lambda }_{p,f,q}(\pi )=D_{KL}(\widehat{\pi }||\pi )\\ =-{\displaystyle \sum _{g,c}}\widehat{\pi }(g|c)log\left(\frac{\pi (g|c)}{\widehat{\pi }(g|c)}\right)\ge 0& (7)\end{array}$

The main insight from these results is that under certain conditions the decision theoretical value of information in an evolutionary context can be written explicitly in terms of information theoretical quantities. While no equivalent analytical result exists for the full model, it seems plausible that the conflict between the information theory and decision theory approaches can be solved by a quantitative model with the long term population growth rate as the function to be optimized.

Discussion and Outlook

The use of information theory tools has been profitable in many branches of biology, and advances in the study of stochasticity in gene expression and microbial growth have provided new test beds for its applicability. Fundamental questions about how organisms manage information on their environments and how evolution can optimize their strategies to respond to uncertain environments can be posed in a more limited but better defined form as they apply to the growth of microorganisms in changing media. This allows precise mathematical formulations that can provide general insight as well as providing experimental means of testing those predictions. In this context, one overarching doubt about the applicability of formal measures of information to situations where the semantic content of a message should be paramount is elegantly resolved by showing an explicit connection between the information theory measure and the decision-theory value of information. Furthermore, increasing numbers of experimental studies are allowing ever more precise questions to be asked and the generality of any claims to be directly explored.

Despite these advances, many open questions remain. Reasonably complete models are very hard to solve analytically, so it remains to be seen what extensions of the results for simple models are possible. Given the increasing parallels with problems in communication and finance, there is large scope for collaborations with specialists in those areas. The tools reviewed here are necessary because for it to be approachable by interdisciplinary collaborations, a formal description of the problem is needed. Since the analytical results presented here give clear predictions but for limited situations, those cases need to be tested experimentally to ensure any further advances rest on a solid foundation. In particular, we propose to expose populations to changing media in different runs where instead of the (average) period the transition probabilities are changed, over a timescale of hundreds of generations. If done for a well characterized system like the lac operon, this would allow for a direct test of the adaptive changes in $\widehat{\pi }(g|c)$.

A longer term goal could be the incorporation of information as a standard quantity alongside mass and energy in optimization arguments in other fields such as behavioral ecology. While much work would need to be done in solidifying and expanding the results mentioned here before they can be used across fields, it could be extremely fruitful. Some of the most powerful types of findings in physical systems are conserved quantities, as they provide the basic limitations to any dynamical process. Should information flow solidify into a similar rule in biology, it could greatly expand the number of cases where an optimization procedure can be used predictively.

Author Contributions

JP wrote the article, and all authors conducted background research and edited the final version.

Funding

This work was partially funded by the Faculty of Science at Universidad de los Andes.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Quastler H. Essays on the Use of Information Theory in Biology. Urbana: University of Illinois Press (1953).

Google Scholar

2. Yang Z, Bielawski JP. Statistical methods for detecting molecular adaptation. Trends Ecol Evol. (2000) 15:496–503. doi: 10.1016/S0169-5347(00)01994-7

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Reiss MJ. Optimization theory in behavioural ecology. J Biol Educ. (1987) 21:241–7. doi: 10.1080/00219266.1987.9654909

CrossRef Full Text | Google Scholar

4. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

5. Howard R. Information value theory. IEEE Trans. Syst. Sci. Cybern. (1966) SSC-2:22–6. doi: 10.1109/TSSC.1966.300074

CrossRef Full Text | Google Scholar

6. Toprak E, Veres A, Yildiz S, Pedraza JM, Chait R, Paulsson J, et al. Building a morbidostat: an automated continuous-culture device for studying bacterial drug resistance under dynamically sustained drug inhibition. Nat Protoc. (2013) 8:555. doi: 10.1038/nprot.2013.021

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Shoresh N, Hegreness M, Kishony R. Evolution exacerbates the paradox of the plankton. Proc Natl Acad Sci USA. (2008) 105:12365–9. doi: 10.1073/pnas.0803032105

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature (2000) 403:339–42. doi: 10.1038/35002131

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Lenski RE, Travisano M. Dynamics of adaptation and diversification: a 10,000-generation experiment with bacterial populations. Proc Natl Acad Sci USA. (1994) 91:6808–14. doi: 10.1073/pnas.91.15.6808

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Cohen D. Optimizing reproduction in a randomly varying environment. J Theor Biol. (1966) 12:119–29. doi: 10.1016/0022-5193(66)90188-3

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Thattai M, van Oudenaarden A. Stochastic gene expression in fluctuating environments. Genetics (2004) 167:523–30. doi: 10.1534/genetics.167.1.523

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Slatkin M. Hedging one's evolutionary bets. Nature (1974) 250:704.

Google Scholar

13. Avlund M, Dodd IB, Semsey S, Sneppen K, Krishna S. Why do phage play dice? J Virol. (2009) 83:11416–20. doi: 10.1128/JVI.01057-09

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Acar M, Mettetal JT, van Oudenaarden A. Stochastic switching as a survival strategy in fluctuating environments. Nat Genet. (2008) 40:471–5. doi: 10.1038/ng.110

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Paulsson J. Summing up the noise in gene networks. Nature (2004) 427:415. doi: 10.1038/nature02257

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Fraser HB, Hirsh AE, Giaever G, Kumm J, Eisen MB. Noise minimization in eukaryotic gene expression. PLoS Biol. (2004) 2:e137. doi: 10.1371/journal.pbio.0020137

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Raser JM, O'Shea EK. Noise in gene expression: origins, consequences, and control. Science (2005) 309:2010–3. doi: 10.1126/science.1105891

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Blake WJ, Balázsi G, Kohanski MA, Isaacs FJ, Murphy KF, Kuang Y, et al. Phenotypic consequences of promoter-mediated transcriptional noise. Mol Cell (2006) 24:853–65. doi: 10.1016/j.molcel.2006.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Lewis K. Persister cells. Annu Rev Microbiol. (2010) 64:357–72. doi: 10.1146/annurev.micro.112408.134306

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. Bacterial persistence as a phenotypic switch. Science (2004) 305:1622–5. doi: 10.1126/science.1099390

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Maynard-Smith J. Optimization theory in evolution. Annu Rev Ecol Syst. (1978) 9:31–56. doi: 10.1146/annurev.es.09.110178.000335

CrossRef Full Text | Google Scholar

22. Gould SJ, Lewontin RC. The Spandrels of San Marco and the panglossian paradigm: a critique of the adaptationist programme. Proc R Soc Lond B Biol Sci. (1979) 205:581–98. doi: 10.1098/rspb.1979.0086

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Maynard-Smith J. The concept of information in biology. Philos Sci. (2000) 67:177–94. doi: 10.1086/392768

CrossRef Full Text | Google Scholar

24. Cerullo MA. The problem with phi: a critique of integrated information theory. PLoS Comput Biol. (2015) 11:e1004286. doi: 10.1371/journal.pcbi.1004286

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sarkar S, editor. Biological information: a skeptical look at some central dogmas of molecular biology. In: The Philosophy and History of Molecular Biology. Dordrecht: Kluwer Academic Publishers (1996). p. 187–231.

26. Gadiraju S, Vyhlidal CA, Leeder JS, Rogan PK. Genome-wide prediction, display and refinement of binding sites with information theory-based models. BMC Bioinformatics (2003) 4:38. doi: 10.1186/1471-2105-4-38

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Rieke F, Warland D, Deruytervansteveninck R, Bialek W. Spikes : Exploring the Neural Code. The MIT Press(1999).

28. Schneider TD, Stormo GD, Gold L, Ehrenfeucht A. Information content of binding sites on nucleotide sequences. J Mol Biol. (1986) 188:415–31. doi: 10.1016/0022-2836(86)90165-8

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Savir Y, Kagan J, Tlusty T. Binding of transcription factors adapts to resolve information-energy tradeoff. J Stat Phys. (2016) 162:1383–94. doi: 10.1007/s10955-015-1388-5

CrossRef Full Text | Google Scholar

30. Seoane LF, Solé RV. Information theory, predictability and the emergence of complex life. R Soc Open Sci. (2018) 5:172221. doi: 10.1098/rsos.172221

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Adami C. The use of information theory in evolutionary biology. Ann N Y Acad Sci. (2012) 1256:49–65. doi: 10.1111/j.1749-6632.2011.06422.x

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Dimitrov AG, Lazar AA, Victor JD. Information theory in neuroscience. J Comput Neurosci. (2011) 30:1–5. doi: 10.1007/s10827-011-0314-3

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Massey JL. Causality, feedback, and directed information. In: Proceedings IEEE International Symposium on Information Theory. Honolulu, HI (1990). p. 303–5.

Google Scholar

34. Fisher RA. On the mathematical foundations of theoretical statistics. Phil Trans R Soc Lond A (1922) 222:309–68. doi: 10.1098/rsta.1922.0009

CrossRef Full Text

35. Kinney JB, Atwal GS. Equitability, mutual information, and the maximal information coefficient. Proc Natl Acad Sci USA. (2014) 111:3354–9. doi: 10.1073/pnas.1309933111

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Day EK, Sosale NG, Lazzara MJ. Cell signaling regulation by protein phosphorylation: a multivariate, heterogeneous, and context-dependent process. Curr Opin Biotechnol. (2016) 40:185–92. doi: 10.1016/j.copbio.2016.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Farkash-Amar S, Zimmer A, Eden E, Cohen A, Geva-Zatorsky N, Cohen L, et al. Noise genetics: inferring protein function by correlating phenotype with protein levels and localization in individual human cells. PLoS Genet. (2014) 10:e1004176. doi: 10.1371/journal.pgen.1004176

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Massicotte R, Whitelaw E, Angers B. DNA methylation: a source of random variation in natural populations. Epigenetics (2011) 6:421–7. doi: 10.4161/epi.6.4.14532

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Cheong R, Rhee A, Wang CJ, Nemenman I, Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science (2011) 334:354–8. doi: 10.1126/science.1204553

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Thomas PJ, Eckford AW. Capacity of a simple intercellular signal transduction channel. arXiv:1411.1650 (2013).

Google Scholar

41. Micali G, Endres RG. Bacterial chemotaxis: information processing, thermodynamics, and behavior. Curr Opin Microbiol. (2016) 30, 8–15. doi: 10.1016/j.mib.2015.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Sprinzak D, Elowitz MB. Reconstruction of genetic circuits. Nature (2005) 438:443–8. doi: 10.1038/nature04335

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Almalki SG, Agrawal DK. Key transcription factors in the differentiation of mesenchymal stem cells. Differ Res Biol Divers. (2016) 92:41–51. doi: 10.1016/j.diff.2016.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Dequéant M-L, Pourquié O. Segmental patterning of the vertebrate embryonic axis. Nat Rev Genet. (2008) 9:370–82. doi: 10.1038/nrg2320

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Feinberg AP, Irizarry RA. Stochastic epigenetic variation as a driving force of development, evolutionary adaptation, and disease. Proc Natl Acad Sci USA. (2010) 107:1757–64. doi: 10.1073/pnas.0906183107

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Raj A, van Oudenaarden A. Stochastic gene expression and its consequences. Cell (2008) 135:216–26. doi: 10.1016/j.cell.2008.09.050

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Okumus B, Landgraf D, Lai GC, Bakshi S, Arias-Castro JC, Yildiz S, et al. Mechanical slowing-down of cytoplasmic diffusion allows in vivo counting of proteins in individual cells. Nat Commun. (2016) 7:11641. doi: 10.1038/ncomms11641

CrossRef Full Text | Google Scholar

48. Raj A, Peskin CS, Tranchina D, Vargas DY, Tyagi S. Stochastic mRNA synthesis in mammalian cells. PLoS Biol. (2006) 4:e309. doi: 10.1371/journal.pbio.0040309

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Tang F, Barbacioru C, Wang Y, Nordman E, Lee C, Xu N, et al. mRNA-Seq whole-transcriptome analysis of a single cell. Nat Methods (2009) 6:377–82. doi: 10.1038/nmeth.1315

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Taniguchi Y, Choi PJ, Li G-W, Chen H, Babu M, Hearn J, et al. Quantifying, E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science (2010) 329:533–8. doi: 10.1126/science.1188308

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Wang P, Robert L, Pelletier J, Dang WL, Taddei F, Wright A, et al. Robust growth of Escherichia coli. Curr Biol. (2010) 20:1099–103. doi: 10.1016/j.cub.2010.04.045

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Brophy JAN, Voigt CA. Principles of genetic circuit design. Nat Methods (2014) 11:508–20. doi: 10.1038/nmeth.2926

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Isalan M, Lemerle C, Serrano L. Engineering gene networks to emulate Drosophila embryonic pattern formation. PLoS Biol. (2005) 3:e64. doi: 10.1371/journal.pbio.0030064

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Mahner M, Bunge M. Foundations of Biophilosophy. Berlin; Heidelberg: Springer Berlin Heidelberg (1997).

Google Scholar

55. Milo R, Phillips R. Cell Biology by the Numbers. New York, NY: Garland Science (2015).

PubMed Abstract | Google Scholar

56. Paulsson J. Models of stochastic gene expression. Phys Life Rev. (2005) 2:157–75. doi: 10.1016/j.plrev.2005.03.003

CrossRef Full Text | Google Scholar

57. Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science (2002) 297:1183–6. doi: 10.1126/science.1070919

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Pedraza JM, van Oudenaarden A. Noise propagation in gene networks. Science (2005) 307:1965–9. doi: 10.1126/science.1109090

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Becskei A, Séraphin B, Serrano L. Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion. EMBO J. (2001) 20:2528–35. doi: 10.1093/emboj/20.10.2528

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Singh A. Negative feedback through mRNA provides the best control of gene-expression noise. IEEE Trans Nanobiosci. (2011) 10:194–200. doi: 10.1109/TNB.2011.2168826

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Ozbudak EM, Thattai M, Lim HN, Shraiman BI, Van Oudenaarden A. Multistability in the lactose utilization network of Escherichia coli. Nature (2004) 427:737–40. doi: 10.1038/nature02298

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Acar M, Becskei A, van Oudenaarden A. Enhancement of cellular memory by reducing stochastic transitions. Nature (2005) 435:228–32. doi: 10.1038/nature03524

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Tkačik G, Callan CG, Bialek W. Information capacity of genetic regulatory elements. Phys Rev E Stat Nonlin Soft Matter Phys. (2008) 78(1 Pt 1):011910. doi: 10.1103/PhysRevE.78.011910

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Prindle A, Hasty J. Making gene circuits sing. Proc Natl Acad Sci USA. (2012) 109:16758–9. doi: 10.1073/pnas.1214118109

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Tishby N, Pereira FC, Bialek W. The information bottleneck method. arXiv:physics/0004057 (2000).

Google Scholar

66. Haccou P, Iwasa Y. Optimal mixed strategies in stochastic environments. Theor Popul Biol. (1995) 47:212–43. doi: 10.1006/tpbi.1995.1009

CrossRef Full Text | Google Scholar

67. Sasaki A, Ellner S. The evolutionarily stable phenotype distribution in a random environment. Evol Int J Org Evol. (1995) 49:337–50. doi: 10.1111/j.1558-5646.1995.tb02246.x

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Kussell E, Leibler S. Phenotypic diversity, population growth, and information in fluctuating environments. Science (2005) 309:2075–20. doi: 10.1126/science.1114383

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Rosenfeld N, Elowitz MB, Alon U. Negative autoregulation speeds the response times of transcription networks. J Mol Biol. (2002) 323:785–93. doi: 10.1016/S0022-2836(02)00994-4

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Dörr T, Lewis K, Vulić M. SOS response induces persistence to fluoroquinolones in Escherichia coli. PLoS Genet (2009) 5:e1000760. doi: 10.1371/journal.pgen.1000760

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Lewontin RC, Cohen D. On population growth in a randomly varying environment. Proc Natl Acad Sci USA. (1969) 62:1056–60. doi: 10.1073/pnas.62.4.1056

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Donaldson-Matasci MC, Bergstrom CT, Lachmann M. The fitness value of information. Oikos Cph Den. (2010) 119:219–30. doi: 10.1111/j.1600-0706.2009.17781.x

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Rivoire O, Leibler S. The value of information for populations in varying environments. J Stat Phys. (2011) 142:1124–66. doi: 10.1007/s10955-011-0166-2

CrossRef Full Text | Google Scholar

74. Cohen SE, Golden SS. Circadian rhythms in cyanobacteria. Microbiol Mol Biol Rev. (2015) 79:373–85. doi: 10.1128/MMBR.00036-15

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Lambert G, Chew J, Rust MJ. Costs of clock-environment misalignment in individual cyanobacterial cells. Biophys J. (2016) 111:883–91. doi: 10.1016/j.bpj.2016.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Taylor SF, Tishby N, Bialek W. Information and fitness. arXiv:0712.4382 (2007).

Google Scholar

77. Dekel E, Alon U. Optimality and evolutionary tuning of the expression level of a protein. Nature (2005) 436:588–92. doi: 10.1038/nature03842

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Blahut RE. Computation of channel capacity and rate distortion functions. IEEE Trans Info Thy. (1972) 18:460–73. doi: 10.1109/TIT.1972.1054855

CrossRef Full Text | Google Scholar

79. Lambert G, Kussell E. Memory and fitness optimization of bacteria under fluctuating environments. PLOS Genet. (2014) 10:e1004556. doi: 10.1371/journal.pgen.1004556

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Oxman E, Alon U, Dekel E. Defined order of evolutionary adaptations: experimental evidence. Evol Int J Org Evol. (2008) 62:1547–54. doi: 10.1111/j.1558-5646.2008.00397.x

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Kelly JL. A new interpretation of information rate. Bell Syst Tech J. (1956) 35:917–26. doi: 10.1002/j.1538-7305.1956.tb03809.x

CrossRef Full Text | Google Scholar

82. Kullback S, Leibler RA. On information and sufficiency. Ann Math Stat. (1951) 22:79–86. doi: 10.1214/aoms/1177729694

CrossRef Full Text | Google Scholar