- Institute for Mechanics of Materials and Structures, TU Wien–Vienna University of Technology, Vienna, Austria
Both the shape of bone organs and the micro-architecture of bone tissue are significantly influenced by the prevailing mechanical loading. In this context, several of the most striking and hence also most debated issues relate to the question how bone is actually able to sense and process its mechanical environment. Among other stimuli, it has been hypothesized that the macroscopic mechanical loading induces pressure gradients in the pore spaces of bone tissue, and that these pressure gradients lead to fluid flow exciting the cells that are located in the pore spaces. Since in vitro tests confirmed that cells subjected to the flow of the surrounding fluid indeed respond in form of altered expression activities, the scientific community has in large part embraced the fluid flow-hypothesis. However, direct experimental evidence as to the actual occurrence of sufficiently fast fluid flow (in order to reach the cell responses observed in vitro) has not been attained so far. In this paper, a multiscale modeling strategy is presented (inspired by the well-established concept of continuum micromechanics), allowing for upscaling (or homogenization) of the fluid flow contributions in the canalicular, lacunar, and vascular pores in terms of a corresponding macroscopic permeability of bone tissue. The same model also allows for proceeding the opposite way, namely for downscaling macroscopically acting pressure gradients to the pore levels. Thus, physiologically relevant mechanical loading conditions can be related straightforwardly to the correspondingly arising pore-scale pressure gradients, and, through considering the resulting pressure gradients in suitable transport laws, also to related fluid velocities. When comparing the such computed fluid velocities with the fluid velocities that were shown to efficiently excite bone cells in vitro, it turns out that pressure-driven fluid flow in the canalicular pores is probably not a potent mechanical stimulus for osteocytes, whereas fluid flow in the vascular pores may indeed reach the required fluid velocities and hence excite the therein residing osteoblasts, osteoclasts, and bone lining cells. In conclusion, this paper provides important, unprecedented insights as to the observation scale-specific cellular mechanosensation in bone.
1. Introduction
Given that the pore spaces of bone are inhabited by biological cells (as well as by hormones, growth factors, and numerous further proteins) [1–3] bone is standardly considered to be a living tissue. The cells, namely osteoclasts, osteoblasts, lining cells, and osteocytes, all of which are often referred to as bone cells, specifically respond to changes of both biochemical and mechanical signals occurring in their immediate environments, in form of decreasing or increasing cell (expression) activities. This implies that bone cells must be equipped with some kind of sensors which enable them to quantitatively measure the aformentioned signals.
Here, we focus on the latter of the two above-introduced types of regulatory signals sensed by bone cells, namely their mechanical stimulation. In this context, one of the major (yet still unresolved) scientific challenges concerns the exact mechanisms by which bone cells are actually able to sense their mechanical environment and process changes thereof. In the late 1980s and early 1990s, respectively, findings regarding the stimulation of different types of cells by fluid flow-induced shear stresses, including endothelial cells [4, 5], were hypothesized to be equally valid for the cells located in bone. The works of Reich and colleagues can be regarded as particularly seminal, confirming that fluid shear stress acting onto osteoblasts can effectively increase the levels of intracellular cyclic adenosine monophosphate (cAMP), prostaglandin E2, and inosital triphosphate, altogether indicating increased osteoblast activity [6, 7]. While fluid shear stress was initially thought to be a potential mechanical stimulus sensed by osteoblasts, see also [8, 9], it did not take long until the hypothesis was advocated that osteocytes (which are considered to be the mechanosensors in bone [10–12]) may be excited by fluid flow-induced shear stresses as well [13]. Klein-Nulend and co-workers were among the first to show the remarkable responsiveness of osteocytes isolated from embryonic chicken and mouse calvariae when subjected to fluid flow (in terms of expression of nitric oxide and prostaglandin E2) [14, 15].
On the one hand, there is no reason to doubt, or even contest these and similar experimental results [16–20] concerning the responsiveness of osteoblasts and osteoctyes to fluid shear stress. On the other hand, however, it seems to be of paramount importance to tackle the question whether the fluid flow conditions considered in the aforementioned in vitro studies also occur in vivo–that is, in the pore spaces of bone in response to physiologically reasonable loading conditions. Addressing this issue experimentally is very challenging, and various experimental modalities have been used for that purpose. In order to study transport processes in the bone marrow of cancellous bone, e.g., magnetic resonance imaging (MRI) techniques have been used; such as diffusion-weighted MRI [21–25], or perfusion-weighted MRI [21, 22]. Transport processes in the network of lacunar and canalicular pores, on the other hand, have been studied mainly based on injecting suitable tracer molecules, and on visualizing, after a certain amount of time (optionally involving mechanical loading), the distribution of the tracer molecules, e.g., by means of fluorescence recovery after photobleaching (FRAP) [26–28]. While the results of the referenced and similar studies are indeed insightful, using them for answering the previously posed question—Do the fluid flow conditions prescribed in in vitro studies also occur in vivo, under physiological loading conditions?—remains problematic. On the one hand, to the best of the authors's knowledge, the aforementioned MRI-based experimental techniques have not yet been applied to study transport processes in the lacunar-canalicular network. And, on the other hand, it may be difficult to clearly distinguish between diffusive and perfusive transport; e.g., the diffusion coefficient in the bone pore fluid may change upon mechanical excitation, see the respective discussion in Scheiner et al. [29] p. 22.
In this paper, an alternative strategy is proposed, based on establishing mathematical relations between the macroscopic mechanical loading (of arbitrary direction and magnitude) and the correspondingly arising velocities of the fluid contained in the various pore systems of bone tissue. For this purpose, the concept of continuum micromechanics, which has already proven remarkably reliable for estimating various properties of bone tissue, including stiffness [30–33], strength [34, 35], viscoelasticity [36], poroelasticity [37], and permeability [38], is utilized. After reviewing the fundamentals of micromechanics, see section 2.1, adaption of continuum micromechanical homogenization for permeability upscaling and pressure gradient downscaling is briefly described in section 2.2. Section 2.3 is then devoted to the development of a multiscale model of bone tissue, on the basis of which the equations presented in section 2.2 are correspondingly specified, see sections 2.4.1–2.4.5, followed by a summary of the required input data, see section 2.5. As regards numerical studies, the multiscale model is first validated based on comparing model-predicted permeabilities to suitable experimental data, see section 3.1. Furthermore, downscaling of pressure gradients is performed, allowing for computation of pore-scale fluid flow velocities, see section 3.2. These velocities are then assessed in terms of their capability of stimulating bone cells, see section 3.3. The paper is concluded by a discussion of the key findings of this paper, of the strengths and limitations of the proposed model, and of potential follow-up future research directions, see section 4.
2. Materials and Methods
2.1. Introduction of Representative Volume Elements
In continuum micromechanics, a material is thought to be macro-homogenous, but micro-heterogenous. Considering an arbitrary volume element hosting such material, this volume element is representative in terms of the physical behavior of the contained material if its characteristic length, ℓRVE, is much larger than the characteristic size of the micro-heterogeneities, dRVE, within the RVE, i.e., ℓRVE ≫ dRVE [39–41]. In particular, ℓRVE must be (at least) 2–3 times larger than dRVE in order to comply with this requirement [42]. On the other hand, ℓRVE must be considerably smaller than the characteristic length of the geometry of a structure composed of the material defined on the RVE, , as well as of the loading acting onto such a structure, . The requirement is satisfyingly fulfilled as long as and , respectively, are (at least) 5 to 10 times larger than ℓRVE [43].
The microstructure of the material contained within a representative volume element (RVE) is typically too complex to describe in its entirety. Instead, quasi-homogeneous material phases are introduced. These material phases exhibit known physical properties, such as volume fractions, mechanical or transport properties, and a variety of different phase morphologies can be established, thereby allowing the introduction of different phase shapes, and interactions between the considered material phases. Continuum micromechanics enables the derivation of mathematical relations which reconcile these conditions, for the eventual estimation of macroscopic physical properties valid on the level of the RVE, based on the corresponding phase properties. This mathematical method is often referred to as homogenization, or upscaling.
Homogenization can be carried out in a sequential fashion if a material phase itself exhibits a heterogeneous microstructure. Then, an additional RVE can be introduced within the respective material phase [32]; the characteristic length of this new RVE, ℓRVE,2, must fulfill the requirement ℓRVE,2 ≤ dRVE, while the principle of scale separation demands that the characteristic length of the heterogeneities within the new RVE, dRVE,2, are again considerably smaller than ℓRVE,2, i.e., dRVE,2 ≪ ℓRVE,2. This leads to a multi-step homogenization scheme.
2.2. Theoretical Foundations of Permeability Upscaling and Pressure Gradient Downscaling
In the following, the concept of continuum micromechanical up- and downscaling, which was originally developed for studying mechanical properties of materials [40, 44], is adapted in order to derive permeability upscaling relations and pressure gradients downscaling relations.
In particular, analogously to classical continuum micromechanics [40, 44], an RVE is subjected to a homogeneous macroscopic pressure gradient, GRADpRVE, implying that at the surface of the RVE, ∂VRVE, microscopic pressures p obey the following boundary condition [45, 46]:
where x is the position vector. It can be shown [38] that Equation (1) leads to a pressure gradient averaging rule, reading as
where VRVE denotes the volume of the RVE. Furthermore, it is supposed that the RVE contains fluid which can move according to potentially arising pressure gradients, thereby following a transport law which can be considered to be the microscopic counterpart to the well-known Darcy law [38, 45]. Hence, the velocity of the fluid at position x, v(x), is defined as
with K(x) being the position-dependent permeability tensor. The fluid is considered to be incompressible and required to fulfill, throughout the entire RVE, mass conservation, implying
Equation (4) allows to derive the velocity averaging relation, see Abdalrahman et al. [38] and Damrongwiriyanupap et al. [47] for details, reading as
Combining Equations (2–5) allows to derive the Darcy law in its classical, macroscopic format [38],
with the homogenized permeability of the RVE defined as
with A(x) as the so-called localization or concentration tensor (originally introduced in the context of linear elasticity [40, 48]), allowing for linearly relating macro- and microscopic pressure gradients,
At this point, it is expedient to simplify the microstructure of the RVE, in terms of introducing material phases and corresponding volume fractions instead of considering the microstructure in minute detail, see section 2.1. Then, the fields of permeability and concentration tensors, K(x) and A(x), can be replaced by corresponding phase-specific tensors, Ki and Ai, requiring to accordingly rewrite Equations (8, 9), yielding
with fi as volume fraction of phase i, and
Finally, the phase-specific pressure gradient concentration tensor Ai is defined based on adapting Eshelby's matrix-inclusion or inhomogeneity problem [49], see also [46],
where 1 is the second-order unit tensor, and is the inhomogeneity tensor relating to phase i. The inhomogeneity tensor depends on the shape of the inhomogeneity, as well as on the permeability of the matrix in which it is embedded, Kmat. Detailed descriptions of how is derived can be found elsewhere [38, 41, 44].
2.3. Multiscale Model of Bone Tissue
Bone is a hierarchically built-up material, made largely out of collagen, hydroxyapatite matrix, and water, and also contains bone marrow, cells, as well as non-collagenous proteins. Two different types of bony structures can be identified in bone organs: The dense and compact cortical bone often forming the shell of bone organs, and the more loosely packed and highly porous trabecular or cancellous bone [50]. A graphical illustration of the hierarchical organization of bone can be found in [29].
Cancellous bone lines the walls of the medullary cavity, where the bone marrow is stored, and has a high surface area due to its inter-trabecular porosity, ranging from 50 to 90 % [51]. Cortical bone, on the other hand, is less porous, with a vascular porosity of a few (typically around 5 %) percent in young adults [52–54]; in the course of aging, the vascular porosity in cortical bone may increase significantly, up to 35% [55]. Vascular pores, as the name already implies, host blood vessels in a branched structure, the main larger branches being aligned along the bone axis called Haversian canals and the smaller Volkmann canals, which are often imagined to be oriented more or less perpendicular to the Haversian canals [56]. The next smaller pores are the lacunae, hosting the osteocytic cell bodies. The lacunar porosity lies within a range of approximately 1.5 to 10 % [57–60], and the diameter of the lacunar pores amounts to a few microns [61, 62]. The even smaller, cylindrically shaped canaliculi are a few hundred nanometers in diameter [63–65], and exhibit a volume fraction of approximately 1–3 % [60, 66, 67]. Remarkably, the canaliculi contain the cell processes of the osteocytes. As canaliculi occur in form of a dense network embedded in the extracellular bone matrix, they allow for effective communication between osteocytes.
At even lower observation scales, further types of pore spaces can be discerned, namely the space between the hydroxyapatite crystals (together forming the so-called extrafibrillar space), and the intramolecular pore space found between collagen molecules, (see e.g., [32, 34, 68, 69]). Both intercrystalline and intermolecular pore spaces are however irrelevant for the work presented in this paper, and are hence neglected subsequently.
Considering the hierarchical organization of bone with regard to the principle of scale separation introduced in section 2.1, it seems reasonable to represent bone tissue by means of three RVEs, see Figure 1:
• The RVE of extralacunar bone matrix consists of canalicular pores, represented as cylindrical, arbitrarily oriented inclusions, which are interpenetrating, exhibiting a characteristic length of m, and of the impermeable extracanalicular bone matrix phase, sometimes referred to as extracellular bone matrix. For the sake of simplicity, the extracanalicular phase is considered to be of spherical shape. Together, these two material phases form the polycrystalline extralacunar matrix which exhibits a characteristic length of m, thereby fulfilling ℓexlac ≫ dcan.
• Together with the lacunar pores (which are approximated as spherical material phase), the material defined on the first RVE, extralacunar bone matrix, forms extravascular bone matrix. The characteristic length of this RVE lies within the range of m, while the characteristic length of the lacunae is m [29, 32–34].
• On an even larger scale of observation, macroscopic bone tissue can be identified at a characteristic length of m. It is composed of vascular pores, represented as cylindrical inhomogeneities with a characteristic length of m, and the extravascular bone matrix. In order to cover different types of bone tissue, such as (osteonal) cortical and trabecular bone, as well as the transition zone in-between, that is endocortical bone, two morphologies are considered. Firstly, the vascular pores are introduced with a preferred, namely longitudinal orientation, and the extravascular bone material acts as a matrix phase hosting the pores as inclusions. This matrix-inclusion-type morphology reflects the situation in cortical bone, if Haversian canals are the dominant type of pore space, and Volkmann canals are negligibly scarce. Secondly, it is considered that vascular pores may also form an interpenetrating pore network of arbitrarily oriented inclusions (which may reflect the situation in endocortical or trabecular bone, but also in cortical bone with more frequent occurrence of Volkmann canals). The extravascular material are then modeled as spherical inclusions in-between.
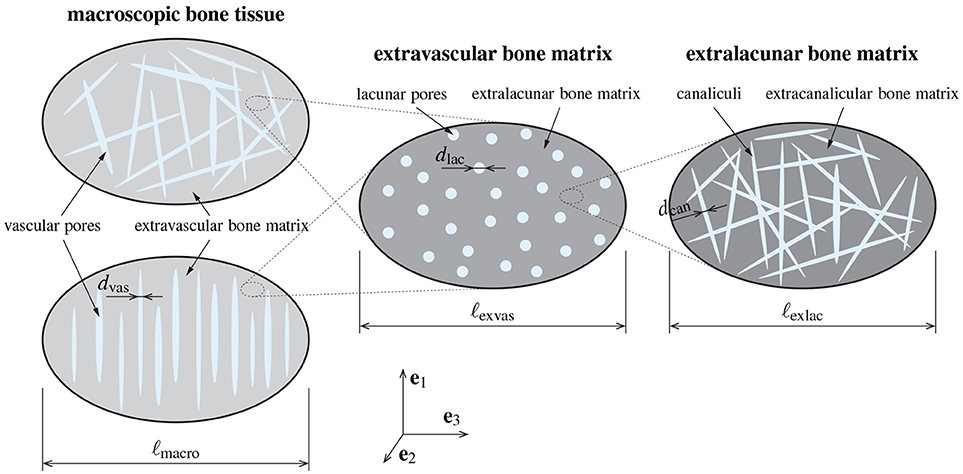
Figure 1. Model representation based on which permeability upscaling and pressure gradient downscaling is performed, including the RVE of macroscopic bone tissue (left), containing vascular pores (oriented arbitrarily or longitudinally) and extravascular matrix, the RVE of extravascular bone material (middle), containing lacunar pores and the extralacunar bone matrix, and the RVE of extralacunar bone material (right), containing canalicular pores and extracanalicular bone matrix.
Notably, similar model representations were used previously in the field of bone (fluid) mechanics, e.g., in order to homogenize bone stiffness [32, 70], poroelasticity [29, 33, 37, 71], viscoelasticity [36], strength [34], and the trabecular permeability [38]. All these works included substantial experimental validation, hence underpinning the soundness of the chosen model representation.
2.4. Derivation of Scaling Relations
Specializing Equations (9–11) for the sequence of RVEs introduced in section 2.3 yields a set of equations which allow, on the one hand, for upscaling the permeability from the length scales of single canaliculi, lacunae, and vascular pores to the length scale of macroscopic bone tissue, and, on the other hand, for downscaling pressure gradients from the length scale of macroscopic bone to the length scales of single vascular pores, lacunae, and canaliculi. The following sections 2.4.1–2.4.4 are devoted to explaining the aforementioned specializations, while the (partly lengthy) equations defining the resulting concentration and permeability tensors are provided in the Supplementary Material of this article.
2.4.1. Extralacunar Bone Matrix
Considering the morphology of the RVE of extralacunar bone matrix as defined in section 2.3, the concentration tensors related to the RVE-defining material phases, canalicular pores and extracanalicular bone matrix, follow from respective utilization of Equation (11), and read as
and
In Equations (12, 13), denotes the volume fraction of the canalicular pores quantified on the RVE of extralacunar bone matrix. It should be noted that, in Equations (12, 13) as well as subsequently, variable ϕ is chosen to represent pore space volume fractions (or porosities) instead of f (which was used in section 2.2), as is usually done in the field of poromechanics. Furthermore, and denote the inhomogeneity tensors of the (cylindrical) canalicular pores and the (spherical) extracanalicular bone matrix, both assumed to be embedded in the polycrystal-type extralacunar matrix, whereby the permeability of the latter is defined through tensor Kexlac = Kexlac1. The inhomogeneity tensors are defined according to the work of Abdalrahman et al. [38], reading as
with unit vectors es (oriented in direction of the cylindrical canaliculus), as well as et and eu (oriented orthogonal both to es and to each other) spanning the base frame of the cylindrical pore, and
As for the permeability tensor Kcan, taking into account pressure gradient-driven fluid flow in the canalicular pores, it is assumed that this fluid flow is appropriately described by the famous law postulated by Hagen [72] and Poiseuille [73], see also [74]. As demonstrated in Abdalrahman et al. [38] and Dormieux and Kondo [45], setting the velocity of the pore fluid equal to the velocity of a pore-scale, microscopic version of the Darcy law gives access to
where rcan is the radius of the canaliculus, and η is the dynamic fluid viscosity (see section 2.5 for some considerations concerning the numerical value of η). Note that Kcan is a Darcy-type, viscosity-afflicted permeability, with m2/(Pa·s) as standard unit, which should not be confused with the intrinsic permeability, which is usually measured in m2. As pointed out in section 2.3, the extracanalicular bone matrix is considered to be impermeable, hence Kexcan = 0. Importantly, the arbitrary orientation of the canalicular pores implies that all quantities related to the canalicular pores (, Kexlac, and Acan) are defined as function of the pore orientation, considered via Euler angles ϑ and φ. Furthermore, for summation over all material phases, it is necessary to integrate over all possible pore orientations, see, e.g., the double integrals in Equations (12, 13). The thereby involved transformations of second-order tensors is explained in detail in the Supplementary Material of this article.
Finally, insertion of Equations (12, 13), as well as of Kexcan = 0 into Equation (9) gives access to the homogenized permeability of extralacunar bone matrix,
On the other hand, the concentration tensors defined through Equations (12, 13) allow for downscaling of pressure gradients from the length scale of extralacunar bone matrix to the constituents of the latter, that is to the canalicular pores and the extracanalicular bone matrix, through
and
where gradpcan(ϑ, φ) are the orientation-dependent pressure gradients in the canalicular pores, gradpexcan is the pressure gradient in the extracanalicular bone matrix, and gradpexlac is the pressure gradient on the RVE of extralacunar bone matrix. Note that, due to the multi-step nature of the homogenization scheme presented in section 2.4, the RVE-scale pressure gradients occurring in section 2.4.1, and also subsequently, are no longer denoted by a gradient operator in capital letters, as introduced, for the sake of clarity, in section 2.2.
2.4.2. Extravascular Bone Matrix
Owing to the distinct matrix-inclusion morphology of the RVE of extravascular bone matrix, the concentration tensors of the lacunar pores and of the extralacunar bone matrix follow as
and
where is the lacunar porosity, quantified on the RVE of extravascular bone matrix, Klac is the permeability tensor related to the lacunar pores, and is the inhomogeneity tensor of the spherical lacunar pores embedded in a matrix exhibiting a permeability which is described by tensor Kexlac. While Kexlac is the outcome of the first homogenization step, see Equation (17) of this paper and Equation (S13) of the Supplementary Material, Klac is chosen according to the work of Markov et al. [75]. They considered spherical inclusions embedded in a porous domain, and analyzed the pressure gradient-driven fluid flow across such a domain by means of a Stokes analysis. The such computed fluid flow was then set equal to a quasi-Darcy law analogous to the strategy proposed in Dormieux and Kondo [45] and Abdalrahman et al. [38] and summarized in section 2.4.1, allowing for back-analysis of a corresponding permeability related to the lacunar pores. In particular, Markov et al. [75] chose the boundary conditions concerning the continuity of the normal pressure and the normal velocity components as suggested in Beavers and Joseph [76] and Saffman [77]. Tying in with these works, the permeability of the lacunar pores follows as
where rlac is the radius of the (spherical) lacunar pores, and λ is the dimensionless, semi-empirical slip coefficient typically varying between 0 and 5, the latter range following from the experiments described in [76]. However, considering the numerical values for Kexlac and rlac that are relevant in the context of the present paper, it can be readily seen that . Hence, it is reasonable to simplify the definition of Klac accordingly, . Finally, inhomogeneity tensor is equal to , , see Equation (15).
Equations (10, 11) give access to the permeability tensor of extravascular bone matrix, Kexvas = Kexvas1, via
and allow to evaluate the pressure gradient downscaling relations on the RVE of extravascular bone matrix,
and
where gradplac and gradpexlac, respectively, are the pressure gradients in the lacunar pores and in the extralacunar bone matrix, respectively, whereas gradpexvas is the pressure gradient on the RVE of extravascular bone matrix.
2.4.3. Macroscopic Bone Tissue–Arbitrarily Oriented Vascular Pores
At the macroscopic level, the case of arbitrarily oriented, interpenetrating vascular pores, embedded in a matrix representing the macroscopic bone tissue (with permeability ), is considered first.
For such an RVE morphology, the concentration tensors related to the vascular pores and to the extravascular bone matrix follow as
and
with as the vascular porosity, quantified on the RVE of macroscopic bone tissue, and , respectively, as the inhomogeneity tensors related to the vascular pores and to the extravascular bone matrix, respectively, and Kvas(ϑ, φ) as the permeability of the vascular pores; note that the components of the inhomogeneity tensor and of the permeability tensor related to the vascular pores depend on the orientation of the pores. Analogously to the inhomogeneity tensors defined on the RVE of extralacunar bone matrix, see section 2.4.1, and are defined as
and
Also, Kvas(ϑ, φ) is defined analogously to Kcan(ϑ, φ), see the corresponding explanations in section 2.4.1, namely through
where rvas is the radius of the vascular pores. The permeability of the extravascular bone matrix is known from the previous homogenization step, Kexvas = Kexvas1, according to Equation (23) of this paper, and Equation (S16) of the Supplementary Material.
The concentration tensors according to Equations (29, 30) are then inserted into Equations (10, 11), in order to derive the permeability tensor of macroscopic bone tissue containing arbitrarily oriented vascular pores,
as well as the pressure gradient downscaling relations allowing to relate the macroscopic pressure gradient gradpmacro to the orientation-dependent pressure gradients in the vascular pores, ,
and to the pressure gradient in the extravascular bone matrix, ,
2.4.4. Macroscopic Bone Tissue–Longitudinally Oriented Vascular Pores
When considering that the vascular pores are oriented longitudinally, as it can be expected for cortical bone in long bones, a distinctive matrix-inclusion morphology emerges, i.e., the vascular pores act as inclusions in a matrix consisting of extravascular bone matrix (which exhibits the permeability Kexvas = Kexvas1). Then, the concentrations tensors related to the vascular pores and to the extravascular bone matrix read as
and
Inhomogeneity tensor is defined analogously to Equation (28),
taking, however, into account that extravascular bone is now acting as matrix phase hosting the vascular pores. Furthermore, Kvas is defined as shown in Equation (30). Note that, in contrast to Equations (26, 27), only one orientation of the vascular pores is considered in Equations (34, 35); hence no coordinate transformation is necessary when considering longitudinally oriented vascular pores.
The above-defined concentration tensors and allow for deriving the upscaled permeability tensor ,
as well as the downscaled pressure gradients in the vascular pores, ,
and in the extravascular bone matrix, ,
Notably, the longitudinal orientation of the vascular pores implies a transversally isotropic permeability tensor . Hence, the main diagonal of includes one longitudinal component, , and two transversal components, , with due to Equation (30); all other components (i.e., with i ≠ j) are zero.
2.4.5. Further Evaluation of the Permeability Up- and Pressure Gradient Downscaling Relations
Inserting Equations (14–16) into Equations (12–13), and the resulting expressions into Equation (17), gives access to the upscaled permeability of extralacunar bone matrix, , see Equation (S13) of the Supplementary Material for details. Inserting Kexlac, according to Equation (15), and of Equation (22) into Equations (20, 21), and the resulting expressions into Equation (23), gives access to the upscaled permeability of extravascular bone matrix, Kexvas, see Equation (S16) of the Supplementary Material for details. Inserting Kexvas, as well as Equations (28–30) into Equations (26, 27), and the resulting expressions into Equation (31), gives access to the upscaled permeability of macroscopic bone tissue containing arbitrarily oriented vascular pores, , see Equation (S25) of the Supplementary Material for details. And, finally, inserting Kexvas, as well as Equations (30, 36) into Equations (34, 35), and the resulting expressions into Equation (37), gives access to the upscaled permeability of macroscopic bone tissue containing longitudinally oriented vascular pores, , see Equations (S28–S30) of the Supplementary Material for details.
The concentration tensors needed for estimating the pressure gradients arising in the canalicular pores in response to pressure gradients defined on the length scale of extralacunar bone matrix, the pressure gradients in the lacunar pores in response to pressure gradients defined on the length scale of extravascular bone matrix, and the pressure gradients in the vascular pores in response to pressure gradients defined on the length scale of macroscopic bone tissue can be found in Equations (S5–S12), (S14), (S15), and (S17–S24) of the Supplementary Material of this paper. Furthermore, combination of Equations (33) or (39) with Equation (24) gives access to the pressure gradients in the lacunar pores in response to macroscopic pressure gradients,
whereas combination of Equations (33) or (39) with Equations (25, 18) gives access to the pressure gradients in the canalicular pores in response to macroscopic pressure gradients,
In Equations (40, 41), superscript “arb/long” expresses that either arbitrarily or longitudinally oriented vascular pores are considered.
2.5. Model Input Parameters
Evaluation of the model elaborated in section 2.4 is based on three categories of model parameters: (i) canalicular, lacunar, and vascular porosities (, , and ); (ii) canalicular, lacunar, and vascular pore radii (rcan, rlac, and rvas); and (iii) the dynamic viscosities of the canalicular, lacunar, and vascular pore fluids (ηcan, ηlac, and ηvas). Physiologically reasonable ranges for the porosities and pore radii have already been defined in section 2.3.
Concerning the pore fluid viscosities, it is assumed that no relevant differences between the considered types of pore spaces occur, i.e., ηcan = ηlac = ηvas = η. This assumption has been introduced tacitly in section 2.4, by not distinguishing between the viscosities related to different pore spaces, compare, e.g., Equations (16), (22), and (30). Furthermore, it is well known that the dynamic viscosity of bulk water amounts to 0.001 Pas; a value that has been used frequently in both experimental and theoretical studies related to the movement of fluid in the lacunar-canalicular pore system of bone [78–80]. However, water is a polarized fluid. As such, it changes its transport behavior when adjacent to electrically charged surfaces (such as the hydroxyapatite crystals, building up extracanalicular bone material). In fact, so-called structured, or ice-type water (of liquid crystalline nature) forms, leading to a higher viscosity and a lower diffusivity in the affected regions, referred to as surface zone [81], or exclusion zone [82]. The thickness of this zone ranges from some hundred micrometers up to a few millimeters [83, 84], as evidenced by several different experimental modalities, see [38] for a brief overview. Moreover, Ichikawa et al. [85] and Ichikawa et al. [83] quantified, by means of molecular dynamics studies (on water molecules which are surrounded by clay-type mineral surfaces), that the viscosity in structured water increases on average by a factor of approximately 7. Hence, given that the pore fluid in bone tissue is quite similar to water, it is assumed that the dynamic viscosity of the fluid contained in all considered pore spaces amounts to η = 0.007 Pa s.
3. Results
3.1. Model Validation–Comparison of Model-Predicted Permeabilities to Experimental and Alternative Computer Simulation Data
First, the model is experimentally validated, based on comparing the model-predicted, upscaled permeabilities to experimentally derived permeabilities of bone tissue on different observation scales. In order to take into account the variability of the model input data, in particular of the canalicular, lacunar, and vascular porosities as well as of the pore radii, the effects of varying these quantities is studied within the following ranges, see also section 2.3: , , for arbitrarily oriented vascular pores, for longitudinally oriented vascular pores, m, m, and m. Entering these values, together with η = 0.007 Pa s into the permeability upscaling relations derived in section 2.4, gives access to the permeabilities of extralacunar bone matrix, of extravascular bone matrix, and of macroscopic bone tissue, see also the Supplementary Material of this paper. The ranges of these permeabilities, stemming from the aforementioned porosity and pore radii variations, are depicted in Figure 2.
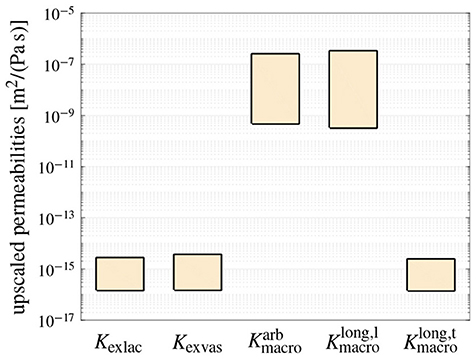
Figure 2. The model-predicted, non-zero components of the isotropic permeability tensors of extralacunar bone matrix (Kexlac), extravascular bone matrix (Kexvas), and macroscopic bone tissue when considering arbitrarily oriented vascular pores (), and of the transversally isotropic permeability tensor of macroscopic bone tissue when considering longitudinally oriented vascular pores ( and ), see Section 2.4 and the Supplementary Material for details; the ranges shown for each permeability highlight the resulting upper and lower limits when varying the canalicular, lacunar, and vascular porosities, and the corresponding pore radii within the physiologically reasonable ranges.
While open literature does not provide experimentally derived permeability data relating to extralacunar bone matrix, respective numerically computed values can be found in Sansalone et al. [86], or deduced from Kaiser et al. [87], agreeing reasonably well with the extralacunar permeabilities predicted by the here presented model. As for extravascular bone matrix, most studies report intrinsic permeabilities ranging from 10−22 to 6.7 × 10−18m2 [78, 79, 88, 89], while optionally, intrinsic permeabilities between 5 × 10−25 to 2.8 × 10−23m2 [80, 90] are reported. Given these substantial variations, and considering a viscosity of η = 0.007 Pa s for converting the Darcy-type permeabilities shown in Figure 2 into intrinsic ones, allows to conclude that the model-predicted extravascular permeabilities agree reasonably well with independent data found in literature. On the macroscopic scale, the model has already successfully undergone comprehensive experimental validation in a previous work [38], thereby considering arbitrarily oriented vascular pores. Furthermore, as can be seen in Figure 2, is very similar to , whereas is, as expected, by orders of magnitude smaller.
3.2. Sensitivities of Downscaled Pressure Gradients and Pore Fluid Velocities
In order to study how macroscopically applied pressure gradients are transferred to the considered material phases, a macroscopic pressure gradient of is inserted into the downscaling relations described in section 2.4.5. In Figure 3, the resulting material phase-scale pressure gradients are shown. It should be noted that in the arbitrarily oriented vascular and canalicular pores the magnitudes of the pressure gradients depend on the pore orientation, and in Figure 3 the respective maximum pressure gradients are shown. When considering, on the one hand, arbitrarily oriented vascular pores, the macroscopic pressure gradient is transferred to the extravascular bone matrix with almost no attenuation, while the pressure gradient in the vascular pores amounts to 0.66 kPa/mm. The pressure gradient arriving in the lacunar pores is virtually zero, while the pressure gradient in the extralacunar bone matrix is amplified as compared to the macroscopic one, to 1.11 kPa/mm. In the canalicular pores, in turn, the pressure gradient amounts to 0.74kPa/mm, while, analogously to the RVE of macroscopic bone tissue, the pressure gradient in the extracanalicular bone matrix is only marginally smaller than the one in the extralacunar bone matrix. On the other hand, for longitudinally oriented vascular pores, all pressure gradients are slightly reduced as compared to arbitrarily oriented vascular pores, except for the pressure gradient in the vascular pores; the latter is exactly zero, due to the fact that for such morphology the prescribed pressure gradient is oriented perpendicular to the vascular pores.
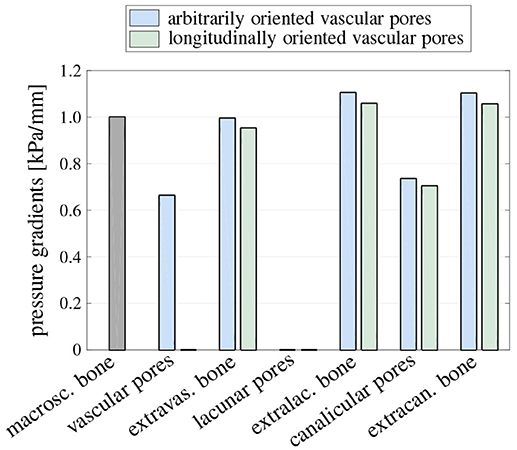
Figure 3. Pressure gradient kPa/mm applied on the level of macroscopic bone tissue, and the corresponding maximum pressure gradients in all considered material phases, for both arbitrarily and longitudinally oriented vascular pores; in the cylindrical (vascular and canalicular) pore phases, the respective maximum pressure gradients in pore direction are shown, thereby considering all possible pore orientations.
It is now interesting to study how the pore-scale pressure gradients translate into corresponding fluid velocities, as well as the sensitivities of these velocities to changes of the canalicular, lacunar, and vascular porosities as well as pore radii. To that end, the porosities and pore radii are varied within the ranges introduced in section 3.1, and pore fluid velocities are calculated by inserting the downscaled canalicular and vascular pressure gradients into v = −[r2/(8η)]dp/ds [38], with s being the longitudinal pore direction; the results of this study are shown in Figure 4. Notably, the downscaled pressure gradients in the lacunar pores are negligibly small, hence presentation and further discussion of the velocities in the lacunar pores is omitted in this paper. The fluid velocities in the canalicular pores increase significantly with increasing radius of the canaliculi (regardless how the vascular pores are oriented), and with increasing vascular porosity (if the vascular pores are oriented longitudinally). Furthermore, they increase slightly with increasing lacunar porosity (regardless how the vascular pores are oriented), and with increasing vascular porosity (if the vascular pores are oriented arbitrarily). Variations of the canalicular porosity, as well as of the lacunar and vascular radii (within physiologically reasonable ranges) do not have noteworthy effects on the related canalicular fluid velocities. The fluid velocity in the arbitrarily oriented vascular pores is effectively influenced only by the vascular pore radius.
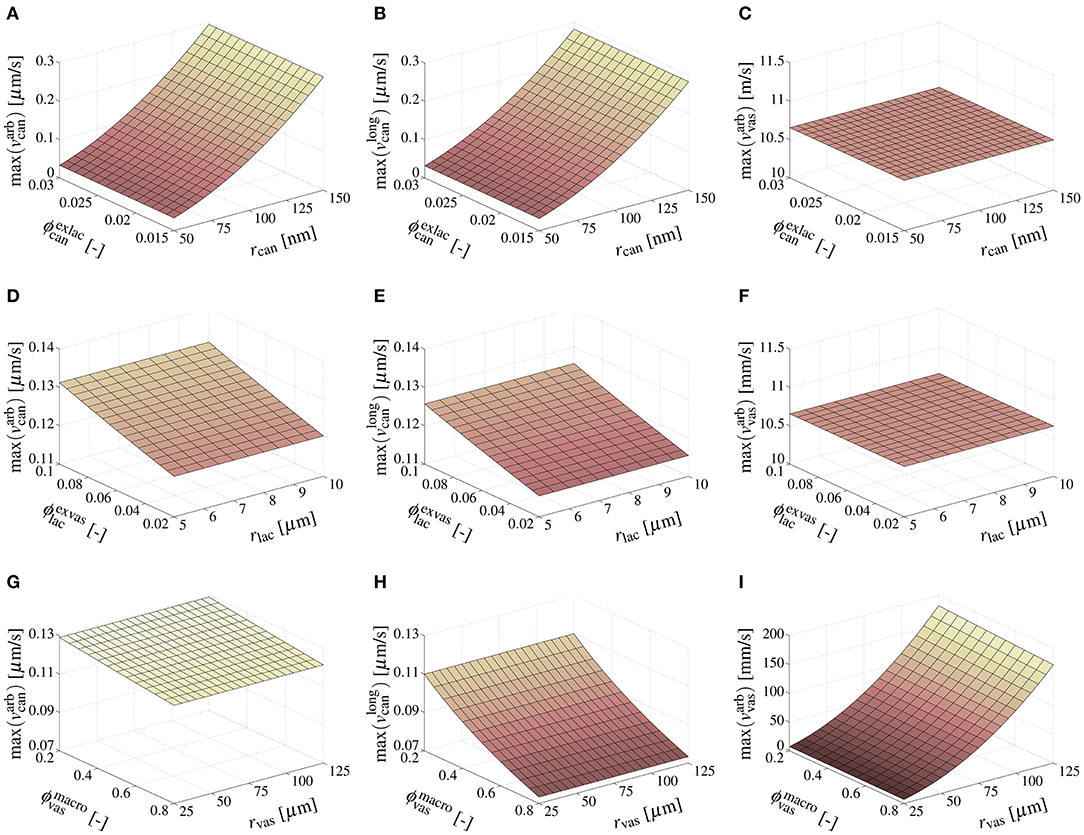
Figure 4. Sensitivities of model-predicted maximum canalicular and vascular pore fluid velocities, in response to the macroscopic pressure gradient kPa/mm, considering the following variations of porosities and pore radii: and m, see (A–C); and m, see (D–F); and m, see (G–I).
3.3. Computation of Pore Fluid Velocities Relating to Physiological Mechanical Loading
In order to check the magnitude of the canalicular and vascular pore fluid velocities provoked by macroscopic loading of physiological magnitude, the latter has to be defined. Based on gait analysis [91], strain gauge measurements [92], and mathematical modeling [93], a (compressive) normal force of N = 700 N, together with a bending moment of M = 50Nm can be considered as typical loading to which a human femur is subjected [94]. Let us consider that in the long, median part of a femur the organ structure resembles an annular beam, with inner radius ri = 5.5mm and outer radius ro = 14.2 mm [95]. To this beam, a base system (ex,ey,ez) is attached, with ex coinciding with the longitudinal axis of the beam. Then, it is assumed that the stress distribution related to the above-mentioned loading can be reasonably calculated by the classical Euler-Bernoulli beam theory [96, 97]. In the framework of this theory, the normal stress in direction of the beam axis is defined as σxx = N/A + (My/Iy)z + (Mz/Iz)y, My and Mz being the bending moments with respect to the y- and z-axes, whereas Iy and Iz are the respective moments of inertia, . Hence, assuming that the aforementioned bending moment acts with respect to the z-axis, the stress gradient in the cross section results to . The corresponding pressure gradient, acting onto macroscopic bone tissue, follows from the hydrostatic part of the stress tensor gradient, , and, hence, .
Utilizing then the downscaling relations established in section 2.4, and evaluating the resulting pore-scale pressure gradients in terms of the corresponding pore fluid velocities, as described in section 3.2, yields the maximum and mean canalicular and vascular pore fluid velocities (considering all possible orientations of the pores): m/s, m/s, m/s, m/s, m/s, and m/s. Notably, previous studies report similar canalicular fluid velocities [28, 98, 99].
4. Discussion
4.1. Interpretation of Results and Key Findings
It has been shown that the model presented in this paper allows for reliable upscaling of the permeability, from the scale of canalicular, lacunar, and vascular pores, to the scale of macroscopic bone tissue, see section 3.1. In particular, the model validity has been corroborated based on comparing model-predicted permeabilities on the extravascular and macroscopic scales to corresponding experimental data, as well as on comparing model-predicted permeabilities on the extralacunar scale to corresponding numerical results.
However, the main focus of this paper is to assess the role of fluid shear stresses in the mechanobiology of bone. For that purpose, it is expedient to compare the canalicular and vascular pore fluid velocities predicted by the model in response to physiological macroscopic loading, see section 3.2, to the fluid velocities which have been shown to excite bone cells in vitro. As can be seen in Table 1, the fluid velocities used in vitro vary substantially between the different studies. Nevertheless, it can be concluded that typically fluid velocities of several tens to hundreds of mm/s are needed to excite osteoblasts. Only one study [103] reports flow velocities in the range of several tens to hundreds μm/s, however in form of a long-term fluid perfusion of a tissue engineering scaffold–physiologically reasonable characteristic loading times of bone [29] suggest that such long-term exposure to constant fluid flow does hardly or not at all occur in vivo. Unfortunately, the papers involving studies on osteocytes neither provide fluid velocities, nor enough information to back-calculate them. However, the provided specifications of the used test set-ups (such as flow rates) suggest that the fluid velocities arising in these studies are also in the aforementioned range.
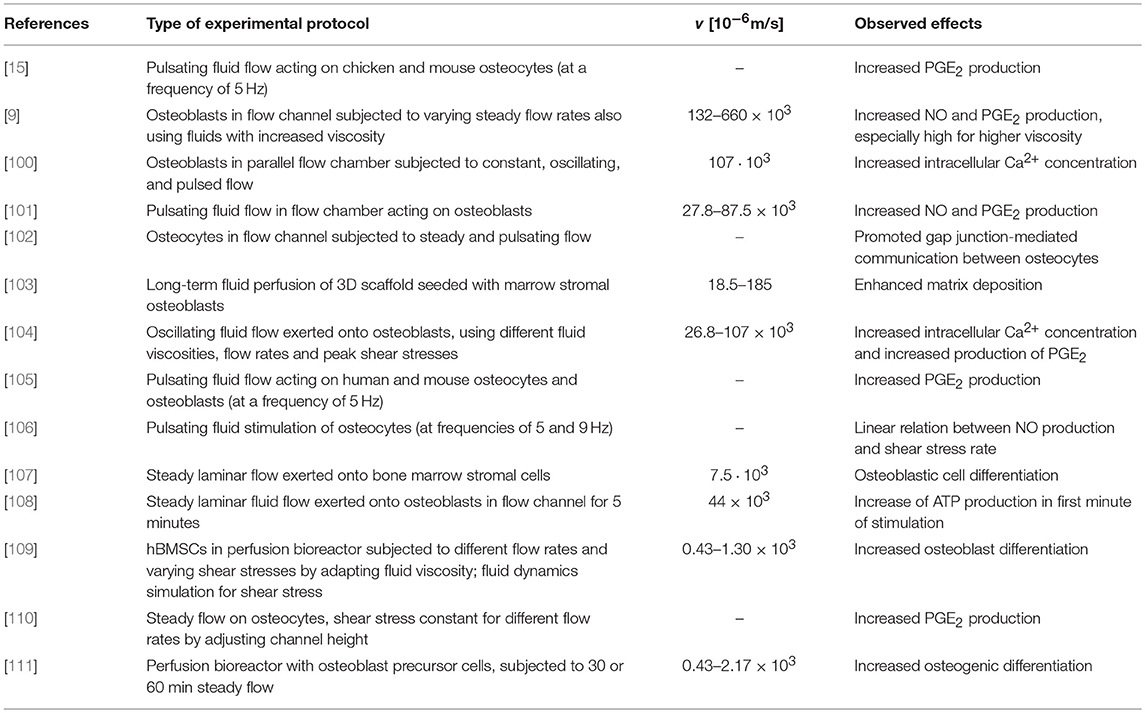
Table 1. In vitro tests showing stimulation of bone cells by fluid flow; studies involving osteocytes neither provide fluid velocities nor provide enough information to back-calculate them.
Remarkably, the computed canalicular pore fluid velocities are separated from the experimentally used ones by orders of magnitude. This suggests that the flow velocities that were shown in vitro to be necessary to provoke some cellular response are not reached in vivo. Hence, it turns out that, according to the model predictions, it is unlikely that osteocytes are effectively stimulated by fluid shear stresses. In this context, it should be mentioned that the model input parameters are subjected to (partly) significant variations. However, the sensitivity studies discussed in section 3.2 and highlight in Figure 4 clearly highlight that varying the canalicular, lacunar, and vascular porosities, as well as the corresponding pore radii, within physiologically reasonable ranges does not lead to the required increase of the canalicular pore fluid velocities. The only remaining input parameter that could differ significantly from the one used in the computation described in section 3.3 is the macroscopic pressure gradient. The one used in this paper, , is clearly a considerable simplification of the real situation in bone. In vivo, pressure gradients are certainly influenced by the exact (non-circular) geometry of the organ, local variations of the microstructure, or the fact that pressure gradients occur anisotropically in all three space directions. Considering these and further (so far neglected) effects could eventually lead to increased canalicular fluid flow velocities – however hardly by the required extent (i.e., by factor ≈103). Furthermore, the model-predicted vascular fluid velocities (in response to macroscopically applied, physiological loading conditions) are indeed high enough to stimulate the bone remodeling-relevant cells which can be found in the vascular pore space (such as osteoblasts, osteoclasts, or bone lining cells). In fact, the model presented in this paper delivers vascular fluid velocities which are by orders of magnitude higher than the ones used in the in vitro studies summarized in Table 1, and also than vascular fluid velocities occurring in vivo, as well as those suggested by numerical studies [112]. A reason for this significant overestimation could be that the chosen morphology on the RVE of macroscopic bone tissue overly facilitates fluid flow, whereas it is nevertheless appropriate in order to accurately predict the macroscopic permeability of bone tissue, see section 3.1. Furthermore, it may be necessary to take into account the actual distribution of the bone microstructure across the studied cross section, from low-porosity cortical bone to high-porosity trabecular bone, in order to obtain a more realistic estimate of the local pressure gradients, and, in further consequence, of the vascular pore fluid velocities. On the other hand, the pressure gradient used in this study does not take into account that in vivo mechanical loading may increase continuously from zero to the peak level (rather than being applied in step-wise fashion) which leads to gradual pore drainage. Despite these limitations, it seems valid to conclude that in the vascular pores, fluid shear stresses are much more likely to excite the therein residing cells than in the canalicular pores.
4.2. Computational Aspects
It should be noted that the homogenization schemes derived on the RVEs of extralacunar bone matrix, see section 2.4.1, and of macroscopic bone tissue considering arbitrarily oriented vascular pores, see section 2.4.3, are of self-consistent nature. Hence, the homogenized permeabilities Kexlac and are defined implicitly, and numerically evaluating the underlying homogenization schemes require, in the general case, a numerical approach. However, specializing the two implicit homogenization schemes, for the respective RVE morphologies and for the assumed fluid flow conditions in the canalicular and vascular spaces, eventually yields explicit definitions of the homogenized permeabilities of extralacunar bone matrix and macroscopic bone tissue considering arbitrarily oriented vascular pores, see Equations (S13, S25) of the Supplementary Material. Hence, the multiscale model presented in this paper is, from a computational point of view, highly efficient – iterative, potentially time-consuming approaches are not needed at all.
4.3. Model Assumptions and Limitations
The remarkable computational efficiency of the concept of continuum micromechanical homogenization comes at a price – as stated in section 2.1, the modeling strategy pursued in this paper does not consider the real microstructure of the studied material in minute detail. Instead, an assembly of so-called material phases is defined. These material phases are assumed to be homogeneous and must represent the real microstructure in the best possible way. In this paper, canalicular and vascular pores are chosen to be represented by long cylinders, while lacunar pores are chosen to be represented by spheres. The bone matrix on the lowest observation scale considered in this model representation, extracanalicular (or, extracellular) bone matrix is assumed to be impermeable. We believe that this approach is a reasonably good compromise between keeping the model representation as simple as possible (in terms of eventually arriving at a mathematical framework which is straightforward to handle), but as complex as necessary (in terms of taking into account the relevant microstructural features). Notably, this view is supported by permeability-based model validation, see section 4.1. Nevertheless, the here presented model does include some limitations (as it is the nature of mathematical models in general). In order to put the results of this paper in better perspective, we discuss these limitations in the following.
As stressed in the preceding paragraph, the permeability of extracanalicular bone is considered to be negligibly small. Strictly speaking, additional pore spaces can be found on smaller observation scales, such as the pore space between hydroxyapatite crystals or even between collagen molecules (see, e.g., [32]) and references therein. It has been argued, e.g., by Lemaire and co-workers [113, 114], that the contribution of the fluid flow in these nanopores may actually be not as negligible as commonly believed. Introducing this additional contribution to the permeability of bone tissue in the here presented model is straightforward, and may be considered in the future, once insights concerning the permeability of the extracanalicular matrix have consolidated.
Considering now the RVE of macroscopic bone tissue, it should be noted that the model presented in this paper does not explicitly distinguish between Haversian and Volkmann canals. Instead, two morphological scenarios are considered on the RVE of macroscopic bone tissue, see Figure 1, which are thought to represent limit cases of the vascular permeability. The first scenario, involving arbitrarily oriented, interpenetrating vascular pores represents, depending on the volume fraction of the vascular pores, trabecular bone, endocortical bone, or cortical bone exhibiting somewhat disordered Haversian and Volkmann canals. The latter representation of vascular pores in cortical bone in a way resemble results from micro-computed tomography (see e.g., [56]), which confirm that it may be difficult to clearly distinguish between Haversian and Volkmann canals. The second scenario, considering that the vascular pores are oriented longitudinally, represents cortical bone tissue with Haversian canals being clearly the dominant kind of vascular pore space, whereas Volkmann canals occur to an negligible extent. Such case hence resembles a (theoretical) extreme example of the multiply reported situation that Volkmann canals are the, by far, secondary kind of vascular pore space [115, 116]. Hence, although just one kind of vascular pore space is considered, the model introduced here covers the whole spectrum of vascular permeability, spanned through physiologically conceivable arrangements of Haversian and Volkmann canals.
Furthermore, in vivo, pores are not solely filled with pore fluid. Lacunar pores contain osteocytes, with the cell processes of the latter stretching into the canalicular pores. Vascular pores, in turn, contain cells, various biochemical factors, the vasculature, and, when considering trabecular (also referred to as cancellous, or spongy bone) bone, the bone marrow, as well as the endosteum. Thus, the physical space which is available for fluid flow is actually (much) smaller than the volume of the pores. One way to take this into account could be to replace the currently considered homogeneous pore spaces by shell-like structures composed of two (or more) layers, with each layer exhibiting different fluid flow characteristics – a similar approach has been successfully applied in in the contexts of stiffness homogenization [117, 118] and strength homogenization [119]. When considering the cell body and the cell processes as completely impermeable, and assuming that pore walls and cell components exhibit the same behavior in terms of friction and slip, solutions for Poiseuille-type flow profiles can be analytically derived [120]. On the other hand, the fluid flow velocities presented in this paper can be regarded as upper bounds, occurring only when the pores contain only pore fluid. The latter observation implies two further conclusions: Firstly, it provides a reasonable explanation for the high fluid flow velocities the model has predicted to occur in the vascular pores; and, secondly, it significantly strengthens the key finding of this paper, namely that osteocytes are unlikely to be sufficiently excited by fluid flow in response to physiological macroscopic loading (considering that in a more physiological canalicular pore milieu fluid flow velocities are probably even lower than the model-predicted ones).
When comparing bulk water to the bone pore fluid, the latter features increased salinity. One of the thereof arising effects is, similar to layered water, an increased fluid viscosity, as compared to bulk water [86]. Hence, considering this effect would further compromise the predicted pore fluid flow velocities. Due to the fact that quantitative information on the effect of fluid salinity on the corresponding viscosity is, to the best of the authors' knowledge, quite diverse and more or less vague—in particular, the combined effect of layered water and pore fluid salinity is unclear and probably remains to be investigated—the respective viscosity increase has not been introduced.
Finally, there are also pore fluid flow-related aspects that have been neglected in this work which have been hypothesized to magnify the effect of pore fluid flow in terms of osteocyte excitation. This concerns, e.g., the pericellular space around the cell processes of osteocytes, for which significant strain amplification effects were predicted by means of theoretical approaches [121]. Furthermore, the network of fibers tethering the cell processes to the canalicular pore walls were suggested to significantly change the fluid flow behavior in the canalicular pores [86, 113]. In another theoretical study, based on fluid flow simulations by means of the Finite Volume method [122], it was concluded that an idealized (i.e., smooth) canalicular pore shape implies, when compared to a more realistic pore shape (gained from transmission electron micrographs) higher fluid velocity but up to 33% lower shear stresses acting onto the pore walls. Also, electrochemical effects were not taken into account. Sansalone and co-workers [86, 87] performed insightful studies as to the fluid flow- and shear stress-related implications of electrical double layers at the pore walls, as well as of biochemical and electrical gradients, highlighting that these effects could provide significant contributions to the overall wall shear stress (while the fluid flow velocity is largely governed by pressure gradients).
4.4. Outlook
Several future research directions are conceivable, aiming at confirming the insights presented in this paper, or at generating even improved insights, by extending and improving the underlying model:
• An optional strategy to compute pore-scale pressure gradients from macroscopically applied mechanical loading could be based on recently published work on poromicromechanical pressure downscaling [29].
• Consideration of more realistic stress distribution on the scale of macroscopic bone tissue would give access to (three-dimensional) distributions of pore-scale fluid flow conditions, thereby improving the significance of the model predictions. The same is true when envisioning a more realistic consideration of the shapes, properties, and internal structure of the pores.
• An extremely insightful addition to the model presented in this paper would be the calculation of the fluid flow-equivalent shear stresses. The classical law of Hagen [72] and Poiseuille [73] actually provides a respective definition of the shear stress acting onto the pore walls. However, since mechanical cell excitation does not occur on the pore walls but rather on the cell itself, using this definition does not seem correct. Some kind of explicit consideration of the cell body and of its processes is deemed essential to that end. The key challenge in such an endeavor would be the translation of the geometrical information available from sufficiently accurate imaging techniques, such as confocal microscopy [123], into corresponding microstructural entities usable in continuum micromechanics-type homogenization.
• It would be highly interesting to use the model for simulating perfusion tests. This could be achieved based on considering the microstructure of a bone specimen according to suitable imaging (such as micro-computed tomography), prescribing suitable macroscopic loading boundary conditions, and simulating the fluid flow behavior in the relevant pore spaces. Comparing the such obtained results to corresponding experimental data, collected, e.g., from perfusion-weighted MRI, would allow for experimental validation of the model. Notably, using a model which is conceptually similar to the one presented in this paper [47], even diffusion tests could be simulated, allowing for further validation of the model representation of bone tissue.
• Eventually, the model presented in this paper could be straightforwardly implemented in modeling approaches dealing with simulation of the bone remodeling process (see, e.g., [124–127]), enabling the latter class of models to consider the mechanobiological process regulation in a more refined, physiologically more meaningful way.
Author Contributions
S-JE Conceptual model design, model implementation, performance of numerical studies, interpretation of the results, as well as drafting the manuscript; SS Conceptual model design, performance of numerical studies, interpretation of the results, and all tasks related to finalizing the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge the TU Wien Library for financial support through its Open Access Funding Program.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00076/full#supplementary-material
References
1. Buckwalter J, Glimcher M, Cooper R, Recker R. Bone biology. Part I: Structure, blood supply, cells, matrix, and mineralization. J Bone Joint Surg A. (1995) 77:1256–75. doi: 10.2106/00004623-199508000-00019
2. Buckwalter J, Glimcher M, Cooper R, Recker R. Bone biology. part II. formation form, modeling, remodeling, and regulation of cell function. J Bone Joint Surg A. (1995) 77:1276–89. doi: 10.2106/00004623-199508000-00020
3. Robling A, Castillo A, Turner C. Biomechanical and molecular regulation of bone remodeling. Ann Rev Biomed Eng. (2006) 8:455–98. doi: 10.1146/annurev.bioeng.8.061505.095721
4. Frangos J, Eskin S, McIntire L, Ives C. Flow effects on prostacyclin production by cultured human endothelial cells. Science (1985) 227:1477–9.
5. Frangos J, McIntire L, Eskin S. Shear stress induced stimulation of mammalian cell metabolism. Biotechnol Bioeng. (1988) 32:1053–60. doi: 10.1002/bit.260320812
6. Reich K, Gay C, Frangos J. Fluid shear stress as a mediator of osteoblast cyclic adenosine monophosphate production. J Cell Physiol. (1990) 143:100–4. doi: 10.1002/jcp.1041430113
7. Reich K, Frangos J. Effect of flow on prostaglandin E2 and inositol trisphosphate levels in osteoblasts. Am J Physiol Cell Physiol. (1991) 261:C428–32. doi: 10.1152/ajpcell.1991.261.3.C428
8. Cowin S, Moss-Salentijn L, Moss M. Candidates for the mechanosensory system in bone. J Biomed Eng. (1991) 113:191–7. doi: 10.1115/1.2891234
9. Smalt R, Mitchell F, Howard R, Chambers T. Induction of NO and prostaglandin E2 in osteoblasts by wall-shear stress but not mechanical strain. Am J Physiol. Endocrinol. Metab. (1997) 273:751–8. doi: 10.1152/ajpendo.1997.273.4.E751
10. Bonewald L, Johnson M. Osteocytes, mechanosensing and Wnt signaling. Bone (2008) 42:606–15. doi: 10.1016/j.bone.2007.12.224
11. Jacobs C, Temiyasathit S, Castillo A. Osteocyte mechanobiology and pericellular mechanics. Ann Rev Biomed Eng. (2010) 12:369–400. doi: 10.1146/annurev-bioeng-070909-105302
13. Hillsley M, Frangos J. Bone tissue engineering: the role of interstitial fluid flow. Biotechnol Bioeng. (1994) 43:573–81. doi: 10.1002/bit.260430706
14. Klein-Nulend J, Van der Plas A, Semeins C, Ajubi N, Frangos J, Nijweide P, et al. Sensitivity of osteocytes to biomechanical stress in vitro. FASEB J. (1995a) 9:441–5. doi: 10.1096/fasebj.9.5.7896017
15. Klein-Nulend J, Semeins C, Ajubi N, Nijweide P, Burger E. Pulsating fluid flow increases nitric oxide (NO) synthesis by osteocytes but not periosteal fibroblasts–correlation with prostaglandin upregulation. Biochem Biophys Res Commun. (1995b) 217:640–8. doi: 10.1006/bbrc.1995.2822
16. Stevens H, Frangos J. Bone Cell responses to fluid flows. In: Helfrich M, Ralston S, editors. Vol. 80, Bone Research Protocols, Methods in Molecular Medicine. Totowa, NJ: Humana Press Inc. (2003). p. 381–98.
17. Tan S, de Vries T, Kuijpers-Jagtman A, Semeins C, Everts V, Klein-Nulend J. Osteocytes subjected to fluid flow inhibit osteoclast formation and bone resorption. Bone (2007) 41:745–51. doi: 10.1016/j.bone.2007.07.019
18. Malone A, Anderson C, Tummala P, Kwon R, Johnston T, Stearns T, et al. Primary cilia mediate mechanosensing in bone cells by a calcium-independent mechanism. Proc Natl Acad Sci USA. (2007) 104:13325–30. doi: 10.1073/pnas.0700636104
19. You L, Temiyasathit S, Lee P, Kim C, Tummala P, Yao W, et al. Osteocytes as mechanosensors in the inhibition of bone resorption due to mechanical loading. Bone (2008) 42:172–9. doi: 10.1016/j.bone.2007.09.047
20. Kamel M, Picconi J, Lara-Castillo N, Johnson M. Activation of β-catenin signaling in MLO-Y4 osteocytic cells versus 2T3 osteoblastic cells by fluid flow shear stress and PGE2:Implications for the study of mechanosensation in bone. Bone (2010) 47:872–81. doi: 10.1016/j.bone.2010.08.007
21. Biffar A, Dietrich O, Sourbron S, Duerr HR, Reiser M, Baur-Melnyk A. Diffusion and perfusion imaging of bone marrow. Eur J Radiol. (2010) 76:323–8. doi: 10.1016/j.ejrad.2010.03.011
22. Sala E, Rockall A, Rangarajan D, Kubik-Huch R. The role of dynamic contrast-enhanced and diffusion weighted magnetic resonance imaging in the female pelvis. Eur J Radiol. (2010) 76:367–85. doi: 10.1016/j.ejrad.2010.01.026
23. Capuani S. Water diffusion in cancellous bone. Microporous Mesoporous Mater. (2013) 178:34–8. doi: 10.1016/j.micromeso.2013.05.016
24. Rebuzzi M, Vinicola V, Taggi F, Sabatini U, Wehrli F, Capuani S. Potential diagnostic role of the MRI-derived internal magnetic field gradient in calcaneus cancellous bone for evaluating postmenopausal osteoporosis at 3 t. Bone (2013) 57:155–63. doi: 10.1016/j.bone.2013.07.027
25. Capuani S, Manenti G, Iundusi R, Tarantino U. Focus in diffusion MR investigations of musculoskeletal tissue to improve osteoporosis diagnosis: a brief practical review. BioMed Res Internat. (2015) 2015:948610. doi: 10.1155/2015/948610
26. Knothe Tate M, Steck R, Forwood M, Niederer P. In vivo demonstration of load-induced fluid flow in the rat tibia and its potential implications for processes associated with functional adaptation. J Exp Biol. (2000) 203:2737–45.
27. Zhou X, Novotny J, Wang L. Anatomic variations of the lacunar-canalicular system influence solute transport in bone. Bone (2009) 45:704–10. doi: 10.1016/j.bone.2009.06.026
28. Kwon R, Frangos J. Quantification of lacunar-canalicular interstitial fluid flow through computational modeling of fluorescence recovery after photobleaching. Cell Mol Bioeng. (2010) 3:296–306. doi: 10.1007/s12195-010-0129-8
29. Scheiner S, Pivonka P, Hellmich C. Poromicromechanics reveals that physiological bone strains induce osteocyte-stimulating lacunar pressure. Biomech Model Mechanobiol. (2016a) 15:9–28. doi: 10.1007/s10237-015-0704-y
30. Hellmich C, Ulm FJ. Micromechanical model for ultra-structural stiffness of mineralized tissues. J Eng Mech ASCE (2002) 128:898–908. doi: 10.1061/(ASCE)0733-9399(2002)128:8(898)
31. Hellmich C, Ulm FJ. Average hydroxyapatite concentration is uniform in the extracollagenous ultrastructure of mineralized tissues: evidence at the 1—10 μm scale. Biomech Model Mechanobiol. (2003) 2:21–36. doi: 10.1007/s10237-002-0025-9
32. Fritsch A, Hellmich C. ‘Universal’ microstructural patterns in cortical and trabecular, extracellular and extravascular bone materials: micromechanics-based prediction of anisotropic elasticity. J Theor Biol. (2007) 244:597–620. doi: 10.1016/j.jtbi.2006.09.013
33. Morin C, Hellmich C. A multiscale poromicromechanical approach to wave propagation and attenuation in bone. Ultrasound (2014) 54:1251–69. doi: 10.1016/j.ultras.2013.12.005
34. Fritsch A, Hellmich C, Dormieux L. Ductile sliding between mineral crystals followed by rupture of collagen crosslinks: experimentally supported micromechanical explanation of bone strength. J Theor Biol. (2009) 260:230–52. doi: 10.1016/j.jtbi.2009.05.021
35. Morin C, Vass V, Hellmich C. Micromechanics of elastoplastic porous polycrystals: Theory, algorithm, and application to osteonal bone. Int J Plast. (2017) 91:238–67. doi: 10.1016/j.ijplas.2017.01.009
36. Eberhardsteiner L, Hellmich C, Scheiner S. Layered water in crystal interfaces as source for bone viscoelasticity: arguments from a multiscale approach. Comput Methods Biomech Biomed Eng. (2014) 17:48–63. doi: 10.1080/10255842.2012.670227
37. Hellmich C, Celundova D, Ulm FJ. Multiporoelasticity of hierarchically structured materials: micromechanical foundations and application to bone. J Eng Mech ASCE. (2009) 135:382–94. doi: 10.1061/(ASCE)EM.1943-7889.0000001
38. Abdalrahman T, Scheiner S, Hellmich C. Is trabecular bone permeability governed by molecular ordering-induced fluid viscosity gain? Arguments from re-evaluation of experimental data in the framework of homogenization theory. J Theor Biol. (2015) 365:433–44. doi: 10.1016/j.jtbi.2014.10.011
39. Hill R. Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids (1963) 11:357–72. doi: 10.1016/0022-5096(63)90036-X
40. Zaoui A. Continuum micromechanics: survey. J Eng Mech (ASCE) (2002) 128:808–16. doi: 10.1061/(ASCE)0733-9399(2002)128:8(808)
42. Drugan W, Willis J. A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites. J Mech Phys Solids (1996) 44:497–524. doi: 10.1016/0022-5096(96)00007-5
43. Kohlhauser C, Hellmich C. Ultrasonic contact pulse transmission for elastic wave velocity and stiffness determination: influence of specimen geometry and porosity. Eng Struct. (2013) 47:115–33. doi: 10.1016/j.engstruct.2012.10.027
44. Dormieux L, Ulm FJ. Applied Micromechanics of Porous Media, CISM Courses and Lectures, Vol. 480. Wien; New York, NY: Springer Verlag (2005).
45. Dormieux L, Kondo D. Approche micromécanique du couplage perméabilité–endommagement [Micromechanical approach to the coupling between permeability and damage]. Compt Rendus Mécan. (2004) 332:135–40. doi: 10.1016/j.crme.2003.11.003
46. Dormieux L, Kondo D. Diffusive transport in disordered media. Application to the determination of the tortuosity and the permeability of cracked materials. In: Applied Micromechanics of Porous Media CISM Courses and Lecture Series, Vol. 480. Wien; New York, NY: Springer-Verlag (2005). p. 83–106.
47. Damrongwiriyanupap N, Scheiner S, Pichler B, Hellmich C. Self-consistent channel approach for upscaling chloride diffusivity in cement pastes. Trans Porous Med (2017) 118:495–518. doi: 10.1007/s11242-017-0867-3
48. Zaoui A. Structural Morphology and Constitutive Behavior of Microheterogeneous Materials. In: Suquet P editor. Continuum Micromechanics, CISM Courses and Lectures, Vol. 377. Wien; New York, NY: Springer Verlag (1997). p. 291–347.
49. Eshelby J. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond A. (1957) 241:376–96. doi: 10.1098/rspa.1957.0133
51. Padilla F, Jenson F, Bousson V, Peyrin F, Laugier P. Relationships of trabecular bone structure with quantitative ultrasound parameters: in vitro study on human proximal femur using transmission and backscatter measurements. Bone (2008) 42:1193–202. doi: 10.1016/j.bone.2007.10.024
52. Feik S, Thomas C, Clement J. Age-related changes in cortical porosity of the midshaft of the human femur. J Anat. (1997) 191:407–16.
53. Stein M, Feik S, Thomas C, Clement J, Wark J. An automated analysis of intracortical porosity in human femoral bone across age. J Bone Miner Res. (1999) 14:624–32.
54. Bousson V, Bergot C, Meunier A, Barbot F, Parlier-Cuau C, Laval-Jeantet A, et al. CT of the middiaphyseal femur: Cortical bone mineral density and relation to porosity. Radiology (2000) 217:179–87. doi: 10.1148/radiology.217.1.r00se11179
55. Cooper D, Thomas C, Clement J, Turinsky A, Sensen C, Hallgrímson B. Age-dependent change in the 3D structure of cortical porosity at the human femoral midshaft. Bone (2007) 40:957–65. doi: 10.1016/j.bone.2006.11.011
56. Cooper D, Turinsky A, Sensen C, Hallgrímsson B. Quantitative 3D analysis of the canal network in cortical bone by micro-computed tomography. Anat Record B New Anat. (2003) 274:169–79. doi: 10.1002/ar.b.10024
57. Schneider P, Stauber M, Voide R, Stampanoni M, Donahue L, Müller R. Ultrastructural properties in cortical bone vary greatly in two inbred strains of mice as assessed by synchrotron light based micro- and nano-CT. J Bone Miner Res. (2007) 22:1557–70. doi: 10.1359/jbmr.070703
58. Tommasini S, Trinward A, Acerbo A, De Carlo F, Miller L, Judex S. Changes in intracortical microporosities induced by pharmaceutical treatment of osteoporosis as detected by high resolution micro-CT. Bone (2012) 50:596–604. doi: 10.1016/j.bone.2011.12.012
59. Tai K, Pelled G, Sheyn D, Bershteyn A, Han L, Kallai I, et al. Nanobiomechanics of repair bone regenerated by genetically modified mesenchymal stem cells. Tissue Eng A. (2008) 14:1709–20. doi: 10.1089/ten.tea.2007.0241
60. Benalla M, Palacio-Mancheno P, Fritton S, Cardoso L, Cowin S. Dynamic permeability of the lacunar-canalicular system in human cortical bone. Biomech Model Mechanobiol. (2013) 13:801–12. doi: 10.1007/s10237-013-0535-7
61. Palacio-Mancheno P, Larriera A, Doty S, Cardoso L, Fritton S. 3D assessment of cortical bone porosity and tissue mineral density using high-resolution μCT: Effects of resolution and threshold method. J Bone Miner Res. (2014) 29:142–50. doi: 10.1002/jbmr.2012
62. Sugawara Y, Kamioka H, Honjo T, Tezuka K, Takano-Yamamoto T. Three-dimensional reconstruction of chick calvarial osteocytes and their cell processes using confocal microscopy. Bone (2005) 36:877–83. doi: 10.1016/j.bone.2004.10.008
63. Marotti G. The original contributions of the scanning electron microscope to the knowledge of bone structure. Boston, MA: Kluwer Academic (1990). p. 19–39.
64. You LD, Weinbaum S, Cowin S, Schaffler M. Ultrastructure of the osteocyte process and its pericellular matrix. Anat Rec A Discov Mol Cell Evol Biol. (2004) 278A:505–13. doi: 10.1002/ar.a.20050
65. Lin Y, Xu S. AFM analysis of the lacunar-canalicular network in demineralized compact bone. J Microsc. (2011) 241:291–302. doi: 10.1111/j.1365-2818.2010.03431.x
66. Schneider P, Meier M, Wepf R, Müller R. Serial FIB/SEM imaging for quantitative 3D assessment of the osteocyte lacuno-canalicular network. Bone (2011) 49:304–11. doi: 10.1016/j.bone.2011.04.005
67. Hesse B, Varga P, Langer M, Pacureanu A, Schrof S, Männicke N, et al. Canalicular network morphology is the major determinant of the spatial distribution of mass density in human bone tissue: Evidence by means of synchrotron radiation phase-contrast nano-CT. J Bone Miner Res. (2015) 30:346–56. doi: 10.1002/jbmr.2324
68. Weiner S, Wagner H. The material bone: Structure-mechanical function relations. Annu Rev Mater Sci. (1998) 28:271–98. doi: 10.1146/annurev.matsci.28.1.271
69. Katz J, Yoon H. Stucture and anisotropic mechanical properties of bone. IEEE Trans Biomed Eng. (1984) 31:878–84. doi: 10.1109/TBME.1984.325252
70. Hellmich C, Barthélémy JF, Dormieux L. Mineral-collagen interactions in elasticity of bone ultrastructure - a continuum micromechanics approach. Eur J Mech A Solids (2004) 23:783–810. doi: 10.1016/j.euromechsol.2004.05.004
71. Hellmich C, Ulm FJ. Drained and undrained poroelastic properties of healthy and pathologial bone: a poro-micromechanical investigation. Trans Porous Med. (2005) 58:243–68. doi: 10.1007/s11242-004-6298-y
72. Hagen G. Über die Bewegung des Wassers in engen cylindrischen Röhren [On the movement of water in narrow cylindrical tubes]. Poggendorf's Annalen der Physik und Chemie (1839) 122:423–4.
73. Poiseuille J. Recherches Expérimentales sur le Mouvement des Liquids Dans les Tubes de très Petits diamètres [Experimental Research on the Movement of Liquids in Tubes of Very Small Diameters]. Mémoires présentés par divers savants à l'Académie Royale des Sciences de l'Institut de France IX (1847) 433–544. In French.
75. Markov M, Kazatchenko E, Mousatov A, Pervago E. Permeability of the fluid-filled inclusions in porous media. Trans Porous Med. (2009) 84:307–17. doi: 10.1007/s11242-009-9503-1
76. Beavers G, Joseph DD. Boundary conditions at a naturally permeable wall. J Fluid Mech. (1967) 30:197–207.
77. Saffman P. On the boundary condition at the surface of a porous medium. Stud Appl Math. (1971) 50:93–101.
78. Gururaja S, Kim H, Swan C, Brnad R, Lakes R. Modeling deformation-induced fluid flow in cortical bone's canalicular-lacunar system. Ann Biomed Eng. (2005) 33:7–25. doi: 10.1007/s10439-005-8959-6
79. Weinbaum S, Cowin S, Zeng Y. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. J Biomech. (1994) 27:339–60.
80. Gardinier J, Townend C, Jen KP, Wu Q, Duncan R, Wang L. In situ permeability measurement of the mammalian lacunar-canalicular system. Bone (2010) 46:1075–81. doi: 10.1016/j.bone.2010.01.371
82. Pollack G. The Fourth Phase of Water Beyond Solid, Liquid, and Vapor Seattle, WA: Ebner and Sons (2013).
83. Ichikawa Y, Kawamura K, Fujii N, Nattavut T. Molecular dynamics and multiscale homogenization analysis of seepage/diffusion problem in bentonite clay. Int J Numer Methods Eng. (2002) 54:1717–49. doi: 10.1002/nme.488
84. Pivonka P, Hellmich C, Smith D. Microscopic effects on chloride diffusivity of cement pastes–a scale-transition analysis. Cement Concrete Res. (2004) 34:2251–60. doi: 10.1016/j.cemconres.2004.04.010
85. Ichikawa Y, Kawamura K, Nakano M, Kitayama K, Fujii N. Molecular behavior and micro/macro analysis of diffusion problem in bentonite. CD-ROM Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering. Barcelona: ECCOMAS (2000).
86. Sansalone V, Kaiser J, Naili S, Lemaire T. Interstitial fluid flow within bone canaliculi and electro-chemo-mechanical features of the canalicular milieu. Biomech Model Mechanobiol. (2013) 12:533–53. doi: 10.1007/s10237-012-0422-7
87. Kaiser J, Lemaire T, Naili S, Sansalone V, Komarova S. Do calcium fluxes within cortical bone affect osteocyte mechanosensitivity? J Theor Biol. (2012) 303:75–86. doi: 10.1016/j.jtbi.2012.03.001
88. Beno T, Yoon Y, Cowin S, Fritton S. Estimation of bone permeability using accurate microstructural measurements. J Biomech. (2006) 39:2378–87. doi: 10.1016/j.jbiomech.2005.08.005
89. Lemaire T, Naïli S, Rémond A. Study of the influence of fibrous pericellular matrix in the cortical interstitial fluid movement with hydroelectrochemical effects. J Biomech Eng. (2008) 130:1–11. doi: 10.1115/1.2838025
90. Gailani G, Benalla M, Mahamud R, Cowin S, Cardoso L. Experimental determination of the permeability in the lacunar–canalicular porosity of bone. J Biomech Eng. (2009) 131:1–7. doi: 10.1115/1.3200908
91. Forner-Cordero A, Koopman H, van der Helm F. Inverse dynamics calculations during gait with restricted ground reaction force information from pressure insoles. Gait Posture (2006) 23:189–99. doi: 10.1016/j.gaitpost.2005.02.002
92. Cordey J, Gautier E. Strain gauges used in the mechanical testing of bones part III: Strain analysis, graphic determination of the neutral axis. Injury (1999) 30:SA21–5. doi: 10.1016/S0020-1383(99)00122-9
93. Duda G, Schneider E, Chao E. Internal forces and moments in the femur during walking. J Biomech. (1997) 30:933–41.
94. Lerebous C, Buenzli P, Scheiner S, Pivonka P. A multiscale mechanobiological model of bone remodelling predicts site-specific bone loss in the femur during osteoporosis and mechanical disuse. Biomech Model Mechanobiol. (2016) 15:43–67. doi: 10.1007/s10237-015-0705-x
95. Huang B, Chang C, Wang F, Lin A, Tsai Y, Huang M, et al. Dynamic characteristics of a hollow femur. Life Sci J. (2012) 9:723–6.
97. Bauchau O, Craig J. Euler-Bernoulli beam theory. In: Barber JR, Klarbring A, editors. Structural Analysis. Solid Mechanics and Its Applications, Vol. 163. Dordrecht: Springer (2009). p. 173–221.
98. Price C, Zhou X, Li W, Wang L. Real-time measurement of solute transport within the lacunar-canalicular system of mechanically loaded bone: direct evidence for load-induced fluid flow. J Bone Miner Res. (2011) 26:277–85. doi: 10.1002/jbmr.211
99. Wang B, Zhou X, Price C, Li W, Pan J, Wang L. Quantifying load-induced solute transport and solute-matrix interaction within the osteocyte lacunar-canalicular system. J Bone Miner Res. (2014) 28:1075–86. doi: 10.1002/jbmr.1804
100. Jacobs C, Yellowley C, Davis B, Zhou Z, Cimbala J, Donahue H. Differential effect of steady versus oscillating flow on bone cells. J Biomech. (1998) 31:969–76.
101. Bakker A, Soejima K, Klein–Nulend J, Burger E. The production of nitric oxide and prostaglandin E2 by primary bone cells is shear stress dependant. J Biomech. (2001) 34:671–7. doi: 10.1016/S0021-9290(00)00231-1
102. Cheng B, Zhao S, Luo J, Sprague E, Bonewald L, Jiang J. Expression of functional gap junctions and regulation by fluid flow in osteocyte–like MLO–Y4 Cells. J Bone Miner Res. (2001) 16:249–59. doi: 10.1359/jbmr.2001.16.2.249
103. Bancroft G, Sikavitsas V, van den Dolder J, Sheffield T, Ambrose C, Jansen J, et al. Fluid flow increases mineralized matrix deposition in 3D perfusion culture of marrow stromal osteoblasts in a dose–dependent manner. Proc Natl Acad Sci USA. (2002) 99:12600–5. doi: 10.1073/pnas.202296599
104. Haut Donahue T, Haut T, Yellowley C, Donahue H, Jacobs C. Mechanosensitivity of bone cells to oscillating fluid flow induced shear stress may be modulated by chemotransport. J Biomech. (2003) 36:1363–71. doi: 10.1016/S0021-9290(03)00118-0
105. Bakker A, Klein–Nulend J, Burger E. Mechanotransduction in bone cells proceeds via activation of COX–2, but not COX–1. Biochem Biophys Res Commun. (2003) 305:677–83. doi: 10.1016/S0006-291X(03)00831-3
106. Bacabac R, Smit T, Mullender M, Dijcks S, Van Loon J, Klein–Nulend J. Nitric oxide production by bone cells is fluid shear stress rate dependent. Biochem Biophys Res Commun. (2004) 315:823–9. doi: 10.1016/j.bbrc.2004.01.138
107. Kreke M, Huckle W, Goldstein A. Fluid flow stimulates expression of osteopontin and bone sialoprotein by bone marrow stromal cells in a temporally dependent manner. Bone (2005) 36:1047–55. doi: 10.1016/j.bone.2005.03.008
108. Genetos D, Geist D, Liu D, Donahue H, Duncan R. Fluid shear–induced ATP secretion mediates prostaglandin release in MC3T3–E1 osteoblasts. J Bone Miner Res. (2005) 20:41–9. doi: 10.1359/JBMR.041009
109. Li D, Tang T, Lu J, Dai K. Effects of flow shear stress and mass transport on the construction of a large–scale tissue–engineered bone in a perfusion bioreactor. Tissue Eng A. (2009) 15:2773–83. doi: 10.1089/ten.tea.2008.0540
110. Xia X, Batra N, Shi Q, Bonewald L, Sprague E, Jiang J. Prostaglandin promotion of osteocyte gap junction function through transcriptional regulation of connexin 43 by glycogen synthase kinase 3/beta–catenin signaling. Mol Cell Biol. (2010) 30:206–19. doi: 10.1128/MCB.01844-08
111. Sinlapabodin S, Amornsudthiwat P, Damrongsakkul S, Kanokpanont S. An axial distribution of seeding, proliferation, and osteogenic differentiation of MC3T3–E1 cells and rat bone marrow–derived mesenchymal stem cells across a 3D Thai silk fibroin/gelatin/hydroxyapatite scaffold in a perfusion bioreactor. Mater Sci Eng C. (2016) 58:960–70. doi: 10.1016/j.msec.2015.09.034
112. Daish C, Blanchard R, Gulati K, Losic D, Findlay D, Harvie D, et al. Estimation of anisotropic permeability in trabecular bone based on microct imaging and pore-scale fluid dynamics simulations. Bone Rep. (2017) 6:129–39. doi: 10.1016/j.bonr.2016.12.002
113. Lemaire T, Lemonnier S, Naili S. On the paradoxical determinations of the lacuno-canalicular permeability of bone. Biomech Model Mechanobiol. (2012) 11:933–46. doi: 10.1007/s10237-011-0363-6
114. Lemaire T, Pham T, Capiez-Lernout E, de Leeuw N, Naili S. Water in hydroxyapatite nanopores: possible implications for interstitial bone fluid flow. J Biomech. (2015) 48:3066–71. doi: 10.1016/j.jbiomech.2015.07.025
115. Swan C, Lakes R, Brand R, Stewart K. Micromechanically based poroelastic modeling of fluid flow in Haversian bone. J Biomech Eng. (2003) 125:25–37. doi: 10.1115/1.1535191
116. Swan C, Kim HJ. Multi-scale micro-mechanical poroelastic modeling of fluid flow in cortical bone. In: Proceedings of the ASME 2004 International Mechanical Engineering Congress and Exposition. Anaheim, CA (2004). p. 79–90.
117. Hervé E, Zaoui A. n-Layered inclusion-based micromechanical modelling. Int J Eng Sci. (1993) 31:1–10.
118. Scheiner S, Komlev V, Gurin A, Hellmich C. Multiscale mathematical modeling in dental tissue engineering: towards computer-aided design of a regenerative system based on hydroxyapatite granules, focusing on early and mid-term stiffness recovery. Front Physiol. (2016b) 7:383. doi: 10.3389/fphys.2016.00383
119. Scheiner S, Komlev V, Hellmich C. Strength increase during ceramic biomaterial-induced bone regeneration: a micromechanical study. Int J Fract. (2016) 202:217–35. doi: 10.1007/s10704-016-0157-z
120. Rosenhead L editor. Laminar Boundary Layers (Fluid Motion Memoirs). Oxford: Oxford University Press (1963).
121. You L, Cowin S, Schaffler M, Weinbaum S. A model for strain amplification in the actin cytoskeleton of osteocytes due to fluid drag on pericellular matrix. J Biomech. (2001) 34:1375–86. doi: 10.1016/S0021-9290(01)00107-5
122. Anderson E, Knothe Tate M. Idealization of pericellular fluid space geometry and dimension results in a profound underprediction of nano-microscale stresses imparted by fluid drag on osteocytes. J Biomech. (2008) 41:1736–46. doi: 10.1016/j.jbiomech.2008.02.035
123. Verbruggen S, Vaughan T, McNamara L. Fluid flow in the osteocyte mechanical environment: a fluid-structure interaction approach. Biomech Model Mechanobiol. (2014) 13:85–97. doi: 10.1007/s10237-013-0487-y
124. Scheiner S, Pivonka P, Hellmich C. Coupling systems biology with multiscale mechanics, for computer simulations of bone remodeling. Comput Methods Appl Mech Eng. (2013) 254:181–96. doi: 10.1016/j.cma.2012.10.015
125. Pivonka P, Buenzli P, Scheiner S, Hellmich C, Dunstan C. The influence of bone surface availability in bone remodelling – a mathematical model including coupled geometrical and biomechanical regulations of bone cells. Eng Struct. (2013) 47:134–47. doi: 10.1016/j.engstruct.2012.09.006
126. Scheiner S, Pivonka P, Smith D, Dunstan C, Hellmich C. Mathematical modeling of postmenopausal osteoporosis and its treatment by the anti-catabolic drug denosumab. Int J Numer Methods Biomed. Eng. (2014) 30:1–27. doi: 10.1002/cnm.2584
Keywords: mechanobiology, osteocytes, pore spaces, pressure gradient, micromechanics, permeability
Citation: Estermann S-J and Scheiner S (2018) Multiscale Modeling Provides Differentiated Insights to Fluid Flow-Driven Stimulation of Bone Cellular Activities. Front. Phys. 6:76. doi: 10.3389/fphy.2018.00076
Received: 29 November 2017; Accepted: 29 June 2018;
Published: 11 September 2018.
Edited by:
Iwona Jasiuk, University of Illinois at Urbana-Champaign, United StatesReviewed by:
Silvia Capuani, Consiglio Nazionale Delle Ricerche (CNR), ItalyVittorio Sansalone, Université Paris-Est Créteil Val de Marne, France
Copyright © 2018 Estermann and Scheiner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Stefan Scheiner, c3RlZmFuLnNjaGVpbmVyQHR1d2llbi5hYy5hdA==
 Sarah-Jane Estermann
Sarah-Jane Estermann Stefan Scheiner
Stefan Scheiner