
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 05 June 2018
Sec. Interdisciplinary Physics
Volume 6 - 2018 | https://doi.org/10.3389/fphy.2018.00053
This article is part of the Research TopicWomen in ScienceView all 9 articles
Macromolecular crowding plays a principal role in a wide range of biological processes including gene expression, chromosomal compaction, and viral infection. However, the impact that crowding has on the dynamics of nucleic acids remains a topic of debate. To address this problem, we use single-molecule fluorescence microscopy and custom particle-tracking algorithms to investigate the impact of varying macromolecular crowding conditions on the transport and conformational dynamics of large DNA molecules. Specifically, we measure the mean-squared center-of-mass displacements, as well as the conformational size, shape, and fluctuations, of individual 115 kbp DNA molecules diffusing through various in vitro solutions of crowding polymers. We determine the role of crowder structure and concentration, as well as ionic conditions, on the diffusion and configurational dynamics of DNA. We find that branched, compact crowders (10 kDa PEG, 420 kDa Ficoll) drive DNA to compact, whereas linear, flexible crowders (10, 500 kDa dextran) cause DNA to elongate. Interestingly, the extent to which DNA mobility is reduced by increasing crowder concentrations appears largely insensitive to crowder structure (branched vs. linear), despite the highly different configurations DNA assumes in each case. We also characterize the role of ionic conditions on crowding-induced DNA dynamics. We show that both DNA diffusion and conformational size exhibit an emergent non-monotonic dependence on salt concentration that is not seen in the absence of crowders.
Biological cells are highly crowded by macromolecules of varying sizes and structures. This complex crowded environment has been shown to directly impact key DNA processes and functions including replication, transcription, transformation, gene expression, and chromosomal compaction [1–6]. Investigating the impact of crowding on DNA is further motivated by the design of gene therapy and drug delivery systems, as well as the production and manipulation of synthetic cells and nanomaterials [2, 3, 7, 8]. Crowding can induce changes in DNA conformations, such as compaction, swelling, and elongation; and alter its diffusivity and intramolecular fluctuations [9, 10, 14]. However, the exact effect that crowding has on DNA mobility and conformation remains poorly understood. The wide range of differing results presented in the literature likely stems from the myriad of sizes and types of crowders, as well as the varying ionic conditions, used in in vitro experiments—both of which directly impact the effect of crowding on DNA.
Because crowding studies are largely motivated by the role crowding plays in cells, several studies have investigated DNA dynamics in vivo [1, 5, 11–13]. While these studies can directly illuminate DNA behavior in cells, the role that each variable (e.g., crowder size, structure, concentration, ionic conditions) plays in the measured dynamics is hard to discern. Thus, researchers have turned to in vitro studies to methodically explore the role of each variable separately [1, 14, 15]. Most in vitro crowding studies use synthetic polymers, similar in size to the majority of small proteins in cells, at concentrations similar to those found in cells (20–40% w/v). Polysaccharides, such as dextran, polyethylene glycol (PEG) and Ficoll, are advantageous as crowders because they are inert, nonbinding, commercially available in a range of molecular weights, and can often be described by basic polymer theory [16–22]. While these crowders are often used interchangeably to mimic cellular crowding, they differ considerably in their structure and conformational shape.
Dextran is a linear, flexible polymer which is reported to assume a random coil conformation in solution with an empirical scaling of hydrodynamic radius with molecular weight of [19, 23, 24]. While this scaling exponent is close to that of an ideal polymer chain (scaling exponent of 0.5), dextran coils have been shown to be highly asymmetric [19]. At high concentrations, dextran can form entanglements more easily than branched crowders of similar molecular weight due to its linear, flexible structure. Further, its asymmetric shape suggests that at high enough concentrations nematic ordering is also more readily accessible than for branched crowders [25]. PEG is a flexible linear polymer with a hydrodynamic radius that scales as . However, at concentrations above ~7% w/v it self-associates to form highly branched structures which are suggested to behave more like hard spheres than random coils [26]. Ficoll is a highly-branched polymer that assumes a compact spherical conformation that can be described by the empirical scaling [18, 20].
A number of previous studies have examined the effects of these crowders on polymer transport, conformation, and stability [27–36]. However, the role these crowders play in the diffusion or conformation of large DNA molecules remains largely unexplored. Further, no previous studies have directly compared the impact that each of these distinctly-shaped crowders has on DNA dynamics. One previous study investigated the role of crowder shape on protein diffusion by measuring the diffusion of heart-shaped BSA and Y-shaped IgG proteins in crowded solutions of either BSA or IgG [37]. Results showed that the varying excluded volume resulting from the differently-shaped proteins played the most important role in diffusion, as opposed to crowder concentration or direct interactions. A previous simulation study examined the effect of crowder shape on the conformation of stiff rod polymers [25]. Results showed that at high concentrations, spherical crowders caused compaction of the polymers, reducing their radius of gyration Rg, while spherocylindrical particles increased Rg. The increase in Rg was thought to be caused by nematic ordering of spherocylindrical particles which allow the polymers to elongate in the direction of ordering.
We previously measured the diffusion and conformational dynamics of DNA crowded by dextran of varying molecular weights and concentrations [38, 39]. We found that the decrease in DNA diffusivity with increasing dextran concentration was actually less than expected based on the increasing viscosity of the crowding solutions [38]. Namely, measured diffusion coefficients followed a weaker scaling with viscosity than the classical Stokes-Einstein scaling D~η−1. This “enhanced” diffusion was coupled with conformational elongation of DNA from its random coil configuration.
While entropically-driven depletion interactions tend to compact large macromolecules to maximize the available volume for the small crowders, elongation or swelling could ensue if enthalpic effects counteract depletion forces. Because DNA is negatively charged, entropy maximization competes with the electrostatic (enthalpic) cost of compaction, which can lead DNA to preferentially elongate rather than compact to reduce its conformational volume in certain cases. Varying the ionic strength of the solution can directly tune the electrostatic cost of compaction via positive ions (e.g., Na+) screening DNA charge. In fact, increased salt concentrations have been shown to be essential to PEG-induced condensation/aggregation of DNA (known as ψ-compaction) [33, 34, 40, 41]. Since the discovery of ψ-compaction [40], there have been numerous experimental [4, 6, 8, 41–51] and theoretical [52–58] studies investigating this phenomenon. Experiments have shown that ψ-compaction of 166 kbp DNA is a first-order transition from random coil configurations to compacted states; and when the concentration and/or molecular weight of PEG is increased the required NaCl concentration for compaction is reduced [41]. The lowest reported NaCl concentration to induce compaction was 50 mM, which required 25% w/v of 11.5 kDa PEG, in contrast to the 300 mM NaCl required when 10% w/v of 3 kDa PEG was used. Magnetic and optical tweezers studies have examined the force required to uncoil compacted 48.5 kbp DNA in the presence of 15–30% w/v PEG and varying concentrations of NaCl [34, 43]. These studies found that this force increased as the PEG molecular weight and NaCl concentration increased (up to 6 kDa PEG and 2 M NaCl). The remaining studies on DNA compaction have focused on the effects of salt in confined conditions [6, 42, 59–63] or in the presence of charged crowders [64–71]. These previous studies have shed important new light on the role that charge screening plays in crowding-induced DNA compaction. However, the interplay between crowder shape and salt concentration has been left completely unexplored. Further, these studies have all focused on steady-state DNA conformations, so the question of how ionic strength impacts the mobility and conformational fluctuations of crowded DNA remains an important open question.
Here, we explore the effect of crowder shape and ionic conditions on the intriguing crowding-induced DNA dynamics that have previously been reported. Specifically, we track the center-of-mass mean-squared displacements, as well as the size and shape of single DNA molecules diffusing in solutions of crowders with varying structural properties and molecular weights (10 kDa dextran, 500 kDa dextran; 10 kDa PEG, 420 kDa Ficoll). Based on the literature, throughout the text we classify PEG and Ficoll as branched crowders and dextrans as linear crowders. We further explore the effect of salt concentration on the measured DNA properties by examining cases of five-fold increased and decreased NaCl under maximally crowded conditions. We show that crowding-induced DNA conformations are highly-dependent on crowder structure, with branched crowders compacting DNA while linear crowders induce elongation. We further show DNA diffusion exhibits a surprising non-monotonic dependence on salt concentration in crowded environments.
All experimental methods and computational analysis, briefly summarized below, are thoroughly described and verified in [38, 39, 72]. Linear 115 kbp DNA molecules are prepared through replication of supercoiled bacterial artificial chromosomes in Escherichia coli, followed by extraction, purification, and enzymatic linearization [39]. A trace amount of DNA is fluorescent-labeled with YOYO-I (Thermo Scientific) and embedded in a solution of 0–40% w/v crowding polymers dissolved in aqueous buffer (10 mM Tris-HCl, 1 mM EDTA, 10 mM NaCl, 4% β-mercaptoethanol). The four different crowders used are: 10 kDa dextran (Sdex), 500 kDa dextran (Ldex), 420 kDa Ficoll, and 10 kDa PEG (all purchased from Sigma Aldrich). For reference, the hydrodynamic radius, Rh, of Sdex, Ldex, PEG, and Ficoll are 2.2, 15.5, 3.2, and 5.6 nm, respectively [16, 18, 19, 24]. Unless indicated, NaCl concentration is 10 mM. The viscosity of each crowded solution was measured using optical tweezers microrheology as described previously [39, 73].
To determine the diffusion coefficients as well as the conformational size, shape and fluctuations of crowded DNA, single embedded DNA molecules were imaged for 30 s at 10 frames per second using a high-speed CCD camera on a Nikon A1R epifluorescence microscope with 60x objective. All presented data are for ensembles of >200 molecules. Using custom-written algorithms (Matlab), we track the center-of-mass (COM) position (x, y), as well as the lengths of the major and minor axes (Rmax and Rmin, respectively) of each molecule over time. We calculate the COM mean-squared displacement in the x and y directions (<Δx2>, <Δy2>) to determine the diffusion coefficient D via <Δx2> = <Δy2> = 2Dt. Error bars are calculated using bootstrapping for 1,000 sub-ensembles [74]. We use Rmax as a measure of the maximum conformational width, and we measure the degree of molecular elongation or asymmetry by comparing Rmax to Rmin. We also define the average conformational size as R = (<Rmax>2 + <Rmin>2)1/2 which we use as a measure of the hydrodynamic radius Rh. Finally, we determine the time-dependence and lengthscales of intramolecular state fluctuations by calculating the ensemble-averaged fluctuation range f(t) = <|Rmax(0)-Rmax(t)|>/<Rmax> for a given lag time t. f(t) can be understood as the relative lengthscale (compared to the conformational size) over which a given molecule fluctuates or “breathes” between different conformational states during a time t. All data presented in Figures 1–4 can be accessed on the Dryad Digital Repository with the identifier: doi: 10.5061/dryad.77g469g.
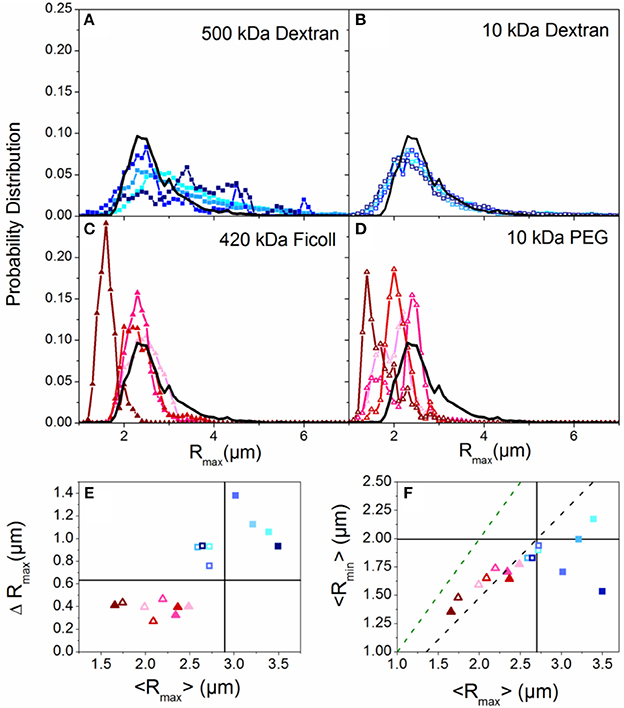
Figure 1. Crowding induces compaction or elongation of DNA dependent on the crowder structure. (A–D) Histograms of major axis lengths (Rmax) for all crowding conditions compared to the buffer condition (black line). Each panel displays results for a different crowder with blue hues denoting linear crowders (A,B; dextrans) and red hues indicating branched crowders (C,D; Ficoll, PEG). Closed symbols indicate high Mw crowders (A,C; 500 kDa dextran, 420 kDa Ficoll) and open symbols denote low Mw crowders (B,D; 10 kDa dextran, 10 kDa PEG). In each panel the color shade increases with increasing crowder concentration (10, 20, 30, 40% w/v). (E) The standard deviation of each Rmax distribution, ΔRmax, vs. the corresponding mean, <Rmax>. The color scheme is the same as (A–D). The buffer condition (0% crowder) value is indicated by the intersection of the horizontal and vertical lines. Symbols above or below the horizontal line indicate increased or decreased ranges in conformational states accessed, and symbols to the left or right of the vertical line indicate crowding-induced compaction or elongation. (F) Phase plot of the mean major and minor axis lengths (<Rmax>,<Rmin>) for each crowded condition. The green dashed line denotes the <Rmax>: <Rmin> ratio for a spherical particle. The black dashed line denotes <Rmax>: <Rmin> for the empirically measured random coil configuration in aqueous buffer. Note that branched crowders (triangles) generally decrease <Rmax> and <Rmax>: <Rmin> indicating more spherical compacted conformations, while linear crowders (squares) tend to elongate DNA.
We first examine the role of crowder structure on DNA conformation and diffusion. To determine the role that crowder structure plays in crowding-induced changes to DNA conformation, we look to the measured major and minor axis lengths Rmax and Rmin. Figures 1A–D shows the distributions of DNA major axis lengths for each crowder type and concentration. There is a noticeable difference between the distributions for branched crowders compared to linear crowders. While branched crowders reduce Rmax (narrowing distributions and shifting them to the left), linear crowders tend to increase Rmax (widening and shifting distributions to the right).
To quantify the degree to which the average major axis length <Rmax> as well as the spread in the distributions (quantified by the standard deviation ΔRmax) vary with crowding, we plot <Rmax> vs. ΔRmax (Figure 1E). The difference between linear and branched crowders is evident: branched crowders decrease ΔRmax and <Rmax>, signifying compaction, while linear crowders tend to increase both quantities, indicating elongation or swelling. Further, elongated or swollen configurations access a wider range of states (larger ΔRmax) than random coil states, while the range of states for compacted configurations is reduced. This reduction is indicative of ordered compaction, in which tight intramolecular packing causes the molecules to fluctuate between fewer states. We note that for Sdex Rmax actually decreases slightly, but ΔRmax still increases appreciably and the distributions show a more pronounced large Rmax tail compared to buffer conditions. Thus, we interpret this data as still demonstrating elongation or swelling rather than compaction. Finally, the (<Rmax>, ΔRmax) data points for all crowders show no discernible trend with crowder concentration, with most data points for 10–40% w/v clustering together. These data indicate that the crowding-induced conformational changes are an all or nothing effect, similar to the discrete first-order phase transition observed in ψ-compaction [41].
To delineate between symmetric swelling vs. elongation (induced by linear crowders), and determine if compacted configurations (induced by branched crowders) are more ellipsoid or spherical in nature than random coils (buffer condition), we compare Rmax to Rmin (Figure 1F). The larger the Rmax:Rmin ratio, the more asymmetric the conformation is. As shown, random coil configurations in buffer conditions exhibit a ~3:2 aspect ratio, as previously predicted and shown [75, 76]. Conversely, compacted conformations induced by branched crowders are more spherical in nature, similar to hard spheres. Linear crowders, on the other hand, markedly increase Rmax:Rmin, signifying elongation rather than symmetric swelling.
Because the spread in our conformational state distributions (ΔRmax) vary for the different crowders, we investigated whether this spread is a result of a heterogeneous ensemble of DNA molecules each assuming a different static conformation, or whether the ensemble is fairly uniform but each molecule transitions between different states over time. To determine the extent to which single molecules transition or “breathe” between different conformational states over time, we measure the change in Rmax for varying lag times t and normalize by <Rmax>. We refer to this quantity as the fluctuation range, f(t) = <|Rmax(0)-Rmax(t)|>/<Rmax>. As shown in Figures 2A,B, f(t) increases over time for all cases and approaches a steady-state value, which we term the steady-state fluctuation range fss (Figure 2C). Thus, the spread in the conformational state data (Figure 1) arises from single molecules breathing between different states over time, rather than a heterogeneous ensemble of static conformations. This result also indicates that the crowding solutions are largely homogenous, so molecules in different regions of the solution exhibit similar conformations. The results shown in Figure 2 also display a marked difference between linear and branched crowders: while Sdex and Ldex increase fss by ~30%, both PEG and Ficoll reduce fss to ~50% of the buffer condition value. These data validate our interpretation that elongated molecules access a broader range of conformational states compared to more rigid compact configurations. It is also notable that while there is a stark difference between the effect of linear crowders vs. branched crowders, the fluctuation length shows little dependence on the concentration or size of crowders. This result is similar to the discrete phase transition seen in Figure 1, and underlines the critical role that crowder structure plays in DNA dynamics.
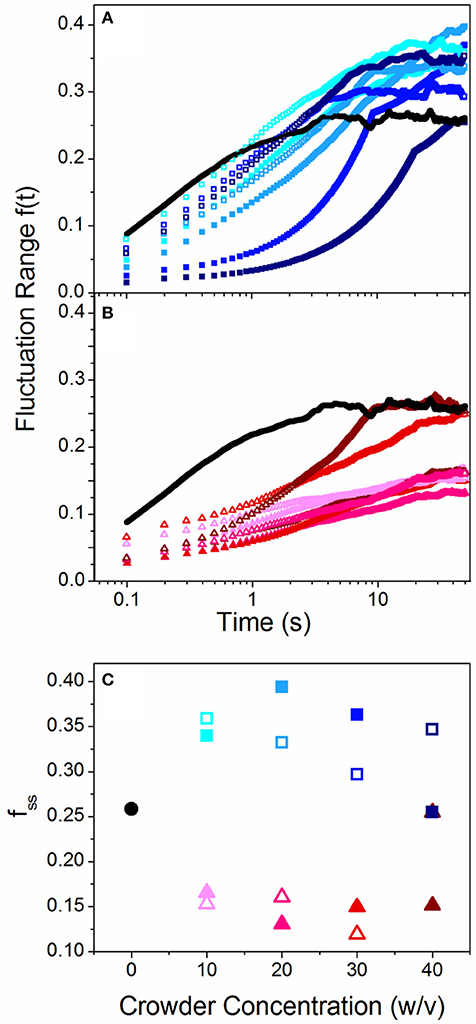
Figure 2. Crowded DNA molecules fluctuate over a range of different conformational states over time with a steady state fluctuation range that depends on crowder structure. (A,B) Fluctuation range, f(t), as a function of time for linear (A) and branched (B) crowders compared to buffer conditions (black lines). Open and closed symbols signify small (10 kDa) and large (~500 kDa) crowders and color shade increases with increasing crowder concentrations (10, 20, 30, 40% w/v). (C) Steady-state fluctuation range, fss [i.e. the terminal plateau values of f(t)], vs. crowder concentration for linear (squares) and branched (triangles) crowders. As shown, linear crowders increase fss from the buffer condition value, while branched crowders reduce fss. These effects are largely independent of crowder size and concentration.
The question remains as to why linear crowders elongate DNA while branched crowders lead to compaction. Both conformations reduce the effective volume the DNA takes up in solution by either stretching into a long thin strand or compacting down to an ordered sphere. This crowding-induced phase transition arises from entropically-driven depletion interactions with the crowders. Namely, the DNA is forced to reduce its configurational volume to maximize the volume, and thus the entropy, of the crowders. Both compaction and elongation reduce the configurational entropy of the DNA from its random coil configuration by reducing the conformational volume and introducing more order, such that the orientation of each DNA segment is not completely independent of its neighbor (as in a random coil). In our previous work we postulated that the crowding-induced elongation arose from the enthalpic cost of compaction due to electrostatic repulsion [39]. However, we show here that the resulting DNA conformation is principally determined by the crowder structure, as the enthalpic contribution remains unchanged in all conditions yet the conformations are dramatically different for the different crowders.
As described in the Introduction, dextrans assume highly asymmetric random coil configurations in solution, compared to the hard sphere configurations of Ficoll and self-associated PEG crowders. If the DNA configurational transitions are entropically-driven then the DNA should assume the shape that allows for the most efficient packing of crowders around the DNA to maximize their available volume. Therefore, the DNA should assume a configuration that most closely matches that of the crowders while still reducing its volume from a random coil. A previous simulation study comparing the effects of spherical vs. cylindrical crowders on the conformational size of short rigid DNA molecules showed that cylindrical crowders elongated DNA while spherical crowders more readily compacted DNA [25]. While these results cannot be directly compared to our study, as our DNA is much larger and more flexible, they suggest that asymmetric crowders promote elongation to maximize the packing efficiency and available volume of the crowders. This study also showed that the presence of the DNA led to local entropically-driven nematic ordering of the crowders around the DNA, which in turn facilitated DNA elongation [25]. In contrast, branched crowders are spherical in nature so packing is most efficient when DNA is likewise spherical. Thus, it appears that different entropy maximization considerations for differently shaped crowders is what drives the crowder-dependent conformational changes rather than the enthalpic costs arising from DNA self-repulsion. Similar conclusions have been drawn from crowding experiments using differently shaped proteins, in which the varying excluded volume resulting from the different crowder shapes played the primary role in determining protein dynamics [37].
We previously found that volume reducing conformational changes in crowded environments were coupled with “enhanced” diffusion in which the scaling of D with viscosity was weaker than the Stokes-Einstein (SE) scaling D~η−1 [38, 39]. We attributed this enhanced diffusion to the reduction in conformational volume of the DNA. Namely, according to the SE relation D = kbT/6πηR for a spherical particle of radius R, a reduction in R leads to an increase in D such that a particle could diffuse faster than expected in increasingly viscous solutions. The diffusion of flexible polymers in solution can likewise be described by the SE relation if R is taken to be the hydrodynamic radius Rh [77]. This relation has shown to hold for DNA and other flexible polymers of varying sizes in Newtonian fluids [24, 77–79]. If a reduced Rh were responsible for the increased diffusion coefficients, and the dynamics could be explained by SE, then the quantity DRh should scale as η−1.
To test this assumption and determine the role of crowder structure on DNA mobility, we examine DNA diffusion coefficients as a function of crowder concentration, conformational size, and solution viscosity (Figure 3). As shown, the diffusion coefficients, D, for all crowders decrease with increasing crowder concentration, as expected given the increasing viscosity of crowded solutions (Figure 3A). However, the scaling of D with η is shallower than η −1. To delineate between the effect of changing conformational sizes and hydrodynamic effects of crowding we scale diffusion coefficients by the corresponding conformational size R. In Figure 3B, we plot vs. where each tilde represents normalization by the corresponding buffer condition value. As shown the data clearly violate SE predictions, with an average scaling for all crowders of D~η−0.5.
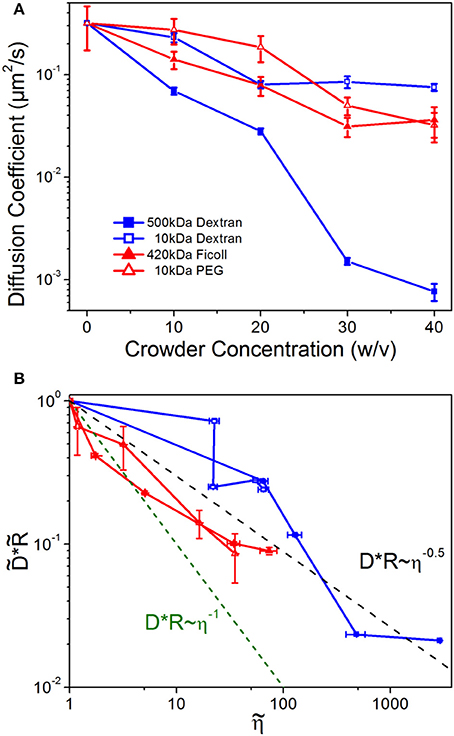
Figure 3. DNA diffusion decreases with increasing crowder concentrations, but universally diffuses faster than predicted by Stokes-Einstein scaling. (A) Diffusion coefficients for DNA crowded by varying concentrations (w/v) of 500 kDa dextran (blue filled squares), 10 kDa dextran (blue open squares), 420 kDa Ficoll (red filled triangles), and 10 kDa PEG (red open triangles). (B) DNA diffusion coefficients D scaled by the empirical DNA size R, vs. crowded solution viscosity η. All quantities are normalized by the corresponding buffer condition value, which we denote by tilde (). The dashed green line indicates the SE relation DR~η−1, while the black dashed line shows the average empirical scaling, D~η−0.5. Note that nearly every value lies above the predicted Stokes-Einstein value.
Violations of the SE relation can arise if the local viscosity that the diffusing particle is experiencing is different than the bulk viscosity, if the crowding fluid exhibits non-Newtonian features such as viscoelasticity or shear-thinning, or if large heterogeneities are present in the fluid [80–82]. We do not expect non-Newtonian properties to play a role in our measurements as previous work has shown that the crowding solutions we are using are largely Newtonian [38]. We also see no evidence of significant spatial heterogeneities based on the distributions of our conformational data (Figure 1) and error analysis of the diffusion coefficients (Figure 3). Instead, our results suggest that the DNA is experiencing a local viscosity that is lower than the bulk viscosity, such that it can evade the SE limited diffusion coefficient. Such scale-dependent viscosity in crowded environments, has been predicted to arise due to the formation of depletion zones surrounding the diffusing particle in which the local concentration of crowders is less than the bulk concentration [81–85]. This microscale effect has been shown to be important in several biological applications including gene regulation [86], kinesin diffusion near microtubules [87], and protein binding kinetics in HeLa cells [85, 88].
We note that the enhanced diffusion effect is more pronounced for linear crowders (Sdex, Ldex) than branched crowders (PEG, Ficoll), especially at low concentrations. This effect likely arises from the varying degrees to which the local viscosity is reduced by the different packing configurations of linear vs. branched crowders. Our results suggest that elongated structures in linear crowders are more efficiently packed, such that the local environment is less concentrated compared to that of compacted structures in spherical crowders. Previous simulations have shown that linear crowders can form nematic clusters surrounding a diffusing probe, which in turn elongates [25]. Aligned linear polymers are less resistant to flow than isotropically-arranged, sterically overlapping linear polymers, and provide more free volume surrounding the DNA, thereby creating a lower viscosity local environment than the equivalent solution of branched crowders. Further, at low viscosities there can be less of a gradient between the local and bulk viscosity, owing to the relatively low concentration of crowders, so the effect of depletion zones would be reduced. Finally, we note the similarity between the viscosities of PEG and Ficoll at equal concentrations, as well as their effect on DNA diffusion, despite their large Mw difference and ~2x difference in Rh (Figure 3B). This result, along with our conformational data (Figures 1, 2), confirms that PEG is indeed self-associating and forming branched structures which more closely mimic the branched structure and size of Ficoll.
Our results presented above appear to be driven primarily by entropic rather than enthalpic contributions to the free energy, so we aimed to vary the enthalpic contribution directly to determine the extent to which enthalpic effects play a role in our results. To do so, we examine the role of salt concentration on DNA crowding by carrying out measurements in the presence of NaCl concentrations that are 5x higher and lower than our standard conditions (10 mM NaCl). According to the wormlike chain model for DNA, as NaCl concentration increases, the persistence length lp should decrease due to Na+ ions partially screening the negatively charged DNA backbone [89]. The reduced electrostatic repulsion between neighboring DNA segments increases the flexibility of the DNA. Because our data show much more of a dependence on crowder structure than concentration (Figures 1–3), in these experiments we fix our crowder concentration at 40% w/v.
As shown in Figures 4A–C, branched crowders induce greater DNA compaction and lead to smaller fss values compared to linear crowders for all salt conditions. Thus, the effects of crowder structure on DNA conformation appear robust to ionic conditions. However, we do find that salt concentration plays a role in the resulting crowding-induced DNA conformations. High salt conditions (50 mM NaCl) enable all crowders to compact DNA (seen as a large drop in <Rmax> and <Rmin>, Figure 4A) and markedly suppress conformational fluctuations (seen as a large drop in fss and ΔRmax, Figures 4B,C). This large change is likely facilitated by the increased flexibility of DNA at high [NaCl]. Because DNA is more flexible it can more easily transition between different conformational states, so it can more readily undergo large changes to its conformation driven by the entropy maximization of the crowders. This effect is in accord with the classic ψ-compaction mechanism in which high salt conditions and crowding are both needed to efficiently induce bulk condensation of DNA [40]. In contrast, at the lowest NaCl concentration (2 mM) the steady-state fluctuation range remains nearly unchanged by crowders (Figure 4C). Low [NaCl] conditions also result in the smallest change to the conformational size of DNA, with DNA undergoing slight compaction in the presence of all crowder types (Figures 4A,B). While it is the enthalpic contribution to the DNA free energy that drives the change in DNA flexibility with varying salt, as it is a result of varying degrees of charge screening, the resulting crowding-induced conformational changes still appear to be driven primarily by the entropy maximization of the crowders. Namely, in all cases spherical crowders induce more compaction than linear crowders due to the different packing efficiencies of the differently shaped crowders (as described above). Further, because compaction at high salt is only seen in the presence of crowders, charge screening is not the principle mechanism for compaction, rather it simply facilitates the ability for the crowders to compact DNA to maximize their entropy.
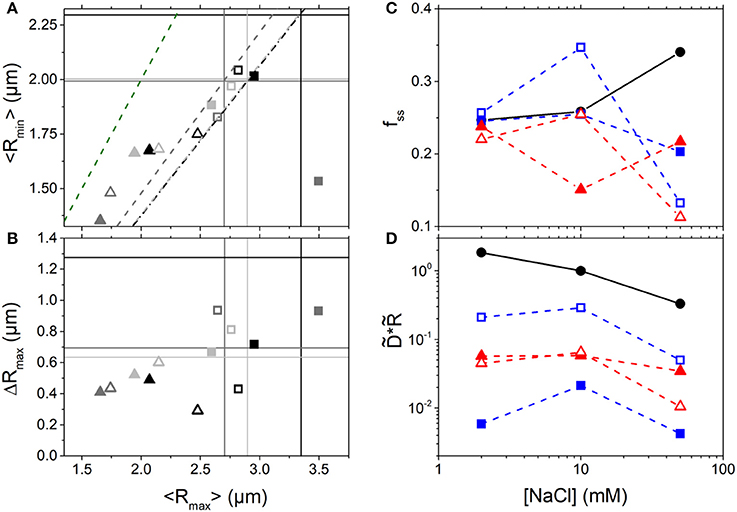
Figure 4. Conformation and mobility of crowded DNA display unexpected non-monotonic dependence on NaCl concentration. (A) Phase plot of the mean major and minor axis lengths (<Rmax>,<Rmin>) for DNA crowded by 10 kDa (open symbols) and ~500 kDa (closed symbols) linear (squares) and branched (triangles) crowders at NaCl concentrations of: 2 mM (light gray), 10 mM (gray), and 50 mM (black). The intersections of the color-coded horizontal and vertical lines denote the buffer condition values at the corresponding salt concentration. The dashed lines show the color-coded <Rmax>: <Rmin> ratio (i.e. degree of sphericity) for the corresponding DNA conformations in buffer conditions. The green dashed line denotes the <Rmax>: <Rmin> ratio for a spherical particle. (B) Phase plot of the mean major axis length <Rmax> and corresponding standard deviation ΔRmax. Colors and symbols are as in (A). As shown, 10 mM salt conditions lead to the most pronounced crowding-induced compaction and elongation (smallest and largest Rmax) compared to lower and higher salt conditions. (C) Steady-state conformational fluctuation range of DNA, fss, as a function of [NaCl] for solutions with no crowders (black circles) and 40% w/v 500 kDa dextran (closed blue squares), 10 kDa dextran (open blue squares), 420 kDa Ficoll (closed red triangles), and 10 kDa PEG (open red triangles). (D) DNA diffusion coefficients D, scaled by the corresponding empirical DNA size R, vs. [NaCl]. D and R are both normalized by the corresponding value in buffer with 10 mM NaCl, denoted by tilde (). Color scheme is as in (C).
To determine the effect of salt-induced conformational changes on DNA mobility we also evaluate the relative diffusion coefficients scaled by the corresponding conformational size, (Figure 4D). Because the varying salt concentrations change the viscosity of the solutions by <1%, one would expect to be constant across all NaCl concentrations if the SE relation were valid in this regime. As shown, we see a surprising non-monotonic dependence of DNA mobility on [NaCl] when crowded: DNA exhibits the fastest rescaled diffusion at 10 mM NaCl. This effect is not seen in buffer conditions in which the mobility decreases with increasing [NaCl]. While 50 mM NaCl induces that largest change in DNA size from its buffer condition value, the most compacted and elongated DNA states are actually seen in 10 mM NaCl. As shown in Figures 4A,B, the 10 mM NaCl data points lie at the extreme left and right-hand sides of the phase plots (low and high <Rmax> values) while the 2 and 50 mM NaCl data are mostly clustered together in the middle of the plot. These extreme conformational state changes likely contribute to the faster diffusion at 10 mM NaCl. However, this effect cannot be explained within the SE framework in which it is simply the changing conformational size that alters the mobility. Rather, we suspect that it is once again due to the varying degrees to which the local viscosity surrounding the DNA is altered in the varying conditions [82, 83]. Future studies will focus on developing quantitative models to fully describe this effect, as well as some of our other presented results, of which we provide qualitative interpretations. However, such theoretical work is outside the scope of the current manuscript.
We have investigated the role of crowder structure, size, and concentration, as well as ionic conditions, on the diffusion and conformational dynamics of large DNA molecules. We crowded 115 kbp DNA with widely used synthetic crowders that can be categorized into linear (dextrans) and branched (Ficoll, PEG) structures of small (10 kDa) and large (~500 kDa) molecular weights. We present a number of intriguing results that have not been previously predicted or observed. We find that linear crowders entropically drive DNA to elongate while branched crowders compact DNA to maximize their entropy. Elongated conformations undergo larger conformational fluctuations than random coils, while compacted configurations are more spherical and access a smaller range of conformational states. These findings are largely independent of crowder concentration and molecular weight. Despite the marked difference in conformational dynamics that DNA exhibits in the presence of different crowders, we find that for both crowder types DNA diffuses faster than expected based on the increasing viscosity of the solutions. We attribute this enhanced diffusion to a combination of entropically-driven conformations that reduce the volume of the DNA as well as a reduced local viscosity surrounding the DNA arising from optimized packing of the crowders. We also find that DNA dynamics exhibit a complex interplay between salt concentration and crowding. In buffer conditions, DNA mobility decreases and the range of conformational states increases with increasing salt (from 2 to 50 mM NaCl). However, upon crowding, DNA diffusion and conformational changes exhibit an emergent non-monotonic dependence on salt concentration, with DNA diffusing the fastest and exhibiting the most extreme compaction or elongation in 10 mM NaCl compared to lower and higher salt concentrations. Our collective results present several complex and unexpected phenomena that are highly relevant to polymer physics and cell biology alike. We hope that these results spur new theoretical investigations to fully understand these intriguing results.
WM collected data, analyzed data, interpreted data, wrote paper. SG prepared samples, collected data, analyzed data. KR prepared samples, collected data. T-CW collected data, analyzed data. RR-A designed experiments, analyzed data, interpreted data, wrote paper.
This research was funded by the Air Force Office of Scientific Research (Young Investigator Program Award No. FA95550-12-1-0315, Biomaterials Award No. FA9550-17-1-0249) and the National Institutes of Health (NNIGMS Award No. R15GM123420).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Ellis RJ. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr Opin Struct Biol. (2001) 11:114–9. doi: 10.1016/S0959-440X(00)00172-X
2. Nakano S, Miyoshi D, Sugimoto N. Effects of molecular crowding on the structures, interactions, and functions of nucleic acids. Chem Rev. (2014) 114:2733–58. doi: 10.1021/cr400113m
3. Miyoshi D, Sugimoto N. Molecular crowding effects on structure and stability of DNA. Biochimie (2008) 90:1040–51. doi: 10.1016/j.biochi.2008.02.009
4. Tan C, Saurabh S, Bruchez MP, Schwartz R, LeDuc P. Molecular crowding shapes gene expression in synthetic cellular nanosystems. Nat Nanotech. (2013) 8:602–8. doi: 10.1038/nnano.2013.132
5. Rivas G, Ferrone F, Herzfeld J. Life in a crowded world. EMBO Rep. (2004) 5:23–7. doi: 10.1038/sj.embor.7400056
6. Pelletier J, Halvorsen K, Ha B-Y, Paparcone R, Sandler SJ, Woldringh CL, et al. Physical manipulation of the Escherichia coli chromosome reveals its soft nature. Proc Natl Acad Sci USA. (2012) 109:E2649–56. doi: 10.1073/pnas.1208689109
7. Heddi B, Phan AT. Structure of human telomeric DNA in crowded solution. J Am Chem Soc. (2011) 133:9824–33. doi: 10.1021/ja200786q
8. Li GW, Berg OG, Elf J. Effects of macromolecular crowding and DNA looping on gene regulation kinetics. Nat Phys. (2009) 5:294–7. doi: 10.1038/nphys1222
9. Zinchenko A. DNA conformational behavior and compaction in biomimetic systems: toward better understanding of DNA packaging in cell. Adv Colloid Interface Sci. (2016) 232:70–9. doi: 10.1016/j.cis.2016.02.005
10. Jorge AF, Nunes SCC, Cova TFGG, Pais AACC. Cooperative action in DNA condensation. Curr Opin Colloid Interface Sci. (2016) 26:66–74. doi: 10.1016/j.cocis.2016.09.014
11. Lukacs GL, Haggie P, Seksek O, Lechardeur D, Freedman N, Verkman A. Size-dependent DNA mobility in cytoplasm and nucleus. J Biol Chem. (2000) 275:1625–9. doi: 10.1074/jbc.275.3.1625
12. Regner BM, Vučinić D, Domnisoru C, Bartol TM, Hetzer MW, Tartakovsky DM, et al. Anomalous diffusion of single particles in cytoplasm. Biophys J. (2013) 104:1652–60. doi: 10.1016/j.bpj.2013.01.049
13. Platani M, Goldberg I, Lamond AI, Swedlow JR. Cajal body dynamics and association with chromatin are ATP-dependent. Nat Cell Biol. (2002) 4:502–8. doi: 10.1038/ncb809
14. Nakano S, Sugimoto N. Model studies of the effects of intracellular crowding on nucleic acid interactions. Mol Biosyst. (2017) 13:32–41. doi: 10.1039/C6MB00654J
15. Minton AP. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J Biol Chem. (2001) 276:10577–80. doi: 10.1074/jbc.R100005200
16. Lee H, Venable RM, Mackerell AD Jr, Pastor RW. Molecular dynamics studies of polyethylene oxide and polyethylene glycol: hydrodynamic radius and shape anisotropy. Biophys J. (2008) 95:1590–9. doi: 10.1529/biophysj.108.133025
17. Azri A, Privat M, Grohens Y, Aubry T. Linear rheological properties of low molecular weight polyethylene glycol solutions. J Colloid Interface Sci. (2013) 393:104–8. doi: 10.1016/j.jcis.2012.10.059
18. Fissell WH, Hofmann CL, Smith R, Chen MH. Size and conformation of Ficoll as determined by size-exclusion chromatography followed by multiangle light scattering. Am J Physiol Renal Physiol. (2010) 298:F205–8. doi: 10.1152/ajprenal.00312.2009
19. Venturoli D, Rippe B. Ficoll and dextran vs. globular proteins as probes for testing glomerular permselectivity: effects of molecular size, shape, charge, and deformability. Am J Physiol Renal Physiol. (2005) 288:F605–13. doi: 10.1152/ajprenal.00171.2004
20. Lavrenko PN, Mikryukova OI, Didenko SA. Hydrodynamic properties and the shape of the molecules of the polysaccharide Ficoll-400 in solution. Polymer Sci USSR. (1986) 28:576–84. doi: 10.1016/0032-3950(86)90183-8
21. Yun SI, Melnichenko YB, Wignall GD. Small-angle neutron scattering from symmetric blends of poly(dimethylsiloxane) and poly(ethylmethylsiloxane). Polymer (2004) 45:7969–77. doi: 10.1016/j.polymer.2004.09.050
22. Ebagninin KW, Benchabane A, Bekkour K. Rheological characterization of poly(ethylene oxide) solutions of different molecular weights. J Colloid Interface Sci. (2009) 336:360–7. doi: 10.1016/j.jcis.2009.03.014
23. Luby-Phelps K, Castle PE, Taylor DL, Lanni F. Hindered diffusion of inert tracer particles in the cytoplasm of mouse 3T3 cells. Proc Natl Acad Sci USA. (1987) 84:4910–3. doi: 10.1073/pnas.84.14.4910
24. Armstrong JK, Wenby RB, Meiselman HJ, Fisher TC. The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophys J. (2004) 87:4259–70. doi: 10.1529/biophysj.104.047746
25. Kang H, Toan NM, Hyeon C, Thirumalai D. Unexpected swelling of Stiff DNA in a polydisperse crowded environment. J Am Chem Soc. (2015) 137:10970–8. doi: 10.1021/jacs.5b04531
26. Azri A, Giamarchi P, Grohens Y, Olier R, Privat M. Polyethylene glycol aggregates in water formed through hydrophobic helical structures. J Colloid Interface Sci. (2012) 379:14–9. doi: 10.1016/j.jcis.2012.04.025
27. Nakano S-I, Karimata H, Ohmichi T, Kawakami J, Sugimoto N. The effect of molecular crowding with nucleotide length and cosolute structure on DNA duplex stability. J Am Chem Soc. (2004) 126:14330–1. doi: 10.1021/ja0463029
28. Gao M, Gnutt D, Orban A, Appel B, Righetti F, Winter R, et al. RNA hairpin folding in the crowded cell. Angew Chem Int Ed Engl. (2016) 55:3224–8. doi: 10.1002/anie.201510847
29. Batra J, Xu K, Zhou HX. Nonadditive effects of mixed crowding on protein stability. Proteins (2009) 77:133–8. doi: 10.1002/prot.22425
30. Yang D, Khan S, Sun Y, Hess K, Shmulevich I, Sood AK, et al. Association of BRCA1 and BRCA2 mutations with survival, chemotherapy sensitivity, and gene mutator phenotype in patients with ovarian cancer EDITORIAL COMMENT. Obstet Gynecol Surv. (2012) 67:164–5. doi: 10.1097/OGX.0b013e31824b70b7
31. Dauty E, Verkman A. Actin cytoskeleton as the principal determinant of size-dependent DNA mobility in cytoplasm: a new barrier for non-viral gene delivery. J Biol Chem. (2005) 280:7823–8. doi: 10.1074/jbc.M412374200
32. Szymanski J, Weiss M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys Rev Lett. (2009) 103:038102. doi: 10.1103/PhysRevLett.103.038102
33. Zinchenko AA, Yoshikawa K. Na+ shows a markedly higher potential than K+ in DNA compaction in a crowded environment. Biophys J. (2005) 88:4118–23. doi: 10.1529/biophysj.104.057323
34. Cheng C, Jun-Li J, Shi-Yong R. Polyethylene glycol and divalent salt-induced RNA reentrant condensation revealed by single molecule measurements. Soft Matter (2015) 11:3927–35. doi: 10.1039/C5SM00619H
35. Ramisetty SK, Dias RS. Synergistic role of DNA-binding protein and macromolecular crowding on DNA condensation. An experimental and theoretical approach. J Mol Liq. (2015) 210:64–73. doi: 10.1016/j.molliq.2015.04.051
36. Wegner AS, Wintraecken K, Spurio R, Woldringh CL, de Vries R, Odijk T. Compaction of isolated Escherichia coli nucleoids: Polymer and H-NS protein synergetics. J Struct Biol. (2016) 194:129–37. doi: 10.1016/j.jsb.2016.02.009
37. Balbo J, Mereghetti P, Herten DP, Wade RC. The shape of protein crowders is a major determinant of protein diffusion. Biophys J. (2013) 104:1576–84. doi: 10.1016/j.bpj.2013.02.041
38. Gorczyca SM, Chapman CD, Robertson-Anderson RM. Universal scaling of crowding-induced DNA mobility is coupled with topology-dependent molecular compaction and elongation. Soft Matter (2015) 11:7762–8. doi: 10.1039/C5SM01882J
39. Chapman CD, Gorczyca S, Robertson-Anderson RM. Crowding induces complex ergodic diffusion and dynamic elongation of large DNA molecules. Biophys J. (2015) 108:1220–8. doi: 10.1016/j.bpj.2015.02.002
40. Lerman LS. A transition to a compact form of DNA in polymer solutions. Proc Natl Acad Sci USA. (1971) 68:1886–90. doi: 10.1073/pnas.68.8.1886
41. Vasilevskaya VV, Khokhlov AR, Matsuzawa Y, Yoshikawa K. Collapse of single DNA molecule in poly(ethylene glycol) solutions. J Chem Phys. (1995) 102:6595–602. doi: 10.1063/1.469375
42. Zhang C, Shao PG, van Kan JA, van der Maarel JR. Macromolecular crowding induced elongation and compaction of single DNA molecules confined in a nanochannel. Proc Natl Acad Sci USA. (2009) 106:16651–6. doi: 10.1073/pnas.0904741106
43. Ojala H, Ziedaite G, Wallin AE, Bamford DH, Haeggstrom E. Optical tweezers reveal force plateau and internal friction in PEG-induced DNA condensation. Eur Biophys J. (2014) 43:71–9. doi: 10.1007/s00249-013-0941-x
44. Xu W, Muller SJ. Polymer-monovalent salt-induced DNA compaction studied via single-molecule microfluidic trapping. Lab Chip (2012) 12:647–51. doi: 10.1039/C2LC20880F
45. Hirano K, Ichikawa M, Ishido T, Ishikawa M, Baba Y, Yoshikawa K. How environmental solution conditions determine the compaction velocity of single DNA molecules. Nucleic Acids Res. (2012) 40:284–9. doi: 10.1093/nar/gkr712
46. Kawakita H, Uneyama T, Kojima M, Morishima K, Masubuchi Y, Watanabe H. Formation of globules and aggregates of DNA chains in DNA/polyethylene glycol/monovalent salt aqueous solutions. J Chem Phys. (2009) 131:094901. doi: 10.1063/1.3216110
47. Saito T, Iwaki T, Yoshikawa K. DNA compaction induced by neutral polymer is retarded more effectively by divalent anion than monovalent anion. Chem Phys Lett. (2008) 465:40–4. doi: 10.1016/j.cplett.2008.09.040
48. Maniatis T, Venable JH Jr, Lerman LS. The structure of psi DNA. J Mol Biol. (1974) 84:37–64. doi: 10.1016/0022-2836(74)90211-3
49. Minagawa K, Matsuzawa Y, Yoshikawa K, Khokhlov AR, Doi M. Direct observation of the coil-globule transition in DNA molecules. J Mol Biol. (1994) 84:37–64. doi: 10.1002/bip.360340410
50. Yoshikawa K, Yoshikawa Y, Koyama Y, Kanbe T. Highly effective compaction of long duplex DNA induced by polyethelene glycol with pendant amino groups. J Am Chem Soc. (1997) 119:6473–7. doi: 10.1021/ja970445w
51. Ramos JÉB, de Vries R, Ruggiero Neto J. DNA PSI-condensation and reentrant decondensation: effect of the PEG degree of polymerization. J Phys Chem. (2005) 109:23661–5. doi: 10.1021/jp0527103
52. de Vries R. Flexible polymer-induced condensation and bundle formation of DNA and F-actin filaments. Biophys J. (2001) 80:1186–94. doi: 10.1016/S0006-3495(01)76095-X
53. Post CB, Zimm BH. Theory of DNA condensation: collapse versus aggregation. Biopolymers (1982) 21:2123–37. doi: 10.1002/bip.360211104
54. Grosberg AY, Erukhimovitch IY, Shakhnovitch EI. On the theory of PSI-condensation. Biopolymers (1982) 21:1487–501. doi: 10.1002/bip.360211207
55. Post CB, Zimm BH. Internal condensation of a single DNA molecule. Biopolymers (1979) 18:1487–501. doi: 10.1002/bip.1979.360180612
56. Naghizadeh J, Massih AR. Concentration-dependent collapse of a large polymer. Phys Rev Lett. (1978) 40:1299–303. doi: 10.1103/PhysRevLett.40.1299
57. Shin J, Cherstvy AG, Metzler R. Polymer looping is controlled by macromolecular crowding, spatial confinement, and chain stiffness. ACS Macro Lett. (2015) 4:202–6. doi: 10.1021/mz500709w
58. Shin J, Cherstvy AG, Metzler R. Kinetics of polymer looping with macromolecular crowding: effects of volume fraction and crowder size. Soft Matter (2015) 11:472–88. doi: 10.1039/c4sm02007c
59. Zhang C, Gong Z, Guttula D, Malar PP, van Kan JA, Doyle PS, et al. Nanouidic compaction of DNA by like-charged protein. J Phys Chem B (2012) 116:3031–6. doi: 10.1021/jp2124907
60. Jones JJ, van der Maarel JR, Doyle PS. Effect of nanochannel geometry on DNA structure in the presence of macromolecular crowding agent. Nano Lett. (2011) 11:5047–53. doi: 10.1021/nl203114f
61. Biswas N, Ichikawa M, Datta A, Sato YT, Yanagisawa M, Yoshikawa K. Phase separation in crowded micro-spheroids: DNA-PEG system. Chem Phys Lett. (2012) 539:157–62. doi: 10.1016/j.cplett.2012.05.033
62. Negishi M, Sakaue T, Takiguchi K, Yoshikawa K. Cooperation between giant DNA molecules and actin filaments in a microsphere. Phys Rev E Stat Nonlinear Soft Matter Phys. (2010) 81(5Pt 1):051921. doi: 10.1103/PhysRevE.81.051921
63. Negishi M, Ichikawa M, Nakajima M, Kojima M, Fukuda T, Yoshikawa K. Phase behavior of crowded like-charged mixed polyelectrolytes in a cell-sized sphere. Phys Rev E Stat Nonlin Soft Matter Phys. (2011) 83:061921. doi: 10.1103/PhysRevE.83.061921
64. de Vries R. Depletion-induced instability in protein-DNA mixtures: influence of protein charge and size. J Chem Phys. (2006) 125:014905. doi: 10.1063/1.2209683
65. de Vries R. DNA compaction by nonbinding macromolecules. Polymer Sci Series C (2012) 54:30–5. doi: 10.1134/S1811238212070016
66. Zinchenko A, Yoshikawa K. Compaction of double-stranded DNA by negatively charged proteins and colloids. Curr Opin Colloid Interface Sci. (2015) 20:60–5. doi: 10.1016/j.cocis.2014.12.005
67. Ichiba Y, Yoshikawa K. Single chain observation on collapse transition in giant DNA induced by negatively-charged polymer. Biochem Biophys Res Commun. (1998) 242:441–5. doi: 10.1006/bbrc.1997.7967
68. Kidoaki S, Yoshikawa K. Folding and unfolding of a giant duplex-DNA in a mixed solution with polycations, polyanions and crowding neutral polymers. Biophys Chem. (1999) 76:133–43. doi: 10.1016/S0301-4622(98)00231-2
69. Yoshikawa K, Hirota S, Makita N, Yoshikawa Y. Compaction of DNA induced by like-charge protein: opposite salt-effect against the polymer-salt-induced condensation with neutral polymer. J Phys Chem Lett. (2010) 1:1763–6. doi: 10.1021/jz100569e
70. Zinchenko A, Tsurnoto K, Murata S, Yoshikawa K. Crowding by anionic nanoparticles causes DNA double-strand instability and compaction. J Phys Chem B (2014) 118:1256–62. doi: 10.1021/jp4107712
71. Barisik M, Atalay S, Beskok A, Qian SZ. Size dependent surface charge properties of silica nanoparticles. J Phys Chem C (2014) 118:1836–42. doi: 10.1021/jp410536n
72. Laib S, Robertson RM, Smith DE. Preparation and characterization of a set of linear DNA molecules for polymer physics and rheology studies. Macromolecules (2006) 39:4115–9. doi: 10.1021/ma0601464
73. Chapman CD, Lee K, Henze D, Smith DE, Robertson-Anderson RM. Onset of non-continuum effects in microrheology of entangled polymer solutions. Macromolecules (2014) 47:1181–6. doi: 10.1021/ma401615m
74. Efron B, Tibshirani R. Statistical Data Analysis in the Computer Age. University of Toronto, Department of Statistics (1990).
75. Haber C, Ruiz SA, Wirtz D. Shape anisotropy of a single random-walk polymer. Proc Natl Acad Sci USA. (2000) 97:10792–5. doi: 10.1073/pnas.190320097
76. Kuhn W. Über die Gestalt fadenförmiger Moleküle in Lösungen. Kolloid Zeitschr. (1934) 68:2–15. doi: 10.1007/BF01451681
77. Doi M, Edwards SF. The Theory of Polymer Dynamics. Oxford: Clarendon Press, Oxford University Press (1988). p. 391.
78. Robertson RM, Laib S, Smith DE. Diffusion of isolated DNA molecules: dependence on length and topology. Proc Natl Acad Sci USA. (2006) 103:7310–4. doi: 10.1073/pnas.0601903103
79. Kam Z, Borochov N, Eisenberg H. Dependence of laser light scattering of DNA on NaCl concentration. Nature (1981) 329:2671–90. doi: 10.1002/bip.1981.360201213
80. Biroli G, Bouchaud JP. Critical fluctuations and breakdown of the Stokes-Einstein relation in the mode-coupling theory of glasses. J Phys Condens Mat. (2007) 19:205101. doi: 10.1088/0953-8984/19/20/205101
81. Tuteja A, Mackay ME, Narayanan S, Asokan S, Wong MS. Breakdown of the continuum Stokes-Einstein relation for nanoparticle diffusion. Nano Lett. (2007) 7:1276–81. doi: 10.1021/nl070192x
82. Kalwarczyk T, Sozanski K, Ochab-Marcinek A, Szymanski J, Tabaka M, Hou S, et al. Motion of nanoprobes in complex liquids within the framework of the length-scale dependent viscosity model. Adv Colloid Interface Sci. (2015) 223:55–63. doi: 10.1016/j.cis.2015.06.007
83. Ochab-Marcinek A, Wieczorek SA, Ziebacz N, Holyst R. The effect of depletion layer on diffusion of nanoparticles in solutions of flexible and polydisperse polymers. Soft Matter (2012) 8:11173–9. doi: 10.1039/c2sm25925g
84. Holyst R, Bielejewska A, Szymanski J, Wilk A, Patkowski A, Gapinski J, et al. Scaling form of viscosity at all length-scales in poly (ethylene glycol) solutions studied by fluorescence correlation spectroscopy and capillary electrophoresis. Phys Chem Chem Phys. (2009) 11:9025–32. doi: 10.1039/b908386c
85. Kalwarczyk T, Ziebacz N, Bielejewska A, Zaboklicka E, Koynov K, Szymanski J, et al. Comparative analysis of viscosity of complex liquids and cytoplasm of mammalian cells at the nanoscale. Nano Lett. (2011) 11:2157–63. doi: 10.1021/nl2008218
86. Zhou HX. Brownian dynamics study of the influences of electrostatic interaction and diffusion on protein-protein association kinetics. Biophys J. (1993) 64:1711–26. doi: 10.1016/S0006-3495(93)81543-1
87. Sozanski K, Ruhnow F, Wisniewska A, Tabaka M, Diez S, Holyst R. Small crowders slow down kinesin-1 stepping by hindering motor domain diffusion. Phys Rev Lett. (2015) 115:218102. doi: 10.1103/PhysRevLett.115.218102
88. Phillip Y, Kiss V, Schreiber G. Protein-binding dynamics imaged in a living cell. Proc Natl Acad Sci USA. (2012) 109:1461–6. doi: 10.1073/pnas.1112171109
Keywords: macromolecular crowding, DNA diffusion, DNA conformation, single-molecule tracking, depletion interactions, fluorescence microscopy, DNA compaction, entropic forces
Citation: Mardoum WM, Gorczyca SM, Regan KE, Wu T-C and Robertson-Anderson RM (2018) Crowding Induces Entropically-Driven Changes to DNA Dynamics That Depend on Crowder Structure and Ionic Conditions. Front. Phys. 6:53. doi: 10.3389/fphy.2018.00053
Received: 20 March 2018; Accepted: 17 May 2018;
Published: 05 June 2018.
Edited by:
Jennifer Lynn Ross, University of Massachusetts Amherst, United StatesReviewed by:
Enrique Hernandez-Lemus, National Institute of Genomic Medicine, MexicoCopyright © 2018 Mardoum, Gorczyca, Regan, Wu and Robertson-Anderson. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rae M. Robertson-Anderson, cmFuZGVyc29uQHNhbmRpZWdvLmVkdQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.