- Department of Economics, Sapporo Gakuin University, Ebetsu, Japan
Sound correlations among six sites on the Japanese short poetry are analyzed in detail. For haiku composed of 5-7-5 syllables, the six sites are occupied by the head vowels on the three phrases as well as by the end sounds (in addition to five vowels, a syllabic nasal being included) on them. For tanka, first, one should divide the entire poem (5-7-5-7-7 syllables) into two parts, namely, the first (5-7-5) and the latter (5-7-7) part. For the six-dimensional array of sounds, there are 203 rhyme patterns possible. Specifically, for corpora of the haiku poetry, the complete works of three haiku poets, all of whom are distinguished in Japan, are selected. For those of the tanka, Collection of Ten Thousand Leaves and The Twenty-One Collections of Waka are chosen. Analyzed results through comparison between the surveyed and the expected frequencies show statistically the strong preference for the arrangements with a far-reaching antirhyming between sounds on the three ends, along with the correlation between those on the heads. In addition to the avoided rhyming, one finds a preference for specific arrangements exhibiting the nearest-neighbor correlations. Subsequently, to manifest the distinctive feature of each corpus, correlation analysis is carried out between frequency distributions of the arrangements. Moreover, in order to explore a statistical rule for the rank-ordered data, fitting is attempted to a long-tail distribution, followed by the Durbin-Watson testing. Quantitative analyses by using Gini's coefficient as well as Shannon's information entropy are also made. Finally, it is shown that the results of the complicated rhyming can be explained in part in comparison with the sound correlation between the first and the latter parts in the full names of Japanese.
Introduction
Along with nearest-neighbor correlations between spins [1, 2], long-range correlations have been found to occur ubiquitously not only in physics but in diverse areas such as biophysics, physiology, economics, and informational science [3–5]. The long-range correlations appear in stochastic processes in which autocorrelation functions decay according to an inverse power law, as opposed to a short-range exponential decay; typical examples of the long-memory effect can be seen in self-similar fractal processes as well as generalized diffusion including fractional Brownian motion [6]. It is interesting to note that long-range correlations have been found in several unexpected areas. For instance, a binary sequence realized by a subscribed rule shows a long-range correlation, where in the limit of infinity the ratio between numbers of two binary symbols does approach exactly the golden ratio 1.6180339 … [7]. Another instance that has attracted our attention in more recent years is found for the possibility of observing long-range correlations in the complex networks modeling texts [8–11]. In comparison with the ubiquity of the long-range correlated systems, those exhibiting the long-range anticorrelations appear limited [12, 13], though the distinction does not belong in the same category with the extreme unbalance between matter and antimatter in the universe. (This fact seems to be also the case with the contrast between the nearest-neighbor correlations vs. the nearest-neighbor anticorrelations [14]). In this paper, instead of interacting spins we consider sound arrangements of poetry. While the well-cited proverb, “There is no rule without exceptions,” includes a logical contradiction due inevitably to its self-reference nature, its parody, “There is no language without poetry,” could not be judged by anyone to include any contradiction. Indeed, irrespective of languages, texts are categorized into prose and verses. Poems take the form of the latter. Conventional poetics has classified world's poetries into triplet (tercet), sestina, sonnet, villanelle, etc. [15]. One can find that in typical European poetry a sound on a line is correlated to that on the same site in other lines, where correlation among syllables on the feet of lines is termed end rhyme (or simply rhyme) whereas the one among consonants on the head syllables is termed alliteration. In the prominent triplet La Divina Commedia [16–18] consisting of 14,233 lines, which was composed by Dante (1265-1321), the rhyming scheme ABA is employed throughout the poem. In Japan, in addition to modern poetry composed of many lines, several forms of the short poetry have traditionally been enjoying general popularity. For example, one enumerates tanka (5-7-5-7-7), sedoka (5-7-7-5-7-7), bussokusekikataika (5-7-5-7-7-7), haiku (5-7-5), senryu (5-7-5), kyoka (5-7-5-7-7), and dodoitsu (7-7-7-5), where the numeral in the bracket indicates the number of syllables in the phrase of each verse; as is seen in the number string, these verses are segmented into phrases with a combination between five and seven syllables. Among these, the matchless twin stars are undoubtedly haiku and tanka [19, 20], which are composed of, respectively, the 17 and the 31 syllables. (Incidentally, both are prime numbers. In particular, the length of the former is pronounced; it could be that it is the shortest poetry in the world. One should compare the length with, for instance, that of the shortest form of Chinese poetry, namely a quatrain composed of 20 characters; according to the rule that a syllable is in principle allotted per character, the poetry consists of syllables with the same number as Chinese characters.) Actually, independently of nationwide and local newspapers, in the literary columns on their pages, there are plenty of two poetries (haiku and tanka) that are constantly submitted by their readers. Moreover, the more surprising fact is that without distinction of age and sex a large number of people including foreigners submit a tanka poem to the New Year's Poetry Party held at the Imperial Court.
In this paper, sound correlations among six sites on the short poetry are analyzed in details both for haiku and for tanka. For corpora of the haiku poetry, the complete works of the three haiku composers, Mantaro Kubota (1889-1963), Shuoshi Mizuhara (1892-1981), and Seishi Yamaguchi (1901-1994), are chosen, all of whom are most outstanding poets in Japan, and therefore, complete works that include several- to ten-thousand poems are readily available [21–23]. It must be emphasized here that in general the larger-scale statistical analysis provides the stronger impact on the quantitative study of languages. For those of the tanka, Collection of Ten Thousand Leaves (N = 4,183; Man'yoshu in Japanese) [24, 25] and The Twenty-One Collections of Waka (N = 33,692; Nijuichidaishu in Japanese) [26–41] are chosen, where N indicates the total number of poems included. The former is known as the oldest collection of poems in Japan, which is said to have been compiled in the eighth century, while the latter were compiled by imperial command between the early Heian period (the tenth century) and the early Muromachi period (the fifteenth century), which are often divided into two parts: The Eight Collections of Waka (N = 9,483) [26–32] and The Thirteen Collections of Waka (N = 24,209) [33–41]. Specifically, for haiku the six sites are occupied by the head vowels on the three phrases as well as by the end sounds (in addition to five vowels, a syllabic nasal being included) on them. However, for tanka, first, one should split the entire poem (5-7-5-7-7) into two parts, namely, the first (5-7-5) and the latter (5-7-7) part; note that the syllabic structure of the former is exactly identical to that of haiku. For the six-dimensional array of sounds, 203 rhyme schemes are possible; the value can be determined by the Bell number B(6) that is obtained sequentially through B(0) = 1, B(1) = 1, B(2) = 2, B(3) = 5, B(4) = 15, as well as B(5) = 52 [42]. It should be mentioned here that analysis on the sound correlation of haiku was reported previously, but has been restricted to the three-dimensional system, i.e., B(3) = 5, where correlations among either heads or feet of the phrases were considered [43], indicating that with this method the nearest-neighbor correlations cannot in principle be dealt with. Although far more computational efforts are required, for revealing the phonological secrets of the Japanese short poetry, the full six-dimensional treatment is indispensable. Analyzed results through comparison between the surveyed and the expected frequencies reveal strong preference for specific arrangements. To put it the other way around, the results indicate, at the same time, strong avoidance for other ones. Subsequently, to manifest the distinctive feature of each corpus, correlations between two distributions in the frequencies of the arrangements are compared through calculation by means of the Peason's coefficient. Moreover, in an effort to explore a statistical rule for the rank-ordered data, fitting is made to a generalized long-tail distribution, followed by the Durbin-Watson testing. Detailed analyses by using Gini's coefficient as well as Shannon's information entropy are also performed. The results are discussed in comparison with the sound correlation between the first and the latter parts in the personal names of Japanese, for which four-dimensional arrangements can be realized.
Generating 6D-Arrangements
To explain how to obtain sound arrangements of haiku, from The Complete Haiku Works of Shuoshi Mizuhara [22], we select two poems
Poem 1: Risshun ya, mezame awaseshi, ake no kane.
Poem 2: Iso no ta wa, aze no yomogi no, haru hayaki.
Here a comma is put in on the boundary between neighboring phrases. Extracting a vowel sound in the first syllable of the head word and the last sound in the end word on each phrase, we obtain the six-dimensional strings
Poem 1: ia;ei;ae,
Poem 2: ia;ao;ai,
where commas in original poems are replaced by semicolons. Subsequently, to explain how to obtain sound arrangements of tanka, from A Collection of Japanese Poetry of a Thousand Years (published in 1188; including 1,282 poems) [31], which is listed as the seventh tanka collection in The Twenty-One Collections of Waka, we select two poems
Poem 3: Haru no kuru, ashita no hara o, miwataseba, kasumi mo kyo zo, tachi hajime keru.
Poem 4: Mimuroyama, tani ni ya haru no, tachi nu ran, yuki no shita mizu, iwa tataku nari.
With the same procedure as that adopted for haiku, we obtain the ten-dimensional strings
Poem 3: au;ao;ia;ao;au,
Poem 4: ia;ao;an;uu;ii.
Here we remark that the total number of the ten-dimensional arrangements can be determined by the Bell number B(10) = 115975 [42], the value of which, however, is found to be too large to deal with. For this reason, we shall split the entire arrangement into the first and the latter strings:
Poem 3: au;ao;ia, ia;ao;au,
Poem 4: ia;ao;an, an;uu;ii.
With this division we can generate twin six-dimensional arrangements per each tanka poem. Finally, we shall rewrite the above strings of haiku and tanka in more symbolic form:
Poem 1: #198 AB;CA;BC,
Poem 2: #152 AB;Bx;BA,
Poem 3: #023 Ax;Ay;zA, #028 xA;Ay;Az,
Poem 4: #028 xA;Ay;Az, #101 xy;AA;BB,
where the numeral on the front of the string indicates the sequential number in the 203 arrangements (#001-#203), which are categorized into 13 groups that follow:
(1) #001 xy;zw;vt,
(2) #002 AA;xy;zw, …, #016 xy;zw;AA,
(3) #017 AA;Ax;yz, …, #036 xy;zA;AA,
(4) #037 AA;AA;xy, …, #051 xy;AA;AA,
(5) #052 AA;AA;Ax, …, #057 xA;AA;AA,
(6) #058 AA;AA;AA,
(7) #059 AA;BB;xy, …, #103 xy;AB;BA,
(8) #104 AA;AB;Bx, …, #139 xA;BB;AA,
(9) #140 AA;BB;Bx, …, #163 xA;BB;BA,
(10) #164 AA;AA;BB, …, #173 AB;BA;AA,
(11) #174 AA;AB;BB, …, #183 AB;BB;AA,
(12) #184 AA;BB;BB, …, #188 AB;BB;BA,
(13) #189 AA;BB;CC, …, #203 AB;CC;BA.
For Poem 1 (haiku) and for Poem 3 (tanka) the procedures explained above are illustrated in Figure 1.

Figure 1. Schematic illustration of generating six-dimensional sound arrangements. (A) Haiku (e.g., Poem 1 in the text). There are five steps that follow. Step 1: Segmenting the poem into three phrases according to 5-7-5 syllables; Step 2: Transliterating the original poem into the Roman alphabet; Step 3: Choosing the head and the end syllables from the three phrases; Step 4: Extracting a vowel from each individual syllable and arranging the six sounds like a string; Step 5: Rewriting the string with a generic form. (B) Tanka (e.g., Poem 3 in the text). There are six steps that follow. Step 1: Segmenting the poem into five phrases according to 5-7-5-7-7 syllables; Step 2: Same as haiku; Step 3: Choosing the head and the end syllables from the five phrases; Step 4: Extracting a vowel from each individual syllable and arranging the 10 sounds like a string; Step 5: Splitting the ten-dimensional arrangement into twin six-dimensional ones; Step 6: Rewriting both strings in more generic form.
Deciding Ranking for Haiku
Prior to presenting analytical results, we shall mention the terminology relevant to the arrangements. First, the term “nearest-neighbor correlation” is defined as those with an identical sound across the boundary between two phrases. For example, arrangements that include A;A, B;B, or C;C meet the requirement, but those including AA;, ;AA, ;BB, or ;CC do not, because all of the latter four represent correlations between two sounds within a single phrase. Next, the term “far-reaching correlation” is defined as the arrangements with identical sounds between the same sites across the phrases. With this definition, examples of the “shortest” far-reaching correlations are given by those including Ai;A, Bi;B, Ci;C, A;iA, B;iB, or C;iC, while those of the “longest” far-reaching correlations are written as Ai;jk;A and A;ij;kA. Here the symbols, i, j, and k, represent A, B, C, x, y, z, and w. Finally, the term “far-reaching anticorrelation” is defined as the arrangements with opposed sounds between the same sites over the three phrases. With this definition, examples of the far-reaching anticorrelations are given by those including, for instance, x;iy;jz, A;ix;jy, x;iA;jB, xi;yj;z, Ai;xj;y, or xi;Aj;B.
The top-twenty and the bottom-twenty rankings of the haiku works are given in Tables 1–6, where ranking is determined by evaluating the relative squared difference between the surveyed (f) and the expected (F) frequencies: (f − F)2/F, the total summation of which yields the chi-square value χ2. The expected values are obtainable analytically from the blending among six sounds (five vowels /u, o, a, e, i/ plus a syllabic nasal /n/); for instance, for Group (3) above-mentioned, computational details of the expected frequencies are given as follows:
where nj (j = u, o, a, e, i, n) indicates the number of the sound /j/. In the tables that follow, the symbol “H” (“E”) denotes sound correlations between the head vowels (the end sounds) of phrases; in particular, those among the three phrases are highlighted by “H” (“E”). In other words, with this notation the single “H” (“E”) or “H” (“E”) without being accompanied by “E” (“H”) or “E” (“H”) signifies that the far-reaching anticorrelations occur between the ends (the heads) of the three phrases in a poem. In addition, the Gothic rank on the top-twenty ranking indicates that the nearest-neighbor correlation does arise on the boundary between adjoining phrases. From Tables 1–6 one can summarize the results as follows:
(1) In the top-twenty ranking of Mantaro Kubota (Table 1), almost all arrangements exhibit far-reaching correlations between head sites on the two or the three phrases (“H,” “H”). One can see an exception, specifically, Rank 18. Those between three phrases, “H,” are seen in Rank 1, 2, 15, and 17. For Rank 15 and 17, simultaneously, the correlations can be seen between the two feet (“E”); all the other arrangements show the far-reaching anticorrelations between the three sounds on the feet. In contrast with the far-reaching phenomena, there exist three arrangements [Rank 6 (#33), 11, and 12 (#17)] showing the nearest-neighbor correlations between adjacent phrases.
(2) In the bottom-twenty ranking of Mantaro (Table 2), all arrangements exhibit far-reaching correlations between end sites on the two or the three phrases (“E,” “E”). To be specific, those among three phrases, “E,” are seen in Rank 202, 200, 199, 193 (#53 & #57), 192, and 189. For Rank 200-198, 193 (#52, #53, & #57), 187, and 185 (#164 & #184), the correlations can also be seen between head sites (“H,” “H”).
(3) In the top-twenty ranking of Shuoshi Mizuhara (Table 3), all arrangements except Rank 15 (#94) show far-reaching correlations between head sites on the phrases (“H,” “H”). Those between three phrases, “H,” can be seen in Rank 1, 7, 8, and 10. At the same time, for Rank 8 and 12, the correlations are seen between feet (“E”); other arrangements show the far-reaching anticorrelations among the three ends. In sharp contrast with the long-range phenomena, there are six arrangements (Rank 2, 7, 10, 11, 17, and 19) that exhibit the nearest-neighbor correlations between the first and the second phrases (Rank 7, 11, 17, and 19) as well as between the second and the last phrases (Rank 2, 10, and 17). Of these, the arrangement of Rank 17 (#104: AA;AB;Bx) is most worth noting because of the dual components, A;A and B;B, being included simultaneously.
(4) In the bottom-twenty ranking of Shuoshi (Table 4), all arrangements except Rank 188 (#64) exhibit far-reaching correlations between end sites on the phrases (“E,” “E”). Specifically, those between three phrases, “E,” are seen in Rank 203, 202, and 193. For Rank 194 (#172 & #184), 190, 187, and 186, the correlations can be seen between head sites (“H,” “H”) as well.
(5) In the top-twenty ranking of Seishi Yamaguchi (Table 5), all arrangements except Rank 12 show far-reaching correlations between the head sites (“H,” “H”). Those between three phrases, “H,” are seen solely in Rank 1 and 2. For Rank 2, 8 (#73), 13, 14, 16, and 17 (#65), the correlations can be seen also between end sites (“E”); other 14 arrangements yield the far-reaching anticorrelations between the three ends. Besides the far-reaching phenomena, it is interesting to note that there exist five arrangements (Rank 10, 13, 15, 19, and 20) showing the nearest-neighbor correlations between the first and the second phrases (Rank 10 and 19) as well as between the second and the last phrases (Rank 13, 15, and 20).
(6) In the bottom-twenty ranking of Seishi (Table 6), all arrangements exhibit far-reaching correlations between the end sites (“E,” “E”). Of them, those among three phrases, “E,” are seen in Rank 201 (#48), 193 (#145), as well as 188-186. For Rank 201 (#46), 193 (#135 & #145), 188, and 185, the correlations can be seen as well between heads (“H”).
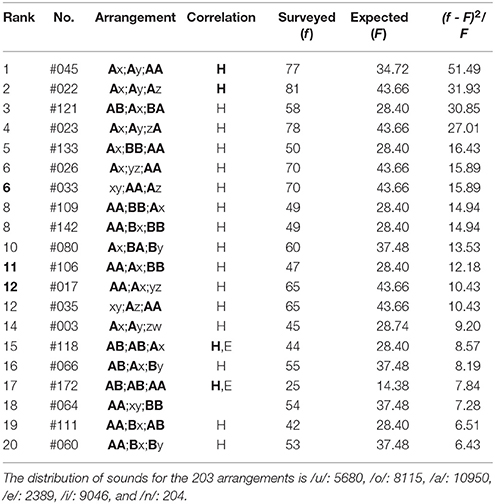
Table 1. The top-twenty arrangements in The Complete Haiku Works of Mantaro Kubota, wherein there are 6064 poems included.
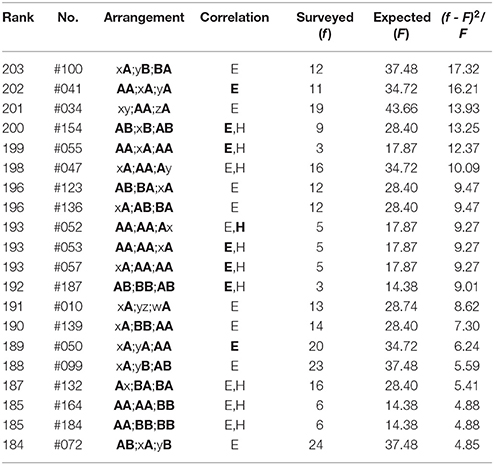
Table 2. The bottom-twenty arrangements in The Complete Haiku Works of Mantaro Kubota, wherein there are 6064 poems included.
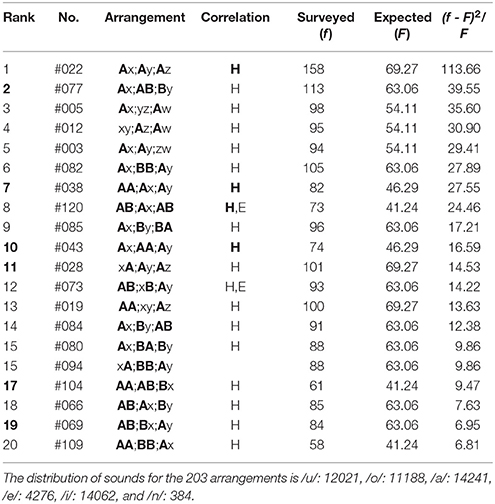
Table 3. The top-twenty arrangements in The Complete Haiku Works of Shuoshi Mizuhara, wherein there are 9362 poems included.
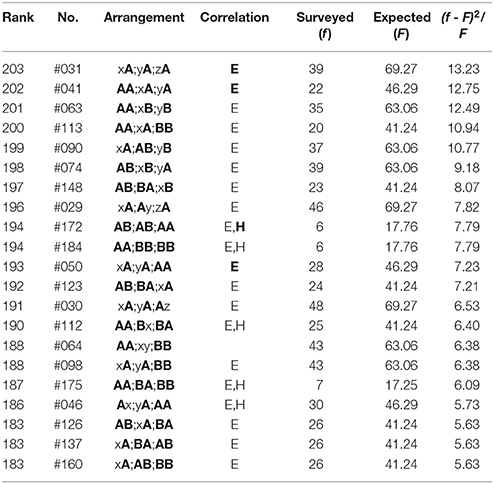
Table 4. The bottom-twenty arrangements in The Complete Haiku Works of Shuoshi Mizuhara, wherein there are 9362 poems included.
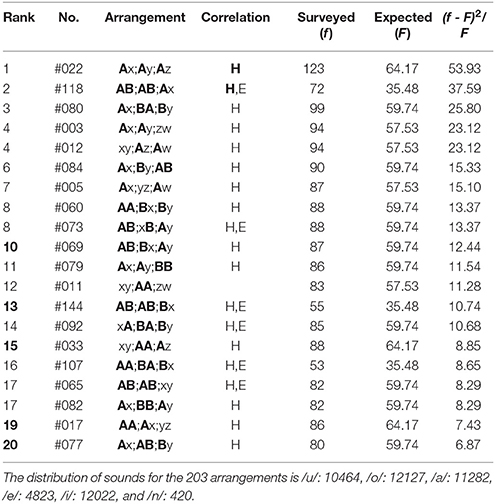
Table 5. The top-twenty arrangements in The Complete Haiku Works of Seishi Yamaguchi, wherein there are 8523 poems included.
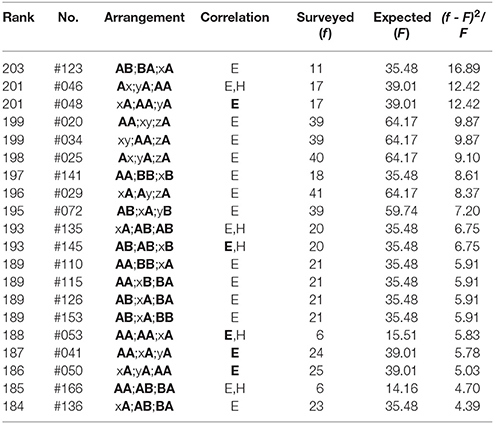
Table 6. The bottom-twenty arrangements in The Complete Haiku Works of Seishi Yamaguchi, wherein there are 8523 poems included.
Deciding Ranking for Tanka
The top-twenty and the bottom-five rankings of the tanka collections are shown in Tables 7–10. Note that to reduce redundancy, for the bottom of tanka, only five rankings are included; the bottom-twenty rankings are given in Supplementary Material as Tables 7'−10', respectively. From Tables 7–10 we conclude as follows:
(1) In the top-twenty ranking of the first three phrases (5-7-5) of poems in Collection of Ten Thousand Leaves (Table 7), all arrangements except Rank 19 (#61) give far-reaching correlations between head sites on the two or the three phrases (“H,” “H”). Of them, those between three phrases, “H,” are seen in Rank 1, 4, 6, 8, 16, and 18. At the same time, for Rank 3-6, 10, 11 (#65), 18, and 19 (#75), the correlations can be seen between feet as well (“E,” “E”); one can find other 12 arrangements to be far-reaching anticorrelated between sounds on the three ends. In contrast with the far-reaching phenomena, there are three arrangements [Rank 7, 8, and 13 (#69)] worthy to be noted, all of which show the nearest-neighbor correlations between the first and the second phrases. Contrary to this, in the bottom-five ranking (Table 7), all arrangements show far-reaching correlations between end sites on the two or the three phrases (“E,” “E”). To be specific, those between three phrases, “E,” are seen in Rank 199, 202, and 203. For Rank 200 and 201, correlations can also be seen between heads (“H,” “H”).
(2) In the top-twenty ranking of the latter three phrases (5-7-7) of poems in Collection of Ten Thousand Leaves (Table 8), most arrangements exhibit far-reaching correlations between head sites on the phrases (“H,” “H”). Exceptions are seen in Rank 4 (#30), 10, and 15. Those between three phrases, “H,” occur in Rank 1, 9, and 14. Simultaneously, for Rank 4 (#30), 7, 9, 14, and 19 (#65), the correlations arise between feet (“E,” “E”); one can see other 15 arrangements being far-reaching anticorrelated between sounds on the three ends. In contrast with the far-reaching phenomena, there are eight arrangements [Rank 4 (#28 & #30), 10, 11, 12 (#106), 15, 16 (#33), and 18] to be emphasized, which show the nearest-neighbor correlations between the first and the second phrases [Rank 4 (#28), 10, 11, 12 (#106), and 15] and between the second and the last phrases [Rank 4 (#30), 16 (#33), and 18]. On the other hand, in the bottom-five ranking (Table 8), all arrangements exhibit far-reaching correlations between end sites on the phrases (“E,” “E”). Specifically, those between three phrases, “E,” are seen in Rank 200. For Rank 199, correlations can also be seen between heads (“H”).
(3) In the top-twenty ranking of the first three phrases (5-7-5) of poems in The Twenty-One Collections of Waka (Table 9), all arrangements except Rank 18 show far-reaching correlations between the head sites (“H,” “H”). Those between three phrases, “H,” are seen in Rank 1, 11, 12, and 20. At the same time, solely for Rank 20 the correlations can also be seen between feet (“E”); one can see other 19 arrangements being far-reaching anticorrelated between sounds on the three ends. In addition to the far-reaching phenomena, there are five arrangements [Rank 2, 5, 12, 15 (#28), and 19] to be noticed, all of which but Rank 5 show the nearest-neighbor correlations between the first and the second phrases. In the bottom-five ranking (Table 9), however, all arrangements exhibit far-reaching correlations between the end sites (“E,” “E”). To be specific, those between the three phrases, “E,” are seen in Rank 200-203. For Rank 200, correlations can also be seen between head sites (“H”). To conclude, in careful comparison between results on Table 7 and those on Table 9 we can understand how the specific sound arrangements had been spontaneously selected through an extremely long-term symmetry-breaking process, and at the same time, how the phonological structure of the present poetry had been self-organized from the eighth to the fifteenth century.
(4) In the top-twenty ranking of the latter three phrases of poems in The Twenty-One Collections of Waka (Table 10), for all arrangements, far-reaching correlations arise between the head sites (“H,” “H”). Those between three phrases, “H,” are found in Rank 1, 5, 8, and 9. Simultaneously, for Rank 8, the correlation can be seen between feet (“E”); one can find other 19 arrangements to be far-reaching anticorrelated between sounds on the three ends. Besides the far-reaching phenomena, there are six arrangements (Rank 5, 7, 13, 14, 18, and 20) to be highlighted. Of these, for arrangements of Rank 5, 13, and 14 the nearest-neighbor correlations occur between the first and the second phrases, while for other three they do between the second and the last phrases. In the bottom-five ranking (Table 10), all arrangements exhibit the far-reaching correlations between the end sites (“E,” “E”). Explicitly those between the three phrases, “E,” are found in Rank 200, 202, and 203. Again, comparison between results in Table 8 and those in Table 10 reveals how the specific arrangements had been selected as well as how the poetry had been organized over a period of the 700 years.
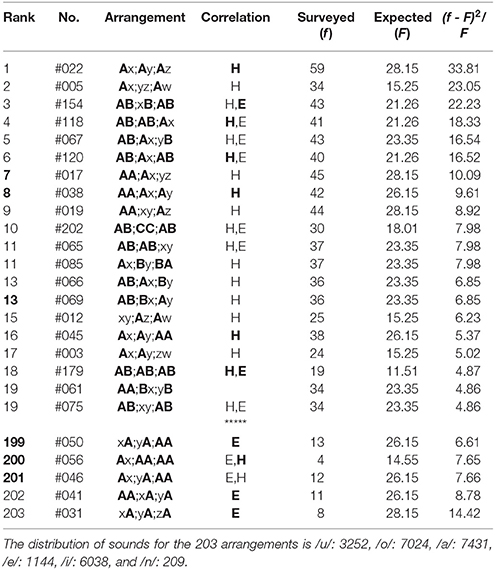
Table 7. The top-twenty and the bottom-five arrangements in the first three phrases (5-7-5) of poems in Collection of Ten Thousand Leaves, wherein there are 4183 tanka poems included.
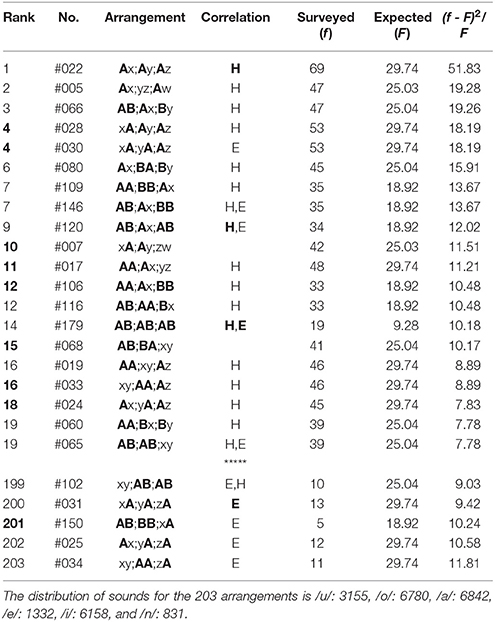
Table 8. The top-twenty and the bottom-five arrangements in the latter three phrases (5-7-7) of poems in Collection of Ten Thousand Leaves, wherein there are 4183 tanka poems included.
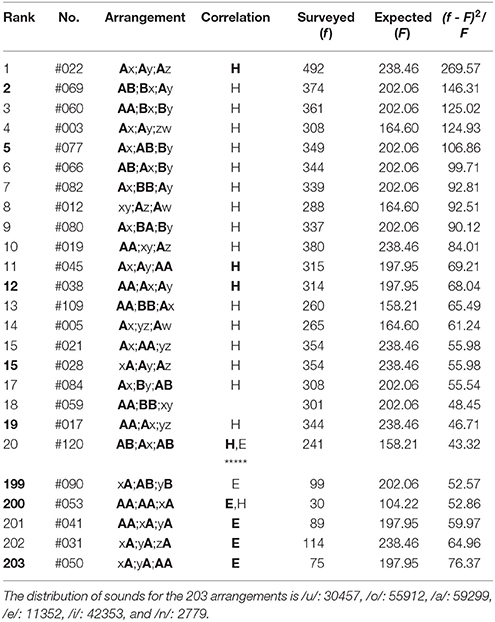
Table 9. The top-twenty and the bottom-five arrangements in the first three phrases (5-7-5) of poems in The Twenty-One Collections of Waka, wherein there are 33692 tanka poems included.
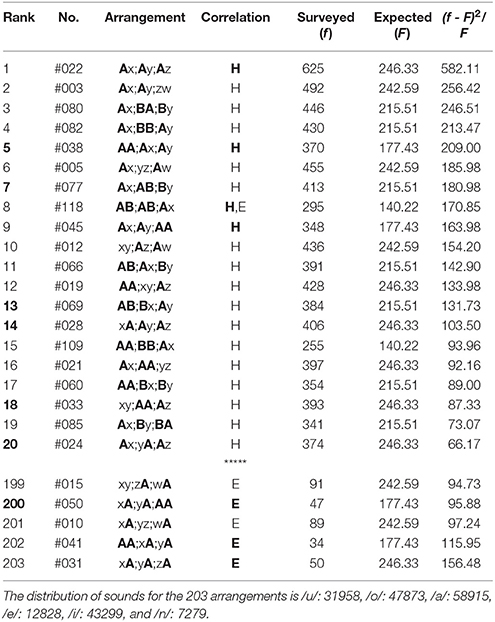
Table 10. The top-twenty and the bottom-five arrangements in the latter three phrases (5-7-7) of poems in The Twenty-One Collections of Waka, wherein there are 33692 tanka poems included.
Comparing Pattern Distributions
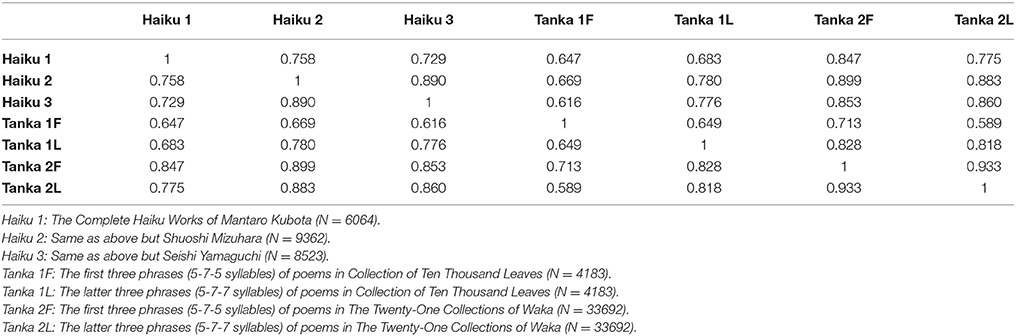
Although above we focus our attention on the top-twenty as well as the bottom-twenty arrangements, in this section we shall make a quantitative comparison between the complete distributions (i.e., #001–#203) of the arrangements. The results are summarized in Table 11. While such methods employing information-theoretical tools as the Hellinger distance as well as the Kullback-Leibler divergence are available, for several reasons we shall adopt the standard theory of two-variable correlation, in which the correlation between two distributions is measured by means of the Peason's method [44]. Namely, the correlation r (−1 ≤ r ≤ 1) is quantified with the covariance divided by the product of the two standard deviations. It is found from Table 11 that for all combinations the correlation is positive (i.e., 0 < r ≤ 1) and is bounded within the range 0.589 ≤ r ≤ 0.933 for the off-diagonal elements in the correlative matrix (note that trivial autocorrelations on the diagonal sites, r = 1, are excluded). Here the strongest correlation, r = 0.933, is seen for the autocorrelation of The Twenty-One Collections of Waka (i.e., Tanka 2F vs. Tanka 2L), whereas the weakest, r = 0.589, is for the cross-correlation between the first three phrases of poems in Collection of Ten Thousand Leaves (Tanka 1F) and the latter three phrases of poems in The Twenty-One Collections of Waka (Tanka 2L). From Table 11 we conclude as follows:
(1) First we shall pay attention to comparison among three combinations of haiku:
For Mantaro (Haiku 1) vs. Shuoshi (Haiku 2), r = 0.758,
For Mantaro (Haiku 1) vs. Seishi (Haiku 3), r = 0.729,
For Shuoshi (Haiku 2) vs. Seishi (Haiku 3), r = 0.890.
Evidently, among the three the correlation is found to be distinguished in the third combination (Haiku 2 vs. Haiku 3). This result is consistent with the fact that the first composer (Mantaro) had belonged to a haiku sect different from that of the other two (Shuoshi and Seishi). The sect to which the latter had belonged originated from an authority on the haiku community, Kyoshi Takahama (1874-1959), and it has been called Little Cuckoo Sect; both Shuoshi and Seishi are the most outstanding poets in the sect. [With Suju Takano (1893-1976) and Seiho Awano (1899-1992) the four poets are referred to as “Four S of Little Cuckoo” or more simply “Four S,” due to the common initial in their pen names.] Finally, it should be mentioned that similarly to the artful fluctuation analysis of network topology and word intermittency [45] the present statistical method might be useful for discriminating composers' styles in the context of stylometry [46].
(2) Next, we shall concentrate on the correlation with the distribution of Collection of Ten Thousand Leaves [24, 25]. What is most interesting in Table 11 is that there are relatively smaller values being seen on the correlations with the distribution of its first three phrases of poems (Tanka 1F), specifically
For Mantaro (Haiku1), r = 0.647,
For Shuoshi (Haiku 2), r = 0.669,
For Seishi (Haiku 3), r = 0.616,
For the latter three phrases of the same poetry (Tanka 1L), r = 0.649,
For the first three phrases of another tanka poetry (Tanka 2F), r = 0.713,
For the latter three phrases of another tanka poetry (Tanka 2L), r = 0.589.
These can be explained by remarking the circumstances peculiar to Collection of Ten Thousand Leaves, the oldest collection of waka including not only tanka but also choka, renga, sedoka, and bussokusekikataika, which is said to have been created in the eighth century and is known as its poetic style typical of the collection, where set epithets termed “pillow words” were used frequently. In addition to poems composed by court poets, Emperors, Imperial Princes and Princesses, and nobles, it includes a number of poems by many amateurs such as local farmers, lower-echelon government clerks, and coast guards, who remained anonymous and were pure of becoming distinguished in a poetic community by means of a rhetorical device. In consequence, those composed by them did not get involved in excessive rhetoric, the feature of which presents a striking contrast to poems in The Twenty-One Collections of Waka [26–41]. They had been compiled from the first half of the tenth century to the middle of the fifteenth century, and are occupied with poems composed by many professional poets having a good command of highly skillful rhetoric.
(3) Finally, to make a comparison among the three haiku collections (Haiku 1, 2, and 3) and The Twenty-One Collections of Waka (Tanka 2F and 2L), from Table 11 we shall pick out relevant values:
For Mantaro (Haiku 1): r = 0.847 (for Tanka 2F) and r = 0.775 (for Tanka 2L),
For Shuoshi (Haiku 2): r = 0.899 (for Tanka 2F) and r = 0.883 (for Tanka 2L),
For Seishi (Haiku 3): r = 0.853 (for Tanka 2F) and r = 0.860 (for Tanka 2L).
Evidently it is found that the distribution of Shuoshi (Haiku 2) shows the strongest correlation with those of the tanka collections being considered.
Testing Rank-Frequency Rules
Prior to exploring a statistical rule in the pattern distributions, in order to manifest the inequality and the diversity of each individual distribution, we take notice of the Gini coefficient G (0 ≤ G ≤ 1) and the Shannon's information entropy H (bit)
where pi = f i/N (i = 1, 2, …, M) with N = f 1 + f 2 + … + fM; p(j) (j = 1, 2, …, M) signify the data put in ascending order. M represents the number of categories; for the six-dimensional system, M = B(6) = 203. Besides H, such quantities as the Reyni's generalized entropy and the Simpson's diversity index will be obtainable, but at least for solving the present problem, there seems to be little merit to investigate. With H (bit) and M the relative entropy h (0 ≤ h ≤ 1) is defined with
The results of G and h are given in Table 12. It is found that the values of G are confined within 0.245 ≤ G ≤ 0.375; for the first three phrases of poems in Collection of Ten Thousand Leaves (Tanka 1F), G gives the minimum (G = 0.245), whereas for the latter three phrases of poems in The Twenty-One Collections of Waka (Tanka 2L), it attains to the maximum (G = 0.375). Comparison between the two tanka collections indicates that in the distribution of arrangements the latter (Tanka 2F and 2L) includes the inequality larger than that in the former (Tanka 1F and 1L); the results of the haiku works lie between the two extremes. In regard of h, irrespective of the kinds of poetry, its magnitude appears relatively high and consequently the values are found to be confined within the noticeably narrow region (i.e., 0.958 ≤ h ≤ 0.982), forming a striking contrast with that of G. Here we can notice that G and h are complementary to each other.
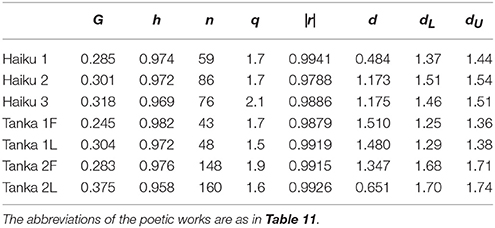
Table 12. List of the Gini coefficient G, the relative entropy h, the number of regression points, n, the optimal exponent of rank-ordered frequency, q, the degree of fit, |r|, the Durbin-Watson ratio d, the lower critical value of the ratio, dL (the 1% point), and its upper counterpart dU.
Subsequently, to generate rank-ordered statistics the frequency data fi (i = 1, 2, …, 203) of sound arrangements should be rearranged in descending order. For instance, for The Complete Haiku Works of Mantaro Kubota (Haiku 1) [21] they are given as
where X represents the rank. These rank-ordered data are used in the subsequent regression analysis. Below we concentrate on the regression of pq vs. log10 X [5, 47–49],
where q, a, and b denote positive parameters. To highlight the link with the Zipf's law [50, 51] the expression will be modified as
with
where e is the Napier's constant. Employing the formula
from Equation (7a) one obtains in the limit of q → 0
with a″ (b″) representing the limit of a′ (b′) as q → 0. Specifically, for b” = 1 the above relation, Equation (9), is reduced to the one that was found for the rank-frequency analysis of word statistics in English texts [50].
The validity of the present regression model can be checked by using the degree of fit, |r| (0 < |r| < 1), together with the Durbin-Watson ratio, d (0 < d < 4). Here the value of |r| is obtainable with the formula for calculating the Peason's correlation coefficient; the Durbin-Watson ratio can be written as [44]
with
where n indicates the summation of regression points, and Y = pq; the hat on Y represents the point on the regression line. With level alpha test being done, it can be judged that if 0 < d < dL (dL is the lower critical value) there exists a positive correlation between adjacent points on the sequence of the residual data ei (i = 1, 2, …, n) and that if dU < d ≤ 2 (dU is the upper critical value) there is no correlation between them. Note that for dL ≤ d ≤ dU any judgment is impossible. Therefore, a null hypothesis that “there is a correlation between the neighboring residual data” is rejected solely for dU < d ≤ 2. (For d > 2, d must be replaced by 4 – d.) For typical levels the two critical values are obtainable from numerical tables available. It should be emphasized here that this test with the ratio d is necessary for discriminating the genuine solution from the spurious one. In what follows, the level 1% test, i.e., α = 0.01, will be adopted. Along with G and h the analyzed results of q, |r|, and d are given in Table 12. The conclusion is that of the seven cases the hypothesis is rejected solely for Tanka 1F and for Tanka 1L, confirming the genuine rank-frequency rule for Collection of Ten Thousand Leaves.
Taking Notice of Given Names
Finally we shall discuss the reason why, as mentioned for the results in Tables 1–10, end sounds on their phrases are strongly anticorrelated both in haiku and in tanka. In summary, this feature can be explained by taking notice of the fact that, along with Finnish, Turkish, and Korean, Japanese belongs to the family of so-called agglutinative languages in which words are loosely agglutinated to a main word with a postpositional word functioning as an auxiliary to the former. According to the conventional Japanese classical literature, the auxiliary particles have been termed te-ni-o-ha by joining four particles (te, ni, o, ha) in sequence, where one should notice the end vowels, /e/, /i/, /o/, /a/, being free from duplication. This indicates that the probability of giving rise to the avoided rhyming could be enhanced if more than one particle are located simultaneously on the end sites of each phrase in a poem. Incidentally the above explanation is consistent with the so-called law of a linked form, which was presented initially by Norinaga Motoori (1730-1801), an authority on the Japanese classics in the middle of the Edo period. Indeed, through careful inspection into his works currently available it may be safely affirmed that the linkage is realized principally between particles with different sounds.
Lastly, we shall discuss why the nearest-neighbor correlations occur between sounds on the boundary of phrases on a poem. Honestly the qualitative explanation of the phenomena seems to be much difficult. As a clue to solve the hard problem, in what follows we shall focus our attention on the sound arrangement of Japanese full names. First, it should be noted that, as in Hungary as well as in other several East-Asian countries, in Japan the given name follows the family name, so that the end sound on the latter adjoins the head on the former. (Note that there is no middle name in the Japanese name.) Tables 13, 14, respectively, manifest the rank-ordered frequency distribution of the sound arrangements in the full names of Japanese men and women that have been registered in the database of Sapporo Gakuin University, Japan. Note that the four sounds on each individual arrangement correspond, in sequence, to (1) the vowel on the head syllable of the family name, (2) the last sound on the end syllable of the family one, (3) the vowel on the head syllable of the given name, and (4) the last sound on the end syllable of the given one, so that the semicolon in the vowel arrangement indicates the boundary between the family (first) and the given (latter) names. Application of this method to, for example, two samples yields
Suzuki Kazuhiko (masculine) → ui;ao → #1: xy;zw,
Koga Manami (feminine) → oa;ai → #5: xA;Ay.
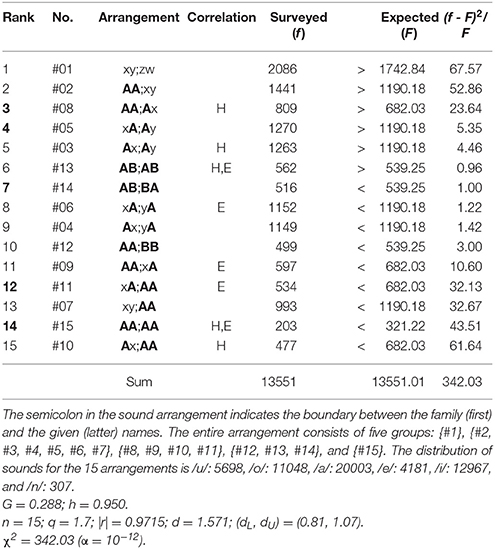
Table 13. Rank-ordered frequency distribution of the sound arrangements in the full names of Japanese men registered in the database of Sapporo Gakuin University.
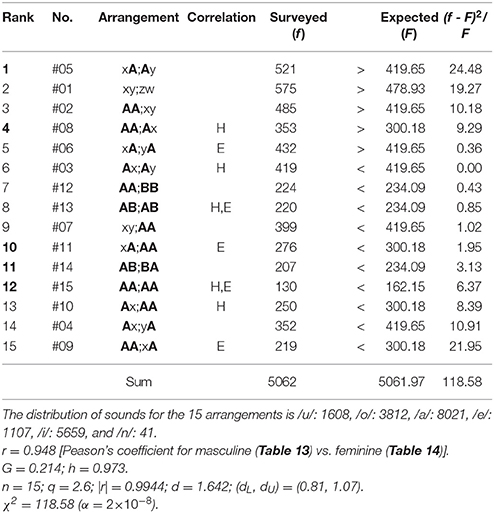
Table 14. Same as Table 13 but the full names of Japanese women registered in the database of Sapporo Gakuin University.
For the four-dimensional analysis the number of the categories is determined by M = B(4) = 15. From the results in Table 13, for the masculine names, remarkable concentration is seen on #1: xy;zw, #2: AA;xy, #8: AA;Ax, #5: xA;Ay, and #3: Ax;Ay, in which there are two arrangements (specifically, #8 and #5) that include the key segment A;A corresponding to the nearest-neighbor correlation. Subsequently, from those in Table 14, for the feminine names, noticeable aggregation is found on #5: xA;Ay, #1: xy;zw; #2: AA;xy, and #8: AA;Ax. Here it should be stressed that again the two arrangements #5 and #8, both of which imply the nearest-neighbor correlation, are included; in particular, the former, #5, does gain the premier place in the score of (f – F)2/F. To conclude, with regard to the preference for the nearest-neighbor sound correlations, coherence is preserved between the sound arrangements of the Japanese short poetry and those of the Japanese names. As a complement, it is well-known that the Japanese Imperial Family has traditionally a preference for the archaic names of the women of Imperial blood, such as Kako, Kiko, and Mako.
Conclusion
Sound correlations among the six sites on the Japanese short poetry have been detailed quantitatively both for haiku and for tanka. For corpora of the haiku poetry, the complete works of the three distinguished haiku composers have been selected. For those of the tanka, Collection of Ten Thousand Leaves and The Twenty-One Collections of Waka have been chosen. Analyzed results through comparison between the surveyed and the expected frequencies have manifested remarkable preference for the arrangements with the far-reaching correlations between heads as well as with the far-reaching anticorrelations between ends. In sharp contrast with the avoided rhyming between the far sites, preference has been found for specific arrangements showing the nearest-neighbor correlations. Subsequently, to reveal the distinctive feature of each corpus, correlation analysis has been carried out between the complete frequency distributions of the arrangements. Moreover, in order to explore a statistical rule for the rank-ordered frequency data, fitting has been made to a long-tail distribution. It has been shown that the results can be explained in comparison with the sound correlation between the first and the latter parts in the names of Japanese.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author should like to thank K. Saito, Secretary-General of Sapporo Gakuin University, for his permission to access the database of students as well as graduates of the university.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2018.00031/full#supplementary-material
References
1. Black-Schaffer AM, Doniach S. Effect of nearest neighbor spin-singlet correlations in conventional grapheme SNS Josephson junctions. Phys Rev B (2009) 79:064502. doi: 10.1103/PhysRevB.79.064502
2. Greif D, Tarruell L, Uehlinger T, Jördens R, Esslinger T. Probing nearest-neighbor correlations of ultracold fermions in an optical lattice. Phys Rev Lett. (2011) 106:145302. doi: 10.1103/PhysRevLett.106.145302
3. Buchler JR, Dufty JW, Kandrup HE. (ed.). Long-Range Correlations in Astrophysical Systems. New York, NY: New York Academy of Sciences (1998).
4. Rangarajan G, Ding M. (ed.). Processes with Long-Range Correlations. Berlin: Springer-Verlag (2003).
8. Kello CT, Brown GDA, Ferrer-i-Cancho R, Holden JG, Linkenkaer-Hansen K, Rhodes T, Van Orden GC. Scaling laws in cognitive sciences. Trends Cogn Sci. (2010) 14:223–32. doi: 10.1016/j.tics.2010.02.005
9. Amancio DR, Oliveira ONJr, Costa LF. Structure-semantics interplay in complex networks and its effects on the predictability of similarity in texts. Physica A (2012) 391:4406–19. doi: 10.1016/j.physa.2012.04.011
10. Amancio DR. Probing the topological properties of complex networks modeling short written texts. PLoS ONE (2015) 10:e0118394. doi: 10.1371/journal.pone.0118394
11. Amancio DR. A complex network approach to stylometry. PLoS ONE (2015) 10:e0136076. doi: 10.1371/journal.pone.0136076
12. Peng C-K, Mietus J, Hausdorff, JM, Havlin S, Stanley HE, Goldberger AL. Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys Rev Lett. (1993) 70:1343–46. doi: 10.1103/PhysRevLett.70.1343
13. Penna TJP, de Oliveira PMC, Sartorelli JC, Gonçalves WM, Pinto RD. Long-range anticorrelations and non-Gaussian behavior of a leaky faucet. Phys Rev E (1995) 52:R2168–71. doi: 10.1103/PhysRevE.52.R2168
14. Shvartsman N, Freund I. Vortices in random wave fields: nearest neighbor anticorrelations. Phys Rev Lett. (1994) 72:1008–11. doi: 10.1103/PhysRevLett.72.1008
30. Kawamura T, Kashiwagi Y, Kudo S. (ed.). Collection of Golden Leaves; Collection of Germs of Written Expression. Tokyo: Iwanami Shoten (1989).
31. Kubota J. (ed.). A Collection of Japanese Poetry of a Thousand Years. Tokyo: Iwanami Shoten (1986).
32. Sasaki N. (ed.). New Collection of Ancient and Modern Japanese Poetry. Tokyo: Iwanami Shoten (1959).
33. Nakagawa H. (ed.). A New Anthology of Japanese Poems Collected by Imperial Command. Tokyo: Meiji Shoin (2005).
34. National Books Inc. (ed.). A Revised and Annotated Anthology of National Poetry, Vol. 5–8: The Thirteen Collections of Waka, Pt.1-4. Tokyo: Kodansha (1976).
36. Iwasa M. (ed.). The Complete Annotation of Collection of Gemlike Leaves, Vol. 1–3. Tokyo: Kasama Shoin (1996).
38. Iwasa M. (ed.). The Complete Annotation of Collection of Elegance, Vol. 1. Tokyo: Kasama Shoin (2002).
39. Iwasa M. (ed.). The Complete Annotation of Collection of Elegance, Vol. 2. Tokyo: Kasama Shoin (2003).
40. Iwasa M. (ed.). The Complete Annotation of Collection of Elegance, Vol. 3. Tokyo: Kasama Shoin (2004).
41. Murao S. (ed.). New More Collection of Ancient and Modern Japanese Poetry. Tokyo: Meiji Shoin (2001).
42. Dickau RM. Bell Number Diagram. (1996). Available online at: http://mathforum.org/advanced/robertd/bell.html
43. Hayata K. Statistical prosody: rhyming pattern selection in Japanese short poetry. Forma (2006) 21:259–73.
45. Amancio DR. Authorship recognition via fluctuation analysis of network topology and word intermittency. J Stat Mech. (2015) 2015:P03005. doi: 10.1088/1742-5468/2015/03/P03005
46. Stamatatos E. A survey of modern authorship attribution methods. J Assoc Inf Sci Technol. (2009) 60:538–56. doi: 10.1002/asi.21001
47. Laherrere J, Sornette D. Stretched exponential distributions in nature and economy: “fat tails” with characteristic scales. Europ Phys J B (1998) 2:525–39.
48. Hayata K. Statistical properties of extremely squeezed configurations: a feature in common between squared squares and neighboring cities. J Phys Soc Jpn. (2003) 72:2114–17. doi: 10.1143/JPSJ.72.2114
49. Hayata K. A time-dependent statistical analysis of the large-scale municipal consolidation. Forma (2010) 25:37–44.
Keywords: quantitative poetics, rhyming scheme, spontaneous pattern selection, rank- frequency rule, long-tail phenomena
Citation: Hayata K (2018) Phonological Complexity in the Japanese Short Poetry: Coexistence Between Nearest-Neighbor Correlations and Far-Reaching Anticorrelations. Front. Phys. 6:31. doi: 10.3389/fphy.2018.00031
Received: 06 February 2018; Accepted: 23 March 2018;
Published: 18 April 2018.
Edited by:
Víctor M. Eguíluz, Instituto de Física Interdisciplinar y Sistemas Complejos (IFISC), SpainReviewed by:
Haroldo Valentin Ribeiro, Universidade Estadual de Maringá, BrazilDiego R. Amancio, Universidade de São Paulo, Brazil
Copyright © 2018 Hayata. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kazuya Hayata, aGF5YXRhQHNndS5hYy5qcA==
 Kazuya Hayata
Kazuya Hayata