The Role of Fractional Time-Derivative Operators on Anomalous Diffusion

The generalized diffusion equations with fractional order derivatives have shown be quite efficient to describe the diffusion in complex systems, with the advantage of producing exact expressions for the underlying diffusive properties. Recently, researchers have proposed different fractional-time operators (namely: the Caputo-Fabrizio and Atangana-Baleanu) which, differently from the well-known Riemann-Liouville operator, are defined by non-singular memory kernels. Here we proposed to use these new operators to generalize the usual diffusion equation. By analyzing the corresponding fractional diffusion equations within the continuous time random walk framework, we obtained waiting time distributions characterized by exponential, stretched exponential, and power-law functions, as well as a crossover between two behaviors. For the mean square displacement, we found crossovers between usual and confined diffusion, and between usual and sub-diffusion. We obtained the exact expressions for the probability distributions, where non-Gaussian and stationary distributions emerged. This former feature is remarkable because the fractional diffusion equation is solved without external forces and subjected to the free diffusion boundary conditions. We have further shown that these new fractional diffusion equations are related to diffusive processes with stochastic resetting, and to fractional diffusion equations with derivatives of distributed order. Thus, our results suggest that these new operators may be a simple and efficient way for incorporating different structural aspects into the system, opening new possibilities for modeling and investigating anomalous diffusive processes.

1. Introduction

The random walk concept is one of the broadest and versatile paradigms to deal with statistical fluctuations. The term “random walk” was coined in 1905 by Pearson [1], but the fundamental relationship between this concept and the usual diffusion equation was reported earlier in the seminal works of Rayleigh [2–4] in sound theory, Bachelier [5] in economics, Einstein [6], and von Smoluchowski [7] in the Brownian motion theory. Due to this intrinsic relation, the usual random walk is characterized by Gaussian, Markovian, and ergodic properties, which lead to a linear time dependence of the mean square displacement, (Δx)² ~ t. The versatility of this concept relies on the possibility of generalizations and extensions to describe systems with one or more characteristics of anomalous diffusion: non-Gaussian distributions; long-range memory effects (non-Markovian); non-ergodicity; divergent mean square displacement (Lévy walks); and nonlinear mean square displacement, (Δx)² ~ t^α (sub-diffusion: α < 1, superdiffusion: α > 1, confined or saturated diffusion: α = 0).

In the context of generalizations, the first landmark is the work proposed in 1965 by Montroll and Weiss [8], in which they introduce the continuous time random walk concept (see [9] for a general overview). This framework is characterized by a joint distribution of jump length and waiting time ψ(x, t), where $\lambda (x)={\int }_0^{\infty }dt\psi (x,t)$ is the jump length distribution and $\omega (t)={\int }_{-\infty }^{\infty }dx\psi (x,t)$ is the waiting time distribution. Subsequently, a connection with a generalized master equation is proposed to discuss memory effects in the continuous time random walk [10–12]; the waiting time distribution ω(t) is strictly related to the memory kernel of the generalized master equation. Moreover, natural extensions of both random walk and continuous time random walk were proposed to study transport properties in systems with structural complexity, such as disordered, random, and fractal environments [13].

The second landmark, “a modern era of the continuous time random walk” according to Kutner and Masoliver [9], is the development of the intrinsic relationship between this formalism and the fractional diffusion equations. Among the seminal works, we have found a simple mention in the work of Klafter et al. [14] on the possibility of having a fractional diffusion equation to describe anomalous transport. However, were Hilfer et al. [15] that, 90 years after Einstein's work [6], established a rigorous and precise connection between the continuous time random walk and the fractional master equation as well as with the fractional diffusion equation (a special case of the former). This result was later extended by Compte [16] in the long-time limit, where it is shown that any decoupled continuous time random walk having no characteristic scale of time or space (power-law memories) corresponds to a time- or space-fractional diffusion equation, respectively with Riemann-Liouville time derivative or Riesz space derivate. The subsequent success and development of the fractional approach are well documented in two review articles by Meztler and Klafter [17, 18], and in several articles by Barkai [19–22].

Since memory effects underlying a continuous time random walk are implicitly considered by the differential operators, the versatility of the fractional formalism is mainly related to two remarkable features. First, this formalism handles very well the physical requirements of a system by dealing boundary conditions and external forces in a simple manner. Second, it takes advantage of traditional tools from mathematical physics and statistics for obtaining exact expressions to describe complex systems with anomalous behaviors. For instance, in the following fractional differential equation

$\begin{array}{ll}\frac{\partial }{\partial t}\rho \left(x,t\right){=}_0{{D}}_t^{1-\alpha }\left({L}\left\{\rho \left(x,t\right)\right\}\right),& (1)\end{array}$

where

$\begin{array}{l}{L}\left\{\rho \left(x,t\right)\right\}=D\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right)-\frac{\partial }{\partial x}\left[F\left(x,t\right)\rho \left(x,t\right)\right],\end{array}$

the nonusual relaxation can be associated with a continuous time random walk where the waiting time distribution is a power-law. This process is also strictly related to the Riemann-Liouville fractional operator [23]

$\begin{array}{ll}{{\displaystyle {}_0{D}}}_t^{1-\alpha }\rho (x,t)=\frac{1}{\Gamma \left(\alpha \right)}\frac{d}{dt}{\displaystyle {\int }_0^t\frac{\rho (x,t\prime )}{{(t-t^{\prime })}^{1-\alpha }}}dt\prime ,& (2)\end{array}$

where 0 < α < 1 is the fractional order exponent (or the anomalous exponent), a quantity that can be interpreted as an index of memory in empirical systems [24]. The fractional operator is also responsible for introducing a nonlinear time dependence in the mean square displacement of the system [17]. Thus, a large class of complex phenomena can be effectively described by extending the standard differential operator to a non-integer order [25–34]; indeed, as pointed out by West [35], the fractional calculus provides a suitable framework to deal with complex systems.

Recently, researchers have made and promoted remarkable progress toward improving experimental techniques for investigating diffusive processes, mainly illustrated by the developments in the single-particle tracking technique [36–39]. Such improvements yield novel insights into transport properties of biological systems [40–42] and nanomaterials [43–45], where the high-resolution of the experiments has found different diffusive behaviors depending on the time scale. In this context, an important question is whether other forms of fractional differential operators (replacing the Riemann-Liouville one) such as those recently-proposed with non-singular kernels [46–51] are suitable to describe the aforementioned situations. To answer this question, we investigate an one-dimensional diffusive process described by the fractional diffusion equation

$\begin{array}{ll}\frac{\partial }{\partial t}\rho \left(x,t\right)=D{{F}}_t^{\alpha }\left(\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right)\right),& (3)\end{array}$

where D is the generalized diffusion coefficient. This equation is also subjected to the free diffusion boundary conditions ρ(±∞, t) = 0 and to the initial condition ρ(x, 0) = φ(x).

The fractional operator in Equation (3) is defined as

$\begin{array}{ll}{{F}}_t^{\alpha }\rho \left(x,t\right)=\frac{\partial }{\partial t}{\displaystyle {\int }_0^t}\rho \left(x,t^{\prime }\right){K}\left(t-t^{\prime }\right)d{t}^{\prime },& (4)\end{array}$

in order to consider situations with singular and non-singular kernels in a unified way. It is worth noting that ${K}$(t) = δ(t) recovers the usual diffusion equation. Here we consider three different forms for the kernel ${K}$(t). The first one is

$\begin{array}{ll}{K}\left(t\right)=t^{\alpha -1}/\Gamma \left(\alpha \right),& (5)\end{array}$

which corresponds to the well-known Riemann-Liouville fractional operator [52] for 0 < α < 1. The second one is

$\begin{array}{ll}{K}\left(t\right)=bexp\left(-\frac{\alpha t}{1-\alpha }\right),& (6)\end{array}$

which corresponds to the fractional operator of Caputo-Fabrizio [46, 53, 54]. As discussed in Caputo and Fabrizio [46], the ratio α/(1 − α) maps the time from the range [0, ∞] to the range [0, 1] (see also [54] for details on the role of the fractional order α).

Finally, the third one is

$\begin{array}{ll}{K}\left(t\right)=b{E}_{\alpha }\left(-\frac{\alpha t^{\alpha }}{1-\alpha }\right),& (7)\end{array}$

where E_α(…) is the Mittag-Leffler function [52]. This kernel corresponds to the fractional operator of Atangana and Baleanu [47]. Further possibilities for the kernel ${K}$(t) are discussed by Gómez-Aguilar et al. [48]. We observe that the Riemann-Liouville operator have a singularity at the origin (t = 0), while the recently-proposed Caputo-Fabrizio and Atangana-Baleanu are non-singular operators [46–51]. In the previous definitions, the parameter b is a normalization constant and α is the fractional order exponent.

Our main goal here is to verify how these different fractional operators modify the fractional diffusion Equation (1) and what are the effect of these choices on the underlying diffusive properties of a system modeled by this equation. The rest of this manuscript is organized as follows. In Section II, we investigate general solutions and processes related with Equation (3) when considering different choices (singular and non-singular) for the kernel ${K}$(t). In Section 3, we present a summary of our results and some concluding remarks.

2. Diffusion and Fractional Operators

We start by noting that the solution of the fractional diffusion Equation (3) in the Fourier-Laplace space is

$\begin{array}{ll}\rho \left(k,s\right)=\frac{\phi \left(k\right)}{s+sD{K}\left(s\right)k^2},& (8)\end{array}$

where ρ(k, s) is the Fourier-Laplace transformation of the probability distribution ρ(x, t). This result can be related to different situations depending on the choice of the kernel ${K}$(s).

Within the continuous time random walk formalism and by following the works of Meztler and Klafter [17], we can show that the waiting time ω(t) and the jump λ(x) probability distribution associated with Equation (3) are (in the Laplace and Fourier spaces)

$\begin{array}{ll}\omega \left(s\right)=\frac{{K}\left(s\right)/{\tau }_c}{1+{K}\left(s\right)/{\tau }_c}& (9)\end{array}$

and $\lambda (k)=1-k^{2}D{\tau }_c$, where τ_c is a characteristic waiting time of the underlying continuous time random walk. We observe that the jump probability distribution is characterized by a Gaussian asymptotic behavior [$\lambda (x)~e^{-x^2/{(2D{\tau }_c)}^2}$] and thus has a finite characteristic jump length, regardless of the choice for the kernel ${K}$(t). On the other hand, the inverse Laplace transform of the waiting time distribution is given by

$\begin{array}{l}\omega \left(t\right)=\frac{1}{{\tau }_c}{\displaystyle {\int }_0^t}d{t}^{\prime }{K}\left(t^{\prime }\right)+{\displaystyle \sum _{n=1}^{\infty }}{\left(-\frac{1}{{\tau }_c}\right)}^n{\displaystyle {\int }_0^t}d{t}_n{K}\left(t-t_n\right)\cdots \\ \times {\displaystyle {\int }_0^{t_4}}d{t}_3{K}\left(t_4-t_3\right){\displaystyle {\int }_0^{t_2}}d{t}_1{K}\left(t_2-t_1\right){K}\left(t_1\right),& (10)\end{array}$

yielding different situations that depends on ${K}$(t).

The choice ${K}$(t) = δ(t) leads to usual diffusion and an exponential distribution for the waiting times

$\begin{array}{ll}\omega \left(t\right)=\frac{1}{{\tau }_c}{e}^{-t/{\tau }_c}.& (11)\end{array}$

For the fractional operator of Riemann-Liouville, we find

$\begin{array}{ll}\omega \left(t\right)=\frac{1}{{\tau }_c}{t}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-\frac{1}{{\tau }_c}{t}^{\alpha }\right),& (12)\end{array}$

where E_α,α(…) is the generalized Mittag-Leffler function [52] whose asymptotic behavior is described by a power-law, ω(t) ~ 1/t^1+α for t → ∞. For the Atangana-Baleanu operator (Equation 7), the waiting time distribution is given by

$\begin{array}{ll}\omega \left(t\right)=\frac{\xi b\gamma }{\pi {\tau }_c}sin\left(\pi \gamma \right){\displaystyle {\int }_0^{\infty }}d\eta \frac{{\eta }^{\gamma }{e}^{-\eta b\left(1-\alpha \right)t/{\tau }_c}}{{\left(1-\eta \right)}^2+2\xi \left(1-\eta \right){\eta }^{\gamma }cos\left(\pi \gamma \right)+{\eta }^{2\gamma }}& (13)\end{array}$

where γ = 1 − α and ξ = αb/τ_c. This expression is very interesting because for small times we have a stretched exponential, that is,

$\begin{array}{ll}\omega \left(t\right)~E_{\alpha }\left(-\frac{\alpha t^{\alpha }}{1-\alpha }\right)~exp\left(-\frac{\alpha t^{\alpha }}{\left(1-\alpha \right)\Gamma \left(\alpha \right)}\right),& (14)\end{array}$

while for long times we have the same power-law behavior of the Riemann-Liouville operator. Thus, the Atangana-Baleanu operator yields a crossover between a stretched exponential and a power-law distribution.

In the case of the Caputo-Fabrizio operator, the connection with the continuous time random walk is more complex and not compatible with its standard interpretation. As we shall discuss later on, the diffusion equation associated with this operator is connected to a diffusive process with stochastic resetting [55, 56], where the waiting time distribution is exponential.

Figure 1 depicts the behavior of the waiting time distribution ω(t) for the different kernels previously-discussed. For long times, we confirm that the operators of Riemann-Liouville and Atangana-Baleanu yield the same power-law decay for ω(t). We further note that the Atangana-Baleanu operator yields a non-divergent ω(t), an interesting feature that is not observed for the singular kernel of Riemann-Liouville.

FIGURE 1

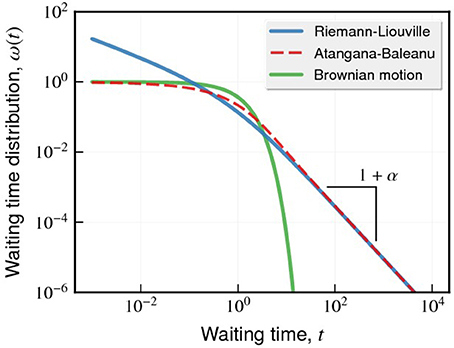
Figure 1. Changes in the waiting time distribution ω(t) caused by the different forms of the kernel ${K}$(t) defining the fractional operator of Equation (4). The different curves correspond the ω(t) when choosing the kernels of Riemann-Liouville (Equation 5, blue), Atangana-Baleanu (Equation 7, red), and the usual (Brownian motion) case [${K}$(t) = δ(t), green]. For simplicity, we have considered τ_c = 1 and α = 1/2. We note that the asymptotic behavior of ω(t) is a power-law for the kernels of Riemann-Liouville and Atangana-Baleanu, that is, ω(t) ~ 1/t^1+α. In the usual, we have an exponential behavior.

We now focus on finding the formal solutions for the fractional diffusion Equation (1) when considering the three different fractional operators. These solutions are obtained by performing the inverse of Fourier and Laplace transforms of the ρ(k, s) expressed in Equation (8), where the Laplace transform of the kernel ${K}$(s) appears. In the well-known case of the Riemann-Liouville operator [17], we have

$\begin{array}{ll}{K}\left(s\right)=s^{-\alpha }& (15)\end{array}$

and consequently

$\begin{array}{ll}\rho \left(x,t\right)={\displaystyle {\int }_{-\infty }^{\infty }}d{x}^{\prime }{G}\left(x-x^{\prime },t\right)\phi \left(x^{\prime }\right),& (16)\end{array}$

where the Green function is

$\begin{array}{ll}{G}\left(x,t\right)=\frac{1}{2\left|x\right|}{\mathrm{\text{H}}}_{1,1}^{1,0}\left[\frac{\left|x\right|}{\sqrt{D{t}^{\alpha }}}{|}_{\left(1,1\right)}^{\left(1,\frac{\alpha }{2}\right)}\right].& (17)\end{array}$

Here H(…) stands for the Fox H-function [57]. Having found the probability distribution, we can show that the mean square displacement is

$\begin{array}{ll}{\left(\Delta x\right)}^2=\langle {\left(x-\langle x\rangle \right)}^2\rangle =\frac{2D{t}^{\alpha }}{\Gamma \left(1+\alpha \right)},& (18)\end{array}$

which corresponds to the typical case of anomalous diffusion, where α < 1 represents sub-diffusion and α → 1 recovers the usual diffusion. The time-dependent behavior of a typical probability distribution ρ(x, t) (with α = 1/2) is shown in Figure 2A. We observe that the Riemann-Liouville operator leads to a tent-shaped distribution, whose tails are longer than the Gaussian distribution of the usual diffusion (Figure 2D). Figure 3 shows the corresponding behavior for mean square displacement of Equation (18), which is a power-law function of the time t with an exponent α.

FIGURE 2

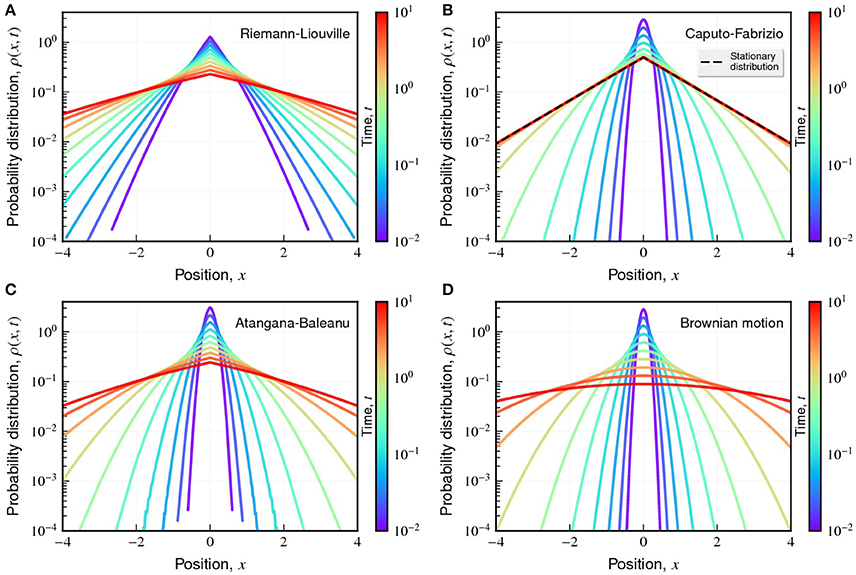
Figure 2. Changes in the profile of probability distribution ρ(x, t) caused by the different fractional time operators. The plots show a typical shape of ρ(x, t) for different values of t (indicated by the color code) when considering the operators of Riemann-Liouville (A), Caputo-Fabrizio (B), Atangana-Baleanu (C), and the usual case (D). For simplicity, we have considered φ(x) = δ(x), α = 1/2, and Db = 1. The dashed line in (B) indicates the stationary solution in the Caputo-Fabrizio (Equation 23).

FIGURE 3

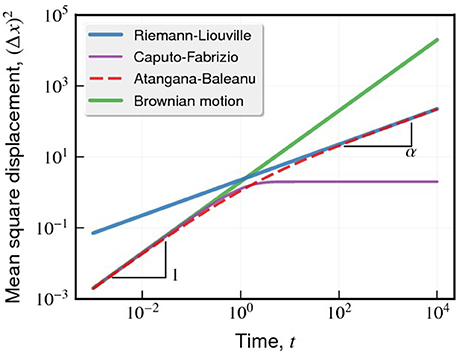
Figure 3. Changes in the evolving behavior of the mean square displacement (Δx)² caused by the different fractional time operators. The curves show (Δx)² vs. t when considering the operators of Riemann-Liouville (blue, Equation 18), Caputo-Fabrizio (purple, Equation 24), Atangana-Baleanu (red, Equation 35), and the usual case [green, (Δx)² ∝ t]. For simplicity, we have considered α = 1/2 and Db = 1. It is worth noting the Atangana-Baleanu operator shows a crossover between usual (for small times) and sub-diffusion (for long time). In the Caputo-Fabrizio case, the diffusion is usual for small times and saturates for large times.

For the Caputo-Fabrizio operator, the Laplace transform of the kernel in Equation (6) is

$\begin{array}{ll}{K}\left(s\right)=\frac{b}{\left(s+\frac{\alpha }{1-\alpha }\right)},& (19)\end{array}$

which substituted into Equation (8) yields

$\begin{array}{ll}\rho \left(k,s\right)=\frac{\left(s+\frac{\alpha }{1-\alpha }\right)\phi \left(k\right)}{s\left(s+\frac{\alpha }{1-\alpha }+Db{k}^2\right)}.& (20)\end{array}$

By performing the inverse Fourier and Laplace transforms, we have

$\begin{array}{l}\rho \left(x,t\right)={\displaystyle {\int }_{-\infty }^{\infty }}d{x}^{\prime }{G}\left(x-x^{\prime },t\right)\phi \left(x^{\prime }\right)\\ +\frac{\alpha }{1-\alpha }{\displaystyle {\int }_0^t}d{t}^{\prime }{\displaystyle {\int }_{-\infty }^{\infty }}d{x}^{\prime }{G}\left(x-x^{\prime },t^{\prime }\right)\phi \left(x^{\prime }\right)& (21)\end{array}$

where the Green function is

$\begin{array}{ll}{G}\left(x,t\right)=\frac{e^{-\frac{\alpha t}{1-\alpha }}}{\sqrt{4\pi Dbt}}{e}^{-\frac{x^2}{4Dbt}},& (22)\end{array}$

A typical shape of this distribution is shown in Figure 2B. We observe that this distribution is very similar to a Gaussian for small times, and exhibits a tent-shape to long times. However, differently from the distribution obtained for the Riemann-Liouville operator (Equations 16 and 17), the distribution obtained from Equations (21) and (22) displays a stationary behavior for t → ∞, that is,

$\begin{array}{ll}\rho \left(x,t\to \infty \right)~{\displaystyle {\int }_{-\infty }^{\infty }}d{x}^{\prime }\phi \left(x^{\prime }\right)e^{-\frac{\alpha |x-x^{\prime }|}{\left(1-\alpha \right)Db}},& (23)\end{array}$

a result that corresponds to confined diffusion. Figure 2B also shows this stationary solution (dashed line); in particular, we observe that the shape of ρ(x, t) is practically constant for t ≳ 5 in that case. This behavior also appears in the mean square displacement

$\begin{array}{ll}{\left(\Delta x\right)}^2=\frac{2Db\left(1-\alpha \right)}{\alpha }\left(1-e^{-\frac{\alpha t}{1-\alpha }}\right),& (24)\end{array}$

which behaves linearly in time for small times and saturates in 2Db(1 − α)/α for long times. Figure 3 illustrates this crossover, a common feature of systems where diffusion is confined or hindered [41, 58]. In particular, the same crossover between usual and confined diffusion is observed in simulations of diffusion with immobile obstacles or obstacles moving according to an Ornstein-Uhlenbeck process [59, 60].

An intriguing feature of the diffusion equation with the Caputo-Fabrizio fractional operator is that it can be related to a diffusion with stochastic resetting [61]. Indeed, we find out that the fractional diffusion Equation (3) with the kernel of Equation (6) can be rewritten as

$\begin{array}{l}\frac{\partial }{\partial t}\rho \left(x,t\right)=Db\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right)\\ -\frac{\alpha }{1-\alpha }Db{\displaystyle {\int }_0^t}d{t}^{\prime }{e}^{-\frac{\alpha }{1-\alpha }\left(t-t^{\prime }\right)}\frac{{\partial }^2}{\partial x^2}\rho \left(x,t^{\prime }\right).& (25)\end{array}$

This equation is essentially the same obtained by Hristov [49] when by analyzing a heat diffusion equation with non-singular memory. Also, by integrating both sides of the fractional diffusion Equation (3), we obtain

$\begin{array}{ll}Db{\displaystyle {\int }_0^t}d{t}^{\prime }{e}^{-\frac{\alpha }{1-\alpha }\left(t-t^{\prime }\right)}\frac{{\partial }^2}{\partial x^2}\rho \left(x,t^{\prime }\right)=\rho \left(x,t\right)-\phi \left(x\right),& (26)\end{array}$

which after substituting into Equation (25) yields

$\begin{array}{ll}\frac{\partial }{\partial t}\rho \left(x,t\right)=Db\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right)-\frac{\alpha }{1-\alpha }\left[\rho \left(x,t\right)-\phi \left(x\right)\right].& (27)\end{array}$

Equation (27) with φ(x) = δ(x − x₀) is the same obtained by Evans and Majumdar [61] when studying a random walker whose position is redefined to the position x₀ with a rate r = α/(1 − α). Thus, the fractional exponent α in the fractional diffusion equation of Caputo-Fabrizio can be related to a well-defined physical quantity (resetting rate).

Also, the mean square displacement of Equation (24) is analogous to results obtained from a random walk description of a diffusive process with stochastic resetting, subjected to an exponential waiting time distribution [55, 56]. As discussed in these works, a suitable continuous time random walk formulation is established by considering a density of particles ${J}$(x, t) whose dynamics is governed by

$\begin{array}{l}{J}\left(x,t\right)=\delta \left(t\right)\delta \left(x\right)+r\delta \left(x\right){\displaystyle {\int }_0^t}d{t}^{\prime }\omega \left(t^{\prime }\right){J}\left(x,t-t^{\prime }\right)\\ +\left(1-r\right){\displaystyle {\int }_0^t}d{t}^{\prime }\psi \left(x^{\prime },t^{\prime }\right){J}\left(x-x^{\prime },t-t^{\prime }\right),& (28)\end{array}$

when particles start the random walk at the origin (x = 0) with $\rho (x,t)={\int }_0^t\Phi (t^{\prime }){J}(x,t-t^{\prime })d{t}^{\prime }$ and $\Phi (t)={\int }_t^{\infty }\omega (t^{\prime })d{t}^{\prime }$. In Equation (28), r is a resetting rate, ψ(x, t) is joint distribution of jump length and waiting time, $\lambda (x)={\int }_0^{\infty }dt\psi (x,t)$ is the jump length distribution, and $\omega (t)={\int }_{-\infty }^{\infty }dx\psi (x,t)$ is waiting time distribution. By considering λ(x) Gaussian and ω(t) exponentially distributed, we can show that this formalism leads to Equation (27). It is worth remarking that by comparison with this framework, we can infer that the diffusion equation with the Caputo-Fabrizio operator leads to the same waiting time distribution of the usual diffusion, that is, an exponential.

Finally, for the Atangana-Baleanu operator, the Laplace transform of the kernel in Equation (7) is

$\begin{array}{ll}{K}\left(s\right)=\frac{b{s}^{\alpha -1}}{\left(s^{\alpha }+\frac{\alpha }{1-\alpha }\right)},& (29)\end{array}$

which substituted into Equation (8) yields

$\begin{array}{ll}\rho \left(k,s\right)=\frac{\left(s^{\alpha }+\frac{\alpha }{1-\alpha }\right)\phi \left(k\right)}{s^{\alpha }\left(s+\frac{\alpha }{1-\alpha }{s}^{1-\alpha }+Db{k}^2\right)},& (30)\end{array}$

the solution for the fractional diffusion Equation (3) in the Fourier-Laplace space. By evaluating the inverse Fourier and Laplace transforms, we obtain

$\begin{array}{l}\rho \left(x,t\right)={\displaystyle {\int }_{-\infty }^{\infty }}d{x}^{\prime }{G}\left(x-x^{\prime },t\right)\phi \left(x^{\prime }\right)\\ +\frac{\alpha }{\Gamma \left(\alpha \right)\left(1-\alpha \right)}{\displaystyle {\int }_0^t}\frac{d{t}^{\prime }}{{\left(t-t^{\prime }\right)}^{1-\alpha }}{\displaystyle {\int }_{-\infty }^{\infty }}d{x}^{\prime }\phi \left(x^{\prime }\right){G}\left(x-x^{\prime },t^{\prime }\right),& (31)\end{array}$

where the Green function is

$\begin{array}{l}{G}\left(x,t\right)=\frac{e^{-\frac{x^2}{4Dbt}}}{\sqrt{4\pi Dbt}}\\ +\frac{1}{\left|x\right|}{\displaystyle \sum _{n=1}^{\infty }}\frac{{\left(-\frac{\alpha }{1-\alpha }\right)}^n}{\Gamma \left(1+n\right)}{t}^{n\alpha }{\mathrm{\text{H}}}_{2,2}^{2,0}\left[\frac{x^2}{Dbt}{|}_{\left(1,2\right),\left(1+n,1\right)}^{\left(1+\alpha n,1\right),\left(1,1\right)}\right].& (32)\end{array}$

Once again, H(…) stands for the Fox H-function [57]. We can also show that for |x| → ∞, Equation (32) is approximated by

$\begin{array}{ll}{G}\left(x,t\right)\approx \frac{1}{\sqrt{4\pi Dbt}}{e}^{-f\left(x,t\right)},& (33)\end{array}$

where

$\begin{array}{ll}f\left(x,t\right)=\frac{x^2}{4Dbt}+\frac{\alpha }{1-\alpha }{t}^{\alpha }{\left(\frac{x^2}{4Dbt}\right)}^{1-\alpha }.& (34)\end{array}$

A typical behavior for the distribution ρ(x, t) for this operator is shown in Figure 2C. Similarly to the Caputo-Fabrizio operator, the profile of ρ(x, t) resembles a Gaussian for small times, while exhibits a tent-shape for long times. However, the distribution does not have a stationary solution for the Atangana-Baleanu operator. This crossover between two behaviors for ρ(x, t) is also present in Equation (34), and can be better quantified by analyzing the mean square displacement. For this operator, we have

$\begin{array}{ll}{\left(\Delta x\right)}^2=2Dbt{E}_{\alpha ,2}\left(-\frac{\alpha }{1-\alpha }{t}^{\alpha }\right),& (35)\end{array}$

where E_α,2(…) is the generalized Mittag-Leffler function [52]. By considering the asymptotic limits of this function, we can show that (Δx)² ~ t for small times, and (Δx)² ~ t^{1 − α} for long times.

This crossover between usual and sub-diffusion is present in several biological systems [62–66] and is also illustrated in Figure 3 for α = 1/2. A similar situation appears in simulations of diffusion with obstacles moving according to a usual random walk [59, 60], where the same crossover between usual and sub-diffusion with α = 1/2 is observed. It is worth mentioning that crossovers between diffusive regimes can also be described by generalized Langevin equations [67] and fractional (with the Riemann-Liouville operator) Kramers equations [19], among other approaches [68, 69]. In particular, the usual Langevin equation [70] predicts a crossover between ballistic and usual diffusion, which has been experimentally observed only in 2011 [71]. However, the diffusion equation in terms of these new operators lead to these crossovers without explicitly considering external forces, inertial effects, and reaction terms.

The fractional diffusion equation with the Atangana-Baleanu operator can be further related to fractional derivatives of distributed order as proposed by Caputo [72, 73] and worked out in Chechkin [68] and Lenzi et al. [69], that is,

$\begin{array}{ll}{\displaystyle {\int }_0^1}d\nu w\left(\nu \right)\frac{{\partial }^{\nu }}{\partial t^{\nu }}\rho \left(x,t\right)=D\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right),& (36)\end{array}$

where w(ν) is the distribution of the fractional order exponent ν and

$\begin{array}{ll}\frac{{\partial }^{\nu }}{\partial t^{\nu }}\rho \left(x,t\right)=\frac{1}{\Gamma \left(1-\nu \right)}{\displaystyle {\int }_0^t}\frac{d{t}^{\prime }}{{\left(t-t^{\prime }\right)}^{\nu }}\frac{\partial }{\partial t^{\prime }}\rho \left(x,t^{\prime }\right)& (37)\end{array}$

is the fractional time derivative of Caputo. Indeed, by substituting the kernel of Equation (7) into Equation (3) and taking the Laplace transform, we have

$\begin{array}{ll}s\rho \left(x,s\right)-\rho \left(x,0\right)=Db\frac{s^{1-\alpha }}{s^{1-\alpha }+\frac{\alpha }{1-\alpha }}\frac{{\partial }^2}{\partial x^2}\rho \left(x,s\right),& (38)\end{array}$

which can be rewritten as

$\begin{array}{l}s\rho \left(x,s\right)-\rho \left(x,0\right)+\frac{\alpha }{1-\alpha }{s}^{-\alpha }\left[s\rho \left(x,s\right)-\rho \left(x,0\right)\right]\\ =Db\frac{{\partial }^2}{\partial x^2}\rho \left(x,s\right).& (39)\end{array}$

By calculating the inverse Laplace transform of the previous equation, we find

$\begin{array}{l}\frac{\partial }{\partial t}\rho \left(x,t\right)+\frac{\alpha }{\Gamma \left(\alpha \right)\left(1-\alpha \right)}{\displaystyle {\int }_0^t}\frac{d{t}^{\prime }}{{\left(t-t^{\prime }\right)}^{1-\alpha }}\frac{\partial }{\partial t^{\prime }}\rho \left(x,t^{\prime }\right)\\ =Db\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right),& (40)\end{array}$

which can also be written as

$\begin{array}{ll}\frac{\partial }{\partial t}\rho \left(x,t\right)+\frac{\alpha }{1-\alpha }\frac{{\partial }^{1-\alpha }}{\partial t^{1-\alpha }}\rho \left(x,t\right)=Db\frac{{\partial }^2}{\partial x^2}\rho \left(x,t\right).& (41)\end{array}$

We note that Equation (41) is a special case of Equation (36) with $w(\nu )=\delta (\nu -1)+\frac{\alpha }{1-\alpha }\delta (\nu +\alpha -1)$. Analogously to results reported here, the solutions of Equation (41) are also characterized by two diffusive regimes [68, 69].

3. Discussion and Conclusions

We presented a detailed investigation of the changes in the fractional diffusion equation when the well-established Riemann-Liouville operator is replaced by the recently-proposed operators of Caputo-Fabrizio and Atangana-Baleanu. These changes are summarized in Table 1. Within the context of the continuous time random walk, we verified that these new fractional operators modify the behavior of the waiting time distribution. In the Caputo-Fabrizio case, we found that the waiting time distribution is described by an exponential distribution; while the Atangana-Baleanu operator yields a distribution that decays as a stretched exponential for small times and as a power-law (with the same exponent of the Riemann-Liouville operator) for long times.

TABLE 1

Table 1. Summary of the changes caused by the different fractional operators on the diffusion Equation (1).

We obtained the exact solutions of the fractional diffusion equation and the time dependence of the mean square displacement when considering these different fractional operators. Our results reveal that these new operators lead to non-Gaussian distributions and different diffusive regimes depending on the time scale. For the Caputo-Fabrizio operator, the probability distribution ρ(x, t) displays a stationary state as well as saturated diffusion for long times. This is a remarkable feature because the fractional diffusion equation is solved without external forces and subjected to the free diffusion boundary conditions. For the Atangana-Baleanu operator, we found a crossover between two diffusive regimes: a usual for small times and a sub-diffusive for long times, a feature observed in several empirical systems.

By properly manipulating the fractional diffusion equations, we demonstrated that the results obtained with these new fractional operators could be connected with other diffusive models. The fractional diffusion equation with the Caputo-Fabrizio operator recovers a diffusive process with stochastic resetting, where the fractional order exponent is directly related to the resetting rate. Also, the equation with the Atangana-Baleanu operator can be associated with a fractional diffusion equation with derivatives of distributed order. Our results thus suggest that these new fractional operators may be a simple and efficient way for incorporating different memory effects, opening new possibilities for modeling and investigating the anomalous diffusive processes.

Author Contributions

All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

AT thanks the financial support of the CNPq under Grant No. 462067/2014-9. HR thanks the financial support of the CNPq under Grant No. 440650/2014-3 and CAPES. EL thanks the financial support of the CNPq under Grant No. 303642/2014-9.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Pearson K. The problem of the random walk. Nature (1905) 72:294. doi: 10.1038/072294b0

CrossRef Full Text | Google Scholar

2. Rayleigh L. On the resultant of a large number of vibrations of the same pitch and arbitrary phase. Philos Mag. (1880) 10:73. doi: 10.1080/14786448008626893

CrossRef Full Text | Google Scholar

3. Rayleigh L. The Theory of Sound, 2nd Edn., Vol. 1. London: Macmillan (1894).

4. Rayleigh L. The problem of the random walk. Nature (1905) 72:318. doi: 10.1038/072318a0

CrossRef Full Text

5. Bachelier L. Théorie de la Spéculation. Ann Sci. (1900) 17:21.

6. Einstein A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann Phys. (1905) 17:549–60. doi: 10.1002/andp.19053220806

CrossRef Full Text | Google Scholar

7. von Smoluchowski M. Zur kinetischen theorie der brownschen molecularbewegung und der suspensionen. Ann Phys. (1906) 21:756–80. doi: 10.1002/andp.19063261405

CrossRef Full Text | Google Scholar

8. Montroll EW, Weiss GH. Random walks on lattices: II. J Math Phys. (1965) 6:167–81. doi: 10.1063/1.1704269

CrossRef Full Text | Google Scholar

9. Kutner R, Masoliver J. The continuous time random walk, still trendy: fifty-year history, state of art and outlook. Eur Phys J B (2017) 50:90. doi: 10.1140/epjb/e2016-70578-3

CrossRef Full Text | Google Scholar

10. Montroll EW, Scher H. Random walks on lattices. IV. Continuous-time walks and influence of absorbing boundaries. J Stat Phys. (1973) 9:101–35. doi: 10.1007/BF01016843

CrossRef Full Text | Google Scholar

11. Kenkre VM, Montroll EW, Shlesinger MF. Generalized master equations for continuous-time random walks. J Stat Phys. (1973) 9:45–50. doi: 10.1007/BF01016796

CrossRef Full Text | Google Scholar

12. Shlesinger MF. Asymptotic solutions of continuous-time random walks. J Stat Phys. (1974) 10:421–34. doi: 10.1007/BF01008803

CrossRef Full Text | Google Scholar

13. Havlin S, Avraham YB. Diffusion and Reactions in Fractals and Disordered Systems. Cambridge: Cambridge University Press (2000).

Google Scholar

14. Klafter J, Blumen A, Shlesinger MF. Stochastic path to anomalous diffusion. Phys Rev A (1987) 35:3081–5. doi: 10.1103/PhysRevA.35.3081

CrossRef Full Text | Google Scholar

15. Hilfer R, Anton L. Fractional master equations and fractal time random walks. Phys Rev E (1995) 51:R848–51. doi: 10.1103/PhysRevE.51.R848

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Compte A. Stochastic foundations of fractional dynamics. Phys Rev E (1996) 53:4191–3. doi: 10.1103/PhysRevE.53.4191

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Meztler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. (2000) 339:1–77. doi: 10.1016/S0370-1573(00)00070-3

CrossRef Full Text | Google Scholar

18. Metzler R, Klafter J. The restaurant at the end of the random walk: recent developments in the descriptions of anomalous transport by fractional dynamics. J Phys A (2004) 37:R161–R208. doi: 10.1088/0305-4470/37/31/R01

CrossRef Full Text | Google Scholar

19. Barkai E, Silbey RJ. Fractional Kramers equation. J Phys Chem B (2000) 104:3866–74. doi: 10.1021/jp993491m

CrossRef Full Text | Google Scholar

20. Barkai E. Fractional Fokker-Planck equation, solution, and application. Phys Rev E (2001) 63:046118. doi: 10.1103/PhysRevE.63.046118

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Barkai E CTRW pathways to the fractional diffusion equation. Chem Phys. (2002) 284:13–27. doi: 10.1016/S0301-0104(02)00533-5

CrossRef Full Text | Google Scholar

22. Sung J, Barkai E, Silbey RJ, Lee S. Fractional dynamics approach to diffusion-assisted reactions in disordered media. J Chem Phys. (2002) 116, 2338–41. doi: 10.1063/1.1448294

CrossRef Full Text | Google Scholar

23. Barkai E, Metzler R, Klafter J. From continuous time random walks to the fractional Fokker-Planck equation. Phys Rev E (2000) 61:132–8. doi: 10.1103/PhysRevE.61.132

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Du M, Wang Z, Zu H. Measuring memory with the order of fractional derivative. Sci Rep. (2013) 3:431. doi: 10.1038/srep03431

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zahran MA. On the derivation of fractional diffusion equation with an absorbent term and a linear external force. Appl Math Model. (2009) 33:3088–92. doi: 10.1016/j.apm.2008.10.013

CrossRef Full Text | Google Scholar

26. Zahran MA, Abulwafa EM, El-Wakil SA. The fractional Fokker Planck equation on comb-like model. Phys A (2003) 323:237–48. doi: 10.1016/S0378-4371(02)02026-5

CrossRef Full Text | Google Scholar

27. El-Wakil SA, Zahran MA, Abulwafa EM. Fractional (space time) diffusion equation on comb-like model. Chaos Solit Fract. (2004) 20:1113–20. doi: 10.1016/j.chaos.2003.09.032

CrossRef Full Text | Google Scholar

28. Villamaina D, Sarracino A, Gradenigo G, Puglisi A, Vulpiani A. On anomalous diffusion and the out of equilibrium response function in one-dimensional models. J Stat Mech. (2011) L01002. doi: 10.1088/1742-5468/2011/01/L01002

CrossRef Full Text | Google Scholar

29. Burioni R, Cassi D, Giusiano G, Regina S. Anomalous diffusion and Hall effect on comb lattices. Phys Rev E (2003) 67:016116. doi: 10.1103/PhysRevE.67.016116

PubMed Abstract | CrossRef Full Text | Google Scholar

30. da Silva LR, Tateishi AA, Lenzi MK, Lenzi EK, da Silva PC. Green function for a non-Markovian Fokker-Planck equation: comb-model and anomalous diffusion. Braz J Phys. (2009) 39:483–7. doi: 10.1590/S0103-97332009000400025

CrossRef Full Text | Google Scholar

31. Iomin A. Subdiffusion on a fractal comb. Phys Rev E (2011) 83:052106. doi: 10.1103/PhysRevE.83.052106

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Baskin E, Iomin A. Superdiffusion on a comb structure. Phys Rev Lett. (2004) 93:120603. doi: 10.1103/PhysRevLett.93.120603

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Tateishi AA, Lenzi EK, Ribeiro HV, Evangelista LR, Mendes RS, da Silva LR. Solutions for a diffusion equation with a backbone term. J Stat Mech. (2011) P02022. doi: 10.1088/1742-5468/2011/02/P02022

CrossRef Full Text | Google Scholar

34. Metzler R, Nonnenmacher TF. Space- and time-fractional diffusion and wave equations, fractional Fokker Planck equations, and physical motivation. Chem Phys. (2002) 284:67–90. doi: 10.1016/S0301-0104(02)00537-2

CrossRef Full Text | Google Scholar

35. West BJ. Fractional Calculus View of Complexity: Tomorrow's Science. London: CRC Press (2016).

Google Scholar

36. Saxton MJ, Jacobson K. Single-particle tracking: applications to membrane dynamics. Annu Rev Biophys Biomol Struct. (1997) 26:373–99. doi: 10.1146/annurev.biophys.26.1.373

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wirtz D. Particle-tracking microrheology of living cells: principles and applications. Annu Rev Biophys. (2009) 38:301–26. doi: 10.1146/annurev.biophys.050708.133724

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Gal N, Lechtman-Goldstein D, Weihs D. Particle tracking in living cells: a review of the mean square displacement method and beyond. Rheol Acta (2013) 52:425–43. doi: 10.1007/s00397-013-0694-6

CrossRef Full Text | Google Scholar

39. Hozé N, Holcman D. Statistical methods for large ensembles of super-resolution stochastic single particle trajectories in cell biology. Annu Rev Stat Appl. (2017) 4:189–223. doi: 10.1146/annurev-statistics-060116-054204

CrossRef Full Text | Google Scholar

40. Höfling F, Franosch T. Anomalous transport in the crowded world of biological cells. Rep Prog Phys. (2013) 76:046602. doi: 10.1088/0034-4885/76/4/046602

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Manzo C, Garcia-Parajo MF. A review of progress in single particle tracking: from methods to biophysical insights. Rep Prog Phys. (2015) 78:124601. doi: 10.1088/0034-4885/78/12/124601

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Shen H, Tauzin LJ, Baiyasi R, Wang W, Moringo N, Shuang B, et al. Single particle tracking: from theory to biophysical applications. Chem Rev. (2017) 117:7331–76. doi: 10.1021/acs.chemrev.6b00815

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zagato E, Forier K, Martens T, Neyts K, Demeester J, De Smedt S, et al. Single-particle tracking for studying nanomaterial dynamics: applications and fundamentals in drug delivery. Nanomedicine (2014) 9:913–27. doi: 10.2217/nnm.14.43

PubMed Abstract | CrossRef Full Text

44. Kaerger J, Ruthven DM, Theodorou DN. Diffusion in Nanoporous Materials. Weinheim: Wiley-VCH Verlag (2012). doi: 10.1002/9783527651276

CrossRef Full Text | Google Scholar

45. Kaerger J, Ruthven D. Diffusion in nanoporous materials: fundamental principles, insights and challenges. New J Chem. (2016) 40:4027–48. doi: 10.1039/C5NJ02836A

CrossRef Full Text | Google Scholar

46. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:73–85. doi: 10.12785/pfda/010201

CrossRef Full Text | Google Scholar

47. Atangana A, Baleanu D. New fractional derivative with non-local and non-singular kernel. Therm Sci. (2016) 20:763–9. doi: 10.2298/TSCI160111018A

CrossRef Full Text | Google Scholar

48. Gómez-Aguilar JF, Atangana A. Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann-Liouville and Liouville-Caputo sense. Eur Phys J Plus (2017) 132:100. doi: 10.1140/epjp/i2017-11371-6

CrossRef Full Text | Google Scholar

49. Hristov J. Transient heat diffusion with a non-singular fading memory: from the Cattaneo constitutive equation with Jeffrey's Kernel to the Caputo-Fabrizio time-fractional derivative. Therm Sci. (2016) 20:757–62. doi: 10.2298/TSCI160112019H

CrossRef Full Text | Google Scholar

50. Gómez-Aguilar JF. Space time fractional diffusion equation using a derivative with nonsingular and regular kernel. Phys A (2017) 465:562–72. doi: 10.1016/j.physa.2016.08.072

CrossRef Full Text

51. Abdeljawada T, Baleanu D. Integration by parts and its applications of a new nonlocal fractional derivative with Mittag-Leffler nonsingular kernel. J Nonlin Sci Appl. (2017) 10:1098–107. doi: 10.22436/jnsa.010.03.20

CrossRef Full Text

52. Podlubny I. Fractional Differential Equations. San Diego, CA; Academic Press (1999).

Google Scholar

53. Hristov J. Derivation of fractional Dodson's equation and beyond: transient mass diffusion with a non-singular memory and exponentially fading-out diffusivity. Progr Fract Differ Appl. (2017) 3:255–70. doi: 10.18576/pfda/030402

CrossRef Full Text

54. Hristov J. Derivatives with Non-Singular kernels from the Caputo - Fabrizio definition and beyond: appraising analysis with emphasis on diffusion models. In: Bhalekar S, editor. Frontiers in Fractional Calculus. Sharjah: Bentham Science Publishers (2017), p. 235–95.

Google Scholar

55. Méndez V, Campos D. Characterization of stationary states in random walks with stochastic resetting. Phys Rev E (2016) 93:022106. doi: 10.1103/PhysRevE.93.022106

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Shkilev VP. Continuous-time random walk under time-dependent resetting. Phys Rev E (2017) 96:012126. doi: 10.1103/PhysRevE.96.012126

CrossRef Full Text | Google Scholar

57. Mathai AM, Saxena RK, Haubold HJ The H-Function: Theory and Applications. New York, NY: Springer (2009).

Google Scholar

58. Mo J, Simha A, Raizen MG. Broadband boundary effects on Brownian motion. Phys Rev E (2015) 92:062106. doi: 10.1103/PhysRevE.92.062106

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Berry H, Chaté H. Anomalous diffusion due to hindering by mobile obstacles undergoing Brownian motion or Ornstein-Uhlenbeck process. Phys Rev E (2014) 89:022708. doi: 10.1103/PhysRevE.89.022708

CrossRef Full Text | Google Scholar

60. Koslover EF, de la Rosa MD, Spakowitz AJ. Crowding and hopping in a protein's diffusive transport on DNA. J Phys A Math Theor. (2017) 50:074005. doi: 10.1088/1751-8121/aa53ee

CrossRef Full Text | Google Scholar

61. Evans MR, Majumdar SN. Diffusion with stochastic resetting. Phys Rev Lett. (2011) 106:160601. doi: 10.1103/PhysRevLett.106.160601

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Skalski GT, Gilliam JF. Modeling diffusive spread in a heterogeneous population: a movement study with stream fish. Ecology (2000) 81:1685–1700. doi: 10.1890/0012-9658(2000)081[1685:MDSIAH]2.0.CO;2

CrossRef Full Text | Google Scholar

63. Upadhyaya A, Rieub JP, Glaziera JA, Sawadac Y. Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates. Phys A (2001) 293:549–58. doi: 10.1016/S0378-4371(01)00009-7

CrossRef Full Text | Google Scholar

64. Mieruszynski S, Digman MA, Gratton E, Jones MR. Characterization of exogenous DNA mobility in live cells through fluctuation correlation spectroscopy. Sci Rep. (2015) 5:13848. doi: 10.1038/srep13848

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Ribeiro HV, Tateishi AA, Alves LGA, Zola RS, Lenzi EK. Investigating the interplay between mechanisms of anomalous diffusion via fractional Brownian walks on a comb-like structure. New J Phys. (2014) 16:093050. doi: 10.1088/1367-2630/16/9/093050

CrossRef Full Text | Google Scholar

66. Alves LG, Scariot DB, Guimaraes RR, Nakamura CV, Mendes RS, Ribeiro HV. Transient superdiffusion and long-range correlations in the motility patterns of trypanosomatid flagellate protozoa. PLoS ONE (2016) 11:e0152092. doi: 10.1371/journal.pone.0152092

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Tateishi AA, Lenzi EK, da Silva LR, Ribeiro HV, Picoli S Jr, Mendes RS. Different diffusive regimes, generalized Langevin and diffusion equations. Phys Rev E (2012) 85:011147. doi: 10.1103/PhysRevE.85.011147

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Chechkin AV, Gorenflo R, Sokolov IM. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys Rev E (2002) 66:046129. doi: 10.1103/PhysRevE.66.046129

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Lenzi EK, Mendes RS, Tsallis C. Crossover in diffusion equation: anomalous and normal behaviors. Phys Rev E (2003) 67:031104. doi: 10.1103/PhysRevE.67.031104

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Bian X, Kimb C, Karniadakis GE. 111 years of Brownian motion. Soft Matt. (2016) 12:6331. doi: 10.1039/C6SM01153E

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Huang R, Chavez I, Taute KM, Lukić B, Jeney S, Raizen MG, Florin EL. Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid. Nat Phys. (2011) 7:576–80. doi: 10.1038/nphys1953

CrossRef Full Text | Google Scholar

72. Caputo M. Mean fractional-order-derivatives differential equations and filters. Ann Univ Ferrara Sez (1995) 41:73–84.

Google Scholar

73. Caputo M. Distributed order differential equations modelling dielectric induction and diffusion. Fract Calc Appl Anal. (2001) 4:421–42.