Risk of Coinfection Outbreaks in Temporal Networks: A Case Study of a Hospital Contact Network

We study the spreading of cooperative infections in an empirical temporal network of contacts between people, including health care workers and patients, in a hospital. The system exhibits a phase transition leading to one or several endemic branches, depending on the connectivity pattern and the temporal correlations. There are two endemic branches in the original setting and the non-cooperative case. However, the cooperative interaction between infections reinforces the upper branch, leading to a smaller epidemic threshold and a higher probability for having a big outbreak. We show the microscopic mechanisms leading to these differences, characterize three different risks, and use the influenza features as an example for this dynamics.

Introduction

Infectious diseases have been a serious problem across the whole history of humankind. Nowadays, 200,000 hospitalizations are directly associated with influenza every year in the United States [1, 2], and a potential pandemic could kill between 50 and 80 million people through a virulence strain similar to the 1918 influenza [3, 4]. However, the complexity of this dynamics is even higher, as infections can interact between themselves in several ways, inducing higher susceptibility or cross-immunity [5–8]. Hospitals, where different diseases are more likely to meet, are risky places for coinfection, that is the concurrent infection of a host with multiple pathogens. Moreover, diseases in hospitals are probably in their most virulent stages, weakening their hosts' immune system such that secondary infections are very likely to occur. Indeed, hospital acquired infections affect, on average, to 10% of the admitted patients [9], while the network defined by the transfer of patients across hospitals may explain the spread of bacterial infections [10]. Coinfection in hospitals has been reported, like the association between Clostridium difficile and vancomycin-resistant Enterococcus [11]. Some studies show that multiple pathogen infections were present in the children hospitalized [12–14]. Pérez-García et al. also reported that co-infection was significantly associated with nosocomial acquisition [15]. This is translated not only in health issues, but also economic costs [16].

In this work, we address the study of contagion processes following the temporal interactions pattern within a hospital. This can help determining the main drivers of this complex interacting spreading process and then preventing these cases. Thus, we are motivated to calculate risks of coinfection outbreaks in a hospital.

Recently, a model for cooperation between two infections has been proposed, with both infections following a dynamics that is an extension of the usual SIR (Susceptible-Infected-Recovered) model [17], but considering that individuals that previously suffered from one infection are more likely to get a second infection than susceptible ones, in a process that is called coinfection [18]. In contrast with usual SIR model applied to a single disease spreading along a network, this dynamics leads to abrupt transitions in several topologies [19, 20]. We study this dynamics in an empirical temporal network, to assess the differences that cooperation between infections can induce in real world. In fact, several studies have shown the differences between temporal and static approaches when dynamical processes occur in networks, changing the characteristic time scales of the processes [21–24]. The temporal correlations have a remarkable effect on cooperation in evolutionary dynamics [25], and the interplay of them with the structure strongly affects the diffusion processes [26]. Nowadays, empirical temporal contact networks in hospital are becoming available for scientific analysis. For instance, Jarynowski and Liljeros made a dataset based on the registry of visits in the hospital, and it was used to specify the interactions between hosts [27]. Also contact networks for disease spreading in hospitals have been studied [28], where the sequence of contacts was aggregated in a daily scale.

Considering these motivations, we apply our cooperative spreading model to an empirical network built from hospital contacts. Then we make another step further and calculate risks of coinfection outbreaks on this hospital contact network, for a general case and the specific case of influenza. The body of the paper is structured in 4 sections, including the description of the empirical network, the definition of the dynamics describing the spreading process, the introduction of the risks that will be assessed and, finally, the results and discussions.

Network Description

The empirical network we study here includes the contacts between N = 75 people in a hospital (46 health care workers and 29 patients) [29]. Contacts are reported by tracking devices when two individuals are located within a distance of 1–1.5 m, and are agreggated in time windows of Δt = 20s. Specifically, 32,424 contacts were recorded along 17,375 intervals, t_max = 96.53h, which gives an average degree per unit time 8.96h⁻¹. This network is described with a temporal adjacency matrix A_ij(t), where A_ij(t) = 1 if individuals i and j are connected at time t and A_ij(t) = 0 otherwise. Note that A_ij(t) = A_ji(t) due to the symmetry of interactions.

This temporal network of contacts has a non-uniform activity on time, having peaks separated by 24h (Figure 1A). In fact, there are valleys of low activity, associated with night, such that dynamics starting here is very likely to die out due to the low number of contacts. This motivates our choice of the recovery probability according to the characteristic time scale for those valleys of 1,000 time intervals (≈5.5h). Specifically, in a SI (Susceptible-Infected) process with transmission probability equal to 1, where one disease is transmitted in every contact between an infected individual and a susceptible one, starting from one initially infected individual, the low activity periods have a constant number of infected individuals, until the morning arrives and new infections occur (Figure 1B).

FIGURE 1

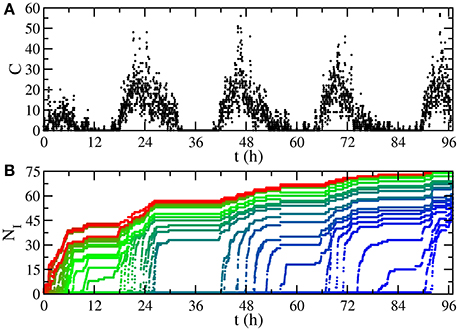
Figure 1. Temporal features of the network. (A) Number of contacts $C(t)={\displaystyle \sum _{i,j>i}}{A}_{ij}(t)$ happening at time t, aggregated for time intervals of 80 s. The low activity periods are valleys associated with night. (B) Number of infected individuals N_I in a SI process with transmission probability equal to 1. Each curve starts from a different initially infected individual, assigning red color to trajectories whose initial infected individual is the first having a contact in the sequence, progressively changing to blue (last).

Dynamics

We consider a model where two infections, ${A}$ and ${B}$, both experiencing SIR dynamics, spread along the temporal contact network (Figure 2). This leads to 9 different states for individuals:

Active states

• A: singly infected with ${A}$

• B: singly infected with ${B}$

• AB: doubly infected with both ${A}$ and ${B}$

• aB: recovered from ${A}$, infected with ${B}$

• Ab: infected with ${A}$, recovered from ${B}$

Inactive states

• S: susceptible

• a: recovered from ${A}$

• b: recovered from ${B}$

• ab: recovered from both ${A}$ anf ${B}$

FIGURE 2

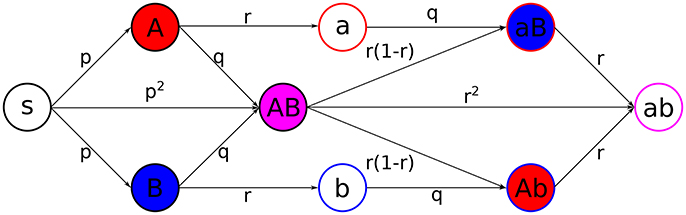
Figure 2. Scheme of the coinfection dynamics. Probabilities of transition, under the exposure to the suitable active states, between different states are depicted in the center of the arrows connecting states. Primary infections, i.e., when a state S gets infected, happen with probability p, secondary infections, which are those from active/recovered for/from one infection to active for the other, happen with probability q, and recovery, from active to inactive states, happens with probability r. Filling colors indicate active states, while stroke colors stand for recovered states (red for infection ${A}$, blue for infection ${B}$, magenta for both).

Individuals can get infected by their active neighbors. The states are updated synchronously according to the following rules:

1. Individuals that are active for ${A}$ infect their susceptible neighbors with probability p (analogous for individuals that are active for ${B}$).

2. Secondary infections will occur when an individual with an active state is connected with an individual which has previously suffered from the other infection, happening with probability q.

3. Recovery from each infection in active individuals will happen independently with probability r.

The case q > p is representative for cooperation between infections, while q = p means two independent spreading processes and q < p would represent cross-immunity.

As several individuals may remain active after the t_max time steps of the empirical network, we repeat the observed interaction pattern until there are no remaining individuals in active states. This means that, for time step t, we will consider the network of interactions A_ij(t mod t_max). Taking into account the analysis performed in Figure 1, we set r = 0.001, such that infections can survive the low activity night period.

Estimation of Risks

We consider three estimators for the risk. First of all, the presence of an outbreak: classical studies of disease spreading show a phase transition from non-endemic to endemic regime, when the transmission probability p is changed; there is a threshold p_c, the critical point, such that for p < p_c there are no outbreaks, while for p > p_c the probability of having an outbreak grows. This epidemic threshold p_c is calculated as the maximum of the susceptibility. Secondly, we will estimate the fraction of the population affected by the outbreak: given a value for p, we compute the period prevalence [30], defined in our study as the fraction of people ρ_ab which has been coinfected in independent realizations in a statistical ensemble. Finally, we analyze the distribution of ρ_ab, i.e., the probability Π_p(ρ_ab) of having an outbreak of size ρ_ab for a given p, that is useful to characterize the probability of having big outbreaks, considering that a realization is a big outbreak when it is in the upper endemic branch on the ρ_ab-p diagram. Π_p(ρ_ab) = 0 for p < p_c and ${\rho }_{ab}>\frac{1}{N}$ (one initially doubly infected individual), and it will grow for values higher than p_c.

Results

We compare two cases: (a) independent spreading (p = q), and (b) strong coinfection (p < q = 1). Both cases lead to similar qualitative results. Interestingly, there are two endemic branches: one growing continuously and another appearing after an abrupt jump (Figures 3A,B). However, a quantitative assessment reveals the differences between the independent (Figure 3A) and cooperative (Figure 3B) cases. First of all, cooperation makes epidemic threshold smaller, such that outbreaks appear for lower values of p when diseases cooperate, meaning that the risk for the presence of an outbreak is higher, as p_c is smaller. Secondly, outbreaks lead to fractions of doubly infected individuals that are almost a 10% higher. Finally, for a given value of p, the probability of having big outbreaks is higher for the cooperating case, as the highest endemic branch includes a higher density in the cooperative case than in the independent case (Figure 4).

FIGURE 3

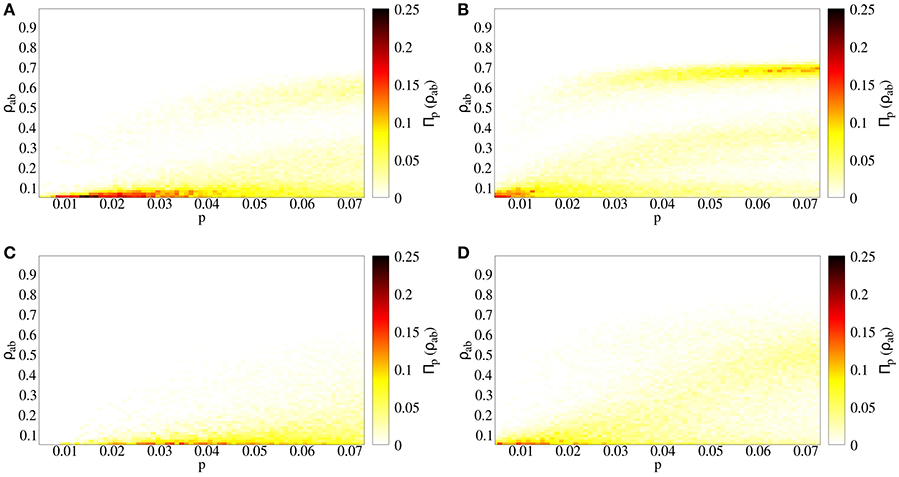
Figure 3. Spreading process in a temporal contact network. Prevalence of doubly infected individuals ρ_ab as a function of primary infection probability p. The color indicates the fraction of realizations taken which reach the value ρ_ab for a given p. (A) Independent spreading, with q = p, (B) coinfection spreading, with q = 1, (C) independent spreading in uncorrelated temporal networks, with q = p, (D) coinfection spreading in uncorrelated temporal networks, with q = 1.

FIGURE 4

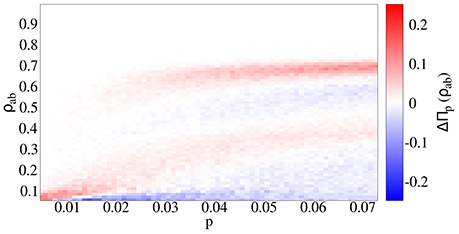
Figure 4. Difference in the prevalence probability ΔΠ_p(ρ_ab) between the cooperative (q = 1) and independent spreading (q = p) cases. In the cooperative case, outbreaks affect a higher fraction of individuals, and happen for a smaller value of the primary infection probability p.

In empirical contact networks, temporal correlations are highly present due to mobility of agents, such that two individuals that are close to each other are more likely to interact soon than when they are in far locations. Moreover, interactions are defined by a time-evolving spatial network, and spatial networks have large values of the clustering coefficient [31], meaning that if i is connected with j and j is connected with k, i is likely to be connected with k. In order to study the effect of the temporal structure of our empirical network on coinfection risks, we randomize the sequence of interactions: for every t, we randomly choose $C(t)={\displaystyle \sum _{i,j>i}}{A}_{ij}(t)$ contacts from the contact list. In this way, we keep constant both the number of contacts C(t) at every t and the probability for two specific individuals to interact, but we break the correlations mentioned above. Comparing the real with the uncorrelated network for the coinfection and independent cases, the transition from non-endemic to endemic regime has an abrupt jump in the empirical network, while the transition is smooth in the randomized network (Figure 3C). This highlights the role of temporal correlations as an important factor for the appearance of highly unexpected risks.

The strong clustering in the high activity periods, which disappears when we break the temporal correlations, makes both infections spread together. In fact, the number of doubly active individuals N_AB(t) (i.e., in state AB) is a high fraction of the total number of active individuals N_I(t) = N_A(t) + N_B(t) + N_AB(t) + N_Ab(t) + N_aB(t) in our system (Figure 5 and inset): even if diseases initially spread following different paths, the strong clustering makes them meet after short paths. However, the low activity periods (i.e., night) are dominated by stochastic recovery processes due to the absence of contacts, leading to a decrease in the number of both active and doubly active individuals. If both infections are able to survive the night (N_I ≠ 0), they may remain active in different individuals (N_AB = 0, blue and orange curves in inset of Figure 5). In next high activity period, the infections will initially spread independently, but if they meet (blue curve on Figure 5), they will continue spreading together, reinforced by the cooperative interaction in the coinfection case (q = 1). As a conclusion, when the spreading process starts from a doubly infected seed on a temporal cluster (high activity period) in our empirical network, the temporal correlations make infections spread together, but in the low activity periods, due to the stochasticity of the recovering process, infections can remain active in the same individuals (state AB), recover totally (state ab) or partially (states Ab and aB). If they continue together (i.e., some AB states remain in the system), or they are able to meet, they can induce similar processes, leading to a high fraction of doubly recovered individuals at the end of the dynamics. In the opposite case, they will spread independently and the fraction of doubly recovered individuals at the end of the dynamics will be lower, just including those that were doubly infected in the first activity period, with a prevalence ρ_ab that will be smaller. Those two cases lead to two endemic branches: the upper branch, happening when diseases meet after the low activity period, and the lower branch, growing more slowly, in the opposite case. The process of infections spreading together is reinforced with a higher probability of getting a secondary disease (q > p), explaining why the highest endemic branch is more probable and appears for a lower value of the control parameter p in the cooperative case (q = 1, Figure 3B), in contrast to the non-interacting case (q = p, Figure 3A).

FIGURE 5

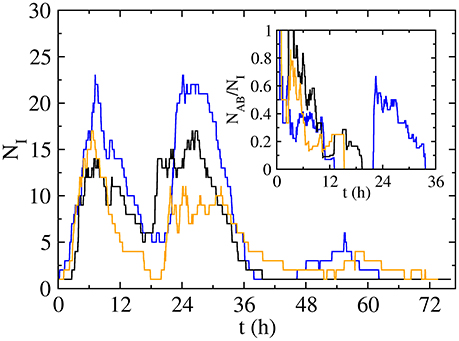
Figure 5. Time evolution of the number of infected individuals N_I for three long-lived realizations with p = 0.06 and q = 1, leading to a final number of infected of 56 (blue curve), 54 (black) and 52 (orange) individuals, while the final number of doubly infected is 50 (blue curve), 21 (black) and 14 (orange) individuals. Inset: time evolution of the fraction doubly active individuals N_AB amongst the total active individuals N_I.

Previous results of this coinfection model on static networks reported the role of dimensionality, such that low-dimensional lattices, with high local clustering, lead to continuous transitions, while discontinuous transitions appear in lattices with dimension higher than three, which have relatively lower values of local clustering [19, 20]. The topology explained these results, as diseases spread independently through long paths in the network and, after infecting a macroscopic fraction of individuals, they meet, coinfecting those individuals due to the high value of q. This leads to two possible solutions for ρ_ab in the region above, but close to the epidemic threshold: if both diseases are not able to meet, ρ_ab ≈ 0, while if they meet, ρ_ab has a high value. In fact, finite system size effects may hide the broad jumps, appearing even in networks with broad degree distributions [32]. In our case, similar mechanisms, including the influence of the temporal connectivity pattern, explain how the cooperative interaction reinforces the upper endemic branch: infections spread together in the temporal clusters associated with high activity periods, while the night valley of activity and the stochastic recovery allow diseases to separate and spread independently, leading to macroscopic coinfection effects in ρ_ab for the cases in which diseases meet again.

After describing the effects of cooperation between infections and temporal correlations on this spreading process, we focus on a specific example. Given that the basic reproductive number of a special influenza strain is R₀ = 2 [33], we estimate the transition probability considering that, for a sufficiently big time window, the network is described by a single giant cluster, and we set a low recovery probability such that an infected individual is able to contact most of the individuals in the system before becoming recovered, leading to $p=\frac{R_0}{N}\approx 0.03$. For this value of p, in the independent infections case the system is below the epidemic threshold, while it is above it for the coinfection case, where the outbreaks leads to ρ_ab = 0.69 of the population at most, with the peak for Π_{p = 0.03}(ρ_ab) in the highest endemic branch at ρ_ab = 0.63. The coinfection case for the uncorrelated network, for this p, is above the epidemic threshold, but leading to lower outbreak prevalence (ρ_ab = 0.61 at most, peak for Π_{p = 0.03}(ρ_ab) in ρ_ab = 0.13), as the prevalence grows continuously with p (Figure 3).

Summary and Conclusion

Mathematical modeling of disease spreading can help understanding how diseases spread in networks and guide policy makers for better strategies to avoid large outbreaks. To bridge the gap, we applied a coinfection model to an empirical network. Then we estimated the risk of coinfection with three indicators: (1) the epidemic threshold that determines whether there is an outbreak or not, (2) the fraction of the population affected by the outbreak and (3) the probability for having a big outbreak.

The combination of cooperation with temporal variables for determining the network of interactions leads to a complex dynamics. In order to determine the role of each of these features, we have splitted our analysis in four cases: (a) cooperative interaction between the infections with temporal correlations, (b) no interaction between the diseases, keeping temporal correlations, (c) cooperative interaction between the infections without temporal correlations, and (d) no interaction between the infections without temporal correlations. Comparing cases (a) and (b), we report a higher risk of double infection for the cooperative case, where the epidemic threshold is smaller, outbreaks lead to a higher fraction of infected individuals and they appear more likely (Figure 4). However, the presence of the abrupt outbreaks both in non-interacting and coinfection cases suggests that several temporal clusters, separated by low activity periods, are formed in the empirical network and the connection of those clusters leads to those abrupt outbreaks. This is confirmed when breaking the correlations in cases (c) and (d), where even with coinfection spreading, for which abrupt outbreaks have been reported under several conditions [18–20], the randomized temporal network lead to a continuous transition between disease-free and epidemic states. This means that the specific sequence and the temporal correlations that the empirical network contains are responsible for the abrupt jumps (Figure 3).

Considering the correlated network, looking at values of p above the epidemic threshold, there is a higher maximum for the prevalence distribution Π_p(ρ_ab), higher bounds for the prevalence if we compare the cooperative case with the independent spreading. We find clear differences between the correlated and uncorrelated cases, as the first experiences a broad transition, while the second is continuous, leading to higher values both for the maximum prevalence and the prevalence at the peak of Π_p(ρ_ab). Surprisingly, the uncorrelated case, that could stand for a static approach, leads to lower values of final fraction of doubly infected individuals, in contrast with other works that study similar models for one disease spreading in empirical temporal networks [34] and references inside.

Our theoretical study combined with real data can in general help policy makers to make public health more efficient and save more public budget. In summary, in our assessment of the risks of coinfection, we have shown how the connectivity pattern and the temporal correlations in the contact network presented in a hospital contact network can increase the risks of coinfection outbreaks. Hence, a good policy for avoiding this risks would consist on minimizing the effect of these correlations, for example organizing nursing teams in vertical while keeping horizontal organization for physician, such that the temporal clusters are disconnected, in contrast with the model in which both nursing and physician teams are organized horizontally. Future studies can address how vaccination, length of stays in hospitals and different recovery probability may alter the risks.

Author Contributions

JPR performed the simulations. JPR, FGh, and VME analyzed the results and wrote the paper.

Funding

JPR acknowledges support from the FPU program of MECD (Spain). JPR and VME received funding from SPASIMM [FIS2016-80067-P (AEI/FEDER, UE)]. FGh acknowledges the support of the German Research Foundation (DFG) for idonate project (project number: 345463468). http://gepris.dfg.de/gepris/projekt/345463468

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Thompson WW, Shay DK, Weintraub E, Brammer L, Cox N, Anderson LJ, et al. Mortality associated with influenza and respiratory syncytial virus in the United States. JAMA (2003) 289:179–86. doi: 10.1001/jama.289.2.179

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Thompson WW, Shay DK, Weintraub E, Brammer L, Bridges CB, Cox NJ, et al. Influenza-associated hospitalizations in the United States. JAMA (2004) 292:1333–40. doi: 10.1001/jama.292.11.1333

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Murray CJ, Lopez AD, Chin B, Feehan D, Hill KH. Estimation of potential global pandemic influenza mortality on the basis of vital registry data from the 1918–20 pandemic: a quantitative analysis. Lancet (2007) 368:2211–8. doi: 10.1016/S0140-6736(06)69895-4

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Parrish CR, Kawaoka Y. The origins of new pandemic viruses: the acquisition of new host ranges by canine parvovirus and influenza A viruses. Annu Rev Microbiol. (2005) 59:553–86. doi: 10.1146/annurev.micro.59.030804.121059

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Recker M, Pybus OG, Nee S, Gupta S. The generation of influenza outbreaks by a network of host immune responses against a limited set of antigenic types. Proc Natl Acad Sci USA. (2007) 104:7711–6. doi: 10.1073/pnas.0702154104

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Newman ME. Threshold effects for two pathogens spreading on a network. Phys Rev Lett. (2005) 95:108701. doi: 10.1103/PhysRevLett.95.108701

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Karrer B, Newman ME. Competing epidemics on complex networks. Phys Rev E (2011) 84:036106. doi: 10.1103/PhysRevE.84.036106

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Sanz J, Xia CY, Meloni S, Moreno Y. Dynamics of interacting diseases. Phys Rev X (2014) 4:041005. doi: 10.1103/PhysRevX.4.041005

CrossRef Full Text | Google Scholar

9. Filetoth Z. Hospital-Acquired Infections. Philadelphia: John Wiley & Sons (2008).

Google Scholar

10. Gracia JF, Onnela JP, Barnett ML, Eguíluz VM, Christakis NA. Spread of pathogens in the patient transfer network of US hospitals. arXiv:150408343. (2015).

Google Scholar

11. Poduval RD, Kamath RP, Corpuz M, Norkus EP, Pitchumoni C. Clostridium difficile and vancomycin-resistant enterococcus: the new nosocomial alliance. Am J Gastroenterol. (2000) 95:3513–5. doi: 10.1111/j.1572-0241.2000.03291.x

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Nascimento MS, Souza AVd, Ferreira AVdS, Rodrigues JC, Abramovici S, Silva Filho LVFd. High rate of viral identification and coinfections in infants with acute bronchiolitis. Clinics (2010) 65:1133–7. doi: 10.1590/S1807-59322010001100014

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Mansbach JM, Piedra PA, Teach SJ, Sullivan AF, Forgey T, Clark S, et al. Prospective multicenter study of viral etiology and hospital length of stay in children with severe bronchiolitis. Arch Pediatr Adolesc Med. (2012) 166:700–6. doi: 10.1001/archpediatrics.2011.1669

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Bonzel L, Tenenbaum T, Schroten H, Schildgen O, Schweitzer-Krantz S, Adams O. Frequent detection of viral coinfection in children hospitalized with acute respiratory tract infection using a real-time polymerase chain reaction. Pediatr Infect Dis J. (2008) 27:589–94. doi: 10.1097/INF.0b013e3181694fb9

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Pérez-García F, Vásquez V, de Egea V, Catalán P, Rodríguez-Sánchez B, Bouza E. Influenza A and B co-infection: a case–control study and review of the literature. Eur J Clin Microbiol Infect Dis. (2016) 35:941–6. doi: 10.1007/s10096-016-2620-1

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Plowman R, Graves N, Griffin M, Roberts J, Swan A, Cookson B, et al. The rate and cost of hospital-acquired infections occurring in patients admitted to selected specialties of a district general hospital in England and the national burden imposed. J Hosp Infect. (2001) 47:198–209. doi: 10.1053/jhin.2000.0881

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kermack WO, McKendrick AG. A contribution to the mathematical theory of epidemics. Proc R Soc Lond A Math Phys Sci. (1927) 115:700–21. doi: 10.1098/rspa.1927.0118

CrossRef Full Text | Google Scholar

18. Chen L, Ghanbarnejad F, Cai W, Grassberger P. Outbreaks of coinfections: The critical role of cooperativity. EPL (2013) 104:50001. doi: 10.1209/0295-5075/104/50001

CrossRef Full Text | Google Scholar

19. Cai W, Chen L, Ghanbarnejad F, Grassberger P. Avalanche outbreaks emerging in cooperative contagions. Nat Phys. (2015) 11:936–40. doi: 10.1038/nphys3457

CrossRef Full Text | Google Scholar

20. Grassberger P, Chen L, Ghanbarnejad F, Cai W. Phase transitions in cooperative coinfections: Simulation results for networks and lattices. Phys Rev E (2016) 93:042316. doi: 10.1103/PhysRevE.93.042316

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Karsai M, Kivelä M, Pan RK, Kaski K, Kertész J, Barabási AL, et al. Small but slow world: How network topology and burstiness slow down spreading. Phys Rev E (2011) 83:025102. doi: 10.1103/PhysRevE.83.025102

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Holme P, Saramäki J. Temporal networks. Phys Rep. (2012) 519:97–125. doi: 10.1016/j.physrep.2012.03.001

CrossRef Full Text | Google Scholar

23. Scholtes I, Wider N, Pfitzner R, Garas A, Tessone CJ, Schweitzer F. Causality-driven slow-down and speed-up of diffusion in non-Markovian temporal networks. Nat Commun. (2014) 5:5024. doi: 10.1038/ncomms6024

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Masuda N. Accelerating coordination in temporal networks by engineering the link order. Sci Rep. (2016) 6:22105. doi: 10.1038/srep22105

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Cardillo A, Petri G, Nicosia V, Sinatra R, Gómez-Gardenes J, Latora V. Evolutionary dynamics of time-resolved social interactions. Phys Rev E (2014) 90:052825. doi: 10.1103/PhysRevE.90.052825

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Delvenne J, Lambiotte R, Rocha L. Diffusion on networked systems is a question of time or structure. Nat Commun. (2015) 6:7366. doi: 10.1038/ncomms8366

CrossRef Full Text | Google Scholar

27. Jarynowski A, Liljeros F. Contact networks and the spread of MRSA in Stockholm hospitals. In: 2015 Second European Network Intelligence Conference, Karlskrona (2015), p. 150–4. doi: 10.1109/ENIC.2015.30

CrossRef Full Text | Google Scholar

28. Obadia T, Silhol R, Opatowski L, Temime L, Legrand J, Thiébaut AC, et al. Detailed contact data and the dissemination of Staphylococcus aureus in hospitals. PLoS Comput Biol. (2015) 11:e1004170. doi: 10.1371/journal.pcbi.1004170

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Vanhems P, Barrat A, Cattuto C, Pinton JF, Khanafer N, Régis C, et al. Estimating potential infection transmission routes in hospital wards using wearable proximity sensors. PLoS ONE (2013) 8:e73970. doi: 10.1371/journal.pone.0073970

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Rothman KJ. Epidemiology: An Introduction. New York, NY: Oxford University Press (2012).

Google Scholar

31. Barthélemy, M Spatial networks. Phys Rep. (2011) 499:1–101. doi: 10.1016/j.physrep.2010.11.002

CrossRef Full Text | Google Scholar

32. Cui PB, Colaiori F, Castellano C. Mutually cooperative epidemics on power-law networks. arXiv:170502840. (2017).

PubMed Abstract | Google Scholar

33. Mills CE, Robins JM, Lipsitch M. Transmissibility of 1918 pandemic influenza. Nature (2004) 432:904–6. doi: 10.1038/nature03063

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Masuda N, Holme P. Predicting and controlling infectious disease epidemics using temporal networks. F1000 Prime Rep. (2013) 5:6. doi: 10.12703/P5-6

PubMed Abstract | CrossRef Full Text | Google Scholar