- Department of Chemistry and Biochemistry, University of Oklahoma, Norman, OK, USA
Magnetic force spectroscopy is a rapidly developing single molecule technique that has found numerous applications at the interface of physics and biology. Since the invention of the first magnetic tweezers, a number of modifications to the approach have helped to relieve the limitations of the original design while amplifying its strengths. Inventive molecular biology solutions further advanced the technique by expanding its possible applications. In its present form, the method can be applied to both single molecules and live cells without resorting to intense irradiation, can be easily multiplexed, accommodates multiple DNAs, displays impressive resolution, and allows a remarkable ease in the stretching and twisting of macromolecules. In this review, we describe the architecture of magnetic tweezers, key requirements for experimental design and analysis of data, and outline several applications of the method that illustrate its versatility.
Introduction
Force spectroscopy has become a powerful approach for studies of single molecules [1–4], macromolecular assemblies [5–7] and even whole cells [8–11]. This approach was pioneered by the invention of optical tweezers, which manipulate dielectric microscopic objects with the help of a focused light beam [12, 13]. Soon thereafter, magnetic tweezers were invented to allow the manipulation of paramagnetic beads using a gradient of magnetic field [14]. The two techniques have been developing head to head to achieve nowadays a remarkable level of sophistication. They have their own unique advantages but, largely, offer similar capabilities and require the same workflow.
The main advantage of optical tweezers is the ease with which single beads can be manipulated and carried around. In contrast, magnetic tweezers are at their best when working with a homogeneous force field. This set-up does not generate a three-dimensional (3D) force trap but allows for easy multiplexing where multiple beads can be observed and manipulated at the same time. In addition, the method does not require intense sample irradiation, accommodates multiple DNAs (or other macromolecules) and allows remarkable ease in the stretching and twisting of macromolecules. This offers unparalleled simplicity and versatility in the design of downstream applications. This review discusses the architecture and use of magnetic tweezers, highlights key requirements for experimental design and provides several examples illustrating their use.
Instrument Configuration
The first magnetic tweezers were assembled in 1996 by Strick, Bensimon and Croquette who used them to explore elasticity of supercoiled DNA [14]. In the original design, the experiment is conducted within a glass flow cell, which is placed atop an inverted microscope with a pair of permanent magnets above it (Figure 1). The flow cell contains DNA molecules stretched between its surface and a paramagnetic bead, and the force is varied by moving the magnets with the help of a motorized drive. Later implementations developed more sophisticated flow chambers and magnetic pole assemblies.
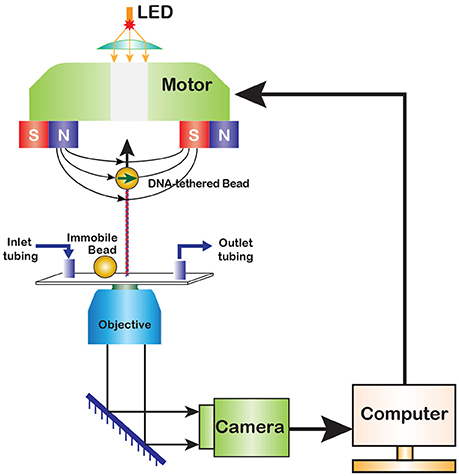
Figure 1. A diagram of magnetic tweezers. A paramagnetic bead is tethered to the surface of a flow cell via a functionalized DNA molecule. A fixed reference bead is attached to the flow cell surface for drift correction. Permanent magnets produce magnetic field that pulls the bead in the direction of the field gradient. The magnets can be translocated or rotated to alter the stretching force or twist the DNA. The motion of the bead is observed in real time via digital camera.
In a typical experiment, the position of the bead is monitored in 3D. This is achieved by computer-assisted analysis of the bead image, which changes not only during horizontal but also vertical displacement of the bead (see below). The changes in DNA extension are recorded in real time, in response to the activity of an enzyme or changes in the applied force. The flow cell is connected to the rest of a microfluidic system, which can be as simple as a single reservoir, or as complicated as the user requires. A light source is usually placed atop of the microscope but can be relocated when needed. The image of the bead is captured using a charge-coupled device (CCD) camera. In recent years, complementary metal oxide semiconductor (CMOS) cameras have been gaining in popularity due to their generally faster response times and the resulting ability to track motion at higher frequencies. To complete the system, a computer program that records the real time motion of the bead and provides control over the magnets is required.
Magnetic Field
Magnetic tweezers can be assembled in a variety of configurations to match diverse experimental needs. The first question that needs to be answered at the design stage is about organization of the magnetic field. This is a key factor that defines performance of the tweezers. The generated force is proportional to the gradient of magnetic field and directed toward the area with the strongest field [1, 15–17]. As a result, magnetic tweezers display different properties depending on the configuration of the field. A single magnet cannot apply torque. When a pair of magnets is employed, the force is directed toward the gap between the magnets, and away from the sample (Figure 2A). For applications that require true capture of the bead and its translocation, a more complex arrangement is needed, with magnets placed around the bead, so that the strongest field can be created in its vicinity [18, 19]. Furthermore, the field strength in this case must be dynamically controlled to ensure efficient confinement of the bead, which necessitates the use of electromagnets.
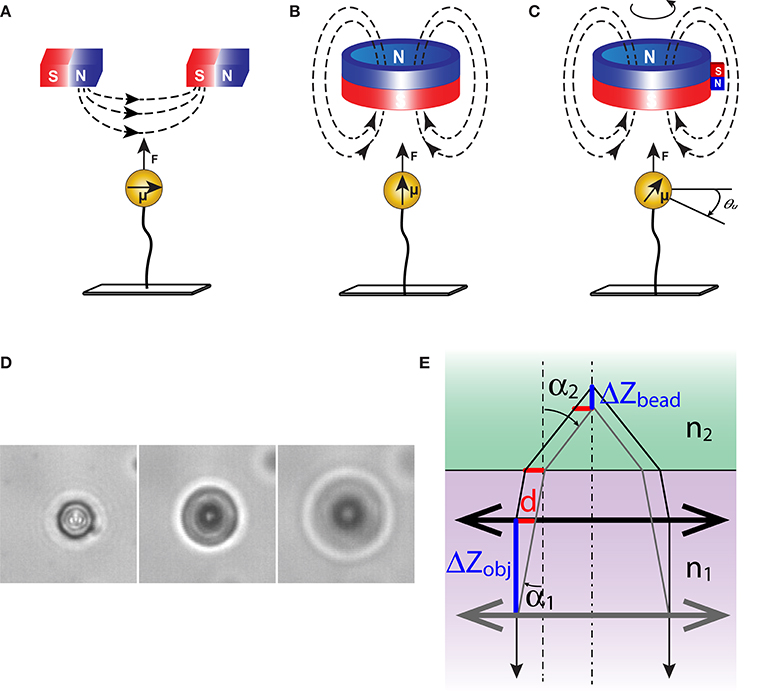
Figure 2. Orientation of magnetic field and magnetic forces. DNA tethered magnetic beads experience a force (F) along the field gradient. (A) A pair of horizontally placed magnets induces a horizontal magnetic moment (μ) in the beads. Due to anisotropic polarization, the induced magnetic moment will be retained by the bead even when the field changes direction. As a result, rotation of the magnets forces rotation of the bead. (B) Cylindrical magnets exert a vertical magnetic field to the tether axis. The vertical magnetic field allows free rotation of the beads around the tether axis. (C) Magnetic torque tweezers apply a small horizontal field gradient in addition to a strong vertical one [26]. The torque generated in the tethered molecule due to its rotation is sufficient to cause a misalignment between the bead and the magnet. (D) Images of a magnetic bead at several separations from the focal plane. Diameter of the diffraction rings changes with vertical displacement of the objective. (E) The shift in focus during translation of an objective. The correction for light refraction can be obtained by combining Snell's law n1sin(α1) = n2sin(α2) and the geometric constraint d = ΔZobjtg(α1) = ΔZbead tg(α2), where n1 and n2 are the refractive indices of the immersion oil and reaction buffer, respectively, and d is the projection of the displacement onto the horizontal plane. For small objects, this yields: ΔZbead/ΔZobj = tg(α1)/tg(α2) ≈ n2/n1.
Orientation of the field is another possible variable. Horizontal magnets induce horizontal magnetic dipole in the bead (Figure 2A). Such beads follow the magnets as the magnets are rotated. This configuration is required if one is interested in twisting macromolecules. Vertical orientation of the field (Figure 2B) produces a torque-free tether, which might be useful in applications where stretching and twisting need to be uncoupled [20].
Using NdFeB magnets and the widely used 2.8 μm beads, one can easily produce forces up to about 20 pN at distances of about 1 mm [10, 21]. This force is sufficient for many single molecule applications and often must not be exceeded since higher forces can induce unwanted conformational transitions in biological specimens [22, 23]. Higher forces can be produced by using bigger beads, reducing the separation between the magnets and the bead (i.e., using flow cells) and optimizing the geometry of magnetic poles. Such modifications, however, often come at a price. Bigger beads, for example, generate greater drag and reduce, therefore, the temporal resolution of the experiment [24]. Likewise, the use of microfabricated devices [18] can produce forces in nN range due to a dramatic decrease in the magnet-to-bead separation but increases the cost of each experiment. Moreover, this arrangement foregoes a significant advantage of conventional tweezers, the ability to conduct experiments at constant force, since variations in magnetic field within the field of view can no longer be neglected.
Of particular interest are electromagnetic tweezers, which employ electromagnets to generate the field [19, 25]. Such instruments use electric current to modulate the strength and direction of the magnetic field and can accommodate efficient feedback loops to generate stable force clamps. With fewer moving parts, reduced vibration and faster control over the magnetic field, electromagnetic tweezers expand possible applications of the technique. Their main disadvantages are a rather significant cost of integration of electromagnets into the tweezers, and the need to control hysteretic effects in the ferromagnetic core of the electromagnet.
Magnetic torque tweezers (MTT) [26] and electromagnetic torque tweezers (eMTT) [27] are newer additions to the field. They expand the capabilities of conventional instruments by allowing direct measurements of the applied torque. This is achieved by introducing a weak horizontal gradient of magnetic field so that the twisted molecules could produce detectable counteracting torque. Following proper calibration, the torque on such molecules could be derived from the misalignment of the rotated bead and the magnet (Figure 2C).
Bead Tracking
The heart of magnetic tweezers is a computer program that tracks the bead in 3D space and reports its position in real time. In a typical experiment, the bead is observed through a static oil immersion objective and its image projected onto a digital camera (Figure 1). To compensate for instrumental drift, one might choose to track simultaneously two beads, one of which is tethered to DNA and the other is stuck to the surface and serves as a reference. In this set up, detecting the horizontal location of the beads is quite straightforward. Most tweezers, however, apply force vertically, making vertical displacements the ones to track. Tracking is achieved by analyzing the image of the bead, which changes depending on bead proximity to the focal plane of the objective (Figure 2D).
Since the size of the beads is comparable to the wavelength of incident light, their images are significantly affected by diffraction [28, 29]. The use of coherent light for illumination accentuates the diffraction rings and thereby increases the effective size of the image. This in turn helps overcome the pixelation limit and increases the precision in locating the bead. These issues, however, rarely limit the experiment and become important only when using small beads or studying stiff tethers. As discussed below, such systems maximize suppression of thermal noise. As a result, the precision of locating the bead begins to affect the overall precision of the instrument.
The instant position of the bead is measured by comparison to a reference set of bead images [30]. These are collected for each bead prior to the experiment. During this initial calibration, the bead is typically held in place at a high force to reduce fluctuations, and the objective is translocated in the Z-direction. The generated stack of images is then processed to produce a reference curve that relates the appearance of the bead to its separation from the focal plane. Thereafter, the objective is held in place and the bead is allowed to fluctuate in response to applied forces. The displacement of the bead linearly relates to the displacement of the objective needed to produce the matching image, ΔZbead = ΔZobj·n2/n1, where n1 and n2 are the refractive indices of the immersion oil and the reaction buffer, respectively (Figure 2E). Using interpolative techniques, one can achieve a precision of the order of 1 nm.
Attachment of DNA to the Surface
Attachment of DNA to both the magnetic bead and the surface of the flow cell is essential for single molecule studies. This is achieved by combining together an unmodified DNA with derivatized DNA handles. Such handles can be prepared in a variety of ways. Perhaps the easiest way involves PCR using modified dNTPs. For the generation of a DNA tether, modified dUTPs such as amino-allyl dUTP, digoxigenin-dUTP (DIG-dUTP), or biotin-dUTP, can be incorporated by enzymatic polymerase chain reaction (PCR) [31–34], primer extension [35] or terminal transferase DNA extension [36]. While ligation of labeled PCR fragments remains a popular protocol, the choice of labeling strategy depends on the nature of experimental design and the required lifetime of the linkage.
The most common method for surface attachment of DNA utilizes the non-covalent interaction between DIG labeled DNA and an anti-digoxigenin antibody coated surface, and between biotin labeled DNA and streptavidin coated magnetic beads. At forces of about 10 pN, the average lifetimes of these interactions are 4 and 18,000 s, respectively [37]. The lifespan of these interactions decreases exponentially with increasing force [37] which significantly reduces the duration of the DIG/anti-DIG attachment and presents a major problem for experiments requiring large forces, such as those involving hairpins.
An alternative approach, in which DNA is covalently attached to both the surface and the magnetic bead, has been developed to achieve longer lifetime of binding. To covalently link DNA to the glass surface, a small fragment of DNA is labeled with amino-allyl-dUTP, digested and ligated to one end of the tethering DNA. Once labeled, the DNA is injected into a glass chamber coated with either silane-PEG-NHS (silane-polyethylene glycol-N-hydroxysuccinimide) [37], or coated with ethanolamine/PEG or NHS-PEG-COOH [34]. In all cases, the primary amine of the amino-allyl-dUTP will react with the coated surface to form a covalent bond. By simply exchanging DIG/anti-DIG binding for covalent attachment to the glass surface, the lifetime is increased dramatically from a few minutes to a few hours [34].
Force Calibration
The force exerted by the tweezers cannot be determined from first principles if only because magnetization varies from one bead to another. Instead, the instrument relies on quantification of Brownian motion of the bead. To this end, the thermal motion of the bead is recorded at several positions of the magnets, quantified to derive the forces acting on the bead, and the measured forces are then used to construct an empirical interpolation function. Different interpolation functions have been employed for the task including high power polynomials [38] and the exponential function F = Fmax exp(AZmag + BZmag2) [30]. In this analysis, the bead must be suspended in solution since its interactions with the surface restrict its motion and leads to abnormal readings [39].
In principle, the force can be calculated from the magnitude of the horizontal bead fluctuations, <δy2>. According to the Equipartition Theorem, αy<δy2> = kT, where αy is the horizontal stiffness of the trap, T is the temperature and k is the Boltzmann constant (Figure 3). For a bead tethered to the surface via a single linkage, the stiffness is proportional to the applied force [14], αy = F/l, where l is the length of the tether, leading to the following relationship:
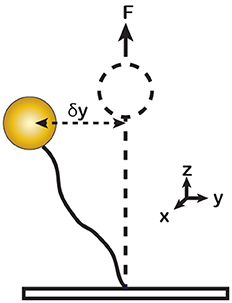
Figure 3. Illustration of Brownian motion of a DNA tethered magnetic bead in solution. δy represents the horizontal displacement of a vertically stretched bead. The tethered bead behaves as a harmonic pendulum with the lateral stiffness αy = F/l. The force (F) can be calculated from the horizontal fluctuation <δy2> of the bead.
Thus, the force can be readily computed once the length of the tether and the variance of fluctuations are known. In practice, however, the utility of Equation (1) is limited due to external vibrations in the instrument, which must be filtered out from the recorded Brownian motion. The most robust way to achieve it is by fitting the fluctuations in the frequency domain.
A detailed description of such analysis and associated problems is presented in Berg-Sorensen and Flyvbjerg [40]. The approach is based on solving the underlying Langevin equation in the frequency domain. Assuming a harmonic force field, the power spectrum of the bead motion is found to be the Lorentzian:
where S(f) is the power spectrum of the bead motion, ζ is the friction coefficient for the bead, and f0 = αy/2πζ is the cutoff frequency of the oscillator. For a spherical particle with the radius r in a liquid with the viscosity η, ζ = 6πηr. Regardless to the shape of the bead, the friction coefficient is related to its diffusion coefficient, D, via the Einstein equation, D = kT/ζ. Integration of Equation (2) over the entire range of frequencies (from zero to infinity) yields Equation (1).
Analysis of Equation (2) leads to important experimental considerations. The shape of a Lorentzian is completely defined by two parameters, its cutoff frequency f0 and the peak value, A = 4kTζ/αy2, which describes the magnitude of low frequency fluctuations, when f ≪ f0. Both of them depend on the stiffness of the trap, αy, and the diffusion coefficient of the bead. Only by multiplying the two can the contribution from viscosity be eliminated, A·f0 = 2kT/παy. Therefore, both A and f0 must be determined in order to derive the force, which requires fitting the power spectrum to the Lorentzian over a broad range of frequencies.
To achieve this, the recorded noise must include high frequency motion, when f ≥ f0. Otherwise, the measured magnitude of Brownian motion would be underrepresented by an unknown factor. This, however, seldom poses a problem because magnetic tweezers produce fairly soft traps (characterized by low f0). For a 3 μm DNA attached to a 3 μm bead and stretched with a 10 pN force, the cutoff frequency is on the order of 10 Hz. For such systems, fluctuations can be accurately recorded using a low end CCD camera. Certain applications, however, require suppression of the noise. This becomes especially important in studies of fast processes or those that involve small changes in DNA length. Such suppression is usually achieved by using higher forces, shorter DNAs and smaller beads [41, 42]. All these factors increase the frequency of fluctuations (Equation 2) and necessitate the use of CMOS or high speed CCD cameras.
DNA Elasticity
DNA stretching by force is largely defined by its polymeric properties. In the simplest, freely-jointed model, a polymer is viewed as a chain of rigid segments connected by completely flexible links (Figure 4A). This model was first proposed by Werner Kuhn in his analysis of rubber elasticity [43] and still remains a cornerstone of polymer physics. The model contains only one parameter, the length of the segment, b, also known as the Kuhn length or statistical segment length. This length serves as an operational measure of polymer rigidity since stiffer polymers remain straight over longer distances and vice versa. The number of the segments can be immediately derived from the length L of the molecule as N = L/b. For long polymers, with N ≫ 1, the model predicts the well-known random coil conformation [44, 45].
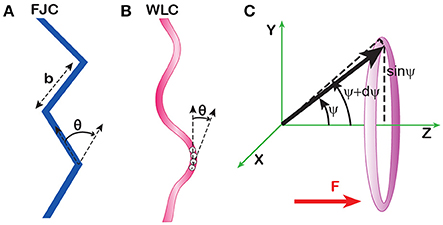
Figure 4. Polymeric models of DNA. (A) The freely jointed (FJC) model views polymers as chains of rigid segments whose orientations are completely uncorrelated with each other. (B) The worm-like chain (WLC) model postulates a constant time-averaged curvature of the chain. The average angle θ between adjacent monomers is a measure of this curvature and the rigidity of the chain. Its magnitude, but not direction, remains constant throughout the chain. (C) Statistical weight of various conformations of a rigid segment in a uniform force field. The number of conformations of the segment confined to the sector between angles ψ and ψ +dψ is proportional to the area of this sector on a unit sphere (shaded). The radius of this sector equals sinψ, and the area is 2π·sinψ dψ.
Statistics of the segment within a random coil is the same as found in any stochastic process, such as diffusion or random flight. Thus, a random coil is characterized by massive fluctuations on the order of the size of the coil itself. The average size of the coil scales with the square root of the polymer length, <R2> = Lb, and is much smaller that the length of the molecule. Double stranded DNA, being naturally straight and fairly rigid, conforms well to the predictions of the model. The length of its Kuhn segment is about 300 bp [46]. Thus, most test molecules will contain at least several Kuhn segments.
The force applied to a polymer distorts the otherwise isotropic orientation of the segments. Extended molecules allow fewer microscopic conformations and generate, as a result, a purely entropic elastic force that resists stretching. The magnitude of the extension can be analytically calculated in the freely jointed model [44]. The distribution function of the segments in the constant force field follows the Boltzmann distribution:
where ΔG is the free energy of the segment in the force field, ψ is the angle between the segment and the direction of the force, b·cosψ is the projection of the segment onto the force, Fb cos ψ is the energy of the segment in the field, and 2π sinψ is the statistical weight of the conformations with the given angle ψ (Figure 4C). The average projection of the segments onto the force field, Lz, can be calculated as:
where (x) is the Langevin function, (x) = coth(x) − 1/x. Since all segments are equally influenced by the force, the relative extension, z = Lz/L, of the chain would be given by:
The result predicts that the relative extension of all polymers follows the same universal function of the product of the force and the polymer rigidity expressed as its statistical length. When comparing different polymers, the more flexible one requires proportionally higher force to achieve the same relative extension. One might also notice that double stranded DNA is a very soft spring. A force as low as 0.1 pN stretches DNA to 60% of its contour length. In the limit of low extensions, when Fb ≪ kT, Equation (5) reduces to a linear dependence
Equation (6) is analogous to Hooke's law, which describes the behavior of an ideal spring. Notably, the Langevin function can be approximated by a straight line up to fairly large extensions, when Fb ≈ kT. Thus, polymers retain their ideal spring behavior for extensions that dramatically exceed their unperturbed size.
Equation (5) poorly describes DNA elasticity at high extensions [47]. This occurs because the freely jointed chain model completely ignores local polymer curvature on scales shorter than the Kuhn length. Such fluctuations, however, significantly distort the shape of both short and highly extended polymers [48, 49].
A much better description of such conformations can be obtained using the worm-like chain model (Figure 4B). The model accounts for local curvature by postulating that the adjacent monomers of the chain bend relative to each other by an average angle θ = <θ2>1/2, which does not change along the chain. This approximation is realistic since one should expect a constant energy associated with each degree of freedom, including bending. Thus, for harmonic fluctuations, αb <θ2> = kT, where αb is the bending rigidity. This equation applies to naturally straight polymers, for which <θ> = 0, and therefore, fluctuations of the bending angle are equal to the angle itself, δθ = θ − <θ> = θ. This model predicts that the correlation in the orientation of non-adjacent monomers in the chain exponentially decays with increasing separation between the monomers:
where u1, un are unit vectors associated with the two monomers, u1·un is their dot product, l is the distance between the monomers along the chain, l0 is the distance between two adjacent monomers, and P is the persistence length. The expression for the end-to-end distance, R, applies both to short and long polymers:
For long polymers, with L ≫ P, <R2> = 2PL. This relationship resembles the aforementioned conclusions of the freely jointed model (<R2> = bL). Thus, the model predicts the same statistics as the freely jointed chain, provided that L ≫ P and b = 2P. For short DNAs, Equation 8 provides a much better estimate of DNA extension.
DNA Stretching
The persistence length is the primary parameter that defines extension of polymers by applied forces. The persistence length of double stranded DNA measured using single molecule stretching agrees well with numerous previous studies [48, 50, 51]. Its value is 45 nm at moderate salt conditions (i.e., above 50 mM NaCl or 1 mM MgCl2), but significantly increases in diluted salt conditions. Double stranded RNA is about 20% stiffer; in 10 mM sodium phosphate solution, its persistence length was estimated as 64 nm, compared to 54 nm for double stranded DNA [52].
The problem of the worm-like chain under tension can be solved only numerically. In practice, data on DNA extension should be fit to the following empirical equation, which agrees with the solution to within 0.1%:
where a2 = −0.5164228, a3 = −2.737418, a4 = 16.07497, a5 = −38.87607, a6 = 39.49944, a7 = −14.17718 [50]. Notably, this equation neglects any volume interaction in DNA. Indeed, such interactions significantly affect conformations of random coils but are virtually non-existent in highly extended molecules.
High forces do not only overpopulate extended conformations of the polymer but also stretch the molecule itself. The elastic modulus (or rather its 1D equivalent) for DNA, K, is fairly high, given the DNA stability, about 1,000 pN [51, 53]. As a result, DNA extensibility becomes relevant only at high tension, when the molecule is about to undergo a force-induced conformational transition. The precision of existing data is insufficient to discriminate between conceivable structural models of extension. Instead, data can be approximated assuming a constant DNA extensibility and replacing z in Equation 9b with z − F/K [51].
Notably, polymeric DNA models discussed in the previous section prove insufficient when applied to stretching experiments using moderately short DNAs [54]. This occurs because DNA attachment to macroscopic objects imposes rather restrictive boundary conditions on the orientation of its ends. Moreover, rotational fluctuations of the tethered bead further restrict DNA conformations in favor of the more extended ones. Due to these factors, the apparent persistence length measured in stretching experiments displays DNA length dependence and is significantly underappreciated, even for molecules as long as several persistence lengths. In such cases, DNA extension must be modeled explicitly or analyzed in the framework of a computer intensive finite worm like chain model [54].
DNA Topology
A signature feature of magnetic tweezers is their ability to quickly and precisely twist macromolecules. This allows researchers to alter DNA supercoiling during the course of the experiment. This in turn better mimics the cellular environment, where DNA is typically topologically constrained [55–58]. However, DNA behavior under tension somewhat differs from that in bulk measurements, when it is unconstrained, an aspect that must be taken into account during experimental design. We provide below a brief synopsis of DNA topology while more detailed reading is available in numerous excellent reviews [55, 59, 60].
The theory of DNA supercoiling was developed for circular DNA but can be readily extended to linear, yet torsionally constrained molecules (i.e., those whose ends do not freely rotate). To achieve this, the ends of the DNA must be attached to both the bead and the flow cell via multiple linkages, so that by rotating the bead, the molecule can be twisted. In such molecules, one strand winds around the other a certain number of times, which can be changed only by rotating the bead or transiently breaking the molecule and passing DNA segments through the resulting gate. This number of intertwining is called the linking number, Lk. In torsionally unstrained DNA, the linking number is directly related to the most stable secondary structure of the molecule. Such DNA is called relaxed, and its linking number is denoted as Lk0. Lk0 is inversely related to the DNA helical repeat, γ, which is the number of base pairs needed to make a full turn within the DNA double helix under given conditions. For DNA composed of N base pairs, Lk0 = N/γ. The difference between Lk and Lk0 describes the extent of torsional deformation of the molecule and is called supercoiling, ΔLk = Lk − Lk0, whereas superhelical density, σ = ΔLk/Lk0, specifies a length independent measure of supercoiling. Inside bacteria, DNA is partially underwound, with σ ≈ −0.05 [61, 62]. Higher levels of torsional stress induce formation of non-canonical structures, such as stretches of melted DNA or Z-DNA (reviewed in [60, 63, 64]).
The linking number can be realized in the form of twist, Tw, and writhe, Wr. These two properties describe DNA topology by approximating it as a ribbon [65, 66] (Figure 5). By convention, the plane of the ribbon is associated with DNA grooves and the edges with the sugar-phosphate backbone. Twist is defined as the rotation of the edges of the ribbon around its axis and writhe describes the anisotropy of the axis in 3D space. Twist is a local property that can be readily related to the local structure of a molecule. It equals the sum of all local rotations between adjacent base pairs measured in turns. In relaxed DNA, Tw0 = N/γ. By contrast, writhe describes the global layout of the chain. It is a measure of chirality and equals zero for flat molecules or those with mirror symmetry. For shapes typical of supercoiled DNA, writhe represents the number of supercoils formed by the axis of the molecule in 3D space, counted as the number of unreducible crossings of the axis averaged through all possible projections of the molecule. This number should not be confused with the number of solenoidal coils formed by the DNA axis. For example, for molecules wrapped n times around a cylinder with a pitch angle αp, Wr = −n·sin(αp) [67].
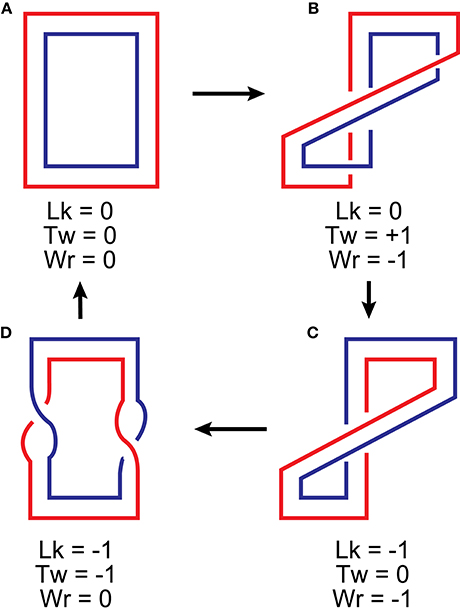
Figure 5. Interplay between linking number, twist and writhe upon deformation of a flattened ribbon. The three properties relate to each other according to Equation (10). Lk is defined as the number of times one edge of the ribbon crosses the surface swept by the other. It changes only when the edges pass through each other (b → c and d → a transitions). Tw is the sum of rotations of the edges around the axis of the ribbon. In flattened structures, it occurs only when the two edges cross, half a turn for each crossing. These can be found in structures b (two right-handed half-turns) and d (two left-handed half-turns). Wr can be evaluated by counting crossings of the ribbon axis (or any of its edges) with itself. These can be found only in structures b and c, each of them containing a single negative crossing. Note that a physical deformation, folding of a ribbon, which is illustrated in transitions a → b and c → d, leads to an interconversion between twist and writhe.
All three properties, Lk, Tw and Wr, can be expressed as line integrals along the ribbon and, therefore, are precise geometric properties. They are related via a simple exact relationship [65]:
Similarly, linking number deficit, ΔLk, partitions between torsional distortions and writhe:
Equation (10b) assumes that DNA is naturally straight and, therefore, Wr0 = 0 when it is relaxed. Thus, formation of supercoils relieves torsional strain in DNA but restricts conformations in favor of the compact ones. ΔTw remains linearly proportional to the applied torque over a broad range of DNA deformations, both for over- and undertwisted DNA [26, 68–71]. Partitioning between twist and writhe is dictated by the balance of torsional and bending rigidities of DNA. In free DNA, about three quarters of linking number deficit are realized as writhe [72, 73].
The torsional rigidity determined from DNA stretching experiments, C = 4.3·10−19 erg·cm [68], tends to be somewhat higher than that derived from the analysis of DNA conformations, 3.1·10−19 erg·cm [74, 75], although lower values of 3.0·10−19 erg·cm and 3.5·10−19 erg·cm have also been reported [76, 77]. The reasons for this discrepancy are not well understood, but could reflect stress-induced changes in DNA mechanical properties. Alternatively, they could be related to changes in DNA conformational statistics imposed by bead attachment, as has been found previously for bending fluctuations of DNA [54].
Analogous to DNA bending fluctuations, the torsional rigidity is sometimes reported in terms of the torsional persistence length, Pt. This value describes how quickly the correlation between the twist of individual base pairs decays along the DNA length (see also Equation 7). Torsional persistence length is related to torsional rigidity by the equation: Pt = 2C/kT, where kT is the Boltzmann factor. Using the value 3.1·10−19 erg·cm determined from bulk measurements, one obtains a DNA torsional persistence length of 150 nm.
Twisting DNA with Magnetic Tweezers
When DNA is twisted using magnetic tweezers, the results are markedly affected by the strength of the stretching force. At low forces, the introduced supercoils induce extrusion of a plectoneme, which contracts the DNA (Figure 6A). This results in characteristically symmetric “hat curves” when DNA extension is plotted against rotation (Figure 6B). For relatively short DNAs, one should expect only one plectoneme within a molecule. This is because the highest DNA curvature (and, hence, the highest energetic penalty for formation) is concentrated in the terminal loop of the plectoneme. It would be energetically unfavorable, therefore, if additional supercoils were initiating new plectonemes instead of being absorbed into the existing one. Under physiological conditions, long supercoiled DNAs produce multiple plectonemes, with the length of each branch averaging about 1.7 kb [72, 73]. A magnetic tweezers study of fluorescently stained DNA [78] revealed that plectonemes are highly dynamic at low stretching forces but become less mobile and less frequent as the force increases. Plectoneme formation is also facilitated by a reduction in the salt concentration, which leads to increased electrostatic repulsion between DNA segments [79].

Figure 6. (A) Magnetic beads attached to one (left), two or three (right) DNAs. Twisting the DNA at low tension induces the extrusion of a plectoneme but leads to structural transitions at high tension. (B) Characteristic hat curves for beads with one attached DNA. At low force, the hat curves are symmetric. At higher forces, untwisting causes DNA melting or formation of Z-DNA whereas overtwisting induces formation of P-DNA, which suppress formation of supercoils and the resulting DNA contraction. (C) A hat curve with a characteristic spike for a bead with two DNAs. Outside of the spike region (|n| > 0.5), DNA extension, z, can be calculated using the equation z2 = − (2E + πD·(|n| − 0.5))2, where n is the rotation of the bead expressed in turns, z0 is the highest DNA extension, which is observed when n equals zero, 2E is the average distance between the anchor points of the two DNAs, and D is the DNA effective diameter [90]. (D) The shape of the spike for beads with two (left) or three (right) DNAs. For beads with two DNAs, DNA extension within the spike (−0.5 < n < 0.5) follows the equation z2 = − 4E2sin2(πn) [90]. With three DNAs, the spike is asymmetric, and only one of its halves can be fit to this equation.
The slope of the hat curves, about 40 nm per turn, can significantly increase at low stretching force [80, 81]. The critical level of DNA supercoiling required to extrude the plectoneme increases with increasing tension. This occurs because the formation of a supercoil reduces the torsional strain in the molecule but also must perform work against the stretching force. The balance of the two energies becomes favorable only above certain level of DNA superhelicity, and this critical level of σ is proportional to the applied force. A more detailed analysis of this phenomenon can be found in Strick et al. [82].
The symmetry of the hat curve disappears at forces above 0.4 pN due to supercoiling-induced structural transitions in DNA. At intermediate forces, these transitions are limited to negatively supercoiled DNA, resulting in asymmetric hat curves. When force exceeds 3 pN, positively supercoiled DNA also undergoes a transition to adopt the P-form, similar to Pauling's early proposal of the DNA structure, where bases are exposed to solution [83].
Notably, these transitions occur at lower levels of DNA supercoiling than in bulk experiments. The main reason for it is the suppression of writhing in stretched DNA. As a result, most of the supercoiling in stretched DNA is absorbed as twist, with very low contribution from writhe. By contrast, the linking number deficit is split 3:1 between writhe and untwisting under native conditions [84–86]. Thus, the same level of torsional strain that triggers structural transitions, would be achieved at 4-fold lower levels of supercoiling when DNA is stretched. From the comparison of the stretching curves for positively and negatively supercoiled DNA, the energy of the transition upon DNA untwisting was estimated as 4 kJ mol−1 bp−1 [82]. This is on par with other estimates for the formation of non-canonical DNA structures that were obtained in the absence of stretching forces [87–89].
Multiple DNAs
Magnetic tweezers offer a convenient tool for handling two or more DNAs. This can be readily achieved by increasing the amount of DNA during its attachment to magnetic beads. Such beads end up tethered to the surface via multiple DNAs. Beads with two DNAs have been used for studies of DNA braiding [80, 90] and various enzymes that require proximity of distant DNA fragments, including DNA topoisomerases [91], condensins and transcription factors [6, 7]. The advantage of this approach is that the DNAs can be brought into contact or pulled apart simply by rotating the magnets. The contact region can be created with either left- or right-handed chirality, as desired, and the length of the overlap can be varied by changing the number of intertwinings between the DNAs.
Beads with multiple DNAs can be recognized by their characteristic hat curves (Figures 6C,D), which remain bell-shaped even at high tension. Indeed, DNA contraction occurs in this case due to geometric restrictions imposed by the intertwining of different DNA strands rather than extrusion of supercoils and, therefore, is not inhibited by stretching force. A detailed analysis of the interplay between supercoil extrusion and DNA braiding can be found in Charvin et al. [90]. The number of attached molecules can be determined from the analysis of force-extension curves. Data-fitting yields a persistence length which is linearly proportional to the number of stretched DNAs. This immediately follows from Equation 7b and the realization that bending several molecules by the same angle requires proportionally more energy.
The beads with two DNAs can also be distinguished from those with more molecules by the analysis of their hat curves [7]. All such molecules are expected to produce a sharp spike at ±0.5 turns (Figure 6C) owing to significant DNA contraction caused by the first crossing of the strands. This spike is expected to be symmetric for beads with two but not three or more DNAs.
Steps in DNA Extension
A common task in single molecule enzymology is to detect single steps of a given DNA motor protein and determine their size. This task is often exacerbated by high noise in the observed DNA extensions. This high noise becomes especially problematic at low forces, when thermal fluctuations are prominent. The use of smaller magnetic beads and shorter DNAs helps partially alleviate this problem [41]. However, much work needs to be done at the signal processing level. Several automatic algorithms have been developed [38, 92–94] that allow hands-free deconvolution of reaction time courses into series of distinct steps, and new algorithms are likely to appear in the future. All these algorithms, however, produce unambiguous results only when the signal is well separated from the noise. In borderline cases, the deconvoluted step sequences contain both false-positive and false-negative steps.
The developed algorithms seek to discard statistically insignificant steps while giving users the opportunity to vary the stringency of noise filtration. Statistical significance of the resulting steps can be evaluated, for example, using the Student's t-test [93, 94]. Such analysis calculates the probability that the two time series that precede and follow the putative step occur so by chance. Steps with a T-value below a preselected threshold are rejected. The T-value must be computed using the generalized least squares approach:
where s is the size of the putative step, σ2 is the variance of the distribution of the measured DNA extensions, N1 and N2 are the numbers of time points before and after the step, and R is a measure of auto-correlation within the time series, xi:
With this in mind, a computer program generally needs to be developed that identifies statistically significant steps within a time course. The steps are typically approximated using the Heaviside function, and the timing of the steps seeks to optimize the statistical significance of the approximation. This approach, however, does not yield a unique solution, because the time interval over which the signal is averaged in Equation (11) depends on whether or not a step has been recognized in the vicinity. As a result, the ultimate deconvolution of a signal into a step series might vary depending on the algorithm.
Several step recognition algorithms have been described in the literature. All of them act iteratively by recognizing steps one at a time. The algorithm in Kerssemakers et al. [92] begins by fitting the biggest step within the entire time course and then works its way down in ever shrinking time intervals. Another approach is to give preference to prospective steps that occur earlier during the time course while seeking to detect them independently of each other [93]. An example of step identification in a noisy signal is shown in Figure 7.
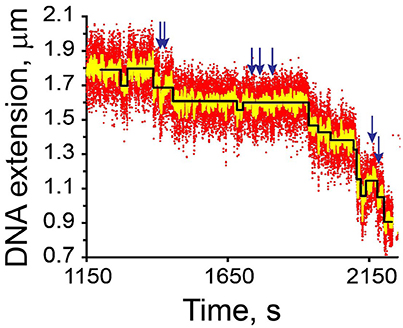
Figure 7. Identification of steps in a noisy time course. The data describe condensation of a 2.8 μm DNA by E. coli condensin MukB against a 0.3 pN force [93]. The recorded time points (red; 25 fps) and filtered at 0.5 Hz (yellow) or approximated as a series of steps (black). The steps were accepted if their T-value exceeds 3, as described in Cui et al. [93]. If the threshold T-value is set at 1, additional steps would be identified (arrows).
Multiple Beads
Magnetic tweezers create a nearly homogeneous field that changes on the sub-millimeter scale, much larger than the specimens used in most studies. This offers an opportunity to handle several beads at once and thereby accelerate the collection of the required statistics. This is a significant advantage since accumulating enough statistics is time-consuming. To be effective, however, the multiplex approach must overcome three challenges [95–97]. First, all beads must be manipulated with a known force. Therefore, the force applied to each bead must be individually measured during calibration to account for the polydispersity in the beads' magnetic properties. Second, the computer program must be able to manage a high data acquisition rate: indeed, the computer must be able to process images of multiple beads and convert them into values of DNA extensions with adequate speed. Third, to increase the number of beads within the field of view, the magnification must be decreased without sacrificing image resolution too much.
To increase the density of beads, a method for targeted DNA tethering has been developed (Figure 8). In this method, a negative stamp of the preferred pattern is created on silicon wafer with electron beam lithography and dry etching [97] (I). Then, a flat elastomeric PDMS (polydimethylsiloxane) stamp is coated with antidigoxigenin antibody on one side, and pressed against the silicon template. In the process, only the desired protein pattern will remain on the PDMS stamp, which is then printed onto a glass slide (II). The surface is then passivated, DIG-labeled DNA is attached to the printed surface (III), and finally the magnetic beads are attached [97]. Targeted DNA tethering helps increase the density of beads within the field of view, in a well-arranged fashion. This prevents bead clumping and allows one to obtain clear images, so that diffraction patterns of numerous beads will remain separated during bead motion.

Figure 8. Targeted DNA tethering [97]. A patterned silicon wafer is first created using electron beam lithography. A solid PDMS layer is then coated with anti- digoxigenin antibody and hard-pressed against the wafer in order to transfer the wafer pattern to the PDMS stamp. The antibody pattern from the PDMS stamp is transferred to a glass slide and used to capture digoxigenin labeled DNA tethered to magnetic beads [97].
Experimental Specifics: Design Issues
Using magnetic tweezers is a real time technique. Therefore, the sequence and duration of DNA twisting and stretching is tailored to specific experiments. However, several questions must be addressed at the design stage. The first and foremost question to be addressed is the choice of the substrate. The first experiments employed arbitrarily picked double stranded DNAs that were terminally labeled with derivatized nucleotides [14, 80]. Such molecules are easy to make and often suffice. In other cases, however, more elaborate structures are needed. Below, we describe several such structures that were used in magnetic tweezer experiments, including DNA with bulges and hairpins, single stranded DNA, RNA, and fluorescently labeled DNA.
The second critical question is whether or not supercoiling will be required. In order to observe supercoiling, one must use DNA with multiply labeled extremities. Such DNA could be cumbersome to produce, especially if the central part of the molecule itself includes multiple elements. If no DNA twisting is needed, however, more efficient labeling strategies can be used, such as filling sticky ends of the molecule via primer extension or extension of the ends by terminal transferase.
Improving the signal-to-noise ratio is a recurrent issue in single molecule experiments. In general, thermal noise in the system can be reduced by using shorter DNA, higher forces and increasing the number of observations. Thus, researchers should select the shortest DNA that would still support the studied reaction. The use of higher forces, however, could be limited by the internal constraints of the system. For example, motors that make large steps often exert only a weak force [6, 93], simply because the work performed by biological motors is often linked to the energy of ATP hydrolysis, ΔGATP ≥ F·s. Moreover, strong forces can induce undesired structural transitions in the system. Stretching DNA by the application of 30 pN force, for example, can lead to DNA unzipping or disruption of protein-DNA interactions.
Similarly, the number of observations can only be productively increased until they remain uncorrelated (Equation 11). At low frequencies, they are limited by the rate of the studied process and are outside of the observer's control. Thus, the time period over which the signal is averaged must not exceed the time between successive steps of the motor in question. At high frequencies, they are limited by the viscosity of the system, which sets the cutoff frequency of the bead's Brownian motion (Equation 2). Collecting data points at faster rates does not improve the signal-to-noise ratio. The cutoff frequency can be somewhat increased by switching to smaller beads owing to their reduced friction. Smaller beads, however, generate lower forces, which limits the experiment in its own way.
Custom DNA Substrates
Depending on the task, various DNAs might need to be prepared. We review below the preparation of several such molecules. For proteins that do not require specific DNA sequences, such as DNA topoisomerases [91, 98] or condensins [6, 7, 93], plasmid DNA or PCR generated dsDNA, multiply labeled with biotin and digoxigenin at the extremities, are often used as target DNA substrates. Instead of sequence specificity, the binding of such proteins often requires DNA supercoiling or braiding, both of which can be achieved by rotation of magnetic beads. Multiple end labeling promotes stronger binding to the surface, and thus a longer-lived twisted state can be attained.
For proteins that require a specific nucleotide sequence, such as RNA polymerase (RNAP) or some DNA looping proteins, more complicated substrates have been incorporated in the experimental design. A DNA looping restriction endonuclease BspMI recognizes the asymmetric sequence 5′-ACCTGC-3′. λ-phage DNA, where this binding sequence occurs 41 times, has been used as a substrate for a magnetic tweezers experiment [99]. High affinity tandem repeats of 601, a nucleosome positioning sequence, helps to localize histones on DNA to form a compact nucleosome. These 601 sequences are convenient for the study of histones if repeatability of protein assembly on DNA is required [2, 3].
For experiments that require single stranded DNA, the substrate can be prepared by thermal denaturation of labeled dsDNA precursors [100] (Figure 9A). In this study, the dsDNA precursor has been heat treated (5 min at 100°C) shortly before injection into the flow chamber, and then quickly chilled and diluted into low salt, ice cold solution. To monitor DNA relaxation by type IA topoisomerase, a bulge of 25 nucleotides has been introduced into a plasmid DNA [101]. The resulting molecule was then digested with restriction endonucleases to generate a linear DNA fragment. The ends of this DNA fragment with the bulge were then multiply tagged with biotin and digoxigenin (Figure 9B).
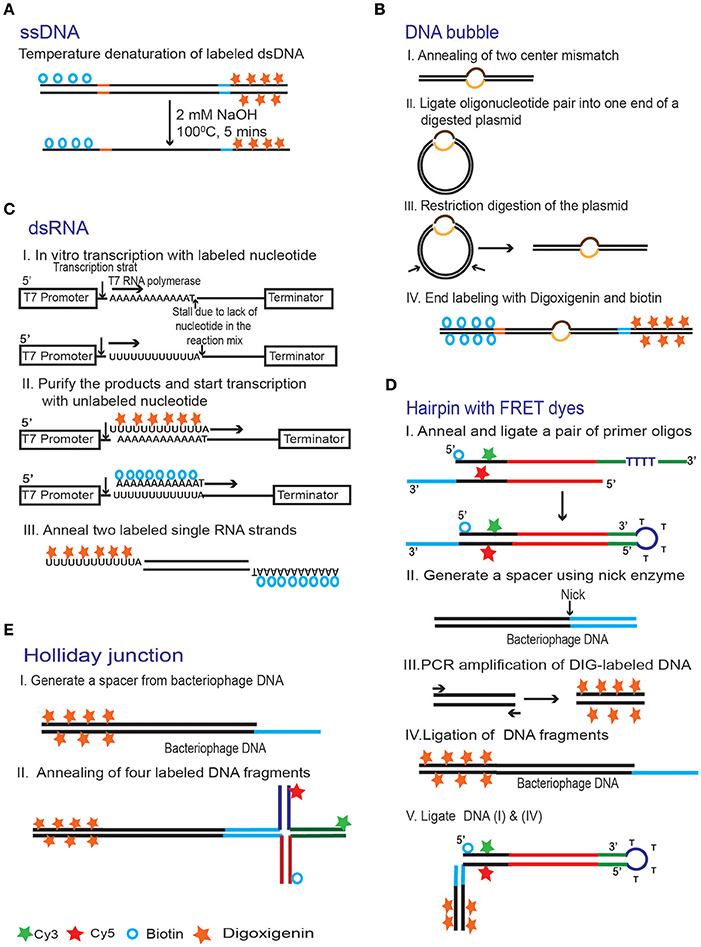
Figure 9. Common strategies for making DNA substrates for magnetic tweezers experiments. (A) Single stranded DNA substrates can be made by thermal denaturation of end labeled dsDNA [100]. (B) A pair of oligonucleotides with a mismatch in the middle was inserted into a plasmid. The DNA was then cut elsewhere and ligated to digoxigenin- and biotin-labeled DNA handles to produce a molecule with a bubble [101]. (C) Production of dsRNA [81]. End labeled ssRNA substrates were prepared using in vitro transcription. The reaction was done in two steps. First, the digoxigenin- and biotin- labeled dUTPs were used, as appropriate, to initiate transcription. The labeled nucleotides were then replaced with a complete set of unlabeled ones and the reaction continued to produce the rest of the molecule. Finally, the labeled ssRNA strands are annealed together in order to create dsRNA substrate. (D) A hairpin with a FRET pair [102]. Two oligonucleotides with biotin, Cy3 and Cy5 incorporated during their synthesis were annealed and then ligated together to produce a looped arm (I). The loop in this structure forms spontaneously, because of the self-complementary stretch separated by four unmatched thymidines in one of the oligos. The second arm for this structure (IV) was created by ligating together a digoxigenin-labeled DNA handle (III) and bacteriophage DNA with a sticky end (II). The two arms were then ligated together taking advantage of the compatible sticky ends (blue). Complementary sequences are shown in the same color. (E) A Holliday junction is prepared by annealing four oligonucleotide strands labeled with Cy3, Cy5 and biotin [102]. A 12 nt overhang on one of the arms is used to attach the structure to a digoxigenin labeled DNA tether.
Production of labeled RNA molecules has been achieved with the help of in vitro transcription [52, 81]. To this end, dsDNA templates were constructed that give rise to complementary RNA strands with unique leader sequences to facilitate further cloning. Following transcription, the two RNA strands were hybridized to generate dsRNA, and the unique ends have been used to attach the molecule to biotin- and digoxegenin-labeled RNA handles [52]. In another approach [26], terminally labeled ssRNAs were generated using a two-step transcription reaction. In the first step, an incomplete mixture of labeled nucleotides (which included biotin- or digoxigenin- derivatized adenosine or uracil triphosphate, as appropriate) was used to generate short, multiply labeled leader fragments. Such reactions stall once the need for the missing nucleotide arises. Thereafter, the labeled nucleotides were replaced with the full complement of the unlabeled ones to generate the body of the molecule (Figure 9C).
Hairpin DNA substrates have been used for studies of DNA unwinding by DNA helicases [30, 94]. These enzymes bind at the junction between single and double stranded DNA. Several approaches were described for the preparation of DNA hairpins. One such method involves primer extension of a 5′-biotin tailed primer annealed to a circular ssDNA using a DNA polymerase. The resulting circular product were linearized by restriction digestion. A short oligo was then ligated between two DNA strands to form a hairpin structure [30].
Another strategy for the preparation of a DNA hairpin is depicted in Figure 9D where biotin and digoxigenin anchoring ends and a pair of FRET (Főrster resonance energy transfer) dyes have been combined into one molecule [102]. This kind of substrate is particularly useful in cases where both force measurement and fluorescent tracking are desirable, such as tracking the movement of DNA motor proteins under force. Here, the DNA hairpin was prepared by combining two separate DNA substrates. The first substrate was made by annealing two matching oligonucleotides, which contain a sticky end, biotin and the cyanine fluorophores (Cy3 and Cy5) on one end and a DNA loop at the other (Figure 9D, I). The second substrate is a DNA spacer with a matching sticky end and digoxigenin-labeled DNA handle (Figure 9D, IV). The two substrates were then ligated together via their matching sticky ends, producing a structure with DIG and biotin on opposite ends (Figure 9D, V).
Another special type of substrate used in magnetic tweezers experiment is the Holliday junction [102]. This structure was created by annealing four oligonucleotides which contain four mutually complementary single stranded regions with biotin and the FRET pair located at the appropriate arms. A bacteriophage DNA spacer with a digoxigenin-labeled DNA handle was attached to the four-arm Holliday junction (Figure 9E).
DNA Stretching Applications of Magnetic Tweezers
Magnetic tweezers are an excellent tool for probing mechanical properties of DNA including: DNA unwinding [103] bending [5] and elasticity [47], activity of DNA topoisomerases [91, 98], DNA condensation [6, 7, 93], and functions of chromatin remodeling enzymes, DNA helicases and translocases [30, 94, 104], RNA polymerase [103, 105], restriction endonucleases [99], and many others. Below, we review several applications of magnetic tweezers that highlight their power and versatility in studies of DNA modifying enzymes. Note that many features uncovered in these studies would be very difficult to reveal using the more traditional biochemical approaches.
Alteration of DNA Topology by DNA Topoisomerase
DNA topoisomerases are not only important for their biomedical applications but are also remarkable molecular machines with an exquisite mechanism of action. These enzymes act by transiently opening a gate in single or double stranded DNA and transporting another piece of DNA through the gate. In the process, they affect the global shape of the bound DNA in a purposeful manner, allowing them to alter mesoscale properties of the molecule. Magnetic tweezers have been used to explore a number of aspects of the topoisomerase reaction.
The mechanism of strand passage is the defining feature of the topoisomerase reaction. Type-1 topoisomerases cleave only one DNA strand and, therefore, can change the DNA linking number in steps of 1 (Figures 10A,B). Type-2 DNA topoisomerases cleave both strands of the double stranded DNA and, hence, change DNA supercoiling in steps of two (Figure 10C). This feature has been recognized early on during topoisomerase studies and helped deduce the reaction mechanism. Bulk measurements, however, always leave room for doubts, especially when it comes to potentially processive or cooperative enzymes. These doubts were dispelled using magnetic tweezers, which helped observe individual reaction events and revealed that type-2 topoisomerases indeed require a DNA crossing for activity and change linking number in steps of two [91]. In contrast, type-1A topoisomerases removed supercoils in steps of 1 and required a bulged or melted piece of DNA [101]. Type-1B enzymes, on the other hand, were able to act on both positively and negatively supercoiled DNA and relaxed DNA in steps of n, in full accord with their postulated controlled rotation mechanism which envisions multiple strand transport events between cleavage and religation [106].
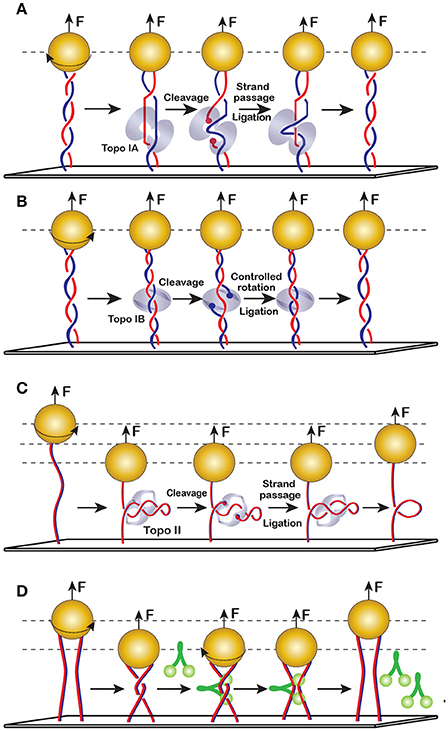
Figure 10. Enzymatic changes to DNA shape and topology. (A) Type-1A topoisomerases (topo IA) require a single stranded DNA region for binding and, therefore, act predominantly on negatively supercoiled DNA. They transport DNA strands strictly once during their cleavage-religation cycle. (B) Topo IB employs controlled rotation mechanism and can relax both positive and negative supercoils. They can transport DNA once or multiple times before religation. Note that topo-1A and topo-1B can act on DNA without a plectoneme. In such cases, their activity is not accompanied by changes in DNA extension. (C) Topo II requires DNA crossings. Each round of topo II reaction changes the DNA linking number by 2, which alters DNA extension. (D) Condensin mediated DNA bridging observed on braided DNAs. Crossing the two DNAs by rotating the bead creates a transient bridge, which can be stabilized by condensins even after the DNAs were untwisted.
Curiously, the rate of type-1A topoisomerases is depressed by the applied torque [101]. This is somewhat counterintuitive since one might expect that DNA stretching should facilitate reactions that break DNA. Indeed, polysaccharide stretching is an important part of lysozyme catalysis. Collagen proteolysis was, similarly, accelerated by applied force [107], as were type-1B topoisomerases [106]. Inhibition by force indicates that topo1As scrunch DNA during catalysis, which requires them to drag the bead against the force. The length of this displacement, as estimated from the force-velocity data, was about two times longer than the enzyme. Apparently, the protein wraps DNA around itself during the reaction.
A striking feature of DNA topoisomerases is their ability to sense DNA topology, which appears to originate from recognition of randomly colliding DNA segments [108]. Perhaps related to it on a structural level is chirality sensing. DNA gyrase, for example, introduces (−) supercoils into DNA at the expense of ATP hydrolysis, which allows it to relax positively supercoiled DNA and swivel relaxed or negatively supercoiled molecules. Topo IV, on the other hand, can relax both positive and negative supercoils but acts much faster with the former [109, 110]. Chirality sensing extends to bimolecular topoisomerase reactions but varies from one enzyme to another. A real time decatenation experiment using two mechanically braided DNA molecules reveals that eukaryotic topo II relaxes left-handed (as found in positively supercoiled DNA) and right-handed (negatively supercoiled) braids at the same rate, whereas E. coli topo IV preferentially relaxes left-handed braids. This result has important implications for the mechanism of topoisomerase involvement in support of DNA replication [91].
DNA Bridging and Condensation by Condensins
Condensins are ubiquitous proteins required for global chromosome organization in a diverse range of organisms. DNA bridging is their central activity that underlies their action inside the cell. To observe DNA bridging using magnetic tweezers [7], two DNAs attached to a single bead were crossed by rotating the bead, resulting in a decrease of DNA extension. The length of DNA is immediately restored after DNA is untwisted. However, the presence of the E. coli condensin MukB delays the restoration of the length, signaling the formation of DNA bridges. The frequency of bridging decreases significantly if the magnets are rotated in the opposite direction. This observation reveals high preference of MukB for positively braided DNAs. This geometric selectivity toward DNA substrates can be compared to E. coli topo IV.
DNA bridging by condensins was also reconstituted using single DNA molecules (Figure 10D). In this case, DNA bridging could be deduced from the large size of DNA condensation steps, but was especially evident during decondensation, which was triggered by high stretching forces [6, 93]. Magnetic tweezers reveal an intriguing feature of condensins that remained elusive during previous studies. It turned out that condensins bind and condense DNA in a highly cooperative manner. Similar to DNA reannealing, condensin reactions proceed in a zippering fashion, where the nucleation step limits the rate of the reaction and propagation follows it very fast [93]. As a result, the time course of DNA condensation includes a characteristic lag, the length of which markedly declines upon even a modest increase in the protein concentration.
RNA Polymerase Mediated DNA Scrunching
Transcription is a fundamental cellular reaction that lies at the heart of life itself. The mechanism of transcription is remarkably complex and includes multiple steps and translocation events. One of such steps was discovered using magnetic tweezers [103, 105]. In this study, the authors reconstituted the initiation of transcription by E. coli RNA polymerase, RNAP, on a stretched DNA. During this process, the initial association of RNAP with the promoter produces the so called closed promoter complex, Pc. The protein then melts about one turn of the DNA double helix to produce the open promoter complex, Po, which is accompanied by the generation of a compensatory positive supercoil (Figure 11A). The addition of nucleotides initiates RNA synthesis and prompts promoter clearance and the formation of the transcription elongation complex, TEC. Escape from the promoter is accompanied by scrunching, when the footprint of RNAP on DNA expands to include additional 9-11 nucleotides, which serve as a template for the leader mRNA.
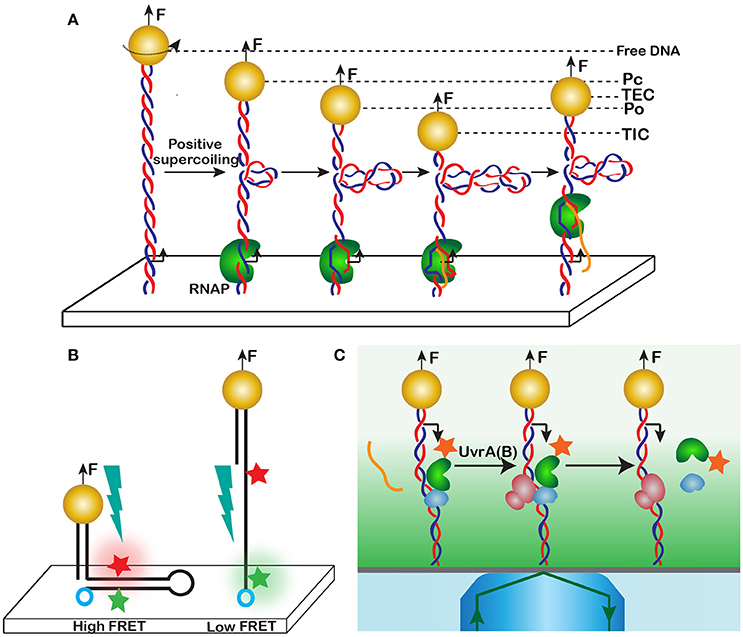
Figure 11. Detecting reaction intermediates through DNA distortion. (A) Promoter unwinding and subsequent scrunching of DNA by RNA polymerase. A dsDNA with an E. coli promoter is tethered in between the surface and a magnetic bead. The bead is rotated once past buckling instability to introduce a supercoil into the molecule. RNA polymerase and nucleotides are then added to the reaction, and various reaction intermediates are detected through their characteristic DNA extension, including the closed promoter complex, Pc, open promoter complex, Po, transcription initiation complex, TIC, and transcription elongation complex, TEC. The DNA extension changes in this case because of the compensatory positive supercoiling that accompanies DNA melting during promoter opening and scrunching. (B) Conformational transitions in a DNA hairpin detected by simultaneous magnetic tweezers and FRET measurements. Formation of the hairpin creates a high FRET state, when fluorescence of the acceptor (red) can be detected. At high forces, the hairpin unravels, and the fluorophores separate beyond the Forster distance. Only the donor (green) will be able to fluoresce. (C) Dynamics of a DNA repair complex detected using a combination of magnetic trapping and single molecule total internal reflection fluorescence (TIRF) imaging. Upon an encounter with a lesion, RNAP stalls, releases the transcript and recruits the Mfd translocase. Mfd then displaces the RNAP from the lesion site. RNAP remains attached to Mfd until UvrA(B) causes the dissolution of the Mfd-RNAP complex. Transient events are detected using fluorophore labeled RNAP and Mfd.
By carefully measuring DNA extension during this process, Revyakin et al. [103, 105] discovered one more intermediate in the reaction, the transcription initiation complex, TIC, which if formed prior to promoter clearance and following successful synthesis of a short leading stretch of mRNA (Figure 11A). Furthermore, they discovered that scrunching generates compensatory positive supercoils, occurs during both successful and abortive initiation of transcription, and proceeds progressively and not as a single step.
To achieve this feat, the authors developed a system capable of reporting changes in DNA extension to a single base pair resolution. They did it by taking advantage of the greater rigidity of supercoiled DNA (Figure 11A). Indeed, extrusion of supercoils removes much slack from DNA and reduces thermal noise [82]. This significantly improves the signal-to-noise ratio and makes possible the detection of very small steps. Another advantage of this system is its ability to distinguish between positive and negative generated supercoils. Indeed, expansion of the transition bubble produces positive compensatory supercoils. These increase the overall DNA supercoiling and decrease its extension only if DNA was initially positively supercoiled. The effect would be opposite on negatively supercoiled DNA.
Another example of measuring changes in DNA extension at single base pair resolution has been reported in a recent study by Dekker et al. [42], who used a bright coherent laser source and a CMOS camera for fast image acquisition to resolve 3 Å steps with a 1 s period for immobile beads melted into the surface and 5 Å steps with a 0.5 s period for dsDNA anchored beads.
Integration of Magnetic Tweezers with Fluorescence Microscopy
Unraveling complex reactions can often benefit from the use of multiple probes. In this respect, simultaneous detection of single molecule fluorescence and deformation offers new possibilities to mechanistic studies. An example of this has been recently reported using DNA hairpin formation for the proof of concept [102].
To observe the event, Kemmerich and coauthors constructed a molecule that contained a self-complementary region of single-stranded DNA with a FRET pair at its borders and DNA handles as needed for stretching (see Figure 9 for details of the construction). Without applied force, the single-stranded region folds into a hairpin, thus bringing the two fluorophores together (Figure 11B). The high-FRET state can then be detected simultaneously with DNA contraction, which accompanies formation of the hairpin. Conversely, an increase in the force melts the hairpin and induces a low-FRET state in the system.
In another example, Strick and coauthors combined magnetic trapping with total internal reflection fluorescence, TIRF, [111–113] to elucidate the mechanism of bacterial transcription-coupled DNA repair (Figure 11C). The use of evanescent light helped detect fluorescence from the tagged proteins while eliminating at the same time the interference from the bead. Magnetic force and fluorescence have been used to provide complementary information, which helped decode a complex sequence of events that unfold during the interaction between RNAP and the Mfd translocase during their encounter with DNA lesions. Specifically, the catalytic properties of RNAP were probed using stretching force, whereas fluorescence was reporting on the composition of the complex.
Non-DNA Applications of Magnetic Tweezers
Magnetic tweezers are most frequently used for studies of DNA and DNA reconfiguring enzymes. However, a number of other applications have been recently described. These include studies of protein folding [5, 114], rotating protein assemblies [115], cellular cortical stiffness [9], cellular mechanotransduction processes [10] and intracellular transport [11]. These applications take advantage of the non-invasive character of the tweezers. Indeed, magnetic tweezers do not require intense sample irradiation, efficiently work in solution, and do not even need a computer for some tasks. We will review in this section several of the applications that do not focus on DNA.
Mechanical Manipulation of Protein-Protein Interactions: Protein Folding
Actin filaments deliver mechanical stability to cells through their gigantic network, and actin crosslinking protein Filamin A (FLNa) participates in this process. Filamin proteins are elastic; they can transmit a signal generated by external stress, or generate their own signals in response to contractile forces produced by the actin network. In a recent study [116], Chen and coworkers demonstrated that mechanical forces induce conformational transition of FLNa domains and proposed that the impairment of domain-domain interaction of the protein might lead to the mechanosensing function of FLNa.
In this study on protein unfolding, an immunoglobulin-like repeat containing a pair of IgFLNa domains, 20 and 21, previously identified as a mechanosensing domain, were tethered in between streptavidin- coated magnetic bead and an NTA-copper coated glass surface by C-terminal biotin and the N-terminal his tag, respectively (Figure 12A). Two handles consisting of repeats of IgFLNa 1-3 were used for surface attachments.
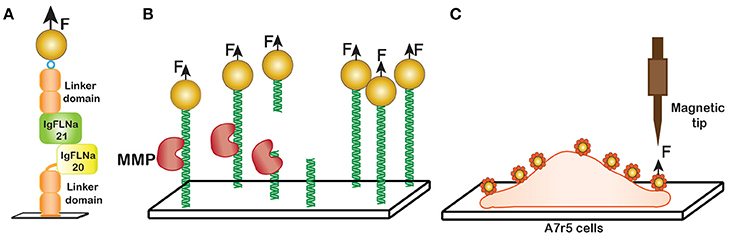
Figure 12. Non-DNA applications. (A) Unfolding of Filamin domains. Domains IgFLNa 20-21 with two handles consisting of domains IgFLNa 1-3 were tethered between a magnetic bead and the surface and then stretched with a magnetic field. (B) The force dependence of collagen proteolysis. MMP protease cuts the collagen trimers at a specific recognition site resulting in the bead detachment. (C) Cellular cortical stiffness measurement in vascular smooth muscle cells (VSMC). Arginine-glycine-aspartic acid (RGD) coated paramagnetic beads were adhered by the transmembrane integrin receptors of the cells. A sharp tip magnetic tweezers exert force on the bead and induce a magnetic moment.
Stretching of this complex revealed that it unfolds in several stages. The interaction between IgFLNa domain 20 and 21 was disrupted at low force, 2-5 pN [117]. Unfolding of domains 20 and 21 required a higher force, 15 pN and 30 pN respectively. Furthermore, distinct kinetic intermediates could be detected during unfolding of domain 21. The existence of these intermediates was proposed to contribute to the mechanism of mechanosensing.
Another strategy to tether a protein was used in unfolding studies of a single neuronal SNARE (soluble N-ethylmaleimide-sensitive factor attachment protein receptor) complex [118]. The SNARE complex acts as a force generating machine for membrane and vesicle fusion, in which the folding energy of SNARE complex rezipping drives the membrane fusion. The SNARE complex, which consist of an α-helix bundle, was produced with cysteins close to its N- and C-terminal ends and then attached to DNA handles using thiol-disulfide exchange. Its further stretching revealed the existence of a metastable folding intermediate with a well pronounced hysteresis in the zipping-rezipping curves. This intermediate was proposed to ensure the directionality of the SNARE complex assembly during force generation.
Collagen Proteolysis
In another study [114], Adhikari and coworkers employed magnetic tweezers to study the effect of external force on collagen proteolysis by matrix metalloproteinase-1 (MMP-1). Mechanical stress is known to have a profound impact on the structure and composition of extra-cellular matrix (ECM), and the proteolytic degradation of ECM by MMPs plays an important role in the progression of cancer cell metastasis [107].
To study collagen proteolysis, a collagen trimer was immobilized to the anti-myc antibody coated surface via 5x myc tag of the protein. An increase in length of 1.5 nm of collagen upon stretching was observed suggesting the unwinding of the collagen triple helix prior to proteolysis [114]. The proteolysis event was detected by the detachment of the beads from the glass surface as a function of time (Figure 12B) and fitted to a single exponential function. Multiple fields were sampled for each measurement. Application of 13 pN stretching force resulted in ~100-fold increase in proteolysis rate by MMP-1. Similar to other cases, the rate of proteolysis followed the Arrhenius equation and increased exponentially with applied force.
Cellular Mechanotransduction Studies
A growing list of applications employs magnetic tweezers for studies of cellular trafficking and mechanosensing. A common approach here is to coat magnetic beads with a compound that ensures their proper intracellular recruitment, take advantage of phagocytosis if the bead destination is intracellular, and then employ a microprobe to apply magnetic forces to the beads. The beads in this case can be used to monitor stiffness of the organelle [10, 11], or simply as a means to stimulate the cell and observe downstream responses [119].
As an example, magnetic tweezers were applied to study stiffness of aortic tissue, which has been linked to cardiovascular disease. To measure cellular cortical stiffness of A7r5 vascular smooth muscle cells, a GRGDNP (H-Gly-Arg-Gly-Asp-Asn-Pro-OH) peptide (RGD), which is required for binding by transmembrane integrin receptor present in A7r5 cells, has been covalently linked to magnetic beads. Then the beads were incubated with the cells at 37°C with 5% CO2 to aid the binding. Here, a magnetic microneedle made of a highly permeable and low hysteresis nickel alloy rod surrounded by a copper solenoid was used as the magnetic tweezers probe (Figure 12C). This probe was placed 150–200 μm from the adherent beads at the time of the measurement. The cortical stiffness was calculated as the stiffness of bead-integrin attachment, a ratio of the force applied to the displacement of the cell-adhered magnetic beads [9]. The results demonstrate that lysophosphatidic acid (LPA), an activator of myosin, increases cell contractility and stimulate cortical stiffness and PP2, a small molecule inhibitor Src-dependent FA recycling, inhibits LPA-induced increase in cortical stiffness.
Summary
Magnetic tweezers are powerful instruments well suited for diverse single molecule applications. They are lauded for their ability to twist macromolecules in addition to stretching. However, they have a number of other unique advantages. In particular, they provide a technical solution that does not use intense irradiation of the sample, which inevitably leads to accelerated degradation. Furthermore, the tweezers generate a nearly homogeneous force field over large distances. As a result, no adjustments are needed during the course of experiment to compensate for enzyme translocation. Additionally, the flow chamber can be readily modified for multiplex applications so that many reactions can be followed in parallel. Finally, magnetic tweezers can handle multiple DNAs as easily as they handle single molecules.
Recent advances in hybrid single molecule techniques, which combine magnetic tweezers with microfluidic systems and fluorescence microscopy, opened new possibilities of experimental design. These advances also helped to solve one of the original weaknesses of the method, its difficulties in generating strong magnetic fields. The use of micromanufactured magnetic poles allows a significant reduction in the separation between the bead and the pole, which helps produce stronger field gradients and stiffer magnetic traps. Thanks to such developments, sub-nanometer resolution has become possible.
The method has few limitations. One of them includes difficulties in working with particles that are susceptible to magnetic fields. Among biomolecules, however, the list of such molecules is rather short and consists mostly of proteins associated with metal clusters. Perhaps the biggest limitation is the rather bulky geometry of the magnetic poles, which must be positioned close to the sample. As a result, combining tweezers with other applications requires a degree of ingenuity. Likewise, carrying beads around using magnetic tweezers remains a challenge and requires a specialized instrument. These limitations, however, are not especially restrictive and only underscore how versatile and powerful the technique truly is.
Author Contributions
RS and VR designed and wrote this manuscript, approved its final version and are responsible for its content.
Funding
This work was supported by the awards for the project number HR14-042 from Oklahoma Center for Advancement of Science and Technology, and HDTRA1-14-1-0019 from the Department of the Defense, Defense Threat Reduction Agency.
Disclaimer
The content of the information does not necessarily reflect the position or the policy of the federal government, and no official endorsement should be inferred.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge the contribution from Viridiana Herrera during initial crafting of the manuscript, are grateful to Casey Stevens for reading it, and are indebted to the reviewers for many excellent suggestions.
References
1. Neuman KC, Nagy A. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nat Methods (2008) 5:491–505. doi: 10.1038/nmeth.1218
2. Kruithof M, Chien FT, Routh A, Logie C, Rhodes D, van Noort J. Single-molecule force spectroscopy reveals a highly compliant helical folding for the 30-nm chromatin fiber. Nat Struct Mol Biol. (2009) 16:534–40. doi: 10.1038/nsmb.1590
3. Meng H, Andresen K, van Noort J. Quantitative analysis of single-molecule force spectroscopy on folded chromatin fibers. Nucleic Acids Res. (2015) 43:3578–90. doi: 10.1093/nar/gkv215
4. Capitanio M, Pavone FS. Interrogating biology with force: single molecule high-resolution measurements with optical tweezers. Biophys J. (2013) 105:1293–303. doi: 10.1016/j.bpj.2013.08.007
5. Le S, Chen H, Cong P, Lin J, Dröge P, Yan J. Mechanosensing of DNA bending in a single specific protein-DNA complex. Sci Rep. (2013) 3:3508. doi: 10.1038/srep03508
6. Strick TR, Kawaguchi T, Hirano T. Real-time detection of single-molecule DNA compaction by condensin I. Curr Biol. (2004) 14:874–80. doi: 10.1016/j.cub.2004.04.038
7. Petrushenko ZM, Cui Y, She W, Rybenkov VV. Mechanics of DNA bridging by bacterial condensin MukBEF in vitro and in singulo. EMBO J. (2010) 29:1126–35. doi: 10.1038/emboj.2009.414
8. Wozniak MA, Chen CS. Mechanotransduction in development: a growing role for contractility. Nat Rev Mol Cell Biol. (2009) 10:34–43. doi: 10.1038/nrm2592
9. Saphirstein RJ, Gao YZ, Jensen MH, Gallant CM, Vetterkind S, Moore JR, et al. The focal adhesion: a regulated component of aortic stiffness. PLoS ONE (2013) 8:e62461. doi: 10.1371/journal.pone.0062461
10. Collins C, Guilluy C, Welch C, O'Brien ET, Hahn K, Superfine R, et al. Localized tensional forces on PECAM-1 elicit a global mechanotransduction response via the integrin-RhoA pathway. Curr Biol. (2012) 22:2087–94. doi: 10.1016/j.cub.2012.08.051
11. Mahowald J, Arcizet D, Heinrich D. Impact of external stimuli and cell micro-architecture on intracellular transport states. Chemphyschem (2009) 10:1559–66. doi: 10.1002/cphc.200900226
12. Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt Lett. (1986) 11:288. doi: 10.1364/OL.11.000288
13. Ashkin A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys J. (1992) 61:569–82. doi: 10.1016/S0006-3495(92)81860-X
14. Strick TR, Allemand J-F, Bensimon D, Croquette V. The elasticity of a single supercoiled DNA molecule. Science (1996) 271:1835–7. doi: 10.1126/science.271.5257.1835
15. Lipfert J, Hao X, Dekker NH. Quantitative modeling and optimization of magnetic tweezers. Biophys J. (2009) 96:5040–9. doi: 10.1016/j.bpj.2009.03.055
16. Gassner AL, Abonnenc M, Chen HX, Morandini J, Josserand J, Rossier JS, et al. Magnetic forces produced by rectangular permanent magnets in static microsystems. Lab Chip (2009) 9:2356–63. doi: 10.1039/b901865d
17. Zacchia NA, Valentine MT. Design and optimization of arrays of neodymium iron boron-based magnets for magnetic tweezers applications. Rev Sci Instrum. (2015) 86:053704. doi: 10.1063/1.4921553
18. Fisher JK, Cribb J, Desai KV, Vicci L, Wilde B, Keller K, et al. Thin-foil magnetic force system for high-numerical-aperture microscopy. Rev Sci Instrum. (2006) 77:nihms8302. doi: 10.1063/1.2166509
19. Gosse C, Croquette V. Magnetic tweezers: micromanipulation and force measurement at the molecular level. Biophys J. (2002) 82:3314–29. doi: 10.1016/S0006-3495(02)75672-5
20. Lipfert J, Wiggin M, Kerssemakers JW, Pedaci F, Dekker NH. Freely orbiting magnetic tweezers to directly monitor changes in the twist of nucleic acids. Nat Commun. (2011) 2:439. doi: 10.1038/ncomms1450
21. Lin J, Valentine MT. Ring-shaped NdFeB-based magnetic tweezers enables oscillatory microrheology measurements. Appl Phys Lett. (2012) 100:201902. doi: 10.1063/1.4717988
22. Case RB, Chang YP, Smith SB, Gore J, Cozzarelli NR, Bustamante C. Retraction. Science (2005) 307:1409. doi: 10.1126/science.307.5714.1409b
23. Bockelmann U, Thomen P, Essevaz-Roulet B, Viasnoff V, Heslot F. Unzipping DNA with optical tweezers: high sequence sensitivity and force flips. Biophys J. (2002) 82:1537–53. doi: 10.1016/S0006-3495(02)75506-9
24. Crut A, Koster DA, Seidel R, Wiggins CH, Dekker NH. Fast dynamics of supercoiled DNA revealed by single-molecule experiments. Proc Natl Acad Sci USA. (2007) 104:11957–62. doi: 10.1073/pnas.0700333104
25. Bijamov A, Shubitidze F, Oliver PM, Vezenov DV. Quantitative modeling of forces in electromagnetic tweezers. J Appl Phys. (2010) 108:104701. doi: 10.1063/1.3510481
26. Lipfert J, Kerssemakers JW, Jager T, Dekker NH. Magnetic torque tweezers: measuring torsional stiffness in DNA and RecA-DNA filaments. Nat Methods (2010) 7:977–80. doi: 10.1038/nmeth.1520
27. Janssen XJ, Lipfert J, Jager T, Daudey R, Beekman J, Dekker NH. Electromagnetic torque tweezers: a versatile approach for measurement of single-molecule twist and torque. Nano Lett. (2012) 12:3634–9. doi: 10.1021/nl301330h
28. Ovryn B, Izen SH. Imaging of transparent spheres through a planar interface using a high-numerical-aperture optical microscope. J Opt Soc Am A Opt Image Sci Vis. (2000) 17:1202–13. doi: 10.1364/JOSAA.17.001202
29. Ovryn B. Three-dimensional forward scattering particle image velocimetry applied to a microscopic field-of-view. Exp Fluids (2000) 29:S175–84. doi: 10.1007/s003480070019
30. Manosas M, Meglio A, Spiering MM, Ding F, Benkovic SJ, Barre FX, et al. Magnetic tweezers for the study of DNA tracking motors. Methods Enzymol. (2010) 475:297–320. doi: 10.1016/S0076-6879(10)75013-8
31. Paik DH, Roskens VA, Perkins TT. Torsionally constrained DNA for single-molecule assays: an efficient, ligation-free method. Nucleic Acids Res. (2013) 41:e179. doi: 10.1093/nar/gkt699
32. Paul N, Yee J. PCR incorporation of modified dNTPs: the substrate properties of biotinylated dNTPs BioTechniques (2010) 48:333–4. doi: 10.2144/000113405
33. Lionnet T, Allemand JF, Revyakin A, Strick TR, Saleh OA, Bensimon D, et al. Magnetic trap construction. Cold Spring Harb Protoc. (2012) 2012:133–8. doi: 10.1101/pdb.prot067496
34. Janissen R, Berghuis BA, Dulin D, Wink M, van Laar T, Dekker NH. Invincible DNA tethers: covalent DNA anchoring for enhanced temporal and force stability in magnetic tweezers experiments. Nucleic Acids Res. (2014) 42:e137. doi: 10.1093/nar/gku677
35. Carey MF, Peterson CL, Smale ST. The Primer Extension Assay. Cold Spring Harbor Laboratory Protocols. Cold Spring, NY: Cold Spring Harbor Laboratory Press (2009).
36. Komura J, Riggs AD. Terminal transferase-dependent PCR: a versatile and sensitive method for in vivo footprinting and detection of DNA adducts. Nucleic Acids Res. (1998) 26:1807–11. doi: 10.1093/nar/26.7.1807
37. Schlingman DJ, Mack AH, Mochrie SG, Regan L. A new method for the covalent attachment of DNA to a surface for single-molecule studies. Colloids Surf B Biointerfaces (2011) 83:91–5. doi: 10.1016/j.colsurfb.2010.11.002
38. Sun Z, Tikhonova EB, Zgurskaya HI, Rybenkov VV. Parallel lipoplex folding pathways revealed using magnetic tweezers. Biomacromolecules (2012). 13:3395–400. doi: 10.1021/bm301155w
39. Burnham DR, De Vlaminck I, Henighan T, Dekker C. Skewed brownian fluctuations in single-molecule magnetic tweezers. PLoS ONE 9:e108271. doi: 10.1371/journal.pone.0108271
40. Berg-Sorensen K, Flyvbjerg H. Power spectrum analysis for optical tweezers. Rev Sci Instrum. (2004) 75:594–612. doi: 10.1063/1.1645654
41. Revyakin A, Ebright RH, Strick TR. Single-molecule DNA nanomanipulation: improved resolution through use of shorter DNA fragments. Nat Methods (2005) 2:127–38. doi: 10.1038/nmeth0205-127
42. Dulin D, Cui TJ, Cnossen J, Docter MW, Lipfert J, Dekker NH. High spatiotemporal-resolution magnetic tweezers: calibration and applications for DNA dynamics. Biophys J. (2015) 109:2113–25. doi: 10.1016/j.bpj.2015.10.018
43. Kuhn W. Über die Gestalt fadenförmiger Moleküle in Losungen (On the shape of filform molecules in solutions). Kolloidzeitschrift (1934) 68:2–15.
46. Hagerman PJ. Flexibility of DNA. Annu Rev Biophys Biophys Chem. (1988) 17:265–86. doi: 10.1146/annurev.bb.17.060188.001405
47. Smith SB, Finzi L, Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science (1992) 258:1122–6. doi: 10.1126/science.1439819
48. Bustamante C, Marko JF, Siggia ED, Smith S. Entropic elasticity of lambda-phage DNA. Science (1994) 265:1599–600. doi: 10.1126/science.8079175
49. Vologodskii A. DNA Extension under the action of an external force. Macromolecules (1994) 27:5623–5. doi: 10.1021/ma00098a016
50. Bouchiat C, Wang MD, Allemand J, Strick T, Block SM, Croquette V. Estimating the persistence length of a worm-like chain molecule from force-extension measurements. Biophys J. (1999) 76(1 Pt 1):409–13. doi: 10.1016/S0006-3495(99)77207-3
51. Wang MD, Yin H, Landick R, Gelles J, Block SM. Stretching DNA with optical tweezers. Biophys J. (1997) 72:1335–46. doi: 10.1016/S0006-3495(97)78780-0
52. Abels JA, Moreno-Herrero F, van der Heijden T, Dekker C, Dekker NH. Single-molecule measurements of the persistence length of double-stranded RNA. Biophys J. (2005) 88:2737–44. doi: 10.1529/biophysj.104.052811
53. Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science (1996) 271:795–9. doi: 10.1126/science.271.5250.795
54. Seol Y, Li J, Nelson PC, Perkins TT, Betterton MD. Elasticity of short DNA molecules: theory and experiment for contour lengths of 0.6-7 microm. Biophys J. (2007) 93:4360–73. doi: 10.1529/biophysj.107.112995
55. Travers A, Muskhelishvili G. DNA structure and function. FEBS J. (2015) 282:2279–95. doi: 10.1111/febs.13307
56. Roca J. The torsional state of DNA within the chromosome. Chromosoma (2011) 120:323–34. doi: 10.1007/s00412-011-0324-y
57. Dillon SC, Dorman CJ. Bacterial nucleoid-associated proteins, nucleoid structure and gene expression. Nat Rev Microbiol. (2010) 8:185–95. doi: 10.1038/nrmicro2261
58. Vologodskii A. DNA supercoiling helps to unlink sister duplexes after replication. Bioessays (2010) 32:9–12. doi: 10.1002/bies.200900143
59. Deweese JE, Osheroff MA, Osheroff N. DNA Topology and topoisomerases: teaching a “knotty” subject. Biochem Mol Biol Educ. (2008) 37:2–10. doi: 10.1002/bmb.20244
61. Bliska JB, Cozzarelli NR. Use of site-specific recombination as a probe of DNA structure and metabolism in vivo. J Mol Biol. (1987) 194:205–18. doi: 10.1016/0022-2836(87)90369-X
62. Sinden RR, Carlson JO, Pettijohn DE. Torsional tension in the DNA double helix measured with trimethylpsoralen in living E. coli cells: analogous measurements in insect and human cells. Cell (1980) 21:773–83. doi: 10.1016/0092-8674(80)90440-7
63. Mirkin SM. Discovery of alternative DNA structures: a heroic decade (1979-1989). Front Biosci. (2008) 13:1064–71. doi: 10.2741/2744
64. Frank-Kamenetskii MD, Mirkin SM. Triplex DNA structures. Annu Rev Biochem. (1995) 64:65–95. doi: 10.1146/annurev.bi.64.070195.000433
65. White JH. Self-linking and the Gauss integral in higher dimensions. Am J Math. (1969) 91:693–728. doi: 10.2307/2373348
66. Fuller FB. Decomposition of the linking of a closed ribbon: a problem of molecular biology. Proc Natl Acad Sci USA. (1978) 75:3557–61. doi: 10.1073/pnas.75.8.3557
68. Bryant Z, Stone MD, Gore J, Smith SB, Cozzarelli NR, Bustamante C. Structural transitions and elasticity from torque measurements on DNA. Nature (2003) 424:338–41. doi: 10.1038/nature01810
69. Oberstrass FC, Fernandes LE, Bryant Z. Torque measurements reveal sequence-specific cooperative transitions in supercoiled DNA. Proc Natl Acad Sci U.S.A. (2012) 109:6106–11. doi: 10.1073/pnas.1113532109
70. Strick TR, Bensimon D, Croquette V. Micro-mechanical measurement of the torsional modulus of DNA. Genetica (1999) 106:57–62. doi: 10.1023/A:1003772626927
71. Cluzel P, Lebrun A, Heller C, Lavery R, Viovy JL, Chatenay D, et al. DNA: an extensible molecule. Science (1996) 271:792–4. doi: 10.1126/science.271.5250.792
72. Vologodskii AV, Cozzarelli NR. Conformational and thermodynamic properties of supercoiled DNA. Annu Rev Biophys Biomol Struct. (1994) 23:609–43. doi: 10.1146/annurev.bb.23.060194.003141
73. Rybenkov VV, Vologodskii AV, Cozzarelli NR. The effect of ionic conditions on the conformations of supercoiled DNA. II. Equilibrium catenation. J Mol Biol. (1997) 267:312–23. doi: 10.1006/jmbi.1996.0877
74. Geggier S, Kotlyar A, Vologodskii A. Temperature dependence of DNA persistence length. Nucleic Acids Res. (2011) 39:1419–26. doi: 10.1093/nar/gkq932
75. Shimada J, Yamakawa H. Moments for DNA topoisomers: the helical wormlike chain. Biopolymers (1988) 27:657–73. doi: 10.1002/bip.360270409
76. Vologodskii AV, Marko JF. Extension of torsionally stressed DNA by external force. Biophys J. (1997) 73:123–32. doi: 10.1016/S0006-3495(97)78053-6
77. Bouchiat C, Mezard M. Elasticity model of a supercoiled DNA molecule. Phys Rev Lett. (1998) 80:1556–9. doi: 10.1103/PhysRevLett.80.1556
78. van Loenhout MT, de Grunt MV, Dekker C. Dynamics of DNA supercoils. Science (2012) 338:94–7. doi: 10.1126/science.1225810
79. Rybenkov VV, Vologodskii AV, Cozzarelli NR. The effect of ionic conditions on DNA helical repeat, effective diameter, and free energy of supercoiling. Nucleic Acids Res. (1997) 25:1412–8. doi: 10.1093/nar/25.7.1412
80. Strick T, Allemand J-F, Bensimon D, Croquette V. Behavior of supercoiled DNA. Biophys J. (1998) 74:2016–28. doi: 10.1016/S0006-3495(98)77908-1
81. Lipfert J, Skinner GM, Keegstra JM, Hensgens T, Jager T, Dulin D, et al. Double-stranded RNA under force and torque: similarities to and striking differences from double-stranded DNA. Proc Natl Acad Sci U.S.A. (2014) 111:15408–13. doi: 10.1073/pnas.1407197111
82. Strick T, Allemand J, Croquette V, Bensimon D. Twisting and stretching single DNA molecules. Prog Biophys Mol Biol. (2000) 74:115–40. doi: 10.1016/S0079-6107(00)00018-3
83. Allemand JF, Bensimon D, Lavery R, Croquette V. Stretched and overwound DNA forms a Pauling-like structure with exposed bases. Proc Natl Acad Sci USA. (1998) 95:14152–7. doi: 10.1073/pnas.95.24.14152
84. Vologodskii AV, Levene SD, Klenin KV, Frank-Kamenetskii M, Cozzarelli NR. Conformational and thermodynamic properties of supercoiled DNA. J Mol Biol. (1992) 227:1224–43. doi: 10.1016/0022-2836(92)90533-P
85. Adrian M, ten Heggeler-Bordier B, Wahli W, Stasiak AZ, Stasiak A, Dubochet J. Direct visualization of supercoiled DNA molecules in solution. EMBO J. (1990) 9:4551–4.
86. Boles TC, White JH, Cozzarelli NR. Structure of plectonemically supercoiled DNA. J Mol Biol. (1990) 213:931–51. doi: 10.1016/S0022-2836(05)80272-4
87. Bauer WR, Benham CJ. The free energy, enthalpy and entropy of native and of partially denatured closed circular DNA. J Mol Biol. (1993). 234:1184–96. doi: 10.1006/jmbi.1993.1669
88. Mirkin SM, Lyamichev VI, Kumarev VP, Kobzev VF, Nosikov VV, Vologodskii AV. The energetics of the B-Z transition in DNA. J Biomol Struct Dyn. (1987) 5:79–88. doi: 10.1080/07391102.1987.10506376
89. Haniford DB, Pulleyblank DE. Facile transition of poly[d(TG·d(CA)] into a left-handed helix in physiological conditions. Nature (1983) 302:632–4. doi: 10.1038/302632a0
90. Charvin G, Vologodskii A, Bensimon D, Croquette V. Braiding DNA: experiments, simulations, and models. Biophys J. (2005) 88:4124–36. doi: 10.1529/biophysj.104.056945
91. Charvin G, Bensimon D, Croquette V. Single-molecule study of DNA unlinking by eukaryotic and prokaryotic type-II topoisomerases. Proc Natl Acad Sci USA. (2003) 100:9820–5. doi: 10.1073/pnas.1631550100
92. Kerssemakers JW, Munteanu EL, Laan L, Noetzel TL, Janson ME, Dogterom M. Assembly dynamics of microtubules at molecular resolution. Nature (2006) 442:709–12. doi: 10.1038/nature04928
93. Cui Y, Petrushenko ZM, Rybenkov VV. MukB acts as a macromolecular clamp in DNA condensation. Nat Struct Mol Biol. (2008) 15:411–8. doi: 10.1038/nsmb.1410
94. Seol Y, Strub MP, Neuman KC. Single molecule measurements of DNA helicase activity with magnetic tweezers and t-test based step-finding analysis. Methods (2016) 105:119–27. doi: 10.1016/j.ymeth.2016.04.030
95. Ribeck N, Saleh OA. Multiplexed single-molecule measurements with magnetic tweezers. Rev Sci Instrum. (2008) 79:094301. doi: 10.1063/1.2981687
96. De Vlaminck I, Henighan T, van Loenhout MT, Burnham DR, Dekker C. Magnetic forces and DNA mechanics in multiplexed magnetic tweezers. PLoS ONE 7:e41432. doi: 10.1371/journal.pone.0041432
97. De Vlaminck I, Henighan T, van Loenhout MT, Pfeiffer I, Huijts J, Kerssemakers JW, et al. Highly parallel magnetic tweezers by targeted DNA tethering. Nano Lett. (2011) 11:5489–93. doi: 10.1021/nl203299e
98. Charvin G, Strick TR, Bensimon D, Croquette V. Topoisomerase IV bends and overtwists DNA upon binding. Biophys J. (2005) 89:384–92. doi: 10.1529/biophysj.105.060202
99. Wang Y, Ran S, Yang G. Single molecular investigation of DNA looping and aggregation by restriction endonuclease BspMI. Sci Rep. (2014) 4:5897. doi: 10.1038/srep05897
100. Maier B, Bensimon D, Croquette V. Replication by a single DNA polymerase of a stretched single-stranded DNA. Proc Natl Acad Sci USA. (2000) 97:12002–7. doi: 10.1073/pnas.97.22.12002
101. Dekker NH, Rybenkov VV, Duguet M, Crisona NJ, Cozzarelli NR, Bensimon D, et al. The mechanism of type IA topoisomerases. Proc Natl Acad Sci USA. (2002) 99:12126–31. doi: 10.1073/pnas.132378799
102. Kemmerich FE, Swoboda M, Kauert DJ, Grieb MS, Hahn S, Schwarz FW, et al. Simultaneous single-molecule force and fluorescence sampling of dna nanostructure conformations using magnetic tweezers. Nano Lett. (2016) 16:381–6. doi: 10.1021/acs.nanolett.5b03956
103. Revyakin A, Ebright RH, Strick TR. Promoter unwinding and promoter clearance by RNA polymerase: detection by single-molecule DNA nanomanipulation. Proc Natl Acad Sci USA. (2004) 101:4776–80. doi: 10.1073/pnas.0307241101
104. Lionnet T, Dawid A, Bigot S, Barre FX, Saleh OA, Heslot F, et al. DNA mechanics as a tool to probe helicase and translocase activity. Nucleic Acids Res. (2006) 34:4232–44. doi: 10.1093/nar/gkl451
105. Revyakin A, Liu C, Ebright RH, Strick TR. Abortive initiation and productive initiation by RNA polymerase involve DNA scrunching. Science (2006) 314:1139–43. doi: 10.1126/science.1131398
106. Koster DA, Croquette V, Dekker C, Shuman S, Dekker NH. Friction and torque govern the relaxation of DNA supercoils by eukaryotic topoisomerase IB. Nature (2005) 434:671–4. doi: 10.1038/nature03395
107. Kessenbrock K, Plaks V, Werb Z. Matrix metalloproteinases: regulators of the tumor microenvironment. Cell (2010) 141:52–67. doi: 10.1016/j.cell.2010.03.015
108. Rybenkov VV, Ullsperger CU, Vologodskii AV, Cozzarelli NR. Simplification of DNA topology below equilibrium values by type II topoisomerases. Science (1997) 277:690–3. doi: 10.1126/science.277.5326.690
109. Nöllmann M, Stone MD, Bryant Z, Gore J, Crisona NJ, Hong SC, et al. Multiple modes of Escherichia coli DNA gyrase activity revealed by force and torque. Nat Struct Mol Biol. (2007) 14:264–71. doi: 10.1038/nsmb1213
110. Corbett KD, Schoeffler AJ, Thomsen ND, Berger JM. The structural basis for substrate specificity in DNA topoisomerase IV. J Mol Biol. (2005) 351:545–61. doi: 10.1016/j.jmb.2005.06.029
111. Graves ET, Duboc C, Fan J, Stransky F, Leroux-Coyau M, Strick TR. A dynamic DNA-repair complex observed by correlative single-molecule nanomanipulation and fluorescence. Nat Struct Mol Biol. (2015) 22:452–7. doi: 10.1038/nsmb.3019
112. Fan J, Leroux-Coyau M, Savery NJ, Strick TR. Reconstruction of bacterial transcription-coupled repair at single-molecule resolution. Nature (2016) 536:234–7. doi: 10.1038/nature19080
113. Duboc C, Graves ET, Strick TR. Simple calibration of TIR field depth using the supercoiling response of DNA. Methods (2016) 105:56–61. doi: 10.1016/j.ymeth.2016.03.028
114. Adhikari AS, Chai J, Dunn AR. Mechanical load induces a 100-fold increase in the rate of collagen proteolysis by MMP-1. J Am Chem Soc. (2011) 133:1686–9. doi: 10.1021/ja109972p
115. Watanabe R, Iino R, Noji H. Phosphate release in F1-ATPase catalytic cycle follows ADP release. Nat Chem Biol. (2010) 6:814–20. doi: 10.1038/nchembio.443
116. Chen H, Chandrasekar S, Sheetz MP, Stossel TP, Nakamura F, Yan J. Mechanical perturbation of filamin A immunoglobulin repeats 20-21 reveals potential non-equilibrium mechanochemical partner binding function. Sci Rep. (2013) 3:1642. doi: 10.1038/srep01642
117. Rognoni L, Stigler J, Pelz B, Ylänne J, Rief M. Dynamic force sensing of filamin revealed in single-molecule experiments. Proc Natl Acad Sci USA. (2012) 109:19679–84. doi: 10.1073/pnas.1211274109
118. Min D, Kim K, Hyeon C, Cho YH, Shin YK, Yoon TY. Mechanical unzipping and rezipping of a single SNARE complex reveals hysteresis as a force-generating mechanism. Nat Commun. (2013) 4:1705. doi: 10.1038/ncomms2692
Keywords: magnetic tweezers, force spectroscopy, single molecule methods, DNA nanomanipulations, DNA supercoiling
Citation: Sarkar R and Rybenkov VV (2016) A Guide to Magnetic Tweezers and Their Applications. Front. Phys. 4:48. doi: 10.3389/fphy.2016.00048
Received: 17 September 2016; Accepted: 22 November 2016;
Published: 06 December 2016.
Edited by:
Mario Nicodemi, Universita' di Napoli “Federico II,” ItalyReviewed by:
Andrea Gamba, Polytechnic University of Turin, ItalyAndrzej Stasiak, University of Lausanne, Switzerland
Keir Cajal Neuman, National Institutes of Health, USA
Copyright © 2016 Sarkar and Rybenkov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Valentin V. Rybenkov, dmFseWFAb3UuZWR1
 Rupa Sarkar
Rupa Sarkar Valentin V. Rybenkov
Valentin V. Rybenkov