Information kinetics—an extension

We present an operator formalism for the recently developed kinetic information theory, construct Poisson brackets between the Liouville 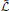and information 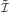operators in μ space, proposing its quantum version. Making use of the universal quantum of time, the Planck time τ_p, a pseudo-energy-time uncertainty relation is constructed. It suggests that tiny amounts of information production may cause large variations in energy. The Hubble time τ_H sets an upper bound on information in the universe.

In Treumann and Baumjohann [1] we have put forward the principles of a physical kinetic theory of information starting from the idea that information is based in the dynamics of many particle N ≫ 1 systems encountered in physics as well as in other domains of nature and society. The basic equation governing the N-particle (Boltzmann-Shannon-) information _N(F_N) = F_N log F_N turned out to be the exact N-particle Liouville equation in Gibbs' 6N-dimensional Γ phase space

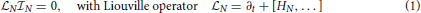
and H_N the N-particle classical Hamiltonian. (In Equation 6 of that work a typo occurred: log_N should be replaced with log F_N, and the sentence following it can be dropped.) We also conjectured that it can be reduced by the methods of the BBGKY hierarchy construction to a one-particle N = 1 kinetic equation in Boltzmann's 6-dimensional (no index) μ phase space

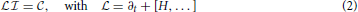
Its non-vanishing right-hand side 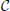≠ 0, an information-production term, we related to the Kolmogorov [2] entropy rate 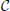= K(), with ≡ ₁.

Effectively, the classical Liouville operator = d/dt ≡ { ˙ } is a total, not a partial time derivative in μ-space yielding

Preference for use of the total time derivative is justified by the equivalence to kinetic theory. For small information production rates, one has K() ≈ K₀, and the μ-space Liouville equation yields the exponentially growing solution (t) ≈ (0) exp[K₀t], where 0 < K₀ = ∑_iλ_i is the total sum of all positive Lyapunov exponents λ_i ≥ 0 of the parts of which the system is constituted. Generally, any exponential growth of (t) with time t, as inferred in low-dimensional systems, holds only for this linear dependence of K on information. Saturation of information at a value _sat ≈ −2K₀/K⁽²⁾ > 0 becomes possible for negative second derivative K⁽²⁾ = d²K/d² < 0, when including the quadratic term in the expansion of K() ≈ K₀ + $\frac{1}{2}$K⁽²⁾² + ….

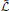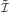We tentatively interpret and as operators , acting to the right on some phase space density function F(p, q). Formally applying the commutator [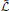, 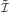] to the phase space density function, keeping in mind that we are dealing with a total time derivative, yields

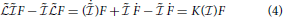
and hence

with the right-hand side as usual understood as multiplied by a unit operator. The Kolmogorov entropy rate appears as the commutator of the Liouville and information operators in μ-phase space, thus describing the kinetic evolution of the Boltzmann-Shannon information operator together with the phase space density.

Applying the same argument to the N-particle Gibbs' Γ-phase space, we have 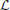_NN = 0. Hence, in Γ space the commutator of the Liouville and information operators vanishes identically:

due to conservation of Shannon information in Γ-space. Other definitions of information than Shannon's, introducing a non-vanishing right hand side in Γ-space, a N-particle Kolmogorov entropy rate K_N, will result in non-vanishing commutators.

There is an important difference between the Liouville and information operators. The former is a differential operator. The latter, instead, refers to the sum over all states of the system; it is thus a (properly normalised) integral operator

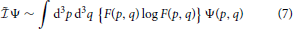
acting on any function Ψ(p, q) that depends on the μ-phase space coordinates.

Wishfully the above commutator should serve as starting point of a quantum theory of information. However, K() is not a fixed constant; it is a variable that depends upon the information itself and thus upon the full dynamics in μ space. One way of generalisation to a quantum version may be via defining

where, with 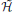_q the quantum Hamiltonian, we introduced von Neumann's quantum Liouville operator 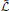_q = ħ ∂_t + i[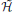_q, …] which acts on the phase-space density matrix $\wide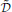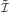hat{\rho }$. Here ≡ K⁻¹, obtained by multiplication with the inverse scalar K⁻¹ from the right, plays the role of a “duration operator” (or time operator), with time not the life-time of a particle, however, as in ordinary quantum mechanics. This expression applies to the quantum evolution of information or, otherwise, duration, the “dynamics of time.” Since information cannot be erased, duration cannot be erased either. It can only accumulate increasing time elapsed. K() ≡ K(p, q) is a function of (p, q); thus the operator 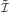in the duration operator 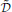= 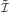K⁻¹ acts on the product K⁻¹$\widehat{\rho }$. The above commutator equation should give rise to an integro-differential equation instead of a partial differential equation.

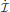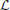Returning to = K(), again referring to as a total time derivative and writing it as Δ = KΔt, with Δt = 2π/Δω = 2πħ/Δϵ, yields Δ · K⁻¹Δϵ = 2πħ. The meaning of energy ϵ in this expression remains unclear thus preventing calling it an energy-information uncertainty relation. On the other hand, (arbitrarily) introducing the universal quantum of time, the Planck time τ_P = $\sqrt{\hslash G/c^5}$ as the shortest (physically motivated) time element, yields

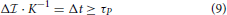
Re-introducing energy, this expression can be written as

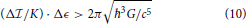
which, formally, is an information-energy uncertainty relation with right hand side a universal constant though again undefined meaning of energy. Physical motivation for the use of the Planck time is based on τ_P being the natural limit of validity of quantum electrodynamics where it merges into quantum gravity. So far the above commutator does not contain any gravity. The appearance of the gravitational constant G in the last expression thus suggests that a proper quantum theory of information (respectively time/duration) cannot be expected prior to a consistent formulation of quantum gravity.

The Planck time, in our choice, imposes an absolute lower bound on the ratio of information change and Kolmogorov entropy rate. In this interpretation, “physical time in information production” can be “generated at the smallest” in τ_P quanta only. We repeat [1] that K = 0 implies Δ = 0, no production of information (nor time, in this interpretation), while K → ∞ is non-physical.

In order to give the above assertion another twist, one may square the second last expression to obtain

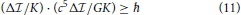
Here, with explicit expression for the energy differential Δϵ = (c⁵/G)(Δ/K) and Δt = Δ/K, the energy-time uncertainty relation ΔϵΔt ≥ ħ is formally reproduced. However, since both its terms on the left contain the ratio Δ/K as the sole variable, this is not a genuine uncertainty relation. This version of the former relation suggests that, due to the huge factor c⁵/G ≈ 10⁵² J s⁻¹ in the energy factor Δϵ, small information changes Δ/K may imply large energy variations—an interesting notion in view of the enormous practical effects any dispersion of information is observed to cause.

Duration is also strictly bound from above by the Hubble time τ_H ≥ Δ/K(), which in the universe with accelerated expansion is itself a function of time. For fixed (average universal) production rate K_U() this bound limits the total amount of information production in the visible universe. Knowledge of the total universal entropy Δ_U provides an estimate of the (average) universal entropy/information production rate (assuming that no information is lost to higher dimensional space—by generation of Klein-Kaluza particles in the bulk of D-brane cosmologies, for instance). Assuming, in particular, exponential growth of the universal entropy throughout its entire evolution (implying K_U ~ K_U0U) yields that K_U0 ≳ τ⁻¹_Hlog{_U(τ_H)/_U0}, with index 0 referring to the beginning.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Treumann RA, Baumjohann W. Kinetic theory of information – the dynamics of information. Front Phys. (2015) 3:19. doi: 10.3389/fphy.2014.00019

CrossRef Full Text | Google Scholar

2. Kolmogorov AN. Entropy per unit time as a metric invariant of automorphism. Dokl Russ Acad Sci. (1959) 124:754–5.