Extending resonant inelastic X-ray scattering to the extreme ultraviolet

In resonant inelastic X-ray scattering (RIXS), core hole resonance modes are used to enhance coupling between photons and low energy electronic degrees of freedom. Resonating with shallow core holes accessed in the extreme ultraviolet (EUV) can provide greatly improved energy resolution at standard resolving power, but has been found to often yield qualitatively different spectra than similar measurements performed with higher energy X-rays. This paper uses experimental data and multiplet-based numerical simulations for the M-edges of Co-, Ni-, and Cu-based Mott insulators to review the properties that distinguish EUV RIXS from more commonly performed higher energy measurements. Key factors such as the origin of the strong EUV elastic line and advantages of EUV spectral functions over soft X-ray RIXS for identifying intrinsic excitation line shapes are discussed.

1. Introduction

Resonant inelastic X-ray scattering (RIXS) is a powerful technique for observing the energy states of many-body quantum materials, which include features such as the momentum-resolved Mott gap and emergent particles composed of diverse combinations of charge, orbital, and spin degrees of freedom [1–28]. In RIXS, incident photons are tuned close to an absorption edge to excite high energy core hole states that rapidly decay into low energy many-body excitations, represented by Raman features in scattered light. The core hole resonance states that make RIXS possible are strongly correlated, and undergo complex time evolution that can have a large impact on the appearance of inelastic spectra [1–6, 8, 15, 28–30]. This paper will explore the properties of RIXS performed with core level resonances found in the extreme ultraviolet (EUV), a regime that is infrequently used for resonant photon scattering, and which has very distinctive scattering matrix elements and core hole time evolution.

Extending the RIXS to the EUV incident energy range (roughly 10 eV < hν < 120 eV) has several very pronounced consequences. The long wavelength of EUV photons makes it possible to achieve superior energy resolution, opening up significant scientific potential discussed in Section 4. Excitation spectral functions observed in the EUV may also be simpler and easier to attribute, with fewer simultaneously excited collective modes (see Section 5). However, resonant elastic scattering (REXS) is extremely strong in the EUV (the reason for this is explained in Section 3), which can be interesting to measure but is mostly a hindrance as it obscures inelastic features below E ≲ 0.1 eV. Inelastic X-ray scattering by contrast has a smaller total cross section in the EUV than in the soft X-ray regime, because of growth in the Auger electron emission rate. Also, EUV photons have insufficient momentum to measure the momentum dispersion of itinerant excitations outside of the Brillouin zone center.

On a more subtle level, EUV RIXS spectra show very different feature intensities than one would find at a corresponding soft X-ray resonance (e.g., comparing the transition metal M- and L- edges). The lifetime of shallow core hole resonance states accessed in the EUV has a complex dependence on incident photon energy [6, 31–33], and can provide the option to access both long and short core hole lifetimes at the same resonance edge. The effective shake-up perturbation caused by shallow core holes also tends to be weaker, and can exclude some classes of excitations that are not directly created by the action of the scattering photon operators (e.g., multi-magnons, phonons, charge transfer modes) [3, 4, 7, 8, 10, 28, 34, 35]. Atomic multiplet (AM) models of RIXS can potentially work better in the EUV, because angular momentum entanglement through multipolar Coulomb interactions is stronger than at the L-edge, and protects multiplet symmetries. These effects will be discussed in Sections 5, 6. Many of our observations about EUV RIXS in this paper are common with earlier studies, and in particular the insightful discussion in Chiuzbaian et al. [16]. However, we have attempted to consider a wider range of effects and provide a broader context with respect to numerics.

2. Materials and Methods

The Mott insulators CoO, NiO, and SrCuO₂ were chosen as model materials for this study, and provide examples of resonance from strongly correlated 3d⁷, 3d⁸, and 3d⁹ systems, respectively. The principle electronic excitations observed in X-ray absorption spectroscopy (XAS) and RIXS with p-symmetry core holes on Co [7, 16], Ni [6, 8, 14, 15, 17, 18, 36], and Cu [8, 9] are closely identified with excitation matrix elements obtained from AM based calculations for a high-spin 2+ valence atomic state perturbed by the crystal field of surrounding oxygen atoms. The compounds CoO and NiO have a rock salt crystal structure, with an octahedral crystal field on the transition metal site, and strong antiferromagnetic superexchange interactions through σ-bonded oxygen atoms. The Cu atoms of SrCuO₂ are found in a quasi-1D [11, 13, 21, 37] network of copper oxide plaquettes that lack apical oxygens. The ground state includes a single hole in the 3d_x²−y² orbital [36], and the energies of dd crystal field states are known from previous RIXS measurements [8].

Samples of SrCuO₂ and NiO were cleaved single crystals. The CoO sample was a bulk-like well ordered CoO film grown on MgO, and transferred to the RIXS chamber vacuum with minimal exposure to the air. The sample was grown by molecular beam epitaxy (MBE) in an ultrahigh vacuum chamber with the base pressure of 2×10⁻¹⁰ torr. Cobalt was evaporated onto a MgO(001) substrate in 2×10⁻⁶ torr oxygen at room temperature. After evaporation, the sample was annealed to 600°C within a 2×10⁻⁶ torr oxygen atmosphere for 30 min, yielding a surface roughness under 1nm measured by atomic force microscopy. Sample thickness was 45 nm, much greater than the ≲10 nm layer over which interface strain and exchange effects may be significant [38], and similar to three times the estimated X-ray penetration depth.

Measurements at the M-edges of Co, Ni, and Cu were performed at the beamline 4.0.3 (MERLIN) RIXS endstation (MERIXS) at the Advanced Light Source (ALS), Lawrence Berkeley National Laboratory. The data were recorded by a VLS based X-ray emission spectrograph equipped with a commercially available CCD detector [39, 40]. Scattering intensity measured at each pixel was normalized to ensure that intensity in the final spectra accurately represents the density of scattered photons per unit energy. Large single crystal samples were measured near room temperature at a pressure of 3×10⁻¹⁰ Torr. The resolution-limited full width at half maximum of the elastic line is better than δE≲35 ± 2 meV for all M-edge measurements. Measurements at the copper K-edge were performed with ~400 meV resolution using beamline 11-XU at SPring-8. All measurements were performed close to room temperature with in-plane polarization in the [001] scattering plane, with scattered photons measured at 90° to the incident beam trajectory. The photon beam had a grazing (NiO) 25° or (CoO, SrCuO₂) 30° angle of incidence to the cleaved [010] face.

3. Specular Reflection and the Elastic Line

The elastic line observed in EUV RIXS experiments is far stronger than elastic intensity under similar measurement conditions in the soft X-ray regime. For example, M-edge resonant scattering from 3d transition metals is performed in the EUV, and typically yields an elastic line that even under ideal conditions is 3 or more orders of magnitude more intense than inelastic RIXS features (see Figure 1C). This contrasts with M-edge atomic multiplet calculations and L-edge soft X-ray data which show that elastic and near-elastic scattering intensity can be within ~1 order of magnitude of inelastic features. In this section, we will explain why a strong elastic tail caused by off-specular reflectivity has been unavoidable in EUV X-ray scattering experiments to date. The incident energy dependence of EUV elastic scattering includes a strong resonant component that can be understood from atomic multiplet caculations [6, 7], meaning that the resonant elastic (REXS) signal could potentially be measured on resonance to study electronic correlations on a length scale similar to the incident photon wavelength (e.g., 20–100 nm). On the other hand, it is a significant source of artifacts in RIXS data when the elastic line is 4 or more orders of magnitude stronger than inelastic features, because the RIXS resolution function is convoluted by surface structure in the area of the focused beam spot.

FIGURE 1

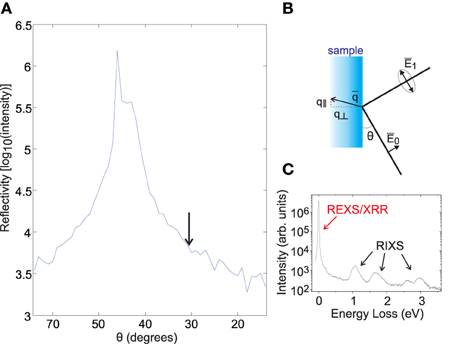
Figure 1. Elastic line and specular reflection. (A) Elastic scattering intensity as a function of θ, the angle between the incident beam and a NiO sample surface, in the 90° scattering geometry shown in (B). Incident polarization is inside the scattering plane, and most specular reflection intensity is found near θ = 45°. (C) The relative intensity of the elastic scattering (REXS) and inelastic excitations on resonance (i.e., M-edge RIXS) is shown for the slightly grazing scattering geometry indicated by the arrow in (A).

To understand the origin of the EUV elastic line, we have measured how the elastic line intensity varies when approaching the specular reflection condition on a cleaved NiO sample (Figure 1). Specular reflection is observed at θ = 45° for the 90° scattering geometry at the MERLIN beamline (see scattering diagram in Figure 1B). The dependence of elastic line intensity on scattering geometry is shown in Figure 1A, revealing that elastic intensity decreases exponentially as the scattering geometry deviates from the specular condition. This trend is common to all sample families we have studied. Similar off-specular and off-Bragg elastic scattering is well-known in the soft X-ray regime, and can provide information about structural and electronic disorder when investigated with techniques such as X-ray photon correlation spectroscopy (XPCS) [41].

However, the tail of specular reflectivity is typically only identified within a few degrees of the specular condition in the soft X-ray regime, and reflection intensity is far weaker than in the EUV [42] due to the roughly n ~ 1 − c λ² dependence of the index of refraction on X-ray wavelength. This leads to an expected increase of about 4 orders of magnitude in the intensity of reflected light at transition metal M-edges relative to L-edges, based on the Fresnel equations (R_EUV/R_X ~ [(n_EUV − 1)/(n_X − 1)]² ~ (λ_EUV/λ_X)⁴ ~ 10⁴). In addition to specular reflection being far stronger in the EUV, the longer wavelengths of EUV photons cause the off-specular elastic tail to cover a much larger solid angle. Surface roughness on a length scale of ~ 1μm is hard to avoid in most samples of interest for RIXS, particularly given the typically ≲ 10 nm penetration depth of EUV photons [42]. In-plane scattering with a wavelength of λ > 1 μm will yield off-specular rays spread over δθ = 3.2° at the nickel M-edge (hν ~ 65 eV) in the scattering geometry used for our measurement, qualitatively comparable to the reflectivity feature width in our data, but would only give δθ = 0.5° at the M-edge. If one factors in a 10⁴ gain in reflected intensity and a factor of ~6 broader rocking curve, it is reasonable to expect off-specular reflectivity tails prominent over several degrees in the soft X-ray regime to cover all solid angles of scattering in the EUV.

The main reason EUV off-specular reflection intensity deviates dramatically from atomic multiplet calculations designed for the X-ray regime is that calculations for the X-ray regime make use of the Born approximation, and specular reflection is specifically derived from non-perturbative physics outside of the Born approximation. If we consider even lower photon energies in the optical regime, the observation of off-specular reflection intensity covering all outgoing solid angles is associated with Lambert's cosine law, and has been known of since the eighteenth century [43].

4. A New Regime of Energy Resolution

A primary incentive to perform RIXS in the EUV regime is that with the same resolving power and qualitatively similar optics, one can achieve energy resolution that is as much as an order of magnitude better than RIXS spectrometers in the soft X-ray regime [39, 40]. At the transition metal M-edge, this has so far enabled studies with energy resolution similar to δE ~ 20 to 30 meV, which is similar to the energy scale of room temperature thermal fluctuations. A principle success of high resolution studies over the last few years has been more detailed observations of how thermal energy changes the appearance of atomic multiplet excitations such as transition metal dd modes. Temperature dependence in dd modes has been linked to thermal lattice expansion and the thermal population of low energy degrees of freedom [7, 45]. The thermal population of low energy electronic degrees of freedom can introduce an intensity tail on the energy gain side (i.e., the leading edge) of excitations in a pattern resembling anti-Stokes scattering. This tail is termed “pseudo-anti-Stokes” emission in Wray et al. [7].

Entering the δE ~ 20 to 30 meV resolution regime also enables the observation of a broader range of many-body effects, such as the interaction between atomic multiplet excitations and other many-body degrees of freedom [7]. Measurements in Figure 2 show that the energy resolution range accessed at the M-edge is sufficient to resolve the decay dynamics of orbital excitations in the cuprate Mott insulator SrCuO₂. The copper oxide lattice of SrCuO₂ has a similar electron configuration to undoped 2D cuprates [36] but electrons are constrained to propagate primarily within one-dimensional chains of corner sharing CuO plaquettes[11, 21, 37]. The momentum dispersion of similar orbital excitations has been studied at the soft X-ray L-edge [20, 21], however energy resolution at that energy did not facilitate a detailed study of excitation line shapes.

FIGURE 2

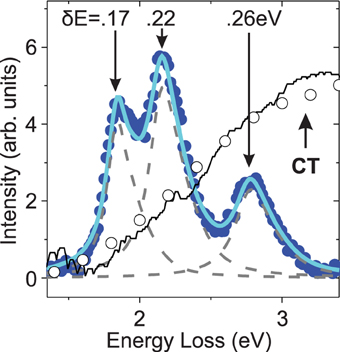
Figure 2. Interacting charge transfer and orbiton modes. The orbital excitations of SrCuO₂ measured with M₃ photons (hν = 75 eV) are fitted by convoluting the intrinsic line shape of excitations in the SrCuO₂ spin chain [9] with the inverse lifetimes (δE) indicated. Dipole induced charge transfer excitations measured from (open circles) K-edge RIXS and (black line) optical ellipsometry from Popovic et al. [44] are overlaid, revealing delocalized charge excitations that orbitons can decay into.

In SrCuO₂, charge transfer excitations and atomic multiplet orbiton excitations overlap in energy close to the Brillouin zone center. This can be seen from overlaying the M-edge spectrum of SrCuO₂ orbitons with measurements of Q = 0 charge transfer modes by copper K-edge RIXS and optical ellipsometry in Figure 2. Energetic overlap with the charge transfer continuum implies that the orbitons observed in this measurement are actually semi-stable “resonance modes.” Degeneracy with the continuum allows resonance modes to delocalize into separately propagating electrons, holes, and spinons, without first absorbing energy from an outside source. If delocalization happened instantaneously, the M-edge RIXS spectrum of SrCuO₂ would largely be shaped by the spectral contour of delocalized states seen in K-edge RIXS (circles in Figure 2). Instead, the experimental results show an M-edge spectrum that strongly resembles expectations from an AM model.

Orbiton line widths fitted in Figure 2 provide a rough estimate of the time scale of charge transfer delocalization from a local orbiton resonance. The leading edge of the lowest energy (3d_xy) excitation does not overlap with a large density of charge transfer excitations, and has a sharper line shape than any other feature in the spectrum, roughly matching a δ = 0.15 ± 0.02 eV Lorentzian. As the energies of the orbitons increase beyond the charge transfer gap energy, a broadening trend is observed. The highest energy excitation (3d_3z²−r²) has the greatest quantum overlap with charge transfer excitations, and the fitted inverse lifetime of δ = 0.26 eV suggest that it can decay into delocalized states on a time scale of ħ/0.26 ± 0.02 eV = 2.5 ± 0.2fs.

The line shapes resolved from SrCuO₂ illustrate the need for adequate resolution to observe how simple atomic excitations decompose into more complex and delocalized many-body states, and are broad enough to also be well resolved at recently developed soft X-ray RIXS spectrometers that achieve ~100 meV resolution [46–49]. Our earlier EUV studies have shown that orbital excitations inside the insulating gap of CoO and NiO have significantly sharper line shapes that are sensitive to thermal fluctuations [7], with a δE ~ 70 meV leading edge contour identified at low temperature for the 1 eV excitation in CoO. Resolving these widths and the larger feature widths in the SrCuO₂ spectrum illustrates the femtosecond time scale on which local multiplet excitations can persist and interact meaningfully with the surrounding many-body environment. Several upcoming soft X-ray spectrometers are anticipated to reveal momentum dispersion in the critically important “thermal1” resolution regime (δE ~ k_B T near or below room temperature) [50–55], and superior energy resolution can also now be achieved with with hard X-rays [56, 57] for certain specific cases such as the iridium L-edge.

5. Shake-up RIXS and Shallow Core Holes

5.1. Classes of Shake-up Excitation, and their Influence on RIXS Excitation Line Shapes

The existence of a core hole can dramatically change valence orbital energies and cause the entire atomic wavefunction of a resonance site to contract, resulting in so-called “shake-up” excitations observed in RIXS. Shake-up excitations include double magnons (see Discussion in Bisogni et al. [28]) and charge transfer excitations at the M- and L- edges (see Figure 4 below), and can have a distinctive pattern of incident energy dependence in RIXS spectra [8]. These excitations have a fractional contribution to scattering intensity in the RIXS spectrum that scales roughly as I ~ K² / Γ² when core hole lifetime is short (|K / Γ| ≪ 1) due to destructive interference in the numerator of the Kramers-Heisenberg scattering equation (see discussion of “indirect” RIXS in Ament et al. [4]). Here, K is a factor determined by the kinetics through which the resonance states evolve to create a particular excitation, and Γ is the intermediate state lifetime.

When low energy shake-up modes such as phonons are coupled to with high probability, they can cause RIXS features to shift in energy, and to adopt new line shapes that are non-trivially convoluted with the shake-up excitation profile. Multi-phonon shake-up has been associated with incident energy dependent shifts of <10 meV [7], ~50 meV [23] and >0.1 eV [22] in excitation energies at the M-, L-, and K-edges of 3d transition metals, respectively, showing that EUV resonant scattering at the M-edge has a particularly mild shake-up effect, and may give the most accurate representation of intrinsic excitation energies and line shapes.

Hartree-Fock calculations can qualitatively explain the degree of shake-up occurring at each edge, as they predict that the radial wavefunction of d-electrons in NiO will contract by (M) 0.6%, (L) 6%, and (K) 11% when core holes of these symmetries are present. The reason the EUV M-edge has the least contraction is that the radial part of the core orbital wavefunction for shallow core holes is quite similar to the radial wavefunction of valence electrons, meaning that the total radial charge density distribution surrounding the scattering site is not greatly disrupted in resonance states. A weak core hole potential has also been proposed in Chiuzbaian et al. [16] to explain the lack of charge transfer excitations in M-edge RIXS on CoO.

Single magnon excitations are also technically shake-up excitations with a kinetic parameter “K” set by the strength of core hole spin orbit coupling. In the soft X-ray RIXS, single magnon excitations are usually not created in the |K / Γ| ≪ 1 regime, so it is not necessary to consider their shake-up nature. In the EUV however, core hole spin orbit coupling tends to be weak, creating a close link between the intensity of single magnon excitations and core hole lifetime.

5.2. Looking for Charge Transfer Excitations Outside the AM Window

To evaluate the degree to which charge transfer shake-up excitations are reduced in EUV RIXS, we examine M-edge scattering data on the model Mott insulators NiO and CoO. Previous experimental studies performed with soft X-rays at the transition metal L-edge (700–900 eV) have noted that charge transfer features from these materials have significant intensity at 4–7 eV energy loss [14, 16–18]. M-edge studies have noted that charge transfer excitations are weak, but stopped short of presenting data that covered the Mott gap feature [15, 16]. Broad-range M-edge RIXS resonance profiles of CoO and NiO are shown in Figure 3, including energies above the insulating gap. All features visible below the insulating band gap energy can be accounted for from AM models (Figure 3B) that do not allow charge transfer, indicating that the materials are qualitatively well described with only a strongly correlated d-orbital basis.

FIGURE 3

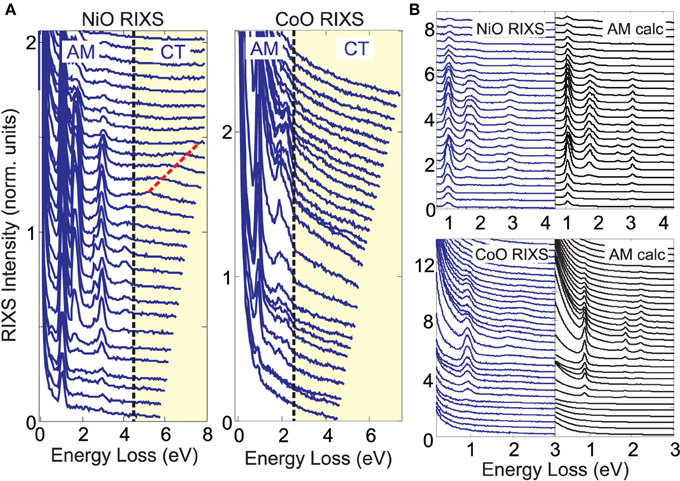
Figure 3. Non-local excited states vanish. (A) (left) NiO RIXS curves measured with hν = 62.5–76 eV photons and (right) CoO curves measured at hν = 56.5–69.5 eV (0.5 eV step) are shown on an expanded scale that emphasizes the yellow-shaded high energy loss region. The band gap is indicated with a dashed line. (B) RIXS data beneath the charge transfer gap have good correspondence with a single-atom atomic multiplet (AM) model (hν is (NiO) 63–75.5 and (CoO) 55–70 eV). Intensity units are defined so that peak features have identical height in (A,B). The relative scattering intensity from NiO vs. CoO cannot be directly compared due to uncontrolled experimental factors (e.g., beam slit widths).

Focusing on energies above the insulating gap (dashed line in Figure 3A) shows that there is remarkably little intensity that could be attributed to charge transfer excitations and other high energy shake-up features. (data at even higher energy loss can be found in Figure 6) A feature that disperses linearly with incident energy, with a slope of ~1, is indicated with a dashed red line on the NiO profile, and has intensity of I_CT ~ 0.02. Intensity fluctuations in the CoO profile also achieve an amplitude of ~0.02, but cannot be definitively identified as RIXS features because of worse signal to noise and due to a large background slope from the elastic line. The 1 eV t_2g to e_g multiplet excitation achieves a peak intensity more than 50 times larger than features above the insulating gap (I_{~1 eV} > 1 ≳ 50I_CT) for both materials.

A very rough upper limit to the spectral intensity of charge transfer features relative to AM RIXS features can be obtained from these data, if we make several assumptions about how charge transfer features manifest in the data. First, we assume that the incident energy dependence of M-edge charge transfer features is not very different from that of the 1 eV feature. Single impurity Anderson model calculations for the M-edge support this assumption. Second, we focus only on the region within 4 eV of the band gap, as this is where most charge transfer intensity is found at the L-edge, with the exception of the high energy emission line. The emission line is far weaker at the M-edge than at the L-edge, and only low energy parts of the emission line are associated with simple metal-ligand charge transfer in recent models [17, 18]. Finally, we assume that the peak intensity of charge transfer excitations is 50% greater than the average intensity of the 4 eV region and, based on the data quality in Figure 3, that a feature with peak intensity greater than 0.01 in several consecutive RIXS curves would be recognizable in the data.

The greatest total charge transfer intensity that could be hidden in the spectra under these assumption is 7 ± 1% and 20 ± 5% of the total intensity of visible inelastic AM RIXS features for NiO and CoO, respectively. Error bars are much larger for CoO, due to inaccuracy in subtracting the elastic tail. Additionally, the dispersive feature observed above the band gap in NiO (Figure 3A) has an integrated intensity that is 3% of the AM features, giving a an estimated range of 3–10% for the fraction of total scattering intensity that can be attributed to charge transfer features in the 3–8 eV energy loss range for NiO. The underlying reasons for decreased charge transfer intensity at the M-edge relative to the L-edge requires some nuance to parse. Figure 4 below will address this question with respect to specific modeling parameters.

FIGURE 4

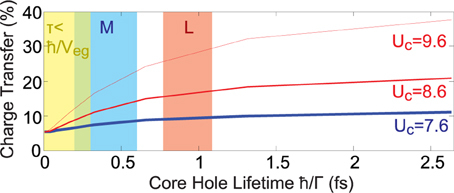
Figure 4. Core shake-up and charge transfer. The intensity of core hole shake-up excitations is simulated as a percentage of total RIXS intensity from 0 to 8 eV energy loss, using the SIAM model. Each plotted point is derived from a calculation in which all intermediate state lifetimes are set to the value indicated on the horizontal axis. The thick blue curve represents a parameter set thought to accurately describe the M-edge of NiO, and red curves use larger core hole potentials.

5.3. Time and Energy Considerations Governing Charge Transfer

Charge transfer can be considered in numerics by augmenting AM calculations with the single Anderson impurity model (SIAM) [58]. We have chosen to implement this model only for NiO in this paper, owing to the detailed study of NiO modeling parameters in Matsubara et al. [17] and other analysis justifying the approach [18]. Modeling parameters follow Matsubara et al. [17], and are described in the Appendix. The SIAM model is well suited to NiO due to factors such as a large semi-classical local spin moment, and a large band gap which is likely to have cleaner charge transfer character than the CoO band gap. By construction in the model, a hole localized next to the scattering site is described by a phase coherent superposition of delocalized states, and the speed at which holes delocalize away from the scattering site in the absence of any binding potential is given by the inverse of the bandwidth factor W. The model does not attempt to define the detailed symmetries and dynamics through which holes delocalize beyond these qualitative parameters, and is not meant to be quantitatively compared with the insulating band gap or the actual distribution of oxygen orbital DOS in band structure.

The intensity of charge transfer excitations in the 0–8 eV energy range as a function of core hole lifetime and the core hole potential is modeled in Figure 4. When core hole lifetime approaches zero, charge transfer excitations shrink to a direct RIXS component that is 5% of the total spectral intensity. The I ~ K² / Γ² time scale that characterizes the onset of shake-up RIXS scattering is very short. A positive second derivative is only found for core hole lifetime values τ < 100as that are much smaller than any of the M- or L-edge intermediate state lifetimes calculated for NiO. Intensity of charge transfer modes grows quickly as core hole lifetime increases from 0as to 300as, corresponding to the inverse metal-ligand hopping parameter ħ/V_eg = 300as. Describing the monopole part of the Coulomb potential with a core hole term U_C estimated previously [17] for the M-edge of NiO and d-orbital Hubbard parameter U_d gives a weak shake-up potential of about U_C − U_d = 0.4 eV, resulting in M-edge predictions that have only ~50% more charge transfer intensity than the τ = 0 direct RIXS value. The weak manifestation of charge transfer excitations at the M-edge relative to the L-edge can be understood because the effective core hole U_C perturbation at the L-edge is larger (8.0 eV in Matsubara et al. [17]), and core hole lifetimes are longer than at the M-edge by a factor of ≳ 2.

Comparing Figure 4 with the experimental upper bound of ~10% on charge transfer intensity in the 4–8 eV region suggests that the core hole potential U_C must be less than 1 eV larger than the Hubbard parameter U_d. Regardless of how precisely accurate this estimate may be, it is interesting to note that in the indicated parameter range, the calculated contribution of shake-up RIXS mechanisms to the charge transfer excitation spectrum is weaker than the non-shake-up RIXS contribution. This is counterintuitive, and is not expected to be the case with soft X-rays at the L-edge. If it proves to be true, then experiments with better signal to noise may in the future use EUV RIXS to obtain spectroscopic information about charge transfer excitations that is not influenced by the incident energy dependence and core hole lifetime dependence that complicate shake-up RIXS spectra.

6. Incident Energy Dependence of Core Hole Lifetime

At present, RIXS spectra are most commonly modeled with the Kramers–Heisenberg equation (see Appendix), which uses second order perturbation theory to limit explicit reference of time dynamics to a reduced set of inverse lifetime parameters (Γ_m). In these treatments, the lifetimes of core hole states are often empirically estimated and assumed to share a single value (Γ_m → Γ). This fixed-lifetime approach produces very good results for most XAS calculations, and only coarse corrections are needed to optimize correspondence with experimental spectra [59–61]. However, the justification for applying the fixed-lifetime approximation to RIXS spectra is far weaker, and theoretical intuition from XAS does not always carry over nicely to RIXS. For example, the sum rule equating RIXS intensity (summed over energy loss and momentum) to the XAS spectrum is broken when core hole lifetimes are incorrect. At resonances in the EUV, a particularly broad range of core hole lifetimes can be observed, and core hole lifetime can vary significantly as a function of incident energy at a given resonance edge [6, 31–33].

Error from the fixed-lifetime approximation is amplified in RIXS spectra relative to other spectroscopies, due to the role lifetime plays in normalizing intensity in the Kramers-Heisenberg equation, and in mediating quantum interference throughout the RIXS spectrum. The qualitative nature of this problem for EUV RIXS studies can be seen by comparing data and theory for the Mott insulator NiO, studied at the nickel M-edge (Figure 5). The features simulated in Figure 5A (middle, right) are excitations of a single Ni²⁺ atom acted on by an octahedral crystal field and weak magnetic exchange field. In the fixed-lifetime calculation (middle panel), resonant intensity at incident energies near 70 eV is more than 5 times too intense relative to experimental data. Relative feature intensities along the energy loss axis also have error in the ballpark of ~50%, when viewed at a single incident photon energy [6].

FIGURE 5

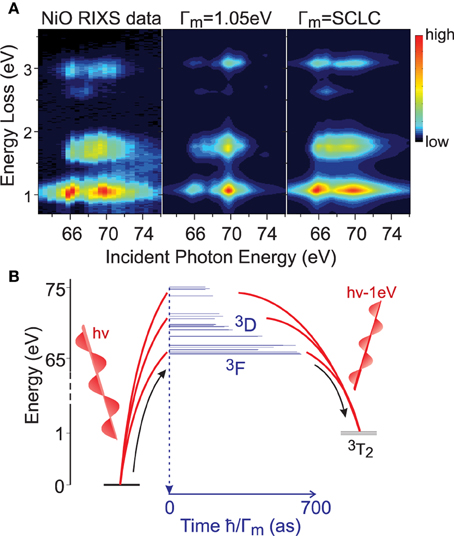
Figure 5. A fingerprint of scattering dynamics. (A) (left) The incident energy dependence of NiO RIXS scattering is compared with (middle) a fixed-lifetime simulation and (right) a self consistent lifetime correction (SCLC) method [6]. (B) A diagram shows resonance pathways by which an incident photon beam can create a 1 eV t_2g to e_g orbital excitation in NiO (³T₂ symmetry excitation). The width of blue bars represents the calculated lifetimes of transiently occupied intermediate states. Intermediate states with significant³F angular momentum symmetry are clustered roughly 3–4 eV below states derived from³D symmetry.

Much better correspondence with data is achieved when the differing decay rates for different resonance states are taken into account [see Figure 5A right), in modeling methods that employ a self consistent lifetime correction (SCLC) for the dependence of core hole decay rate on the multiplet symmetry (see [6, 31, 32] and Appendix). Figure 5B illustrates the scattering channels that underlie M-edge scattering in nickel oxide. Due to uncertainty principle between time and energy, the sub-femtosecond time scale of the scattering process allows intermediate states with energies distributed over several electron volts to be simultaneously occupied. Scattering intensity thus depends greatly on the constructive or destructive interference that results from the system simultaneously evolving through multiple scattering paths. The accuracy of numerical simulations in turn depends on the accuracy with which resonance state time evolution is understood.

The study in Gupta et al. [33] has shown that the rate of autoionization (e.g., charge transfer shake-up) rather than true core hole decay can be the limiting factor on the apparent core hole lifetime that broadens atomic multiplet RIXS excitations along the incident energy axis. In these processes, higher energy resonance modes of EUV RIXS evolve rapidly into autoionized states that can no longer decay into low energy RIXS excitations, resulting in a RIXS spectrum that is dominated by high energy excitations (e.g., 5–15 eV). The rapid creation of high energy excitations is made possible when core hole resonance states are distributed over a ≳ 10 eV incident energy range, so that transitions between different core hole states can free up sufficient energy. This effect has been known of for a long time at the transition metal L-edge [59], and is a prominent factor in numerics for mid-transition metals (e.g., the Mn M-edge) and for N- and O- edges of many f-electron systems.

However, as discussed in Section 5, we have not observed evidence for the same physics in EUV RIXS on late transition metals (d7–d9 valence). The lack of high energy inelastic features that might represent final states of autoionization can be seen over a broader energy range in Figure 6, confirming that intrinsic core hole decay matrix elements are responsible for the distribution of resonance state lifetimes. The principle resonance states accessed at the M-edges of Cu, Ni, and Co for d7 to d9 electronic occupation are spread out over just ~5eV for each material, and may not provide enough energy in core-core transitions for autoionization to be a significant factor.

FIGURE 6

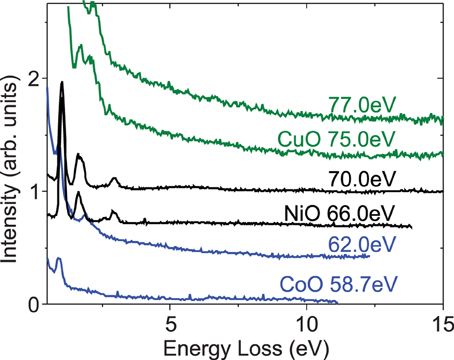
Figure 6. No features at large energy loss. RIXS spectra are extended to large energy loss at incident energies that correspond roughly to the two principle inelastic resonance maxima for CuO, NiO, and CoO. Small fluctuations near the statistical noise threshold at large energy loss (E ≳ 5 eV) should not be analyzed quantitatively, as they tend to come from multiple reflection of the elastic line off of the analyzer vacuum sheath.

7. Summary

In summary, data from the MERLIN beamline are used to explore the properties of resonant inelastic scattering in the extreme ultraviolet photon energy range, with specific examples and numerical simulations presented for the Cu, Ni, and Co M-edges. These data are used to discuss a wide range of topics, including the origin and significance of the strong elastic line found in EUV RIXS, the scientific significance of superior energy resolution obtained in the EUV, and the matrix elements for RIXS scattering in the EUV. The origin of incident energy dependence in core hole lifetime for RIXS involving shallow core holes is discussed with respect to simulations and data that cover an unprecedented energy loss window for the materials studied. The tunability of core hole lifetime is a useful phenomenon for distinguishing between shake-up and non shake-up RIXS features, and for spectroscopic approaches that make use of the core hole as an approximate clock of ultrafast phenomena [30].

An accurate understanding of resonant scattering in the EUV is of increasing importance with the recent advances of short wavelength optics [39, 62, 63] and the availability of ultrashort UV and X-ray pulses [64]. As the state of the art in flux and energy resolution at RIXS beamlines continues to improve, we expect that line shape effects recently identified via EUV RIXS (e.g., on the incident energy axis) will also be measured in the soft X-ray regime and charted as a function of momentum. The dependence of core hole decay rate on multiplet symmetries that vary within a given resonance edge (discussed in Section 6) will be smaller in the soft X-ray regime, but may also be identified within transition metal L-edges as high flux facilitates the study of incident energy dependence.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The Advanced Light Source is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. The Cu K-edge RIXS experiments at SPring-8 were performed at BL11XU with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (Proposal No. 2007A3502 and 2007B3502).

References

1. Tsutsui K, Tohyama T, Maekawa S. Resonant inelastic x-ray scattering in one-dimensional copper oxides. Phys Rev B (2000) 61:7180. doi: 10.1103/PhysRevB.61.7180

CrossRef Full Text | Google Scholar

2. Ishii K, Tsutsui K, Endoh Y, Tohyama T, Maekawa S, Hoesch M, et al. Momentum dependence of charge excitations in the electron-doped superconductor Nd_1.85Ce_0.15CuO₄: a resonant inelastic X-ray scattering study. Phys Rev Lett. (2005) 94:207003. doi: 10.1103/PhysRevLett.94.207003

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Ament LJP, Forte F, van den Brink J. Ultrashort lifetime expansion for indirect resonant inelastic x-ray scattering. Phys Rev B (2007) 75:115118. doi: 10.1103/PhysRevB.75.115118

CrossRef Full Text | Google Scholar

4. Ament LJP, van Veenendaal M, Devereaux, TP, Hill JP, van den Brink J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev Mod Phys. (2011) 83:705. doi: 10.1103/RevModPhys.83.705

CrossRef Full Text | Google Scholar

5. Jia CJ, Chen C-C, Sorini AP, Moritz B, Devereaux TP. Uncovering selective excitations using the resonant profile of indirect inelastic x-ray scattering in correlated materials: observing two-magnon scattering and relation to the dynamical structure factor. New J Phys. (2012) 14:113038. doi: 10.1088/1367-2630/14/11/113038

CrossRef Full Text | Google Scholar

6. Wray LA, Yang W, Eisaki H, Hussain Z, Chuang Y-D. Multiplet resonance lifetimes in resonant inelastic x-ray scattering involving shallow core levels. Phys Rev B (2012) 86:195130. doi: 10.1103/PhysRevB.86.195130

CrossRef Full Text | Google Scholar

7. Wray LA, Li J, Qiu ZQ, Wen J, Xu Z, Gu G, et al. Measurement of the spectral line shapes for orbital excitations in the Mott insulator CoO using high-resolution resonant inelastic X-ray scattering. Phys Rev B (2013) 88:035105. doi: 10.1103/PhysRevB.88.035105

CrossRef Full Text | Google Scholar

8. Wray LA, Huang S-W, Xia Y, Hasan MZ, Mathy C, Eisaki H, et al. Experimental signatures of phase interference and subfemtosecond time dynamics on the incident energy axis of resonant inelastic x-ray scattering. Phys Rev B (2015) 91:035131. doi: 10.1103/PhysRevB.91.035131

CrossRef Full Text | Google Scholar

9. Wray LA, Jarrige I, Ikeuchi K, Ishii K, Shvyd'ko Y, Xia Y, et al. Disentangling a quantum antiferromagnet with resonant inelastic X-ray scattering. (2012) Available online at: http://arxiv.org/abs/1203.2397

10. Hasan MZ, Isaacs ED, Shen Z-X, Miller LL, Tsutsui K, Tohyama T, et al. Electronic structure of Mott insulators studied by inelastic X-ray scattering. Science (2000) 288:1811. doi: 10.1126/science.288.5472.1811

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hasan MZ, Montano PA, Isaacs ED, Shen Z-X, Eisaki H, Sinha SK, et al. Momentum-resolved charge excitations in a prototype one-dimensional Mott insulator. Phys Rev Lett. (2002) 88:177403. doi: 10.1103/PhysRevLett.88.177403

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Kim YJ, Hill JP, Komiya S, Ando Y, Casa D, Gog T, et al. Doping dependence of charge-transfer excitations in La_2-xSr_xCuO₄. Phys Rev B (2004) 70:094524. doi: 10.1103/PhysRevB.70.094524

CrossRef Full Text | Google Scholar

13. Kim Y-J, Hill JP, Benthien H, Essler FHL, Jeckelmann E, Choi HS, et al. Resonant inelastic X-ray scattering of the holon-antiholon continuum in SrCuO₂. Phys Rev Lett. (2004) 92:137402. doi: 10.1103/PhysRevLett.92.137402

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ghiringhelli G, Matsubara M, Dallera C, Fracassi F, Gusmeroli R, Piazzalunga A, et al. NiO as a test case for high resolution resonant inelastic soft X-ray scattering. J Phys Condens Matter (2005) 17:5397. doi: 10.1088/0953-8984/17/35/007

CrossRef Full Text | Google Scholar

15. Chiuzbăian SG, Ghiringhelli G, Dallera C, Grioni M, Amann P, Wang X, et al. Localized electronic excitations in NiO studied with resonant inelastic X-ray scattering at the Ni M threshold: evidence of spin flip. Phys Rev Lett. (2005) 95:197402. doi: 10.1103/PhysRevLett.95.197402

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chiuzbaian SG, Schmitt T, Matsubara M, Kotani A, Ghiringhelli G, Dallera C, et al. Combining M- and L-edge resonant inelastic x-ray scattering for studies of 3d transition metal compounds. Phys Rev B (2008) 78:245102. doi: 10.1103/PhysRevB.78.245102

CrossRef Full Text | Google Scholar

17. Matsubara M, Uozumi T, Kotani A, Parlebas JC. Charge transfer excitation in resonant X-ray emission spectroscopy of NiO. J Phys Soc Japan (2005) 74:2052. doi: 10.1143/JPSJ.74.2052

CrossRef Full Text | Google Scholar

18. Magnuson M, Butorin SM, Agui A, Nordgren J. Resonant soft x-ray Raman scattering of NiO. J Phys Condens Matter (2002) 14:3669. doi: 10.1088/0953-8984/14/13/324

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Li YW, Qian D, Wray L, Hsieh D, Xia Y, Kaga Y, et al. X-ray imaging of dispersive charge modes in a doped Mott insulator near the antiferromagnet/superconductor transition. Phys Rev B (2008) 78:073104. doi: 10.1103/PhysRevB.78.073104

CrossRef Full Text | Google Scholar

20. Wohlfeld K, Daghofer M, Nishimoto S, Khaliullin G, van den Brink J. Intrinsic coupling of orbital excitations to spin fluctuations in Mott insulators. Phys Rev Lett. (2011) 107:147201. doi: 10.1103/PhysRevLett.107.147201

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Schlappa J, Wohlfeld K, Zhou KJ, Mourigal M, Haverkort MW, Strocov VN, et al. Spin-orbital separation in the quasi-one-dimensional Mott insulator Sr₂CuO₃. Nature (2012) 485:82. doi: 10.1038/nature10974

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hancock JN, Chabot-Couture G, Greven M. Lattice coupling and Franck-Condon effects in K-edge resonant inelastic X-ray scattering. New J Phys. (2010) 12:033001. doi: 10.1088/1367-2630/12/3/033001

CrossRef Full Text | Google Scholar

23. Lee JJ, Moritz B, Lee WS, Yi M, Jia CJ, Sorini AP, et al. Charge-orbital-lattice coupling effects in the dd-excitation profile of one dimensional cuprates. Phys Rev B (2014) 89:041104(R). doi: 10.1103/PhysRevB.89.041104

CrossRef Full Text | Google Scholar

24. Braicovich L, van den Brink J, Bisogni V, Sala MM, Ament LJP, Brookes NB, et al. Magnetic excitations and phase separation in the underdoped La_2-xSr_xCuO₄ superconductor measured by resonant inelastic X-ray scattering. Phys Rev Lett. (2010) 104:077002. doi: 10.1103/PhysRevLett.104.077002

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Le Tacon M, Ghiringhelli G, Chaloupka J, Sala MM, Hinkov V, Haverkort MW, et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat Phys. (2011) 7:725. doi: 10.1038/nphys2041

CrossRef Full Text | Google Scholar

26. Dean MPM, Springell RS, Monney C, Zhou KJ, Pereiro J, Božović I, et al. Spin excitations in a single La₂CuO₄ layer. Nat Mater. (2012) 11:850. doi: 10.1038/nmat3409

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Dean MPM, Dellea G, Springell RS, Yakhou-Harris F, Kummer K, Brookes NB, et al. Persistence of magnetic excitations in La_2-xSr_xCuO₄ from the undoped insulator to the heavily overdoped non-superconducting metal. Nat Mater. (2013) 12:1019. doi: 10.1038/nmat3723

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Bisogni V, Kourtis S, Monney C, Zhou K, Kraus R, Sekar C, et al. Femtosecond dynamics of magnetic excitations from resonant inelastic x-ray scattering in CaCu₂O₃. Phys Rev Lett. (2014) 112:147401. doi: 10.1103/PhysRevLett.112.147401

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Benjamin D, Abanin D, Abbamonte P, Demler E. Microscopic theory of resonant soft-X-ray scattering in materials with charge order: the example of charge stripes in high-temperature cuprate superconductors. Phys Rev Lett. (2013) 110:137002. doi: 10.1103/PhysRevLett.110.137002

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Braicovich L, Ghiringhelli G, Tagliaferri A, van der Laan G, Annese E, Brookes NB. Femtosecond dynamics in ferromagnetic metals investigated with soft X-ray resonant emission. Phys Rev Lett. (2005) 95:267402. doi: 10.1103/PhysRevLett.95.267402

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Okada K, Kotani A, Ogasawara H, Seino Y, Thole BT. Auger decay of quasiparticle states: calculation of the Ni 3p photoemission spectrum in NiCl₂. Phys Rev B (1993) 47:6203.

PubMed Abstract | Google Scholar

32. Ogasawara H, Kotani A, Thole, BT. Lifetime effect on the multiplet structure of 4d x-ray-photoemission spectra in heavy rare-earth elements. Phys Rev B (1994) 50:12332. doi: 10.1103/PhysRevB.50.12332

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Gupta SS, Bradley JA, Haverkort MW, Seidler GT, Tanaka A, Sawatzky GA. Coexistence of bound and virtual-bound states in shallow-core to valence x-ray spectroscopies. Phys Rev B (2011) 84:075134. doi: 10.1103/PhysRevB.84.075134

CrossRef Full Text | Google Scholar

34. van Veenendaal MA, Eskes H, Sawatzky GA. Strong nonlocal contributions to Cu 2p photoelectron spectroscopy. Phys Rev B (1993) 47:11462. doi: 10.1103/PhysRevB.47.11462

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Ament LJP, van Veenendaal M, van den Brink J. Determining the electron-phonon coupling strength from resonant inelastic X-ray scattering at transition metal L-edges. Europhys Lett. (2011) 95:27008. doi: 10.1209/0295-5075/95/27008

CrossRef Full Text | Google Scholar

36. Knupfer M, Neudert R, Kielwein M, Haffner S, Golden MS, Fink J, et al. Site-specific unoccupied electronic structure of one-dimensional SrCuO₂. Phys Rev B (1997) 55:R7291. doi: 10.1103/PhysRevB.55.R7291

CrossRef Full Text | Google Scholar

37. Kim BJ, Koh H, Rotenberg E, Oh S-J, Eisaki H, Motoyama N, et al. Distinct spinon and holon dispersions in photoemission spectral functions from one-dimensional SrCuO₂. Nat Phys. (2006) 2:397. doi: 10.1038/nphys316

CrossRef Full Text | Google Scholar

38. van der Zaag PJ, Feiner LF, Wolf RM, Borchers JA, Ijiri Y, Erwin RW. The blocking and Néel temperature in exchange-biased Fe₃O₄/CoO multilayers. Phys B Condens Matter (2000) 276:638. doi: 10.1016/S0921-4526(99)01392-7

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Chuang Y-D, Pepper J, McKinney W, Hussain Z, Gullikson E, Batson P, et al. High-resolution soft X-ray emission spectrograph at advanced light source. J Phys Chem Solid (2005) 66:2173. doi: 10.1016/j.jpcs.2005.09.051

CrossRef Full Text | Google Scholar

40. Chuang Y-D, Wray LA, Denlinger J, Hussain, Z. Resonant inelastic X-ray scattering spectroscopy at MERLIN beamline at the advanced light source. Synchrotron Radiat News (2012) 25:23. doi: 10.1080/08940886.2012.700844

CrossRef Full Text | Google Scholar

41. Grübel G, Zontone F. Correlation spectroscopy with coherent X-rays. J Alloys Comp. (2004) 362:3. doi: 10.1016/S0925-8388(03)00555-3

CrossRef Full Text | Google Scholar

42. Henke BL, Gullikson EM, Davis JC. X-ray interactions: photoabsorption, scattering, transmission, and reflection at E=50-30000 eV, Z=1-92. Atomic Data Nucl Data Tables (1993) 54:181–342. doi: 10.1006/adnd.1993.1013

CrossRef Full Text | Google Scholar

43. It is worth noting that due to the large deviation of index of refraction from 1 in the optical regime, Lambert's law involves multiple reflection scattering channels that may not be relevant in the EUV. (see K. E. Torrance and E. M. Sparrow, J. Opt. Soc. Am. 57:1105 (1967))

44. Popović ZV, Ivanov VA, Konstantinović MJ, Cantarero A, Martínez-Pastor J, Olguín D, et al. Optical studies of gap, hopping energies, and the Anderson-Hubbard parameter in the zigzag-chain compound SrCuO₂. Phys Rev B (2001) 63:165105. doi: 10.1103/PhysRevB.63.165105

CrossRef Full Text | Google Scholar

45. Huotari S, Simonelli L, Sahle CJ, Sala MM, Verbeni R, Monaco G. Temperature dependence of crystal field excitations in CuO. J Phys Condens Matter (2014) 26:165501. doi: 10.1088/0953-8984/26/16/165501

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ghiringhelli G, Piazzalunga A, Dallera C, Trezzi G, Braicovich L, Schmitt T, et al. SAXES, a high resolution spectrometer for resonant x-ray emission in the 400-1600eV energy range. Rev Sci Instrum. (2006) 77:113108. doi: 10.1063/1.2372731

CrossRef Full Text | Google Scholar

47. Strocov VN, Schmitt T, Flechsig U, Schmidt T, Imhof A, Chen Q, et al. High-resolution soft X-ray beamline ADRESS at the Swiss Light Source for resonant inelastic X-ray scattering and angle-resolved photoelectron spectroscopies. J Synchrotron Radiat. (2010) 17:631. doi: 10.1107/S0909049510019862

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Chiuzbăian SG, Hague CF, Avila A, Delaunay R, Jaouen N, and Sacchi M, et al. Design and performance of AERHA, a high acceptance high resolution soft x-ray spectrometer. Rev Sci Instrum. (2014) 85:043108. doi: 10.1063/1.4871362

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Harada Y, Kobayashi M, Niwa H, Senba Y, Ohashi H, Tokushima T, et al. Ultrahigh resolution soft x-ray emission spectrometer at BL07LSU in SPring-8. Rev Sci Instrum. (2012) 83:013116. doi: 10.1063/1.3680559

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Warwick T, Chuang Y-D, Voronov DL, Padmore HA. A multiplexed high-resolution imaging spectrometer for resonant inelastic soft X-ray scattering spectroscopy. J Synchrotron Radiat. (2014) 21:736. doi: 10.1107/S1600577514009692

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Information on the upcoming NSLS-II SIX beamline and CENTURION spectrometer can be found at “http://www.bnl.gov/ps/nsls2/beamlines/files/pdf/02ID-SIX.pdf”

52. Information on the upcoming DLS I21 RIXS beamline can be found at “http://www.diamond.ac.uk/Beamlines/Spectroscopy/I21.html”

53. Braicovich L, Minola M, Dellea G, Le Tacon M, Sala MM, Morawe C, et al. The simultaneous measurement of energy and linear polarization of the scattered radiation in resonant inelastic soft x-ray scattering. Rev Sci Instrum. (2014) 85:115104. doi: 10.1063/1.4900959

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Lai CH, Fung HS, Wu WB, Huang HY, Fu HW, Lin SW, et al. Highly efficient beamline and spectrometer for inelastic soft X-ray scattering at high resolution. J Synchrotron Radiat. (2014) 21:325. doi: 10.1107/S1600577513030877

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Information on the upcoming MAX IV SPECIES beamline RIXS spectrometer can be found at “https://www.maxiv.se/node/1505”

56. Shvyd'ko YV, Hill JP, Burns CA, Coburn DS, Brajuskovic B, Casa D, et al. MERIX - Next generation medium energy resolution inelastic X-ray scattering instrument at the APS. J Electron Spectrosc Relat Phenom. (2013) 188:140.

Google Scholar

57. Information on PETRA III P01 RIXS capabilities can be found at “http://photon-science.desy.de/facilities/petra_iii/beamlines/p01_dynamics/inelastic_x_ray_scattering_station/rixs_spectrometer/index_eng.html”

58. Anderson PW. Localized magnetic states in metals. Phys Rev. (1961) 124:41. doi: 10.1103/PhysRev.124.41

CrossRef Full Text | Google Scholar

59. Zaanen J, Sawatzky GA. Strong interference between decay channels and valence-electron rearrangements in core-hole spectroscopy. Phys Rev B (1986) 33:8074. doi: 10.1103/PhysRevB.33.8074

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Braicovich L, Taguchi M, Borgatti F, Ghiringhelli G, Tagliaferri A, Brookes NB, et al. Resonant Raman scattering at the L thresholds with final 3s hole in 3d²⁺ systems. II. The CoO case in the whole L_2,3 region. Phys Rev B (2001) 63:245115. doi: 10.1103/PhysRevB.63.245115

CrossRef Full Text | Google Scholar

61. Taguchi M, Braicovich L, Borgatti F, Ghiringhelli G, Tagliaferri A, Brookes NB, et al. Resonant Raman scattering at the L thresholds with final 3s hole in 3d²⁺ systems. I. Configuration interaction with two 3p hole final states in different systems. Phys Rev B (2001) 63:245114. doi: 10.1103/PhysRevB.63.245114

CrossRef Full Text | Google Scholar

62. Osugi M, Tanaka K, Sakaya N, Hamamoto K, Watanabe T, Kinoshita H. Resolution enhancement of extreme ultraviolet microscope using an extreme ultraviolet beam splitter. Jpn J Appl Phys. (2008) 47:4872. doi: 10.1143/JJAP.47.4872

CrossRef Full Text | Google Scholar

63. Gautier J, Delmotte F, Roulliay M, Bridou F, Ravet M-F, Jérome A. Study of normal incidence of three-component multilayer mirrors in the range 20-40 nm. Appl Opt. (2005) 44:384. doi: 10.1364/AO.44.000384

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Morlens A-S, López-Martens R, Boyko O, Zeitoun P, Balcou P, Varjú K, et al. Design and characterization of extreme-ultraviolet broadband mirrors for attosecond science. Opt Lett. (2006) 31:1558.

PubMed Abstract | Google Scholar

65. Shen ZX, List RS, Dessau DS, Wells BO, Jepsen O, Arko AJ, et al. Electronic structure of NiO: correlation and band effects. Phys Rev B (1991) 44:3604. doi: 10.1103/PhysRevB.44.3604

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Eder R. Correlated band structure of NiO, CoO, and MnO by variational cluster approximation. Phys Rev B (2008) 78:115111. doi: 10.1103/PhysRevB.78.115111

CrossRef Full Text | Google Scholar

67. Fujimori A, Minami F. Valence-band photoemission and optical absorption in nickel compounds. Phys Rev B (1984) 30:957. doi: 10.1103/PhysRevB.30.957

CrossRef Full Text | Google Scholar

68. Sakurai J, Buyers WJL, Cowley RA, and Dolling G. Crystal dynamics and magnetic excitations in cobaltous oxide. Phys Rev. (1968) 167:510. doi: 10.1103/PhysRev.167.510

CrossRef Full Text | Google Scholar

69. Rechtin MD, Averbach BL. Short-range magnetic order in CoO. Phys Rev B (1972) 5:2693. doi: 10.1103/PhysRevB.5.2693

CrossRef Full Text | Google Scholar

70. Srinivasan G, Seehra MS. Nature of magnetic transitions in MnO, Fe_zO, CoO, and NiO. Phys Rev B (1983) 28:6542. doi: 10.1103/PhysRevB.28.6542

CrossRef Full Text | Google Scholar

71. Sala MM, Bisogni V, Aruta C, Balestrino G, Berger H, Brookes NB, et al. Energy and symmetry of dd excitations in undoped layered cuprates measured by Cu L₃ resonant inelastic x-ray scattering. New J Phys. (2011) 13:043026. doi: 10.1088/1367-2630/13/4/043026

PubMed Abstract | CrossRef Full Text | Google Scholar

Appendix

Computational Details

The AM calculations in this paper closely resemble numerics in Wray et al. [6, 7, 9]. Scattering is evaluated using the Kramers-Heisenberg equation:

$\begin{array}{cc}\begin{array}{l}{R}_f(E,h\nu )\propto {\displaystyle \sum _g{\left|{\displaystyle \sum _m\frac{\langle f|T^{†}|m\rangle \langle m|T|g\rangle }{h\nu -E_m+i{\Gamma }_m/2}}\right|}^2}\\ \times \frac{\frac{1}{2\pi }{\Gamma }_f}{{(E-E_f)}^2+{(\frac{1}{2}{\Gamma }_f)}^2}\end{array}& \left(1\right)\end{array}$

The quantity inside absolute value brackets represents the matrix elements for quantum paths from the ground state |g〉 to a final state |f〉, through short-lived intermediate states indexed by |m〉. Incident photon energy is written as hν, the excitation energy is E, and the inverse final state excitation lifetime is Γ_f. The incident photon operator T couples to the polarization of the incident photon beam, and the outgoing photon operator T^† couples to the resultant polarization of scattered photons. Effects of quantum interference appear in the spectrum when inverse intermediate state lifetimes (Γ_m) are similar to the separation between intermediate state energies (E_m).

The crystal field in AM calculations is described by (CoO) 10Dq = 0.96 and (NiO) 1.03 eV. In the SIAM implementation for NiO, coupling with the ligand band reduces the effective 10Dq value to 0.53 eV. Values of 10Dq are chosen to match the sharp onset lineshape of the ~1 eV t_2g to e_g excitation in experimental spectra, as described in Chiuzbăian et al. [15], Wray et al. [6, 7]. The calculations use atomic values of inter-d-orbital Slater-Condon interaction parameters (F2(dd),F4(dd)) for the SIAM, and scale them to 80% for AM simulations (64% of bare Hartree-Fock parameters). We have found that 3p-3d interactions (G1(pd),G3(pd),F2(pd)) require an unusually large correction at the M-edge, and are estimated at (NiO) 70% and (CoO) 65% of atomic values for the AM calculations, and 80% of nominal atomic values for the SIAM. The 3p spin orbit coupling strength is larger than first principles estimates, likely due to positive 4s-shell valence, and has been set to (CoO) 1.5 eV, (NiO) 1.6 eV, and (SrCuO₂) 1.8 eV.

Core hole lifetimes (Γ_m) are estimated from the dipole valence-to-core transition matrix element via the method described in Wray et al. [6]. Using an empirical dipole decay rate constant that corresponds to a lifetime of Γ ~ 2.5 eV for d¹⁰ electron configurations gives very good correspondence with incident energy line shapes in cuprate, nickelate, and cobaltate compounds [6, 7, 9]. This approach is highly phenomenological, and does not attempt to comprehensively consider how decay occurs via Auger emission, which is numerically complex for shallow, radially-large core holes. Our preliminary calculations show that in the EUV, unconventional Auger channels involving electrons in ligand orbitals can have similar intensity to intraatomic Auger. Moreover, it is easy to show that ~1 Å scale electronic correlations in the ground state wavefunction that are not described by a d-orbital basis also have significant structure on the length scale of Auger electron wavelengths in the EUV, and are very important to consider (though numerically intractable). We hope that these issues will be addressed with theoretical rigor in future studies.

Parameters of the SIAM model mostly follow the treatment in Matsubara et al. [17]. We define a ligand band with W = 3 eV bandwidth, similar to the maximum dispersion observed for an oxygen derived band in recent analysis of NiO [65, 66]. Hopping between e_g orbitals and the nearest neighbor ligand states with corresponding symmetry is V_eg = 2.2 eV (V_t2g = −V_eg/2), and is reduced by 10% when a core hole is present. The core hole monopole potential (Slater Condon F0) is U_C = 7.6 eV, and the d-orbital Hubbard U parameter is U_d = 7.2 eV. The state basis is limited to allow a maximum of 1 ligand hole, as in Magnuson et al. [18], and the flat ligand band density of states distribution is approximated by 10 discrete energies (N = 10). The ground state density of oxygen holes within this model matches the experimentally based estimate of 0.2 [67].

Interatomic spin interactions are considered by incorporating an external exchange field of J* = 0.0126 eV for CoO [68, 69] and a rough estimate of J* = 0.1 eV for NiO. Type 2 phase transitions at (CoO) T_N ~ 290K and (NiO) 524K [70] preserve local spin correlations and do not have a pronounced effect on M-edge RIXS scattering features near room temperature [7]. The quasi-1D spin lattice and large spin interactions of SrCuO₂ result in corrections to the self energy contour of orbitons [20, 21], but do not behave as a static exchange field for most cuprate orbiton symmetries [71]. These self energy corrections are convoluted with Lorentzians representing orbiton lifetime in the Figure 2 fit curves, following the implementation in Wray et al. [9] of the model in Wohlfeld et al. [20].