For whom will the Bayesian agents vote?

Within an agent-based model where moral classifications are socially learned, we ask if a population of agents behaves in a way that may be compared with conservative or liberal positions in the real political spectrum. We assume that agents first experience a formative period, in which they adjust their learning style acting as supervised Bayesian adaptive learners. The formative phase is followed by a period of social influence by reinforcement learning. By comparing data generated by the agents with data from a sample of 15,000 Moral Foundation questionnaires we found the following. (1) The number of information exchanges in the formative phase correlates positively with statistics identifying liberals in the social influence phase. This is consistent with recent evidence that connects the dopamine receptor D4-7R gene, political orientation and early age social clique size. (2) The learning algorithms that result from the formative phase vary in the way they treat novelty and corroborative information with more conservative-like agents treating it more equally than liberal-like agents. This is consistent with the correlation between political affiliation and the Openness personality trait reported in the literature. (3) Under the increase of a model parameter interpreted as an external pressure, the statistics of liberal agents resemble more those of conservative agents, consistent with reports on the consequences of external threats on measures of conservatism. We also show that in the social influence phase liberal-like agents readapt much faster than conservative-like agents when subjected to changes on the relevant set of moral issues. This suggests a verifiable dynamical criterium for attaching liberal or conservative labels to groups.

1. Introduction

A central controversy in moral psychology and sociology deals with understanding the variety of moral values and whether adherence to one set or another have a genetic origin or arise from social interactions. Political affiliation has been associated to social interaction, to genetics and to the combination of both (e.g., 1–5). We address questions about early age socialization, cognitive styles and political orientation within a Moral Foundation theory (MFT) perspective using agent-based modeling and techniques from information theory. The present work is culturally situated within the fields of sociophysics [6–8] and computational social sciences [9–11] and is a companion to our previous work [12–14].

In a series of papers Haidt and coworkers [15–21] have described MFT, an empirically driven theory dealing with the foundations of moral psychology. It aims to understand statistically significant differences in moral valuations of social issues and their association to coordinates of the political spectrum. The core tenet of the theory is that moral issues, which are valued mostly in an intuitive manner, can be parsed into a number of discrete dimensions, at least five, possibly six or even more. According to Kohlberg and Turiel [22], Power et al. [23], and Gilligan [24] dimensions representing care/harm and fairness/cheating should be enough to span the space of moral issues. Shweder et al. [25] argued that the dimensions should be three instead.

The MFT states that dimensions representing loyalty/betrayal, authority/subversion and sanctity/degradation should also be included in the moral space. The care/harm and fairness/cheating dimensions are statistically more important for liberals than the rest, and each dimension of the entire set is of similar importance for conservatives. Culture wars would be a consequence of these differences.

Consideration of other political cultures, such as libertarians leads to yet other dimensions, such as liberty/oppression [26]. Political affiliation is also correlated with some characteristics of the Big Five personality traits. Openness and liberal values appear together frequently while Conscientiousness and conservatism are positively associated (e.g., 27). Further associations between cognitive learning styles and political affiliation have been suggested by EEG experiments [28].

In constructing the Motivated Social-Cognitive perspective Jost et al. [29], Jost and Amodio [30] make the assumption “that conservative ideologies—like virtually all other belief systems—are adopted in part because they satisfy some psychological needs.” We have also followed in our previous work [13, 14] a motivation driven approach with a totally different methodology: studying mathematically the dynamics of agent-based models using information theory. We considered the discomfort associated to disagreement [31] and the motivating pressure was to reduce pain associated to social exclusion. This was implemented by a learning dynamics designed to maximize a utility function or, equivalently, minimize an energy-like function. Haslam [32] correctly argues that not all social figuring is or should be a matter of cost/benefit calculation. In a third person description, within a mathematical language, we calculate, but the social agent does not calculate, it just acts and the dynamics proceeds as if agents were actually maximizing a utility function. Similarly, a rock falls, we calculate its motion, the rock doesn't.

In our previous approach we characterized in a simplified society of agents the effects of different learning styles on the statistics of their opinions about a set of issues. We will call the artificial data set the data obtained by simulation of the agents. The analytical and numerical results were compared to data gathered by the Moral Foundation Questionnaire project of Haidt and collaborators (http://www.yourmorals.org), to which we will refer as the empirical data set. Agents learning with an algorithm that treated new and corroborative information in the same way, exhibited (a) less dispersion of opinions, (b) longer times to readapt under changes of the issues under discussion and (c) histograms of opinions very similar to those of self declared conservatives in the empirical data set. On the other end of the spectrum of cognitive styles, agents that could be thought to score higher in an Openness personality trait, since they gave more importance to new data than to corroborative data, (a) showed greater dispersion of opinions, (b) readapted faster after changes of the issues and (c) were statistically similar to self declared liberals.

Note that we avoided the difficult task of theoretically predefining conservative or liberal. We just took a pragmatic route, comparing the results of our model with empirical data where subjects had declared their belief about their positions in the political spectrum. In other words, a society of agents is classified as conservative or liberal by the proximity of their statistical signatures to those obtained from the Moral Foundation Questionnaires of groups who believe and declared to be of a certain political affiliation.

In this paper we address the following question: why are different cognitive strategies present in the population? Distal causes could be such as the advantages of societies with a higher cohesive set of values due to conservatives and shorter readaptations due to liberals. If we ask for more proximate causes, genetics or heterogeneous social interactions are possible explanations. A discussion by Smith et al. [33] illustrates the long path between genetics and opinions about specific issues, including four intermediate levels: biological, cognitive/information processing, personality/values and ideology with the environment influencing each one.

Fowler and collaborators presented evidence for interactions between genetics and politics. In Dawes and Fowler [34] they link the DRD2 dopamine receptor to partisanship hereditability. More relevant to our present study, is their analysis of data [35] from the National Longitudinal Adolescent Health study indicating that a certain allele (7 repetitions long allele) of the dopamine receptor gene DRD4 may have just that kind of influence. For those having two copies of the allele, the number of friends during early age condition the probability of their self declared political affiliation as an adult. The direction is such that those that had a larger number of friends are associated to a larger probability of being a liberal as an adult.

Here we aim at explaining the diversity in moral valuation within our agent based framework by adopting an information theory point of view, in particular we consider an artificial society composed by interacting Bayesian information processing agents. Each agent has a set of social neighbors and exchanges information in the form of opinions about issues. Learning means that when the information brought by the opinion of a social neighbor arrives, there are certain changes in the weights attributed to each moral dimension.

The main results about the learning process following from this approach are two. First, that the learning algorithm is not static but adaptive. It depends on the number of opinions to which an agent has been exposed in social interactions. Second, that for different numbers of such opinions, the difference of the ensuing learning algorithms can be described by the different modulation given to opinions that carry novelty of information relative to opinions that carry corroborative information. Figure 1-Left shows the modulation function for different number of social interactions. The modulation function is a measure of the overall scale of the changes of the weights for the moral dimensions elicited by a particular issue and opinion of a social partner. Including the possibility of errors in communication, a Bayesian learner with the information that there might be imperfect communication, acts with suspicion and ignores disagreeing opinions on issues about which it has a strong opinion (Figure 1-Right).

FIGURE 1

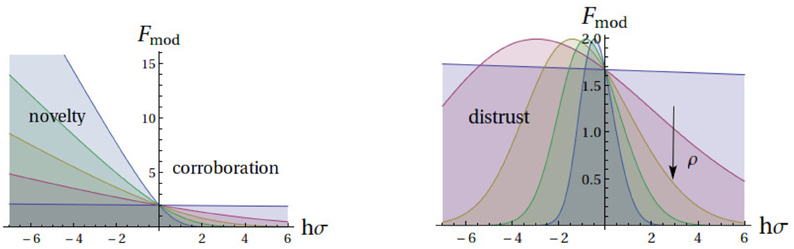
Figure 1. The modulation function depends on a measure of novelty and on the number of social opinion exchanges. Left: Complete confidence on the information received. Right: Agent assumes noisy communication with received opinions randomly inverted with probability of 20%. The vertical axes are modulation functions and horizontal axes represent agent prior opinion (h) times the sign (σ) of an opinion received in an exchange. Social interactions with opinions where hσ < 0 bring new information, those with hσ > 0 are corroborative. The different curves are drawn for several exchange counts measured by ρ which increases as shown by the arrow (↓). The modulation function changes from almost a constant, for very small number of opinion exchanges, to a very asymmetrical form where repetitive information causes almost no change at all and novelty leads to intense modulation as far as hσ is not too negative, when distrust sets in.

The agents of our model are Bayesian during an early window of time we call the formative phase. Each “young” agent is exposed to a random number of social information exchanges. At the end of the formative phase the learning algorithm stops evolving and agents enter the social influence phase. Agents, each with its particular fixed learning algorithm determined by the random socialization in the formative phase, exchange information about a set of issues and continue learning. After a time where a steady state has been achieved, we collect statistical information about the state of the society in the form of histograms of opinions (the artificial data set, ADS). A similar set of statistics can be extracted from the set of questions about moral issues (the empirical data set, EDS) collected by Haidt and collaborators from the Moral Foundation project (http://www.yourmorals.org) as done in Caticha and Vicente [13], Vicente et al. [14]. Numerical comparisons of the statistics permit identifying a class of agents with a group of respondents with a given declared political affiliation. The conclusion is that the number of opinion exchanges in the formative phase is correlated with the political affiliation of the corresponding group of the responders. Agents with large number of opinion exchanges in the formative phase are identified with liberals after the social influence phase, those with a small number are identified with conservatives.

In Section 2 and Appendix we present the mathematical aspects of the theory, first the Bayesian algorithm of learning that evolves during the formative phase, then the description of the social influence phase where agents interact. In Section 3 we present the results and describe the comparison to the data obtained from the Moral Foundation questionnaires. We end this paper with a discussion of the results, the limitations of the theory and possible extensions.

2. Model and Methods

2.1. Adaptive Agents

Each agent is endowed with a learning system and a set of weights. They exchange information, learning and teaching at different instances, about a set of issues, represented each by a set of numbers. Each number represents the bearing of the issue on one of the moral dimensions. The dimension of the moral space, according to MFT is around five or six. The development of the mathematical theory can be done for a general number of dimensions d_m. A choice has to be made in order to compare with data, and since we are only comparing with a set of questionnaires of conservatives and liberals, will use d_m = 5 in the numerical part of the calculations. So, a statement or issue to be morally judged, at a time labeled by μ is represented as a vector in moral space x_μ = (x_1,μ, x_2,μ, x_3,μ, x_4,μ, x_5,μ) with five components. For a particular agent, call it i, the moral state of the agent, called the moral matrix in MFT, is also a vector ω_i = (ω_1,i, ω_2,i, ω_3,i, ω_4,i, ω_5,i).

Moral judgements are taken to be intuitive, fast, not based on intricate rules. We suppose opinions to be constructed by the average of the components of the issue, weighted by the values of the moral dimensions: $h_{i,\mu }={\displaystyle {\sum }_{a=1}^{d_m}{\omega }_{a,i}{x}_{a,\mu }}$ is the opinion of agent i about issue x_μ. Furthermore, we introduce the sign, for or against, of the opinion σ_i,μ = sign(h_i,μ) about the issue.

We model social encounters when agent i receives information y_μ = (σ_j,μ, x_μ) emitted by the social partner j. Since the length of the vector x_μ does not alter the opinions σ, we take all issues to be unit length.

Call D_μ = {y₁, y₂, ….y_μ} the set of all such pairs received until that time. To take into account our limited access to information we have to use a probabilistic framework. Let P(ω|D_μ) describe our knowledge of the vector of moral dimensions ω conditional on the information the agent received until now D_μ, composed of all the pairs up to time μ. Now a new pair y_μ+1 is received and the probability of having a particular moral dimension ω changes. That is the essence of learning. The basic relation of inference is drawn from Bayes theorem. If P(ω|D_μ) is the probability posterior to the consideration of the data set D_μ and prior to the inclusion of the information contained in the pair y_μ+1, the basic assumption in Bayesian learning is to use the old posterior P(ω|D_μ) as the new prior. Then we can write for the updated distribution of the receiving agent

$\begin{array}{cc}P(\omega |D_{\mu +1})\propto P(\omega |D_{\mu })P({\sigma }_{i,\mu +1}={\sigma }_{j,\mu +1}|\omega ,D_{\mu },x_{\mu +1})& (1)\end{array}$

The likelihood P(σ_{iμ + 1} = σ_{j,μ + 1}|ω, D_μ, x_{μ + 1}) describes the probability that agent i would have opinion σ_{iμ + 1} = σ_{j,μ + 1} about issue x_{μ + 1} if its moral vector were ω.

For simplicity we consider an approximation where the probability distributions are multivariate Gaussians. This family can be described by two objects: a mean vector ($\widehat{\omega }$) and a covariance matrix (C). Now the dynamics of learning can be simply written by giving the changes in these two quantities due to the incorporation of the information in the example y_{μ + 1}. After some manipulations (see the Appendix and 36, the learning dynamics of agent i is described in terms of the components by

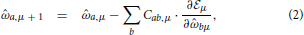
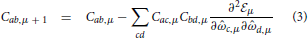
and 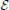_μ, that can be called the learning energy or cost, is given by

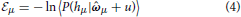
where h_μ = ∑_a$\widehat{\omega }$_a,μx_a,μ+1 is the opinion of the agent about issue x_μ+1 before receiving the opinion of the social partner. The average, represented by the angular brackets, is over the gaussian variable u with zero mean and covariance C_ab,μ. Note that 〈P(h_μ|$\widehat{\omega }$ + u)〉_μ is also called the evidence. It is in the likelihood that enters the information about how an issue and a moral vector give rise to an opinion and the noise process that is corrupting the communication.

Different types of noise can enter in the communication process. Here we suppose the case of multiplicative noise where a fraction ϵ of the opinions are inverted. The form of the learning potential that results from assuming agents that are Bayesian optimal learners can then be written as

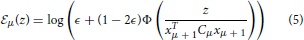
where z = σ_{j,μ + 1}h_i,μ and Φ is the cumulative distribution of the gaussian 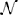(0, 1). To simplify the interpretation of the results, at the expense of small degradation in the performance of the learning algorithm we consider the case where the covariance has the the from C_μ = C_μ1, an overall factor C_μ times a unit matrix. In this approximation x^T_{μ + 1}C_μx_{μ + 1} = C_μ. Then the dynamics becomes

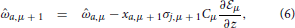
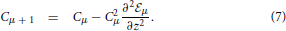
This dynamics and variations for other learning scenarios has been extensively analyzed in Kinouchi and Caticha [37], Opper [36], Kinouchi and Caticha [38], Copelli and Caticha [39], Vicente et al. [40], Biehl et al. [41], Biehl and Schwarze [42], Caticha and de Oliveira [43], de Oliveira and Caticha [44], and Engel and den Broeck [45]. We now make some comments that are relevant for our present purposes.

We introduce the modulation function (Figure 1) 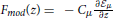and write the dynamics as

$\begin{array}{cc}{\widehat{\omega }}_{a,\mu +1}={\widehat{\omega }}_{a,\mu }+x_{a,\mu +1}{\sigma }_{j,\mu +1}{F}_{mod}(z_{\mu }),& (8)\end{array}$

$\begin{array}{cc}{C}_{\mu +1}=C_{\mu }+C_{\mu }\frac{\partial F_{mod}(z_{\mu })}{\partial z_{\mu }}.& (9)\end{array}$

Learning is now seen as a modulated Hebbian learning, where changes in the weights are done in the direction of the vector x_μ+1, if the social partner's opinion σ_μ+1 about it is positive and in the opposite direction it the opinion is negative. In Figure 1, the modulation function

$\begin{array}{cc}{F}_{mod}(z_{\mu })=\frac{\left(1-2ϵ\right)\exp -\frac{z_{\mu }^2}{2C_{\mu }^2}}{ϵ+\left(1-2ϵ\right)\Phi \left(\frac{z_{\mu }}{C_{\mu }}\right)}& (10)\end{array}$

is plotted as a function of z. Note that z takes positive values if the opinion of the agent and its social partner are the same and is negative if there is disagreement. If the absolute value of z is large the agent can be said to be very sure about its opinion since small changes in the issue will not change its classification.

But more strikingly, the modulation function depends on C. In Figure 1 we present F_mod(z) for different values of $\rho =1/\sqrt{1+C^2}$, a convenient variable since it takes values between zero and one. It is close to zero when the agent's opinion has probability around one half of agreeing with that of the social partner. As learning occurs, ρ increases toward one. It can be shown that ρ is related to the probability e_g of the opinions being different on a random issue, and e_g goes to zero as ρ → 1. In particular $e_g=\frac{1}{\pi }{\text{accos}}^{-1}\rho$ for large d_m and uniform and independently distributed examples and it remains a useful variable in other conditions.

2.2. Formative Phase

Here we describe within a Bayesian framework the way agents process information. We suppose that issues are parsed into a set of five numbers. An issue labeled μ is represented by $x_{\mu }={\left\{x_{a\mu }\right\}}_{a=1,\dots 5}$, each x_aμ describing the bearing of its content on a moral dimension. Agents emit opinions in a fast, automatic, intuitive manner independently of intricate if-then rules. In the model this is done by summing over the five dimensions the content of each moral dimension of the issue, weighted by the importance the agent attributes to each foundation. The moral state of agent i at time t, called the moral matrix in MFT, is also a vector ${\omega }_i(t)={\left\{{\omega }_{a,i}(t)\right\}}_{a=1,\dots 5}$. The opinion of agent i about issue μ is $h_{i,\mu }={\displaystyle {\sum }_{a=1}^5{\omega }_{a,i}{x}_{a,\mu }}$ and its sign σ_i,μ = sign(h_i,μ) shows whether an agent is for or against an issue.

During a social encounter in the formative phase an agent i receives information y_μ = (σ_j,μ, x_μ) emitted by the social partner j. Learning occurs in order to decrease disagreement over issues. Within this learning scenario, we hypothesize that evolutionary pressures to increase the prediction of the opinions of others would select learning algorithms near Bayesian optimality (see 46 and 47). As shown in Appendix the resulting learning algorithm that approximates a full Bayesian use of the available information, can be described in two different ways. One as a motivational algorithm where a cost or energy like function 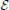is decreased by the changes elicited by learning. The other as a modulated Hebbian learning algorithm with the central concept, the modulation function F_mod (Figure 1), being a measure of the importance attributed to a given issue and the opinion of the interlocutor. In terms of the moral matrix $\widehat{\omega }$_a(t) and a measure of the full social experience C(t), both ways are:

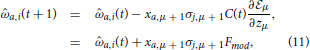
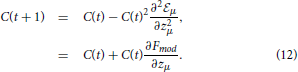
The modulation function and the cost are related by 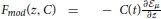where z_μ = σ_j,μ+1h_i,μ measures the concurrence/disagreement between agents i, the receiving agent, and agent j the opinion emitting agent. C(t) is related to the width of the posterior distribution and decreases as learning occurs. We also use $\rho (t)=1/\sqrt{1+C{(t)}^2}$, a convenient variable since it takes values between zero and one. It is close to zero when an agent had a small number of social encounters and approaches one as the number increases. Hence the modulation function and the cost are functions of z and ρ.

The main results of this paper derive from the fact that the modulation function of the Bayesian algorithm (1) is not the same throughout the learning period and changes as more information is incorporated and depends on the number of social encounters; and (2) it depends on the novelty that the opinion of the social partner carries. These two aspects are clear in Figure 1. Right, where the modulation function is plotted as a function of z = h_iσ_j, for different fixed values of ρ, which measures the number of social interactions. Note that z = |h_i|σ_iσ_j measures the strength |h_i| of the opinion held by i and the σ_iσ_j which is positive if the opinion σ_i prior to learning agent i is the same as the that of agent j and the information is corroborative, and z < 0 if the opinions are opposite and the arriving information is considered a novelty.

2.3. Social Influence Phase

We consider that the information exchanges in the formative phase occur at random and thus the effective ρ for each agent is a random number. Now we freeze the evolution of the modulation function, ρ or equivalently C is fixed at a particular value for each agent. We consider the agents to start a new phase in their lives where the value of ρ does not change anymore. The agents in the formative phase learned to learn and now they just learn from each other. The validity of this supposition as something that represents the developments of adolescents has to be investigated in an independent way. It loosely rings with Piagetian overtones [48].

We also consider the fact that people tend to interact with the likes [49]. The likes here would mean agents with similar learning styles, so we consider as a nonessential simplification, a system of agents all with the same ρ each one in a site of a social lattice, exchanging information and then investigate the effect of changing ρ. The dynamics of information exchange is analogous to some proposals found in the literature [50–52] and differs from Vicente et al. [12], Caticha and Vicente [13], Vicente et al. [14] in the learning process that here follows the Bayesian algorithm described above.

We suppose that a society discusses a set of P issues. Parsing of an issue into a vector might be subjective, expressed by the fact that agent i obtains a vector x_i. Exchange of information between agents is about the average vector

$\begin{array}{cc}Z\propto \frac{1}{P}{\displaystyle \sum _{\mu =1}^P}{x}_i^{\mu },& (13)\end{array}$

which we suppose for simplicity to be independent of the agent, since fluctuations due to subjective parsing, if unbiased, tend to cancel out. We call Z the Zeitgeist vector since it captures the contributions of all issues that are currently being discussed by the model society. Without any loss it will be normalized to unit length. The opinion of agent k about the Zeitgeist is

$\begin{array}{cc}{h}_k=Z·w_k& (14)\end{array}$

and its sign is denoted by σ_k = sign(h_k). We now consider a Metropolis-like stochastic dynamics of information exchange. Pick at random one agent, call i. Pick its social partner, call it j uniformly from its social neighbors. Now choose a d_m dimensional vector u drawn uniformly on a ball of radius κ. A trial weight vector is defined by

$\begin{array}{cc}T=\frac{w_i(t)+u}{|w_i(t)+u|}& (15)\end{array}$

and accepted as the new weight vector, w_i(t + 1) = T if the learning energy : Δ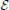: = 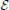(T,σ_j) − 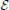(w_i(t), σ_j) ≤ 0. If Δ 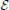> 0 the change is accepted with probability exp − βΔ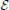. In analogy to Equation (5)

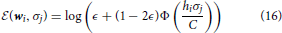
This is looped randomly over the whole population. A technical comment is that it is not obvious if this dynamics leads to an equilibrium state since the energy 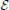is not symmetric with respect to the interchange of the two actor agents: the emitter and the receiver of the information. However, numerically, order parameters rapidly converge to values that remain stationary during thousands of iterations, a time scale that we consider sufficient to study a steady state and further to consider the effects of Zeitgeist changes and readaptations. Within certain limits, κ controls the acceptance rate and thus the time scales to reach stationary values.

The value of β sets the scale of fluctuations of the energy 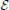. If β is large, even small changes Δ 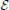have large effects and large changes will not be possible, and if β is small, then large fluctuations may be easily accepted. Our interpretation is that β serves as a pressure to accommodate and conform to the opinion of others. Large β means strict conformity, while in a small β regime, tolerance to fluctuations in conformity are accepted.

The conjugate parameter β, determines the scale of tolerance to fluctuations in the cost 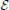, that is, it determines how important it is to conform to the opinions of others agents and eventually sets the scale of fluctuations of an agent's moral vector around the Zeitgeist.

2.4. Simulation

The artificial data is generated by the following procedure. We suppose that agents are characterized by a learning algorithm parametrized by ρ depending on the number of social interactions they experienced during the formative phase. We also suppose that agents only interact with counterparts holding equal ρ. We choose a random social undirected graph from an ensemble here taken to be generated by a Barabasi-Albert model with N = 400 and m = 10. Our results are not strongly dependent on the details of the social graph topology [14].

Agents start the social influence phase with moral weights that are represented by unitary vectors ω_i with random positive overlaps with a fixed Zeitgeist vector Z. The social influence dynamics is implemented as a Markov Chain Monte Carlo process as follows. At each step an edge 〈ij〉 of the social graph is randomly and uniformly chosen. One of its vertices (let it be i) is then marked as the influenced agent with probability 1/2. The influenced agent chooses a random unit vector ω′_i and changes her moral weights ω_i with probability given by min{1, exp (−βΔ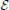)}, where 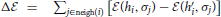. Note that the agent has complete access to his opinion h_i, but only knows the sign of the influencer opinion σ_j. Observe also that the pressure parameter β regulates the acceptance rate in the transition. High pressure β makes moral representation changes more difficult.

Data are collected after the system reaches equilibrium. We typically wait T_term = 6× 10⁴N interactions before gathering uncorrelated samples for time averaged opinions h_i that are used to build the histograms depicted in Figure 2. To guarantee that samples are uncorrelated we calculate autocorrelation times τ and then select properly spaced T_term/τ samples. The whole procedure is repeated a n times until 500 independent samples are drawn (n = 4 being the minimum for the data we report). Our codes and preprocessed data are available at https://github.com/jonataseduardo/BayesianSociety. Raw data for the Moral Foundations survey can be obtained from http://www.yourmorals.org.

FIGURE 2

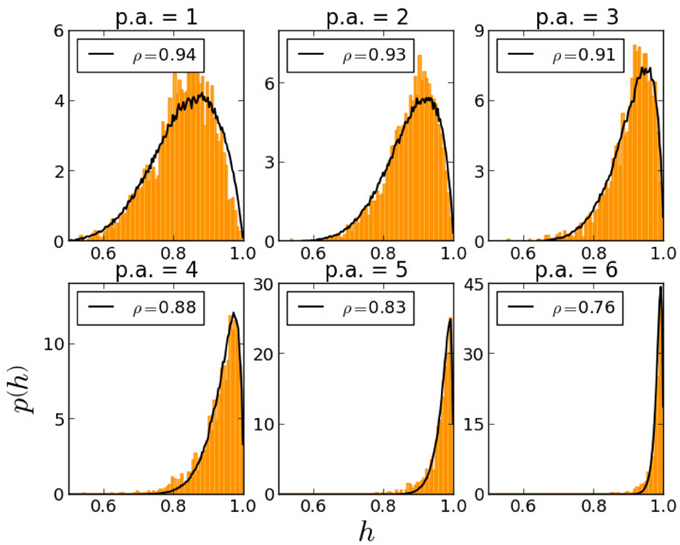
Figure 2. Comparison with empirical data. Empirical opinions (histograms in orange) correspond to the overlap between moral weights obtained by MFT questionnaires and the average weight of the most conservative group (Zeitgeist direction Z). The histogram obtained by simulating social influence in a social network with homogeneous learning styles (homogeneous ρ) and computing overlaps between moral weights of a the agents and a given Zeitgeist direction (Z = (1, 1, 1, 1, 1) in the simulation) are represented by the black line. In each graph we find ρ that best fits the empirical histogram for pressure β = 3.8 and for each political affiliation group. Simulations are performed on a Barabási-Albert network with N = 400 and average degree 20.

2.5. Confrontation Between Artificial and Empirical Data

A society of agents is characterized by the values of ρ, measuring the effective socialization in the formative phase, and of β that sets the pressure on the society during the social influence phase. While in a society different agents with different ρ's and feeling different β's will interact, it is a reasonable first approximation to consider that people will more likely interact in a meaningful manner with those that are more similar.

In a steady state of a society of agents, changes in the moral matrices still occur, but the distribution P_ADS(h|ρ, β) of opinions about the Zeitgeist are stable in time. From 15,000 MFT questionnaires (MFTQ, see [14] for a description of this data set) we obtained the data and the following information. (i) {w_a}_a=1…5, the (normalized) weights of the moral matrix and the political affiliation of each respondent. (ii) The empirical Zeitgeist vector (Z_e = {Z_a}_a=1…5) defined as the average weight vector of the most conservative group. (iii) The empirical Zeitgeist opinion h^e = ∑_aw_aZ_a for each respondent. (iv) The empirical distribution of opinions P_EDS(h|pa) is obtained for each of the political affiliations pa.

A distance between the two distributions is measured

$\begin{array}{cc}D\left(\rho ,\beta ;pa\right)={\displaystyle \sum _{h\in bins}{\left(P_{ADS}\left(h|\rho ,\beta \right)-P_{EDS}\left(h|pa\right)\right)}^2}.& (17)\end{array}$

by summing the quadratic difference over a set of bins of h. Figures 2, 3 are obtained by identifying the value of pa for the regions on the ρ − β space where D(ρ, β; pa) is smallest. If the smallest D(ρ, β; pa) is larger than a threshold value of identification (e.g., 0.1) then the point is not identified to any political affiliation.

FIGURE 3

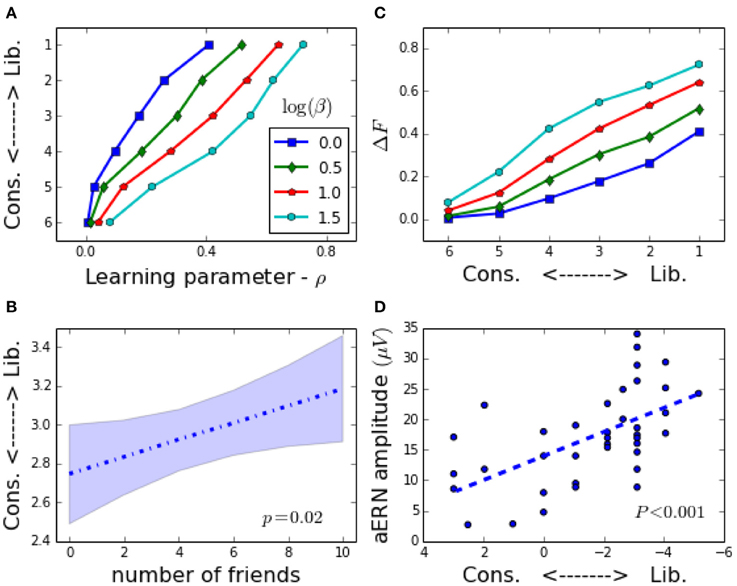
Figure 3. Model vs. data. Model results: Panels (A) and (C) show results from the model. Panels (B) and (D) are observational results from data published in Settle et al. [35] and Amodio et al. [28], respectively. (A) Model: Political affiliation (pa = 1-Liberal, pa = 7-Very Conservative) is correlated to ρ, which is a measure of the number of social information exchanges in the formative phase of the agents' lives. This occurs for a wide range β values. (B) Data: Number of friendships in people with the two alleles of DRD4-7R correlates with liberalism [35]. (C) Model: Difference between average modulation in novel and corroborative situations, ΔF = 〈F_mod〉_novelty − 〈F_mod〉_{corroboration}. correlates with liberalism (see Section 3.4). (D) Data: magnitude of ERN difference between novelty and corroboration in a go-no-go task from Amodio et al. [28] correlates with liberalism.

3. Results

3.1. Learning Dynamics

We started with Bayesian learning and obtained two equivalent descriptions of the learning dynamics describing changes in the weights of the moral dimensions. The dynamics described in Equation (11) can be seen to be a gradient descent: changes of the weights are in the direction of decreasing a quantity 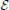that can be interpreted as an energy, a cost or a pain.

We claim that this motivational (or utilitarian) form of learning can be useful to understand what is occurring. Then for each example the change occurs in the direction which tends to reduce the error of classification, to increase conformism or to reduce pain derived from disagreement. But it is just a mathematical fact that may go along uninterpreted and be described just as a Bayesian inspired learning. We can describe the falling rock as moving along a trajectory that decreases potential energy. It is not the rock that is being utilitarian or motivated to reduce an energy, but it is our description using energy that seems utilitarian. The motivation lies in our third person description.

3.2. The Modulation Function

By using the idea of the modulation function we described (Equation 12) the same learning dynamics differently. The modulation function measures the importance of the information carried by the example. It could be thought in a loose way as representing the signal from something like an amygdala, which would signal more strongly in case the example causes surprise due to the novelty of an unexpected result.

In addition to measuring surprise, it is striking that it depends on $\rho (t)=1/\sqrt{1+C{(t)}^2}$. What is striking about a ρ dependent modulation is that in a static scenario and for an agent with only one social partner we can prove [37] that ρ increases with the number of information exchanges, and this still holds numerically when learning from several correlated social partners.

We now analyze the case shown in Figure 1-Left for noiseless communication. At the beginning of the learning process the modulation function is flat. Every piece of information, every example receives the same modulation. Being right or wrong is of little consequence in the manner in which the information is incorporated. As learning occurs, from the information exchange with social partners, the modulation function decreases for positive z and increases for negative z. Examples that carry new information start getting a higher modulation. Those that were predicted correctly, are less effective in fostering changes in the weights of the moral vector. Examples carrying new information make larger impacts, those that corroborate the opinion of the agent, have a smaller influence. As ρ increases this effect is amplified.

In Figure 1-Right a noisy communication channel is introduced. With probability ϵ (equal to 0.2 in the figure), the received opinion is flipped. But the agent doesn't know which specific examples are corrupted. The Bayesian algorithms permits the incorporation of this information, the result is a distrust effect. If the agent is very sure about its opinion (large absolute value of z), but it differs from that of the social partner (z < 0), it tends to disregard the example by doing smaller changes in the weights. This increases with the value of the noise level and with ρ.

To sum it up, the modulation has three characteristics which we list in decreasing order of importance. The modulation function depends on

1. Novelty/Corroboration: a measure of whether the example carries new information (z < 0) or is corroborative (z > 0),

2. Socialization in the formative phase: a measure of the number of information exchanges (ρ),

3. Trust/distrust: a measure of the reliability attributed to the social partners. Given ϵ, if z is too negative, the example is not considered new information but rather it is distrusted and its effect is small.

We have analyzed the simple dynamics where the covariance is represented by a single parameter C or equivalently ρ. This is probably a good approximation but it is reasonable to assume that the dimensions may be interdependent. For example caring for a member of the group may be larger than for a member of another group, also cheating an authority figure may be different than cheating a common member of the group. This can be modeled by off diagonal terms in the covariance matrix, that mix the moral dimensions of care and loyalty, in the first case or the fairness and authority dimensions in the second. It is not clear at this point whether this means that there are different neural circuits that deal with the dimensions but are interconnected, or if there exists combinations of dimensions that are independent. This last option seems attractive from a mathematical point of view, being just another case where diagonalization is useful. However, the existence of interacting circuits is probably more in accord with the fact that evolved language attributes specific names to them and not to their combinations.

3.3. The Political Affiliation of Bayesian Agents

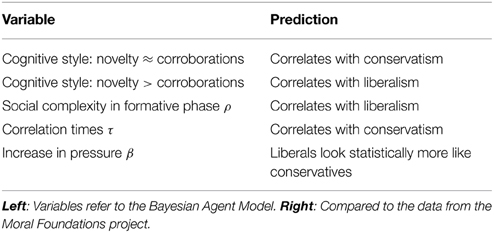
Agents, of course, do not have a political affiliation. However, we can measure the distribution of opinions P_ADS(h_i|ρ, β) after the formative phase, about the Zeitgeist vector for a society of agents all with the same value of ρ and pressure β. Now we have a statistical signature that can be compared to a similar signature extracted from the data of the Moral Foundation questionnaires for each political affiliation group. This is similar to the methodology we used in Caticha and Vicente [13] and Vicente et al. [14]. This results in the identification for fixed β, of the measure ρ of the formative phase, and the self-declared political affiliation of the respondents of the questionnaires. This is done for several values of β and the result is shown in Figures 2, 3. It is clear that the populations of agents with small value of ρ, or small number of social information exchanges, are close to conservatives and those populations with high ρ or large number of social information exchanges, are more likely to be identified with liberals. Note that this is not a one to one identification. We are not saying that a given agent's value of ρ determines political affiliations, but rather that this subset of the population will have a distribution of opinions consistent with such identification.

3.4. Comparing ERN and the Modulation Function

The modulation function determines the size of the weight changes during learning. We define the average of the modulation function for novelty 〈F_mod〉_novelty and 〈F_mod〉_{corroboration} by

$\begin{array}{cc}\begin{array}{l}\langle F_{mod}{}_{novelty}\rangle =\frac{{\displaystyle {\int }_{-\infty }^0{F}_{mod}}(z)P(z)dz}{{\displaystyle {\int }_{-\infty }^{\infty }{F}_{mod}}(z)P(z)dz},\\ \langle F_{mod}{}_{corroboration}\rangle =\frac{{\displaystyle {\int }_0^{\infty }{F}_{mod}}(z)P(z)dz}{{\displaystyle {\int }_{-\infty }^{\infty }{F}_{mod}}(z)P(z)dz}.\end{array}& (18)\end{array}$

For a uniform distribution of examples, and with the normalization of ω, the distribution P(z) of z = hσ, is the gaussian distribution with zero mean and unit variance. Since the modulation function depends on ρ, the difference

$\begin{array}{cc}\Delta F={\langle F_{mod}\rangle }_{novelty}-{\langle F_{mod}\rangle }_{corroboration}& (19)\end{array}$

can be identified to a political affiliation. This is shown in Figure 3C. This is the closest we can come theoretically to defining within the model a quantity similar to the Error Related Negativity (ERN) measured by Amodio et al. [28] which reports differences between measured EEG signals of unexpected and expected situations conditional on self-declared political affiliations. In Figure 3D we show the results from Amodio et al. [28] for the magnitude of the ERN signal vs. political affiliations.

3.5. The Phase Diagram

The phase diagram is the instrument used to represent the variety of possible collective behaviors of systems composed of many interacting units, in particular a society of agents. The phase boundary separates regions of totally different properties. In Figure 4-Left we show the phase diagram in the space of parameters (ρ, β). Above the transition line which is the lower line, the society of agents has an ordered phase. That there is some coherence of opinions in the society is shown by the fact that the average value of the opinions is not zero. Below the transition line the model society is disordered in the sense that opinions are so varied that they average to zero, opinions are not shared, the Zeitgeist is not clear. This phase, the opposite of the ordered phase, resembles the anomie of Durkheim. The stripes follow regions where the statistical signatures are similar to a certain political affiliation group.

FIGURE 4

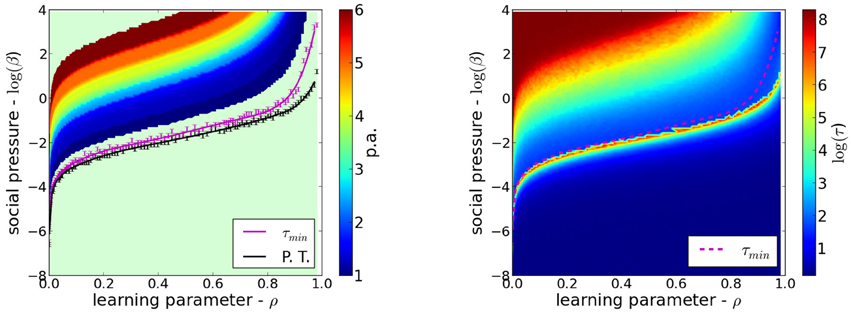
Figure 4. Phase diagram and relaxation times. Left: The phase diagram in the space ρ, a measure of the complexity of socialization vs. the pressure β. The stripes represent regions of the space of parameters where agents could be statistically identified with a group with a given political affiliation. The lower line represents the boundary between order (above) and disordered (below) societies. Below the transition line, and for very large β, no identification with MFT questionnaire respondents was found. Right: Color coded relaxation times after changes in the set of moral issues. Note that at the transition relaxation times are very large. This is called critical slowing down. For the agents identified with respondents of the MFTQ, the lowest times correspond to those liberal identified agents and the largest times to conservative identified agents. The line just above the transition shows the locus of minimum correlation time as a function of β, for fixed ρ.

3.6. Readaptation Times

What is it that conservatives conserve? If a society of agents identified with conservatives (low ρ) were to readapt after changes faster than one identified with liberals, our theory would have to be thrown away. But it is a result of our theory that liberal-like societies are faster than conservative-likes in readapting.

Several approximately equivalent ways of defining relevant measures of readaptations times can be introduced and we have looked at two such measurements and obtained similar results. After a steady state was achieved and the steady state distribution P_ADS(h|ρ, β) is measured, the Zeitgeist Z_old is changed to a new Zeitgeist z_new. Call this time t = 0. After a sweep of information exchanges of all the agents, t increases by one unit, the distribution of opinions about the new Zeitgeist P_t(h) is measured. A distance between the two distributions is measured

$\begin{array}{cc}D(t)={\displaystyle \sum _{h\in bins}{\left(P_t\left(h\right)-P_{ADS}\left(h|\rho ,\beta \right)\right)}^2}.& (20)\end{array}$

by summing the quadratic difference over a set of bins. As usual the relaxation is exponential so we parametrize D(t) = D₀e^−t/T in terms of the adaptation time T which depends on ρ and β. For more about this measure see [14].

A second possibility is the correlation time, defined by measuring the decay in time of the time correlations. These are defined by the difference between the expected value of the product of the moral vector at two different times and the product of their expected values c(t) = 〈m(t′ + t)m(t′)〉 − 〈m(t′ + t)〉 〈m(t′)〉 which also decays exponentially as c(t) ∝ exp(−t/τ) with a characteristic relaxation time τ(β, ρ). Figure 4-Right shows the result of measuring numerically the relaxation times of the different populations. At the transition line the relaxation time grows beyond any limit as ever increasing populations are considered. This is called critical slowing down. Bellow the transition, the system is disordered and after the Zeitgeist change, it returns very quickly to the steady state. This temporally and spatially uncorrelated region is uninteresting from the point of view that no data for an analogous population in this region is currently available. Above the transition line, as we move to larger β with fixed ρ, τ goes down very fast, attaining its minimum values near the regions of ultraliberals and then has a monotonous rise into the conservative region. The shape of the regions where τ remains approximately constant are similar in shape to the regions in the phase diagram identified with a given political affiliation. This suggests that political affiliation could be empirically characterized by collective relaxation time that increases as the political spectrum is transversed from groups conventionally labeled as liberals to those labeled as conservatives.

3.7. Threats: Conservative Shift Under Increase of Pressure

The pressure parameter β determines how important it is to conform to the opinions of others. A more detailed modeling of the agents could make a difference between informational or normative peer pressure. Or the differences between situational or dispositional attributions of β. Economical or environmental pressures could influence how the the social environment is perceived. Coarsely, β describes the overall motivation that sets the scales of adaptation of beliefs. However, it is set, it controls how strongly the agent should conform to other opinions or to the overall current Zeitgeist. Technically, it determines the scale of tolerance to fluctuations in the cost function 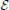. Equivalently β sets the scale of fluctuations of an agent's moral vector around the Zeitgeist.

We can model the effect of an external event that threatens the group to which the agent belongs by considering that the pressure β increases. The effects of the threat in the political affiliation of the agents, shown in Figure 5-Left is that the population will shift toward the conservative end of the spectrum. We supposed a fixed distribution of the number of social information exchanges ρ, and the effect on the distribution of political affiliations before and after a threat which increases the peer pressure β. Our model predicts also that under the perceived decrease of an external threat the populations will shift toward the more liberal region.

FIGURE 5

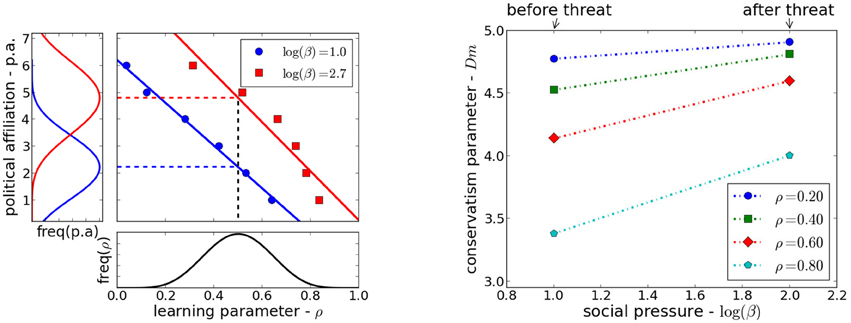
Figure 5. Threats. Left: The level of conservatism changes with pressure. If the population has a distribution of social encounters as shown in the bottom panel, the resulting distributions of political affiliations changes, for different pressures as shown in the left panel. Right: The effective number of moral dimensions for two values of the pressure, before and after an external threat. If a threat leads to increased pressure, the statistical signature of liberals agents will look more like that of conservatives.

We have defined the effective number of moral dimensions of a group with a given political affiliation. This is done by averaging the weights over all members of the population and multiplying by the number of moral dimensions d_m = 5, $Dm=\frac{1}{N}{\displaystyle {\sum }_{a,j}{\omega }_{a,i}}$. For groups of agents that are identified with conservatives, the effective moral dimension is near 4.8. For those identified with liberals it is near 3.5. Both increase under increase of the peer pressure parameter β as shown in Figure 5-Right. This is in qualitative agreement with experiments reported in Bonanno and Jost [53], Nail and McGregor [54], Nail et al. [55] and further work in Van der Toorn et al. [56].

4. Discussion

The main characteristic of Entropic inference and the Bayesian approach to information theory is that the mathematical structure to represent beliefs in the absence of complete information [57, 58], if manifest inconsistency is to be avoided, is probability theory. As presented in Section 2, a Bayesian study of the learning dynamics of moral classifications can be described as the changes in the weight parameters for each dimension that lead to a decrease in the cost, interpreted as psychological discomfort, caused by differences of opinions.

The main result we presented here is that the cognitive style of the Bayesian agent depends on the complexity of the social interactions in the formative phase and cognitive style induces a statistical association to political affiliation. The formative phase is a mimic of the pre-adolescent phase in the life of an agent and the social influence phase is a mimic of the post-adolescence. During the social influence phase the agent's cognitive style is crystallized, so that it ceases to change, although the agent is still capable of learning, then it follows that statistically the agents when identified with respondents of the MFTQ, with the social complexity of the formative phase being positively correlated with liberalism. This is exciting since in Settle et al. [35] the number of childhood friends is positively correlated to liberalism, at least for those that have two alleles of the DRD4-R7 gene. They cautiously withhold from claiming that a gene for political ideology was identified and just claim that evidence points to a gene-environment interaction.

Within the context of Settle et al. [35] what is the genetic interpretation of our results? Our methods do not address this problem. Genetically, having two long R7 DRD4 alleles, may contribute to making the number of friends a proxy for social complexity in the formative phase. But some other genes may contribute to Openness, with influence on the number of friends, thereby influencing the cognitive style with respect to the differences of learning novelty and corroborations. But our approach does not address this mechanism nor those by which other phenotypes become conservative or liberal. What we say is that Bayesian optimal learning predicts that number of social interactions in the formative phase will correlate with liberalism in the social influence phase. But, why should agents be Bayesian optimal? An answer can be given based on the results of first, [37] where the functional optimization of the learning process was obtained, second [36], where a related algorithm was shown to be the online version of the Bayes algorithm and third [46] where, using evolutionary programming, the authors showed that perceptrons evolving under pressure for having larger generalization ability, were driven to learning algorithms that resembled Bayesian optimal algorithms both in functional form and performance. Thus, if learning algorithms for moral classification from examples, are subject to evolutionary pressures for better generalization, Bayesian optimal like algorithms will be approximated. Cognitive styles will then depend on social interactions at the earlier phase in the life of the agent. A question that remains is why there would be a formative phase, for learning how to learn and setting overall parameters, and a social influence phase, for actual learning. These questions are outside of our scope and will need other methods and inputs.

What are the predictions of the model? These are summarized in Table 1. Relaxation times were never used in the theoretical formulation of the problem. They are a physical consequence of the social information exchanges and hence a prediction of the model. Different cognitive styles, through social interactions, lead to different adaptation times. The existence of a phase transition between an ordered moral phase and a moral disordered phase might not be observable since societies morally disordered might not exist. However, this model can be applied to other culturally relevant landscapes, where groups on both sides of the divide might be found. A question that remains is if in those contexts, pressure will lead to Bayesian optimality resulting in cognitive style diversity.

TABLE 1

Table 1. Predictions of the model of Bayesian Agents.

Another prediction of the model is that under an increase of β, the peer pressure, a society as a group will tend to seem statistically more conservative, as shown in Figure 5. This effect of peer pressure increase might be behind the results of Bonanno and Jost [53] and Nail and McGregor [54] about the increased conservatism of subjects that were exposed to the 9/11 attack. However, Nail et al. [55] show that there is no need for social interaction in order to become more conservative, suggesting that our interpretation of β as peer pressure could be extended to a self-regulated parameter that is adjusted dynamically from information about social context.

An empirical definition and consequent measure of pressure might be done following the methodology of Gelfand et al. [59] where nations were classified on a tight/loose scale. Analysis of morality data sets for individual countries could point out if our pressure and their tight/loose scale are related. Since we use only USA citizens questionnaires, we are not able to address this question here, leaving the issue for a forthcoming paper.

An important characteristic of our model is that it is semantically free. Just or loyal in the mathematical space where the agents are defined are concepts devoid of meaning. We believe that this aspect has to be addressed from an evolutionary perspective in order to understand the emergence of the dimensions and hence provide our mathematical backbone of a semantic dressing.

Funding

This research received support from the Center for the Study of Natural and Artificial Information Processing Systems of the University of São Paulo (CNAIPS NAP-USP). JC received support from a FAPESP fellowship.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

It is a pleasure to thank Jonathan Haidt, Jesse Graham and the YourMorals.org team for letting us play with their data, Vitor B. P. Leite for discussions about possible genetic basis of political ideology, Marcus V. Baldo for discussions about learning and Paul Nail for comments on threats.

References

1. Hyman H. Political Socialization. New York, NY: The Free Press (1959).

Google Scholar

2. Fowler J, Baker L, Dawes C. Genetic variation in political participation. Am Polit J Rev. (2008) 102:233–48. doi: 10.1017/S0003055408080209

CrossRef Full Text | Google Scholar

3. Alford JR, Funk CL, Hibbing JR. Are Political Orientations Genetically Transmitted? Am Polit Sci Rev. (2005) 99:153–67. doi: 10.1017/S0003055405051579

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

4. Hatemi PK, Hibbing JR, Medland SE, Keller MC, Alford JR, Smith KB, et al. Not by twins alone: using the extended family design to investigate genetic influence on political beliefs. Am J Polit Sci. (2010) 54:798–814. doi: 10.1111/j.1540-5907.2010.00461.x

CrossRef Full Text | Google Scholar

5. Hatemi PK, Gillespie NA, Eaves LJ, Maher BS, Webb BT, Heath AC, et al. A genome-wide analysis of liberal and conservative political attitudes. J Polit. (2011) 73:271–85. doi: 10.1017/S0022381610001015

CrossRef Full Text | Google Scholar

6. Galam S. Sociophysics: A Physicist's Modeling of Psycho-Political Phenomena. New York, NY: Springer (2012).

Google Scholar

7. Sen P, Chakrabarti BK. Sociophysics: An Introduction. Oxford: Oxford University Press (2013).

Google Scholar

8. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys. (2009) 81:591–646. doi: 10.1103/RevModPhys.81.591

CrossRef Full Text | Google Scholar

9. Epstein JM. Generative Social Science: Studies in Agent-Based Computational Modeling. Princeton, NJ: Princeton University Press (2006).

Google Scholar

10. Epstein JM. Agent Zero: Toward Neurocognitive Foundations for Generative Social Science. Princeton, NJ: Princeton University Press (2014).

Google Scholar

11. Gilbert N, Troitzsch K. Simulation for the Social Scientist. New York, NY: Open University Press (2005).

Google Scholar

12. Vicente R, Martins ACR, Caticha N. Opinion dynamics of learning agents: does seeking consensus lead to disagreement? J Stat Mech. (2009) P03015. doi: 10.1088/1742-5468/2009/03/P03015

CrossRef Full Text | Google Scholar

13. Caticha N, Vicente R. Agent-based social psychology:from neurocognitive processes to social data. Adv Complex Syst. (2011) 14:711–31. doi: 10.1142/S0219525911003190

CrossRef Full Text | Google Scholar

14. Vicente R, Susemihl A, Jericó JP, Caticha N. Moral foundations in an interacting neural networks society: a statistical mechanics analysis. Physica A (2014) 400:124–38. doi: 10.1016/j.physa.2014.01.013

CrossRef Full Text | Google Scholar

15. Haidt J. The emotional dog and its rational tail: a social intuitionist approach to moral judgment. Psychol Rev. (2001) 108:814–34. doi: 10.1037/0033-295X.108.4.814

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

16. Haidt J. Intuitive ethics: how innately prepared intuitions generate culturally variable virtues. Daedalus (2004) 133:55–66. doi: 10.1162/0011526042365555

CrossRef Full Text | Google Scholar

17. Haidt J. The new synthesis in moral psychology. Science (2007) 316:998–1002. doi: 10.1126/science.1137651

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

18. Haidt J, Graham J. Planet of the Durkheimians, where community, authority, and sacredness are foundations of morality. In: Jost JT, Kay AC, Thorisdottir H, editors. Social and Psychological Bases of Ideology. Oxford: Oxford University Press (2009). p. 371–401.

19. Haidt J, Kesebir S. Morality. In: Fiske ST, Gilbert DT, Lindzey G, editors. Handbook of Social Psychology. Vol 2. New York, NY: Wiley (2010). p. 797–832.

Google Scholar

20. Graham J, Haidt J, Nosek B. Liberals and conservatives rely on different sets of moral foundations. J Pers Soc Psychol. (2009) 96:1029–46. doi: 10.1037/a0015141

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

21. Graham J, Nosek BA, Haidt J, Iyer R, Koleva S, Ditto PH. Mapping the moral domain. J Pers Soc Psychol. (2011) 101:366–85. doi: 10.1037/a0021847

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

22. Kohlberg L, Turiel E. Moral development and moral education. In: Lesser GS editor. Psychology and Educatiuonal Practice. Glenview, IL: Scott, Foresman (1971) p. 410–465.

23. Power F, Higgins A, Kohlberg L. Lawrence Kohlberg's Approach to Moral Education. New York, NY: Columbia University Press (1989).

24. Gilligan C. In a Different Voice: Psychological Theory and Women's Development. Cambridge: Harvard University Press (1982).

25. Shweder RA, Munch NC, Mahapatra M, Park L. Big Three of morality (Autonomy, Community, Divinity) and the Big Three explanations of suffering. In: Brandt AM, Rozin P, editors. Morality and Health. New York, NY: Routledge (1997) p. 119–167.

26. Iyer R, Koleva S, Graham J, Ditto P, Haidt J. Understanding libertarian morality: the psychological roots of an individualist ideology. PLoS ONE (2012) 7:e42366. doi: 10.1371/journal.pone.0042366

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

27. Gerber A, Huber G, Raso C, Ha SE. Personality and political behavior. Soc Sci Res Netw. (2009). doi: 10.2139/ssrn.1412829. (in press).

CrossRef Full Text | Google Scholar

28. Amodio DM, Jost JT, Master SL, Yec CM. Neurocognitive correlates of liberalism and conservatism. Nat Neurosci. (2007) 10:1246–7. doi: 10.1038/nn1979

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

29. Jost JT, Glaser J, Kruglanski AW, Sulloway FJ. Political conservatism as motivated social cognition. Psychol Bull. (2003) 129:339–75. doi: 10.1037/0033-2909.129.3.339

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

30. Jost J, Amodio D. Political ideology as motivated social cognition: behavioral and neuroscientific evidence. Motiv Emot. (2011) 36:55–64. doi: 10.1007/s11031-011-9260-7

CrossRef Full Text | Google Scholar

31. Eisenberger N, Lieberman M, Williams K. Does rejection hurt? An fMRI study of social exclusion. Science (2003) 302:290–2. doi: 10.1126/science.1089134

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

32. Haslam N. A grammar of social relations. Transcult Psychiatr Res Rev. (1995) 32:41. doi: 10.1177/136346159503200102

CrossRef Full Text | Google Scholar

33. Smith KB, Oxley DR, Hibbing MV, Alford JR, Hibbing JR. Linking genetics and political attitudes: reconceptualizing political ideology. Polit Psychol. (2011) 32:369–97. doi: 10.1111/j.1467-9221.2010.00821.x

CrossRef Full Text | Google Scholar

34. Dawes C, Fowler J. Partisanship, voting, and the dopamine D2 receptor gene. J Polit. (2009) 71:1157. doi: 10.1017/S002238160909094X

CrossRef Full Text | Google Scholar

35. Settle JE, Dawes CT, Christakis NA, Fowler JH. Friendships moderate an association between a dopamine gene variant and political ideology. J Polit. (2010) 72:1189–98. doi: 10.1017/S0022381610000617

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

36. Opper M. On-line versus Off-line Learning from random examples: general results. Phys Rev Lett. (1996) 77:4671–4. doi: 10.1103/PhysRevLett.77.4671

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

37. Kinouchi O, Caticha N. Optimal generalization in perceptrons. J Phys A. (1992) 25:6243. doi: 10.1088/0305-4470/25/23/020

CrossRef Full Text | Google Scholar

38. Kinouchi O, Caticha N. Lower bounds for generalization with drifting rules. J Phys A. (1993) 26:6161. doi: 10.1088/0305-4470/26/22/017

CrossRef Full Text

39. Copelli M, Caticha N. On-line learning in the committee machine. J Phys A. (1995) 28:1615.

PubMed Abstract | Full Text | Google Scholar

40. Vicente R, Kinouchi O, Caticha N. Statistical mechanics of online learning of drifting concepts: a variational approach. Mach Learn. (1998) 32:179. doi: 10.1023/A:1007428731714

CrossRef Full Text | Google Scholar

41. Biehl M, Riegler P, Stechert M. Learning from noisy data: an exactly solvable model. Phys Rev E. (1995) 52:R4624–7.

PubMed Abstract | Full Text | Google Scholar

42. Biehl M, Schwarze H. Learning by on-line gradient descent. J Phys A. (1995) 28:643–56. doi: 10.1088/0305-4470/28/3/018

CrossRef Full Text | Google Scholar

43. Caticha N, de Oliveira E. Gradient descent learning in and out of equilibrium. Phys Rev E. (2001) 63:061905. doi: 10.1103/PhysRevE.63.061905

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

44. de Oliveira E, Caticha N. Inference from aging information. IEEE Trans Neural Netw. (2010) 21:1015–20. doi: 10.1109/TNN.2010.2046422

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

45. Engel A, den Broeck CV. Statistical Mechanics of Learning. Cambridge: Cambridge University Press (2001).

Google Scholar

46. Neirotti J, Caticha N. Dynamics of the evolution of learning algorithms by selection. Phys Rev E. (2001) 67:041912. doi: 10.1103/PhysRevE.67.041912

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

47. Yu AJ. Adaptive behavior: human act as Bayesian learners. Curr Biol. (2007) 17:R977–80. doi: 10.1016/j.cub.2007.09.007

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

48. Piaget J. The Moral Judgment of the Child. New York, NY: The Free Press (1965).

49. Abrams D, Wetherel M, Cochrane S, Hogg MA, Turner JC. Knowing what to think by knowing who you are: Self-categorization and the nature of norm formation, conformity and group polarization. Br J Soc Psychol. (1990) 29:97–119. doi: 10.1111/j.2044-8309.1990.tb00892.x

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

50. Martins ACR. Continuous opinions and discrete actions in opinion dynamics problems. Int J Mod Phys C. (2008) 19:617–24. doi: 10.1142/S0129183108012339

CrossRef Full Text | Google Scholar

51. Martins ACR, de Pereira CB, Vicente R. An opinion dynamics model for the diffusion of innovations. Physica A. (2009) 388:3225–32. doi: 10.1016/j.physa.2009.04.007

CrossRef Full Text | Google Scholar

52. Lallouache M, Chakrabarti AS, Chakrabarti A, Chakraborti A, Chakrabarti BK. Opinion formation in kinetic exchange mmodel: spontaneous symmetry-breaking transition. Phys Rev E. (2010) 82:056112. doi: 10.1103/PhysRevE.82.056112

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

53. Bonanno G, Jost J. Conservative shift among high-exposure survivors of the September 11th terrorist attacks. Basic Appl Soc Psychol. (2006) 28:311–23. doi: 10.1207/s15324834basp2804/4

CrossRef Full Text | Google Scholar

54. Nail P, McGregor I. Conservative shift among liberals and conservatives following 9/11/01. Soc Justice Res. (2009) 22:231–40. doi: 10.1007/s11211-009-0098-z

CrossRef Full Text | Google Scholar

55. Nail PR, McGregorb I, Drinkwatera AE, Steelea GM, Thompson AW. Threat causes liberals to think like conservatives. J Exp Soc Psychol. (2009) 45:901–7. doi: 10.1016/j.jesp.2009.04.013

CrossRef Full Text | Google Scholar

56. Van der Toorn J, Nail PR, Liviatan I, Jost JT. My country, right or wrong: does activating system justification motivation eliminates the liberal-conservative gap in patriotic attachment? J Exp Soc Psychol (2014). 54:50–60. doi: 10.1016/j.jesp.2014.04.003

CrossRef Full Text | Google Scholar

57. Jaynes ET. Probability Theory: The Logic of Science. Cambridge: Cambridge University Press (2003).

Google Scholar

58. Caticha A. Lectures on Probability, Entropy, and Statistical Physics (2008). arXiv:0808.0012 [physics.data-an].

59. Gelfand MJ, Raver JL, Nishii L, Leslie LM, Lun J, Lim BC, et al. Differences between tight and loose cultures: a 33-nation study. Science (2011) 332:1100–4. doi: 10.1126/science.1197754

PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar

Appendix

Bayesian inspired learning algorithms

For the learning set D_t = (y₀,…,y_{t − 1}) of independently chosen vectors and their opinions, the likelihood is a product

$\begin{array}{cc}P(D_t|\omega )={\displaystyle \prod _{i=0}^{t-1}P}(y_i|\omega )& (\text{A}1)\end{array}$

where ω is the set parameters to be inferred. The data comes in ordered pairs y_t = (σ_j,t, x_t) where σ_j,t is positive if agent j considers issue x_t as a morally acceptable issue and negative otherwise; x_t = (x¹_t, …, x^N_t) is a five dimensional vector. Our choice of N = 5 is determined by Moral Foundation theory.

Bayesian inference derives from the application of Bayes theorem in order to incorporate information that permits updating from a prior to a posterior distribution:

$\begin{array}{cc}P(\omega |D_t)=\frac{P(\omega )P(D_t|\omega )}{{\displaystyle \int \text{ d}}\omega \prime P(\omega \prime )P(D_t|\omega \prime )}& (\text{A}2)\end{array}$

In Online learning we consider the updating of the distribution due to the addition of a single example pair y_{t + 1}

$\begin{array}{cc}P(\omega |D_{t+1})=\frac{P(\omega |D_t)P(y_t|\omega )}{{\displaystyle \int d}\omega \prime P(\omega \prime |D_t)P(y_t|\omega \prime )}.& (\text{A}3)\end{array}$

The amount of memory needed to store the whole posterior can be prohibitively large and following Opper [36] we consider a simplification where the posterior is constrained to belong to a parametric family, which we take to be the N dimensional multivariate Gaussian.

If at a certain stage our knowledge is codified into one such Gaussian,

$\begin{array}{cc}\begin{array}{l}{P}_G(\omega |D_t)=\frac{1}{|2\pi \det C_t{|}^{\frac{1}{2}}}\\ \times \exp \left(-\frac{1}{2}{\left(\omega -{\widehat{\omega }}_t\right)}^T{C}_t^{-1}\left(\omega -{\widehat{\omega }}_t\right)\right)\end{array}& (\text{A}4)\end{array}$

a Bayesian update will in general take the posterior out of the Gaussian space. Then a new Gaussian posterior is chosen is such a way that the information loss is minimized. Thus, the learning step is comprised of two sub-steps:

• New example drives the posterior out of the Gaussian space:

$\begin{array}{cc}P(\omega |D_{t+1}):=P(\omega |D_t,y_t)=\frac{P_G(\omega |D_t)P(y_t|\omega )}{{\displaystyle \int \text{ d}}\omega \prime P_G(\omega \prime |D_t)P(y_t|\omega \prime )}& (\text{A}5)\end{array}$

• Project back to Gaussian space:

$\begin{array}{cc}P(\omega |D_{t+1})\to P_G(\omega |D_{t+1})& (\text{A}6)\end{array}$

The projection step is done using the Kullback-Leibler divergence or equivalently, by maximizing the cross entropy:

$\begin{array}{cc}\begin{array}{l}KL\left[P\left(\omega |D_{t+1}\right)||P_G\left(\omega |D_{t+1}\right)\right]\\ ={\displaystyle \int \text{d}}\omega P(\omega |D_t,y_t)\log \frac{P(\omega |D_{t+1})}{P_G(\omega |D_{t+1})}\end{array}& (\text{A}7)\end{array}$

The minimization of the KL divergence results in projecting into the Gaussian with the same mean and covariance vector as the non-Gaussian posterior:

$\begin{array}{cc}\begin{array}{l}{\widehat{\omega }}_{t+1}=\frac{{\displaystyle \int \text{d}}\omega \omega P(\omega |D_{t+1})P(y_t|\omega )}{{\displaystyle \int \text{d}}\omega P(\omega |D_{t+1})P(y_t|\omega )}\\ C_{t+1}=\frac{{\displaystyle \int \text{ d}}\omega \omega {\omega }^{T}P(\omega |D_{t+1})P(y_t|\omega )}{{\displaystyle \int \text{ d}}\omega P(\omega |D_{t+1})P(y_t|\omega )}-{\widehat{\omega }}_{t+1}{\widehat{\omega }}_{t+1}^T.\end{array}& (\text{A}8)\end{array}$