Bosonic coherent motions in the Universe

We review the role of fundamental spin-0 bosons as bosonic coherent motion (BCM) in the Universe. The fundamental spin-0 bosons have the potential to account for the baryon number generation, cold dark matter (CDM) via BCM, inflation, and dark energy. Among these, we pay particular attention to the CDM possibility because it can be experimentally tested with the current experimental techniques. We also comment on the panoply of the other roles of spin-0 bosons–such as those for cosmic accelerations at early and late times.

1. Introduction

Recent cosmological observations [1, 2] confirm the eight decade old Zwicky's proposal [3] that the Universe contains a large amount of dark matter (DM). The DM profile has been measured accurately enough to pinpoint DM to “it is cold dark matter (CDM) [1].” The bosonic coherent motion (BCM) can be CDM [4–6] if the coherent-boson lifetime is long enough to have survived until now [7–10]. The axion proposed to solve the strong CP problem [11–14] is fitting to this BCM scenario [15]. The BCM is one of many possibilities of CDM scenarios [15] which accounts for only 27% in the energy pie of the Universe. The dominant portion, 68%, in the energy pie is the homogeneous energy density, at least up to the 10³ Mpc scale, which is usually referred to dark energy. Dark energy (DE) being homogeneous cannot be accounted for by corpuscular particles but may be accountable by the cosmological constant or by some vacuum expectation value (VEV) of spin-0 boson(s) [16–22]. The visible particles (mostly atoms in the energy count) constitute only 5% in the energy pie.

If we accept the Big Bang cosmology from the earliest possible time, 10⁻⁴³ s, the success of the Standard Model of particle physics is based on the assumption of very tiny DE of order less than 10⁻⁴⁶ GeV⁴ because the age of the Universe is very long ≃ 13.8 Gy [1, 2]. So, the DE problem or the theoretical cosmological constant problem [23] is not only the problem in cosmology but also a problem in particle physics. Out of despair, many adopt the anthropic scenario for the cosmological constant problem [24–26]. For the anthropic solution to work, the cosmological constant must be a free undetermined parameter in particle physics, as integration constants of Hawking [27], Kim et al. [28] and Kim [29]. In a deterministic theory such as in string theory, possible cosmological constants must be allowed near 0 for our Universe to have adopted one of these, which is the reason trying to have as many as 10¹²⁰ models, to pack the vacua with separation between them by (10⁻³ eV)⁴, from string theory [26]. But, all those 10¹²⁰ vacua must allow three family Standard Models, and satisfy the known SM phenomena such as the grand unified theory (GUT) scale weak mixing angle sin² θ_W = 3/8 [30–32], etc. But, we have only a handful of minimal supersymmetric Standard Models from string theory satisfying the requirements [33–37]. Or, a Standard Model solution with DE ≃ 10⁻⁴⁷ GeV⁴ has to be found so that the anthropic argument chooses it. This search seems more difficult than finding a vanishing cosmological constant solution theoretically. At present, we can say that the anthopic solution in string theory has not worked out yet. Therefore, in the Standard Model and in its supergravity extension, it is fair to say that the cosmological constant is assumed to be zero.

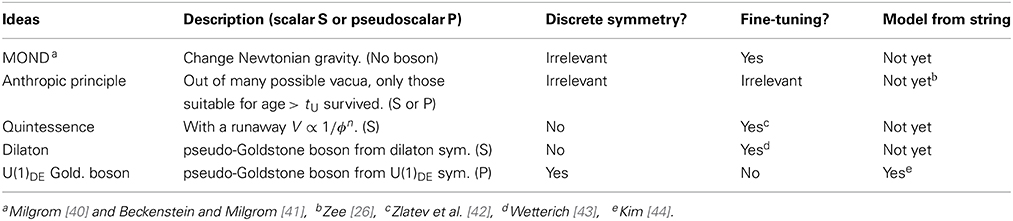
By observing the luminosities of Type-I supernovae [38, 39], the recent acceleration of the Universe has been established. So, explaining the DE scale of 10⁻⁴⁷ GeV⁴ − 10⁻⁴⁶ GeV⁴ became an important topic [19–21]. In Table 1, we list several ideas proposed to account for this recent acceleration of the Universe. Both the high scale inflation [45–47] and the recent acceleration [38, 39] in the Universe are based on the assumption of vanishing cosmological constant.

TABLE 1

Table 1. Typical DE models with a few pseudo-Goldstone bosons originating from global symmetries.

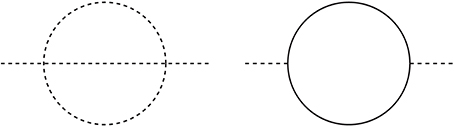
To determine the VEV of a scalar field, say ϕ, one must consider all the allowed effective terms at low energy. At each interaction point, suitable symmetry requirements must be satisfied. A typical mass scale of ϕ is given by the effective mass term m²|ϕ|². In Figure 1, we consider only two diagrams with the dimension 4 (d = 4) couplings. If each d = 4 vertex of Figure 1 satisfies the global phase symmetry, the two-loop and one-loop mass terms do not break the global symmetry. On the other hand, each d = 4 vertex satisfies the dilaton symmetry (requiring just d = 4 couplings) but the diagrams of Figure 1 are d = 2 terms which of course break the dilaton symmetry. One well-known model breaking the dilaton symmetry at the one-loop quantum level, including the d ≥ 6 terms, is the Coleman-Weinberg model [48]. Therefore, it is not likely that a consistent calculation of a small DE scale can be performed by introducing the dilaton symmetry. However, some global phase symmetry may be suitable for this.

FIGURE 1

Figure 1. Diagrams leading to dimension 2 interactions with dimension 4 coupling at each vertex.

In Section 2, we present the focus points of this review: the BCM scenarios and the axion detection experiments. In Section 3, we point out the difficulty of obtaining zero cosmological constant theoretically. In Section 4, we mini-review the inflationary cosmology, in particular in view of the recent BICEP2 data. In Section 5, we discuss the subject of this review: why the role of fundamental spin-0 particles are important in cosmology.

2. Spin-0 Boson Filling the Universe

After the discovery of a fundamental spin-0 scalar particle (the Brout-Englert-Higgs boson) at the LHC, it is timely to study the roles of fundamental spin-0 bosons in the Universe. It is very interesting to note that fundamental spin-0 bosons have been employed to account for the mothers of atoms (i.e., baryon number generation via the Affleck-Dine mechanism [49]), CDM via BCM [4], DE via a transient cosmological constant [50–54], and even the vacuum energy needed for the high scale inflation [45–47]. Among these, we focus on CDM via BCM in this review because similar ideas can be applicable to DE and inflation models. Another attractive point discussing CDM via BCM is that it can be experimentally proved in the near future [55].

We are familiar with the ether idea of the late 19th Century, filling out the Universe. The VEV idea of spin-0 particles used for breaking global symmetries [56] and gauge symmetries [57, 58] is a kind of ether. If a scalar field ϕ has a universal value over the entire Universe, any operation of the type “Poincare transformation” does not notice a change. Thus, the VEV of a scalar field, 〈ϕ〉, respects the Poincare symmetry. But, if ϕ is a complex field, then the VEV breaks the phase transformation symmetry, i.e., breaks a global phase symmetry [56]. Even though the Brout-Englert-Higgs mechanism [57–60] for breaking gauge symmetries is not a monopoly of spin-0 particles [61–63], now the role of spin-0 particles becomes more important, especially after a hint of large tensor-to-scalar ratio r, based on the BICEP2 observation [64].

Let us denote scalar and pseudoscalar particles as s and a, respectively. Scalar particles transform under the parity operation as P : s(x) → + s(−x), and pseudoscalar particles transform as P : a(x) → − a(−x). If they are components of a complex field, it is usually represented as the radial and phase fields, respectively, ϕ = se^ia/f where f is a mass parameter. Thus, the complex field transforms under parity as P: ϕ(x) → ϕ*(−x). Any pseudoscalar field represented as a phase can be represented by an angle field with the angle defined in the range [0, 2Nπ), where N is the domain-wall number. A Goldstone boson arising from breaking a global phase symmetry by the VEV v is a pseudoscalar field a defined as

$\begin{array}{cc}\langle \varphi \rangle =\frac{v+s}{\sqrt{2}}{e}^{ia/f}, \langle s\rangle =0, \langle a\rangle =[0,2N\pi f).& \left(1\right)\end{array}$

2.1. Cosmology with BCM

On the flat Friedmann-Lemaitre-Robertson-Walker cosmological background space described by the line element ds² = − dt² + a²(t)δ_ijdxⁱ dx^j, the evolution of the classical scalar field ϕ, (i.e., the evolution of the VEV of ϕ), is given by

$\begin{array}{cc}\frac{d^2}{d{t}^2}\langle \varphi \rangle +3H\frac{d}{dt}\langle \varphi \rangle +V^{\prime }(\langle \varphi \rangle )=0,& \left(2\right)\end{array}$

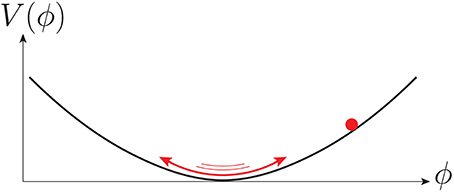
where H = ȧ/a is the Hubble parameter and V′ = (d/d 〈 ϕ〉)V is a derivative of the potential V (a dot represents a derivative with respect to the cosmic time t). With a discrete symmetry ϕ → −ϕ, the leading term of V′ is the mass term m² 〈 ϕ 〉. When 〈 ϕ 〉 moves very slowly, we can neglect the second derivative term, and the evolution equation gives 3H $\dot{\varphi }$ ≃ − m² ϕ. 〈 ϕ 〉 starts to change rapidly when H becomes small enough to satisfy 3H≃ m. After this condition is met, 〈 ϕ 〉 oscillates rapidly, as shown in Figure 2, which is interpreted as the BCM of ϕ.

FIGURE 2

Figure 2. After t₁, the BCM potential of 〈ϕ〉 at the red bullet oscillates around the minimum.

As mentioned above, the VEV 〈 ϕ 〉 is assumed to be the same over the entire Universe for the Poincare invariance, otherwise the invariance is broken. In the Universe, this homogeneity is subtly broken. The inflation manages different scales of quantum fluctuations enter the horizon at different scales, basically breaking the homogeneity. A given scale condenses gravitationally. The VEV in that scale evolves according to Equation (2), and describes the BCM of 〈ϕ 〉.

From the Friedmann equation we have 3H²M²_P = ρ, where ρ is the energy density of the Universe and M_P is the reduced Planck mass (M_P = 2.4 × 10¹⁸ GeV). Denoting the time at the onset of oscillations of 〈ϕ〉 as t₁, the condition for determining t₁ is

$\begin{array}{cc}\sqrt{\frac{3\rho (t_1)}{M_{\text{P}}^2}}=m(t_1).& \left(3\right)\end{array}$

These oscillations are equivalent to a gas of ϕ particles of low-momentum. This kind of spin-0 particle coherent motion was first discussed in Preskill et al. [4], Abbott and Sikivie [5] and Dine and Fischler [6] for the case ϕ = axion. It is known that the BCM behaves like CDM because of the low-momentum. Thus, the number and energy densities are given by

$\begin{array}{cc}n=m{\langle \varphi \rangle }^2,\rho =m^2{\langle \varphi \rangle }^2.& \left(4\right)\end{array}$

We denote the current age of the Universe as t_U. Depending on t₁ and t_U, we can classify BCMs as

• BCM: If t₁ < t_U, the currently oscillating vacuum 〈ϕ〉 is BCM. The BCM can be classified into the following two sub-categories.

⋆ BCM1: The lifetime of ϕ is long enough, τ_ϕ > t_U. Then, the oscillating BCM contributes to the CDM amount. The QCD axion belongs here.

⋆ BCM2: The lifetime of ϕ is short, τ_ϕ < t_U. Then, all ϕ quanta decayed already, producing SM particles. The inflaton with τ_ϕ ~ 10⁻³⁶ s belongs here and reheating after inflation gives the beginning of the radiation-dominated Universe.

• CCtmp: Temporary cosmological constant. On the other hand, if 〈ϕ〉 has not oscillated yet, then t₁ > t_U and 〈ϕ〉 stays there now, behaves like a cosmological constant, but it is a temporary phenomenon and will eventually become BCM1 after t₁. For this to be satisfied, the mass is around 10⁻³³ eV with a trans-Planckian decay constant [65]. If V(〈ϕ〉) describes CCtmp, the equation of state w_ϕ, characterized by the field energy density ${\rho }_{\varphi }=\frac{1}{2}{\dot{\varphi }}^2+V(\varphi )$ and the pressure $P_{\varphi }=\frac{1}{2}{\dot{\varphi }}^2-V(\varphi )$, is a useful parameter,

$\begin{array}{cc}{w}_{\varphi }\equiv \frac{P_{\varphi }}{{\rho }_{\varphi }}=\frac{\frac{1}{2}{\dot{\varphi }}^2-V(\varphi )}{\frac{1}{2}{\dot{\varphi }}^2+V(\varphi )}.& \left(5\right)\end{array}$

Provided that $\frac{1}{2}{\dot{\varphi }}^2\ll V(\varphi )$, w_ϕ is close to −1, behaving like the cosmological constant. In order to realize the recent acceleration, we require the condition $w_{\varphi }<-\frac{1}{3}$.

2.2. Scalar Particles

The Brout-Englert-Higgs boson is the only known fundamental scalar field. The other scalar most widely used in particle theory is dilaton, the scalar Goldstone boson arising from breaking the dilatonic symmetry. The effect of dilatonic symmetry on the cosmological constant problem has been discussed extensively in Wetterich [43]. For the solution, however, a fine-tuning is needed. The obvious effect of a VEV of a scalar field s in cosmology is the universal constant on the right-hand-side of the Einstein equation.

The scalar-field cosmology in the presence of a barotropic perfect fluid was studied in 1980–1990s [43, 66–76], even before the discovery of the recent cosmic acceleration. This was chiefly motivated by the “missing matter problem” in 1980s. In 1990, Fukugita et al. [77] tested cosmological models against observations of the number count of faint galaxies and showed that these data favor the Universe with low matter density (i.e., matter is missing). In the abstract of their paper they stated that “Furthermore, it is shown that the best agreement with the data is obtained with a sizable cosmological constant, including the case of zero curvature model as predicted by inflation.” In addition, it was already known in the early 1990s that the presence of a cosmological constant can make the age of the Universe longer such that it is consistent with the age of oldest globular clusters.

If the cosmological constant originates from a vacuum energy appearing in particle physics, it is vastly larger than the today's average cosmological density [23]. Because of this problem, people tried to construct dynamical cosmological constant models in which the energy density of cosmological constant varies in time, basically belonging to a kind of CCtmp. For example, if we consider a dilaton field ϕ, the cosmological constant depends on ϕ by transforming the dilatonic action to the so-called Einstein-frame action (in which the dilaton does not have a direct coupling with the Ricci scalar) [43, 67].

Exponential potentials often arise from the curvature of internal spaces associated with the geometry of extra dimensions (so called “modulus” fields) [78, 79]. Inspired by this, the exponential potential V(s) = V₀ e^{−λ sM_P} has been used, with constant parameters V₀ and λ. There are two distinct fixed points on the flat Friedmann-Lemaitre-Robertson-Walker cosmological background space [19, 76]: (a) the scaling solution, and (b) the scalar-field dominated solution.

For λ² > 3(1 + w_m), where w_m is the equation of state for a background fluid, the solutions approach the scaling fixed point (a), characterized by the field density parameter Ω_s = 3(1 + w_m)/λ² and the field equation of state w_s = w_m [69, 73, 76]. Even for the initial conditions where ρ_s is larger than ρ_m in the early radiation-dominated era, the field eventually enters the scaling regime in which ρ_s is proportional to ρ_m with ρ_s/ρ_m = constant < 1. The field energy density of the scaling solution contributes to the total energy density of the Universe, but it does not lead to the cosmic acceleration. For λ² < 3(1 + w_m), there exists the scalar-field dominated fixed point (b), characterized by Ω_s = 1 and w_s = −1 + λ²/3. The late-time cosmic acceleration can be realized for λ² < 2. Since in this case the point (b) is also stable, the scalar field can be the source of DE. For λ² < 2, the scalar potential is quite shallow, so the field density in the early Universe needs to be much smaller than the background energy density (unlike the scaling solution discussed above).

After the discovery of the recent cosmic acceleration in 1998, the cosmological dynamics of “quintessence” (a canonical scalar field responsible for DE) were studied in detail for several different potentials [80, 81]. One example is the inverse power-law potential V(s) = M^{4 + n}s⁻ⁿ, where M and n are positive constants. This potential can arise in globally supersymmetric QCD theories [82]¹. The Universe enters the stage of cosmic acceleration for the field value larger than s₀ ≈ M_P. Since V(s₀) is of the order of H²₀M²_P, one can estimate the mass scale M as M ≈ 10^{−(46 − 19n)/(4 + n)} GeV. For n = O(1), this energy scale can be compatible with that appearing in particle physics.

In the presence of a perfect fluid with the equation of state w_m, there exists a so-called tracker solution for the potential V(s) = M^{4 + n}s⁻ⁿ. The tracker is characterized by a common, cosmic evolutionary trajectory that attracts solutions with a wide range of initial conditions [81]. The field equation of state along the tracker is given by w_s = (w_mn − 2)/(n + 2), which corresponds to w_s = −2/(n + 2) > − 1 during the matter era. The slope of the potential λ = −M_P V,_s/V = nM_P/s gets smaller with the growth of s, so w_s approaches −1 in the future. The inverse power-law potential belongs to a class of freezing quintessence models [83] in which the evolution of the field gradually slows down.

There is another class of quintessence models, dubbed thawing models [83], in which the field has been frozen by Hubble friction and then it starts to evolve after the Hubble parameter drops below the field mass m. In this case the field equation of state w_s is close to −1 at the initial stage, but it starts to grow at the late cosmological epoch. The field mass m_s responsible for dark energy corresponds to m_s ≃ 10⁻³³ eV [65]. The representative potential of thawing models is that of a pseudo-scalar field arising from breaking the global U(1) symmetry (which we will explain more details in Section 2.3).

If we consider a scalar field ϕ non-minimally coupled to the Ricci scalar R (like dilaton), this gives rise to a coupling with non-relativistic matter in the Einstein frame [84]. The fifth force induced by such a matter coupling needs to be suppressed in the solar system. There are several ways to suppress the propagation of the fifth force in local regions of the Universe.

One is the so-called chameleon mechanism [85], under which the mass of a scalar degree of freedom is different depending on the matter densities in the surrounding environment. If the effective mass is sufficiently large in the regions of high density, the coupling between the field and non-relativistic matter can be suppressed by having a thin shell inside a spherically symmetric body. In Brans-Dicke theory (including f(R) gravity) [86] it is possible to suppress the propagation of the fifth force by designing the field potential V(ϕ) appropriately [87–92].

Another is the so-called Vainshtein mechanism [93], under which non-linear scalar-field self interactions can suppress the fifth force at short distances even in the absence of the field potential. The self interactions of the form (∂ ϕ)² □ ϕ, which correspond to the Lagrangian of covariant Galileons [94], can lead to the decoupling of the field ϕ from matter within a radius much larger than the solar-system scale [95–98].

2.3. Pseudoscalar Particles

Most pseudoscalar particles observed so far are pseudo-Goldstone bosons. Let a, Λ and f, respectively, be a Goldstone boson from a spontaneously-broken global U(1) symmetry, the dominant explicit symmetry breaking mass parameter, and the decay constant. Then, the mass of a is

$\begin{array}{cc}{m}_a=c_a\frac{{\Lambda }^2}{f},& \left(6\right)\end{array}$

where c_a is the number given by the explicit symmetry breaking terms. For the QCD axion, the breaking of the U(1) symmetry is given by the QCD anomaly and we have c_a Λ² = [Z^1/2/(1 + Z)] f_π m_π with Z = m_u/m_d where f_π, m_π, m_u, m_d are neutral-pion decay constant, its mass, and u and d quark masses [14]. If the explicit breaking term is given by V_br = −(Λ^{4 − n} ϕⁿ + h.c.)/2, then we have m_a = (f/Λ)^n/2 (nΛ²/f). As shown in Figure 1, the pseudo-Goldstone boson arising from a global symmetry U(1)_gl does not appear in the loops if each vertex satisfies U(1)_gl. But, it is known that all global symmetries are approximate [44, 99–102]. Most strong explicit breaking may be from the anomaly of the type U(1)_gl-G-G, where G is a non-Abelian gauge group.

The most waited-for pseudoscalar particle is the very light axion in the axion window because its discovery will confirm at least three: (1) a physical confirmation of instanton solutions of non-Abelian gauge theories [103], (2) ´t Hooft solution [104] of the U(1) problem of QCD [105], and (3) at least some portion of CDM in the Universe. The particle axion was first appreciated by Weinberg and Wilczek in the Ben Lee Memorial Conference in October, 1977 [106], using the Peccei-Quinn (PQ) symmetry [107]. If G is QCD, the symmetry U(1)_gl is called the PQ symmetry U(1)_PQ and the pseudo-Goldstone boson a related to U(1)_PQ is called the QCD axion. The axion is needed to understand the strong CP problem of “Why is the neutron electric diplole moment so small even though the gluon interactions (in the presence of instanton solutions of QCD) allow a neutron-size dipole moment?” In early days, three kinds of solutions to the strong CP problem were admitted [11]: the calculable solution, the massless up quark case, and the axion solution. The calculable solutions have not provided yet an acceptable model with sufficiently small neutron electric dipole moment. The massless up quark case is not favored in the global fit [14]. The remaining axion solution is checked in various cases as discussed in the next Subsect.

Field theory examples on axions with renormalizable couplings corresponding to BCM1 are usually classified to the KSVZ and DFSZ models [7–10]. But, this classification is too simple. There can be many KSVZ and DFSZ type models with one type of quark representations [108]. One may introduce many different types of quarks also for axion phenomenology.

Therefore, it is better to have a theory predicting definite PQ charges of the quarks in a full theory. The most attractive proposal along this line is the string compactification. Here, the PQ global symmetry is determined once the compactification scheme is presented. Standard models obtained from string compactification include many quarks beyond the Standard Model spectrum, in particular numerous singlet fields. Along this line, several years ago a QCD axion including non-renormalizable terms was studied and the axion-photon-photon coupling has been calculated with an approximate U(1)_PQ symmetry [109]. Recently, an exact U(1)_PQ symmetry has been studied in a string compactification where the axion-photon-photon coupling has been calculated below the PQ symmetry breaking scale [110],

$\begin{array}{cc}{c}_{a\gamma \gamma }=\frac{1123}{388}-1.98\simeq 0.91.& \left(7\right)\end{array}$

We expect that more calculations of c_aγγ will be performed in string models with the property of successful Standard Model phenomenologies, which will guide us where to look for the QCD axion [55].

Dark energy can be the case of CCtmp in the above classification. Pseudoscalar CCtmp have been discussed already more than a decade ago in Kim and Nilles [50], Choi [54] and Nomura et al. [111]. But, a more plausible analysis, looking into the detail of string compactification, has been presented recently [44, 102, 112].

The field mass m_a responsible for dark energy corresponds to m_a ≃ 10⁻³³ eV [65]. Meanwhile, if the axion field is responsible for CDM, the typical mass scale is between 10⁻⁵ eV and 10⁻² eV [14]. In string theory there are many ultralight axions possibly down to the Hubble scale H₀ = 10⁻³³ eV [113]. Axions in the mass range between 10⁻²⁸ and 10⁻¹⁸ eV become non-relativistic at a later cosmological epoch relative to the standard CDM. Such a light scalar field leads to the suppression of the CDM power spectrum on small scales [113–115] (like light massive neutrinos), so there is an observational signature for ultralight axions if the axion potential is of the form [1 − cos(a/f_a)]³ [112].²

2.4. Axion Detection

Figure 3 captures the idea behind the main experimental axion dark matter detection effort. There are two equivalent pictures describing the axion to photon conversion in the presence of a Direct-Current (DC) magnetic field B [116–118], briefly described here: The axion decays to two photons through the triangle anomaly. Its lifetime, for an axion mass in the μeV range, is of order 10⁵⁰ s, much larger than the lifetime of our Universe. This decay rate can be significantly enhanced in the presence of a DC B-field via the inverse Primakov effect [116]. This decay rate is additionally enhanced by the density of the final states, e.g., the quality factor Q of a resonant microwave cavity when its resonant frequency coincides with the axion field oscillation frequency.

FIGURE 3

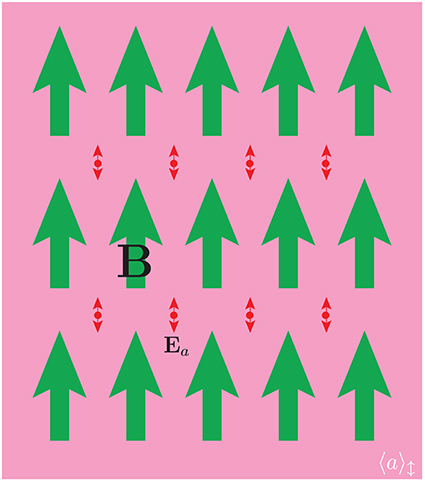
Figure 3. The magnetic and electric field behavior used in the axion detection experiments. The CP violating effect is ∝ B · E, and the oscillating tiny E over the constant large B is schematically drawn. The E follows the oscillation of the classical axion field 〈 a 〉.

In the second picture the axion couples to the product of E · B, where E is an electric field. In the presence of a DC magnetic field there is an oscillating electric field appearing with the same frequency as the axion field. If the DC magnetic field is of finite extent, then the oscillating E-field induces an azimuthal oscillating magnetic field due to Maxwell's equations. If there is a resonant microwave cavity at the same boundary and with the same resonant frequency, it then provides feedback that enhances the oscillating E-field by the quality factor of the cavity [117, 118]. The power conversion of the axion DM to microwave photons estimated by the two methods is the same and it is given by

$\begin{array}{cc}{P}_{a\to \gamma }=g_{a\gamma \gamma }^2\left(\frac{{\rho }_a}{m_a}\right)B_0^{2}V{C}_j{Q}_L,& \left(8\right)\end{array}$

where Q_L is the cavity loaded quality factor, C_j is the mode filling factor, g_{a γ γ} is the axion-photon-photon coupling constant, ρ_a is the axion DM local density, m_a is the axion mass, B₀ is the strength of the DC magnetic field and V the volume of the cavity.

The expected power conversion P_{a → γ} is extra-ordinarily small, but nonetheless it can be within the present experimental capabilities for an axion mass in the 1–20 μ eV range. Have we known the axion mass with a 1 part per million (ppm) accuracy, it would take less than a day to detect it if axions were more than 10% of the DM. The main issue is that, barring the BICEP2 results [119, 120], we have no such information. The best-suited axion DM mass is below about 1 meV all the way to about 1 μeV, spanning three orders of magnitude with a potential line width of about 1 ppm. Clearly, scanning the whole axion mass range will require too many steps, and therefore the sensitivity needs to be very high at each step.

Furthermore, in some theoretical scenarios, the axion DM mass is not constrained from below and can be very light, well below 1 μeV. In addition to the microwave cavity method, which is mostly applicable between 1 and 20 μeV, other methods include looking for axions emitted by Sun's core, and astrophysical limits, as axions can provide another channel of energy loss, significantly altering the star lifetime. An overview of the present experimental/astrophysical limits of the axion coupling constant vs. the axion mass are given in Figure 4.

FIGURE 4

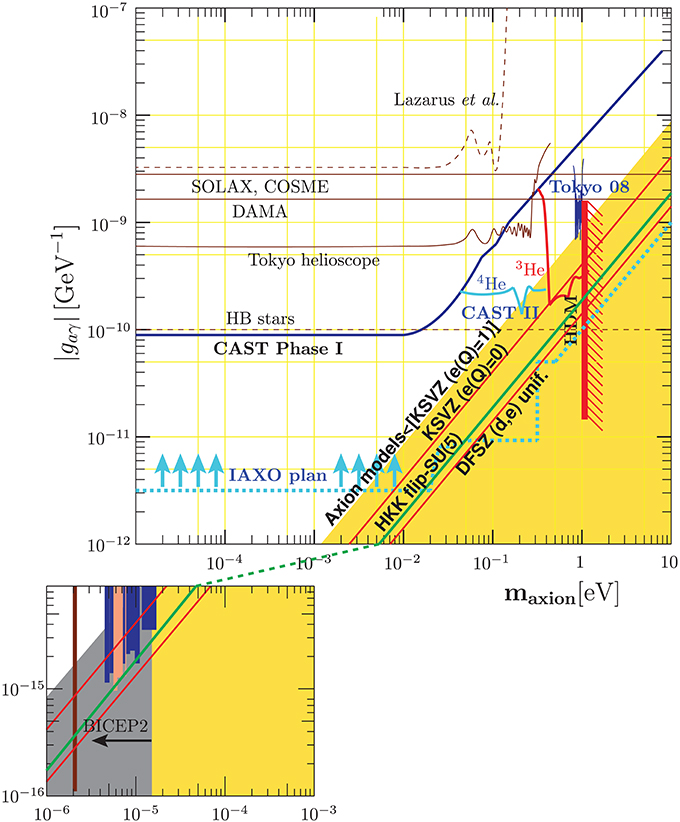
Figure 4. Experimental/astrophysical limits of g_aγ vs. m_a [15]. The experiments giving the limits are shown. The KSVZ and DFSZ lines are from Kim [108], and the string calculation is the green line [110]. The limit of the yellow region is the largest one from kim [108]. The excluded gray region is from Marsh et al. [119] and Vissineli and Gondolo [120], allowing a factor 5 generosity due to the domain wall annihilation problem [165]. The astrophysics lines in the bigger box represent that the regions above those lines are excluded.

Looking at Equation (8), it is clear there is a number of possible improvements one can make in this method: (i) Increase the magnetic field value, (ii) Increase the magnetic field volume, and (iii) Increase the cavity quality factor. The pioneering axion DM experiments that started in the late 1980's [121, 122] probed an axion DM candidate in a limited mass region, assuming a stronger axion to photon coupling than is required by theory by roughly two orders of magnitude.

Over a period of more than 15 years, the dominant axion dark matter experiment (ADMX), currently located at the University of Washington and ADMX-HF located at Yale University, have made several conceptual improvements and have improved on those limits. The second generation ADMX experiment, owing to the development of very low noise SQUID amplifiers just below 1 GHz [123] and a number of additional smaller developments, has reached the boundaries of a plausible axion DM candidates. Currently implementing a dilution refrigerator to their system is expected to allow them to either detect or exclude an axion comprising 100% of the DM for masses in the range 1–20 μeV.

The new Center for Axion and Precision Physics (CAPP)³ established by the Institute for Basic Science in South Korea⁴, plans to either detect or exclude an axion DM component down to the 10% level for a similar axion mass range. This will be achieved by Semertzidis [55] (a) Development of a 25 T and then a 35 T solenoidal magnet compared to the currently used 8–9 T solenoidal magnets, (b) Substantially improving, roughly by an order of magnitude, the quality factor of the microwave cavities in the presence of strong magnetic fields, and (c) Constructing and running a toroidal cavity with a large volume and a reasonable B-field value so that the overall product B² V is an order of magnitude larger than present values.

The commonly used NbTi superconducting cable has a critical current that falls very rapidly as the magnetic field increases above 10 T, making it unsuitable to obtain higher B-field strengths. However, recent developments with high T_c cables makes possible achieving much higher current densities at large B-field values, when they are cooled at low temperatures around 4 K. This is an experimental method fueled by the energy-storage field and prototype magnets are already under development. CAPP is collaborating with the Magnet Division of Brookhaven National Laboratory to develop a 10 cm inner bore diameter capable of producing around 25 T of magnetic field. Preliminary tests on different high T_c cables are providing encouraging results that the goal can be met. The expected time period for this development is of order of 5 years, after which we develop a separate magnet with a goal of achieving 35 T peak magnetic field, albeit with smaller inner bore diameter. The next step would be to configure a toroidal magnetic field, optimizing the use of the magnetic field as the fringe field is minimized in that geometry. Preliminary cable testing results also point to this geometry for achieving the highest possible magnetic field values. The time scale for this development is of order 10 years.

The presently used cavities have a quality factor between 50 and 100 K. It has been reported by ADMX that they are developing cavities with thin-film superconducting coatings on the vertical side walls with the goal of increasing the cavity quality factor by roughly a factor of five. This is possible when the B-field is shaped to be aligned with the vertical wall, minimizing the transverse B-field below about 100 Gauss. Further increases of the quality factor are hindered by the top/bottom surfaces of the right-cylindrical cavity as the magnetic field angle traversing the surface is very close to 90°. Our plan to further improve upon this achievement is two-fold: First, develop a toroidal cavity where the B-field can be shaped along the cavity walls reducing the transverse B-field below the required level. If that is possible, the quality factor can be increased by several orders of magnitude. Second, the top/bottom plates are going to be treated in a way that the B-field can penetrate it without affecting the superconducting layer on the inside of the cavity. Again, the quality factor can potentially increase by several orders of magnitude.

The expected axion width is of order 1 ppm, i.e., the axion quality factor is a bit better than 10⁶. Therefore, the best one can do is to produce a cavity with the same quality factor, so the best one can expect is to gain a factor of 10–20 in the axion to photon power conversion. The scanning speed goes as the square root of the quality factor since there are more steps required in order to cover all possible frequencies, i.e., the best one can expect to do is a scanning speed improvement factor between three and five.

BICEP2 results favor axion masses in the meV range, albeit with only 1–10% of DM composed of axions. This fact makes it particularly difficult to detect it as the volume of microwave cavities are particularly small and not of much practical use at those frequencies, plus the axion DM density is very weak. If the BICEP2 results turn out to be confirmed,⁵ one could follow a different strategy in detecting axions [124]. If the axion mass were to be found, then one could launch a dedicated axion DM experiment within a very small axion mass range having much higher chances of success.

3. The Cosmological Constant Problem and String Theory

In order to realize the present-day cosmic acceleration with the cosmological constant Λ, we require that Λ is of the order of H²₀, i.e., Λ ≈ H²₀ = (2.1332h × 10⁻⁴² GeV)², where h ≈ 0.7. This corresponds to the energy density ρ_Λ ≈ Λ M²_P ≈ 10⁻¹²⁰M⁴_P. Even before the discovery of the present-day cosmic acceleration, Weinberg [24] put the bound on ρ_Λ, as

$\begin{array}{cc}-2\times {10}^{-120}{M}_{\text{P}}^4\lesssim {\rho }_{\Lambda }\lesssim 6\times {10}^{-118}{M}_{\text{P}}^4.& \left(9\right)\end{array}$

The lower bound comes from the fact that the negative cosmological constant does not lead to the collapse of the Universe today. The upper bound corresponds to the requirement that the vacuum energy does not dominate over the matter density for redshifts z larger than 1 to realize the successful structure formation.

There have been attempts to explain the very low values of ρ_Λ ranging the Weinberg bound (9). For example, Bousso and Polchinski [126] employed the 4-form field F_{μ ν λ σ} with the energy density F_{μ ν λ σ}F^{μ ν λ σ}/48 = c²/2, where c is a constant. In the context of string theory, there are “electric charges” (membranes) sourcing the 4-form field dual to “magnetic charges” (5-branes). The constant c can be quantized in integer (n) multiples of the membrane charge q, such that c = nq.

Bousso and Polchinski introduced J 4-form fields together with J membrane species with charges q₁, q₂, …, q_J. The number J can be as large as 100 in string theory. Since the flux energy density of each charge is given by n²_iq²_i/2, the effective cosmological constant reads

$\begin{array}{cc}\Lambda ={\Lambda }_b+{\displaystyle \sum _{i=1}^J{n}_i^2}{q}_i^2/2,& \left(10\right)\end{array}$

where Λ_b is the bare cosmological constant. For the anti de Sitter minimum with Λ_b < 0, there exist integers n_i satisfying

$\begin{array}{cc}2|{\Lambda }_b|<{\displaystyle \sum _{i=1}^J{n}_i^2}{q}_i^2<2(|{\Lambda }_b|+\Delta \Lambda ),& \left(11\right)\end{array}$

where ΔΛ ≃⁻¹²³ in the unit M_P = 1.

If we consider a J-dimensional grid with axes corresponding to n_iq_i, the displacement of the 4-form field is given by discrete grid points with integers n_i. The region (11) corresponds to a thin-shell characterized by the radius $r=\sqrt{2|{\Lambda }_b|}$ and the width $\Delta r=\Delta \Lambda /\sqrt{2|{\Lambda }_b|}$. The volume of the thin-shell is

$\begin{array}{cc}{V}_S={\Omega }_{J-1}{r}^{J-1}\Delta r={\Omega }_{J-1}|2{\Lambda }_b{|}^{J/2-1}\Delta \Lambda ,& \left(12\right)\end{array}$

where Ω_{J − 1} = 2π^J/2/Γ(J/2) is the area of a unit (J − 1)-dimensional sphere. A grid cell has a volume $V_C={\displaystyle {\prod }_{i=1}^J{q}_i}$. There is at least one value of Λ for V_C < V_S, i.e.,

$\begin{array}{cc}{\displaystyle \prod _{i=1}^J{q}_i}<\frac{2{\pi }^{J/2}}{\Gamma (J/2)}|2{\Lambda }_b{|}^{J/2-1}\Delta \Lambda .& \left(13\right)\end{array}$

When J = 100, |Λ_b| = 1 and ΔV = 10⁻¹²³ with equal charges (q_i = q, for i = 1, 2, …, J), the condition (13) is satisfied for q < 0.035. Since the charge $\sqrt{q}$ has the dimension of mass from Equation (10), this condition translates to $\sqrt{q}$ < 0.19 in units of M_P. Thus, the presence of many 4-form fields allows the possibility of realizing a small effective cosmological constant.

The idea of Bousso and Polchinski is based on the flux energy density originating from multiple 4-form fields. This idea was extended to the so-called flux compactification on a Calabi-Yau manifold in type II string theory. In the presence of fluxes, Kachru et al. [127] first set up a supersymmetric anti de Sitter (AdS) vacuum with all moduli fields fixed. Then, they obtained a de Sitter vacuum by adding an anti D3-brane in a warped geometry to lift up the AdS state.

There are hundreds of different 3-cycles on the Calabi-Yau manifold in the flux compactification. A macroscopic observer can view a 5-brane wrapping a 3-cycle as a 2-brane (membrane). The 5-brane can wrap any of these 3-cycles, which gives rise to hundreds of different membranes in four-dimensional space-time. The number of vacua appearing in string theory can be extremely large. For 500 three-cycles with each cycle wrapped by up to 10 fluxes, we have 10⁵⁰⁰ vacua.

The possible presence of such a large amount of vacua led to the notion of so-called string landscape [128]. This landscape includes so many possible configurations of local minima, among which our Universe may correspond to one of them. Each vacuum in the string landscape has different matter and coupling constant. The Standard Model is not predicted uniquely in this picture. The argument is that we may be able to find a vacuum with an extremely small energy density among 10⁵⁰⁰ vacua. However, this anthropic argument depends on “Those packed near Λ = 0 out of 10⁵⁰⁰ vacua describe particle phenomenology correctly, in particular with three chiral families and sin² θ_W = 3/8,” otherwise the landscpe vacua differring by ΔΛ describe unacceptable universes. From this reasoning, the string landscape is commented in Table 1 as “not yet” established.

A general problem with the anthropic arguments is that they are often applied to a single parameter while fixing all the others. A parameter value that is ruled out in one case may be acceptable if something else is changed at the same time. In this sense, it is not clear that the anthropic arguments of Λ provide a satisfactory answer to the cosmological constant problem.

As commented before, the DE scale may be accountable from highly suppressed non-renormalizable terms in string-allowed discrete symmetries [44, 102] if the true vacuum has zero cosmological constant. In this sense, the theoretical solution toward the vanishing cosmological constant is more difficult to solve than obtaining a tiny DE scale on top of the vanishing cosmological constant [23, 26].

4. Inflation

The possibility of an exponential expansion of the Universe was known [129–133] even before the influential paper of Guth [45] which advocates diluting away the GUT scale monopoles [134]. For example, in the abstract of the Kazanas's paper [132], it is stated that “…In particular it is shown that under certain conditions this expansion law is exponential. It is further argued that under reasonable assumptions for the mass of the associated Higgs boson this expansion stage could last long enough to potentially account for the observed isotropy of the universe.” In the papers of Sato [130, 131], diluting away topological defects such as monopoles and domain walls was stressed after the advent of the modern GUT model [135, 136]. In the Guth's paper [45] it was clearly emphasized that the inflationary paradigm can address the solutions for the homogeneous, horizon and flatness problems.

The scalar field responsible for inflation is called “inflaton.” The inflaton field is a superposition of quanta of all possible wave lengths. A quantum fluctuating scale inflates exponentially and after passing the horizon, it is stretched exponentially with an almost scale-invariant form [137–141] and the frozen-scale still inflates exponentially (see [142] for a review). Different fluctuating scales go out of the horizon at different cosmic times and their exponentially stretched scales are correlated.

After the end of inflation, the quantum fluctuations enter the horizon again and become the sources of density perturbations. The prediction of nearly scale-invariant primordial perturbations generated during inflation was consistent with the temperature anisotropies of Cosmic Microwave Background (CMB) observed by the COBE satellite [143]. The recent WMAP and the Planck data of CMB refined the temperature anisotropies to very high accuracy [1, 2]⁶.

The observables and the constraints implied by inflation are

• A sufficient inflation, requiring the large e-fold number, N_e > 70, for addressing horizon and flatness problems.

• The amplitude of temperature anisotropies δ T/T ≃ 10⁻⁵, for galaxy formation with CDM.

• The spectral index of scalar perturbations n_s ≃ 0.96, from WMAP and Planck data.

• The tensor-to-scalar ratio r ≲ 0.2, from WMAP and Planck data.

• The non-linear estimator of scalar non-Gaussianities for the local shape f^local_NL = 2.7 ± 5.8 (68% CL), from Planck data.

As long as the slow-roll conditions are satisfied, the single-field inflationary scenario generally gives rise to local non-Gaussianities with |f^local_NL| much smaller than 1 even for most general scalar-tensor theories with second order equations of motion [145–147]. Hence the slow-roll single-field models are consistent with the Planck bound of non-Gaussianities. Using the observational bounds of n_s and r, we can distinguish between many single-field inflationary models [148–150]. For example, the self-coupling potential V(ϕ) = λ ϕ⁴/4 [151] and hybrid inflation [152] with n_s > 1 are disfavored from the data.

The amplitude of tensor perturbations is given by P_h = 2H²/(π² M²_P), so the detection of gravitational waves in CMB observations implies that the energy scale of inflation is directly known [153–157]. Since the B-mode polarization of CMB is generated by tensor perturbations but not by scalar perturbations, the B-mode detection is a smoking gun for the existence of primordial gravitational waves.

If the tensor-to-scalar ratio r is smaller than the order of 0.01, it is not easy to detect the CMB B-mode polarization.⁷ If r is detected in the range r > 0.05, then the energy scale during inflation corresponds to the GUT scale. The great interest in the announcement of r ~ 0.16 from the BICEP2 group [64] is because of the implication that the Universe once passed the vacuum energy scale of 10¹⁶ GeV. Even though the GUT scale M_GUT is humongous from our TeV scale Standard Model, it is tiny from the point of gravity scale, the Planck mass M_P. Because of the micro density perturbation, the vacuum energy at the scale (10¹⁶ GeV)⁴ leads to r ~ O(0.1). This phenomenon of the GUT scale energy density during inflation is usually parametrized by chaotic inflation with the potential $V(\varphi )=\frac{1}{2}{m}^2{\varphi }^2$ [151].

If a large r of order 0.2 is detected, the field value in the ϕ² chaotic inflation is bounded from below, i.e., 〈ϕ〉 > 15M_P, which is known as the “Lyth bound” [158]. This situation is shown in Figure 5, where the energy density at the inflationary epoch is the GUT scale. The field value 〈ϕ〉 > 15M_P is trans-Planckian and the energy density at M_P is tiny. So, one needs a fine-tuning in the ϕ² chaotic inflation. Introducing a confining force at a GUT scale, a heavy axion for the inflaton with a potential bounded from above was proposed [159], which is called natural inflation. In this scenario, the energy density has the upper bound of order M_GUT⁴ as shown in Figure 6A. One period of the inflaton in this case is of order M_GUT, and hence the Lyth bound is violated. To remedy this, two confining forces are introduced with two heavy axions with the resulting potential [160],

$\begin{array}{cc}\begin{array}{l}V=-{\Lambda }_1^4\cos \left(\alpha \frac{a_1}{F_1}+\beta \frac{a_2}{F_2}\right)\\ -{\Lambda }_2^4\cos \left(\gamma \frac{a_1}{F_1}+\delta \frac{a_2}{F_2}\right)+\text{constant},\end{array}& \left(14\right)\end{array}$

FIGURE 5

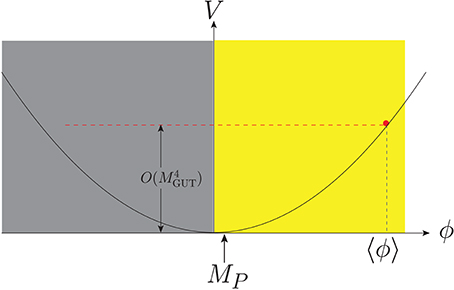
Figure 5. The chaotic inflation with m² ϕ² [151]. The red bullet is the Lyth bound which is far above M_P.

FIGURE 6

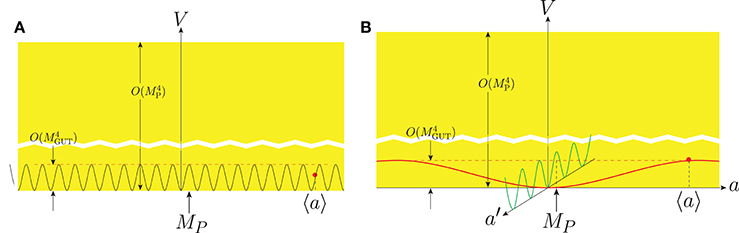
Figure 6. (A) The natural inflation of Freese et al. [159]; (B) The 2-flation [160]. The red bullet in the 2-flation is an O(1) value of 〈 a 〉/f_a.

where α, β, γ, and δ are determined by the corresponding PQ symmetries of two heavy axions a₁ and a₂. Even though we allow O(1) couplings, the GUT mass scales can lead to M_P with the probability of ~1%. With mass parameters of 50M_GUT, we would obtain 50M_P with the probability of ~1%. This is the Kim-Nilles-Peloso 2-flation model [160]. The probability of the 2-flation model with a large decay constant, i.e., f_ϕ >15M_P to occur as shown in Figure 6B, is about 1%. The green-potential in Figure 6B is the other heavy axion potential. It can be generalized to N-flation [161].

The axionic topological defects in the anthropic window [25, 162] can be diluted away if inflation occurs below the anthropic window scale. With the GUT scale energy density during inflation, however, this dilution mechanism does not work. With the GUT energy scale inflation as implied by the BICEP2 [64], it could have pinned down to f_a ~ 10¹¹ GeV [119, 120], using the numerical calculation of radiating axions from axionic string-wall system [163]. In the numerical calculation, the Vilenkin-Everett mechanism [164] of erasing the horizon scale string has not been taken into account. In addition, the hidden-sector confining force can erase horizon scale axionic strings such that the QCD axion domain wall is not a serious cosmological problem [165]. The hidden-sector solution needs the hidden-sector domain-wall number of N_h = 1, which is possible in string compactification with an anomalous U(1) [166].

In addition to pinning down the upper bound on f_a, the GUT scale inflation provokes a question, “What is the symmetry which naturally satisfies the Lyth bound [158]?” Lyth considered this problem with respect to the η parameter [167]. But, there exists a more fundamental question. In an ultra-violet completed theory such as string theory, every parameter is calculable. If we consider the ϕ² chaotic inflation of Figure 5, there is a question, “Why do we neglect other terms?” In string theory, only discrete symmetries are permitted by the compactification process. For example, a term ϕ¹⁰⁴/M¹⁰⁰_P can be possible if the discrete symmetries allow it. But with the trans-Planckian value, for example 〈 ϕ 〉 ~ 31, the coefficient must be tuned to 1 out of 10¹²⁷, which is as bad as the cosmological constant problem.

Fortunately, there is another way for inflation to occur. We must choose the hilltop inflation, but sacrificing the single-field inflaton. It is not so bad in view of the fact that the 2-flation model already introduced two axions in the inflaton sector. Then, the inflating region is near origin such that the minimum at f_DE is far away from the origin. In the region [0, f_DE] the vacuum energy is of order M⁴_GUT. This can be obtained from the condition on the quantum numbers of the assumed discrete symmetry [168]. The inflaton rolls in the yellow region in Figure 7 where the inflaton takes a green curve in the two-inflatons space.

FIGURE 7

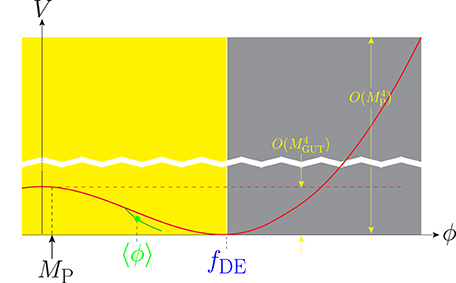
Figure 7. The hilltop inflation [159]. The green bullet is the point whose effects are observed by the BICEP2 group.

5. Discussion

After the discovery of the fundamental Brout-Englert-Higgs boson, which is represented as H_u and H_d (= H^†_u in non − SUSY case), we reviewed the cosmological role of spin-0 bosons. This finding hints the possibility of numerous spin-0 bosons (ϕ) at the GUT scale. Spin-0 bosons at the GUT scale of the canonical dimension 1 can have more important effects to low energy physics compared to those of spin-$\frac{1}{2}$ fermions of the canonical dimension $\frac{3}{2}$ (Dirac fermions ψ, ψ for example) at the GUT scale. For example, the spin-0 contribution

$\begin{array}{cc}\frac{{\varphi }^{2n}}{M_{\text{P}}^{2n+2m-4}}{(H_d{H}_u)}^m& \left(15\right)\end{array}$

dominates the fermion contribution $\frac{{\psi }^n{\overline{\psi }}^n}{M_{\text{P}}^{3n+2m-4}}{(H_d{H}_u)}^m$ for n, m ≥ 1. In addition, the existence of fundamental spin-0 bosons at the GUT scale may be extended to a larger symmetry: supersymmetric GUTs, or minimal supersymmetric Standard Models from string compactification. The interactions of the singlet fields only can take a SUSY superpotential, for example with GUT scale singlets ϕ and trans-Planckian singlets Φ for simplicity [168]

$\begin{array}{cc}W={\displaystyle \sum _i\frac{{\varphi }^{a_i}}{M_{\text{P}}^{a_i+{\ell }_i-3}}}{\Phi }^{{\ell }_i}.& \left(16\right)\end{array}$

The rationale leading to the forms of Equations (15) and (16) are the discrete symmetries obtained from string compactification [44],⁸ which guarantees the absence of gravity obstruction of discrete symmetries, for example via wormholes [99]. The form of the interactionis (16) can lead to inflation with trans-Planckian decay constant with a multi-field hilltop potential, i.e., BCM2. The form of the interactionis (15) can lead to QCD axion via BCM1, and the DE scale via CCtmp. The fundamental scalars at the TeV, GUT and trans-Planckian scales allow all scenarios presented in Subsection 2.1. These are worked out on top of vanishing cosmological constant, which is assumed in any particle physics models. At present, we do not have any persuasive hint toward a theoretical solution of the vanishing cosmological constant. Any theory for the vanishing cosmological constant must satisfy the requirements of particle phenomenology we used in this review.

The fundamental scalars may be detectable if their couplings to gluons are appreciable. The front runner in the search of fundamental scalars hinting high energy (GUT or intermediate) scales is the QCD axion which couples to the gluon anomaly.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Jihn E. Kim is supported in part by the National Research Foundation (NRF) grant funded by the Korean Government (MEST) (No. 2005-0093841) and by the IBS (IBS-R017-D1-2014-a00), Yannis K. Semertzidis is supported by the IBS (IBS-R017-D1-2014-a00), and Shinji Tsujikawa is supported by the Grant-in-Aid for Scientific Research from JSPS (No. 24540286).

Footnotes

1. ^However, the scalar in this case is composite.

2. ^For this specific form, one needs fine-tunings between domain wall number one, two, and three terms in the potential.

3. ^http://capp.ibs.re.kr/html/capp_en/

4. ^http://www.ibs.re.kr/eng.do/

5. ^We note that the recent Planck-dust report extrapolated to the BICEP2 field gives the dust contribution similar to r ≈ 2 without the dust contribution [125].

6. ^From the Planck data the existence of CDM was also confirmed (by 7 σ [144]) better than any other data.

7. ^However, the future observations like LiteBIRD may reach this range.

8. ^See, also, the discrete gauge symmetries in the field theory language [101].

References

1. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F, et al. (Planck Collaboration). Planck 2013 results XXII: constraints on inflation. (2013) [arXiv:1303.5082 [astro-ph.CO]].

Google Scholar

2. Hinshaw G, Larson D, Komatsu E, Spergel DN, Bennett CL, Dunkley J, et al. (WMAP Collaboration). Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological parameter results. Astrophys J Suppl. (2013) 208:19. doi: 10.1088/0067-0049/208/2/19

CrossRef Full Text | Google Scholar

3. Zwicky F. Spectral displacement of extra galactic nebulae. Helv Phys Acta (1933) 6:110.

4. Preskill J, Wise MB, Wilczek F. Cosmology of the invisible axion. Phys Lett B (1983) 120:127–32. doi: 10.1016/0370-2693(83)90637-8

CrossRef Full Text | Google Scholar

5. Abbott LF, Sikivie PA. Cosmological bound on the invisible axion. Phys Lett B (1983) 120:133–6. doi: 10.1016/0370-2693(83)90638-X

CrossRef Full Text | Google Scholar

6. Dine M, Fischler W. The not so harmless axion. (1983) Phys Lett B 120:137–41. doi: 10.1016/0370-2693(83)90639-1

CrossRef Full Text | Google Scholar

7. Kim JE. Weak interaction singlet and strong CP invariance. Phys Lett B (1979) 43:103–7. doi: 10.1103/PhysRevLett.43.103

CrossRef Full Text | Google Scholar

8. Shifman MA, Vainstein VI, Zakharov VI. Can confinement ensure natural CP invariance of strong interactions?. Nucl Phys B (1980) 166:4933. doi: 10.1016/0550-3213(80)90209-6

CrossRef Full Text | Google Scholar

9. Zhitnitsky AP. On possible suppression of the axion hadron interactions. (In Russian) Yad. Fiz. (1980) 31:497–504. Sov J Nucl Phys. 31:260.

10. Dine M, Fischler W, Srednicki M. A simple solution to the strong CP problem with a harmless axion. Phys Lett B (1981) 104:199–202. doi: 10.1016/0370-2693(81)90590-6

CrossRef Full Text | Google Scholar

11. Kim JE. Light pseudoscalars, particle physics and cosmology. (1986) Phys Rep. 150:1–177. doi: 10.1016/0370-1573(87)90017-2

CrossRef Full Text | Google Scholar

12. Cheng H-Y. The strong CP problem revisited. (1988) Phys Rep. 158:1–89. doi: 10.1016/0370-1573(88)90135-4

CrossRef Full Text | Google Scholar

13. Peccei RD. CP Violation. In: C. Jarlskog, editors. Adv. Ser. Direct. High Energy Phys. Singapore: World Scientific (1989). p. 503–51.

14. Kim JE, Carosi G. Axions and the strong CP problem. Rev Mod Phys. (2010) 82:557–602. doi: 10.1103/RevModPhys.82.557

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

15. Baer H, Choi K-Y, Kim JE, Roszkowski L. Dark matter production in the early Universe: beyond the thermal WIMP paradigm. [arXiv:1407.0017 [hep-ph]].

16. Sanhi V, Starobinsky A. The case for a positive cosmological Λ term. Int J Mod Phys D (2000) 9:373–444. doi: 10.1142/S0218271800000542

CrossRef Full Text | Google Scholar

17. Peebles P, Ratra B. The cosmological constant and dark energy. Rev Mod Phys. (2003) 75:559–606. doi: 10.1103/RevModPhys.75.559

CrossRef Full Text | Google Scholar

18. Padmanabhan T. Cosmological constant: the weight of the vacuum. Phys Rep. (2003) 380:235–320. doi: 10.1016/S0370-1573(03)00120-0

CrossRef Full Text | Google Scholar

19. Copeland EJ, Sami M, Tsujikawa S. Dynamics of dark energy. Int J Mod Phys D (2006) 15:1753–936. doi: 10.1142/S021827180600942X

CrossRef Full Text | Google Scholar

20. Silvestri A, Trodden M. Approaches to understanding cosmic acceleration. Rept Prog Phys. (2009) 72:096901. doi: 10.1088/0034-4885/72/9/096901

CrossRef Full Text | Google Scholar

21. Caldwell RR, Kamionkowski M. The physics of cosmic acceleration. Ann Rev Nucl. (2009) 59:397–429. doi: 10.1146/annurev-nucl-010709-151330

CrossRef Full Text | Google Scholar

22. Tsujikawa S. Dark energy: investigation and modeling. Astrophys Space Sci Library (2011) 370:331–402. doi: 10.1007/978-90-481-8685-3-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

23. Weinberg S. The cosmological constant problem. (1989) 61:1–23. doi: 10.1103/RevModPhys.61.1

CrossRef Full Text | Google Scholar

24. Weinberg S. Anthropic bound on the cosmological constant. Phys Rev Lett. (1987) 59:2607–10. doi: 10.1103/PhysRevLett.59.2607

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

25. Tegmark M, Aguirre A, Rees M, Wilczek F. Dimensionless constants, cosmology and other dark matters. Phys Rev D (2006) 73:023505. doi: 10.1103/PhysRevD.73.023505

CrossRef Full Text | Google Scholar

26. Zee A. Einstein Gravity in a Knutshell. Princeton, NJ: Princeton University Press (2013).

27. Hawking SW. The cosmological constant is probably zero. Phys Lett B (1984) 134:403–4. doi: 10.1016/0370-2693(84)91370-4

CrossRef Full Text | Google Scholar

28. Kim JE, Kyae B, Lee HM. Randall-Sundrum model for selftuning the cosmological constant. Phys Rev Lett. (2000) 86:4223–6. doi: 10.1103/PhysRevLett.86.4223

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

29. Kim JE. Cosmological constant is probably adjustable in brane worlds. Phys Rev D (2009) 81:123018. doi: 10.1103/PhysRevD.81.123018

CrossRef Full Text | Google Scholar

30. Kim JE, Langacker P, Levine M, Williams HH. A Theoretical and experimental review of the weak neutral current: a determination of its Structure and limits on deviations from the minimal SU(2)_L × U(1) Electroweak Theory. Rev Mod Phys. (1981) 53:211–52. doi: 10.1103/RevModPhys.53.211

CrossRef Full Text | Google Scholar

31. Langacker P, Luo M-X. Implications of precision electroweak experiments for M_t, ρ₀, sin² θ_W and grand unification. Phys Rev D (1991) 44:817–22. doi: 10.1103/PhysRevD.44.817

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

32. Kim JE. Z₃ orbifold construction of SU(3)³ GUT with ${\sin }^2{\theta }_W^0=\frac{3}{8}$. Phys Lett B (2003) 564:35–41. doi: 10.1016/S0370-2693(03)00567-7

CrossRef Full Text

33. Kobayashi T, Raby S, Zhang R. Searching for realistic 4d string models with a Pati-Salam symmetry – Orbifold grand unified theories from heterotic string compactification on a Z₆ orbifold. Nucl Phys B (2005) 704:3–55. doi: 10.1016/j.nuclphysb.2004.10.035

CrossRef Full Text | Google Scholar

34. Kim JE, Kyae B. Flipped SU(5) from Z_12-I orbifold with Wilson line. Nucl Phys B (2007) 770:47–82. doi: 10.1016/j.nuclphysb.2007.02.008

CrossRef Full Text | Google Scholar

35. Huh J-H, Kim JE, Kyae B. SU(5)_flip × SU(5)′ from Z_12−I. Phys Rev D (2009) 80:115012. doi: 10.1103/PhysRevD.80.115012

CrossRef Full Text | Google Scholar

36. Lebedev O, Nilles HP, Ramo-Sanches S, Raby S, Ratz M, Vaudrevange PKS, et al. A mini-landscape of exact MSSM spectra in heterotic orbifolds. Phys Lett B (2007) 645:88–94. doi: 10.1016/j.physletb.2006.12.012

CrossRef Full Text | Google Scholar

37. Nilles HP, Ramo-Sanches S, Ratz M, Vaudrevange PKS. From strings to the MSSM. Euro Phys J C (2009) 59:249–67. doi: 10.1140/epjc/s10052-008-0740-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

38. Perlmutter S, Aldering G, Goldhaber G, Knop AR, Nugent P, Castro PG, et al. (Supernova Cosmology Project). Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys J. (1999) 517:565–86. doi: 10.1086/307221

CrossRef Full Text | Google Scholar

39. Riess1 AG, Filippenko AV, Challis P, Clocchiatti A, Diercks A, Garnavich PM, et al. (Supernova Search Team). Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astrophys J. (1998) 116:1009–38. doi: 10.1086/300499

CrossRef Full Text | Google Scholar

40. Milgrom MA. Modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys J. (1983) 270:365–70. doi: 10.1086/161130

CrossRef Full Text | Google Scholar

41. Beckenstein J, Milgrom M. Does the missing mass problem signal the breakdown of Newtonian gravity?. Astrophys J. (1984) 286:7–14. doi: 10.1086/162570

CrossRef Full Text

42. Zlatev I, Wang L, Stenhardt PJ. Quintessence, cosmic coincidence, and the cosmological constant. Phys Rev Lett. (1998) 82:896–9. doi: 10.1103/PhysRevLett.82.896

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

43. Wetterich C. Cosmology and the fate of dilatation symmetry. Nucl Phys B (1988) 302:668–96. doi: 10.1016/0550-3213(88)90193-9

CrossRef Full Text | Google Scholar

44. Kim JE, Nilles HP. Dark energy from approximate U(1)_de symmetry. Phys Lett B (2014) 730:53–8. doi: 10.1016/j.physletb.2014.01.031

CrossRef Full Text | Google Scholar

45. Guth A. The inflationary universe: a possible solution to the Horizon and flatness problems. Phys Rev D (1981) 23:347–56. doi: 10.1103/PhysRevD.23.347

CrossRef Full Text | Google Scholar

46. Linde AD. A new inflationary universe scenario: a possible solution of the Horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys Lett B (1982) 108:389–93. doi: 10.1016/0370-2693(82)91219-9

CrossRef Full Text | Google Scholar

47. Albrecht A, Steinhardt PJ. Cosmology for grand unified theories with radiatively induced symmetry breaking. Phys Rev Lett. (1982) 48:1220–3. doi: 10.1103/PhysRevLett.48.1220

CrossRef Full Text | Google Scholar

48. Coleman SR, Weinberg EJ. Radiative corrections as the origin of spontaneous symmetry breaking. Phys Rev D (1973) 7:1888–910. doi: 10.1103/PhysRevD.7.1888

CrossRef Full Text | Google Scholar

49. Affleck I, Dine M. A new mechanism for baryogenesis. Nucl Phys B (1985) 249:361. doi: 10.1016/0550-3213(85)90021-5

CrossRef Full Text | Google Scholar

50. Kim JE, Nilles HP. A quintessential axion. Phys Lett B (2003) 553:1–6. doi: 10.1016/S0370-2693(02)03148-9

CrossRef Full Text | Google Scholar

51. Kim JE. Axion and almost massless quark as ingredients of quintessence. JHEP (1999) 9905:022. doi: 10.1088/1126-6708/1999/05/022

CrossRef Full Text | Google Scholar

52. Kim JE. Model dependent axion as quintessence with almost massless hidden sector quarks. JHEP (2000) 0006:016. doi: 10.1088/1126-6708/2000/06/016

CrossRef Full Text | Google Scholar

53. Kim JE, Nilles HP. Axionic dark energy and a composite QCD axion. JCAP (2009) 0905:010. doi: 10.1088/1475-7516/2009/05/010

CrossRef Full Text | Google Scholar

54. Choi K. String or M theory axion as a quintessence. Phys Rev D (2000) 62:043509. doi: 10.1103/PhysRevD.62.043509

CrossRef Full Text | Google Scholar

55. Semertzidis Y. Talk Presented at “10th Patras Workshop on Axions, WIMPs, and WISPs,” CERN, 29 June – 4 July. Geneva (2014).

56. Goldstone J. Field theories with superconductor solutions. Nuovo Cim. (1961) 19:154–64. doi: 10.1007/BF02812722

CrossRef Full Text | Google Scholar

57. Higgs PW. Broken symmetries, massless particles and gauge fields. Phys Lett B (1964) 12:132–3. doi: 10.1016/0031-9163(64)91136-9;

CrossRef Full Text

58. Higgs PW. Broken symmetries and the masses of gauge bosons. Phys Rev Lett. (1964) 13:508–9. doi: 10.1103/PhysRevLett.13.508

CrossRef Full Text

59. Brout R, Englert F. Broken symmetry and the mass of gauge vector mesons. Phys Rev Lett. (1964) 13:321–3. doi: 10.1103/PhysRevLett.13.321

CrossRef Full Text | Google Scholar

60. Guralnik GS, Hagen CR, Kibble TWB. Global conservation laws and massless particles. Phys Rev Lett. (1964) 13:585–7. doi: 10.1103/PhysRevLett.13.585

CrossRef Full Text

61. Susskind L. Mass without scalars. Phys Rev D (1979) 20:237–52. doi: 10.1016/0550-3213(79)90364-X

CrossRef Full Text | Google Scholar

62. Weinberg S. Implications of dynamical symmetry breaking: an addendum. Phys Rev D (1979) 19:1277–80. doi: 10.1103/PhysRevD.19.1277

CrossRef Full Text | Google Scholar

63. Weinberg S. Implications of dynamical symmetry breaking: an addendum. Phys Rev D (1976) 13:974–96. doi: 10.1103/PhysRevD.13.974

CrossRef Full Text | Google Scholar

64. Ade PAR, Aikin RW, Barkats D, Benton SJ, Bischoff CA, Bock JJ, et al. (BICEP2 Collaboration). BICEP2 I: detection Of B-mode polarization at degree angular scales. Phys Rev Lett. (2014) 112:241101. doi: 10.1103/PhysRevLett.112.241101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

65. Carroll SM. Quintessence and the rest of the world. Phys Rev Lett. (1998) 81:3067–70. doi: 10.1103/PhysRevLett.81.3067

CrossRef Full Text | Google Scholar

66. Fujii Y. Origin of the gravitational constant and particle masses in scale invariant scalar–tensor theory. Phys Rev D (1982) 26:2580–8. doi: 10.1103/PhysRevD.26.2580

CrossRef Full Text | Google Scholar

67. Fujii Y, Nishioka T. Model of a decaying cosmological constant. Phys Rev D (1990) 42:361–70. doi: 10.1103/PhysRevD.42.361

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

68. Ford LH. Cosmological constant damping by unstable scalar fields. Phys Rev D (1987) 35:2339–44. doi: 10.1103/PhysRevD.35.2339

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

69. Peebles PJE, Ratra B. Cosmology with a time variable cosmological constant. Astrophys J. (1988) 325:L17. doi: 10.1086/185100

CrossRef Full Text | Google Scholar

70. Ratra B, Peebles PJE. Cosmological consequences of a rolling homogeneous scalar field. Phys Rev D (1988) 37:3406–27. doi: 10.1103/PhysRevD.37.3406

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

71. Chiba T, Sugiyama N, Nakamura T. Cosmology with x matter. Mon Not R Astron Soc. (1997) 289:L5–9. doi: 10.1093/mnras/289.2.L5

CrossRef Full Text | Google Scholar

72. Chiba T, Sugiyama N, Nakamura T. Observational tests of x matter models. Mon Not R Astron Soc. (1998) 301:72–80. doi: 10.1046/j.1365-8711.1998.02012.x

CrossRef Full Text | Google Scholar

73. Ferreira PG, Joyce M. Structure formation with a selftuning scalar field. Phys Rev Lett. (1997) 79:4740–3. doi: 10.1103/PhysRevLett.79.4740

CrossRef Full Text | Google Scholar

74. Ferreira PG, Joyce M. Cosmology with a primordial scaling field. Phys Rev D (1998) 58:023503. doi: 10.1103/PhysRevD.58.023503

CrossRef Full Text | Google Scholar

75. Caldwell RR, Dave R, Steinhardt PJ. Cosmological imprint of an energy component with general equation of state. Phys Rev Lett. (1998) 80:1582–5. doi: 10.1103/PhysRevLett.80.1582

CrossRef Full Text | Google Scholar

76. Copeland EJ, Liddle AR, Wands D. Exponential potentials and cosmological scaling solutions. Phys Rev D (1998) 57:4686–90. doi: 10.1103/PhysRevD.57.4686

CrossRef Full Text | Google Scholar

77. Fukugita M, Takahara F, Yamashita K, Yoshii Y. Test for the cosmological constant with the number count of faint galaxies. Astrophys J. (1990) 361:L1–4. doi: 10.1086/185813

CrossRef Full Text | Google Scholar

78. Green MB, Schwarz JH, Witten E. Superstring Theory. Bonn: Cambridge University Press (1987).

Google Scholar

79. Olive KA. Inflation. Phys Rep. 190:347–403. doi: 10.1016/0370-1573(90)90144-Q

CrossRef Full Text

80. Zlatev I, Wang L-M, Steinhardt PJ. Quintessence, cosmic coincidence, and the cosmological constant. Phys Rev Lett. (1999) 82:896–9. doi: 10.1103/PhysRevLett.82.896

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

81. Steinhardt PJ, Wang L-M, Zlatev I. Cosmological tracking solutions. Phys Rev D (1999) 59:123504. doi: 10.1103/PhysRevD.59.123504

CrossRef Full Text | Google Scholar

82. Binetruy P. Models of dynamical supersymmetry breaking and quintessence. Phys Rev D (1999) 60:063502. doi: 10.1103/PhysRevD.60.063502

CrossRef Full Text | Google Scholar

83. Caldwell RR, Linder EV. The limits of quintessence. Phys Rev Lett. (2005) 95:141301. doi: 10.1103/PhysRevLett.95.141301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

84. Amendola L. Scaling solutions in general nonminimal coupling theories. Phys Rev D (1999) 60:043501. doi: 10.1103/PhysRevD.60.043501

CrossRef Full Text | Google Scholar

85. Khoury J, Weltman A. Chameleon fields: awaiting surprises for tests of gravity in space. Phys Rev Lett. (2004) 93:171104. doi: 10.1103/PhysRevLett.93.171104

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

86. Brans C, Dicke R. Mach's principle and a relativistic theory of gravitation. Phys Rev D (1961) 124:925–35. doi: 10.1103/PhysRev.124.925

CrossRef Full Text | Google Scholar

87. Khoury J, Weltman A. Chameleon cosmology. Phys Rev D (2004) 69:044026. doi: 10.1103/PhysRevD.69.044026

CrossRef Full Text | Google Scholar

88. Hu W, Sawicki I. Models of f(R) cosmic acceleration that evade solar-system tests. Phys Rev D (2007) 76:064004. doi: 10.1103/PhysRevD.76.064004

CrossRef Full Text | Google Scholar

89. Capozziello S, Tsujikawa S. Solar system and equivalence principle constraints on f(R) gravity by chameleon approach. Phys Rev D (2008) 77:107501. doi: 10.1103/PhysRevD.77.107501

CrossRef Full Text | Google Scholar

90. Gannouji R, Moraes B, Mota D, Polarski D, Tsujikawa S, Winther H. Chameleon dark energy models with characteristic signatures. Phys Rev D (2010) 82:124006. doi: 10.1103/PhysRevD.82.124006

CrossRef Full Text | Google Scholar

91. Sotiriou TP, Faraoni V. f(R) theories of gravity. 2010 82:451–97. doi: 10.1103/RevModPhys.82.451

CrossRef Full Text | Google Scholar

92. De Felice A, Tsujikawa S. f(R) theories. Living Rev Rel. (2010) 13:3. doi: 10.12942/lrr-2010-3

CrossRef Full Text

93. Vainshtein A. To the problem of nonvanishing gravitation mass. Phys Lett B (1972) 39:393–4. doi: 10.1016/0370-2693(72)90147-5

CrossRef Full Text | Google Scholar

94. Deffayet C, Esposito-Farese G, Vikman A. Covariant galileon. Phys Rev D (2009) 79:084003. doi: 10.1103/PhysRevD.79.084003

CrossRef Full Text | Google Scholar

95. Nicolis A, Rattazzi R, Trincherini E. The Galileon as a local modification of gravity. Phys Rev D (2009) 79:064036. doi: 10.1103/PhysRevD.79.064036

CrossRef Full Text | Google Scholar

96. Kimura R, Kobayashi T, Yamamoto K. Vainshtein screening in a cosmological background in the most general second-order scalar-tensor theory. Phys Rev D (2012) 85:024023. doi: 10.1103/PhysRevD.85.024023

CrossRef Full Text | Google Scholar

97. De Felice A, Kase R, Tsujikawa S, Vainshtein mechanism in second-order scalar-tensor theories. Phys Rev D (2012) 85:044059. doi: 10.1103/PhysRevD.85.044059

CrossRef Full Text | Google Scholar

98. Kase R, Tsujikawa S, Screening the fifth force in the Horndeski's most general scalar-tensor theories. JCAP (2013) 1308:054. doi: 10.1088/1475-7516/2013/08/054

CrossRef Full Text | Google Scholar

99. Kim JE. Abelian discrete symmetries Z_N and Z_nR from string orbifolds. Phys Lett B (2013) 726:450–5. doi: 10.1016/j.physletb.2013.08.039

CrossRef Full Text | Google Scholar

100. Dias AG, Machado ACB, Nishi CC, Ringwald A, Vaudrevange PKS. The quest for an intermediate-scale accidental axion and further ALPs. JHEP (2014) 1406:037. doi: 10.1007/JHEP06(2014)037

CrossRef Full Text | Google Scholar

101. Krauss LM, Wilczek F. Discrete gauge symmetry in continuum theories. Phys Rev Lett. (1989) 62:1221–3. doi: 10.1103/PhysRevLett.62.1221

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

102. Kim JE. Modeling the small dark energy scale with a quintessential pseudoscalar boson. J Korean Phys Soc. (2014) 64:795–805. doi: 10.3938/jkps.64.795

CrossRef Full Text | Google Scholar

103. Belavin AA, Polyakov A, Schwartz A, Tyupkin Y. Pseudoparticle solutions of the Yang-Mills equations. Phys Lett B (1975) 59:85–7. doi: 10.1016/0370-2693(75)90163-X

CrossRef Full Text | Google Scholar

104. ´t Hooft G. How instantons solve the U(1) problem. Phys Rep. (1986) 142:357–87. doi: 10.1016/0370-1573(86)90117-1

CrossRef Full Text | Google Scholar

105. Weinberg S. The U(1) problem. Phys Rev D (1975) 11:3583–93. doi: 10.1103/PhysRevD.11.3583

CrossRef Full Text | Google Scholar

106. Weinberg S, Wilczek F. Unification of Elementary Forces and Gauge Theories. D. B. Cline and F. E. Mills, editors. London: Harwood Academic Publishers (1980).

Google Scholar

107. Peccei RD, Quinn HR. CP conservation in the presence of instantons. Phys Rev Lett. (1977) 38:1440–3. doi: 10.1103/PhysRevLett.38.1440

CrossRef Full Text

108. Kim JE. Constraints on very light axions from cavity experiments. Phys Rev D (1998) 58:055006 doi: 10.1103/PhysRevD.58.055006

CrossRef Full Text | Google Scholar

109. Choi KS, Kim IW, Kim JE. String compactification, QCD axion and axion-photon-photon coupling. JHEP (2007) 0703:116. doi: 10.1088/1126-6708/2007/03/116

CrossRef Full Text | Google Scholar

110. Kim JE. Calculation of axion-photon-photon coupling in string theory. Phys Lett B (2014) 735:95–100. doi: 10.1016/j.physletb.2014.06.021

CrossRef Full Text | Google Scholar

111. Nomura Y, Watari T, Yanagida T. Quintessence axion potential induced by electroweak instanton effects. Phys Lett B (2000) 484:103. doi: 10.1016/S0370-2693(00)00605-5

CrossRef Full Text | Google Scholar

112. Kamionkowski M, Pradler J, Walker DGE. Dark energy from string axiverse. [arXiv: 1409.0549[hep-ph]].

113. Arvanitaki A, Dimopoulos S, Dubovsky S, Kaloper N, March-Russell J. String axiverse. Phys Rev D (2010) 81:123530. doi: 10.1103/PhysRevD.81.123530

CrossRef Full Text | Google Scholar

114. Amendola L, Barbieri R. Dark matter from an ultra-light pseudo-Goldsone-boson. Phys Lett B (2006) 642:192–6. doi: 10.1016/j.physletb.2006.08.069

CrossRef Full Text | Google Scholar

115. Hu W, Barkana R, Gruzinov A. Cold and fuzzy dark matter. Phys Rev Lett. (2000) 85:1158–61. doi: 10.1103/PhysRevLett.85.1158

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

116. Sikivie P. Experimental tests of the invisible axion. Phys Rev Lett. Phys Rev Lett. (1983) 51:1415–7. Erratum. 52:695 (1984). doi: 10.1103/PhysRevLett.51.1415

CrossRef Full Text | Google Scholar

117. Krauss L, Moody J, Wilczek F, Morris EB. Calculations for cosmic axion detection. Phys Rev Lett. (1985) 55:1797–1800. doi: 10.1103/PhysRevLett.55.1797

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

118. Hong J, Kim JE, Nam S, Semertzidis KY. Calculations of resonance enhancement factor in axion-search tube-experiments. (2014) [arXiv:1403.1576 [hep-ph]].

Google Scholar

119. Marsh DJE, Grin D, Hlozek R, Ferreira PG. Tensor detection severely constrains axion dark matter. Phys Rev Lett. (2014) 113:011801. doi: 10.1103/PhysRevLett.113.011801

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

120. Vissineli L, Gondolo P. Axion cold dark matter in view of BICEP2 results. Phys Rev Lett. (2014) 113:011802. doi: 10.1103/PhysRevLett.113.011802

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

121. Melissinos AC, Depanfilis S, Moskowitz BE, Rogers JT, Semertzidis YK, Wuensch W, et al. (Rochester-Brookhaven-Fermilab Collaboration). Limits on the abundance and coupling of cosmic axions at 4.5 < m_a < 5.0 μeV. Phys Rev Lett. (1987) 59:839. doi: 10.1103/PhysRevLett.59.839

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

122. Hagmann C, Sikivie P, Sullivan NS, and Tanner DB. (Florida Group). Results from a search for cosmic axions. Phys Rev D (1990) 42:1297–1300. doi: 10.1103/PhysRevD.42.1297

CrossRef Full Text | Google Scholar

123. Clarke J. Then and Now. Int J Mod Phys D (2010) 24:3999–4038. doi: 10.1142/S0217979210056438

CrossRef Full Text | Google Scholar

124. Arvanitaki A, Geraci AA. Resonant detection of axion mediated forces with nuclear magnetic resonance. [arXiv: 1403.1290 [hep-ph]].

125. Adam R, Ade PAR, Aghanim N, Arnaud M, Aumont J, Baccigalupi C, et al. (Planck Collaboration). Planck intermediate results, XXX: the angular power spectrum of polarized dust emission at intermediate and high galactic latitudes. (2014) arXiv: 1409.5738 [astro-ph.CO].

Google Scholar

126. Bousso R, Polchinski J. Quantization of four form fluxes and dynamical neutralization of the cosmological constant. JHEP (2000) 0006:006. doi: 10.1088/1126-6708/2000/06/006

CrossRef Full Text | Google Scholar

127. Kachru S, Kallosh R, Linde A, Trivedi S. De Sitter vacua in string theory. Phys Rev D (2003) 68:046005. doi: 10.1103/PhysRevD.68.046005

CrossRef Full Text

128. Susskind L. The anthropic landscape of string theory. In: BJ Carr, editors. Universe or Multiverse? Cambridge: Cambridge University Press (2009) 247–266.

Google Scholar

129. Lemaitre G. Annales de la Society Scientifique de Bruxelles (1933) 47A:49 [English in Gen. Rel. Grav. (1997) 29:641.

130. Sato K. Cosmological baryon number domain structure and the first order phase transition of a vacuum. Phys Lett B (1981) 99:66–70. doi: 10.1016/0370-2693(81)90805-4

CrossRef Full Text | Google Scholar

131. Sato K. First order phase transition of a vacuum and expansion of the universe. Mon Not R Astron Soc. (1981) 195:467–79.

Google Scholar

132. Kazanas D. Dynamics of the universe and spontaneous symmetry breaking. Astrophys J. (1980) 241:L59–63. doi: 10.1086/183361

CrossRef Full Text | Google Scholar

133. Starobinsky AA. A new type of isotropic cosmological models without singularity. Phys Lett B (1980) 91:99–102. doi: 10.1016/0370-2693(80)90670-X

CrossRef Full Text | Google Scholar

134. Preskill J. Cosmological production of superheavy magnetic monopoles. Phys Rev Lett. (1979) 43:1365–8. doi: 10.1103/PhysRevLett.43.1365

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

135. Georgi H, Glashow SL. Unity of all elementary particle forces. Phys Rev Lett. (1974) 32:438–41. doi: 10.1103/PhysRevLett.32.438

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

136. Pati J, Salam A. Unified lepton-hadron symmetry and a gauge theory of the basic interactions. Phys Rev D (1973) 8:1240–51. doi: 10.1103/PhysRevD.8.1240

CrossRef Full Text | Google Scholar

137. Mukhanov VF, Chibisov GV. Quantum fluctuation and nonsingular universe (In Russian). Pis'ma Zh. Eksp. Teor. Fiz. (1981) 33:549–53 [JETP Lett. (1981) 33:532–535].

Google Scholar

138. Hawking SW. The development of irregularities in a single bubble inflationary universe. Phys Lett B (1982) 115:295–7. doi: 10.1016/0370-2693(82)90373-2

CrossRef Full Text | Google Scholar

139. Starobinsky AA. Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations. Phys Lett B (1982) 117:175–8. doi: 10.1016/0370-2693(82)90541-X

CrossRef Full Text | Google Scholar

140. Guth AH, Pi S-Y. Fluctuations in the new inflationary universe. Phys Rev Lett. (1982) 49:1110–3. doi: 10.1103/PhysRevLett.49.1110

CrossRef Full Text | Google Scholar

141. Bardeen J, Steinhardt P, Turner M. Spontaneous creation of almost scale - free density perturbations in an inflationary universe. Phys Rev D (1983) 28:679. doi: 10.1103/PhysRevD.28.679

CrossRef Full Text | Google Scholar

142. Bassett B, Tsujikawa S, Wands D. Inflation dynamics and reheating. Rev Mod Phys. (2006) 78:537–89. doi: 10.1103/RevModPhys.78.537

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

143. Smoot GF, Bennett CL, Kogut A, Wright EL, Aymon J, Boggess NW, et al. Structure in the COBE differential microwave radiometer first year maps. Astrophys J. (1992) 396:L1–5. doi: 10.1086/186504

CrossRef Full Text | Google Scholar

144. Turner MS. Talk Presented at “The 5 Year Celebration of Bethe Center.” Bonn: University Bonn (2014).

145. Creminelli P, Zaldarriaga M. Single field consistency relation for the 3-point function. JCAP (2004) 0410:006. doi: 10.1088/1475-7516/2004/10/006

CrossRef Full Text | Google Scholar

146. Chen X, Huang M, Kachru S, and Shiu G. Observational signatures and non-Gaussianities of general single field inflation. JCAP (2007) 0701:002. doi: 10.1088/1475-7516/2007/01/002

CrossRef Full Text | Google Scholar

147. De Felice A, Tsujikawa S. Shapes of primordial non-Gaussianities in the Horndeski's most general scalar-tensor theories. JCAP (2013) 1303:030. doi: 10.1088/1475-7516/2013/03/030

CrossRef Full Text | Google Scholar

148. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F, et al. Planck 2013 results. XXII. Constraints on inflation. [arXiv:1303.5082 [astro-ph.CO]].

149. Tsujikawa S, Ohashi J, Kuroyanagi S, De Felice A. Planck constraints on single-field inflation. Phys Rev D (2013) 88:023529. doi: 10.1103/PhysRevD.88.023529

CrossRef Full Text | Google Scholar

150. Tsujikawa S. Distinguishing between inflationary models from cosmic microwave background. PTEP (2014) 6:06B104. doi: 10.1093/ptep/ptu047

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

151. Linde AD. Chaotic inflation. Phys Lett B (1983) 129:177–81. doi: 10.1016/0370-2693(83)90837-7

CrossRef Full Text | Google Scholar

152. Linde AD. Hybrid inflation. Phys Rev D (1994) 49:748–54. doi: 10.1103/PhysRevD.49.748

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

153. Grishchuk LP. Amplification of gravitational waves in an istropic universe. Zh. Eksp. Teor. Fiz. (1974) 67:825–38 [Sov. Phys. J. Exp. Theor. Phys. (1975) 40:409–15]

Google Scholar

154. Starobinsky AA. Spectrum of relict gravitational radiation and the early state of the universe. Zh. Eksp. Teor. Fiz. Pisma Red. (1979) 30:719–23 [JETP Lett. (1979) 30:682–85].

Google Scholar

155. Rubakov VA, Sazhin MV, Veryaskin AV. Graviton creation in the inflationary universe and the grand unification scale. Phys Lett B (1982) 115:189–92. doi: 10.1016/0370-2693(82)90641-4

CrossRef Full Text | Google Scholar

156. Fabbri R, Pollock MD. The effect of primordially produced gravitons upon the anisotropy of the cosmological microwave background radiation. Phys Lett B (1983) 125:445–8. doi: 10.1016/0370-2693(83)91322-9

CrossRef Full Text | Google Scholar

157. Abbott LF, Wise MB. Constraints on generalized inflationary cosmologies. Nucl Phys B (1984) 244:541–8. doi: 10.1016/0550-3213(84)90329-8

CrossRef Full Text | Google Scholar

158. Lyth DH. What would we learn by detecting a gravitational wave signal in the cosmic microwave background anisotropy?. Phys Rev Lett. (1997) 78:1861–3. doi: 10.1103/PhysRevLett.78.1861

CrossRef Full Text | Google Scholar

159. Freese K, Frieman JA, Orlinto AV. Natural inflation with pseudo Nambu–Goldstone bosons. Phys Rev Lett. (1990) 65:3233–6. doi: 10.1103/PhysRevLett.65.3233

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

160. Kim JE, Nilles HP, Peloso M. Completing natural inflation. JCAP (2005) 0501:005. doi: 10.1088/1475-7516/2005/01/005

CrossRef Full Text | Google Scholar

161. Dimopoulos S, Kachru S, McGreevy J, Wacker JG. N-flation. JCAP (2008) 0808:003. doi: 10.1088/1475-7516/2008/08/003

CrossRef Full Text | Google Scholar

162. Pi S-Y. Inflation without tears. Phys Rev Lett. (1984) 52:1725–8. doi: 10.1103/PhysRevLett.52.1725

CrossRef Full Text | Google Scholar

163. Hiramatsu T, Kawasaki M, Saikawa K, Sekiguchi T. Axion cosmology with long-lived domain walls. Phys Rev D (2012) 85:105020. doi: 10.1088/1475-7516/2013/01/001

CrossRef Full Text | Google Scholar

164. Vilenkin A, Everett AE. Cosmic strings and domain walls in models with Goldstone and PseudoGoldstone bosons. Phys Rev Lett. (1982) 48:1867–70. doi: 10.1103/PhysRevLett.48.1867

CrossRef Full Text | Google Scholar

165. Barr SM, Kim JE. New confining force solution of QCD domain wall problem. (2014) [arXiv:1407.4311 [hep-ph]].

Google Scholar

166. Kim JE. High scale inflation, model-independent string axion, and QCD axion with domain wall number one. Phys Lett B (2014) 734:68–71. doi: 10.1016/j.physletb.2014.05.033

CrossRef Full Text | Google Scholar

167. Lyth DH. BICEP2, the curvature perturbation and supersymmetry. [arXiv:1403.7323 [hep-ph]]

168. Kim JE. The inflation point in U(1)_de hilltop potential assisted by chaoton, BICEP2 data, and trans-Planckian decay constant. Phys Lett B (2014) 737:1–5. doi: 10.1016/j.physletb.2014.08.025

CrossRef Full Text | Google Scholar