High spatial resolution imaging of light localization in hyperuniform disordered patterns of circular air pores in a dielectric slab

Granchi, Nicoletta; Spalding, Richard; Stokkereit, Kris; Lodde, Matteo; Petruzzella, Maurangelo; Otten, Frank V.; Sapienza, Riccardo; Fiore, Andrea; Florescu, Marian; Intonti, Francesca

doi:10.3389/fphot.2023.1199411

ORIGINAL RESEARCH article

Front. Photonics, 14 June 2023

Sec. Plasmonics

Volume 4 - 2023 | https://doi.org/10.3389/fphot.2023.1199411

This article is part of the Research Topic Advances in Plasmonics: a European Collection View all 5 articles

High spatial resolution imaging of light localization in hyperuniform disordered patterns of circular air pores in a dielectric slab

Nicoletta Granchi^1,2*

Richard Spalding³

Kris Stokkereit³

Matteo Lodde⁴

Maurangelo Petruzzella⁴

Frank V. Otten⁴

Riccardo Sapienza⁵

Andrea Fiore⁴

Marian Florescu³

Francesca Intonti^1,2

¹Department of Physics and Astronomy, University of Florence, Sesto Fiorentino, Italy
²European Laboratory for Non-Linear Spectroscopy - LENS, University of Florence, Sesto Fiorentino, Italy
³Department of Physics, Advanced Technology Institute, University of Surrey, Surrey, United Kingdom
⁴Department of Applied Physics and Science Education, Eindhoven Hendrik Casimir Institute, Eindhoven University of Technology, Eindhoven, Netherlands
⁵The Blackett Laboratory, Department of Physics, Imperial College London, London, United Kingdom

Hyperuniform disordered photonic structures are a peculiar category of disordered photonic heterostructures located between random structures and ordered photonic crystals. These materials, thanks to the presence of a photonic bandgap, exhibit the advantages of random and ordered structures since they have been shown to support in a small spatial footprint a high density of Anderson-localized modes, which naturally occur at the bandgap edges with peculiar features like relatively high Q/V ratios. Different localization behaviors have been recently reported in hyperuniform disordered luminescent materials, with a well-established and widely studied design, based on disordered networks. Here, we explore an alternative design, based on circular holes of different sizes hyperuniformely distributed, that we investigate theoretically and experimentally by means of scanning near-field optical microscopy. We report that the spectral features of hyperuniform disordered networks can also be extended to a different design, which, in turn, displays pseudo-photonic bandgaps and light localization. The ability of generating different kinds of hyperuniform disordered photonic systems that share the same theoretical and experimental optical features can largely extend practical potentialities and integration in many optoelectronic applications.

1 Introduction

Recently, disordered dielectric heterostructures with structural correlations, which fill the gap between random structures and photonic crystals, have attracted a lot of attention (Yu et al., 2020) (Vynck et al., 2021). A particular class among disordered photonic materials is called hyperuniform disordered (HuD) photonic structures (Torquato, 2018; Torquato and Stillinger, 2003). A point pattern in real space is hyperuniform if, within a spherical sampling window of radius $R$ (in $d$ dimensions), the number variance ${σ (R)}^{2}$ for large $R$ increases slower than the window volume (i.e., slower than $R^{d}$ ) (Torquato and Stillinger, 2003). This means that in Fourier space, the structure factor, $S (k)$ , approaches zero as $|k|$ → 0, which is the reason of transparency at long wavelength. HuD systems have recently been shown to display large isotropic photonic band gaps (PBGs) and optical transparency (Florescu et al., 2009; Froufe-Pérez et al., 2016). It has been demonstrated that the combination of hyperuniformity, short-range geometric order, and uniform local topology can lead to a complete PBG, by considering that PBGs arise within the limit of the large dielectric constant ratio (Florescu et al., 2009). In particular, their formation is associated with Mie resonances (Kuznetsov et al., 2012; Liu and Kivshar, 2018; Granchi et al., 2021; Granchi et al., 2023a) of the single scattering centers composing the structure as they open whenever the scattered field is out of phase with the incident field, and no propagation channel exists for light. The presence of short-range correlations in hyperuniformity results in peculiar phenomena, such as topologically protected electronic states (Mitchell et al., 2018), polarization selectivity (Gerasimenko et al., 2019), lasing (Froufe-Pérez et al., 2017), glassy electronic quantum-state transitions (Zhou et al., 2016), Anderson localization of light (Degl'Innocenti et al., 2016), and a full photonic band gap for light propagation (Froufe-Pérez et al., 2017; Mitchell et al., 2018; Gerasimenko et al., 2019; Granchi et al., 2023a), and emerges in different fabrication approaches (Rumi et al., 2019) (Salvalaglio et al., 2020; Piechulla et al., 2018). These materials that share features of photonic crystals and random systems are characterized by tailored light transport, from diffusive transport to Anderson localization. Among the several experimental photonic realizations of HuD structures (Muller et al., 2013; Castro-Lopez et al., 2017; Milošević et al., 2019; Tavakoli et al., 2022; Granchi et al., 2023b), quantitative experimental demonstrations of different regimes of light transport within a single HuD structure, from a PBG to Anderson-like localization (Anderson, 1958), and to transport regimes such as diffusive multiple scattering, have been proposed in the microwave and telecom wavelength regime (Aubry et al., 2020; Haberko et al., 2020; Granchi et al., 2022). In particular, the investigation of HuD network structures with a well-established and widely studied design highlighted that these correlated disorder systems are promising since they combine the small spatial footprint typical of random modes with Q/V ratios comparable with photonic crystal cavities for the Anderson-localized modes localized at the PBG edges. This result was so far obtained for modes supported by HuD networks. Here, we explore an alternative HuD design, based on circular holes of different sizes hyperuniformely distributed. We study the HuD systems realized on two dielectric parallel membranes optically activated with the insertion of InAs quantum dots, by means of scanning near-field optical microscopy (SNOM). The membranes are patterned with the novel HuD design based on circular holes instead of networks. We show how this HuD design is characterized by the spectral region of strongly depleted density of states (DOSs), at the edges of which high density strongly localized Anderson modes arise with relatively high Q factors (10³). Our work also focuses on another important aspect of disordered photonics. Although Maxwell’s equations have exact solutions for any dielectric problem, in real random structures, experiments usually unveil large deviations in the resonances from the nominal design due to unavoidable fabrication-induced disorder. As a consequence, an exact prediction of where the photons will localize in samples is almost impossible. The aspect of predictability of photonic modes motivated an entire field of optoelectronic research, whose aim has been to make the deterministic control of random resonances possible despite unpredictable spatial distributions. It has been recently demonstrated that the modes supported by HuD networks on a dielectric slab not only are intrinsically reproducible but differently for modes arising from disorder, and they exhibit spatial distribution extremely robust to local perturbation and disorder with respect to their ordered and disordered counterparts (Granchi et al., 2022). Here, we propose a study of HuD samples with the circular hole design and investigate the supported resonances and their spatial distributions in nominally identical structures, demonstrating that not only tightly localized modes exhibit this behavior but also delocalized resonances spectrally far from the PBG are as reproducible and resilient with respect to fabrication-induced disorder. Notably, we show how the spectral features of HuD networks, which show complete PBG, can be extended to HuD design, which, on the contrary, exhibits pseudo-PBGs.

2 Materials and methods

2.1 Theoretical design

The 2D hyperuniform disordered photonic structure is generated under periodic boundary conditions in a square of side $L$ , employing $a = L / \sqrt{N}$ as a characteristic length scale such that all patterns have point density $1 / a^{2}$ , where $N$ is the number of scattering centers in the supercell. We use the protocol described in Florescu et al. (2009) to generate the design. We then calculate the photonic band structure using the 2D eigenmode expansion software MPB (Johnson and Joannopoulos, 2001) for a supercell of side $a \sqrt{N}$ using the associated high-symmetry points of the resulting Brillouin zone (of characteristic size $2 π / (a \sqrt{N})$ ). In addition, transmission spectra are calculated by 2D MPB simulations.

2.2 Sample fabrication

The sample was grown by molecular-beam epitaxy on a GaAs (001) wafer and consists of two GaAs membranes separated by a Al_0.7Ga_0.3As sacrificial layer, on top of a Al_0.7Ga_0.3As sacrificial layer (Joannopoulos et al., 2011; Midolo and Fiore, 2014; Petruzzella et al., 2016; Petruzzella et al., 2017). High-density InAs quantum dots (QDs) are embedded in the middle of the upper membrane and act as an optically active medium. The photoluminescence (PL) emission of the QDs ranges from 1,100 to 1,350 nm. The HuD structure was defined by electron-beam lithography, reactive-ion etching, and subsequent selective etching of the sacrificial layers. The slab thickness and the intermembrane separation distance are, respectively, t = 130 nm and d = 105 nm (details on the scanning electron microscopy (SEM) investigation on similar samples are given in Granchi et al. (2022).

2.3 Finite element method simulations

To simulate the 3D structure along with its optical properties, we use finite element method (FEM) simulations through the commercial software application COMSOL Multiphysics (Zobenica et al., 2017) to obtain information on the eigenvalues and eigenvectors of the system. The double-membrane structure was simulated by modeling one membrane and then imposing perfect electric conductor (PEC) conditions in the plane between the two membranes in order to detect antisymmetric solutions.

2.4 Scanning near-field optical microscopy

A commercial SNOM (Twinsnom, Omicron) is used in illumination/collection geometry. The spatially resolved optical maps were recorded by scanning the probe tip over the sample at a fixed distance (few tens of nm). The sample is excited by a laser diode at 785 nm, both the excitation and the signal collection occur through the tip, and the collected signal is dispersed using a spectrometer and collected by a cooled InGaAs array. At every tip position, the entire spectrum of the sample is collected with a spectral resolution of 0.1 nm. The SNOM tip-collecting area, which has a lateral size of about 250 nm, is the estimated spatial resolution of our system.

3 Results and discussion

The 2D design of the HuD pattern under study, containing $N$ = 500 points, with $a$ = 360 nm and filling fraction $f f$ = 0.27%, is shown in Figure 1A. The point pattern we use contains $N$ = 500 points and belongs to a further subcategory of HuD systems, known as “stealthy” (Degl'Innocenti et al., 2016; COMSOL, 2019), whose name relates to their property of being transparent to incident radiation for a certain range of wave vectors $k$ . Specifically, it is called a stealthy point pattern with a structure factor $S (k)$ (Granchi et al., 2022) that is statistically isotropic, continuous, and precisely equal to zero for a finite range of wavenumbers smaller than a certain wave vector $k_{C}$ , i.e., $S (k < k_{C}) = 0$ . The stealthiness parameter $χ$ is defined as the ratio between the number of $k$ vectors for which the structure factor S(k) is constrained to vanish and the total number of $k$ vectors. In the design of Figure 1A, the stealthiness parameter is $χ$ = 0.5. On the left panel of Figure 1B, we report the bandstructure of the design in (a), while the transmission spectrum is shown in the right panel of Figure 1B. The two panels are in fairly good agreement since the suppression of the transmission over a range of frequencies indicates the presence of a spectral region of strongly depleted density of states (with small PBGs clearly visible), as predicted by the bandstructure calculations (details on the theoretical design and bandstructure calculations are given in Section 2). However, it would be imprecise to call the whole region a complete bandgap; we, therefore, refer to it as a photonic pseudo-gap. The physical reason underlying this can be understood by considering a network structure of constant wall thickness (Florescu et al., 2009), which exhibit a full PBG. By coercing it to become a hole structure (i.e., the polygonal holes in the network structure of constant thickness are deformed and acquire a circular shape), we introduce dielectric walls of varying thicknesses throughout the sample. In this process, the electromagnetic “resonances,” which were previously established in the constant thickness network walls and had an identical resonant frequency, need to accommodate the dielectric domains of varying thicknesses present between the holes in the structure. This perturbs their “resonant” frequency and causes the band edges of the gap to fluctuate widely, giving rise to states inside the gap, hence reducing its size. The additional states created are not sufficient in number to cover the whole band gap spectral region, and there will still be residual small band gap regions left. Although there are many applications of structures presenting large and complete PBGs, here we are focusing on exploring the physics of the Anderson localization phenomenon, and understanding if and how the features of Anderson modes in the hyperuniform systems are preserved even in the presence of a pseudo-gap.

FIGURE 1

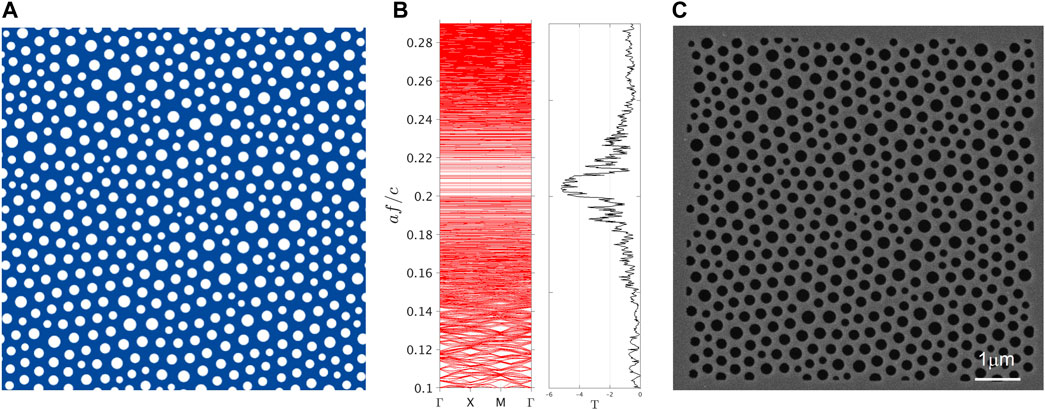
FIGURE 1. (A) Sketch of the theoretical design of the studied hyperuniform disordered network, which constitutes the elementary cell, with the length scale $a = 360 n m$ and filling fraction $f f = 0.27 %$ and $N p o i n t s = 500$ . (B) Left panel: 2D bandstructure (MPB) corresponding to the design in (A). Right panel: 2D transmission spectrum. (C) SEM image showing the top view of the sample and zoom on the pattern. The bottom left inset shows the sketch of the double membranes, with thickness t and distance d.

We fabricated the samples (details on fabrication can be found in Section 2) based on the HuD design of Figure 1A. The samples consist in two GaAs parallel membranes patterned with air circular holes, following the theoretical design. Vertical etching ensures that the hole patterns in the two parallel membranes have the same nominal design. Interestingly, double-membrane photonic systems have been recently proposed as promising devices for sensing and metrology applications, for the possibility that they offer the possibility of achieving a deterministic control of the supported coupled modes (Midolo and Fiore, 2014; Petruzzella et al., 2016; Petruzzella et al., 2017; Batten et al., 2008; Balestri et al., 2019). By patterning the double membranes with the HuD design, we simply include HuD systems into the large plethora of practical applications, which focus on post-fabrication control of photonic modes. A top view SEM image of the fabricated sample, where only the upper membrane is visible, is reported in Figure 1C, along with a zoom on the patterned area and with a sketch of the double membrane system. The structural parameters are reported in Section 2.2.

When using a double-membrane system, the symmetry of the problem leads to the splitting into symmetric and antisymmetric modes, which are vertically delocalized over the two membranes. It has been proven both theoretically and experimentally that the modes arising from the coupling between parallel membranes inherit the in-plane spatial distributions of the modes supported by the original single membrane (Balestri et al., 2019). For this reason, the results here presented can also be extended to single-membrane structures. For the sake of simplicity, we focus only on antisymmetric solutions.

Previous works highlighted that photonic HuD systems support a variety of transport regimes and a photonic band gap (Florescu et al., 2009; Degl'Innocenti et al., 2016). Specifically, Anderson-localized modes with relatively high Q factors occur naturally at the PBG edges and are predicted to spread over a few cells of HuD structures (Granchi et al., 2019; COMSOL, 2019). These modes are distinguishable as below or above the PBG due to the electric field being concentrated in the dielectric or air fraction, respectively. As the modes step away from the PBG, they enter a diffusive regime and consequently spatially spread over the entire structure and exhibit lower Q factors (Granchi et al., 2022). Here, we study the localization of Anderson modes arising in the pseudo-gap region at the lower edge of a small PBG and concentrated in the dielectric part of the sample. To explore the localization properties of these modes, we calculate the (antisymmetric) solutions of the 3D double-membrane HuD system by means of FEM simulations. A sketch of the simulation domain, in which we exploit the mirror symmetry of the system to simulate only half of the structure, is shown in Figure 2A (Section 2.3). For each eigensolution obtained with FEM simulations, we extract the central wavelength, spectral width, and electric field amplitude of the modes supported by the HuD system. With these data, we can reconstruct the spectrum of the system by representing every mode with a Lorentzian curve with every single-mode wavelength, spectral bandwidth, and amplitude, and plotting them as a function of wavelength. The resulting spectrum, which is reported in Figure 2A, exhibits a high density of modes, a feature which is typical of disordered systems. The yellow band highlights the presence of the small PBG since no mode is detected in that spectral window. Many peaks are present in the spectrum, with Q factors ranging from 200 to 3,000. Around $λ =$ 1,180 nm, sharp peaks are clearly visible, and as wavelength increases, the modes become spectrally broader.

FIGURE 2

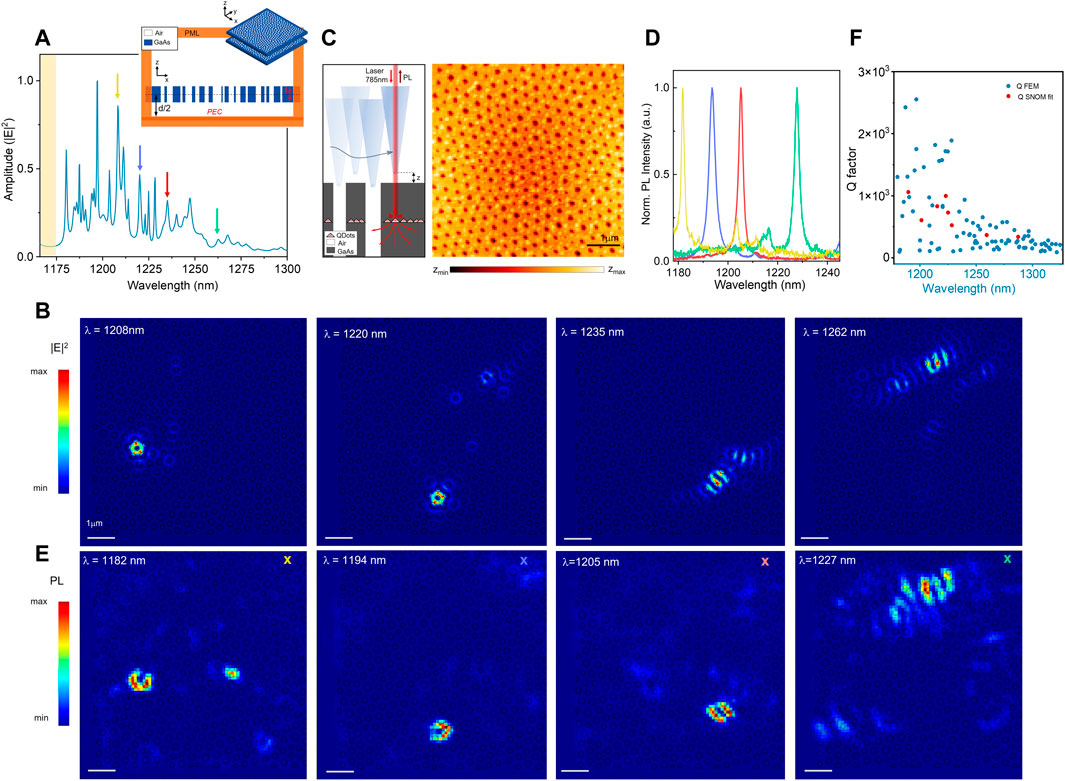
FIGURE 2. (A) Spectrum of the system reconstructed through Lorentzian curves plotted with central wavelength, spectral width, and amplitude obtained with FEM simulations. The yellow bar highlights the presence of the photonic band gap (PBG). A sketch of the simulated model is shown on the upper right side. (B) FEM maps of the electric field intensity of four dielectric modes ( $λ =$ 1,208 nm, $λ =$ 1,220 nm, $λ =$ 1,235 nm, and $λ =$ 1,262 nm) located on the lower edge of the PBG. (C) Sketch of the SNOM setup used in illumination/collection configuration. On the right: SNOM topography of the investigated sample. (D) SNOM PL spectra of four modes collected at the positions of the maximum PL intensity in PL maps reported in (E). (E) SNOM PL maps filtered around the central wavelengths of the peaks in (D), $λ =$ 1,175.0 nm, $λ =$ 1,194.0 nm, $λ =$ 1,205.0 nm, and $λ =$ 1,227.0 nm. (F) Theoretical Qs (blue dots) and experimental Qs (red dots) trend with respect to the wavelength.

We select a few solutions, distinguishable for the peculiar and localized spatial profile, and plot the corresponding electric field intensity spatial distribution in Figure 2B. The modes are spectrally located around $λ =$ 1,208 nm, $λ =$ 1,220 nm, $λ =$ 1,235 nm, and $λ =$ 1,262 nm, and their theoretical Q factors are, respectively, 1,000, 750, 800, and 500. The simulated maps superimposed to the design (Figure 2B) show that these modes are concentrated in the dielectric part of the structure.

In order to experimentally characterize light localization at the lower PBG edge of the sample, we employed a room temperature SNOM in an illumination-collection geometry (Figure 2C). Details on the experimental setup can be found in Section 2. In our experimental setup, spatially resolved optical maps are recorded by scanning the probe tip over the sample at a fixed distance (few tens of nm). This technique allows performing hyper-spectral imaging (HSI), that is, we collect a full spectrum of the photonic local density of states (LDOS) of a system for any spatial pixel of the near-field map. This allows reconstructing hyperspectral maps that can either be filtered around a single wavelength, for example, the central wavelength of a single peak, or around a broad spectral interval. Moreover, during the scan, a topographical map is recorded simultaneously with the acquisition of the optical signal. The topography of the studied sample is reported on the right of Figure 2C. We performed a 10 $μ$ m × 10 $μ$ m scan with spatial steps of 100 nm on the sample. Figure 2D shows the four PL spectra corresponding to the selected modes predicted by theory, and by filtering the hyperspectral map around the central wavelength of each peak ( $λ =$ 1,175.0 nm, $λ =$ 1,194.0 nm, $λ =$ 1,205.0 nm, and $λ =$ 1,227.0 nm), we obtain the PL SNOM maps of Figure 2E that represent the near-field spatial distribution of the electric field intensity of the modes (Florescu et al., 2013). The spectra of Figure 2D were acquired in correspondence of the mode maximum intensity hotspots. It should be noted that there is a wavelength shift of 20–30 nm between measurements and simulations, which is to be attributed to EBL effects determining air hole sizes bigger than the nominal size (Intonti et al., 2008). Despite this wavelength shift, the FEM spatial profiles (Figure 2B) are quite in good agreement with the SNOM PL maps (Figure 2E), reproducing important submicrometric features that allow distinguishing every mode. Moreover, by performing Lorentzian fits on the peaks of Figure 2D, we can extract the experimental Q factors of the modes, obtaining values in good match with the theoretical values, respectively, Q = 1,000, 500, 700, and 600, and, coherently with what has been shown in previous works, calculations confirm that the Q-factor of modes decreases as their wavelength increases. This is further observable in the plot of Figure 2F, in which we report the trend of theoretical and selected experimental Qs with respect to the wavelength (the wavelength axis of experimental Qs has been rescaled properly).

An important aspect of HuD modes is the mode predictability for the design and their robustness against fabrication-induced disorder (Granchi et al., 2022). Here, we address this matter by performing SNOM measurement on two nominally identical samples that we label as Replica 1 and Replica 2. We investigate the two replicas and demonstrate that the same modes can be observed in the two samples as a confirmation of recently shown results based on simulations regarding the mode robustness to fabrication-induced disorder (Rumi et al., 2019). Some examples of the reproducible modes are given in Figure 3. In particular, we exploit the combination of the near-field HSI technique with the topographic imaging of the samples to align different maps at the nanoscale. Moreover, for every tip position, we calculate the PL enhancement spectrum by dividing the recorded near-field spectrum by one of the QDs (Granchi et al., 2022). In this way, it is possible to also reconstruct PL enhancement maps. In Figure 3A, we report the PL enhancement spectra acquired at the position of maximum intensity of the PL signal of the selected mode in the replica (in blue), compared with respect to its counterpart in the original structure (in red). Correspondingly, the panels of Figure 3B show the SNOM PL enhancement maps acquired at the central wavelengths of the red peaks in Replica 1, respectively, λ = 1,183.6 nm, λ = 1,196.0 nm, λ = 1,205.0 nm, and λ = 1,263.0 nm. In Figure 3C, we show instead the SNOM PL maps acquired at the central wavelengths of the blue peaks in Replica 2, respectively, λ = 1,179.9 nm, λ = 1,196.0 nm, λ = 1,206.0 nm, and λ = 1,265.4 nm. The similarity of the submicrometric details of the most variable shapes in the field distributions of the replicas is evident for all the four considered modes, not only in the brightest spots but also throughout the zones with a lower signal. Notably, the first three considered modes are strongly localized and exhibit a very high PL enhancement factor well reproduced in both replicas, and this reaches a maximum value of $\approx$ 40, which is double the value reported previously in the literature (Granchi et al., 2022). The fourth mode of Figure 3 has a lower PL enhancement ( $\approx 7 - 9$ ) and is spatially delocalized all over the sample. This is because it belongs to a spectral region where the diffusive regime is dominant. As a matter of fact, the localization scale of modes is also important when considering the effect of disorder and this is the reason for which we also report on the reproducibility of a delocalized mode (the fourth in Figure 3, λ $\approx$ 1,263 nm). Thanks to our analysis, it is possible to deduce not only about the robustness of Anderson-localized modes in HuD, which extend on a smaller scale with respect to one on which the fabrication-induced disorder acts, but also delocalized modes, corresponding to the diffusive transport regime, share the same property.

FIGURE 3

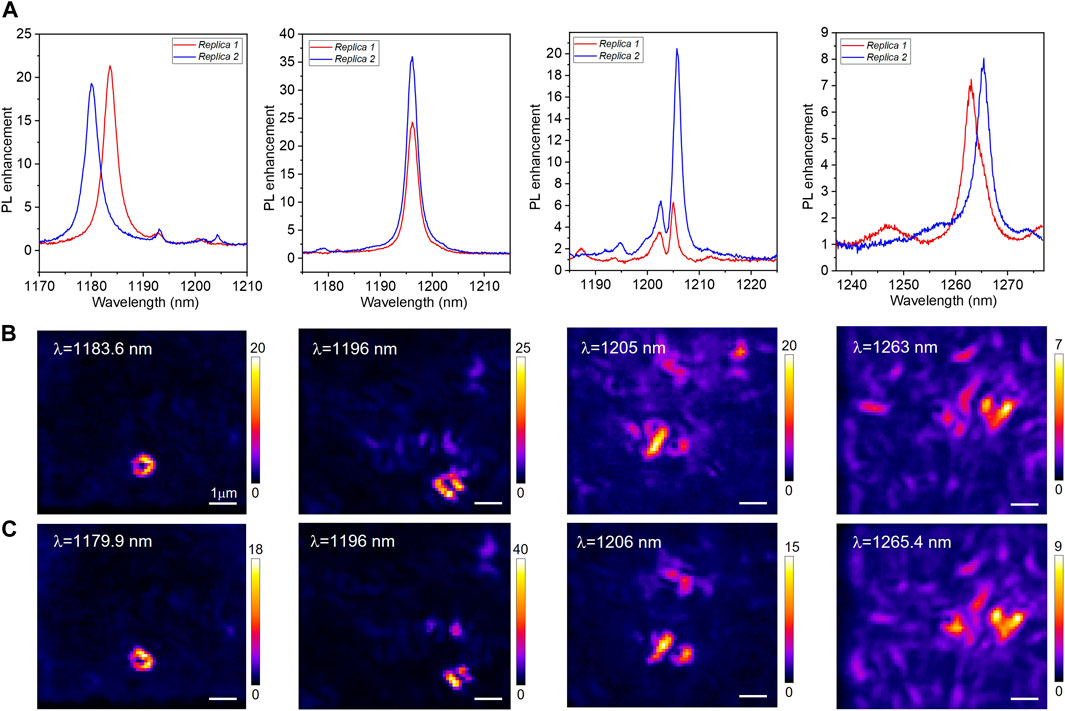
FIGURE 3. (A) PL enhancement spectra of four different modes acquired in the point of maximum intensity of each. The spectra of Replica 1 are represented in red, and those of Replica 2 are represented in blue. Panels in (B,C) are the SNOM PL enhancement maps filtered around the central wavelengths of the red (blue) peaks in Replica 1 (Replica 2), specifically λ = 1,183.6 nm (λ = 1,179.9 nm), λ = 1,196.0 nm (λ = 1,196.0 nm), λ = 1,205.0 nm (λ = 1,205.0), and λ = 1,263.0 nm (λ = 1,265.4).

4 Conclusion

In conclusion, in this work, we explored light localization features in HuD luminescent materials in an alternative design exploiting circular holes of different sizes in a HuD pattern. By means of theoretical simulations and SNOM HSI, we have predicted and detected the formation of the high density of Anderson-localized modes at the pseudo-gap lower edge, featuring Q factors of the order of 10³. Our analysis shows that these modes exhibit a high degree of robustness against the fabrication-induced disorder and that they share this feature also with delocalized resonances spectrally far from the pseudo-gap and relative to a diffusive regime of light transport. The ability of generating different kinds of hyperuniform disordered photonic systems that supports modes sharing the same optical features might constitute a step toward the inclusion of hyperuniform materials into promising platforms for optoelectronic applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

NG conducted the experiments, numerical simulations, and contributed to the writing of the manuscript, and the interpretation of results. RSp and KS conducted numerical simulations and designed the structure. ML and MP fabricated the semiconductor structure. FI and MF supervised the work and contributed to the writing of the manuscript and interpretation of the results. AF and RSa contributed to the supervision of the work. All authors contributed to the article and approved the submitted version.

Funding

FI acknowledges funding provided by PNRR project I-PHOQS (CUP B53C22001750006).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, P. W. (1958). Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505. doi:10.1103/physrev.109.1492