
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Photonics, 17 March 2023
Sec. Optical Nanostructures
Volume 4 - 2023 | https://doi.org/10.3389/fphot.2023.1081521
This article is part of the Research TopicGlobal Excellence in Photonics: EuropeView all 4 articles
The optical properties of vanadium dioxide (VO2) can be tuned via metal-insulator transition. In this work, different types of one-dimensional photonic structure-based microcavities that embed vanadium dioxide have been studied in the spectral range between 900 nm and 2000 nm. In particular, VO2 has been sandwiched between: i) two photonic crystals made of SiO2 and ZrO2; ii) two aperiodic structures made of SiO2 and ZrO2 that follow the Thue-Morse sequence; iii) two disordered photonic structures, made of SiO2 and ZrO2 in which the disorder is introduced either by a random sequence of the two materials or by a random variation of the thicknesses of the layers; iv) two four material-based photonic crystals made of SiO2, Al2O3, Y2O3, and ZrO2. The ordered structures i and iv show, respectively, one and two intense transmission valleys with defect modes, while the aperiodic and disordered structures ii and iii show a manifold of transmission valleys due to their complex layered configurations. The metal-insulator transition of VO2, controlled by temperature, results in a modulation of the optical properties of the microcavities.
Crystalline vanadium dioxide (VO2) shows a thermochromic phase transition around 68°C (341 K) (Morin, 1959). The phase transition is related to a structural crystal change from a monoclinic insulating phase to a tetragonal (rutile) metallic phase (Briggs et al., 2010; Currie et al., 2017). From an optical point of view, the phase transition of VO2 results in a change from an insulating semi-transparent material to a metallic more lossy and reflective material (Verleur et al., 1968; Currie et al., 2017). The VO2 phase transition can be exploited for several applications, such as smart windows, steep-slope devices for micro-electronics, neuromorphic computing devices, reconfigurable radiofrequency switches, optical limiters, and metasurfaces (Liu et al., 2018; Lu et al., 2021; Li et al., 2023; Tognazzi et al., 2023).
A method to utilize the VO2 switchable optical properties is the integration of such material in photonic crystals (John, 1987; Yablonovitch, 1987; Joannopoulos, 2008). In photonic crystals, the periodic modulation of the refractive index in one, two or three dimensions gives rise to energy regions in which light is not transmitted through the crystal. The integration of materials with switchable optical properties in the infrared, such as photochromic polymers (Toccafondi et al., 2014) and infrared plasmonic nanomaterials (Guo et al., 2016; Kriegel et al., 2016), in one-dimensional photonic crystals has been proposed previously (Kriegel and Scotognella, 2018). Furthermore, the deposition of a VO2 layer onto a one-dimensional photonic crystal has been theoretically studied by Rashidi et al. (2018) and experimentally studied by Singh et al. (Singh et al.(2020).
In this work, different types of one-dimensional photonic microcavities (Boucher et al., 2009) are proposed, in which a layer of VO2 is embedded between two photonic crystals, two aperiodic Thue-Morse photonic structures, two disordered photonic structures, and two four-material based photonic crystals. The wavelength dependent refractive indexes of all the employed materials have been implemented. The light transmission of the microcavities has been simulated via the transfer matrix method. The modulation of the transmission spectra of the microcavities due the VO2 metal-insulator phase transition has been highlighted.
The light transmission of the different microcavities in the spectral range between 900 nm and 2000 nm has been studied with the transfer matrix method (Born et al., 1999; Xiao et al., 2016; Paternò et al., 2019). The system is glass/multilayer/air with light impinging the sample surface orthogonally. The characteristic matrix of the multilayer is written as
with k=(1,…,N) and N number of layers. The parameters
with
The parameters
The wavelength dependent refractive indexes of vanadium dioxide in the metal phase and in the insulating phase (30 °C) and in the metallic phase (100 °C) have been taken from Ref. (Briggs et al., 2010). The employment of the two refractive indexes in the transfer matrix method allows to simulate the optical properties of the different photonic structures in the two temperature regimes.
In Figure 1 the light transmission spectrum for the microcavity (SiO2/ZrO2)5/VO2/(ZrO2/SiO2)5 is shown. The black solid curve is related to VO2 in the insulating phase, while the blue dashed curve is related to VO2 in the metallic phase. The two phases correspond to a temperature of the material of 30°C for the insulating phase and a temperature of 100 °C for the metallic phase, respectively, as reported in Ref. (Briggs et al., 2010). In the microcavity the thickness of the silicon dioxide layers is 220 nm, the thickness of the zirconium dioxide layers is 165 nm, while the thickness of the vanadium dioxide layers is 55 nm.
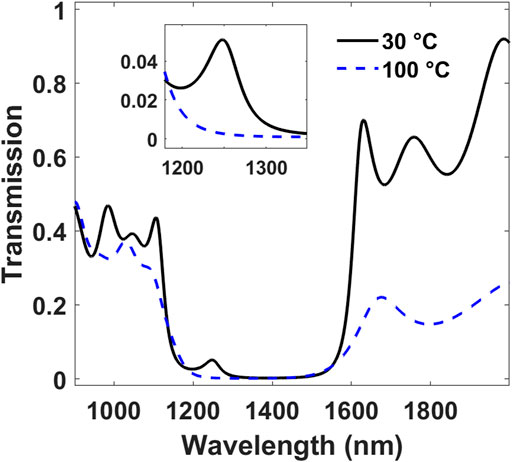
FIGURE 1. Light transmission spectra for the microcavity (SiO2/ZrO2)5/VO2/(ZrO2/SiO2)5 with VO2 in the insulating phase (at 30°C, black solid curve) and in the metallic phase (at 100°C, blue dashed curve).
In the microcavity configuration, the insulating VO2 based microcavity shows a defect mode at around 1,250 nm within the photonic band gap of the structure (i.e., the intense transmission valley between 1,100 nm and 1,600 nm). The intensity of the defect mode is in agreement with experimental values shown in microcavities for coherent photoluminescence (Chiasera et al., 2019). On the other hand, for light filtering, the defect mode intensity is not high enough, and higher values are required for this type of application. The defect mode is magnified in the inset of Figure 1. Instead, for the metallic VO2 based microcavity the defect mode is suppressed. Noteworthy, the transmission at wavelengths longer than 1,600 nm is weaker in the metallic VO2 phase because of its infrared absorption.
In Figure 2 the transmission spectrum for the aperiodic microcavity that follows the Thue-Morse sequence is depicted. The VO2 layer is sandwiched between two photonic structures with the sequence of layers ABBABAABBAABABBABAABABBAABBABAAB (Steurer and Sutter-Widmer, 2007) (A = SiO2; B = ZrO2). The layer thicknesses are the same ones of the periodic structure. The black solid curve is related to VO2 in the insulating phase, while the blue dashed curve is related to VO2 in the metallic phase. The transmission spectra are slightly modified with the VO2 from the insulating to the metallic phase, with the suppression of peaks around 1,100 and 1,600 nm.
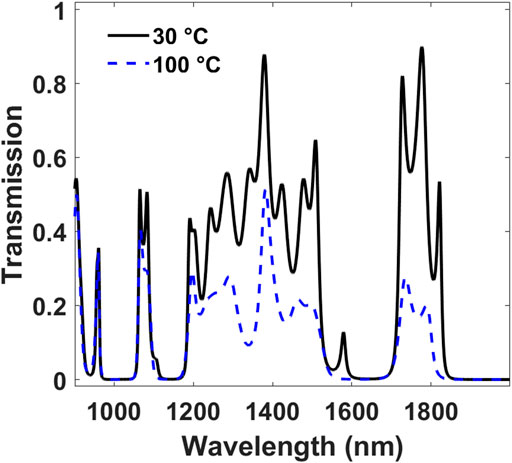
FIGURE 2. Light transmission spectra for the
Thue-Morse aperiodic microcavity
ABBABAABBAABABBABAABABBAABBABAAB/
VO2/ABBABAABBAABABBABAABABBAABBABAAB
(A = SiO2; B = ZrO2) with VO2 in the insulating phase (at 30°C, black solid curve)
and in the metallic phase (at 100°C, blue dashed curve).
In Figure 3A the transmission spectra for the disordered microcavity, in which VO2 is embedded between one-dimensional disordered photonic structures are shown (Wiersma et al., 2005; Wiersma, 2013). The proposed structure follows the sequence BBABBAABBBABBBBA/VO2/BABAABBBBABBBABA. Also in this case, the layer thicknesses are the same ones of the periodic structure and the black solid curves correspond to the insulating phase of VO2, while the blue dashed curves to the metallic phase of VO2. The transmission spectrum with VO2 in the insulating phase shows eight peaks in the studied range (900–2000 nm). With the transition from insulator to metal the suppression of most of the transmission peaks is noticeable.
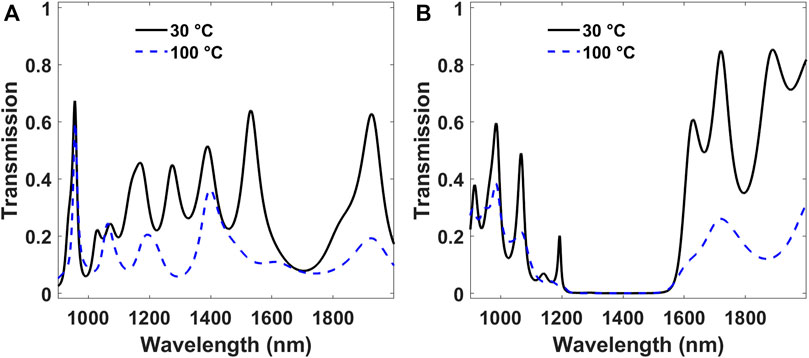
FIGURE 3. (A) Light transmission spectra for the disordered microcavity BBABBAABBBABBBBA/VO2/
BABAABBBBABBBABA (A = SiO2; B = ZrO2) with VO2 in the insulating phase (at 30°C, black solid curve) and in the metallic phase (at 100°C, blue dashed curve). (B) Light transmission spectra for the microcavity (SiO2/ZrO2)5/VO2/(ZrO2/SiO2)5, in which a random variation of the thicknesses is introduced, with VO2 in the insulating phase (at 30°C, black solid curve) and in the metallic phase (at 100°C, blue dashed curve).
In Figure 3B is shown the transmission spectra of the microcavity (SiO2/ZrO2)5/VO2/(ZrO2/SiO2)5, in which a random variation of the thicknesses is introduced (Faist et al., 1989; Chiasera et al., 2015). For the SiO2 layers the thickness follows
In Figure 4A the transmission spectrum of the four material-based microcavity (SiO2/Al2O3/Y2O3/ZrO2)6/VO2/(ZrO2/Y2O3/Al2O3/SiO2)6 is shown. The thickness of SiO2 layers is 275.9 nm, the thickness of Al2O3 layers is 228.6 nm, the thickness of Y2O3 layers is 210.5 nm, the thickness of ZrO2 layers is 190.5 nm, and the thickness of VO2 layers is 45.9 nm. As shown in previous reports, four-material photonic crystals show a manifold of gaps (Kriegel and Scotognella, 2015). In fact, with this structure, in the wavelength interval between 900 nm and 2000 nm two intense photonic band gaps are observable, compared to the single photonic band gap of the microcavity (Figure 1). In this case, the defect modes of the two photonic band gaps show a red shift and a remarkable intensity increase. In Figure 4B the transmission spectrum of the four material-based microcavity is shown in logarithmic scale to highlight the large modulation depth of the transmission peak at around 1,100 nm and 1,600 nm for the metallic phases of vanadium dioxide.
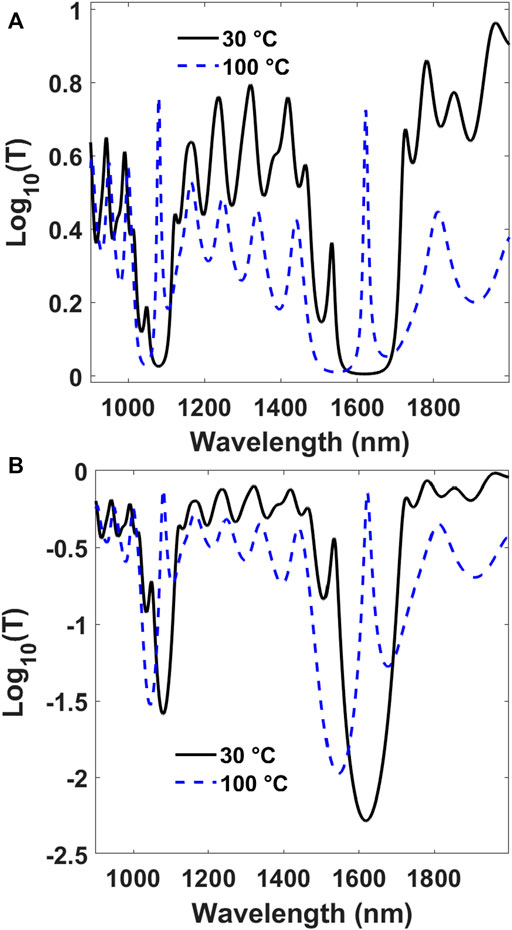
FIGURE 4. (A) Light transmission spectra for the
four-material photonic crystal based microcavity
(SiO2/Al2O3/Y2O3/ZrO2)6/
VO2/(ZrO2/Y2O3/Al2O3/SiO2)6 with VO2 in the insulating phase
(at 30°C, black solid curve) and in the metallic
phase (at 100°C, blue dashed curve). (B) Light transmission spectra for the four-material photonic crystal based microcavity in logarithmic scale.
In this work it has been studied the light transmission of different one-dimensional photonic microcavities that embed vanadium dioxide by means of the transfer matrix method. The four types of microcavities include periodic photonic crystals, aperiodic structures, disordered structures, and four-material-based photonic crystals. The different structures have been chosen in order to exploit their particular optical properties: An intense photonic bandgap with a defect for the microcavities including photonic crystals, a multiplicity of transmission valleys in the case of the microcavity with aperiodic structures, the occurrence of several transmission peaks, or a broader photonic band gap, in the case of microcavities with disordered structures, a doublet of photonic band gaps in the case of microcavities with four-material-based photonic structures. The transmission of VO2 from insulator to metal, achievable via a temperature increase, leads to a modulation of the transmission spectra, noticeable with shifts and suppressions of transmission peaks. The modulation of the transmission spectra of the microcavities can be exploited for smart windows and temperature-controlled switches. Moreover, the photonic structure can be also used as temperature sensor since it has been studied by Currie et al. the temperature dependent refractive index dispersion of vanadium dioxide (Currie et al., 2017).
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
FS is the sole author of the manuscript. FS conceived the idea, performed the simulations, analysed the data, wrote the manuscript.
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 816313).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Born, M., Wolf, E., Bhatia, A. B., Clemmow, P. C., Gabor, D., Stokes, A. R., et al. (1999). Principles of optics: Electromagnetic theory of propagation, interference and diffraction of light. 7th ed. Cambridge, UK: Cambridge University Press. doi:10.1017/CBO9781139644181
Boucher, Y. G., Chiasera, A., Ferrari, M., and Righini, G. C. (2009). Photoluminescence spectra of an optically pumped erbium-doped micro-cavity with SiO2/TiO2 distributed Bragg reflectors. J. Luminescence 129, 1989–1993. doi:10.1016/j.jlumin.2009.04.085
Briggs, R. M., Pryce, I. M., and Atwater, H. A. (2010). Compact silicon photonic waveguide modulator based on the vanadium dioxide metal-insulator phase transition. Opt. Express, OE 18, 11192–11201. doi:10.1364/OE.18.011192
Chiasera, A., Meroni, C., Scotognella, F., Boucher, Y. G., Galzerano, G., Lukowiak, A., et al. (2019). Coherent emission from fully Er3+ doped monolithic 1-D dielectric microcavity fabricated by rf-sputtering. Opt. Mater. 87, 107–111. doi:10.1016/j.optmat.2018.04.057
Chiasera, A., Scotognella, F., Criante, L., Varas, S., Valle, G. D., Ramponi, R., et al. (2015). Disorder in photonic structures induced by random layer thickness. Sci. Adv. mater 7, 1207–1212. doi:10.1166/sam.2015.2249
Currie, M., Mastro, M. A., and Wheeler, V. D. (2017). Characterizing the tunable refractive index of vanadium dioxide. Opt. Mater Express, OME 7, 1697–1707. doi:10.1364/OME.7.001697
Faist, J., Ganière, J -D., Buffat, Ph, Sampson, S., and Reinhart, F -K. (1989). Characterization of GaAs/(GaAs)n(AlAs)msurface-emitting laser structures through reflectivity and high-resolution electron microscopy measurements. J. Appl. Phys. 66, 1023–1032. doi:10.1063/1.343488
Guo, P., Schaller, R. D., Ocola, L. E., Diroll, B. T., Ketterson, J. B., and Chang, R. P. H. (2016). Large optical nonlinearity of ITO nanorods for sub-picosecond all-optical modulation of the full-visible spectrum. Nat. Commun. 7, 12892–12892_10. doi:10.1038/ncomms12892
Joannopoulos, J. D. (Editor) (2008). Photonic crystals: Molding the flow of light. 2nd ed. (Princeton, NJ, USA: Princeton University Press).
John, S. (1987). Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 58, 2486–2489. doi:10.1103/PhysRevLett.58.2486
Kriegel, I., and Scotognella, F. (2015). Band gap splitting and average transmission lowering in ordered and disordered one-dimensional photonic structures composed by more than two materials with the same optical thickness. Opt. Commun. 338, 523–527. doi:10.1016/j.optcom.2014.10.045
Kriegel, I., and Scotognella, F. (2018). Light-induced switching in pDTE–FICO 1D photonic structures. Opt. Commun. 410, 703–706. doi:10.1016/j.optcom.2017.11.019
Kriegel, I., Urso, C., Viola, D., De Trizio, L., Scotognella, F., Cerullo, G., et al. (2016). Ultrafast photodoping and plasmon dynamics in fluorine–indium codoped cadmium oxide nanocrystals for all-optical signal manipulation at optical communication wavelengths. J. Phys. Chem. Lett. 7, 3873–3881. doi:10.1021/acs.jpclett.6b01904
Li, B., Camacho-Morales, R., Li, N., Tognazzi, A., Gandolfi, M., Ceglia, D. de, et al. (2023). Fundamental limits for transmission modulation in VO2 metasurfaces. Phot. Res. PRJ 11, B40–B49. doi:10.1364/PRJ.474328
Liu, K., Lee, S., Yang, S., Delaire, O., and Wu, J. (2018). Recent progresses on physics and applications of vanadium dioxide. Mater. Today 21, 875–896. doi:10.1016/j.mattod.2018.03.029
Lu, H., Clark, S., Guo, Y., and Robertson, J. (2021). The metal–insulator phase change in vanadium dioxide and its applications. J. Appl. Phys. 129, 240902. doi:10.1063/5.0027674
Malitson, I. H. (1965). Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. JOSA 55, 1205–1209. doi:10.1364/JOSA.55.001205
Malitson, I. H. (1962). Refraction and dispersion of synthetic sapphire. J. Opt. Soc. Am. JOSA 52, 1377–1379. doi:10.1364/JOSA.52.001377
Morin, F. J. (1959). Oxides which show a metal-to-insulator transition at the neel temperature. Phys. Rev. Lett. 3, 34–36. doi:10.1103/PhysRevLett.3.34
Nigara, Y. (1968). Measurement of the optical constants of yttrium oxide. Jpn. J. Appl. Phys. 7, 404. doi:10.1143/JJAP.7.404
Paternò, G. M., Moscardi, L., Donini, S., Ariodanti, D., Kriegel, I., Zani, M., et al. (2019). Hybrid one-dimensional plasmonic–photonic crystals for optical detection of bacterial contaminants. J. Phys. Chem. Lett. 10, 4980–4986. doi:10.1021/acs.jpclett.9b01612
Rashidi, A., Hatef, A., and Namdar, A. (2018). On the enhancement of light absorption in vanadium dioxide/1D photonic crystal composite nanostructures. J. Phys. D. Appl. Phys. 51, 375102. doi:10.1088/1361-6463/aad70a
Singh, D. U., Bhoite, O., and Narayanan, R. (2020). Temperature tunable optical transmission using IR based 1D photonic crystals of VO2 nanostructures. J. Phys. D. Appl. Phys. 53, 245106. doi:10.1088/1361-6463/ab7d69
Steurer, W., and Sutter-Widmer, D. (2007). Photonic and phononic quasicrystals. J. Phys. D. Appl. Phys. 40, R229–R247. doi:10.1088/0022-3727/40/13/R01
Tan, C. Z. (1998). Determination of refractive index of silica glass for infrared wavelengths by IR spectroscopy. J. Non-Crystalline Solids 223, 158–163. doi:10.1016/S0022-3093(97)00438-9
Toccafondi, C., Occhi, L., Cavalleri, O., Penco, A., Castagna, R., Bianco, A., et al. (2014). Photochromic and photomechanical responses of an amorphous diarylethene-based polymer: A spectroscopic ellipsometry investigation of ultrathin films. J. Mater Chem. C 2, 4692–4698. doi:10.1039/C4TC00371C
Tognazzi, A., Gandolfi, M., Li, B., Ambrosio, G., Franceschini, P., Camacho-Morales, R., et al. (2023). Opto-thermal dynamics of thin-film optical limiters based on the VO2 phase transition. Opt. Mater Express, OME 13, 41–52. doi:10.1364/OME.472347
Verleur, H. W., Barker, A. S., and Berglund, C. N. (1968). Optical properties of VO2between 0.25 and 5 eV. Phys. Rev. 172, 788–798. doi:10.1103/PhysRev.172.788
Wiersma, D. S., Sapienza, R., Mujumdar, S., Colocci, M., Ghulinyan, M., and Pavesi, L. (2005). Optics of nanostructured dielectrics. J. Opt. A: Pure Appl. Opt. 7, S190–S197. doi:10.1088/1464-4258/7/2/025
Wood, D. L., and Nassau, K. (1982). Refractive index of cubic zirconia stabilized with yttria. Appl. Opt. AO 21, 2978–2981. doi:10.1364/AO.21.002978
Xiao, X., Wenjun, W., Shuhong, L., Wanquan, Z., Dong, Z., Qianqian, D., et al. (2016). Investigation of defect modes with Al2O3 and TiO2 in one-dimensional photonic crystals. Optik 127, 135–138. doi:10.1016/j.ijleo.2015.10.005
Keywords: photonic cristals, vanadium oxide, metal-insulating transition, microcavities, transfer matrix method
Citation: Scotognella F (2023) Vanadium oxide metal-insulator phase transition in different types of one-dimensional photonic microcavities. Front. Photonics 4:1081521. doi: 10.3389/fphot.2023.1081521
Received: 27 October 2022; Accepted: 03 March 2023;
Published: 17 March 2023.
Edited by:
Lei Kang, The Pennsylvania State University (PSU), United StatesReviewed by:
Arezou Rashidi, University of Mazandaran, IranCopyright © 2023 Scotognella. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Scotognella, ZnJhbmNlc2NvLnNjb3RvZ25lbGxhQHBvbGltaS5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.