Engineered octave frequency comb in integrated chalcogenide dual-ring microresonators

Octave-spanning Kerr combs bridging the spectral windows of the near-infrared region (NIR) and the mid-infrared (MIR) region are expected in a number of applications, including high-capacity coherent optical communications, and gas molecular absorption footprints. Here, we propose novel concentric dual-ring microresonators (DRMs) for advanced dispersion engineering to tailor the comb spectral profile. The dispersion can be flexibly engineered not only by the cross-section of the DRMs, but also by the gap between concentric dual-ring microresonators, which provides a new path to geometrically control the spectral profile of the soliton Kerr combs. An octave-spanning Kerr soliton microcomb with multi-dispersive waves has been achieved numerically covering from the telecommunication band (1224 nm) to the mid-infrared band region (2913 nm) with a −40 dB bandwidth of 1265 nm. Our results are promising to fully understand the nonlinear dynamics in hybrid modes in DRMs, which helps control broadband comb formation.

Introduction

Microresonator-based Kerr combs (microcombs) have attracted significant research interest in the past decades, which enables the generation of the mode-locked laser pulse in chip-scale photonic devices at milliwatt-level power (Fortier and Baumann, 2019). Dissipative Kerr solitons (DKSs) in microresonators have been demonstrated for high-quality laser sources with high coherence and large bandwidth, originating from the double balance between the dispersion and nonlinearity as well as the cavity losses and the parametric gain (Kippenberg et al., 2018). Up-to-date, soliton microcombs have revolutionized various applications, including large-capacity optical communications (Marin-Palomo et al., 2017; Geng et al., 2022), precision metrology, molecular spectroscopy (Suh et al., 2016; Dutt et al., 2018; Yu et al., 2018), massively parallel LiDAR (Feldmann et al., 2021), chip-scale frequency synthesizer (Spencer et al., 2018), etc., (Tanabe et al., 2019; Shastri et al., 2021). Specifically, octave-spanning soliton microcombs enable the high signal-to-noise ratio via phase locking of carrier-envelope-offset frequency (f_ceo), which becomes a significant task (Liu et al., 2021).

Bright soliton generation in integrated microresonators, benefitted from cavity-enhanced nonlinear efficiency and lithographically controlled accurate dispersion engineering, has advantages in generating high coherent broadband frequency combs in chip-scale footprint (Brasch et al., 2016; Okubo et al., 2018). The broad and flat comb spectra are required in many applications, which need highly careful dispersion engineering. With the aid of dispersive waves (DWs), octave-spanning microcombs have been demonstrated in many nonlinear photonic platforms (Li et al., 2017; Pfeiffer et al., 2017; Yu et al., 2019; Liu et al., 2021; Weng et al., 2021; Cai et al., 2022). However, the large dispersion barrier between the pump and the locations of DWs inevitably results in a decrease in the spectral flatness of the soliton microcombs. Many attempts at advanced dispersion engineering have been proposed, including slot waveguides (Zheng et al., 2008; De Leonardis and Passaro, 2011; Zhang et al., 2013; Wang et al., 2016), bilayer structures (Guo et al., 2016), and multi-cladding schemes (Jafari and Zarifkar, 2016; Liang et al., 2016; Wang et al., 2021). Recently, multiple zero group velocity wavelengths have been proven to facilitate flat and broadband microcomb generation, which are theoretically achieved in integrated microresonators with the above-mentioned methods. However, these microresonators with complex structures are sensitive to fabrication tolerance and remain challenging in high-quality (Q) factor photonic systems. Recently, the concentric dual-ring microresonators (DRMs) (Soltani et al., 2016; Kim et al., 2017; Ding and Feng, 2020; Saha et al., 2021) are proposed to potentially manipulate the group velocity dispersion by controlling the mode coupling between the hybrid waveguides, providing additional degrees of freedom for geometric design in comparison to single-ring microresonators (SRMs). However, tailoring the bandwidth and flatness of the soliton microcombs in this attractive structure, has not been explored yet.

In this work, broadband and flat optical frequency comb generation in DRMs based on a home-developed chalcogenide glass (Ge₂₅Sb₁₅S₆₀), due to its wide transmission window from 0.5 to 10 μm, is theoretically investigated to obtain an octave-range microcomb spanning the near-infrared and the mid-infrared (MIR) region for various applications including coherent optical communications (Kong et al., 2022), and gas molecular absorption footprints (Tan et al., 2021). The characteristics of supermode coupling and integrated dispersion of DRMs are studied to achieve local anomalous dispersion by mode hybridization between the inner and outer microresonators in DRM systems. Accordingly, multiple DWs can be attained by introducing local anomalous dispersion in the strong normal dispersion regime in MIR, leading to beyond-octave flat frequency comb generation spanning from 1224 to 2913 nm with a −40 dB bandwidth of 1265 nm. Moreover, the comb power at a specific spectral region in concentric DRMs is enhanced, which is potential for a broad range of applications, such as coherent optical communications. Our results provide a novel route to achieve broadband-integrated microcombs with a user-defined target spectral profile.

Operation principle of supermode hybridization in DRMs

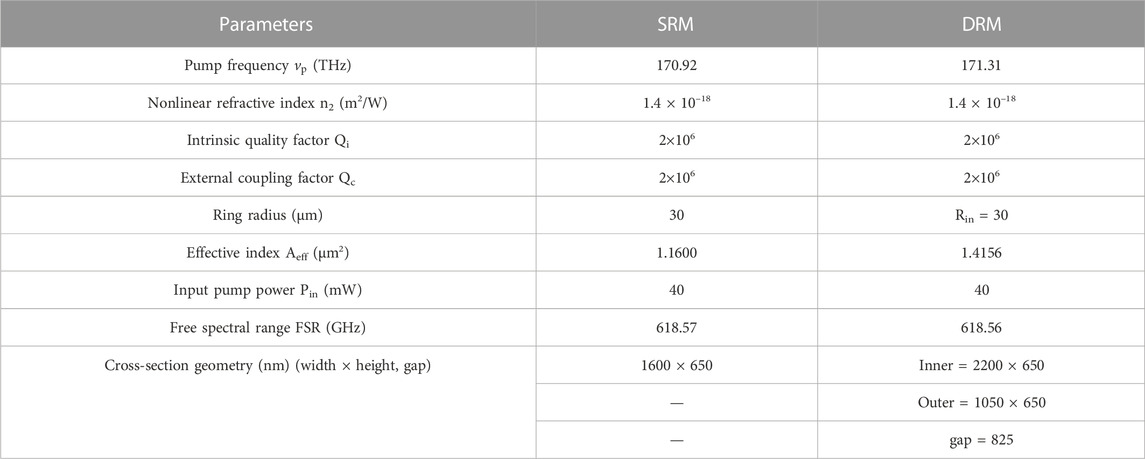
The structure of the DRM is shown in Figure 1A, which is composed of two concentrically placed microring resonators with a certain distance and an independent coupling bus waveguide. The new home-developed chalcogenide glass-Ge₂₅Sb₁₀S₆₅ is chosen as the core, and the air upper cladding is used to reduce material absorption in MIR, see Figure 1B. The system is driven by a continuous-wave laser for broadband frequency comb generation.

FIGURE 1

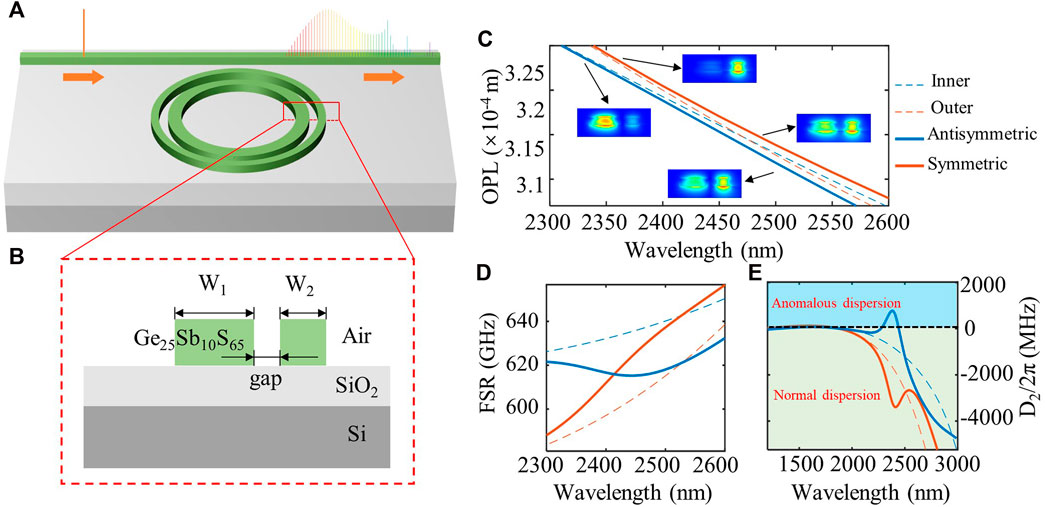
FIGURE 1. Schematic of the proposed DRM and characterization of supermode hybridization. The DRM has an inner ring of radius R = 30 μm, an inner ring width of W₁ = 2200 nm, a height of H = 650 nm, a gap of 850 nm, and an outer ring of W₂ = 1050 nm. (A) 3D profile of the DRM. (B) Cross section of the DRM based on Ge₂₅Sb₁₀S₆₅ material on insulator. (C) The variation of optical path lengths (OPLs) and corresponding electric mode field distributions. The dashed lines are the calculated OPLs of the TM₀₀ modes in the inner and outer SRM, respectively. The solid lines are OPLs of antisymmetric and symmetric supermodes in the DRM. (D) The calculated free spectral ranges (FSRs) and (E) group velocity dispersion (D₂) of the fundamental transverse magnetic modes (TM₀₀).

Local dispersion profiles can be engineered by adequately designing the structural parameters of DRM and introducing mode hybridization. Here, the fundamental quasi-transverse magnetic mode (TM₀₀) mode is taken into consideration. In the absence of the coupling of the inner and the outer microresonators, the optical path lengths (OPLs) of the independent inner and the outer microresonators (SRM) can be described as the following, respectively (Kim et al., 2017),

${\mathrm{O}\mathrm{P}\mathrm{L}}_{\mathrm{i}\mathrm{n}}=2\mathrm{\pi }{R}_{\mathrm{i}\mathrm{n}}{n}_{\mathrm{i}\mathrm{n}}(1)$

${\mathrm{O}\mathrm{P}\mathrm{L}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=2\mathrm{\pi }{R}_{\mathrm{o}\mathrm{u}\mathrm{t}}{n}_{\mathrm{o}\mathrm{u}\mathrm{t}}(2)$

where OPL_in and OPL_out represent the OPLs of the inner and outer microresonator, respectively. $R_{\mathrm{i}\mathrm{n}}$ and $R_{\mathrm{o}\mathrm{u}\mathrm{t}}$ denote their ring radius. The $n_{\mathrm{i}\mathrm{n}}$ and $n_{\mathrm{o}\mathrm{u}\mathrm{t}}$ are the effective mode refractive indices. The mode coupling between hybrid waveguides occurs at the regime where OPLs of the individual inner and outer SRMs are equal (Kim et al., 2017).

We perform the modified dispersion simulation of the DRM based on the structural parameters of R = 30 μm, W₁ = 2200 nm, H = 650 nm, gap = 850 nm, and W₂ = 1050 nm. A cross point of the calculated OPLs of the TM₀₀ modes for two separate SRMs appears at the wavelength of around 2.4 μm, see Figure 1C. To characterize the formation of mode hybridization, the free spectral ranges and group velocity dispersion of the DRM are investigated. The resonance frequencies of microresonators are determined by Pfeiffer et al. (2017),

${\omega }_{\mu }={\omega }_{\mathrm{s}}+D_1\mu +\frac{1}{2}{D}_2{\mu }^2+\dots (3)$

Where $D_1/2\pi$ is equivalent to the free spectral range of microresonators, $D_k\left(k\ge 2\right)$ is the k-order dispersion coefficient, ${\omega }_{s\left(u\right)}$ is the angular resonant frequency for pump mode and other modes, and $\mu$ is the relative mode number. The integrated dispersion D_int including the full-order dispersion term, can be calculated by Pfeiffer et al. (2017), Cai et al. (2022),

$D_{\mathrm{int}}={\omega }_{\mu }-{\omega }_{\mathrm{s}}-D_1\mu ={\displaystyle \sum }_{k=2}^{\infty }\frac{1}{k!}{D}_k{\mu }^k(4)$

The broadband and flat spectral envelope of microcomb rely on dispersive wave generation by tailoring the integrated dispersion engineering, which will be discussed in parts 3 and 4. Here, we investigate the impact of mode hybridization on second-order dispersion (D₂). In the DRM system, the modes in the inner and outer microresonator will divert to each other as wavelength increases and generate the resonant mode hybridization between the coupled waveguides. Compared with the individual microresonators, the mode distributions in DRMs show the superposition of the original modes in inner and outer microresonators (inset of Figure 1C), which are defined as symmetric and antisymmetric supermodes. As the mode hybridization modifies the effective index of supermodes, their eigenfrequencies shift slightly from the original uncoupled modes in SRMs accordingly (Saha et al., 2021). Hence, local FSRs change remarkably, and the crosstalk of FSRs arises to modify the second-order dispersion of supermodes. The FSRs of the hybrid symmetric and anti-symmetric modes of the DRMs vary in two distinct ways as wavelength increases. In the mode coupling region, the FSR of the anti-symmetric mode is decreasing with wavelength, which is the origin of anomalous dispersion ($\frac{\partial FSR}{\partial \lambda }<0$) (Fujii and Tanabe, 2020), while the symmetric mode features normal dispersion ($\frac{\partial FSR}{\partial \lambda }>0$), see Figure 1D. The symmetric supermode features strong normal dispersion (D₂ < 0) around the mode coupling region, while the antisymmetric supermode undergoes a period of strong anomalous dispersion (D₂ > 0), see Figure 1E. Therefore, the antisymmetric mode of the DRMs can introduce anomalous dispersion in the strong normal dispersion region and be utilized to modify the integrated dispersion D_int profile of the microresonators. In the DRMs system, the symmetric mode is more likely to be excited because the outer ring is closer to the bus waveguide (Kim et al., 2017). Here, a pulley coupling scheme based on adiabatic mode conversion has been proposed to excite the anti-symmetric mode efficiently for the DRMs (Figure 2A). The widths of the inner and outer of the DRMs are adiabatically tapered simultaneously in the coupling region. As a result, the light in the bus waveguide is first transferred into the outer ring, and then gradually coupled to the inner ring of DMRs to excite anti-symmetric mode as the widths of the DRMs are increasing adiabatically, see Figure 2B.

FIGURE 2

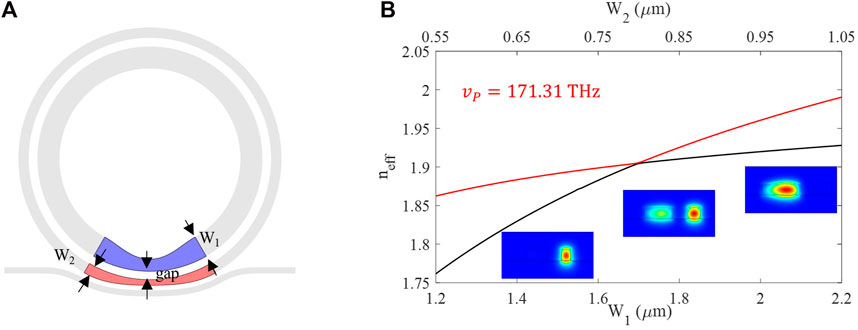
FIGURE 2. Schematic of external coupling of the hybrid modes in the DRMs. (A) An adiabatic tapering section is marked in a colored region. (B) Simulated effective index in the tapered section for exciting anti-symmetric mode.

Dispersion engineering and fabrication tolerances

The local dispersion at the specific wavelength of the DRMs can be adjusted by tailoring structural parameters of the two microresonators, including the inner ring width (W₁), outer ring width (W₂), gap and thickness (h) in the DRMs. The dispersion engineering is most sensitive to “h” and is least sensitive to “W₁”. By carefully designing four structural parameters, mode hybridization can be achieved in the MIR region to tailor the shape of the microcombs, see Figure 3. Moreover, considering the antisymmetric mode in the same DRM in part 2, increasing the outer ring width W₂ or the gap will push the coupling region to a longer wavelength, see Figures 3A, C. It is worth noting that the dispersion profile far from the coupling wavelength remains unchanged. Four zero-integrated dispersion wavelengths with a flat spectral shape can be observed by optimizing the geometric parameters of the microresonators, see Figures 3B, D. When the structure of the inner ring is fixed, the local anomalous dispersion and integrated dispersion with a tunable coupling position for antisymmetric mode are favourable by adjusting the gap and W₂.

FIGURE 3

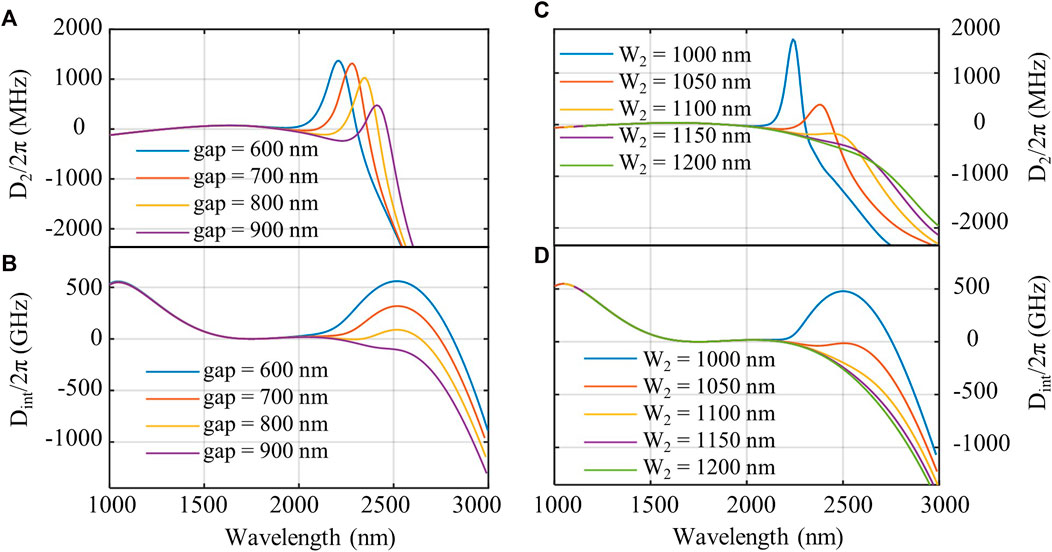
FIGURE 3. Dispersion profiles of the DRMs with structural parameters varying at near R = 30 μm, W₁ = 2200 nm, H = 650 nm, gap = 850 nm, W₂ = 1050 nm. (A), (B) The variations of D₂ and D_int of antisymmetric modes with the gap. (C), (D) The variations of the D₂ and D_int of antisymmetric mode with W₂.

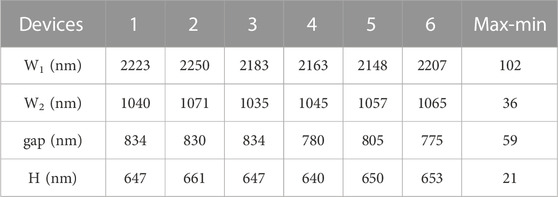
To analyze the fabrication tolerances of the DRMs, we randomly and independently tune the four structural parameters (W₁, W₂, gap, and h) of the DRMs, which is repeated six times (Guo et al., 2019). The variation of integrated dispersion due to the dimension tolerance is smaller than 200 GHz for all six devices, which still enables the generation of engineered dispersive waves near the wavelength of 2500 nm, see Figure 4 and Table 1. As a result, the proposed DRMs have a large fabrication tolerance to support broadband soliton microcomb generation.

FIGURE 4

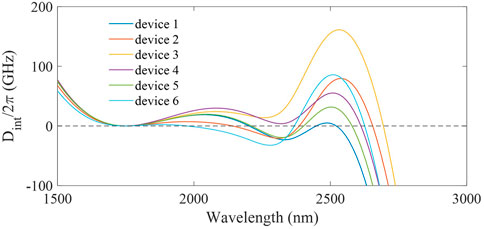
FIGURE 4. Integrated dispersion profiles of the six DRM devices with different structural parameters correspond to Table 1.

TABLE 1

TABLE 1. Six different DRM devices with randomly changed geometric parameters.

We also provide a practical fabrication process for the DRMs (Xia et al., 2022a; Xia et al., 2022b). First, the GeSbS film is thermally evaporated on the silicon substrate with 3 μm silicon oxide layer. The deposition rate is set to approximately 5A/second and thereby the variation of thickness can be precisely controlled at ± 5 nm when the total thickness of the film is 800 nm (Zhang et al., 2021). Furthermore, a dry etch trimming scheme can be utilized to finely change the thickness of GeSbS film (Moille et al., 2021). Then, a photoresist (ARP-6200) with a thickness of ca. 800 nm is coated on the GeSbS film. After that, the waveguide structure is patterned on the ARP layer using electron-beam lithography (EBL) and then transferred to GeSbS layer by inductively coupled plasma (ICP) reactive ion etcher (ICP-RIE). Afterward, an ICP-RIE is used to remove the residual resist. The dimensional accuracy of W₁, W₂, and gap for the DRMs can be controlled within 20 nm. Therefore, the geometric dispersion engineering for broadband microcombs generation can be fulfilled by the typical fabrication process of integrated chalcogenide microresonators.

Flat and broadband frequency comb generation

Generally, higher-order dispersion plays a significant role in the generation of DWs, which can tune the spectral shape (Grassani et al., 2019; Okawachi et al., 2022). Here, we investigate the influence of dispersion engineering of DRMs on the frequency comb generation, especially on multiple DWs generation.

A phase-matching condition between the soliton pulse and DW is required for the generation of DWs, which is defined as (Guo et al., 2018),

$\beta \left({\omega }_{\mathrm{d}}\right)=\beta \left({\omega }_{\mathrm{s}}\right)+\frac{\left({\omega }_{\mathrm{d}}-{\omega }_{\mathrm{s}}\right)}{v_{\mathrm{g}}}+\frac{\gamma P}{2}(5)$

where $\beta$ is the propagation constant of light, ${\omega }_d$ and ${\omega }_s$ are the angular frequencies of DW and pump light, v_g denotes the group velocity, P is pump power, $\gamma$ is the nonlinear coefficient. The phase mismatching induced by nonlinear phase shift $\gamma P$/2, can be negligible under low pump power. Therefore, the spectral position (${\omega }_d$) of the DW generation is approximately given by linear phase-mismatching conditions in the fiber system, as defined in Eq. 5 without the third term on the right-hand side (Erkintalo et al., 2012). In chip-based microresonator systems, this linear phase-matching condition is analogous to the integrated dispersion D_int(μ_DW) = 0 in Eq. 4, where μ_DW is the relative mode number of DWs (Brasch et al., 2016).

Then, we numerically simulate the spectral and time dynamic of Kerr frequency comb in concentric DRMs and SRMs by mean-field LLE model (Coen et al., 2013; Guo et al., 2017; Kovach et al., 2020),

$\frac{\partial A}{\partial t}=-\left(\frac{\kappa }{2}-\mathrm{i}\Delta \right)A+{\sum }_{k\ge 2}{\left(-\mathrm{i}\right)}^{\mathrm{k}+1}\frac{D_{\mathrm{k}}}{k!}{\left(\frac{\partial }{\partial \theta }\right)}^k\mathrm{A}+\mathrm{i}{g}_0{\left|A\right|}^{2}A+\sqrt{k_{\mathrm{c}}}{S}_{\mathrm{i}\mathrm{n}}(6)$

where |A|² is the intracavity photon number, $t=n{T}_{\mathrm{R}}$ is the slow time with T_R representing the roundtrip time and n representing the number of T_R in simulation. $\theta =\frac{2\pi \tau }{T_{\mathrm{R}}}$ is the angular location of the light field envelope in microresonators with $\tau$ representing the fast time of light. $\mathrm{\Delta }={\omega }_{\mathrm{p}}-{\omega }_0$ is the frequency detuning between the pump and the cold cavity resonance. Generally, the relationship between the actual intracavity energy field |E|² (S.I. unit: W) and the intracavity photon number |A|² (S.I. unit: 1) is ${\left|E\right|}^2={\left|A\right|}^2\cdot \hslash \omega /T_R$, where $\hslash \omega$ is the energy of a single photon (Guo et al., 2017). Generally, the pump frequency scan from blue detuning ($\mathrm{\Delta }>0$) to red detuning ($\mathrm{\Delta }<0$) for frequency comb excitation, where the nonlinear thermal phase shift is not included in our model because it makes little difference to the bandwidth of frequency comb (Xia et al., 2022a). $g_0=\frac{\mathrm{\hslash }{\omega }^{2}c{n}_2}{n_{\mathrm{g}}^2{V}_{\mathrm{e}\mathrm{f}\mathrm{f}}}$ is the Kerr gain coefficient related to the nonlinear refractive index n₂ and effective modal volume V_eff. The cavity total decay rate $\kappa ={\kappa }_0+{\kappa }_c=\frac{\omega }{Q_0}+\frac{\omega }{Q_c}$ is composed of two parts, the intrinsic decay rate ${\kappa }_0$ and external coupling rate ${\kappa }_c$, which can be derived from the quality factor $Q_0$ and $Q_c$, respectively. In this work, the pump frequency linearly detunes from $5\kappa$ to $-45\kappa$ to trigger the formation of microcomb, and the simulation parameters used in our model are listed in Table 2. Here, the home-developed chalcogenide glass material (Ge₂₅Sb₁₅S₆₀) was reported for integrated nonlinear photonics including integrated Raman lasers and Kerr frequency combs in microresonators (microcombs), which have been demonstrated in our previous works (Xia et al., 2022a; Xia et al., 2022b). The measured intrinsic Q and coupling Q of GeSbS microring resonators with a radius of 100 μm are 2.3 × 10⁶ and 4.0 × 10⁶, respectively. In this work, both the intrinsic Q and coupling Q of our dual-ring Ge₂₅Sb₁₅S₆₀ microresonators are chosen as 2 × 10⁶ for simulations. The nonlinear refractive index of Ge₂₅Sb₁₅S₆₀ film is also obtained in ref. Xia et al. (2022a), which was measured using the Z-scan method. To achieve a broadband microcomb covering the NIR and MIR region in the DRMs, a 1.75-μm pump laser is utilized, which can be available from a commercial DFB continuous-wave laser and a home-developed all-fiber short-wavelength (1650–1800 nm) thulium-doped fiber amplifier (TDFA) (Kong et al., 2022).

TABLE 2

TABLE 2. Simulated geometric parameters of the SRM and DRM.

We first analyzed the integrated dispersion in a traditional microresonator with R = 30 μm, W₁ = 1600 nm, and H = 650 nm, see Figure 5A. The maximum phase mismatching between the pump and DW reaches ∼70 GHz, resulting in strong power depression of the spectral comb lines, which hinders the access of octave frequency comb with high flatness. Therefore, when DW moves farther from the pump wavelength, the spectral region between the pump wavelength and DW will show a larger phase mismatching, causing more energy discrepancy among the comb lines (Guo et al., 2018; Grassani et al., 2019; Guo et al., 2020). For comparison, in DRM with R = 30 μm, W₁ = 2200 nm, H = 650 nm, W₂ = 1050 nm, gap = 825 nm, a flat integrated dispersion curve can be realized with D₂/2π = 57.77 MHz, and D₃/2π = 1.84 MHz by creating an additional anomalous dispersion region in the long wavelength, see the upper panel in Figure 5B. Three zero integrated dispersion points (excluding pump wavelength) are observed in the wavelength range from 2000 to 3000 nm, allowing an overall flat dispersion spectral shape and a smaller phase mismatching (∼20 GHz) compared with the SRM.

FIGURE 5

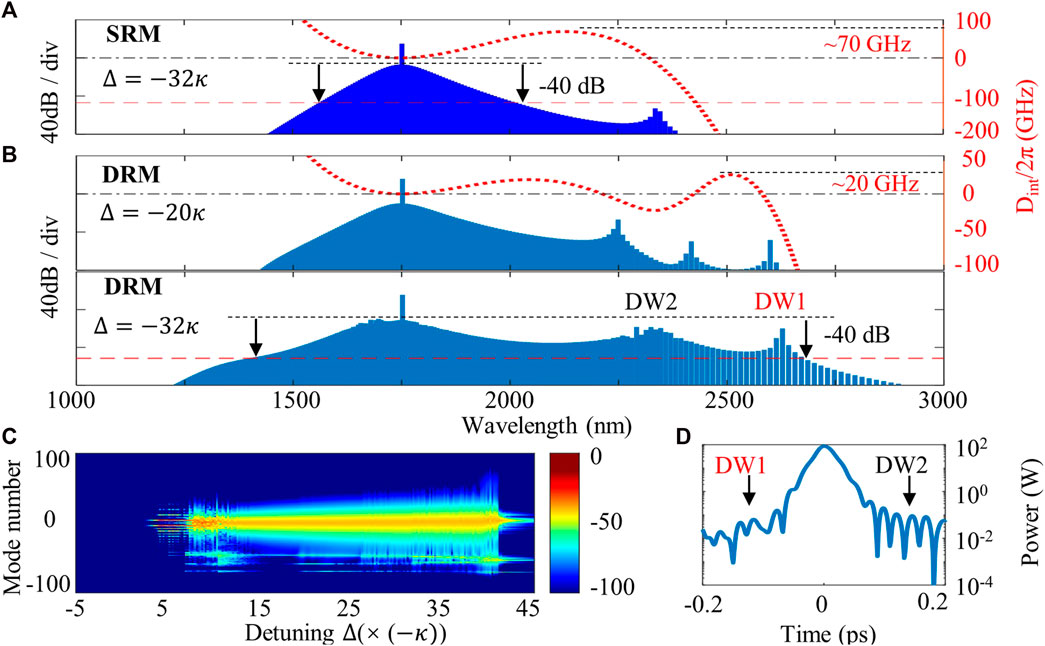
FIGURE 5. The generations of optical frequency combs in different microresonators. (A) The integrated dispersion (right axis) and frequency comb spectrum (left axis) of the SRM at the detuning $\mathrm{\Delta }=-32\kappa$ with a −40 dB bandwidth of only 449.89 nm (1564.84–2014.73 nm). (B) Upper panel: the integrated dispersion of DRM with a flat and small dispersion configuration (right axis). The corresponding frequency comb spectrum from LLE simulation at detuning $\mathrm{\Delta }=-32\kappa$ (left axis) features multiple DWs at phase-matching wavelengths. Lower panel: octave comb spectrum ranging from 1227.25 to 2912.87 nm at the same detuning $\mathrm{\Delta }=-32\kappa$ as the spectrum in (A), with a −40 dB bandwidth of 1265.84 nm (1405.63–2671.47 nm). (C) Spectral evolution with detuning in the DRM. The pump frequency detunes from $5\kappa$ to $-45\kappa$. (D) The temporal waveform at $\mathrm{\Delta }=-32\kappa$, indicates two typical DWs tails (labeled as DW1 and DW2) along with a soliton pulse.

In the numerical simulation, mode-locked octave frequency comb with a −40 dB bandwidth of 1265.84 nm (99.82 THz) and 620 GHz comb lines spacing can be obtained in DRM when the pump detuning is swept to $-32\kappa$, see the lower panel in Figure 5B. Because of the high Kerr nonlinearity of chalcogenide material, the driving pump power for such broadband soliton microcomb is 40 mW. The microcomb in the SRM has a typical sech² spectral envelope and the comb power decreases monotonously as comb frequencies are farther away from the pump frequency, see Figure 5A. While the soliton microcomb based on the DRMs features wide bandwidth with a flatter envelope at the same detuning. Generally, the spectral flatness of microcombs can be evaluated by the ratio of the geometric mean to the arithmetic mean of the power spectrum in a certain wavelength range (Tian et al., 2015),

$SFM=\frac{{\left[{\displaystyle \prod }_{k=1}^N{S}_k^2\right]}^{\frac{1}{N}}}{\left[\frac{1}{N}{\displaystyle \sum }_{k=1}^N{S}_k^2\right]}(7)$

Where SFM and S_k denote the spectral flatness and power of each comb line, respectively. As SFM is closer to 1, the spectrum is flatter. The SFM of the simulated octave micrcomb in the DRM was calculated to be 0.645, while SFM = 0.593 for microcomb in the SRM. The dynamic behavior of DWs spectral evolution can be observed as the pump laser detunes from $5\kappa$ to $-45\kappa$, see Figure 5C. At small detuning $-20\kappa$, three DWs emerge at the spectral position corresponding to D_int = 0, as shown in the upper panel in Figure 5B. As the pump wavelength moves further into red detuning, two gradually merge into one with higher comb line power (Figure 5D) due to the power-dependent nonlinear phase shift (Anderson et al., 2022). Taking the detuning effect into account, we can confirm that the spectral position of DWs is determined by $D_{\mathrm{int}}\left(\mu \right)=\mathrm{\Delta }$ (Anderson et al., 2022). In the temporal domain, the soliton pulse is characterized by two kinds of DW tails (DW1 and DW2) sitting on the background of continuous waves (Anderson et al., 2022), see Figure 5D. The peculiar structures of spectral and temporal profiles in the DRM improve the understanding of broadband soliton comb with multiple DWs. It also highlights the utility of DRMs as a feasible scheme to extend spectral region deep into the MIR footprint region for molecular spectroscopy.

Furthermore, the DWs position can be flexibly tuned while keeping the large bandwidth in the DRMs to meet the high demands of practical applications. For example, the integrated dispersion curves at ∼2500 nm are engineered to adjust the number and the position of the zero integrated dispersion points by increasing the width of the outer microresonator of the DRMs, see Figure 6A, broadband (octave) DKS spectra accompanied by the generation of DW can be observed correspondingly when the width of the outer microresonator is 1060 nm. Moreover, as W₂ decreases, the positions of the DWs tend to shift to longer wavelengths, giving rise to beyond-octave DKS, see Figure 6B. Therefore, devisable DKS states can be obtained by tailoring the spectral profile of DWs, allowing for the extension of spectral coverage and boosting comb outpower at the desired wavelengths (Okawachi et al., 2022).

FIGURE 6

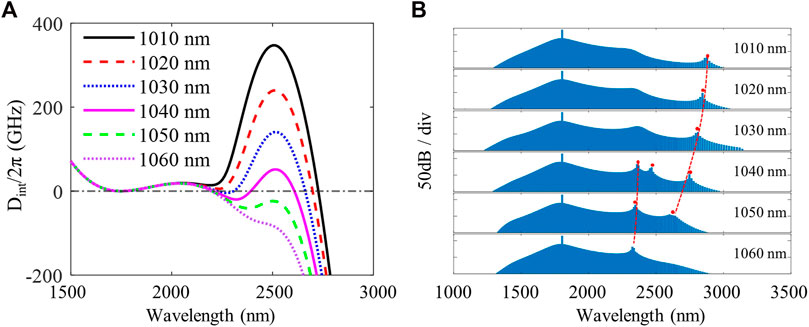
FIGURE 6. The spectral location tailoring of DWs by changing the outer microresonator width W2 in the DRMs. (A) Integrated dispersion curves with W₂ varying from 1010 to 1060 nm. The other simulated parameters are fixed at R = 30 μm, W₁ = 2200 nm, H = 650 nm, and gap = 800 nm. (B) The corresponding output spectra with different W₂. Tuning “W₂” allows desired spectral shaping of frequency combs and enhancement of the comb power at the target wavelengths. The pump detuning is fixed at $-32\kappa$ for comparison.

Conclusion

In summary, we have systematically investigated the effect of advanced dispersion engineering of the DRMs on the spectral evolution of soliton microcombs generation. By introducing the mode hybridization, the dispersion can be spectrally optimized in favour of generating multiple dispersive waves. Octave-spanning Kerr combs with the target shape can be realized numerically by geometrically controlling the DRMs. This flexible DRMs structure enables mode coupling in hybrid waveguides and control of the spectral location of the dispersive wave, which is critical in broadband soliton microcombs generation.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZW built the theoretical simulation model of concentric microring resonators. LL performed numerical simulations and processed the data. ZW, LL, and DX wrote the manuscript together. The work was done under the supervision of BZ. All authors contributed to the revision of the manuscript.

Funding

This work was supported by Key Project in Broadband Communication and New Network of the Ministry of Science and Technology (MOST) (2018YFB1801003), the National Key R&D Program of China under Grant (2019YFA0706301), National Science Foundation of China (NSFC) (U2001601, 61975242, 61525502, 11974234), the Science Foundation of Guangzhou City (202002030103).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, M. H., Weng, W., Lihachev, G., Tikan, A., Liu, J., and Kippenberg, T. J. (2022). Zero dispersion Kerr solitons in optical microresonators. Nat. Commun. 13, 4764. doi:10.1038/s41467-022-31916-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Brasch, V., Geiselmann, M., Herr, T., Lihachev, G., Pfeiffer, M. H. P., Gorodetsky, M. L., et al. (2016). Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science 351, 357–360. doi:10.1126/science.aad4811

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, L., Li, J., Wang, R., and Li, Q. (2022). Octave-spanning microcomb generation in 4H-silicon-carbide-on-insulator photonics platform. Photonics Res. 10, 870–876. doi:10.1364/PRJ.449267

CrossRef Full Text | Google Scholar

Coen, S., Randle, H. G., Sylvestre, T., and Erkintalo, M. (2013). Modeling of octave-spanning Kerr frequency combs using a generalized mean-field Lugiato–Lefever model. Opt. Lett. 38, 37–39. doi:10.1364/OL.38.000037

PubMed Abstract | CrossRef Full Text | Google Scholar

De Leonardis, F., and Passaro, V. (2011). Dispersion engineered silicon nanocrystal slot waveguides for soliton ultrafast optical processing. Adv. Optoelectron. 2011, 1–9. doi:10.1155/2011/751498

CrossRef Full Text | Google Scholar

Ding, X., and Feng, S. (2020). Dispersion engineering in asymmetric dual-width Si3N4 waveguide with high confinement based on super-mode theory. Opt. Commun. 464, 125474. doi:10.1016/j.optcom.2020.125474

CrossRef Full Text | Google Scholar

Dutt, A., Joshi, C., Ji, X., Cardenas, J., Okawachi, Y., Luke, K., et al. (2018). On-chip dual-comb source for spectroscopy. Sci. Adv. 4, e1701858. doi:10.1126/sciadv.1701858

PubMed Abstract | CrossRef Full Text | Google Scholar

Erkintalo, M., Xu, Y. Q., Murdoch, S. G., Dudley, J. M., and Genty, G. (2012). Cascaded phase matching and nonlinear symmetry breaking in fiber frequency combs. Phys. Rev. Lett. 109, 223904. doi:10.1103/PhysRevLett.109.223904

PubMed Abstract | CrossRef Full Text | Google Scholar

Feldmann, J., Youngblood, N., Karpov, M., Gehring, H., Li, X., Stappers, M., et al. (2021). Parallel convolutional processing using an integrated photonic tensor core. Nature 589, 52–58. doi:10.1038/s41586-020-03070-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Fortier, T., and Baumann, E. (2019). 20 years of developments in optical frequency comb technology and applications. Commun. Phys. 2, 153. doi:10.1038/s42005-019-0249-y

CrossRef Full Text | Google Scholar

Fujii, S., and Tanabe, T. (2020). Dispersion engineering and measurement of whispering gallery mode microresonator for Kerr frequency comb generation. Nanophotonics 9, 1087–1104. doi:10.1515/nanoph-2019-0497

CrossRef Full Text | Google Scholar

Geng, Y., Zhou, H., Han, X., Cui, W., Zhang, Q., Liu, B., et al. (2022). Coherent optical communications using coherence-cloned Kerr soliton microcombs. Nat. Commun. 13, 1070–1078. doi:10.1038/s41467-022-28712-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Grassani, D., Tagkoudi, E., Guo, H., Herkommer, C., Yang, F., Kippenberg, T. J., et al. (2019). Mid-infrared gas spectroscopy using efficient fiber laser driven photonic chip-based supercontinuum. Nat. Commun. 10, 1553. doi:10.1038/s41467-019-09590-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, H., Herkommer, C., Billat, A., Grassani, D., Zhang, C., Pfeiffer, M. H. P., et al. (2018). Mid-infrared frequency comb via coherent dispersive wave generation in silicon nitride nanophotonic waveguides. Nat. Photonics 12, 330–335. doi:10.1038/s41566-018-0144-1

CrossRef Full Text | Google Scholar

Guo, H., Karpov, M., Lucas, E., Kordts, A., Pfeiffer, M., Brasch, V., et al. (2017). Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat. Phys. 13, 94–102. doi:10.1038/nphys3893

CrossRef Full Text | Google Scholar

Guo, H., Weng, W., Liu, J., Yang, F., Hansel, W., Bres, C. S., et al. (2020). Nanophotonic supercontinuum-based mid-infrared dual-comb spectroscopy. Optica 7, 1181–1188. doi:10.1364/OPTICA.396542

CrossRef Full Text | Google Scholar

Guo, Y., Jafari, Z., Agarwal, A. M., Kimerling, L. C., Li, G., Michel, J., et al. (2016). Bilayer dispersion-flattened waveguides with four zero-dispersion wavelengths. Opt. Lett. 41, 4939–4942. doi:10.1364/OL.41.004939

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Jafari, Z., Xu, L., Bao, C., Liao, P., Li, G., et al. (2019). Ultra-flat dispersion in an integrated waveguide with five and six zero-dispersion wavelengths for mid-infrared photonics. Photonics Res. 7, 1279–1286. doi:10.1364/PRJ.7.001279

CrossRef Full Text | Google Scholar

Jafari, Z., and Zarifkar, A. (2016). Fabrication-friendly subwavelength-structure-assisted waveguide for dispersion engineering. Appl. Opt. 55, 9084–9090. doi:10.1364/AO.55.009084

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Han, K., Wang, C., Jaramillo-Villegas, J. A., Xue, X., Bao, C., et al. (2017). Dispersion engineering and frequency comb generation in thin silicon nitride concentric microresonators. Nat. Commun. 8, 372–378. doi:10.1038/s41467-017-00491-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kippenberg, T. J., Gaeta, A. L., Lipson, M., and Gorodetsky, M. L. (2018). Dissipative Kerr solitons in optical microresonators. Science 361, eaan8083. doi:10.1126/science.aan8083

PubMed Abstract | CrossRef Full Text | Google Scholar

Kong, D., Liu, Y., Ren, Z., Jung, Y., Kim, C., Chen, Y., et al. (2022). Super-broadband on-chip continuous spectral translation unlocking coherent optical communications beyond conventional telecom bands. Nat. Commun. 13, 4139. doi:10.1038/s41467-022-31884-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kovach, A., Chen, D., He, J., Choi, H., Dogan, A. H., Ghasemkhani, M., et al. (2020). Emerging material systems for integrated optical Kerr frequency combs. Adv. Opt. Photonics 12, 135–222. doi:10.1364/AOP.376924

CrossRef Full Text | Google Scholar

Li, Q., Briles, T. C., Westly, D. A., Drake, T. E., Stone, J. R., Ilic, B. R., et al. (2017). Stably accessing octave-spanning microresonator frequency combs in the soliton regime. Optica 4, 193–203. doi:10.1364/OPTICA.4.000193

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, H., He, Y., Luo, R., and Lin, Q. (2016). Ultra-broadband dispersion engineering of nanophotonic waveguides. Opt. Express 24, 29444–29451. doi:10.1364/OE.24.029444

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Gong, Z., Bruch, A. W., Surya, J. B., Lu, J., and Tang, H. X. (2021). Aluminum nitride nanophotonics for beyond-octave soliton microcomb generation and self-referencing. Nat. Commun. 12, 5428. doi:10.1038/s41467-021-25751-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Marin-Palomo, P., Kemal, J. N., Karpov, M., Kordts, A., Pfeifle, J., Pfeiffer, M. H. P., et al. (2017). Microresonator-based solitons for massively parallel coherent optical communications. Nature 546, 274–279. doi:10.1038/nature22387

PubMed Abstract | CrossRef Full Text | Google Scholar

Moille, G., Westly, D., Orji, N. G., and Srinivasan, K. (2021). Tailoring broadband Kerr soliton microcombs via post-fabrication tuning of the geometric dispersion. Appl. Phys. Lett. 119, 121103. doi:10.1063/5.0061238

CrossRef Full Text | Google Scholar

Okawachi, Y., Kim, B. Y., Zhao, Y., Jang, J., Ji, X., Lipson, M., et al. (2022). Active tuning of dispersive waves in Kerr soliton combs. Opt. Lett. 47, 2234–2237. doi:10.1364/OL.456609

PubMed Abstract | CrossRef Full Text | Google Scholar

Okubo, S., Onae, A., Nakamura, K., Udem, T., and Inaba, H. (2018). Offset-free optical frequency comb self-referencing with an f-2f interferometer. Optica 5, 188–192. doi:10.1364/OPTICA.5.000188

CrossRef Full Text | Google Scholar

Pfeiffer, M. H., Herkommer, C., Liu, J., Guo, H., Karpov, M., Lucas, E., et al. (2017). Octave-spanning dissipative Kerr soliton frequency combs in Si_3N_4 microresonators. Optica 4, 684–691. doi:10.1364/OPTICA.4.000684

CrossRef Full Text | Google Scholar

Saha, M., Roy, S., and Varshney, S. K. (2021). Intracavity field dynamics near avoided mode crossing in a concentric silicon-nitride ring resonator. Phys. Rev. A 104, 033514. doi:10.1103/PhysRevA.104.033514

CrossRef Full Text | Google Scholar

Shastri, B. J., Tait, A. N., Ferreira de Lima, T., Pernice, W. H. P., Bhaskaran, H., Wright, C. D., et al. (2021). Photonics for artificial intelligence and neuromorphic computing. Nat. Photonics 15, 102–114. doi:10.1038/s41566-020-00754-y

CrossRef Full Text | Google Scholar

Soltani, M., Matsko, A., and Maleki, L. (2016). Enabling arbitrary wavelength frequency combs on chip. Laser & Photonics Rev. 10, 158–162. doi:10.1002/lpor.201500226

CrossRef Full Text | Google Scholar

Spencer, D. T., Drake, T., Briles, T. C., Stone, J., Sinclair, L. C., Fredrick, C., et al. (2018). An optical-frequency synthesizer using integrated photonics. Nature 557, 81–85. doi:10.1038/s41586-018-0065-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Suh, M.-G., Yang, Q.-F., Yang, K. Y., Yi, X., and Vahala, K. J. (2016). Microresonator soliton dual-comb spectroscopy. Science 354, 600–603. doi:10.1126/science.aah6516

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, T., Yuan, Z., Zhang, H., Yan, G., Zhou, S., An, N., et al. (2021). Multispecies and individual gas molecule detection using Stokes solitons in a graphene over-modal microresonator. Nat. Commun. 12, 6716–6718. doi:10.1038/s41467-021-26740-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanabe, T., Fujii, S., and Suzuki, R. (2019). Review on microresonator frequency combs. Jpn. J. Appl. Phys. 58, SJ0801. doi:10.7567/1347-4065/ab2aca

CrossRef Full Text | Google Scholar

Tian, L., Wei, L., and Guoying, F. (2015). Numerical simulation of supercontinuum generation in liquid-filled photonic crystal fibers with a normal flat dispersion profile. Opt. Commun. 334, 196–202. doi:10.1016/j.optcom.2014.07.080

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, M., Lu, L., Li, M., Wang, J., Zhou, F., et al. (2016). Ultra-flat and broad optical frequency combs generation based on novel dispersion-flattened double-slot microring resonator. Appl. Phys. B 122, 11–16. doi:10.1007/s00340-015-6295-6

CrossRef Full Text | Google Scholar

Wang, Z., Du, J., Shen, W., Liu, J., and He, Z. (2021). Efficient design for integrated photonic waveguides with agile dispersion. Sensors 21, 6651. doi:10.3390/s21196651

PubMed Abstract | CrossRef Full Text | Google Scholar

Weng, H., Liu, J., Afridi, A. A., Li, J., Dai, J., Ma, X., et al. (2021). Directly accessing octave-spanning dissipative Kerr soliton frequency combs in an AlN microresonator. Photonics Res. 9, 1351–1357. doi:10.1364/PRJ.427567

CrossRef Full Text | Google Scholar

Xia, D., Huang, Y., Zhang, B., Zeng, P., Zhao, J., Yang, Z., et al. (2022). Engineered Raman lasing in photonic integrated chalcogenide microresonators. Laser & Photonics Rev. 16, 2100443. doi:10.1002/lpor.202100443

CrossRef Full Text | Google Scholar

Xia, D., Yang, Z., Zeng, P., Zhang, B., Wu, J., Wang, Z., et al. (2022). Integrated chalcogenide photonics for microresonator soliton combs. Laser Photonics Rev. 2022, 2200219. doi:10.1002/lpor.202200219

CrossRef Full Text | Google Scholar

Yu, M., Okawachi, Y., Griffith, A. G., Picque, N., Lipson, M., and Gaeta, A. L. (2018). Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 9, 1869. doi:10.1038/s41467-018-04350-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, S.-P., Briles, T. C., Moille, G. T., Lu, X., Diddams, S. A., Srinivasan, K., et al. (2019). Tuning Kerr-soliton frequency combs to atomic resonances. Phys. Rev. Appl. 11, 044017. doi:10.1103/PhysRevApplied.11.044017

CrossRef Full Text | Google Scholar

Zhang, B., Zeng, P., Yang, Z., Xia, D., Zhao, J., Sun, Y., et al. (2021). On-chip chalcogenide microresonators with low-threshold parametric oscillation. Photonics Res. 9, 1272–1279. doi:10.1364/PRJ.422435

CrossRef Full Text | Google Scholar

Zhang, L., Bao, C., Singh, V., Mu, J., Yang, C., Agarwal, A. M., et al. (2013). Generation of two-cycle pulses and octave-spanning frequency combs in a dispersion-flattened micro-resonator. Opt. Lett. 38, 5122–5125. doi:10.1364/OL.38.005122

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Z., Iqbal, M., and Liu, J. (2008). Dispersion characteristics of SOI-based slot optical waveguides. Opt. Commun. 281, 5151–5155. doi:10.1016/j.optcom.2008.07.003

CrossRef Full Text | Google Scholar