Generation of counterpropagating and spectrally uncorrelated photon-pair states by spontaneous four-wave mixing in photonic crystal waveguides

In this work, we propose and theoretically analyze a new scheme for generation of counterpropagating photon pairs in photonic crystal waveguides through the process of spontaneous four-wave mixing. Using the fundamental properties of periodic Bloch modes in a standard photonic crystal waveguide, we demonstrate how modal phase-matching can be reached between forward-propagating pump modes and counterpropagating signal and idler modes, for generation of degenerate and non-degenerate photon pairs. We then show how this scheme can be used for generation of photon pairs that are nearly uncorrelated in the spectral degree of freedom. Such a source will be highly interesting as a heralded source of single photons, especially as the spectrally separable signal and idler photons are also spatially separated directly at the source. We conduct our investigation based on a design in silicon, yet our design concept is general and can in principle be applied to any nanostructured material platform.

1 Introduction

Sources of heralded single photons are an important resource for optical quantum technologies, e.g., for generation of cluster states Nielsen (2004) and Greenberger–Horne–Zeilinger states Varnava et al. (2008) for optical quantum computation, for boson sampling Brod et al. (2019), and quantum communication protocols Wang et al. (2006); Pant et al. (2017). Such sources are based on spontaneous photon-pair generation in nonlinear materials, where pairs of photons are generated commonly through the processes of spontaneous parametric down-conversion (SPDC) in materials with χ⁽²⁾-nonlinearity or spontaneous four-wave mixing (SFWM) in materials with χ⁽³⁾-nonlinearity Castelletto and Scholten (2008); Zhang et al. (2012); Signorini and Pavesi (2020). In both cases, the nonlinear material is optically pumped. In SPDC, a pump photon of frequency ω_P can split into a pair of photons, commonly called signal and idler, with frequencies ω_S and ω_I, respectively, such that conservation of energy ω_P = ω_S + ω_I is preserved. In SFWM, two pump photons, with frequencies ω_P1 and ω_P2, can combine and split into a pair of signal and idler photons such that ω_P1 + ω_P2 = ω_S + ω_I. For efficient nonlinear interaction, conservation of momentum, also known as the phase-matching condition, should also be satisfied between the wave-vectors of the photonic modes, which for SPDC and SFWM takes the form Δk = k_P (ω_P) − k_S (ω_S) − k_I (ω_I) = 0 and Δk = k_P1 (ω_P1) + k_P2 (ω_P2) − k_S (ω_S) − k_I (ω_I) = 0, respectively.

Since photon-pair generation through SPDC and SFWM is probabilistic, heralding is used to determine when or if a pair is generated, where the detection of one of the photons in the pair heralds the presence of the other one. For the output heralded single photon to be useful for quantum applications, the two photons in a pair must be spectrally uncorrelated, otherwise detection of one photon can randomly collapse the state of the other photon, and hence create a mixed state at the output, instead of the commonly desired pure single-photon state Signorini and Pavesi (2020). However, due to the combination of conservation of energy and phase-matching conditions, signal and idler photons generated through SPDC or SFWM are commonly entangled in the spectral degree of freedom Law et al. (2000). In general, such a two-photon state can be described as $\left|\psi \right.⟩\propto \iint d{\omega }_{S}d{\omega }_I\mathrm{J}\mathrm{S}\mathrm{A}({\omega }_S,{\omega }_I)\left|S,{\omega }_S\right.⟩\left|I,{\omega }_I\right.⟩$ (removing its vacuum part and the proportionality coefficients that indicate the overall probability of the process), where JSA is the joint-spectral amplitude of the photon-pair state, describing the spectral correlation between the signal and idler photons Law et al. (2000). Having a spectrally uncorrelated pair is equivalent to having a separable/factorable JSA, namely JSA (ω_S, ω_I) = u (ω_S) × v (ω_I) Grice et al. (2001); U’Ren et al. (2005). One way of creating spectrally pure single photons at the output of the heralded source is by using narrowband spectral filters at the output Aboussouan et al. (2010), yet this reduces the source brightness and limits the heralding efficiency Meyer-Scott et al. (2017). A better method is to engineer the dispersion properties of the optical modes of the system to directly generate spectrally uncorrelated pairs Grice et al. (2001); U’Ren et al. (2005). In the following, we focus our explanation on generating factorable states in waveguide systems with propagating waves, but it has to be mentioned that factorable states can also be generated in resonator systems Vernon et al. (2017); Christensen et al. (2018), where resonators typically allow for higher power efficiencies for the source, yet they are more sensitive to temperature and fabrication inaccuracies.

In waveguide systems, a prerequisite for the generation of spectrally factorable pairs is to satisfy the following relation between the group indices of the signal, idler, and pump modes: n_g,S < n_g,P < n_g,I or n_g,I < n_g,P < n_g,S Grice et al. (2001); U’Ren et al. (2005). The group index is related to the group velocity through $v_g=\frac{d\omega }{dk}=\frac{c}{n_g}$, with c being the vacuum speed of light. To minimize the spectral correlations, a condition often known as asymmetric group-velocity matching (AGVM) is sought after, where we either have n_g,I ≠ n_g,P = n_g,S or n_g,I = n_g,P ≠ n_g,S Zhang et al. (2012). AGVM can be reached in different systems, such as bulk crystals Mosley et al. (2008); Kaneda et al. (2016), photonic crystal fibers Garay-Palmett et al. (2007), nanostructured wavegudies Svozilík et al. (2011); Kang et al. (2014); Kumar et al. (2022), and photonic crystal waveguides Saravi et al. (2019), with different degrees of versatility. The bulk crystals used for SPDC offer the least degree of versatility, as AGVM is only attained in certain crystals (such as KDP Mosley et al. (2008) and KTP Kaneda et al. (2016)) and at certain frequency ranges limited by the dispersion of the material’s permittivity. The constraints can be reduced by using micro- and nanostructured optical systems, where the dispersion of the guided modes can be more dominantly controlled by the geometry of the structure, yet such structures are still limiting. For example, AGVM with SPDC in nanostructured ridge waveguides is limited to material platforms that can implement quasi-phase-matching (QPM). This requires to change the nonlinear susceptibility of the material periodically (such as in lithium niobate through periodic poling Younesi et al. (2021)), as QPM is needed as an extra degree of freedom to reach both phase-matching and AGVM conditions Svozilík et al. (2011); Kang et al. (2014); Kumar et al. (2022). Moreover, in pair generation based on SFWM in waveguide systems, to the best of our knowledge AGVM is only reached for non-degenerate photon-pair generation Garay-Palmett et al. (2007). Overall, in all such waveguide systems, there are constraints on the frequency ranges where the AGVM condition can be reached, as the dispersion relations of the guided modes are still a strong function of the dispersion properties of the material and there is only a limited manipulation of the dispersion relation of guided modes that can be achieved in regular waveguides.

A way to overcome these limitations is to use the counterpropagating (CP) configuration Christ et al. (2009), in which the waveguide system is phase-matched such that one photon in the pair is propagating in the forward direction, e.g., the signal, and the idler in the backward direction. This configuration creates an effect similar to the AGVM case with n_g,S = n_g,P, where here instead of bringing n_g,S close to n_g,P, we bring n_g,I, being a negative number, much further from the signal and pump group indices, which are positive numbers. This effectively makes |n_g,I − n_g,P|≪|n_g,S − n_g,P|, which has an equivalent effect as the AGVM condition for creating spectrally uncorrelated pairs, but without being limited by the dispersion of the modes. Moreover, the CP configuration will be of additional value for a heralded source of single photons, as the spectrally separable signal and idler photons are also spatially separated directly at the source. The problem, however, is that due to the negative wave-vector of the backward-propagating modes, satisfying the phase-matching condition is very complicated. One way is by QPM in χ⁽²⁾-materials with submicron-sized poling periods, which is technologically challenging Nagy and Reano (2020); Zhao et al. (2020); Younesi et al. (2021). Only recently fully guided uncorrelated pair-generation in the CP configuration was demonstrated, but using larger micron-sized poling periods that allow for higher-order and consequently less efficient QPM Luo et al. (2020); Liu et al. (2021). Nevertheless, this limits the use of the CP configuration to material platforms that can be poled to such small periods. Another way would be to use free-space pumping from above the sample for reducing the wave-vector of the pump waves Lanco et al. (2006), which was also used for demonstrating the generation of factorable pairs Belhassen et al. (2018) and polarization-entangled photon pairs Orieux et al. (2013). Yet, this method is fundamentally a non-integrated method and not appealing for large-scale implementations. There is also a proposal for CP SFWM based on pumping the structure from two sides with CP pump pulses Monroy-Ruz et al. (2016), although due to the specific configuration of CP pumping the generation of pairs is limited to frequencies close to that of the pump pulses.

Photonic crystal waveguides (PCWs) have been proposed as a structure that can reach CP phase-matching in a fully integrated way using modal phase-matching and without the need for periodic poling, where specific designs have been proposed for direct generation of path-entangled Bell states Saravi et al. (2017a) and near-factorable CP photon pairs Saravi et al. (2019), both through the process of SPDC in a PCW made of a χ⁽²⁾-material. The proposed schemes use the fundamental properties of guided Bloch modes, where each Bloch mode can have both positive- and negative-valued wave-vectors. This allows to satisfy the phase-matching condition in a CP configuration, involving forward-propagating (FP) pump, FP signal, and backward-propagating (BP) idler modes. Importantly, PCWs are highly versatile in controlling the group indices of the guided modes, far beyond what can be done with ridge waveguides Li et al. (2008). The capability for group-index engineering in PCWs was in fact used to satisfy CP phase-matching together with AGVM between the signal and pump modes, allowing the generation of highly factorable photon pairs Saravi et al. (2019). The problem, however, with the SPDC-based designs was, that due to the large difference between the frequencies of the signal/idler and the pump mode, the pump mode will be above the light line and inherently a leaky mode Saravi et al. (2015). This eventually limits the interaction length and hence the efficiency of such photon-pair sources. To reduce the pump mode leakage, a double-slot structure was proposed Saravi et al. (2017b); Saravi et al. (2019), which increases the interaction length. Nevertheless, due to the suspended narrow central waveguide, such double-slot designs have challenging fabrication prospects compared to a standard PCW, and the interaction length still remains limited due to the limited decay length of the leaky pump mode.

In our work, we propose and theoretically analyze a new scheme for generation of CP photon pairs in PCWs through the process of SFWM. SFWM has the advantage that the frequencies of all participating modes can be close to one another, and hence we can have all the participating modes below the light line and fully guided. This allows to use a standard W1 photonic crystal waveguide, where one row of holes is missing from the photonic crystal slab. To enable CP phase-matching for a four-wave-mixing process, we propose the use of TM-like index-guided modes of the structure for the pump modes and the TE-like gap-guided mode for the signal and idler modes. We then show that simply by a proper choice of the thickness of the photonic crystal slab, one can satisfy the CP phase-matching condition between the TM-like and TE-like modes. This is shown schematically in Figure 1. We numerically demonstrate this based on a design in silicon.

FIGURE 1

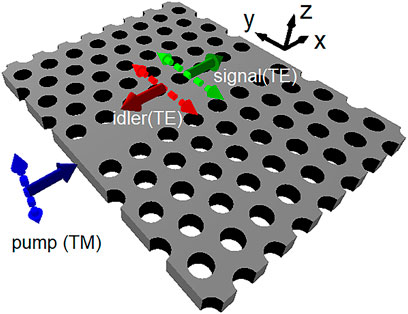
FIGURE 1. Scheme of counterpropagating photon-pair generation in a photonic crystal waveguide through spontaneous four-wave mixing. The solid arrows indicate the direction of propagation for each of the involved modes. The dashed arrows indicate the dominant polarization direction for the modes.

In the first part of our paper, we show the mechanism for phase-matching a CP SFWM process in a standard silicon PCW, both for the generation of frequency non-degenerate photon pairs by degenerate pumping and also for generating degenerate photon pairs by non-degenerate pumping. Afterwards, we discuss the spectral properties of the photon pairs and the many different possibilities in this system for generation of factorable photon pairs. We then calculate the JSA of the photon pairs for specific CP scenarios that also satisfy AGVM and demonstrate near-factorable states. In both cases, we numerically demonstrate the generation of spectrally narrow single photons with central wavelengths in the telecom range and sub-nanometer bandwidths, in a short PCW of below 400 μm length. Finally, we also calculate the absolute efficiency of pair generation in such a structure. At the very end, we also discuss some of the other possibilities of this highly versatile scheme for generation of quantum light.

2 Counterpropagating phase-matching in photonic crystal waveguides for spontaneous four-wave mixing

Here we show how our proposed phase-matching scheme works. Before going on to describe the mechanism, let us describe our system. We are using a standard W1 photonic crystal waveguide (PCW), which is formed by removing one row of holes from a photonic crystal slab that is suspended in free space. The photonic crystal slab of thickness h is made of a periodic array of holes, with radius r and periodicity a (the distance between closest hole neighbours is a), arranged in a hexagonal lattice. This is shown schematically in Figure 1, where we take x as the propagation direction along the direction of the removed row of holes. Such a structure supports Bloch modes propagating along the x-direction, with a pseudo-periodic electric field profile $\mathit{E}(\mathit{r},\omega )=\mathit{e}(\mathit{r},\omega )\exp [ik(\omega )x]={\sum }_{n=-\infty }^{+\infty }{\mathit{C}}_n(y,z,\omega )\exp [i(k(\omega )+2\pi n/a)x]$, where $\mathit{e}(\mathit{r})=\mathit{e}(\mathit{r}+a\widehat{\mathbf{x}})$ is periodic with the periodicity a. k(ω) is the wave-vector of that particular mode at frequency ω in the first Brillouin zone (BZ), where the first BZ is defined as $-\frac{\pi }{a}\le k\le \frac{\pi }{a}$. The band diagram of Bloch modes repeat themselves in the other BZs, such that k(ω) = k(ω) + 2π/a. Moreover, the band diagram is also symmetric around k = 0 for reciprocal materials, such that k(ω) = −k(ω). Since e(r) is periodic, it can be expanded into a Fourier series, with vectorial x-invariant coefficients C_n. These are the Bloch harmonics (BH) of the Bloch mode Yariv and Yeh (1977). Essentially, one can imagine that a Bloch mode is composed of non-periodic waveguide-like modes with mode profiles C_n(y, z, ω) and wave-vectors k_n(ω) ≡ k(ω) + 2πn/a. For indexing the BHs, we take n = 0 to correspond to the BH with a wave-vector in the first BZ. As can be seen, in principle a Bloch mode can include BHs with both positive- and negative-valued k_n wave-vectors, which contribution to the Bloch mode is determined by the strength of their C_n coefficients. The overall direction of propagation of a Bloch mode is determined by the sign of its group velocity $v_g=\frac{d\omega }{dk}$. Hence, a mode with either positive- or negative-valued sign of this derivative can include both positive- and negative-valued k_n wave-vectors. This is the core idea used for reaching CP phase-matching for SPDC in Saravi et al. (2017a); Saravi et al. (2019). We also use this core principle here.

To do this for SFWM, we have to find the proper set of modes that can satisfy the CP phase-matching condition. To find the Bloch modes in the system, we use the MIT Photonic Bands (MPB) package Johnson and Joannopoulos (2001), where we look for Bloch modes with a wave-vector along the x-direction in a unit-cell of the size a, $10\sqrt{3}a$, and 6a in the x, y, and z directions, respectively. The band diagram for photonic crystals is often presented in normalized quantities, such as shown in Figure 2, where the frequency of ω is expressed in units of 2πc/a and the wave-vector k is expressed in units of 2π/a. Hence, the normalized frequencies take the value of $\frac{\omega a}{2\pi c}=\frac{a}{\lambda }$, where λ is the free-space wavelength, and normalized wave-vectors take the value of $\frac{ka}{2\pi }$. The first BZ in normalized units is then within −0.5 ≤ k ≤ 0.5. The spatial dimensions can also be described in units normalized to a. In fact, finding the band diagram of PCWs can be done independent of the periodicity a using all normalized quantities Joannopoulos et al. (2011). If the physical effect of interest is happening at a normalized frequency of ω_norm, and we want to choose the physical dimensions of the PCW such that this normalized frequency coincides with the physical free-space wavelength of λ₀, then we have to choose a such that a = λ₀ × ω_norm. Yet this choice is not so arbitrary, since the simulation in MPB has to be done by assigning a non-dispersive permittivity ɛ to the material. Hence, from the start of the design one has to choose a target physical wavelength of operation, λ₀, and then use the actual permittivity of the underlying material at that wavelength, ɛ(λ₀), in the simulation. a can then be chosen such that a ω_norm of interest coincides with λ₀. In this way, the simulation will be an exact representation of the PCWs behaviour at λ₀ and an approximation for the wavelengths around it. This will be a good approximation if ɛ(λ) of the underlying material is not strongly dispersive around λ₀ and we are not deviating too far from λ₀. In our design, we choose λ₀ = 1.55 μm, as the telecom range is a wavelength range of interest for many quantum communication and computation applications. We set the relative permittivity to ɛ = (3.694)², which corresponds to that of amorphous silicon (from the company Tafelmaier) at λ₀ = 1.55 μm. We emphasize that our design concept is general and not specific to a material or certain permittivity values and could be implemented in other nanostructured material platforms (potentially by changing the slab thickness, as we will discuss), especially in III-V semiconductors like GaAs and GaP, which have a high permittivity and very strong χ⁽³⁾ nonlinearities, both comparable to silicon.

FIGURE 2

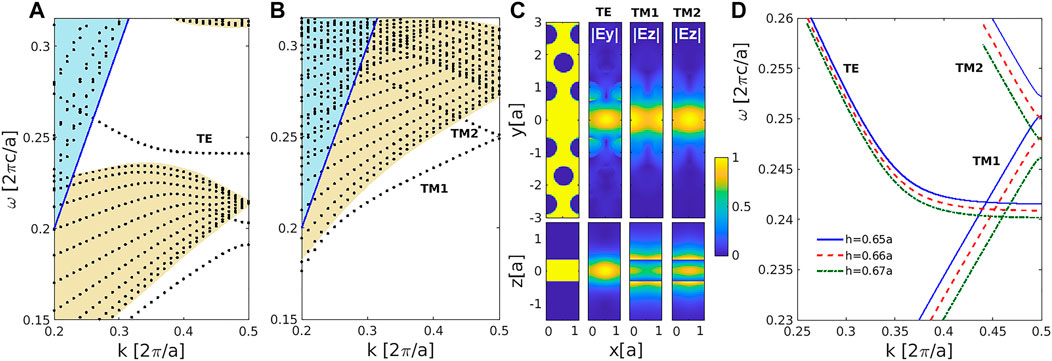
FIGURE 2. Band diagram of the (A) TE-like and (B) TM-like modes of a W1 photonic crystal waveguide (relative permittivity ɛ = (3.694)², slab thickness h = 0.66a, hole radius r = 0.3a). Our guided modes of interest are marked as TE, TM1, and TM2. (C) The profile of the dominant electric field component for our guided modes of interest, shown in the xy and xz planes, along with the permittivity profile of the photonic crystal waveguide. (D) The band diagram of the TE, TM1, and TM2 modes for different slab thicknesses, showing the relative movement of the TM bands with respect to the TE band.

We now analyze the modes of the PCW. The modes in a vertically mirror-symmetric PCW can be categorized into TE-like and TM-like modes, which can more simply be thought of as modes with dominant E_y and E_z components of the electric field, respectively. There is a more systematic description to these modes based on the symmetry of their field components, which can be found elsewhere Joannopoulos et al. (2011). In our case, we are looking only for TE-like (TM-like) modes, where the profile of the E_y (E_z) electric field component has an even mirror symmetry across the xy and xz planes. This ensures a better input and output coupling for the modes of the system and better overlap between the mode profiles of the different modes for having a more efficient nonlinear interaction. More technically, TE-like (TM-like) modes of that symmetry are also referred to as z-even-y-odd (z-odd-y-even) modes Joannopoulos et al. (2011). The band diagrams for these TE-like and TM-like modes are shown in Figures 2A,B, respectively. The blue shaded region in each plot shows the regions with leaky modes above the light line (the blue line), which are modes that couple to the surrounding free-space. The yellow-shaded regions correspond to leaky modes that couple to the modes of the photonic crystal slab and also modes of the photonic crystal slab that will exist without the line defect. Only isolated lines indicate truly guided modes that are confined to the central line defect. Our guided modes of interest are marked as TE, TM1, and TM2, which dominant electric field profiles are shown in Figure 2C. The TE mode falls within the bandgap frequency range of the photonic crystal slab for TE-like modes, hence it is guided by the bandgap effect in the y-direction and total internal reflection in the z-direction. Due to the strong interaction with the periodic photonic crystal slab, such TE modes have considerable negative- and positive-valued wave-vector BHs for both forward- and backward-propagating modes Saravi et al. (2017b); Saravi et al. (2019), and will be the choice for the signal and idler modes here. To reach the CP phase-matching and also to be able to reach the AGVM condition, we choose the TM1 and TM2 modes as the pump modes. These are index-guided modes, which have lower frequency than all the TM-like slab modes of the photonic crystal (the slab modes are in the yellow-shaded region in Figure 2B) and are guided by the fact that the surrounding photonic crystal slab has a lower average permittivity than the central line defect. By changing the thickness of the slab, one can shift the TM1 and TM2 modes in frequency with respect to the TE mode, as the TM modes with their dominant E_z components are more sensitive to the change in the z-direction. This is shown in Figure 2D, which shows how the TM bands move with respect to the TE band by changing the slab thickness h. For our chosen permittivity, a slab thickness of h = 0.66a brings the index-guided TM modes to a frequency range where they can be used for phase-matching the CP process, as will be demonstrated in the following. Moreover, the slab thickness is used here to fine tune the position of the TM modes with respect to TE modes, to also get the AGVM condition, which will also be shown in the following. We note, that in all the following cases, we are using a design with h = 0.66a.

In the following we explain how CP phase-matching for SFWM can be reached in two scenarios, one with degenerate pumping for generation of non-degenerate signal and idler photons and the other case with non-degenerate pumping for generation of degenerate signal and idler photons. We start with the case of degenerate pumping. We show the band diagram of the involved modes in Figure 3A. We have color-coded the different modes for better distinction in the different plots. For our idler mode, we choose the backward-propagating TE mode (red line), in the first BZ. The sign of the group velocity indicates that this is a backward-propagating mode. This TE mode also has a forward-propagating counterpart in the neighboring BZ (green line), which we choose as our signal mode. We also see the forward-propagating TM1 (blue curve, called pump1) and TM2 (purple curve, called pump2) modes in this graph. The TM1 and TM2 modes also have backward-propagating counterparts that are their mirror symmetric version around the edge of the BZ (k = π/a), which we do not show here, as they are not used in our scheme. Figure 3B shows the group index of the forward-propagating modes. The markers in Figure 3A indicate an example of points that satisfy the phase-matching condition between the FP signal, BP idler, and FP pump1 mode, such that k_S + k_I = 2k_P1, while at the same time satisfying the conservation of energy ω_S + ω_I = 2ω_P1. To better understand the physics, we take a look at the BH distribution of the modes, shown in Figure 3C. To be specific, we are showing the z-component of C (y, z) for the TM modes and the y-component of C (y, z) for the TE modes, all at the center of the transversal coordinate y = z = 0. For example, C_0,P1 is shorthand for z ⋅C_0,P1 (y = 0, z = 0). The amplitudes of the BHs are normalized, such that the dominant BH for each mode takes the value of 1. For example, C_0,P1 is the strongest BH of the pump1 mode, which takes the value of 1, and the value of C_−1,P1 is normalized with respect to C_0,P1. We show the dominant BHs for the modes in Figure 3C. As we can see, the FP signal and pump modes have their strongest BH at positive-valued wave-vector values of k_S and k_P1, respectively. Importantly, the BP idler mode has a weaker, yet substantial, BH with a positive-valued wave-vector at k_I (C_0,I). This allows for phase-matching between the C_1,S, C_0,I, and C_0,P1 BHs. The profiles of these BHs are shown in Figure 3D. Here, we show the dominant polarization component for each mode, namely the absolute values of z ⋅C_0,P1 (y, z), y ⋅C_1,S (y, z), and y ⋅C_0,I (y, z). As can be seen, all modes have a strong field concentration around y = z = 0, which allows a high overlap between the mode profiles of the BHs for an efficient nonlinear interaction between them. We note that the C_0,S, C_−1,I, and C_−1,P1 BHs are also phase-matched, as k_S − 1 + k_I − 1 = 2 (k_P1 − 1), but their contribution is weaker than C_1,S, C_0,I, and C_0,P1, due to the smaller BH amplitudes in combination. It is important to also note that such a nonlinear process between z-polarized pump fields and y-polarized signal and idler fields can be mediated by the ${\chi }_{\mathit{zzyy}}^{(3)}$ of the third-order nonlinear susceptibility tensor Boyd (2008). Such cross-polarized processes have been used for pair-generation through SFWM Garay-Palmett et al. (2007). Finally, in our work we are neglecting the potential effects from self- and cross-phase modulation that can shift the phase-matching condition with increasing input pump powers Garay-Palmett et al. (2007), by assuming that we are operating in a weak pumping regime. Considering these power-dependent effects is beyond the scope of our work here, as we are mainly aiming for introducing the main physics of this new scheme. Finally, it is important to note that the particular points we chose to demonstrate our general phase-matching scheme also satisfy the AGVM condition. This can be seen in Figure 3B, where we marked the chosen points in the group-index curves for the pump and the signal modes. The two modes have a very close group index, with n_g,S ≈ 7.37 and n_g,P1 ≈ 7.29, which is used to achieve a highly factorable JSA, as will be shown in the next section.

FIGURE 3

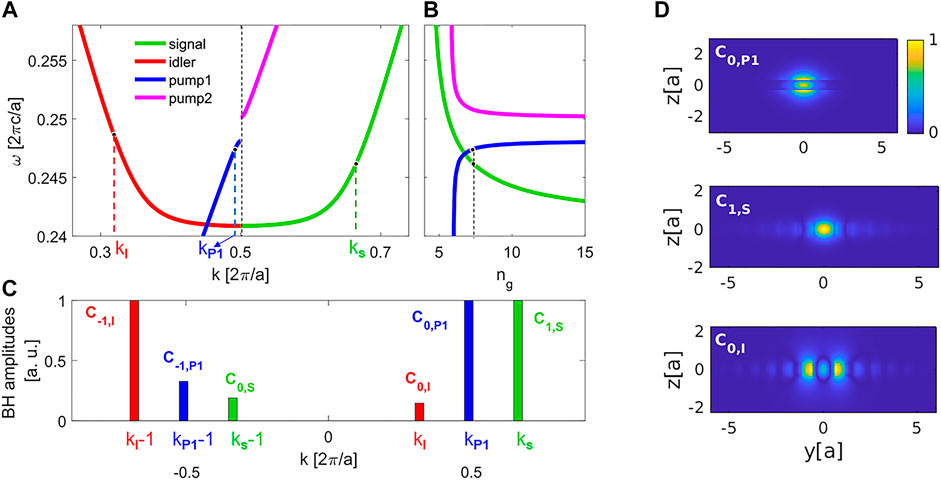
FIGURE 3. Explaining the phase-matching mechanism for generating non-degenerate counterpropagating photon pairs. Here we show the case with degenerate pumping in mode TM1. (A) Shows the band diagram of the idler in the backward-propagating TE mode (red), the signal in the forward-propagating TE mode (green), and the pump in the forward-propagating TM1 mode (blue). The markers indicate a combination where modes are phase-matched, with k_S + k_I = 2k_P1. (B) Group index of the forward-propagating modes. The markers indicate the same points as marked in (A) for the signal and pump modes, showing that they also have matching group indices, in addition to being phase-matched. (C) The position and amplitude of the main Bloch harmonics (BH) for the modes. (D) The field profile of the BHs that make the dominant contribution to the process.

We now explain how phase-matching with non-degenerate pumping for generation of CP degenerate signal and idler photons can be achieved. We show the same band diagram from Figure 3A again in Figure 4A, but marking different points in the bands that satisfy the phase-matching condition k_S + k_I = k_P1 + k_P2 and conservation of energy condition ω_S + ω_I = 2ω_S = ω_P1 + ω_P2. In this case, one of the pump beams for the SFWM process will be in the forward-propagating TM1 mode and the other in the forward-propagating TM2 mode. It is interesting to note that the frequency-degenerate counterpropagating signal and idler modes at ω_S = ω_I will have the following relation between their wave-vectors $k_S=\frac{2\pi }{a}-k_I$ due to the mirror-symmetry of the band diagram around the edge of the BZ. This means that we also have the following relation between the two pump mode wave-vectors $k_{P1}+k_{P2}=k_S+k_I=\frac{2\pi }{a}$. The BH distribution of the modes is shown in Figure 4C. As can be seen, the dominant contribution to the process will be from the phase-matching between the C_1,S, C_0,I, C_0,P1, and C_1,P2 BHs. The profiles of these BHs are shown in Figure 4D, namely the absolute values of z ⋅C_0,P1 (y, z), z ⋅C_1,P2 (y, z), y ⋅C_1,S (y, z), and y ⋅C_0,I (y, z). Once again, all modes have a strong field concentration around y = z = 0 for an efficient overlap. We note that the C_0,S, C_−1,I, C_−1,P1, and C_0,P2 BHs are also phase-matched, as k_S − 1 + k_I − 1 = k_P1 − 1 + k_P2 − 1, but with a weaker contribution due to their smaller BH amplitudes. Finally, Figure 4B shows the group index of the forward-propagating modes, where we see a near-AGVM between the signal and the pump2 modes, with n_g,S ≈ 5.88 and n_g,P2 ≈ 5.90. This will be used to achieve a highly factorable JSA in this scenario.

FIGURE 4

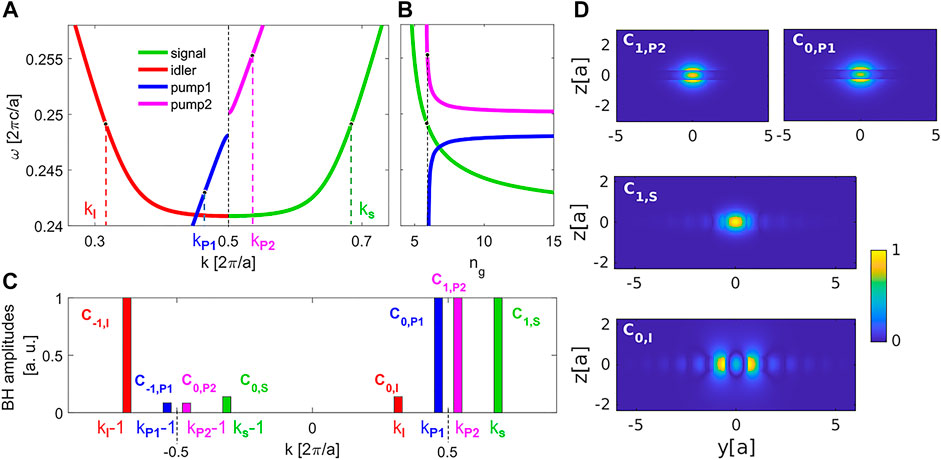
FIGURE 4. Explaining the phase-matching mechanism for generating degenerate counterpropagating photon pairs. Here we show the case with non-degenerate pumping using both TM1 and TM2 modes. (A) Shows the band diagram of the idler in the backward-propagating TE mode (red), the signal in the forward-propagating TE mode (green), and the pumps in the forward-propagating TM1 (blue) and TM2 (purple) modes. The markers indicate a combination where modes are phase-matched, with k_S + k_I = k_P1 + k_P2. (B) Group index of the forward-propagating modes. The markers indicate the same points as marked in (A) for the signal and pump in the TM2 mode, showing that these two modes also have matching group indices. (C) The position and amplitude of the main Bloch harmonics (BH) for the modes. (D) The field profile of the BHs that make the dominant contribution to the process.

3 Nearly uncorrelated joint spectral amplitudes

In this section, we will calculate the JSA of the two-photon state, where we focus on the two specific group-index-matched cases shown in the previous section. The JSA of the two-photon state from the SFWM can be found from the following expression Garay-Palmett et al. (2007):

$\mathrm{J}\mathrm{S}\mathrm{A}\left({\omega }_S,{\omega }_I\right)=\int d{\omega }^{\prime }{\alpha }_1\left({\omega }^{\prime }\right){\alpha }_2\left({\omega }_S+{\omega }_S-{\omega }^{\prime }\right)\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{c}\left[\mathrm{\Delta }k\left({\omega }^{\prime },{\omega }_S,{\omega }_I\right)\frac{L}{2}\right]\exp \left[i\mathrm{\Delta }k\left({\omega }^{\prime },{\omega }_S,{\omega }_I\right)\frac{L}{2}\right].(1)$

Firstly, it should be emphasized that this relation assumes that the JSA has a narrow enough spectral width, such that the other properties of the modes such as their mode profile or group index can be considered a constant over this spectral range. Hence, they can be pulled out of the frequency integral and treated as a proportionality constant. We will see this coefficient when we are calculating the overall pair generation efficiency in this structure at the end of this work. This point aside, in the above equation, L is the length of the structure. α_1,2(ω) are the spectral amplitudes of the pump pulses, which could be the same with degenerate pumping or different with non-degenerate pumping. The phase-mismatch function will take different forms based on which mode combinations are used for pumping, namely if both pumps are in the pump1 mode we have Δk (ω′, ω_S, ω_I) = k_P1 (ω′) + k_P1 (ω_S + ω_I − ω′) − k_S (ω_S) − k_I (ω_I), if both pumps are in the pump2 mode we have Δk (ω′, ω_S, ω_I) = k_P2 (ω′) + k_P2 (ω_S + ω_I − ω′) − k_S (ω_S) − k_I (ω_I), and if both pump1 and pump2 modes are used for pumping we get Δk (ω′, ω_S, ω_I) = k_P1 (ω′) + k_P2 (ω_S + ω_I − ω′) − k_S (ω_S) − k_I (ω_I). Although the JSA depends on the choice of the pump pulse spectra, a fixed property of the device itself is its joint phase-matching spectrum (JPS), being sinc [Δk (ω′, ω_S, ω_I)L/2] exp [iΔk (ω′, ω_S, ω_I)L/2]. Let us first have a look at the JPS for different configurations. More specifically, we plot the curve corresponding to the maximum of the JPS, which corresponds to the points with Δk = 0. To plot these curves in the two-dimensional ω_S, ω_I space, we have to assign values to ω′. This choice will correspond to different pumping configurations. ${\omega }^{\prime }=\frac{{\omega }_S+{\omega }_I}{2}$ represents the phase-matching curve for a degenerate pumping case. If the degenerate pumping is in pump1 mode, the curve of interest will be 2$k_{P1}(\frac{{\omega }_S+{\omega }_I}{2})-k_S({\omega }_S)-k_I({\omega }_I)=0$, which is calculated for our structure and shown in Figure 5A (blue curve). If the degenerate pumping is in pump2, the curve of interest will be 2$k_{P2}(\frac{{\omega }_S+{\omega }_I}{2})-k_S({\omega }_S)-k_I({\omega }_I)=0$, which is also shown in Figure 5A (purple curve). The dashed line in these plots correspond to the ω_S = ω_I line, which corresponds to degenerate photon-pair generation. For non-degenerate pumping, we can fix the frequency of one of the pump beams, and vary the other one, which in practice corresponds to using a continuous wave (CW) pump field for one of the pump beams. In Figure 5B we plot the maximum of the JPS for the case with a fixed pump in the pump2 mode at ${\omega }_{P2}=0.258\frac{2\pi c}{a}$, where the frequency of the pump1 mode can vary. The curve corresponds to $k_{P1}({\omega }_S+{\omega }_I-0.258\frac{2\pi c}{a})+k_{P2}(0.258\frac{2\pi c}{a})-k_S({\omega }_S)-k_I({\omega }_I)=0$. In Figure 5C we plot the maximum of the JPS for the case with a fixed pump in the pump1 mode at ${\omega }_{P1}=0.243\frac{2\pi c}{a}$, where the frequency of the pump2 mode can vary. The curve corresponds to $k_{P2}({\omega }_S+{\omega }_I-0.243\frac{2\pi c}{a})+k_{P1}(0.243\frac{2\pi c}{a})-k_S({\omega }_S)-k_I({\omega }_I)=0$.

FIGURE 5

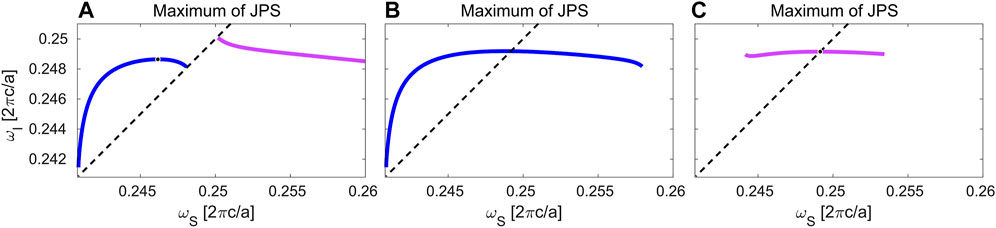
FIGURE 5. The maximum of the joint phase-matching spectrum (JPS), showing the curve of Δk =0, for different pumping scenarios. (A) Degenerate pumping in the TM1 mode (blue) and in the TM2 mode (purple). The marked point on the blue curve corresponds to the group-index-matched phase-matched scenario shown in Figure 3. (B) Non-degenerate pumping, by varying the pump frequency in TM1 and having a fixed pump in TM2 at ${\omega }_{P2}=0.258\frac{2\pi c}{a}$. (C) Non-degenerate pumping, by varying the pump frequency in TM2 and having a fixed pump in TM1 at ${\omega }_{P1}=0.243\frac{2\pi c}{a}$. The marked point around the middle of the purple curve corresponds to the group-index-matched phase-matched scenario shown in Figure 4, where the signal and idler photons have equal central frequencies. The dashed line in all plots is the ω_S = ω_I line.

There are a number of important points that should be discussed about these JPSs. Firstly, that the limited range of the curves is associated to the fact that the guided modes exist over limited frequency ranges. The TE mode’s frequency is bounded from the lower side by its bandgap (where the mode gets to k = π/a) and from the higher side by the fact that it goes above the light line and becomes leaky. The TM1 mode’s frequency is only bounded from the higher side by its bandgap. The TM2 mode’s frequency is bounded from the lower side by its bandgap and from the higher side by the fact that it goes into the slab-mode region and starts leaking into the photonic crystal slab. Hence, considering these modes only over regions where they are fully guided results in a limited range of the JPS curves. The most important property of the JPS curves that relates to the possibility for uncorrelated pair generation is the angle θ that the JPS maximum curve makes with the ω_S axis. For factorable pair generation to be possible we must have 0 ≤ θ ≤ 90°, where this angle relates to the group indices of the modes through $\theta =-{\tan }^{-1}\left(\frac{n_{g,P}-n_{g,S}}{n_{g,P}-n_{g,I}}\right)$ Christ et al. (2009). An angle of θ = 0 (θ = 90) degrees corresponds to AGVM between the pump and the signal (idler) mode. The marked points in Figures 5A,C, correspond to the group-index-matched phase-matching scenarios shown in Figures 3, 4, respectively, where we have θ = 0. In fact, there is a wide variety of angles that can be reached with a single design, as the TE mode goes over a large range of group indices as it approaches the band edge, where the mode enters the slow-light region and the group index theoretically diverges. However, this is only the case if there are no sources of losses, such as disorder in fabrication, which can increasingly reduce the propagation losses of the slow light modes and overall limit the performance of nonlinear interactions Saravi et al. (2016). Nevertheless, the lower left side of both of the blue curves in Figures 5A,B corresponds to such a region, where both the FP signal and BP idler are going into the slow light region, but the phase-matching frequency for the FP signal is closer to the band edge, making its group index much higher than the idler, such that |n_g,P − n_g,S| > |n_g,P − n_g,I| = |n_g,P + |n_g,I‖, which makes θ approach 90°. This in principle can have the same effect as AGVM with θ = 0, however, since these regions deal with very slow modes close to the bande edge they can in practice experience strong losses. Nevertheless, the important point is that due to the strong variations in n_g there is a wide variety of θ angles at different frequencies that can be chosen along the blue JPS curves shown in Figures 5A,B, for reaching factorable states, which allows for choosing the central frequencies and bandwidths of the resulting factorable photons with respect to one another. In the following, we calculate the JSA for the two explained cases with AGVM between pump and signal, where all modes have moderate group indices below 10, to show that highly factorable states can be reached in these structures.

We calculate the JSA from Eq. 1. We take the normalized length of the structure as L/a = N, with N = 1,000 periods. For the case of degenerate pumping shown in Figure 3, we take a pump pulse centered around ${\omega }_{P1}=0.2474\frac{2\pi c}{a}$, with a Gaussian spectrum with FWHM of $\mathrm{\Delta }{\omega }_{P1}=1.66\times 10^{-4}\frac{2\pi c}{a}$ for its spectral intensity. We show the resulting joint spectral intensity (JSI), which is JSI = |JSA|², in Figure 6A. Such shapes for the JSI, which look like a horizontal or vertical elongated ellipse, commonly result in highly uncorrelated pairs. To quantify the degree of spectral entanglement between the signal and idler, we perform a Schmidt decomposition on the JSA Law et al. (2000); Grice et al. (2001), such that $\mathrm{J}\mathrm{S}\mathrm{A}({\omega }_S,{\omega }_I)={\sum }_n\sqrt{{\mathrm{\Lambda }}_n}{u}_n({\omega }_S)v_n({\omega }_I)$, with ∑_nΛ_n = 1, where Λ_n is the probability of having a certain pair of spectral Schmidt modes in the JSA. The ideal uncorrelated pair has just one pair of Schmidt modes with Λ₁ = 1. Doing the Schmidt decomposition on this JSA results in a highly dominant Schmidt mode pair with near-unity value of probability Λ₁ = 0.9766. The next pair of Schmidt modes have a very low probability of Λ₂ = 0.0098. To give one number for quantifying the degree of spectral entanglement, one can calculate the purity $P={\sum }_n{\mathrm{\Lambda }}_n^2$. A purity of P = 1 corresponds to a fully factorable state. Here we calculate the purity of P = 0.954, which is very close to unity and comparable to the state of the art designs for factorable pair generation Christ et al. (2009); Kang et al. (2014); Garay-Palmett et al. (2007). At this point, we can now choose a value for the periodicity of the structure, to get some physical values from the normalized quantities. We set the periodicity to a = 383.47 nm to coincide the pump central wavelength to 1.55 μm. With this choice, we plot the spectral intensity of the pump and the dominant Schmidt modes of the signal and idler photons as a function of wavelength in Figure 6B. In terms of free-space wavelength, the FWHM of the pump pulse is Δλ_P1 = 1.0 nm, and the bandwidths of the resulting signal and idler photons (the dominant Schmidt modes to be precise) are Δλ_S = 1.5 nm and Δλ_I = 0.13 nm, respectively.

FIGURE 6

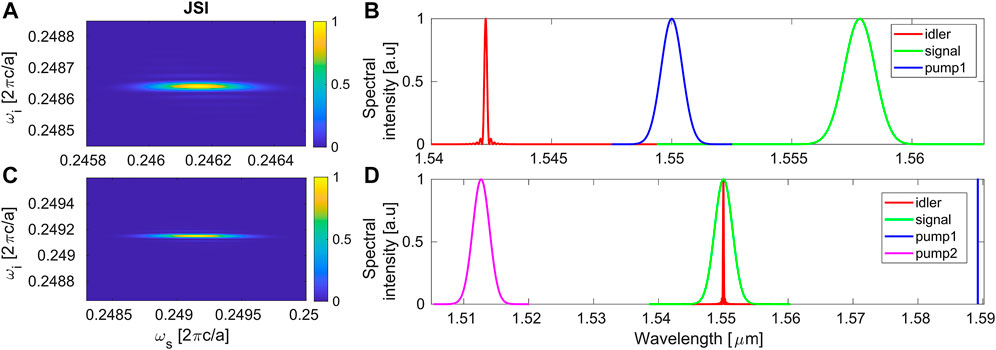
FIGURE 6. (A) Joint spectral intensity (JSI) for degenerate pumping with a pulsed pump in mode TM1, which creates non-degenerate pairs. The frequency combination corresponds to the case shown in Figure 3. The purity calculated from Schmidt mode decomposition is P = 0.954. (B) The spectral intensity of the pump and the dominant Schmidt modes of the signal and idler photons for the case in (A). The periodicity is set to a = 383.47 nm to set the pump central wavelength to 1.55 μm. (C) JSI for non-degenerate pumping, with a CW pump in mode TM1 and a pulsed pump in mode TM2, which creates pairs with degenerate central frequencies. The frequency combination corresponds to the case shown in Figure 4. The purity calculated from Schmidt mode decomposition is P = 0.975. (D) The spectral intensity of the pump and the dominant Schmidt modes of the signal and idler photons for the case in (C). The periodicity is set to a = 386.18 nm to set the signal/idler central wavelengths to 1.55 μm. The narrow blue line corresponds to the wavelength of the CW pump in mode TM1.

For the case of non-degenerate pumping shown in Figure 4, we take a pump pulse in mode TM2 centered around ${\omega }_{P2}=0.2553\frac{2\pi c}{a}$, with a Gaussian spectrum with a FWHM of $\mathrm{\Delta }{\omega }_{P1}=5.16\times 10^{-4}\frac{2\pi c}{a}$ for its spectral intensity, and a single-frequency pump beam in the TM1 mode at ${\omega }_{P1}=0.243\frac{2\pi c}{a}$. We show the resulting JSI in Figure 6C. Doing the Schmidt decomposition on this JSA results in a near-unity value of probability Λ₁ = 0.9874 for the dominant Schmidt pair. The next pair of Schmidt modes have a very low probability of Λ₂ = 0.0080. For this JSA we calculate the purity of P = 0.975, which is even better than the previous case. To get physical values from the normalized quantities, we set the periodicity to a = 386.18 nm, which sets the signal/idler central wavelengths to 1.55 μm. With this choice, we plot the spectral intensity of the pumps and the dominant Schmidt modes of the signal and idler photons as a function of wavelength in Figure 6D. In terms of free-space wavelength, the FWHM of the pump pulse in mode TM2 (shown by purple curve) is Δλ_P2 = 3.0 nm, and the bandwidths of the resulting signal and idler photons are Δλ_S = 3.2 nm and Δλ_I = 0.15 nm, respectively. The narrow blue line corresponds to the wavelength of the CW pump in mode TM1.

4 Calculation of pair-generation efficiency

In this section, we calculate the efficiency of generating spectrally uncorrelated pairs in the proposed structure. Specifically, we do this for the degenerate pumping scenario, with spectral properties shown in Figures 6A,B. We use the formulation developed for description of SPDC in photonic crystal waveguides in Saravi et al. (2017b), and adapt it to describe the SFWM case. To do this, we start with the SFWM Hamiltonian, ${\widehat{H}}_{NL}(t)\approx -3{ϵ}_0\int d\mathit{r}{\chi }_{\mathit{zzyy}}^{(3)}(\mathit{r})E_{P,z}^{(+)}(\mathit{r},t)E_{P,z}^{(+)}(\mathit{r},t){\widehat{E}}_{S,y}^{(-)}(\mathit{r},t){\widehat{E}}_{I,y}^{(-)}(\mathit{r},t)+H.c.$Christensen (2018), which is the nonlinear Hamiltonian of SFWM with degenerate pumping. Here we only take into account the contribution from the dominant polarization components of the modes, mediated by ${\chi }_{\mathit{zzyy}}^{(3)}={\chi }_{\mathit{yyyy}}^{(3)}/3$. For the positive-frequency part of the classical pump pulse we use ${\mathit{E}}_P^{(+)}(\mathit{r},t)\approx A_P{\mathit{e}}_P(\mathit{r},{\omega }_{P,0}){\int }_0^{+\infty }d\omega \alpha (\omega )e^{ik(\omega )x-i\omega t}$, with $\alpha (\omega )=\exp (-{(\omega -{\omega }_{P,0})}^2/2{\sigma }_P^2)$ being the spectral envelope of the pump at the central frequency ω_P,0 with bandwidth σ_P. In our case, the pump bandwidth is narrow enough that we can approximate its field profile as being the field profile at its central frequency. If P_peak is the peak power of the pump pulse at its center, x = 0 and t = 0, then we can find the pump intensity$A_P^2=\frac{P_{\text{peak}}}{4\pi {\sigma }_P^{2}c}\frac{n_{g,P}({\omega }_{P,0})}{{\int }_{\mathrm{\Omega }}d\mathbf{r}{ϵ}_0\epsilon (\mathit{r},{\omega }_{P,0})|{\mathbf{e}}_P(\mathit{r},{\omega }_{P,0}){|}^2/a}$, where we used a similar normalization approach as in Saravi et al. (2015). We note that the volume integral ${\int }_{\mathrm{\Omega }}d\mathbf{r}={\int }_0^{a}dx{\int }_{-\infty }^{+\infty }dy{\int }_{-\infty }^{+\infty }dz$ is taken over the volume of one unit cell of the photonic crystal waveguide. We then take a similar approach as in Saravi et al. (2017a) for calculating the biphoton state $\left|\psi \right.⟩$ in photonic crystals (neglecting the material dispersion), which itself is based on a perturbative pair-generation formalism Yang et al. (2008) combined with a quantization formalism for Bloch modes Sipe et al. (2004), with only changing the SPDC Hamiltonian to the SFWM Hamiltonian. The result for the probability of generating a photon pair is

$⟨\psi \left|\psi \right.⟩\approx G\iint d{\omega }_{S}d{\omega }_I|\mathrm{J}\mathrm{S}\mathrm{A}\left({\omega }_S,{\omega }_I\right){|}^2,(2)$

with

$G=\frac{{\left|{\int }_{\mathrm{\Omega }}d\mathbf{r}{e}_{P,z}^2\left(\mathit{r}\right)e_{S,y}^{\ast }\left(\mathit{r}\right)e_{I,y}^{\ast }\left(\mathit{r}\right)/a\right|}^2}{{\mathcal{E}}_P^2{\mathcal{E}}_I{\mathcal{E}}_S}{\left|\frac{3{\mu }_{0}L{\chi }_{\mathit{zzyy}}^{\left(3\right)}{P}_{\text{peak}}}{8\pi {\sigma }_P^2}\right|}^2|n_{g,P}^2{n}_{g,I}{n}_{g,S}|{\omega }_{I,0}{\omega }_{S,0}.(3)$

Here, ${\mathcal{E}}_q={\int }_{\mathrm{\Omega }}d\mathbf{r}\epsilon (\mathit{r},{\omega }_{q,0})|{\mathbf{e}}_q(\mathit{r},{\omega }_{q,0}){|}^2/a$, with q = P, S, I. The Bloch mode profiles and the group indices are evaluated at the central frequencies for the pump, signal, and idler, being ω_P,0, ω_S,0, and ω_I,0, respectively. This is a good approximation in our case, as the JSA has a very narrow spectral band compared to the spectral functionality of these quantities. The JSA in this equation has the same expression as in Eq. 1.

We now calculate the pair generation probability from Eq. 2 for the case of the degenerate pumped structure with the JSA shown in Figure 6A. The periodicity is set to a = 383.47 nm to fix the pump central wavelength to 1.55 μm. The structure chosen there was N = 1,000 periods long, which results in the physical length of L = N × a ≈ 383 μm. The chosen Gaussian spectrum with a FHWM of $\mathrm{\Delta }{\omega }_{P1}=1.66\times 10^{-4}\frac{2\pi c}{a}$ corresponds to ${\sigma }_P=10^{-4}\frac{2\pi c}{a}$, which results in the FWHM of the pump pulse intensity being Δλ_P = 1.0 nm, as shown in Figure 6B. The group indices are n_g,I = −6.04, n_g,S = 7.37, and n_g,p = 7.29. For the nonlinear coefficient, we take n₂ = 7.43 × 10^–17 m²/W for the nonlinear index of amorphous silicon Wang and Foster (2012). Using $n_2[\frac{{\mathrm{m}}^2}{\mathrm{W}}]=\frac{283}{\epsilon }{\chi }_{\mathit{yyyy}}^{(3)}[\frac{{\mathrm{m}}^2}{{\mathrm{V}}^2}]$ Boyd (2008), with ɛ = (3.694)², we find the nonlinear susceptibility ${\chi }_{\mathit{yyyy}}^{(3)}=3.58\times 10^{-18}$ m²/V², which gives ${\chi }_{\mathit{zzyy}}^{(3)}=1.19\times 10^{-18}$ m²/V² for the cross-polarized nonlinear susceptibility coefficient. With a peak pump pulse power of P_peak = 1 W, we find the generation probability of about 1.4 × 10^–3 counts per input pump pulse. Assuming a 80 MHz repetition rate for the pump laser, the average pump power will be about 0.3 mW and the pair-generation rate will be about 115 KHz.

We compare this theoretically calculated efficiency with the measurements from a pulsed SFWM experiment on an amorphous silicon ridge waveguide, with comparable transverse dimensions and pump pulse bandwidths, but with approximately an order of magnitude larger length Wang et al. (2014). In this case, a comparable generation rate was measured, yet with an order of magnitude lower pump pulse energy due to the longer length of the ridge waveguide. It should be pointed out, that the effect of the lower value of the cross-polarized nonlinear susceptibility in our scheme and the lower overlap integral due to the use of non-dominant Bloch harmonics is effectively balanced by the effect of larger group indices in the PCW.

5 Conclusion and discussion

We have proposed a novel scheme for reaching CP phase-matching for photon-pair generation through SFWM in a standard photonic crystal waveguide, where we have performed the design and numerical demonstration of this scheme in a silicon PCW. We have then showed that asymmetric group-velocity matching can be reached in this structure, and have numerically demonstrated the generation of highly spectrally uncorrelated photon-pair states, where the pair can have both degenerate and non-degenerate central frequencies.

An important part of our design is the use of index-guided TM modes of the PCW, which allow us to reach both the CP phase-matching condition and the AGVM condition. We emphasize that the region of interest in the design was reached only by tuning the slab thickness in a standard W1 PCW, and we have not even tapped into the well-known dispersion-engineering capability of PCWs, which can shape the group-index spectra of the guided modes through changing the in-slab design parameters (such as the position or radius of the rows of holes neighbouring the central line defect) Li et al. (2008); Schulz et al. (2010). Adding this degree of freedom to the design can open up even more possibilities in engineering the properties of the factorable state.

An interesting property of the design is that the pump and the signal/idler modes are cross polarized. Hence, the polarization degree of freedom can also be used, in addition to spectral filtering, to filter out the pump field from the two-photon state. Even more interesting, is the fact that in both of the cases we presented with degenerate and non-degenerate pumping, one can fully avoid the unwanted photon pairs that are usually generated around the pump beam frequency due to trivial phase-matching of the pump mode with itself. This is due to the fact that in the case shown in Figure 3, the frequency of the idler photon, and in the case shown in Figure 4, the frequency of both of the signal and idler photons fall within the bandgap of the TM modes. It has been shown that if one of the photons in a pair falls within the bandgap region of a mode, pair generation will be fully suppressed at both frequencies of the pair in that mode Helt et al. (2017); Saravi et al. (2017b). This means that pair generation in the TM modes themselves will be suppressed at the frequencies where we generate pairs in the TE mode. The bandgap-suppression effect has been proposed previously to suppress unwanted pair generation channels Helt et al. (2017), although it has to be noticed that the extent of this suppression can be limited by underlying losses of the system, which reduce the effectiveness of the bandgap modes Saravi et al. (2017a).

It should also be noted that, although we have used the same TE mode for the CP signal and idler, which consequently generates the pair in a close spectral range, we are not limited to such a configuration. For example, to separate the signal and idler frequencies even further, one can imagine a scenario, with the signal photon in the low-frequency TE index-guided modes (the lowest guided bands in Figure 2A) and the idler photon in the gap-guided TE mode, while having the pump mode somewhere in the TM1 mode, which could be positioned in the needed frequency range with a proper choice of the slab thickness, as was done in this work. We do not investigate such scenarios here, yet we want to point this out as an example of the plethora of possibilities for generation of CP photons pairs in such PCWs based on SFWM.

We strongly emphasize, that although we do our demonstration based on a design in silicon, our design concept is general and can in principle be applied to any nanostructured material platform. Other candidates could be III-V semiconductor material platforms, such as aluminium gallium arsenide Kultavewuti et al. (2016) and gallium phosphide Wilson et al. (2019), which also have comparable χ⁽³⁾ coefficients to silicon and also a comparable linear refractive index. Such silicon Xiong et al. (2011); Collins et al. (2013); He et al. (2014) and III-V semiconductor Clark et al. (2013) photonic crystal waveguides have already been fabricated and used for conventional co-propagating photon-pair generation. This shows that an experimental demonstration of our proposed scheme is feasible.

Aside from heralded single-photon sources, the CP configuration is of interest for other applications, e.g. for creating a mirrorless optical parametric oscillator Canalias and Pasiskevicius (2007), which can then be used as a narrowband source of squeezed light Gatti et al. (2017). In particular, recently there is a rising interest for creating purely single- and two-mode squeezed light sources for Gaussian boson sampling Vaidya et al. (2020); Zhong et al. (2020). Such sources in essence require that the two squeezed beams are spectrally factorable from one another. Hence, the source presented here could also be a candidate for such applications if it is operating in a higher-gain regime of pumping that surpasses the probabilistic pair-generation regime. Finally, the CP scheme involving different modes for the signal and idler was used in Saravi et al. (2017b) to propose a design for direct generation of path-entangled Bell states through SPDC in PCWs. The same concept could potentially be extended to SFWM for generation of path-entangled Bell states.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SS, FS, and TP have developed the concept. SS, YZ, and XC have done the designs and the numerical simulations. SS, MA, YZ, and XC have performed the data analysis. SS have wrote the first draft of the manuscript, and MA contributed to some parts of the manuscript preparation. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The authors acknowledge funding from the German Federal Ministry of Education and Research (BMBF) under the project identifiers 13N14877 (QuanIm4Life), 13N16108 (PhoQuant); from the German Research Foundation (DFG) under the project identifiers PE 1524/13-1 (NanoPair), SE 2749/1-1 (NanoSPDC), 398816777-SFB 1375 (NOA); and from the Thuringian Ministry for Economic Affairs, Science and Digital Society under the project identifier 2021 FGI 0043 (Quantum Hub Thuringia).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aboussouan, P., Alibart, O., Ostrowsky, D. B., Baldi, P., and Tanzilli, S. (2010). High-visibility two-photon interference at a telecom wavelength using picosecond-regime separated sources. Phys. Rev. A 81, 021801. doi:10.1103/PhysRevA.81.021801

CrossRef Full Text | Google Scholar

Belhassen, J., Baboux, F., Yao, Q., Amanti, M., Favero, I., Lemaître, A., et al. (2018). On-chip III-V monolithic integration of heralded single photon sources and beamsplitters. Appl. Phys. Lett. 112, 071105. doi:10.1063/1.5015951

CrossRef Full Text | Google Scholar

Boyd, R. W. (2008). Nonlinear optics. Third Edition. Burlington: Academic Press. Third edition edn.

Google Scholar

Brod, D. J., Galvão, E. F., Crespi, A., Osellame, R., Spagnolo, N., and Sciarrino, F. (2019). Photonic implementation of boson sampling: a review. Adv. Photonics 1, 034001. doi:10.1117/1.AP.1.3.034001

CrossRef Full Text | Google Scholar

Canalias, C., and Pasiskevicius, V. (2007). Mirrorless optical parametric oscillator. Nat. Photonics 1, 459–462. doi:10.1038/nphoton.2007.137

CrossRef Full Text | Google Scholar

Castelletto, S. A., and Scholten, R. E. (2008). Heralded single photon sources: a route towards quantum communication technology and photon standards. Eur. Phys. J. Appl. Phys. 41, 181–194. doi:10.1051/epjap:2008029

CrossRef Full Text | Google Scholar

Christ, A., Eckstein, A., Mosley, P. J., and Silberhorn, C. (2009). Pure single photon generation by type-I PDC with backward-wave amplification. Opt. Express 17, 3441. doi:10.1364/OE.17.003441

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen, J. B., Koefoed, J. G., Rottwitt, K., and McKinstrie, C. J. (2018). Engineering spectrally unentangled photon pairs from nonlinear microring resonators by pump manipulation. Opt. Lett. 43, 859. doi:10.1364/OL.43.000859

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen, J. (2018). Tailored four-wave-mixing processes for optical quantum information science. Ph.D. thesis.

Google Scholar

Clark, A. S., Husko, C., Collins, M. J., Lehoucq, G., Xavier, S., De Rossi, A., et al. (2013). Heralded single-photon source in a III-V photonic crystal. Opt. Lett. 38, 649. doi:10.1364/OL.38.000649

PubMed Abstract | CrossRef Full Text | Google Scholar

Collins, M. J., Xiong, C., Rey, I. H., Vo, T. D., He, J., Shahnia, S., et al. (2013). Integrated spatial multiplexing of heralded single-photon sources. Nat. Commun. 4, 2582. doi:10.1038/ncomms3582

PubMed Abstract | CrossRef Full Text | Google Scholar

Garay-Palmett, K., McGuinness, H. J., Cohen, O., Lundeen, J. S., Rangel-Rojo, R., U’Ren, A. B., et al. (2007). Photon pair-state preparation with tailored spectral properties by spontaneous four-wave mixing in photonic-crystal fiber. Opt. Express 15, 14870. doi:10.1364/OE.15.014870

PubMed Abstract | CrossRef Full Text | Google Scholar

Gatti, A., Corti, T., and Brambilla, E. (2017). Squeezing and Einstein-Podolsky-Rosen correlation in the mirrorless optical parametric oscillator. Phys. Rev. A . Coll. Park. 96, 013820. doi:10.1103/PhysRevA.96.013820

CrossRef Full Text | Google Scholar

Grice, W. P., U’Ren, A. B., and Walmsley, I. A. (2001). Eliminating frequency and space-time correlations in multiphoton states. Phys. Rev. A 64, 063815. doi:10.1103/PhysRevA.64.063815

CrossRef Full Text | Google Scholar

He, J., Clark, A. S., Collins, M. J., Li, J., Krauss, T. F., Eggleton, B. J., et al. (2014). Degenerate photon-pair generation in an ultracompact silicon photonic crystal waveguide. Opt. Lett. 39, 3575. doi:10.1364/OL.39.003575

PubMed Abstract | CrossRef Full Text | Google Scholar

Helt, L. G., Brańczyk, A. M., Liscidini, M., and Steel, M. J. (2017). Parasitic photon-pair suppression via photonic stop-band engineering. Phys. Rev. Lett. 118, 073603. doi:10.1103/PhysRevLett.118.073603

PubMed Abstract | CrossRef Full Text | Google Scholar

Joannopoulos, J., Johnson, S., Winn, J., and Meade, R. (2011). emphPhotonic crystals: Molding the flow of light. United States: Princeton University Press.

Google Scholar

Johnson, S. G., and Joannopoulos, J. D. (2001). Block-iterative frequency-domain methods for maxwell’s equations in a planewave basis. Opt. Express 8, 173–190. doi:10.1364/OE.8.000173

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaneda, F., Garay-Palmett, K., U’Ren, A. B., and Kwiat, P. G. (2016). Heralded single-photon source utilizing highly nondegenerate, spectrally factorable spontaneous parametric downconversion. Opt. Express 24, 10733. doi:10.1364/OE.24.010733

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, D., Pang, A., Zhao, Y., and Helmy, A. S. (2014). Two-photon quantum state engineering in nonlinear photonic nanowires. J. Opt. Soc. Am. B 31, 1581. doi:10.1364/JOSAB.31.001581

CrossRef Full Text | Google Scholar

Kultavewuti, P., Zhu, E. Y., Qian, L., Pusino, V., Sorel, M., and Stewart Aitchison, J. (2016). Correlated photon pair generation in AlGaAs nanowaveguides via spontaneous four-wave mixing. Opt. Express 24, 3365. doi:10.1364/OE.24.003365

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, P., Younesi, M., Saravi, S., Setzpfandt, F., and Pertsch, T. (2022). Group index matched frequency conversion in lithium niobate on insulator waveguides. arXiv e-printsarXiv:2203.04885.

Google Scholar

Lanco, L., Ducci, S., Likforman, J.-P., Marcadet, X., van Houwelingen, J. A. W., Zbinden, H., et al. (2006). Semiconductor waveguide source of counterpropagating twin photons. Phys. Rev. Lett. 97, 173901. doi:10.1103/PhysRevLett.97.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

Law, C. K., Walmsley, I. A., and Eberly, J. H. (2000). Continuous frequency entanglement: Effective finite hilbert space and entropy control. Phys. Rev. Lett. 84, 5304–5307. doi:10.1103/PhysRevLett.84.5304

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., White, T. P., O’Faolain, L., Gomez-Iglesias, A., and Krauss, T. F. (2008). Systematic design of flat band slow light in photonic crystal waveguides. Opt. Express 16, 6227. doi:10.1364/OE.16.006227

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y.-C., Guo, D.-J., Ren, K.-Q., Yang, R., Shang, M., Zhou, W., et al. (2021). Observation of frequency-uncorrelated photon pairs generated by counter-propagating spontaneous parametric down-conversion. Sci. Rep. 11, 12628. doi:10.1038/s41598-021-92141-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, K.-H., Ansari, V., Massaro, M., Santandrea, M., Eigner, C., Ricken, R., et al. (2020). Counter-propagating photon pair generation in a nonlinear waveguide. Opt. Express 28, 3215. doi:10.1364/OE.378789

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyer-Scott, E., Montaut, N., Tiedau, J., Sansoni, L., Herrmann, H., Bartley, T. J., et al. (2017). Limits on the heralding efficiencies and spectral purities of spectrally filtered single photons from photon-pair sources. Phys. Rev. A 95, 061803. doi:10.1103/PhysRevA.95.061803

CrossRef Full Text | Google Scholar

Monroy-Ruz, J., Garay-Palmett, K., and U’Ren, A. B. (2016). Counter-propagating spontaneous four wave mixing: Photon-pair factorability and ultra-narrowband single photons. New J. Phys. 18, 103026. doi:10.1088/1367-2630/18/10/103026

CrossRef Full Text | Google Scholar

Mosley, P. J., Lundeen, J. S., Smith, B. J., Wasylczyk, P., U’Ren, A. B., Silberhorn, C., et al. (2008). Heralded generation of ultrafast single photons in pure quantum states. Phys. Rev. Lett. 100, 133601. doi:10.1103/PhysRevLett.100.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagy, J. T., and Reano, R. M. (2020). Submicrometer periodic poling of lithium niobate thin films with bipolar preconditioning pulses. Opt. Mat. Express 10, 1911. doi:10.1364/OME.394724

CrossRef Full Text | Google Scholar

Nielsen, M. A. (2004). Optical quantum computation using cluster states. Phys. Rev. Lett. 93, 040503. doi:10.1103/PhysRevLett.93.040503

PubMed Abstract | CrossRef Full Text | Google Scholar

Orieux, A., Eckstein, A., Lemaître, A., Filloux, P., Favero, I., Leo, G., et al. (2013). Direct Bell states generation on a III-V semiconductor chip at room temperature. Phys. Rev. Lett. 110, 160502. doi:10.1103/PhysRevLett.110.160502

PubMed Abstract | CrossRef Full Text | Google Scholar

Pant, M., Krovi, H., Englund, D., and Guha, S. (2017). Rate-distance tradeoff and resource costs for all-optical quantum repeaters. Phys. Rev. A 95, 012304. doi:10.1103/PhysRevA.95.012304

CrossRef Full Text | Google Scholar

Saravi, S., Diziain, S., Zilk, M., Setzpfandt, F., and Pertsch, T. (2015). Phase-matched second-harmonic generation in slow-light photonic crystal waveguides. Phys. Rev. A 92, 063821. doi:10.1103/PhysRevA.92.063821

CrossRef Full Text | Google Scholar

Saravi, S., Pertsch, T., and Setzpfandt, F. (2017a). Generation of counterpropagating path-entangled photon pairs in a single periodic waveguide. Phys. Rev. Lett. 118, 183603. doi:10.1103/PhysRevLett.118.183603

PubMed Abstract | CrossRef Full Text | Google Scholar

Saravi, S., Pertsch, T., and Setzpfandt, F. (2019). Photonic crystal waveguides as sources of counterpropagating factorizable biphoton states. Opt. Lett. 44, 69. doi:10.1364/OL.44.000069

PubMed Abstract | CrossRef Full Text | Google Scholar

Saravi, S., Poddubny, A. N., Pertsch, T., Setzpfandt, F., and Sukhorukov, A. A. (2017b). Atom-mediated spontaneous parametric down-conversion in periodic waveguides. Opt. Lett. 42, 4724. doi:10.1364/OL.42.004724

PubMed Abstract | CrossRef Full Text | Google Scholar

Saravi, S., Quintero-Bermudez, R., Setzpfandt, F., Asger Mortensen, N., and Pertsch, T. (2016). Effect of loss on slow-light-enhanced second-harmonic generation in periodic nanostructures. Opt. Lett. 41, 3110. doi:10.1364/OL.41.003110

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulz, S. A., O’Faolain, L., Beggs, D. M., White, T. P., Melloni, A., and Krauss, T. F. (2010). Dispersion engineered slow light in photonic crystals: a comparison. J. Opt. 12, 104004. doi:10.1088/2040-8978/12/10/104004

CrossRef Full Text | Google Scholar

Signorini, S., and Pavesi, L. (2020). On-chip heralded single photon sources. AVS Quantum Sci. 2, 041701. doi:10.1116/5.0018594

CrossRef Full Text | Google Scholar

Sipe, J. E., Bhat, N. A., Chak, P., and Pereira, S. (2004). Effective field theory for the nonlinear optical properties of photonic crystals. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 69, 016604. doi:10.1103/PhysRevE.69.016604

PubMed Abstract | CrossRef Full Text | Google Scholar

Svozilík, J., Hendrych, M., Helmy, A. S., and Torres, J. P. (2011). Generation of paired photons in a quantum separable state in Bragg reflection waveguides. Opt. Express 19, 3115. doi:10.1364/OE.19.003115

PubMed Abstract | CrossRef Full Text | Google Scholar

U’Ren, A. B., Silberhorn, C., Erdmann, R., Grice, W. P., Walmsley, I. A., Banaszek, K., et al. (2005). Generation of pure-state single-photon wavepackets by conditional preparation based on spontaneous parametric downconversion. Laser Phys. 15, 146–161.

Google Scholar

Vaidya, V. D., Morrison, B., Helt, L. G., Shahrokshahi, R., Mahler, D. H., Collins, M. J., et al. (2020). Broadband quadrature-squeezed vacuum and nonclassical photon number correlations from a nanophotonic device. Sci. Adv. 6, eaba9186. doi:10.1126/sciadv.aba9186

PubMed Abstract | CrossRef Full Text | Google Scholar

Varnava, M., Browne, D. E., and Rudolph, T. (2008). How good must single photon sources and detectors be for efficient linear optical quantum computation? Phys. Rev. Lett. 100, 060502. doi:10.1103/PhysRevLett.100.060502

PubMed Abstract | CrossRef Full Text | Google Scholar

Vernon, Z., Menotti, M., Tison, C. C., Steidle, J. A., Fanto, M. L., Thomas, P. M., et al. (2017). Truly unentangled photon pairs without spectral filtering. Opt. Lett. 42, 3638. doi:10.1364/OL.42.003638

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Zhang, Q., and Tang, C.-j. (2006). Multiparty controlled quantum secure direct communication using Greenberger Horne Zeilinger state. Opt. Commun. 266, 732–737. doi:10.1016/j.optcom.2006.05.035

CrossRef Full Text | Google Scholar

Wang, K.-Y., and Foster, A. C. (2012). Ultralow power continuous-wave frequency conversion in hydrogenated amorphous silicon waveguides. Opt. Lett. 37, 1331. doi:10.1364/OL.37.001331

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, K.-Y., Velev, V. G., Lee, K. F., Kowligy, A. S., Kumar, P., Foster, M. A., et al. (2014). Multichannel photon-pair generation using hydrogenated amorphous silicon waveguides. Opt. Lett. 39, 914. doi:10.1364/OL.39.000914

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, D. J., Schneider, K., Hönl, S., Anderson, M., Baumgartner, Y., Czornomaz, L., et al. (2019). Integrated gallium phosphide nonlinear photonics. Nat. Photonics 14, 57–62. doi:10.1038/s41566-019-0537-9

CrossRef Full Text | Google Scholar

Xiong, C., Monat, C., Clark, A. S., Grillet, C., Marshall, G. D., Steel, M. J., et al. (2011). Slow-light enhanced correlated photon pair generation in a silicon photonic crystal waveguide. Opt. Lett. 36, 3413–3415. doi:10.1364/OL.36.003413

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Liscidini, M., and Sipe, J. E. (2008). Spontaneous parametric down-conversion in waveguides: A backward heisenberg picture approach. Phys. Rev. A . Coll. Park. 77, 033808. doi:10.1103/PhysRevA.77.033808

CrossRef Full Text | Google Scholar

Yariv, A., and Yeh, P. (1977). Electromagnetic propagation in periodic stratified media. ii. birefringence, phase matching, and x-ray lasers. J. Opt. Soc. Am. 67, 438–447. doi:10.1364/JOSA.67.000438

CrossRef Full Text | Google Scholar

Younesi, M., Geiss, R., Rajaee, S., Setzpfandt, F., Chen, Y.-H., and Pertsch, T. (2021). Periodic poling with a micrometer-range period in thin-film lithium niobate on insulator. J. Opt. Soc. Am. B 38, 685. doi:10.1364/JOSAB.414298

CrossRef Full Text | Google Scholar

Zhang, L., Söller, C., Cohen, O., Smith, B. J., and Walmsley, I. A. (2012). Heralded generation of single photons in pure quantum states. J. Mod. Opt. 59, 1525–1537. doi:10.1080/09500340.2012.679707

CrossRef Full Text | Google Scholar

Zhao, J., Rüsing, M., Roeper, M., Eng, L. M., and Mookherjea, S. (2020). Poling thin-film x-cut lithium niobate for quasi-phase matching with sub-micrometer periodicity. J. Appl. Phys. 127, 193104. doi:10.1063/1.5143266

CrossRef Full Text | Google Scholar

Zhong, H.-S., Wang, H., Deng, Y.-H., Chen, M.-C., Peng, L.-C., Luo, Y.-H., et al. (2020). Quantum computational advantage using photons. Science 370, 1460–1463. doi:10.1126/science.abe8770

PubMed Abstract | CrossRef Full Text | Google Scholar