Group-index-matched frequency conversion in lithium niobate on insulator waveguides

Sources of spectrally engineered photonic states are a key resource in several quantum technologies. Of particular importance are the so-called factorizable biphoton states, which possess no spectral entanglement and hence, are ideal for heralded generation of high-purity single photons. An essential prerequisite for generating these states through nonlinear frequency conversion is the control over the group indices of the photonic modes of the source. Here, we show that thin-film lithium niobate on insulator (LNOI) is an excellent platform for this purpose. We design and fabricate periodically poled ridge waveguides in LNOI to demonstrate group index engineering of its guided photonic modes and harness this control to experimentally realize on-chip group index matched type-II sum-frequency generation (SFG). Also, we numerically study the role of the top cladding layer in tuning the dispersion properties of the ridge waveguide structures and reveal a distinctive difference between the air and silica-clad designs which are currently among the two most common device cladding configurations in LNOI. We expect that these results will be relevant for various classical and quantum applications where dispersion control is crucial in tailoring the nonlinear response of the LNOI-based devices.

1 Introduction

The field of integrated linear and nonlinear optics has seen rapid technological progress based on recent developments in the thin-film lithium niobate on insulator (LNOI) photonic platform (Zhang et al., 2017; Wang et al., 2018a; Saravi et al., 2021). Improvements in microfabrication techniques have enabled reliable monolithic fabrication of nanoscale low-loss optical waveguide structures with typical cross-sectional dimensions below 1 μm². This promises to truly meet the requirements in high on-chip integration density, high performance and scalability of fabrication (Luke et al., 2020). More crucially, lithium niobate (LN), being a χ⁽²⁾-nonlinear material, allows an array of integrated nonlinear optical applications such as classical frequency conversion (Geiss et al., 2015; Wang et al., 2018b), on-chip frequency comb creation (Zhang et al., 2019), supercontinuum generation, (Yu et al., 2019; Escalé et al., 2020), and photon-pair generation with strong spectral entanglement and high generation rates (Zhao et al., 2020) through efficient spontaneous parametric down-conversion (SPDC).

Apart from high conversion efficiencies (Wang et al., 2018b; Rao et al., 2019), an often needed capability in classical and quantum nonlinear frequency conversion processes is control over the spectral characteristics of the generated light. This is especially relevant for quantum applications requiring generation of spectrally tailored quantum states. A preeminent example of such an application is the heralded generation of high purity single-photon states through SPDC. In SPDC, a higher energy pump (P) photon at frequency ω_P spontaneously splits into a pair of lower energy photons, called signal (S) and idler (I) with frequencies ω_S and ω_I inside a χ⁽²⁾-medium, such that ω_P = ω_S + ω_I. If the SPDC process is engineered to eliminate the spectral entanglement between the two photons, such that the generated two-photon joint state is spectrally factorizable, then the generation of a spectrally pure single-photon state can be heralded by detecting the other photon of the pair (U’Ren et al., 2005; Mosley et al., 2008).

Spectral engineering of SPDC to produce such factorizable states requires careful manipulation of the group indices (n_g) of pump, signal and the idler modes such that either the condition ${\mathrm{n}}_g^{\text{S}}\le {\mathrm{n}}_g^{\text{P}}\le {\mathrm{n}}_g^{\text{I}}$ or ${\mathrm{n}}_g^{\text{I}}\le {\mathrm{n}}_g^{\text{P}}\le {\mathrm{n}}_g^{\text{S}}$ can be fulfilled (Grice et al., 2001). In general, achieving such control over the dispersion properties of a χ⁽²⁾ nonlinear source at wavelengths of interest is not always possible.

Ridge waveguides in LNOI allow broad control over the dispersion of its optical modes (Jankowski et al., 2020). This is in contrast to the conventional low-index contrast in-diffused waveguides in LN, where the dispersion properties of the modes are mostly dominated by that of the bulk LN material. In the case of LNOI, tight modal confinement of light in subwavelength dimension waveguiding structures can lead to dispersion engineering opportunities. Through geometry-induced dispersion control, LNOI ridge waveguides can allow manipulation of group velocity and group-velocity dispersion of the modes. In recent works, this dispersion engineering capability has received special attention (Jankowski et al., 2021). Through appropriate waveguide design, dispersion parameters have been optimized to significantly enlarge the bandwidth of second harmonic generation and SPDC processes compared to that in the bulk medium (Solntsev et al., 2011; Jankowski et al., 2020; Javid et al., 2021; Ledezma et al., 2021).

So far, most of the experimental efforts towards dispersion engineering in LNOI nanophotonics have been focused on the so-called type-0 processes to exploit its highest nonlinear tensor element, d₃₃. However, a type-0 process restricts the range of possibilities in dispersion control since it does not fully leverage the strong birefringence of ridge waveguides. In particular, to satisfy the factorizability condition for generation of frequency-degenerate signal and idler photons, the two photons have to be generated in two different modes to first realize different group indices for them, and then try to engineer the pump group index to a value between them. For this scenario, a type-II process is needed, which utilizes the d₃₁ element of the nonlinear tensor and involves two orthogonally polarized modes for the signal and idler photons: the transverse magnetic (TM) and transverse electric (TE) modes. In fact, it has been theoretically shown that by exploiting the geometry-dependent birefringence of the modes in LNOI ridge waveguides, the group indices can be tailored to satisfy the condition for generation of factorizable photon-pairs (Kang et al., 2014).

In this work, we experimentally demonstrate the dispersion-engineering capability of LNOI ridge waveguides for spectral control of type-II frequency conversion processes. Specifically, we show that in a type-II process, the group indices of the signal and pump modes can be made equal, ${\mathrm{n}}_g^{\text{P}}={\mathrm{n}}_g^{\text{S}}$, through a suitable choice of the design parameters. We verify this control experimentally by mapping the spectral properties of the type-II process in sum-frequency generation (SFG) experiments, where the waveguides are excited at the signal and idler wavelengths and pump photons are generated through the SFG process. We show that the signal and pump modes of the waveguides have group indices that are nearly equal to each other. This shows the capability of LNOI waveguides for dispersion engineering of type-II frequency conversion. The group index matching demonstrated here is highly relevant for realizing on-chip sources of spectrally pure single photons as it is required for the generation of factorizable photon-pair states through SPDC (Mosley et al., 2008). Since modal-confinement is crucial in controlling the group indices of the modes, we also perform a numerical analysis of the effect of top-cladding layer and waveguide dimensions on group index. It is shown that while air-clad higher-index contrast ridge waveguides offer more diverse control, the silica-clad waveguides can offer higher robustness to device dimension variations. Finally, we perform a numerical analysis of the biphoton states which can be generated in these waveguides through SPDC and provide quantitative estimates for the heralded single photon purity to highlight the potential of our tested systems for quantum technologies.

2 Materials and methods

2.1 Phase-matching function

To study the effect of dispersion engineering on the spectral features of type-II frequency conversion, we start by describing the corresponding SPDC process. The biphoton state |ψ⟩ generated in SPDC is described in the frequency domain as |ψ⟩ = ∬ dω_Sdω_IJ (ω_S, ω_I)|1⟩_S|1⟩_I, where the joint spectral amplitude (JSA), J (ω_S, ω_I), contains information about spectral entanglement between the signal-idler pair produced from the pump photon (Grice et al., 2001). The JSA can be shown to be J (ω_S, ω_I) ∝ A_p (ω_P = ω_S + ω_I) × ϕ(ω_S, ω_I) with A_p (ω_P) being the pump photon spectral amplitude and ϕ(ω_S, ω_I) being the phase matching function (PMF). If the factorizability condition on the group indices of the photonic modes is fulfilled, the shape of the resulting PMF enables the generation of a spectrally factorizable state with J (ω_S, ω_I) = u (ω_S) × v (ω_I).

The PMF for a quasi-phase-matched (QPM) type-II frequency conversion process depends on the phase-mismatch vector ΔK and length L of the waveguide, and is given by ϕ = sinc (ΔKL/2) × exp (−iΔKL/2), where ΔK (ω_S, ω_I) = K^S(ω_S) + K^I(ω_I) − K^P(ω_P) + (2π/Λ). Here, K^i=P,S,I are the wave vectors of the respective modes of the waveguide. For QPM-assisted frequency conversion the nonlinearity of the waveguide is periodically inverted with a period of Λ along its length though a technique called periodic poling. The resulting nonlinear grating vector (2π/Λ) compensates for the mismatch of the effective indices of the waveguide modes leading to efficient frequency conversion. QPM, which is a well established technique in bulk LN, has recently been adapted to the LNOI thin-film platform (Wang et al., 2018b; Rao et al., 2019; Younesi et al., 2021). This decouples the phase-matching requirement from the dispersion control such that the geometry of the waveguide can be used to control the group velocities of the modes to modify the spectral dependence of the PMF while the central phase-matching wavelengths can be fixed through the choice of the QPM period Λ so that ΔK = 0.

Since the quantum process of SPDC and its reverse classical process of SFG share the same PMF, by virtue of the quantum-classical correspondence principle (Lenzini et al., 2018), the experimental investigation of the PMF for SPDC is also possible by studying the corresponding SFG process. This immensely reduces the experimental effort in probing the spectral dependence of the PMF. The SFG intensity, I_SFG, is related to ϕ(ω_S, ω_I) as I_SFG ∝|ϕ(ω_S, ω_I)|² = sinc² (ΔKL/2). Vanishing ΔK maximizes the sinc function and leads to the largest SFG intensity. Thus ΔK (ω_S, ω_I) = 0 gives the relation between the signal and idler frequency defining the phase-matching-curve (PMC) of the SFG and SPDC processes. The slope of the PMC is related to the group indices as (U’Ren et al., 2005)

$\theta ={\tan }^{-1}\left\{-\left({\mathrm{n}}_g^{\text{P}}-{\mathrm{n}}_g^{\text{S}}\right)/\left({\mathrm{n}}_g^{\text{P}}-{\mathrm{n}}_g^{\text{I}}\right)\right\},(1)$

thus directly revealing the effect of group-index engineering on the spectrum of biphoton state generated in SPDC. We depict this schematically in Figure 1. The pump amplitude A_p (ω_p), shown in Figure 1A is oriented at a fixed angle of −45° with respect to the ω_S-axis due to energy conservation, ω_p = ω_S + ω_I. On the other hand, the slope of the PMC can be tuned through dispersion control to lie in the range 0° ≤ θ ≤ 90° as is required to reach the factorizability condition. This is shown in Figure 1B by the blue solid line overlaid on the two-dimensional plot for the PMF ϕ(ω_S, ω_I). In this case the slope is around 20°. The resulting JSA J (ω_S, ω_I) of the signal-idler pair is displayed in Figure 1C. It is composed of a central circular-looking high intensity lobe surrounded by several smaller intensity lobes along the −45° diagonal.

FIGURE 1

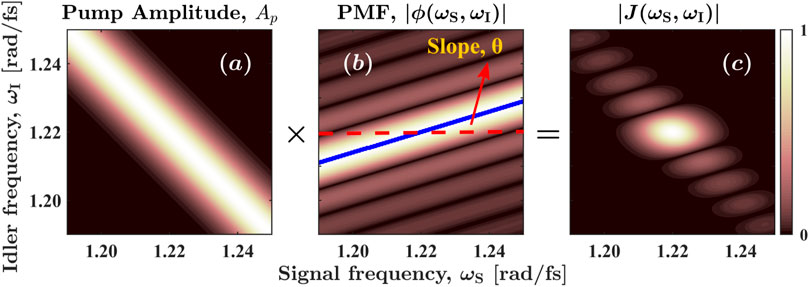
FIGURE 1. Schematic of the JSA, J = A_p × ϕ, of a biphoton state. (A) Gaussian pump spectral amplitude, A_p (B) PMF, ϕ, of a type-II frequency conversion process. The blue solid line, referred to as the PMC, is oriented at an angle of θ with the ω_S-axis (represented schematically by the horizontal red dashed line) and represents the maximum of PMF. (C) Resulting JSA of the signal-idler pair.

The factorizability of J (ω_S, ω_I) can be optimized for a given PMF by choosing an appropriate spectral bandwidth of the pump (Grice et al., 2001). In general, the extent of this optimal factorizability and consequently, the purity of the heralded single photon states is larger for the two extreme cases when the slope of PMC is either θ = 0° or θ = 90° compared to other slopes in the range 0° ≤ θ ≤ 90° (Jankowski et al., 2021). These specific cases can be achieved through group index matching, ${\mathrm{n}}_g^{\text{P}}={\mathrm{n}}_g^{\text{S}}\ne {\mathrm{n}}_g^{\text{I}}$ and ${\mathrm{n}}_g^{\text{P}}={\mathrm{n}}_g^{\text{I}}\ne {\mathrm{n}}_g^{\text{S}}$ respectively. Here, we demonstrate the first case, where the group indices of the pump and signal are nearly matched while that of the idler is smaller, ${\mathrm{n}}_g^{\text{P}}\approx {\mathrm{n}}_g^{\text{S}}>{\mathrm{n}}_g^{\text{I}}$, leading to PMC slope of θ ≈ 0°.

2.2 Group-index matching

We consider an x-cut LNOI thin-film geometry as shown in Figure 2A for design and fabrication of the ridge waveguides. The waveguide has a fixed height of H = 600 nm and is cladded from the top with a thick silica layer. We ought to point out here that this particular choice of fixed height for the fabrication of waveguides was primarily due to issues related to the unavailability of commercial LNOI wafers in other thicknesses. The top width of the waveguide shown in Figure 2A is W = 1,275 nm. The fundamental modes at the three wavelengths involved in type-II frequency mixing are shown in Figure 2B. To phase match the process we used a QPM period of Λ = 3 μm which results in phase matching of the signal and idler waves at the central wavelength of λ_S = λ_I = 1,542 nm to generate the pump at half of their wavelength through the SFG process. The length of the waveguide is L = 4 mm.

FIGURE 2

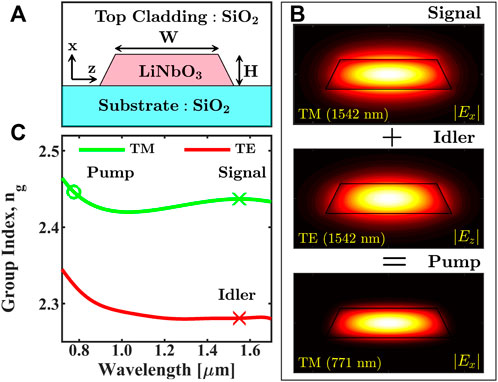
FIGURE 2. (A) Schematic of the LNOI ridge waveguide in x-cut thin-film with top width W = 1,275 nm, height H = 600 nm and the base side-wall angle of 72°. (B) The three fundamental modes of the waveguide involved in a type-II SFG process. (C) Variation of group index with wavelength for TE and TM modes. Group index of the TM pump mode at the wavelength of 771 nm and that of the TM signal mode at the wavelength of 1,542 nm are nearly matched.

Figure 2C shows the dependence of the group index n_g of TE and TM modes of the waveguide on the wavelength. The green curve belongs to the TM mode on which we have marked the position of signal and pump by green cross and circle respectively. The corresponding group index ${\mathrm{n}}_g^{\text{I}}$ of the idler is highlighted on the red curve belonging to the TE mode by a red cross. We note that the green curve shows an interesting behaviour, such that it first decreases with wavelength till about λ ≈ 1 μm and then shows an increase. As a result ${\mathrm{n}}_g^{\text{S}}$ and ${\mathrm{n}}_g^{\text{P}}$ can be matched. Such dependence of group index on wavelength can be understood by noting that n_g is given by ${\mathrm{n}}_g(\lambda )=\mathrm{n}(\lambda )-\lambda \frac{d\mathrm{n}(\lambda )}{d\lambda }$, where n(λ) is the effective index of the mode. Due to the weaker modal confinement with increasing wavelength, the effective index of modes of the LNOI ridge waveguides decreases appreciably with increasing wavelength. This confinement-induced dispersion can be substantial for waveguides of sub-micrometer dimensions and thus, the $-\lambda \frac{d\mathrm{n}(\lambda )}{d\lambda }$ contribution to n_g can be significant and enough to compensate for the decrease in the effective index n(λ) with increasing wavelength. This explains the non-monotonic behaviour of the group index n_g for the TM mode shown in Figure 2C. For shorter wavelengths till about λ ≈ 1 μm, the $-\lambda \frac{d\mathrm{n}(\lambda )}{d\lambda }$ contribution is small and thus n_g decreases with increasing wavelength. However, when the wavelength becomes large the confinement-induced dispersion term grows in magnitude and this leads to an increasing n_g with increasing wavelength in the range of about λ ≈ 1 μm to λ ≈ 1.6 μm. Further increasing the wavelength again leads to a reduced n_g because the mode of the waveguide is predominantly residing in the cladding which strongly reduces the magnitude of $|\frac{d\mathrm{n}(\lambda )}{d\lambda }|$. It can be noted from Figure 2C that n_g for the TE mode does not increase like the TM mode for the wavelengths larger than λ ≈ 1 μm. In fact it only shows a very small change with increasing wavelength. The reason for this difference again lies in the transverse confinement of the modes in the waveguide. Since the height of the considered waveguide is smaller than its width, the magnitude of the $-\lambda \frac{d\mathrm{n}(\lambda )}{d\lambda }$ term for the TM mode is larger compared to that for the TE mode. As a consequence although the group index n_g for the TM mode increases with increasing wavelength in the intermediate wavelength range of λ ≈ 1 μm to λ ≈ 1.6 μm, the n_g for the TE mode remains nearly constant since its $-\lambda \frac{d\mathrm{n}(\lambda )}{d\lambda }$ term contribution is only large enough to compensate for the decrease in the effective index n(λ) with increasing wavelength. For the design presented here, we calculate the group indices of pump and signal to be ${\mathrm{n}}_g^{\text{P}}=2.447$ and ${\mathrm{n}}_g^{\text{S}}=2.437$, while ${\mathrm{n}}_g^{\text{I}}=2.281$ is significantly smaller. Using these values we estimate the slope of the PMC using Eq. (1) to be θ = −3.45°. As we discuss later, although the resulting slope θ is quite small in this design, a perfect group-index matching θ = 0 is also possible for waveguides of height H = 700 nm in the considered silica-clad waveguide configuration.

We now look at the influence of the waveguide dimensions on the group indices with an aim to investigate the tunability of the PMC slope. We consider waveguides with silica and air top cladding since the index-contrast between the core and surroundings is significantly different in these cases, which affects their dispersion properties. In Figure 3A we show the variation of the slope θ with the top width of the waveguide for the fixed height of H = 600 nm. Here, by choosing appropriate poling periods Λ, the central signal and idler phase-matching wavelength for all the waveguides is kept equal to 1,542 nm for calculating and comparing the PMC slopes. The blue solid curve represents the silica-clad case where the minimal slope of θ ≈ − 3° is attained for a waveguide width of W = 950 nm. The red square on this curve represent the design we discussed before with a width of W = 1,275 nm. We note that although W = 1,275 nm is not the optimal case for the waveguide of fixed height considered here, the difference between their slopes is quite small. On the other hand, the air-clad case displayed by the black dotted curve shows much higher sensitivity to the waveguide width and thus allows wider tunability of the slope. Remarkably, θ in the air-clad case is positive and has a larger magnitude meaning that ${\mathrm{n}}_g^{\text{S}}$ is substantially greater than ${\mathrm{n}}_g^{\text{P}}$ in contrast to the silica cladding case. The contour plots in Figures 3B,C show the dependence of the slope on the height and width of the waveguide for silica and air-clad cases respectively. In the case of silica cladding the attainable slope is either negative or can be zero, whereas with the air cladding the waveguides allow more broader control over the group indices such that one can achieve negative, zero or even positive PMC slopes by choosing appropriate dimensions for the waveguide. Comparing these two cladding cases also shows that the silica-clad design can offer a more robust way for group index matching with θ ≈ 0, since there exists a globally optimal waveguide design with dimensions W = 775 nm and H = 700 nm. In this case, sensitivity to variations in the device dimensions or the wavelength of operation is quite low compared to the air-clad case. Hence, the silica-clad waveguide design can be beneficial for realizing complex optical circuits that integrate sources of classical or quantum states of light with the electro-optic modulators (Wang et al., 2018a; Wang et al., 2018c) on the same chip.

FIGURE 3

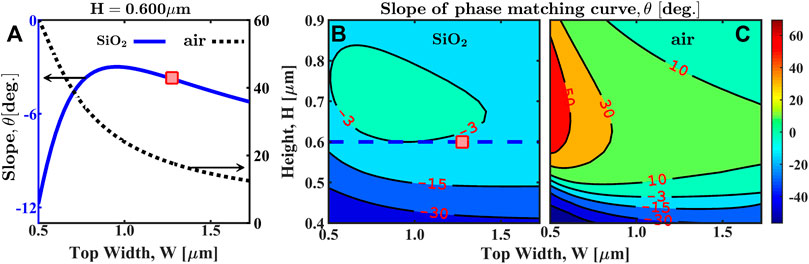
FIGURE 3. Slope θ of PMC for type-II degenerate-frequency SFG with the fundamental wavelength of 1,542 nm. (A) Variation of the slope with waveguide width W for a fixed height H for the silica cladding (blue solid curve) and air cladding (black dotted curve) cases. The red square denotes the waveguide of width W = 1,275 nm. (B)–(C) Dependence of PMC slope on height and width of waveguide for silica and air cladding designs respectively. The blue dashed line in (B) indicates the silica-clad waveguides of constant height H = 600 nm.

2.3 SFG experiments

We experimentally confirm group-index matching by performing SFG experiments. This is done for four waveguides having widths W in the range 1,275 nm–1,380 nm and the same height H = 600 nm. They have silica cladding on the top. Since their QPM period was the same, Λ = 3 μm, their central signal-idler phase-matching wavelengths are different.

For SFG experiments we combine two independent continuous-wave tunable lasers using a fiber-based polarization beam combiner and couple them simultaneously into the waveguide with the help of a lensed tip single mode fiber. Their polarization state is controlled individually on the input side using two fiber-based polarization controllers so that one of them excites the fundamental TM mode (signal) while the other excites the TE mode (idler) of the waveguide. The waveguide chip and the lensed fiber are placed on 3-axis translation stages to optimize the coupling. On the output side, a broadband collecting objective was placed to collect the signal and idler beams and the sum-frequency radiation (pump). The lower wavelength SFG beam is then separated from the higher wavelength fundamental beams using a longpass dichroic beamsplitter whose pass edge is around 1 μm. Finally, the signal and idler beams, which are in orthogonal polarization, are separated using a polarization beamsplitter and the power of the three beams is measured using appropriate power meters.

3 Results and discussions

3.1 Experimental validation of dispersion engineering and near group-index matching

We present the result of such a measurement for the waveguide of width W = 1,275 nm as a two-dimensional plot in Figure 4A. This is obtained by sweeping the wavelength of the lasers from 1,490 nm to 1,610 nm. The normalized SFG intensity essentially represents the PMF ϕ(λ_S, λ_I) such that its maximum maps out the PMC of the SFG process. We can see that the SFG intensity produces a band which is oriented nearly flat along the horizontal direction parallel to the signal frequency axis. This clearly shows that the signal and pump are nearly group index matched. The solid blue curve overlaid on the SFG plot is the numerically calculated PMC while the dashed red line is a horizontal line parallel to the ω_S axis. The numerically calculated slope of the PMC is quite small, being approximately equal to θ ≈ − 3°, as is shown in the figure.

FIGURE 4

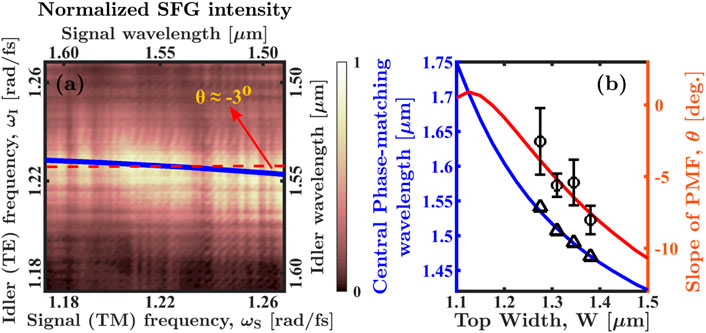
FIGURE 4. (A) Normalized SFG intensity from the waveguide of width W = 1,275 nm for varying signal and idler wavelengths. The solid blue curve is the theoretical PMC and θ denotes its slope. (B) Central phase-matching wavelength for SFG (blue curve) and the corresponding slope of the PMC (red curve) for waveguides of different widths. All waveguides were fabricated with a constant QPM period of Λ = 3 μm and the calculations are performed for different waveguide widths with this constant poling period for comparison.

To obtain the value of the slope θ from experiments, we first determine the experimental PMC. This is extracted from the SFG experimental data by determining the idler wavelength which maximizes the SFG intensity for each signal wavelength. Then a linear function is fitted to the experimental PMC to get its slope θ. For the experimental PMF shown in Figure 4A the slope determined in this manner is found to be θ = −2.5° which is in good agreement with numerical calculations. Further, we performed similar SFG experiments for other three waveguides of larger widths to acquire their experimental PMCs, which we then used to calculate the corresponding slopes.

In Figure 4B we show the result of such analysis for all the four waveguides investigated experimentally in this work. The solid blue curve in the figure shows the central signal-idler phase-matching wavelengths for SFG, defined as the signal-idler wavelength λ_S = λ_I which results in phase matching ΔK = 0, for waveguides of different widths. Since the QPM period is the same, Λ = 3 μm, for all the fabricated waveguides, their central phase-matching wavelengths varies. The black triangles correspond to the different waveguides studied experimentally. The theoretical slope of their PMC is also shown in the figure by the solid red curve. The black circles on this curve denote the experimentally observed slopes θ obtained from the SFG measurements as described before. We see, that with an increase in waveguide width the slope of the PMC grows in magnitude. However, its variation is small such that increasing the width from W = 1,275 nm–1,380 nm changes θ from about −3° to −8°. Notably, the central phase-matching wavelength changes appreciably from around 1,540 nm–1,460 nm with increasing waveguide width. Such dispersion characteristics allow the central wavelength of nonlinear frequency conversion to be easily tuned while still approximately maintaining the group-index matching through an appropriate waveguide design.

We point out that the experimental SFG intensity shown in Figure 4A differs from the well-known sinc² shape of the PMF. This is due to the presence of loss. We ascertain the magnitude of these losses for signal and idler by performing Fabry-Perot interference measurement (Hu et al., 2009). From the visibility of fringes in transmission of spectral intensity, we estimate these to be 20 dB/cm and 26 dB/cm, for idler and signal respectively. The main source of the losses is the roughness on the side-walls of the waveguides. By improving the etching parameters this can be minimized in future versions of the device as would be necessary for quantum applications. Lossy guiding modes of the waveguide also affect the conversion efficiency of SFG. The normalized conversion efficiency, which is defined as $\eta =P_{\text{P}}/\left(P_{\text{S}}{P}_{\text{I}}{L}^2\right)$, is estimated to be about 560% W⁻¹cm⁻² if the waveguides were lossless. Here, P_P,S,I are the respective powers of the three modes. The value of the conversion efficiency η given here is much larger than unity since it is normalized by the square of the length L² of the waveguide. Using this normalized efficiency we can also calculate the absolute conversion efficiency, $P_{\text{P}}/\left(P_{\text{S}}{P}_{\text{I}}\right)$, for the SFG process. For the waveguide of length L = 4 mm, taking the signal and idler powers to be 1 mW respectively, results in a pump power of P_P = 0.9 μW. Thus, for the nanophotonic ridge waveguide considered here the absolute conversion efficiency is $P_{\text{P}}/\left(P_{\text{S}}{P}_{\text{I}}\right)=0.9W^{-1}$. When compared with the type-II SFG in low-index contrast LN waveguides, this is more than an order of magnitude larger (Chung et al., 2020). On the other hand, for similar nanophotonic LN ridge waveguides designed for type-0 second harmonic generation, the conversion efficiencies are about 10 times larger than that calculated here for the type-II SFG (Wang et al., 2018b; Rao et al., 2019). This is primarily due to the larger magnitude of the d₃₃ nonlinear element of LN employed in type-0 processes compared to the d₃₁ element used in this work for realizing type-II SFG. The experimentally observed efficiency, however, is only 4% W⁻¹cm⁻². The theoretically estimated η assuming a lossless waveguide agrees with the observed efficiency when we take into account the optical losses of the modes, their individual collection efficiencies and limited transmission through the collecting objective.

3.2 Estimated purity of the heralded single photon state

We have, so far, demonstrated a near-zero slope θ of the PMC and its tunability with the dimensions of the waveguide through SFG experiments. We now consider the corresponding SPDC process and provide an analysis of the effect of this slope on the purity of the heralded single photon states by investigating the JSA of the resulting biphoton state in these dispersion-engineered waveguides.

The degree of spectral entanglement between signal and idler photons can be quantified by performing a Schmidt decomposition of the JSA J (ω_S, ω_I) into a set of orthogonal basis functions u_n (ω_S) and v_n (ω_I) such that $J({\omega }_{\text{S}},{\omega }_{\text{I}})=\sum _n\sqrt{{\lambda }_n}{u}_n({\omega }_{\text{S}})v_n({\omega }_{\text{I}})$ (U’Ren et al., 2005; Mosley et al., 2008; Grice et al., 2001). The distribution of Schmidt eigenvalues λ_n over the various joint spectral modes n in the decomposition is responsible for the spectral entanglement. To get a pure heralded single photon state by detecting its partner photon the joint-state should ideally be composed of just a single joint spectral mode. Such a state is completely factorizable and thus, has zero entanglement. Alternatively, the purity of the heralded single photon state given by $\sum _n{\lambda }_n^2=1$ is maximum in this case. In general, JSA J (ω_S, ω_I), with lower spectral entanglement results in a higher purity value for the heralded single photon state which is desirable for single photon sources.

In Figure 5A we show the numerically calculated joint spectral intensity |J (ω_S, ω_I)|² for the waveguide with height H = 600 nm and width W = 1,275 nm. The slope of the PMC for this waveguide is θ = −3.45° and the resulting JSA for a pump pulse with spectral width of Δλ_p = 6 nm resembles an ellipse. The purity of the heralded single photon state for this JSA is calculated to be 0.79. We note that the particular value of Δλ_p chosen for this case provides the maximum purity for the given angle θ and length L = 4 mm of the waveguide (Grice et al., 2001). This is shown explicitly in Figure 5D by the red solid curve which shows the dependence of purity on pump spectral width for this waveguide. It can be seen that purity value reaches a maximum for the chosen pump width Δλ_p. We note that the maximum purity attainable is limited due to the small negative nonzero slope θ of the PMC in this case. By using the most optimal waveguide dimension of height H = 700 nm and width W = 775 nm, we have shown that the slope can be made equal to zero and thus, the purity can be further improved. We show the corresponding |J (ω_S, ω_I)|² for this case in Figure 5B for a typical pump width of Δλ_p = 10 nm. The major axis of the elliptical-looking joint spectral intensity in this case is oriented horizontally and thus, a higher purity value of 0.94 is attained. Interestingly, it is possible to further increase the purity in this case by increasing the pump spectral width. This is depicted by the blue solid curve in Figure 5D, which shows that by increasing Δλ_p beyond 10 nm, the purity can be improved. It should be noted that although we have restricted the purity plot in Figures 5A–D to a maximum pump spectral width of 15 nm, this is not the pump bandwidth that maximizes the purity for the case of exact group-index matching. In fact, increasing Δλ_p beyond 15 nm would lead to increased purity as long as the difference between the group indices of the pump and the signal does not become large enough such that the slope of the PMC becomes nonzero. This is because exact group-index matching is strictly true only at the central phase matching wavelengths. With increasing Δλ_p, the signal photon bandwidth increases and at some point the group-index mismatch between signal and pump becomes significant such that the elliptical |J (ω_S, ω_I)|² shown in Figure 5B no longer remains oriented completely horizontally. This in turn limits the maximum purity of the heralded signal photons.

FIGURE 5

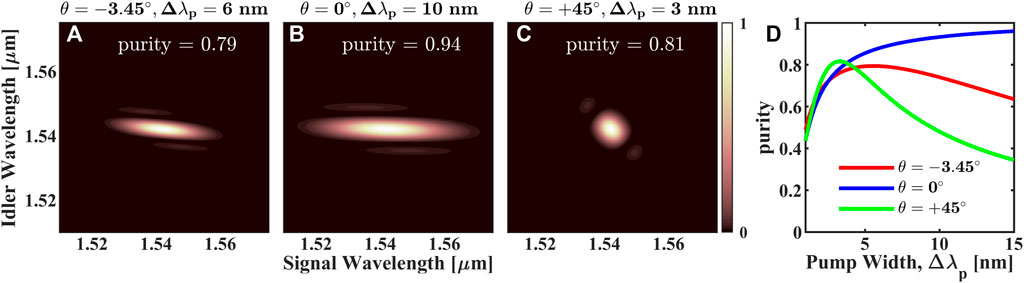
FIGURE 5. Joint spectral intensity resulting from phase matching functions whose slope is (A) θ = −3.45° (waveguide height H = 600 nm, width W = 1,275 nm with silica cladding), (B) θ = 0 (H = 700 nm, W = 775 nm with silica cladding) and (C) θ = +45° (H = 700 nm, W = 650 nm with air cladding). (D) The dependence of heralded single photon purity on the spectral bandwidth of the pump for the three PMC slopes θ.

We should highlight that the two cases we considered in Figures 5A,B are for waveguides with a cladding layer of silica. As we have shown in Figure 3B such a design can fulfill group-index matching but can not provide a positive PMC slope θ. In contrast, for the air-cladded case, shown in Figures 3A,C positive slope θ can be realized. We now consider such a air-cladded waveguide with the height of H = 700 nm and width W = 650 nm for which the slope is θ = 45°. Its joint spectral intensity is shown in Figure 5C for a pump width of Δλ_p = 3 nm. Unlike the two cases discussed for the silica-clad design, the central lobe of the JSA is circular in this case. Its purity, which is maximised for the chosen pump width, is estimated to be 0.81. Also the dependence of purity on pump width, shown by the green solid curve in Figure 5D, shows a stronger variation with changing Δλ_p compared to the other two cases.

It is evident that, in general, group-index matching θ = 0° can lead to higher purity for the heralded single photon state. By suppressing the smaller side lobes of the JSA which arise from sinc² shape of the PMF, the purity can be further increased. This can be achieved by employing appropriately apodized QPM poling pattern to realize a Gaussian-shaped PMF instead of the usual sinc-shaped one (Jankowski et al., 2021). In the resulting JSA, the sides lobes are largely suppressed in this case and much higher purity can be achieved for the heralded state. We would like to point out that during the review process of this work, we became aware of similar work where factorizable two-photon states where experimentally demonstrated in LNOI waveguides (Xin et al., 2022).

4 Conclusion

In conclusion, we have presented the concept of group-index matching for thin-film LNOI ridge waveguides and experimentally demonstrated its application in tuning the phase-matching curve of a type-II SFG process. This is highly relevant for the generation of factorizable biphoton states to realize heralded sources of spectrally pure single photons. We show that the waveguide dimensions together with the choice of the top cladding layer determine the extent of control over the group indices of waveguide modes. In particular, we find a waveguide geometry that is optimal for group-index matching and shows high robustness to variations in waveguide dimensions. Finally, we theoretically analyse photon-pair generation through SPDC in the group-index engineered waveguides and provide estimates for the purity of the heralded single photon states to highlight its application in quantum technologies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PK, SS, and FS contributed to conception and design of the study. MY contributed to the fabrication of the samples. PK designed and built the experimental setup, performed the experiments and analysed the data. All authors contributed to the preparation of the manuscript.

Funding

The authors acknowledge funding from the German Federal Ministry of Education and Research (BMBF) under the project identifiers 13N14877 (QuanIm4Life), 13N16108 (PhoQuant); from the German Research Foundation (DFG) under the project identifiers PE 1524/13-1 (NanoPair), SE 2749/1-1 (NanoSPDC), 398816777-SFB 1,375 (NOA); and from the Thuringian Ministry for Economic Affairs, Science and Digital Society under the project identifier 2021 FGI 0043 (Quantum Hub Thuringia).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chung, H. P., Kumar, P., Wang, K., Bernard, O., Shirpurkar, C., Su, W. C., et al. (2020). Spectral mapping of polarization-correlated photon-pair sources using quantum-classical correspondence. Arxiv. doi:10.48550/ARXIV.2007.00880

CrossRef Full Text | Google Scholar

Escalé, M. R., Kaufmann, F., Jiang, H., Pohl, D., and Grange, R. (2020). Generation of 280 THz-spanning near-ultraviolet light in lithium niobate-on-insulator waveguides with sub-100 pJ pulses. Apl. Photonics 5, 121301. doi:10.1063/5.0028776

CrossRef Full Text | Google Scholar

Geiss, R., Saravi, S., Sergeyev, A., Diziain, S., Setzpfandt, F., Schrempel, F., et al. (2015). Fabrication of nanoscale lithium niobate waveguides for second-harmonic generation. Opt. Lett. 40, 2715. doi:10.1364/ol.40.002715

PubMed Abstract | CrossRef Full Text | Google Scholar

Grice, W. P., U’Ren, A. B., and Walmsley, I. A. (2001). Eliminating frequency and space-time correlations in multiphoton states. Phys. Rev. A . Coll. Park. 64, 063815. doi:10.1103/physreva.64.063815

CrossRef Full Text | Google Scholar

Hu, H., Ricken, R., and Sohler, W. (2009). Lithium niobate photonic wires. Opt. Express 17, 24261. doi:10.1364/oe.17.024261

PubMed Abstract | CrossRef Full Text | Google Scholar

Jankowski, M., Langrock, C., Desiatov, B., Marandi, A., Wang, C., Zhang, M., et al. (2020). Ultrabroadband nonlinear optics in nanophotonic periodically poled lithium niobate waveguides. Optica 7, 40. doi:10.1364/optica.7.000040

CrossRef Full Text | Google Scholar

Jankowski, M., Mishra, J., and Fejer, M. M. (2021). Dispersion-engineered χ⁽²⁾ nanophotonics: A flexible tool for nonclassical light. J. Phys. Photonics 3, 042005. doi:10.1088/2515-7647/ac1729

CrossRef Full Text | Google Scholar

Javid, U. A., Ling, J., Staffa, J., Li, M., He, Y., Lin, Q., et al. (2021). Ultrabroadband entangled photons on a nanophotonic chip. Phys. Rev. Lett. 127, 183601. doi:10.1103/physrevlett.127.183601

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, D., Pang, A., Zhao, Y., and Helmy, A. S. (2014). Two-photon quantum state engineering in nonlinear photonic nanowires. J. Opt. Soc. Am. B 31, 1581. doi:10.1364/josab.31.001581

CrossRef Full Text | Google Scholar

Ledezma, L., Sekine, R., Guo, Q., Nehra, R., Jahani, S., and Marandi, A. (2021). Intense optical parametric amplification in dispersion engineered nanophotonic lithium niobate waveguides.

Google Scholar

Lenzini, F., Poddubny, A. N., Titchener, J., Fisher, P., Boes, A., Kasture, S., et al. (2018). Direct characterization of a nonlinear photonic circuit’s wave function with laser light. Light. Sci. Appl. 7, 17143. doi:10.1038/lsa.2017.143

PubMed Abstract | CrossRef Full Text | Google Scholar

Luke, K., Kharel, P., Reimer, C., He, L., Loncar, M., Zhang, M., et al. (2020). Wafer-scale low-loss lithium niobate photonic integrated circuits. Opt. Express 28, 24452. doi:10.1364/oe.401959

PubMed Abstract | CrossRef Full Text | Google Scholar

Mosley, P. J., Lundeen, J. S., Smith, B. J., Wasylczyk, P., U’Ren, A. B., Silberhorn, C., et al. (2008). Heralded generation of ultrafast single photons in pure quantum states. Phys. Rev. Lett. 100, 133601. doi:10.1103/physrevlett.100.133601

PubMed Abstract | CrossRef Full Text | Google Scholar

Rao, A., Abdelsalam, K., Sjaardema, T., Honardoost, A., Camacho-Gonzalez, G. F., Fathpour, S., et al. (2019). Actively-monitored periodic-poling in thin-film lithium niobate photonic waveguides with ultrahigh nonlinear conversion efficiency of 4600 %w-1cm-2. Opt. Express 27, 25920. doi:10.1364/oe.27.025920

PubMed Abstract | CrossRef Full Text | Google Scholar

Saravi, S., Pertsch, T., and Setzpfandt, F. (2021). Lithium niobate on insulator: An emerging platform for integrated quantum photonics. Adv. Opt. Mater. 9, 2100789. doi:10.1002/adom.202100789

CrossRef Full Text | Google Scholar

Solntsev, A. S., Sukhorukov, A. A., Neshev, D. N., Iliew, R., Geiss, R., Pertsch, T., et al. (2011). Cascaded third harmonic generation in lithium niobate nanowaveguides. Appl. Phys. Lett. 98, 231110. doi:10.1063/1.3597627

CrossRef Full Text | Google Scholar

U’Ren, A., Silberhorn, C., Banaszek, K., Walmsley, I., Erdmann, R., Grice, W., et al. (2005). Generation of pure-state single-photon wavepackets by conditional preparation based on spontaneous parametric downconversion. Laser Phys. 15, 146–161.

Google Scholar

Wang, C., Langrock, C., Marandi, A., Jankowski, M., Zhang, M., Desiatov, B., et al. (2018). Ultrahigh-efficiency wavelength conversion in nanophotonic periodically poled lithium niobate waveguides. Optica 5, 1438. doi:10.1364/optica.5.001438

CrossRef Full Text | Google Scholar

Wang, C., Zhang, M., Chen, X., Bertrand, M., Shams-Ansari, A., Chandrasekhar, S., et al. (2018). Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 562, 101–104. doi:10.1038/s41586-018-0551-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Zhang, M., Stern, B., Lipson, M., and Lončar, M. (2018). Nanophotonic lithium niobate electro-optic modulators. Opt. Express 26, 1547. doi:10.1364/oe.26.001547

PubMed Abstract | CrossRef Full Text | Google Scholar

Xin, C. J., Mishra, J., Chen, C., Zhu, D., Shams-Ansari, A., Langrock, C., et al. (2022). Spectrally separable photon-pair generation in dispersion engineered thin-film lithium niobate. Opt. Lett. 47, 2830. doi:10.1364/ol.456873

PubMed Abstract | CrossRef Full Text | Google Scholar

Younesi, M., Geiss, R., Rajaee, S., Setzpfandt, F., Chen, Y. H., Pertsch, T., et al. (2021). Periodic poling with a micrometer-range period in thin-film lithium niobate on insulator. J. Opt. Soc. Am. B 38, 685. doi:10.1364/josab.414298

CrossRef Full Text | Google Scholar

Yu, M., Desiatov, B., Okawachi, Y., Gaeta, A. L., and Lončar, M. (2019). Coherent two-octave-spanning supercontinuum generation in lithium-niobate waveguides. Opt. Lett. 44, 1222. doi:10.1364/ol.44.001222

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., Buscaino, B., Wang, C., Shams-Ansari, A., Reimer, C., Zhu, R., et al. (2019). Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 568, 373–377. doi:10.1038/s41586-019-1008-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, M., Wang, C., Cheng, R., Shams-Ansari, A., and Lončar, M. (2017). Monolithic ultra-high-q lithium niobate microring resonator. Optica 4, 1536. doi:10.1364/optica.4.001536

CrossRef Full Text | Google Scholar

Zhao, J., Ma, C., Rüsing, M., and Mookherjea, S. (2020). High quality entangled photon pair generation in periodically poled thin-film lithium niobate waveguides. Phys. Rev. Lett. 124, 163603. doi:10.1103/physrevlett.124.163603

PubMed Abstract | CrossRef Full Text | Google Scholar