High-throughput artifact-free slightly off-axis holographic imaging based on Fourier ptychographic reconstruction

Slightly off-axis digital holographic microscopy (DHM) has recently gained considerable attention due to its unique ability to improve the space-bandwidth product (SBP) of the imaging system while separating the object information from the background intensity to a certain extent. In order to obtain a decent image reconstruction, the spectral aliasing problem still needs to be addressed, which, however, is difficult to be achieved by the conventional linear Fourier domain filtering. To this end, in this paper, we propose a high-throughput artifact-free slightly off-axis holographic reconstruction method based on Fourier ptychographic microscopy (FPM). Inspired by the nonlinear optimized phase reconstruction algorithm of FPM, we perform constrained updates between the real and Fourier domains in an iterative manner to reconstruct the complex amplitude by the hologram intensity. Experimental results on live HeLa cell samples show that the proposed method can provide higher reconstruction accuracy and better image quality compared with the conventional Fourier method and the Kramers–Kronig (KK) relation-based method.

Introduction

In the field of optical microscopy, quantitative phase imaging (QPI) is an essential tool for biomedical research, possessing the distinctive ability of optical thickness measurement of live cells without exogenous contrast agents (Lee et al., 2013; Zuo et al., 2015; Sun et al., 2017; Zuo et al., 2017; Fan et al., 2019; Zuo et al., 2020). As a classical QPI technique, digital holographic microscopy (DHM) (Cuche et al., 1999; Mann et al., 2005; Chen et al., 2011) combines the principle of interferometry and holography, allowing for single-shot digital recording and numerical reconstruction of the object wavefront to quantitatively recover amplitude and phase with high accuracy in real time. Based on the off-axis architecture, DHM introduces an additional coherent reference beam that is tilted superimposed with the object beam, which encodes the invisible phase information into an interferogram. Capture the intensity signal of the hologram by imaging devices such as a CCD and then perform phase demodulation with fringe analysis algorithms.

During the hologram acquisition process, the intensity of the two coherent beams (often referred to as the zero-order term) and the object complex amplitude information are superimposed on the recorded signal simultaneously (Gao et al., 2013). Conventional off-axis holography completely separates the real image from its twin image and zero-order term in the spatial frequency domain by adjusting the tilt angle. Combining band-pass filtering and deconvolution to realize high-speed single-shot measurement, i.e. Fourier method (Takeda et al., 1982). However, the linear solution involves solely Fourier domain filtering , sacrificing the utilization of spatial bandwidth. The imaging throughput is quantitatively described by the space-bandwidth product (SBP), which varies with the recovery method and the modulation direction of the reference beam. Since the zero-order has a bandwidth of twice the one of the imaging term (the twin images), the maximum spatial bandwidth achieved by this linear solution is $\frac{N}{2+3\sqrt{2}}$ (Pavillon et al., 2009) for a region of N × N pixels with uniform sampling in the absence of spectral overlap. The limited bandwidth of the off-axis system is inefficient regarding the SBP of the complex amplitude image. It is negative for enhancing the imaging resolution, while the realization of real-time high-throughput imaging is the fundamental target constantly pursued in the development of microscopic imaging technology (Trusiak, 2021).

To improve the SBP of off-axis holography, spectral aliasing of zero-order with diffraction terms in the spatial frequency domain is unavoidable, which leads to a loss of imaging quality, such as reduced resolution or produced artifacts. So how to make full use of the spatial bandwidth and achieve artifact-free imaging while maintaining the diffraction limit resolution is a crucial issue. Various zero-order suppression methods have been proposed (Trusiak et al., 2020). The nonlinear filtering (Pavillon et al., 2009) in the cepstral domain can confine the object wave modulation to one quadrant of the spectrum and enhance the utilization of spatial bandwidth to $\frac{N}{4}$. Alternatively, the zero-order can be suppressed by subtracting the object intensity from the hologram with the reconstructed object wavefront in an iterative manner, loosening the constraints on bandwidth (Pavillon et al., 2010). Furthermore, on the basis of the nonlinear filtering method, high SBP off-axis holographic imaging can be achieved by exploiting the Kramers–Kronig (KK) relations (Baek et al., 2019). With the zero-padding operation in the frequency domain, the spectral aliasing is substantially reduced without an iterative process or imposing any restriction on objects, which theoretically increases the spatial bandwidth to $\frac{N}{2+\sqrt{2}}$. However, these methods are not applicable when the intensity of the reference beam is smaller than that of the object beam since the power series of the object-reference ratio is divergent in the Fourier domain.

With the proposal of phase retrieval (Fienup, 1982; Bauschke et al., 2002; Shechtman et al., 2015), nonlinear optimization algorithms provide a new demodulation perspective on optical phase microscopy. A particularly classic method in this field to recover phase from a single intensity measurement is the Gechberg-Saxton (GS) algorithm (Gerchberg, 1972, 1971), and related improved algorithms have also been proposed (Gonsalves, 1976; Fienup, 1978). These methods are based on nonlinear optimal iterations, which usually define a cost function similar to the intensity difference, and reconstruct the phase by constrained updates back and forth between the intensity in the spatial domain and aperture in the frequency domain. Nonlinear optimal iterative reconstruction methods have been widely applied in the field of QPI, such as lens-free microscopic imaging (Ozcan and Demirci, 2008; Seo et al., 2009) and Fourier ptychographic microscopy (FPM) (Zheng et al., 2013), etc. The original solutions to FPM are based on the gradient descent method, which retrieves the phase information of the samples by alternating iterations in the real and Fourier spaces, and is a highly representative integration of nonlinear optimization algorithms and QPI techniques.

Nevertheless, nonlinear optimization algorithms are rarely reported in holographic phase recovery since conventional DHM already has convenient demodulation methods (Fourier method for off-axis holography (Takeda et al., 1982) and phase-shift method for on-axis holography (Hariharan et al., 1987)), which can recover the phase in a single step without complicated iterative processes (Latychevskaia, 2019). However, when breaking the SBP limitation of conventional off-axis holography, the Fourier method cannot reconstruct the phase correctly due to the aliasing of spectral information. Therefore, nonlinear optimization algorithms are considered to solve the above problem. We present and experimentally demonstrate a QPI technique for high-throughput artifact-free slightly off-axis holographic imaging based on a nonlinear optimization algorithm similar to Fourier ptychographic reconstruction. Inspired by the phase retrieval process of FPM, the complex amplitude recovery is viewed as a nonlinear optimization problem to be solved by a method like the GS algorithm. In the premise that the linear method cannot correctly solve for the object wavefront, the proposed optimal iterative solution algorithm is more universal with no restrictions on the intensity of two coherent beams and unconstrained spectral configuration, which is distinct from all previous off-axis holography phase recovery methods.

Principle

Based on the nonlinear iterative solution of FPM, first built the forward mathematical modeling of the off-axis digital holographic imaging process. The spectrum of the object beam that reaches the camera target surface is O(u, v)P(u, v), where O (u, v) is the spectrum of the complex amplitude distribution of the measured object, P(u, v) represents the pupil function defined by the NA of the microscope objective and the illumination wavelength, and (u, v) denotes the frequency domain coordinates. The corresponding complex amplitude of the object beam is $O(x,y){=\mathcal{F}}^{-1}\left[O(u,v)P(u,v)\right]$, where ${\mathcal{F}}^{-1}$ denotes inverse Fourier transform. The reference beam is considered as a quasi-plane wave with a tilt angle θ to the object beam, which is expressed as R(x, y) = |R| exp(−ik sin θx). According to the interference principle of coherent superposition, the complex amplitude distribution of the hologram is

$U\left(x,y\right)=O\left(x,y\right)+R\left(x,y\right)(1)$

where the complex amplitude of the reference beam is reconstructed by the amplitude information obtained from the captured intensity image of the reference beam and the offset of ±1-order in the hologram spectrum. So R (x, y) is regarded as a known quantity for the subsequent calculations.

Since only the intensity distribution of the optical wavefield can be converted to a digital signal while the phase information is completely lost during the camera recording process, the complex wavefront requires some phase recovery methods for reconstruction. We learn from the nonlinear optimization idea of FPM and use the alternating projection method similar to the GS iterative algorithm, which recognize the complex amplitude reconstruction of the hologram as a nonlinear optimization problem. Essentially, the proposed phase recovery method for the slightly off-axis holography is to define a cost function that will converge to a minimum by updating functions back and forth between the real and Fourier spaces.

Next, we specify the objective cost function and the optimal solution algorithm used in the proposed iterative method. Define the cost function with the purpose of minimizing the amplitude error

$\epsilon \left(O\right)=\sum _{x,y}{\left|\sqrt{I\left(x,y\right)}-\left|F^{-1}\left[O\left(u,v\right)P\left(u,v\right)\right]+R\left(x,y\right)\right|\right|}^2.(2)$

where $I(x,y)={\left|U(x,y)\right|}^2$ is the intensity of the hologram. As the iterations proceed, the amplitude of the hologram reconstructed from the object complex wavefront to be recovered will gradually approach that of the captured hologram. Theoretically, the cost function, i.e., the amplitude error function, can eventually converge to zero, at which point the hologram complex amplitude update also converges to the real distribution.

Then we derive the update equation for the nonlinear optimization solution algorithm mentioned above. According to Parseval’s theorem, the cost function ɛ can be simplified as

$\epsilon \left(O\right)=\sum _{u,v}{‖U^u\left(u,v\right)-U^e\left(u,v\right)‖}^2(3)$

where U^e(u, v) = O(u, v)P(u, v) + R(u, v) represents the subspectrum before the update and U^u(u, v) represents the subspectrum after the update exploiting the captured hologram intensity I (x, y). The update process is expressed by the equation $U^u(x,y)=\sqrt{I(x,y)}\frac{U^e(x,y)}{\left|U^e(x,y)\right|}$.

The first-order derivative of the cost function is thus a component of Eq 11 and can be expressed as

${\nabla }_O\epsilon \left(O\right)=-\left[P^{\ast }\left(u,v\right)\left(U^u\left(u,v\right)-U^e\left(u,v\right)\right)\right].(4)$

The derivation process is explained in Appendix A. By minimizing the derivative with the gradient descent method to make it infinitely close to zero, thus the cost function Eq 2 can be reduced to the minimum value.

Finally, we achieve the update equation for the hologram complex amplitude distribution

$U\left(u,v\right)=U\left(u,v\right)+\alpha \frac{{\left|P\left(u,v\right)\right|}^2}{{\left|P\left(u,v\right)\right|}_{\max }^2}\frac{P^{\ast }\left(u,v\right)}{{\left|P\left(u,v\right)\right|}^2+\delta }\left[U^u\left(u,v\right)-U^e\left(u,v\right)\right].(5)$

α is the update step length and usually ranges from 0.5 to 1. Values of α around 1 (not greater than 1) works well in our simulations and experiments. δ is a regularization parameter (a minimal value near 0) to prevent the denominator from going to zero. It should be noted that the P(u, v) in Eqs 3–5 is a mask function for spectrum selection of the numerical reconstruction in the actual phase recovery process (the ideal state is the above-mentioned pupil function determined by NA).

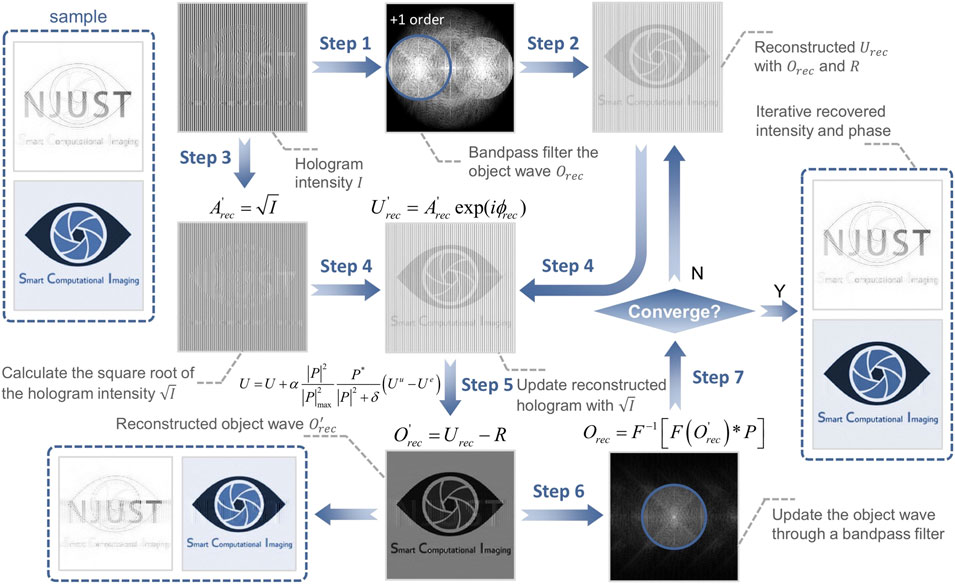
The iterative procedures derived from Eq 5 are shown in algorithm 1 and Figure 1 as an example for the case where the value of update step α is 1. During the iterative process, the square root of the intensity of the recorded digital hologram is always employed to update the reconstructed complex amplitude. Based on the gradient descent method, the cost function gradually converges to zero by updating functions back and forth between the real and Fourier spaces. Then the complex amplitude distribution of the hologram is reconstructed to recover the phase information of the sample.

FIGURE 1

FIGURE 1. Flow chart of the nonlinear optimization iterative algorithm for phase recovery.

Exploiting the nonlinear optimization algorithm, we can construct an slightly off-axis holographic system with extreme resolution that makes full use of the space bandwidth, in which the spectral configuration of the twin images is exactly tangent at the origin without overlapping by diagonal modulation of the reference beam and selection of suitable system parameters. In other words, it is able to iteratively reconstruct the object complex amplitude while guaranteeing a maximum spatial bandwidth of $\frac{N}{2+\sqrt{2}}$, and there is no additional requirement for the intensity of the object and reference beam in the iterative process.

ALGORITHM 1

Algorithm 1. Nonlinear optimization iterative algorithm based on FPM for slightly off-axis DHM phase recovery

Simulation

Simulations are carried out to verify the validity and effectiveness of the proposed algorithm. To investigate the performance of the proposed method for phase demodulation at R < O, we choose the case of R/O = 0.7 for simulation and compare the reconstruction results with that of the conventional off-axis method and KK method. The simulation results are shown in Figure 2. Figure 2A1, A2 are used as amplitude image and phase image respectively to generate the hologram [Figue 2A3]. Here we used a vertical reference beam modulation in these simulations and the spectrum of the hologram is shown in Figure 2A4. To compare the QPI results of the above methods more intuitively, we also calculated the root mean square error (RMSE) images of the reconstructed amplitude and phase. It is obvious that the proposed algorithm can reconstruct the complex amplitude image of the object wave with high accuracy and its errors are almost indistinguishable to the naked eye, as shown in Figures 2B1–B4. In contrast, the conventional off-axis method has many artifacts in the reconstructed amplitude and phase due to the inability to suppress the 0-order term [Figures 2C1–C4], and the results of the KK method not only have artifacts, but also a constant term error on the background of the amplitude image [Figures 2D1–D4].

FIGURE 2

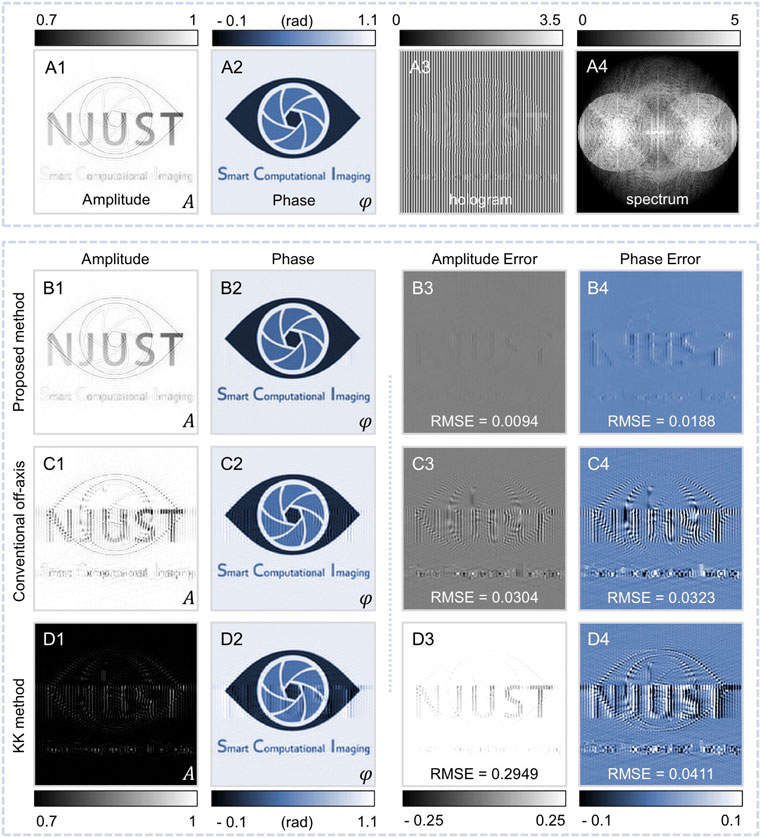
FIGURE 2. Comparison of the simulation results of the proposed method, conventional off-axis method and KK method in case of R/O = 0.7. (A1,A2) Simulated amplitude and phase. (A3) Hologram simulated with (A1,A2). (A4) Spectrum of the hologram. (B1–B4) Reconstructed amplitude, phase and the corresponding errors with the proposed method. (C1–C4) Reconstructed amplitude, phase and the corresponding errors with conventional off-axis method. (D1–D4) Reconstructed amplitude, phase and the corresponding errors with KK method.

In order to further verify the stability, convergence, and robustness properties of the proposed nonlinear optimization algorithm, and further compare the effectiveness of the above methods at an arbitrary reference-object ratio (R/O), we simulate all cases with R/O from 0 to 1.2 and plotted the correlation curves demonstrated in Figure 3. It can be seen that the blue curve always lies above the curves of the other colors and tends to be close to one even when the intensity of the reference beam is as small as almost one-tenth of the object beam, much higher than the other curves. This shows that the proposed method is applicable to all reference-object ratios and has better performance than the linear methods even when R > O. We also compare the convergence of the RMSE between the proposed iterative method and Pavillon method for the case of R/O = 0.7 and R/O = 0.9 of the hologram in Figure 4 and display the best reconstruction result during the iteration (R/O = 0.7). It is obvious that the RMSE of the Pavillon method is divergent when R/O = 0.7 and its best result still has serious artifacts. In comparison, our method has a stable declining RMSE trend and maintains a very small error, which means that the RMSE converges in only 10 iterations, ensuring the efficiency of phase recovery. (RMSE 0.0188 rad, total computation time 0.035s with a 2.60 GHz laptop).

FIGURE 3

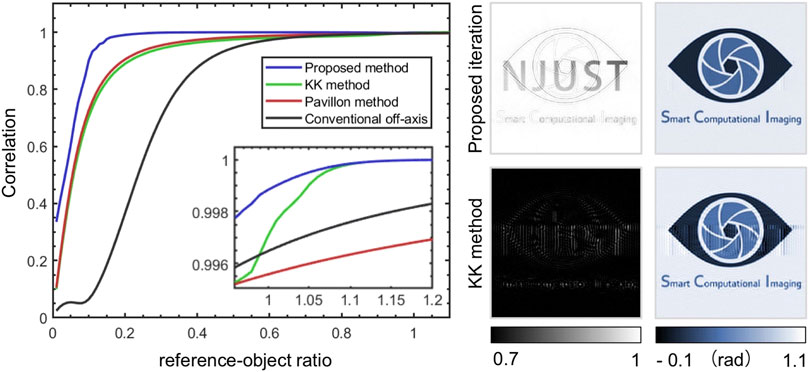
FIGURE 3. Correlation curves of the proposed method, KK method, Pavillon method and conventional Fourier method.

FIGURE 4

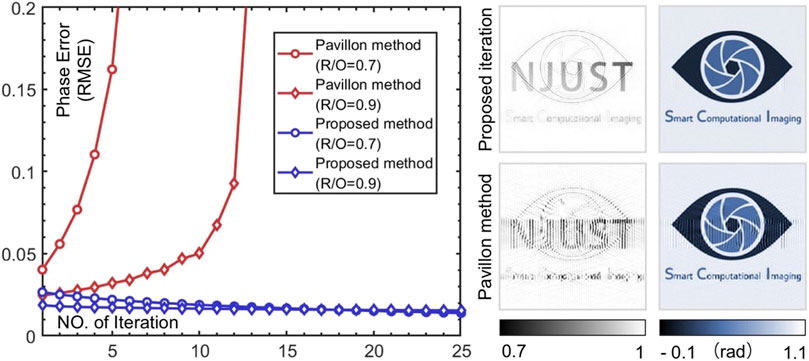
FIGURE 4. Comparison between two iterative methods. Left: RMSE curves versus the iteration number for the case of R/O = 0.7 and R/O = 0.9 of the hologram. Right: the best reconstruction results for the case of R/O = 0.7.

Let’s specifically analyze why the Pavillon method and KK method are not applicable in the case of object-reference ratios (O/R) greater than or equal to 1. The parasitic terms of the error between the estimator and the object 0-order of the Pavillon method are powers of O/R that must meet the conditions of O < R to not diverge. The nonlinear filtering and KK methods convert the extraction of +1-order to the solution of $\log \left(1+O/R\right)$, which is a power series of O/R through Taylor expansion. When O/R < 1, ${\left(O/R\right)}^n$ decreases rapidly with increasing order n and decays outward in the spectrum along the modulation direction, with the overflow superimposed on its conjugate image on the other side of the spectrum. The KK method ensures the continuity and integrity of higher-order terms in the frequency domain by zero-padding. Nevertheless, if O/R ≥ 1, the higher-order terms tend to diverge and overlap severely with the conjugate term. As a result, the Hilbert transform (HT) cannot separate $\log \left(1+O/R\right)$ and thus the residual intensity information will damage the accuracy of phase recovery. Therefore, only when the reference-object ratio is greater than 1, the convergence of the Pavillon method can be guaranteed and high precision recovery of the KK method can be ensured. In addition, the KK method should change the direction of the zero-padding operation and HT for different spectral configurations, so the parameters have to be adjusted according to the imaging system in practice.

Experiment

To demonstrate the capability of the nonlinear optimization algorithm, various samples are imaged, under the condition where the zero-order and diffraction terms severely overlap in the frequency space. Digital holographic smart computational light microscope (DH-SCLM) (Fan et al., 2021) developed by SCILab is used to acquire the hologram. The beam is transmitted by the objective lens (UPLanSAPO ×10/0.4NA, Olympus, Japan) and recorded by the camera (The Imaging Source DMK 23U274, 1600 × 1200, 4.4 μm). The central wavelength of the illumination is 532 nm. With these system parameters, adjust the tilt angle of the reference beam until the imaging term is diagonally tangent in the frequency space to achieve maximum utilization of the spatial bandwidth. The biggest advantage of the proposed method is the relaxed restriction on the reference-object ratio, so we conduct the experiments under the same conditions as the simulation (R/O = 0.7). Complex amplitudes are recovered by the proposed method, the KK method, and the conventional off-axis method, respectively. For comparison, an identical interferogram per sample is used for the three methods. In addition, the intensity of the reference beam is recorded for the subsequent phase reconstruction algorithm, which needs to be measured only once.

Interferogram of a standard phase resolution target (QPT^TM, Benchmark Technologies Corporation, United States , RIn = 1.52) is imaged as shown in Figure 5. The proposed iterative method recovers the quantitative phase with high accuracy in the case of reaching the theoretical resolution of the holographic imaging system and without excess background [Figures 5A1, A2]. However, since the reference-object ratio of the system is less than 1, the KK method cannot suppress all the 0-order so that the reconstructed phase image still carries some artifacts formed by the intensity information of the hologram [Figures 5B1, B2]. And in the conventional method, the recovered phase image has severe artifacts [Figures 5C1, C2] due to the lack of ability to remove the part of the 0-order term that overlaps with the +1-order in the frequency domain by bandpass filtering. In this case, the slightly off-axis hologram has a fringe pattern with high spatial frequency [Figure 5D1] and a spectral configuration with the maximum SBP [Figure 5D2].

FIGURE 5

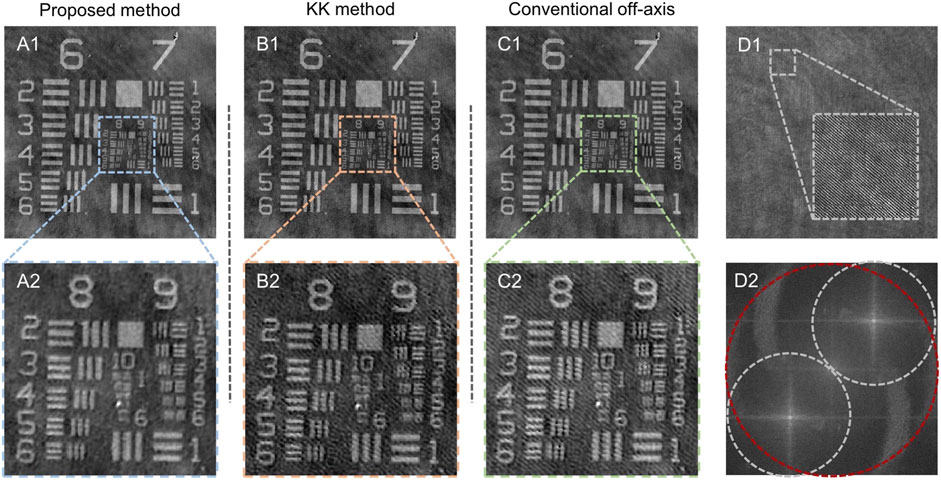
FIGURE 5. Comparison of the experimental results of the proposed method, KK method and conventional Fourier method. (A1) Reconstructed phase with the proposed method. (A2) The enlarged sub-region of interest of the reconstructed phase in (A1). (B1) Reconstructed phase with KK method. (B2) The enlarged sub-region of interest of the reconstructed phase in (B1). (C1) Reconstructed phase with conventional off-axis method. (C2) The enlarged sub-region of interest of the reconstructed phase in (C1). (D1) Hologram in the experimental condition. (D2) Fourier transform of (D1) (red circle indicates 0-order, white circles indicate ±1-order).

Then the nonlinear optimization algorithm is applied to the QPI of live HeLa cells as shown in Figure 6. The phase images reconstructed by the proposed iterative method are shown in Figures 6A1–A3, which obtain the internal structure of the cells without any artifacts since the unwanted zero-order term is completely suppressed. The field of view (FoV) of Figure 6A1 is 0.33 × 0.44 mm with a diffraction-limited size of 0.81 μm. The SBP of the complex amplitude image is 257000 pixels [the area of the FoV, 0.1452 mm², multiplied by the area of the spatial frequency band, π(NA/λ)²]. For comparison, the KK method can suppress the zero-order term to some extent, but it cannot converge and result in blurring or even loss of cell details and obvious artifacts in the background [Figures 6B1–B3]. When the phase is recovered by the conventional method, simple filtering retains some of the intensity information of the object beam and reference beam, thus drastically reducing the correctness of the phase reconstruction [Figures 6C1–C3].

FIGURE 6

FIGURE 6. Comparison of the experimental results of the proposed method, KK method and conventional off-axis method. (A1) Reconstructed phase with the proposed method. (A2,A3) The sub-regions of interest of phase in (A1). (B1) Reconstructed phase with KK method. (B2), (B3) The sub-regions of interest of phase in (B1). (C1) Reconstructed phase with conventional off-axis method (magnification = 10). (C2,C3) The sub-regions of interest of phase in (C1). (D1) Reconstructed phase with conventional off-axis method (magnification = 20). (D2) The sub-regions of interest of phase in (D1).

Finally, we perform an experiment to verify the enhancement in the SBP of the proposed method. For imaging, an Olympus 20× (0.4 NA) objective lens is adopted. The total magnification of the setup is kept at 20, identical to the magnification of the objective lens. Adjust the tilt angle of the reference beam to generate an absolute diagonal off-axis hologram with the ±1-order completely separated from the 0-order. Image the same HeLa sample with the system and conduct phase recovery by the conventional off-axis method. The measured quantitative phase image is shown in Figures 6D1, D2, which is almost the same as that reconstructed by our proposed nonlinear optimization method in a diagonal tangent spectral configuration. The ×10 and ×20 objectives have the same numerical aperture, which means both achieve the same lateral resolution. However, the difference in objective magnification results in the FoV and SBP at ×20 objective reduced to 1/4 of that at ×10 objective, where SBP is only 64200 pixels. In contrast, the proposed method provide a 4-fold increase in the SBP compared to the conventional method while performing the phase recovery correctly.

Discussion and conclusion

We have demonstrated a QPI technique for high-SBP slightly off-axis DHM based on Fourier ptychographic reconstruction. Exploiting the reconstruction principle of FPM, the optimal iterative solution algorithm reconstructs an exact complex amplitude of the object wavefront without imposing any constraint on the reference-object ratio. It effectively utilizes the spatial bandwidth to provide a 4-fold increase in the SBP compared to the linear solution and achieve the ultimate maximum bandwidth in all off-axis holography since there is no requirement for spectral configuration. The nonlinear optimization algorithm is experimentally demonstrated to have high accuracy at an arbitrary reference-object ratio and can realize high-throughput artifact-free imaging with spectral aliasing.

The optimal iterative solution algorithm is fundamentally different from previous methods for zero-order suppression under the spectral overlap in slightly off-axis holography. The suppression principle of the nonlinear filtering and KK method involves constructing an intermediate function whose Taylor expansion is a power series of the object-reference ratio. Nonlinear filtering first proposes the idea of taking the logarithm of the intensity ratio of the hologram to the reference beam, which transforms the product into a sum, allowing for the subsequent separation of the interference terms from the zero-order term. The KK method brilliantly proves the analyticity of the intermediate function, i. e., a variant of the object-reference ratio, in the upper half-plane, thus guaranteeing the KK relationship between the real and imaginary parts of the intermediate function. However, these must be based on the condition that the object-reference ratio is less than 1. Otherwise, the higher-order terms will diverge in the frequency domain and severely overlap with other terms as the order increases. Similarly, the error between the estimator and the object zero-order in the Pavillon method contains a power series of the object-reference ratio, which also converges only under this condition.

In contrast, the proposed method uses the nonlinear optimization algorithm to derive the update equation by forward modeling the process of holographic imaging. As long as the spectrum of the +1-order and -1-order do not overlap (which is sufficiently fulfilled by all off-axis holographic systems), the optimal iterative solution algorithm can be applied. During the phase recovery process, the reconstructed hologram amplitude gradually approximates the recorded true value by iteration until the error converges to zero, i.e., the measured complex amplitude is exact. The nonlinear optimization iteration is unconstrained for object-reference ratio and spectral configuration, which greatly relaxes the requirements on the system parameters and exhibits enhanced robustness to system errors.

The proposed method can be combined with other techniques for further improvement. Referring to the adaptive step-size strategy introduced by Zuo (Zuo et al., 2016) et al., the stability and robustness of the phase reconstruction towards noise can be enhanced by altering the fixed step-size to an adaptive step-size. OU (Ou et al., 2014) et al. propose the embedded pupil function recovery (EPRY), which is expected to be combined with the proposed method to reconstruct the aberration of the objective lens while recovering the quantitative phase of the object. In addition, the integration of nonlinear optimization with synthetic aperture digital holography can also be considered to improve the spatial resolution (Gao and Yuan, 2022). We envision that the proposed method will benefit off-axis holographic imaging with an enhanced SBP and contribute to the combination of nonlinear optimal phase reconstruction algorithm with more QPI techniques for application in large-scale studies of cells and other fields.

Data availability statement

The original contributions presented in the study are included in the article further inquiries can be directed to the corresponding authors.

Author contributions

CZ conceived the idea. QS did the experiments. CZ, JS, and QC supervised the project. All the authors contributed to discussion on the results for this manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (61905115, 62105151, 62175109, U21B2033), Leading Technology of Jiangsu Basic Research Plan (BK20192003), Youth Foundation of Jiangsu Province (BK20190445, BK20210338), Fundamental Research Funds for the Central Universities (30920032101), and Open Research Fund of Jiangsu Key Laboratory of Spectral Imaging and Intelligent Sense (JSGP202105, JSGP202201).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix A: Gradient calculation

Eq 3 can be transformed as follows (coordinates are omitted for convenience):

$\epsilon \left(O\right)=\sum {‖U^u-U^e‖}^2=\sum \left({\left|U^e\right|}^2-2\sqrt{I}\left|U^e\right|+I\right).(6)$

Then calculate the derivative of ɛ with respect to O, and it can then be expressed as

${\nabla }_O\epsilon \left(O\right)=\sum {\left[\frac{\partial \epsilon \left(O\right)}{\partial O}\right]}^{\ast }.(7)$

The equation in parentheses in Eq. 7 can be decomposed into three parts combined with Eq. 6 as follows:

$\frac{\partial {\left|U^e\right|}^2}{\partial O}=\frac{\partial {\left|OP+R\right|}^2}{\partial O}=O^{\ast }{\left|P\right|}^2+P{R}^{\ast }(8)$

$\frac{\partial \left(2\sqrt{I}\left|U^e\right|\right)}{\partial O}=2\sqrt{I}\frac{\partial \left|OP+R\right|}{\partial O}=\sqrt{I}P\frac{O^{\ast }{P}^{\ast }+R^{\ast }}{\left|OP+R\right|}(9)$

$\frac{\partial I}{\partial O}=0(10)$

By plugging these three terms into Eq. 6, the gradient of ɛ with respect to O becomes

${\nabla }_O\epsilon \left(O\right)=\sum \left(O{\left|P\right|}^2+P^{\ast }R-\sqrt{I}{P}^{\ast }\frac{OP+R}{\left|OP+R\right|}\right)=\sum \left[P^{\ast }\left(U^e-U^u\right)\right].(11)$

References

Baek, Y., Lee, K., Shin, S., and Park, Y. (2019). Kramers–kronig holographic imaging for high-space-bandwidth product. Optica 6, 45. doi:10.1364/optica.6.000045

CrossRef Full Text | Google Scholar

Bauschke, H. H., Combettes, P. L., and Luke, D. R. (2002). Phase retrieval, error reduction algorithm, and fienup variants: a view from convex optimization. J. Opt. Soc. Am. A 19, 1334–13345. doi:10.1364/josaa.19.001334

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, N., Yeom, J., Jung, J.-H., Park, J.-H., and Lee, B. (2011). Resolution comparison between integral-imaging-based hologram synthesis methods using rectangular and hexagonal lens arrays. Opt. Express 19, 26917–26927. doi:10.1364/oe.19.026917

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuche, E., Bevilacqua, F., and Depeursinge, C. (1999). Digital holography for quantitative phase-contrast imaging. Opt. Lett. 24, 291. doi:10.1364/ol.24.000291

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, Y., Li, J., Lu, L., Sun, J., Hu, Y., Zhang, J., et al. (2021). Smart computational light microscopes (sclms) of smart computational imaging laboratory (scilab). PhotoniX 2, 19. doi:10.1186/s43074-021-00040-2

CrossRef Full Text | Google Scholar

Fan, Y., Sun, J., Chen, Q., Pan, X., Tian, L., Zuo, C., et al. (2019). Optimal illumination scheme for isotropic quantitative differential phase contrast microscopy. Photonics Res. 7, 890–904. doi:10.1364/prj.7.000890

CrossRef Full Text | Google Scholar

Fienup, J. R. (1982). Phase retrieval algorithms: a comparison. Appl. Opt. 21, 2758. doi:10.1364/ao.21.002758

PubMed Abstract | CrossRef Full Text | Google Scholar

Fienup, J. R. (1978). Reconstruction of an object from the modulus of its fourier transform. Opt. Lett. 3, 27–29. doi:10.1364/ol.3.000027

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, P., Pedrini, G., and Osten, W. (2013). Structured illumination for resolution enhancement and autofocusing in digital holographic microscopy. Opt. Lett. 38, 1328–1330. doi:10.1364/ol.38.001328

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, P., and Yuan, C. (2022). Resolution enhancement of digital holographic microscopy via synthetic aperture: a review. gxjzz. 3, 105. doi:10.37188/lam.2022.006

CrossRef Full Text | Google Scholar

Gerchberg, R. W. (1972). A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246.

Google Scholar

Gerchberg, R. W. (1971). Phase determination for image and diffraction plane pictures in the electron microscope. Opt. Stuttg. 34, 275.

Google Scholar

Gonsalves, R. (1976). Phase retrieval from modulus data. J. Opt. Soc. Am. 66, 961. doi:10.1364/josa.66.000961

CrossRef Full Text | Google Scholar

Hariharan, P., Oreb, B. F., and Eiju, T. (1987). Digital phase-shifting interferometry: a simple error-compensating phase calculation algorithm. Appl. Opt. 26, 2504. doi:10.1364/ao.26.002504

PubMed Abstract | CrossRef Full Text | Google Scholar

Latychevskaia, T. (2019). Iterative phase retrieval for digital holography: tutorial. J. Opt. Soc. Am. A 36, D31–D40. doi:10.1364/josaa.36.000d31

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K., Kim, K., Jung, J., Heo, J., Cho, S., Lee, S., et al. (2013). Quantitative phase imaging techniques for the study of cell pathophysiology: from principles to applications. Sensors 13, 4170–4191. doi:10.3390/s130404170

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann, C. J., Yu, L., Lo, C.-M., and Kim, M. K. (2005). High-resolution quantitative phase-contrast microscopy by digital holography. Opt. Express 13, 8693. doi:10.1364/opex.13.008693

PubMed Abstract | CrossRef Full Text | Google Scholar

Ou, X., Zheng, G., and Yang, C. (2014). Embedded pupil function recovery for fourier ptychographic microscopy. Opt. Express 22, 4960–4972. doi:10.1364/oe.22.004960

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozcan, A., and Demirci, U. (2008). Ultra wide-field lens-free monitoring of cells on-chip. Lab. Chip 8, 98–106. doi:10.1039/b713695a

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavillon, N., Arfire, C., Bergoënd, I., and Depeursinge, C. (2010). Iterative method for zero-order suppression in off-axis digital holography. Opt. Express 18, 15318–15331. doi:10.1364/oe.18.015318

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavillon, N., Seelamantula, C. S., Kühn, J., Unser, M., and Depeursinge, C. (2009). Suppression of the zero-order term in off-axis digital holography through nonlinear filtering. Appl. Opt. 48, H186–H195. doi:10.1364/ao.48.00h186

PubMed Abstract | CrossRef Full Text | Google Scholar

Seo, S., Su, T.-W., Tseng, D. K., Erlinger, A., and Ozcan, A. (2009). Lensfree holographic imaging for on-chip cytometry and diagnostics. Lab. Chip 9, 777–787. doi:10.1039/b813943a

PubMed Abstract | CrossRef Full Text | Google Scholar

Shechtman, Y., Eldar, Y. C., Cohen, O., Chapman, H. N., Miao, J., Segev, M., et al. (2015). Phase retrieval with application to optical imaging: a contemporary overview. IEEE Signal Process. Mag. 32, 87–109. doi:10.1109/msp.2014.2352673

CrossRef Full Text | Google Scholar

Sun, J., Zuo, C., Zhang, L., and Chen, Q. (2017). Resolution-enhanced fourier ptychographic microscopy based on high-numerical-aperture illuminations. Sci. Rep. 7, 1187. doi:10.1038/s41598-017-01346-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Takeda, M., Ina, H., and Kobayashi, S. (1982). Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 72, 156. doi:10.1364/josa.72.000156

CrossRef Full Text | Google Scholar

Trusiak, M., Cywińska, M., Mico, V., Picazo-Bueno, J. Á., Zuo, C., Zdańkowski, P., et al. (2020). Variational hilbert quantitative phase imaging. Sci. Rep. 10, 13955. doi:10.1038/s41598-020-69717-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Trusiak, M. (2021). Fringe analysis: single-shot or two-frames? quantitative phase imaging answers. Opt. Express 29, 18192–18211. doi:10.1364/oe.423336

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, G., Horstmeyer, R., and Yang, C. (2013). Wide-field, high-resolution fourier ptychographic microscopy. Nat. Photonics 7, 739–745. doi:10.1038/nphoton.2013.187

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, C., Li, J., Sun, J., Fan, Y., Zhang, J., Lu, L., et al. (2020). Transport of intensity equation: a tutorial. Opt. Lasers Eng. 135, 106187. doi:10.1016/j.optlaseng.2020.106187

CrossRef Full Text | Google Scholar

Zuo, C., Sun, J., and Chen, Q. (2016). Adaptive step-size strategy for noise-robust fourier ptychographic microscopy. Opt. Express 24, 20724–20744. doi:10.1364/oe.24.020724

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, C., Sun, J., Li, J., Zhang, J., Asundi, A., Chen, Q., et al. (2017). High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci. Rep. 7, 7654. doi:10.1038/s41598-017-06837-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, C., Sun, J., Zhang, J., Hu, Y., and Chen, Q. (2015). Lensless phase microscopy and diffraction tomography with multi-angle and multi-wavelength illuminations using a led matrix. Opt. Express 23, 14314–14328. doi:10.1364/oe.23.014314

PubMed Abstract | CrossRef Full Text | Google Scholar