Coherent Noise Suppression of Single-Shot Digital Holographic Phase Via an Untrained Self-Supervised Network

In digital holography, the coherent noise affects the measurement accuracy and reliability greatly due to the high spatial and temporal coherence of the laser. Especially, compared with the speckle noise of intensity in digital holography, the coherent noise of phase contains more medium- and low-frequency characteristics, which hinders the effectiveness of noise suppression algorithms. Here, we propose a single-shot untrained self-supervised network (SUSNet) for the coherent noise suppression of phase, requiring only one noisy phase map to complete the optimization and learning. The SUSNet can smoothen and suppress the background fluctuations, parasitic fringes, and diffraction loops in a noisy phase and shows good generalization performance for samples with different shapes, sizes, and phase ranges. Compared with the traditional algorithms and the ground truth-supervised neural network (DnCNN), the SUSNet has the best noise suppression performance and background smoothing effect. As a result, the SUSNet can suppress the fluctuation range to ∼20% of the original range.

Introduction

Coherent noise is a vexing problem and has attracted many researchers in solving it. However, there is still no perfect solution for the coherent noise problem nowadays due to the high spatial and temporal coherence of the laser. In digital holography, coherent noise will lead to haphazardly distributed granular noise in the reproduced intensity, named as speckle noise, and the background fluctuations, parasitic fringes, and diffraction loops in the reconstructed phase, which we simply refer to as the coherent noise of phase. If the random fluctuation in intensity or phase is generated due to the object itself, it does not change over time. At this point, the fluctuation actually contains detailed object information. However, if the fluctuation is generated due to other factors within the system, it needs to be suppressed as much as possible to reduce the effect on observation and measurement. For speckle noise suppression, there are some methods, such as the averaging ideas with multiwavelength (Nomura et al., 2008), multi-polarization (Xiao et al., 2011), multi-angle illumination (Kang et al., 2007; Feng et al., 2009), slight displacements (Pan et al., 2011), and numerical multi-look (Bianco et al., 2013), and the decoherence idea with the replaced laser source (Kemper et al., 2008; Remmersmann et al., 2009; Langehanenberg et al., 2010). Nevertheless, the averaging method always requires capturing a large number of holograms for suppression, while the decoherence method requires replacing the light emitting diode (LED) as the laser source which will limit the interference range of measurement, although those methods may be useful in suppressing the coherent noise of phase relatively.

In addition to optical methods, digital image processing approaches are also helpful in solving the coherent noise problem. The image processing methods mainly adopt the filtering idea, according to the theory of information optics, considering the differences between the distribution and characteristics of object and noise in the signal domain. At present, they are divided into the space-domain filtering-based (Darakis and Soraghan, 2006; Shortt et al., 2006; Uzan et al., 2013), transform-domain filtering-based (Maycock et al., 2007; Sharma et al., 2008; Choi et al., 2010), and deep learning–based methods (Zhang et al., 2017; Jeon et al., 2018; Wang et al., 2019; Montresor et al., 2020; Yin et al., 2020). Especially, the deep learning–based methods have achieved excellent performance over the traditional algorithms as soon as they appeared (Di et al., 2021). For example, Wang et al. discussed the suppression and resistance of deep neural networks to additional Gaussian and salt-and-pepper noises in phase unwrapping (Wang et al., 2019); Montresor et al. applied a residual network (DnCNN) (Zhang et al., 2017) to compare the generalization capability among three models, which were trained by the natural images with Gaussian noise, the noise-free fringe patterns with added Gaussian noise, and the phase data with realistic speckle noise, (Montresor et al., 2020); Yin et al. used the Noise2Noise strategy (Lehtinen et al., 2018) to reduce the speckle noises in computer-generated holography and digital holography without noise-free data as the ground truth (Yin et al., 2020).

Nevertheless, the low-level speckle noise has some statistical similarity with the regular additional noises, such as Gaussian noise, uniform noise, and salt-and-pepper noise, which have many high-frequency and low-correlation characteristics. Compared with these noises, the additional coherent phase noise may contain more medium- and low-frequency characteristics and some non-stationary features, such as background fluctuations, parasitic fringes, and diffraction loops. Facing these problems, it is difficult to play a good generalization with the network model only trained under high-frequency noise. Moreover, most of the existing deep learning methods are ground truth–supervised training with a large amount of data, but it is difficult and time-consuming to get the noise-free data or other noisy data additionally in practice.

Is it possible to train the network with one single image? We have tried to train a network to predict the diffraction distance from a pair of images for autofocusing (Tang et al., 2022), inspired by the deep image prior (Ulyanov et al., 2017). Facing the noise suppression requirements of the single-shot phase of digital holography, here, we propose a single-shot untrained self-supervised network (SUSNet). The SUSNet only needs a noisy phase for learning and optimization and can generalize to various samples with different noise disturbances. We describe the physical generation of coherent noise and our denoising model in Section 2. Subsequently, we measure some objects through a common-path off-axis digital holographic microscope system and compare and analyze the denoising results of various samples, including different shapes, sizes, and phase ranges, by traditional algorithms, DnCNN and SUSNet in Section 3.

Principle and Method

Physical Generation of Coherent Noise

In the recording stage of a digital hologram, the object wavefront O(x, y) and the reference wavefront R(x, y) interfere on the target plane of the camera, and the intensity distribution I(x, y) of the obtained hologram can be expressed as

$I\left(x,y\right)={\left|\mathit{O}\left(x,y\right)\right|}^2+{\left|\mathit{R}\left(x,y\right)\right|}^2+\mathit{O}\left(x,y\right){\mathit{R}}^{\ast }\left(x,y\right)+{\mathit{O}}^{\ast }\left(x,y\right)\mathit{R}\left(x,y\right),(1)$

where (x, y) is the coordinates of the recording plane and the symbol ^* describes the complex conjugation. In the reconstruction stage, the reconstructed object wavefront U_d (ξ, η) can be expressed as follows:

$U_d\left(\xi ,\eta \right)=\frac{\exp \left(\mathrm{j}kd\right)}{\mathrm{j}\lambda d}\exp \left[\mathrm{j}\frac{k}{2d}\left({\xi }^2+{\eta }^2\right)\right]\cdot \mathrm{FT}\left\{R\left(x,y\right)I\left(x,y\right)\exp \left[\mathrm{j}\frac{k}{2d}\left(x^2+y^2\right)\right]\right\},(2)$

where (ξ, η) is the coordinates of the object plane, d is the distance from the recording plane to the object plane, k = 2π/λ is the wave number, λ is the wavelength, and FT $\{\cdot \}$ is the Fourier transform operation. Ideally, the reconstructed wavefront U_d (ξ, η) is equivalent to the initial object wavefront U_o(ξ, η). However, a series of sub-waves occur when the laser beam passes through (or reflects from) some uneven or non-smooth objects and will be scattered by dust particles in the air. These sub-waves have subtle optical path differences, and coherent superposition occurs between sub-waves due to the high coherence of the laser, which is eventually recorded in the hologram. The additional components result in random fluctuations in reconstructed intensity and phase, called the coherent noise. In fact, the reconstructed wavefront U_d(ξ, η) is the product of the ideal object wavefront U_o(ξ, η) and the random complex amplitude U_n(ξ, η) of noise

$U_d\left(\xi ,\eta \right)=U_o\left(\xi ,\eta \right)\cdot U_n\left(\xi ,\eta \right)=A_o\exp \left(\mathrm{j}{\phi }_o\right)\cdot A_n\exp \left(\mathrm{j}{\phi }_n\right)=A_o{A}_n\exp \left[\mathrm{j}\left({\phi }_o+{\phi }_n\right)\right],(3)$

where A_o and φ_o are the amplitude and phase of the object wavefront, while A_n and φ_n are those of the noisy complex amplitude, respectively. The phase distribution of the reconstructed wavefront is obtained as

$\phi \left(\xi ,\eta \right)=\arctan \left\{\frac{\mathrm{Im}\left[U_d\left(\xi ,\eta \right)\right]}{\mathrm{Re}\left[U_d\left(\xi ,\eta \right)\right]}\right\}\left[\mathrm{mod}\left(2\text{π}\right)\right]={\phi }_o\left(\xi ,\eta \right)+{\phi }_n\left(\xi ,\eta \right),(4)$

where Im ($\cdot$) and Re $(\cdot )$ take the real and imaginary parts of the complex amplitude, respectively, and mod $(\cdot )$ is the remainder function. It is obvious that the measured noisy phase φ(ξ, η) obtained by digital holography is the sum of the true object phase φ_o (ξ, η) and coherent noise term φ_n (ξ, η). The presence of a coherent noise term will introduce additional phenomena, such as random fluctuations in the phase background, parasitic interference fringes, and dust diffraction loops, and decrease the signal-to-noise ratio of the whole phase map. In particular, the confidence of measurement is reduced for those objects with a small spatial scale or phase changes due to the noise drowning.

Single-Shot Untrained Self-Supervised Network

The traditional deep neural network is almost trained under the supervision of ground truth, based on a large amount of standard data. The learning process of the network can be formulized as

${\mathrm{\theta }}^{\ast }=\arg \underset{\theta }{\min }E\left[f_{\theta }\left(\phi \right);\overline{\phi }\right],{\phi }_o^{\prime }=f_{{\mathrm{\theta }}^{\ast }}\left(\phi \right),(5)$

where φ and $\overline{\theta }$ are the input and ground truth of the network, respectively; θ is the learnable parameter for optimization; θ^* is the suitable parameter after learning; $E[\cdot ]$ is the denoising task term; and φ^′_o is the final noise-free phase by the network $f_{{\mathrm{\theta }}^{\mathrm{*}}}(\cdot )$. In general, the ground truth can be the true object phase φ_o or another measured noisy phase φ^′ which consists of the same true phase φ_o and another noise term φ^′_n, named as the Noise2Noise strategy (Lehtinen et al., 2018; Yin et al., 2020). However, either the true phase or another noisy phase is extremely difficult to obtain consistently with the large demand of datasets. Moreover, the diversity of the datasets limits the generalization capability of the trained network model. Although the neural network can greatly outperform the traditional algorithms on specific problems, its application is still resistant in practice.

Here, we focus on the problems of dataset requirement, ground truth, and generalization capability and propose the single-shot untrained self-supervised network (SUSNet). The learning process is changed as

${\mathrm{\theta }}^{\mathrm{*}}=\arg \underset{\theta }{\min }E\left[f_{\theta }\left(z\right);\phi \right],{\phi }_o^{\prime }=f_{{\mathrm{\theta }}^{\mathrm{*}}}\left(z\right),(6)$

where the noisy phase φ is set as the ground truth to supervise the optimization and z is a constant matrix with the same size as the ground truth, which is set as a random uniform noise during each training. The implementation procedure for learning and optimization is shown in Figure 1A, and the details of the U-shaped SUSNet structure are clearly shown in Figure 1B. The constant noise z and the noisy phase φ are regarded as the input and ground truth, respectively. During each step of learning, low-level random Gaussian noise is added in the input and ground truth to make the optimization more robust. It is regarded as a self-supervised way because no additional data acquisition is required except one noisy phase. Moreover, unlike the traditional network which needs to be trained first for a long time before implementing, SUSNet can directly optimize and achieve the denoising task using only one single-shot noisy phase with a little time. Moreover, it can generalize to arbitrary objects with targeting and adaptation for better results.

FIGURE 1

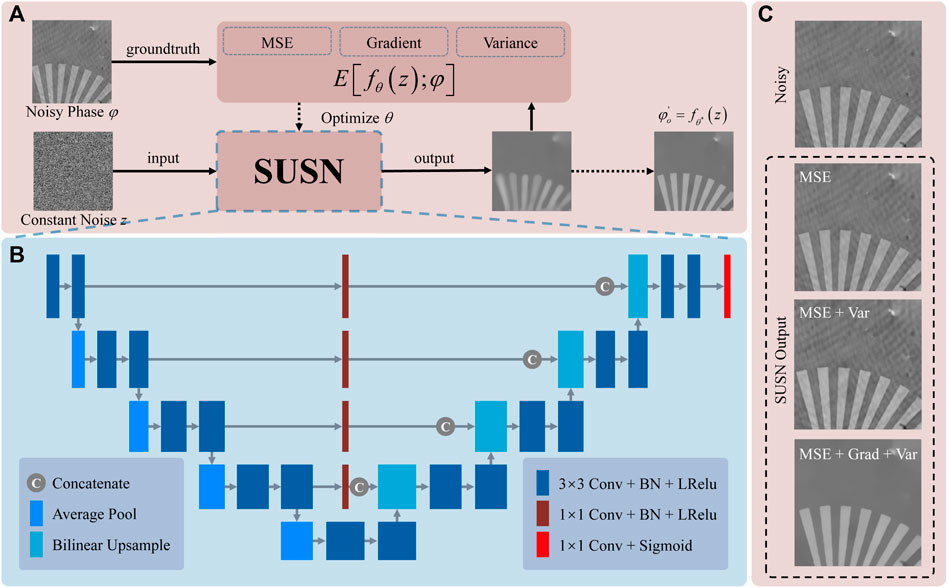
FIGURE 1. Schematic diagram of the single-shot untrained self-supervised network (SUSNet). (A) Implementation procedure for learning and optimization. (B) Details for the U-shaped network structure. (C) Different outputs by the SUSNet with the same learning parameters except loss function.

The denoising task term $E[\cdot ]$ can be quantitatively represented by the sum of loss functions as

$E\left[f_{\theta }\left(z\right);\phi \right]=\mathrm{MSE}\left[f_{\theta }\left(z\right),\phi \right]+{\beta }_1\cdot \mathrm{Grad}\left[f_{\theta }\left(z\right)\right]+{\beta }_2\cdot \mathrm{Var}\left[f_{\theta }\left(z\right)\right],(7)$

$\mathrm{MSE}\left[f_{\theta }\left(z\right),\phi \right]=\frac{{\Vert f_{\theta }\left(z\right)-\phi \Vert }_2^2}{M\cdot N},(8)$

$\mathrm{Grad}\left[f_{\theta }\left(z\right)\right]=\frac{{\displaystyle {\sum }_1^M{\displaystyle {\sum }_1^N\sqrt{G_{\xi }^2+G_{\eta }^2}}}}{M\cdot N}\text{,}\{\begin{array}{c}{G}_{\xi }={\mathrm{g}}_{\mathit{\xi }}\ast f_{\theta }\left(z\right)\\ G_{\eta }={\mathrm{g}}_{\mathit{\eta }}\ast f_{\theta }\left(z\right)\end{array},(9)$

$\mathrm{Var}\left[f_{\theta }\left(z\right)\right]=\frac{{\displaystyle {\sum }_1^M{\displaystyle {\sum }_1^N{\left[f_{\theta }\left(z\right)-\mu \right]}^2}}}{M\cdot N},\mu =\frac{{\displaystyle {\sum }_1^M{\displaystyle {\sum }_1^N{f}_{\theta }\left(z\right)}}}{M\cdot N}.(10)$

Where MSE $(\cdot )$, Grad $(\cdot )$, and Var $(\cdot )$ are the mean squared error function, tenengrad gradient function, and variance function, respectively; μ is the mean value; M and N are the numbers of pixels; and β₁ and β₂ are the hyperparameters to balance the influence of different loss functions. In Eq. 9, G_ξ and G_η are the gradients in the horizontal and vertical directions, respectively, which are obtained by the convolution * with Sobel operators g_ξ and g_η. The effect of SUSNet with different loss functions is shown in Figure 1C. It is clear that SUSNet with MSE or MSE + Var just generates the noisy phase without noise suppression, while SUSNet with MSE + Grad + Var suppresses and smoothens the background fluctuations, parasitic fringes, and other coherent noise phenomena effectively. In brief, the MSE term allows SUSNet to learn quickly from the noise z to the object phase information, and the edge gradient of the output is computed and minimized to abandon overfitting the coherent noise by the Grad term. The Var term plays a role in balancing the smoothing effect caused by the Grad term in the late training period. The initial learning rate is 0.002 and subsequently reduces by one-tenth every 100 steps with the Adam optimizer. β₁ = 0.02 and β₂ = -0.15 are used with possible fine-tuning. The optimization process takes ∼35 s for 400 steps with the Intel Core i7-10700K CPU and NVIDIA GeForce RTX 1080Ti GPU.

Experimental Setup

Here, we implement the common-path off-axis digital holographic microscope system for the hologram capture and noisy phase acquisition, as shown in Figure 2B. A green light beam from a diode-pumped solid-state laser (Cobolt Samba ™ 50 532 nm, Linewidth <1 MHz) is collimated by a lens and is incident to the sample. Then, the laser is magnified and collimated again with the microscope objective (Mitutoyo M Plan Apo ×50) and the tube lens, and a non-polarized beam splitter (NPBS) is used to form the common-path structure. The wave is refracted and reflected by the NPBS placed at an angle of 45° and finally divided into two parts. The camera (Basler acA 2040-90 μm) is placed on a suitable plane to capture the in-focus image of the sample. This common-path setup benefits the object-free region of the other half spot as the reference wavefront, so the propagation path of the object and reference wavefronts is the same. The common-path design can improve the stability of the system simply and greatly but requires the sample to be sparse and sacrifices half of the field of view (FOV) (Zhang et al., 2021). After hologram acquisition, the double-exposure method is implemented to compensate the system aberration, and the measured noisy phases of different samples are obtained by numerical reconstruction according to Eqs 1–4.

FIGURE 2

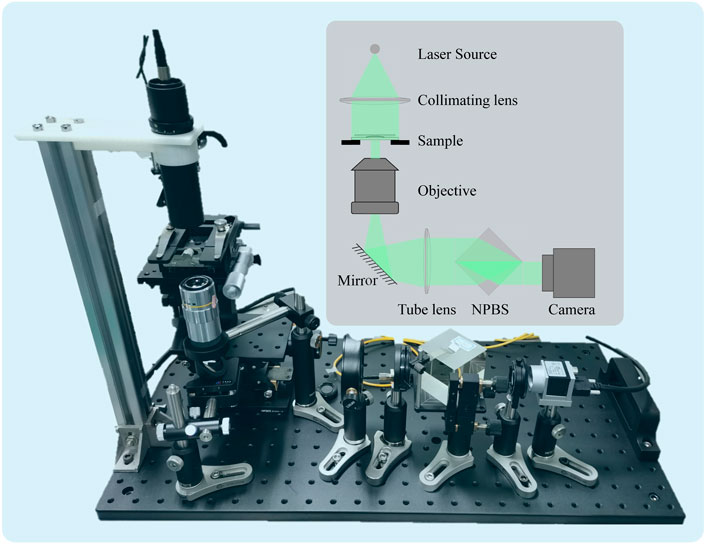
FIGURE 2. Common-path off-axis digital holographic microscope system for hologram capture and noisy phase acquisition. NPBS: non-polarized beam splitter.

Experimental Results

Noise Suppression With Various Samples

Here, we measure four samples, including microlens, cell, cake structure, and star structure, to obtain the noisy phases of various samples. The microlens array has a maximum height of 5 μm and a refractive index of 1.458, while the cake and star structures are both on the benchmark quantitative phase target with the refractive index of 1.52. The HT22 cells after overnight culturing have a uniform refractive index of 1.375, while the cell culture has a refractive index of 1.3377 (Lue et al., 2012). To observe the actual denoising effect of SUSNet, we take several traditional noise suppression algorithms for comparison, including BM3D (Dabov et al., 2007), non-local means filtering (NLM) (Uzan et al., 2013), median filtering (MF) (Darakis and Soraghan, 2006), and DnCNN (Zhang et al., 2017).

From Figure 3A, it is obvious that all noisy phases have background fluctuations, parasitic fringes, and even some damage defects. Intuitively, the BM3D, MF, and DnCNN can relatively suppress the fluctuations and fringes and improve the overall signal-to-noise ratio, but their actual effect is limited with insufficient smoothing and fringe residue. In comparison, the NLM is the most effective one among these noise suppression algorithms, but there are still some gaps compared with the SUSNet. We set several truncated lines on these phases and converted them to the height distribution along the lines in Figure 3B. From the truncated lines of microlens, the coherent noise is not drastic because the phase change of microlens is much larger than the fluctuation caused by the noise. However, these fluctuations on the truncated lines of cell, cake, and star structures are more pronounced and intense. In contrast, the red curves of the SUSNet ensure a flatter curve than other algorithms with the same fundamental shape. We select the truncated lines of the cell to calculate the ranges $\left(R=\mathrm{Max}(\cdot )-\mathrm{Min}(\cdot )\right)$ as the reference values of background fluctuation. The noisy phase of the cell has 0.980 rad fluctuation, and the denoising results of BM3D, NLM, MF, and DnCNN have 0.292, 0.342, 0.588, and 0.265 rad fluctuations, respectively, while the noise-free phase of the SUSNet has 0.235 rad fluctuation, which is only 23.9% of the original range.

FIGURE 3

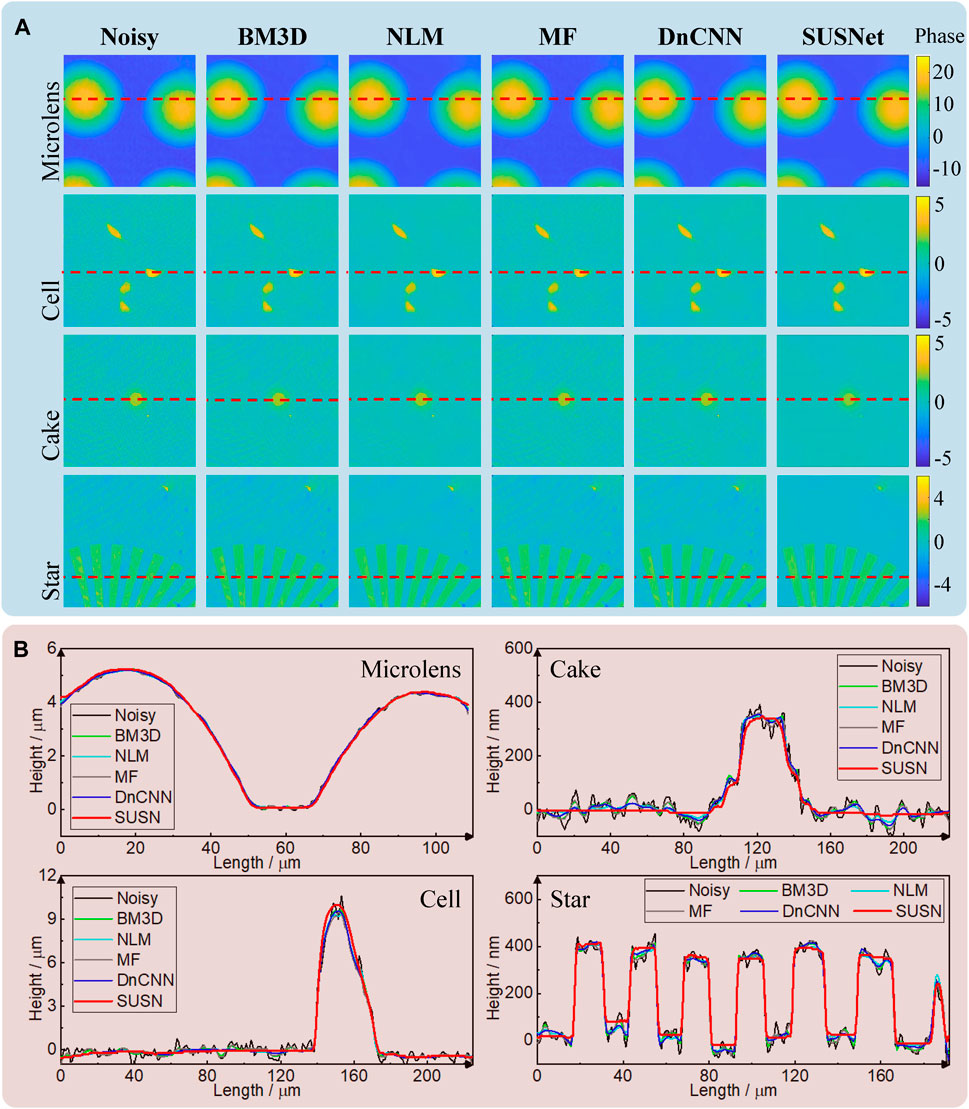
FIGURE 3. Comparison of different noise suppression algorithms on experimental holographic phases with 532-nm green laser illumination. (A) Noisy phase maps of microlens, cell, cake, and star samples and their denoise results with BM3D, NLM, MF, DnCNN, and SUSNet. (B) Comparison of the height distribution along the truncated lines in (A).

It is clear that SUSNet can effectively generalize and suppress noise for various samples of different shapes, sizes, and phase variations, which has reached the generalization capability of traditional algorithms, such as BM3D, MF, and NLM, and the neural network model, such as DnCNN, trained by a large amount of data. Another advantage of SUSNet is that it does not require a prior evaluation of the noise level, while the traditional algorithms need this prior as one hyperparameter for adjustment. For example, the results in Figure 3A are calculated using the standard deviation of 10 as a prior. The DnCNN is more necessary to load the corresponding model trained by the dataset with a similar noise level because the traditional neural networks limited by the dataset have difficulty generalizing to other noise levels and types beyond the training set. In contrast, the SUSNet prioritizes the extraction of object information while ignoring the noises during learning, even if the noises are not all high frequencies. As for the calculation cost, the SUSNet needs ∼35 s for 400 steps of optimization, while BM3D, NLM, MF, and DnCNN spend 0.3, 30, 0.02, 8.35 s in calculating by CPU, respectively.

Noise Suppression at Another Level of Noise

Here, we change a red diode laser with a wavelength of 640 nm (Changchun New Industries, MRL-III-640-100 mW, Linewidth <4.4 GHz) as the source of the common-path off-axis digital holographic microscope system and re-measure the previous samples as shown in Section 3.1. The actual coherence length of the green laser is thousands of times longer than that of the red laser in the experiment, so the noisy phase obtained under the red laser will have different noise levels and distributions. The noisy phases and their denoising results of all algorithms, including SUSNet, are shown in Figure 4A. Compared with those under the green laser, the noises under the red laser have less parasitic fringes and damage defects, and the background fluctuations have lower amplitudes and higher frequencies. Intuitively, the performance of the SUSNet is still comparable to, or even better than that of these traditional algorithms. From Figure 4B, the effect of background fluctuations is evident in truncated lines, even affecting the fundamental shape. However, the red curves of the SUSNet are the flattest and smoothest compared with other color curves, especially in the blue truncated lines of the cell. We also calculate the range of curves in the blue truncated lines of the cell as the reference values of background fluctuations. The noisy phase has 0.878 rad fluctuation, and the denoising results of BM3D, NLM, MF, and DnCNN have 0.228, 0.300, 0.376, and 0.242 rad fluctuations, respectively, while the noise-free phase of the SUSNet has 0.125 rad fluctuation, which is only 14.2% of the original range. It is obvious that the SUSNet has a very powerful smoothing ability for fluctuations by ensuring accurate object information. However, SUSNet still has some shortcomings to be researched and overcome. It may not apply to the detailed structures (e.g., scratch and damage) as objects, and its smooth effect will bring some impact for some small-sized objects. In general, in the case of a single-shot noisy phase, it is surprising enough that an untrained network can learn a noise-free phase directly from a noisy image with the self-supervised method, not to mention that its noise suppression performance is relatively excellent.

FIGURE 4

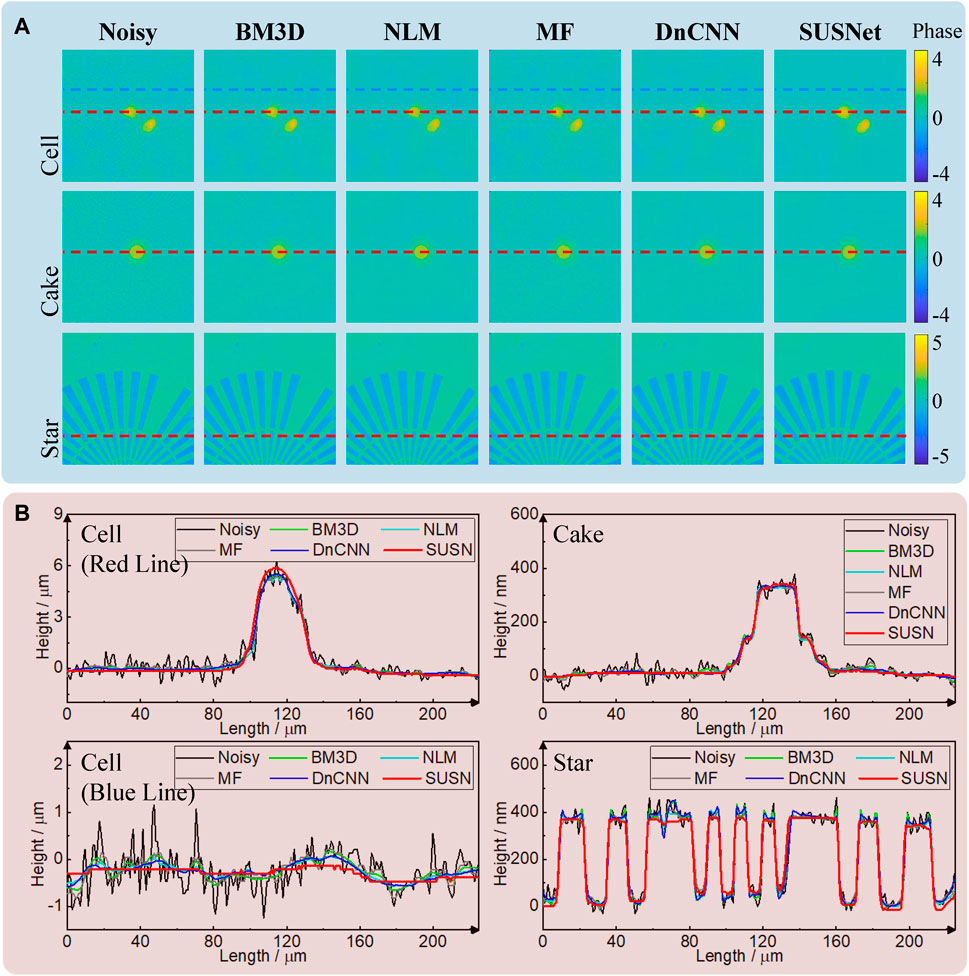
FIGURE 4. Comparison of different noise suppression algorithms on experimental holographic phases with 640-nm red laser illumination. (A) Noisy phase maps of cell, cake, and star samples, and their denoise results with BM3D, NLM, MF, DnCNN, and SUSNet. (B) Comparison of height distribution along the truncated lines in (A).

Conclusion

In summary, we propose an untrained self-supervised network SUSNet for the coherent noise suppression of the phase map in digital holography. The proposed SUSNet can smooth and suppress background fluctuations, parasitic fringes, and diffraction loops and has good generalization performance for the samples with different shapes, sizes, and phase ranges. Compared with the conventional algorithms, such as BM3D, NLM, and MF, and the ground truth–supervised neural network DnCNN, the SUSNet has the best noise suppression performance and background smoothing effect. As a result, the SUSNet can reduce the fluctuation range to ∼20% of the original range. The most important point is that SUSNet requires only one noisy phase to complete the optimization and learning without the ground truth and a large amount of data, which is the main challenge of traditional neural networks in applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

JT wrote the draft of the manuscript. JT and JW contributed to data analysis. JT and JZhang performed the experiments. JD and JZhao conceived and supervised the project. All the authors edited the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant No. 61927810, Grant No. 62075183).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bianco, V., Paturzo, M., Memmolo, P., Finizio, A., Ferraro, P., and Javidi, B. (2013). Random Resampling Masks: a Non-bayesian One-Shot Strategy for Noise Reduction in Digital Holography. Opt. Lett. 38, 619–621. doi:10.1364/OL.38.000619

PubMed Abstract | CrossRef Full Text | Google Scholar

Choi, H. J., Seo, Y. H., and Kim, D. W. (2010). Noise Reduction for Digital Holograms in a Discrete Cosine Transform (DCT) Domain. Opt. Appl. 40, 991–1005. doi:10.1117/12.850803

CrossRef Full Text | Google Scholar

Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K. (2007). Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 16, 2080–2095. doi:10.1109/tip.2007.901238

PubMed Abstract | CrossRef Full Text | Google Scholar

Darakis, E., and Soraghan, J. J. (2006). Compression of Interference Patterns with Application to Phase-Shifting Digital Holography. Appl. Opt. 45, 2437–2443. doi:10.1364/AO.45.002437

PubMed Abstract | CrossRef Full Text | Google Scholar

Di, J., Tang, J., Wu, J., Wang, K., Ren, Z., Zhang, M., et al. (2021). Research Progress in the Applications of Convolutional Neural Networks in Optional Information Processing. Laser optoelectron. 58, 1600001. doi:10.3788/LOP202158.1600001

CrossRef Full Text | Google Scholar

Feng, P., Wen, X., and Lu, R. (2009). Long-working-distance Synthetic Aperture Fresnel off-axis Digital Holography. Opt. Express 17, 5473–5480. doi:10.1364/OE.17.005473

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeon, W., Jeong, W., Son, K., and Yang, H. (2018). Speckle Noise Reduction for Digital Holographic Images Using Multi-Scale Convolutional Neural Networks. Opt. Lett. 43, 4240–4243. doi:10.1364/OL.43.004240

PubMed Abstract | CrossRef Full Text | Google Scholar

Kang, X., Kang, X., and Tay, C. J. (2007). Speckle Noise Reduction in Digital Holography by Multiple Holograms. Opt. Eng. 46, 115801. doi:10.1117/1.2802060

CrossRef Full Text | Google Scholar

Kemper, B., Stürwald, S., Remmersmann, C., Langehanenberg, P., and von Bally, G. (2008). Characterisation of Light Emitting Diodes (LEDs) for Application in Digital Holographic Microscopy for Inspection of Micro and Nanostructured Surfaces. Opt. Lasers Eng. 46, 499–507. doi:10.1016/j.optlaseng.2008.03.007

CrossRef Full Text | Google Scholar

Langehanenberg, P., Bally, G. v., and Kemper, B. (2010). Application of Partially Coherent Light in Live Cell Imaging with Digital Holographic Microscopy. J. Mod. Opt. 57, 709–717. doi:10.1080/09500341003605411

CrossRef Full Text | Google Scholar

Lehtinen, J., Munkberg, J., Hasselgren, J., Laine, S., Karras, T., Aittala, M., et al. (2018). “Noise2Noise: Learning Image Restoration without Clean Data,” in Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm Sweden, 10-15 July 2018, 4620–4631. doi:10.48550/arXiv.1803.041897

CrossRef Full Text | Google Scholar

Lue, N., Kang, J. W., Hillman, T. R., Dasari, R. R., and Yaqoob, Z. (2012). Single-shot Quantitative Dispersion Phase Microscopy. Appl. Phys. Lett. 101, 084101. doi:10.1063/1.4745785

CrossRef Full Text | Google Scholar

Maycock, J., Hennelly, B. M., McDonald, J. B., Frauel, Y., Castro, A., Javidi, B., et al. (2007). Reduction of Speckle in Digital Holography by Discrete Fourier Filtering. J. Opt. Soc. Am. A 24, 1617–1622. doi:10.1364/JOSAA.24.001617

PubMed Abstract | CrossRef Full Text | Google Scholar

Montresor, S., Tahon, M., Laurent, A., and Picart, P. (2020). Computational De-noising Based on Deep Learning for Phase Data in Digital Holographic Interferometry. Apl. Photonics 5, 030802. doi:10.1063/1.5140645

CrossRef Full Text | Google Scholar

Nomura, T., Okamura, M., Nitanai, E., and Numata, T. (2008). Image Quality Improvement of Digital Holography by Superposition of Reconstructed Images Obtained by Multiple Wavelengths. Appl. Opt. 47, D38–D43. doi:10.1364/AO.47.000D38

PubMed Abstract | CrossRef Full Text | Google Scholar

Pan, F., Xiao, W., Liu, S., Wang, F., Rong, L., and Li, R. (2011). Coherent Noise Reduction in Digital Holographic Phase Contrast Microscopy by Slightly Shifting Object. Opt. Express. 19, 3862–3869. doi:10.1364/OE.19.003862

PubMed Abstract | CrossRef Full Text | Google Scholar

Remmersmann, C., Stürwald, S., Kemper, B., Langehanenberg, P., and von Bally, G. (2009). Phase Noise Optimization in Temporal Phase-Shifting Digital Holography with Partial Coherence Light Sources and its Application in Quantitative Cell Imaging. Appl. Opt. 48, 1463–1472. doi:10.1364/AO.48.001463

PubMed Abstract | CrossRef Full Text | Google Scholar

Sharma, A., Sheoran, G., Jaffery, Z. A., and Moinuddin, (2008). Improvement of Signal-To-Noise Ratio in Digital Holography Using Wavelet Transform. Opt. Lasers Eng. 46, 42–47. doi:10.1016/j.optlaseng.2007.07.004

CrossRef Full Text | Google Scholar

Shortt, A. E., Naughton, T. J., and Javidi, B. (2006). A Companding Approach for Nonuniform Quantization of Digital Holograms of Three-Dimensional Objects. Opt. Express 14, 5129–5134. doi:10.1364/OE.14.005129

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, J., Wu, J., Zhang, J., Ren, Z., Di, J., and Zhao, J. (2022). Single-shot Diffraction Autofocusing: Distance Prediction via an Untrained Physics-Enhanced Network. IEEE Photonics J. 14, 1–6. doi:10.1109/JPHOT.2021.3138548

CrossRef Full Text | Google Scholar

Ulyanov, D., Vedaldi, A., and Lempitsky, V. (2017). “Improved Texture Networks: Maximizing Quality and Diversity in Feed-Forward Stylization and Texture Synthesis,” in Proceedings of the IEEE conference on computer vision and pattern recognition, San Francisco, CA, USA, 18-20 June 1996, 9446–9454. doi:10.1109/CVPR.2017.437

CrossRef Full Text | Google Scholar

Uzan, A., Rivenson, Y., and Stern, A. (2013). Speckle Denoising in Digital Holography by Nonlocal Means Filtering. Appl. Opt. 52, A195–A200. doi:10.1364/AO.52.00A195

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, K., Li, Y., Kemao, Q., Di, J., and Zhao, J. (2019). One-step Robust Deep Learning Phase Unwrapping. Opt. Express 27, 15100–15115. doi:10.1364/OE.27.015100

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, W., Zhang, J., Rong, L., Pan, F., Shuo Liu, S., Wang, F., et al. (2011). Improvement of Speckle Noise Suppression in Digital Holography by Rotating Linear Polarization State. Chin. Opt. Lett. 9, 60903–060901. doi:10.3788/COL201109.060901

CrossRef Full Text | Google Scholar

Yin, D., Gu, Z., Zhang, Y., Gu, F., Nie, S., Feng, S., et al. (2020). Speckle Noise Reduction in Coherent Imaging Based on Deep Learning without Clean Data. Opt. Lasers Eng. 133, 106151. doi:10.1016/j.optlaseng.2020.106151

CrossRef Full Text | Google Scholar

Zhang, J., Dai, S., Ma, C., XI, T., Di, J., and Zhao, J. (2021). A Review of Common-Path off-axis Digital Holography: Towards High Stable Optical Instrument Manufacturing. Light. Adv. Manu. 2, 333–349. doi:10.37188/lam.2021.023

CrossRef Full Text | Google Scholar

Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L. (2017). Beyond a Gaussian Denoiser: Residual Learning of Deep Cnn for Image Denoising. IEEE Trans. Image Process. 26, 3142–3155. doi:10.1109/TIP.2017.2662206

PubMed Abstract | CrossRef Full Text | Google Scholar