Transverse Traveling-Wave and Standing-Wave Ray-Wave Geometric Beams

Ray-wave geometric beam is an exotic kind of structured light with ray-wave duality and coupled diverse degrees of freedom (DoFs), which has attracted intense attention due to its potential applications in theories and applications. This work offers a new insight that the traditional ray-wave geometric beams can be seen as the transverse standing-wave (SW) beams, and can be decomposed into the superposition of transverse traveling-wave (TW) beams. We construct a generalized model for transverse TW and SW ray-wave geometric beams in the wave picture. In experiment, we exploit a digital hologram system with more flexible tunable DoFs to generate the transverse TW and SW beams, inspiring the exploration for the spatial wave structure of more complex structured light.

1 Introduction

Structured light with multiple controllable degrees of freedom (DoFs) has attracted wide attention in both fundamental theories and technological applications such as optical manipulation, communication, quantum-classical entanglement, and the analogy between classical optics and quantum mechanics (Shen et al., 2021a; Shen et al., 2021b; Forbes et al., 2021; Lourenço-Martins et al., 2021; Shen and Rosales-Guzmán, 2022). In the structured light family, the identified ray-wave geometric beam, as the classical analogy of quantum SU(2) coherent state (Bužek and Quang, 1989; Fox and Choi, 2000), has intriguing ray-wave duality (Babington, 2018), multiple tunable DoFs (Wan et al., 2021) and wide potential applications (Shen, 2021). Ray-wave geometric beam can be described by both ray and wave representation in optics (Shen et al., 2020a), and expressed as the superposition of eigenmodes analogous to the distribution of bosons in SU(2) coherent state in mathematic (Wodkiewicz and Eberly, 1985). There are many identified ray-wave geometric beams such as multi-path ray-wave geometric beams (Chen et al., 2019a), multi-axis ray-wave geometric beams (Tuan et al., 2018), and Lissajous-to-trochoidal geometric beams (Chen et al., 2006; Chen, 2011). Besides, multifarious novel ray-wave geometric beams have been proposed to enrich the structured light family, such as ray-wave vector vortex beams (Shen et al., 2020b) and astigmatic hybrid vector vortex beams (Wang et al., 2021b). In addition to constructing exotic ray-wave beams, the spatial wave structure is also an interesting topic. Recently, a unified mode evolution of azimuthally traveling-wave (TW) and standing-wave (SW) ray-wave beams has been proposed, which newly constructs ray-wave geometric beams with ray-splitting/fusion and provides a deep insight into the azimuthally spatial structure of ray-wave geometric beams (Wang et al., 2021a). However, the study on transverse wave structure of ray-wave geometric beams has not been reported.

Generally, SW refers to a superposition of 2 TWs, which could be understood via some simple mathematical formulas. For f_±(x) = g_c(x) ±ig_s(x), f_±(x) is the TW function, g_c(x) and g_s(x) are SW functions, which could also be expressed as g_c(x) = [f₊(x) + f₋(x)]/2, g_s(x) = [f₊(x) − f₋(x)]/(2i). In a word, SW and TW functions are mathematical analogies to g_c(x) and g_s(x), respectively. The concepts of TW and SW manifest themselves in structured light as well. For example, azimuthally TW vortex beams can be expressed as A(r) exp ± iℓθ, and azimuthally SW vortex beams can be expressed as A(r) cos ℓθ and A(r) sin ℓθ, where A(r) is the complex amplitude and ℓ is the topological charge (Wang et al., 2021a). For another example, Bessel beams also have radial TW component as $[J_n(k_{r}r)\pm \text{i}{N}_n(k_{r}r)]{\text{e}}^{\text{i}(\ell \theta +k_{z}z)}$, and radial SW component as $J_n(k_{r}r){\text{e}}^{\text{i}(\ell \theta +k_{z}z)}$ and $N_n(k_{r}r){\text{e}}^{\text{i}(\ell \theta +k_{z}z)}$, where $k_r^2+k_z^2=k^2$, k = 2π/λ the wave number, J_n(r) and N_n(r) are Bessel function and Neumann function as two independent solutions of Bessel function, respectively (Chávez-Cerda et al., 1996). Besides, the Laguerre-Gaussian (LG) beams, Hermite-Gaussian (HG) beams and Airy beams also have the corresponding radial (or transverse) TW and SW beams (Richards, 2002; Mendoza-Hernández et al., 2019; Ugalde-Ontiveros et al., 2021). Note that TW and SW beams have key applications such as the coherent perfect absorption of light (Vetlugin, 2021), classical analogy of quantum entanglement (Chen et al., 2021), interpretation of the self-healing origin in wave picture (Mendoza-Hernández et al., 2019; Ugalde-Ontiveros et al., 2021) and dispersive soliton solutions in optical fibers (Tang, 2021). Therefore, it is of great importance to study the SW and TW forms of ray-wave geometric beams for extending the Frontier of structured light. Besides, ray-wave geometric beams were generated in a degenerate laser resonator originally (Chen et al., 2004, 2006; Tuan et al., 2018), but there are some limits on the tunability (Wan et al., 2020) and a lack of a generalized model in the wave picture for more exotic beams (Chen et al., 2019b).

In this paper, we construct a theoretical framework for the transverse TW and SW ray-wave geometric beams, which provides a physical insight in the wave picture. Besides, we generate these beams via a digital hologram system in experiment, with more flexible tunability. We first analyze the transverse TW and SW Hermite-Laguerre-Gaussian (HLG) beams as the eigenmodes of ray-wave geometric beams (Section 2.1), and then propose a generalized model for the transverse TW and SW ray-wave geometric beams (Section 2.2). Furthermore, we experimentally generate these transverse TW and SW beams by the digital holography method with a liquid-crystal spatial light modulator (LC-SLM) (Section 3) (Ren et al., 2015; Wan et al., 2020; Javidi et al., 2021). Our work can be easily extended to investigate the spatial wave structure of more complex structured light, further enriching the structured light family.

2 Theoretical Framework

2.1 Transverse Wave Structure of Hermite-Laguerre-Gaussian Beams

The ray-wave geometric beams are the superposition of eigenmodes under the frequency-degenerate condition (Chen et al., 2004). As such, we analyze the transverse TW and SW forms of eigenmodes firstly. HLG beams are the typical eigenmodes of the paraxial wave equation (PWE), which describe the tunable spatial mode evolution between HG beams and LG beams. In mathematics, HLG beams could be expressed as the superposition of HG beams (Chen, 2011):

${\text{HLG}}_{n,m,l}\left(x,y,z|\alpha ,\beta \right)={\text{e}}^{\text{i}\frac{n+m}{2}\alpha }\sum _{k=0}^{n+m}{\text{e}}^{\text{i}k\alpha }{d}_{k-\frac{n+m}{2},\frac{n-m}{2}}^{\frac{n+m}{2}}\left(\beta \right){\text{HG}}_{k,n+m-k,l}\left(x,y,z\right),(1)$

where HLG_n,m,l (x, y, z|α, β) represents the complex field of HLG beams with transverse indices (n, m) and longitudinal indices l, (α, β) are tunable parameters of spatial mode evolution between HG beams and LG beams that HLG_n,m,l (x, y, z|α, β) would tend to LG beams for (α = π/2, β = π/2) and HG beams for α = 0 or β = 0, where $d_{k-\frac{n+m}{2},\frac{n-m}{2}}^{\frac{n+m}{2}}\left(\beta \right)$ are the elements of Wigner d-matrix as (Chen, 2011):

$d_{k-\frac{n+m}{2},\frac{n-m}{2}}^{\frac{n+m}{2}}\left(\beta \right)=\sqrt{k!\left(n+m-k\right)!n!m!}\times \sum _{\upsilon =\max \left(0,k-n\right)}^{\min \left(m,k\right)}\frac{{\left(-1\right)}^{\upsilon }{\left[\cos \left(\beta /2\right)\right]}^{m+k-2\upsilon }{\left[\sin \left(\beta /2\right)\right]}^{n-k+2\upsilon }}{\upsilon !\left(m-\upsilon \right)!\left(k-\upsilon \right)!\left(n-k+\upsilon \right)!}.(2)$

In this way, one can describe the transverse wave structure of HLG beams, using the transverse wave structure of HG beams that are further expressed as (Ugalde-Ontiveros et al., 2021):

${\text{HG}}_{n,m,l}\left(x,y,z\right)=\frac{1}{4}\sum _{i,j}{\text{TWHG}}_{n,m,l}^{i,j}\left(x,y,z\right),(3)$

where i, j = 1, 2, and ${\text{TWHG}}_{n,m,l}^{i,j}(x,y,z)$ represents the decomposed components as Ugalde-Ontiveros et al. (2021):

${\text{TWHG}}_{n,m,l}^{i,j}\left(x,y,z\right)=\frac{C_{n,m}}{w\left(z\right)}{\text{e}}^{-\frac{{\tilde{x}}^2+{\tilde{y}}^2}{2}}H{H}_n^i\left(\tilde{x}\right)H{H}_m^j\left(\tilde{y}\right){\text{e}}^{\left[\text{i}{\tilde{k}}_{n,m,l}\tilde{z}-\text{i}\left(n+m+1\right)\vartheta \left(z\right)\right]},(4)$

where $C_{n,m}=\sqrt{\pi 2^{n+m-1}n!m!}$ is the normalized factor, (x, y, z) is the Cartesian coordinates, $\tilde{x}=\sqrt{2}x/w(z)$, $\tilde{y}=\sqrt{2}y/w(z)$, $\tilde{z}=z+[(x^2+y^2)z]/[2(z^2+z_R^2)]$, ${\tilde{k}}_{n,m,l}=2\pi {\omega }_{n,m,l}/c$, ω_n,m,l = (n + m + 1)ω₀ + (l + 1/2)ω_z, ω₀ and ω_z are transverse and longitudinal mode frequency spacings, c is the light speed, ϑ(z) = tan⁻¹ (z/z_R) is the Gouy phase, $w(z)=w_0\sqrt{1+{(z/z_R)}^2}$ is the Gaussian beam waist, z_R is the Rayleigh rang, λ is the light wavelength. ${HH}_n^i(\cdot )$ is the Hankel-like Hermite polynomial of nth order as ${HH}_n^i(\cdot )=H_n(\cdot )\pm \text{i}N{H}_n(\cdot )$, where H_n(⋅) and NH_n(⋅) are the first and second solutions of the Hermite differential equation, i = 1, 2 for the sign of“+” and“−”, respectively (Ugalde-Ontiveros et al., 2021).

Note that H_n(⋅) and NH_n(⋅) are the transverse SW functions analogous to g_c(x) and g_s(x), and ${HH}_n^i(\cdot )$ is the transverse TW function analogous to f_±(x), respectively. Since the analytical expression of HG beams requires the multiplication of two Hermite functions defined in x −, y − directions, there would be four decomposed components as defined in Eq. 4. The decomposed components of HG beams in Eq. 4 could be called the transverse TW HG beams. Besides, the sum of four transverse TW HG beams in Eq. 3 is equivalent to the traditional HG beams, due to ${\sum }_{i,j}{HH}_n^i(x){HH}_m^j(y)=H_n(x)H_m(y)$. Thus, the traditional HG beams could be called the transverse SW HG beams, alternatively. Based on the transverse TW HG beams, the transverse TW HLG beams could be obtained as:

${\text{TWHLG}}_{n,m,l}^{i,j}\left(x,y,z|\alpha ,\beta \right)={\text{e}}^{\text{i}\frac{n+m}{2}\alpha }\sum _{k=0}^{n+m}{\text{e}}^{\text{i}k\alpha }{d}_{k-\frac{n+m}{2},\frac{n-m}{2}}^{\frac{n+m}{2}}\left(\beta \right){\text{TWHG}}_{k,n+m-k,l}^{i,j}\left(x,y,z\right).(5)$

The sum of four transverse TW HLG beams is equivalent to the traditional HLG beams in Eq. 1, which could also be called the transverse SW HLG beams. The simulated results of transverse TW and SW HLG beams are shown in Figure 1, where the intensity and phase at z = 0 plane are shown in rows Figures 1A–F, respectively. The horizontal and vertical axes of subplots are x- and y-axis and ranges from −4.2w₀ to 4.2w₀. The corresponding parameters are (n, m) = (5, 6), α = π/2, and the rows from top to bottom correspond to HG-HLG-LG beam evolution with β = 0, π/4, π/2. The subplots labeled with (i, j) in columns 1-4 are transverse TW HLG beams as defined in Eq. 5, and the column 5 corresponds to transverse SW HLG beams. The transverse TW HG beams have almost rectangular intensity profiles with different phase distributions, as shown in the Figures 1A,D, 1–4, while their superposition as SW HG beams have arrayed intensity profiles, as shown in Figures 1A5. In comparison, the transverse TW HLG beams have different intensity and phase distributions, which are superposed to form the transverse SW HLG beams with elliptical arrayed intensity profiles, as shown in Figures 1B,E, 1–5. The transverse TW LG beams could be divided into two groups with same intensity distributions (Figures 1C1–C4) but different phases (Figures 1F1–F4), which can constitute LG beams with ring-like intensity profiles and spiral phase distributions as shown in Figures 1C5,F5.

FIGURE 1

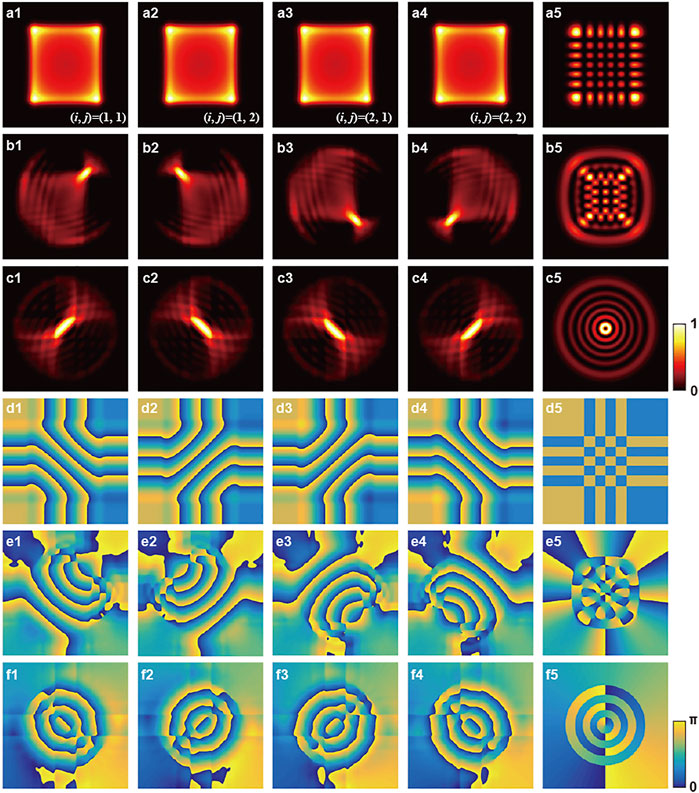
FIGURE 1. Transverse wave structure of HLG beams. Subplots (A1–C4) correspond to the intensities of transverse TW HLG beams with (n, m) = (5, 6), α = π/2, β = 0, π/4, π/2 from top to bottom, respectively. Subplots (A5,B5,C5) correspond to the intensities of transverse SW HLG beams. The subplots in rows (D–F) are the phases corresponding to the intensities shown in rows (A–C) (Colormap: darkness to brightness means 0 to 1 for intensity, and − π to π for phase).

2.2 Transverse Wave Structure of Ray-Wave Geometric Beams

In the above subsection, we have analyzed the transverse wave structure of HLG beams and proposed the transverse TW HLG beams, which allows us to further explore the transverse wave structure of complex ray-wave geometric beams as the superposed spatial wave packet. There are three typical kinds of ray-wave geometric beams, which are the so-called multi-path ray-wave geometric beams (Chen et al., 2019a), multi-axis ray-wave geometric beams (Tuan et al., 2018), and Lissajous-to-trochoidal geometric beams (Chen et al., 2006; Chen, 2011). Here we would decompose these exotic ray-wave beams into the superposition of transverse TW components. By selecting the transverse TW HLG beams as eigenmodes, the transverse TW ray-wave geometric beams can be expressed mathematically as (Bužek and Quang, 1989):

${\psi }_{n,m,l}^{i,j}\left(x,y,z|N,\varphi ,\alpha ,\beta \right)=\frac{1}{2^{N/2}}\sum _{K=0}^N{\left(\begin{array}{c}\hfill N\hfill \\ \hfill K\hfill \end{array}\right)}^{\frac{1}{2}}{\text{e}}^{\text{i}K\varphi }{\text{TWHLG}}_{n+pK,m+qK,l-sK}^{i,j}\left(x,y,z|\alpha ,\beta \right),(6)$

where ϕ is the coherent phase, N is an integer which represents the number of superposed eigenmodes in ray-wave geometric beams, analogous to the number of bosons in quantum SU(2) coherent state (Wodkiewicz and Eberly, 1985; Bužek and Quang, 1989), (p, q, s) are three integers about frequency-degenerate condition (Chen et al., 2004). The sum of four transverse TW ray-wave geometric beams (subplots labeled with (i, j) in columns 1-4 in Figure 2) as defined in Eq. 6 is equivalent to traditional ray-wave geometric beams (subplots in column 5 in Figure 2), which could be called transverse SW ray-wave geometric beams, where the horizontal and vertical axes of subplots are x- and y-axis, (α, β) = (π/2, 0) for rows (Figures 2A,D,G), (π/2, π/4) for rows (Figures 2B,E,H), (π/2, π/2) for rows (Figures 2C,F,I), respectively. The rows a-c, d-f, and g-i of the Figure 2 are ray-wave multi-path geometric beams (n = 5, m = 0, ϕ = 0, p = 3, q = 0, M = 4, (x, y) ranges from −4.2w₀ to 4.2w₀), ray-wave multi-axis geometric beams (n = 25, m = 5, ϕ = 0, p = 3, q = 0, M = 6, (x, y) ranges from − 8w₀ to 8w₀) and ray-wave Lissajous-to-trochoidal geometric beams (n = 25, m = 5, ϕ = π/2, p = −1, q = 4, M = 6, (x, y) ranges from − 8w₀ to 8w₀), respectively. The simulation ranges and the parameters are set for clear illustration. The beams that intensity located on segmented curves, are explained in the ray picture (Chen et al., 2019b). Here we demonstrate that these beams with segmented curved intensity are the transverse TW ray-wave geometric beams in the wave picture. Our generalized model provides a physical insight in the wave picture for the ray-wave geometric beams, which would be experimentally generated in the next section.

FIGURE 2

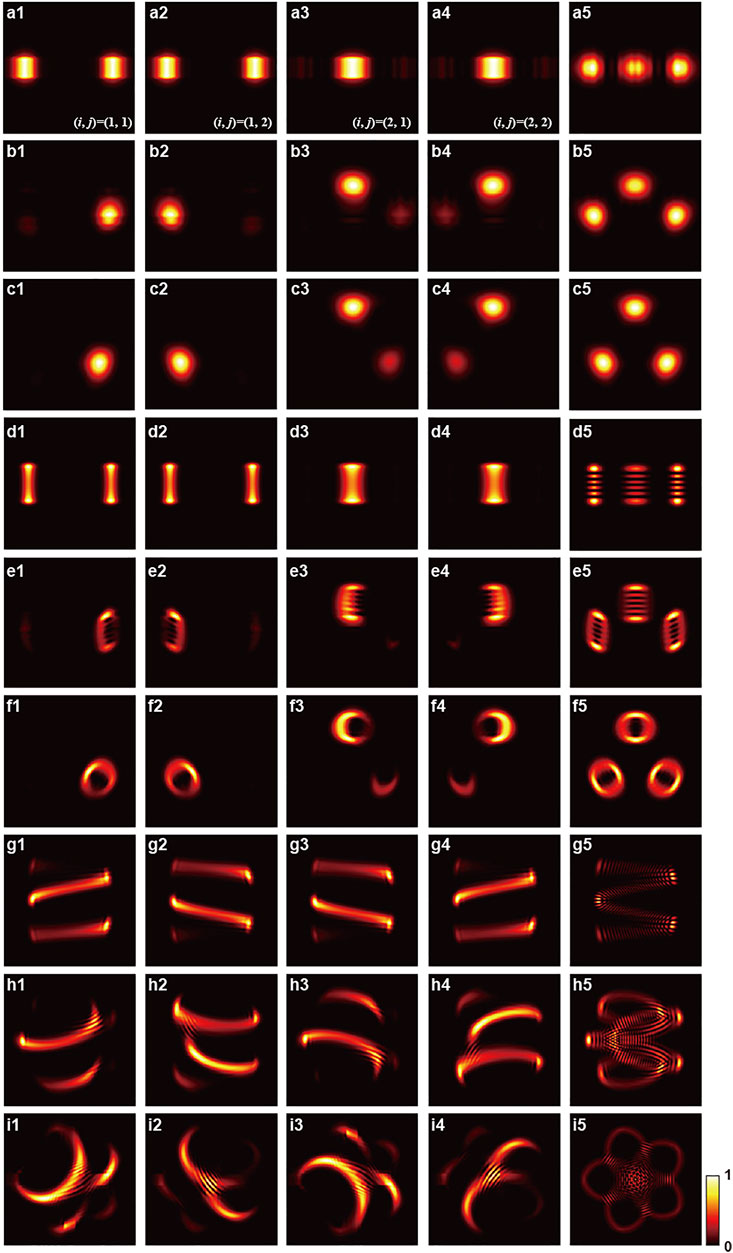
FIGURE 2. Transverse intensity of ray-wave geometric beams. The subplots in columns (A1–I5) are transverse TW (labeled with (i, j)) and SW ray-wave geometric beams, respectively (Colormap: darkness to brightness means 0 to 1 for intensity).

3 Experiment

We exploit a digital hologram system to generate the transverse TW and SW beams, since this method could generate various exotic beams flexibly, just by changing the mask loaded on the SLM (Chen et al., 2004, 2006; Tuan et al., 2018). In comparsion, the traditional method based on laser resonator requires to tune the length of cavity, pump position and power, and gain for generating various exotic beams, while some ray-wave beams cannot be generated in the cavity (Wan et al., 2020). Therefore, the digital hologram system is an effective and compact setup for the generation and modulation of structured light. The experimental setup based on LC-SLM is shown in Figure 3. LC-SLM is a type of opto-electrical device for phase modulation, which is regulated by the extraordinary refractive index of liquid crystal cells (Aulbach et al., 2017). Exploiting SLM to generate complex beams requires masks, which are essentially computer-generated holograms (Arrizón et al., 2007). There are several methods to generate masks, as introduced in (Arrizón et al., 2007; Markus Fratz et al., 2021; Trolinger, 2021). The masks used in this paper can be expressed as (Arrizón et al., 2007; Wan et al., 2020):

$f_{\text{mask}}\left(x,y\right)={\text{e}}^{\text{i}{J}_1^{-1}\left[CA\left(x,y\right)\right]\sin \left[\mathrm{\Phi }\left(x,y\right)+2\pi \left(u_{x}x+v_{y}y\right)\right]},(7)$

where C = 0.5819 is a constant (Arrizón et al., 2007; Wan et al., 2020), A (x, y) and Φ(x, y) are complex amplitude and phase distributions of light, u_x and u_y are spatial frequency coordinates. Lens L1 and L2 expand the beam emitted by the source, and the collimated beam is modulated by the mask loaded on SLM. The lenses L3 and L4 compose a 4f system. The aperture (AP) is placed at the Fourier plane of L3 to extract +1st-order diffraction component, as shown in the inset with blue box in the Figure 3, where only three diffraction orders are displayed. The target structured light exists in the +1st-order diffracting component, which is imaged by L4 and then recorded by CCD. The generation of planar multi-path ray-wave geometric beams is selected as an example shown in the right insets, where the insets are the mask loaded on SLM, enlarged view of the mask, and the experimental pattern recorded by CCD from top to bottom, respectively. A 1064-nm laser source (2 W) is used in this experiment and the generated beams are linear-polarized. The SLM (Meadowlark Optics) have 1920 × 1,152 pixels and (u_x, u_y) = (5, 0) for the masks loaded. The results recorded by CCD are about 300 × 300 pixels. The focal length of L1 to L4 is 20 mm, 120 mm, 120 mm, 60 mm, respectively.

FIGURE 3

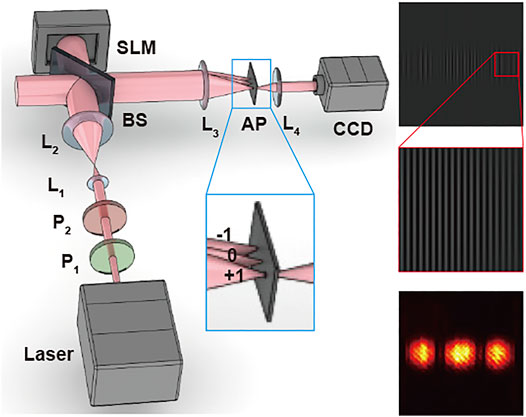
FIGURE 3. Experimental setup. P1-P2, polarizers; L1-L4, lens; BS, beam splitter; SLM, spatial light modulator; AP, aperture for filtering; CCD, charge coupled device camera. The blue rectangle highlights the filtering aperture, with the details of extracting + 1st-order diffraction component. The right insets exhibit the mask loaded on SLM, enlarged view of the mask, and the experimental pattern recorded by CCD from top to bottom, respectively.

Experimental results of transverse TW and SW HLG beams and ray-wave geometric beams are shown in Figure 4, where subplots labelled with (i, j) in rows 1-4 of each section are transverse TW beams and the subplots in 5th row are transverse SW beams. The first section of Figures 4A–C exhibits experimental results of HLG beams corresponding to the simulated results as shown in Figure 1, where subplots a1-a5, b1-b5, c1-c5 are transverse TW and SW HG, HLG and LG beams, respectively. The other three sections of Figure 4 exhibit the transverse TW and SW ray-wave geometric beams generated in experiment, corresponding to the simulated results as shown in Figure 2, where the subplots d1-d5, e1-e5, f1-f5 are transverse TW and SW ray-wave multi-path geometric beams, the subplots g1-g5, h1-h5, i1-i5 are transverse TW and SW ray-wave multi-axis geometric beams, and the subplots j1-j5, k1-k5, p1-p5 are transverse TW and SW ray-wave Lissajous-to-trochoidal geometric beams, respectively.

FIGURE 4

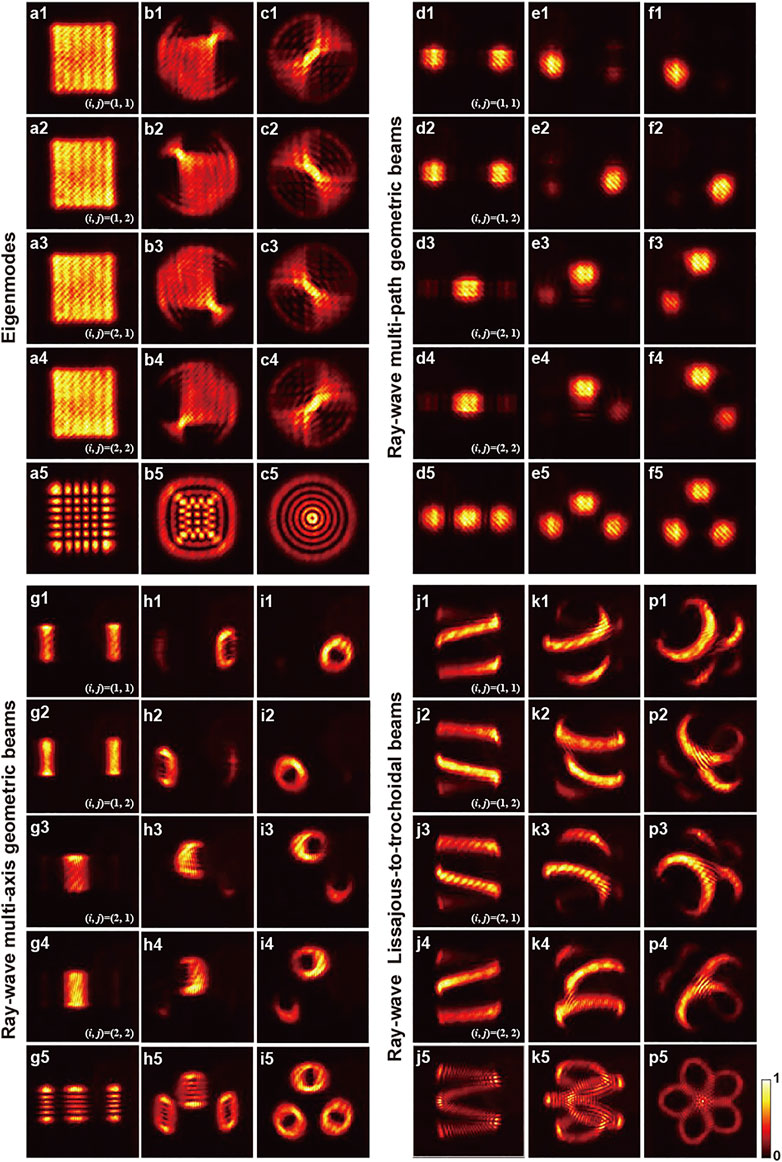
FIGURE 4. Experimental results of the transverse TW and SW beams of HLG beams, multi-path geometric beams, multi-axis geometric beams and Lissajous-to-trochoidal geometric beams. The subplots labeled with (i, j) in rows (A1–A4) to (P1–P4) of each section are transverse TW beams, and subplots in row (A5–P5) are SW beams (Colormap: darkness to brightness means 0 to 1 for intensity).

4 Discussion

The theoretical framework presented in this work decomposes traditional transverse SW ray-wave geometric beams into transverse TW geometric beams, which enriches the structured light family and provides a physical insight for the ray-wave beams. The generalized model demonstrates that the beams with segmented curved intensity in the laser resonator (Chen et al., 2019b) are transverse TW ray-wave geometric beams, essentially. Furthermore, our theoretical framework has the potential to unveil more classes. For instance, it can be applied to non-diffraction resonant geometric beams based on Bessel beams (Chen et al., 2012; Liang and Lin, 2020) since Bessel function J_n(r) and Neumann function N_n(r) can be seen as radial SW functions, and J_n(r) ±iN_n(r) can be seen as radial TW functions (Chávez-Cerda et al., 1996). For another instance, the first kind of Airy function Ai (⋅) and the second kind of Airy function Bi(⋅) could be used to construct transverse (radial) TW and SW Airy beams and their coherent spatial wave packet (Richards, 2002). We can also investigate generalized transverse wave structure in astigmatic and vector fields (Droop et al., 2021), as well as hybrid coherent state (Shen et al., 2020b). Besides, our newly proposed TW ans SW beams have multi- controllable DoFs, which is significant for extending the potential applications such as optical communication and manipulation.

In summary, we propose the transverse TW HLG beams and three kinds of exotic transverse TW ray-wave geometric beams, providing a physical insight for spatial wave structure of structured light, which are demonstrated in theoretical simulation and experiment. Our work has strong extensibility to explore spatial wave structure of more structured light such as non-diffracting beams, providing a powerful tool for exploring the frontiers of structured light.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

ZaW performed the theoretical analysis and experiment. ZeW and ZS also contributed to the experiment. XF leaded this work. All authors participated in the analysis of results and manuscript writing.

Funding

Funded by National Natural Science Foundation of China (61975087).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Sabino Chavez-Cerda for useful discussion.

References

Arrizón, V., Ruiz, U., Carrada, R., and González, L. A. (2007). Pixelated Phase Computer Holograms for the Accurate Encoding of Scalar Complex fields. J. Opt. Soc. America A 24, 3500–3507. doi:10.1364/josaa.24.003500

CrossRef Full Text | Google Scholar

Aulbach, L., Bloise, F. S., Lu, M., Wang, S., and Koch, A. W. (2017). “Structural Influence of a Spatial Light Modulator on Generated Wavefronts for Speckle-Based Shape Measurement,” in Automated Visual Inspection and Machine Vision II. Editors J. Beyerer, and F. P. León (Munich, Germany: International Society for Optics and Photonics (SPIE), 10334, 16–27.

Google Scholar

Babington, J. (2018). Ray-wave Duality in Classical Optics: Crossing the Feynman Bridge. Opt. Lett. 43, 5591–5594. doi:10.1364/ol.43.005591

PubMed Abstract | CrossRef Full Text | Google Scholar

Bužek, V., and Quang, T. (1989). Generalized Coherent State for Bosonic Realization of SU(2) Lie Algebra. J. Opt. Soc. America B 6, 2447–2449.

Google Scholar

Chávez-Cerda, S., McDonald, G., and New, G. (1996). Nondiffracting Beams: Travelling, Standing, Rotating and Spiral Waves. Opt. Commun. 123, 225–233. doi:10.1016/0030-4018(95)00538-2

CrossRef Full Text | Google Scholar

Chen, Y.-F. (2011). Geometry of Classical Periodic Orbits and Quantum Coherent States in Coupled Oscillators with SU(2) Transformations. Phys. Rev. A 83, 032124. doi:10.1103/physreva.83.032124

CrossRef Full Text | Google Scholar

Chen, Y.-F., Jiang, C., Lan, Y.-P., and Huang, K.-F. (2004). Wave Representation of Geometrical Laser Beam Trajectories in a Hemiconfocal Cavity. Phys. Rev. A 69, 053807. doi:10.1103/physreva.69.053807

CrossRef Full Text | Google Scholar

Chen, Y. F., Hsieh, M. X., Ke, H. T., Yu, Y. T., Liang, H. C., and Huang, K. F. (2021). Quantum Entanglement by a Beam Splitter Analogous to Laser Mode Transformation by a Cylindrical Lens. Opt. Lett. 46, 5129–5132. doi:10.1364/ol.439322

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y. F., Li, S. C., Hsieh, Y. H., Tung, J. C., Liang, H. C., and Huang, K. F. (2019a). Laser Wave-Packet Representation to Unify Eigenmodes and Geometric Modes in Spherical Cavities. Opt. Lett. 44, 2649–2652. doi:10.1364/ol.44.002649

CrossRef Full Text | Google Scholar

Chen, Y. F., Lin, Y. C., Zhuang, W. Z., Liang, H. C., Su, K. W., and Huang, K. F. (2012). Generation of Large Orbital Angular Momentum from Superposed Bessel Beams Corresponding to Resonant Geometric Modes. Phys. Rev. A 85, 043833. doi:10.1103/physreva.85.043833

CrossRef Full Text | Google Scholar

Chen, Y. F., Lu, T. H., Su, K. W., and Huang, K. F. (2006). Devil's Staircase in Three-Dimensional Coherent Waves Localized on Lissajous Parametric Surfaces. Phys. Rev. Lett. 96, 213902. doi:10.1103/physrevlett.96.213902

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y. F., Tung, J. C., Hsieh, M. X., Hsieh, Y. H., Liang, H. C., and Huang, K. F. (2019b). Generalized Wave-Packet Formulation with ray-wave Connections for Geometric Modes in Degenerate Astigmatic Laser Resonators. Opt. Lett. 44, 5366–5369. doi:10.1364/ol.44.005366

PubMed Abstract | CrossRef Full Text | Google Scholar

Droop, R., Asché, E., Otte, E., and Denz, C. (2021). Shaping Light in 3d Space by Counter-propagation. Sci. Rep. 11, 1–11. doi:10.1038/s41598-021-97313-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Forbes, A., de Oliveira, M., and Dennis, M. R. (2021). Structured Light. Nat. Photon. 15, 253–262. doi:10.1038/s41566-021-00780-4

CrossRef Full Text | Google Scholar

Fox, R. F., and Choi, M. H. (2000). Generalized Coherent States and Quantum-Classical Correspondence. Phys. Rev. A 61, 032107. doi:10.1103/physreva.61.032107

CrossRef Full Text | Google Scholar

Javidi, B., Carnicer, A., Anand, A., Barbastathis, G., Chen, W., Ferraro, P., et al. (2021). Roadmap on Digital Holography [Invited]. Opt. Express 29, 35078–35118. doi:10.1364/oe.435915

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, H.-C., and Lin, H.-Y. (2020). Generation of Resonant Geometric Modes from off-axis Pumped Degenerate Cavity Nd:yvo4 Lasers with External Mode Converters. Opt. Lett. 45, 2307–2310. doi:10.1364/ol.390278

PubMed Abstract | CrossRef Full Text | Google Scholar

Lourenço-Martins, H., Gérard, D., and Kociak, M. (2021). Optical Polarization Analogue in Free Electron Beams. Nat. Phys. 17, 598–603. doi:10.1038/s41567-021-01163-w

CrossRef Full Text | Google Scholar

Markus Fratz, A. B., Tobias, Seyler., and Carl, D. (2021). Digital Holography in Production: an Overview. Light: Adv. Manufacturing 2, 283. doi:10.37188/lam.2021.015

CrossRef Full Text | Google Scholar

Mendoza-Hernández, J., Arroyo-Carrasco, M. L., Iturbe-Castillo, M. D., and Chávez-Cerda, S. (2019). Structured Light Beams Constituted of Incoming and Outgoing Waves. Phys. Rev. A 100, 053847. doi:10.1103/physreva.100.053847

CrossRef Full Text | Google Scholar

Ren, Y.-X., Lu, R.-D., and Gong, L. (2015). Tailoring Light with a Digital Micromirror Device. Annalen Der Physik 527, 447–470. doi:10.1002/andp.201500111

CrossRef Full Text | Google Scholar

Richards, D. (2002). Advanced Mathematical Methods with Maple. Cambridge University Press.

Google Scholar

Shen, Y., Hou, Y., Papasimakis, N., and Zheludev, N. I. (2021a). Supertoroidal Light Pulses as Electromagnetic Skyrmions Propagating in Free Space. Nat. Commun. 12, 1–9. doi:10.1038/s41467-021-26037-w

CrossRef Full Text | Google Scholar

Shen, Y. (2021). Rays, Waves, SU(2) Symmetry and Geometry: Toolkits for Structured Light. J. Opt. 23, 124004. doi:10.1088/2040-8986/ac3676

CrossRef Full Text | Google Scholar

Shen, Y., and Rosales-Guzmán, C. (2022). Nonseparable States of Light: From Quantum to Classical. Hoboken, NJ, United States: Wiley Online Library.

Google Scholar

Shen, Y., Wang, Z., Fu, X., Naidoo, D., and Forbes, A. (2020a). SU(2) Poincaré Sphere: A Generalized Representation for Multidimensional Structured Light. Phys. Rev. A 102, 031501. doi:10.1103/physreva.102.031501

CrossRef Full Text | Google Scholar

Shen, Y., Wang, Z., Yang, X., Nape, I., Naidoo, D., Fu, X., et al. (2021b). Classically Entangled Vectorial Structured Light towards Multiple Degrees of Freedom and Higher Dimensions. Light: Sci. Appl. 10, 1–10. doi:10.1364/cleo_si.2021.sth1b.1

CrossRef Full Text | Google Scholar

Shen, Y., Yang, X., Naidoo, D., Fu, X., and Forbes, A. (2020b). Structured ray-wave Vector Vortex Beams in Multiple Degrees of freedom from a Laser. Optica 7, 820–831. doi:10.1364/optica.382994

CrossRef Full Text | Google Scholar

Tang, L. (2021). Dynamical Behavior and Traveling Wave Solutions in Optical Fibers with Schrödinger-Hirota Equation. Optik 245, 167750. doi:10.1016/j.ijleo.2021.167750

CrossRef Full Text | Google Scholar

Trolinger, J. D. (2021). The Language of Holography. Light: Advanced Manufacturing 2. doi:10.37188/lam.2021.034

CrossRef Full Text | Google Scholar

Tuan, P. H., Hsieh, Y. H., Lai, Y. H., Huang, K. F., and Chen, Y. F. (2018). Characterization and Generation of High-Power Multi-axis Vortex Beams by Using off-axis Pumped Degenerate Cavities with External Astigmatic Mode Converter. Opt. Express 26, 20481–20491. doi:10.1364/oe.26.020481

PubMed Abstract | CrossRef Full Text | Google Scholar

Ugalde-Ontiveros, J. A., Jaimes-Nájera, A., Luo, S., Gómez-Correa, J. E., Pu, J., and Chávez-Cerda, S. (2021). What Are the Traveling Waves Composing the Hermite-Gauss Beams that Make Them Structured Wavefields? Opt. Express 29, 29068–29081. doi:10.1364/oe.424782

PubMed Abstract | CrossRef Full Text | Google Scholar

Vetlugin, A. N. (2021). Coherent Perfect Absorption of Quantum Light. Phys. Rev. A 104, 013716. doi:10.1103/physreva.104.013716

CrossRef Full Text | Google Scholar

Wan, Z., Shen, Y., Wang, Z., and Fu, X. (2021). Digitally Controlled ray-wave Geometric Beams as Higher-Dimensional Information Carriers. Laser Beam Shaping XXI 11818, 118180B. International Society for Optics and Photonics. doi:10.1117/12.2596429

CrossRef Full Text | Google Scholar

Wan, Z., Wang, Z., Yang, X., Shen, Y., and Fu, X. (2020). Digitally Tailoring Arbitrary Structured Light of Generalized ray-wave Duality. Opt. Express 28, 31043–31056. doi:10.1364/oe.400587

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Shen, Y., Liu, Q., and Fu, X. (2021a). To Unify Azimuthally Traveling-Wave and Standing-Wave Structured Light by ray-wave Duality. J. Opt. 23, 115604. doi:10.1088/2040-8986/ac160b

CrossRef Full Text | Google Scholar

Wang, Z., Shen, Y., Naidoo, D., Fu, X., and Forbes, A. (2021b). Astigmatic Hybrid SU(2) Vector Vortex Beams: towards Versatile Structures in Longitudinally Variant Polarized Optics. Opt. Express 29, 315–329. doi:10.1364/oe.414674

PubMed Abstract | CrossRef Full Text | Google Scholar

Wodkiewicz, K., and Eberly, J. H. (1985). Coherent States, Squeezed Fluctuations, and the SU(2) Am SU(1,1) Groups in Quantum-Optics Applications. J. Opt. Soc. Am. B 2, 458–466. doi:10.1364/josab.2.000458

CrossRef Full Text | Google Scholar