Elimination of Quadratic Phase Aberration in Digital Holographic Microscopy by Using Transport of Intensity

We propose to reconstruct 3D images by combining the merits of transport of intensity and digital holography. The proposed method solves the transport-of-intensity equation by using digital holographic reconstructed images as inputs. Our simulation and experimental results show that this method can eliminate quadratic phase aberration introduced by the microscope objective in digital holographic microscopy. This proposed phase retrieval method is free of phase unwrapping process. It is thus efficient in removing quadratic phase aberration introduced by the microscope objective.

1 Introduction

Holography was invented in 1948 by Dennis Gabor (1948) to improve the resolution of an electron microscope. Leith and Upatnieks (1964) proposed off-axis illumination with an off-axis reference beam, thus eliminating the spectral overlap of the zeroth-order beam and the twin image inherent in Gabor’s in-line configuration. Schnars and Jüptner (1994) first used a CCD camera to capture a hologram and subsequently reconstruct the hologram numerically. They termed the technique as Digital Holography (DH).

In order to improve the transverse resolution of holographic measurements, digital holographic microscopy (DHM) was developed. In combination with microscopy, DHM provides label-free, quantitative phase imaging (Cuche et al., 1999; Mann et al., 2005). Even though DHM has significant advantages such as being simple, non-intrusive, and dynamic. However, quadratic phase aberration introduced by the microscope objective is a great issue (Zuo et al., 2013a). In addressing this issue, quadratic error compensation method has been applied (Zhou et al., 2009). It includes an optical design compensation (Rappaz et al., 2005) such as the use of a telecentric architecture (Sánchez-Ortiga et al., 2011) and a tunable lens compensation (Deng et al., 2017). The removal of quadratic phase aberration by software-based methods has also been investigated (Liu et al., 2018). Computer simulations of quadratic phase compensation (Colomb et al., 2006; Wang et al., 2019), least squares surface fitting compensation (Di et al., 2009), and automatic spectral energy analysis (Liu et al., 2014) have also been proven successfully. Most recently, deep learning compensation based on convolutional neural network has also shown great success (Nguyen et al., 2017). While these methods are promising, they mostly involve post processing steps for the quadratic phase removal, e.g., after holographic reconstruction. It is also feasible that intensity images can be reconstructed from a digital hologram to provide inputs for the transport-of-intensity equation (TIE) for unwrapped phase recovery. By doing this, we avoid shifting the sample or the camera in the experiment (Yan et al., 2019). In this research, we combine DH and TIE (DH-TIE) algorithm with regularization parameters. The TIE is a second-order elliptic partial differential equation for the phase φ. We use a fast method based on FFT to solve the TIE. Within the method of DH-TIE, a single hologram can provide phase retrieval without phase unwrapping (Zhou et al., 2018; Yan et al., 2019; Zuo et al., 2020; Lu et al., 2021).

Many scholars have combined digital holography and TIE in many applications. In the works by Zuo et al., TIE was invoked following the numerical reconstruction and propagation of the digital hologram, and the absolute phase without 2π discontinuities has been directly recovered (Zuo et al., 2013b). Whittkopp et al. described a microscopic setup implementing phase imaging by DHM and TIE, which allowed the results of both measurements to be quantitatively compared for either live cell or static samples (Wittkopp et al., 2020). Gupta et al. combined TIE with DH to overcome the artifacts caused by TIE phase recovery under low-light conditions by reconstructing the desired multiple out-of-focus intensity maps from the captured coaxial digital holograms (Gupta et al., 2020; Gupta and Nishchal, 2021). Kelly et al. (2013) compared Fresnel-based digital holography and phase retrieval from TIE. All these studies provide a lot of new ideas and methods for DH-TIE applications. In this paper, we employ the technique of DH-TIE to eliminate quadratic phase aberration introduced by a microscope objective in DHM. However, a suitable regularization parameter $\gamma$ needs to be selected during the TIE phase retrieval process. By simulating the quadratic phase with different curvature factors, we provide some analysis for the appropriate selection of the regularization parameter. We will also present experimental results to verify our idea. In Section 2, we present some of the key formulas of the DH-TIE algorithm. In Section 3, a simulated phase object is used for the demonstration of the removal of quadratic phase aberration caused by a microscope objective in the DH system. In particular, we compare results using the DH-TIE and DH methods. We also analyze the effect of zero padding on phase retrieval. In Section 4, experimental results on a USAF resolution chart as a sample are presented to show the effectiveness of quadratic phase aberration removal. In the last section, we make some concluding remarks.

2 Key Formulas of DH-TIE Algorithm

In DH, a laser beam illuminates an object and the amplitude (${\mathit{A}}_{\mathit{o}}$) and phase (${\mathit{\phi }}_{\mathit{o}}$) of the light waves on the holographic plane form the object wave are as follows:

${\mathit{O}}_{\mathit{o}}\left(\mathit{x},\mathit{y}\right)={\mathit{A}}_{\mathit{o}}\left(\mathit{x},\mathit{y}\right)\mathit{exp}\left[\mathit{i}{\mathit{\phi }}_{\mathit{o}}\left(\mathit{x},\mathit{y}\right)\right].(1)$

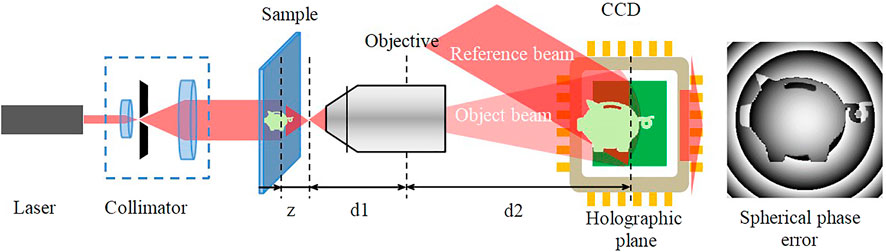
In DHM (Figure 1), the object wave is magnified on the holographic plane by a microscope objective (MO), and the image of the object beam satisfies the rule of lens imaging. The wavefront of the object wave therefore contains an additional quadratic phase aberration introduced by the microscope objective and is given by

$\mathit{O}\left(\mathit{x},\mathit{y}\right)={\mathit{A}}_{\mathit{o}}\left(\frac{\mathit{x}}{\mathit{M}},\frac{\mathit{y}}{\mathit{M}}\right)\mathit{exp}\left[\mathit{i}{\mathit{\phi }}_{\mathit{o}}\left(\frac{\mathit{x}}{\mathit{M}},\frac{\mathit{y}}{\mathit{M}}\right)\right]\mathit{ exp}\left\{\frac{\mathit{ik}}{2\mathit{\mu }}\left[{\mathit{x}}^2+{\mathit{y}}^2\right]\right\}\mathit{ },\mathit{ }(2)$

where $\mathit{M}$ is the magnification of the microscope objective, $\mathit{\mu }$ is the radius of curvature of quadratic phase aberration (also called the quadratic phase aberration factor) introduced by the microscope objective, and $k$ is the wave number of the laser. In off-axis holography, there is an angle between the reference beam and the holographic plane, which generates a linear phase reference wave on the holographic plane:

$\mathit{R}\left(\mathit{x},\mathit{y}\right)={\mathit{A}}_{\mathit{r}}\mathit{exp}\left[\mathit{ik}\left({\mathit{t}}_{\mathit{x}}\mathit{x}+{\mathit{t}}_{\mathit{y}}\mathit{y}\right)\right]\mathit{ },\mathit{ }(3)$

where ${\mathit{t}}_{\mathit{x}}$ and ${\mathit{t}}_{\mathit{y}}$ are the inclination factors along the $\mathit{x}$ and $\mathit{y}$ directions, respectively.

FIGURE 1

FIGURE 1. Diagram of digital holographic plane microscopy.

For off-axis holography, the digital hologram is generated through the interference between the object wave and the reference wave given by

$\mathit{H}\left(\mathit{x},\mathit{y}\right)={\left|\mathit{R}\left(\mathit{x},\mathit{y}\right)\right|}^2+{\left|\mathit{O}\left(\mathit{x},\mathit{y}\right)\right|}^2+{\mathit{R}}^{\mathit{*}}\left(\mathit{x},\mathit{y}\right)\mathit{O}\left(\mathit{x},\mathit{y}\right)+\mathit{R}\left(\mathit{x},\mathit{y}\right){\mathit{O}}^{\mathit{*}}\left(\mathit{x},\mathit{y}\right),(4)$

where ${\mathit{R}}^{\mathit{*}}\left(\mathit{x},\mathit{y}\right)\mathit{O}\left(\mathit{x},\mathit{y}\right)$ and $\mathit{R}\left(\mathit{x},\mathit{y}\right){\mathit{O}}^{\mathit{*}}\left(\mathit{x},\mathit{y}\right)$ are the positive and negative first order images, respectively (Nguyen et al., 2017). We have used a Fourier spectrum window filter to extract the positive first order image of the hologram. Moreover, the tilted phase (with factors ${\mathit{t}}_{\mathit{x}}$, ${\mathit{t}}_{\mathit{y}}$ ) of the reference light can be eliminated by a Fourier frequency shift. The distribution of the filtered complex amplitude (${\mathit{H}}^{\mathit{F}}\left(\mathit{x},\mathit{y}\right)$) on the holographic plane is then given by

${\mathit{H}}^{\mathit{F}}\left(\mathit{x},\mathit{y}\right)={\mathit{F}}^{-1}\left\{{\mathit{F}}^{\mathit{filter}}\left[{\mathit{R}}^{\mathit{*}}\left(\mathit{x},\mathit{y}\right)\cdot \mathit{O}\left(\mathit{x},\mathit{y}\right)\right]\right\}\mathit{ }={\mathit{A}}_{\mathit{r}}{\mathit{A}}_0\left(\frac{\mathit{x}}{\mathit{M}},\frac{\mathit{y}}{\mathit{M}}\right)\mathit{exp}\left[\mathit{i}{\mathit{\phi }}_0\left(\frac{\mathit{x}}{\mathit{M}},\frac{\mathit{y}}{\mathit{M}}\right)\right]\mathit{ exp}\left[\frac{\mathit{ik}}{2\mathit{\mu }}\left({\mathit{x}}^2+{\mathit{y}}^2\right)\right] .(5)$

Finally, the complex amplitude distribution of the original sample needs to be calculated by a convolution formula under paraxial approximations based on Kirchhoff scalar diffraction (Poon and Liu, 2014). The diffraction process can be regarded as a linear and space invariant system. After illuminating the hologram with $\mathit{R}$. The reconstructed image is given by

$\begin{array}{c} \mathit{O}\mathrm{’}\left(\mathit{x},\mathit{y}\right)=\int \int \mathit{R}\cdot {\mathit{H}}^{\mathit{F}}\cdot {\mathit{g}}_{\mathit{z}}\left(\mathit{x}-{\mathit{x}}_{\mathit{z}},y-{\mathit{y}}_{\mathit{z}};z\right)d{\mathit{x}}_{\mathit{z}}d{\mathit{y}}_{\mathit{z}}, \end{array}(6)$

where

$\mathit{ }{\mathit{g}}_{\mathit{z}}\left(\mathit{x},\mathit{y};\mathit{z}\right)=\frac{1}{\mathit{i\lambda }}\frac{\mathit{exp}\left(\mathit{ik}\sqrt{{\mathit{x}}^2+{\mathit{y}}^2+{\mathit{z}}^2}\right)}{\sqrt{{\mathit{x}}^2+{\mathit{y}}^2+{\mathit{z}}^2}},(7)$

is the point spread function in free space. Note that the quadratic phase aberration, $\mathit{exp}\left\{\frac{\mathit{ik}}{2\mathit{\mu }}\left[{\mathit{x}}^2+{\mathit{y}}^2\right]\right\}$, is contained in ${\mathit{H}}^{\mathit{F}}$. The angular spectrum numerical propagation method is used to propagate a small distance $\mathrm{\Delta }z$, the value of $\mathrm{\Delta }z$ cannot be too small in the case of intensity measurement noise, otherwise the differential estimation of the light intensity will be drowned by the noise. However, when the value of $\mathrm{\Delta }z$ is too large, the phase ambiguity effect will become more obvious. In light of this, we choose $\Delta z$ between the intensity measurement noise and nonlinear error as follows:

$\mathit{ }\frac{\mathit{k\sigma }}{\sqrt{2}\mathit{I}{\mathit{\nabla }}^2\mathit{\phi }}<\mathrm{\Delta }\mathit{Z}\ll \frac{1}{\mathit{\pi \lambda }{\mathit{f}}_{\mathit{max}}^2}\mathit{ },\mathit{ }(8)$

where $\mathit{I}\left(\mathit{x},\mathit{y};\mathit{z}\right)$ is the intensity distribution around the image plane, and $\mathit{\phi }(\mathit{x},\mathit{y};\mathit{z})$ is the corresponding phase distribution of the phase object. The upper limit of the defocused distance is determined by the highest spatial frequency of the object f_max, and the lower limit is determined by the intensity measurement noise (assuming Gaussian noise of standard deviation σ). The next two defocused intensities from the focal plane are generated by the angular spectrum method (ASM) numerically, giving $\mathbf{I}\left(\mathbf{x},\mathbf{y};\mathbf{z}+\mathbf{\Delta }\mathbf{z}\right)$ and $\mathbf{I}\left(\mathbf{x},\mathbf{y};\mathbf{z-}\mathbf{\Delta }\mathbf{z}\right)$. The two intensities are used as input data to solve the TIE. The axial differential intensity $\frac{\partial \mathbf{I}}{\partial \mathbf{Z}}$ is estimated by the following central finite difference method:

$\frac{\partial \mathit{I}}{\partial \mathit{Z}}\approx \frac{\mathit{I}\left(\mathit{x},\mathit{y};\mathit{z}+\mathrm{\Delta }\mathit{z}\right)-\mathit{I}\left(\mathit{x},\mathit{y};\mathit{z}-\mathrm{\Delta }\mathit{z}\right)}{2\mathrm{\Delta }\mathit{z}}.\mathit{ }(9)$

Figure 1 shows a diagram of the digital holographic microscopy system. The laser passes through the beam collimator and is divided into two beams, one of which passes through the object sample and is magnified by the microscope, and the other, which does not pass through the object, is served as a reference beam at the CCD to obtain the hologram of the sample. Furthermore in Figure 1, z is the reconstruction distance, d1 is the object distance, and d2 is the image distance.

The transport-of-intensity equation (TIE) is an elliptic partial differential equation (Zuo et al., 2014). In order to improve the speed of solving the equation, it can be approximated by the following Poisson equation:

$\mathit{\nabla }\left(\mathit{I}\mathit{\nabla }\mathit{\phi }\right)=-\frac{2\mathit{\pi }}{\mathit{\lambda }}\frac{\partial \mathit{I}}{\partial \mathit{z}} ,(10)$

where $\frac{\mathit{\partial }\mathit{I}}{\mathbf{\partial }\mathit{Z}}$, as shown in Eq. 9, can be approximated as the difference of defocused image intensities in two planes. The phase of the object can be reconstructed using the FFT-based Poisson solver (Teague, 1983; Zhou et al., 2018):

$\mathit{ \phi }={\mathbf{ℱ}}^{-1}\left\{\frac{{\mathit{f}}_{\mathit{x}}^2+{\mathit{f}}_{\mathit{y}}^2}{{\left({\mathit{f}}_{\mathit{x}}^2+{\mathit{f}}_{\mathit{y}}^2\right)}^2+\mathit{\gamma }}\mathbf{ℱ}\left\{\frac{\mathit{k}}{{\mathit{I}}_{\mathit{o}}}\cdot \frac{\partial \mathit{I}}{\partial \mathit{z}}\right\}\right\},(11)$

where $\mathbf{ℱ}$ and ${\mathbf{ℱ}}^{-1}$ denotes forward and inverse Fourier transform notations, respectively. $\mathit{\gamma }$ is the regularization parameter, an important factor under the Tikhonov-regularization treatment. ${\mathit{f}}_{\mathit{x}}$ and ${\mathit{f}}_{\mathit{y}}$ are the spatial frequencies in the $\mathit{x}$ and $\mathit{y}$ directions, respectively. ${\mathit{I}}_{\mathit{o}}$ is the intensity distribution at the focused plane and usually can be taken as the average intensities of the two defocused planes. Since the TIE is being solved using Fourier transforms, the boundary conditions are implicitly assumed as the same as that for the existence of the Fourier transform of the function (Banerjee, 2022). The Tikhonov-regularization treatment is commonly used to remove very low frequency artifacts, and in the next Sections, we will demonstrate that the treatment can also filter out the slowly varying feature corresponding to spherical phase aberration introduced by the microscope objective in the DH system.

3 Simulation Analysis

We have simulated a sine grating as a sample. The sinusoidal grating is expressed as follows:

$\mathit{t}\left(\mathit{x},\mathit{y}\right)=\{\begin{array}{c}{\mathit{e}}^{\mathit{j}\mathit{sin}\mathit{\omega x}}\mathit{sin}\mathit{\omega x}>0\\ 0 \mathit{sin}\mathit{\omega x}\le 0\end{array} . (12)$

The wavelength used is 632.8 $nm$. The square size of the hologram is 1,024 pixels ×1,024 pixels with the pixel size of 4.65 $\mu m$. The defocused distances are $\mathrm{\Delta }z$ = ±1 mm. Quadratic phase aberration with spherical factor μ = 150 is shown in Figure 2A. We add quadratic phase aberration on the object phase (sine grating of two periods) shown in Figure 2C, to simulate the object after imaged by the microscope objective, as shown in Figure 2D. Figure 2E is a line trace across center of wrapped quadratic phase aberration from Figure 2B. Figure 2F is the line trace of the object phase from Figure 2C. Figure 2G shows the line trace of the wrapped object phase mixed with quadratic phase aberration. An off-axis reference beam is simulated to interfere with the aberrated object complex amplitude. The digital hologram is shown in Figure 2H, with 50 mm recording distance and the zeroth-order term in the hologram has been eliminated. The complex amplitude distributions of the focal plane and the defocused planes can be obtained by multiplying the digital hologram with the reconstructed reference light and perform the convolution reconstruction process for different distances.

FIGURE 2

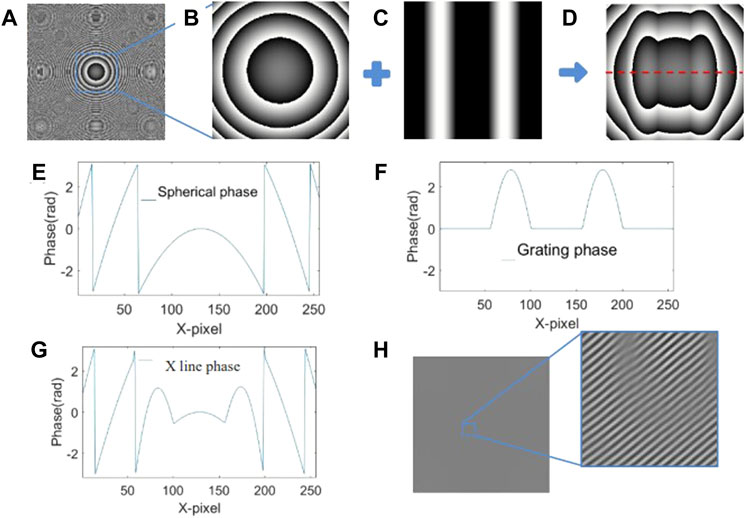
FIGURE 2. Simulation of object wave and digital hologram. (A) Quadratic phase aberration simulated as the effect due to the microscope objective (wrapped), (B) Spherical phase map in center 256 × 256 region, (C) Object phase (sine grating function of two periods) located at the center of 256 × 256 region, (D) Wrapped phase map of quadratic phase combined with object. (E) Line trace of the quadratic phase extracted from the red line in (B). (F) Line trace of the sine grating object from (C), (G) Line trace of the combined phase extracted from the red line of (D). (H) Simulated off axis digital hologram map with 50 mm recording distance.

As shown in Figures 3A–C, in the holographic reconstruction process, the simulated phase of the object wave modulates the intensity image, but quadratic phase aberration added to the object only affects the boundary region of the phase retrieval. Figure 3A is the intensity image with 50 mm reconstruction distance equal to the recording distance. Figures 3B,C are the intensity image with 49 and 51 mm reconstruction distance, respectively. We solve the TIE to calculate the object phase with three intensity images. Figures 3D,E show the phase retrieval by DH-TIE with $\Delta z$ = ±1 mm from vertical view and the 3-D profile view, respectively. In general, we observe that the center area of phase retrieval yields fairly accurate results. Around the boundary region phase retrieval is, however, associated with large errors as evidenced by Figure 3F, where we present line traces of simulated object (Green), DH (Blue) and DH-TIE (Red) phase results.

FIGURE 3

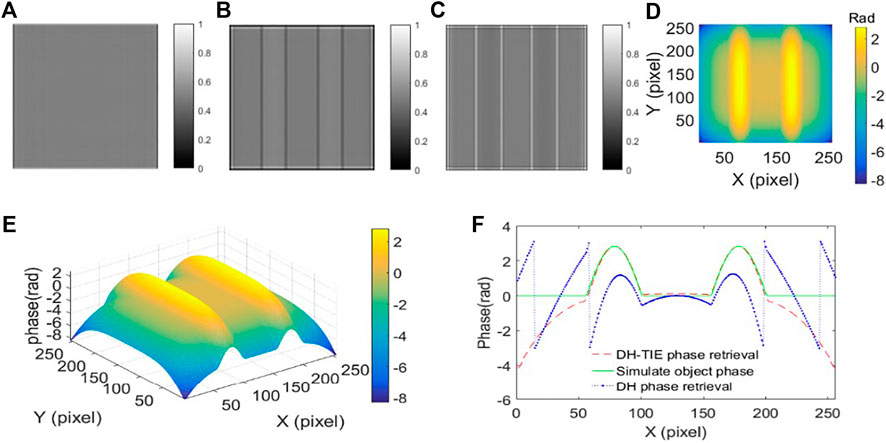
FIGURE 3. Holographic reconstruction intensity images and TIE phase retrieval results. (A) Reconstruction intensity image (256 × 256 size of the center of the region) with 50 mm reconstruction distance. (B) Reconstruction intensity image with 49 mm reconstruction distance. (C) Reconstruction intensity image with 51 mm reconstruction distance. (D) Phase retrieval by DH-TIE with 1 mm Δz (vertical view). (E) 3D profile view of (D). (F) Line traces of simulated object (Green), DH (Blue) and DH-TIE (Red) retrieval phase.

As it turns out, the DH-TIE phase retrieval is improved drastically by zero padding. We summarize the results in Figure 4. In Figure 4A, we have used a 256 × 256 image. In Figures 4B–D, we perform zero padding on the image file in Figure 4A to have 512 × 512, 768 × 768, 1,024 × 1,024 image files, respectively. It is evident that phase retrieval of using 512 × 512, 768 × 768, 1,024 × 1,024 image files are better than that from the 256 × 256 image file, and the reconstruction effect of 512 × 512 image file is the best among them. It is also clear that quadratic phase aberration added to the object does not impact phase retrieval using the DH-TIE method. Simulation results show that the DH-TIE method can effectively eliminate quadratic phase aberration in DHM, greatly simplifying the phase reconstruction process of real objects. Zero padding provides a larger uniform background on the original image file and can achieve better retrieval results.

FIGURE 4

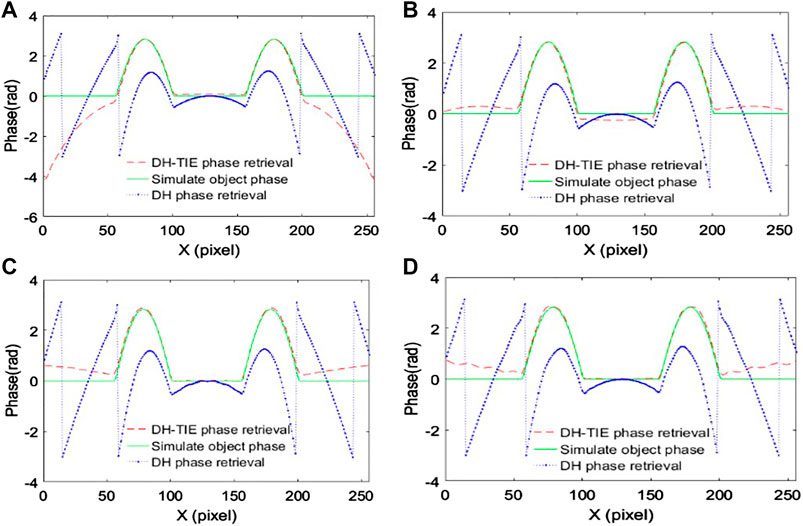
FIGURE 4. Reconstruction under zero padding of different sizes and the line traces of simulated object (Green), DH (Blue) and DH-TIE (Red) phase retrieval. Reconstruction intensity images are with Δz = 1 mm. (A) The image file is 256 × 256. (B) The image file is 512 × 512. (C) The image file is 768 × 768. (D) The image file is 1,024 × 1,024.

We also study the reconstruction effectiveness due to the regularization parameter under different severities of quadratic phase aberration. A two-dimensional correlation coefficient $\mathit{r}\left(\mathit{A},\mathit{B}\right)$ can effectively represent the similarity between the retrieved phase and the original phase (ground truth) and it is given by

$\mathit{r}\left(\mathit{A},\mathit{B}\right)=\frac{{{\displaystyle \sum }}_{\mathit{m}}{{\displaystyle \sum }}_{\mathit{n}}\left({\mathit{A}}_{\mathit{mn}}-\overline{\mathit{A}}\right)\left({\mathit{B}}_{\mathit{mn}}-\overline{\mathit{B}}\right)}{\sqrt{{\left({{\displaystyle \sum }}_{\mathit{m}}{{\displaystyle \sum }}_{\mathit{n}}\left({\mathit{A}}_{\mathit{mn}}-\overline{\mathit{A}}\right)\right)}^2{\left({{\displaystyle \sum }}_{\mathit{m}}{{\displaystyle \sum }}_{\mathit{n}}\left({\mathit{B}}_{\mathit{mn}}-\overline{\mathit{B}}\right)\right)}^2}}, (13)$

where $\mathit{A}$, $\mathit{B}$ are two arrays in the same size, $\overline{\mathit{A}}$ is the mean of A, and $\overline{\mathit{B}}$ is the mean of B. When the correlation coefficient is closer to one, DH-TIE achieves better phase reconstruction. Figure 5A shows that when the quadratic phase aberration factor μ = 400, the correlation coefficient is higher when the regularization parameter is 100–1,000, and the reconstruction effect is better. When the regularization parameter is 0.1–90 or more than 1,000, the correlation coefficient becomes lower with adverse reconstruction quality. Figure 6A shows that when the quadratic phase aberration factor μ = 1,500, the regularization parameter is optimized around 100. Figure 7A shows that when the quadratic phase aberration factor μ = 7,000, the regularization parameter is optimized around 1,000.

FIGURE 5

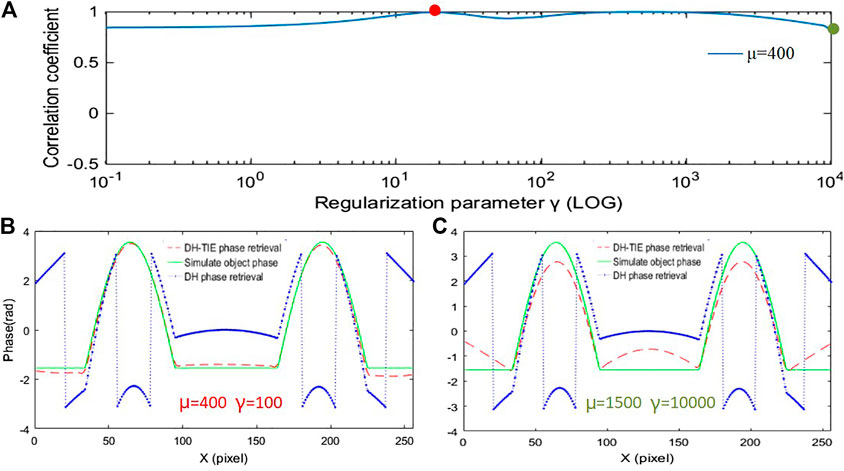
FIGURE 5. (A) Correlation coefficient plots corresponding to different regularization parameters when the quadratic phase aberration factor μ = 400. (B) Reconstruction results, line traces when the value of the regularization parameter γ is taken as 100. (C) Reconstruction results, line traces when the value of the regularization parameter γ is taken as 10,000.

FIGURE 6

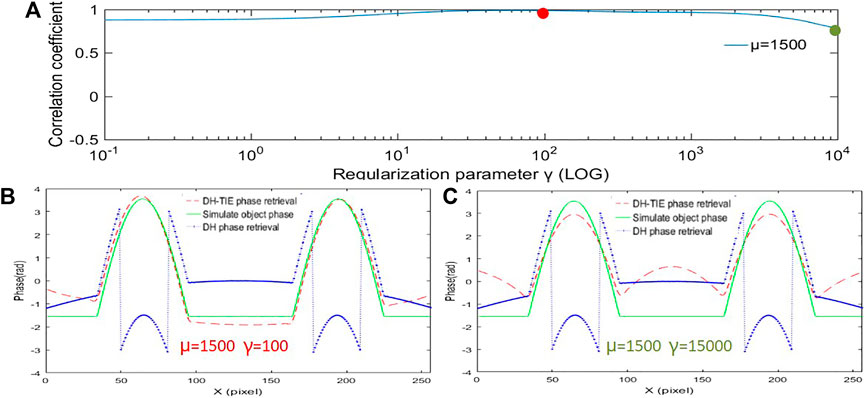
FIGURE 6. (A) Correlation coefficient plots corresponding to different regularization parameters when the quadratic phase aberration factor μ = 1,500. (B) Reconstruction results, line traces when the value of the regularization parameter γ is taken as 100. (C) Reconstruction results, line traces when the value of the regularization parameter γ is taken as 15,000.

FIGURE 7

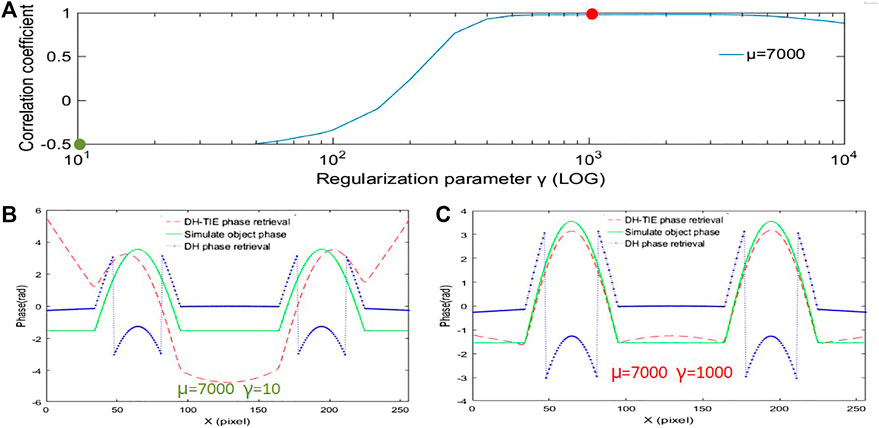
FIGURE 7. (A) Correlation coefficient plots corresponding to different regularization parameters when the quadratic phase aberration factor μ = 7,000. (B) Reconstruction results, line traces when the value of the regularization parameter is taken as 10. (C) Reconstruction results when taking the red point in (A), line trace when the value of the regularization parameter is taken as 1,000.

4 Experiment and Results

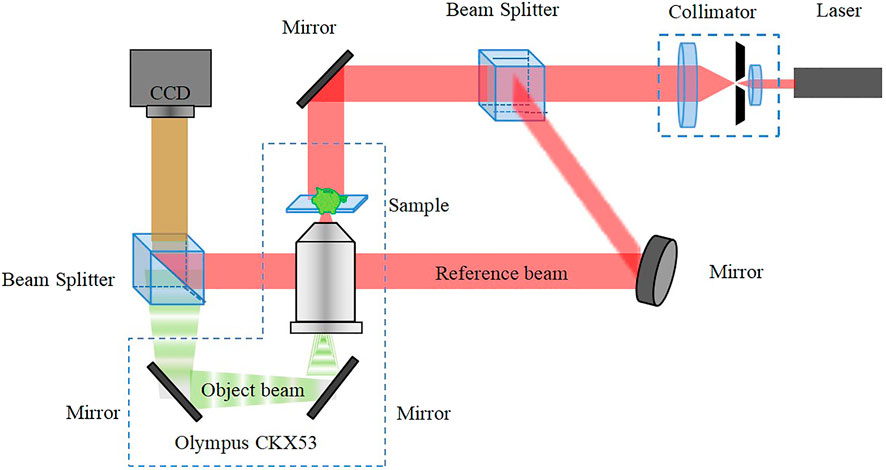
To verify the effectiveness of the proposed method, a DHM system of off-axis Mach-Zehnder interferometer combined with an inverted microscopy (Olympus CKX53) has been constructed. The wavelength of He-Ne laser source (Da Heng DH-NH250) is 632.8 nm$nm$. The resolution of the CCD (Da Heng MER-500-7UM) is 2592(H)×1944(V) with single pixel size 2.2 $\mu m$ × 2.2 $\mu m$. The off-axis digital holographic system setup is shown in Figure 8.

FIGURE 8

FIGURE 8. Diagram of off-axis digital holographic microscopy system setup.

A collimated laser beam is divided into two beams after passing through a laser collimator and a beam-splitting prism. One of the beams is reflected by a reflector mirror and modulated by the sample phase to become the object beam, where the object wavefront (green) is magnified by an Olympus microscope and diffracted onto the CCD plane. The other beam is used as the reference light. An off-axis angle between the two beams is created to form an interference between the object and reference light waves on the CCD plane.

The actual off-axis digital holographic system is shown in Figure 9. The light beam emitted by the laser passes through a collimator and then passes through a beamsplitter (BS) which is divided into an object beam and a reference beam. The object beam passes through another beamsplitter and passes down through the object and the microscope, while the reference beam passes through the two beamsplitters and is incident onto the CCD together with the object beam (green arrow) to form an interference beam. In the system, the laser enters the Olympus microscope through a mirror, and by this way, the laser replaces the original light source of the microscope with vertical incidence, and the inverted microscope has been used to form a post-amplification digital holographic microscope. The merit of using an inverted microscope is that the microscope objective lens can be flexibly switched to change the magnification of the system.

FIGURE 9

FIGURE 9. Experimental setup diagram of off-axis digital holographic microscopy system.

We have obtained the holograms of a USAF 1951 resolution chart (Edmund Optics) using the holographic microscope. The digital holograms that we have captured under ×4 and ×10 microscope objectives are shown in Figures 10A,B, respectively. Figures 10C,D are the spectra of these two holograms, respectively, and Figures 10E,F are the focused intensity reconstructed images of Figures 10A,B, respectively.

FIGURE 10

FIGURE 10. Recorded holograms, two-dimensional spectra and reconstructed intensity images. (A) Hologram under X4 MO with 20 mm recording distance, (B) Hologram under ×10 MO with 30 mm recording distance, (C,D) are the two-dimensional spectra of holograms (A,B), respectively, (E) Focused intensity reconstructed image of (A), (F) Focused intensity reconstructed image of (B).

In the DH-TIE phase retrieval process, we have used a focused image and two defocused images with 1 mm away from the focused image. We have reconstructed two holograms (Figures 10A,B) by the DH and DH-TIE methods. Figures 11A,B are the DH retrieved phase, and Figures 11C,D are the DH-TIE retrieved phase. In the DH-TIE phase reconstruction, the regulation parameter has been set to 5,000.

FIGURE 11

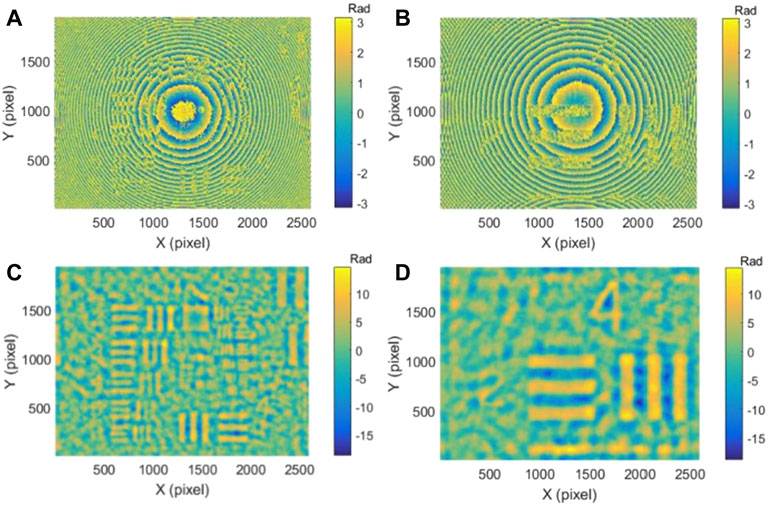
FIGURE 11. Phase retrievals of DH and DH-TIE. (A,B) are the DH phase map retrievals from Figures 10A,B, respectively. (C,D) are the DH-TIE phase map retrievals from Figures 10A,B.

It can be seen in Figures 11A,B that quadratic phase aberration is sharp in the DH reconstruction. Quadratic phase aberration introduced by the microscope objective is so strong that the phase information of the objects have been completely buried. Under the ×4 and ×10 microscope objective, quadratic phase aberration has different curvatures. The quadratic phase factor in Figure 11A is μ = 200, and the quadratic phase factor in Figure 11B is μ = 400. This problem does not exist in the phase retrieval process using DH-TIE as quadratic phase aberration has been eliminated and the object phase has been retrieved successfully as shown in Figures 11C,D. In order to verify the effect of different regularization parameters on the reconstruction phase, we compare reconstructions when γ = 1,000 and γ = 10,000 under the ×10 microscope objective. It can be seen from Figure 12 that reconstruction is worse when γ = 10,000 as compared to that when γ = 1,000. Clearly, regularization parameter plays an important role in reconstruction.

FIGURE 12

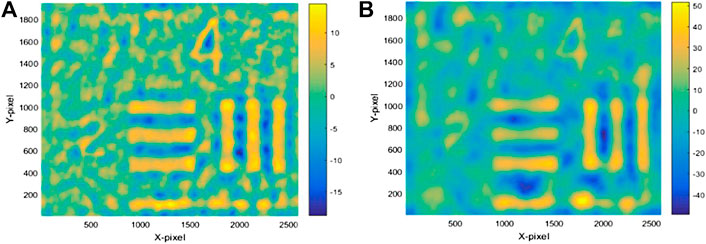
FIGURE 12. Phase retrievals of DH-TIE under ×10 MO. (A) Phase map retrieval when γ = 1,000 (B) Phase map retrieval when γ = 10,000.

5 Concluding Remarks

Off-axis DHM simulation results show that, for quadratic phase aberration generated by a microscope objective, the DH-TIE method along with regularization can effectively eliminate quadratic phase aberration. The unique advantage of DH-TIE is that phase unwrapping is not needed. In contrast, conventional DH phase retrieval method is not able to remove quadratic phase aberration since there is no such process (regularization within TIE) for the removal of the quadratic phase. We have performed simulations that provide guidance for the proper selection of the regularization process under the TIE.

Through optical experimental results, along with regularization the DH-TIE method shows consistency in phase retrieval under quadratic phase aberration introduced by the microscope objective in the DH system. It should be noted that the uniformity of the beam brightness in the holographic plane should affect the accuracy of the DH-TIE reconstruction, because only when the light intensity is uniformly distributed on the hologram plane, the TIE equation can then be directly reduced to a Poisson equation, which can be solved directly by using Fourier transforms. This aspect should be further studied.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

WZ, HZ, and T-CP contributed to conception and design of the study. CW organized the database. YY performed the statistical analysis. SL wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This project was supported by the National Natural Science Foundation of China (No.51775326 and No.61975112); the Major State Research Development Program of China (2020YFE024600); Shanghai Key Laboratory of Intelligent Manufacturing and Robotics.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Banerjee, P. P. (2022). University of Dayton.[Private Communications]. Dayton, Ohio: University of Dayton.

Google Scholar

Colomb, T., Kühn, J., Charrière, F., Depeursinge, C., Marquet, P., and Aspert, N. (2006). Total Aberrations Compensation in Digital Holographic Microscopy with a Reference Conjugated Hologram. Opt. Express 14, 4300. doi:10.1364/oe.14.004300

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuche, E., Marquet, P., and Depeursinge, C. (1999). Simultaneous Amplitude-Contrast and Quantitative Phase-Contrast Microscopy by Numerical Reconstruction of Fresnel off-axis Holograms. Appl. Opt. 38, 6994–7001. doi:10.1364/ao.38.006994

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, D., Peng, J., Qu, W., Wu, Y., Liu, X., He, W., et al. (2017). Simple and Flexible Phase Compensation for Digital Holographic Microscopy with Electrically Tunable Lens. Appl. Opt. 56, 6007. doi:10.1364/AO.56.006007

PubMed Abstract | CrossRef Full Text | Google Scholar

Di, J., Zhao, J., Sun, W., Jiang, H., and Yan, X. (2009). Phase Aberration Compensation of Digital Holographic Microscopy Based on Least Squares Surface Fitting. Opt. Commun. 282, 3873–3877. doi:10.1016/j.optcom.2009.06.049

CrossRef Full Text | Google Scholar

Gabor, D. (1948). A New Microscopic Principle. Nature. 161, 777–778. doi:10.1038/161777a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Gupta, A. K., Nishchal, N. K., and Banerjee, P. P. (2020). Transport of Intensity Equation Based Photon-Counting Phase Imaging. OSA Continuum. 3, 236–245. doi:10.1364/OSAC.383527

CrossRef Full Text | Google Scholar

Gupta, A. K., and Nishchal, N. K. (2021). Low-light Phase Imaging Using In-Line Digital Holography and the Transport of Intensity Equation. J. Opt. 23, 025701. doi:10.1088/2040-8986/abe18a

CrossRef Full Text | Google Scholar

Kelly, D. P., Megel, L., Meinecke, T., and Sinzinger, S. (2013). A Theoretical Comparison of Fresnel Based Digital Holography and Phase Retrieval from the Transport of Intensity Equation. Proc. SPIE. 8833, 88330G. doi:10.1117/12.2024855

CrossRef Full Text | Google Scholar

Leith, E. N., and Upatnieks, J. (1964). Wavefront Reconstruction with Diffused Illumination and Three-Dimensional Objects*. J. Opt. Soc. Am. 54, 1295–1301. doi:10.1364/JOSA.54.001295

CrossRef Full Text | Google Scholar

Liu, S., Xiao, W., and Pan, F. (2014). Automatic Compensation of Phase Aberrations in Digital Holographic Microscopy for Living Cells Investigation by Using Spectral Energy Analysis. Opt. Laser Technology. 57, 169–174. doi:10.1016/j.optlastec.2013.10.014

CrossRef Full Text | Google Scholar

Liu, Y., Wang, Z., and Huang, J. (2018). Recent Progress on Aberration Compensation and Coherent Noise Suppression in Digital Holography. Appl. Sci. 8, 444. doi:10.3390/app8030444

CrossRef Full Text | Google Scholar

Lu, L., Fan, Y., Sun, J., Zhang, J., Wu, X., Chen, Q., et al. (2021). Accurate Quantitative Phase Imaging by the Transport of Intensity Equation: a Mixed-Transfer-Function Approach. Opt. Lett. 46, 1740–1743. doi:10.1364/OL.422095

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann, C. J., Yu, L., Lo, C.-M., and Kim, M. K. (2005). High-resolution Quantitative Phase-Contrast Microscopy by Digital Holography. Opt. Express. 13, 8693–8698. doi:10.1364/opex.13.008693

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, T., Bui, V., Lam, V., Raub, C. B., Chang, L.-C., and Nehmetallah, G. (2017). Automatic Phase Aberration Compensation for Digital Holographic Microscopy Based on Deep Learning Background Detection. Opt. Express. 25, 15043–15057. doi:10.1364/OE.25.015043

PubMed Abstract | CrossRef Full Text | Google Scholar

Poon, T.-C., and Liu, J.-P. (2014). Introduction to Modern Digital Holography with MATLAB. Cambridge, UK: Cambridge University Press.

Google Scholar

Rappaz, B., Marquet, P., Cuche, E., Emery, Y., Depeursinge, C., and Magistretti, P. J. (2005). Measurement of the Integral Refractive index and Dynamic Cell Morphometry of Living Cells with Digital Holographic Microscopy. Opt. Express. 13, 9361–9373. doi:10.1364/opex.13.009361

PubMed Abstract | CrossRef Full Text | Google Scholar

Sánchez-Ortiga, E., Ferraro, P., Martínez-Corral, M., Saavedra, G., and Doblas, A. (2011). Digital Holographic Microscopy with Pure-Optical Spherical Phase Compensation. J. Opt. Soc. Am. A. 28, 1410–1417. doi:10.1364/JOSAA.28.001410

CrossRef Full Text | Google Scholar

Schnars, U., and Jüptner, W. (1994). Direct Recording of Holograms by a CCD Target and Numerical Reconstruction. Appl. Opt. 33, 179–181. doi:10.1364/AO.33.000179

PubMed Abstract | CrossRef Full Text | Google Scholar

Teague, M. R. (1983). Deterministic Phase Retrieval: a Green's Function Solution. J. Opt. Soc. Am. 73, 1434–1441. doi:10.1364/JOSA.73.001434

CrossRef Full Text | Google Scholar

Wang, H., Dong, Z., Wang, X., Lou, Y., and Xi, S. (2019). Phase Compensation in Digital Holographic Microscopy Using a Quantitative Evaluation Metric. Opt. Commun. 430, 262–267. doi:10.1016/j.optcom.2018.08.061

CrossRef Full Text | Google Scholar

Wittkopp, J. M., Khoo, T. C., Carney, S., Pisila, K., Bahreini, S. J., Tubbesing, K., et al. (2020). Comparative Phase Imaging of Live Cells by Digital Holographic Microscopy and Transport of Intensity Equation Methods. Opt. Express 28, 6123–6133. doi:10.1364/OE.385854

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, K., Yu, Y., Huang, C., Sui, L., Qian, K., and Asundi, A. (2019). Fringe Pattern Denoising Based on Deep Learning. Opt. Commun. 437, 148–152. doi:10.1016/j.optcom.2018.12.058

CrossRef Full Text | Google Scholar

Zhou, W.-J., Guan, X., Liu, F., Yu, Y., Zhang, H., Poon, T.-C., et al. (2018). Phase Retrieval Based on Transport of Intensity and Digital Holography. Appl. Opt. 57, A229. doi:10.1364/AO.57.00A229

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, W., Yu, Y., and Asundi, A. (2009). Study on Aberration Suppressing Methods in Digital Micro-holography. Opt. Lasers Eng. 47, 264–270. doi:10.1016/j.optlaseng.2008.04.026

CrossRef Full Text | Google Scholar

Zuo, C., Chen, Q., Li, H., Qu, W., and Asundi, A. (2014). Boundary-artifact-free Phase Retrieval with the Transport of Intensity Equation II: Applications to Microlens Characterization. Opt. Express 22, 18310–18324. doi:10.1364/OE.22.018310

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, C., Chen, Q., Qu, W., and Asundi, A. (2013a). Direct Continuous Phase Demodulation in Digital Holography with Use of the Transport-Of-Intensity Equation. Opt. Commun. 309, 221–226. doi:10.1016/j.optcom.2013.07.013

CrossRef Full Text | Google Scholar

Zuo, C., Chen, Q., Qu, W., and Asundi, A. (2013b). Phase Aberration Compensation in Digital Holographic Microscopy Based on Principal Component Analysis. Opt. Lett. 38, 1724–1726. doi:10.1364/OL.38.001724

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, C., Li, J., Sun, J., Fan, Y., Zhang, J., Lu, L., et al. (2020). Transport of Intensity Equation: a Tutorial. Opt. Lasers Eng. 135, 106187. doi:10.1016/j.optlaseng.2020.106187

CrossRef Full Text | Google Scholar