Compact Computational Holographic Display

Holographic display is an ultimate three-dimensional (3D) display technique that can produce the wavefront of 3D objects. The dynamic holographic display usually requires a spatial light modulator (SLM) with a following 4f system to eliminate the unnecessary orders produced by the grating structure of the SLM. We present a technique that displays the images without the 4f system. We detect the unnecessary wavefield by phase-shifting holography and suppress it using computational optimization. Experimental results are presented to verify the proposed method.

1 Introduction

Holography could create a light field identical to the one generated by a real three-dimensional (3D) object. Thus, it is regarded as the ultimate display technique for 3D displays (Hong et al., 2011). One of the most challenging issues in holographic displays is modulating the complex wavefield at wavelength-scale, pixel by pixel, yielding ultra-high spatial resolution. The typical light modulation devices are spatial light modulators (SLMs) or digital micromirror devices (DMDs). The commercial SLMs or DMDs are mainly phase-only or amplitude-only, and the practical realization of a complex one is challenging. Various approaches have been reported to conduct complex field modulation in optical or computational manners (Hsueh and Sawchuk, 1978; Juday et al., 1991; Gregory et al., 1992; Neto et al., 1996; de Bougrenet de la Tocnaye and Dupont, 1997; Arrizón et al., 1998; Birch et al., 2000; Hsieh, 2007; Bingxia Wang et al., 2021). The optical approaches usually achieve complex modulation by integrating and controlling phase-only or amplitude-only SLMs in different ways (Juday et al., 1991; Gregory et al., 1992; Neto et al., 1996; de Bougrenet de la Tocnaye and Dupont, 1997; Hsieh, 2007), while the computational techniques convert the complex field into equivalent phase-only (Hsueh and Sawchuk, 1978; Birch et al., 2000) or amplitude-only (Arrizón et al., 1998; Bingxia Wang et al., 2021) ones that adapt to the physical constraints of commercial light modulators. The latter is also referred to as hologram encoding. Analytical solutions and computational optimization are two main approaches for hologram encoding. Detour phase (Arrizón et al., 1998; Bingxia Wang et al., 2021) and double-phase methods (Hsueh and Sawchuk, 1978; Song et al., 2012; Mendoza-Yero et al., 2014) are typical analytical techniques, which are fast but with compromised qualities, and can be easily applied to arbitrary complex holograms. Optimization techniques such as Gerchberg–Saxton (GS) (Gerchberg, 2002; Sun et al., 2018; Chen et al., 2020; Wu et al., 2021) are time-consuming with improved image quality. However, these are difficult to be applied to arbitrary complex fields (Chakravarthula et al., 2019). The rasterization structure of SLM or DMD also introduces multiple orders. The fill factor of the pixels results in the zero-order issue, which interferes with and distorts the modulated light wave. To improve the displayed image quality, it requires suppression of the zero-order. The 4f optical filter system (Arrizón et al., 2007; Liang et al., 2012; Ronzitti et al., 2012; Siemion et al., 2012; Improso et al., 2014) is a common approach that can block the zero-order in the Fourier plane. The 4f system and other variants of zero-order blocking techniques result in a non-accessible region in the final reconstruction because any part of the desired pattern near the zero-order area would also be affected. An ideal solution would be to create a correction beam with the same profile as the zero-order together with the desired target (Palima and Daria, 2007), which could create a destructive interference with the unwanted beam. However, developing complex field optimization may be the barrier to this approach (Improso et al., 2017).

Herein, we propose a computational holographic display technique that integrates phase-shifting holography and automatic differentiable (AD) optimization. The former helps us detect the unwanted complex wavefield in a holographic display system, and the latter achieves complex field optimization to suppress the unwanted wavefields. It shows that optimization through AD can obtain a phase-only hologram that acts equally as a complex field in an efficient way. In the simulation, the peak signal-to-noise (PSNR) and structural similarity index measure (SSIM) can reach 50 dB and 0.9 in around one second. Thanks to the powerful AD optimization, we can achieve comparable image quality in hologram display while deputing the 4f system. We present the methodology in Section 2 and experimental results in Section 3.

2 Methods

Figure 1A represents a typical holographic display system, wherein a laser light beam illuminates an SLM that shows the holograms. The diffracted light goes through a 4f system and reproduces the desired objects. The 4f system, as denoted by the dashed rectangle in Figures 1A, is used to block unwanted terms induced by the rasterized SLM and its limited fill factor. It usually keeps only the first order of the diffraction (Zaperty et al., 2018). The 4f makes the system bulky and may introduce extra aberrations if the focal lengths of the lenses are small. Therefore, it is demanded to be eliminated. The ideal display system is shown in Figure 1B.

FIGURE 1

FIGURE 1. Holographic display with (A) and without (B) 4f system.

However, without the 4f system, the detected images along the optical axis is an interference pattern between the directly reflected beam and the diffracted beam from the SLM, as shown in Figure 2 and Eq. 1:

$I(x,y)=|\mathcal{P}\left(u_{dead}(x,y),z\right)+\mathcal{P}\left(u_{active}(x,y),z\right){|}^2,(1)$

FIGURE 2

FIGURE 2. Zero-order issue in holographic display systems with an SLM.

where $u_{dead}(x,y)=A(x,y)e^{j{\varphi }_{dead}(x,y)}$ and $u_{active}(x,y)=A(x,y)e^{j{\varphi }_{active}(x,y)}$ are the beams from the dead area and activate area of the SLM, respectively, $\mathcal{P}(\cdot ,z)$ is the free-space propagator of a complex amplitude of a wavefield with a distance z (described in Section 2.3), and I(x, y) is the detected image in the camera sensor. The proposed method detects the complex amplitude of the wavefield u_dead(x, y) and eliminates it with a computational optimization approach. It should be mentioned that u_dead(x, y) is not only the directly reflected beam from the SLM but also contains some system aberrations. We obtain it through phase-shifting holography. With the known u_dead(x, y), the computationally designed phase hologram displayed by the active area of the SLM can cancel it in the camera plane. We achieve this by automatic differentiable complex field optimization. The following two sub-sections describe the proposed method in more detail.

2.1 Unwanted Wavefront Detection

Figure 2 and Eq. 1 show the unwanted complex amplitude of the wavefield we want to suppress is an interference pattern. Obtaining it is a holographic imaging problem. Therefore, we introduce the four-step phase-shifting holography (Yamaguchi and Zhang, 1997; Jeong et al., 2008) to measure it. We treat the wavefield u_dead(x, y) at the camera sensor plane as the target and the wavefield from the SLM active area as the reference beam and perform phase-shifting hologram recording. The four holograms are taken by shifting the reference beams’ phase with a step of 0.5π; that is, α is of 0π, 0.5π, π and 1.5π, respectively. Thus, the captured holograms under phase-shifting α can be represented by

$\begin{array}{ll}\hfill I(x,y;\alpha )& =|u_{dead}(x,y)+u_{active}(x,y;\alpha ){|}^2\hfill \\ \hfill & =|A_{dead}(x,y){|}^2+|A_{active}(x,y;\alpha ){|}^2+\hfill \\ \hfill & =2A_{dead}(x,y)A_{active}(x,y;\alpha )\cos ({\varphi }_{dead}(x,y)-{\varphi }_{active}(x,y)-\alpha ).\hfill \end{array}(2)$

Thus, the phase and amplitude of the light beam of $u_{dead}(x,y)=A_{dead}{e}^{j{\varphi }_{dead}(x,y)}$ can be obtained by (Jeong et al., 2008)

$\begin{array}{ll}\hfill {\varphi }_{dead}(x,y)& ={\tan }^{-1}\left(\frac{I(x,y;0.5\pi )-I(x,y;1.5\pi )}{I(x,y;0)-I(x,y;\pi )}\right),\hfill \end{array}(3)$

$\begin{array}{ll}\hfill A_{dead}(x,y)& =\frac{1}{4}\frac{I(x,y;0)-I(x,y;\pi )}{\cos \left({\varphi }_{dead}(x,y)-{\varphi }_{active}(x,y)\right)}.\hfill \end{array}(4)$

It should be mentioned that we suppose the dead area of the SLM acts as a “mirror.” However, the cover glass of the SLMs may be imperfect, which could result in an inaccurate estimation of the zero-order.

2.2 Unwanted Wavefront Suppression Through Automatic Differentiable Optimization

With the detected complex amplitude of the wavefield u_dead(x, y), we need to calculate a desired phase only hologram that can be loaded into the active area of the SLM to produce the desired image after interfering with u_dead(x, y). Suppose b is the known target, the problem is to find a phase ϕ(x, y), such that for a known distance z, the interference between the propagated wavefield and u_dead(x, y) approaches the target b, which can be presented as

${\min }_{\varphi }\mathcal{L}(\varphi )=\Vert |\mathcal{P}(e^{j\varphi },z)+u_{dead}(x,y){|}^2-b{\Vert }^2,(5)$

We can optimize the above equation using a gradient descent. At iteration n, update ϕⁿ⁺¹ given a step size τ:

${\varphi }^{n+1}\leftarrow {\varphi }^n-\tau \nabla \mathcal{L}({\varphi }^n),(6)$

with the derivatives of

$\nabla \mathcal{L}({\varphi }^n)={\left.\frac{\partial \mathcal{L}}{\partial \varphi }\right|}_{\varphi ={\varphi }^n}.(7)$

Computing $\frac{\partial \mathcal{L}}{\partial \varphi }$ is critical because the partial derivatives indicate how the phase affects the error metric locally. The analytic expression of Eq. 7 is typically derived by writing an explicit expression for the error metric $\mathcal{L}(\varphi )$ and symbolically differentiating with respect to each of the input parameters. Herein, we can expand Eq. 7 using the chain rule as follows:

$\frac{\partial \mathcal{L}}{\partial \varphi }=\frac{\partial \mathcal{L}}{\partial x_7}\frac{\partial x_7}{\partial x_6}\frac{\partial x_6}{\partial x_5}\frac{\partial x_5}{\partial x_4}\frac{\partial x_4}{\partial x_3}\frac{\partial x_3}{\partial x_2}\frac{\partial x_2}{\partial x_1}\frac{\partial x_1}{\partial \varphi },(8)$

where

$\begin{array}{cc}\hfill x_1& =\exp (j\varphi )\hfill \\ \hfill x_2& =\mathcal{F}\left\{x_1\right\}\hfill \\ \hfill x_3& =x_2◦H\hfill \\ \hfill x_4& ={\mathcal{F}}^{-1}\left\{x_3\right\}\hfill \\ \hfill x_5& =x_4+u_{dead}\hfill \\ \hfill x_6& =|x_5{|}^2\hfill \\ \hfill x_7& =x_6-y\hfill \\ \hfill \mathcal{L}& =|x_7{|}^2,\hfill \end{array}(9)$

where H is the transfer function of free-space wave propagation, ◦ is the element-wise product, and $\mathcal{F}$ and ${\mathcal{F}}^{-1}$ are the Fourier and inverse Fourier operator, respectively. Calculating Eq. 8 is mathematically straightforward, but somewhat laborious. Herein, we apply the reverse-mode AD (Griewank and Walther, 2008), which is a cheap technique for a computing derivative of a scalar function with many variables by the chain rule (Blennow, 2018; Congli Wang et al., 2021). From Eqs 8, 9, it is clear that we need to optimize real-valued loss functions with complex variables, that is, $f(z):\mathbb{C}\to \mathbb{R}$. However, a non-constant real-valued function of a complex variable is not (complex) analytic and therefore is not differentiable. Generally, the same real-valued function viewed as a function of the real-valued real and imaginary components of the complex variable can have a (real) gradient when partial derivatives are taken with respect to those two (real) components, that is, $f(z)=f(x,y):{\mathbb{R}}^2\to \mathbb{R}$. However, taking the real or imaginary part of a complex number (Peng et al., 2020; Chen et al., 2021), do not satisfy the Cauchy–Riemann equations and cannot be addressed via a complex differentiation. In this work, we use the Wirtinger derivative (Remmert, 1991; Kreutz-Delgado, 2009), which can rewrite a real differentiable function f(z) as two-variable holomorphic function f(z, z*), where z = x + jy and z* = x − jy. We can use the chain rule to establish a relationship between partial derivatives of $\frac{\partial }{\partial z},\frac{\partial }{\partial z^{*}}$ and the partial derivatives with respect to the real and imaginary components of z:

$\begin{array}{cc}\hfill \frac{\partial }{\partial x}& =\frac{\partial z}{\partial x}\frac{\partial }{\partial z}+\frac{\partial z^{*}}{\partial x}\frac{\partial }{\partial z^{*}}=\frac{\partial }{\partial z}+\frac{\partial }{\partial z^{*}}\hfill \\ \hfill \frac{\partial }{\partial y}& =\frac{\partial z}{\partial y}\frac{\partial }{\partial z}+\frac{\partial z^{*}}{\partial y}\frac{\partial }{\partial z^{*}}=1j\times \left(\frac{\partial }{\partial z}+\frac{\partial }{\partial z^{*}}\right)\hfill \end{array}(10)$

From the aforementioned equations, we get the classic definition of Wirtinger calculus:

$\begin{array}{c}\hfill \frac{\partial }{\partial z}=\frac{1}{2}\left(\frac{\partial }{\partial x}-1j\times \frac{\partial }{\partial y}\right)\\ \hfill \frac{\partial }{\partial z^{*}}=\frac{1}{2}\left(\frac{\partial }{\partial x}+1j\times \frac{\partial }{\partial y}\right)\end{array}(11)$

For step s and loss L, we have $z_{n+1}=z_n-s\times \frac{\partial L}{\partial z^{*}}$. This tells us that we can simplify the complex variable update formula above to only refer to the conjugate Wirtinger derivative $\frac{\partial L}{\partial z^{*}}$, giving us exactly the step we take in optimization.

The complex numbers are represented by the cascading of real and imaginary parts in the last dimension. The derivative implementation of the complex elementary functions follows the gradient rules in Table 1 of Jurling and Fienup (2014). We implement the proposed method with PyTorch 1.8 (Chilamkurthy and Tanamala, 2019), while the derivatives are calculated automatically. All presented results in the following sections were performed on a workstation with an Intel Core i7-6820 CPU and an NVIDIA GTX1080 GPU. Figure 3 shows the image quality of the proposed AD and the traditional Gerchberg–Saxton (GS) concerning the computation time. It takes around one second to optimize one 1,024 × 1,024 hologram with a PSNR ratio more significant than 70 dB and SSIM larger than 0.8. In comparison, the GS method can hardly reach a PSNR larger than 20 dB and SSIM larger than 0.6.

FIGURE 3

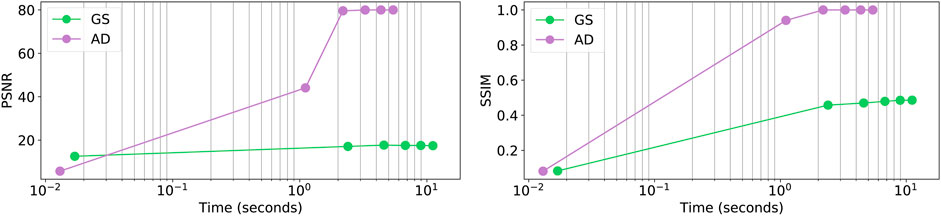
FIGURE 3. Image quality of the proposed AD and the traditional Gerchberg–Saxton (GS) versus computation time.

2.3 Free-Space Wavefield Diffraction

The wave propagation mentioned in the previous sections is free-space diffraction and is implemented with the angular spectrum method (ASM) of the Rayleigh–Sommerfeld diffraction (Goodman, 2005):

$u(x,y)={\int }_{z_1}^{z_2}{\mathcal{F}}^{-1}\left\{\mathcal{F}\left\{u(x,y,z)\right\}H(f_x,f_y,z-z_1)\right\}dz,(12)$

where u(x, y, z) is the complex amplitude at a plane located at z, $\mathcal{F}$ is the Fourier transform, and H is the ASM transfer function given by

$H(f_x,f_y,z)=\left\{\begin{array}{cc}\exp \left(j2\pi z\sqrt{\frac{1}{{\lambda }^2}-(f_x^2+f_y^2)}\right),\hfill & \sqrt{f_x^2+f_y^2}<\frac{1}{\lambda },\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.(13)$

3 Experiments

The SLM in the experiment is HOLOEYE PLUTO with a full resolution of 1,920 × 1,080 pixels and 8 µm pixel pitch. Moreover, the image sensor is Point Grey Research GS3-U3-50S5C, with a resolution of 2,248 × 2,048 pixels and 3.45 µm pixel pitch. The light source was a laser diode with a center wavelength of 532 nm, and the image sensor distance was 250 mm away from the SLM. The four phases used for detection u_dead(x, y) are shown in the above row of Figure 4A, and the corresponding captured holograms are shown in the below row. The phase-shifting hologram reconstruction is shown in Figure 4B, and the propagated wavefield at the SLM plane is shown in Figure 4C. We conducted a calibration to match the size difference between the image sensor and the SLM.

FIGURE 4

FIGURE 4. Four phases and the holograms (A), and the calculated wavefield at the image sensor (B) and SLM (C) planes.

For a target image shown in Figure 5A, we calculated the phase-only holograms without and with the unwanted term suppression, which are shown in the left column of Figures 5B,C. Whether the difference between the conventional and the proposed method is optimizing the zero-order term or not, the computational calculation time is the same. However, we conducted the phase-shifting holography in the proposed method to obtain the zero-order field. The calculation time can be overlooked, but the capture takes time. This can be improved by automatically synchronizing and controlling the SLM and the camera. The corresponding experimentally reconstructed images are shown in the right columns. Comparing the proposed method with the conventional one, we can observe less background noise in Figure 5C, indicating that the proposed technique suppresses some of the unwanted terms. However, some noise still exists, which may be due to the inaccurate modeling of the optical system. This could be improved if we further consider the laser speckle and the SLM’s fill factor that reflects only part of the incident light wave.

FIGURE 5

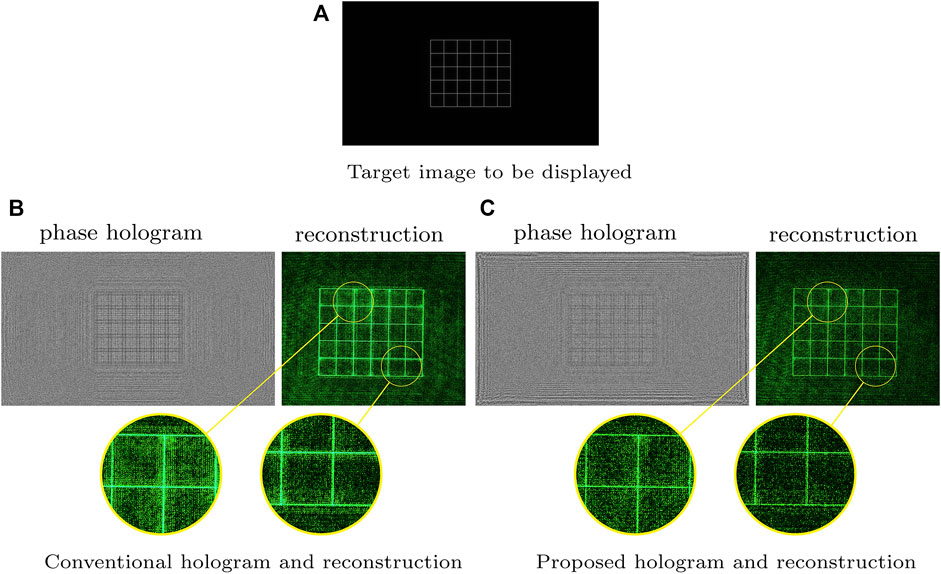
FIGURE 5. Experimental results of conventional (B) and proposed (C) methods for displaying a target image (A).

4 Discussion and Conclusion

We presented a computational holographic display technology that can achieve a lightweight holographic display with high quality. The results show that the automatic differentiable complex wavefield optimization can suppress the unwanted wavefield with the assistance of phase-shifting holography. The automatic differentiable complex wavefield optimization can also be applied to other optical systems requiring aberration or system error corrections.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

NC proposed the idea and conducted the simulation and experiments. CW and WH worked together on the manuscript writing.

Funding

This work was supported by the KAUST individual baseline funding.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arrizón, V., Kinne, S., and Sinzinger, S. (1998). Efficient Detour-phase Encoding of One-Dimensional Multilevel Phase Diffractive Elements. Appl. Opt. 37, 5454. doi:10.1364/ao.37.005454

PubMed Abstract | CrossRef Full Text | Google Scholar

Arrizón, V., Ruiz, U., Carrada, R., and González, L. A. (2007). Pixelated Phase Computer Holograms for the Accurate Encoding of Scalar Complex fields. J. Opt. Soc. Am. A. 24, 3500. doi:10.1364/josaa.24.003500

CrossRef Full Text | Google Scholar

Birch, P., Young, R., Chatwin, C., Farsari, M., Budgett, D., and Richardson, J. (2000). Fully Complex Optical Modulation with an Analogue Ferroelectric Liquid crystal Spatial Light Modulator. Opt. Commun. 175, 347–352. doi:10.1016/s0030-4018(00)00478-810.1016/s0030-4018(00)00478-8

CrossRef Full Text | Google Scholar

Blennow, M. (2018). Mathematical Methods for Physics and Engineering. New York, NY: CRC Press. doi:10.1201/b22209

CrossRef Full Text | Google Scholar

Chakravarthula, P., Peng, Y., Kollin, J., Fuchs, H., and Heide, F. (2019). Wirtinger Holography for Near-Eye Displays. ACM Trans. Graph. 38, 1–13. doi:10.1145/3355089.3356539

CrossRef Full Text | Google Scholar

Chen, C., Lee, B., Li, N.-N., Chae, M., Wang, D., Wang, Q.-H., et al. (2021). Multi-depth Hologram Generation Using Stochastic Gradient Descent Algorithm with Complex Loss Function. Opt. Express, 29, 15089. doi:10.1364/oe.425077

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Zhang, H., Cao, L., and Jin, G. (2020). Non-iterative Phase Hologram Generation with Optimized Phase Modulation. Opt. Express 28, 11380. doi:10.1364/oe.391518

PubMed Abstract | CrossRef Full Text | Google Scholar

Chilamkurthy, S., and Tanamala, S. (2019). Deep Learning and Medical Diagnosis - Authors' Reply. The Lancet 394, 1711. doi:10.1016/s0140-6736(19)32614-510.1016/s0140-6736(19)32614-5

CrossRef Full Text | Google Scholar

de Bougrenet de la Tocnaye, J. L., and Dupont, L. (1997). Complex Amplitude Modulation by Use of Liquid-crystal Spatial Light Modulators. Appl. Opt. 36, 1730. doi:10.1364/ao.36.001730

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerchberg, R. W. (2002). A New Approach to Phase Retrieval of a Wave Front. J. Mod. Opt. 49, 1185–1196. doi:10.1080/09500340110114425

CrossRef Full Text | Google Scholar

Goodman, J. (2005). Introduction to Fourier Optics. Englewood, Colo: Roberts & Co.

Google Scholar

Gregory, D. A., Kirsch, J. C., and Tam, E. C. (1992). Full Complex Modulation Using Liquid-crystal Televisions. Appl. Opt. 31, 163. doi:10.1364/ao.31.000163

PubMed Abstract | CrossRef Full Text | Google Scholar

Griewank, A., and Walther, A. (2008). Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. University City, Philadelphia: Society for Industrial and Applied Mathematics. doi:10.1137/1.9780898717761

CrossRef Full Text | Google Scholar

Hong, J., Kim, Y., Choi, H.-J., Hahn, J., Park, J.-H., Kim, H., et al. (2011). Three-dimensional Display Technologies of Recent Interest: Principles, Status, and Issues [invited]. Appl. Opt. 50, H87. doi:10.1364/ao.50.000h87

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsieh, M.-L. (2007). Improvement of the Complex Modulated Characteristic of Cascaded Liquid crystal Spatial Light Modulators by Using a Novel Amplitude Compensated Technique. Opt. Eng. 46, 070501. doi:10.1117/1.2750658

CrossRef Full Text | Google Scholar

Hsueh, C. K., and Sawchuk, A. A. (1978). Computer-generated Double-phase Holograms. Appl. Opt. 17, 3874. doi:10.1364/ao.17.00387410.1364/ao.17.003874

PubMed Abstract | CrossRef Full Text | Google Scholar

Improso, W. D. G. D., Tapang, G. A., and Saloma, C. A. (2017). “Suppression of Zeroth-Order Diffraction in Phase-Only Spatial Light Modulator via Destructive Interference with a Correction Beam,” in Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (Porto, Portugal: SCITEPRESS - Science and Technology Publications). doi:10.5220/0006129802080214

CrossRef Full Text | Google Scholar

Improso, W. D. G., Hilario, P. L. A., and Tapang, G. (2014). “Zero Order Diffraction Suppression in a Phase-Only Spatial Light Modulator via the GS Algorithm,” in Frontiers in Optics 2014 (Tucson, AZ: OSA). doi:10.1364/fio.2014.ftu4c.3

CrossRef Full Text | Google Scholar

Jeong, M.-O., Kim, N., and Park, J.-H. (2008). Elemental Image Synthesis for Integral Imaging Using Phase-Shifting Digital Holography. J. Opt. Soc. Korea 12, 275–280. doi:10.3807/josk.2008.12.4.275

CrossRef Full Text | Google Scholar

Juday, R. D., and Florence, J. M. (1991). “Full-complex Modulation with Two One-Parameter Slms,” in Wave Propagation and Scattering in Varied Media II. Editor VK. Varadan (San Diego, CA: SPIE). doi:10.1117/12.49656

CrossRef Full Text | Google Scholar

Jurling, A. S., and Fienup, J. R. (2014). Applications of Algorithmic Differentiation to Phase Retrieval Algorithms. J. Opt. Soc. Am. A. 31, 1348. doi:10.1364/josaa.31.001348

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Kreutz-Delgado, K. (2009). The Complex Gradient Operator and the Cr-Calculus. ArXiv.

Google Scholar

Liang, J., Wu, S.-Y., Fatemi, F. K., and Becker, M. F. (2012). Suppression of the Zero-Order Diffracted Beam from a Pixelated Spatial Light Modulator by Phase Compression. Appl. Opt. 51, 3294. doi:10.1364/ao.51.003294

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendoza-Yero, O., Mínguez-Vega, G., and Lancis, J. (2014). Encoding Complex fields by Using a Phase-Only Optical Element. Opt. Lett. 39, 1740. doi:10.1364/ol.39.001740

PubMed Abstract | CrossRef Full Text | Google Scholar

Neto, L. G., Roberge, D., and Sheng, Y. (1996). Full-range, Continuous, Complex Modulation by the Use of Two Coupled-Mode Liquid-crystal Televisions. Appl. Opt. 35, 4567. doi:10.1364/ao.35.004567

PubMed Abstract | CrossRef Full Text | Google Scholar

Palima, D., and Daria, V. R. (2007). Holographic Projection of Arbitrary Light Patterns with a Suppressed Zero-Order Beam. Appl. Opt. 46, 4197. doi:10.1364/ao.46.004197

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Y., Choi, S., Padmanaban, N., Kim, J., and Wetzstein, G. (2020). “Neural Holography,” in ACM SIGGRAPH 2020 Emerging Technologies (Virtual Event, United States: ACM). doi:10.1145/3388534.3407295

CrossRef Full Text | Google Scholar

Remmert, R. (1991). Theory of Complex Functions. New York, NY: Springer New York.

Google Scholar

Ronzitti, E., Guillon, M., de Sars, V., and Emiliani, V. (2012). LCoS Nematic SLM Characterization and Modeling for Diffraction Efficiency Optimization, Zero and Ghost Orders Suppression. Opt. Express 20, 17843. doi:10.1364/oe.20.017843

PubMed Abstract | CrossRef Full Text | Google Scholar

Siemion, A., Sypek, M., Suszek, J., Makowski, M., Siemion, A., Kolodziejczyk, A., et al. (2012). Diffuserless Holographic Projection Working on Twin Spatial Light Modulators. Opt. Lett. 37, 5064. doi:10.1364/ol.37.005064

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, H., Sung, G., Choi, S., Won, K., Lee, H.-S., and Kim, H. (2012). Optimal Synthesis of Double-phase Computer Generated Holograms Using a Phase-Only Spatial Light Modulator with Grating Filter. Opt. Express 20, 29844. doi:10.1364/oe.20.029844

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, P., Chang, S., Liu, S., Tao, X., Wang, C., and Zheng, Z. (2018). Holographic Near-Eye Display System Based on Double-Convergence Light Gerchberg-saxton Algorithm. Opt. Express 26, 10140. doi:10.1364/oe.26.010140

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, B., Hong, X., Wang, K., Chen, X., Liu, S., Krolikowski, W., et al. (2021). Nonlinear Detour Phase Holography. Nanoscale 13, 2693–2702. doi:10.1039/d0nr07069f

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Chen, N., and Heidrich, W. (2021). Towards Self-Calibrated Lens Metrology by Differentiable Refractive Deflectometry. Opt. Express 29, 30284–30295. doi:10.1364/oe.433237

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, Y., Wang, J., Chen, C., Liu, C.-J., Jin, F.-M., and Chen, N. (2021). Adaptive Weighted Gerchberg-saxton Algorithm for Generation of Phase-Only Hologram with Artifacts Suppression. Opt. Express 29, 1412. doi:10.1364/oe.413723

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamaguchi, I., and Zhang, T. (1997). Phase-shifting Digital Holography. Opt. Lett. 22, 1268. doi:10.1364/ol.22.001268

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaperty, W., and Kozacki, T. (2018). “Numerical Model of Diffraction Effects of Pixelated Phase-Only Spatial Light Modulators,” in Speckle 2018: VII International Conference on Speckle Metrology. Editors M Józwik, L. R Jaroszewicz, and M Kujawińska (Janów Podlaski, Poland: SPIE). doi:10.1117/12.2319739

CrossRef Full Text | Google Scholar