Frequency-to-Time Mapping Technique for Direct Spectral Characterization of Biphoton States From Pulsed Spontaneous Parametric Processes

The well-established frequency-to-time mapping technique is employed as a convenient and time-efficient method to directly characterize the spectral correlations of biphoton states from a pulsed-excited spontaneous parametric down-conversion process. We were enabled by this technique to implement for the first time, the spectral Hanbury-Brown and Twiss measurement, revealing directly the single frequency-mode bandwidth of the biphoton state.

Introduction

The characterization of spectral and temporal properties of biphoton states generated in spontaneous parametric down-conversion (SPDC) or spontaneous four-wave mixing (SFWM) is essential to assess their utility towards different applications in quantum information processing and metrology. For example, the joint spectral intensity (JSI) of biphoton states should often be tailor-made in order to achieve quantum interference of high visibility (Metcalf et al., 2013; Joshi et al., 2020; Khodadad Kashi et al., 2021). To date the characterization techniques have been primarily based on successive and time-consuming frequency scans over the biphoton state spectrum. Spectral filtering of photonpairs yields inefficient detection rates, which degrades the signal-to-noise ratio (SNR) and in turn restricts the accessible spectral resolution. In addition, the limited frequency-bandwidth of the filtering devices further constraints the spectral resolution of the scheme. In alternative characterization techniques, such as the one based on position-to-frequency mapping, a low spectral resolution per pixel/detector as well as a low frequency sampling rate are the main limitations (Johnsen et al., 2014). In another approach, which relies on Fourier spectroscopy, a very low spectral resolution paired with measurement instability and long integration time to reconstruct the JSI can be identified (Wasilewski et al., 2006; Eckstein et al., 2014). In methods based on stimulated SPDC or SFWM, despite the contribution of seed light in providing high generation rates and hence enabling a fast implementation, the stimulated emission itself appears as a source of noise due to the spatial and spectral overlap with photonpairs originating from the parametric process (Eckstein et al., 2014; Jizan et al., 2015; Kaneda et al., 2020).

In this paper, we demonstrate the first-time experimental implementation of spectral Hanbury Brown and Twiss (HBT) interferometry via the well-established frequency-to-time mapping (FTM) technique (Leaird et al., 2011; Goda, K. and Jalali, B. 2013; Goda et al., 2009; Mahjoubfar et al., 2017), also commonly referred to as dispersive Fourier transform (DFT) (Wetzel et al., 2012; Godin et al., 2013; Nguyen et al., 2013), which relies on chromatic dispersion to translate the frequency components of an optical spectrum onto a time-stretched temporal waveform (Lu et al., 2018; Goda, K. and Jalali, B., 2013). The FTM had been previously demonstrated (Valencia et al., 2002; Brida et al., 2006; Baek et al., 2008) and employed as a technique to characterize the JSI of parametric processes (Avenhaus et al., 2009; Eckstein et al., 2014). However, in these implementations the spectral resolution was limited due to the employment of avalanche photo detectors with large timing jitters, which to be compensated for, required additional lengths of the dispersion compensating fiber (DCF) at the cost of large amounts of loss imposed on the measurement. In our present work, the FTM technique enabled us to directly (through only a single coincidence measurement) characterize the single frequency-mode bandwidth and the spectral correlations of a biphoton state generated in a pulsed-driven SPDC process within a periodically-poled lithium niobate (PPLN) waveguide.

The frequency components of the biphoton state are temporally resolved post-propagation through a DCF. The fine timing resolution of our singlephoton detection system allows for the spectrally-resolved detection and thus the direct frequency-mapping of the biphoton state in time. In particular, this technique enables the spectral characterization of biphoton states without the need to perform time-consuming successive frequency scans with expensive filtering devices. Specifically, this is achieved through only a single coincidence measurement over the SPDC biphoton spectrum: contrary to the hitherto commonly-adopted schemes composed of successive scans over the frequency distribution of the biphoton state, in our approach the time-resolved coincident detections are exploited to directly reconstruct the signal-idler JSI, to gain access to the coincidence to accidental ratio (CAR), and to directly implement the spectral HBT interferometry (Silva et al., 2016). Importantly, for the first time we directly measure and demonstrate the dependency of the second-order auto-correlation function $g^{\left(2\right)}\left(\Delta \nu \right)$ on the spectral difference $\Delta \nu$ of the frequency components within the signal spectrum of the biphoton state, in contrast to the common demonstrations that exhibit the variations of $g^{\left(2\right)}\left(\tau \right)$ as function of delay $\tau$ between the photons’ arrival times at the detectors (Jeltes et al., 2007; Bromberg et al., 2010; Silva et al., 2016; Abbas and Wang 2021). It is important to note that the $g^{\left(2\right)}\left(\Delta \nu \right)$ function incorporates information regarding the spectral correlations, which can be used to determine the single frequency-mode bandwidth of the system, whereas the $g^{\left(2\right)}\left(\tau \right)$ contains information over the temporal correlations and as a result, for impure states, the Fourier transformation does not hold between the two, $\mathrm{ℱ}\left\{g^{\left(2\right)}\left(\tau \right)\right\}\ne g^{\left(2\right)}\left(\Delta \nu \right)$.

Experimental Setup

The experimental setup (see Figure 1A) consisted of a PPLN waveguide excited by a 10 $\text{μW}$ pulsed mode-locked laser (50 MHz repetition rate) whose spectral bandwidth was filtered to a full-width at half-maximum (FWHM) of ${\delta }_{pump}$ = 200 GHz and aligned at the center wavelength of ${\lambda }_{pump}$ = 778.8 nm. Through type-0 SPDC processes within the PPLN, photons of the excitation pulse-train were down-converted to highly time-frequency correlated photon pairs. The frequency distribution of the created photon-pairs spans over a bandwidth of several THz, which is determined by the SPDC phase-matching bandwidth. Cascaded with the PPLN, a DCF was placed—with GDD = 960 ps/nm (GDD as group delay dispersion), and 6.5 dB loss measured for one passage through the fiber—which allowed for the formation of a scaled and temporally-resolved replica of the SPDC biphoton spectrum. With the use of a programmable waveshaper (Finisar Waveshaper 4000S), a bandpass filter with arbitrary $\Delta i{n}_{SPDC}$ = 800 GHz bandwidth was defined to filter-out the SPDC biphoton spectrum symmetric to its degeneracy point ${\lambda }_d$ = 1,557.6 nm (see Figure 1B). Specifically, the higher- (lower-) frequency spectral window, i.e., the signal (idler) spectrum with $\Delta f_{signal\left(idler\right)}$ = 400 GHz bandwidth, was split 50:50 in to separate ports on the waveshaper and was directed towards the superconducting nanowire single photon detectors (SNSPDs) D1 and D2 (D3 and D4). A start-stop timing electronics unit (Swabian Instruments; time-tagger module) with its operation synchronized with the laser repetition-rate, was employed to collect the coincident detections. The total integration time for the single coincidence measurement was 11 h.

FIGURE 1

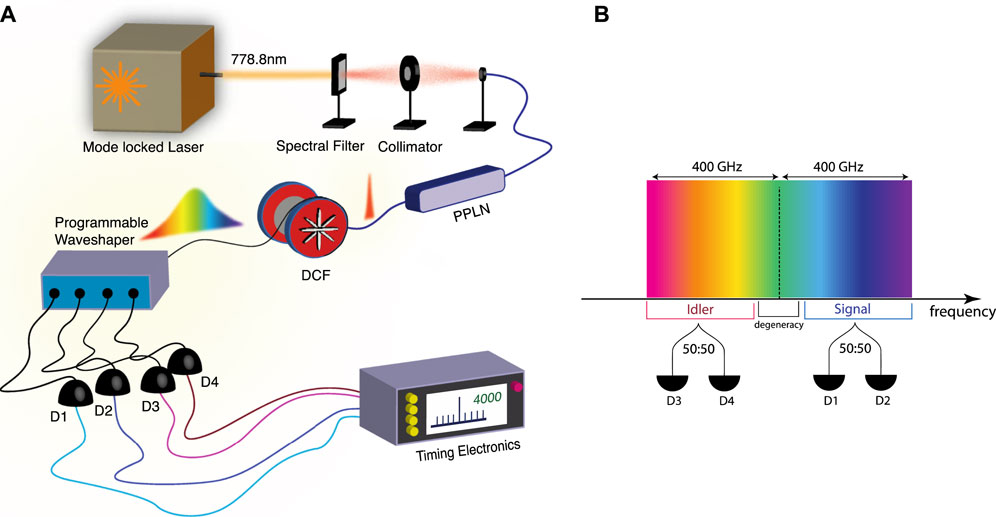
FIGURE 1. (A) Experimental setup which employs the FTM technique to characterize the SPDC biphoton spectrum (see main text for more details). (B) Spectral configuration defined with the use of a programmable waveshaper for characterization of the SPDC biphoton spectrum. The signal (idler) spectral intensity with $\Delta f_{signal\left(idler\right)}=400$ GHz bandwidth is half-split on two different output ports on the waveshaper and directed towards the detectors D1 and D2 (D3 and D4) (PPLN: periodically-poled lithium niobate; DCF: dispersion compensating fiber).

Frequency-to-Time Mapping

The frequency-to-time mapped replica of the signal and idler spectra are shown in Figure 2. The frequency components within the signal and idler spectrum ($\Delta f_{signal\left(idler\right)}$ = 400 GHz) disperse through the DCF and create time-resolved detections in synchronization with the laser repetition rate of 50 MHz, hence over the pulse period of $T_{pulse}$ = 20 ns.

FIGURE 2

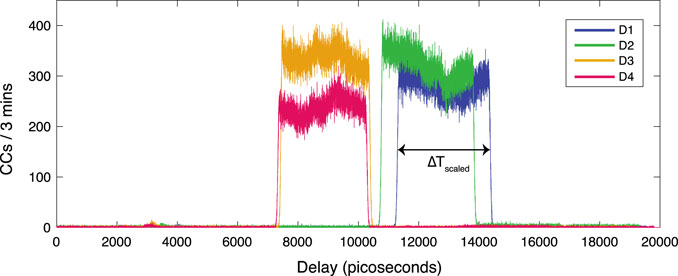
FIGURE 2. Time-stretched replica of the signal and idler spectra. The $\Delta {\mathit{T}}_{\mathit{scaled}\left(\mathit{idler}\right)}$ = 400 GHz-bandwidth of the signal and idler spectra are mapped onto a temporally-scaled intensity profile of $\Delta {\mathit{T}}_{\mathit{scaled}}$ = 3,300 ps width, corresponding to a FTM coefficient of $C_{FTM}\mathrm{\sim }$0.1212 GHz/ps. The slight deviation between the intensity profiles can be ascribed to the systems electronics, slight difference in detectors’ timing resolution or the optical path lengths, as well as the polarization sensitivity of the SNSPDs. Detections on detectors D1 and D2 (D3 and D4) correspond to the signal (idler) spectrum with higher (lower) frequency. Considering a normal dispersion, the higher-frequency nature of the signal spectrum is reflected in its larger delay in comparison to the idler spectrum.

By relating the time-scaled replica of $\Delta T_{scaled}\mathit{ }\sim$ 3,300 ps temporal-width to the initial undispersed spectral bandwidth of $\Delta f_{signal\left(idler\right)}$ = 400 GHz, a FTM correspondence of $C_{FTM}\sim$ 0.1212 GHz/ps was measured for the system, which is in good agreement with the 960 ps/nm GDD of the DCF. Considering the timing resolution $t_r$ = 25 ps of our SNSPDs, the net spectral resolution of ${\nu }_r \sim$ 3.03 GHz is measured for the whole single-photon spectrometer, that is the combination of the SNSPDs with the DCF.

It is important to note that the frequency resolving capability achievable with our spectrometer is 29 and 10 times higher than those reported in the articles by Avenhaus et al. (2009) and Eckstein et al. (2014), respectively. In these experiments the detectors' timing jitter of 180 and 250 ps have restricted the achievable spectral resolutions to $\sim$89.8 GHz and $\sim$ 28.89 GHz at $\sim$1,550 nm wavelength. The large timing jitter of the detection system required the employment of DCF with much larger GDD as well as the decrease of the pulsed-laser repetion rate to obviate the possibilty of pulse overalpping. Besides limited spectral resolution, this also leads to the loss of information as well as considerable overhead in the measurement integration time. It is important to note that in our setup the repetion rate of 50 MHz allowed for a maximum temporal broadening of 20 ns such that no adjacent pulses would overlap.

By comparison, the presented system here allows a more efficient demonstration of FTM-assisted spectral characterization of parametric processes, mitigating in a more efficient way the effects of loss by having incorporated an infrastructure of better specifications.

Second-Order Auto-Correlation Function

Propagation of the SPDC biphoton state spectrum through the DCF led to time-resolved detection of its frequency components. As a result, by probing the collected two-fold coincident events on detectors D1 and D2, we were able to directly measure the spectral second-order auto-correlation function (Silva et al., 2016)

$g^{\left(2\right)}\left({\nu }_1,{\nu }_2\right)=\mathit{ }\frac{\langle {\widehat{a}}^{†}\left({\nu }_1\right) {\widehat{a}}^{†}\left({\nu }_2\right)\widehat{a}\left({\nu }_2\right)\widehat{a}\left({\nu }_1\right)\rangle }{\langle {\widehat{a}}^{†}\left({\nu }_1\right)\widehat{a}\left({\nu }_1\right)\rangle \langle {\widehat{a}}^{†}\left({\nu }_2\right)\widehat{a}\left({\nu }_2\right)\rangle }$

associated with the signal field. Figure 3A illustrates the dependency of $g^{\left(2\right)}({\nu }_1,{\nu }_2)$ on frequency offsets ${\nu }_1$ and ${\nu }_2$ with respect to the SPDC degeneracy point, ${\lambda }_d$ = 1,557.6 nm, and starting from ${\nu }_1= {\nu }_2$ = 50 GHz to exclude the coincidence counts coming from signal-idler frequency correlations.

FIGURE 3

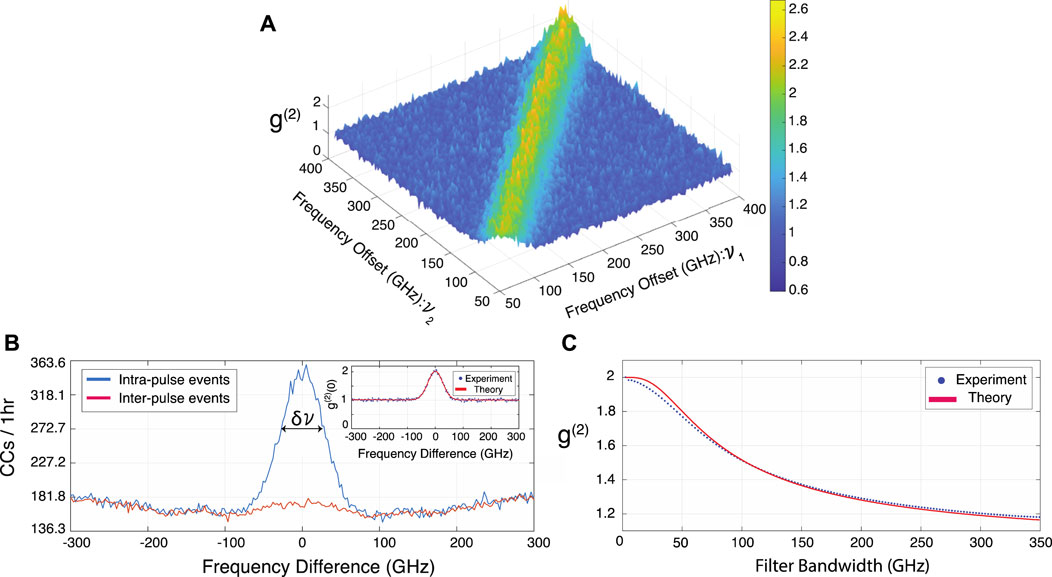
FIGURE 3. (A) Spectral second-order auto-correlation ${\mathit{g}}^{\left(2\right)}({\mathit{\nu }}_1,{\mathit{\nu }}_2)$ as a function of the photons frequency offset ${\mathit{\nu }}_1$ and ${\mathit{\nu }}_2$ from the SPDC degeneracy point, ${\mathit{\lambda }}_{\mathit{d}}$ = 1,557.6 nm. (B) Coincidence detection rate as function of frequency difference $\Delta \mathit{\nu }$ between the spectral components of the signal spectrum. The inset Figure illustrates the dependency of ${\mathit{g}}^{\left(2\right)}$ ($\Delta \mathit{\nu }$) on $\Delta \mathit{\nu }$. (C) Variation of ${\mathit{g}}^{\left(2\right)}\left(\Delta \mathit{f}\right)$ as a function of the spectral filter bandwidth $\Delta \mathit{f}$. In panel (B), the FWHM of $\mathit{\delta \nu }$ = 57.18 $\pm$ 0.94 $\mathit{ }$GHz is the single frequency-mode bandwidth of our system (see text for more details).

In Figure 3B, the total intra- and inter-pulse coincidence counts as function of spectral difference $\Delta \nu$ is shown, i.e. ${\nu }_1=\nu$ and ${\nu }_2=\nu$ + $\Delta \nu$. The intra-pulse events refer to coincidence detections that have occurred within the same pulse period, whereas the inter-pulse events correspond to coincidence events between different pulses. For the case of intra-pulse events and at zero-frequency difference, $\Delta \nu =0$, an increased number of coincidence detections is observed. The ratio of the intra- to the inter-pulse coincidence counts reaches $g^{\left(2\right)}\left(0\right)$ = 2.0756 $\pm$ 0.0587 (see the inset of Figure 3B). The FWHM of the spectrum at which the peak number of intra-pulse events were collected relates to the single frequency-mode bandwidth of the system. With a Lorentzian fit, we could directly determine the single frequency-mode bandwidth $\delta \nu$ = 57.18 $\pm$ 0.94 GHz. This value was additionally verified by comparison with the conventional measurement of the $g^{\left(2\right)}\left(\Delta f\right)$ function, observing its dependency on the spectral filter bandwidth $\Delta f$, and by fitting a theoretical model (Zielnicki et al., 2018) to the experimental data (see Figure 3C). It is important to note that in our approach, we were able to demonstrate the $g^{\left(2\right)}\left(\Delta \nu \right)$ function for various frequency modes of the same spectral differences. This is in contrast to the conventionally performed measurements of the $g^{\left(2\right)}\left(\Delta f\right)$ where the gradual widening of the filter bandwidth is implemented on an arbitrarily selected single frequency component of the measured field (Bruno et al., 2014; Schwartz et al., 2018; Meyer-Scott et al., 2017).

Assuming an undispersed SPDC biphoton spectrum with a total signal bandwidth of $\Delta f_{signal}$ = $400$ GHz, under Gaussian profile approximation, the corresponding transform-limited temporal modes should be of approximately $\delta t\approx$ 1.1 ps temporal width. Moreover, under such conditions, the single frequency-mode bandwidth of our system, $\delta \nu$ = 57.18 $\pm$ 0.94 GHz, would correspond to a $\Delta \tau \approx$ 7.7 ps-wide wave packet (See Figures 4A,B). In light of the timing resolution $t_r$ = 25 ps of our single-photon detectors, the temporal wave packet would thus be unresolvable by our detection system. This suggests that by measuring the $g^{\left(2\right)}$ ($\tau$) as function of delay $\tau$ between the photons’ arrival times at the detectors, the determination of the single frequency-mode bandwidth would lead to incorrect values. It should be noted that with a FTM factor of $C_{FTM}\approx$ 0.1212 GHz/ps and for the timing resolution $t_r$ = 25 ps of our SNSPDs, the whole single-photon spectrometer composed of SNSPDs and the DCF allows for the frequency resolution of ${\nu }_r$ ≈ 3.03 GHz, which guarantees the reliable measurement of $\delta \nu$ = 57.18 $\pm$ 0.94 $$GHz as the single frequency-mode bandwidth.

FIGURE 4

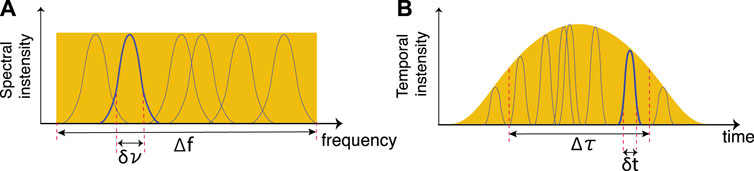
FIGURE 4. Schematic illustration of the signal (A) spectral and its reciprocal (B) temporal intensity profiles under the assumption of propagation through a non-dispersive medium. The undispersed signal spectrum ($\Delta f_{signal}$ = 400 GHz) and the single frequency-mode bandwidth of $\delta \nu$ = 57.18 $\pm 0.94$ GHz correspond to a temporal intensity profile with FWHM of $\Delta \tau$ = 7.7 ps and composed of transform-limited temporal modes with $\delta t=1.1\text{ps}$ temporal width (see main text for more details).

With this demonstration, we lay particular stress on the necessity of system calibration prior to spectral characterization of biphoton states. For single photon detectors with timing resolution that exceeds the reciprocal of the biphoton state spectrum, the accuracy of the measured single frequency-mode bandwidth is undermined if gauged via observing the dependency of the $g^{\left(2\right)}\left(\tau \right)$ as function of delay $\tau$ in coincident detections. This highlights the advantage of the FTM technique for reliable spectral characterization of biphoton states generated from parametric processes.

Joint Spectral Intensity and Coincidence to Accidental Ratio

The FTM technique allows for a direct measurement of the JSI and the CAR. The time-resolved coincidence events corresponding to the high-purity signal-idler photon pairs were collected to reconstruct the JSI and to obtain the CAR of our photon-pair source.

In Figure 5A, the JSI of the signal and idler photons is illustrated as function of their symmetric positive and negative frequency offset from the degeneracy point, ${\lambda }_d$ = 1,557.6 nm, respectively. The diagram in Figure 5B illustrates the total signal-idler intra- and inter-pulse coincidence counts versus the spectral difference between the absolute values of the signal and idler frequency offsets from the degeneracy point. At perfectly symmetric spectral distance from the degeneracy point, where the frequency anti-correlation lies, the ratio between the intra- (actual) and inter-pulse (accidental) coincidence counts is measured to be $\sim$ 80 (see inset in Figure 5B), equivalent to $\sim$19.03-dB SNR.

FIGURE 5

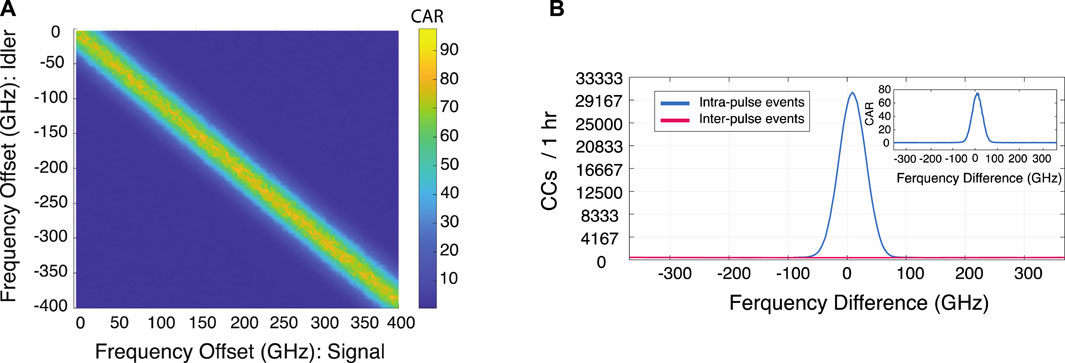
FIGURE 5. (A) Joint Spectral Intensity coincidence to accidental ratio (CAR) versus signal and idler frequency offset from the SPDC degeneracy point ${\mathit{\lambda }}_{\mathit{d}}$ = 1,557.6 nm (B) Coincidence count rate corresponding to the intra-pulse and inter-pulse coincident events versus the spectral difference between the signal and idler frequency offset from the degeneracy point. The inset in panel (B) demonstrates the ratio of intra-pulse (actual) to inter-pulse (accidental) coincidence events (CAR).

It is important to note that the FTM technique is merely considered for spectral characterization of broad spectra such as biphoton state spectra of ultra-short pulsed-excited parametric processes and for sources where the temporal width of the photons’ wave packets fall below the temporal resolution of the detection system. In particular, spectral characterization of photon pairs generated in high Q-factor (Q > 1000000) resonators (Puckett et al., 2021) as well as from continuous wave-driven parametric processes are practicable neither with FTM technique nor via the state-of-the-art programmable filters, owing to the ultra-narrow line-widths of the modes that fall in the order of kHz. These systems are better characterized directly in the time-domain.

Conclusion

To date the HBT interferometry had been entirely performed by probing temporal correlations, together with variable spectral filtering. In this research we were enabled by the FTM technique to show for the first time the direct measurement of the spectral second-order autocorrelation function. Via a single coincidence measurement, we performed direct spectral characterization of a biphoton state from pulsed-excited SPDC process. To this end, time-resolved intra- and inter-pulse coincidence detections were collected on-the-fly in synchronization with the pulsed-laser repetition rate, and by relying on the fine timing resolution of our SNSPDs, $t_r$ = 25 ps. In this work, the importance of system calibration prior to spectral characterization was highlighted; With a single-photon detection system of a timing resolution longer than the reciprocal of the biphoton state spectrum, precise determination of the single frequency-mode bandwidth will not be reliably achievable via time-domain analysis. In this regard, our single-photon spectrometer provided a frequency resolution of ${\nu }_r\approx$ 3.03 GHz, which confirms the accuracy of our spectral HBT experiment in determining $\delta \nu$ = 57.18 $\pm$ 0.94 GHz as the single frequency-mode bandwidth. As a result, we were able to demonstrate the efficient application of the FTM technique for spectral characterization of parametric processes, revealing its potentiality by making use of elaborate experimental infrastructure that could establish a better trade-off between loss and spectral resolution. In this implementation higher spectral resolution could be achievable with longer DCF (or larger GDD values), however at the cost of additional and in turn quadratic overhead in integration time. In addition, applying higher pump powers could also improve the integration time, considering the fact that the HBT interferometry is intrinsically power-independent. This, however does not hold true for the JSI reconstruction as the CAR would degrade consequently.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AK performed the conception and design of the study with contributions of MK. AK performed the experiment, the data analysis and wrote the manuscript. LS, RH, and BW provided input and contributed to discussion. MK supervised and coordinated the project. All authors contributed to the revision of the manuscript.

Funding

AK and MK acknowledge funding from the German Federal Ministry of Education and Research, Quantum Futur Program (PQuMAL). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 950618 (STREAMLINE project) and No. 947603 (QFreC project). BW further acknowledges the support of the French ANR through the OPTIMAL project (ANR-20-CE30-0004) and the Région Nouvelle-Aquitaine (SCIR & SPINAL projects).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbas, A., and Wang, L.-G. (2021). Hanbury Brown and Twiss Effect in the Spatiotemporal Domain II: The Effect of Spatiotemporal Coupling. OSA Continuum 4 (8), 2221. doi:10.1364/osac.434377

CrossRef Full Text | Google Scholar

Avenhaus, M., Eckstein, A., Mosley, P. J., and Silberhorn, C. (2009). Fiber-assisted Single-Photon Spectrograph. Opt. Lett. 34 (18), 2873–2875. doi:10.1364/ol.34.002873

PubMed Abstract | CrossRef Full Text | Google Scholar

Baek, S.-Y., Kwon, O., and Kim, Y.-H. (2008). Nonlocal Dispersion Control of a Single-Photon Waveform. Phys. Rev. A. 78 (1), 1–4. doi:10.1103/PhysRevA.78.013816

CrossRef Full Text | Google Scholar

Brida, G., Chekhova, M. V., Genovese, M., Gramegna, M., and Krivitsky, L. A. (2006). Dispersion Spreading of Biphotons in Optical Fibers and Two-Photon Interference. Phys. Rev. Lett. 96 (14), 1–4. doi:10.1103/PhysRevLett.96.143601

PubMed Abstract | CrossRef Full Text | Google Scholar

Bromberg, Y., Lahini, Y., Small, E., and Silberberg, Y. (2010). Hanbury Brown and Twiss Interferometry with Interacting Photons. Nat. Photon 4 (10), 721–726. doi:10.1038/nphoton.2010.195

CrossRef Full Text | Google Scholar

Bruno, N., Martin, A., Guerreiro, T., Sanguinetti, B., and Thew, R. T. (2014). Pulsed Source of Spectrally Uncorrelated and Indistinguishable Photons at Telecom Wavelengths. Opt. Express 22 (14), 17246. doi:10.1364/oe.22.017246

PubMed Abstract | CrossRef Full Text | Google Scholar

Eckstein, A., Boucher, G., Lemaître, A., Filloux, P., Favero, I., Leo, G., et al. (2014). High-Resolution Spectral Characterization of Two Photon States via Classical Measurements. Laser Photon. Rev. 8 (5), L76–L80. doi:10.1002/lpor.201400057

CrossRef Full Text | Google Scholar

Goda, K., and Jalali, B. (2013). Dispersive Fourier Transformation for Fast Continuous Single-Shot Measurements. Nat. Photon 7 (2), 102–112. doi:10.1038/nphoton.2012.359

CrossRef Full Text | Google Scholar

Goda, K., Solli, D. R., Tsia, K. K., and Jalali, B. (2009). Theory of Amplified Dispersive Fourier Transformation. Phys. Rev. A. 80 (4). doi:10.1103/PhysRevA.80.043821

CrossRef Full Text | Google Scholar

Godin, T., Wetzel, B., Sylvestre, T., Larger, L., Kudlinski, A., Mussot, A., et al. (2013). Real Time Noise and Wavelength Correlations in Octave-Spanning Supercontinuum Generation. Opt. Express 21 (15), 18452. doi:10.1364/oe.21.018452

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeltes, T., McNamara, J. M., Hogervorst, W., Vassen, W., Krachmalnicoff, V., Schellekens, M., et al. (2007). Comparison of the Hanbury Brown-Twiss Effect for Bosons and Fermions. Nature 445 (7126), 402–405. doi:10.1038/nature05513

PubMed Abstract | CrossRef Full Text | Google Scholar

Jizan, I., Helt, L. G., Xiong, C., Collins, M. J., Choi, D.-Y., Joon Chae, C., et al. (2015). Bi-Photon Spectral Correlation Measurements from a Silicon Nanowire in the Quantum and Classical Regimes. Sci. Rep. 5 (July), 1–9. doi:10.1038/srep12557

CrossRef Full Text | Google Scholar

Johnsen, K. D., Kolenderski, P., Scarcella, C., Thibault, M., Tosi, A., and Jennewein, T. (2014). Time and Spectrum-Resolving Multiphoton Correlator for 300-900 Nm. J. Appl. Phys. 116 (14), 143101. doi:10.1063/1.4897296

CrossRef Full Text | Google Scholar

Joshi, C., Farsi, A., Dutt, A., Kim, B. Y., Ji, X., Zhao, Y., et al. (2020). Frequency-Domain Quantum Interference with Correlated Photons from an Integrated Microresonator. Phys. Rev. Lett. 124 (14), 143601. doi:10.1103/PhysRevLett.124.143601

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaneda, F., Oikawa, J., Yabuno, M., China, F., Miki, S., Terai, H., et al. (2020). Spectral Characterization of Photon-Pair Sources via Classical Sum-Frequency Generation. Opt. Express 28 (26), 38993. doi:10.1364/oe.412448

PubMed Abstract | CrossRef Full Text | Google Scholar

Khodadad Kashi, A., and Kues, M. (2021). Spectral Hong-Ou-Mandel Interference between Independently Generated Single Photons for Scalable Frequency‐Domain Quantum Processing. Laser Photon. Rev. 15 (5), 2000464–2000466. doi:10.1002/lpor.202000464

CrossRef Full Text | Google Scholar

Torres-Company, V., Leaird, D. E., and Weiner, A. M. (2011). Dispersion Requirements in Coherent Frequency-To-Time Mapping. Opt. Express 19 (24), 24718. doi:10.1364/oe.19.024718

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, H.-H., Odele, O. D., Leaird, D. E., and Weiner, A. M. (2018). Arbitrary Shaping of Biphoton Correlations Using Near-Field Frequency-To-Time Mapping. Opt. Lett. 43 (4), 743. doi:10.1364/ol.43.000743

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahjoubfar, A., Churkin, D. V., Barland, S., Broderick, N., Turitsyn, S. K., and Jalali, B. (2017). Time Stretch and its Applications. Nat. Photon 11 (6), 341–351. doi:10.1038/nphoton.2017.76

CrossRef Full Text | Google Scholar

Metcalf, B. J., Thomas-Peter, N., Spring, J. B., Kundys, D., Broome, M. A., Humphreys, P. C., et al. (2013). Multiphoton Quantum Interference in a Multiport Integrated Photonic Device. Nat. Commun. 4. doi:10.1038/ncomms2349

CrossRef Full Text | Google Scholar

Meyer-Scott, E., Montaut, N., Tiedau, J., Sansoni, L., Herrmann, H., Bartley, T. J., and Silberhorn, C. (2017). Limits on the Heralding Efficiencies and Spectral Purities of Spectrally Filtered Single Photons from Photon-Pair Sources. Phys. Rev. A. 95 (6), 1–8. doi:10.1103/PhysRevA.95.061803

CrossRef Full Text | Google Scholar

Nguyen, D. M., Godin, T., Toenger, S., Combes, Y., Wetzel, B., Sylvestre, T., et al. (2013). Incoherent Resonant Seeding of Modulation Instability in Optical Fiber. Opt. Lett. 38 (24), 5338. doi:10.1364/ol.38.005338

PubMed Abstract | CrossRef Full Text | Google Scholar

Puckett, M. W., Liu, K., Chauhan, N., Zhao, Q., Jin, N., Cheng, H., et al. (2021). 422 Million Intrinsic Quality Factor Planar Integrated All-Waveguide Resonator with Sub-MHz Linewidth. Nat. Commun. 12 (1), 1–8. doi:10.1038/s41467-021-21205-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwartz, M., Schmidt, E., Rengstl, U., Hornung, F., Hepp, S., Portalupi, S. L., et al. (2018). Fully On-Chip Single-Photon Hanbury-Brown and Twiss Experiment on a Monolithic Semiconductor-Superconductor Platform. Nano Lett. 18 (11), 6892–6897. doi:10.1021/acs.nanolett.8b02794

PubMed Abstract | CrossRef Full Text | Google Scholar

Silva, B., Sánchez Muñoz, C., Ballarini, D., González-Tudela, A., De Giorgi, M., Gigli, G., et al. (2016). The Colored Hanbury Brown-Twiss Effect. Sci. Rep. 6, 1–9. doi:10.1038/srep37980

PubMed Abstract | CrossRef Full Text | Google Scholar

Valencia, A., Chekhova, M. V., Trifonov, A., and Shih, Y. (2002). Entangled Two-Photon Wave Packet in a Dispersive Medium. Phys. Rev. Lett. 88 (18), 1836011–1836014. doi:10.1103/PhysRevLett.88.183601

CrossRef Full Text | Google Scholar

Wasilewski, W., Wasylczyk, P., Kolenderski, P., Banaszek, K., and Radzewicz, C. (2006). Joint Spectrum of Photon Pairs Measured by Coincidence Fourier Spectroscopy. Opt. Lett. 31 (8), 1130. doi:10.1364/ol.31.001130

PubMed Abstract | CrossRef Full Text | Google Scholar

Wetzel, B., Stefani, A., Larger, L., Lacourt, P. A., Merolla, J. M., Sylvestre, T., et al. (2012). Real-Time Full Bandwidth Measurement of Spectral Noise in Supercontinuum Generation. Sci. Rep. 2, 1–7. doi:10.1038/srep00882

CrossRef Full Text | Google Scholar

Zielnicki, K., Garay-Palmett, K., Cruz-Delgado, D., Cruz-Ramirez, H., O’Boyle, M. F., Fang, B., et al. (2018). Joint Spectral Characterization of Photon-Pair Sources. J. Mod. Opt. 65 (10), 1141–1160. doi:10.1080/09500340.2018.1437228

CrossRef Full Text | Google Scholar