Visual Cryptography Using Binary Amplitude-Only Holograms

Visual cryptography (VC) is developed to be a promising approach to encoding secret information using pixel expansion rules. The useful information can be directly rendered based on human vision without the usage of decryption algorithms. However, many VC schemes cannot withstand occlusion attacks. In this paper, a new VC scheme is proposed using binary amplitude-only holograms (AOHs) generated by a modified Gerchberg-Saxton algorithm (MGSA). During the encryption, a secret image is divided into a group of unrecognizable and mutually-unrelated shares, and then the generated shares are further converted to binary AOHs using the MGSA. During image extraction, binary AOHs are logically superimposed to form a stacked hologram, and then the secret image can be extracted from the stacked hologram. Different from conventional VC schemes, the proposed VC scheme converts a secret image into binary AOHs. Due to the redundancy of the generated binary AOHs, the proposed method is numerically and experimentally verified to be feasible and effective, and possesses high robustness against occlusion attacks.

Introduction

Information security plays an important role nowadays, and has attracted much current attention (Javidi, 1997; Alfalou and Brosseau, 2009; Chen et al., 2014). One promising approach to realizing information security is optical encryption, which exploits physical properties of light (e.g., amplitude, phase, frequency and polarization) to secure information (Javidi, 1997; Alfalou and Brosseau, 2009; Chen et al., 2014). Owing to the striking properties of optical means, optical encryption opens up a new research perspective for information security in the field of data transmission and data storage. Since double random phase encoding (DRPE) was demonstrated (Refregier and Javidi, 1995), its variations have been continuously developed in different domains, e.g., Fresnel domain and fractional Fourier domain (Situ and Zhang, 2004; Wang et al., 2014). Other optical technology-based encryption schemes have been studied based on DRPE architecture, e.g., diffractive imaging and computer-generated hologram (Johnson and Brasher, 1996; Zhang and Wang, 2008; Chen et al., 2010; Xi et al., 2017). However, many optical encryption schemes use digital decryption algorithms to decode secret information. There is also a high demand of new types of cryptographic schemes, which could enable the authorized users to realize decryption of secret information in a simple way. Since visual cryptography (VC) was developed (Naor and Shamir, 1995), there are many relevant studies for its applications. The VC offers a feasible and straightforward solution for the decryption of secret information based on human vision (Naor and Shamir, 1995; Blundo et al., 2000; Hou, 2003; Wan et al., 2018; Yang et al., 2018; Jiao et al., 2019; Li et al., 2019; Jiao et al., 2020). The first visual cryptographic technique was proposed by Naor and Shamir in 1995, which broke up a secret image into multiple shares (i.e., visual key images) (Naor and Shamir, 1995). Subsequently, the secret image can be directly and visually decrypted by overlapping all the shares. In practice, these visual key images are printed onto separate transparent sheets, and then the secret image can be decoded by overlaying these sheets. It is worth mentioning that no meaningful information about the secret image can be retrieved from any one of the shares. The VC has been rapidly developed, and recent developments of VC are focused on the generation of visual key images. In the developed VC techniques, the generated visual key images can be random binary patterns, natural binary images, grayscale images and color images (Naor and Shamir, 1995; Blundo et al., 2000; Hou, 2003). Moreover, visual key images can be further designed using quick response patterns or phase holograms (Wan et al., 2018; Jiao et al., 2020). The visual key images are printed onto holographic optical elements (HOEs) or metasurface, and then the secret images can be visually decoded when these visual key images are overlapped (Yang et al., 2018; Li et al., 2019). Although VC scheme provides an effective way to realize encryption by using pixel expansion rule and decode the secret information based on human vision, conventional VC techniques could have some disadvantages. It is required that visual key images should be printed onto transparent sheets but not opaque materials (Naor and Shamir, 1995; Blundo et al., 2000; Hou, 2003). There are also some concerns with visual key images printed on HOEs or meta-devices, e.g., fabrication difficulty (Yang et al., 2018; Li et al., 2019). Furthermore, many VC techniques have a risk due to information occlusion, which usually happens in data transmission and data storage. Therefore, the potential of VC schemes has not been fully explored. It is desirable that new VC schemes can be continuously proposed to explore the potentials with enhanced robustness and reduced fabrication difficulty.

In this paper, we propose a new VC scheme using binary amplitude-only holograms (AOHs) with a modified Gerchberg-Saxton algorithm (MGSA). During the encryption, a secret image is expanded into a set of random binary patterns using pixel expansion rule, and then these random binary patterns are transformed into binary AOHs using the designed MGSA. Owing to the redundancy of binary AOHs, a high level of robustness is achieved in the proposed method to withstand occlusion attacks. During image extraction, binary AOHs are logically superimposed to form a stacked hologram, and then the secret image can be extracted from the stacked hologram. Feasibility and effectiveness of the proposed method are fully demonstrated in numerical simulations and optical experiments. It is numerically and experimentally verified that the proposed VC scheme can achieve high robustness to withstand occlusion attacks. It is believed that the proposed method could provide a promising solution for visual cryptography.

Principles

Conventional VC Scheme

Conventional VC scheme is developed based on pixel expansion rules to expand each pixel to be a set of sub-pixels (Naor and Shamir, 1995). Figure 1 shows a typical example of conventional VC scheme. A secret image with 64 × 64 pixels in Figure 1A is encrypted into two random binary shares with 256 × 256 pixels (i.e., visual key images) in Figures 1B,C. In this case, each pixel is expanded to be four sub-pixels. As can be seen in Figures 1B,C, no information about original secret image can be visually obtained from visual key images. If the two shares (i.e., visual key images) are overlapped, the secret image can be visually rendered as shown in Figure 1D. However, many conventional VC schemes are proven to be vulnerable to occlusion attacks owing to the dependence on expansion rules of pixels. Furthermore, high fabrication difficulty of the shares could also limit the application of VC schemes. It is desirable that VC schemes can be developed with enhanced robustness and reduced fabrication difficulty.

FIGURE 1

FIGURE 1. A typical example for conventional VC scheme to encrypt a secret image into two visual key images, and then the secret image can be retrieved by overlapping these two visual key images. (A) A secret image. (B) and (C) Two visual key images generated by using conventional VC scheme. (D) A retrieved image obtained by overlapping (B) and (C).

The Proposed VC Scheme Using Binary AOHs via MGSA

Here, the redundancy of digital holograms is applied to enhance capability of VC scheme to withstand occlusion attacks. To reduce fabrication difficulty, binary AOHs rather than phase-only holograms are integrated into VC scheme to convert visual key images into binary AOHs. Figure 2 shows a schematic of the proposed MGSA to generate binary AOHs (Xu et al., 2020; Zhou et al., 2021). A target image with a random phase φ^random is inverse Fourier transformed, and then the generated phase φ¹ is constrained by a cosine function to form an amplitude-only pattern cos (φ¹). To reduce complexity of amplitude retrieval, amplitude-only pattern cos (φ¹) is binarized to generate a binary AOH φ². With the usage of Fourier transform to the binary AOH φ², new complex amplitude can be obtained and an updated phase φ^update is correspondingly retrieved. Then, the updated phase φ^update together with the target image is inverse Fourier transformed in a new iteration. When a preset condition is satisfied, the final binary AOH is used as an optimal binary AOH of the target image. To solve the twin-image problem, the target image can be placed at the upper left corner. Since the redundancy of digital holograms provides high robustness, the generated binary AOHs can be used for secret-image retrieval, e.g., under occlusion attacks (Gerritsen et al., 1968; Kreis, 2005; Schnars and Jüptner, 2005; Hwang et al., 2009; Xu et al., 2017; Xu et al., 2020; Zhou et al., 2021).

FIGURE 2

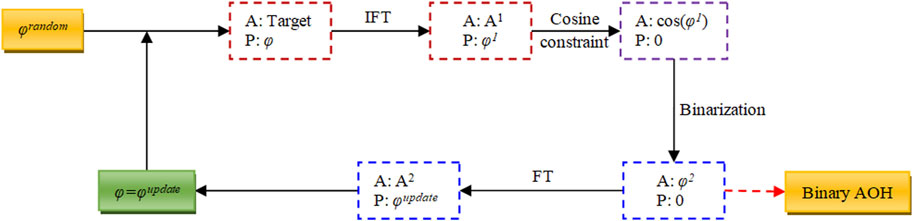
FIGURE 2. A schematic of the designed MGSA to generate binary AOHs. A: Amplitude; P: phase; IFT: Inverse Fourier transform; FT: Fourier transform.

Owing to the generation of binary AOHs to withstand occlusion attacks, a new VC scheme is proposed by integrating binary AOHs into VC scheme. Figure 3 shows a flow chart for the proposed VC scheme using binary AOHs with the MGSA. During the encryption, a secret image is encoded into a set of visual key images (i.e., Share 1, … , Share n) using conventional VC scheme. Then, the visual key images are further processed by the designed MGSA, yielding n binary AOHs (i.e., H₁, … , H_n). The binary AOHs are used as new shares to be delivered to the authorized users in the proposed VC scheme. During image extraction, a logical operation (e.g., AND, OR, or XOR) is implemented on these new shares (i.e., binary AOHs) to generate a stacked hologram. Finally, an image can be retrieved from the stacked hologram to visually render information of the secret image.

FIGURE 3

FIGURE 3. A flow chart for the proposed VC scheme using binary AOHs via MGSA.

Results and Discussion

Simulation Results and Discussion

To verify feasibility and effectiveness of the proposed VC scheme, numerical simulation is first conducted. Figure 4 shows a schematic of the proposed VC scheme. For the sake of brevity, encoding a secret image into only two shares is conducted. In addition, an AND operation is adopted to illustrate the proposed VC scheme. It is worth noting that the generated stacked hologram is still a binary AOH when an AND operation is applied. By using conventional VC algorithm, a secret image with 64 × 64 pixels is encoded into two visual key images (i.e., Share 1 and Share 2 with 256 × 256 pixels). Then, these two shares are converted to binary AOHs (i.e., H₁ and H₂) to further enhance the robustness. Here, size of binary AOHs is 512 × 512 pixels to avoid the overlapping with twin image. To extract the secret image, the two binary AOHs are collected and processed by an AND operation to generate a stacked hologram with 512 × 512 pixels. Finally, an image can be retrieved from the stacked hologram to visually render information of the secret image.

FIGURE 4

FIGURE 4. A schematic of the proposed VC scheme using two shares.

By using the proposed VC scheme, each secret image can be encoded into a pair of binary AOHs, and then the two binary AOHs are delivered to two authorized users. When the pair of binary AOHs is collected and processed by an AND operation, a stacked hologram can be generated. Then, the generated stacked hologram can be further used for the retrieval of the secret image. Figure 5 shows several secret images (64 × 64 pixels) encoded by using the proposed VC scheme into binary AOHs (512 × 512 pixels). As can be seen in Figures 5A,B,E,F,I,J, three secret images have been respectively converted to binary AOHs, which do not visually render any information about secret images. To extract the secret images, an AND operation is implemented to each pair of binary AOHs (i.e., Figures 5A,B, Figures 5E,F and Figures 5I,J) to generate the stacked holograms as respectively shown in Figures 5C,G,K. Finally, the corresponding images are retrieved from the stacked holograms by using Fourier transform, as shown in Figures 5D,H,L. It is illustrated that the retrieved images can clearly render information of the secret images based on human vision. To quantitatively evaluate the retrieved images, peak signal-to-noise ratio (PSNR) is calculated. Since twin images are generated in the retrieved images as shown in Figures 5D,H,L, only area of interest (i.e., the top left corner with 256 × 256 pixels) is used. Meanwhile, original secret images are resized from 64 × 64 pixels to 256 × 256 pixels to calculate PSNR. PSNR values of the retrieved images in Figures 5D,H,L are 10.30, 14.08 and 14.88 dB, respectively.

FIGURE 5

FIGURE 5. Typical examples of the proposed VC scheme. (A, E, I) Binary AOHs H₁. (B, F, J) Binary AOHs H₂. (C, G, K) Stacked holograms respectively generated by an AND operation between (A) and (B) (E) and (F), and (I) and (J). (D, H, L). The retrieved images obtained by respectively using Fourier transform to (C, G, K).

The proposed method uses binary AOHs to enhance robustness of VC schemes. When Fourier transform is directly Figure 6 applied to retrieve the shares from binary AOHs, it is also studied whether secret images can be extracted by overlapping the retrieved shares without the usage of logical operations. For a comparison, original secret images used in Figure 6 are the same as those used in Figure 5. Figures 6A,B,F,G,K,L show three pairs of binary AOHs, and the images in Figures 6C,D,H,I,M,N are obtained by directly using Fourier transform to the images in Figures 6A,B,F,G,K,L, respectively. Then, the image retrieval is conducted by overlapping Figures 6C,D,H,I,M,N, respectively. As can be seen in Figures 6E,J,O, no information about secret images can be visually rendered in the retrieved images without the usage of logical operations. Therefore, it is compulsory for the proposed VC scheme to use logical operations for secret-image retrieval. It is also demonstrated that the proposed VC scheme is feasible and effective.

FIGURE 6

FIGURE 6. Secret images retrieved without the usage of logical operations. (A, F, K) Binary AOHs H₁. (B, G, L) Binary AOHs H₂. (C, H, M) Share 1 respectively extracted from (A, F, K). (D, I, N) Share 2 respectively extracted from (B, G, L). (E, J, O) The images obtained by respectively overlapping (C) and (D), (H) and (I), and (M) and (N).

Experimental Results and Discussion

Optical experiments are also conducted to demonstrate feasibility and effectiveness of the proposed VC scheme. Figure 7 shows a schematic experimental setup for extracting secret images from the stacked holograms. He-Ne laser beam (Newport, R-30993) with wavelength of 633.0 nm is expanded and collimated. The collimated optical wave is reflected by a mirror to illuminate an amplitude-only spatial light modulator (SLM, Holoeye LC-R720). The stacked holograms are sequentially embedded into the SLM. Then, the modulated wave propagates through a lens (f = 10.0 cm), and is recorded by a CCD camera with 1,280 × 1,024 pixels and pixel size of 5.30 μm (Thorlabs, DCC3240M). When the pairs of binary AOHs are collected, stacked holograms are generated by applying an AND operation. The secret images are experimentally retrieved from the stacked holograms. Figures 8A–D show the stacked holograms generated by using binary AOHs, and Figures 8E–H show the corresponding images recorded by CCD camera. Information of the secret images is visually recognized, which is sufficient in optical encryption field. To quantitatively evaluate quality of the retrieved images in optical experiments, visibility is used and calculated by (Kellock et al., 2011; Ghaleh et al., 2018)

$\mathrm{V}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}=\frac{<{\mathrm{I}}_{\mathrm{s}}>-<{\mathrm{I}}_{\mathrm{b}}>}{<{\mathrm{I}}_{\mathrm{s}}>+<{\mathrm{I}}_{\mathrm{b}}>}(1)$

where I_s and I_b respectively denote intensity in the signal part and background part, and average intensity is respectively denoted as <I_s> and <I_b>. Visibility of the retrieved images in Figures 8E–H is 0.17, 0.16, 0.19 and 0.22, respectively.

FIGURE 7

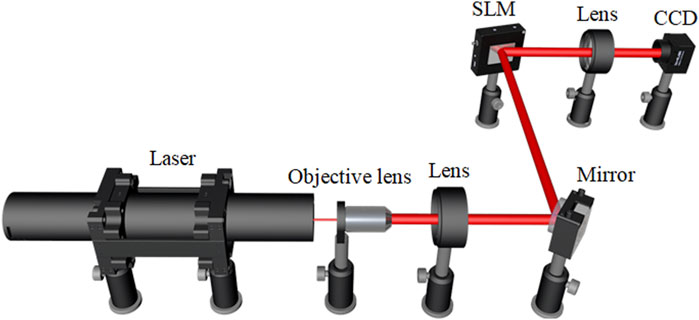
FIGURE 7. A schematic optical setup for retrieving secret images from the stacked holograms. CCD: charge-coupled device.

FIGURE 8

FIGURE 8. The four images retrieved in optical experiments. (A-D) The stacked holograms. (E-H) The retrieved images respectively corresponding to (A-D).

In optical experiments, Fourier transform of binary AOHs for image retrieval without the usage of logical operations is also investigated. Figures 9A,B show two binary AOHs corresponding to a secret image ‘EIE’. Then, binary AOHs in Figures 9A,B are experimentally Fourier transformed to retrieve the shares as shown in Figures 9C,D, respectively. Finally, the retrieved shares are overlapped to extract the secret image, and the retrieved image is shown in Figure 9E. As can be seen in Figure 9E, the retrieved image cannot visually provide any information about secret image ‘EIE’. It is experimentally verified that secret images cannot be retrieved without the usage of logical operations, and Fourier transform of binary AOHs will not result in information leakage.

FIGURE 9

FIGURE 9. The proposed VC scheme without the usage of logical operations. (A) and (B) Binary AOHs H₁, and H₂ for a secret image ‘EIE’. (C) and (D) The retrieved shares experimentally obtained respectively using Fourier transform to (A) and (B). (E) A retrieved image by overlapping (C) and (D).

Since occlusion of binary AOHs could happen during data transmission or data storage, occlusion attacks have also been experimentally conducted to demonstrate robustness of the proposed VC scheme. Here, a secret image ‘EIE’ is used and tested, and its corresponding binary AOHs are shown in Figures 9A,B. Figures 10A–E show the stacked holograms generated by occlusion contamination of the first binary AOH H₁ in Figure 9A, when the second binary AOH H₂ in Figure 9B remains unchanged. When the first binary AOH is respectively occluded with 3.81% (100 × 100 pixels), 15.26% (200 × 200 pixels), 34.33% (300 × 300 pixels), 61.04% (400 × 400 pixels) and 77.25% (450 × 450 pixels), the generated stacked holograms are correspondingly occluded at the top left corner as shown in Figures 10A–E. The secret images are experimentally retrieved and shown in Figures 10F–J. When occlusion percentage of the first binary AOH is lower than 61.04%, the retrieved images can still be recognized as shown in Figures 10F–I. Figure 11 shows the performance of the proposed VC scheme, when the second binary AOH in Figure 9B is occluded from 3.81 to 77.25% and the first binary AOH in Figure 9A remains unchanged. In this case, the corresponding stacked holograms are generated and shown in Figures 11A–E. It is also demonstrated that information of the secret image can be extracted when occlusion percentage of the second binary AOH is lower than 61.04%, as shown in Figures 11F–I.

FIGURE 10

FIGURE 10. Occlusion contamination on the first binary AOH in Figure 9A when the second binary AOH in Figure 9B remains unchanged in optical experiments. (A-E) The stacked holograms generated when occlusion percentage of 3.81, 15.26, 34.33, 61.04 and 77.25% is respectively used. (F-J) The retrieved images experimentally obtained respectively corresponding to (A-E).

FIGURE 11

FIGURE 11. Occlusion contamination on the second binary AOH in Figure 9B when the first binary AOH in Figure 9A remains unchanged in optical experiments. (A-E) The stacked holograms generated when occlusion percentage of 3.81, 15.26, 34.33, 61.04 and 77.25% is respectively used. (F-J) The retrieved images experimentally obtained respectively corresponding to (A-E).

Figure 12 shows the effect of occlusion attacks on visibility of the retrieved images in optical experiments. In Figure 12A, only the first binary AOH in Figure 9A is occluded with the increased percentage from 0.000381 to 95.37%, and the occluded region is from the upper left to the lower right. As can be seen in Figure 12A, there is a downward trend of visibility values from 0.21 to 0.06. The same trend is found for the occlusion attack on the second binary AOH, as shown in Figure 12B. Although quality of the retrieved images decreases with the increased occlusion percentage, effective information of the secret images can still be visually recognized from the retrieved images, as can be seen in Figures 10F–J and 11F–J. Therefore, it is experimentally verified that the proposed VC scheme possesses high robustness against occlusion attacks.

FIGURE 12

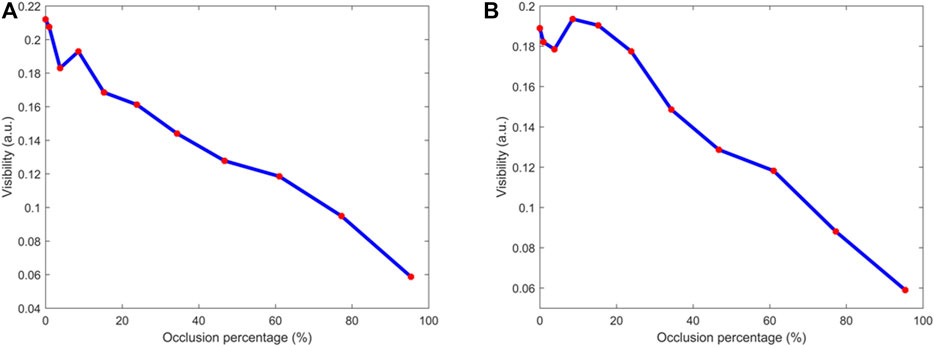
FIGURE 12. Occlusion attacks. (A) A relationship between occlusion percentage and visibility of the retrieved images when only the first binary AOH in Figure 9A is occluded. (B) A relationship between occlusion percentage and visibility of the retrieved images when only the second binary AOH in Figure 9B is occluded.

In practice, both binary AOHs could be occluded at the same time. Optical experiments are further conducted to demonstrate performance of the proposed VC scheme when occlusion attacks on the two binary AOHs happen, and experimental results are shown in Figures 13A–H. For instance, the first binary AOH is occluded by 3.81% as shown in Figure 13A, and the second binary AOH is occluded by 46.73% (350 × 350 pixels) as shown in Figure 13B. By using an AND operation between Figures 13A,B, a stacked hologram is obtained and shown in Figure 13C. Therefore, an image can be experimentally retrieved and shown in Figure 13D to visually render information of the secret image. When occlusion percentage for the first binary AOH is 34.33% and that for the second binary AOH is 61.04%, a retrieved image still can visually render information of secret image as shown in Figure 13H. It is experimentally verified that the proposed VC scheme is robust against occlusion attacks.

FIGURE 13

FIGURE 13. Occlusion attacks on both binary AOHs (i.e., those in Figures 9A,B) in optical experiments. (A) The first binary AOH occluded by 3.81%. (B) The second binary AOH occluded by 46.73% (350 × 350 pixels). (C) A stacked hologram generated by using (A) and (B). (D) A retrieved image experimentally obtained from (C). (E) The first binary AOH occluded by 34.33%. (F) The second binary AOH occluded by 61.04%. (G) A stacked hologram generated by using (E) and (F). (H) A retrieved image experimentally obtained from (G).

Conclusion

In this paper, a new VC scheme has been proposed by using binary AOHs with the MGSA. During the encryption, a secret image can be divided into a group of unrecognizable and mutually-unrelated shares by using conventional VC schemes, and then the generated shares are further converted to binary AOHs using the MGSA. During image extraction, binary AOHs are logically superimposed to form a stacked hologram, and then an image can be directly extracted from the stacked hologram to visually render information of the secret image. Numerical simulations and optical experiments have been conducted to demonstrate validity of the proposed VC scheme. Owing to the usage of binary AOHs, the proposed VC scheme can reduce fabrication difficulty when metasurface devices or other materials are used, and is also able to withstand occlusion attacks and noise contamination.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

LZ conducted data recording and validation, developed methodology, and wrote original draft. YX conducted data validation, and reviewed and edited the writing. ZP reviewed and edited the writing. YC reviewed and edited the writing. WC developed methodology, reviewed and edited the writing, and supervised research project.

Funding

This work was supported by Hong Kong Research Grants Council (C5011-19G) and The Hong Kong Polytechnic University (G-R006, 4-R006, 4-ZZLF, 1-W167).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alfalou, A., and Brosseau, C. (2009). Optical Image Compression and Encryption Methods. Adv. Opt. Photon. 1 (3), 589–636. doi:10.1364/AOP.1.000589

CrossRef Full Text | Google Scholar

Blundo, C., De Santis, A., and Naor, M. (2000). Visual Cryptography for Grey Level Images. Inf. Process. Lett. 75 (6), 255–259. doi:10.1016/S0020-0190(00)00108-3

CrossRef Full Text | Google Scholar

Chen, W., Chen, X., and Sheppard, C. J. R. (2010). Optical Image Encryption Based on Diffractive Imaging. Opt. Lett. 35 (22), 3817–3819. doi:10.1364/OL.35.003817

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W., Javidi, B., and Chen, X. (2014). Advances in Optical Security Systems. Adv. Opt. Photon. 6 (2), 120–155. doi:10.1364/AOP.6.000120

CrossRef Full Text | Google Scholar

Gerritsen, H. J., Hannan, W. J., and Ramberg, E. G. (1968). Elimination of Speckle Noise in Holograms with Redundancy. Appl. Opt. 7 (11), 2301–2311. doi:10.1364/AO.7.002301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghaleh, S. R., Ahmadi-Kandjani, S., Kheradmand, R., and Olyaeefar, B. (2018). Improved Edge Detection in Computational Ghost Imaging by Introducing Orbital Angular Momentum. Appl. Opt. 57 (32), 9609–9614. doi:10.1364/AO.57.009609

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, Y.-C. (2003). Visual Cryptography for Color Images. Pattern Recognition 36 (7), 1619–1629. doi:10.1016/s0031-3203(02)00258-3

CrossRef Full Text | Google Scholar

Hwang, H.-E., Chang, H. T., and Lie, W.-N. (2009). Multiple-image Encryption and Multiplexing Using a Modified Gerchberg-Saxton Algorithm and Phase Modulation in Fresnel-Transform Domain. Opt. Lett. 34 (24), 3917–3919. doi:10.1364/OL.34.003917

PubMed Abstract | CrossRef Full Text | Google Scholar

Javidi, B. (1997). Securing Information with Optical Technologies. Phys. Today 50 (3), 27–32. doi:10.1063/1.881691

CrossRef Full Text | Google Scholar

Jiao, S., Feng, J., Gao, Y., Lei, T., and Yuan, X. (2020). Visual Cryptography in Single-Pixel Imaging. Opt. Express 28 (5), 7301–7313. doi:10.1364/OE.383240

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, S., Zhou, C., Shi, Y., Zou, W., and Li, X. (2019). Review on Optical Image Hiding and Watermarking Techniques. Opt. Laser Tech. 109, 370–380. doi:10.1016/j.optlastec.2018.08.011

CrossRef Full Text | Google Scholar

Johnson, E. G., and Brasher, J. D. (1996). Phase Encryption of Biometrics in Diffractive Optical Elements. Opt. Lett. 21 (16), 1271–1273. doi:10.1364/OL.21.001271

PubMed Abstract | CrossRef Full Text | Google Scholar

Kellock, H., Setälä, T., Shirai, T., and Friberg, A. T. (2011). Higher-order Ghost Imaging with Partially Polarized Classical Light. Proc. SPIE 8171, 81710Q. doi:10.1117/12.896826

CrossRef Full Text | Google Scholar

Kreis, T. (2005). Handbook of Holographic Interferometry: Optical and Digital Methods. Weinheim, Germany: Wiley VCH, 35–219. doi:10.1002/3527604154.ch4

CrossRef Full Text | Google Scholar

Li, Z., Dong, G., Yang, D., Li, G., Shi, S., Bi, K., et al. (2019). Efficient Dielectric Metasurface Hologram for Visual-Cryptographic Image Hiding. Opt. Express 27 (14), 19212–19217. doi:10.1364/OE.27.019212

PubMed Abstract | CrossRef Full Text | Google Scholar

Naor, M., and Shamir, A. (1995). Visual Cryptography. Adv. Cryptography–Eurocrypt 950 (7), 1–12. doi:10.1007/BFb0053419

CrossRef Full Text | Google Scholar

Refregier, P., and Javidi, B. (1995). Optical Image Encryption Based on Input Plane and Fourier Plane Random Encoding. Opt. Lett. 20 (7), 767–769. doi:10.1364/OL.20.000767

PubMed Abstract | CrossRef Full Text | Google Scholar

Schnars, U., and Jüptner, W. P. O. (2005). Digital Holography: Digital Hologram Recording, Numerical Reconstruction, and Related Techniques. Berlin: Springer. doi:10.1007/b138284

CrossRef Full Text | Google Scholar

Situ, G., and Zhang, J. (2004). Double Random-phase Encoding in the Fresnel Domain. Opt. Lett. 29 (14), 1584–1586. doi:10.1364/OL.29.001584

PubMed Abstract | CrossRef Full Text | Google Scholar

Wan, S., Lu, Y., Yan, X., Wang, Y., and Chang, C. (2018). Visual Secret Sharing Scheme for (K,n) Threshold Based on QR Code with Multiple Decryptions. J. Real-time Image Proc. 14 (1), 25–40. doi:10.1007/s11554-017-0678-3

CrossRef Full Text | Google Scholar

Wang, X., Chen, W., and Chen, X. (2014). Fractional Fourier Domain Optical Image Hiding Using Phase Retrieval Algorithm Based on Iterative Nonlinear Double Random Phase Encoding. Opt. Express 22 (19), 22981–22995. doi:10.1364/OE.22.022981

PubMed Abstract | CrossRef Full Text | Google Scholar

Xi, S., Wang, X., Song, L., Zhu, Z., Zhu, B., Huang, S., et al. (2017). Experimental Study on Optical Image Encryption with Asymmetric Double Random Phase and Computer-Generated Hologram. Opt. Express 25 (7), 8212–8222. doi:10.1364/OE.25.008212

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, W., Luo, Y., Li, T., Wang, H., and Shi, Y. (2017). Multiple-image Hiding by Using Single-Shot Ptychography in Transform Domain. IEEE Photon. J. 9 (3), 1–10. doi:10.1109/JPHOT.2017.2695398

CrossRef Full Text | Google Scholar

Xu, Z., Huang, L., Li, X., Tang, C., Wei, Q., and Wang, Y. (2020). Quantitatively Correlated Amplitude Holography Based on Photon Sieves. Adv. Opt. Mater. 8 (2), 1901169. doi:10.1002/adom.201901169

CrossRef Full Text | Google Scholar

Yang, N., Gao, Q., and Shi, Y. (2018). Visual-cryptographic Image Hiding with Holographic Optical Elements. Opt. Express 26 (24), 31995–32006. doi:10.1364/OE.26.031995

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., and Wang, B. (2008). Optical Image Encryption Based on Interference. Opt. Lett. 33 (21), 2443–2445. doi:10.1364/OL.33.002443

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, L., Xiao, Y., Pan, Z., Cao, Y., and Chen, W. (2021). Optical Hiding Based on Single-Input Multiple-Output and Binary Amplitude-Only Holograms via the Modified Gerchberg-Saxton Algorithm. Opt. Express 29 (16), 25675–25696. doi:10.1364/OE.428564

PubMed Abstract | CrossRef Full Text | Google Scholar