- 1Maj Institute of Pharmacology, Polish Academy of Sciences, Kraków, Poland
- 2Faculty of Pharmacy, Chair of Technology and Biotechnology of Medical Remedies, Jagiellonian University Medical College in Krakow, Kraków, Poland
An increasing number of crystal structures available on one side, and the boost of computational power available for computer-aided drug design tasks on the other, have caused that the structure-based drug design tools are intensively used in the drug development pipelines. Docking and molecular dynamics simulations, key representatives of the structure-based approaches, provide detailed information about the potential interaction of a ligand with a target receptor. However, at the same time, they require a three-dimensional structure of a protein and a relatively high amount of computational resources. Nowadays, as both docking and molecular dynamics are much more extensively used, the amount of data output from these procedures is also growing. Therefore, there are also more and more approaches that facilitate the analysis and interpretation of the results of structure-based tools. In this review, we will comprehensively summarize approaches for handling molecular dynamics simulations output. It will cover both statistical and machine-learning-based tools, as well as various forms of depiction of molecular dynamics output.
Introduction
Structure-based drug design is becoming an indispensable part of virtual screening campaigns, due to the expanding possibilities of carrying out experiments from this path. It is related both to the achievements in the field of crystallography (expressed by the increasing number of deposited crystal structures), but also to the availability of the computational power and more efficient computational algorithms. Structure-based tools, with their key representatives—docking and molecular dynamics simulations–are a great source of information on the possible interaction schemes occurring between ligand and target receptors (Yang, 2014; Wang et al., 2018).
Molecular docking is a technique that aims to predict the optimal binding mode(s) of a ligand in the respective receptor (Morris and Lim-Wilby, 2008; Guedes et al., 2014; Ferreira et al., 2015). As the docking methodology relies on minimizing free energy of the ligand-receptor complex, the obtained structure can constitute a good starting point for more detailed analysis of ligand-protein interactions during molecular dynamics (MD) simulations (Santos et al., 2019; Wang et al., 2019). Moreover, as most docking tools provide limited flexibility of the target, MD can explore conformational space and generate an ensemble of receptor conformations, which could further be used during screening of chemical databases (Amaro et al., 2018; Acharya et al., 2020). The so-called ensemble sampling has not only increased the hit rate and, thus, improved the quality of virtual screening, but has also allowed efficient docking to the so-called “difficult protein targets” (Fu et al., 2014; Ellingson et al., 2015; Uehara and Tanaka, 2017; Bhattarai et al., 2020).
MD is an approach that relies on simulating dynamical changes of the system and capturing its evolution in time. MD offers an insight into the movement of the ligand-receptor complex at an atomistic level. Furthermore, it enables quantitative estimation of parameters that cannot be established in wet-lab experiments, e.g., values of torsional angles to describe flexibility, solvent accessible surface area to predict stability, or change in the entropy for distinct structures, such as water molecule in particular location (Ferreira et al., 2015; Leimkuhler and Matthews, 2016; Hollingsworth and Dror, 2018). The basis of the classical MD methodology is solving the Newton’s motion equations for each atom in the system, where the potential energy and forces of interacting particles are from the force-field definitions (Sutmann, 2002; Lindahl, 2008). These approximations are necessary to balance between the required accuracy and optimal speed of simulations’ performance. Moreover, MD timestep should be very small—1–10 fs – in order to minimize errors related to the potential energy estimation (Binder et al., 2004; Leimkuhler and Matthews, 2016). Huge numbers of timesteps, which are required for even relatively short simulations, contribute to the consumption of a great amount of computational resources. Fortunately, due to the increasing computational power and possibilities to perform simulations with the use of graphical processing units (GPU), MD simulations reached a millisecond time scale allowing to investigate events such as protein folding (Figure 1; Lindahl, 2008).
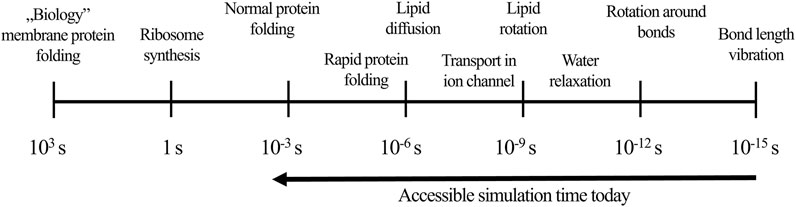
FIGURE 1. The influence of simulation time on events occurring during MD (according to Lindahl, 2008).
Thus, the amount of data produced by MD has dramatically increased over recent years and is far beyond the accessibility of manual analysis. For this reason, it is crucial to develop automatic tools for post-processing of such data. Great numbers of approaches are offered specifically by the software for MD simulations. Nevertheless, a lot of new independent methods for automated analysis have appeared recently, which are based on various statistical methods and machine learning (ML).
ML approaches are nowadays used at each stage of the drug design process and development (Ballester, 2019; Vamathevan et al., 2019; Patel et al., 2020). Their most common application involves the evaluation of compound potential bioactivity in ligand-based virtual screening (Melville et al., 2009; Carpenter and Huang, 2018; Hussain et al., 2021); however, they are also widely applied in the evaluation of compound physicochemical and ADMET properties (Göller et al., 2020; Göller et al., 2022; Jia and Gao, 2022). The ML role in computer-aided drug design is not limited to the assessment of compound libraries, but a number of generative approaches is used to enumerate new sets of potentially active compounds (Baskin, 2020). Moreover, ML can help in the compound optimization and indication of features, which are important for a particular type of activity, thanks to the wide range of interpretability tools (Hudson, 2021). ML methods also support structure-based path of virtual screening tasks – they assist in the detection of ligand-protein interaction patterns characteristic for considered activity profiles (Khamis et al., 2015; Khamis and Gomaa, 2015; Khamis et al., 2016), as well as in the detection of complex relationships between ligand-protein interaction schemes occurring during MD simulations (Podlewska et al., 2020; Kucwaj-Brysz et al., 2021).
In this review, we comprehensively summarize existing approaches to automatic handling of MD simulations’ outputs. We will describe approaches available within the MD software, but our main focus is on the automatic statistical and ML-based post-processing tools.
Tools Available Within the MD Software or Packages Dedicated To MD Output Analysis
Numerous software packages are able to perform MD simulations. The list of the most popular programs includes GROMACS (Abraham et al., 2015), HyperChem (Laxmi and Priyadarshy, 2002), AMBER (Case et al., 2005), LAMMPS (Thompson et al., 2021), CHARMM (Brooks et al., 2009), DL_POLY (Todorov et al., 2006), HOOMD (Glaser et al., 2015), TINKER (Lagardère et al., 2018), NAMD (Phillips et al., 2005), and Desmond (Bowers et al., 2006). The resulting simulation trajectory can then be analyzed at different levels – from the qualitative visualization of changes occurring in the modeled system to detailed investigation of variations in atom positions and ligand-protein interactions. Due to the high amount of data produced during MD simulations (of up to several terabytes size), programs for MD analysis should also be able to efficiently deal with such data volumes.
The list of the most known packages for MD simulations analysis opens VMD [Visual Molecular Dynamics (Humphrey et al., 1996)], developed by the Theoretical and Computational Biophysics Group at the University of Illinois at Urbana-Champaign. VMD is a program designed for interactive visualization and analysis of biomolecular systems including processing of very large systems (composed of up to billion particles). The software is written in C and C++ (source code available) and is distributed free of charge. Convenient graphical interface supports performing various types of coordinate analysis on Unix, MacOS, and Windows operating system, along with NVIDIA OptiX and CUDA support. In addition to the built-in analysis tools applicable to trajectories processing, VMD has a broad collection of plugins and scripts (VMD Plugin Library, 2021, n. d.; VMD Script Library (2021), n. d.).
Execution of Tcl and Python scripts and implementation of developed plugins enables adjustement of VMD capabilities to users’ needs without recompiling the source code. Both types of tools are distributed under an open-source license, unless otherwise stated. Moreover, researchers are encouraged to develop and share new utilities in order to support the growth of the VMD community and development of the software. VMD plugins are divided into the “molfile” plugins, which enable working with multiple file formats of molecular data, and scripting extensions used to perform requested tasks. Plugins dedicated to data analysis allow performing various calculations: from RMSD (RMSD Tool, RMSD Trajectory Tool) to electrostatic potentials (APBSRun, Delphi Force) and IR spectral density (IRSpecGUI). Resulting outcomes can be visualized through generated plots—GofRGUI, NAMD Plot, RamaPlot, Timeline—or as maps—Contact Map, VolMap, HeatMapper, PMEpot. There are also plugins capable of analysing free-energy perturbation calculations (AlaScan, ParseFEP) and obtaining data on proteins—Intervor (extracts and displays protein-protein interface), SurfVol (measures surface area and volume of proteins), and NetworkView (shows protein interaction networks). Developed statistical tools visualize clusters of structure conformations (Clustering Tool) or perform normal mode visualization and comparative analysis (NMWiz). VMD has constantly been developed: the latest version (1.9.3) includes introduction of the following major features: introduction of new QwikMD plugin connecting VMD with MD program NAMD, enabling quick preparation of common molecular simulations; the TopoTools plugin used for automated topology conversion from CHARMM to GROMACS: the new TachyonL-OSPray ray tracing engine for generating high quality renderings of molecular systems containing hundreds millions of particles; and OpenGL rendering for parallel visualization runs on “headless” clouds and petascale computers.
PTRAJ (Process TRAJectory) is another example of a tool enabling post-processing of MD data (Roe et al., 2013). It was dedicated for the analysis of the AMBER output. Its successor, CPPTRAJ, emerged as a response to the growing trajectory sizes, offering a wider range of functionalities and more efficient data processing. In contrast to PTRAJ (written primarily in C), CPPTRAJ code is based on C++ and the whole program structure was reorganized to facilitate the addition of new functionalities. The programs and their source code are freely available under the GNU General Public License version 3 and are distributed within the AmberTools21. The strong point of CPPTRAJ is batch-processing, which allows the use of remote sites for analysis and possibility of combining various types of commands, trajectories, and topologies in the same run. Other important features of CPPTRAJ are: the availability of MPI, OpenMP, and CUDA parallelization, support for implementation of variables and loops, and possibility to apply atom masking to specify which part of the system should be analyzed. The number of developed commands applicable for MD data analysis is great, including simple calculations, such as estimation of the number of hydrogen bonds (hbond), and multiple examples of more complex tools, such as performing non-linear curve fitting (curvefit, multicurve) and linear regression (regress), matrix based calculations (crosscorr, diagmatrix, hausdorff, modes), estimating auto-/cross-correlation (autocorr, correlationcoe, timecorr), creating histograms (hist, kde, multihist), and many more (Case et al., 2021). CPPTRAJ development has resulted in new features, among which are: rewritten code expanding clustering capabilities, ability to RMS-fit grids onto coordinates, automatic calculation of multiple puckers, speeding up the non-bonded energy calculation, enhancing the performance of the permutedihedrals and randomizeions commands, and automation of downloading and building external libraries in CPPTRAJ (2021).
MDAnalysis is an object-oriented library developed for the analysis of MD trajectories and protein structures (Michaud-Agrawal et al., 2011). The package is written in Python and Cython and uses NumPy arrays to expand its functionality. MDAnalysis is available under the GNU General Public License version 2.0 (https://github.com/MDAnalysis/mdanalysis). The analysis modules are capable of assessing distances and contacts (e.g., calculating path similarity, which reveals geometric similarity of trajectories useful for identification of patterns in trajectory), performing dimensionality reduction and carrying out volumetric analysis (e.g., linear density estimation). Other modules analyze the structure of macromolecules (such as HELANAL (Sugeta and Miyazawa, 1967; Bansal et al., 2000)—a tool for the analysis of protein helices), polymers (including determination of the polymer persistence length), nucleic acids and, finally, membrane and membrane proteins (namely, HOLE (Stelzl et al., 2014), a suite of tools used to assess pore dimensions of the holes as a function of time). Recently MDAnalysis announced the introduction of a command-line interface in answer to user needs, and a number of supported analysis modules is provided in the documentation.
MDTraj (McGibbon et al., 2015) is a Python library applied for MD trajectory manipulation and analysis, whose goal is to provide interafce between MD data and modern tools and programs for statistical analysis and visualization based on Python. MDTraj is licensed under the Lesser GNU General Public License (LGPL v2.1+) on GitHub (https://github.com/mdtraj/mdtraj). MDTraj works with every possible MD data format, focusing on speed and efficient performance and providing multiple analysis possibilities. Available functions identify hydrogen bonds, compute distances to create residue-residue contact maps, assess secondary structure of the protein and assign code according to the implemented Dictionary (Kabsch and Sander, 1983), calculate solvent-accessible surface area (SASA) and NMR scalar coupling, as well as determine nematic order parameters, which describe the orientational order of a system from 0 to 1. Another special feature is the particularly fast RMSD computations due to performance optimization based on Haque at al. (2014) along with C/C++ code implementation. Moreover, MDTraj documentation gives access to 14 notebooks containing analysis examples with executable code—e.g., PCA with scikit-learn ML library followed by plotting data using Matplotlib.
LOOS (Lightweight Object-Oriented Structure-analysis) (Romo et al., 2014; Grossfield and Romo, 2021) aims at enabling rapid development and testing of new tools for MD analysis. Additionally, the program includes a number of easy-to-use prebuilt applications. As LOOS is a C++ library, its combination with Python interface (PyLOOS) resulted in high performance and simplicity of use and further development. Moreover, the C++ layers could be used independently for even more efficient utilization of resources. LOOS is freely distributed under the GPLv3 license and is available via GitHub (https://github.com/GrossfieldLab/loos). In LOOS, 140 prebuilt tools are grouped into the following categories: macromolecule tools (e.g., computation of the radial distribution function), hydrogen bonding handling, principal component analysis (PCA), elastic network models (ENM), clustering, assessment of statistical error (e.g., block-averaged standard error calculations), and convergence. The tools included in the "membrane systems" category are dedicated for analyzing lipid bilayers and associated systems (e.g., calculation of molecular order parameters. Furthermore, 2D Voronoi decomposition tools are used to obtain data within a particular membrane slice. 3D density distributions tools generate 3D histograms from MD trajectories. They were originally created for visualization of water distribution; however, they are able to estimate membrane lipid density as well.
Pteros (Yesylevskyy, 2012; Yesylevskyy, 2015) is a high-performance molecular modeling library available for C++ and Python. It lets users analyse MD data and develop new analysis tools with the assistance of the easy-to-use APIs in both of the above-mentioned programming languages. In order to accelerate the analysis process, Pteros asynchronously reads files with MD trajectories and performs analysis tasks in parallel. Analysis plugins are completely independent and, besides typical calculations, provide more specific manipulations. For example, they enable assessing properties related to curvature with the Curvature plugin, which computes mean and Gaussian curvatures of various lipid aggregates, smooths membrane surfaces, and calculates other properties of molecules embedded into the lipid membrane. While the above-mentioned plugin is not open-source, Pteros is a free software distributed under Artistic License and available at GitHub (https://github.com/yesint/pteros).
Till now, we have described exclusively open source software and libraries, which serve as powerful and freely available tools for MD output analysis. Nevertheless, some commercial software is also worth mentioning, e.g., Molecular Operating Environment (MOE) [Molecular Operating Environment (MOE), 2019], Desmond (Schrödinger Release 2021–4: Desmond Molecular Dynamics System, 2021), and CHARMM (Brooks et al., 2009). MOE constitutes a platform for integrated computer-aided molecular design with vast capabilities: QSAR models generation, virtual screening, protein engineering, homology modeling, as well as carrying out MD simulations. However, MOE offers limited opportunities for MD analysis, as only Free Energy Calculations along with Torsion Scan and Analysis are mentioned at the official software webpage. Greater analysis possibilities are provided by Desmond—a commercial software available without cost for non-commercial use, developed by D. E. Shaw Research for high-speed MD simulations of biological systems. Desmond offers multiple panels for different post-processing operations, such as Trajectory Frame Clustering Panel, Simulation Quality Analysis Panel (enabling estimation of potential energy, temperature, pressure, etc.), Simulation Event Analysis Panel (enabling calculation of geometric and energy-based properties, e.g., RMSF, hydrogen bonds, Coulomb energy), and Radial Distribution Function Panel. What is more, Desmond provides distinct panels for metadynamics and replica exchange simulations analysis, and Python scripts applicable for PCA, density profile calculations, and others. The advantages of MD data analysis in Desmond are its detailed tutorials, intuitive GUI, and conveniency of some tools, such as Simulation Interaction Diagram. Its output is saved as a pdf file, which contains results of protein-ligand system analysis in the form of colored plots, together with the short explanation of the meaning of each calculated property.
Plenty of other software and tools are useful in MD data analysis; among them are GROMACS (Abraham et al., 2015) and CHARMM (Brooks et al., 2009)— well-known MD programs capable of performing analysis tasks as well. Carma (Glykos, 2006) is a lightweight program written in C along with its graphical user interface grcarma (Koukos and Glykos, 2013) and Wordom (Seeber et al., 2007; Seeber et al., 2011) - a simple and fast command-line utility. MMTSB (Feig and Karanicolas, 2004) is a set of tools for enhanced sampling and multiscale molecular modeling approaches, while Simulaid (Mezei, 2010) is a program for carrying out analysis tasks of multiple types and MD trajectory data manipulation. MMTK (Hinsen, 2000), the Molecular Modeling Toolkit, contains MD analysis scripts; both Bio3D package (Grant et al., 2006) written in R language, and Python toolkit. MD-Tracks (Verstraelen et al., 2008) provides statistical analysis of MD data, and ST-Analyzer (Jeong et al., 2014) is an intuitive and simple web-based GUI environment, with nine analysis modules for extraction of various parameters from MD output.
Machine Learning—Classes of Models Used in the Structure-Based Drug Design
ML methods have become an integral element of structure-based path of drug design, and they assist in the analysis of both docking and MD simulations (Dutta and Bose, 2021). The general task of ML is to detect relationships and complex patterns in large datasets. As the amount of data produced in the structure-based path has recently grown enormously, the application of ML methods for MD outcome analysis is becoming more and more popular. Within ML methods, we can also distinguish deep learning (DL) algorithms with their main usage in computer-aided drug design to generate examples of new potential ligands via generative approaches.
The most popular classes of ML models applied in the broadly understood campaigns for searching for new drugs include:
1) Bayesian models—a collection of models based on the Bayes’ theorem. It defines the probability of an event on the basis of prior knowledge of conditions, which might be influencing this event. The Bayes’ theorem in its simplest form (taking into account only two events, A and B) can be described using the following equation:
where P (A|B) is a conditional probability of occurrence of event A, given that B is true; P(B|A) is a conditional probability of occurrence of event B, given that B is true; and P(A) and P(B) are probabilities of occurrence A and B, respectively, without any conditions (P(B) > 0).
Bayes’ theorem for a higher number of events adopts the following form:
If B, T1,…,Tn are such events that:
P(B) > 0,
In drug design approaches, Bayes’ theorem is most often used within the Naïve Bayes algorithm. In such a case, Bayes’ theorem is used together with an assumption of events (features) independence (Berrar, 2019).
Another concept using Bayes’ theorem is Bayesian statistics, in which all observed and unobserved parameters of a statistical model are given a joint probability distribution (prior and data distribution). Bayesian statistics expresses probability as a degree of belief, and Bayes’ theorem is used to assign a probability distribution to quantitatively describe this degree of belief in the form of a set of parameters (van de Schoot et al., 2021).
The Bayesian concept is also used in fuzzy clustering (Glenn et al., 2015).
2) K-nearest neighbors methods – based on the determination of distances between an evaluated sample and representatives of the training set. In its simplest form (K = 1), the evaluated sample is assigned to the class of its closest neighbor from the training set (or value of the considered parameter of the closest neighbor is returned in the case of regression). If a higher number of examples closest to the query is considered (K > 1), voting for the most frequent class label is carried out (classification) or values of evaluated parameters are averaged (regression)–Figure 2 a (Cover and Hart, 1967; Hall et al., 2008).
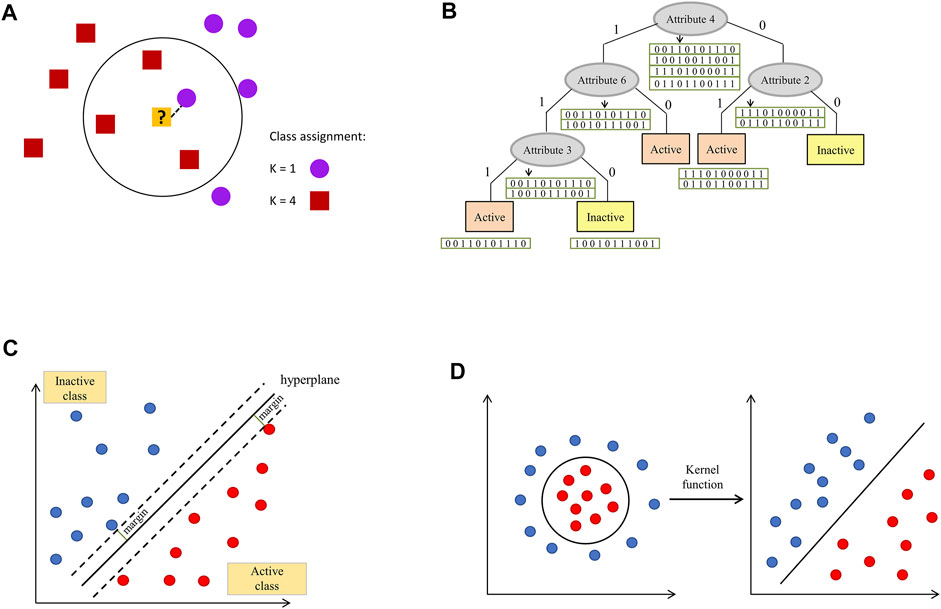
FIGURE 2. Visualization of selected ML algorithms: (A) k-nearest neighbor, (B) decision tree, (C) hyperplane with the highest separation margin constructed within the support vector machines algorithm implementation, (D) data transformation to the space, in which they are linearly separable with the use of the kernel function.
In MD studies, k-nearest neighbors algorithm is also used in clustering procedures aimed at the formation of groups of geometrically similar conformations (Keller et al., 2010).
3) Trees—tree-based algorithms are considered to be one of the most efficient and most broadly used types of ML models. Their important advantage is their simplicity and ease of interpretation, which play a role in drug design protocols (e.g., by the possibility of indication of features important for a particular compound activity). Predictions can be made using one decision tree or multiple tress (as it is in the case of Random Forest). Attributes for a root and subsequent nodes are selected on the basis of their discrimination power (at each level, a feature which provides the best distinguishment between considered classes is selected). Evaluation of new examples is carried out via checking values of features present in the subsequent nodes -Figure 2B (Breiman et al., 1984; Quinlan, 1986).
4) Neural networks—neural networks search for relationships in data in such a way that they mimic the processes occurring in the human brain. Their neurons are constituted by a mathematical function, which collects and classifies information. Such artificial neurons are interconnected (such connections reflect biological synapses, called edges) and they have the ability to communicate with each other. A neuron (node) receives a signal, processes it, and passes the respective information to the connected neurons. Typically, neurons are organized into layers, and the signal is passed from the input layer (the first one) to the output layer (the last one) (Hopfield, 1982).
A special type of neural network that has recently gained enormous popularity is deep neural network (DNN) with “deep” referring to the application of multiple layers in the network (LeCun et al., 2015; Schmidhuber, 2015).
Neural networks concept is also applied in unsupervised approaches for MD data clustering, e.g., in the form of Self Organizing Maps (SOMs) (Hyvönen et al., 2001; Fraccalvieri et al., 2013; Mallet et al., 2021). In order not to lose the topological properties of the input space, a neighborhood function is used.
5) Support Vector Machines (SVM)—an algorithm according to which each data item constitutes a point in n-dimensional space (n is equal to the number of features), with coordinates defined by the particular feature value. The task of the model is to find a hyperplane, which discriminates example classes with the highest margin (Figure 2C). As linear discrimination is often not possible, a kernel function needs to be applied in order to transform the input into a space of higher dimension, so an inseparable problem is converted into a separable one–Figure 2D (Cortes and Vapnik, 1995).
Clustering and Reduction of Data Dimensionality
The most common approach to use the automatic post-processing of the MD simulations output is the reduction of dimensionality and clustering (Amadei et al., 1993; Lange and Grubmüller, 2006).
Clustering
Clustering, from its assumptions, is an unsupervised technique of finding patterns and relationships in data. In contrast to the previously described techniques, clustering does not require the presence of the training set, as its aim is to form subgroups of similar objects. Clustering algorithms use various “distance” measures to evaluate object similarity. Two main groups of clustering approaches can be distinguished, namely partitional and hierarchical, both of which can be carried out in the bottom-up agglomerative way or using a top-down divisive approach (Kaufman and Rousseeuw, 1990). Another group of data grouping methods are density-based schemes, in which the clusters refer to the peaks of the probability distribution (or free energy minima) from which the data are collected (Sander, 2011; Glielmo et al., 2021). In MD simulations, such probability peaks typically correspond to metastable states of the system. An example application of density-based clustering to the analysis of MD data is density-based spatial clustering of applications with noise (DBSCAN) (Ester et al., 1996; Schubert et al., 2017), in which the clusters are defined as regions with density above the particular threshold. Such an approach was used to find representative structures from MD simulations and analyze MD trajectories (Wang et al., 2013). MD trajectories have also been analyzed by the density peak clustering.
The most popular partitional clustering technique is the K-means algorithm. Clustering in this approach starts from the random placement of K initial centroids. Then, K clusters are formed iteratively in such a way that a point which is closest to a particular centroid is added to the respective cluster, and a new centroid for each cluster is determined. When the cluster membership does not change (the convergence is obtained), the process is stopped. The drawback of K-means clustering is the dependence of the final outcome on the initial choice of the centroids. Problems might also occur when significant variations in the cluster sizes or densities appear, when data outliers are present, or when the ‘natural’ clusters have non-spherical shapes (Hartigan and Wong, 1979; Huang, 1998).
The starting point of agglomerative hierarchical clustering is a formation of singleton clusters from each object from the dataset. Then, iterative linkage of the nearest clusters is carried out, until the whole dataset constitutes one group. On the basis of the resulting dendrogram, the final division of data is produced. Hierarchical clustering is deterministic, but it requires high computational power and storage abilities, which limits its application to small datasets.
The most popular metric used to evaluate MD simulations’ output in terms of data proximity is Root Mean Square Deviation (RMSD). Despite the presence of some drawbacks [e.g., incidents of wrong conclusions when applied to equilibrium evaluation (Grossfield and Zuckerman, 2009)], it is still the most frequently used method for comparison of conformation similarity. Several different solutions were also proposed, such as the application of Euclidean Distances Matrices (EDM) (de Souza et al., 2017); however, they have not gained such wide popularity as RMSD.
Evaluation of Clustering Approaches
The evaluation of clustering is not easy, as falling into the group of unsupervised approaches, clustering does not refer to true labels. One group of cluster assessment methods is the so-called “internal evaluation,” where clusters are evaluated on the basis of the clustered data. In general, in such an evaluation, the highest scores are assigned to the approaches which produce clusters of high similarity between particular cluster elements and low similarity between elements belonging to different clusters (Rand, 1971). An example of internal measure of clustering quality is Davies-Bouldin index (DB) (Davies and Bouldin, 1979):
with n being the number of clusters, ci, cj being centroids of clusters i and j, respectively; σi refers to the average distance of elements belonging to cluster i to its centroid ci; and d (ci,cj) is the distance between centroids of clusters i and j. The lower the values of DB index, the better they are.
Another approach of the assessment of clustering quality is external evaluation, which refers to pieces of information that were not used during clustering. External evaluation can be based on the known class labels or on some benchmark datasets. However, if the true class labels are known, the clustering is actually not needed (de Souto et al., 2012).
Before the application of methods for clustering evaluation, the dataset should be examined in terms of the clustering tendency. If the dataset is composed of the uniformly distributed points (therefore, there is no clustering tendency present), then the identified clusters may be invalid. In order to verify the clustering tendency, the Hopkins test (Hopkins and Skellam, 1954) can be used (statistical test for spatial randomness of a variable).
Reduction of Data Dimensionality
Principal Component Analysis (PCA) is an approach for the reduction of the data dimensionality via transformation of a large set of variables into a smaller one, preserving as much information of the original set as possible (Ichiye and Karplus, 1991; Jolliffe, 2002; Jolliffe and Cadima, 2016). The goal is obtained via extraction of important information from the data table and its representation in the form of new orthogonal (linearly independent) variables (principal components). Then, the relationships between observations and variables can be displayed in the form of points in the maps. PCA is based on the assumption that the phenomena of interest can be explained by variances and covariances between original variables from the dataset. PCA is often applied before performing the clustering procedure. In MD-related applications, PCA is responsible for extracting the dominant modes in the molecule motion. It should be pointed out that, during the MD, the Cartesian positions of all atoms of the simulated system (of a size of thousands or even millions of atoms) are recorded in every time step, which indicates the importance of application of post-processing methods. If the dimensionality reduction is carried out properly, all relevant information is preserved, and the analysis of the MD output is valid.
Another approach for reduction of data dimensionality is multidimensional scaling (MDS), which determines the data space of lower dimension with the best possible preservation of the pairwise distances between data points (Young and Householder, 1938; Torgerson, 1952). Its mode of action is closely related to PCA; however, for MDS it is sufficient to provide a pairwise distance between points (their exact positions are not necessary).
PCA and MDS are representatives of linear methods of data dimensionality reduction; however, there is also a number of non-linear approaches to this task, with such examples as isometric features mapping (Tenenbaum et al., 2000), kernel PCA (Schölkopf et al., 1998), diffusion map (Coifman et al., 2005; Coifman and Lafon, 2006), and t-Distributed Stochastic Neighbor Embedding (t-SNE) (van der Maaten and Hinton, 2008). Low-dimensional spaces to embed high-dimensional data are also more and more often determined using DL approaches. One of the most popular DL techniques for reduction of data dimensionality is autoencoder (Kramer, 1991). Autoencoder maps input configuration to representation of lower dimension and then maps it back to the original space via respective decoder. Low-dimensional representation is learned via minimization of error between the original data points and data points obtained by the application of the above-mentioned decoder. Another DL-based approach for reduction of data dimensionality falls into the group of generative neural networks. Its representatives include Variational Autoencoders (VAEs) (Lopez et al., 2018) and Generative Adversarial Networks (GANs) (Goodfellow, et al., 2014).
Examples of Clustering and Data Dimensionality Reduction for MD Output Analysis
Unsupervised procedures are widely applied in the MD outcome analysis, due to the above-mentioned problem of the vast amount of data produced during simulations: clustering data into groups gathering similar conformations obtained during MD, and reduction of data dimensionality which lowers the number of features considered. Both these approaches help in the analysis of MD output.
The problem of clustering MD data emerged quite early. The first reports of clustering MD output were released in the early 1990s (Gordon and Somorjai, 1992; Torda and van Gunstered, 1994). Various groups also compared effectiveness of various clustering algorithms (Shao et al., 2007; Keller et al., 2010; Abramyan et al., 2016). Nowadays, clustering of MD data has become a standard procedure applied in order to facilitate interpretation and analysis of MD trajectories (Bruno et al., 2011; De Paris et al., 2015a; De Paris et al., 2015b; Rudling et al., 2018; Takemura et al., 2018; Evangelista et al., 2019; Yoshino et al., 2019; Bekker et al., 2020; Roither et al., 2020; Araki et al., 2021; Mallet et al., 2021; Wu et al., 2021) and new algorithms to improve this procedure are constantly developed.
Dimensionality reduction of MD data with the use of PCA was also first used in the early 90s (Ichiye and Karplus, 1991; Amadei et al., 1993) and since that time its application in MD output analysis has been constantly growing (Das and Mukhopadhyay, 2007; Chiappori et al., 2010; Kim et al., 2010; Casoni et al., 2013; Ng et al., 2013; Novikov et al., 2013; Bhakat et al., 2014; Sittel et al., 2014; Ernst et al., 2015; Chaturvedi et al., 2017; Cossio-Pérez et al., 2017; Fakhar et al., 2017; Chen, 2018; Cholko et al., 2018; An et al., 2019; Barletta et al., 2019; Girdhar et al., 2019; Karnati and Wang, 2019; Lipiński et al., 2019; Martínez-Archundia et al., 2019; Wu et al., 2019; Magudeeswaran and Poomani, 2020; David et al., 2021; Majumder and Giri, 2021). Although PCA is the most popular approach applied to handle MD trajectories, other data dimensionality reduction methods are also used in the MD field. Pisani et al. used MDS to examine conformational landscapes of CDK2 (Pisani et al., 2016) and Bécavin et al. improved the application of MDS for MD data by using singular value decomposition. MDS in the context of MD was also described by Troyer and Cohen (1995), Andrecut (2009), Tribello and Gasparotto (2019), and Srivastava et al. (2020). There are also examples of the application of other approaches: isometric feature mapping (Stamati et al., 2010), kernel PCA (Antoniou and Schwartz, 2011), diffusion map (Rohrdanz et al., 2011; Zheng et al., 2011; Zheng et al., 2013a; Zheng et al., 2013b; Preto and Clementi, 2014), t-SNE (Zhou et al., 2018; Zhou et al., 2019; Spiwok and Kříž, 2020), and VAE (Hernández et al., 2018; Shamsi et al., 2018; Moritsugu, 2021; Tian et al., 2021).
Markov State Modeling
Markov state modeling (MSM) (Pande et al., 2010; Husic and Pande, 2018) is another approach widely applied in the MD-based studies. MSM can be used to characterize events that occur at longer timescales than available computational power to perform such long simulation. Such MDs are simulated as transitions between a set of discrete stable states. The MSM parametrization can be performed via running several short MDs, which can be computed in parallel. The main difficulty in the MSM application is definition of the above-mentioned stable states (Abella et al., 2020). In general, MSM is an approach for modeling random processes with the use of the Markov assumption, which is when the present state is given, all following states are independent of all past states. MSMs describe the stochastic dynamics of a biomolecular system using two objects: a discretization of the high-dimensional molecular state space into n disjoint conformational sets and a model of the stochastic transitions between these states [usually described by a matrix of conditional transition probabilities (Chodera and Noé, 2014)].
Examples of MSM applications in drug design include: examination of the binding kinetics of the trypsin inhibitor benzamidine (Buch et al., 2011), description of the multiple unbinding pathways of ligands dissociating from FKBP (Huang and Caflisch, 2011), examination of substrate binding mechanism of HIV-1 protease (Pietrucci et al., 2009), analysis of binding pathways of opiates to µ-opioid receptors (Barati et al., 2018), reconstruction of binding process of alprenolol to the beta2-adrenergic receptor (Bernetti et al., 2019), membrane-mediated ligand unbinding of the PK-11195 ligand from the translocator protein (TSPO) (Dixon et al., 2021), study of the two bromodomain-inhibitor systems using multiple docked starting poses (Dickson, 2018), examination of the unbinding kinetics of a p38 MAP kinase type II inhibitor (Casasnovas et al., 2017), examination of ligand-induced active-inactive conformation change of beta-2 adrenergic receptor (Bai et al., 2014), and investigation of the interplay of conformational change and ligand-binding kinetics for the serine protease trypsin and its competitive inhibitor benzamidine (Plattner and Noé, 2015).
Examples of ML-Based Analysis of MD
The proper representation of MD outcome opens the door to the wide range of possibilities in terms of the post-processing approaches. Podlewska et al. (2020) and Kucwaj-Brysz et al. (2021) analyzed ligand-receptor contact patterns occurring during MD simulations and examined them with reference to the modeled property. Via the calculation of the Pearson’s correlation coefficient between the contact frequencies and values of examined parameters, the highest correlated residues (considered as the most important for the modeled property) were detected. Scheme of the above-described protocol is presented in Figure 3. At first, each simulation frame was represented with the use of the Structural Interaction Fingerprints (Singh et al., 2006). Then, for each amino acid, the contact frequency during simulation was calculated. Finally, for each protein residue, the Pearson’s correlation coefficients between the respective contact frequency and values of the evaluated compound parameters were determined. The highest correlated positions were indicated as those which should be considered in detail during the further design of compounds of particular activity profile.
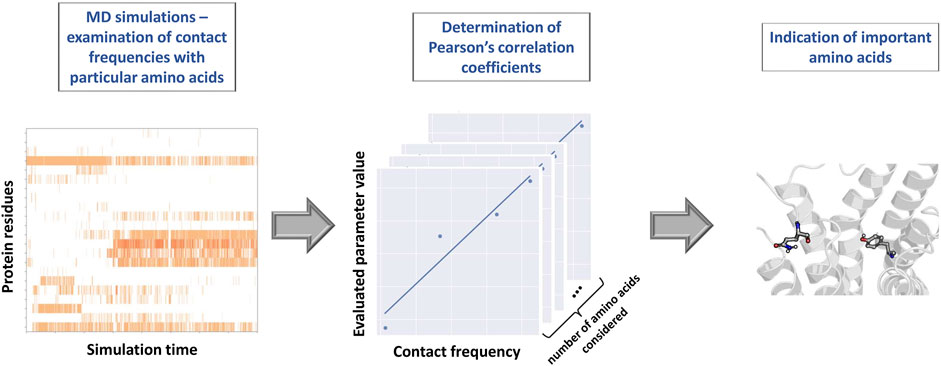
FIGURE 3. Scheme of the protocol for indication of the important amino acids on the basis of the contact frequency with particular amino acids during MD simulations.
Riniker (2017) developed a molecular dynamics fingerprint (MDFP) to combine MD approach with ML methods. MDFPs were obtained via the extraction of three properties from MD trajectories: intramolecular and total potential energy of the solute, radius of gyration, and solvent-accessible surface area resulting in a vector of floats. The fingerprint also contained information on the distribution of each property, characterized by its average, standard deviation, and median values. In addition, MDFP was enriched with standard 2D fingerprints: Morgan fingerprints and 2D-counts fingerprints from RDKit (number of heavy atoms, number of rotatable bonds, number of N, O, F, P, S, Cl, Br, and I atoms in the compound). Such representation constituted an input for ML models, which were trained to predict solvation free energies in five different solvents (water, octanol, chloroform, hexadecane, and cyclohexane) and partition coefficient in octanol/water, hexadecane/water, and cyclohexane/water.
MDFP was also used by Gebhardt et al. (2020). In this approach, ML was combined with the atomistic MD simulations encoded with MDFPs enabling the large-scale free-energy calculations. The so-called ML/MDFP method overcomes limitations related to free-energy estimation with MD – high computational expense and imperfections of force-fields. ML models are able to detect systematic force field errors caused by specific chemical groups and, afterwards, decrease their influence on final prediction. Moreover, ML models provide efficient and fast calculations when working with fingerprints databases; as an example, Gebhart et al. utilized the distributions of potential energy of the solute, radius of gyration, and SASA, which were generated from MD data. The outcomes proved that ML/MDFP approach predicted free-energy not worse or even slightly better than rigorous free-energy simulations and two models, namely quantum chemistry-based COSMO-RS. When two models for free energy predictions (COSMO-RS and UNIFAC) were compared with the support vector regression (SVR), it appeared that the latter one demonstrated the best results. The other application of fingerprints extracted from MD could be distinguishing active compounds, as Jamal et al. (2019) proved on the example of caspase-8 ligands. MD descriptors determined in this work were analogous to those obtained by Gebhardt et al. Moreover, fingerprints of different types were also calculated for reference. Multiple combinations of 2D, 3D, and MD descriptors were used to train two ML models: artificial neural networks and Random Forest. MD descriptors used individually showed better performance than being combined with other 2D/3D descriptors, which proved applicability of MD descriptors for lead prioritization and optimization of caspase-8 ligands.
Ash and Fourches (2017) made benefits of combination of MD and chemical descriptors to generate innovative QSAR models based on MD data, resulting in the construction of the so-called hyperpredictive MDQSAR models. The researchers in their work hypothesized that exploring dynamic noncovalent protein-ligand interactions would help to distinguish active compounds from non-active. A set of ERK2 inhibitors served as a case study, after previous unsuccessful attempts to rank them using conventional QSAR and sophisticated molecular docking techniques. Each ligand was docked in the ERK2 binding site using Glide, then 20 ns simulations of obtained ligand-protein complexes were performed in Desmond. MDs were followed by the extraction of descriptors on the basis of MD data with KNIME, such as traditional 1D-MACCS fingerprints, as well as 2D RDKit, 3D-D Moments and 3D-WHIM descriptors. The results indicate that MD descriptors successfully tackled the primary challenge and clearly pointed out the most active ligands. The hierarchical clustering highlighted similarities between MD descriptors and activities; furthermore, MD descriptors turned out to be useful in the identification of activity cliffs in all descriptor spaces. The research underlines the importance of further investigation of the MD descriptors usage, which could lead to implementation of new highly effective MDQSAR models in the future computer-aided drug design workflows.
MD data were also used by Vitek et al. (2013) to develop Support Vector Regression (SVR) model for water molecule energy estimation and by Jamroz et al. (2012) to examine fluctuations of protein residues during simulation.
Exploring protein conformations is extremely useful in understanding protein structure and function. However, to capture conformational changes we would need to perform long-time simulations and overcome multiple high energy barriers between local energy minima, which is related to the consumption of significant amounts of computational resources. Traditionally, enhanced sampling methods are exploited to solve these problems; however, their efficiency requires improvement (Yang et al., 2019). Fortunately, owing to technology advances, numerous novel efficient techniques have been developed. For example, a number of DL-based, approaches have already been proposed, such as variational autoencoders (VAEs), which significantly increases sampling “power”, if combined with MD potential. Tian et al. (2021) demonstrated successful protein sampling with VAEs on the example of adenosine kinase (ADK) conformational change from its closed state to the open one. Decoded conformations were similar to the training ones. Additionally, the latent space provided by VAEs could serve as a starting point for new simulations and studying of unexplored conformational spaces. VAEs application allows to perform short simulations of 20 ns and reach sampling efficiency comparable to a single long MD simulation. Another example of analysis of MD trajectories of proteins applies the Bayesian interference method to perform structural fitting for removing time-dependent translational and rotational movements (Miyashita and Yonezawa, 2017). On the other hand, Perez et al. (2015) combined MD with Bayesian interference to speed up simulation. The combination of Bayesian interference with MD simulations was also used by Shevchuk and Hub (2017) to refine structures and ensembles against small-angle X-ray scattering (SAXS) data.
Proteins change their conformations upon the influence of many factors, such as temperature, pH, and more importantly as a consequence of molecular recognition due to ligand binding (Doms et al., 1985; Takeda et al., 1989; Andersen et al., 1990). What is more, the ligand-protein complex is formed by the induced fit of both molecules, and the resulting protein conformations depend on the structure of the ligand (Bosshard, 2001). Conformational dynamics of proteins have a profound effect on cell functioning, such as in the case of G-protein coupled receptors (GPCRs), which transduce external signals into cells by activation of specific cellular pathways. The binding of different ligands stabilizes certain conformational state, which results in the elicitation of distinct signalling—a phenomenon called functional signalling, or biased agonism (Hilger et al., 2018; Wootten et al., 2018). An essential role of GPCRs in signal transmission highlights the importance of understanding how ligand binding alters protein conformations, in order to design new GPCR ligands, which would target desired pathways and avoid others, potentially causing side effects. MD is perfectly suited for perceiving ligand-protein conformational change; however, the difficulty lies in the necessity to analyze long-scale MD simulations, which are required to capture tiny structural changes, responsible for functional signalling. Plante et al. (2019) successfully applied deep neural networks (DNNs), to analyze MD data. MD output was transformed into the pixel representation, which is interpretable by the state-of-art DL object-recognition technology. When the method was applied to the pharmacological classification of 5-HT2A and D2 receptors ligands, among which were full, partial, and inverse agonists, DNN achieved near-perfect accuracy, classifying correctly >99% frames. Moreover, the sensitivity analysis identified the molecular determinants, which were considered by the model as the most important for the correct prediction. Even if the study has limited scope, including only eight ligands and two receptors, it gives hope for the highly accurate and efficient estimation of ligand-protein functional selectivity with the help of DNN.
Allostery is called the second secret of life (Fenton, 2008), as it is crucial for the adaptation of living organisms to changing environmental conditions by altering multiple cell functions, like enzyme catalysis, cell signalling, gene transcription, and others (Goodey and Benkovic, 2008; Nussinov et al., 2014). Designing allosteric drugs is a challenging task for multiple reasons. First of all, classical docking alone is unable to predict how orthosteric binding sites would adjust to allosteric modulation, and, importantly, which functional effect ligands would exert on protein’s function (Nussinov and Tsai, 2013; Lu et al., 2019; Sheik et al., 2020). Luckily, MD simulations give insight into the nature of allosteric perturbations; moreover, the application of ML algorithms to MD data expands possibilities to extract valuable information from long-scale simulations. Recently conducted research proved that such a combined MD-ML approach is able to efficiently determine ligand’s functional activity and models explaining ligand efficacy can be constructed. Marchetti et al. (2021) brought together the benefits of ensemble docking, MD and ML, in order to predict whether a set of ligands would inhibit or activate molecular chaperone Hsp90. MD of Hsp90 with several ligands was followed by cluster analysis of the obtained metatrajectory, subsequently, representative protein conformations were chosen for ensemble docking. The features obtained from docking, notably docking score, RMS, and RMSD, were used for training a supervised model, which served as a classification tool. Among three popular algorithms—logistic regression, SVM, and Random Forest - SVM reached the highest accuracy (0.9), as well as showed the best performance. On the other hand, attempts to classify ligands on the basis of separate features or chemometrics properties (here, molecular fingerprints) were far less efficient. In contrast, Ferraro et al. (2021) aimed to predict allosteric ligand functionality quantitatively. A computational experiment was performed on the allosteric modulators of the molecular chaperone TRAP1, which had similar affinities, but inhibited ATPase function with different efficacy. Two ML algorithms–Naïve Bayes and SVM–were applied to extract the local dynamic patterns responsible for the allosteric perturbation. The models were trained and validated on MD simulations of the perturbed and unperturbed systems. Whereas the discriminative SVM models qualitatively assessed the disparities between the perturbed and unperturbed ensembles, the implementation of the generative Naïve Bayes model produced a linear regression model with a 0.71 correlation between predicted states in the inhibitor-bound trajectories (TPR percentage) and the TRAP1 inhibition percentage. Additionally, Naïve Bayes could estimate the weight of ligand effects on each feature, which would support the identification of the features crucial for the allosteric propagation. Therefore, ML expands the possibilities of computer-aided drug design of allosteric modulators and could bring drug design to a new level with limited experimental testing.
The number of proteins with unknown functions is increasing due to the advances in bioinformatics, especially in the field of structural genomics. Identification of binding pockets could potentially be the key to understanding which functions specific proteins carry out. The FEATURE (Wei and Altman, 1998) is an ML-based algorithm for the identification of Ca2+-binding sites, utilizing the Bayesian scoring scheme. The FEATURE prediction does not depend on the sequence or structure, as the models examine local 3D physicochemical environment and that is why they are able to recognize diverse binding sites. However, the applications of the algorithm were limited to static structures, until Glazer et al. (2008) applied MD to improve the FEATURE detection ability by increasing structural diversity. The hypothesis was tested on parvalbumin β – an EF-hand Ca2+-binding protein, which has two Ca2+-binding sites–and MD-assisted calcium-binding pockets recognition. Moreover, relatively small time steps were characterized by significant change in the FEATURE scores, meaning that the FEATURE is very sensitive to small conformational changes, which might have an impact on calcium binding. These promising results could help to implement MD methodology in the exploration of protein functions.
Researchers’ efforts and technological advancement resulted in the development of a framework designed to support performing of MD simulations by means of ML algorithms – TorchMD (Doerr et al., 2021). Since the toolset is written in PyTorch (Paszke et al., 2019), it can be easily integrated with other models from this ML library. Among essential features of the framework is TorchMD-Net, which takes advantage of training neural network potential in order to improve force-field development. Furthermore, TorchMD enables running simulations with end-to-end differentiability of parameters, beneficial for the performance of steered and highly constrained MD simulations, sensitivity analysis, and others. Additionally, TorchMD with implemented neural network potential is used for coarse-grained MD simulations, which are helpful in studying protein folding and exploring conformational space. Code, step-by-step tutorials, and data are available at GitHub (https://www.github.com/torchmd).
Conclusion
Both intense growth in the amount of data, as well as increasing capabilities of various algorithms to detect patterns and relationships in various sets of information, dramatically increased the popularity of automatic approaches for MD outcome analysis. The output of such experiments consists of billions of timesteps, and recorded positions and velocities of thousands of atoms. Therefore, extracting important information from such a data package can be very challenging, and so the application of various post-processing approaches is needed. The post-processing protocols can help in the finding of non-obvious ligand-protein interaction patterns, detection of rare conformational states, or examining dependence of conformational changes of the examined system in time. Moreover, thanks to the post-processing approaches, the prediction of the system behavior in longer time scales than modeled can be made.
However, given all the advantages of ML approaches, we should still be aware of their limitations and pay attention to data used for models training, as it will substantially define the quality of the outcome. Importantly, ML models could have limited transferability and must be applied to other types of data carefully. Nevertheless, application of ML to MD data is undoubtedly the future, which makes the potential of MD applications almost unlimited.
Author Contributions
HB: literature search; preparation of the manuscript draft, review, editing, figures preparation; SP: literature search, preparation of the manuscript, review, editing, figures preparation, supervision.
Funding
The study was supported by the grant OPUS 2018/31/B/NZ2/00165 financed by the National Science Centre, Poland (www.ncn.gov.pl).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abella, J. R., Antunes, D., Jackson, K., Lizée, G., Clementi, C., and Kavraki, L. E. (2020). Markov State Modeling Reveals Alternative Unbinding Pathways for Peptide-MHC Complexes. Proc. Natl. Acad. Sci. U S A. 117 (48), 30610–30618. doi:10.1073/pnas.2007246117
Abraham, M. J., Murtola, T., Schulz, R., Páll, S., Smith, J. C., Hess, B., et al. (2015). GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 1-2, 19–25. doi:10.1016/j.softx.2015.06.001
Abramyan, T. M., Snyder, J. A., Thyparambil, A. A., Stuart, S. J., and Latour, R. A. (2016). Cluster Analysis of Molecular Simulation Trajectories for Systems where Both Conformation and Orientation of the Sampled States Are Important. J. Comput. Chem. 37 (21), 1973–1982. doi:10.1002/jcc.24416
Acharya, A., Agarwal, R., Baker, M., Baudry, J., Bhowmik, D., Boehm, S., et al. (2020). Supercomputer-based Ensemble Docking Drug Discovery Pipeline with Application to COVID-19. ChemRxiv 60 (12), 5832–5352. doi:10.26434/chemrxiv.12725465.v1
Amadei, A., Linssen, A. B., and Berendsen, H. J. (1993). Essential Dynamics of Proteins. Proteins 17 (4), 412–425. doi:10.1002/prot.340170408
Amaro, R. E., Baudry, J., Chodera, J., Demir, Ö., McCammon, J. A., Miao, Y., et al. (2018). Ensemble Docking in Drug Discovery. Biophys. J. 114 (10), 2271–2278. doi:10.1016/j.bpj.2018.02.038
An, Y., Jessen, H. J., Wang, H., Shears, S. B., and Kireev, D. (2019). Dynamics of Substrate Processing by PPIP5K2, a Versatile Catalytic Machine. Structure 27 (6), 1022–e2. e2. doi:10.1016/j.str.2019.03.007
Andersen, B. F., Baker, H. M., Morris, G. E., Rumball, S. V., and Baker, E. N. (1990). Apolactoferrin Structure Demonstrates Ligand-Induced Conformational Change in Transferrins. Nature 344 (6268), 784–787. doi:10.1038/344784a0
Andrecut, M. (2009). Molecular Dynamics Multidimensional Scaling. Phys. Lett. A 373 (23-24), 2001–2006. doi:10.1016/j.physleta.2009.04.007
Antoniou, D., and Schwartz, S. D. (2011). Response to Comment on “Towards Identification of the Reaction Coordinate Directly from the Transition State Ensemble Using the Kernel PCA Method” by D. Antoniou and S. Schwartz, J. Phys. Chem. B. 115, 2465-2469 (2011). J. Phys. Chem. B 115 (10), 12674–12675. doi:10.1021/jp207463g
Araki, M., Matsumoto, S., Bekker, G. J., Isaka, Y., Sagae, Y., Kamiya, N., et al. (2021). Exploring Ligand Binding Pathways on Proteins Using Hypersound-Accelerated Molecular Dynamics. Nat. Commun. 12 (1), 2793. doi:10.1038/s41467-021-23157-1
Ash, J., and Fourches, D. (2017). Characterizing the Chemical Space of ERK2 Kinase Inhibitors Using Descriptors Computed from Molecular Dynamics Trajectories. J. Chem. Inf. Model. 57 (6), 1286–1299. doi:10.1021/acs.jcim.7b00048
Bai, Q., Pérez-Sánchez, H., Zhang, Y., Shao, Y., Shi, D., Liu, H., et al. (2014). Ligand Induced Change of β2 Adrenergic Receptor from Active to Inactive Conformation and its Implication for the Closed/open State of the Water Channel: Insight from Molecular Dynamics Simulation, Free Energy Calculation and Markov State Model Analysis. Phys. Chem. Chem. Phys. 16 (30), 15874–15885. doi:10.1039/c4cp01185f
Ballester, P. J. (2019). Machine Learning for Molecular Modelling in Drug Design. Biomolecules 9 (6), 216. doi:10.3390/biom9060216
Bansal, M., Kumar, S., and Velavan, R. (2000). HELANAL: a Program to Characterize helix Geometry in Proteins. J. Biomol. Struct. Dyn. 17 (5), 811–819. doi:10.1080/07391102.2000.10506570
Barati Farimani, A., Feinberg, E., and Pande, V. (2018). Binding Pathway of Opiates to μ-Opioid Receptors Revealed by Machine Learning. Biophysical J. 114 (3), 62a–63a. doi:10.1016/j.bpj.2017.11.390
Barletta, G. P., Franchini, G., Corsico, B., and Fernandez-Alberti, S. (2019). Fatty Acid and Retinol-Binding Protein: Unusual Protein Conformational and Cavity Changes Dictated by Ligand Fluctuations. J. Chem. Inf. Model. 59 (8), 3545–3555. doi:10.1021/acs.jcim.9b00364
Baskin, I. I. (2020). The Power of Deep Learning to Ligand-Based Novel Drug Discovery. Expert Opin. Drug Discov. 15 (7), 755–764. doi:10.1080/17460441.2020.1745183
Bekker, G. J., Araki, M., Oshima, K., Okuno, Y., and Kamiya, N. (2020). Exhaustive Search of the Configurational Space of Heat-Shock Protein 90 with its Inhibitor by Multicanonical Molecular Dynamics Based Dynamic Docking. J. Comput. Chem. 41 (17), 1606–1615. doi:10.1002/jcc.26203
Bernetti, M., Masetti, M., Recanatini, M., Amaro, R. E., and Cavalli, A. (2019). An Integrated Markov State Model and Path Metadynamics Approach to Characterize Drug Binding Processes. J. Chem. Theor. Comput. 15 (10), 5689–5702. doi:10.1021/acs.jctc.9b00450
Berrar, D. (2019). “Bayes’ Theorem and Naive Bayes Classifier,” in Encyclopedia of Bioinformatics and Computational Biology. Editors S. Ranganathan, M. Gribskov, K. Nakai, and C. Schönbach (Wadern: Academic Press), 403–412. doi:10.1016/b978-0-12-809633-8.20473-1
Bhakat, S., Martin, A. J., and Soliman, M. E. (2014). An Integrated Molecular Dynamics, Principal Component Analysis and Residue Interaction Network Approach Reveals the Impact of M184V Mutation on HIV Reverse Transcriptase Resistance to Lamivudine. Mol. Biosyst. 10 (8), 2215–2228. doi:10.1039/c4mb00253a
Bhattarai, A., Wang, J., and Miao, Y. (2020). Retrospective Ensemble Docking of Allosteric Modulators in an Adenosine G-Protein-Coupled Receptor. Biochim. Biophys. Acta Gen. Subj. 1864 (8), 129615. doi:10.1016/j.bbagen.2020.129615
Binder, K., Horbach, J., Kob, W., Paul, W., and Varnik, F. (2004). Molecular Dynamics Simulations. J. Phys. Condens. Matter 16 (5), S429–S453. doi:10.1088/0953-8984/16/5/006
Bosshard, H. R. (2001). Molecular Recognition by Induced Fit: How Fit Is the Concept. News Physiol. Sci. 16 (4), 171–173. doi:10.1152/physiologyonline.2001.16.4.171
Bowers, K. J., Chow, D. E., Xu, H., Dror, R. O., Eastwood, M. P., Gregersen, B. A., et al. (2006). “Scalable Algorithms for Molecular Dynamics Simulations on Commodity Clusters,” in SC '06: Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, 43. doi:10.1109/SC.2006.54
Breiman, L., Friedman, J. H., Olshen, R. A., and Stone, C. J. (1984). Classification and Regression Trees. 1st ed. New York: Routledge.
Brooks, B. R., Brooks, C. L., Mackerell, A. D., Nilsson, L., Petrella, R. J., Roux, B., et al. (2009). CHARMM: the Biomolecular Simulation Program. J. Comput. Chem. 30 (10), 1545–1614. doi:10.1002/jcc.21287
Bruno, A., Beato, C., and Costantino, G. (2011). Molecular Dynamics Simulations and Docking Studies on 3D Models of the Heterodimeric and Homodimeric 5-HT(2A) Receptor Subtype. Future Med. Chem. 3 (6), 665–681. doi:10.4155/fmc.11.27
Buch, I., Giorgino, T., and de Fabritiis, G. (2011). Complete Reconstruction of an Enzyme-Inhibitor Binding Process by Molecular Dynamics Simulations. Proc. Natl. Acad. Sci. U S A. 108, 10184–10189. doi:10.1073/pnas.1103547108
Carpenter, K. A., and Huang, X., (2018). Machine Learning-Based Virtual Screening and its Applications to Alzheimer's Drug Discovery: A Review. Curr. Pharm. Des. 24 (28), 3347–3358. doi:10.2174/1381612824666180607124038
Casasnovas, R., Limongelli, V., Tiwary, P., Carloni, P., and Parrinello, M. (2017). Unbinding Kinetics of a P38 MAP Kinase Type II Inhibitor from Metadynamics Simulations. J. Am. Chem. Soc. 139 (13), 4780–4788. doi:10.1021/jacs.6b12950
Case, D. A., Cheatham, T. E., Darden, T., Gohlke, H., Luo, R., and Merz, K. M.. (2005). The Amber Biomolecular Simulation Programs. J. Comput. Chem. 26(16), 1668. doi:10.1002/jcc.20290
Case, D. A., Aktulga, H. M., Belfon, K., Ben-Shalom, I. Y., Brozell, S. R., Cerutti, D. S., et al. (2021). Amber 2021. San Francisco: University of California.
Casoni, A., Clerici, F., and Contini, A. (2013). Molecular Dynamic Simulation of mGluR5 Amino Terminal Domain: Essential Dynamics Analysis Captures the Agonist or Antagonist Behaviour of Ligands. J. Mol. Graph. Model. 41, 72–78. doi:10.1016/j.jmgm.2013.02.002
Chaturvedi, N., Yadav, B. S., Pandey, P. N., and Tripathi, V. (2017). The Effect of β-glucan and its Potential Analog on the Structure of Dectin-1 Receptor. J. Mol. Graph. Model. 74, 315–325. doi:10.1016/j.jmgm.2017.04.014
Chen, J. (2018). Functional Roles of Magnesium Binding to Extracellular Signal-Regulated Kinase 2 Explored by Molecular Dynamics Simulations and Principal Component Analysis. J. Biomol. Struct. Dyn. 36 (2), 351–361. doi:10.1080/07391102.2016.1277783
Chiappori, F., Merelli, I., Milanesi, L., and Rovida, E. (2010). Exploring the Role of the Phospholipid Ligand in Endothelial Protein C Receptor: a Molecular Dynamics Study. Proteins 78 (12), 2679–2690. doi:10.1002/prot.22782
Chodera, J. D., and Noé, F. (2014). Markov State Models of Biomolecular Conformational Dynamics. Curr. Opin. Struct. Biol. 25, 135–144. doi:10.1016/j.sbi.2014.04.002
Cholko, T., Chen, W., Tang, Z., and Chang, C. A. (2018). A Molecular Dynamics Investigation of CDK8/CycC and Ligand Binding: Conformational Flexibility and Implication in Drug Discovery. J. Comput. Aided Mol. Des. 32 (6), 671–685. doi:10.1007/s10822-018-0120-3
Coifman, R. R., and Lafon, S. (2006). Diffusion Maps. Appl. Comput. Harmon. Anal. 21 (1), 5–30. doi:10.1016/j.acha.2006.04.006
Coifman, R. R., Lafon, S., Lee, A. B., Maggioni, M., Nadler, B., Warner, F., et al. (2005). Geometric Diffusions as a Tool for Harmonic Analysis and Structure Definition of Data: Diffusion Maps. Proc. Natl. Acad. Sci. U. S. A. 102 (21), 7426–7431. doi:10.1073/pnas.0500334102
Cortes, C., and Vapnik, V. N. (1995). Support-vector Networks. Mach. Learn. 20 (3), 273–297. doi:10.1007/BF00994018
Cossio-Pérez, R., Palma, J., and Pierdominici-Sottile, G. (2017). Consistent Principal Component Modes from Molecular Dynamics Simulations of Proteins. J. Chem. Inf. Model. 57 (4), 826–834. doi:10.1021/acs.jcim.6b00646
Cover, T. M., and Hart, P. E. (1967). Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theor. 13 (1), 21–27. doi:10.1109/TIT.1967.1053964
CPPTRAJ (2021). CPPTRAJ Wiki. Available at: https://github.com/Amber-MD/cpptraj/wiki (Accessed December 22, 2021).
Das, A., and Mukhopadhyay, C. (2007). Application of Principal Component Analysis in Protein Unfolding: an All-Atom Molecular Dynamics Simulation Study. J. Chem. Phys. 127 (16), 165103. doi:10.1063/1.2796165
David, C. C., Avery, C. S., and Jacobs, D. J. (2021). JEDi: Java Essential Dynamics Inspector - a Molecular Trajectory Analysis Toolkit. BMC Bioinform 22 (1), 226. doi:10.1186/s12859-021-04140-5
Davies, D. L., and Bouldin, D. W. (1979). A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-1 (2), 224–227. doi:10.1109/TPAMI.1979.4766909
De Paris, R., Quevedo, C. V., Ruiz, D. D. A., and Norberto de Souza, O. (2015a). An Effective Approach for Clustering InhA Molecular Dynamics Trajectory Using Substrate-Binding Cavity Features. PLoS ONE 10 (7), e0133172. doi:10.1371/journal.pone.0133172
De Paris, R., Quevedo, C. V., Ruiz, D. D., Norberto de Souza, O., and Barros, R. C. (2015b). Clustering Molecular Dynamics Trajectories for Optimizing Docking Experiments. Comput. Intell. Neurosci. 2015, 916240. doi:10.1155/2015/916240
de Souto, M. C. P., Coelho, A. L. V., Faceli, K., Sakata, T. C., Bonadia, V., and Costa, I. G. (2012). A Comparison of External Clustering Evaluation Indices in the Context of Imbalanced Data Sets. Braz. Symp. Neural Networks 2012, 49–54. doi:10.1109/SBRN.2012.25
de Souza, V. C., Golliat, L., and Goliatt, P. V. Z. C. (2017). “Clustering Algorithms Applied on Analysis of Protein Molecular Dynamics,” in Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI), 1–6.
Dickson, A. (2018). Mapping the Ligand Binding Landscape. Biophys. J. 115 (9), 1707–1719. doi:10.1016/j.bpj.2018.09.021
Dixon, T., Uyar, A., Ferguson-Miller, S., and Dickson, A. (2021). Membrane-Mediated Ligand Unbinding of the PK-11195 Ligand from TSPO. Biophys. J. 120 (1), 158–167. doi:10.1016/j.bpj.2020.11.015
Desmond Molecular Dynamics System, (2021). Maestro-Desmond Interoperability Tools. New York, NY: Schrödinger.
Doerr, S., Majewski, M., Pérez, A., Krämer, A., Clementi, C., Noe, F., et al. (2021). TorchMD: A Deep Learning Framework for Molecular Simulations. J. Chem. Theor. Comput. 17 (4), 2355–2363. doi:10.1021/acs.jctc.0c01343
Doms, R. W., Helenius, A., and White, J. (1985). Membrane Fusion Activity of the Influenza Virus Hemagglutinin. The Low pH-Induced Conformational Change. J. Biol. Chem. 260 (5), 2973–2981. doi:10.1016/s0021-9258(18)89461-3
Dutta, S., and Bose, K. (2021). Remodelling Structure-Based Drug Design Using Machine Learning. Emerg. Top. Life Sci. 5 (1), 13–27. doi:10.1042/ETLS20200253
Ellingson, S. R., Miao, Y., Baudry, J., and Smith, J. C. (2015). Multi-conformer Ensemble Docking to Difficult Protein Targets. J. Phys. Chem. B. 119 (3), 1026–1034. doi:10.1021/jp506511p
Ernst, M., Sittel, F., and Stock, G. (2015). Contact- and Distance-Based Principal Component Analysis of Protein Dynamics. J. Chem. Phys. 143 (24), 244114. doi:10.1063/1.4938249
Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Kdd-96 Proc. 96, 226–231. doi:10.5555/3001460.3001507
Evangelista, F. W., Ellingson, S. R., Smith, J. C., and Baudry, J. (2019). Ensemble Docking in Drug Discovery: How Many Protein Configurations from Molecular Dynamics Simulations Are Needed to Reproduce Known Ligand Binding. J. Phys. Chem. B. 123 (25), 5189–5195. doi:10.1021/acs.jpcb.8b11491
Fakhar, Z., Govender, T., Maguire, G. E. M., Lamichhane, G., Walker, R. C., Kruger, H. G., et al. (2017). Differential Flap Dynamics in L,d-Transpeptidase2 from mycobacterium Tuberculosis Revealed by Molecular Dynamics. Mol. Biosyst. 13 (6), 1223–1234. doi:10.1039/c7mb00110j
Feig, M., Karanicolas, J., and Brooks, C. L. (2004). MMTSB Tool Set: Enhanced Sampling and Multiscale Modeling Methods for Applications in Structural Biology. J. Mol. Graph. Model. 22 (5), 377–395. doi:10.1016/j.jmgm.2003.12.005
Fenton, A. W. (2008). Allostery: an Illustrated Definition for the ‘second Secret of Life. Trends Biochem. Sci. 33 (9), 420–425. doi:10.1016/j.tibs.2008.05.009
Ferraro, M., Moroni, E., Ippoliti, E., Rinaldi, S., Sanchez-Martin, C., Rasola, A., et al. (2021). Machine Learning of Allosteric Effects: the Analysis of Ligand-Induced Dynamics to Predict Functional Effects in TRAP1. J. Phys. Chem. B. 125 (1), 101–114. doi:10.1021/acs.jpcb.0c09742
Ferreira, L. G., Dos Santos, R. N., Oliva, G., and Andricopulo, A. D. (2015). Molecular Docking and Structure-Based Drug Design Strategies. Molecules 20 (7), 13384–13421. doi:10.3390/molecules200713384
Fraccalvieri, D., Bonati, L., and Stella, F. (2013). “Self Organizing Maps to Efficiently Cluster and Functionally Interpret Protein Conformational Ensembles,” in In Proceedings Wivace. arXiv:1309.7122. doi:10.4204/eptcs.130.13
Fu, G., Sivaprakasam, P., Dale, O. R., Manly, S. P., Cutler, S. J., and Doerksen, R. J. (2014). Pharmacophore Modeling, Ensemble Docking, Virtual Screening, and Biological Evaluation on Glycogen Synthase Kinase‐3β. Mol. Inform. 33 (9), 610–626. doi:10.1002/minf.201400044
Gebhardt, J., Kiesel, M., Riniker, S., and Hansen, N. (2020). Combining Molecular Dynamics and Machine Learning to Predict Self-Solvation Free Energies and Limiting Activity Coefficients. J. Chem. Inf. Model. 60 (11), 5319–5330. doi:10.1021/acs.jcim.0c00479
Girdhar, K., Dehury, B., Kumar, S. M., Daniel, V. P., Choubey, A., Dogra, S., et al. (2019). Novel Insights into the Dynamics Behavior of Glucagon-like Peptide-1 Receptor with its Small Molecule Agonists. J. Biomol. Struct. Dyn. 37 (15), 3976–3986. doi:10.1080/07391102.2018.1532818
Glaser, J., Nguyen, T. D., Anderson, J. A., Lui, P., Spiga, F., Millan, J. A., et al. (2015). Strong Scaling of General-Purpose Molecular Dynamics Simulations on GPUs. Comput. Phys. Commun. 192, 97–107. doi:10.1016/j.cpc.2015.02.028
Glazer, D. S., Radmer, R. J., and Altman, R. B. (2008). Combining Molecular Dynamics and Machine Learning to Improve Protein Function Recognition. Pac. Symp. Biocomput. 13, 332–343. doi:10.1249/jsr.0b013e31818f03c5
Glenn, T. C., Zare, A., and Gader, P. D. (2015). Bayesian Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 23 (5), 1545–1561. doi:10.1109/TFUZZ.2014.2370676
Glielmo, A., Husic, B. E., Rodriguez, A., Clementi, C., Noé, F., and Laio, A. (2021). Unsupervised Learning Methods for Molecular Simulation Data. Chem. Rev. 121 (16), 9722–9758. doi:10.1021/acs.chemrev.0c01195
Glykos, N. M. (2006). Software News and Updates Carma: A Molecular Dynamics Analysis Program. J. Comput. Chem. 27 (14), 1765–1768. doi:10.1002/jcc.20482
Göller, A. H., Kuhnke, L., Montanari, F., Bonin, A., Schneckener, S., Ter Laak, A., et al. (2020). Bayer's In Silico ADMET Platform: a Journey of Machine Learning over the Past Two Decades. Drug Discov. Today 25 (9), 1702–1709. doi:10.1016/j.drudis.2020.07.001
Göller, A. H., Kuhnke, L., Ter Laak, A., Meier, K., and Hillisch, A. (2022). Machine Learning Applied to the Modeling of Pharmacological and ADMET Endpoints. Methods Mol. Biol. 2390, 61–101. doi:10.1007/978-1-0716-1787-8_2
Goodey, N. M., and Benkovic, S. J. (2008). Allosteric Regulation and Catalysis Emerge via a Common Route. Nat. Chem. Biol. 4 (8), 474–482. doi:10.1038/nchembio.98
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative Adversarial Nets. Adv. Neural Inf. Process. Syst. 27, 2672–2680. doi:10.3156/jsoft.29.5_177_2
Gordon, H. L., and Somorjai, R. L. (1992). Fuzzy Cluster Analysis of Molecular Dynamics Trajectories. Proteins 14 (2), 249–264. doi:10.1002/prot.340140211
Grant, B. J., Rodrigues, A. P. C., ElSawy, K. M., McCammon, J. A., and Caves, L. S. D. (2006). Bio3d: an R Package for the Comparative Analysis of Protein Structures. Bioinformatics 22 (21), 2695–2696. doi:10.1093/bioinformatics/btl461
Grossfield, A., and Romo, T. D. (2021). Loos, a Better Tool to Analyze Molecular Dynamics Simulations. Biophys. J. 120 (3), 178a. doi:10.1016/j.bpj.2020.11.1245
Grossfield, A., and Zuckerman, D. M. (2009). Quantifying Uncertainty and Sampling Quality in Biomolecular Simulations. Annu. Rep. Comput. Chem. 5, 23–48. doi:10.1016/S1574-1400(09)00502-7
Guedes, I. A., de Magalhães, C. S., and Dardenne, L. E. (2014). Receptor–ligand Molecular Docking. Biophys. Rev. 6 (1), 75–87. doi:10.1007/s12551-013-0130-2
Hall, P., Park, B. U., and Samworth, R. J. (2008). Choice of Neighbor Order in Nearest-Neighbor Classification. Ann. Stat. 36 (5), 2135–2152. doi:10.1214/07-AOS537
Haque, I. S., Beauchamp, K. A., and Pande, V. S. (2014). A Fast 3× N Matrix Multiply Routine for Calculation of Protein RMSD. Biorxiv 8631. doi:10.1101/008631
Hartigan, A., and Wong, M. A. (1979). A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 28 (1), 100–108. doi:10.2307/2346830
Hernández, C. X., Wayment-Steele, H. K., Sultan, M. M., Husic, B. E., and Pande, V. S. (2018). Variational Encoding of Complex Dynamics. Phys. Rev. E. 97 (6-1), 062412. doi:10.1103/PhysRevE.97.062412
Hilger, D., Masureel, M., and Kobilka, B. K. (2018). Structure and Dynamics of GPCR Signaling Complexes. Nat. Struct. Mol. Biol. 25 (1), 4–12. doi:10.1038/s41594-017-0011-7
Hinsen, K. (2000). The Molecular Modeling Toolkit: a New Approach to Molecular Simulations. J. Comput. Chem. 21 (2), 79–85. doi:10.1002/(SICI)1096-987X(20000130)21:2<79::AID-JCC1>3.0.CO;2-B
Hollingsworth, S. A., and Dror, R. O. (2018). Molecular Dynamics Simulation for All. Neuron 99 (6), 1129–1143. doi:10.1016/j.neuron.2018.08.011
Hopfield, J. J. (1982). Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc. Natl. Acad. Sci. U.S.A. 79 (8), 2554–2558. doi:10.1073/pnas.79.8.2554
Hopkins, B., and Skellam, J. G. (1954). A New Method for Determining the Type of Distribution of Plant Individuals. Ann. Bot. 18 (2), 213–227. doi:10.1093/oxfordjournals.aob.a083391
Huang, D., and Caflisch, A. (2011). The Free Energy Landscape of Small Molecule Unbinding. Plos Comput. Biol. 7 (2), e1002002. doi:10.1371/journal.pcbi.1002002
Huang, Z. (1998). Extensions to the K-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Discov. 2 (3), 283–304. doi:10.1023/A:1009769707641
Hudson, I. L. (2021). Data Integration Using Advances in Machine Learning in Drug Discovery and Molecular Biology. Methods Mol. Biol. 2190, 167–184. doi:10.1007/978-1-0716-0826-5_7
Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: Visual Molecular Dynamics. J. Mol. Graph. 14 (1), 33–38. doi:10.1016/0263-7855(96)00018-5
Husic, B. E., and Pande, V. S. (2018). Markov State Models: From an Art to a Science. J. Am. Chem. Soc. 140 (7), 2386–2396. doi:10.1021/jacs.7b12191
Hussain, W., Rasool, N., and Khan, Y. D. (2021). Insights into Machine Learning-Based Approaches for Virtual Screening in Drug Discovery: Existing Strategies and Streamlining through FP-CADD. Curr. Drug Discov. Technol. 18 (4), 463–472. doi:10.2174/1570163817666200806165934
Hyvönen, M. T., Hiltunen, Y., El-Deredy, W., Ojala, T., Vaara, J., Kovanen, P. T., et al. (2001). Application of Self-Organizing Maps in Conformational Analysis of Lipids. J. Am. Chem. Soc. 123 (5), 810–816. doi:10.1021/ja0025853
Ichiye, T., and Karplus, M. (1991). Collective Motions in Proteins: a Covariance Analysis of Atomic Fluctuations in Molecular Dynamics and normal Mode Simulations. Proteins 11 (3), 205–217. doi:10.1002/prot.340110305
Jamal, S., Grover, A., and Grover, S. (2019). Machine Learning from Molecular Dynamics Trajectories to Predict Caspase-8 Inhibitors against Alzheimer’s Disease. Front. Pharmacol. 10, 780. doi:10.3389/fphar.2019.00780
Jeong, J. C., Jo, S., Wu, E. L., Qi, Y., Monje‐Galvan, V., Yeom, M. S., et al. (2014). ST‐analyzer: A Web‐based User Interface for Simulation Trajectory Analysis. J. Comput. Chem. 35 (12), 957–963. doi:10.1002/jcc.23584
Jia, L., and Gao, H. (2022). Machine Learning for In Silico ADMET Prediction. Methods Mol. Biol. 2390, 447–460. doi:10.1007/978-1-0716-1787-8_20
Jolliffe, I. T., and Cadima, J. (2016). Principal Component Analysis: a Review and Recent Developments. Phil. Trans. R. Soc. A. 374 (2065), 20150202. doi:10.1098/rsta.2015.0202
Kabsch, W., and Sander, C. (1983). Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen‐bonded and Geometrical Features. Biopolym. Orig. Res. Biomol. 22 (12), 2577–2637. doi:10.1002/bip.360221211
Karnati, K. R., and Wang, Y. (2019). Structural and Binding Insights into HIV-1 Protease and P2-Ligand Interactions through Molecular Dynamics Simulations, Binding Free Energy and Principal Component Analysis. J. Mol. Graph. Model. 92, 112–122. doi:10.1016/j.jmgm.2019.07.008
Kaufman, L., and Rousseeuw, P. J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis. Hoboken, NJ: John Willey & Sons.
Keller, B., Daura, X., and van Gunsteren, W. F. (2010). Comparing Geometric and Kinetic Cluster Algorithms for Molecular Simulation Data. J. Chem. Phys. 132 (7), 074110. doi:10.1063/1.3301140
Khamis, M. A., Gomaa, W., and Ahmed, W. F. (2015). Machine Learning in Computational Docking. Artif. Intell. Med. 63 (3), 135–152. doi:10.1016/j.artmed.2015.02.002
Khamis, M. A., and Gomaa, W. (2015). Comparative Assessment of Machine-Learning Scoring Functions on PDBbind 2013. Eng. Appl. Artif. Intell. 45 (C), 136–151. doi:10.1016/j.engappai.2015.06.021
Khamis, M., Gomaa, W., and Galal, B. (2016). Deep Learning Is Competing Random forest in Computational Docking. New Borg El-Arab City, Egypt: arXiv:1608.06665.
Kim, H. J., Choi, M. Y., Kim, H. J., and Llinás, M. (2010). Conformational Dynamics and Ligand Binding in the Multi-Domain Protein PDC109. PLoS One 5 (2), e9180. doi:10.1371/journal.pone.0009180
Koukos, P. I., and Glykos, N. M. (2013). Grcarma: a Fully Automated Task‐oriented Interface for the Analysis of Molecular Dynamics Trajectories. J. Comput. Chem. 34 (26), 2310–2312. doi:10.1002/jcc.23381
Kramer, M. A. (1991). Nonlinear Principal Component Analysis Using Autoassociative Neural Networks. Aiche J. 37, 233–243. doi:10.1002/aic.690370209
Kucwaj-Brysz, K., Dela, A., Podlewska, S., Bednarski, M., Siwek, A., Satała, G., et al. (2021). The Structural Determinants for α1-adrenergic/serotonin Receptors Activity Among Phenylpiperazine-Hydantoin Derivatives. Molecules 26 (22), 7025. doi:10.3390/molecules26227025
Lagardère, L., Jolly, L.-H., Lipparini, F., Aviat, F., Stamm, B., Jing, Z. F., et al. (2018). Tinker-HP: A Massively Parallel Molecular Dynamics Package for Multiscale Simulations of Large Complex Systems with Advanced Point Dipole Polarizable Force Fields. Chem. Sci. 9 (4), 956–972. doi:10.1039/c7sc04531j
Lange, O. F., and Grubmüller, H. (2006). Can Principal Components Yield a Dimension Reduced Description of Protein Dynamics on Long Time Scales? J. Phys. Chem. B. 110 (45), 22842–22852. doi:10.1021/jp062548j
Laxmi, D., and Priyadarshy, S. (2002). HyperChem 6.03. Biotech. Softw. Internet Rep. 3 (1), 5–9. doi:10.1089/152791602317250351
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521 (7553), 436–444. doi:10.1038/nature14539
Lindahl, E. R. (2008). Molecular Dynamics Simulations. Methods Mol. Biol. 443, 3–23. doi:10.1007/978-1-59745-177-2_1
Lipiński, P. F. J., Jarończyk, M., Dobrowolski, J. C., and Sadlej, J. (2019). Molecular Dynamics of Fentanyl Bound to μ-opioid Receptor. J. Mol. Model. 25 (5), 144. doi:10.1007/s00894-019-3999-2
Lopez, R., Regier, J., Jordan, M. I., and Yosef, N. (2018). Information Constraints on Auto-Encoding Variational Bayes. Adv. Neural Inf. Process. Syst. 31, 6114–6125.
Lu, S., Shen, Q., and Zhang, J. (2019). Allosteric Methods and Their Applications: Facilitating the Discovery of Allosteric Drugs and the Investigation of Allosteric Mechanisms. Acc. Chem. Res. 52 (2), 492–500. doi:10.1021/acs.accounts.8b00570
Magudeeswaran, S., and Poomani, K. (2020). Binding Mechanism of Spinosine and Venenatine Molecules with P300 HAT Enzyme: Molecular Screening, Molecular Dynamics and Free-Energy Analysis. J. Cel. Biochem. 121 (2), 1759–1777. doi:10.1002/jcb.29412
Majumder, S., and Giri, K. (2021). An Insight into the Binding Mechanism of Viprinin and its Morpholine and Piperidine Derivatives with HIV-1 VPR: Molecular Dynamics Simulation, Principal Component Analysis and Binding Free Energy Calculation Study. J. Biomol. Struct. Dyn., 1–13. doi:10.1080/07391102.2021.1954553
Mallet, V., Nilges, M., and Bouvier, G. (2021). Quicksom: Self-Organizing Maps on GPUs for Clustering of Molecular Dynamics Trajectories. Bioinformatics 37 (14), 2064–2065. doi:10.1093/bioinformatics/btaa925
Marchetti, F., Moroni, E., Pandini, A., and Colombo, G. (2021). Machine Learning Prediction of Allosteric Drug Activity from Molecular Dynamics. J. Phys. Chem. Lett. 12 (15), 3724–3732. doi:10.1021/acs.jpclett.1c00045
Martínez-Archundia, M., Correa-Basurto, J., Montaño, S., and Rosas-Trigueros, J. L. (2019). Studying the Collective Motions of the Adenosine A2A Receptor as a Result of Ligand Binding Using Principal Component Analysis. J. Biomol. Struct. Dyn. 37 (18), 4685–4700. doi:10.1080/07391102.2018.1564700
McGibbon, R. T., Beauchamp, K. A., Harrigan, M. P., Klein, C., Swails, J. M., Hernández, C. X., et al. (2015). MDTraj: a Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 109 (8), 1528–1532. doi:10.1016/j.bpj.2015.08.015
Melville, J. L., Burke, E. K., and Hirst, J. D. (2009). Machine Learning in Virtual Screening. Comb. Chem. High Throughput Screen. 12 (4), 332–343. doi:10.2174/138620709788167980
Mezei, M. (2010). Simulaid: a Simulation Facilitator and Analysis Program. J. Comput. Chem. 31 (14), 2658–2668. doi:10.1002/jcc.21551
Michaud-Agrawal, N., Denning, E. J., Woolf, T. B., and Beckstein, O. (2011). MDAnalysis: a Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem. 32 (10), 2319–2327. doi:10.1002/jcc.21787
Miyashita, N., and Yonezawa, Y. (2017). On-the-fly Analysis of Molecular Dynamics Simulation Trajectories of Proteins Using the Bayesian Inference Method. J. Chem. Phys. 147 (12), 124108. doi:10.1063/1.4997099
Moritsugu, K. (2021). Multiscale Enhanced Sampling Using Machine Learning. Life (Basel) 11 (10), 1076. doi:10.3390/life11101076
Morris, G. M., and Lim-Wilby, M. (2008). Molecular Docking. Methods Mol. Biol. 443, 365–382. doi:10.1007/978-1-59745-177-2_19
Ng, H. W., Laughton, C. A., and Doughty, S. W. (2013). Molecular Dynamics Simulations of the Adenosine A2a Receptor: Structural Stability, Sampling, and Convergence. J. Chem. Inf. Model. 53 (5), 1168–1178. doi:10.1021/ci300610w
Novikov, G. V., Sivozhelezov, V. S., and Shaitan, K. V. (2013). Study of Structural Dynamics of Ligand-Activated Membrane Receptors by Means of Principal Component Analysis. Biochemistry (Mosc) 78 (4), 403–411. doi:10.1134/S0006297913040093
Nussinov, R., and Tsai, C.-J. (2013). Allostery in Disease and in Drug Discovery. Cell 153 (2), 293–305. doi:10.1016/j.cell.2013.03.034
Nussinov, R., Tsai, C.-J., and Liu, J. (2014). Principles of Allosteric Interactions in Cell Signaling. J. Am. Chem. Soc. 136 (51), 17692–17701. doi:10.1021/ja510028c
Pande, V. S., Beauchamp, K., and Bowman, G. R. (2010). Everything You Wanted to Know about Markov State Models but Were Afraid to Ask. Methods 52 (1), 99–105. doi:10.1016/j.ymeth.2010.06.002
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). “PyTorch: An Imperative Style, High-Performance Deep Learning Library,” in Advances in Neural Information Processing Systems. Editors H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Vancouver: Curran Associates, Inc.), 8024–8035. 32.
Patel, L., Shukla, T., Huang, X., Ussery, D. W., and Wang, S. (2020). Machine Learning Methods in Drug Discovery. Molecules 25 (22), 5277. doi:10.3390/molecules25225277
Perez, A., MacCallum, J. L., and Dill, K. A. (2015). Accelerating Molecular Simulations of Proteins Using Bayesian Inference on Weak Information. PNAS 112 (38), 11846–11851. doi:10.1073/pnas.1515561112
Phillips, J. C., Braun, R., Wang, W., Gumbart, J., Tajkhorshid, E., Villa, E., et al. (2005). Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 26 (16), 1781–1802. doi:10.1002/jcc.20289
Pietrucci, F., Marinelli, F., Carloni, P., and Laio, A. (2009). Substrate Binding Mechanism of HIV-1 Protease from Explicit-Solvent Atomistic Simulations. J. Am. Chem. Soc. 131 (33), 11811–11818. doi:10.1021/ja903045y
Pisani, P., Caporuscio, F., Carlino, L., and Rastelli, G. (2016). Molecular Dynamics Simulations and Classical Multidimensional Scaling Unveil New Metastable States in the Conformational Landscape of CDK2. PLoS One 11 (4), e0154066. doi:10.1371/journal.pone.0154066
Plante, A., Shore, D. M., Morra, G., Khelashvili, G., and Weinstein, H. (2019). A Machine Learning Approach for the Discovery of Ligand-Specific Functional Mechanisms of GPCRs. Molecules 24 (11), 2097. doi:10.3390/molecules24112097
Plattner, N., and Noé, F. (2015). Protein Conformational Plasticity and Complex Ligand-Binding Kinetics Explored by Atomistic Simulations and Markov Models. Nat. Commun. 6, 7653. doi:10.1038/ncomms8653
Podlewska, S., Latacz, G., Łażewska, D., Kieć-Kononowicz, K., and Handzlik, J. (2020). In Silico and In Vitro Studies on Interaction of Novel Non-Imidazole Histamine H3R Antagonists with CYP3A4. Bioorg. Med. Chem. Lett. 30 (11), 127147. doi:10.1016/j.bmcl.2020.127147
Preto, J., and Clementi, C. (2014). Fast Recovery of Free Energy Landscapes via Diffusion-Map-Directed Molecular Dynamics. Phys. Chem. Chem. Phys. 16 (36), 19181–19191. doi:10.1039/c3cp54520b
Rand, W. M. (1971). Objective Criteria for the Evaluation of Clustering Methods. J. Am. Stat. Assoc. 66 (336), 846–850. doi:10.1080/01621459.1971.10482356
Riniker, S. (2017). Molecular Dynamics Fingerprints (MDFP): Machine Learning from MD Data to Predict Free-Energy Differences. J. Chem. Inf. Model. 57 (4), 726–741. doi:10.1021/acs.jcim.6b00778
Roe, D. R., and Cheatham, T. E. (2013). PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theor. 9 (7), 3084–3095. doi:10.1021/ct400341p
Rohrdanz, M. A., Zheng, W., Maggioni, M., and Clementi, C. (2011). Determination of Reaction Coordinates via Locally Scaled Diffusion Map. J. Chem. Phys. 134 (12), 124116. doi:10.1063/1.3569857
Roither, B., Oostenbrink, C., and Schreiner, W. (2020). Molecular Dynamics of the Immune Checkpoint Programmed Cell Death Protein I, PD-1: Conformational Changes of the BC-Loop upon Binding of the Ligand PD-L1 and the Monoclonal Antibody Nivolumab. BMC Bioinform 21 (Suppl. 17), 557. doi:10.1186/s12859-020-03904-9
Romo, T. D., Leioatts, N., and Grossfield, A. (2014). Lightweight Object Oriented Structure Analysis: Tools for Building Tools to Analyze Molecular Dynamics Simulations. J. Comput. Chem. 35 (32), 2305–2318. doi:10.1002/jcc.23753
Rudling, A., Orro, A., and Carlsson, J. (2018). Prediction of Ordered Water Molecules in Protein Binding Sites from Molecular Dynamics Simulations: The Impact of Ligand Binding on Hydration Networks. J. Chem. Inf. Model. 58 (2), 350–361. doi:10.1021/acs.jcim.7b00520
Sander, J. (2011). in Density-Based Clustering” in Encyclopedia of Machine Learning. Editors C. Sammut, and G. I. Webb (Boston: Springer).
Santos, L. H. S., Ferreira, R. S., and Caffarena, E. R. (2019). Integrating Molecular Docking and Molecular Dynamics Simulations. Methods Mol. Biol. 2053, 13–34. doi:10.1007/978-1-4939-9752-7_2
Schmidhuber, J. (2015). Deep Learning in Neural Networks: An Overview. Neural Netw. 61, 85–117. doi:10.1016/j.neunet.2014.09.003
Schölkopf, B., Smola, A., and Müller, K. (1998). Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 10 (5), 1299–1319. doi:10.1162/089976698300017467
Schubert, E., Sander, J., Ester, M., Kriegel, H. P., and Xu, X. (2017). DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. 42 (3), 19. doi:10.1145/3068335
Seeber, M., Cecchini, M., Rao, F., Settanni, G., and Caflisch, A. (2007). Wordom: A Program for Efficient Analysis of Molecular Dynamics Simulations. Bioinformatics 23 (19), 2625–2627. doi:10.1093/bioinformatics/btm378
Seeber, M., Felline, A., Raimondi, F., Muff, S., Friedman, R., Rao, F., et al. (2011). Wordom: A User‐friendly Program for the Analysis of Molecular Structures, Trajectories, and Free Energy Surfaces. J. Comput. Chem. 32 (6), 1183–1194. doi:10.1002/jcc.21688
Shamsi, Z., Cheng, K. J., and Shukla, D. (2018). Reinforcement Learning Based Adaptive Sampling: REAPing Rewards by Exploring Protein Conformational Landscapes. J. Phys. Chem. B 122 (35), 8386–8395. doi:10.1021/acs.jpcb.8b06521
Shao, J., Tanner, S. W., Thompson, N., and Cheatham, T. E. (2007). Clustering Molecular Dynamics Trajectories: 1. Characterizing the Performance of Different Clustering Algorithms. J. Chem. Theor. Comput. 3 (6), 2312–2334. doi:10.1021/ct700119m
Sheik, A. O., Veldman, W., Manyumwa, C., Khairallah, A., Agajanian, S., Oluyemi, O., et al. (2020). Integrated Computational Approaches and Tools for Allosteric Drug Discovery. Int. J. Mol. Sci. 21 (3), 847. doi:10.3390/ijms21030847
Shevchuk, R., and Hub, J. S. (2017). Bayesian Refinement of Protein Structures and Ensembles against SAXS Data Using Molecular Dynamics. PLOS Comput. Biol. 13 (10), e1005800. doi:10.1371/journal.pcbi.1005800
Singh, J., Deng, Z., Narale, G., and Chuaqui, C. (2006). Structural Interaction Fingerprints: a New Approach to Organizing, Mining, Analyzing, and Designing Protein-Small Molecule Complexes. Chem. Biol. Drug Des. 67 (1), 5–12. doi:10.1111/j.1747-0285.2005.00323.x
Sittel, F., Jain, A., and Stock, G. (2014). Principal Component Analysis of Molecular Dynamics: on the Use of Cartesian vs. Internal Coordinates. J. Chem. Phys. 141 (1), 014111. doi:10.1063/1.4885338
Spiwok, V., and Kříž, P. (2020). Time-Lagged T-Distributed Stochastic Neighbor Embedding (T-SNE) of Molecular Simulation Trajectories. Front. Mol. Biosci. 7, 132. doi:10.3389/fmolb.2020.00132
Srivastava, A., Bala, S., Motomura, H., Kohda, D., Tama, F., and Miyashita, O. (2020). Conformational Ensemble of an Intrinsically Flexible Loop in Mitochondrial Import Protein Tim21 Studied by Modeling and Molecular Dynamics Simulations. Biochim. Biophys. Acta Gen. Subj. 1864 (2), 129417. doi:10.1016/j.bbagen.2019.129417
Stamati, H., Clementi, C., and Kavraki, L. E. (2010). Application of Nonlinear Dimensionality Reduction to Characterize the Confonrmational Landscape of Small Peptides. Proteins 78 (2), 223–235. doi:10.1002/prot.22526
Stelzl, L. S., Fowler, P. W., Sansom, M. S. P., and Beckstein, O. (2014). Flexible gates Generate Occluded Intermediates in the Transport Cycle of LacY. J. Mol. Biol. 426 (3), 735–751. doi:10.1016/j.jmb.2013.10.024
Sugeta, H., and Miyazawa, T. (1967). General Method for Calculating Helical Parameters of Polymer Chains from Bond Lengths, Bond Angles, and Internal‐Rotation Angles. Biopolym. Orig. Res. Biomol. 5 (7), 673–679. doi:10.1002/BIP.1967.360050708
Sutmann, G. (2002). “Classical Molecular Dynamics,” in Quantum Simulations of Complex Many-Body Systems: From Theory to Algorithms. Editors J. Grotendorst, D. Marx, and A. Muramatsu (Jülich: John von Neumann Institute for Computing), 211–254.
Takeda, K., Wada, A., Yamamoto, K., Moriyama, Y., and Aoki, K. (1989). Conformational Change of Bovine Serum Albumin by Heat Treatment. J. Protein Chem. 8 (5), 653–659. doi:10.1007/BF01025605
Takemura, K., Sato, C., and Kitao, A. (2018). ColDock: Concentrated Ligand Docking with All-Atom Molecular Dynamics Simulation. J. Phys. Chem. B. 122 (29), 7191–7200. doi:10.1021/acs.jpcb.8b02756
Tenenbaum, J. B., de Silva, V., and Langford, J. C. (2000). A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 290, 2319–2323. doi:10.1126/science.290.5500.2319
Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2021). LAMMPS-A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 271, 108171. doi:10.1016/j.cpc.2021.108171
Tian, H., Jiang, X., Trozzi, F., Xiao, S., Larson, E. C., and Tao, P. (2021). Explore Protein Conformational Space with Variational Autoencoder. Front. Mol. Biosci. 8, 781635. doi:10.3389/fmolb.2021.781635
Todorov, I. T., Smith, W., Trachenko, K., and Dove, M. T. (2006). DL_POLY_3: New Dimensions in Molecular Dynamics Simulations via Massive Parallelism. J. Mater. Chem. 16 (20), 1911–1918. doi:10.1039/B517931A
Torda, A. E., and van Gunstered, W. F. (1994). Algorithms for Clustering Molecular Dynamics Configurations. J. Comput. Chem. 15 (12), 1331–1340. doi:10.1002/jcc.540151203
Torgerson, W. S. (1952). Multidimensional Scaling: I. Theory and Method. Psychometrika 17, 401–419. doi:10.1007/BF02288916
Tribello, G. A., and Gasparotto, P. (2019). Using Dimensionality Reduction to Analyze Protein Trajectories. Front. Mol. Biosci. 6, 46. doi:10.3389/fmolb.2019.00046
Troyer, J. M., and Cohen, F. E. (1995). Protein Conformational Landscapes: Energy Minimization and Clustering of a Long Molecular Dynamics Trajectory. Proteins Struct. Funct. Bioinform. 23, 97–110. doi:10.1002/prot.340230111
Uehara, S., and Tanaka, S. (2017). Cosolvent-based Molecular Dynamics for Ensemble Docking: Practical Method for Generating Druggable Protein Conformations. J. Chem. Inf. Model. 57 (4), 742–756. doi:10.1021/acs.jcim.6b00791
Vamathevan, J., Clark, D., Czodrowski, P., Dunham, I., Ferran, E., Lee, G., et al. (2019). Applications of Machine Learning in Drug Discovery and Development. Nat. Rev. Drug Discov. 18 (6), 463–477. doi:10.1038/s41573-019-0024-5
van de Schoot, R., Depaoli, S., King, R., Kramer, B., Märtens, K., and Tadesse, M. G. (2021). Bayesian Statistics and Modelling. Nat. Rev. Methods Primers 1, 1–26. doi:10.1038/s43586-020-00001-2
van der Maaten, L., and Hinton, G. (2008). Visualizing Data Using T-SNE. J. Mach. Learn. Res. 9 (86), 2579–2605.
Verstraelen, T., Van Houteghem, M., Van Speybroeck, V., and Waroquier, M. (2008). Md-tracks: a Productive Solution for the Advanced Analysis of Molecular Dynamics and Monte Carlo Simulations. J. Chem. Inf. Model. 48 (12), 2414–2424. doi:10.1021/ci800233y
Vitek, A., Stachon, M., Krömer, P., and Snáel, V. (2013). “Towards the Modeling of Atomic and Molecular Clusters Energy by Support Vector Regression,” in 2013 5th International Conference on Intelligent Networking and Collaborative Systems, 121–126. doi:10.1109/INCoS.2013.26
VMD Plugin Library, (2021). Theoretical and Computational Biophysics Group. Available at: https://www.ks.uiuc.edu/Research/vmd/plugins/ (Accessed December 22, 2021).
VMD Script Library (2021). Theoretical and Computational Biophysics Group. Available at: https://www.ks.uiuc.edu/Research/vmd/script_library (Accessed December 22, 2021).
Wang, K., Chodera, J. D., Yang, Y., and Shirts, M. R. (2013). Identifying Ligand Binding Sites and Poses Using GPU-Accelerated Hamiltonian Replica Exchange Molecular Dynamics. J. Comput.-Aided Mol. Des. 27 (12), 989–1007. doi:10.1007/s10822-013-9689-8
Wang, W., Gan, N., Sun, Q., Wu, D., Gan, R., Zhang, M., et al. (2019). Study on the Interaction of Ertugliflozin with Human Serum Albumin In Vitro by Multispectroscopic Methods, Molecular Docking, and Molecular Dynamics Simulation. Spectrochim. Acta A. Mol. Biomol. Spectrosc. 219, 83–90. doi:10.1016/j.saa.2019.04.047
Wang, X., Song, K., Li, L., and Chen, L. (2018). Structure-Based Drug Design Strategies and Challenges. Curr. Top. Med. Chem. 18 (12), 998–1006. doi:10.2174/1568026618666180813152921
Wei, L., and Altman, R. B. (1998). Recognizing Protein Binding Sites Using Statistical Descriptions of Their 3D Environments. Pac. Symp. Biocomput., 497–508.
Wootten, D., Christopoulos, A., Marti-Solano, M., Babu, M. M., and Sexton, P. M. (2018). Mechanisms of Signalling and Biased Agonism in G Protein-Coupled Receptors. Nat. Rev. Mol. Cell Biol. 19 (10), 638–653. doi:10.1038/s41580-018-0049-3
Wu, W., Han, L., Wang, C., Wen, X., Sun, H., and Yuan, H. (2019). Structural Insights into Ligand Binding Features of Dual FABP4/5 Inhibitors by Molecular Dynamics Simulations. J. Biomol. Struct. Dyn. 37 (18), 4790–4800. doi:10.1080/07391102.2018.1561328
Wu, X., Zheng, Z., Guo, T., Wang, K., and Zhang, Y. (2021). Molecular Dynamics Simulation of Lentinan and its Interaction with the Innate Receptor Dectin-1. Int. J. Biol. Macromol. 171, 527–538. doi:10.1016/j.ijbiomac.2021.01.032
Yang, G. F. (2014). Structure-based Drug Design: Strategies and Challenges. Curr. Pharm. Des. 20 (5), 685–686. doi:10.2174/138161282005140214161643
Yang, Y. I., Shao, Q., Zhang, J., Yang, L., and Gao, Y. Q. (2019). Enhanced Sampling in Molecular Dynamics. J. Chem. Phys. 151 (7), 70902. doi:10.1063/1.5109531
Yesylevskyy, S. O. (2015). Pteros 2.0: Evolution of the Fast Parallel Molecular Analysis Library for C++ and Python. J. Comput. Chem. 36 (19), 1480–1488. doi:10.1002/jcc.23943
Yesylevskyy, S. O. (2012). Pteros: Fast and Easy to Use Open‐source C++ Library for Molecular Analysis. J. Comput. Chem. 33 (19), 1632–1636. doi:10.1002/jcc.22989
Yoshino, R., Yasuo, N., and Sekijima, M. (2019). Molecular Dynamics Simulation Reveals the Mechanism by Which the Infuenza Cap-Dependent Endonuclease Acquires Resistance Against Baloxavir Marboxil. Sci. Rep. 9 (1), 17464. doi:10.1038/s41598-019-53945-1
Young, G., and Householder, A. S. (1938). Discussion of a Set of Points in Terms of Their Mutual Distances. Psychometrika 3, 19–22. doi:10.1007/BF02287916
Zheng, W., Qi, B., Rohrdanz, M. A., Caflisch, A., Dinner, A. R., and Clementi, C. (2011). Delineation of Folding Pathways of a β-sheet Miniprotein. J. Phys. Chem. B 115 (44), 3065–13074. doi:10.1021/jp2076935
Zheng, W., Rohrdanz, M. A., and Clementi, C. (2013a). Rapid Exploration of Configuration Space with Diffusion-Map-Directed Molecular Dynamics. J. Phys. Chem. B 117 (42), 12769–12776. doi:10.1021/jp401911h
Zheng, W., Vargiu, A. V., Rohrdanz, M. A., Carloni, P., and Clementi, C. (2013b). Molecular Recognition of DNA by Ligands: Roughness and Complexity of the Free Energy Profile. J. Chem. Phys. 139 (14), 145102. doi:10.1063/1.4824106
Zhou, H., Wang, F., Bennett, D. I., and Tao, P. (2019). Directed Kinetic Transition Network Model. J. Chem. Phys. 151 (14), 144112. doi:10.1063/1.5110896
Keywords: molecular dynamics, machine learning, structure-based drug design, clustering, data dimensionality reduction, interaction fingerprints
Citation: Baltrukevich H and Podlewska S (2022) From Data to Knowledge: Systematic Review of Tools for Automatic Analysis of Molecular Dynamics Output. Front. Pharmacol. 13:844293. doi: 10.3389/fphar.2022.844293
Received: 27 December 2021; Accepted: 26 January 2022;
Published: 10 March 2022.
Edited by:
Adriano D. Andricopulo, University of Sao Paulo, BrazilReviewed by:
Mohamed AbdElAziz Khamis Omar, Egypt-Japan University of Science and Technology, EgyptRafael Doležal, University of Hradec Králové, Czechia
Copyright © 2022 Baltrukevich and Podlewska. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sabina Podlewska, c211c3pAaWYtcGFuLmtyYWtvdy5wbA==
 Hanna Baltrukevich
Hanna Baltrukevich Sabina Podlewska
Sabina Podlewska