- 1Institute of Nuclear Engineering and Science, National Tsing Hua University, Hsinchu, Taiwan
- 2Research and Development Center, Heron Neutron Medical Corporation, Zhubei, Taiwan
- 3Department of Heavy Particles and Radiation Oncology, Taipei Veterans General Hospital, Taipei, Taiwan
- 4School of Medicine, National Yang Ming Chiao Tung University, Hsinchu, Taiwan
The tumor control probability (TCP) model has been used for estimating the response of the radiation (photon) therapy for a given treatment dose (distribution). In Taiwan, boron neutron capture therapy (BNCT) is still at the stage of the clinical trials without standard dose prescription. In this study, universal survival curve (USC) model was selected as the TCP model for BNCT. The tumor response and dose distribution from protocol I of the clinical trial of the recurrent head and neck (H&N) cancer conducted by Taipei Veterans General Hospital and National Tsing Hua University were used to verify the TCP model established in this study. The results showed that, using the USC model as a biological model of dose conversion, the TCP calculated by the generalized Equivalent Uniform Dose (gEUD)–based TCP model can be used to well correlate the relationship between the tumor response and dose distribution of the patients of recurrent H&N cancer. The result shows that 25% and 60% of TCP correspond to partial response and complete response of H&N cancer, respectively. This study also indicated that, when BNCT was used to treat recurrent H&N cancer, the minimum dose was an important factor on the efficacy of the treatment. Minimum dose of 18 Gy-w corresponds to at least 60% of TCP.
1 Introduction
The tumor control probability (TCP) model has been used for estimating the response of the radiation therapy since 1980. More models were developed when more clinical data were collected. In Taiwan, unlike photon therapy, boron neutron capture therapy (BNCT) is still at the stage of the clinical trials without standard prescription dose. The major difference between BNCT and photon therapy is the mechanism of the energy deposited from the interaction. BNCT uses the nuclear reaction of the 10B isotope with thermal neutron to produce two high-energy heavy nuclei, alpha (1.84 MeV), and lithium (0.85 MeV), which can release whole kinetic energy in a very short range (10 μm–20 μm). In 2020, boronophenylalanine (BPA), which is a tumor-targeted 10B-enriched drug, was approved as a new drug of BNCT in Japan (1). The neutron generator was also approved as a new medical device at the same time (2). In current BNCT protocol, BPA drug is to be injected to the patient for 2h to accumulate high enough 10B in the tumor before the neutron irradiation. The ratio of the drug concentration between tumor uptake and normal tissue uptake can be larger than 2.5. The weighted dose (Gy-w) of BNCT is commonly calculated by using the relative biological effectiveness (RBE) of the neutron, 3.2, and compound biological effectiveness (CBE) of the BPA for tumor and normal tissue, 3.8 and 1.3, respectively.
The purpose of this study is to establish a TCP model (3) for BNCT and use a clinical trial result to verify it. The clinical trial result used is the protocol I of the clinical trial (NCT01173172) of the re-current head and neck (H&N) cancer conducted by Taipei Veterans General Hospital and National Tsing Hua University during 2010–2014. It was a two-fraction BNCT treatment protocol. Totally, 17 patients were treated. The prescribed dose for tumor is 80% of tumor volume reaching 20 Gy-w. The principles for the normal tissues and critical organs are to minimize the volumes of the skin and mucosa receiving >10 Gy-w per fraction and limiting the maximum dose of the optic nerve/chiasma to be less than 8 Gy-w per fraction. The efficacy of this clinical trial is 71% (4) of positive response [complete response (CR) and partial response (PR)]. The most common acute adverse events were low-grade oral mucositis, radiation dermatitis, and alopecia. The most common grade 3 late adverse event was cranial neuropathy. No grade 4 late adverse events were observed.
2 Materials and methods
2.1 Cell survival curve model
In 1976, Douglas and Fowler (5) proposed a linear quadratic (LQ) model to describe the biological effect of conventionally fractionated radiotherapy (CFRT). Cell death by radiation was described by two mechanisms. One is single-strand break, where cell death is proportional to dose-level squared. Another is double-strand break, where cell death is proportional to the dose level. However, according to the large dose protocol used by stereotactic body radiation therapy (SBRT) since 2000, LQ model cannot predict biological effect well for large dose in one fraction. More models were then proposed to correct this.
A. Universal survival curve model
Universal survival curve (USC) model was proposed by Park (6) in 2008. This model combines LQ model for low-dose range and multi-target model for high-dose range. The transition dose DT connecting LQ model and multi-target model can be described in Equation 1.
where S is survival fraction, d is dose, α and β are the coefficients, Dq is the intercept when lnS is 0 for multi-target model, -1/D0 is the slope of multi-target model.
B. Linear quadratic linear model
Linear quadratic linear (LQL) model was proposed by Astrahan (7) in 2008. It is similar to USC model but with different high dose model as shown in Equation 2.
Where γ is the slope of LQ model at DT.
C. Padé linear quadratic model
Belkić used Padé approximation to expand LQ model to Padé linear quadratic (PLQ) model (8) in 2013 as shown in Equation 3.
In order to investigate which model is suitable for the H&N cancer, the squamous cell carcinoma (SCC) survival fraction data of FaDu cell from Saleh (9) in 2015 is selected. The results are shown in Figure 1. Standard error of estimator is used to evaluate the models. The USC model, which has the smallest error, is used in the following step to evaluate biological effectiveness. The coefficients of USC model are listed in Table 1.
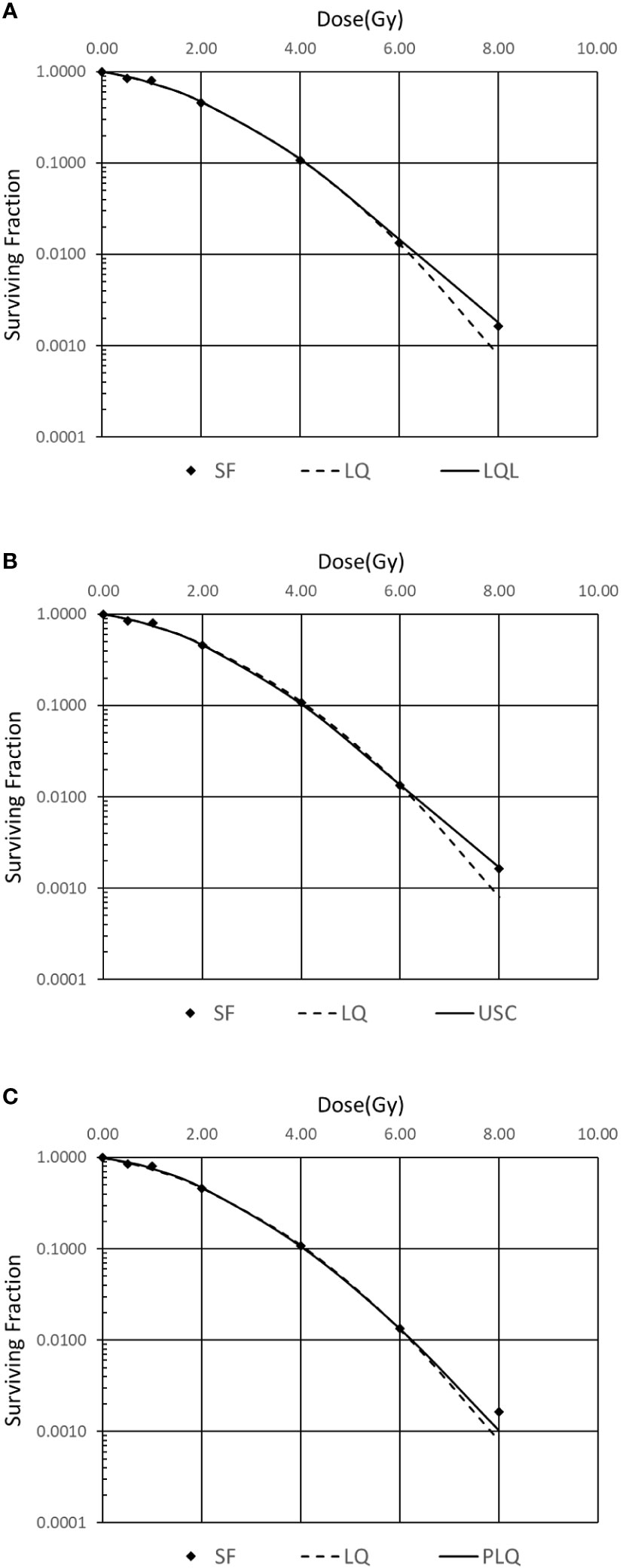
Figure 1 Comparison of different survival curve models for FaDu cell. (A) Linear quadratic linear (LQL) model, (B) universal survival curve (USC) model, (C) Padé linear quadratic (PLQ) model.
2.2 Biological effective dose
The biological effective dose (BED) represents the dose required for a given biological effect E if the dose were to be delivered by infinitely small doses per fraction. For USC model, the BED can be described by Equation 4 for total dose (D) or summation of multiple fractional dose (nd).
For single high-dose delivery of BNCT (DBNCT), which usually is larger than DT, BED of BNCT can be described as
Note that DBNCT is the weighted dose, defined as the sum of the physical dose components multiplied by weighting factors (including RBE and CBE’s). After combining Equations 4 and 5, the equivalent dose in 2 Gy fraction (EQD2) for BNCT can be described by Equation 6 when nd = EQD2 and d = 2 Gy:
2.3 Tumor control probability model
According to the logistic formula by Suit (10) in 1965, TCP model with uniform dose (D) in a volume can be described by Equation 7.
where is the dose for which there is a 50% response, describes the slope of the dose-response curves at the dose of . For SCC, the coefficients are listed below (11).
Unlike photon therapy, non-uniform dose of tumor must be considered due to the drug and neutron flux distribution in tumor and typical single beam portal for BNCT. Niemierko (12) proposed a generalized Equivalent Uniform Dose (gEUD) as shown in Equation 8,
where is fractional volume, N is total number of fractional volume, is the dose of , is the tissue-specific parameter, for example, −13 for SCC (13). When plugging in gEUD into Equation 7, the EUD-based TCP for non-uniform dose distribution becomes.
Note that, since of Equation 8 is negative for tumor, gEUD will be mostly affected by the minimum dose of tumor.
There are other existing methods to calculate TCP in addition to generalized EUD-based TCP, for example, subvolumed-based TCP (14). It is found in this study that results of generalized EUD-based TCP, which gives more weight to the minimum tumor dose, correlate well with the clinical results.
Therefore, the procedure for calculating TCP is below:
1) Based on dose-volume histogram (DVH), of BNCT dose report, one can convert into equivalent dose in 2 Gy fraction, EQD2, using Equation 6.
2) Because in the tumor is non-uniform, one can calculate gEUD using Equation 8 and then obtain TCP using Equation 9.
3 Results and discussions
The DVH data of 11 patients with SCC of protocol 1 of BNCT clinical trial for recurrent H&N cancer is used to calculate TCP based on the method developed above. Comparing to the photon therapy, the tumor dose distribution of BNCT is usually non-uniform, especially in large tumors.
The result is shown in Table 2 together with response of patients and the minimum dose delivered to the tumors during treatment. Although DBNCT,min has large weight in determine gEUD [Equation 8], DBNCT,min alone cannot predict TCP directly. The whole dose distribution in tumor is needed to calculate gEUD and then TCP. For example, patients 8 and 15 have very close DBNCT,min, 9.2 and 9.4, respectively, but their gEUD are quite different due to different tumor dose distribution. For patient 8, 15% of tumor dose are below 18.5 Gy-w, while patient 15 have only 2% of tumor dose below 18.5 Gy-w. Therefore, the gEUD of patient 8 is only 31 Gy, while for patient 15 is 44.7 Gy. The resulting TCP of patient 8 is only 4.4, of patient 15 is 40.9. Clinical result shows that patient 8 is stable disease (SD) and patient 15 is PR.
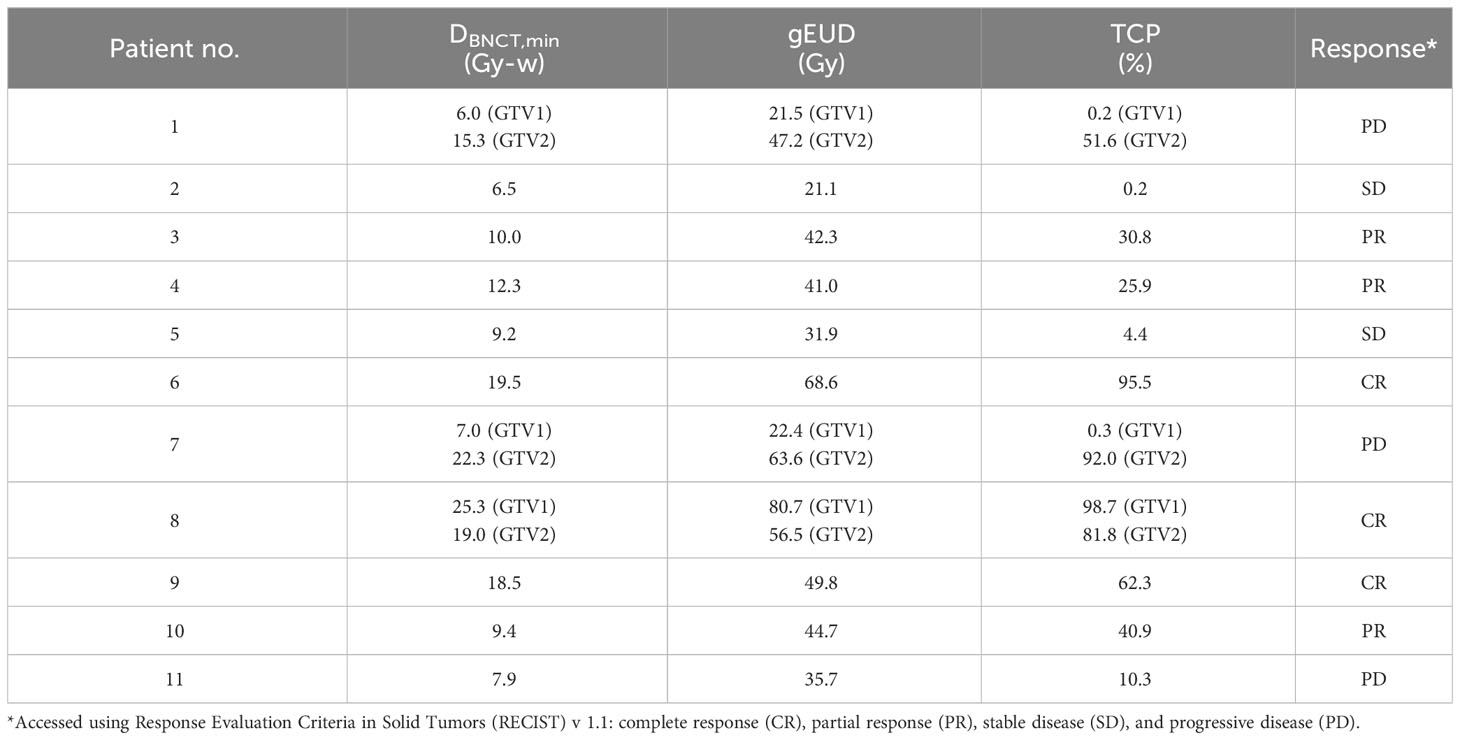
Table 2 Results of generalized EUD-based TCP for protocol 1 of clinical trial of recurrent H&N cancer.
The results in Table 2 show that 25% and 60% of TCP correspond to PR and CR of H&N cancer, respectively. When BNCT was used to treat recurrent H&N cancer, the minimum dose was an important factor on the efficacy of the treatment. Minimum tumor dose of 18 Gy-w corresponds to at least 60% of TCP.
4 Conclusions
In the radiation therapy field, BNCT is still a new treatment modality and lack of enough clinical data for evaluating the delivered dose related to the patient response. In this study, a BNCT TCP model is established based on the TCP models of photon therapy through the equivalent dose conversion. The TCP calculated using the dose distribution from protocol I of the clinical trial of the recurrent H&N cancer correlates well with the tumor response of the clinical results. The proper TCP range for the prescription dose with good tumor response can be obtained when implementing this model into the BNCT treatment planning system to accumulate more clinical data.
The parameters used in generalized EUD-based TCP model are all based on photon therapy, the cell killing mechanism of which is different from BNCT. More biological data on BNCT is needed.
In future clinical treatment of BNCT, the tumor dose distribution of treatment planning result can be used through this model to calculate TCP to predict outcomes. Preferred treatment plans can then be selected.
Data availability statement
The data analyzed in this study is subject to the following licenses/restrictions: Clinical trial results involving patients information. Requests to access these datasets should be directed to L-WW,bHd3YW5nQHZnaHRwZS5nb3YudHc=.
Ethics statement
Ethical approval was not required for the studies involving humans because this study is a dosimetry research based on a published clinical study, clinical trial [NCT01173172]. Only dose/response data were retrieved. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required from the participants or the participants’ legal guardians/next of kin in accordance with the national legislation and institutional requirements because all patients are de-identified. No identifiable human data was shown in this study.
Author contributions
Conceptualization, F-YH and Y-WHL; methodology, F-YH and Y-WHL; formal analysis, F-YH and Y-WHL; resources, F-YH, Y-WHL, and L-WW (principle investigator of this clinical trial); data curation, F-YH and Y-WHL; writing—original draft preparation, F-YH, Y-WHL, and T-YL; writing—review and editing, Y-WHL and T-YL; visualization, F-YH; supervision, Y-WHL; project administration, Y-WHL; funding acquisition, Y-WHL. Software, F-YH and T-YL. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
The authors would like to thank Dr. Y.W. Chen for inclusion patients into the clinical trial.
Conflict of interest
Author Y-WHL is employed by the company Heron Neutron Medical Corporation. Author T-YL was employed by the company Heron Medical Corporation.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Pharmaceutical Division, Safety and Environmental Health Bureau of the Ministry of Health, Labour and Welfare. Report on the Deliberation Results: Steboronine 9000 mg/300 mL for Infusion (2020). Available at: https://www.pmda.go.jp/files/000237990.pdf.
2. Medical Device Evaluation Division, Pharmaceutical Safety and Environmental Health Bureau of the Ministry of Health, Labour and Welfare. Report on the Deliberation Results. NeuCure BNCT System (2020). Available at: https://www.pmda.go.jp/files/000237994.pdf.
3. Hsu FY. Application and Analysis of Tumor Control Probability Model and Normal Tissue Complication Probability Model for Boron Neutron Capture Therapy. National Tsing Hua University (2019). Master Thesis: Hsinchu, Taiwan.
4. Wang LW, Chen YW, Ho CY, Liu YWH, Chou FI, Liu YH, et al. Fractionated boron neutron capture therapy in locally recurrent head and neck cancer: A prospective phase I/II trial. Int J Radiat Oncology Biology Phys (2016) 95:396–403. doi: 10.1016/j.ijrobp.2016.02.028
5. Douglas BG, Fowler JF. The effect of multiple small doses of X rays on skin reactions in the mouse and a basic interpretation. Radiat. Res (1976) 66:401. doi: 10.1667/RRAV10.1
6. Park C, Papiez L, Zhang S, Story M, Timmerman RD. Universal survival curve and single fraction equivalent dose: useful tools in understanding potency of ablative radiotherapy. Int J Radiat. Oncol Biol Phys (2008) 70:847–52. doi: 10.1016/j.ijrobp.2007.10.059
7. Astrahan M. Some implications of linear-quadratic-linear radiation dose-response with regard to hypofractionation. Med Phys (2008) 35:4161–72. doi: 10.1118/1.2969065
8. Belkić D, Belkić K. Mechanistic repair-based padé Linear-quadratic model for cell response to radiation damage. Adv Quantum Chem (2013) 65:407–49. doi: 10.1016/B978-0-12-396455-7.00014-5
9. Saleh EM. Inhibition of topoisomerase IIα sensitizes FaDu cells to ionizing radiation by diminishing DNA repair. Tumor Biol (2015) 36:8985–92. doi: 10.1007/s13277-015-3587-8
10. Suit HD, Shalek RJ, Wette R. Radiation response of C3H mouse mammary carcinoma evaluated in terms of cellular radiation sensitivity. Cell Radiat. Biol (1965), 514–30.
11. Taghian A, duBois W, Budach W, Baumann M, Freeman J, Suit H. In vivo radiation sensitivity of glioblastoma multiforme. Int J Radiat. Oncol Biol Phys (1995) 32:99–104. doi: 10.1016/0360-3016(94)00494-6
13. Anbumani S, Raj N. AN, Prabhakar GS, Anchineyan P, Bilimagga RS, Palled RS, et al. Quantification of uncertainties in conventional plan evaluation methods in Intensity Modulated Radiation Therapy. J Buon (2014) 19:297–303.
Keywords: tumor control probability, boron neutron capture therapy, head and neck cancer, clinical trial, biological effective dose
Citation: Hsu F-Y, Liu Y-WH, Lin T-Y and Wang L-W (2024) Development of a tumor control probability model for boron neutron capture therapy of head and neck cancer. Front. Oncol. 13:1249074. doi: 10.3389/fonc.2023.1249074
Received: 28 June 2023; Accepted: 26 December 2023;
Published: 29 February 2024.
Edited by:
Timothy James Kinsella, Brown University, United StatesReviewed by:
Tsubasa Watanabe, Kyoto University, JapanSunyoung Jang, The Pennsylvania State University, United States
Copyright © 2024 Hsu, Liu, Lin and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yen-Wan Hsueh Liu, eXdobGl1QGdtYWlsLmNvbQ==; WXZvbm5lLkhzdWVoQGhlcm9uLW5ldXRyb24uY29t
 Fang-Ying Hsu1
Fang-Ying Hsu1 Yen-Wan Hsueh Liu
Yen-Wan Hsueh Liu Tzung-Yi Lin
Tzung-Yi Lin