On-the-fly thermal expansion for Monte Carlo multi-physics reactor simulations

In this study, we present on-the-fly thermal expansion methodology for direct Monte Carlo coupled multi-physics reactor simulations. This approach allows the problem geometry to be thermally expanded on-the-fly during particle tracking using local temperatures, such as pin-averaged temperatures, obtained from the thermal-hydraulics solver. Numerical experiments demonstrated that modeling thermal expansion with local temperatures for thermal expansion improves the accuracy of reactor simulations, both for reactor eigenvalue and pin powers, compared to using global core-averaged temperatures. Additionally, the use of thermal expansion also improves the isothermal temperature coefficients, making them approximately 0.77 pcm/K closer to the measured data. Finally, results for depletion problems showed that incorporating thermal expansion in direct reactor modeling enhances the predicted critical boron concentration, particularly at high power and higher fuel burnup. These findings suggest that including thermal expansion in reactor modeling is essential for improving the fidelity of simulations.

1 Introduction

Thermal expansion (TE) significantly impacts reactor physics modeling, not only for fast reactors but also, to a certain extent, for Light Water Reactors (LWRs). This is because the geometric reactor design information is usually provided at room temperature, while the actual reactor core operates at much higher temperatures. At full power, the nominal fuel temperature is around 900 K, and the coolant temperature is around 580 K. This large temperature gap causes all components in the reactor vessel to thermally expand. For example, the core plate expands radially, causing the assembly pitch to expand. The grid spacers within an assembly also expand, altering the pin pitch within the lattice (Palmtag et al., 2017). Furthermore, the fuel pellet and fuel rod cladding expand in both radial and axial directions. In fact, Smith and Forget have asserted that TE must be modeled to achieve accurate high-fidelity simulation capability (Smith and Forget, 2013).

Thermal expansion modelling has long been incorporated into industry best practice two-step methodology for LWRs analyses. In this approach, the thermal expansion is already accounted for during lattices physics calculations to generate the few-group cross section for certain operating reactor temperatures. However, the direct the Monte Carlo (MC) coupled multi-physics simulations present a challenge: local temperatures are determined from thermal-hydraulic feedback, so they are not known a priori and are usually non-uniform within reactor core. To address this challenge, typical TE modeling in direct coupled multi-physics simulations is often achieved by manually adjusting input files to uniformly expand reactor core geometry and modify material densities. This approach commonly uses core-averaged nominal temperatures, as demonstrated in the work by (Palmtag et al., 2017).

In Palmtag’s work, thermal expansion was implemented by processing the XML input files for the Consortium for Advanced Simulation of LWRs (CASL) core simulator code, VERA-CS, to uniformly adjust the core dimensions and material densities. This process is accomplished by VERAIn ASCII input preprocessor. However, VERAin only allows thermal expansion at a specific and uniform temperature, typically the core-averaged temperature, before beginning the simulations. Parametric studies were performed to evaluate the effects of thermal expansion due to various parameters, including fuel enrichment, diluted boron concentration in the coolant, coolant density, and fuel temperature. The study claimed that thermal expansion effects are adequately captured by uniformly expanding the materials from cold conditions to the average hot conditions. However, as this paper will demonstrate, the accuracy of the solutions, both for reactor eigenvalue and pin powers, can be improved if local temperatures, instead of core-averaged temperatures, are used for thermal expansion. Another drawback of using the input preprocessor is that if calculations need to be repeated at different power levels, the inputs must be reprocessed to obtain the correct expanded reactor dimensions and material densities.

Many other studies (Fiorina et al., 2019; Guo et al., 2021; Ma et al., 2021) have implemented thermal expansion using thermo-mechanical solvers in computational fluid dynamics (CFD) codes such as OpenFOAM or ANSYS. In general, these works employed a neutronic solver to obtain power, followed by a CFD code as the thermal-hydraulic (TH) solver and a mechanical solver to perform material deformation due to temperature changes. However, due to their reliance on direct CFD simulations, these approaches are likely suitable only for small cores, like those in heat pipe or modular reactors. The computational requirements for this method would be exponentially more expensive for larger cores.

Another noteworthy study on reactor simulations with thermal expansion modeling is the work conducted by Idaho National Laboratory (Cole et al., 2021). In this study, they modeled feedback mechanisms that include Doppler effects, radial expansion due to the displacement of the support plate, and axial expansion from the displacement of fuel pins for Unprotected Loss of Flow (ULOF) transient simulations in typical sodium fast reactors. A 2D BISON thermomechanical model of the 316 stainless steel support plate was used to simulate mesh displacement and its effect on the core assembly pitch. Meanwhile, fuel expansion was modeled using a 3D BISON thermomechanical model of the fuel pins. To integrate these models into a multi-physics simulation, they employed the MOOSE multi-app system (Permann et al., 2020), with Griffin, the neutronics solver, serving as the main application.

In this paper, we propose on-the-fly thermal expansion for MC coupled multi-physics reactor simulations, with a focus on pressurized water reactors (PWRs). The proposed method dynamically expands the reactor problem geometry during particle tracking, improving accuracy by using local temperatures, either pin-averaged or assembly-averaged. The proposed method also incurs negligible additional computational time. The method has been implemented into the MCS code (Lee et al., 2020) to provide solutions at both assembly and core levels, as well as for whole-core depletion using restart calculations. MCS is a neutron/photon transport code that was developed at Ulsan National Institute of Science and Technology (UNIST) with capabilities of performing multi-physics and multi-cycle reactor analyses (Lee et al., 2017; Yu et al., 2020a; Yu et al., 2020b). The solutions are valuable for evaluating the influence of thermal expansion on the accuracy of direct MC coupled multi-physics reactor simulations. Additionally, they assess the effects of using local temperatures for thermal expansion on accuracy improvements.

2 Methodology

2.1 Theory and thermal expansion coefficients

The physical modelling for the linear thermal expansion of solid materials with an isotropic crystal structure is given by:

$L=L_0\left[1+{\mathrm{\alpha }}_L\left(T-T_{ref}\right)\right],(1)$

where $L$ is the final length at temperature $T$, $L_0$ is the initial length at reference temperature $T_{ref}$, and ${\mathrm{\alpha }}_L$ is the coefficient of linear thermal expansion. Similarly, the physical modelling for area thermal expansion, such as fuel pellet area, is given by:

$A=A_0{\left[1+{\alpha }_L\left(T-T_{ref}\right)\right]}^2.(2)$

When materials are expanded, the mass must be preserved. Therefore, the material densities need to be modified to be consistent with the expanded dimensions. The density is modified according to:

$\mathrm{\rho }={\mathrm{\rho }}_0\frac{V_0}{V},(3)$

where $\mathrm{\rho }$ and $V$ in Equation 3 are thermally expanded density and volume respectively, while ${\mathrm{\rho }}_0$ and $V_0$ are initial density and volume, respectively. The thermally expanded volume can be calculated using the expanded length $L$ and area $A$, shown in Equations 1, 2 respectively.

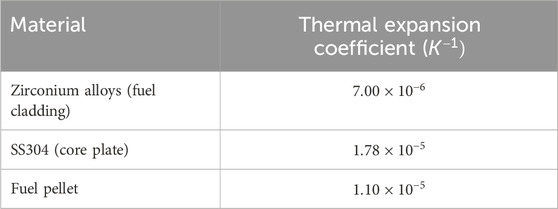
The thermal expansion coefficients of materials used in reactors are crucial for accurate thermal expansion modeling. Detailed descriptions of the correlations used to determine these coefficients for typical materials in LWRs are well described in the reference (Palmtag et al., 2017). However, this work adopted the thermal expansion coefficients used in the STREAM code (Choi et al., 2021). These thermal expansion coefficients are summarized in Table 1.

Table 1

Table 1. Thermal expansion coefficients used in this study.

Note that these thermal expansion coefficients are quite close to those described in reference (Palmtag et al., 2017). Additionally, this study limits the thermal expansion modelling to fuel pellet, cladding, pin pitch and assembly pitch thermal expansion. The dimensions of absorber materials such control rods and burnable absorbers are assumed to remain constant.

2.2 Thermal-hydraulics coupling

MCS is a neutron/photon transport code that can be coupled with both TH1D (Ryu et al., 2015) and COBRA-TF (CTF) (Salko et al., 2015). TH1D is a simple one-dimensional, single closed-channel thermal-hydraulics (TH) solver that does not account for cross-flow, coolant vaporization, and pressure drop across the channel. In contrast, CTF is a more sophisticated TH solver that addresses these limitations in TH1D.

Both TH1D and CTF are internally coupled with MCS, allowing data transfers between MCS and the TH solvers to occur automatically. Although the solvers must be compiled separately, they are linked through a static library. Linear power from MCS is transferred to the TH solvers, while TH parameters are updated by TH solvers and returned to MCS. These data transfers are performed at the pin-by-pin level.

Since data transfers are performed at the pin-by-pin level, MCS multi-physics coupling always uses a single pin cell as the channel for TH coupling. For example, in a single fuel assembly with a 17 × 17 configuration, including 24 guide tubes and one instrumentation tube, a total of 264 channels are modeled for TH coupling.

The reactor’s TH parameters are updated regularly after several cycles of MCS particle tracking. During MCS particle tracking, fission power is tallied in both inactive and active cycles. In inactive cycles, the power tally is not accumulated, meaning that the tally from the last TH update is discarded. In contrast, during active cycles, when both the fission source and TH parameters have converged, the fission power tally is accumulated. The fission power is tallied for each cell in the fuel pellets and then converted into linear powers. These linear powers are passed to the TH solvers to update the reactor’s TH parameters. These procedures are repeated until all cycles are completed.

2.3 Implementation

Many MC codes, such as MCS, use Constructive Solid Geometry (CSG) to define the geometry of reactor problems. Performing non-uniform geometrical expansion using local temperatures in CSG presents a challenge because a single surface can be reused to form multiple cells within a universe, and a universe can be repeatedly used to define a lattice. Consequently, modifications to a particular surface, such as those resulting from thermal expansion, can affect all cells, universes, and lattices that utilize the modified surface. One possible solution to avoid this issue is by creating copies of surfaces and cells, so that every cell can be expanded according to their respective local temperatures. However, this approach is cumbersome for large reactor problems and would consume more memory.

To address this problem, on-the-fly thermal expansion is introduced. In this approach, when a particle enters a particular pin, the geometry of fuel pellet and cladding in that fuel pin are expanded using the corresponding local temperatures, which can be either pin-averaged or assembly-averaged temperatures. Similarly, the pin and assembly pitches where the particle is located are also expanded according to the assembly-averaged and core-averaged temperatures, respectively. In both the pin-averaged and assembly-averaged temperature cases, the average temperatures are calculated in both the axial and radial directions using volume-weighted averaging.

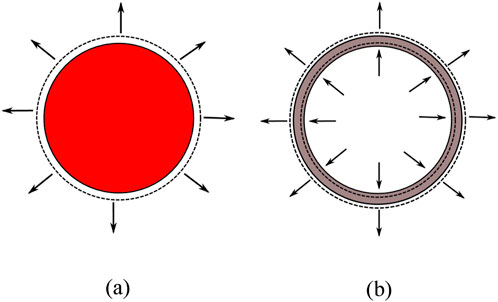
In the implementation in MCS, the fuel pellet expanded both in radial and axial directions, while the cladding is expanded only in the radial direction, with the inner and outer radius assumed to expand equally. It should be noted that geometry deformation is assumed to be uniform both radially and axially, which implies that fuel cladding ballooning is not considered. These expansions are illustrated in Figure 1.

Figure 1

Figure 1. The radial expansion of (A) fuel pellet, and (B) cladding.

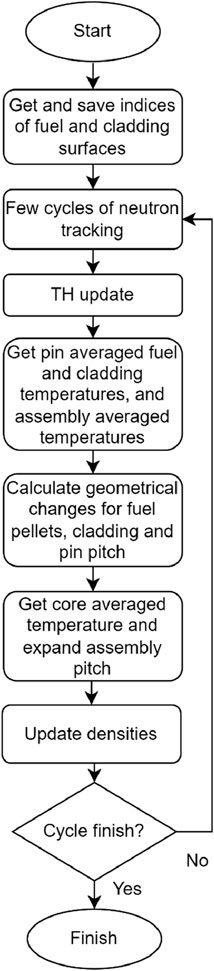
Figure 2 is a flow chart illustrating the calculation of geometrical changes due to thermal expansion. Initially, after several cycles of neutron tracking, the TH solver is executed to determine the temperature distribution. This temperature distribution is then used to calculate pin-averaged fuel pellet and cladding temperatures, which are subsequently utilized to determine the corresponding expansion-induced geometrical changes in fuel pellets and cladding. Similarly, assembly-averaged temperatures are used to compute the geometrical changes in pin-pitch. Following this, core-averaged temperatures are used to thermally expand the assembly pitches uniformly. Finally, the material densities are updated to ensure the preservation of material mass throughout the process. These steps are repeated iteratively until all cycles are completed.

Figure 2

Figure 2. Calculation of geometrical changes due to thermal expansion.

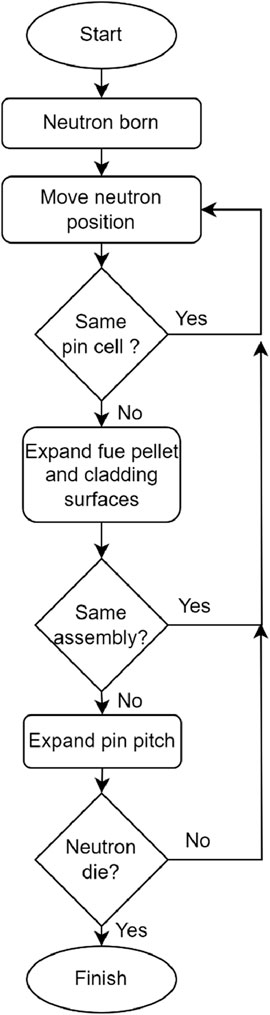
Once the geometrical changes due to thermal expansion are calculated during the TH update, this information is used to thermally expand the core geometry on-the-fly during subsequent cycles of neutron tracking. When a neutron is located in a pin cell after performing a random walk, MCS checks whether it originated from another pin cell or from the same one. If it originated from another pin cell, the fuel pellet and cladding surfaces in that pin cell are expanded based on the previously calculated geometrical changes. Additionally, if the neutron came from another assembly, the pin pitches within that assembly are uniformly expanded as well. These steps are summarized in Figure 3.

Figure 3

Figure 3. On-the-fly thermal expansion during neutron tracking.

3 Results and discussion

To evaluate the effects of TE modelling on MC coupled multi-physics reactor simulations, several test problems were developed. The test problems include assembly and core problems, as well as depletion problems with restart cases. The problem geometries and material compositions were adopted from the Virtual Environment for Reactor Applications (VERA) core physics benchmark (Godfrey, 2014). Additionally, ENDF/B-VII.1 was used for the MCS cross section library.

In all problems considered in this study, the TH parameters are updated every 500 cycles of MCS particle tracking. In MCS, the fuel pellets are axially discretized into 25 equidistant cells without radial discretization, where fission power is tallied. While the TH solvers discretize the problem axially into 25 equidistant meshes corresponding to the MCS cells. Additionally, in the TH solvers, the fuel pellets are radially discretized into 10 equidistant rings, while the cladding and gap are each represented by a single ring to numerically solve the heat conduction equation.

3.1 Small lattice problem

This small lattice problem consists of a 2 x 2 pin cells with two different fuel enrichments: 3.1% wt. fuel enrichment in all fuel pins, except for the bottom-left pin, which has 2.1% wt. enrichment, as shown in Figure 4. The pin geometry and material compositions are based on the VERA benchmark, with a 0.4 cm inter-lattice gap. The boron concentration diluted in the coolant is 1,300 ppm. This problem simulated $4\times {10}^4$ particles per cycle, with a total of 14,500 cycles, of which 2,500 were designated as active cycles.

Figure 4

Figure 4. Small lattice problem geometry.

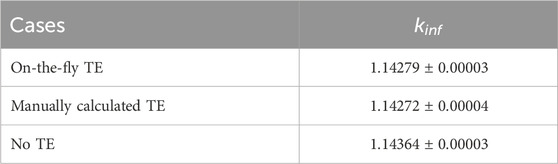
This simple problem is designed to evaluate the implementation of TE in the MC code MCS by comparing the solutions from on-the-fly TE in MCS to those from manually calculated TE. In the manual calculations, the geometrical expansions and expanded material densities were manually computed based on the pin-averaged temperatures from the on-the-fly thermal expansion calculation results. Note that the varying fuel enrichments in this problem result in non-uniform pin-averaged temperatures. A new MCS input file was then created using these manually calculated geometrical expansions and expanded material densities to include the equivalent TE.

Table 2 presents the results for small lattice problem. As observed, the on-the-fly TE and manually calculated TE produce very similar infinite multiplication factors, with only a 7 pcm difference, which is well within the given statistical uncertainty. For comparison, the result without TE is also given that shows a difference of more than 80 pcm compared to the TE cases. These results confirm that on-the-fly TE is correctly implemented in the MCS code.

Table 2

Table 2. Small lattice problems infinite multiplication factors.

3.2 Assembly problem

This test problem aims to assess the effects of TE at the assembly level. It is based on a problem similar to problem six of the VERA benchmark. The problem geometry also includes non-fuel structural materials such as the pin plenum, nozzles, core plates, and bottom and top reflectors. The effects of TE will be evaluated for different boron concentrations and fuel enrichments, with the reactor condition set at Hot Full Power (HFP). Note that the calculations for this problem simulated $4\times {10}^4$ particles per cycle, with a total of 14,500 cycles, of which 2,500 cycles were designated as active.

Table 3, 4 display the assembly reactivity differences due to TE for varying boron concentrations and fuel enrichment levels, respectively. Table 3 shows that as boron concentration increases, the reactivity difference decreases. This effect occurs because the moderator volume containing boron expands with an increase in pin pitch. When the moderator has a high concentration of boron, the overall neutron absorptions would increase, resulting in a lower eigenvalue. Conversely, lower boron concentrations reduce neutron absorption and enhance neutron moderation, resulting in a higher eigenvalue. It has been well known that reactivity differences from TE are highly dependent on boron concentration in the reactor. Similarly, Table 4 shows that higher fuel enrichment levels lead to a more positive reactivity difference from TE. These trends in reactivity differences due to TE for varying boron concentrations and fuel temperatures are consistent with those found in reference (Palmtag et al., 2017).

Table 3

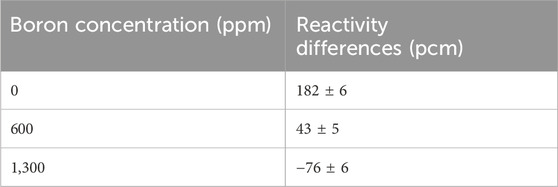
Table 3. Assembly reactivity differences due to TE (TE - no TE) for various boron concentrations using 3.1% wt. enriched fuel.

Table 4

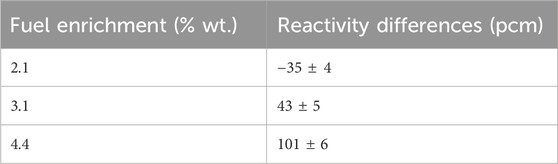
Table 4. Assembly reactivity differences due to TE (TE - no TE) for different fuel enrichment levels at a boron concentration of 600 ppm.

3.3 Core problem

The core problem specifications are similar to those of problem 7 of the VERA benchmark, with the operating condition set at HFP. However, instead of determining the critical boron concentration, this study calculates the eigenvalues using a critical boron concentration of 860 ppm.

The effect of thermal expansion on the core problem will be evaluated at several expansion temperatures as can be seen in Table 5. For the core-averaged case, the core-averaged nominal reactor temperature at HFP is used, with the fuel expansion temperature set at 900 K and the coolant and cladding expansion temperatures set at 583 K. The assembly-averaged case uses assembly-averaged temperatures for geometry expansion in each assembly, while the pin-averaged case uses pin-averaged temperatures for geometry expansion in each pin cell. All cases simulated $3\times {10}^5$ particles per cycle, with a total of 42,000 cycles, of which 38,000 cycles were designated as active. This results in a maximum relative standard deviation of 0.8% in the radial pin powers.

Table 5

Table 5. Core problem eigenvalues and pin-power power errors.

The results for this problem are compiled in Table 5. The pin-power errors were calculated relative to the pin-averaged case. As shown in the table, when thermal expansion is not considered, the eigenvalue is overestimated compared to the pin-averaged case, and the errors at the pin level are more pronounced. Using core-averaged nominal temperatures greatly improves the eigenvalue, with less than a 10 pcm difference from the pin-wise case and the pin errors are also reduced. The results are further improved when local temperatures at the assembly level are used for geometry expansion; this approach results in only a 4 pcm difference in the eigenvalue and a 0.3% RMS pin error. It can also be seen that as the spatial resolution of expansion temperatures increases, both the eigenvalue and pin powers converge to those of the pin-wise case.

The radial pin-power errors relative to the pin-averaged case are shown in Figure 5. As can be observed, the no-TE case underestimates the pin powers at the core periphery by as much as −4.8%, while overestimating the pin powers at the core center. The pin powers from the core-averaged case are fairly accurate; however, there are still some areas with noticeable deviations. Lastly, the assembly-averaged case produces pin-power solutions quite close to the pin-averaged case. It is also important to note that the running time of the pin-wise case is only 0.9% longer compared to the no-TE case. Therefore, the introduction of on-the-fly thermal expansion incurs virtually no additional computational cost.

Figure 5

Figure 5. Radial pin-power errors distributions relative to the pin-averaged case for (A) No TE case, (B) core-averaged case, and (C) assembly-averaged case.

3.4 Isothermal temperature coefficient

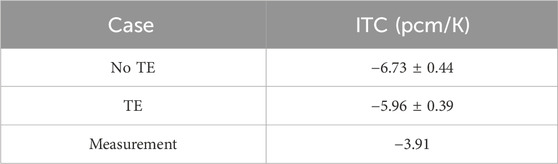
This problem quantifies the effect of TE on the isothermal temperature coefficient (ITC). ITC is the change in the reactivity per unit change in the fuel and moderator temperature (ANSI/ANS-19.6.1-2005, 2005). ITC measurements are performed during HZP reactor physics tests to determine if the measured ITC is consistent with the calculated value (Hong, 2010).

In this study, the ITC measurement in the VERA benchmark was modeled for cases with and without TE. The reactor used in this benchmark is Watts Bar Unit 1, a Westinghouse PWR. The measured ITC was obtained during cycle 1, with all fresh fuel. The ITC was calculated using isothermal temperatures of 560 K and 570 K, with a boron concentration of 1,291 ppm.

To ensure statistical reliability, the ITC mean and the corresponding standard deviations were obtained by performing five runs for each case, with random seeds for each run. This resulted in a total of 25 ITC samples, from which the mean and standard deviation were calculated. For each run, there were 14,500 cycles, of which 2,500 cycles were inactive, with 40,000 particle histories simulated for every cycle. The results are displayed and compared against measurement result in Table 6.

Table 6

Table 6. Calculated ITCs compared with the measured value.

As indicated in the table, core modeling with TE makes the ITC more accurate and closer to measurement data. Furthermore, the results demonstrate that TE modeling makes the ITC more positive by 0.77 pcm/K. This ITC difference is slightly higher compared to the findings from reference (Palmtag et al., 2017), which reported that TE modeling makes the ITC 0.5–0.6 pcm/K more positive.

Although the ITC solutions for both the TE and No TE cases deviate significantly from the reported measured value, they are still comparable to the results of other MC calculations. For example, the ITC solution from KENO without TE is 5.72 pcm/K (Godfrey, 2014).

3.5 Depletion problem

Exercise 3 of the TVA Watts Bar Unit 1 multi-physics depletion benchmark (Albagami et al., 2021) was adopted to investigate the effect of TE on the boron letdown curve during reactor depletion. Restart cases from whole-core pin-by-pin depletion without TE were run at 0, 221.1, and 392.3 effective full power days (EFPDs) for cases with and without TE. This depletion problem simulated $6\times {10}^4$ particles per cycles, with a total of 5,000 cycles, of which 2,500 were active cycles.

MCS, coupled with the CTF thermal-hydraulics solver (Salko et al., 2015), was used to solve this problem. The work on MCS/CTF multi-physics coupling was done in the previous studies (Yu et al., 2017). The results were compared against the measured values obtained from reference (Godfrey, 2014) and are presented in Table 7.

Table 7

Table 7. Critical boron concentrations for depletion problem.

As shown in the table, direct core modeling with TE yields more accurate predictions for this depletion whole-core problem, particularly as power increases and fuel burnup progresses. At the beginning of the cycle (BOC), core modeling with TE underestimates the measured critical boron concentration (CBC) by 22 ppm, which is slightly higher than the 13-ppm underestimation observed with core modeling without TE. This higher CBC underestimation in the TE model at BOC is attributed to the high boron concentration and zero power at the start of the cycle. However, as the fuel cycle progresses and power increases, core modeling with TE offers more precise CBC solutions. For instance, at the end of the cycle (EOC), the TE model underestimates the CBC by just 3 ppm, compared to a 27-ppm underestimation by the model without TE. These results indicate that direct core modeling with TE provides more accurate solutions, particularly at full power and higher fuel burnup levels.

These solutions can be further improved by dividing the fuel pellet into multiple radial rings to more accurately model the radial fuel temperature distribution within the pellet. This radial temperature variation is essential for correctly capturing the spatial self-shielding effect. Another study (Imron and Lee, 2025) reported that accurate spatial self-shielding modeling can increase the reactor eigenvalue by 50–80 pcm at HFP, which corresponds to approximately 5–8 ppm of boron concentration in typical PWR reactor problems.

4 Conclusion

This study presents an on-the-fly thermal expansion methodology for direct MC coupled multi-physics simulations implemented in the MCS code. The methodology was described and evaluated on several reactor problems. The trends in reactivity differences due to thermal expansion for varying boron concentrations and fuel temperatures, as well as the improvement in calculated ITC with thermal expansion, are consistent with previous studies. While using core-averaged temperatures for expansion is fairly accurate, the accuracy can be further improved by using local temperatures. Finally, this study shows that incorporating thermal expansion improves the solutions for depletion problems, especially at high power and high fuel burnup.

Thermal expansion for control rods and burnable poison rods will be included in future work. The inclusion of thermal expansion for control rods is particularly important for obtaining more accurate axial power distribution, which is often ignored in most current LWR analyses. Therefore, further studies are necessary to evaluate thermal expansion for other parts of the reactor core to achieve higher-fidelity reactor analyses.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MI: Writing–original draft, Visualization, Validation, Software, Methodology, Investigation, Formal Analysis, Data curation, Conceptualization. DL: Writing–review and editing, Supervision, Resources, Project administration, Funding acquisition, Conceptualization.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by KOREA HYDRO & NUCLEAR POWER CO., LTD (No. 2022-Tech-13). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

During the preparation of this manuscript, the author(s) used ChatGPT-4o to improve the readability and clarity of the writing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albagami, T., Rouxelin, P., Abarca, A., Holler, D., Moloko, L., Avramova, M., et al. (2021). TVA Watts bar unit 1 multi-physics multi- cycle depletion benchmark version 2.2. Paris, France: OECD Nuclear Energy Agency.

Google Scholar

ANSI/ANS-19.6.1-2005 (2005). Reload startup physics tests for pressurized water reactors. American Nuclear Society.

Google Scholar

Choi, S., Kim, W., Choe, J., Lee, W., Kim, H., Ebiwonjumi, B., et al. (2021). Development of high-fidelity neutron transport code STREAM. Comput. Phys. Commun. 264, 107915. doi:10.1016/j.cpc.2021.107915

CrossRef Full Text | Google Scholar

Cole, M. M., Lin, C.-S., and Ortensi, J. (2021). NRC multiphysics Analysis capability deployment FY 2021 - Part 2. Idaho Falls, Idaho: Idaho National Laboratory.

Google Scholar

Fiorina, C., Radman, S., Koc, M. Z., and Pautz, A. (2019). “Detailed modelling of expansion reactivity feedback in fast reactors using OpenFOAM,” in International conference on mathematics and computational methods applied to nuclear science and engineering (M&C 2019) (Portland, OR), 1434–1442.

Google Scholar

Godfrey, A. T. (2014). VERA core physics benchmark progression problem specifications. U.S. Department of Energy.

Google Scholar

Guo, Y., Li, Z., Huang, S., Liu, M., and Wang, K. (2021). A new neutronics-thermal-mechanics multi-physics coupling method for heat pipe cooled reactor based on RMC and OpenFOAM. Prog. Nucl. Energy 139, 103842. doi:10.1016/j.pnucene.2021.103842

CrossRef Full Text | Google Scholar

Hong, S.-K. (2010). “Advanced on-line isothermal temperature coefficient measurement for A physics test,” in Transactions of the Korean nuclear society autumn meeting (South Korea: Jeju), 135–136.

Google Scholar

Imron, M., and Lee, D. (2025). Monte Carlo coupled multi-physics with spatially continuous material properties. Ann. Nucl. Energy 210, 110856. doi:10.1016/j.anucene.2024.110856

CrossRef Full Text | Google Scholar

Lee, H., Kim, W., Zhang, P., Khassenov, A., Park, J., Yu, J., et al. (2017). “Preliminary simulation results of BEAVRS three-dimensional Cycle 1 whole core depletion by UNIST Monte Carlo code MCS,” in Proceeding of international conference on mathematics and computational methods (M&C 2017) (South Korea: Jeju).

Google Scholar

Lee, H., Kim, W., Zhang, P., Lemaire, M., Khassenov, A., Yu, J., et al. (2020). MCS – a Monte Carlo particle transport code for large-scale power reactor analysis. Ann. Nucl. Energy 139, 107276. doi:10.1016/J.ANUCENE.2019.107276

CrossRef Full Text | Google Scholar

Ma, Y., Han, W., Xie, B., Yu, H., Liu, M., He, X., et al. (2021). Coupled neutronic, thermal-mechanical and heat pipe analysis of a heat pipe cooled reactor. Nucl. Eng. Des. 384, 111473. doi:10.1016/j.nucengdes.2021.111473

CrossRef Full Text | Google Scholar

Palmtag, S., Kochunas, B., Jabaay, D., Han, Z., and Downar, T. (2017). “Modeling thermal expansion in VERA-CS,” in Proceeding of international conference on mathematics and computational methods (M&C 2017) (South Korea: Jeju).

Google Scholar

Permann, C. J., Gaston, D. R., Andrš, D., Carlsen, R. W., Kong, F., Lindsay, A. D., et al. (2020). MOOSE: enabling massively parallel multiphysics simulation. SoftwareX 11, 100430. doi:10.1016/j.softx.2020.100430

CrossRef Full Text | Google Scholar

Ryu, M., Jung, Y. S., Cho, H. H., and Joo, H. G. (2015). Solution of the BEAVRS benchmark using the nTRACER direct whole core calculation code. J. Nucl. Sci. Technol. 52, 961–969. doi:10.1080/00223131.2015.1038664

CrossRef Full Text | Google Scholar

Salko, R. K., Lange, T., Kucukboyaci, V., Sung, Y., Palmtag, S., Gehin, J., et al. (2015). “Development of COBRA-TF for modeling full-core, reactor operating cycles,” in 5th topical meeting on advances in nuclear fuel management, ANFM 2015 (American Nuclear Society), 178–194.

Google Scholar

Smith, K., and Forget, B. (2013). “Challenges in the development of high-fidelity LWR core neutronics tools,” in International conference on mathematics and computational methods applied to nuclear science and engineering (M&C 2013). (Sun Valley, ID).

Google Scholar

Yu, J., Lee, H., Kim, H., Peng, Z., and Lee, D. (2020a). Coupled neutronics–thermal-hydraulic simulation of BEAVRS cycle 1 depletion by the MCS/CTF code system. Nucl. Technol. 206, 728–742. doi:10.1080/00295450.2019.1677107

CrossRef Full Text | Google Scholar

Yu, J., Lee, H., Kim, H., Zhang, P., and Lee, D. (2017). “Preliminary validation of MCS multi-physics coupling capability with CTF,” in Proceedings of the reactor physics asia 2017 (RPHA17) conference, (chengdu, China: reactor physics asia conference organizer).

Google Scholar

Yu, J., Lee, H., Kim, H., Zhang, P., and Lee, D. (2020b). Simulations of BEAVRS benchmark cycle 2 depletion with MCS/CTF coupling system. Nucl. Eng. Technol. 52, 661–673. doi:10.1016/J.NET.2019.09.007

CrossRef Full Text | Google Scholar