EURAD State-of-the-Art Report: Assessment of the chemical evolution at the disposal cell scale – part II – gaining insights into the geochemical evolution

Long time frames are to be considered in the safety and performance assessment of deep geological disposal of intermediate and high level radioactive waste. Geochemical conditions will change in the waste, conditioning matrix, waste package, engineered barriers and the host rock–all components present at the disposal cell scale. This aspect of geological disposal was the focus of the work package ACED (Assessment of chemical evolution of intermediate level (ILW) and high level (HLW) waste at disposal cell scale) in the EURAD project (the European Joint Programme on Radioactive Waste Management). The first part of this review provided a narrative of the geochemical evolution of the disposal cell. In this second part, an overview is given about methods and approaches that can be used to gain further insights into the processes driving the geochemical evolution, more in particular (i) laboratory and in-situ experiments, (ii) archaeological and natural analogues, and (iii) modelling tools. The review concludes with a short discussion on the consequences on material properties, waste forms and radionuclide mobility.

1 Introduction

The most preferable end point for the safe and sustainable management of intermediate (ILW) and high level (HLW) radioactive waste is in many national programmes the disposal in a deep geological repository (DGR). Such DGR consists of an engineered barrier system and a host rock to contain and isolate the radioactive waste. Given the time scales over which safety and performance studies have to be assessed (tens of thousands to hundreds of thousands of years) and the potentially large chemical gradients that exist between materials within the engineered barrier system and the host rock, assessing the evolution of geochemical alteration is potentially a very valid input towards safety and performance assessment, assessing safety margins and optimization including the properties of the materials in the engineered barrier (Neeft et al., 2024). Within the framework of the European Joint Programme on Radioactive Waste Management (EURAD), the work package ACED (Assessment of chemical evolution of intermediate level (ILW) and high level (HLW) waste at disposal cell scale) looked at the disposal cell scale, i.e., waste packages and their immediate surrounding engineered barrier system and host rock (see Figure 1). In the first part of this state-of-the-art on ACED, Neeft et al. (2024) described some main characteristics of disposal cells for DGR in European national programmes in Part I. For HLW, only vitrified HLW is considered; spent fuel is out of scope in this review. Stainless steel canisters with vitrified HLW were encapsulated in carbon steel overpacks. These overpacks were surrounded with buffers made of concrete or bentonite. Only metallic and organic ILW processed with processed with cementitious materials was considered in ACED. Engineered barriers interfaced clay of granitic rock. Furthermore, a state-of-the-art understanding of processes occurring at the interface between two materials (e.g., glass-steel, concrete-clay, etc.) was provided in Part I. Based on this, a generic narrative spatial-temporal evolution of ILW and HLW was presented.

Figure 1

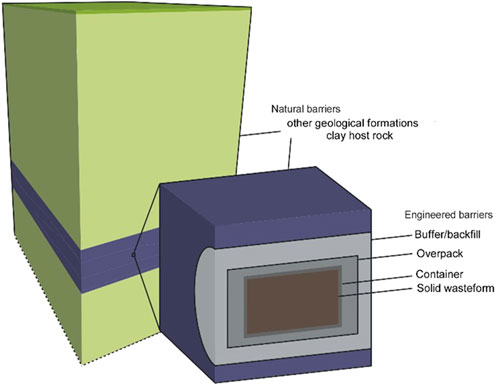
Figure 1. The general concept of the multibarrier system for geological disposal of radioactive waste–the waste package (solid waste form, container, overpack), the host rock (blue) and other geological formations (green) (adapted from Chapman and Hooper, 2012).

The second part of the review focusses on how information about the chemical evolution at the disposal cell scale can be obtained for relevant time and spatial scales. The conceptualizations of the chemical evolution of disposal cells have been extracted from understanding experimental results from a geological disposal perspective. Measurements can be performed on materials in contact with geological disposal representative environments. Determination of the representativeness of these environments requires quantification of the radiological, chemical, physical properties of these materials as well as their environments. There is a lot of literature available with experimental results in which this quantification, for example, radiological quantification, has not been performed. This lack in quantification makes the use of these literature sources for the conceptualization of the chemical evolution of disposal cells speculative. It may be very likely that the described processes do not occur. For example, a too high radiation dose rate had been used, or the concentration in dissolved chemical species to which materials have been exposed are too low (for example, distilled water, lack in dissolved silica) or too high. Also, many measurements have been performed under unrealistic physical conditions from a geological disposal perspective, for example, polished surfaces of metals. Polishing of metallic ILW is never done before disposal, there is usually an existing oxide layer on these metals that limits the corrosion rate. Research time is then devoted into generation of this oxide layer that already exists. The experimental results obtained in this period may not be representative for the disposal of waste.

The experimental period may be too small to observe the processes relevant for disposal. Archaeological or natural analogues give experimental evidence over time scales (much) longer than is typically available in laboratory or in-situ experiments. The information that can be gained from analogues highly depends on the amount of activities that are performed in this area. A natural analogue working group was working in the 3^rd and 4^th EURATOM framework programmes and most studies were focussing on representative studies for radionuclide migration. Natural Analogue network (NAnet) in the 5^th framework programme included more work on the durability of materials. They had made an analogue matrix for the near-field with analogues for each barrier, and such a matrix for the far-field with analogues for radionuclide migration in different types of host rocks. The analogue matrix for the near-field contained a specific section on the degradation of the engineered barriers (NAnet, 2006). Currently, the natural analogue working group operates without funding by the European Commission. Their website (www.natural-analogues.com) aims to contain all the available information on analogues.

The archaeological and natural analogues described in this review are limited to the alteration mechanisms of engineered materials used in the disposal cells and types of waste discussed in this report. The described analogue studies can be used for the description of a conceptual model of their alteration mechanisms in the chemical evolution of the disposal cells. The alteration rate during disposal can in some cases also be determined from natural analogues, provided that the key components for their alteration are understood and are representative for disposal. Frequently, however, the initial and boundary conditions are not known in sufficient detail to determine this rate. Analogue studies can be used to verify the mathematical models that are used to assess the chemical evolution on the long-term, i.e., are the processes sufficiently understood.

Another method to obtain insights into the long-term large-scale geochemical evolution under disposal conditions is through modelling. Although models are based on knowledge on phenomena obtained mainly via experimental approaches, the strength of models is to integrate knowledge and evaluate interacting processes at large scale and long time scales. In the framework of geochemical processes, so-called coupled reactive transport models are in particular useful tools.

2 Laboratory experiments/in-situ experiments

2.1 Long-term and in-situ experiments

Natural and archaeological analogues are in-situ long-term experiments that last over time frames relevant for the long-term in geological disposal of radioactive waste. Features that are important on the long-term such as the transformed medium or alteration zone in clay or concrete when exposed to steel can be observed (Chitty et al., 2005; Dillmann et al., 2014; Neff et al., 2004). Also the understanding of processes of materials interfacing concrete, granite (see Neeft et al., 2024) and clay (see Neeft et al., 2024) have been deduced primarily from the investigations on the Maqarin natural analogue. But not every old material or site can be an analogue. Quantitative knowledge on the chemical and physical properties of the engineered barriers and host rocks are needed to justify the research on the materials and site. The investigation of sites with natural and archaeological analogues requires an understanding of the relevant processes during the implementation of geological disposal of radioactive waste and in the phase when the disposal facility is closed. The main disadvantage of analogues is the lack of information about the initial conditions, which makes it difficult to extract quantitative information for the performance assessment of the disposal of waste.

Transport properties within the host rock and engineered barriers are a key issue in the chemical evolution of disposal cells since it has a high impact on how there can be contact between the pore water and the waste form and when. The ‘how’ determines the chemical and physical conditions for the alteration mechanism of the waste form. The ‘when’ determines the radionuclides that are left and consequently the potential radionuclide release rate. The quantification of the transport properties can depend on the sample size since the heterogeneities on a large scale can have a high impact on these properties. In-situ experiments in underground research laboratories (URLs) can therefore provide the most reliable determination of the (initial) transport properties for the chemical evolution of the disposal cells and its consequences on the radionuclide release rate from the waste forms as well the as the radionuclide migration rate through the engineered and natural barriers.

In the context of radioactive waste disposal, a URL is an underground facility for conducting experiments to establish and demonstrate the feasibility of constructing and operating a deep geological repository (NEA, 2013; NEA, 2001). URLs provide a realistic environment for testing the selected technical approaches and materials, as well as characterising the properties of the host rock (e.g., regarding (hydro)-geology, geochemistry, rock mechanics) and its response to perturbations. Furthermore, they serve to provide data to understand the behaviour and assess the performance of the repository system and the interactions between its components, to demonstrate the robustness of the design and to build confidence in the understanding of the important processes (e.g., Blechschmidt and Vomvoris (2010), NEA (2013), Delay et al. (2014), Mayer et al. (2023)).

Two broad categories of URLs can be distinguished: generic and site-specific URLs. Generic URLs are built for generic research and testing purposes at locations not considered as potential disposal sites but provide the opportunity to enhance the understanding of the respective host rock type and to perform experiments at representative scales under realistic conditions to support disposal elsewhere. Examples for generic URLs in clay or clay rocks comprise the Mont Terri underground rock laboratory in Opalinus Clay in Switzerland (Bossart et al., 2017), the HADES underground research facility situated in Boom Clay in Belgium (Van Geet et al., 2023), and the Tournemire experimental facility in Toarcian clay rocks in France (NEA, 2013). Generic URLs in crystalline rocks (granite) include the Äspö Hard Rock Laboratory (Sweden), the Grimsel Test Site (Switzerland) and the KURT research tunnel (South Korea) (Blechschmidt and Vomvoris, 2010; NEA, 2013). Site-specific URLs are facilities that are implemented at or close to potential waste disposal sites. Site-specific URLS have the advantage that the experiments are performed in the actual conditions of the future repository, broadening the scope and impact of research, development and demonstration conducted in these URLs. Site specific URLs include the URL in the ONKALO URL in crystalline rocks in Eurajoki, Finland, and the URL in Callovo-Oxfordian claystones at the Bure site (Meuse/Haute Marne, France) (NEA, 2013). Some examples for research performed in URLs relevant to the geochemical evolution of disposal cells are given below.

Research in URLs include experiments up to the disposal cell scale (1:2 or even 1:1) and are conducted up to several decades. Examples of full-scale experiments addressing the response of bentonite buffer and host rock to the thermal load imposed by HLW disposal comprise the ‘Full-Scale Emplacement’ (FE) experiment at the Mont Terri rock laboratory, the ‘Full-Scale Engineered Barriers Experiment’ (FEBEX) at the GTS. The FE experiment simulates construction, waste emplacement, backfilling and early post-closure evolution of a spent fuel/vitrified HLW disposal tunnel aiming at the investigation of repository-induced thermo-hydro-mechanical (THM) coupled effects on the clay host rock and the validation of coupled THM models (Müller et al., 2017). The FEBEX experiment started in 1998 to study the behaviour of the near-field components (EBS, host rock) is based on the Spanish reference concept for the disposal of high-level radioactive waste in crystalline rocks, i.e., waste canisters emplaced horizontally in drifts surrounded by highly compacted bentonite blocks (Huertas et al., 2000; Samper et al., 2008).

Examples for in-situ experiments addressing the corrosion of metals/canister materials in repository environments include the IC and IC-A experiments in Mont Terri (Necib et al., 2017) and the MaCoTe materials corrosion test in the GTS (Reddy et al., 2021). Interactions between cementitious materials, near field materials and host rocks were addressed, e.g., in the CI experiment at Mont Terri (Mäder et al., 2017) and the LCS (Long-term Cement Studies) experiments at the GTS (e.g., Soler and Mäder (2007), Watson et al. (2018)).

In the CORALUS project at the HADES underground research facility, the performance of HLW glasses in conditions representative for those expected in a disposal system are investigated since 1998. In this experiment, the combined effects of radiation, heat and interacting near-field materials on vitrified HLW behaviour, radionuclide leaching and migration under disposal conditions are studied (e.g., van Iseghem et al. (2001), Valcke et al. (2006)).

2.2 Laboratory experiments

There have been many experimental results obtained on a laboratory scale. The initial and boundary conditions in a laboratory set-up are usually known, which allows a robust interpretation of the monitored parameters. The main disadvantage of laboratory experiments is the restricted period in time. Extremes in radiological, chemical, physical and microbiological conditions are often used in order to observe ‘something’ within a few days, months or years. These conditions may not be representative for the quantification of processes during geological disposal of radioactive waste. The set-up conditions for a laboratory experiment with the purpose to provide a quantification of a process, e.g., the corrosion rate of steel, requires quantitative knowledge on the radiological, chemical and physical properties of the waste and the chemical and physical properties of the engineered barriers and host rock. An assessment of the potential of microbial activity needs to be made for each set-up and also whether microbial activity would be relevant for geological disposal of waste and why. Quantification in properties has sometimes been made for example, (Smart et al., 2017), but frequently this quantification has not been made. An example is the refereed literature for the effect of γ radiation on bentonite properties [discussed in Section 3 in Neeft et al. (2024)] of more than 10–20 Gy h^-1 or 2.98 kGy h^-1. Such high radiation fields may not be relevant for disposal of waste. In the same section, it was also explained why processes such as radiation enhanced corrosion of steel are not likely to occur, i.e., the required radiation fields and access to water are not present during disposal of waste.

Laboratory tests require the understanding of the relevant processes in order to structure an experimental set-up in which representative results for geological disposal can be generated. Monitoring variables need to be carefully selected in order to investigate the phenomena that are relevant. Some illustrative examples with an impact on the determination of the radionuclide release rate for vitrified waste and the assumed durability for carbon steel overpack are provided below.

2.2.1 Vitrified waste form

Almost all laboratory studies investigating the interaction of porous media with vitrified waste forms are leaching experiments in liquids. The understanding of the alteration mechanism of natural analogue studies on basaltic glasses highlighted the importance of silica saturation. All host rock and engineered pore waters are saturated in silica and therefore leaching experiments of samples in glass in distilled water would overestimate the alteration rate, especially if the leachate solution would be stirred. The dissolved concentrations of silicon, sodium, aluminium, iron and calcium in representative blank solution are usually too large to monitor a change in their concentrations and therefore the dissolved boron concentration is monitored to determine the glass dissolution rate (Van Iseghem et al., 1992). However, the dissolved boron does not represent the behaviour of glass dissolution, since the boron is not incorporated in the altered glass layers (Conradt et al., 1986). The alteration rate of vitrified waste can be determined with rising boron concentration, but this information provides limited knowledge on the potential radionuclide release, since the majority of the radionuclides that are dissolved as cationic species is sorbed by the alteration layer. The long-term boron release rate measured from vitrified waste forms exposed to silicon saturated solutions can therefore only be representative for the radionuclide release rate of anionic dissolved species if a reactive solid phase is absent. It requires some time to build up the alteration layer by which the early measured boron release rates are too large to be representative for the long-term in the post-closure phase.

These leaching experiments lack solid near-field phases. These phases such as steel and corrosion products are present in a HLW disposal cell and their influence may result in larger alteration rates of vitrified waste forms, due to enhanced sorption of dissolved cationic complexes that can no longer be used for building the alteration layer. The glass dissolution rates that are determined without these solid phases may initially therefore be too optimistic for geological disposal, if the diffusion of water is not the rate-limiting step, since access of water is required for the alteration. The interfacial area between the vitrified waste form and steel is, however, limited in the disposal cell. After complete coverage of the corroded steel surfaces with dissolved cationic complexes from the vitrified waste form, the glass alteration rate is envisaged to decline till the long-term boron release rate.

2.2.2 Steel

2.2.2.1 Sample preparation and its impact on the corrosion rate

Most laboratory experiments with steel start with polished surfaces (Swanton et al., 2015) in order to have a well-defined initial condition of the sample. This polishing removes the iron oxide-layer that was generated by atmospheric dry oxidation before its use, for example, to make well-engineered reinforced concrete with ribbed carbon steel bars or iron-oxide layers that are formed on stainless steel after neutron irradiation in a nuclear plant. These layers can be passivation films that were present prior to disposal. The corrosion rate of steel can be several orders in magnitude larger without these films. It can take 4–6 months before a constant corrosion rate is observed (Johnson and King, 2008), if no dissolved calcium is present in the leachate (Kreis, 1991). This period to obtain a steady state can be more than 4 years for compacted clay (Johnson and King, 2008). This period in time is necessary to make the passivation film to obtain the long-term corrosion rate that is representative for disposal.

Another frequently used sample preparation methodology is acid etching. Rinsing with a 10% HCl-methanol solution is used to remove the iron oxide layer (King et al., 1973) that is naturally present. The weight loss from these samples in solutions containing iron sulphides becomes negligible after 30 days, probably because steel became passivated during the corrosion process. The impact of such type of research is that concrete made with a cement blended with Blast Furnace Slag (BFS) has not been accepted for disposal of waste, because iron sulphides within the cement have been observed to depolarise the water reduction reaction and thereby accelerate corrosion by absorbing hydrogen (Marsh et al., 1986). In reality, the rest potential of carbon steel has been measured to be achieved immediately for steel embedded in a grout mixture made with a BFS-blended cement. For carbon steel that is surrounded by mixtures of OPC/Pulverized Fly Ash (PFA) and OPC/Lime, it may take some time before entrapped oxygen is sufficiently consumed to obtain the rest potential of steel at anaerobic, alkaline conditions. Moreover, the iron oxide magnetite is expected for anaerobic, alkaline conditions (see Pourbaix diagrams in Neeft et al. (2024)) and is actually measured by Raman spectroscopy on the surface of carbon steel embedded in BFS-blended cement, but not on surfaces of steel that have been embedded in the mixtures OPC/PFA and OPC/Lime within the same experimental period (Naish et al., 1991).

2.2.2.2 Liquid phase versus solid phase

The solid phase restricts the access of species that may react with steel. There can be aerobic corrosion of steel in the operational phase and also for a small period in the post-closure phase of the chemical evolution of disposal cells. This corrosion process can be rendered due to insufficient access of oxygen towards steel with which for example, the pits in carbon steel are larger for surfaces exposed to solutions than to bentonite; after 2 years exposure the depth of these pits was 3.7 mm for solutions and 0.5 mm for bentonite (Marsh et al., 1991). This insufficient access of oxygen towards the steel surface can be caused by the slow diffusion of oxygen in water-saturated bentonite as well as traces of pyrite present within bentonite that reacted with oxygen.

The benefit of the performance of the corrosion experiments performed in liquids is that the actual corrosion rate can be monitored with the measured hydrogen gas release with negligible loss in time by diffusion of hydrogen to the measurement device. The disadvantage of using only liquids is that the solid phases can increase the corrosion rate by sorption of dissolved iron if these solid phases contain charged minerals such as clays and cement hydration phases and if the diffusion of water required for the corrosion process is not the rate-limiting step.

2.2.2.3 Monitoring variable for the quantification of the corrosion rate

Long-term corrosion rates for carbon steel exposed to alkaline, anaerobic solutions are smaller than 0.1 µm per year using hydrogen evolution measurements. Corrosion rates for carbon steel exposed to concrete are limited to weight loss and electrochemical measurements (Swanton et al., 2015). Electrochemical measurements overestimate the actual corrosion rate, especially when the corrosion rates are smaller than 1 µm per year. Corrosion experiments that have achieved steady state have a total corrosion rate smaller than 0.57 µm per year using weight loss (Naish et al., 1991). These corrosion rates include the initial active corrosion phase in which the corrosion rate has been measured to be 3 orders in magnitude larger than the steady state corrosion rate. The measured corrosion rates by weight loss can at least be one order in magnitude larger than the measured corrosion rate by hydrogen release (Kaneko et al., 2004; Kursten and Druyts, 2015). Determination of the corrosion rate with hydrogen evolution measurements has been performed for carbon steel in concrete for a period of 500 days (Kaneko et al., 2004) but not for carbon steel in clay. The hydrogen generation rate was extremely small despite the fact that accuracy was high, i.e. 0.001 µm per year. Delay in the arrival of hydrogen by the measurement device makes it hard to measure the corrosion rate.

3 Archaeological and natural analogues

3.1 Vitrified waste forms

Of all natural volcanic glasses, basaltic glass has a similar SiO₂ content as the vitrified waste form (e.g., (Lutze et al., 1987; Havlova et al., 2007; Laciok, 2004). The alteration mechanism of basaltic glass is the same as expected for the vitrified waste form, except that the alteration product is named differently, i.e., palagonite, which is a mixture of clay minerals and zeolites. Palagonite occurs as rims of varying thickness around glass fragments. Fe-rich smectites are abundant for basaltic glass interfacing sediments (Fe-Mg saponites being the most common) and zeolites are common in both fresh water and sea water altered basaltic glass. These rims are representative for the glass passivation layer that is formed when vitrified waste is exposed to pore water. The alteration rate depends on dissolved silica concentration. Clay pore water is saturated in dissolved silica [see Section 2 in Supplementary Materials of Neeft et al. (2024)] and alteration rates of 0.1 µm per 1,000 years are representative. The rate of palagonitization highly depends on temperature, doubling for every 12 °C increase, which is similar to the ‘palagonitization’ of borosilicate glass, in which a doubling of the alteration rate for every 10 °C has been found. The measured rate at 100 °C was 3 µm per year (Lutze et al., 1987).

There are also two main differences between natural glass and vitrified waste forms: there is no natural glass that has the same high boron content or radionuclide content as the vitrified waste form. These differences may however have no influences on the alteration mechanism since:

1) The release of boron from vitrified waste forms does not give a representative glass dissolution rate, since boron is not contained in the glass passivation layer (Conradt et al., 1986). Consequently, boron does not take part in a representative glass degradation mechanism;

2) Glass is a metastable solid with no clear crystalline structure in which atoms can be displaced from their lattice position to weaken its strength. As explained in Neeft et al. (2024), the temperature of glass at disposal is too high to have remnants of radiation damage that are detrimental to the physical resistance of glass. Radiation rather works as a network modifier. The high radionuclide content is only a chemical additional feature and that is also present in natural glass. Radioactive and nonradioactive glasses have the same corrosion time- and temperature dependence (Vernaz et al., 1996).

The alteration rates measured for natural basaltic glasses are also more representative for disposal than archaeological glasses, since the exposure environments of archaeological glasses are more near the surface and less representative for deep disposal with, for example, a higher water circulation and oxygenated conditions (Laciok and Dalton, 2005).

3.2 Steel

There are mainly archaeological analogues for steel, since native iron rarely occurs, e.g., upon precipitation from a Fe-rich magma that has been isolated from groundwater, it is usually incorporated into various oxides and silicate compounds. An exception is Disko Island (Greenland) in which native iron has been coated by micrometer sized magnetite and goethite layers (Ahonen, 2004a). The most famous archaeological analogues are the 2000 year old iron nails from Inchtuhil (Scotland) that clearly provided the evidence for the difference in corrosion rates at oxidising and reducing conditions (Hooker, 2003c). There are also many other examples that elucidated this feature including the impact of cementation and the presence of sulphides (Crossland, 2005; Dillmann et al., 2014). The corrosion behaviour of carbon steel is similar as that of iron, there are just more slag inclusions in iron than in carbon steel.

The understanding of the corrosion process of carbon steel and interaction with the relevant surrounding media clay and concrete that were described in Deissmann et al. (2021) and Neeft et al. (2024) could not have been made without the described archaeological analogues (Neff et al., 2004; Chitty et al., 2005). The determination of corrosion rates may, however, not be as exact as can be determined from laboratory experiments, since the corrosion rates are determined with the amount of measured iron near the interface, but the clay and cementitious material can also contain iron, i.e., may not be corroded iron, and the dimensions of the iron specimens are not always known. In addition, the initial corrosion process can have a corrosion rate that is three orders in magnitude larger than the steady state corrosion rate. The long-term corrosion rate can then be easily overestimated if the total corroded amount of iron is attributed to the whole period.

Stainless steel has a higher corrosion resistance than carbon steel due to the alloying of iron with chromium, nickel and molybdenum. It is a new material for which any archaeological analogue would not be as old as previously described for carbon steel. The corrosion product, chromite, is however frequently found, e.g., in mafic and ultramafic rocks (Ahonen, 2004b). Research on such naturally occurring compounds revealed that solid solutions of these spinel types frequently exist and that these types are hard to distinguish with Raman spectroscopy; additional chemical analysis is necessary to identify the chemical compositions of spinel (Wang et al., 2004). These natural analogue studies put the laboratory studies performed on carbon steel in the eighties in a slightly different perspective (Naish et al., 1991), since only Raman spectroscopy was used to identify the corrosion product but its chemical composition can be slightly different from pure magnetite that also has a spinel type structure e.g., magnetite containing traces of calcium or perhaps even CaFe₂O₄.

3.3 Bentonite

Bentonite is an abundant material usually formed by hydrothermal alteration of volcanic ash; there are bentonite mines to explore this material. For disposal, bentonite is compressed in order to achieve a sufficiently high density to limit microbial activity (see Neeft et al. (2024)). In the early post-closure phase, there is also a thermal transient and associated dehydration. In NAnet, characteristics of a few bentonite deposits have been identified (NaNET, 2006):

1. Deposits which have been intruded by small igneous bodies to generate a thermal peak approximating the thermal transient from the waste;

2. Deposits in contact with deep, reducing groundwaters, where groundwater bentonite interactions can be studied;

3. Naturally compressed bentonite, where its long-term hydraulic properties may be investigated; and

4. Deposits, where bentonite is in contact with other materials, which are analogues to components of the engineered barrier system to investigate possible interactions.

The thermal effect found in natural analogues in Isle of Skye (Scotland) (Wouters and Verheyen, 2004), Col du Perthus (France) (Trotignon et al., 2004), Busachi (Italy) (Wouters et al., 2005a) and Kinnekulle (Sweden) is the transformation of montmorillonite into illite (Wouters et al., 2005b). The understanding of this transformation indicated that a sufficient supply of potassium is needed for this transformation. The Supplementary Material Section 2 in Neeft et al. (2024) shows that granitic and clay pore waters are deficient in potassium, but cementitious pore waters are not. The inflow of granitic pore water into bentonite is limited due to desaturation of the buffer by the heating power of the waste. The mineralogical transformation is therefore negligible for HLW disposal cells in granitic host rocks (SKB, 1999) but this transformation could be relevant for the bentonite-shotcrete interface for HLW disposal cells in indurated clay host rocks and concrete-poorly indurated clay interfaces.

Concerning the second aspect, all poorly indurated clay formations at disposal depth are considered suitable analogues such as the Boom Clay and Ypresian Clay formation, since the main clay mineral in poorly indurated clays is smectite and no mineral transformation is induced by the reducing conditions.

The analogue for the third aspect is the Dunarobba Forest (Italy). This analogue is a collection of more than 2 million year old trees that had been preserved in compacted clay, due to the prevailing anaerobic conditions, limited nutrient supply and diffusion dominant transport regime. The trees were protected against microbial degradation and had therefore cellulose contents similar to present-day wood (Lombardi and Valentini, 1996; De Putter et al., 1997; Hooker, 2003a).

The analogues to investigate the possible interactions between bentonite and other components of the engineered barrier system are for the investigated disposal cells limited to carbon steel and concrete. The interaction between soil and iron (Neff et al., 2004) could be suitable analogues, but the focus was mainly on the iron and less on the clay minerals in the soils. Interaction with concrete is described in the next paragraph.

3.4 Concrete

3.4.1 Durability

The natural analogue for Ordinary Portland cement (OPC), which is the main component of CEM-I based cement, is the generation of lime (CaO) from limestone or chalk by a thermal source, i.e., metamorphism, and that this lime came in contact with groundwater. The Maqarin (Jordan) natural analogue project provided the evidence of three concrete leaching stages as identified earlier (see Neeft et al. (2024) and references therein): high pH Na/KOH leachates, Ca(OH)₂ buffered. and silicate-dominated leachates. This analogue also shows the formation of thaumasite (Kamei et al., 2010) except that thaumasite is here a fracture filling mineral (Milodowski et al., 2015) rather than a mineral that deteriorates concrete by its expansive crystallisation volume as modelled for geological disposal facilities (Höglund, 2014). When the limestone contains silicates such as flint nodules or chert, the metamorphism can result into calcium-silicates such as larnite (β-Ca₂SiO₄) that upon hydration form C-S-H gels. Scawt Hill (Northern Ireland) is such a location in which C-S-H gels have been formed about 58 million years ago. This analogue also showed that precipitated calcite as a result of carbonation may surround C-S-H gels by which these poorly-crystalline gels are protected from further carbonation (Knight, 2003).

The past Roman Empire has left a lot of archaeological concrete in Europe. One of the most famous concrete structures showing the durability of concrete is the Pantheon in Rome. Although exposed to ordinary air for almost 1900 years, it clearly shows that carbonation of concrete may not impact its performance if well engineered. The inside of the dome is a perfect analogue for the operational phase of the disposal facility in which the performance of the lining in the disposal facility can be hardly affected by carbonation.

The outside of the dome is exposed to weathering waters; the resulting leaching process is representative for disposal, if the dissolved calcium concentration in host rock pore water is smaller than the dissolved concertation in concrete pore water. This case is present for some countries [see Supplementary Material Section 2 in Neeft et al. (2024)].

3.4.1.1 Cement

The durability of Roman concrete has been attributed to rigid quality control, low water to cement ratio, expert placement and compaction and the type of cement. Many Roman concrete is made of cement in which a part of the lime (CaO) has been replaced by natural pozzolans (Rassineux et al., 1989). Natural pozzolans are siliceous and/or aluminous earth materials: volcanic glass, zeolite minerals, opaline chert, and diatomaceous earths. They form part of a broader class of supplemental cementitious materials (SCM) such as fly ash and blast furnace slag. These SCMs can be considered as natural pozzolans. Concrete made with blended cements such as CEM II and CEM III are therefore more representative for Roman concrete than CEM I based concrete. The water in the concrete recipe in old Roman maritime concretes was seawater and the formation of Al-tobermorite, a C-A-S-H mineral in the cementitious matrix has attributed to its durability (Mulcahy et al., 2017). Also mortars to bind stone blocks in Hadrian’s wall have C-S-H phases (Mallinson and Davies, 1987), but these phases were mostly derived from the calcination of siliceous limestones during the production of the lime and, to a lesser extent, by reaction of fine-grained reactive silicate aggregate (Jull and Lees, 1990; Hooker, 2003c). The aggregate was chert (Mallinson and Davies, 1987) that has a very high reactive surface area. It can be similar to silica fume that is used as an addition to make concrete, e.g., in plugs (Vehmas and Itälä, 2019). It becomes clear from the investigations on historical and current concrete that cement containing lime (CaO) and pozzolan (very fine-grained reactive SiO₂ such as slag) results into C-S-H phases with a refined pore structure. This pore structure minimizes the rate of ingress of species that could alter the chemistry of concrete and therefore contributes to its durability.

Stone blocks are held together by a cementitious mortar in Hadrian’s wall from the Roman empire (Hooker, 2003b). This wall contains in parts mortars that are still hard and sampling need to be performed by coring (Jull and Lees, 1990), but also parts that are softer (Mallinson and Davies, 1987). These parts as well as younger structures, e.g., almost thousand year-old churches such as Reading Abbey, are soft and crumble and the concrete structures would not survive the lithostatic load in the underground. Apart from carbonation, these cementitious materials are also exposed to weathering waters that enhance leaching (Rassineux et al., 1989), since the calcium concentration in, for example, rain water is smaller than in concrete pore water.

The old cements used to manufacture concrete and mortars have larger grain sizes than modern cements (Mallinson and Davies, 1987). There were therefore more non-hydrated phases present just after manufacturing than in modern concrete, which leaves the possibility for fracture sealing.

Many examinations of historical concrete show calcite precipitation by atmospheric carbonation, e.g., Hadrian’s wall. The empirical laws for carbonation found in historical concrete can be relevant for the operational phase of the disposal facility, e.g., for shotcrete. Hardened concrete segments and the outside of concrete containers are polished to facilitate their lifting with vacuum techniques for their emplacement. The polishing effect for the long-term has been listed for historical concrete by the formation of closely knitted carbonation products that reduced the permeability and therefore enhances the durability of concrete (Mallinson and Davies, 1987).

Many natural (e.g., Scawt Hill and Maqarin) and archaeological (e.g., Pantheon in Rome) studies, are available with a chemical composition for concrete that are used or intended to be used in geological disposal facilities but their exposure conditions are usually without ingress of dissolved magnesium and chlorine (Milodowski et al., 2015), which is expected for disposal cells in granitic and many clay host rocks [see Supplementary Materials section 2 in Neeft et al. (2024), host rock pore water]. The exception is the Roman marine infrastructure but that type of concrete has been made with seawater and not tap water.

Portland cements were first manufactured in the middle of the 19^th century (Rassineux et al., 1989) around 1840s (Steadman, 1989). The oldest available materials that can be compared with concrete made with modern cements such as CEM I are therefore less than 200 years old.

3.4.1.2 Aggregates

Aggregates are used for all cementitious materials used in the disposal cells, except sometimes for the waste form. The strength of concrete is determined by the strength of the aggregates and the bonding between the cementitious phase and these aggregates. Aggregates of limestone are used in the concrete buffer (Van Humbeeck et al., 2007). These limestones can contribute in buffering the pH between 8.5 and 10.5. Aggregates of quartz are used in concrete segments and backfill (Verhoef et al., 2014). Examined historical concrete contained basalt, granite or feldspars as aggregates by which the knowledge on the long-term behaviour of quartz aggregates in a cementitious matrix is scarce. An exception is the flint gravel that together with limestone, was used as aggregates for Reading Abbey; a church in England built in 1121. Like some of the dressed stones for building Hadrian’s wall, the cementitious phase of Reading Abbey has become crumbly and washed away, leaving the appearance of these flint aggregates. But also, quartz grains have been flown within the cement mixture to make concrete, e.g., Camiros concrete 500 BC (Mallinson and Davies, 1987). The surface of the grain reacted with the cementitious matrix, i.e., ‘was eaten away’. A rim of reacted material is visible since the reaction proceeded not further. Such reaction rims have also been observed in Roman concrete with aggregates of pumice and feldspars. The idea is that these reaction rims are generated during hardening until thickening of a reaction rim of hydrates covers the external surface; the reaction is then slowed down considerably and proceeds through a diffusion controlled process (Mulcahy et al., 2017). The reactive surface area of quartz aggregates is insignificant compared to the reactive surface area of fly ash or blast furnace slag used in blended cements, so these slags can react completely, while there are only rims visible for the aggregates. Again, from Reading Abbey, when the reactive surface area is large as in chert, 3 different types of reactions with lime have been identified (Mallinson and Davies, 1987):

1) densified carbonate, which may have originally been C-S-H, with a thickness of about 1 mm;

2) a porous amorphous rim;

3) internal cracking of smaller flints, which leaves the residual material very porous.

Aggregates of silica and feldspars in cementitious matrices usually have a very low porosity and examined rims at these dense aggregates have been attributed to reactions taking place during hardening (Mallinson and Davies, 1987; Mulcahy et al., 2017). These reacted rims may provide the necessary bonding between aggregates and cementitious phase for the strength of concrete but are also hardly noticed in the investigations of concrete. Also limestone, basalt and granitic rock have been used as aggregates. Extensive cracking of historical concrete has been attributed to cement shrinkage by drying (dehydration) and carbonation leaving voids between aggregates and the cementitious phase initially made of pure lime. Aggregates remain mainly unaffected (Mallinson and Davies, 1987).

3.4.2 Effect of high-pH leachates on clay host rock and granitic host rocks

Clay host rocks and granitic host rocks are both alumina-silicate bearing rocks. Detailed investigation and understanding of the processes taking place in Maqarin (Jordan) elucidated the potential sequence of secondary mineral formation by interaction with alkaline fluids and alumina-silicate bearing rocks: C-S-H phases, low in Ca C-S-H phases, C-A-S-H, low Si/Al zeolite and high Si/Al zeolite as a function of pH (Savage, 1998; Milodowski et al., 1998). This description is (Figure 2) similar to the identified concrete-bentonite interaction and concrete-granite interaction as discussed in Neeft et al. (2024) and references therein.

Figure 2

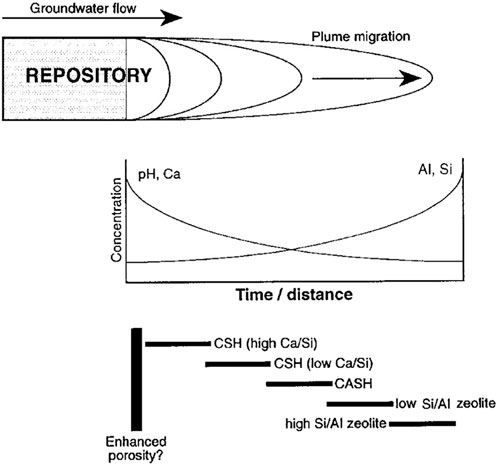
Figure 2. Schematic diagram of hyperalkaline plume migration from a cementitious repository for radioactive wastes, showing hypothesised variation in fluid composition and alteration mineralogy in space and time (Savage, 1998).

The sedimentary rock through which the hyperalkaline waters in the Maqarin analogue was more porous than the envisaged clay host rocks and the clay mineralogy in this sedimentary rock was dominated by illite and kaolinite. These clay minerals are also the dominating ones in indurated clays [see Supplementary Material Section 3 in Neeft et al. (2024)]. The chemical processes are therefore considered to be similar but the speed of the processes is significantly smaller, due to the low diffusion values in indurated clays as well as in concrete. Also the precipitation of calcite within concrete by ingress of bicarbonate from clay pore water would reduce the alkaline leachates. This analogue also revealed the reactivity of different mineralogical components. For example, quartz, K-feldspar and plagioclase are present in granitic host rocks [see Supplementary Material Section 3 in Neeft et al. (2024)] but quartz and K-feldspar react more with hyperalkaline waters than plagioclase. The reactive surface area has a high impact on the observed alteration, e.g., chert clasts are composed of fine-grained or cryptocrystalline quartz and have reacted into C-S-H gels (Milodowski et al., 1998). The natural analogues in Cyprus and Philippines in which hyperalkaline waters were passing clay deposits, similar to bentonite, showed minimal mineralogical alteration in a period of 10⁵–10⁶ years due to the low permeability of these clay deposits (Milodowski et al., 2015).

3.5 Organic waste

Organic matter can be considered as a potential nutrient source for microbes, if the usable energy to breakdown the organic molecules provides sufficient energy. Microbial degradation of organic waste can therefore be a primary process for the potential release of radionuclides. A division is made between addition polymers and condensation polymers to distinguish the potential microbial degradation (see also Neeft et al., 2024).

An example of an addition polymer that is also a predominant organic ILW-type is spent ion exchange resin. Natural resins are solidified products of higher plants with a great resistance to chemical attack and resins can also withstand decomposition by microbes. There is however not an analogue for cemented resins.

An example of a condensation polymer is cellulose (e.g., wood, paper). This type of organic waste is in exceptional cases ILW (Neeft et al., 2024). The Dunarobba forest analogue, previously described in Section 3.3, showed the good preservation of wood by lack of fluid flow and anaerobic conditions. These two features can also be provided by the conditioning grout for organic waste; the chemical corrosion of the steel drums can generate the required reducing conditions, if the cement did not contain traces of pyrite. There is the potential alteration of vegetable debris, i.e., condensation polymers, into polysaccharides by migrating alkaline fluids in Khushaym Matruk (Jordan) (Källström and Lindgren, 2014). Such alkaline migration is expected to take place for ILW disposal cells in granite, in which the conditioning grout had been extensively fractured due to the lithostatic load and mechanical degradation by the ingress of dissolved species that had reacted with the cementitious matrix.

4 Integration in modelling tools

Reactive transport models couple transport processes (advection, hydrodynamic dispersion, diffusion) with geochemical processes (thermodynamic equilibrium, kinetic processes). Such models are emerging for about 40 years and have found applications in many environmental and engineering applications including geological disposal of radioactive waste. Some recent publications give an overview of the background, methods and available codes of reactive transport codes (Steefel et al., 2015a) and an overview of applications in the field of disposal of radioactive waste (Bildstein et al., 2019; Claret et al., 2018; De Windt and Spycher, 2019). Overall, during the last 10 years, coupled reactive transport with a large flexibility to include several equilibrium and kinetic processes are applied for many engineered systems at different spatial and temporal scales including applications relevant to geological disposal of radioactive waste. For background on the mathematical and numerical models, the reader is also referred to Anderson and Crerar (1993), Lichtner (1996), Steefel and MacQuarrie (1996) and Leal et al. (2017) for the basic mathematical and numerical formulations of geochemical and reactive transport equations.

As described in the previous sections, the chemical evolution in a disposal cell is not only governed by transport and geochemical processes, but also by water flow and absorption, multiphase flow phenomena and heat transfer. An overview of the key mathematical formulations of these processes is given in Section 4.1. Some selected codes that have been used in the context of geological disposal of radioactive waste or to describe relevant processes at interface, waste package, and disposal cell scales are described in the Supplementary Materials.

4.1 Governing equations for simulating water flow, heat transport, solute transport and geochemistry

The key processes in the conceptual model of the chemical evolution at an interface, of waste packages (under disposal conditions), or of disposal cells are transport of water (fluid flow), advective and diffuse transport of dissolved species (solutes) between the interfacing materials and reactions between these dissolved species and minerals within these materials.

Other processes, such as fluid flow but also sorption determine the speed in which the materials can be altered. For HLW, also the impact of temperature on these key processes needs to be assessed. The release mechanism and rate of radionuclides from the waste forms are determined by the chemical evolution of materials in the vicinity of the waste form in the disposal cell.

4.1.1 Continuum models

The scope of the reactive transport models described in this report is limited to continuum-scale models. In such an approach, the micro-heterogeneities between different phases (e.g., aqueous phase, solids or even different minerals) are not represented in an explicit way by geometries and boundaries, but are averaged over a representative volume such that the porous medium properties vary continuously in space. These averaging can be orientation dependent, i.e., anisotropy of the porous media properties can be included in continuum-scale models.

On the other hand, there are pore-scale models in which pores and solids are represented explicitly, which currently are also coupled with geochemical solvers to simulate reactive transport at the pore scale (e.g., Molins et al., 2017; Patel et al., 2018a; Seigneur et al., 2017). The codes use different approaches for flow (Navier-Stokes versus a continuum constitutive equations defeind by Darcy’s Law) or transport (molecular diffusion in liquid phase versus effective diffusion in a porous medium). Obviously, this approach cannot be applied to a large scale due to the current computational power limits and the necessity to achieve calculational results within hours, days of perhaps weeks. Computational power will increase by which pore-scale models may be used in the future at disposal cell scale.

4.1.2 Fluid flow

This section describes equations for single-phase flow in porous media and through fractures. The mathematical formulation of a multiphase model is not covered; the mathematical model for single-phase flow of water is given for fully and partially water-saturated porous media.

4.1.2.1 Variably-saturated single-phase flow

When assuming a passive air phase and neglecting hysteresis, the mass conservation equation combined by the Darcy-Buckingham equation results in the Richards equation for variably saturated water flow in porous media:

$\begin{array}{l}\frac{\mathsf{\partial }{\theta }_{\mathrm{w}}}{\mathrm{\partial }t}=\nabla \cdot {\mathbf{q}}_{\mathrm{w}}-Q_{\mathrm{w}}\\ =\nabla \cdot \left[\mathbf{K}\left(\nabla h+{\mathbf{e}}_{\mathrm{z}}\right)\right]-Q_{\mathrm{w}}\end{array}(1)$

where θ_w is the water content (m³ m^-3), t is time (s), q_w is the vector with the volumetric water flux density (m³ kg^-2 s), Q_w is the sink/source term (m³ m^-3 s^-1), K is the hydraulic conductivity (m s^-1) tensor, h is the pressure head (negative for unsaturated conditions) (m), and e_z is a unit vector in the vertical direction. The water content is sometimes expressed as:

${\mathsf{\theta }}_{\mathrm{w}}=\eta S_{\mathrm{w}}(2)$

where η is the porosity (m³ (void) m^-3 (system)) and S_w is the degree of water saturation (m³(water)m^-3 (void)). To solve Equation 1, material properties expressing the relation between the water content and pressure head (or capillary pressure, ψ Pa), for negative values of pressure head), called the moisture retention curve or the (aqueous) saturation function and the relation between the hydraulic conductivity and the pressure head/capillary pressure are required. These relations are mostly defined as closed-form formulations with a number of material-specific parameters. For the saturation curves (S_w(h) or S_w(ψ)), many different functional forms exists; some of them are implemented in reactive transport codes, e.g., the formalism of van Genuchten (1980) or Brooks and Corey (1964). The hydraulic conductivity curve requires typically the saturated hydraulic conductivity K_s (m s^-1) and a functional form of the relative conductivity, i.e., the change of hydraulic conductivity with pressure head. The standard method is to use a pore-size distribution models that calculates the relative hydraulic conductivity from the moisture retention model (e.g., Mualem, 1976; Burdine, 1953, see also van Genuchten et al., 1991).

4.1.2.2 Liquid flow in fully and variably saturated fractured media

Micro and macro cracks or fractures can develop or are present in engineered (e.g., concrete) and geological formations as a result of interactive physical, chemical and mechanical processes. As the existence of fracture networks forms preferential pathways for water flow and/or contaminant/constituent leaching, such networks are of particular concern for the long-term performance and chemical evolution of disposal facilities.

The effect of fracture networks on the release of contaminant fluxes is not univocal and depends on interplay between fracture network characteristics, matrix properties, regional hydraulic conditions and location of encapsulated wastes. Different flow patterns develop for different rates of water infiltration. If the water flux is low relative to the saturated hydraulic conductivity of the fracture, the fracture will not act as a preferential pathway: the fracture will be unsaturated with very low unsaturated hydraulic conductivity (only film or corner flow, Or and Tuller (2000); Tuller and Or (2001)). The unsaturated hydraulic conductivity of the fracture can be lower than the (un)saturated hydraulic conductivity of the matrix and flow might be primarily through the matrix domain (hydraulic conductivity might be very low, and transport is then mainly via diffusion). On the other hand, a water flux high enough to saturate the fractures might result in fractures becoming effective pathways for rapid advective-dominated migration of radionuclides (at least, if saturated hydraulic conductivity of fractures is higher than that of the matrix). The relative importance of fracture flow versus matrix flow in the light of their saturation properties has been studied in Cey et al. (2006), Or et al. (2005) or Perko et al. (2017). Under water-saturated conditions, the condition to be expected in a geological disposal facility in the long-term, flow and transport is mainly in the fractures (when saturated hydraulic conductivity of the fractures is larger, see Cey et al. (2006), Or et al. (2005) or Perko et al. (2017)). However, under unsaturated conditions, the main flow and transport path can be in the matrix domain as well, depending on fracture properties (e.g., roughness), matrix hydraulic properties and pressures.

Several modelling approaches have been proposed to model flow and transport through fractured porous media. The hydrogeological mathematical models for flow and transport through fractured porous media fall into one of three broad classes: (a) equivalent (or single) continuum models and derivatives as dual-porosity and dual-permeability (or multiple) continuum models (e.g., Šimůnek and van Genuchten, 2008), (b) discrete network simulation models either as single fracture or fracture network models (e.g., Sudicky and Mclaren, 1992), and (c) hybrid models (e.g., Oda, 1985). The equivalent continuum models require volume-averaged hydraulic properties that reflect the large-scale average effects of fractures whilst the discrete models need mainly information about the geometric characteristics of fractures. The hybrid models need both sets of information.

4.1.2.2.1 Explicit modelling of saturated single phase flow in fractured systems

As an example, governing equations for the explicit representation of flow in fractures and surrounding rock matrix are given here. The fractures are assumed to be always saturated although in reality this may be unlikely. The saturated hydraulic conductivity of macro fractures with widths of the order of hundreds of µm is typically several orders of magnitude larger than that of a porous matrix. This means that larger fractures will drain out water quicker than the porous matrix, which holds water by suction.

The governing equation for the flow is based on Darcy’s law in both the matrix (Equation 3) and in fractures (Equation 4) (Seetharam et al., 2014). The flow through fractures is modelled using tangential derivatives which define the flow along the interior boundaries representing fractures within a porous matrix. Equation 5 is essentially an averaging of conservation equation across the fracture thickness (see Martin et al. (2005) for derivation).

${\mathsf{\rho }}_{l}S\frac{\mathit{\partial }p}{\mathit{\partial }t}=-\nabla \cdot {\rho }_l\mathbf{u}(3)$

$\mathbf{u}=-\frac{K_s}{{\rho }_{l}g}\nabla p(4)$

${\mathsf{\rho }}_{l}S{d}_f\frac{\mathit{\partial }p}{\mathit{\partial }t}=-{\nabla }_T\cdot {\rho }_l{\mathbf{u}}_{\mathbf{T}}$

${\mathbf{u}}_T=-d_f\frac{K_f}{{\rho }_{l}g}{\nabla }_{T}p(5)$

${\mathsf{K}}_f=\frac{{\rho }_{l}g{d}_f^2}{24\mu }$

where p is the total pressure (Pa) which is the dependent variable, ρ_l is the density of water (kg m^-3), S is the storage coefficient (Pa⁻¹), u is the Darcy’s velocity vector (m s^-1) in the matrix, K_s is the saturated hydraulic conductivity of the concrete matrix (m s^-1), g is gravitational acceleration (m s^-2), d_f is the fracture width (m), K_f (m s^-1) is the hydraulic conductivity of a single fracture for planar fractures (Walton and Seitz, 1991), µ is the dynamic viscosity of water (kgm^-1s^-1), u_T is the tangential velocity vector and ∇_T denotes the gradient operator restricted to the fracture’s tangential plane. The dependent variable, p, is same in both the matrix and fractures. The storage coefficient S is put to a very low number representing water compressibility. A recent overview on treatment of fractures is given in Ahusborde et al. (2021).

4.1.3 Heat transfer

Taking into account the main heat transport processes (conduction in the solid matrix, transport by the fluid phase, conduction in the fluid phase) and assuming the same temperature in the aqueous, solid and gaseous phase, the heat transport equation can be written as:

$\frac{\mathsf{\partial }{c}_{\mathrm{p}}{\rho }_{\mathrm{p}}T}{\partial t}=\nabla \cdot \left(\mathbf{\lambda }\nabla T-c_{\mathrm{w}}{\rho }_{\mathrm{w}}\mathbf{q}T\right)(6)$

where T is temperature [K], c_p is the specific heat capacity of the porous media [J kg^-1 K⁻¹], ρ_p is the mass per unit volume [kg m^-3], c_w is the specific heat capacity of water [J kg^-1 K⁻¹], ρ_w is the mass of water per unit volume [kg m^-3], λ is the thermal conductivity tensor [W m^-1 K⁻¹] and θ is the water content. Please note that this heat transfer equation can only be solved by taking into account fluid flow. Excluding the fluid flow and solving this equation solely with properties for saturated and non-saturated porous media provides a range in temperatures of materials as a function of time. However, only estimates of the correct temperature will be obtained; for water saturated media, the temperature will be underestimated whereas in unsaturated media, it will be overestimated. The range in temperature values obtained by this approximated can be acceptably small enough considering other uncertainties. This is a more simple calculation and less time consuming than including fluid flow. In unsaturated porous media, in addition to transport of heat by conduction, heat can be transported in the gas phase via vapour transport and may become an important component of heat transport in unsaturated low permeable media (e.g., Collin et al. (2002)). Note that this transport process is not included in Equation 6.

4.1.4 Solute transport

In most reactive transport codes, transport is defined in terms of total concentration instead of transport of each individual aqueous species. The number of transport equations then equals the number of primary species or components. This number is equal to the total number of aqueous species, N_a, minus the number of linearly independent reaction equations between species in chemical equilibrium (see Section 4.1.5). As such, the total number of aqueous species, N_a, is divided between N_p primary species and N_a – N_p = N_x secondary species. The total concentration C_w,i of the ith primary species is then defined as:

${\mathsf{C}}_{\mathrm{w}i}=c_{\mathrm{w}i}+{\displaystyle \sum _{j=1}^{N_{\mathrm{x}}}}{\nu }_{ji}{c}_{\mathrm{w}j}$

where v_ji is the stoichiometric coefficient (i.e., the number of moles of the ith primary species in the jth secondary species).

The general solute transport equation for transport of mobile components for a single phase system (liquid phase) can be written as:

$\frac{\mathsf{\partial }{\theta }_{\mathrm{w}}{C}_{\mathrm{w},i}}{\mathrm{\partial }t}=L\left(C_{\mathrm{w},i}\right)+R_i(7)$

where L () is the linear transport operator, and R (mol m^-3 s^-1) is a sink/source term for geochemical reactions (Section 4.1.5). These reactions can change the microstructure e.g., a local change in porosity.

The transport operator for the aqueous phase consists of a hydrodynamic dispersion and an advective component:

$L\left(\right)=\nabla \cdot \left({\theta }_{\mathrm{w}}{\mathbf{D}}_{\text{hd}}\nabla \cdot C_{\mathrm{w}i}\right)-\nabla \cdot \left(\mathbf{q}{C}_{\mathrm{w}i}\right)(8)$

where D_hd is the hydrodynamic dispersion tensor (m² s^-1), and the other symbols as defined before.

The hydrodynamic dispersion includes molecular diffusion in the aqueous phase, corrected for the tortuosity of the porous media and mechanical dispersion due to small scale variations in fluid velocities and travel paths.

Tortuosity multiplied with the molecular diffusion coefficient of the aqueous phase is often indicated by the term pore diffusion coefficient D_p or diffusion coefficients in porous media. This parameter is crucial for the assessment of chemical evolution of disposal cells in a geological disposal system as diffusion is often the most important transport process. Water flow and thus advective transport are usually of minor importance for geological disposal facilities in clay systems due to the absence of strong hydraulic gradients and the low permeable host-rock and engineered barriers; advective flow could be relevant for granite host rocks when fractures are present.

This simplified transport operator assumes that individual diffusion coefficients of charged (ions) and uncharged complexes in water can be replaced by one average molecular diffusion coefficient for all primary species in order to ensure charge neutral transport. Instead of using the phenomenological Fick’s law, the Nernst-Planck equations can be used that consider specific diffusion coefficients for each ion/complex and achieve charge neutrality of transport by calculation of cross-diffusion coefficients for charged species (Samson and Marchand, 2007; Liu et al., 2011; Steefel et al., 2015a). In addition, the gradient of the chemical potential is accounted for instead of the gradient in concentration (Steefel et al., 2015a). The diffusive term in Equation (8) contains, beside the Fickian diffusion term, a term related to the gradient in electrostatic potential (related to Nernst-Planck) and a term related to the gradient in activity coefficients (Appelo, 2017; Samson and Marchand, 2007). A recent example of using the Nernst-Planck equation (only electrochemical effects, no chemical activity gradient) for geochemical changes over a cement-clay interface was presented by Idiart et al. (2020). The effect of electrochemical effects was clearly visible for non-reactive ions such as the mobility of Cl⁻. When the ion concentrations are controlled by mineral phases, the effect of including electrochemical effects is limited.

4.1.4.1 Microstructure and diffusivity

Pore diffusion coefficients can be obtained by experimental in- or through diffusion experiments but these measurements are only valid for the microstructure of the porous media during the experiment. There exist different models to predict the tortuosity from continuum properties of the porous media. For saturated media, variants of Archie’s law (Archie, 1942) using an exponential relation on porosity are available in many reactive transport models. Models proposed by Milington and Quirk (Millington and Quirk, 1961) or Moldrup (Moldrup et al., 2000; Moldrup et al., 1997) account for water saturation degree of the porous media. It is important to note that these models or their parameters are mainly empirical in nature and using them predictive outside their calibration or measurement region (other materials or other range of porosity) is highly uncertain.

For cement-based materials, there exist alternative models adapted to the specificities of the material, see e.g., Patel et al. (2016) for an overview of models for diffusivity in saturated Portlandite cement and concrete. Some models are fitted on numerical (pore-scale models) such as Garboczi and Bentz (1992) or based on effective media theory, accounting for different characteristics as different types of porosity, phases and aggregates [e.g., Bejaoui and Bary (2007), Oh and Jang (2004), Stora et al. (2009)]. In general, such models are not always implemented in the numerical codes.

Geochemical reactions can cause a local change in the microstructure; specifically solid phase dissolution/precipitation/transformation reactions (see Sections 4.1.5.2 and 4.1.5.6.1) can locally change e.g., the pore size distribution and porosity and thus solute migration can locally decrease or increase. The influence on solute diffusion is via the total porosity (area available for diffusion) and the tortuosity coefficient (see Section 5.1.1.2).

4.1.4.2 Mechanical dispersion

Mechanical dispersion is calculated from the average velocity in the principal direction multiplied by the longitudinal or transversal dispersivity, α_L or α_T [L] respectively (Bear, 1972). The components of the dispersion tensor, D_ij, are given by

$D_{ij}={\alpha }_{\mathrm{T}}v{\delta }_{\mathrm{i}\mathrm{j}}+\left({\alpha }_{\mathrm{L}}-{\alpha }_{\mathrm{T}}\right)\frac{v_j{v}_i}{v}+{\tau }_{\mathrm{w}}{D}_{\mathrm{w}}{\delta }_{\mathrm{i}\mathrm{j}}$

where v, v_i and v_j are the average velocity, and the velocity in the i and j direction, respectively, τ_w is the aqueous tortuosity factor which depends on microstructure but also on water content, D_w is the molecular diffusion coefficient in the aqueous phase, and δ_ij is the Kronecker delta.

4.1.5 Geochemical processes

The geochemical reaction term in Equation 7, R_i, accounts for heterogeneous equilibrium or kinetic geochemical reactions or homogeneous kinetic reactions. Homogeneous (aqueous) equilibrium reactions do not change the concentration of the primary species and therefore, there is no need to include them in a sink/source term in transport Equation 7 for master species. Typical heterogeneous reactions taken into account in reactive transport models are (Steefel et al., 2015b) ion exchange, surface complexation, aqueous-gas exchange, mineral dynamics, and solid-solutions; most of them treated both in equilibrium or kinetically-controlled. Typical homogeneous kinetic reactions are radioactive decay and (microbiologically-mediated) kinetic degradation of, e.g., organics, or oxidation-reduction reactions.

In what follows, we give an overview of the most important geochemical reactions that are typically being accounted for in reactive transport models. We choose here to express equilibrium in terms of the law of mass-action equations.

4.1.5.1 Aqueous reactions

The activity of aqueous species is crucial for many other geochemical processes. Several theories and models are published to calculate activity correction coefficients of aqueous species such as based on Debye-Hückel theory, specific ion interaction (SIT) model or Pitzer equations. Most basic handbooks on aquatic chemistry and geochemistry contain information about the different low and high ionic strength activity correction models for aqueous species (Anderson and Crerar, 1993; Appelo and Postma, 2005). Thermodynamic equilibrium between the aqueous and the solid phase or kinetic reactions are for example, expressed in terms of activities rather than component concentration or species concentrations. Aqueous equilibrium reactions are written as:

${\mathit{A}}_{\mathit{j}}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{{\mathit{N}}_{\mathit{p}}}}{\mathit{\nu }}_{\mathit{j}\mathit{i}}{\mathit{A}}_{\mathit{i}}$

where A_i and A_j are the chemical formulae of the primary and secondary species, respectively. When thermodynamic equilibrium is obtained (i.e., at the minimum of the Gibbs free energy of the system), the concentrations of the secondary species are obtained via the law of mass-action equation as:

$c_j=\frac{{\displaystyle \prod _{i=1}^{N_{\mathrm{p}}}}{\left({\gamma }_i{c}_i\right)}^{{\nu }_{ji}}}{K_j{\gamma }_j}$

where K_j is the equilibrium constant for the reaction and γ_i and γ_j are the activity correction coefficients for the primary and secondary species, respectively². Activity correction coefficients relate the concentration of the species to the activities which are used in the definition of the equilibrium constant (activity a_i = γ_ic_i).

4.1.5.2 Mineral precipitation and dissolution

The composition and amount of the solid phase assemblage and its evolution are important variables for flow and transport parameters (as the amount and distribution of solid phases determine the microstructure) and for the sorption of aqueous species (capacity for sorption is defined by the type of minerals and their properties).

The general equation for a mineral dissolution and precipitation reaction is written as:

$M_l={\displaystyle \sum _{k=1}^{N_l}}{\nu }_{kl}{A}_k$

where M represents the chemical formula of the mineral and N_l is the number of aqueous species in the reaction equation. The equilibrium constant is again expressed as the ratio of the activity product of the reactants (right hand-side) and the product (the mineral at the left hand side). The activity of a pure phase is equal to 1, thus at equilibrium, following law of mass-action equation is satisfied:

${\mathsf{K}}_l={\displaystyle \prod _{k=1}^{N_{\mathrm{l}}}}{\left({\gamma }_k{c}_k\right)}^{{\nu }_{kl}}$

A solid-solution is a solid phase consisting of variable mixing of pure end-member minerals. The activity of an end-member in a solid solution is different from 1 and is related to the mole fraction in the solid-solution:

${\mathsf{a}}_i={\gamma }_i{X}_i/X_i^0$

where a_i is the activity of the end member in solid-solution, X_i is the mole fraction and X_i⁰ is the mole fraction at standard state (assumed to be 1). In an ideal solid solution, the activity correction factor γ_i equals 1 and thus the activity equals the mole fraction of the end member. For a non-ideal solution, the activity correction factor is related to the excess free-energy of mixing due to non-ideality. The non-ideality is described with semi-empirical models for binary, ternary, symmetric and asymmetric systems. One of the most often used models to calculate the activity correction factors for a binary non-ideal solid solution is based on Guggenheim series expansion (Glynn, 1991) but other models are also included in reactive transport models (e.g., via GEM3K (Kulik et al., 2013) and the TSolMod library (Wagner et al., 2012)). One particularity of non-ideal solid solutions is that the unmixing of phases is sometimes more stable than the one-phase solid solution leading to an immiscibility or a phase separation.

Mineral precipitation and dissolution reactions can alter the microstructure and local porosity and have an influence on material properties including permeability and solute transport parameters (see Section 5.1.1) or even heat transport parameters.

Beside the equilibrium assumption discussed in this section, dissolution or precipitation rates are often slow compared to envisaged time scales (e.g., during transport calculations), meaning that time is required to reach equilibrium. In that case, a kinetic formulation is required which is discussed in Section 4.1.5.6.1 The need to implement kinetic rather than equilibrium reactions depends on many factors including the time and spatial scale (experimental studies, ∼months to year) at the interface scale may need rather a kinetic than equilibrium implementation), minerals involved (fast kinetics such as calcite compared to slow kinetics for e.g., clay minerals), and the overall goals/endpoints of a particular assessment. The dimensionless Damköhler number expresses the ratio of the transport (advective-dispersive) time over the reaction time; if this ratio is large, local equilibrium can be assumed (Sanchez-Vila et al., 2007). Note that small-scale heterogeneity can also contribute to a need to incorporate (heterogeneous) kinetics, specifically when mixing in the complete pore space is long compared to reaction time (diffusive time over reaction rate (Dentz et al., 2011a; Dentz et al., 2011b)).

4.1.5.3 Ion exchange

The ion exchange process is a charge-neutral exchange of ions between the aqueous phase and exchange sites at the surface of solid phases. The site capacity of a surface is thus always occupied with species of the opposite charge such that the surface is charge neutral. Although this process also includes the exchange of anions at a positively charged surface, the cation exchange process (exchange of cations at a negatively charged surface of e.g., a clay mineral) is more common. In general form, the exchange reaction can be written as:

${\mathit{\nu }}_{{\mathit{A}}_{\mathit{j}}}{\mathit{A}}_{\mathit{k}}{\mathit{X}}_{{\mathit{\nu }}_{{\mathit{A}}_{\mathit{k}}}}+{\mathit{\nu }}_{{\mathit{A}}_{\mathit{k}}}{\mathit{A}}_{\mathit{j}}\rightleftharpoons {\mathit{\nu }}_{{\mathit{A}}_{\mathit{k}}}{\mathit{A}}_{\mathit{j}}{\mathit{X}}_{{\mathit{\nu }}_{{\mathit{A}}_{\mathit{j}}}}+{\mathit{\nu }}_{{\mathit{A}}_{\mathit{j}}}{\mathit{A}}_{\mathit{k}}$

where X denotes the ion exchanger (with unit charge), A_k and A_j denote aqueous species with opposite charge than that of the exchanger, and v_Aj and v_Ak are the stoichiometry coefficients. The equilibrium constant is written as:

$K=\frac{{\left({\mathrm{A}}_j{\mathrm{X}}_{{\nu }_{{\mathrm{A}}_j}}\right)}^{{\nu }_{{\mathrm{A}}_k}}{\left({\mathrm{A}}_k\right)}^{{\nu }_{{\mathrm{A}}_j}}}{{\left({\mathrm{A}}_k{\mathrm{X}}_{{\nu }_{{\mathrm{A}}_k}}\right)}^{{\nu }_{{\mathrm{A}}_j}}{\left({\mathrm{A}}_j\right)}^{{\nu }_{{\mathrm{A}}_k}}}$

where () denotes activity. There are different conventions for calculating the activity correction coefficients for the exchange coefficients called Gaines-Thomas, Gapon or Vanselow conventions (see (Appelo and Postma, 2005; Sposito, 1981)). The Rothmund-Kornfeld model accounts for changing selectivity with site occupancy (Bloom and Mansell, 2001; Bond, 1995). Alternatively, different exchange sites can be defined, each with different selectivity coefficients. At low concentrations, the high selective sites are first filled up; less selective sites are filled up at higher concentrations. The three-site exchange model for Cs sorption on illite of Bradbury and Baeyens (2000) is often applied to describe Cs sorption in clay host formations (e.g., Maes et al. (2008)).

Exchange reactions can be treated kinetically as well, although it is generally assumed that these reactions are fast enough to be treated as equilibrium reactions. However, in a continuum approach, for heterogeneous media, time for mixing of the solutes in the complete pore space might be too long.

4.1.5.4 Surface complexation

Surface complexation is an important process as it describes sorption of major and trace elements as a function of the prevailing geochemical conditions near the solid phase surface. A major difference with exchange processes is that protons, cations and anions are released without compensation by other ions in equivalent properties (as opposed to exchange processes, Appelo and Postma (2005)). The surfaces can be positively or negatively charged (variable charged solid) depending on the pH of the pore solution. Such variable charged solids exist for both natural and engineered materials. Variable charged solids for natural subsurface systems are clays, oxides and organic matter. Also most materials for the technical barriers in subsurface systems contains such variable charged solids such as cement hydration phases (Missana et al., 2019; Olmeda et al., 2019).

In surface reactions, aqueous species bind to functional groups on the surface; as an example an equation of a metal sorbing on a surface hydroxyl site (≡OH):

$\equiv XOH+M^z\leftrightarrow \equiv XO{M}^{z-1}+H^{+}$

Similar to aqueous complexes, the degree of surface complexation depends on the chemical affinity between the aqueous species and the surface functional group and on the electrostatic effects near the solid surface due to the surface charges. These two factors are represented in surface complexation models via following mass action analogue:

$\begin{array}{l}{\mathsf{K}}_a=\frac{\left(\equiv XO{M}^{z-1}\right)\left(H^{+}\right)}{\left(\equiv XOH\right)\left(M^z\right)}{e}^{-\frac{zF{\psi }_0}{RT}}\\ =K_{\mathrm{int}}{K}_{coel}\end{array}$

where K_a is the apparent equilibrium constant, K_int is the intrinsic equilibrium constant, and K_coel represents the electrostatic component. Note that the adsorption reaction can also be written in terms of Gibbs free energy. The key point is to relate the charge distribution near the solid surface to the potential in order to calculate equilibrium. This gives rise to surface complexation models that differ in the way the division is made between charged surface and bulk solutions and the charge/potential relations that are used. The four most common models are the constant-capacitance model (CCM), the diffuse double layer model (DDL), the triple layer model (TLM) and the CD-MUSIC model (Goldberg et al., 2007).

In one layer models, all adsorbed ions are located on a single plane and the surface charge density at that single plane is used to calculate the surface potential by assuming a constant capacitance (CCM) or a variable capacitance calculated with the potential-charge relationship given by the Gouy-Chapman theory that depends on the ionic strength. It represents the diffuse layer of ions balancing the charge of the surface. Other models account for sorption directly to the surface (inner complexes, typically for H⁺ and OH⁻) and one or two additional planes (outer complexes). The Basic Stern Model (BSM) has one additional plane (inner plane) with a constant capacitance between the surface and inner planes and neglect any potential change between the inner plane and the outer plane where the diffuse layer starts¹. The TLM assumes a second capacity between the inner and outer layer. The CD-MUSIC model (Hiemstra and Van Riemsdijk, 2006; Hiemstra and Van Riemsdijk, 1996) distributes the charge of an adsorbed ion between different planes.

Most reactive transport models include one or more of these models to calculate K_coel. However, note that surface complexation models are also often implemented neglecting the electrostatic forces (i.e., K_coel = 1) or diffuse layer calculations.

Surface complexation reactions can be treated kinetically as well, although it is generally assumed that these reactions are fast enough to be treated as equilibrium reactions. However, in a continuum approach, for heterogeneous media, time for mixing of the solutes in the complete pore space might be too long. One possible way is for example, by a multi-rate multi-transport type of model as illustrated in (Greskowiak et al., 2015) for U sorption.

4.1.5.5 Gas reactions

When a gaseous phase is present, exchange between a component G_i in the gaseous phase and a component A_i in the aqueous phase:

${\mathit{G}}_{\mathit{i}}\leftrightarrow {\mathit{A}}_{\mathit{i}}$

is in most cases treated as equilibrium condition. Equilibrium is obtained when the ratio of the activities of the aqueous species in the reaction equation over the ratio of the fugacities of the gaseous species equals 1. Under the assumption of a mixture of ideal gases, the fugacity coefficient is 1 and the fugacity of a gas equals the partial pressure of the gas. For total gas pressures below 10 atm, the fugacity coefficient will be close to 1 (Appelo et al., 2014). For larger total gas pressures, fugacity correction factors can be calculated with the Peng and Robinson equation of state (Peng and Robinson, 1976).

Gaseous components are typically generated or consumed by kinetic reactions such as corrosion or degradation of organics acting for example, as electron acceptors (see Sections 4.1.5.6.2 and 4.1.5.6.3).

4.1.5.6 Kinetic processes

4.1.5.6.1 Kinetic dissolution/precipitation of solid phases (minerals)

Dissolution of minerals in porous media is often treated as a kinetic process. The dissolution kinetics are controlled by the reactions taking place at the surface of the minerals–surface-controlled reactions–and diffusion processes through different layers covering the reactive minerals–transport-controlled reactions (Mayer et al., 2002). Micro-scale transport processes may occur across a stagnant water layer or through surface coatings or alteration rims (Murphy et al., 1989). The reader is referred to several general textbooks (Brantley et al., 2008; Lasaga, 1998; Rimstidt, 2013) for more details on geochemical kinetics in general, and mineral kinetics specifically, and to Cama and Ganor (2015) for details on clay minerals. A general form of a surface-controlled kinetic reaction accounting for effects of reactive surface areas, temperature, different reaction mechanisms and dependence on solution saturation state is (Lasaga, 1998):

$r=S\left({\displaystyle \sum _j}{A}_j{e}^{-E_{\mathrm{a},j}/RT}{\displaystyle \prod _i}{a}_i^{n_{i,j}}f\left(\mathrm{\Omega }\right)\right)(9)$

where r is the dissolution/precipitation rate [mol s^-1 m^-3], and the factors at the right hand side are:

• S–the reactive surface area [m² m^-3] which can be treated as a constant term, or a changing value (for spherical particles with uniform dissolution, the value changes according to (m/m₀)^(2/3)

• Temperature dependence described by an Arrhenius equation where parameter A_j is the Arrhenius pre-exponential factor [mol L-² T^-1], E_a,j is the apparent activation energy [J mol^-1], R is the universal gas constant [J mol^-1 K⁻¹] and T is temperature [K]

• One or more terms representing different mechanisms (e.g., different catalyst for dissolution) where a is the activity of a given species, and n_i,j is an empirical constant.

• A factor that represents the effect of the saturation state of the solution via saturation ratio Ω.

The reaction rate for many minerals depends on the pH. Palandri and Kharaka (2004), for example, defined 3 terms in Equation 9 related to H⁺, H₂O and OH⁻ promoting reactions for which the coefficients n_i,j are obtained by a piecewise linear regression on measured reaction rates.

One of the most commonly used expressions of f(Ω) is (Brantley et al., 2008; Oelkers et al., 2009):

$f\left(\mathrm{\Omega }\right)={\left(1-{\mathrm{\Omega }}^p\right)}^q(10)$

where p and q are empirical constants, often assumed to be equal to 1. When an aqueous phase is in equilibrium with a mineral, Equation 10 equals zero and the reaction rate is zero. The sign of Equation 10 is positive or negative in case of, respectively, over- or undersaturation enabling to simulate precipitation or dissolution. Note that Equation 10 limits the dissolution rate to a constant value when far from equilibrium, whereas the precipitation rate will increase with deviation from equilibrium.

4.1.5.6.2 Degradation of organics

The fate of organics present in the waste can be described by kinetic rate equations including Monod terms for electron donor and acceptor concentrations (Small and Abrahamsen-Mills, 2018). A general from of such equation is:

$R=Q_{\max }B\frac{\left[E_{\mathrm{D}}\right]}{K_{\mathrm{D}}+\left[E_{\mathrm{D}}\right]}\frac{\left[E_{\mathrm{A}}\right]}{K_{\mathrm{A}}+\left[E_{\mathrm{A}}\right]}{I}_{\mathrm{B}}\prod \left(I_X\right)f_{\mathrm{T}}$

where R is the degradation rate [M T^-1 L^-3], Q_max is the maximum rate [M M_B^-1T^-1], B is the biomass [M_B L^-3], [E_D] and [E_A] are the concentrations of the electron donor and acceptor [M L^-3], K_D and K_A are the half-saturation constants for the electron donor and acceptor [M L^-3], the factor I_B accounts for rate reduction when the microbial biomass is too large due to e.g., pore restrictions (see e.g., (Brovelli et al., 2009; Pham, 2018; Ben Moshe et al., 2021) for different functional forms). I_X are inhibition factors, typically in the form of (K_X/(K_X+[X]) with K_X the half saturation constant) which can control a redox sequence to suppress reactions when higher energy-yielding terminal electron acceptors are still present (e.g., (De Blanc et al., 1996; Bhanja et al., 2019; Small and Abrahamsen-Mills, 2018)), but may also include terms related to toxicity or pH (e.g., Maia et al. (2016) or Small and Abrahamsen-Mills (2018)). Control of the rate by the pore water composition can be considered as well by including a thermodynamic potential factor into the equation taking into account the Gibbs free energy of the electron transfer reaction and energy required for ATP synthesis (Jin and Bethke, 2007; Jin and Bethke, 2005; Jin and Bethke, 2003). The last factor f_T accounts for temperature effects and is typically described by Arrhenius’ law. Note also that many variants exist for this particular equation, ranging from first-order definition to competitive effects (De Blanc et al., 1996). Or et al. (2007) reviews factors that are related to these reactions in unsaturated porous media. Mathematically, a yield factor links the growth of biomass to the rate of degradation.

4.1.5.6.3 Dissolution of non-porous materials (steel)

Metallic iron in low carbon or weakly alloyed steels is never under equilibrium in contact with aqueous solutions, both under oxic and anoxic redox conditions. It will be subjected to corrosion such as generalized or pitting corrosion processes. This disequilibrium also requires a kinetic treatment of these type of reactions. The challenge is the representation of a non-porous material in a reactive transport model at the continuum scale.

Corrosion of metallic alloys in oxic and anoxic conditions under repository conditions are often simplified to the reaction equations given in section 3.2.1 (Equations 1 and 2) in Neeft et al. (2024). Often, steel corrosion in reactive transport models is described with a zero-order constant rate model, although some studies also investigated rates depending on solution composition (Wilson et al., 2015) or diffusion through the corrosion layer (Peña et al., 2008). The corrosion products are then simulated by either assuming equilibrium or kinetic precipitation reactions. In addition, in reactive transport models, it is conceptualized as a porous medium to enable transfer from Fe from the solid to the aqueous phase and diffusion into the neighbouring cells. Also the movement of the steel interface is a complex and challenging aspect not often taken into account in numerical studies on steel-bentonite, steel-clay, steel-cement and steel-glass interfaces. A step forward can be expected when electrochemical corrosion models (Bataillon et al., 2010; Macdonald et al., 2011) are introduced into reactive transport models (see also Ahusborde et al., 2021).

4.2 Tools and databases

4.2.1 Codes

In the last 3 decades, several codes have been developed that can handle the processes discussed in Section 4.1 in an integrated way. Such codes are typically called coupled reactive transport codes. An overview of some available codes was given in Steefel et al. (2015) and a more recent update of codes with additional features and new references is given in the Supplementary Material.

4.2.2 Databases

The engineered materials are not in equilibrium with the host rock. The chemical evolution for the disposal cell is slowly progressing towards an equilibrium between the engineered materials and host rock. The expected geochemical reactions can be derived by calculating the stability of the evolved minerals as a function of pH, redox potential, concentration of dissolved solutes, temperature and pressure. There are several thermodynamic databases that have thermodynamic data to calculate the stabilities of the minerals. Geochemical models use these thermodynamic data to calculate the concentration of solutes in equilibrium with the minerals. Deviation of these concentration of solids will result in either a dissolution or precipitation of a mineral. Thermodynamic databases are therefore the cornerstone for reactive transport models and the establishment of internally consistent databases contributed significantly to geochemistry and is of uttermost importance for incorporation into reactive transport modelling (Oelkers et al., 2009). In many of the above mentioned codes, some available databases are derived from the SUPCRT92 thermodynamic database (Johnson et al., 1992) or one of the later versions of it (Zimmer et al., 2016). SUPCRT92 or later versions are also available in codes based on minimization of Gibbs free energy as GEMS² (Kulik et al., 2013; Wagner et al., 2012) and Reaktoro (Leal et al., 2017). Zhang et al. (2020) provides a software to convert SUPCRTBL (Zimmer et al., 2016) to PHREEQC-readable databases in the requested P-T range³.

The aim here is not to give an overview of all available database, but just to list a few databases that are frequently used in the framework of geological disposal:

• Thermoddem⁴: The database is developed by BRGM (Blanc et al., 2012) and contains reactions and thermodynamic data for a temperature range up to 300 °C. Phases for cement materials, clay minerals and zeolites are included. The database is also extended with information on surface complexation and cation exchange reactions. The database is available in the formats for PHREEQC, Crunchflow, ToughReact⁵ (Xu et al., 2011; Xu et al., 2006), Chess (Van der Lee, 1998), and The Geochemist’s Workbench⁶.

• ThermoChimie⁷: The database was initiated by Andra in 1995, but also RWM and Ondraf/Niras joined the “ThermoChimie consortium”. The ThermoChimie database is specifically developed for conditions relevant within radioactive waste repositories, i.e., applied over a pH range between 6 and 14, temperatures below 80°C and Eh in the range of −0.5 to +0.5 V (Giffaut et al., 2014). It includes information on host-rock mineral phases, bentonites, cements and their evolving secondary phases (Blanc et al., 2015), and on radionuclides (Grive et al., 2015). The current version (v12a)⁸ is available for several geochemical codes including PHREEQC, Crunchflow, ToughReact, Chess and The Geochemist’s Workbench.

• PSI/Nagra Chemical Thermodynamic Data Base⁹: This database is developed in the framework of ongoing safety assessments for planned LLW, ILW and HLW repositories in Switzerland (Hummel et al., 2002; Thoenen et al., 2014). The database is available in PHREEQC and GEMS format. The latest version of the PSI/Nagra chemical thermodynamic database 2020 includes an extended list of rock-forming minerals, specifically clays and zeolites, imported from Thermoddem TDB.

• CEMDATA18.1: This database is specifically for hydrated solid phases in Portland cement systems (Lothenbach et al., 2019). It contains thermodynamic data for C-S-H, AFm and AFt phases, hydrogarnet, hydrotalcite, zeolites, and M-S-H in a temperature range between 0°C and 100 °C. Several solid-solution models are implemented to represent these phases. The database is available in GEMS, PHREEQC and Geochemist’s Workbench format. At 25 °C, it is fully consistent with the PSI/Nagra Chemical Thermodynamic Data Base. These databases are recently also supplemented by new databases for zeolites¹⁰ (Ma and Lothenbach, 2021; Ma and Lothenbach, 2020b; Ma and Lothenbach, 2020a).

• THEREDA¹¹ (Thermodynamic Reference Database): This is a joint effort to build an internally consistent reference database that could be used in geochemical and reactive transport codes for processes in the near and far field of different host rock types envisaged as potential sites for final repositories in Germany, including high ionic strength conditions (Moog et al., 2015). It is available in PHREEQC, Geochemist’s Workbench and ToughReact format.

• NEA TDB (Nuclear Energy Agency Thermodynamic DataBase): This is a joint effort between different countries (nowadays 12) in which thermodynamic data with a sufficient quality are included in a database. The elements and compounds that need to be investigated are determined by the different countries. The selection of data is performed by a group of experts with a high track record in relevant scientific publications. The data have been put in a Phreeqc-formatted file (Martinez et al., 2019). The database is not complete for a safety assessment of geological disposal of radioactive waste, but databases such as ThermoChimie and PSI/Nagra Chemical Thermodynamic Data Base have included these NEA TDB data due to the high quality assurance of the NEA TDB data.

Some focussed studies compiled thermodynamic information for some specific applications. De Windt et al. (2015) compiled data for complexation of short-chained organics in a cementitious system (simplified CEM I).

For chemical kinetics, we mention here two relevant compilations:

• A compilation by Marty et al. (2015b) for minerals relevant to clay rich rocks and cements. Parameters were provided for both the linear regression model and the regression curve model. The kinetic parameters are consistent with the ThermoChimie database and are available in three different formats (for PHREEQC, CrunchFlow and ToughReact).

• A compilation for more than 100 minerals provided in PHREEQC format¹² by Zhang et al. (2019) based on the work of Palandri and Kharaka (2004), mostly based on the kinetic rate (Equation 9).

For kinetics of dissolution of the C-S-H phase in cement, the study of Trapote-Barreira et al. (2016) provides information on rate parameters as function of the Ca/Si ratio of the C-S-H phase.

4.3 Modelling the geochemical evolution of materials

In this section, we discuss shortly some of the approaches for geochemical modelling of relevant materials in radioactive waste disposal context.

4.3.1 Vitrified glass

Dissolution of the glass matrix is modelled with relatively simple models using an apparent Si equilibrium concentration together with a simple diffusion-based model (Liu et al., 2019; Liu et al., 2015; Mann et al., 2019). From a numerical point of view, such a diffusion-based dissolution model only needs one first order ordinary differential equation which can be solved, e.g., with Runge-Kutta methods implemented as kinetic reaction in PHREEQC. Thus this model can be easily combined into reactive transport models based on PHREEQC coupling. On the other hand, the GRAAL model (Frugier et al., 2008) includes more dissolution mechanisms especially for early dissolution stages. This model assumes that glass dissolution is controlled by the affinity of a passivating reactive interface (PRI). This model has been successfully integrated into the reactive transport code HYTEC (Frugier et al., 2018) and potentially can be integrated into other reactive transport codes as well (e.g., PHREEQC (Debure et al., 2018)). The study of Repina et al. (2020) includes fractures in the glass into HYTEC and the GRAAL dissolution model.

4.3.2 Cement-based materials

During the last decade, a solid basis for modelling cementitious system in the frame of radioactive waste disposal became available, specifically because of the development of internally consistent and complete databases (Lothenbach and Zajac, 2019). Originally, databases were for ordinary Portland cement systems, but advancements have been made to include phases relevant for other systems including M-S-H (Roosz et al., 2018), blended cements, C-(N)-A-S-H (Myers et al., 2013; Roosz et al., 2018), or high Na, Cl or nitrate concentrations (Balonis et al., 2011; Balonis et al., 2010; De Weerdt et al., 2019). More recently, a sub-lattice C-S-H model was proposed that also includes the uptake of alkalis (Miron et al., 2022; Kulik et al., 2022). Thermodynamic models are used to define the initial properties (phases, cementitious pore water composition, porosity) of the hardened cement paste based on clinker oxide composition, supplementary cementitious materials, water cement ratio etc. Lothenbach and Zajac (2019) and references therein shows ample examples. As an alternative for calculating the equilibrium assemblage after full hydration, the kinetic hydration processes itself can be modelled as well. This is mainly based on empirical rate equations (e.g., Lothenbach and Winnefeld, 2006); some recent tools allow for user-friendly environments to calculate these initial conditions or the hydration process, e.g., the CemGEMS web app¹³ (Kulik et al., 2021) or HYDCEM (Holmes et al., 2020). Please note that thermodynamic equilibrium may not have been achieved as experimental results of fabricated cement pastes have shown. Especially the pH of cementitious pore water of fabricated concrete - made with so-called low pH formulations made with blended cements - can be higher than modelled.

Chemical evolution of the hydrated cementitious materials due to interaction with the environment is often assessed with reaction path type of models in which the evolution of the cement phases and pore water composition is expressed as a function of reaction progress such as amount of reacted CO₂ (mimicking carbonation), amount of water (leaching), or specific reactants (NaCl, sulphate) (Elakneswaran et al., 2018; Han et al., 2021; Jacques et al., 2010; Ke et al., 2020; von Greve-Dierfeld et al., 2020). Although transport processes are neglected in a reaction path model, it provides insights into some of the complex alterations that can occur during chemical ageing and alteration of cementitious materials. Evaluating the stability of cementitious phases with changing temperatures is assessed with a reaction path model where the path variable is temperature (Lothenbach et al., 2008).

Combination of these modelling approaches with a coupled reactive transport model is straightforward and has been used in many studies, either by considering the cementitious material only with some fixed boundary conditions, either interacting with its surrounding including materials relevant for waste disposal (see section 4.3.4 and also Neeft et al. (2024)). Again, kinetic hydration processes can be combined with thermodynamic equilibrium for hydrated phases, as in Li et al. (2021).

4.3.3 Clay systems

Porewater chemistry is often calculated based on equilibrium with the primary clay minerals, protonation and deprotonation at clay edges (e.g., Bradbury and Baeyens, 2003) and cation exchange processes, the latter may strongly be coupled to the pore water chemistry as illustrated for Boom Clay (Frederickx et al., 2018). Pore water chemistry studies have been done for natural clay systems (see Tournassat et al. (2015) for a general overview and for specific clay-rocks COx (Gaucher et al., 2009), Boom Clay (Wang et al., 2023; De Craen et al., 2004), Opalinus Clay (Pearson et al., 2011), Tournemire (Tremosa et al., 2012)) and bentonite (e.g., FEBEX (Fernández et al., 2011)). Thermodynamic data is available in some of the databases mentioned in Section 4.2. Additional information on thermodynamic and kinetic data is given in Jenni et al. (2019). Recently, Blanc et al. (2021) presented a tool to estimate thermodynamic properties of clay minerals, including interstratified illite/smectite minerals and illustrated it in a reactive transport model example.

Modelling evolution of clay systems is mainly based on kinetic dissolution and precipitation of the primary clay minerals, their alterations and secondary phase formation using an equation similar to Equation 9 for surface controlled kinetics, or alternative forms accounting for diffusion-controlled kinetics [including the notion of a shrinking core model, see Mayer et al. (2002); Liu et al. (2014) or Ngo et al. (2015)]. In addition, other processes are sometimes taken into account such as protonation and deprotonation processes at clay edge sites (e.g., Wang et al., 2010), Ostwald ripening processes (e.g., Savage et al., 2010) and the coupling between precipitation/dissolution and cation exchange (e.g., Benbow et al., 2019).

Most modelling work is related to assess the impact of cementitious pore water on the clay mineralogy (e.g., Bildstein and Claret (2015); Marty et al. (2015a); Deissmann et al. (2021) and references therein), but also on the fate of Fe in the clay barrier resulting from steel corrosion (see Section 4.3.4.3).

4.3.4 Modelling reactions at the material interfaces

A recent overview of modelling work on interfaces between different materials relevant for disposal cells was given in Deissmann et al. (2021).

4.3.4.1 Glass-steel interface

The key point in modelling the glass-steel interface is the uptake of Si by the corrosion products as this influences the glass dissolution models. Some models accounted for the sorption of Si on the corrosion products (De Windt et al., 2006; Grambow, 1987; Grambow et al., 1987; Jordan and Rammensee, 1998; Jordan et al., 2007; Mayant, 2009; Mayant et al., 2008; Philippini et al., 2006) which can capture typically the glass alteration rate up to a given point at which a certain saturation point is reached of the magnetite sites. After that, magnetite could be partially transformed in another iron oxide with larger sorption capacity or precipitation of Fe silicates (Rebiscoul et al., 2015; Godon et al., 2013). Including the later in the reaction network led indeed to better predictions of glass alteration rates (Godon et al., 2013).

4.3.4.2 Steel-concrete interface

Up to our best knowledge, no coupled reactive transport simulations for iron/steel corrosion in alkaline and anoxic conditions (i.e., for conditions relevant in a disposal cell) have been found in literature.

4.3.4.3 Steel-clay interface

Extensive experimental studies and numerical models of the steel/iron-bentonite interactions under typical HLW-EBS conditions and the effects of corrosion products on the bentonite have been performed in the last 2 decades (Bildstein et al., 2016; Bildstein et al., 2006; Lu et al., 2011; Marty et al., 2010; Montes-H et al., 2005; Ngo et al., 2015; Ngo et al., 2014; Savage et al., 2010; Wersin et al., 2008; Wilson et al., 2006; Balmer et al., 2017; Cuevas et al., 2016; Fernández et al., 2018; Kaufhold et al., 2018; Mon et al., 2017; Samper et al., 2016). Bildstein et al. (2019) presented a comprehensive review of the reactive transport modelling studied at the iron-clay interface at the lab scale and at the scale of the disposal cell for waste repositories. They conclude that: (1) The most abundant corrosion product predicted by the models in the long-term is magnetite, sometimes with Fe-carbonates (siderite) and Fe-silicates (greenalite), sometimes incorporating Al (berthierine, cronstedtite); (2) Primary minerals in clay are often destabilized in favour of Fe-phyllosilicates or zeolites if they are allowed to precipitate; (3) Numerical studies often differ on the precise nature of the main secondary minerals; (4) The transformation of clay minerals into Fe-chlorite, and the timing, very much depend on whether it is included as a secondary mineral (in which case it is the most stable phase and precipitates from the beginning of the simulation) or it results from a ripening process; (5) One of the most sensitive parameters is the corrosion rate; (6) The extent of the perturbation is always predicted to be limited to a few centimetres, up to 20 cm into the clay barrier; and (7) Porosity clogging is considered in some simulations under different assumptions. Bildstein et al. (2019) also pointed out that a complete inhibition of the corrosion process has never been observed in experiments, even if a dense corrosion product layer is often identified, and the ubiquity of magnetite in simulation results as the dominant corrosion product in the long-term is questioned by many experimental results and archaeological analogues. Section 5.3 in Deissmann et al. (2021) provides further details on different modelling studies for this kind of interface.

4.3.4.4 Steel-granite interface

As noted Neeft et al. (2024), there is not direct interface between steel and granite in repository concepts. Therefore, no further discussion on models that would include explicitly this interface is given here.

4.3.4.5 Cement (mortar)-clay interface

This interface has been included in many modelling studies using a continuum-scale approach both for laboratory experiments, in-situ studies and long-term predictions. A recent overview of these modelling studies was presented in Deissmann et al. (2021). For the concrete part, most studies were done for OPC-CEMI (high pH) for which today excellent databases (see Section 4.2) exist, which now include also phases previously not considered in simulations (M-S-H phases, several C-A-S-H phases). In addition, numerical studies including a concrete/clay interface are available for different host rocks such as Boom Clay (Read et al., 2001; Wang et al., 2010), Opalinus Clay (Berner et al., 2013; Dauzeres et al., 2016; Jenni et al., 2017; Kosakowski and Berner, 2013; Trotignon et al., 2007), or Callovo-Oxfordian clay (Idiart et al., 2020; Marty et al., 2015a; Marty et al., 2014; Marty et al., 2009; Trotignon et al., 2007). When compared to experimental results, numerical studies are, in general, able to capture the mineralogical transformation pathways and the change in porosity (cf. Bildstein et al., 2019). With respect to the long-term predictions, although starting from different geometries and assumptions on evolutionary paths, models predict consistently a limited thickness of the altered zone, type of mineralogical transformation and porosity changes.

4.3.4.6 Cement (mortar)-granite interface

As mentioned in Section 4.2.2, modelling the geochemical alterations in cement-based materials are well-established because of the fast development of high-quality thermodynamic databases for cement phases (see Section 4.2.2). Coupling them in a coupled reactive transport model enables prediction of the degradation fronts as was done in the study of Höglund (2014) for leaching with a granite type of water. Also several modelling studies have been performed for the effect of the alkaline plume on crystalline rocks (Soler et al., 2006; Watson et al., 2017). The choice of reactive minerals is crucial to assess the extent of the perturbation (Chen et al., 2015). However, simulations shown that the model for the evolution of an alkaline plume in a host rock is largely consistent with experimental observations.

5 How to use the gained knowledge from assessing the chemical evolution?

This section describes what we can learn from assessing the chemical evolution besides the chemical evolution as such. We focus on two topics: how chemical evolution is linked to material properties and how it is linked to radionuclide mobility.

5.1 Impact on material properties

5.1.1 Physical and transport properties

The geochemical gradients between different materials in a disposal facility induce geochemical alterations with logically effects on different physical properties. More and more, reactive transport codes implement these coupled effects (Georget et al., 2017; Seigneur et al., 2019; Xie et al., 2015) and studies in the framework of radioactive waste disposal apply this in their modelling studies (e.g., Águila et al. (2020) and references in the description of different tools in the Supplementary Materials). Although the underlying pore-scale is the driver for these changes, the discussion focusses here on how it can be implemented in continuum-scale reactive transport models. For a recent in-depth discussion on parameterization of evolving porous media, we refer to Seigneur et al. (2019).

5.1.1.1 Porosity

Dissolution and precipitation of solid phases will lead to changes in the porosity of the porous medium. At every time and location, the porosity is calculated from:

$\eta =1-{\displaystyle \sum _i^{N_m}}{m}_i{V}_i(11)$

where η is the total porosity [L³ L^-3], N_m the number of solid phases, m_i is the number of moles of a given solid phase per unit volume [M L^-3] and V_i is the molar volume of the solid phase [L³ M^-1]. When the continuum domain is split into different domains (dual porosity (Šimůnek and van Genuchten, 2008), multiple interacting continua (Pruess and Narasimhan, 1985), multi rate mass transfer framework (De Dreuzy et al., 2013; Haggerty and Gorelick, 1995)), a porosity for each domain can be calculated.

• The simple equation for porosity (Equation 11) needs some further refinement for some particular properties of a porous medium:

• For a multiscale material as concrete, different types of porosity are defined with gel porosity as the porosity that is within the C-S-H phases; one may also distinguish between the porosity in the bulk of the hardened cement paste, and a more open structure in the interfacial transition zone;

• Also fractures contribute to porosity, and have to be treated in a continuum model as separate domains (as referenced above), or as part of the equivalent continuum model;

• In swelling materials (clay), fracture opening and porosity depend also on the water saturation degree and the aqueous composition. Porosity changes due to bentonite swelling was taken into account via a state surface approach in Samper et al. (2020).

5.1.1.2 Diffusion coefficient

Diffusion coefficients in porous media may vary in time of space due to:

• Changes in temperature, typically described by an Arrhenius type of equation

• Changes in water saturation degree, typically described by Millington-Quirk

• Changes in microstructure and porosity, the former linked to tortuosity.

Reminding the equation of the effective diffusion coefficient: θD^p:

$\theta D^{\mathrm{p}}=\theta {\tau }_{\mathrm{s}}{\tau }_{\mathrm{p}}{D}_{\mathrm{w}}$

where τ_s is the factor accounting for saturation degree [-] and τ_p the factor for the pore structure. The most widely used formula to link τ_p to porosity η is Archie’s law (Archie, 1942; Xie et al., 2015):

${\mathsf{\tau }}_{\mathrm{p}}={\eta }^{{\alpha }_{\mathrm{c}}}$

where α_c is the cementation factor which is an empirical factor. There exist a number of other relations as well; some examples are given in Seigneur et al. (2019). Some models use the concept of a critical porosity below which diffusion does not occur (e.g., Bentz and Garboczi, 1991).

Models for tortuosity for cement, mortar and concrete have been developed taking into account the multiscale nature of cement (gel pores in C-S-H, capillary porosity) and mortar or concrete (aggregates, interfacial transition zone) using so-called effective media theories (see Patel et al. (2016) for a review). These models have been evaluated for initial conditions (e.g., after 28 days of hardening), there applicability for evolving media is less validated. However, as information on the different mineralogical phases are available in reactive transport models, in theory, they can be used in these models as well (e.g., Perko et al., 2010).

Beside parameterization via experimental results, relations and models can be obtained via pore-scale or microscale modelling that represent explicitly the underlying microstructure (Matyka et al., 2008). Recent pore-scale models for ageing of cement explore the evolution of microstructure and transport parameters (Patel et al., 2021; Patel et al., 2018b; Seigneur et al., 2017) and derive functional relations (Bentz and Garboczi, 1991; Seigneur et al., 2017) (see also Ahusborde et al., 2021). A new route is to using deep learning techniques to relate tortuosity to porosity (Graczyk and Matyka, 2020).

5.1.1.3 Hydraulic conductivity

Similar to diffusivity, hydraulic conductivity depends also on different factors that may change in time and space:

• Changes in temperature and solution composition that effect e.g., viscosity

• Changes in water saturation degree, typically described by models based on statistical pore size distributions (Burdine, 1953; Mualem, 1976)

• Changes in microstructure and porosity

Focussing here on saturated hydraulic conductivity, K_s [L T^-1], and changes due to microstructural and porosity evolution, the change in K_s can be described by a scaling factor α_K:

${\mathsf{\alpha }}_K=\frac{K_{\mathrm{s}}\left(t\right)}{K_{\mathrm{s},0}}=\frac{f\left(\eta \left(t\right)\right)}{f\left({\eta }_0\left(t\right)\right)}$

where the subscript 0 refers to the initial values. The most common models are based on total porosity, and the Kozeny-Carman relation is one of the most often used:

${\mathsf{\alpha }}_K=\frac{\eta {\left(t\right)}^3{\left(1-\eta \left(t_0\right)\right)}^2}{\eta {\left(t_0\right)}^3{\left(1-\eta \left(t\right)\right)}^2}$

However, many relations have been proposed in literature, and we refer to MacQuarrie and Mayer (2005) and Hommel et al. (2018) for an overview.

Another group of models uses the statistical pore-size distribution rather than the total porosity for updating hydraulic conductivity. Precipitation and dissolution will alter the statistical pore size distribution because of changes in pore radii. Consequently, the saturated and unsaturated hydraulic conductivity (and moisture retention characteristic) change when calculated with for example, the model of Mualem (Mualem, 1976) or Burdini (Burdine, 1953). This approach, introduced for saturated conditions by Taylor and Jaffe (1990), has been extended to unsaturated conditions as well by Freedman et al. (2004) and Wissmeier and Barry (2009). The latter model, called the selective radius shift model, assumes that precipitation/dissolution only occurs in the water-saturated region of the pore size distribution, whereas the former did not made a distinction between the wet and dry regions. When applied to the van Genuchten pore size distribution model, Wissmeier and Barry (2009) predicted changes in K_s and the empirical α_VG and n parameter of the van Genuchten model (van Genuchten, 1980); however, the approach is complicated for unsaturated conditions as a refitting of these parameters is needed when the pore-size distribution is altered. For fully saturated conditions, closed-form equations are obtained (Wissmeier and Barry, 2010):

${\mathsf{\alpha }}_{\text{VG}}={\alpha }_{\text{VG},0}{\left(\frac{\left(\eta -{\theta }_r\right)}{\left({\eta }_0-{\theta }_r\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$

and

${\mathsf{K}}_{\mathrm{s}}=K_{\mathrm{s},0}\frac{\sqrt{\eta }{\alpha }_{\text{VG}}^2{\left(\eta -{\theta }_{\mathrm{r}}\right)}^2}{\sqrt{{\eta }_0}{\alpha }_{\text{VG},0}^2{\left({\eta }_0-{\theta }_{\mathrm{r}}\right)}^2}$

where 0 denotes the initial values, and θ_r is the residual water content. This has been implemented to simulate leaching from cementitious materials in Perko et al. (2010). A recent application for cementitious materials for leaching and carbonation is given in Michel et al. (2021).

Liquid configuration-based models (Tuller and Or, 2002; Tuller and Or, 2001) that are based on statistical distributions of geometrically objects to represent the pores potentially offer also a basis for recalculating hydraulic properties during material alterations, but no applications have been found at this stage in the literature.

For saturated fractures, a local cubic law for rough fractures (i.e., fractures with spatially variable apertures) is used to predict the saturated hydraulic conductivity (Oron and Berkowitz, 1998). Liquid configuration-based models offer a physical based approach for estimating unsaturated hydraulic properties of a single fracture or a fracture network (Tuller and Or, 2002; Or and Tuller, 2000). We refer to Deng and Spycher (2019) for an overview of integrating fracture and geochemical fracture evolution into reactive transport models and consequences for the hydraulic (and other) properties.

5.1.2 Mechanical consequences

It is well acknowledged that the mechanical behaviour of cementitious materials is intimately linked to their micro, meso and macrostructural characteristics. These structural characteristics in turn depend on the chemical stability of the material. Therefore, any chemical perturbation will have an effect on the mechanical behaviour of the material such as strength, stiffness, etc. Moreover, it is the nature of the chemical perturbation (e.g., decalcification, sulphate attack) that governs the mechanical behaviour and hence the knowledge of evolution of field variables such as chemical concentrations in the liquid or solid phase is a pre-requisite. The manner in which the chemical field variables predicted by geochemical models (simplified or detailed) are used by some mechanical models are herein demonstrated for two degradation processes relevant to geological disposal: (i) decalcification, and (ii) sulphate attack. The principle in general remains the same for any other degradation processes such as alkali-aggregate reaction, etc.

5.1.2.1 Decalcification

Decalcification is characterized by a decrease in Young’s modulus, compressive strength, cohesion, failure stress, plastic yield stress in deviatoric shearing and pore collapse yield stress (Carde et al., 1996; Heukamp et al., 2003; Heukamp et al., 2001; Huang and Qian, 2011; Ulm et al., 1999; Xie et al., 2008; Gerard et al., 1996), including decalcification shrinkage (Phung, 2015; Rougelot et al., 2010).

From an empirical point of view, Walton et al. (Walton et al., 1990) assumed that the concrete loses half of its strength when 33% of portlandite (CH) is depleted.

There are a number of models that estimate specific mechanical properties (e.g., Young’s modulus) as a function of leached calcium, which are then used in coupled chemo-mechanical models to study mechanical stability of a specimen or a structure. For instance, Gerard et al. (1996) proposed the following relationship between overall Young’s modulus with the initial Young’s modulus of the material and a chemical damage function d_ch.

$E=E_0\left(1-d_{\text{ch}}\right)$

$\left(1-d_{\text{ch}}\right)$ vs liquid Ca²⁺ is obtained using micro-hardness experiments on leached cement paste samples. Similarly, Ulm et al. (1999) considered chemical damage and chemical shrinkage by considering loss of stiffness as a function of solid Ca concentration using the rule of mixtures and homogenization rule as follows:

$E=V{E}^{\mathrm{p}}+\left(1-V\right)E^{\mathrm{s}}{\left(1-\eta \right)}^3$

where E is the overall modulus, $E^{\mathrm{p}}$ is the modulus of the portlandite, V is the portlandite volume ratio and $\left(1-\eta \right)$ is the volume ratio occupied by the solid part of modulus $E^s$. They were also the first to propose a link between the solid Ca and irreversible damage of the material referred to as chemical softening, within the framework of chemo-plasticity. The latter simply means that the yield function is not only a function of stresses (as in typical elasto-plastic approaches) but also on solid Ca that can be obtained from a geochemical model.

Stora et al. (2009) used interaction direct derivation estimate to estimate bulk, shear and Young’s modulus of leached concrete, which essentially uses the time dependent volume fractions of CH, unhydrated clinkers, capillary pores, AFt, C₄AH₁₃, hydrogarnet, AFm and CSH, in combination with measured properties of Young’s modulus of the material. These moduli form inputs to a constitutive law (effective stress-strain relationship) in the standard mechanical equilibrium equation.

5.1.2.2 Sulphate attack

Sulphate attack occurs if the C₃A concentration has not been limited for the use of concrete in a sulphate rich environment. The formation of ettringite, gypsum or thaumasite will result in expansive forces (Bensted et al., 2007). Thus, a key input to all mechanical models of sulphate attack is the amount of ettringite formed. Tixier and Mobasher (2003) used the following expression to compute volumetric strain, ${\epsilon }_v$, due to external sulphate attack.

${\mathsf{\epsilon }}_{\mathrm{v}}\left(x,t\right)=\left(C_{\mathrm{a}}-C_{\mathrm{a}0}{\displaystyle \sum _P}{\left(\frac{\Delta V}{V}\right)}_P\right)$

${\left(\frac{\mathsf{\Delta }V}{V}\right)}_P=\frac{\frac{1}{m_{\mathrm{v},\text{ettringite}}}}{\frac{1}{m_{\mathrm{v},P}}+\frac{a}{m_{\mathrm{v},\text{gypsum}}}}-1$

where $m_{\mathrm{v}}$ represents the molar volume, P is the specific aluminate phase (C₄ASH₁₂, C₃A, C₄AH₁₃, C₃AH₆), ‘‘a’’ is the stoichiometric proportion of the calcium aluminates and gypsum, $C_{\mathrm{a}0}$ is the initial amount of calcium aluminates, and $C_{\mathrm{a}}$ is the current amount of calcium aluminates–all of which are outputs from a geochemical model. The volumetric strain can then be used in the standard mechanical equilibrium equation (not shown) to estimate the impact on stresses and cracking.

Whilst the model of Tixier and Mobasher takes into account changes in molar volume of ettringite and gypsum, Sarkar et al. (2010) consider the change in molar volume of all solid phases [Table 2 in Sarkar et al. (2010)] in the hardened cement paste and hence their contribution to the overall volumetric strain as follows:

${\mathsf{\epsilon }}_{\mathrm{v}}=\frac{\left[\left\{{\displaystyle \sum _{m=1}^M}\left(V_m-V_m^{\text{init}}\right)\right\}-b\varnothing V\right]}{V}$

where M is the number of solid phases, V is the representative volume element (total volume), $V_m^{\text{init}}$ and $V_m$ are the initial and current volumes of the m^th solid phase, b is a calibration parameter and $\varnothing$ is the capillary porosity. If the parameter b = 1, the newly formed solid phases do not contribute to the overall expansion until all the capillary pores are filled with them. Sarkar et al. (2010) used the volumetric strain to determine the loss of stiffness of the material, which was then used in the standard mechanical equilibrium equation to study damage initiation/growth.

Bary (2008) proposed a combined leaching and external sulphate attack model, which couples simplified leaching and sulphate attack reactions with a mechanical model based on combined damage and poroelasticity approach. The leaching problem is solved using dissolved Ca²⁺ as the primary variable (e.g., Mainguy et al., 2000) and the sulphate attack problem is solved using dissolved SO₄^2- as the primary variable. Unlike the approaches discussed above, the model here is based on the concept of crystallization pressure resulting from interaction between growing AFm crystals and the surrounding C-S-H matrix, which is hypothesized to generate macroscopic swelling. They use the crystallization pressure expressed by Correns’s equation involving the ratio between the activity product $Q_{reac}$ and the equilibrium constant of the considered chemical reaction $K_{reac}$ (Equations 6 and 7 in Bary (2008)).

${\mathsf{p}}_{\mathrm{c}}=\frac{RT}{V_{\text{crys}}}\ln \left(\frac{Q_{\text{reac}}}{K_{\text{reac}}}\right)$

where $V_{\text{crys}}$ the molar volume of the growing crystal, R and T is are the gas constant and temperature, respectively. The crystallization pressure is substituted in the following effective stress equation based on poroelasticity.

$\sigma =\left(1-D\right)\left(\mathbf{K}:\mathbf{\epsilon }-{\alpha }_{\text{AFm}}{p}_{\mathrm{c}}\mathbf{1}\right)$

where D is a scalar damage parameter linked to the elastic constants, K is the standard 4^th order stiffness tensor, $\mathrm{\epsilon }$ is the standard 2^nd order strain tensor, ${\alpha }_{\text{AFm}}$ is the interaction coefficient of the AFm phase, which is essentially a function of the volume fraction of the AFm phase and the microstructure of the hardened cement paste. In conclusion, their model not only requires mass action equations for the secondary phases ettringite and gypsum, but also the volume fractions of ettringite.

5.1.2.3 Concluding perspective

Using the decalcification and sulphate attack mechanisms as examples, this section clearly brought out the link between geochemical models (simplified or detailed) and mechanical models proposed by various researchers. Note however, that in disposal cells, either other processes might occur as well or that they occur simultaneously (e.g., decalcification together with carbonation). Also, by good choice of the cement type, some processes are of less importance in some circumstances (e.g., sulphate attack). In general, the evolution of liquid concentrations of primary chemical variables, solid phase concentrations of the reaction products, molar volumes of solid phases and volume fractions of various phases are seen to form minimum inputs to any mechanical model. Although not discussed, many of the fully coupled chemo-mechanical models are capable of considering mechanical response on the flow and transport behaviour. In such models, either the crack density or the actual crack width forms an input to permeability and diffusivity.

5.2 Impact on waste form and radionuclide mobility

The impact on the fate and mobility of radionuclide in a disposal system is depending on the following important aspects:

• The change in transport properties due to microstructural alterations (see previous section) including the physical/mechanical properties of the waste forms themselves

• The change in speciation of radionuclides due to changes in the aqueous composition

• The change in amount of sorption sites due to dissolution and precipitation of minerals.

• Gas generation and transport that may influence transport at the disposal cell scale and in the host rock.

It is not within the scope of this paper to summarize these effects for different radionuclides. The main message is that, based on a quantification of the above mentioned changes, the effects on radionuclide fate and mobility can be assessed in a quantitative way using the same or similar model concepts and tools as discussed in Section 4. Similar to modelling the geochemical evolution of materials, process understanding, models, parameters and thermodynamic data are crucial. This has been or is still an important research subject.

Without being exhaustive, we guide the reader to the following information:

• Cementitious system: information on speciation of radionuclides during different ageing stages of concrete, together with processes regarding the sorption or immobilization processes, is summarized in Ochs et al. (2016). Results of the CEBAMA project are summarized in Grambow et al. (2020). Altmaier et al. (2021) provides additional references including the interaction with organics as well.

• Clay and Crystalline rocks: The theoretical background of sorption on clay minerals is given in many textbooks (Appelo and Postma, 2005); the reader is also referenced to Borisover and Davis (2015). Finally, the state-of-the-art report by Maes et al. (2021) and Maes et al. (2024) contains a large bibliographic review to many aspects of radionuclide fate and mobility.

6 Concluding summary

The safety and performance of deep geological disposal systems of intermediate and high level radioactive waste have to be assessed for long-time frames (several tens-of-thousands to hundreds-of-thousands of years). Inevitable, geochemical alterations will occur in the disposal system which may affect different aspects related to safety and performance. Part I of this series (Neeft et al., 2024) discussed the state-of-the-art of our knowledge on geochemical processes that occur at interfaces between materials in the engineered barriers and the host rock and presented a narrative of the geochemical evolution. Part II of this state-of-the-art presented (i) how information on the geochemical evolution can be obtained (experimental studies, archaeological or natural analogues and through modelling) and (ii) gave examples how it can be used to evaluate consequences of geochemical alteration.

Clay host rocks and granitic host rocks are both alumina-silicate bearing rocks. Detailed investigation and understanding of the processes taking place in Maqarin (Jordan) elucidated the potential sequence of secondary mineral formation by interaction with alkaline fluids and alumina-silicate bearing rocks: C-S-H phases, low in Ca C-S-H phases, C-A-S-H, low Si/Al zeolite and high Si/Al zeolite as a function of pH. The low permeability in clay host rocks ensures that the mineralogical alteration is minimal in a period of 100,000 till 1 million years. The secondary mineral formation takes place within the fractures of granitic host rocks.

Formation of an alteration layer on the surface of steel takes place when steel is in contact with pore water. It takes some time to form this alteration layer and to achieve a constant alteration rate in a laboratory setup, especially if samples are prepared to obtain a well-defined initial condition for example, polishing of steel and acid etching. In practice, there is always a metal-oxide layer present on steel before disposal.

An alteration layer is a passivating layer with the smallest possible alteration rate in that medium. Another word for alteration layer in the literature is ‘dense product layer’. A constant alteration rate is representative for the long-term. This alteration rate is a steady state between the dissolution of the alteration layer interfacing a porous medium and the formation of the alteration layer from the virgin material. The concentration of dissolved species is in equilibrium with the formed minerals in the alteration layer for example, magnetite in case of steel. Dissolved species migrate away from the interface by diffusion in porous media to areas with a smaller concentration in these dissolved species. This migration from the interface can be enhanced by sorption of these dissolved species in porous media. Sorption by porous media can therefore result into larger alteration rates.

Like steel, formation of an alteration layer on the surfaces of glass takes place when glass is in contact with pore water, except that the alteration layer is composed of a diffusion gel layer and secondary mineral precipitates such as clay minerals and zeolites. Like steel, it may also take some time to form this alteration layer and to achieve a constant alteration rate in a laboratory setup. Relevant alteration rates have been obtained from natural analogues and depend on the silicon concentration in porous media. In a laboratory set-up, the liquids to which a simulant of the vitrified waste form is exposed can be chosen to be depleted in dissolved silicon. This set-up will not lead to an alteration rate that is representative for disposal since all porous media are saturated in silicon. After fracture of the carbon steel overpack, glass in the vicinity of steel can have higher alteration rates. The radionuclides dissolved as cationic complexes are, however, incorporated in the alteration layer of glass. Consequently, the containment of these radionuclides has been transformed from the engineered waste form into the naturally formed secondary mineral precipitates.

Author contributions

GD: Conceptualization, Writing–original draft, Writing–review and editing. EN: Conceptualization, Writing–original draft, Writing–review and editing. DJ: Conceptualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The manuscript was prepared within the framework of the work package ACED within EURAD (European Joint Programme on Radioactive Waste Management); Grant Agreement No 847593.

Acknowledgments

This work is based on additional deliverables from the work package ACED of EURAD (mentioned in reference list) and on discussions during the work package meetings. The authors acknowledge all partners from the work package ACED for their fruitful discussions and input and contribution to the work package ACED. In particular, we thank the users of the codes discussed in this paper for providing input for description and main references of their codes.

Conflict of interest

EN was employed by the COVRA.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2024.1433257/full#supplementary-material

Footnotes

¹Terminology indicates also, beside the surface plane, the Inner Helmholtz Plane (IHP) for sorption of the hydrated ions and an Outer Helmholtz Plane (OHP) that is the beginning of the diffuse layer.

²http://gems.web.psi.ch/

³https://models.earth.indiana.edu/superphreeqc.php

⁴https://thermoddem.brgm.fr/

⁵https://tough.lbl.gov/software/toughreact/

⁶https://www.gwb.com/

⁷https://www.thermochimie-tdb.com/

⁸August 2023

⁹https://www.psi.ch/en/les/database

¹⁰https://www.empa.ch/web/s308/zeolite

¹¹https://www.thereda.de/en/

¹²https://github.com/HydrogeoIU/PHREEQC-Kinetic-Library

¹³https://cemgems.org/

References

Águila, J. F., Samper, J., Mon, A., and Montenegro, L. (2020). Dynamic update of flow and transport parameters in reactive transport simulations of radioactive waste repositories. Appl. Geochem. 117, 104585. doi:10.1016/j.apgeochem.2020.104585

CrossRef Full Text | Google Scholar

Ahonen, L. (2004a). Disko Island (Greenland) Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Ahonen, L. (2004b). Josephinite Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Ahusborde, E., Amaziane, B., Baksay, A., Bator, G., Becker, D., Bednar, A., et al. (2021). State of the Art Report in the fields of numerical analysis and scientific computing. Final version as of 16/02/2020 of deliverable D4.1 of the HORIZON 2020 project EURAD. EC Grant agreement no: 847593.

Google Scholar

Altmaier, M., Blin, V., Garcia, D., Henocq, P., Missana, T., Ricard, D., et al. (2021). SOTA on cement-organic-radionuclide interactions. Final version as 19.05.2021 Deliv. D3.1 HORIZON 2020 Proj. EURAD. EC Grant Agreem. no, 847593.

Google Scholar

Anderson, G. M., and Crerar, D. A. (1993). Thermodynamics in geochemistry: the equilibrium model. Oxford, UK: Oxford University Press.

CrossRef Full Text | Google Scholar

Appelo, C. A. J. (2017). Solute transport solved with the Nernst-Planck equation for concrete pores with ‘free’ water and a double layer. Cem. Concr. Res. 101, 102–113. doi:10.1016/j.cemconres.2017.08.030

CrossRef Full Text | Google Scholar

Appelo, C. A. J., Parkhurst, D. L., and Post, V. E. A. (2014). Equations for calculating hydrogeochemical reactions of minerals and gases such as CO2 at high pressures and temperatures. Geochimica Cosmochimica Acta 125, 49–67. doi:10.1016/j.gca.2013.10.003

CrossRef Full Text | Google Scholar

Appelo, C. A. J., and Postma, D. (2005). Geochemistry, groundwater and pollution. 2nd edition. Amsterdam, Netherlands: A.A. Balkema Publishers.

Google Scholar

Archie, G. E. (1942). The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 164, 54–62. doi:10.2118/942054-g

CrossRef Full Text | Google Scholar

Balmer, S., Kaufhold, S., and Dohrmann, R. (2017). Cement-bentonite-iron interactions on small scale tests for testing performance of bentonites as a barrier in high-level radioactive waste repository concepts. Appl. Clay Sci. 135, 427–436. doi:10.1016/j.clay.2016.10.028

CrossRef Full Text | Google Scholar

Balonis, M., Lothenbach, B., LA Saout, G., and Glasser, F. P. (2010). Impact of chloride on the mineralogy of hydrated Portland cement systems. Cem. Concr. Res. 40, 1009–1022. doi:10.1016/j.cemconres.2010.03.002

CrossRef Full Text | Google Scholar

Balonis, M., Mędala, M., and Glasser, F. P. (2011). Influence of calcium nitrate and nitrite on the constitution of AFm and AFt cement hydrates. Adv. Cem. Res. 23, 129–143. doi:10.1680/adcr.10.00002

CrossRef Full Text | Google Scholar

Bary, B. (2008). Simplified coupled chemo-mechanical modeling of cement pastes behavior subjected to combined leaching and external sulfate attack. Int. J. Numer. Anal. Methods Geomechanics 32, 1791–1816. doi:10.1002/nag.696

CrossRef Full Text | Google Scholar

Bataillon, C., Bouchon, F., Chainais-Hillairet, C., Desgranges, C., Hoarau, E., Martin, F., et al. (2010). Corrosion modelling of iron based alloy in nuclear waste repository. Electrochimica Acta 55, 4451–4467. doi:10.1016/j.electacta.2010.02.087

CrossRef Full Text | Google Scholar

Bear, J. (1972). Dynamics of fluids in porous media. New York, USA: Dover Publications, INC.

Google Scholar

Bejaoui, S., and Bary, B. (2007). Modeling of the link between microstructure and effective diffusivity of cement pastes using a simplified composite model. Cem. Concr. Res. 37, 469–480. doi:10.1016/j.cemconres.2006.06.004

CrossRef Full Text | Google Scholar

Benbow, S., Wilson, J., Metcalfe, R., and Lehikoinen, J. (2019). Avoiding unrealistic behaviour in coupled reactive-transport simulations of cation exchange and mineral kinetics in clays. Clay Miner. 54, 83–93. doi:10.1180/clm.2019.7

CrossRef Full Text | Google Scholar

Ben Moshe, S., Weisbrod, N., and Furman, A. (2021). Optimization of soil aquifer treatment (SAT) operation using a reactive transport model. Vadose Zone J. 20, e20095. doi:10.1002/vzj2.20095

CrossRef Full Text | Google Scholar

Bensted, J., Rbrough, A., and Page, M. M. (2007). “4 - chemical degradation of concrete,” in Durability of concrete and cement composites. Editors C. L. PAGE, and M. M. PAGE (Cambridge, UK: Woodhead Publishing).

Google Scholar

Bentz, D. P., and Garboczi, E. J. (1991). Percolation of phases in a three-dimensional cement paste microstructural model. Cem. Concr. Res. 21, 325–344. doi:10.1016/0008-8846(91)90014-9

CrossRef Full Text | Google Scholar

Berner, U., Kulik, D. A., and Kosakowski, G. (2013). Geochemical impact of a low-pH cement liner on the near field of a repository for spent fuel and high-level radioactive waste. Phys. Chem. Earth, Parts A/B/C 64, 46–56. doi:10.1016/j.pce.2013.03.007

CrossRef Full Text | Google Scholar

Bhanja, S. N., Wang, J., Shrestha, N. K., and Zhang, X. (2019). Microbial kinetics and thermodynamic (MKT) processes for soil organic matter decomposition and dynamic oxidation-reduction potential: model descriptions and applications to soil N 2 O emissions. Environ. Pollut. 247, 812–823. doi:10.1016/j.envpol.2019.01.062

PubMed Abstract | CrossRef Full Text | Google Scholar

Bildstein, O., and Claret, F. (2015). “Chapter 5 - stability of clay barriers under chemical perturbations,”. Natural and engineered clay barriers. Developments in clay science. Editors C. TOURNASSAT, C. I. STEEFEL, I. C. BOURG, and F. BERGAYA, 6, 155–188.

Google Scholar

Bildstein, O., Claret, F., and Frugier, P. (2019). RTM for waste repositories. Rev. Mineralogy Geochem. 85, 419–457. doi:10.2138/rmg.2019.85.14

CrossRef Full Text | Google Scholar

Bildstein, O., Lartigue, J. E., Schlegel, M. L., Bataillon, C., Cochepin, B., Munier, I., et al. (2016). Gaining insight into corrosion processes from numerical simulations of an integrated iron-claystone experiment. Geol. Soc. 443, 253–267. doi:10.1144/sp443.2

CrossRef Full Text | Google Scholar

Bildstein, O., Trotignon, L., Perronnet, M., and Jullien, M. (2006). Modelling iron-clay interactions in deep geological disposal conditions. Phys. Chem. Earth 31, 618–625. doi:10.1016/j.pce.2006.04.014

CrossRef Full Text | Google Scholar

Blanc, P., Gherardi, F., Vieillard, P., Marty, N. C. M., Gailhanou, H., Gaboreau, S., et al. (2021). Thermodynamics for clay minerals: calculation tools and application to the case of illite/smectite interstratified minerals. Appl. Geochem. 130, 104986. doi:10.1016/j.apgeochem.2021.104986

CrossRef Full Text | Google Scholar

Blanc, P., Lassin, A., Piantone, P., Azaroual, M., Jacquemet, N., Fabbri, A., et al. (2012). Thermoddem: a geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 27, 2107–2116. doi:10.1016/j.apgeochem.2012.06.002

CrossRef Full Text | Google Scholar

Blanc, P., Vieillard, P., Gailhanou, H., Gaboreau, S., Marty, N., Claret, F., et al. (2015). ThermoChimie database developments in the framework of cement/clay interactions. Appl. Geochem. 55, 95–107. doi:10.1016/j.apgeochem.2014.12.006

CrossRef Full Text | Google Scholar

Blechschmidt, I., and Vomvoris, S. (2010). “Underground research facilities and rock laboratories for the development of geological disposal concepts and repository systems,” in Geological repository systems for safe disposal of spent nuclear fuels and radioactive waste. Editors J. AHN, and M. J. APTED (Cambridge: Woodhead Publishing).

Google Scholar

Bloom, S. A., and Mansell, R. S. (2001). An algorithm for generating cation exchange isotherms from binary selectivity coefficients. Soil Sci. Soc. Am. J. 65, 1426–1429. doi:10.2136/sssaj2001.6551426x

CrossRef Full Text | Google Scholar

Bond, W. J. (1995). On the Rothmund-Kornfeld description of cation exchange. Soil Sci. Soc. Am. J. 59, 436–443. doi:10.2136/sssaj1995.03615995005900020024x

CrossRef Full Text | Google Scholar

Borisover, M., and Davis, J. A. (2015). “Chapter 2 - adsorption of inorganic and organic solutes by clay minerals,”. Natural and engineered clay barriers Developments in clay science. Editors C. TOURNASSAT, C. I. STEEFEL, I. C. BOURG, and F. BERGAYA, 6, 33–70.

Google Scholar

Bossart, P., Bernier, F., Birkholzer, J., Bruggeman, C., Connolly, P., Dewonck, S., et al. (2017). Mont Terri rock laboratory, 20 years of research: introduction, site characteristics and overview of experiments. Swiss J. Geosciences 110, 3–22. doi:10.1007/978-3-319-70458-6_1

CrossRef Full Text | Google Scholar

Bradbury, M. H., and Baeyens, B. (2000). A generalised sorption model for the concentration dependent uptake of caesium by argillaceous rocks. J. Contam. Hydrology 42, 141–163. doi:10.1016/s0169-7722(99)00094-7

CrossRef Full Text | Google Scholar

Bradbury, M. H., and Baeyens, B. (2003). Porewater chemistry in compacted re-saturated MX-80 bentonite. J. Contam. Hydrology 61, 329–338. doi:10.1016/s0169-7722(02)00125-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Brantley, S. L., Kubicki, J. D., and White, A. F. (2008). Kinetics of water-rock interaction. New York, NY: Springer.

Google Scholar

Brooks, R. H., and Corey, A. (1964). “Hydraulic properties of porous media,” in Hydrol. Paper, No. 3. Fort Collins, CO: Colorado State Univ.

Google Scholar

Brovelli, A., Malaguerra, F., and Barry, D. A. (2009). Bioclogging in porous media: model development and sensitivity to initial conditions. Environ. Model. & Softw. 24, 611–626. doi:10.1016/j.envsoft.2008.10.001

CrossRef Full Text | Google Scholar

Burdine, N. T. (1953). Relative permeability calculations from pore-size distribution data. Petrol. Trans. Am. Inst. Min. Eng. 198, 71–78. doi:10.2118/225-g

CrossRef Full Text | Google Scholar

Cama, J., and Ganor, J. (2015). “Chapter 4 - dissolution kinetics of clay minerals,”. Natural and engineered clay barriers, Developments in clay science. Editors C. TOURNASSAT, C. I. STEEFEL, I. C. BOURG, and F. BERGAYA, 6, 101–153.

Google Scholar

Carde, C., Francois, R., and Torrenti, J. M. (1996). Leaching of both calcium hydroxide and C-S-H from cement paste: modeling the mechanical behavior. Cem. Concr. Res. 26, 1257–1268. doi:10.1016/0008-8846(96)00095-6

CrossRef Full Text | Google Scholar

Cey, E., Rudolph, D., and Therrien, R. (2006). Simulation of groundwater recharge dynamics in partially saturated fractured soils incorporating spatially variable fracture apertures. Water Resour. Res. 42, W09413. doi:10.1029/2005wr004589

CrossRef Full Text | Google Scholar

Chen, X., Thornton, S. F., and Small, J. (2015). Influence of hyper-alkaline pH leachate on mineral and porosity evolution in the chemically disturbed zone developed in the near-field host rock for a nuclear waste repository. Transp. Porous Media 107, 489–505. doi:10.1007/s11242-014-0450-0

CrossRef Full Text | Google Scholar

Chitty, W.-J., Dillmann, P., L’Hostis, V., and Lombard, C. (2005). Long-term corrosion resistance of metallic reinforcements in concrete—a study of corrosion mechanisms based on archaeological artefacts. Corros. Sci. 47, 1555–1581. doi:10.1016/j.corsci.2004.07.032

CrossRef Full Text | Google Scholar

Claret, F., Marty, N., and Tournassat, C. (2018). “Modeling the long-term stability of multi-barrier systems for nuclear waste disposal in geological clay formations,” in Reactive transport modeling: applications in subsurface energy and environmental problems. Editors X. YITIAN, W. FIONA, X. TIANFU, and C. STEEFEL (New York, USA: John Wiley & Sons Ltd).

CrossRef Full Text | Google Scholar

Collin, F., Li, X. L., Radu, J. P., and Charlier, R. (2002). Thermo-hydro-mechanical coupling in clay barriers. Eng. Geol. 64, 179–193. doi:10.1016/s0013-7952(01)00124-7

CrossRef Full Text | Google Scholar

Conradt, R., Roggendorf, H., and Ostertag, R. (1986). “The basic corrosion mechanisms of HLW glasses,”. EUR-10680 (Commission of the European Communities). (CEC).

Google Scholar

Crossland, I. C. (2005). “Long-term corrosion of iron and copper,” in The 10th international conference on environmental remediation and radioactive waste management. Glasgow (Scotland).

Google Scholar

Cuevas, J., Ruiz, A. I., Fernández, R., Torres, E., Escribano, A., Regadío, M., et al. (2016). Lime mortar-compacted bentonite–magnetite interfaces: an experimental study focused on the understanding of the EBS long-term performance for high-level nuclear waste isolation DGR concept. Appl. Clay Sci. 124-125, 79–93. doi:10.1016/j.clay.2016.01.043

CrossRef Full Text | Google Scholar

Dauzeres, A., Achiedo, G., Nied, D., Bernard, E., Alahrache, S., and Lothenbach, B. (2016). Magnesium perturbation in low-pH concretes placed in clayey environment-solid characterizations and modeling. Cem. Concr. Res. 79, 137–150. doi:10.1016/j.cemconres.2015.09.002

CrossRef Full Text | Google Scholar

De Blanc, P. C., Mckinney, D. C., and Speitel, J. R. G. E. (1996). “Chapter 1 Modeling subsurface biodegradation of non-aqueous phase liquids,”. Advances in porous media. Editor M. Y. CORAPCIOGLU (Elsevier Science), Vol. 3, 1–86. doi:10.1016/s1873-975x(96)80003-5

CrossRef Full Text | Google Scholar

Debure, M., DE Windt, L., Frugier, P., and Gin, S. (2018). Mechanisms involved in the increase of borosilicate glass alteration by interaction with the Callovian-Oxfordian clayey fraction. Appl. Geochem. 98, 206–220. doi:10.1016/j.apgeochem.2018.09.014

CrossRef Full Text | Google Scholar

De Craen, M., Wang, L., VAN Geet, M., and Moors, H. (2004). Geochemistry of Boom clay pore water at the mol site. Mol, Belgium: SCKCEN-BLG-990: SCK•CEN.

Google Scholar

De Dreuzy, J. R., Rapaport, A., Babey, T., and Harmand, J. (2013). Influence of porosity structures on mixing-induced reactivity at chemical equilibrium in mobile/immobile Multi-Rate Mass Transfer (MRMT) and Multiple INteracting Continua (MINC) models. Water Resour. Res. 49, 8511–8530. doi:10.1002/2013wr013808

CrossRef Full Text | Google Scholar

Deissmann, G., Mouheb, N. A., Martin, C., Turrero, M. J., Torres, E., Kursten, B., et al. (2021). Experiments and numerical model studies on interfaces. Final version as of 12.05.2021 of deliverable D2.5 of the HORIZON 2020 project EURAD. EC Grant agreement no: 847593.

Google Scholar

Delay, J., Bossart, P., Ling, L. X., Blechschmidt, I., Ohlsson, M., Vinsot, A., et al. (2014). Three decades of underground research laboratories: what have we learned? Special Publications, 400. London: Geological Society, 7–32.

Google Scholar

Deng, H., and Spycher, N. (2019). Modeling reactive transport processes in fractures. React. Transp. Nat. Eng. Syst. 85, 49–74. doi:10.2138/rmg.2019.85.3

CrossRef Full Text | Google Scholar

Dentz, M., Gouze, P., and Carrera, J. (2011a). Effective non-local reaction kinetics for transport in physically and chemically heterogeneous media. J. Contam. Hydrology 120-121, 222–236. doi:10.1016/j.jconhyd.2010.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Dentz, M., LE Borgne, T., Englert, A., and Bijeljic, B. (2011b). Mixing, spreading and reaction in heterogeneous media: a brief review. J. Contam. Hydrology 120-121, 1–17. doi:10.1016/j.jconhyd.2010.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

De Putter, T., Grainger, P., Lombardi, S., Manfroy, P., and Valentini, G. (1997). Fourth European conference on management and disposal of radioactive waste, 17543. EUR.

Google Scholar

De Weerdt, K., Lothenbach, B., and Geiker, M. R. (2019). Comparing chloride ingress from seawater and NaCl solution in Portland cement mortar. Cem. Concr. Res. 115, 80–89. doi:10.1016/j.cemconres.2018.09.014

CrossRef Full Text | Google Scholar

De Windt, L., Bertron, A., Larreur-Cayol, S., and Escadeillas, G. (2015). Interactions between hydrated cement paste and organic acids: thermodynamic data and speciation modeling. Cem. Concr. Res. 69, 25–36. doi:10.1016/j.cemconres.2014.12.001

CrossRef Full Text | Google Scholar

De Windt, L., Leclercq, S., and VAN DER Lee, J. (2006). Assessing the durability of nuclear glass with respect to silica controlling processes in a clayey underground disposal. Mater. Res. Soc. Symposium Proc. 932, 931–320. doi:10.1557/proc-932-93.1

CrossRef Full Text | Google Scholar

De Windt, L., and Spycher, N. F. (2019). Reactive transport modeling: a key performance assessment tool for the geologic disposal of nuclear waste. Elements 15, 99–102. doi:10.2138/gselements.15.2.99

CrossRef Full Text | Google Scholar

Dillmann, P., Neff, D., and Féron, D. (2014). Archaeological analogues and corrosion prediction: from past to future. A review. Corros. Eng. Sci. Technol. 49, 567–576. doi:10.1179/1743278214y.0000000214

CrossRef Full Text | Google Scholar

Elakneswaran, Y., Owaki, E., and Nawa, T. (2018). Modelling long-term durability performance of cementitious materials under sodium sulphate interaction. Appl. Sci. 8, 2597. doi:10.3390/app8122597

CrossRef Full Text | Google Scholar

Fernández, A. M., Cuevas, J., and Rivas, P. (2011). Pore water chemistry of the febex bentonite. MRS Online Proc. Libr. 663, 573. doi:10.1557/proc-663-573

CrossRef Full Text | Google Scholar

Fernández, A. M., Kaufhold, S., Sánchez-Ledesma, D. M., Rey, J. J., Melón, A., Robredo, L. M., et al. (2018). Evolution of the THC conditions in the FEBEX in situ test after 18 years of experiment: smectite crystallochemical modifications after interactions of the bentonite with a C-steel heater at 100 °C. Appl. Geochem. 98, 152–171. doi:10.1016/j.apgeochem.2018.09.008

CrossRef Full Text | Google Scholar

Frederickx, L., Honty, M., DE Craen, M., Dohrmann, R., and Elsen, J. (2018). Relating the cation exchange properties of the Boom clay (Belgium) to mineralogy and pore-water chemistry. Clays Clay Minerals 66, 449–465. doi:10.1346/ccmn.2018.064111

CrossRef Full Text | Google Scholar

Freedman, V. L., Bacon, D. H., Saripalli, K. P., and Meyer, P. D. (2004). A film depositional model of permeability for mineral reactions in unsaturated media. Vadose Zone J. 3, 1414–1424. doi:10.2113/3.4.1414

CrossRef Full Text | Google Scholar

Frugier, P., Gin, S., Minet, Y., Chave, T., Bonin, B., Godon, N., et al. (2008). SON68 nuclear glass dissolution kinetics: current state of knowledge and basis of the new GRAAL model. J. Nucl. Mater. 380, 8–21. doi:10.1016/j.jnucmat.2008.06.044

CrossRef Full Text | Google Scholar

Frugier, P., Minet, Y., Rajmohan, N., Godon, N., and Gin, S. (2018). Modeling glass corrosion with GRAAL. npj Mater. Degrad. 2, 35. doi:10.1038/s41529-018-0056-z

CrossRef Full Text | Google Scholar

Garboczi, E. J., and Bentz, D. P. (1992). Computer simulation of the diffusivity of cement-based materials. J. Material Sci. 27, 2083–2092. doi:10.1007/bf01117921

CrossRef Full Text | Google Scholar

Gaucher, E. C., Tournassat, C., Pearson, F. J., Blanc, P., Crouzet, C., Lerouge, C., et al. (2009). A robust model for pore-water chemistry of clayrock. Geochimica Cosmochimica Acta 73, 6470–6487. doi:10.1016/j.gca.2009.07.021

CrossRef Full Text | Google Scholar

Georget, F., Prévost, J. H., and Huet, B. (2017). A reactive transport simulator for variable porosity problems. Comput. Geosci. 21, 95–116. doi:10.1007/s10596-016-9596-x

CrossRef Full Text | Google Scholar

Gerard, B., Didry, O., Marchand, J., Breysse, D., and Hornain, H. (1996). Modelling the long-term durability of concrete barriers for radioactive waste disposals. EDF-96NB00149, EDF, Fr.

Google Scholar

Giffaut, E., Grive, M., Blanc, P., Vieillard, P., Colas, E., Gailhanou, H., et al. (2014). Andra thermodynamic database for performance assessment: ThermoChimie. Appl. Geochem. 49, 225–236. doi:10.1016/j.apgeochem.2014.05.007

CrossRef Full Text | Google Scholar

Glynn, P. D. (1991). MBSSAS: a code for the computation of margules parameters and equilibrium relations in binary solid-solution aqueous-solution systems. Comput. & Geosciences 17, 907–966. doi:10.1016/0098-3004(91)90090-z

CrossRef Full Text | Google Scholar

Godon, N., Gin, S., Rebiscoul, D., and Frugier, P. (2013). SON68 glass alteration enhanced by magnetite. Proc. Fourteenth Int. Symposium Water-Rock Interact. Wri 14 (7), 300–303. doi:10.1016/j.proeps.2013.03.039

CrossRef Full Text | Google Scholar

Goldberg, S., Criscenti, L. J., Turner, D. R., Davis, J. A., and Cantrell, K. J. (2007). Adsorption - desorption processes in subsurface reactive transport modeling. Vadose Zone J. 6, 407–435. doi:10.2136/vzj2006.0085

CrossRef Full Text | Google Scholar

Graczyk, K. M., and Matyka, M. (2020). Predicting porosity, permeability, and tortuosity of porous media from images by deep learning. Sci. Rep. 10, 21488. doi:10.1038/s41598-020-78415-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Grambow, B. (1987). “Nuclear waste glass dissolution: mechanism, model and application,” in JSS-TR--87-02. Sweden: Swedish Nuclear Fuel and Waste Management Co.

Google Scholar

Grambow, B., López-García, M., Olmeda, J., Grivé, M., Marty, N. C. M., Grangeon, S., et al. (2020). Retention and diffusion of radioactive and toxic species on cementitious systems: main outcome of the CEBAMA project. Appl. Geochem. 112, 104480. doi:10.1016/j.apgeochem.2019.104480

CrossRef Full Text | Google Scholar

Grambow, B., Zwicky, H. U., Bart, G., Björner, I. K., and Werme, L. O. (1987). Modeling of the effect of iron corrosion products on nuclear waste glass performance. Mater. Res. Soc. Symposium Proc. 84, 471–481. doi:10.1557/proc-84-471

CrossRef Full Text | Google Scholar

Greskowiak, J., Gwo, J., Jacques, D., Yin, J., and Mayer, K. U. (2015). A benchmark for multi-rate surface complexation and 1D dual-domain multi-component reactive transport of U(VI). Comput. Geosci. 19, 585–597. doi:10.1007/s10596-014-9457-4

CrossRef Full Text | Google Scholar

Grive, M., Duro, L., Colas, E., and Giffaut, E. (2015). Thermodynamic data selection applied to radionuclides and chemotoxic elements: an overview of the ThermoChimie-TDB. Appl. Geochem. 55, 85–94. doi:10.1016/j.apgeochem.2014.12.017

CrossRef Full Text | Google Scholar

Haggerty, R., and Gorelick, S. M. (1995). Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Water Resour. Res. 31, 2383–2400. doi:10.1029/95wr10583

CrossRef Full Text | Google Scholar

Han, S.-C., Jo, Y., and Yun, J.-I. (2021). Chemical degradation of fly ash blended concrete with the seasonal variation of rainwater in a radioactive waste repository: a thermodynamic modeling approach. Cem. Concr. Res. 141, 106326. doi:10.1016/j.cemconres.2020.106326

CrossRef Full Text | Google Scholar

Havlova, V., Knight, L., Laciok, A., Cervinka, R., and Vokal, A. (2007). Analogue evidence relevant to UK HLW glass waste forms. Available at: https://www.natural-analogues.com/nawg-library/glass.

Google Scholar

Heukamp, F. H., Ulm, F. J., and Germaine, J. T. (2001). Mechanical properties of calcium-leached cement pastes: triaxial stress states and the influence of the pore pressures. Cem. Concr. Res. 31, 767–774. doi:10.1016/s0008-8846(01)00472-0

CrossRef Full Text | Google Scholar

Heukamp, F. H., Ulm, F.-J., and Germaine, J. T. (2003). Poroplastic properties of calcium-leached cement-based materials. Cem. Concr. Res. 33, 1155–1173. doi:10.1016/s0008-8846(03)00024-3

CrossRef Full Text | Google Scholar

Hiemstra, T., and Vanriemsdijk, W. H. (1996). A surface structural approach to ion adsorption: the charge distribution (CD) model. J. Colloid Interface Sci. 179, 488–508. doi:10.1006/jcis.1996.0242

CrossRef Full Text | Google Scholar

Hiemstra, T., and VAN Riemsdijk, W. H. (2006). On the relationship between charge distribution, surface hydration, and the structure of the interface of metal hydroxides. J. Colloid Interface Sci. 301, 1–18. doi:10.1016/j.jcis.2006.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Höglund, L. O. (2014). The impact of concrete degradation on the BMA barrier functions, R-13-40. Sweden: SKB.

Google Scholar

Holmes, N., Kelliher, D., and Tyrer, M. (2020). Simulating cement hydration using HYDCEM. Constr. Build. Mater. 239, 117811. doi:10.1016/j.conbuildmat.2019.117811

CrossRef Full Text | Google Scholar

Hommel, J., Coltman, E., and Class, H. (2018). Porosity–permeability relations for evolving pore space: a review with a focus on (Bio-)geochemically altered porous media. Transp. Porous Media 124, 589–629. doi:10.1007/s11242-018-1086-2

CrossRef Full Text | Google Scholar

HOOKER (2003a). Dunarobba. Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Hooker, P. (2003b). Hadrian's wall. Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Hooker, P. (2003c). Inchtuthil roman fort (scotland). Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Huang, B., and Qian, C. (2011). Experiment study of chemo-mechanical coupling behavior of leached concrete. Constr. Build. Mater. 25, 2649–2654. doi:10.1016/j.conbuildmat.2010.12.014

CrossRef Full Text | Google Scholar

Huertas, F., Fuentes-Cantillana, J. L., Jullien, F., Rivas, P., Linares, J. P. F., Ghoreychi, M., et al. (2000). Implementation of the full-scale emplacement (FE) experiment at the Mont Terri rock laboratory. Brussels: European Commission.

Google Scholar

Hummel, W., Berner, U., Curti, E., Pearson, F. J., and Thoenen, T. (2002). Nagra/PSI chemical thermodynamic data base 01/01. USA: Universal Publishers/uPUBLISH.com.

Google Scholar

Idiart, A., Lavina, M., Kosakowski, G., Cochepin, B., Meeussen, J. C. L., Samper, J., et al. (2020). Reactive transport modelling of a low-pH concrete/clay interface. Appl. Geochem. 115, 104562. doi:10.1016/j.apgeochem.2020.104562

CrossRef Full Text | Google Scholar

Jacques, D., Wang, L., Martens, E., and Mallants, D. (2010). Modelling chemical degradation of concrete during leaching with rain and soil water types. Cem. Concr. Res. 40, 1306–1313. doi:10.1016/j.cemconres.2010.02.008

CrossRef Full Text | Google Scholar

Jenni, A., Gimmi, T., Alt-Epping, P., Mäder, U., and Cloet, V. (2017). Interaction of ordinary Portland cement and Opalinus Clay: dual porosity modelling compared to experimental data. Phys. Chem. Earth 99, 22–37. doi:10.1016/j.pce.2017.01.004

CrossRef Full Text | Google Scholar

Jenni, A., Wersin, P., Thoenen, T., Baeyens, B., Ferrari, A., Gimmi, T. U. K. M., et al. (2019). Bentonite backfill performance in a high-level waste repository: a geochemical perspective. Wettingen, Switzerland: NAGRA. Technical Report 19-03.

Google Scholar

Jin, Q., and Bethke, C. M. (2003). A new rate law describing microbial respiration. Appl. Environ. Microbiol. 69, 2340–2348. doi:10.1128/aem.69.4.2340-2348.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2005). Predicting the rate of microbial respiration in geochemical environments. Geochimica Cosmochimica Acta 69, 1133–1143. doi:10.1016/j.gca.2004.08.010

CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2007). The thermodynamics and kinetics of microbial metabolism. Am. J. Sci. 307, 643–677. doi:10.2475/04.2007.01

CrossRef Full Text | Google Scholar

Johnson, J. W., Oelkers, E. H., and Helgeson, H. C. (1992). SUPCRT92: a software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000°C. Comput. Geosciences 18, 899–947. doi:10.1016/0098-3004(92)90029-q

CrossRef Full Text | Google Scholar

Johnson, L., and King, F. (2008). The effect of the evolution of environmental conditions on the corrosion evolutionary path in a repository for spent fuel and high-level waste in Opalinus Clay. J. Nucl. Mater. 379, 9–15. doi:10.1016/j.jnucmat.2008.06.003

CrossRef Full Text | Google Scholar

Jordan, G., and Rammensee, W. (1998). Dissolution rates of calcite (104) obtained by scanning force microscopy: microtopography-based dissolution kinetics on surfaces with anisotropic step velocities. Geochimica Cosmochimica Acta 62, 941–947. doi:10.1016/s0016-7037(98)00030-1

CrossRef Full Text | Google Scholar

Jordan, N., Marmier, N., Lomenech, C., Giffaut, E., and Ehrhardt, J. J. (2007). Sorption of silicates on goethite, hematite, and magnetite: experiments and modelling. J. Colloid Interface Sci. 312, 224–229. doi:10.1016/j.jcis.2007.03.053

PubMed Abstract | CrossRef Full Text | Google Scholar

Jull, S. Ρ., and Lees, Τ. Ρ. (1990). Studies of historic concrete. Commission of the European Communities - Nuclear Science and Technology. EUR--12972.

Google Scholar

Källström, K., and Lindgren, M. (2014). Waste form and packaging process report for the safety assessment SR-PSU. Sweden: TR-14-03, SKB.

Google Scholar

Kamei, G., Alexander, W. R., Clark, I. D., Degnan, P., Elie, M., Khoury, H., et al. (2010). “Natural analogues of cement: overview of the unique systems in Jordan,” in ASME 2010 13th international conference on environmental remediation and radioactive waste management.

Google Scholar

Kaneko, M., Miura, N., Fujiwara, A., and Yamamoto, M. (2004). Evaluation of gas generation rate by metal corrosion in the reducing environment. TWMC-TRE-03003, NEA.

Google Scholar

Kaufhold, S., Dohrmann, R., Ufer, K., and Kober, F. (2018). Interactions of bentonite with metal and concrete from the FEBEX experiment: mineralogical and geochemical investigations of selected sampling sites. Clay Miner. 53, 745–763. doi:10.1180/clm.2018.54

CrossRef Full Text | Google Scholar

Ke, X., Bernal, S. A., Provis, J. L., and Lothenbach, B. (2020). Thermodynamic modelling of phase evolution in alkali-activated slag cements exposed to carbon dioxide. Cem. Concr. Res. 136, 106158. doi:10.1016/j.cemconres.2020.106158

CrossRef Full Text | Google Scholar

Knight, L. (2003). Scwat Hill Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Kosakowski, G., and Berner, U. (2013). The evolution of clay rock/cement interfaces in a cementitious repository for low- and intermediate level radioactive waste. Phys. Chem. Earth, Parts A/B/C 64, 65–86. doi:10.1016/j.pce.2013.01.003

CrossRef Full Text | Google Scholar

Kreis, P. (1991). Hydrogen evolution from corrosion of iron and steel in low/intermediate level waste repositories. Switzerland: NAGRA. NAGRA Technical Report 91-21.

Google Scholar

Kulik, D. A., Miron, G. D., and Lothenbach, B. (2022). A structurally-consistent CASH+ sublattice solid solution model for fully hydrated C-S-H phases: thermodynamic basis, methods, and Ca-Si-H2O core sub-model. Cem. Concr. Res. 151, 106585. doi:10.1016/j.cemconres.2021.106585

CrossRef Full Text | Google Scholar

Kulik, D. A., Wagner, T., Dmytrieva, S. V., Kosakowski, G., Hingerl, F. F., Chudnenko, K. V., et al. (2013). GEM-Selektor geochemical modeling package: revised algorithm and GEMS3K numerical kernel for coupled simulation codes. Comput. Geosci. 17, 1–24.

Google Scholar

Kulik, D. A., Winnefeld, F., Kulik, A., Miron, G. D., and Lothenbach, B. (2021). CemGEMS – an easy-to-use web application for thermodynamic modeling of cementitious materials. RILEM Tech. Lett. 6, 36–52. doi:10.21809/rilemtechlett.2021.140

CrossRef Full Text | Google Scholar

Kursten, B., and Druyts, F. (2015). Assessment of the uniform corrosion behaviour of carbon steel radioactive waste packages with respect to the disposal concept in the geological Dutch Boom Clay formation. Netherlands: OPERA-PU-SCK513, COVRA.

Google Scholar

Laciok, A. (2004). Glasses: natural Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Laciok, A., and Dalton, J. (2005). Glasses: archeological and historical Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Lasaga, A. C. (1998). Kinetic theory in the earth sciences. Princeton, NJ: Princeton University Press.

Google Scholar

Leal, A. M. M., Kulik, D. A., Smith, W. R., and Saar, M. O. (2017). An overview of computational methods for chemical equilibrium and kinetic calculations for geochemical and reactive transport modeling. Pure Appl. Chem. 89, 597–643. doi:10.1515/pac-2016-1107

CrossRef Full Text | Google Scholar

Lichtner, P. C. (1996). Continuum formulation of multicomponent-multiphase reactive transport. Reviews in mineralogy and geochemistry, Editors P. C. LICHTNER, C. STEEFEL, and E. H. OELKERS, 34, 1–81.

Google Scholar

Liu, S. H., Ferrand, K., and Lemmens, K. (2015). Transport- and surface reaction-controlled SON68 glass dissolution at 30°C and 70°C and pH=13.7. Appl. Geochem. 61, 302–311. doi:10.1016/j.apgeochem.2015.06.014

CrossRef Full Text | Google Scholar

Liu, C., Shang, J., and Zachara, J. M. (2011). Multispecies diffusion models: a study of uranyl species diffusion. Water Resour. 47, 1–16. doi:10.1029/2011wr010575

CrossRef Full Text | Google Scholar

Liu, S., Ferrand, K., Aertsens, M., Jacques, D., and Lemmens, K. (2019). Diffusion models for the early-stage SON68 glass dissolution in a hyper-alkaline solution. Appl. Geochem. 111, 104439. doi:10.1016/j.apgeochem.2019.104439

CrossRef Full Text | Google Scholar

Liu, S., Jacques, D., Govaerts, J., and Wang, L. (2014). Conceptual model analysis of interaction at a concrete-Boom Clay interface. Phys. Chem. Earth 70-71, 150–159. doi:10.1016/j.pce.2013.11.009

CrossRef Full Text | Google Scholar

Li, X., Shui, Z., Gao, X., and Ling, G. (2021). Hydration implanted reactive transport modelling in saturated cement-based materials. Constr. Build. Mater. 275, 122185. doi:10.1016/j.conbuildmat.2020.122185

CrossRef Full Text | Google Scholar

Lombardi, S., and Valentini, G. (1996). “The Dunarobbe forest as natural analogue: analysis of the geoenvironmental factors controlling the wood preservation,” in Sixth EC Natural analogue working group meeting. Proceedings of an international workshop held in Santa Fe, 16761. New Mexico, USA: EUR.

Google Scholar

Lothenbach, B., Kulik, D. A., Matschei, T., Balonis, M., Baquerizo, L., Dilnesa, B., et al. (2019). Cemdata18: a chemical thermodynamic database for hydrated Portland cements and alkali-activated materials. Cem. Concr. Res. 115, 472–506. doi:10.1016/j.cemconres.2018.04.018

CrossRef Full Text | Google Scholar

Lothenbach, B., Matschei, T., Möschner, G., and Glasser, F. P. (2008). Thermodynamic modelling of the effect of temperature on the hydration and porosity of Portland cement. Cem. Concr. Res. 38, 1–18. doi:10.1016/j.cemconres.2007.08.017

CrossRef Full Text | Google Scholar

Lothenbach, B., and Winnefeld, F. (2006). Thermodynamic modelling of the hydration of Portland cement. Cem. Concr. Res. 36, 209–226. doi:10.1016/j.cemconres.2005.03.001

CrossRef Full Text | Google Scholar

Lothenbach, B., and Zajac, M. (2019). Application of thermodynamic modelling to hydrated cements. Cem. Concr. Res. 123, 105779. doi:10.1016/j.cemconres.2019.105779

CrossRef Full Text | Google Scholar

Lu, C. H., Samper, J., Fritz, B., Clement, A., and Montenegro, L. (2011). Interactions of corrosion products and bentonite: an extended multicomponent reactive transport model. Phys. Chem. Earth 36, 1661–1668. doi:10.1016/j.pce.2011.07.013

CrossRef Full Text | Google Scholar

Lutze, V., Grambow, B., Ewing, R. C., and Jercinovic, M. J. (1987). “Natural analogues in radioactive waste disposal,” in Commission of the European communities - radioactive waste management series. Editors B. CÔME, and N. A. CHAPMAN

Google Scholar

Ma, B., and Lothenbach, B. (2020a). Synthesis, characterization, and thermodynamic study of selected Na-based zeolites. Cem. Concr. Res. 135, 106111. doi:10.1016/j.cemconres.2020.106111

CrossRef Full Text | Google Scholar

Ma, B., and Lothenbach, B. (2020b). Thermodynamic study of cement/rock interactions using experimentally generated solubility data of zeolites. Cem. Concr. Res. 135, 106149. doi:10.1016/j.cemconres.2020.106149

CrossRef Full Text | Google Scholar

Ma, B., and Lothenbach, B. (2021). Synthesis, characterization, and thermodynamic study of selected K-based zeolites. Cem. Concr. Res. 148, 106537. doi:10.1016/j.cemconres.2021.106537

CrossRef Full Text | Google Scholar

Macdonald, D. D., Urquidi-Macdonald, M., Engelhardt, G. R., Azizi, O., Saleh, A., Almazooqi, A., et al. (2011). Some important issues in electrochemistry of carbon steel in simulated concrete pore water Part 1-theoretical issues. Corros. Eng. Sci. Technol. 46, 98–103. doi:10.1179/1743278211y.0000000002

CrossRef Full Text | Google Scholar

Macquarrie, K. T. B., and Mayer, K. U. (2005). Reactive transport modeling in fractured rock: a state-of-the-science review. Earth-science Rev. 72, 189–227. doi:10.1016/j.earscirev.2005.07.003

CrossRef Full Text | Google Scholar

Mäder, U., Jenni, A., Lerouge, C., Gaboreau, S., Miyoshi, S., Kimura, Y., et al. (2017). 5-year chemico-physical evolution of concrete–claystone interfaces, Mont Terri rock laboratory (Switzerland). Swiss J. Geosciences 110, 307–327. doi:10.1007/s00015-016-0240-5

CrossRef Full Text | Google Scholar

Maes, N., Churakov, S., Glaus, M., Baeyens, B., Dähn, R., Grangeon, S., et al. (2024). EURAD state-of-the-art report on the understanding of radionuclide retention and transport in clay and crystalline rocks. Front. Nucl. Eng. 3. doi:10.3389/fnuen.2024.1417827

CrossRef Full Text | Google Scholar

Maes, N., Glaus, M. A., Baeyens, B., Marques Fernandes, M., Churakov, S., Dähn, R., et al. (2021). State-of-the-Art report on the understanding of radionuclide retention and transport in clay and crystalline rocks. Final version as of 30.04.2021 of deliverable D5.1 of the HORIZON 2020 project EURAD. EC Grant agreement.847593

Google Scholar

Maes, N., Salah, S., Jacques, D., Aertsens, M., Vangompel, M., DE Canniere, P., et al. (2008). Retention of Cs in Boom Clay: comparison of data from batch sorption tests and diffusion experiments on intact clay cores. Phys. Chem. Earth, Parts A/B/C 33, S149–S155. doi:10.1016/j.pce.2008.10.002

CrossRef Full Text | Google Scholar

Maia, F., Puigdomènech, I., and Molinero, J. (2016). Modelling rates of bacterial sulphide production using lactate and hydrogen as energy sources, 16-05. Sweden: SKB TR.

Google Scholar

Mainguy, M., Tognazzi, C., Torrenti, J. M., and Adenot, F. (2000). Modelling of leaching in pure cement paste and mortar. Cem. Concr. Res. 30, 83–90. doi:10.1016/s0008-8846(99)00208-2

CrossRef Full Text | Google Scholar

Mallinson, L. G., and Davies, I. L. (1987). “A historical examination of concrete,” in Nuclear science and technology. Commission of the European Communities.

Google Scholar

Mann, C., Ferrand, K., Liu, S., Eskelsen, J. R., Pierce, E., Lemmens, K., et al. (2019). Influence of young cement water on the corrosion of the International Simple Glass. Npj Mater. Degrad. 3, 5. doi:10.1038/s41529-018-0059-9

CrossRef Full Text | Google Scholar

Marsh, G. P., Taylor, K. J., Sharland, S. M., and Diver, A. J. (1991). Corrosion of carbon steel overpacks for the geological disposal of radioactive waste Task 3 Characterization of radioactive waste forms A series of final reports (1985-89) No 29, Nuclear Science and technology. Commission of the European Communities.

Google Scholar

Marsh, G. P., Taylor, K. J., Shrland, S. M., and Tasker, P. W. (1986). An approach for evaluating the general and localised corrosion of carbon-steel containers for nuclear waste disposal. MRS Online Proc. Libr. 84, 227–238. doi:10.1557/proc-84-227

CrossRef Full Text | Google Scholar

Martinez, J. S., Santillan, E. F., Bossant, M., Costa, D., and Ragoussi, M. E. (2019). The new electronic database of the NEA Thermochemical Database Project. Appl. Geochem. 107, 159–170. doi:10.1016/j.apgeochem.2019.05.007

CrossRef Full Text | Google Scholar

Martin, V., Jaffre, J., and Roberts, J. E. (2005). Modeling fractures and barriers as interfaces for flow in porous media. Siam J. Sci. Comput. 26, 1667–1691. doi:10.1137/s1064827503429363

CrossRef Full Text | Google Scholar

Marty, N. C. M., Bildstein, O., Blanc, P., Claret, F., Cochepin, B., Gaucher, E. C., et al. (2015a). Benchmarks for multicomponent reactive transport across a cement/clay interface. Comput. Geosci. 19, 635–653. doi:10.1007/s10596-014-9463-6

CrossRef Full Text | Google Scholar

Marty, N. C. M., Claret, F., Lassin, A., Tremosa, J., Blanc, P., Madé, B., et al. (2015b). A database of dissolution and precipitation rates for clay-rocks minerals. Appl. Geochem. 55, 108–118. doi:10.1016/j.apgeochem.2014.10.012

CrossRef Full Text | Google Scholar

Marty, N. C. M., Fritz, B., Clément, A., and Michau, N. (2010). Modelling the long term alteration of the engineered bentonite barrier in an underground radioactive waste repository. Appl. Clay Sci. 47, 82–90. doi:10.1016/j.clay.2008.10.002

CrossRef Full Text | Google Scholar

Marty, N. C. M., Munier, I., Gaucher, E. C., Tournassat, C., Gaboreau, S., Vong, C. Q., et al. (2014). Simulation of cement/clay interactions: feedback on the increasing complexity of modelling strategies. Transp. Porous Media 104, 385–405. doi:10.1007/s11242-014-0340-5

CrossRef Full Text | Google Scholar

Marty, N. C. M., Tournassat, C., Burnol, A., Giffaut, E., and Gaucher, E. C. (2009). Influence of reaction kinetics and mesh refinement on the numerical modelling of concrete/clay interactions. J. Hydrology 364, 58–72. doi:10.1016/j.jhydrol.2008.10.013

CrossRef Full Text | Google Scholar

Matyka, M., Khalili, A., and Koza, Z. (2008). Tortuosity-porosity relation in porous media flow. Phys. Rev. E 78, 026306. doi:10.1103/physreve.78.026306

PubMed Abstract | CrossRef Full Text | Google Scholar

Mayant, C. (2009). Étude des propriétés de rétention et de transport de la magnétite dans un état compacté. Nantes, France: University of Nantes.

Google Scholar

Mayant, C., Grambow, B., Abdelouas, A., Ribet, S., and Ledercq, S. (2008). Surface site density, silicic acid retention and transport properties of compacted magnetite powder. Phys. Chem. Earth 33, 991–999. doi:10.1016/j.pce.2008.05.011

CrossRef Full Text | Google Scholar

Mayer, K. U., Frind, E. O., and Blowes, D. W. (2002). Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions. Water Resour. Res. 38, 1174. doi:10.1029/2001WR000862

CrossRef Full Text | Google Scholar

Mayer, S. J., Van Marcke, P., Jung, H., Thompson, P., and Acharya, G. (2023). Important roles of underground research laboratories for the geological disposal of radioactive wastes: an international perspective, 536. United Kingdom: Geological Society, London, Special Publications, 297–309.

CrossRef Full Text | Google Scholar

Michel, A., Marcos-Meson, V., Kunther, W., and Geiker, M. R. (2021). Microstructural changes and mass transport in cement-based materials: a modeling approach. Cem. Concr. Res. 139, 106285. doi:10.1016/j.cemconres.2020.106285

CrossRef Full Text | Google Scholar

Millington, R. J., and Quirk, J. P. (1961). Permeability of porous solids. Trans. Faraday Soc. 57, 1200–1206. doi:10.1039/tf9615701200

CrossRef Full Text | Google Scholar

Milodowski, A. E., Alexander, W. R., West, J. M., Shaw, R. P., Mcevoy, F. M., Scheidegger, J. M., et al. (2015). A catalogue of analogues for radioactive waste management. Keyworth, Nottingham, United Kingdom: British Geologcial Survey.

Google Scholar

Milodowski, A. E., Hyslop, E. K., Pearce, J. M., Wetton, P. D., Kemp, S. J., Longworth, G., et al. (1998). in Magarin natural analogue study: phase III Volume I. Editor J. A. T. SMELLIE (Sweden: TR-98-04), 135–180.

Google Scholar

Miron, G. D., Kulik, D. A., Yan, Y., Tits, J., and Lothenbach, B. (2022). Extensions of CASH+ thermodynamic solid solution model for the uptake of alkali metals and alkaline earth metals in C-S-H. Cem. Concr. Res. 152, 106667. doi:10.1016/j.cemconres.2021.106667

CrossRef Full Text | Google Scholar

Missana, T., Garcia-Gutierrez, M., Mingarro, M., and Alonso, U. (2019). Selenite retention and cation coadsorption effects under alkaline conditions generated by cementitious materials: the case of C-S-H phases. Acs Omega 4, 13418–13425. doi:10.1021/acsomega.9b01637

PubMed Abstract | CrossRef Full Text | Google Scholar

Moldrup, P., Olesen, T., Gamst, J., Schjonning, P., Yamaguchi, T., and Rolston, D. E. (2000). Predicting the gas diffusion coefficient in repacked soil: water-induced linear reduction model. Soil Sci. Soc. Am. J. 64, 1588–1594. doi:10.2136/sssaj2000.6451588x

CrossRef Full Text | Google Scholar

Moldrup, P., Olesen, T., Rolston, D. E., and Yamaguchi, T. (1997). Modeling diffusion and reaction in soils .7. Predicting gas and ion diffusivity in undisturbed and sieved soils. Soil Sci. 162, 632–640. doi:10.1097/00010694-199709000-00004

CrossRef Full Text | Google Scholar

Molins, S., Trebotich, D., Miller, G. H., and Steefel, C. I. (2017). Mineralogical and transport controls on the evolution of porous media texture using direct numerical simulation. Water Resour. Res. 53, 3645–3661. doi:10.1002/2016wr020323

CrossRef Full Text | Google Scholar

Mon, A., Samper, J., Montenegro, L., Naves, A., and Fernández, J. (2017). Long-term non-isothermal reactive transport model of compacted bentonite, concrete and corrosion products in a HLW repository in clay. J. Contam. Hydrology 197, 1–16. doi:10.1016/j.jconhyd.2016.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Montes-H, G., Fritz, B., Clement, A., and Michau, N. (2005). Modeling of transport and reaction in an engineered barrier for radioactive waste confinement. Appl. Clay Sci. 29, 155–171. doi:10.1016/j.clay.2005.01.004

CrossRef Full Text | Google Scholar

Moog, H. C., Bok, F., Marquardt, C. M., and Brendler, V. (2015). Disposal of nuclear waste in host rock formations featuring high-saline solutions – implementation of a thermodynamic reference database (THEREDA). Appl. Geochem. 55, 72–84. doi:10.1016/j.apgeochem.2014.12.016

CrossRef Full Text | Google Scholar

Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12, 513–522. doi:10.1029/wr012i003p00513

CrossRef Full Text | Google Scholar

Mulcahy, S. R., Jackson, M. D., Chen, H., Li, Y., Cappelletti, P., Wenk, H. R., et al. (2017). Phillipsite and Al-tobermorite mineral cements produced through low-temperature water-rock reactions in roman marine concrete. Am. Mineralogist 102, 1435–1450. doi:10.2138/am-2017-5993ccby

CrossRef Full Text | Google Scholar

Müller, H. R., Garitte, B., Vogt, T., Köhler, S., Sakak, T., Weber, H., et al. (2017). Implementation of the full-scale emplacement (FE) experiment at the Mont Terri rock laboratory. Swiss J. Geosciences 110, 287–306. doi:10.1007/s00015-016-0251-2

CrossRef Full Text | Google Scholar

Murphy, W. M., Oelkers, E. H., and Lichtner, P. C. (1989). Surface-reaction versus diffusion control of mineral dissolution and growth-rates in geochemical processes. Chem. Geol. 78, 357–380. doi:10.1016/0009-2541(89)90069-7

CrossRef Full Text | Google Scholar

Myers, R. J., Bernal, S. A., San Nicolas, R., and Provis, J. L. (2013). Generalized structural description of calcium-sodium aluminosilicate hydrate gels: the cross-linked substituted tobermorite model. Langmuir 29, 5294–5306. doi:10.1021/la4000473

PubMed Abstract | CrossRef Full Text | Google Scholar

Naish, C. C., Balkwill, P. H., O'Brien, T. M., Taylor, K. J., and Marsh, G. P. (1991). The anaerobic corrosion of carbon steel in concrete, Task 3: characterization of waste forms.

Google Scholar

NANET (2006). Analogues for the near-field of a repository WP1 of the European community under the ‘competitive and sustainable growth. Programme. 1998-2002).

Google Scholar

NEA (2001). The role of underground laboratories in nuclear waste disposal programmes. France: OECD.

Google Scholar

NEA (2013). Underground research laboratories (URL). France: NEA/RWM/R(2013)2, OECD-NEA

Google Scholar

Necib, S., Diomidis, N., Keech, P., and Nakayama, M. (2017). Corrosion of carbon steel in clay environments relevant to radioactive waste geological disposals, Mont Terri rock laboratory (Switzerland). Swiss J. Geosciences 110, 329–342. doi:10.1007/s00015-016-0259-7

CrossRef Full Text | Google Scholar

Neeft, E., Deissmann, G., and Jacques, D. (2024). Assessment of the chemical evolution at the disposal cell scale – Part I – processes at interfaces and evolution at disposal cell scale. Front. Nucl. Eng. this issue.

Google Scholar

Neff, D., Reguer, S., Bellot-Gurlet, L., Dillmann, P., and Bertholon, R. (2004). Structural characterization of corrosion products on archaeological iron: an integrated analytical approach to establish corrosion forms. J. Raman Spectrosc. 35, 739–745. doi:10.1002/jrs.1130

CrossRef Full Text | Google Scholar

Ngo, V. V., Clément, A., Michau, N., and Fritz, B. (2015). Kinetic modeling of interactions between iron, clay and water: comparison with data from batch experiments. Appl. Geochem. 53, 13–26. doi:10.1016/j.apgeochem.2014.12.003

CrossRef Full Text | Google Scholar

Ngo, V. V., Delalande, M., Clement, A., Michau, N., and Fritz, B. (2014). Coupled transport-reaction modeling of the long-term interaction between iron, bentonite and Callovo-Oxfordian claystone in radioactive waste confinement systems. Appl. Clay Sci. 101, 430–443. doi:10.1016/j.clay.2014.08.020

CrossRef Full Text | Google Scholar

Ochs, M., Mallants, D., and Wang, L. (2016). Radionuclide and metal sorption on cement and concrete. Springer.

Google Scholar

Oda, M. (1985). Permeability tensor for discontinuous rock masses. Geotechnique 35, 483–495. doi:10.1680/geot.1985.35.4.483

CrossRef Full Text | Google Scholar

Oelkers, E. H., Benezeth, P., and Pokrovski, G. S. (2009). Thermodynamic databases for water-rock interaction. Rev. Mineral. Geochem 70, 1–46. doi:10.2138/rmg.2009.70.1

CrossRef Full Text | Google Scholar

Oh, B. H., and Jang, S. Y. (2004). Prediction of diffusivity of concrete based on simple analytic equations. Cem. Concr. Res. 34, 463–480. doi:10.1016/j.cemconres.2003.08.026

CrossRef Full Text | Google Scholar

Olmeda, J., Missana, T., Grandia, F., Grive, M., Garcia-Gutierrez, M., Mingarro, M., et al. (2019). Radium retention by blended cement pastes and pure phases (C-S-H and C-A-S-H gels): experimental assessment and modelling exercises. Appl. Geochem. 105, 45–54. doi:10.1016/j.apgeochem.2019.04.004

CrossRef Full Text | Google Scholar

Or, D., Smets, B. F., Wraith, J. M., Dechesne, A., and Friedman, S. P. (2007). Physical constraints affecting bacterial habitats and activity in unsaturated porous media – a review. Adv. Water Resour. 30, 1505–1527. doi:10.1016/j.advwatres.2006.05.025

CrossRef Full Text | Google Scholar

Or, D., and Tuller, M. (2000). Flow in unsaturated fractured porous media: hydraulic conductivity of rough surfaces. Water Resour. Res. 36, 1165–1177. doi:10.1029/2000wr900020

CrossRef Full Text | Google Scholar

Or, D., Tuller, M., and Fedors, R. (2005). Seepage into drifts and tunnels in unsaturated fractured rock. Water Resour. Res. 41, W05022. doi:10.1029/2004wr003689

CrossRef Full Text | Google Scholar

Oron, A. P., and Berkowitz, B. (1998). Flow in rock fractures: the local cubic law assumption reexamined. Water Resour. Res. 34, 2811–2825. doi:10.1029/98wr02285

CrossRef Full Text | Google Scholar

Palandri, J. L., and Kharaka, Y. K. (2004). A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling. Menlo Park, CA: U.S. Geological Survey. Open File Report 2004-1068.

Google Scholar

Patel, R. A., Churakov, S. V., and Prasianakis, N. I. (2021). A multi-level pore scale reactive transport model for the investigation of combined leaching and carbonation of cement paste. Cem. Concr. Compos. 115, 103831. doi:10.1016/j.cemconcomp.2020.103831

CrossRef Full Text | Google Scholar

Patel, R. A., Perko, J., Jacques, D., DE Schutter, G., Ye, G., and VAN Breugel, K. (2018a). A three-dimensional lattice Boltzmann method based reactive transport model to simulate changes in cement paste microstructure due to calcium leaching. Constr. Build. Mater. 166, 158–170. doi:10.1016/j.conbuildmat.2018.01.114

CrossRef Full Text | Google Scholar

Patel, R. A., Perko, J., Jacques, D., DE Schutter, G., Ye, G., and VAN Bruegel, K. (2018b). Effective diffusivity of cement pastes from virtual microstructures: role of gel porosity and capillary pore percolation. Constr. Build. Mater. 165, 833–845. doi:10.1016/j.conbuildmat.2018.01.010

CrossRef Full Text | Google Scholar

Patel, R., Phung, Q. T., Seetharam, S. C., Perko, J., Jacques, D., Maes, N., et al. (2016). Diffusivity of saturated ordinary Portland cement-based materials: a critical review of experimental and analytical modelling approaches. Cem. Concr. Res. 90, 52–72. doi:10.1016/j.cemconres.2016.09.015

CrossRef Full Text | Google Scholar

Pearson, F. J., Tournassat, C., and Gaucher, E. C. (2011). Biogeochemical processes in a Clay formation in situ experiment: Part E - equilibrium controls on chemistry of pore water from the Opalinus clay, Mont Terri underground research laboratory, Switzerland. Appl. Geochem. 26, 990–1008. doi:10.1016/j.apgeochem.2011.03.008

CrossRef Full Text | Google Scholar

Peña, J., Torres, E., Turrero, M. J., Escribano, A., and Martín, P. L. (2008). Kinetic modelling of the attenuation of carbon steel canister corrosion due to diffusive transport through corrosion product layers. Corros. Sci. 50, 2197–2204. doi:10.1016/j.corsci.2008.06.004

CrossRef Full Text | Google Scholar

Peng, D.-Y., and Robinson, D. B. (1976). A new two-constant equation of state. Industrial Eng. Chem. Fundam. 15, 59–64. doi:10.1021/i160057a011

CrossRef Full Text | Google Scholar

Perko, J., Jacques, D., and Govaerts, J. (2017). Water saturation and flow in a surface disposal facility - numerical study for the Dessel repository. Mol, Belgium: SCK•CEN ER-0355.

Google Scholar

Perko, J., Jacques, D., Seetharam, S. C., and Mallants, D. (2010). Long-term evolution of the near surface disposal facility at Dessel. Belgioum: NIROND-TR 2010–04 E, ONDRAF/NIRAS.

Google Scholar

Pham, H. L. (2018). Operation of biofilters: a numerical approach to some couplings between hydrodynamic and biofilm growth modeling. PhD. France: Université Grenoble Alpes.

Google Scholar

Philippini, V., Naveau, A., Catalette, H., and Leclercq, S. (2006). Sorption of silicon on magnetite and other corrosion products of iron. J. Nucl. Mater. 348, 60–69. doi:10.1016/j.jnucmat.2005.09.002

CrossRef Full Text | Google Scholar

Phung, Q. T. (2015). Effects of Carbonation and calcium Leaching on Microstructure and transport Properties of cement pastes. PhD. Ghent, Belgium: Ghent University.

Google Scholar

Pruess, K., and Narasimhan, T. N. (1985). A practical method for modeling fluid and heat-flow in fractured porous-media. Soc. Petroleum Eng. J. 25, 14–26. doi:10.2118/10509-pa

CrossRef Full Text | Google Scholar

Rassineux, F., Petit, J. C., and Meunier, A. (1989). Ancient analogues of modern cement: calcium hydrosilicates in mortars and concretes from gallo–roman thermal baths of western France. J. Am. Ceram. Soc. 72, 1026–1032. doi:10.1111/j.1151-2916.1989.tb06263.x

CrossRef Full Text | Google Scholar

Read, D., Glasser, F. P., Ayora, C., Guardiola, M. T., and Sneyers, A. (2001). Mineralogical and microstructural changes accompanying the interaction of Boom Clay with ordinary Portland cement. Adv. Cem. Res. 13, 175–183. doi:10.1680/adcr.2001.13.4.175

CrossRef Full Text | Google Scholar

Rebiscoul, D., Tormos, V., Godon, N., Mestre, J. P., Cabie, M., Amiard, G., et al. (2015). Reactive transport processes occurring during nuclear glass alteration in presence of magnetite. Appl. Geochem. 58, 26–37. doi:10.1016/j.apgeochem.2015.02.018

CrossRef Full Text | Google Scholar

Reddy, B., Pdovani, C., Rance, A. P., Smart, N., Cook, A., Haynes, H. M., et al. (2021). The anaerobic corrosion of candidate disposal canister materials in compacted bentonite exposed to natural granitic porewater containing native microbial populations. Mater. Corros. 72, 361–382. doi:10.1002/maco.202011798

CrossRef Full Text | Google Scholar

Repina, M., Bouyer, F., and Lagneau, V. (2020). Reactive transport modeling of glass alteration in a fractured vitrified nuclear glass canister: from upscaling to experimental validation. J. Nucl. Mater. 528, 151869. doi:10.1016/j.jnucmat.2019.151869

CrossRef Full Text | Google Scholar

Rimstidt, J. D. (2013). Geochemical rate models: an introduction to geochemical kinetics. Cambridge, UK: Cambridge University Press.

Google Scholar

Roosz, C., Vieillard, P., Blanc, P., Gaboreau, S., Gailhanou, H., Braithwaite, D., et al. (2018). Thermodynamic properties of C-S-H, C-A-S-H and M-S-H phases: results from direct measurements and predictive modelling. Appl. Geochem. 92, 140–156. doi:10.1016/j.apgeochem.2018.03.004

CrossRef Full Text | Google Scholar

Rougelot, T., Burlion, N., Bernard, D., and Skoczylas, F. (2010). About microcracking due to leaching in cementitious composites: X-ray microtomography description and numerical approach. Cem. Concr. Res. 40, 271–283. doi:10.1016/j.cemconres.2009.09.021

CrossRef Full Text | Google Scholar

Samper, J., Mon, A., and Montenegro, L. (2020). A coupled THMC model of the geochemical interactions of concrete and bentonite after 13 years of FEBEX plug operation. Appl. Geochem. 121, 104687. doi:10.1016/j.apgeochem.2020.104687

CrossRef Full Text | Google Scholar

Samper, J., Naves, A., Montenegro, L., and Mon, A. (2016). Reactive transport modelling of the long-term interactions of corrosion products and compacted bentonite in a HLW repository in granite: uncertainties and relevance for performance assessment. Appl. Geochem. 67, 42–51. doi:10.1016/j.apgeochem.2016.02.001

CrossRef Full Text | Google Scholar

Samper, J., Zheng, L., Montenegro, L., Fernandez, A. M., and Rivas, P. (2008). Coupled thermo-hydro-chemical models of compacted bentonite after FEBEX in situ test. Appl. Geochem. 23, 1186–1201. doi:10.1016/j.apgeochem.2007.11.010

CrossRef Full Text | Google Scholar

Samson, E., and Marchand, J. (2007). Modeling the effect of temperature on ionic transport in cementitious materials. Cem. Concr. Res. 37, 455–468. doi:10.1016/j.cemconres.2006.11.008

CrossRef Full Text | Google Scholar

Sanchez-Vila, X., Dentz, M., and Donado, L. D. (2007). Transport-controlled reaction rates under local non-equilibrium conditions. Geophys. Res. Lett. 34, 2007GL029410. doi:10.1029/2007gl029410

CrossRef Full Text | Google Scholar

Sarkar, S., Mahadevan, S., Meeussen, J. C. L., VAN DER Sloot, H., and Kosson, D. S. (2010). Numerical simulation of cementitious materials degradation under external sulfate attack. Cem. Concr. Compos. 32, 241–252. doi:10.1016/j.cemconcomp.2009.12.005

CrossRef Full Text | Google Scholar

Savage, D. (1998). in Maqarin natural analogue study: phase III. SKB. Editor J. A. T. SMELLIE (Sweden).

Google Scholar

Savage, D., Watson, C., Benbow, S., and Wilson, J. (2010). Modelling iron-bentonite interactions. Appl. Clay Sci. 47, 91–98. doi:10.1016/j.clay.2008.03.011

CrossRef Full Text | Google Scholar

Seetharam, S. C., Perko, J., Jacques, D., and Mallants, D. (2014). Influence of fracture networks on radionuclide transport from solidified waste forms. Nucl. Eng. Des. 270, 162–175. doi:10.1016/j.nucengdes.2013.12.048

CrossRef Full Text | Google Scholar

Seigneur, N., L’Hôpital, E., Dauzères, A., Sammaljärvi, J., Voutilainen, M., Labeau, P. E., et al. (2017). Transport properties evolution of cement model system under degradation - incorporation of a pore-scale approach into reactive transport modelling. Phys. Chem. Earth, Parts A/B/C 99, 95–109. doi:10.1016/j.pce.2017.05.007

CrossRef Full Text | Google Scholar

Seigneur, N., Mayer, K. U., and Steefel, C. I. (2019). Reactive transport in evolving porous media. React. Transp. Nat. Eng. Syst. 85, 197–238. doi:10.2138/rmg.2019.85.7

CrossRef Full Text | Google Scholar

Šimůnek, J., and VAN Genuchten, M. T. (2008). Modeling nonequilibrium flow and transport processes using HYDRUS. Vadose Zone J. 7, 782–797. doi:10.2136/vzj2007.0074

CrossRef Full Text | Google Scholar

SKB (1999). Deep repository for spent nuclear fuel. SR 97 - Post closue safety. Vol 1 and 2. SKB TR-99-06. Sweden: SKB

Google Scholar

Small, J. S., and Abrahamsen-Mills, L. (2018). Modelling of microbial processes relevant to ILW disposal. Deliv. D1.8 MIND Proj.

Google Scholar

Smart, N. R., Reddy, B., Rance, A. P., Nixon, D. J., Frutschi, M., Bernier-Latmani, R., et al. (2017). The anaerobic corrosion of carbon steel in compacted bentonite exposed to natural Opalinus Clay porewater containing native microbial populations. Corros. Eng. Sci. Technol. 52, 101–112. doi:10.1080/1478422x.2017.1315233

CrossRef Full Text | Google Scholar

Soler, J. M., and Mäder, U. (2007). Mineralogical alteration and associated permeability changes induced by a high-pH plume: modeling of a granite core infiltration experiment. Appl. Geochem. 22, 17–29. doi:10.1016/j.apgeochem.2006.07.015

CrossRef Full Text | Google Scholar

Soler, J. M., Pfingsten, W., Paris, B., Mäder, U. K., Frieg, B., Neall, F., et al. (2006). HPF-Experiment: modelling report. Wettingen, Switzerland: NAGRA.

Google Scholar

Sposito, G. (1981). The thermodynamics of soil solutions. Oxford: Oxford University Press.

Google Scholar

Steadman, J. A. (1989). “CEC Natural analogue working group second meeting,” in Commission of the European communities - nuclear science and technology. Editors B. CÔME, and N. A. CHAPMAN

Google Scholar

Steefel, C. I., Appelo, C. A. J., Arora, B., Jacques, D., Kalbacher, T., Kolditz, O., et al. (2015a). Reactive transport codes for subsurface environmental simulation. Comput. Geosci. 19, 445–478. doi:10.1007/s10596-014-9443-x

CrossRef Full Text | Google Scholar

Steefel, C. I., Yabusaki, S. B., and Mayer, K. U. (2015b). Reactive transport benchmarks for subsurface environmental simulation. Comput. Geosci. 19, 439–443. doi:10.1007/s10596-015-9499-2

CrossRef Full Text | Google Scholar

Steefel, C., and Macquarrie, K. T. B. (1996). “Approaches to modeling of reactive transport in porous media,” in Reviews in mineralogy and geochemistry. Editors P. C. LICHTNER, C. STEEFEL, and E. H. OELKERS

Google Scholar

Stora, E., Bary, B., He, Q. C., Deville, E., and Montarnal, P. (2009). Modelling and simulations of the chemo-mechanical behaviour of leached cement-based materials: leaching process and induced loss of stiffness. Cem. Concr. Res. 39, 763–772. doi:10.1016/j.cemconres.2009.05.010

CrossRef Full Text | Google Scholar

Sudicky, E. A., and Mclaren, R. G. (1992). The laplace transform galerkin technique for large-scale simulation of mass-transport in discretely fractured porous formations. Water Resour. Res. 28, 499–514. doi:10.1029/91wr02560

CrossRef Full Text | Google Scholar

Swanton, S. W., Baston, G. M. N., and Smart, N. R. 2015. Rates of steel corrosion and carbon-14 release from irradiated steels – state of the art review D2.1 from CArbon-14 Source Term project from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement no. 604779.

Google Scholar

Taylor, S. W., and Jaffe, P. R. (1990). Biofilm growth and the related changes in the physical properties of a porous medium 3. Dispersivity and model verification. Water Resour. Res. 26, 2171–2180. doi:10.1029/wr026i009p02171

CrossRef Full Text | Google Scholar

Thoenen, T., Hummel, W., Berner, U., and Curti, E. (2014). The PSI/nagra chemical thermodynamic database 12/07. Switzerland: PSI.

Google Scholar

Tixier, R., and Mobasher, B. (2003). Modeling of damage in cement-based materials subjected to external sulfate attack. II: comparison with experiments. J. Mater. Civ. Eng. 15, 314–322. doi:10.1061/(asce)0899-1561(2003)15:4(314)

CrossRef Full Text | Google Scholar

Tournassat, C., Vinsot, A., Gaucher, E. C., and Altmann, S. (2015). “Chapter 3 - chemical conditions in clay-rocks,” in Developments in clay science. Editors C. TOURNASSAT, C. I. STEEFEL, I. C. BOURG, and F. BERGAYA (Elsevier).

Google Scholar

Trapote-Barreira, A., Cama, J., Soler, J. M., and Lothenbach, B. (2016). Degradation of mortar under advective flow: column experiments and reactive transport modeling. Cem. Concr. Res. 81, 81–93. doi:10.1016/j.cemconres.2015.12.002

CrossRef Full Text | Google Scholar

Tremosa, J., Arcos, D., Matray, J. M., Bensenouci, F., Gaucher, E. C., Tournassat, C., and Hadi, J. (2012). Geochemical characterization and modelling of the Toarcian/Domerian porewater at the Tournemire underground research laboratory. Applied Geochemistry 27 (7), 1417–1431.

CrossRef Full Text | Google Scholar

Trotignon, L., Devallois, V., Peycelon, H., Tiffreau, C., and Bourbon, X. (2007). Predicting the long term durability of concrete engineered barriers in a geological repository for radioactive waste. Phys. Chem. Earth 32, 259–274. doi:10.1016/j.pce.2006.02.049

CrossRef Full Text | Google Scholar

Trotignon, L., Techer, I., and Kohler, E. (2004). Col du Perthus Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Tuller, M., and Or, D. (2001). Hydraulic conductivity of variably saturated porous media: film and corner flow in angular pore space. Water Resour. Res. 37, 1257–1276. doi:10.1029/2000wr900328

CrossRef Full Text | Google Scholar

Tuller, M., and Or, D. (2002). Unsaturated hydraulic conductivity of structured porous media: a review of liquid configuration–based models. Vadose Zone J. 1, 14–37. doi:10.2113/1.1.14

CrossRef Full Text | Google Scholar

Ulm, F.-J., Torrenti, J.-M., and Adenot, F. (1999). Chemoporoplasticity of calcium leaching in concrete. J. Eng. Mech. 125, 1200–1211. doi:10.1061/(asce)0733-9399(1999)125:10(1200)

CrossRef Full Text | Google Scholar

Valcke, E., Smets, S., Labat, S., Lemmens, K., VAN Iseghem, P., Thomas, P., et al. (2006). CORALUS: an integrated in situ corrosion test on α-active HLW glass. Mater. Res. Soc. Symposium Proc. 932, 1181. doi:10.1557/proc-932-118.1

CrossRef Full Text | Google Scholar

Van der Lee, J. (1998). Thermodynamic and mathematical concepts of CHESS.

Google Scholar

Van Geet, M., Bruggeman, C., and DE Craen, M. (2023). Geological disposal of radioactive waste in deep clay formations: celebrating 40 years of RD&D in the Belgian URL HADES, 536. United Kingdom: Geological Society, London, Special Publications, 1–10.

CrossRef Full Text | Google Scholar

van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

van Genuchten, M. T., Leij, F. J., and Yates, S. R. (1991). The RETC code for quantifying the hydraulic functions of unsaturated. Soils.

Google Scholar

van Humbeeck, H., DE Bock, C., and Bastiaens, W. (2007) Demonstrating the construction and backfilling feasibility of the supercontainer design for HLW, 2B.14.

Google Scholar

van Iseghem, P., Berghman, K., Lemmens, K., Timmermans, W., and Wang, L. (1992). Laboratory and in-situ interaction between simulated waste glasses and clay Task 3 Characterization of radioactive waste forms A series of final reports (1985-89) No 21. Commission of the European Communities - Nuclear science and technology.

Google Scholar

van Iseghem, P., Valcke, E., and Lodding, A. (2001). In situ testing of the chemical durability of vitrified high-level waste in a Boom Clay formation in Belgium: discussion of recent data and concept of a new test. J. Nucl. Mater. 298, 86–94. doi:10.1016/s0022-3115(01)00618-3

CrossRef Full Text | Google Scholar

Vehmas, T., and Itälä, A. (2019). “Compositional parameters for solid solution C-S-H and the applicability to thermodynamic modelling,” in KIT scientific reports 7752: Proceedings of the second workshop of the horizon 2020 cebama project. Germany, 293–300.

Google Scholar

Verhoef, E. V., DE Bruin, A. M. G., Wiegers, R. B., Neeft, E. A. C., and Deissmann, G. (2014). Cementitious materials in OPERA disposal concept. OPERA-PG-COV020, COVRA, Neth.

Google Scholar

Vernaz, E., Grambow, Β., Lutze, W., Lemmens, K., and VAN Iseghem, P. (1996). in Assessment of the long-term durability of radioactive waste glass. Editor T. MCMENAMIN (European Commission).

Google Scholar

von Greve-Dierfeld, S., Lothenbach, B., Vollpracht, A., Wu, B., Huet, B., Andrade, C., et al. (2020). Understanding the carbonation of concrete with supplementary cementitious materials: a critical review by RILEM TC 281-CCC. Mater. Struct. 53, 136. doi:10.1617/s11527-020-01558-w

CrossRef Full Text | Google Scholar

Wagner, T., Kulik, D. A., Hingerl, F. F., and Dmytrieva, S. V. (2012). GEM-Selektor geochemical modeling package: TSolMod library and data interface for multicomponent phase models. Can. Mineral. 50, 1173–1195. doi:10.3749/canmin.50.5.1173

CrossRef Full Text | Google Scholar

Walton, J. C., Plansky, L. E., and Smith, R. W. (1990). Models for estimation of service life of concrete barriers in low-level radioactive waste disposal. NUREG/CR-5542, EGG-2597. USA: US NRC.

Google Scholar

Walton, J. C., and Seitz, R. R. (1991). Performance of intact and partially degraded concrete barriers. Limiting Fluid Flow. NUREG/CR- 5445, TI92–016245.

Google Scholar

Wang, A., Kuebler, K. E., Jolliff, B. L., and Haskin, L. A. (2004). Raman spectroscopy of Fe-Ti-Cr-oxides, case study: martian meteorite EETA79001. Am. Mineralogist 89, 665–680. doi:10.2138/am-2004-5-601

CrossRef Full Text | Google Scholar

Wang, L., Honty, M., DE Craen, M., and Frederickx, L. (2023). Boom Clay pore-water geochemistry at the Mol site: chemical equilibrium constraints on the concentrations of major elements. Appl. Geochem. 148, 105541. doi:10.1016/j.apgeochem.2022.105541

CrossRef Full Text | Google Scholar

Wang, L., Jacques, D., and DE Cannière, P. (2010). Effects of an alkaline plume on the Boom Clay as a potential host formation for geological disposal of radioactive waste. SCK-CEN-ER-28, SCK•CEN, Belg.

Google Scholar

Watson, C., Savage, D., and Wilson, J. (2017). Geochemical modelling of the LCS experiment. Quintessa Rep. QRS-1523D-2 , Henley-on-Thames, U. K Quintessa.

Google Scholar

Watson, C., Wilson, J., Savage, D., and Norris, S. (2018). Coupled reactive transport modelling of the international Long-Term Cement Studies project experiment and implications for radioactive waste disposal. Appl. Geochem. 97, 134–146. doi:10.1016/j.apgeochem.2018.08.014

CrossRef Full Text | Google Scholar

Wersin, P., Birgersson, M., Karnland, O., and Snellman, M. (2008). Impact of corrosion-derived iron on the bentonite buffer within the KBS-3H disposal concept. Sweden: SKB. SKB report TR-08–34.

Google Scholar

Wilson, J. C., Benbow, S., Sasamoto, H., Savage, D., and Watson, C. (2015). Thermodynamic and fully-coupled reactive transport models of a steel–bentonite interface. Appl. Geochem. 61, 10–28. doi:10.1016/j.apgeochem.2015.05.005

CrossRef Full Text | Google Scholar

Wilson, J., Savage, D., Cuadros, J., Shibata, M., and Ragnarsdottir, K. V. (2006). The effect of iron on montmorillonite stability. (I) Background and thermodynamic considerations. Geochimica Cosmochimica Acta 70, 306–322. doi:10.1016/j.gca.2005.10.003

CrossRef Full Text | Google Scholar

Wissmeier, L., and Barry, D. A. (2009). Effect of mineral reactions on the hydraulic properties of unsaturated soils: model development and application. Adv. Water Resour. 32, 1241–1254. doi:10.1016/j.advwatres.2009.05.004

CrossRef Full Text | Google Scholar

Wissmeier, L., and Barry, D. A. (2010). Implementation of variably saturated flow into PHREEQC for the simulation of biogeochemical reactions in the vadose zone. Environ. Model. & Softw. 25, 526–538. doi:10.1016/j.envsoft.2009.10.001

CrossRef Full Text | Google Scholar

Wouters, L., and Verheyen, A. (2004). Isle of Skye Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Wouters, L., Verheyen, A., and Dalton, J. (2005a). Busachi (sardinia) Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Wouters, L., Verheyen, A., and Dalton, J. (2005b). Kinnekulle Available at: http://www.natural-analogues.com/nawg-library/na-overviews/analoguereview.

Google Scholar

Xie, S. Y., Shao, J. F., and Burlion, N. (2008). Experimental study of mechanical behaviour of cement paste under compressive stress and chemical degradation. Cem. Concr. Res. 38, 1416–1423. doi:10.1016/j.cemconres.2008.06.011

CrossRef Full Text | Google Scholar

Xie, M., Mayer, K. U., Claret, F., Alt-Epping, P., Jacques, D., Steefel, C., et al. (2015). Implementation and evaluation of permeability-porosity and tortuosity-porosity relationships linked to mineral dissolution-precipitation. Comput. Geosci. 19, 655–671. doi:10.1007/s10596-014-9458-3

CrossRef Full Text | Google Scholar

Xu, T. F., Sonnenthal, E., Spycher, N., and Pruess, K. (2006). TOUGHREACT - a simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: applications to geothermal injectivity and CO2 geological sequestration. Comput. & Geosciences 32, 145–165. doi:10.1016/j.cageo.2005.06.014

CrossRef Full Text | Google Scholar

Xu, T. F., Spycher, N., Sonnenthal, E., Zhang, G. X., Zheng, L. E., and Pruess, K. (2011). TOUGHREACT Version 2.0: a simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. & Geosciences 37, 763–774. doi:10.1016/j.cageo.2010.10.007

CrossRef Full Text | Google Scholar

Zhang, G., Lu, P., Zhang, Y., Tu, K., and Zhu, C. (2020). SupPhreeqc: a program for generating customized Phreeqc thermodynamic datasets from Supcrtbl and extending calculations to elevated pressures and temperatures. Comput. & Geosciences 143, 104560. doi:10.1016/j.cageo.2020.104560

CrossRef Full Text | Google Scholar

Zhang, Y., Hu, B., Teng, Y., Tu, K., and Zhu, C. (2019). A library of BASIC scripts of reaction rates for geochemical modeling using phreeqc. Comput. & Geosciences 133, 104316. doi:10.1016/j.cageo.2019.104316

CrossRef Full Text | Google Scholar

Zimmer, K., Zhang, Y., Lu, P., Chen, Y., Zhang, G., Dalkilic, M., et al. (2016). SUPCRTBL: a revised and extended thermodynamic dataset and software package of SUPCRT92. Comput. & Geosciences 90, 97–111. doi:10.1016/j.cageo.2016.02.013

CrossRef Full Text | Google Scholar