Acceleration performance results of the SN nodal transport solvers in MOSASAUR code system for lead-based reactor cores

To address the efficiency bottleneck encountered in reactor design calculations for the newly developed lead-based reactor neutronics analysis code system MOSASAUR, we recently developed acceleration functions based on various coarse-mesh finite difference (CMFD) methods and spatial domain decomposition parallel algorithm. However, the applicability of these improvements to different lead-based reactors remains to be analyzed. This work collected and established core models for various types of lead-based reactor. Based on different SN nodal transport solvers, we analyzed the acceleration performance of different CMFD methods, different CPU cores, and the combination of CMFD and parallel calculation. The results indicated that the impact of different CMFD acceleration or parallel acceleration on the calculation accuracy was negligible; the rCMFD method had good stability and convergence rate, achieving speedup of several to dozens; parallel efficiency was related to the number of meshes, and for large reactor cores, superlinear speedup was achieved with 200 CPU cores; rCMFD and parallel computing could achieve combined speedup, with 200 cores achieving speedup of hundreds to thousands, typically completing a reactor core transport calculation in 1 min.

1 Introduction

As a candidate for the fourth-generation nuclear reactor system, lead-based fast reactors offer multiple advantages in reactor physics and thermal hydraulics. These advantages include achieving fuel breeding and transmutation of high-level radioactive waste, achieving high power density at normal pressure, and facilitating natural circulation for heat transfer. The design of lead-cooled fast reactors is dependent on reliable reactor analysis code for analyzing, verifying, and optimizing the reactor core design.

To obtain an optimized reactor core design within a reasonable time, the efficiency of reactor core transport calculation is crucial. Directly performing whole-core high-fidelity transport calculations would bring huge computational costs. Existing fast reactor physical analysis codes mostly adopt an assembly-homogenized strategy. First, energy spectrum calculations are performed for different typical assemblies to obtain assembly-homogenized multigroup cross sections. Then, based on these cross sections, whole-core three-dimensional transport calculations are performed to obtain key core physical parameters.

Due to the homogeneous nature of assembly cross sections, the transport nodal methods based on coarse mesh usually have higher efficiency than fine mesh methods. Existing fast reactor physical analysis codes mostly adopt PN/SPN variational nodal method (VNM) and SN nodal method (SNM) for reactor core transport calculation. For example, the US fast reactor analysis code DIF3D adopts the DIF3D-VARIANT (Smith et al., 2014) solver based on the PN/SPN SNM (Zhang and Li, 2022), the French fast reactor analysis system ERANOS adopts the TGV/VARIANT (Ruggieri et al., 2006) solver based on the PN/SPN VNM, Japan and Russia have developed NSHEX (Todorova et al., 2004) and CORNER (Bereznev, 2016) codes based on SNM with hexagonal-prism mesh for fast reactor physics analysis. And the fast reactor analysis codes of XJTU (Zheng et al., 2018) and NPIC (Zhang et al., 2023) have adopted the SNM based on triangular-prism, hexagonal-prism, and quadrangular-prism meshes. Both the VNM and the SNM can achieve high accuracy at a relatively fast speed. However, SNM code usually only requires a few GB instead of the tens of GB of the VNM code for typical fast reactors (Smith et al., 2014; Todorova et al., 2004; Xu et al., 2018).

The SN nodal method mentioned here is derived from the earlier discrete nodal transport method (DNTM) (Lawrence, 1986). It has been extended to hexagonal-prism (Todorova et al., 2004; Bereznev, 2016; Xu et al., 2020) and triangular-prism (Lu and Wu, 2007) meshes and has been applied and developed in several fast reactor analysis codes. Starting from the multigroup neutron transport equation, SNM discretizes angle variables of the neutron transport equation by the discrete-ordinates (SN) method and discretizes spatial variables with coarse meshes. Besides, it performs transverse integral and polynomial expansion within each coarse mesh, generating a set of moderately coupled equations that can be solved using iterative methods.

The traditional solution process for SNM involves multi-layer iteration, which involves nested processes of fission source iteration, energy group sweeping, scattering source iteration, angle sweeping, and mesh sweeping from the outer level to the inner level. For large fast reactors, the degrees of freedom for discrete variables by SNM discretization can reach 109, a single reactor core transport calculation can often take several hours. However, in nuclear design calculations, multiple reactor core transport calculations are necessary to couple with other field calculations expect for neutronics, resulting in unbearable calculation times. To enhance the efficiency of reactor core transport calculations using SNM, two approaches can be adopted. Firstly, the number of iterative iterations can be reduced through the application of coarse-mesh finite difference (CMFD) acceleration or similar techniques (Xu et al., 2018; Xu et al., 2020; Xu et al., 2022a). Secondly, the calculation time for each iteration can be minimized by utilizing parallel computing (Xu et al., 2020; Xu et al., 2022b; Qiao et al., 2021).

This research is rooted in the MOSASAUR (Zhang et al., 2023) code system developed by NPIC for lead-bismuth fast reactor neutronics analysis. The system follows a two-step process centered on assembly homogenization. Initially, an ultrafine-group energy spectrum calculation is conducted to derive assembly-homogenized cross-section parameters. Subsequently, a substantial number of three-dimensional multigroup transport calculations are executed to ascertain critical physical parameters across varying burnup conditions. The transport solver of the code system primarily comprises SNMs designed for triangular-prism and hexagonal-prism meshes.

Recently, we have upgraded the MOSASAUR code system, and implemented several CMFD acceleration and MPI parallel acceleration methods for the triangular-prism mesh solver and hexagonal-prism mesh solver respectively. The relevant methods will be introduced in another recent paper. In order to analyze the applicability of these acceleration methods for different types of lead-based fast reactors, we collected and established different types of lead-based reactor core models, and then tested the performance of various acceleration methods using different transport solvers including the triangular prism mesh solver and the hexagonal prism mesh solver. This article will systematically introduce these performance results and provide suggestions for code usage and further development.

The following text first introduces the lead-based reactor core models used in this article in Section 2, as well as the SN nodal method, the different CMFD acceleration methods, MPI parallel algorithms, acceleration performance parameters. Then, it presents the acceleration performance results in Section 3. Finally, it discusses and summarizes the results in Section 4.

2 Materials and methods

The effectiveness of acceleration methods, especially the CMFD acceleration methods, is influenced by factors such as the overall size of the computational core, mesh size, and the type of energy spectrum. To analyze the applicability of acceleration methods to different types of lead-based cores, four lead-based core models were selected, each with different geometric and energy spectrum characteristics. This section will provide a detailed introduction to the main features of these cores. For the sake of completeness, this section will also briefly introduce the SN nodal transport solvers, the characteristics of different acceleration methods, as well as the related performance parameters.

2.1 Lead-based reactor cores

2.1.1 RBEC-M core

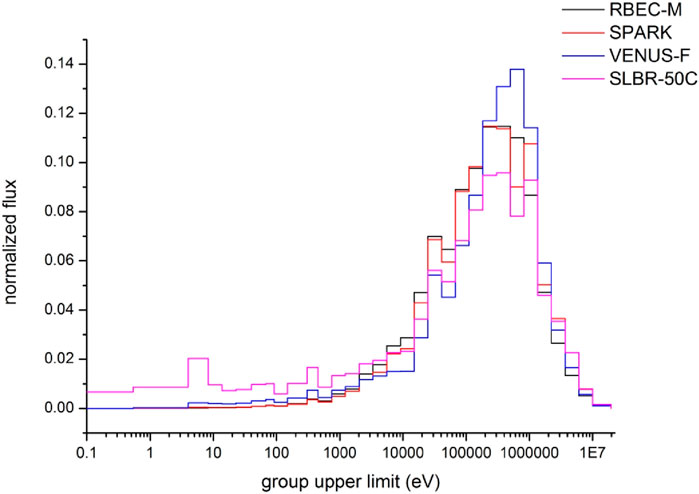
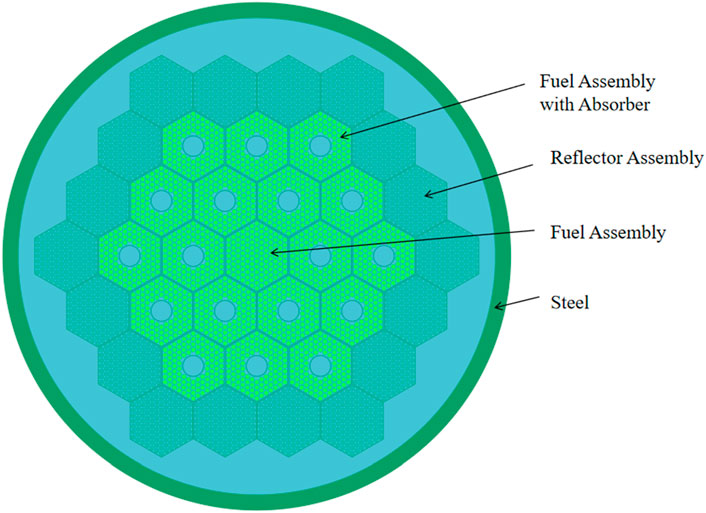
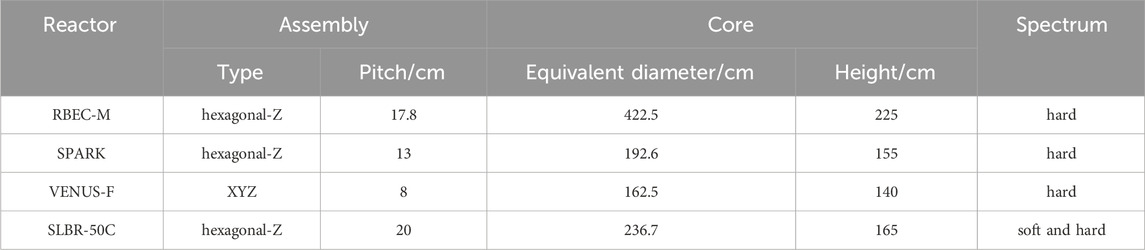
The RBEC-M (Sienicki et al., 2006) core is a lead-bismuth-cooled design proposed by the Kurchatov Institute in Russia (RRC KI) and has been recognized by the International Atomic Energy Agency (IAEA) as a neutronics benchmark. The core is designed for a thermal power of 900 MW. The core model has an equivalent diameter of 422.524 cm and a height of 225 cm, making it relatively large in size. The core is comprised of hexagonal assemblies, with a center-to-center distance of 17.8 cm between the assemblies. The core is composed of uranium-plutonium mixed nitride fuel, lead-bismuth eutectic (LBE) coolant, steel cladding, and structural materials. The radial arrangement of the core consists of inner fuel assemblies, middle fuel assemblies, outer fuel assemblies, breeding assemblies, and reflector assemblies, as depicted in Figure 1. The axial arrangement mainly comprises the active region, axial breeding region, lower plenum region, and upper duct region. The energy spectrum distribution, shown in Figure 2, indicates a relatively high distribution in the high-energy region above 0.1MeV, suggesting a hard energy spectrum.

Figure 1

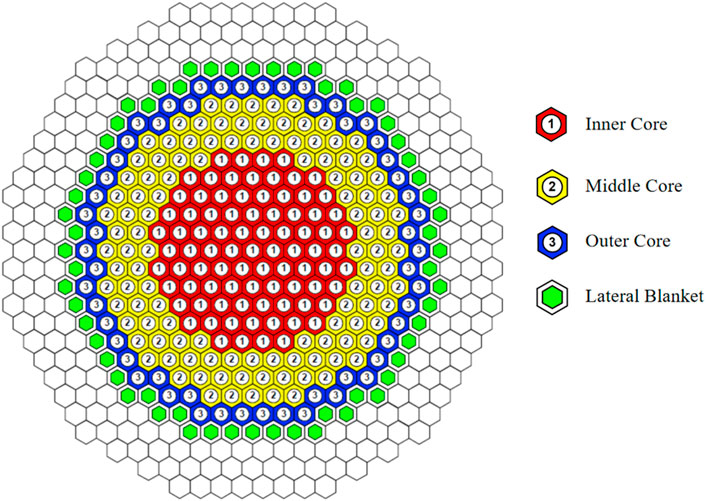
Figure 1. Core Configuration of 900 MWt RBEC-M design (Sienicki et al., 2006).

Figure 2

Figure 2. Neutron energy spectra for different lead-based reactor cores.

2.1.2 SPARK core

The core is a concept LBE cooled small core published in literature (Zhou et al., 2018), with a design thermal power of 20 MW and the capability for uninterrupted operation for 20 years without refueling. The equivalent diameter of the core model is 192.571 cm, with a height of 155 cm, making it relatively small in size. The core is comprised of hexagonal assemblies, with a center-to-center distance of 13 cm between the assemblies. The core consists mainly of UO2 fuel, lead-bismuth alloy coolant, stainless steel cladding and structural materials, Al2O3 (MgO is recommended in the literature, but due to the lack of Mg isotopes in the current database, it is replaced by Al2O3) reflector and B4C shield. The radial arrangement of the core is shown in Figure 3, mainly comprising fuel assemblies, reflector assemblies, shield assemblies, heat pipe assemblies, control assemblies, and safety assemblies. The axial arrangement mainly comprises the active region, upper plenum region, and upper and lower reflector regions. The energy spectrum distribution of the core is shown in Figure 2, with a relatively high distribution in the high-energy region above 0.1MeV, indicating a hard energy spectrum.

Figure 3

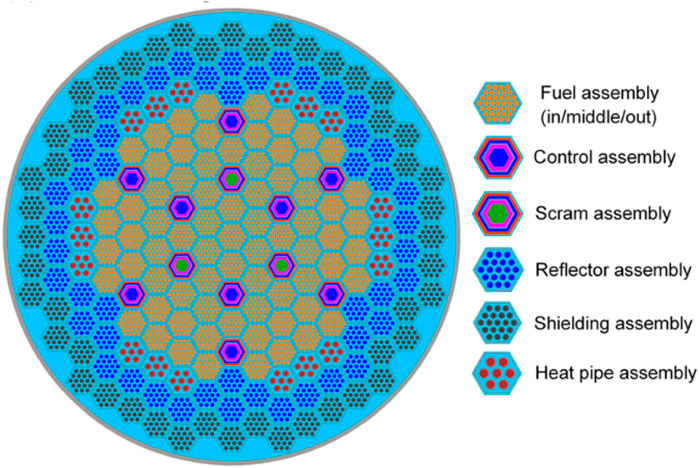
Figure 3. Core Configuration of SPARK (Zhou et al., 2018).

2.1.3 VENUS-F core

The VENUS-F (Sarotto et al., 2018; Zhou et al., 2018) core is one of the Fast Reactor Experiments for hYbrid Applications (FREYA), which is a collaborative project co-funded by the European Commission within the seventh Framework Programme (FP7) of the EURopean ATOMic energy community (EURATOM). Due to limited parameters provided in the literature, the main core parameters for this paper are estimated with reference to the CC5 core of the VENUS-F facility. The core has a side length of 144 cm, a height of 140 cm, making it relatively small in size. And the core consists of square assemblies with a side length of 8 cm. The core materials mainly include metallic uranium fuel, lead blocks, stainless steel vessel, air, and B4C control rods. The radial assembly arrangement is shown in Figure 4 and can be divided into fuel assemblies, Pb reflector assemblies, stainless steel Pb reflector assemblies, control rod assemblies, safety rod assemblies, and absorber rod assemblies. The axial arrangement is relatively simple, with the active region of the core at a height of 60cm, with a 10 cm thick steel layer adjacent to the top and bottom of the core, and 30 cm thick lead layers at the bottom and top ends. The energy spectrum distribution of the core is shown in Figure 2, indicating a higher distribution in the high-energy region above 0.1 MeV compared to the RBEC-M and SPARK cores, suggesting a significantly harder energy spectrum.

Figure 4

Figure 4. Core Configuration of VENUS-F.

2.1.4 SLBR-50C core

This is a self-designed small LBE-cooled reactor core with a designed thermal power of 50 MW. The equivalent diameter of the core model is approximately 236.675 cm with a height of 165 cm, making the core relatively small in size. The core consists of hexagonal assemblies with a center-to-center distance of 20 cm, and incorporates internal control rod design, resulting in larger assembly sizes. The core materials mainly include UO2 fuel, lead-bismuth eutectic coolant, stainless steel, reflector and absorbers within the assemblies. The core arrangement is illustrated in Figure 5. The energy spectrum distribution of the core is shown in Figure 2, indicating a significantly higher distribution in the medium to low energy region below 0.1 MeV compared to other lead-based cores, categorizing it as a mixed energy spectrum core.

Figure 5

Figure 5. Core Configuration of SLBR-50C.

2.1.5 Summary of core characteristics

The comparison of energy spectra for different cores is shown in Figure 2. Based on the graph, it is evident that the VENUS-F core has a high distribution in the high-energy region above 0.1MeV, indicating a hard spectrum. The energy spectra of the RBEC-M and SPARK cores are similar, with a relatively high distribution in the high-energy region above 0.1MeV, signifying a hard spectrum. In comparison to other fast spectrum cores, the SLBR-50C core exhibits a significantly higher distribution in the medium to low energy range below 0.1MeV, classifying it as a mixed spectrum core. A summary of the geometric and energy spectrum characteristics of different cores is presented in Table 1, showcasing the diverse assembly types, core sizes, and energy spectrum characteristics of the selected cores, providing broad coverage.

Table 1

Table 1. Summary of geometry and spectrum characteristics of different lead-based reactor cores.

2.2 SN nodal method

In MOSASAUR, two SN nodal transport solvers have been integrated: one (Tri-solver) based on triangular prism meshes and another (Hex-solver) based on a hexagonal prism meshes. The SN nodal method (Lu and Wu, 2007; Xu et al., 2022a) begins its derivation from the multigroup SN form of the neutron transport equation. For instance, in the context of the most common eigenvalue problems, the equation takes the following form as shown in Eq. 1:

$\begin{array}{l}{\mathit{\Omega }}^m\nabla {\psi }_g^m\left(\mathit{r}\right)+{\mathrm{\Sigma }}_{t,g}\left(\mathit{r}\right){\psi }_g^m\left(\mathit{r}\right)=\frac{{\chi }_g\left(\mathit{r}\right)}{4\pi k}{\displaystyle \sum _{g^{\prime }=1}^{N_g}}\nu {\mathrm{\Sigma }}_{f,g^{\prime }}\left(\mathit{r}\right){\displaystyle \sum _{m=1}^{N_m}}{\omega }^m{\psi }_{g^{\prime }}^m\left(\mathit{r}\right)\\ +{\displaystyle \sum _{l=0}^{N_l}}{\displaystyle \sum _{k=-l}^l}{Y}_{lk}\left({\mathit{\Omega }}^m\right){\displaystyle \sum _{g^{\prime }=1}^{N_g}}{\mathrm{\Sigma }}_{s,g^{\prime }-g,l}\left(\mathit{r}\right){\displaystyle \sum _{m=1}^{N_m}}{\omega }^m{\psi }_{g^{\prime }}^m\left(\mathit{r}\right)Y_{lk}^{*}\left({\mathit{\Omega }}^m\right)\end{array}(1)$

In the equation, ${\mathit{\Omega }}^m$ represents the directional vector for the $m$-th angle, ${\psi }_g^m\left(\mathit{r}\right)$ represents the neutron flux for the gth energy group of angle m at spatial position $\mathit{r}$, ${\mathrm{\Sigma }}_{t,g}\left(\mathit{r}\right)$ represents the total reaction cross-section for the gth energy group at spatial position $\mathit{r}$, ${\chi }_g\left(\mathit{r}\right)$ represents the fission neutron fraction at spatial position $\mathit{r}$ for the gth energy group, $k$ represents the eigenvalue, $N_g$ represents the total number of energy groups, $\nu {\mathrm{\Sigma }}_{f,g^{\prime }}\left(\mathit{r}\right)$ represents the fission neutron production cross-section for the gth energy group at spatial position $\mathit{r}$, ${\omega }^m$ represents the integration weight for the $m$-th angle, $N_m$ represents the total number of discrete angles, $N_l$ represents the anisotropic scattering order, $Y_{lk}\left({\mathit{\Omega }}^m\right)$ represents the spherical harmonic function, ${\mathrm{\Sigma }}_{s,g^{\prime }-g,l}\left(\mathit{r}\right)$ represents the $l$-th order scattering cross-section from the g'-th energy group to the gth energy group at spatial position $\mathit{r}$, and $Y_{lk}^{*}\left({\mathit{\Omega }}^m\right)$ represents the conjugate spherical harmonic function. By performing transverse integral and polynomial expansion within different meshes, a series of nodal response equations can be obtained. Then, through well-organized iterative and sweeping computations, the discrete variables can be solved.

2.3 CMFD methods

The CMFD methods mentioned here not only includes the traditional CMFD (Smith, 2002) method, but also includes the methods similar to the traditional CMFD method. The CMFD methods accelerate the convergence of transport variables by repeatedly solving the transport corrected diffusion coarse-mesh finite difference problem. For different types of core transport problems, it can usually achieve several to hundreds of times acceleration speedup. However, the traditional CMFD method has poor convergence stability, and in recent years, many improved CMFD methods have emerged. Besides the traditional CMFD method, we have implemented the adCMFD (Jarrett et al., 2016) method, the odCMFD (Zhu et al., 2016) method and the rCMFD (Xu et al., 2022c) method.

The process of accelerating transport calculations with different CMFD methods is similar. For regular eigenvalue problems, the efficiency of power iteration is often sluggish. In such cases, an additional CMFD diffusion eigenvalue problem calculation can be performed swiftly before each power iteration update of eigenvalues and fission sources. Although the model error of the CMFD diffusion equations is greater than that of the transport nodal equations, the incorporation of correction terms based on the transport solution into the CMFD diffusion equation allows for the rapid acquisition of eigenvalue and coarse-mesh fluxes that are comparable to those of the transport nodal solution. In turn, these updated eigenvalue and fluxes refine the results obtained through power iteration, thus accelerating the convergence of the power iteration process.

The main difference among these methods lies in the calculation equation of diffusion coefficient. For the traditional CMFD method, the equation below is used to calculate the diffusion coefficient at the mesh interface:

$D_{K_d+1/2}=\frac{2D_K{D}_{K_d+1}{h}_{K_d+1/2}}{h_{K_d}{D}_{K_d+1}+h_{K_d+1}{D}_K}(2)$

In the equation, $D$ represents the diffusion coefficient, $D_K$ and $D_{K_d+1}$ respectively represent the diffusion coefficients within mesh $K$ and mesh $K_d+1$, $D_{K_d+1/2}$ represents the diffusion coefficient at the interface between the two meshes, $h_{K_d}$ and $h_{K_d+1}$ are the mesh sizes of the two meshes along coordinate direction $d$, while $h_{K_d+1/2}$ is the average of $h_{K_d}$ and $h_{K_d+1}$.

For adCMFD and odCMFD, the diffusion coefficient at the mesh interface is still calculated using Eq. 2, but the diffusion coefficient within the mesh is corrected as shown in Eq. 3:

$D_{K_d}^{\prime }=D_K+\theta h_{K_d}(3)$

where $D_{K_d}^{\prime }$ is the corrected diffusion coefficient that would be employed in Eq. 2 and $\theta$ is the correction factor. For the adCMFD method, $\theta$ is a fixed empirical value, such as 0.2. While for the odCMFD method, the one-dimensional step characteristic method is used as the basis for Fourier analysis of single-group homogenous model problems. The optimization objective is to minimize the spectral radius of convergence, and an optimized fitting formula is obtained for the correction factor as shown in Eq. 4:

${\theta }_{K_d}=\left\{\begin{array}{l}0,{\tau }_{K_d}<1\\ {\displaystyle \sum _{i=1}^6}{a}_i{\left({\tau }_{K_d}\right)}^i,1\le {\tau }_{K_d}<14\\ 0.127,{\tau }_{K_d}\ge 14\end{array}\right.(4)$

where, $a_i$ is the fitting coefficient, and the specific value can be found in literature. ${\tau }_{K_d}$ is the optical thickness of the mesh.

For the rCMFD method, in order to avoid the non-physical phenomenon of increasing neutron flux difference but decreasing neutron flow, resulting in non-convergence, the following equation instead Eq. 2 is used to dynamically calculate the diffusion coefficient at the mesh interface as shown in Eq. 5:

$D_{K_d+1/2}=\max \left[\frac{2D_K{D}_{K_d+1}}{h_{K_d}{D}_{K_d+1}+h_{K_d+1}{D}_K},\frac{5}{2}\max \left(-\frac{J_{K_d+1/2}^{SN}}{{\varphi }_{K_d+1}^{SN}},\frac{J_{K_d+1/2}^{SN}}{{\varphi }_K^{SN}}\right)\right](5)$

where $J_{K_d+1/2}^{SN}$ is the neutron current at the mesh interface obtained by the transport calculation, and ${\varphi }_K^{SN}$ and ${\varphi }_{K_d+1}^{SN}$ are the neutron flux of mesh $K$ and mesh $K_d+1$ respectively obtained by the transport calculation.

2.4 MPI parallel algorithms

The common parallel standards for CPUs include OpenMP and MPI. OpenMP adopts the shared memory parallel programming model, which is suitable for CPU parallelization within a single computing node. However, MPI adopts the communication-based parallel programming model, enabling large-scale parallelization among CPU cores across multiple nodes. We have implemented parallel SN nodal calculation and CMFD calculation based on MPI.

To achieve large-scale parallelization, we perform spatial domain decomposition for triangular-Z or hexagonal-Z meshes. The specific MPI parallel algorithm is described as follows: iterative calculations are performed on each CPU core, but MPI communication is conducted at key points. The main communication points are in the outer and inner iteration convergence judgments, as well as after each angle sweeping. Although the SN method can maintain the sweeping order of the domain decomposition using the pipeline idea, for reactor core problems with a relatively small number of meshes, frequent communication at each angle will greatly reduce parallel efficiency. Therefore, we conduct communication of surface fluxes after all angle sweepings, which significantly reduces the number of communications and improves parallel efficiency. However, this block-Jacobian style algorithm destroys the original SN sweeping order, causing the increase of the number of iterations. To address this problem, we further adopt the boundary flux prediction method (Qiao et al., 2021), which performs flux extrapolation for scattering source iterations on domain boundaries to compensate for the iterative degradation of domain boundary fluxes caused by domain decomposition. The equation for flux extrapolation is shown in Eq. 6:

${\psi }_g^{\left(l+1\right)}={\psi }_g^{\left(l\right)}+{\mathrm{\Sigma }}_{t,g}^{-1}\left(Q_{s,g-g}^{\left(l\right)}-Q_{s,g-g}^{\left(l-1\right)}\right)(6)$

where ${\psi }_g^{\left(l+1\right)}$ is the angular flux of group $g$ after extrapolation, ${\psi }_g^{\left(l\right)}$ is the angular flux of group $g$ before extrapolation, ${\mathrm{\Sigma }}_{t,g}^{-1}$ is the reciprocal of the total reaction cross section of group $g$, $Q_{s,g-g}^{\left(l\right)}$ is the self-scattering source of the lth scattering source iteration, and $Q_{s,g-g}^{\left(l-1\right)}$ is the self-scattering source of the $\left(l-1\right)$-th scattering source iteration calculation.

When CMFD methods are enabled, the time for diffusion calculation is also considerable, making it necessary to parallel diffusion calculation by spatial domain decomposition. As the computational workload is smaller for diffusion calculation than transport calculation, the cost of frequent communication will be more significant. Here, we further reduce the communication volume by performing boundary flux communication after each energy group sweeping of the CMFD calculation.

2.5 Performance parameters

To quantitatively measure the acceleration effect, we will adopt the commonly used concept of speedup. The speedup is defined as shown in Eq. 7:

$\text{SP}=T_0/T_1(7)$

where SP represents the speedup, which is the ratio of the computation time without acceleration to the computation time with acceleration. Here the acceleration includes various CMFD accelerations, MPI parallel acceleration, as well as the combination of CMFD and MPI parallel accelerations. The acceleration is effective only when the speedup is greater than 1.

For MPI parallel acceleration, people usually also care about the relationship between the speedup and the number of CPU cores used. Therefore, this paper will also use parallel efficiency to measure parallel acceleration performance. The definition of parallel efficiency is shown in Eq. 8:

$\text{PE}=\left(\text{SP}/n\right)\times 100\%(8)$

where PE is the parallel efficiency, n is the number of CPU cores used. Parallel efficiency is the speedup brought by each CPU core.

3 Results

For the different lead-based cores introduced before, we used the multigroup cross-section generation module in MOSASAUR to generate 33 groups of first-order anisotropic scattering cross sections, and then performed full-core neutron transport calculations under different conditions. For different cores, we considered different transport solvers, different CMFD methods, and different CPU core counts during the calculations. The results are presented in this section.

All calculations were performed on a parallel platform of Intel (R) Xeon (R) CPU E5-2660 v3 @ 2.60 GHz. The S4 quadrature of the transport solvers was adopted during the calculations. When using the Tri-solver, a hexagonal mesh was discretized with six triangular meshes, and a square mesh was discretized with four triangular meshes. When using the Hex-solver, the variables within the mesh were expanded with a second-order polynomial.

3.1 Acceleration performance of different CMFD methods

First, we examined the acceleration performance of different CMFD methods based on one CPU core. For each reactor core, we used different solvers to calculate a benchmark case without CMFD and parallel. To verify the acceleration performance of the acceleration methods with minimal loss of accuracy, for the benchmark case, we set the iteration control parameters with the principle of achieving high accuracy. The scattering source iteration limit was set to a large value of 1,000 to prevent precision loss due to internal iterations not converging and the fission convergence error limits were set to about 10–7 to 10-6. However, when enabling CMFD acceleration, we set the iteration control parameters with the principle of achieving high efficiency. In these cases, the scattering source iteration limit was set to 3-5 and the fission convergence error limits were set to almost the same as the cases without CMFD.

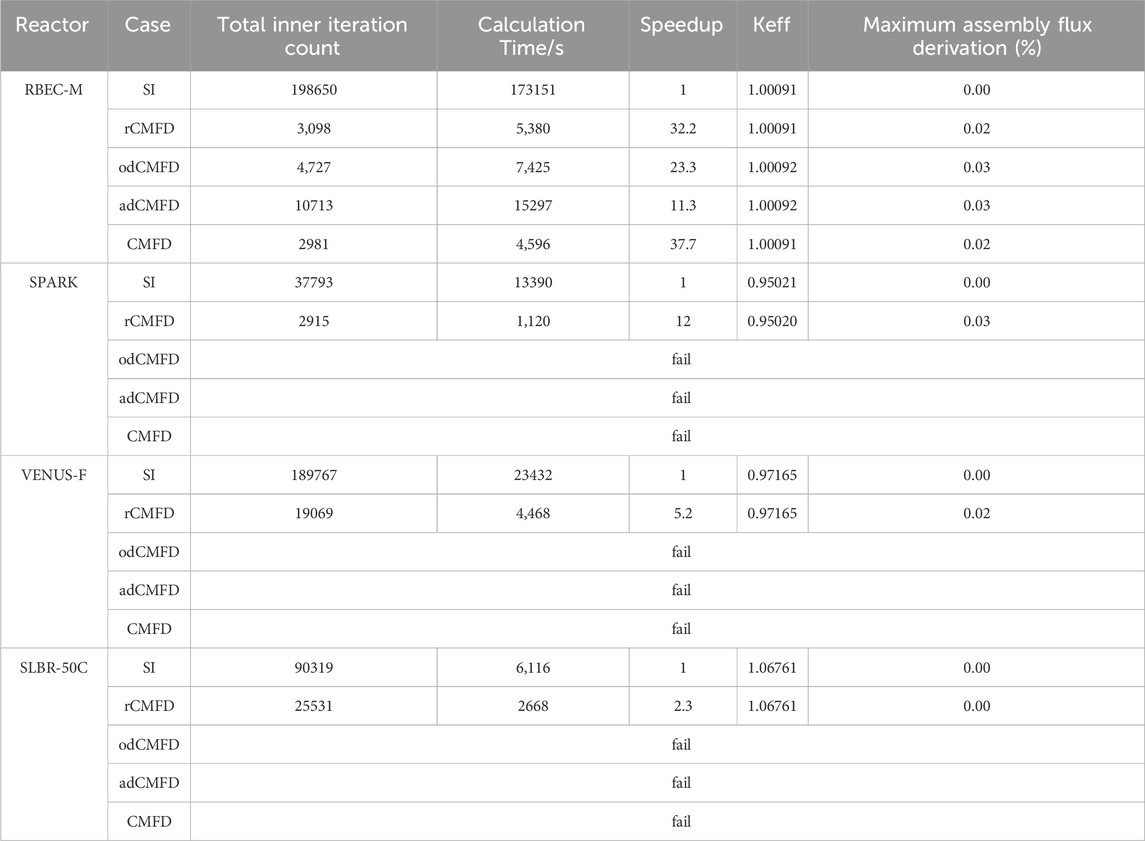
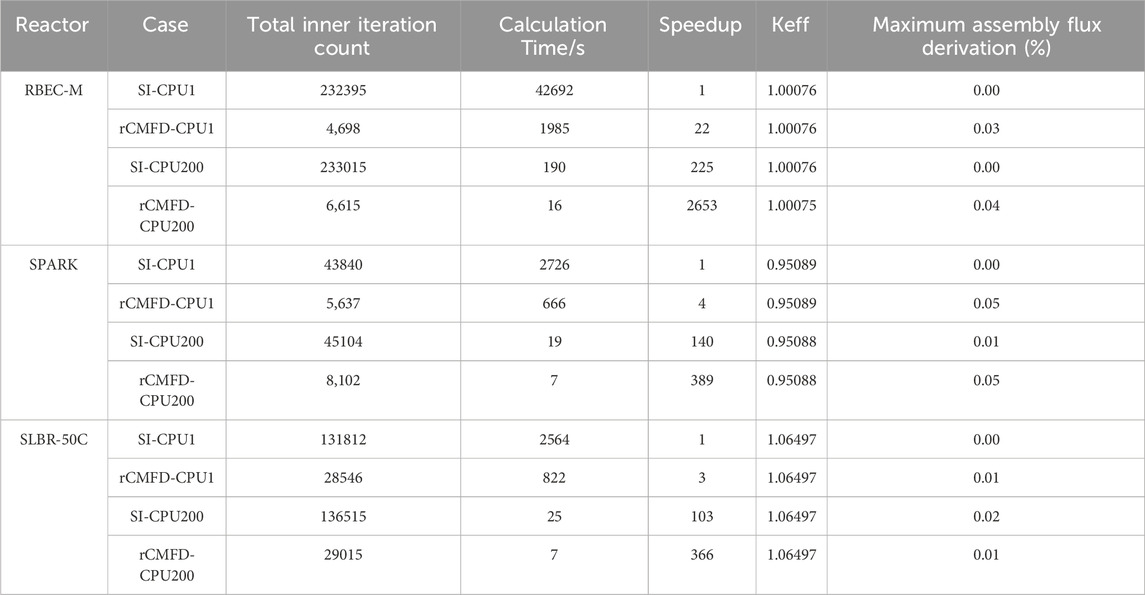
When utilizing the Tri-solver, the computational results for distinct reactor cores are presented in Table 2. Among them, SI represents the case that nothing acceleration is engaged, while rCMFD, odCMFD, adCMFD, and CMFD represent cases that different coarse mesh acceleration is activated. The Total Inner Iteration Count signifies the total number of inner iterations, with each inner iteration requiring a sweeping of all meshes at all angles, which is the most time-consuming part of the calculation. The Maximum Assembly Flux Derivation indicates the maximum relative deviation of the assembly flux calculated under different conditions in comparison to the benchmark case. For the large lead-based reactor core RBEC-M, the traditional CMFD method demonstrated the most effective acceleration, achieving a speedup of 37.7. The rCMFD method aligned closely with the traditional CMFD method, attaining a speedup of 32.2. However, the odCMFD and adCMFD methods exhibited comparatively reduced acceleration effects. Notably, the deviations in keff before and after acceleration did not exceed 1 pcm, and the maximum radial assembly normalized flux deviation was about 0.03%.

Table 2

Table 2. Acceleration performance results of Tri-solver with different CMFD methods.

In the case of smaller reactor cores, such as SPARK, rCMFD demonstrated consistent convergence, achieving a 12-fold speedup. Other methods failed to converge. The deviation in keff before and after rCMFD acceleration remained below 1 pcm, with the maximum radial assembly normalized flux deviations sitting at approximately 0.03%. When applied to reactor cores with harder spectrum, like VENUS-F, and smaller mixed spectrum cores, like SLBR-50C, only rCMFD could converge with minimal loss of accuracy. However, the acceleration speedups were relatively small.

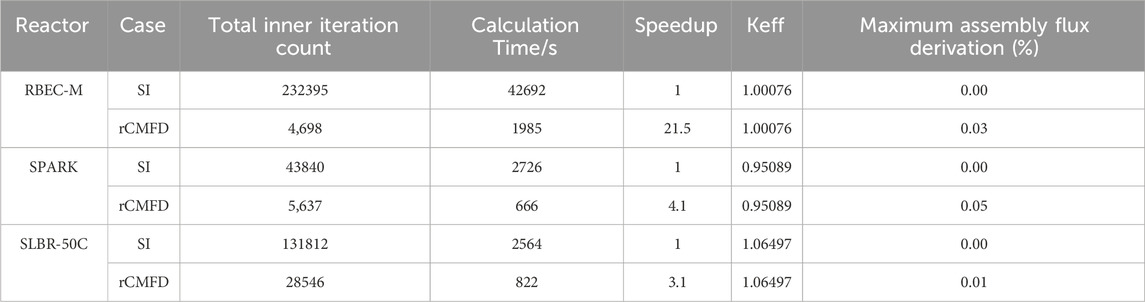
When utilizing the Hex-solver, computational results by rCMFD method for distinct reactor cores are provided in Table 3. Due to mesh constraints, VENUS-F reactor core was excluded from calculations. Notably, the computational results obtained via Hex-solver aligned closely with those obtained via Tri-solver. rCMFD ensured accurate convergence with minimal loss in accuracy. For RBEC-M reactor core, it achieved a speedup of 21.5. For SPARK and SLBR-50C reactor cores, it achieved a speedup of 4.1 and 3.1, respectively.

Table 3

Table 3. Acceleration Performance Results of Hex-solver with rCMFD Method.

3.2 Acceleration performance of MPI parallel

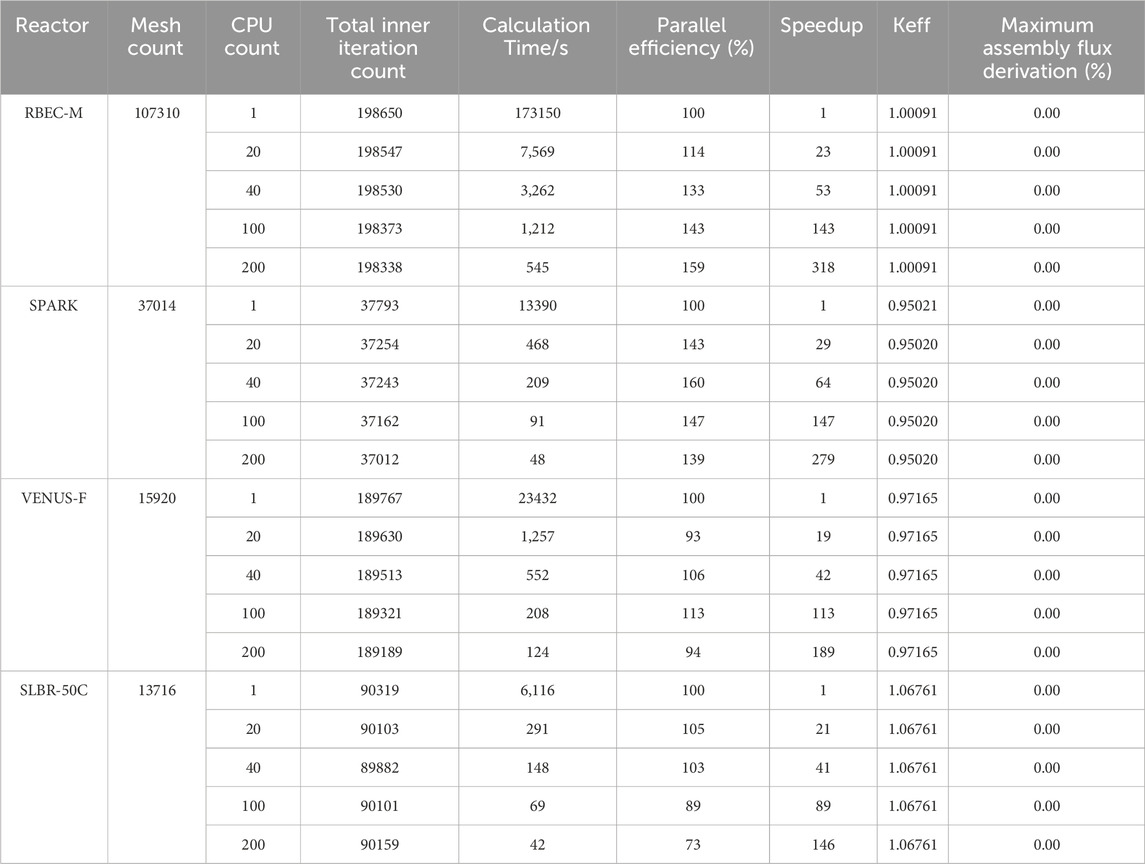
First, we conducted calculations without any CMFD acceleration, using different numbers of CPU cores. When using the Tri-solver, the results are summarized in Table 4. For different reactor cores, the impact of MPI parallel on keff was less than 1 pcm, and the assembly normalized flux deviations were less than 0.01%. For the RBEC-M reactor core, 200 CPU cores achieved a parallel efficiency of 159%, with a parallel speedup of 318, reducing the calculation time from 173,150 s on a single core to 545 s. For the SPARK reactor core, 200 CPU cores achieved a parallel efficiency of 139%, with a parallel speedup of 279, reducing the calculation time from 133,900 s on a single core to 48 s. For the VENUS-F reactor core, 200 cores achieved a parallel efficiency of 94%, with a parallel speedup of 189, reducing the calculation time from 234,320 s on a single core to 124 s. For the SLBR-50C reactor core, 200 cores achieved a parallel efficiency of 73%, with a parallel speedup of 146, reducing the calculation time from 61,160 s on a single core to 42 s. The acceleration effect for large reactor core was better than we expected and superliner speedups (Yan and Regueiro, 2018) were observed.

Table 4

Table 4. Acceleration Performance Results of Tri-solver with Different CPU cores.

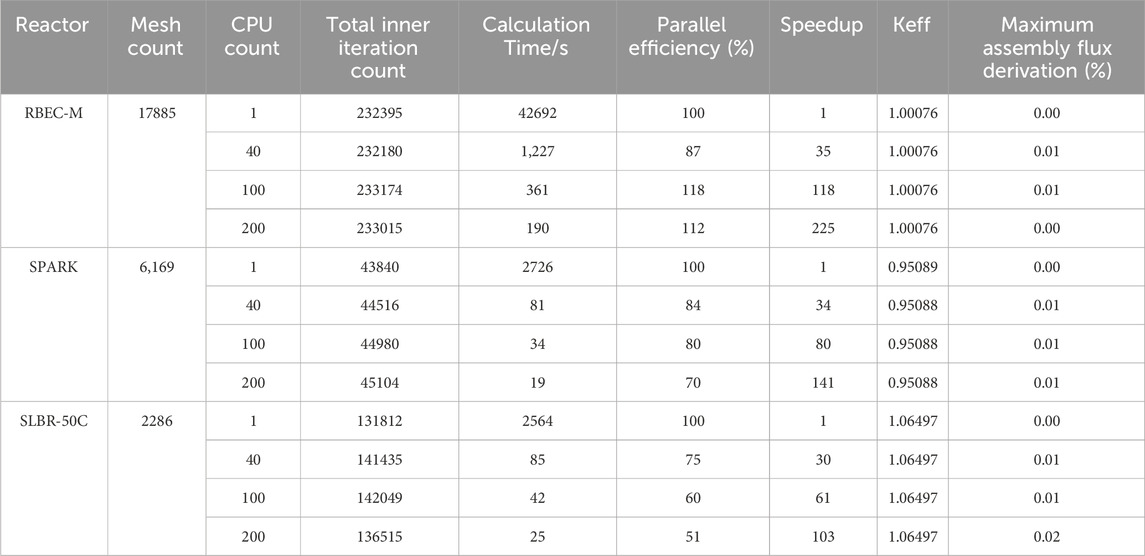
When using the Hex-solver, the results are summarized in Table 5. Similar to the Tri-solver case, for different reactor cores, the impact of parallel processing on keff was less than 1 pcm, and the assembly normalized flux deviations were less than 0.02%. For the RBEC-M reactor core, 200 CPU cores achieved a parallel efficiency of 112%, with a parallel speedup of 225, reducing the calculation time from 426,920 s on a single core to 190 s. For the SPARK reactor core, 200 CPU cores achieved a parallel efficiency of 70%, with a parallel speedup of 141, reducing the calculation time from 272,600 s on a single core to 19 s. For the SLBR-50C reactor core, 200 CPU cores achieved a parallel efficiency of 51%, with a parallel speedup of 103, reducing the calculation time from 256,400 s on a single core to 25 s. Due to the smaller number of meshes when using the Hex-solver compared to the Tri-solver, superlinear parallel efficiency is only observed when calculating large reactor cores such as RBEC-M. For small cores such as SLBR-50C, the parallel efficiency with 200 CPU cores is only 51%, but fortunately, when the number of meshes is small, the computational workload is also smaller, resulting in a final calculation time of only 25 s.

Table 5

Table 5. Acceleration Performance Results of Hex-solver with Different CPU cores.

3.3 Combined acceleration performance of rCMFD and MPI parallel

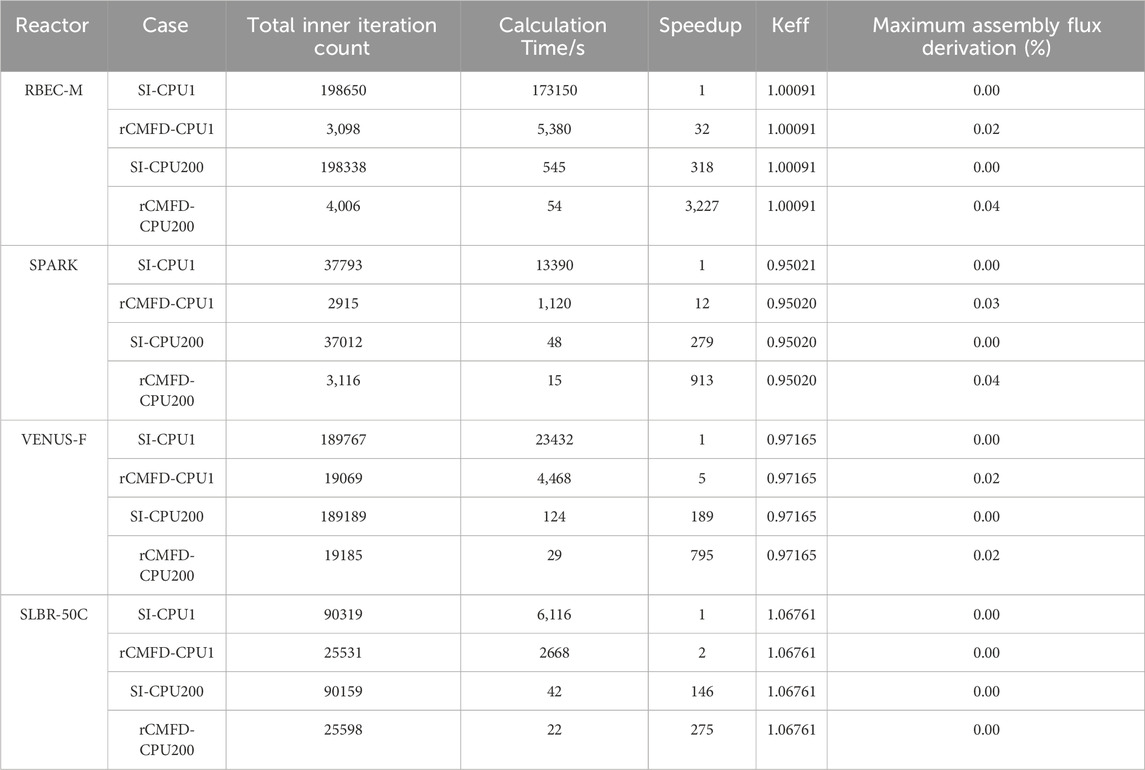
Finally, we investigate the acceleration effect of enabling both rCMFD and MPI parallel computing. For the Tri-solver, the computational results for different reactor cores are summarized in Table 6. SI-CPU1 represents the case of single-core computation without rCMFD, rCMFD-CPU1 represents the case of single-core computation with rCMFD enabled, SI-CPU200 represents the case of 200-core computation without rCMFD, and rCMFD-CPU200 represents the case of 200-core computation with rCMFD enabled. For all reactor cores, the combined acceleration of rCMFD and MPI parallel introduced minimal loss in accuracy, with keff deviations of no more than 1 pcm and assembly normalized flux deviations of no more than 0.04%. For the RBEC-M reactor core, the combined speedup was 3,227, with a calculation time of 54 s. For the SPARK reactor core, the combined speedup was 913, with a calculation time of 15 s. For the VENUS-F reactor core, the combined speedup was 795, with a calculation time of 29 s. For the SLBR-50C reactor core, the combined speedup was 275, with a calculation time of 22 s.

Table 6

Table 6. Combined acceleration performance results of Tri-solver.

For the Hex-solver, the computational results for different reactor cores are summarized in Table 7. Similar to the Tri-solver case, the combination of acceleration introduced minimal loss in accuracy, with keff deviations of no more than 1 pcm and assembly normalized flux deviations of no more than 0.05%. For the RBEC-M reactor core, the combined speedup was 2653, with a calculation time of 16 s. For the SPARK reactor core, the combined acceleration speed was 389, with a calculation time of 7 s. For the SLBR-50C reactor core, the combined speedup was 366, with a calculation time of 7 s.

Table 7

Table 7. Combined acceleration performance results of Hex-solver.

4 Discussion

Based on lead-based reactor cores of different sizes and energy spectra, such as LBE-cooled cores RBEC-M, SPARK, SLBR-50C and lead-based reactor core VENUS-F, we first analyzed the acceleration performance of different CMFD methods, then the acceleration performance of multi-core parallel computing, and finally the combined acceleration performance of CMFD and multi-core parallel computing.

Compared with traditional CMFD, adCMFD and odCMFD methods, the rCMFD method achieved both high stability and speedup. For the large reactor RBEC-M, Tri-solver achieved a speedup of 32.2 by rCMFD, and Hex-solver achieved a speedup of 21.5 by rCMFD. However, for small reactors, the acceleration effect is limited. For example, for the SLBR-50C reactor core, the speedup with Tri-solver by rCMFD is 2, and the speedup with Hex-solver by rCMFD is 3.1.

The efficiency of multi-core parallel acceleration is positively related to the number of meshes. For the reactor RBEC-M with a large number of meshes, the parallel efficiency of Tri-solver reached 159%, and for Hex-solver, the parallel efficiency reached 112%. For the reactor SLBR-50C with the smallest number of meshes, the parallel efficiency of Tri-solver was 73%, and for Hex-solver, the parallel efficiency was 51%.

Superlinear speedups were observed, which was caused by several factors. The main reason is likely the “high-CPU-low-memory” (Yan and Regueiro, 2018) characteristics of the spatial domain decomposition algorithm that more high-speed caches are efficiently utilized during multi-core calculations. As shown in Tables 4, 5, when the number of meshes is reduced, the utilization rate of the cache during single-core calculations is already high, and the communication costs will be even higher, resulting in the disappearance of this superlinear speedup. Additionally, as shown in Tables 4, 5, the reduction in iteration counts during multi-core calculations due to the boundary flux prediction method would also contribute.

When both rCMFD and MPI parallel are performed simultaneously, a combined speedup can be achieved. For the reactor RBEC-M with the best acceleration effect, when using 200 CPU cores for rCMFD calculation, the combined speedup of Tri-solver was 3,227 with a calculation time of 54 s, and for Hex-solver, the combined speedup was 2653 with a calculation time of 16 s. For the reactor SLBR-50C with the worst acceleration effect, when using 200 cores for rCMFD calculation, the combined speedup of Tri-solver was 275 with a calculation time of 22 s, and for Hex-solver, the combined speedup was 366 with a calculation time of 7 s; The accelerations have minimal impact on the calculation accuracy. When the outer iteration convergence error limit was about 10–6 to 10-7, the deviations in keff caused by rCMFD or parallel computing were within 1 pcm, and the maximum deviations in normalized assembly flux were within 0.05%. Moreover, the accuracy loss caused by MPI parallel was significantly smaller than that caused by CMFD.

The numerical results of this research show that the acceleration effect is influenced by various factors. Overall, the speedup by different CMFD methods and MPI parallel efficiency of large reactor cores are higher than those of small reactor cores. The energy spectrum and mesh size have an impact on the acceleration effect, but the specific law is complex, and the results of this study are not sufficient to provide a clear pattern. Based on the current assembly-homogenized strategy for fast reactor neutronics calculation, for different types of lead-bismuth reactor cores, when rCMFD acceleration and MPI parallel acceleration are enabled, the SN nodal transport solvers in MOSASAUR have the ability to complete a 3D whole-core multigroup transport calculation in 1 minute, which can efficiently complete nuclear design work. As far as we know, such computational efficiency is currently leading. For example, recent similar research (Sugino and Takino, 2020) showed that about 10 times speedup was obtained after coupling diffusion acceleration and parallel acceleration, and the transport calculation time for a three-dimensional fast reactor was still much longer than 1 minute.

However, for the possible future lattice-homogenized strategy for fast reactor neutronics calculation, the computational workload of small reactor cores will increase significantly due to the increase in mesh counts, and it will be necessary to further study more suitable acceleration methods for small reactor cores. Furthermore, the test cases presented in this paper are confined to the issues surrounding the lead-based fast reactor under regular state. Our testing experience indicates that while the heterogeneity of the reactor core, caused by factors such as burnup, temperature variations, voids, and control rods, has minimal impact on parallel performance, it may slightly increase the probability of rCMFD failure, and sodium-cooled fast reactors may yield similar conclusions to those of lead-based reactors. Nevertheless, more specific testing in the future is necessary to arrive at definitive conclusions regarding those issues.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BW: Writing–original draft. ZX: Writing–review and editing, Validation, Software. LW: Writing–review and editing. BZ: Writing–review and editing, Methodology. LL: Writing–review and editing, Software, Resources. CZ: Writing–review and editing, Visualization.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Natural Science Foundation of Henan Province (232300420347) and the National Natural Science Foundation of China (12075228).

Acknowledgments

We are grateful to Dr. Hongbo Zhang and Mr. Yutao Huang from NPIC for their assistance in utilizing parallel platform, and to Dr. Shengcheng Zhou from Institute of Applied Physics and Computational Mathematics in Beijing and Dr. Kui Hu from North China Electric Power University for their assistance in modeling the SPARK reactor core and RBEC-M reactor core, respectively.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bereznev, V. P. (2016). Nodal SN-method for HEX-Z geometry. Nucl. Energy Technol. 2 (1), 20–23. doi:10.1016/j.nucet.2016.03.004

CrossRef Full Text | Google Scholar

Jarrett, M., Kochunas, B., Zhu, A., and Downar, T. (2016). Analysis of stabilization techniques for CMFD acceleration of neutron transport problems. Nucl. Sci. Eng. 184 (2), 208–227. doi:10.13182/nse16-51

CrossRef Full Text | Google Scholar

Lawrence, R. D. (1986). Progress in nodal methods for the solution of the neutron diffusion and transport equations. Prog. Nucl. Energy 17 (3), 271–301. doi:10.1016/0149-1970(86)90034-x

CrossRef Full Text | Google Scholar

Lu, H. L., and Wu, H. C. (2007). A nodal SN transport method for three-dimensional triangular-z geometry. Nucl. Eng. Des. 237 (8), 830–839. doi:10.1016/j.nucengdes.2006.10.025

CrossRef Full Text | Google Scholar

Qiao, L., Zheng, Y., Wu, H., Wang, Y., and Du, X. (2021). Improved block-Jacobi parallel algorithm for the S nodal method with unstructured mesh. Prog. Nucl. Energy 133, 103629. doi:10.1016/j.pnucene.2021.103629

CrossRef Full Text | Google Scholar

Ruggieri, J. M., Tommasi, J., Lebrat, J. F., et al. (2006). ERANOS 2.1: International code system for GEN IV fast reactor analysis. Proc. ICAPP 6, 2432–2439.

Google Scholar

Sarotto, M., Kochetkov, A., Krása, A., Bianchini, G., Fabrizio, V., Carta, M., et al. (2018). The neutronic modelling of the VENUS-F critical core experiments with the ERANOS deterministic code (FREYA EU FP7 project). Ann. Nucl. Energy 121, 626–637. doi:10.1016/j.anucene.2018.07.046

CrossRef Full Text | Google Scholar

Sienicki, J. J., Moisseytsev, A., Yang, W. S., et al. (2006). Status report on the small secure transportable autonomous reactor (SSTAR)/Lead-Cooled fast reactor (LFR) and supporting research and development. Argonne Natl. Lab. ANL-GenIV-089.

Google Scholar

Smith, K. S. (2002). Full-core, 2-D, LWR core calculations with CASMO-4E. Seoul, Korea: PHYSOR.

Google Scholar

Smith, M. A., Lewis, E. E., and Shemon, E. R. (2014). DIF3D-VARIANT 11.0: a decade of updates. Argonne, IL (United States): Argonne National Lab.ANL.

Google Scholar

Sugino, K., and Takino, K. (2020). Development of neutron transport calculation codes for 3-D hexagonal geometry (2). Improvement and enhancement of the MINISTRI code. Jpn. At. Energy Agency.

Google Scholar

Todorova, G., Nishi, H., and Ishibashi, J. (2004). Transport criticality analysis of FBR MONJU initial critical core in whole core simulation by NSHEX and GMVP. J. Nucl. Sci. Technol. 41 (4), 493–501. doi:10.3327/jnst.41.493

CrossRef Full Text | Google Scholar

Xu, Z. T., Wu, H. C., Zheng, Y. Q., and He, M. (2018). “Development of an optimized transport solver in SARAX for fast reactor analysis,” in International Conference on Nuclear Engineering, American, August 4–8, 2024 (American Society of Mechanical Engineers). doi:10.1115/icone26-82380

CrossRef Full Text | Google Scholar

Xu, Z. T., Wu, H. C., Zheng, Y. Q., and Zhang, Q. (2022a). A stable condition and adaptive diffusion coefficients for the coarse-mesh finite difference method. Front. Energy Res. 10, 836363. doi:10.3389/fenrg.2022.836363

CrossRef Full Text | Google Scholar

Xu, Z. T., Wu, H. C., Zheng, Y. Q., and Zhang, Q. (2022c). A stable condition and adaptive diffusion coefficients for the coarse-mesh finite difference method. Front. Energy Res. 10, 836363. doi:10.3389/fenrg.2022.836363

CrossRef Full Text | Google Scholar

Xu, Z. T., Zheng, Y., and Q Wu, H. C. (2022b). An IFDF accelerated parallel nodal SN method for XYZ geometry in SARAX code system. Ann. Nucl. Energy 166, 108710. doi:10.1016/j.anucene.2021.108710

CrossRef Full Text | Google Scholar

Xu, Z. T., Zheng, Y. Q., Wang, Y. P., and Wu, H. (2020). IFDF acceleration method with adaptive diffusion coefficients for SN nodal calculation in SARAX code system. Ann. Nucl. Energy 136, 107056. doi:10.1016/j.anucene.2019.107056

CrossRef Full Text | Google Scholar

Yan, B. C., and Regueiro, R. A. (2018). Superlinear speedup phenomenon in parallel 3D Discrete Element Method (DEM) simulations of complex-shaped particles. Parallel Comput. 75, 61–87. doi:10.1016/j.parco.2018.03.007

CrossRef Full Text | Google Scholar

Zhang, B., Wang, L. J., Lou, L., Zhao, C., Peng, X., Yan, M., et al. (2023). Development and verification of lead-bismuth cooled fast reactor calculation code system Mosasaur. Front. Energy Res. 10, 1055405. doi:10.3389/fenrg.2022.1055405

CrossRef Full Text | Google Scholar

Zhang, T. F., and Li, Z. P. (2022). Variational nodal methods for neutron transport: 40 years in review. Nucl. Eng. Technol. 54, 3181–3204. doi:10.1016/j.net.2022.04.012

CrossRef Full Text | Google Scholar

Zheng, Y. Q., Du, X. N., Xu, Z. T., Zhou, S., Liu, Y., Wan, C., et al. (2018). SARAX: a new code for fast reactor analysis part I: methods. Nucl. Eng. Des. 340, 421–430. doi:10.1016/j.nucengdes.2018.10.008

CrossRef Full Text | Google Scholar

Zhou, S., Chen, R., Shao, Y., Cao, L., Bai, B., and Wu, H. (2018). Conceptual core design study of an innovative small transportable lead-bismuth cooled fast reactor (SPARK) for remote power supply. Int. J. Energy Res. 42 (11), 3672–3687. doi:10.1002/er.4119

CrossRef Full Text | Google Scholar

Zhu, A., Jarrett, M., Xu, Y. L., Kochunas, B., Larsen, E., and Downar, T. (2016). An optimally diffusive Coarse Mesh Finite Difference method to accelerate neutron transport calculations. Ann. Nucl. Energy 95, 116–124. doi:10.1016/j.anucene.2016.05.004

CrossRef Full Text | Google Scholar