Beryllium solubility and hydrolysis in dilute to concentrated CaCl2 solutions: thermodynamic description in cementitious systems

The solubility and hydrolysis of Be(II) was investigated from undersaturation conditions in alkaline, dilute to concentrated CaCl₂ solutions (0.05–3.5 M). Experiments were performed with α-Be(OH)₂(cr) under Ar atmosphere at T = (22 ± 2)°C. Aqueous Be speciation was further investigated by means of molecular dynamics (MD) calculations. For the most diluted CaCl₂ systems (0.05 and 0.25 M), a solubility minimum is observed at pH_m ≈ 9.5 {with [Be(II)] ≈ 10⁻⁷ M}, consistent with solubility data previously reported in NaCl and KCl solutions. Above this pH_m, and at higher CaCl₂ concentrations, a steep increase in the solubility with a slope of ∼ +2 is observed, hinting towards the predominance of the moiety [Be(OH)₄^2–] in the aqueous phase. In NaCl and KCl systems, this hydrolysis species prevails only above pH_m ∼ 13, thus supporting the formation of ternary complex/es Ca–Be(II)–OH(aq) in CaCl₂ solutions. The analysis of solubility data in combination with MD calculations underpin the key role of the complex Ca₂[Be(OH)₄]²⁺ in alkaline to hyperalkaline systems containing Ca. In combination with our previous work in NaCl–NaOH and KCl–KOH systems, complete chemical, thermodynamic and (SIT) activity models are derived for the first time for the system Be²⁺–Ca²⁺–Na⁺–K⁺–H⁺–Cl^––OH^––H₂O(l). This model provides an accurate and robust tool for the evaluation of Be(II) solubility and speciation in a diversity of geochemical conditions, including source term calculations of beryllium in the context of repositories for nuclear waste disposal with a high cement inventory.

1 Introduction

Beryllium is a widely used metal in test and research fission reactors as neutron reflector/moderator. It is characterized by a relatively low thermal neutron absorption cross section and unique chemical and structural properties (Beeston, 1970; Chandler et al., 2009). During the reactor operation, ⁹Be undergoes (n, 2n) and (n, α) nuclear reactions resulting in the generation of large quantities of ⁴He, ³He and ³H. This leads to the swelling of beryllium components with the corresponding alteration of their mechanical properties. The disposal of these components results in specific streams of nuclear waste containing a significant inventory of chemotoxic beryllium (Beeston, 1970; Longhurst et al., 2003; Chandler et al., 2009).

In contrast to the rest of the alkali-earth element series and due to its very small ionic radii (r_Be²⁺ = 0.27 Å, for a coordination number (CN) of 4) (Shannon, 1976; Alderighi et al., 2000), beryllium is characterized by very strong hydrolysis. This results in an amphoteric behaviour involving the formation of positively- and negatively-charged hydrolysis species. Several solubility and potentiometric studies previously investigated the solubility and hydrolysis of beryllium in acidic to near-neutral pH conditions, deriving thermodynamic data for the hydrolysis species Be_n(OH)_m^2n–m, with (n,m) = (1,1), (1,2), (2,1), (3,3), (5,6) and (6,8) (Mattock, 1954; Gilbert and Garrett, 1956; Kakihana and Sillen, 1956; Schindler and Garett, 1960; Carell and Olin, 1961; Schwarzenbach, 1962; Hietanen and Sillen, 1964; Bertin et al., 1967; Mesmer and Baes, 1967; Ohtaki, 1967; Ohtaki and Kato, 1967; Lanza and Carpéni, 1968; Pâris and Gregoire, 1968; Schwarzenbach and Wenger, 1969; Kakihana and Maeda, 1970; Tsukuda et al., 1975; Vanni et al., 1975; Baes and Mesmer, 1976; Bruno et al., 1987b; Bruno, 1987; Chinea et al., 1997; Brown and Ekberg, 2016). A significantly scarcer number of studies investigated the hydrolysis of Be(II) in alkaline to hyperalkaline conditions (Gilbert and Garrett, 1956; Green and Alexander, 1965; Bruno et al., 1987a), where the hydrolysis species Be(OH)₃^– and Be(OH)₄^2– are expected to prevail. In our recent solubility and ⁹Be-NMR study, we systematically investigated the solubility and hydrolysis of Be(II) in dilute to concentrated NaCl–NaOH and KCl–KOH systems. Experiments were conducted with a well-defined solid phase, α-Be(OH)₂(cr), and extended from acidic to hyperalkaline conditions (Çevirim-Papaioannou et al., 2020). In combination with previous studies available in the literature, chemical, thermodynamic and (SIT) activity models for the system Be²⁺–Na⁺–K⁺–H⁺–Cl^––OH^––H₂O(l) were derived.

Cementitious materials are widely used in underground repositories for nuclear waste disposal for the stabilization of the waste and for construction purposes. Upon contact with groundwater, cement materials undergo degradation through a sequence of dissolution reactions. In the degradation stage I, the dissolution of K- and Na-oxides/hydroxides imposes hyperalkaline conditions (pH ≈ 13.3) and high alkali content in the pore water. The degradation stage II is characterized by a pore water composition buffered by portlandite at pH ≈ 12.5 and [Ca]_tot ≈ 2∙10⁻² M. After the complete dissolution of portlandite, the degradation stage III is dominated by the incongruent dissolution of calcium silicate hydrate (C-S-H) phases, with Ca:Si ratios of ≈1.6 to ≈0.6 and 12.5 ≤ pH ≤ 10. In the context of waste disposal in rock salt formations, the corrosion of cementitious waste forms has been reported to potentially generate CaCl₂-rich brines (up to 4 M) in combination with very high pH values (pH_m ≈ 12, with pH_m = –log [H⁺] in molal units) (Neck et al., 2009; Bube et al., 2013). Intermediate ionic strength conditions (I = 2–3 M) are also found in Cretaceous argillites in Northern Germany (Brewitz, 1980), with pore waters mostly dominated by NaCl and CaCl₂.

Previous studies investigating the solubility and hydrolysis of transition metals, lanthanides and actinides in alkaline, concentrated CaCl₂ systems have shown the formation and predominance of highly hydrolysed moieties stabilized by the coordination with Ca²⁺ ions. Using a combination of solubility and TRLFS studies, Neck and co-workers reported the formation of the ternary complexes Ca[M(III)(OH)₃]²⁺, Ca₂[M(III)(OH)₄]³⁺ and Ca₃[M(III)(OH)₆]³⁺ (with M = Nd, Am, Cm and Pu) in concentrated CaCl₂ solutions (Rabung et al., 2008; Neck et al., 2009). The formation of analogous ternary complexes of tetravalent metal ions, e.g., Ca₄[An(IV)(OH)₈]⁴⁺ (An(IV) = Th(IV), Pu(IV) and Np(IV)), Ca₃[Zr(IV)(OH)₆]⁴⁺ and Ca₃[Tc(IV)O(OH)₅]³⁺, has been reported to increase the solubility of the corresponding hydrous oxides by several orders of magnitude in alkaline CaCl₂ solutions (Brendebach et al., 2007; Altmaier et al., 2008; Fellhauer et al., 2010; Fellhauer, 2013; Yalcintas et al., 2016). In spite of the weaker hydrolysis of the pentavalent actinides, Fellhauer and co-workers observed the formation of the ternary complexes Ca[Np(V)O₂(OH)₂]⁺ and Ca₃[Np(V)O₂(OH)₅]²⁺ in alkaline, concentrated CaCl₂ solutions (Fellhauer et al., 2016a; Fellhauer et al., 2016b). Spectroscopic evidence for the participation of Ca²⁺ in the formation of inner-sphere complexes was provided for Cm(III), Zr(IV), Th(IV) and Np(V), whereas DFT calculations underpin the stability of such complexes in the case of Tc(IV). All investigations above emphasize the key role of Ca²⁺ in the stabilization of highly hydrolyzed metal ions in concentrated CaCl₂ systems with high pH, regardless of the oxidation state of the metal ion. In the case of Zr(IV) and possibly due to the stronger hydrolysis of this metal ion, the ternary complex/es Ca–Zr(IV)–OH become predominant at [CaCl₂] > 10⁻² M, which emphasizes their relevance also in dilute cementitious systems.

The behaviour of beryllium in aqueous solutions at the molecular level has been investigated in a number of computational studies. Beryllium preferentially coordinates ligands in tetrahedral geometry, has strong hydrolysing and polarising abilities, and shows complex pH-dependent solution chemistry (Marx et al., 1997; Alderighi et al., 2000; Jin et al., 2015; Perera et al., 2017). In our previous studies, it was shown that in cementitious environment Ca²⁺ ions play a key role in the uptake of Be(II) by C-S-H phases (Çevirim-Papaioannou et al., 2021a; Çevirim-Papaioannou et al., 2021b). Together with evidences gained for M(III), M(IV) and M(V) systems, this anticipates the possible formation of previously unreported ternary complexes Ca–Be(II)–OH in alkaline CaCl₂ solutions. Through a combination of experimental solubility studies, molecular dynamics calculations and thermodynamic modelling, this work aims at providing a comprehensive understanding of the solution chemistry of beryllium in Ca-containing alkaline systems representative of cementitious environments with low to elevated ionic strength conditions.

2 Experimental

2.1 Chemicals

All samples were prepared, stored and handled in an Ar-glove box (O₂ < 1 ppm) at T = (22 ± 2)°C. All solutions were prepared with purified water (Milli-Q academic, Millipore, 18.2 MΩ) purged with Ar for at least 1 h to remove CO₂(g). Beryllium sulfate tetrahydrate (BeSO₄∙H₂O, 99.99% purity) and calcium chloride (CaCl₂∙H₂O) EMSURE^® were purchased from Merck. Calcium hydroxide (Ca(OH)₂) was purchased from Sigma-Aldrich.

2.2 pH measurements

A combination pH electrode (ROSS Orion with 3.0 M KCl as filling solution) was used to determine the proton concentration ([H⁺] in mol∙kg^–1, with pH_m = –log [H⁺]). The pH electrode was calibrated using commercial pH buffers (pH = 1–12, Merck). In salt solutions of ionic strength I ≥ 0.1 mol kg^–1, the measured pH value (pH_exp) is an operational apparent value related to [H⁺] by pH_m = pH_exp + A_m. The values A_m entail both the activity coefficient of H⁺ and the liquid junction potential of the electrode at a given background electrolyte concentration and temperature. A_m values reported by Altmaier and co-workers for CaCl₂ systems were used for the determination of pH_m (Altmaier et al., 2008).

2.3 Solid phase preparation and characterization. Solubility experiments with α-Be(OH)₂(cr)

The solid phase used for undersaturation solubility experiments, α-Be(OH)₂(cr), was precipitated by slow addition of a 0.35 M BeSO₄ solution to a 2.0 M carbonate-free NaOH solution with a final pH ≈ 10.5. After an ageing time of ≈2 months, the solid phase was washed thoroughly with slightly alkaline water (pH ≈ 9.5) to remove the residues of the matrix solution (Na₂SO₄ and NaOH), and characterized by X-ray diffraction (XRD). Details on the preparation and characterization of the solid phase used in this work were provided in our previous study (Çevirim-Papaioannou et al., 2020).

A total of 30 independent batch samples were prepared by contacting 0.5–5 mg of α-Be(OH)₂(cr) to alkaline CaCl₂ solutions (0.05, 0.25, 1.0 and 3.5 M) with 8.9 ≤ pH_m ≤ 11.8. Be(II) concentrations and pH_m values were monitored regularly from 7 to 337 days. In each sampling, aliquots (100–500 µL) of the supernatant of each sample were pipetted into 10 kD filters (2–3 nm cut-off Nanosep^®, Pall Life Sciences), centrifuged for 10 min at 6000 g, and diluted (1:100 and 1:4000) with 2% ultrapure HNO₃ before the quantification by inductively coupled plasma mass spectrometry (ICP-MS, PerkinElmer ELAN 610). The detection limit of the technique ranged between 10^−6.5 and 10⁻⁸ M, depending upon the dilution factors applied at different CaCl₂ concentrations. Equilibrium conditions were assumed after repeated measurements over time with constant [Be] and pH_m values, typically after 372 days. After attaining equilibrium conditions, the solid phase of a selected sample (1.0 M CaCl₂, pH_m = 11.1) was characterized by XRD. For this purpose, an aliquot of the solid phase (≈1–2 mg) was washed 7 times with ethanol (0.5–1 mL) under Ar atmosphere in order to remove the background electrolyte, i.e., CaCl₂. After the last cleaning step, the washed solid phase was re-suspended in ethanol, deposited on the XRD sample holder and left drying for a few minutes inside the glovebox. The XRD diffractogram was collected using a Bruker D8 Advance X-Ray powder diffractometer (Cu anode) within the range 2θ = 2–80⁰, incremental steps of 0.02 and a measurement time of 0.4 s per step.

2.4 Computational methods

The simulation model was built in a box with dimensions of 43 Å × 43 Å × 49 Å, which contained 3,120 water molecules with 3 Be(OH)₄^2–, 50 Ca²⁺, and 84 Cl^–randomly distributed ions. This approximately corresponds to 1 M CaCl₂ and 0.05 M beryllium ion concentration. The high concentration of Be(II) is required in the simulations for better statistical sampling, and is in line with experimental observations in concentrated CaCl₂ solutions. The total electroneutrality of the simulation cell was ensured by balancing the number of counterions. Periodic boundary conditions were applied in three dimensions. Water was described using the extended simple point charge (SPC/E) model (Berendsen et al., 1987). The 12-6-4 Lennard-Jones-type nonbonded parameters for Ca²⁺ and Be²⁺ for SPC/E water, which include the contribution from the ion-induced dipole interaction, were taken from Li and Merz (Li and Merz, 2014; Li et al., 2020). Standard Lorenz-Berthelot mixing rules (Allen and Tildesley, 2017) were applied to calculate short-range Lennard-Jones interactions between the unlike atoms (with a cut-off distance of 1.4 nm). Long-range electrostatic forces were evaluated using the Ewald summation method. All molecular dynamics (MD) simulations were performed using the LAMMPS software package (3 March 2020 version) (Plimpton, 1995). Model equilibration was carefully monitored by assessing the temperature, pressure, kinetic and potential energy of the system, and dimensions of the simulation box, in order to confirm that these parameters reach their equilibrium steady state values on average (Braun et al., 2019). The Newtonian equations of the atomic motions were numerically integrated with a time step of 1 fs, and the model systems were initially equilibrated for 5 ns in the isobaric–isothermal statistical ensemble (NPT), then for 5 ns in the canonical ensemble (NVT). Temperature and pressure were constrained using the Nose-Hoover thermostat and barostat (Braun et al., 2019) at ambient conditions (T = 295 K, p = 0.1 MPa). The production run was performed in the NVT ensemble for 5 ns, and the trajectory was recorded every 500 fs. To describe local structural properties, radial distribution functions for pairs of atoms, and running coordination numbers were calculated from the recorded trajectory. The VMD software package (version 1.9.3) has been used for visualisation (Humphrey et al., 1996).

3 Results and discussion

3.1 Solid phase characterization

XRD patterns collected for the beryllium solid phase equilibrated in 1.0 M CaCl₂ at pH_m = 11.1 and 3.5 M CaCl₂ at pH_m = 10.6 are shown in Figure 1, together with the diffractograms previously reported for α-Be(OH)₂(cr) in Bear and Turnbull (1965) and in our previous study (Çevirim-Papaioannou et al., 2020). The main features of this sample are in excellent agreement with the patterns previously reported for α-Be(OH)₂(cr). This observation confirms that the starting material used in the experiments, α-Be(OH)₂(cr), is the solid phase controlling the solubility of beryllium also in CaCl₂ systems.

FIGURE 1

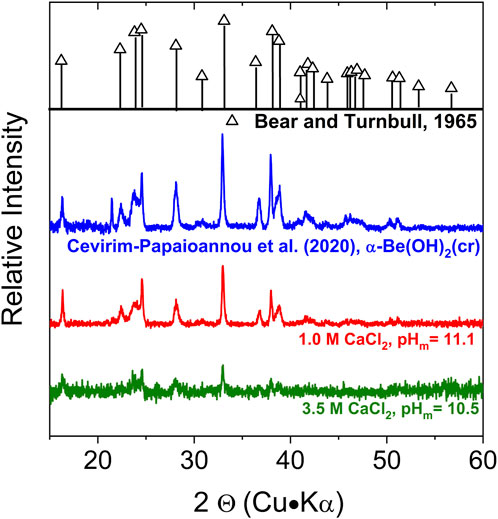
FIGURE 1. X-Ray diffraction patterns of the solid phase recovered from the solubility sample equilibrated in 1.0 M CaCl₂ at pH_m = 11.1, together with reference patterns reported for α-Be(OH)₂(cr) (Bear and Turnbull, 1965) and patterns obtained in our previous study (Çevirim-Papaioannou et al., 2020).

3.2 Solubility experiments

Figure 2 shows the experimental solubility data determined in alkaline CaCl₂ solutions with 8.9 ≤ pH_m ≤ 11.8, together with the solubility curve of α-Be(OH)₂(cr) at I = 0 calculated using the thermodynamic model reported in (Çevirim-Papaioannou et al., 2020) (see Supplementary Tables SI-S1, S2 in the Supplementary Material). The solubility of Be(II) in 0.05 M CaCl₂ shows a pH-independent behaviour within 9 ≤ pH_m ≤ 10.5, which is in good agreement with the calculated solubility line and can be assigned to the solubility reaction α-Be(OH)₂(cr) ⇔ Be(OH)₂(aq). Above pH ≈ 10.5, the solubility in 0.05 M CaCl₂ increases steadily with a slope of ≈ +2 (as log [Be(II] vs. pH_m), in disagreement with the slope of +1 observed for NaCl/KCl systems within the same pH-range and also predicted by the calculated solubility line. This observation reflects that in CaCl₂ solutions the solubility of the α-Be(OH)₂(cr) phase is dominated by an equilibrium reaction involving the release of 2 H⁺. A well-defined slope of ≈ +2 is also observed for all other CaCl₂ systems investigated in this work, with the highest solubility being achieved in 3.5 M CaCl₂ solutions. Our experimental observations in CaCl₂ systems and the direct comparison with solubility data in NaCl/KCl solutions support the earlier predominance of the [Be(OH)₄]^2– moiety in the former systems, expectedly as a result of its stabilization by Ca²⁺ ions. This is in line with previous observations reported in the literature for strongly hydrolyzing metal ions, e.g., M(III), M(IV) and M(V) (Altmaier et al., 2008; Neck et al., 2009; Fellhauer et al., 2010; Fellhauer, 2013; Yalcintas et al., 2016).

FIGURE 2

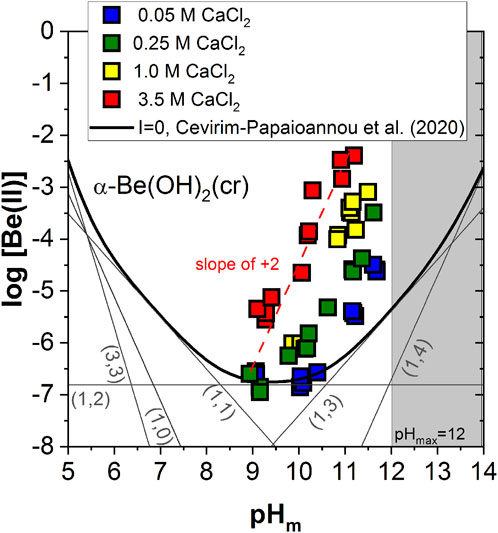
FIGURE 2. Experimental Be(II) solubility data obtained in the present work in 0.05, 0.25, 1.0 and 3.5 M CaCl₂ solutions with 8.9 ≤ pH_m ≤ 11.8. Solid thick line corresponds to the solubility curve of α-Be(OH)₂(cr) at I = 0 calculated with thermodynamic data reported in Çevirim-Papaioannou et al. (2020). Dashed red line indicates the slope analysis performed in this study. Shadowed area represents the precipitation of Ca(OH)₂(s) [at (CaCl₂) ≤ 2 M] or Ca–OH–Cl(s) solid phases. Uncertainties of individual measurements are within the size of the symbols.

3.3 MD calculations of the system Ca²⁺–Be(OH)₄^2––Cl^––H₂O(l)

The local structure of a solution can be described by means of the radial distribution functions of the ion-ion and ion-water pairs. The RDF shows the probability of finding atoms at curtain distance during simulation time, and allows to calculate time-averaged coordination numbers. Figure 3 presents calculation results for Be²⁺ ions in CaCl₂ aqueous solution.

FIGURE 3

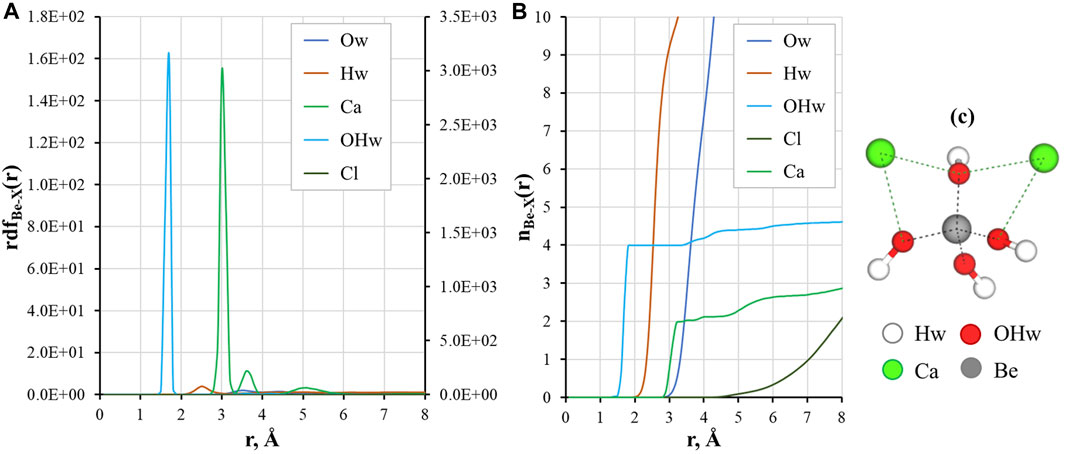
FIGURE 3. Local structural properties of Be(OH)₄^2– in a CaCl₂ solution: (A) radial distribution functions (the secondary axes show rdf(r) for the Be-OHw pair); (B) running coordination numbers for Be-X atom pairs, where X is O, H, Cl, and Ca; (C) Simulation snapshot of the complex, water molecules omitted for clarity.

Figures 3A, B shows that the interaction of Be²⁺ with hydroxyl ions is strong and was stable during all the simulation time. There are 4 oxygen atoms of the aqueous hydroxyl ions in the first coordination sphere of Be²⁺ at r ≈ 1.7 Å. This result agrees well with the reported distances between Be²⁺ and hydroxyl ions calculated by DFT (Jin et al., 2015). The oxygen atoms of the first shell are coordinated with other solution molecules through hydrogen bonding (Hw peak at distances around 2–3 Å) to the second solvation shell (small Ow peak at r ≈ 3–4 Å). As it can be seen from Figures 3A, B, there is a low probability of binding between Be²⁺ and Cl⁻ions: no distinct peak of chloride ions was recorded, and Cl⁻presence was only found at r > 5 Å.

Three peaks for Ca²⁺ are found in the outer coordination sphere of Be²⁺: a high-intensity peak at r ≈ 3.1 Å, a small peak between 3 Å and 4 Å, and very broad peak of very low intensity around 5 Å. The first peak corresponds to binding of two calcium cations with oxygens of the hydroxyl ions in bidentate coordination, as can be seen in the snapshot from simulations (Figure 3C). The peak between 3 and 4 Å is the coordination of Ca²⁺ with a single hydroxyl group. The broad peak after 5 Å stands for Ca²⁺ ions in the solution that are not bound to the complex. We have previously shown that Ca²⁺ plays a crucial role in the sorption of Be(II) in cementitious systems (Çevirim-Papaioannou et al., 2021a; Çevirim-Papaioannou et al., 2021b). The surface of C-S-H provides a more structured environment, where both ions and water molecules are coordinated with the surface in the sorption layer increasing the probability for Be hydroxyl species to form complex with multiple Ca²⁺ ions (up to three). From the results of this study, it can be concluded that in the solution complexes of Be(OH)₄^2– with two Ca²⁺ are dominant, while binding of the third calcium cation remains possible, which is reflected in the slightly higher value of running coordination for the Be-Ca pair (n ≈ 2.2 at a distance of 4 Å).

3.4 Chemical, thermodynamic and SIT activity models

The specific ion interaction theory (SIT) (Ciavatta, 1980) based on the Brønsted-Guggenheim-Scatchard model is used in this study to account for ion interactions in systems at I > 0. This is also the method adopted for ion strength corrections within the NEA-TDB project (Grenthe et al., 2020). In SIT, the activity coefficient of a given ion j (γ_j) is calculated according to:

$lo\mathrm{g}{\mathrm{\gamma }}_j=-z_j^{2}D+{\sum }_k\epsilon \left(j,k,I_m\right)m_k(1)$

where z_j is the charge of the ion j, D is the Debye-Hückel term ($D=\frac{0.509\sqrt{I_m}}{1+1.5\sqrt{I_m}}$), m_k is the molality of the oppositely charged ion k, and ε(j, k, I_m) is the specific ion interaction parameter. The Debye Hückel term in Equation 1 accounts for the electrostatic, non-specific long-range interactions prevailing in dilute systems, whereas the term ${\sum }_k\epsilon \left(j,k,I_m\right)m_k$ accounts for short-range, non-electrostatic interactions that become relevant at higher ionic strength conditions. The SIT coefficient ε(j, k, I_m) reflects also differences between ions of the same charge but different size. The applicability of the SIT approach is often considered limited to I_m ≤ 3.5 mol kg^–1, although previous studies have reported reliable results for 1:1 and 1:2 electrolytes (including CaCl₂ systems) up to I_m ≈ 13.5 mol kg^–1 (Neck et al., 2009; Fellhauer et al., 2010; Yalcintas et al., 2016; Altmaier et al., 2017).

Based on the slope analysis discussed in Section 3.1 and considering that α-Be(OH)₂(cr) is the solid phase controlling the solubility in all investigated systems, the equilibrium reaction (2) is proposed to describe the solubility of Be(II) in CaCl₂ solutions above pH_m ≈ 9–10 (depending upon salt concentration). As reflected in reaction (2), the number of Ca-atoms participating in the complexation reaction (n) is unknown and must be included in the optimization process.

$\mathrm{\alpha }-\text{Be}{\left(\text{OH}\right)}_2\left(\text{cr}\right)+{\text{nCa}}^{2+}+2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\iff {\text{Ca}}_{\mathrm{n}}\mathrm{B}\mathrm{e}{\left(\text{OH}\right)}_4^{\left(2\mathrm{n}–2\right)}+2{\mathrm{H}}^{+}(2)$

with

${\log }^{*}{K}_{\mathrm{s},{\mathrm{C}\mathrm{a}}_{\mathrm{n}}\mathrm{B}\mathrm{e}{\left(\mathrm{O}\mathrm{H}\right)}_4^{\left(2\mathrm{n}-2\right)}}^{\prime }=\log \left[{\text{Ca}}_{\mathrm{n}}\mathrm{B}\mathrm{e}{\left(\text{OH}\right)}_4^{2\mathrm{n}–2}\right]+2\log \left[{\mathrm{H}}^{+}\right]–\text{\hspace{0.17em}nlog\hspace{0.17em}}\left[{\text{Ca}}^{2+}\right](3)$

$lo{g}^{*}{K}_{s,{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}^{°}=lo{g}^{*}{K}_{s,{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}^{\prime }+\mathit{log}{\gamma }_{{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}+2\mathit{log}{\gamma }_{H^{+}}$

$-nlog{\gamma }_{C{a}^{2+}}-2\mathit{log}{a}_w(4)$

$lo{g}^{*}{K}_{s,{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}^{\prime }-\Delta z^{2}D-2\mathit{log}{a}_w=lo{g}^{*}{K}_{s,{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}^{°}-\Delta \epsilon m_{C{l}^{-}}(5)$

Conditional solubility constants, log ^*K′_s,CanBe(OH)4⁽²ⁿ⁻²⁾, were determined from the experimental solubility data obtained in 0.05, 0.25, 1.0 and 3.5 M CaCl₂ using the minimization function ∑((log [Be]_exp–log [Be]_calc)²)^1/2. Three different chemical models were considered in the calculations, assuming the predominance of the ternary complexes Ca_nBe(OH)₄⁽²ⁿ⁻²⁾ with n = 1–3 in the aqueous phase. The SIT-plot was used to derive the solubility constant at the reference state, log ^*K°_s,CanBe(OH)4^(2n-2), and corresponding SIT ion interaction coefficient/s based on the linear regression (log ^*K′_s,CanBe(OH)4^(2n-2) + Δz²D—2 log a_w) vs. [Cl⁻] (in molal units). The SIT ion interaction coefficients of the ternary complexes Ca_nBe(OH)₄⁽²ⁿ⁻²⁾ were calculated from the slope of the linear regression (–Δε) in combination with ε(H⁺, Cl⁻) = (0.12 ± 0.01) kg∙mol^–1, ε(Ca²⁺, Cl⁻) = (0.14 ± 0.01) kg∙mol^–1 and a_w values as reported in the NEA-TDB (Grenthe et al., 2020). The criteria considered for the selection of the chemical model describing the solubility of Be(II) in CaCl₂ was based on:

(i) minimization of the quality parameter (Δ) calculated as $\sum \left|lo{g}^{*}{K}_{s,{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}^{\prime ,\exp }\right.-\left.\mathit{log}{K}_{s,{Ca}_{n}Be{\left(OH\right)}_4^{\left(2n-2\right)}}^{\prime ,\text{calc}}\right|$ (Fellhauer et al., 2010; Fellhauer, 2013; Yalcintas et al., 2016),

(ii) reasonable values of the SIT interaction coefficients, considering charge analogies described in Hummel (2009), and

(iii) smooth shape of the plot log ^*K′_s,CanBe(OH)4^(2n-2) vs. [Cl⁻]

Table 1 shows the conditional solubility constants, log ^*K′_s,CanBe(OH)4^(2n-2), determined for each chemical model and background electrolyte concentration, together with log ^*K°_s,CanBe(OH)4^(2n-2), ε(Ca_nBe(OH)₄⁽²ⁿ⁻²⁾, Ca²⁺/Cl⁻) and the quality parameter (Δ). The SIT-plot as well as the representation of log ^*K′_s,CanBe(OH)4^(2n-2) vs. [Cl⁻] for the three chemical models evaluated in this work are shown in Supplementary Figures SI-S1, S2 of the Supporting Information.

TABLE 1

TABLE 1. Values of log *K′_s,CanBe(OH)4^(2n-2) determined from solubility data of Be(II) in 0.05–3.5 M CaCl₂ solutions for the chemical models assuming the formation of the ternary complexes Ca[Be(OH)₄](aq), Ca₂[Be(OH)₄]²⁺ or Ca₃[Be(OH)₄]⁴⁺. Equilibrium constants in the reference state, log *K’_{s,CanBe(OH)4(2n-2)} and SIT coefficients as determined from the corresponding SIT-plots (see Supplementary Figures SI-S1 in the Supporting Information). Quality parameter (Δ) calculated for each chemical model as described in the text.

Table 1 shows very large values of the quality parameter (Δ) for the chemical models including the aqueous complexes CaBe(OH)₄(aq) and Ca₃Be(OH)₄⁴⁺, which reflect the significant deviations between experimental and calculated log *K′_s,CanBe(OH)4^(2n-2) for these systems (see also Supplementary Figures SI-S1 in the Supplementary Material). Note that although values of ε(i, j) = 0 for neutral species are considered per definition in SIT, a number of neutral species with ε(i, j) ≠ 0 are reported in the NEA-TDB books (see for instance Grenthe et al., 2020), and this cannot be considered as criteria to reject a specific chemical model. The chemical model including the complex Ca₂[Be(OH)₄]²⁺ shows the lowest value of Δ, a reasonable SIT coefficient, as well as a smooth shape of the plot log ^*K′_s,CanBe(OH)4^(2n-2) vs. [Cl⁻] (see Supplementary Figures SI-S2). This outcome is in agreement with the MD calculations summarized in Section 3.3, which predict the predominance of an aqueous complex with two Ca-atoms. The same model calculations described above but excluding solubility data in 3.5 M CaCl₂ were also performed in order to remain within the range of ionic strength normally considered for SIT. The best fit was obtained again for the chemical model including the complex Ca₂[Be(OH)₄]²⁺ (see Supplementary Figures SI-S3; Supplementary Tables SI-S4). Consistent values of log *K°_{s,Ca2[Be(OH)4}]²⁺ and ε(Ca₂[Be(OH)₄]²⁺, Cl⁻) were obtained using both datasets, and thus the model derived including also solubility data in 3.5 M CaCl₂ was finally favored.

The chemical reaction (6) and corresponding thermodynamic functions are thus considered for the extension of the thermodynamic and activity models reported in Çevirim-Papaioannou et al. (2020) to the system Be²⁺–Ca²⁺–Na⁺–K⁺–H⁺–Cl^––OH^––H₂O(l)^.

$\mathrm{\alpha }-\text{Be}{\left(\text{OH}\right)}_2\left(\text{cr}\right)+2{\text{Ca}}^{2+}+2{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\iff {\text{Ca}}_2\mathrm{B}\mathrm{e}{\left(\text{OH}\right)}_4^{2+}+2{\mathrm{H}}^{+}(6)$

$\log *K_{\mathrm{s},{\mathrm{C}\mathrm{a}}_{\mathrm{n}}\mathrm{B}\mathrm{e}{\left(\text{OH}\right)}_4^{\left(2\mathrm{n}-2\right)}}^{°}=–\left(25.13\pm 0.27\right)$

$\mathrm{\epsilon }\left({\text{Ca}}_2{\left[\text{Be}{\left(\text{OH}\right)}_4\right]}^{2+},{\text{Cl}}^{–}\right)=\left(0.00\pm 0.15\right)\text{\hspace{0.17em}kg}\bullet {\text{mol}}^{–1}$

Figures 4A–D shows the excellent agreement between the experimental solubility data determined in 0.05–3.5 M CaCl₂ solutions with solubility calculations conducted using the thermodynamic and activity models derived in Çevirim-Papaioannou et al. (2020) and extended in this work. Future work will target the development of a Pitzer activity model for this system, which is clearly favored for the description of brine systems.

FIGURE 4

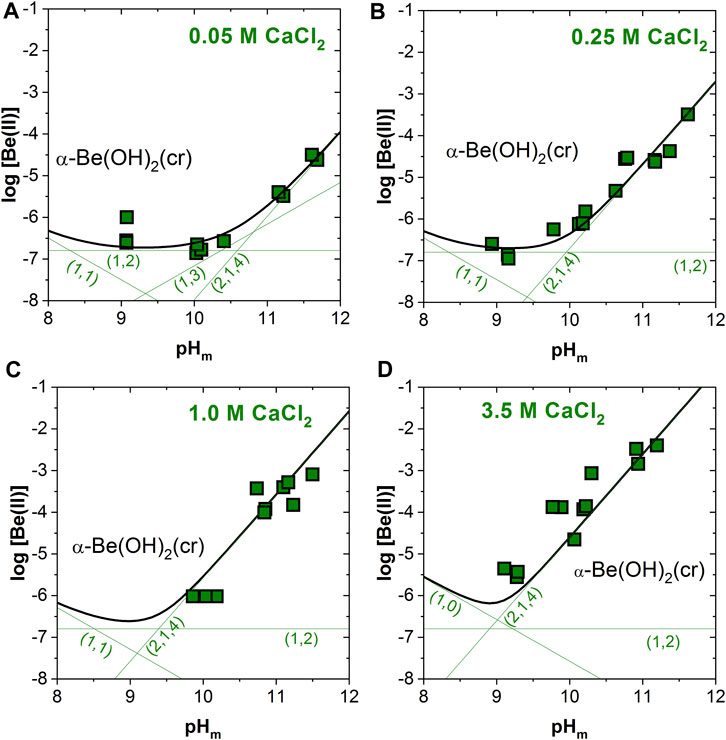
FIGURE 4. Experimental and calculated solubility of α-Be(OH)₂(cr) in (A) 0.05, (B) 0.25, (C) 1.0 and (D) 3.5 M CaCl₂ solutions. Calculations conducted using the thermodynamic and activity models derived in Çevirim-Papaioannou et al. (2020) and extended in this work. Uncertainties of individual measurements are within the size of the symbols.

3.5 Speciation of beryllium in cementitious systems

C-S-H phases of various compositions determine the most relevant properties of cement pastes in ordinary Portland and blended systems. The non-ideal multisite CASH + solid solution model (Miron et al., 2022a; Miron et al., 2022b; Kulik et al., 2022) can accurately model the C-S-H solubility, water content and elemental uptake accounting for the continuous change of solid and pore solution compositions as a function of pH, alkali concentration, and Ca/Si ratio in the system. In the present work, the CASH + model is used to compute the evolution of a pore solution composition assuming the degradation of a Portland cement in a repository setting defined by low ionic strength conditions. This is done by removing alkalis and of Ca from the system (Ca-Si-Na-K-H₂O) in equilibrium with C-S-H to produce the change of the pore solution composition (Figures 5A, B) as a function of [H⁺], present at different cement degradation stages. At the starting point the pore solution composition in equilibrium with a hydrated Portland cement is taken from (Vollpracht et al., 2016) and has a pH = 13.40 and [NaOH + KOH] = 0.555 M (with K/Na = 2). Alkalis are then removed and the pH decreases to a value of 12.4, when the system is in equilibrium with high Ca/Si C-S-H and portlandite. In natural systems, the pore solution composition is buffered at this condition until all portlandite is dissolved. By removing Ca from the system, after the full dissolution of portlandite, the composition of C-S-H goes towards lower Ca/Si ratios and the pH of the solution decreases to 9.8 at which point the system is in equilibrium with low Ca/Si C-S-H and amorphous silica. The evolution of the pore water composition obtained from calculations with the CASH + solid solution model in combination with the thermodynamic and activity models derived in this work and reported in Çevirim-Papaioannou et al. (2020) have been used to calculate the aqueous speciation of beryllium throughout the complete degradation process of cement (see Figure 5C).

FIGURE 5

FIGURE 5. (A) Evolution of the Ca/Si ratio in C-S-H phases and (B) simulated pore solution composition as a function of pH during the process of cement degradation. (C) Fraction diagram of Be(II) within 9.8 ≤ pH_m ≤ 13.5 for the pore water composition shown in (B), as calculated using the thermodynamic and activity models derived in Çevirim-Papaioannou et al. (2020) and extended in this work.

Figure 5C shows that the hydrolysis species Be(OH)_3⁻ and (to less extent) Be(OH)₄²⁻ prevail within the degradation stage I of cement, characterized by very high pH and low Ca concentration. Due to the enhanced Ca concentration defined by the equilibrium with portlandite, the ternary complex Ca₂[Be(OH)₄]²⁺ dominates the aqueous speciation of Be(II) within the degradation stage II, as well as in the early steps of the degradation stage III at pH > 12.1. With the decrease in Ca concentration, the hydrolysis species Be(OH)_3⁻ becomes predominant again at 10.6 ≤ pH ≤ 12.1, in systems controlled by C-S-H phases with Ca:Si = 0.80–1.27. Below pH ≈ 10.6, the neutral species Be(OH)₂(aq) becomes predominant until the full degradation of cement.

Note that CASH + has not been yet verified for calculating systems with concentrated CaCl₂ solutions. In particular, the evolution of C-S-H and other cement phases at high Ca concentrations remains ill-defined. Although this contribution has focused on the SIT activity model, the development of the corresponding Pitzer activity model for the system Be²⁺–Ca²⁺–Na⁺–K⁺–H⁺–Cl^––OH^––H₂O(l) is foreseen in the next phase of this study. Pitzer formalism is clearly favored for the description of high-saline systems. Efforts dedicated to the thermodynamic modelling of cementitious systems in high saline conditions are also on-going in the context of the THEREDA Reference Database project (Moog et al., 2015).

4 Summary and conclusion

The solubility and hydrolysis of Be(II) in dilute to concentrated CaCl₂ solutions (0.05–3.5 M) was investigated using a combination of undersaturation solubility experiments with α-Be(OH)₂(cr) and molecular dynamics (MD) calculations. The solubility of Be(II) in 0.05 M CaCl₂ shows a pH-independent behaviour in weakly alkaline systems (9 ≤ pH_m ≤ 10.5), which corresponds to the solubility equilibrium α-Be(OH)₂(cr) ⇔ Be(OH)₂(aq). These observations are in excellent agreement with previous solubility experiments in NaCl and KCl solutions. A steep increase of the solubility with a slope of ≈ +2 (as log [Be(II)] vs. pH_m) is observed above pH_m ≈ 10.5 and at higher CaCl₂ concentrations. At pH_m ≈ 12, this results in solubility values significantly higher (1–4 orders of magnitude, depending upon CaCl₂ concentration) than those reported previously for analogous NaCl and KCl systems (Çevirim-Papaioannou et al., 2020). In line with previous studies in the literature on M(III), M(IV) and M(V) metal ions in CaCl₂ systems, these observations unequivocally point towards the formation and predominance of ternary complexes of the type Ca_nBe(OH)₄⁽²ⁿ⁻²⁾ in alkaline to hyperalkaline systems containing Ca. MD calculations show the coordination of two Ca-ions in the second coordination sphere of Be²⁺ at r ≈ 3.1 Å. These Ca-ions are coordinated in bi-dentate mode to the hydroxyl groups of the [Be(OH)₄]^2– moiety. Consistently with MD calculations, the fit of solubility data indicates the predominance of the complex Ca₂[Be(OH)₄]²⁺ in the investigated CaCl₂ systems.

In combination with data previously reported in (Çevirim-Papaioannou et al., 2020), chemical, thermodynamic and (SIT) activity models are derived in this work for the system Be²⁺–Ca²⁺–Na⁺–K⁺–H⁺–Cl^––OH^––H₂O(l). These new Be(II) models allow the precise characterization of the solubility and speciation of beryllium throughout all degradation stages of cement, as analysed in this paper for low ionic strengths systems. This can be used for source term estimations of beryllium in the context of nuclear waste disposal, as well as input parameter for advanced surface complexation or solid-solution sublattice models for the retention of beryllium in cementitious systems.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

NÇ-P: Methodology, Investigation, Writing–Original Draft. IA: Simulation, Investigation, Writing–Original Draft. GM: Investigation, Writing–Original Draft. XG: Conceptualization, Writing–Review and Editing, Supervision, Project administration. MA: Writing–Review and Editing, Project administration, Funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

The research leading to these results has received funding from the European Union’s European Atomic Energy Community’s (Euratom) Horizon 2020 Programme (NFRP-2014/2015) under grant agreement, 662147—Cebama.

Acknowledgments

Frank Geyer, Annika Fried and Cornelia Beiser (all KIT–INE) are gratefully acknowledged for the ICP–MS and ICP–OES measurements. We thank Bianca Schacherl for her support on sample preparation. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology. The authors acknowledge support by the state of Baden-Wurttemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster).

Conflict of interest

The author XG declared that they were an editorial board member of Frontiers at the time of submission. This had no impact on the peer review process and the final decision.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2023.1192463/full#supplementary-material

References

Alderighi, L., Gans, P., Midollini, S., and Vacca, A. (2000). “Aqueous solution chemistry of beryllium,” in Main chemistry group, advances in inorganic chemistry, vol 50. Editors A. G. Sykes, and A. Cowley (San Diego: Academic Press), 110–172.

CrossRef Full Text | Google Scholar

Allen, R., and Tildesley, D. J. (2017). Computer simulation of liquids. 2nd edition. New York: Oxford University Press, 626.

Google Scholar

Altmaier, M., Neck, V., and Fanghanel, T. (2008). Solubility of Zr(IV), Th(IV) and Pu(IV) hydrous oxides in CaCl₂ solutions and the formation of ternary Ca-M(IV)-OH complexes. Radiochim. Acta 96, 541–550. doi:10.1524/ract.2008.1535

CrossRef Full Text | Google Scholar

Altmaier, M., Yalcintas, E., Gaona, X., Neck, V., Müller, R., Schlieker, M., et al. (2017). Solubility of U(VI) in chloride solutions. I. The stable oxides/hydroxides in NaCl systems, solubility products, hydrolysis constants and SIT coefficients. J. Chem. Thermodyn. 114, 2–13. doi:10.1016/j.jct.2017.05.039

CrossRef Full Text | Google Scholar

Baes, C. F., and Mesmer, R. E. (1976). The hydrolysis of cations. New York: John Wiley and Sons.

Google Scholar

Bear, I. J., and Turnbull, A. G. (1965). The heats of formation of beryllium compounds. I. Beryllium hydroxides. J. Phys. Chem. 69, 2828–2833. doi:10.1021/j100893a004

CrossRef Full Text | Google Scholar

Beeston, J. M. (1970). Beryllium metal as a neutron moderator and reflector material. Nucl. Eng. Des. 14, 445–474. doi:10.1016/0029-5493(70)90161-5

CrossRef Full Text | Google Scholar

Berendsen, H. J. C., Grigera, J. R., and Straatsma, T. P. (1987). The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271. doi:10.1021/j100308a038

CrossRef Full Text | Google Scholar

Bertin, F., Thomas, G., and Merlin, J. C. (1967). Studies on beryllium complexes. I. Solvolysis of Be²⁺ ions in aqueous media. J. C. Bull. Soc. Chim. Fr. 2393.

Google Scholar

Braun, E., Gilmer, J., Mayes, H. B., Mobley, D. L., Monroe, J. I., Prasad, S., et al. (2019). Best practices for foundations in molecular simulations [article v1.0]. Living J. Comp. Mol. Sci. 1, 5957. doi:10.33011/livecoms.1.1.5957

PubMed Abstract | CrossRef Full Text | Google Scholar

Brendebach, B., Altmaier, M., Rothe, J., Neck, V., and Denecke, M. A. (2007). EXAFS study of aqueous Zr^IV and Th^IV complexes in alkaline CaCl₂ solutions: ca₃[Zr(OH)₆]⁴⁺ and Ca₄[Th(OH)₈]⁴⁺. Inorg. Chem. 46, 6804–6810. doi:10.1021/ic070318t

PubMed Abstract | CrossRef Full Text | Google Scholar

Brewitz, W. (1980). Zusammenfassender zwischenbericht, GSF T 114. Braunschweig: Ges. f. Strahlen-und Umweltforschung.

Google Scholar

Brown, P. L., and Ekberg, C. (2016). Hydrolysis of metal ions. Weinheim: Wiley-VCH Verlag GmbH.

Google Scholar

Bruno, J. (1987). Beryllium(II) hydrolysis in 3.0 mol·dm^-3 perchlorate. J. Chem. Soc. Dalton Trans. 1987, 2431–2437. doi:10.1039/dt9870002431

CrossRef Full Text | Google Scholar

Bruno, J., Grenthe, I., and Munoz, M. (1987a). Studies of metal carbonate equilibria. Part 16. The beryllium(II) - water-carbon dioxide(g) system in neutral-to-alkaline 3.0 mol dm^-3 perchlorate media at 25^oC. J. Chem. Soc. Dalton Trans. 1987, 2445–2449. doi:10.1039/dt9870002445

CrossRef Full Text | Google Scholar

Bruno, J., Grenthe, I., Sandstrom, M., and Ferri, D. (1987b). Studies of metal carbonate equilibria. 15. The beryllium(II)- water-carbon dioxide(g) system in acidic 3.0 mol dm^-3 perchlorate media. J. Chem. Soc. Dalton Trans. 1987, 2439–2444. doi:10.1039/dt9870002439

CrossRef Full Text | Google Scholar

Bube, C., Metz, V., Bohnert, E., Garbev, K., Schild, D., and Kienzler, B. (2013). Long-term cement corrosion in chloride-rich solutions relevant to radioactive waste disposal in rock salt - leaching experiments and thermodynamic simulations. Phys. Chem. Earth 64, 87–94. doi:10.1016/j.pce.2012.11.001

CrossRef Full Text | Google Scholar

Carell, B., Olin, A., and Valen, K. (1961). Studies on the hydrolysis of metal ions. 37. Application of the self-medium method to the hydrolysis of beryllium perchlorate. Acta Chem. Scand. 15, 1875–1884. doi:10.3891/acta.chem.scand.15-1875

CrossRef Full Text | Google Scholar

Çevirim-Papaioannou, N., Androniuk, I., Han, S., Mouheb, N. A., Gaboreau, S., Um, W., et al. (2021a). Sorption of beryllium in cementitious systems relevant for nuclear waste disposal: quantitative description and mechanistic understanding. Chemosphere 282, 131094. doi:10.1016/j.chemosphere.2021.131094

PubMed Abstract | CrossRef Full Text | Google Scholar

Çevirim-Papaioannou, N., Gaona, X., Böttle, M., Bethune Yalcintas, E., Schild, D., Adam, C., et al. (2020). Thermodynamic description of Be(II) solubility and hydrolysis in acidic to hyperalkaline NaCl and KCl solutions. Appl. Geochem. 117, 104601–104613. doi:10.1016/j.apgeochem.2020.104601

CrossRef Full Text | Google Scholar

Çevirim-Papaioannou, N., Han, S., Androniuk, I., Um, W., Altmaier, M., and Gaona, X. (2021b). Uptake of Be(II) by cement in degradation stage I: wet-chemistry and molecular dynamics studies. Minerals 11, 1149. doi:10.3390/min11101149

CrossRef Full Text | Google Scholar

Chandler, D., Primm, R. T., and Maldonado, G. I. (2009). Reactivity accountability attributed to beryllium reflector poisons in the high flux isotope reactor. Oak Ridge, USA: ORNL Report. TM-2009/188.

Google Scholar

Chinea, E., Dominguez, S., Mederos, A., Brito, F., Sanchez, A., Ienco, A., et al. (1997). Hydrolysis of beryllium(II) in DMSO:H₂O. Main. Group Mater. Chem. 20, 11–17. doi:10.1515/mgmc.1997.20.1.11

CrossRef Full Text | Google Scholar

Ciavatta, L. (1980). The specific interaction theory in evaluating ionic equilibria. Ann. Chim-Rome 70, 551–567.

Google Scholar

Fellhauer, D., Altmaier, M., Gaona, X., Lutzenkirchen, J., and Fanghanel, T. (2016a). Np(V) solubility, speciation and solid phase formation in alkaline CaCl₂ solutions. Part II: thermodynamics and implications for source term estimations of nuclear waste disposal. Radiochim. Acta 104, 381–397. doi:10.1515/ract-2015-2490

CrossRef Full Text | Google Scholar

Fellhauer, D., Neck, V., Altmaier, M., Lutzenkirchen, J., and Fanghanel, T. (2010). Solubility of tetravalent actinides in alkaline CaCl₂ solutions and formation of Ca₄[an(OH)₈]⁴⁺ complexes: A study of Np(IV) and Pu(IV) under reducing conditions and the systematic trend in the an(IV) series. Radiochim. Acta 98, 541–548. doi:10.1524/ract.2010.1751

CrossRef Full Text | Google Scholar

Fellhauer, D., Rothe, J., Altmaier, M., Neck, V., Runke, J., Wiss, T., et al. (2016b). Np(V) solubility, speciation and solid phase formation in alkaline CaCl₂ solutions. Part I: experimental results. Radiochim. Acta 104, 355–379. doi:10.1515/ract-2015-2489

CrossRef Full Text | Google Scholar

Fellhauer, D. (2013). Untersuchungen zur Redoxchemie und Löslichkeit von Neptunium und Plutonium. PhD thesis. Germany: University of Heidelberg.

Google Scholar

Gilbert, R. A., and Garrett, A. B. (1956). The equilibria of the metastable crystalline form of beryllium hydroxide - Be(OH)₂ in hydrochloric acid, perchloric acid and sodium hydroxide solutions at 25°C. J. Am. Chem. Soc. 78, 5501–5505. doi:10.1021/ja01602a012

CrossRef Full Text | Google Scholar

Green, R. W., and Alexander, P. W. (1965). Schiff base equilibria .2. Beryllium complexes of N-N-butylsalicylideneimine and hydrolysis of Be²⁺ ion. Aust. J. Chem. 18, 651–659. doi:10.1071/ch9650651

CrossRef Full Text | Google Scholar

Grenthe, I., Gaona, X., Plyasunov, A. V., Rao, L., Run-de, W. H., Grambow, B., et al. (2020). Second update on the chemical thermodynamics of uranium, neptunium, plutonium, americium and technetium. Paris, France 2020: OECD Publications. OECD Nuclear Energy Agency Paris.

Google Scholar

Hietanen, S., Sillen, L. G., Toplin, I., Melera, A., and Nilsson, L. (1964). Studies on the hydrolysis of metal ions. 52. A recalculation of emf data on beryllium hydrolysis. Acta Chem. Scand. 18, 1015–1016. doi:10.3891/acta.chem.scand.18-1015

CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graph. 14, 33–38. doi:10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, X. Y., Liao, R. B., Wu, H., Huang, Z. J., and Zhang, H. (2015). Structures and formation mechanisms of aquo/hydroxo oligomeric beryllium in aqueous solution: A density functional theory study. J. Mol. Model. 21, 232. doi:10.1007/s00894-015-2779-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kakihana, H., and Maeda, M. (1970). The hydrolysis of the beryllium ion in heavy water. Bull. Chem. Soc. Jpn. 43, 109–113. doi:10.1246/bcsj.43.109

CrossRef Full Text | Google Scholar

Kakihana, H., Sillen, L. G., Ormerod, J. G., Stenhagen, E., and Thorell, B. (1956). Studies on the hydrolysis of metal ions. XVI. The hydrolysis of the beryllium ion, Be2+. Acta Chem. Scand. 10, 985–1005. doi:10.3891/acta.chem.scand.10-0985

CrossRef Full Text | Google Scholar

Kulik, D. A., Miron, G. D., and Lothenbach, B. (2022). A structurally-consistent CASH+ sublattice solid solution model for fully hydrated C-S-H phases: thermodynamic basis, methods, and Ca-Si-H₂O core sub-model. Cem. Conc. Res. 151, 106585. doi:10.1016/j.cemconres.2021.106585

CrossRef Full Text | Google Scholar

Lanza, E., and Carpéni, G. (1968). Recherches sur le point isohydruque et les equilibres de condensation ou association-XXV. Etude electromerique de l'hydroxoxomplexation du cation (Be. aq)²⁺ Electrochim. Acta 13, 519–533. doi:10.1016/0013-4686(68)87023-9

CrossRef Full Text | Google Scholar

Li, P. F., and Merz, K. M. (2014). Taking into account the ion-induced dipole interaction in the nonbonded model of ions. J. Chem. Theory Comput. 10, 289–297. doi:10.1021/ct400751u

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Song, L. F., Li, P. F., and Merz, K. M. (2020). Systematic parametrization of divalent metal ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB water models. J. Chem. Theory Comput. 16, 4429–4442. doi:10.1021/acs.jctc.0c00194

PubMed Abstract | CrossRef Full Text | Google Scholar

Longhurst, G. R., Carboneau, M. I., and Mullen, C. K. (2003). “Challenges for disposal of irradiated beryllium,” in Proceedings of the 6th IEA Workshop on Beryllium Technology, Mizayaki, Japan, Dec. 2-5.

Google Scholar

Marx, D., Sprik, M., and Parrinello, M. (1997). Ab initio molecular dynamics of ion solvation. The case of Be²⁺ in water. Chem. Phys. Lett. 273, 360–366. doi:10.1016/s0009-2614(97)00618-0

CrossRef Full Text | Google Scholar

Mattock, G. (1954). The hydrolysis and aggregation of the beryllium ion. J. Am. Chem. Soc. 76, 4835–4838. doi:10.1021/ja01648a019

CrossRef Full Text | Google Scholar

Mesmer, R. E., and Baes, C. F. (1967). Hydrolysis of beryllium(II) in 1 m NaCl. Chem: Inorganic Chemistry Inorg.

Google Scholar

Miron, G. D., Kulik, D. A., and Lothenbach, B. (2022a). Porewater compositions of Portland cement with and without silica fume calculated using the fine-tuned CASH+NK solid solution model. Mat. Struct. 55, 212. doi:10.1617/s11527-022-02045-0

CrossRef Full Text | Google Scholar

Miron, G. D., Kulik, D. A., Yan, Y., Tits, J., and Lothenbach, B. (2022b). Extensions of CASH+ thermodynamic solid solution model for the uptake of alkali metals and alkaline earth metals in C-S-H. Cem. Conc. Res. 152, 106667. doi:10.1016/j.cemconres.2021.106667

CrossRef Full Text | Google Scholar

Moog, H. C., Bok, F., Marquardt, C. M., and Brendler, V. (2015). Disposal of nuclear waste in host rock formations featuring high-saline solutions - implementation of a thermodynamic reference database (THEREDA). Appl. Geochem. 55, 72–84. doi:10.1016/j.apgeochem.2014.12.016

CrossRef Full Text | Google Scholar

Neck, V., Altmaier, M., Rabung, T., Lutzenkirchen, J., and Fanghanel, T. (2009). Thermodynamics of trivalent actinides and neodymium in NaCl, MgCl₂, and CaCl₂ solutions: solubility, hydrolysis, and ternary Ca-M(III)-OH complexes. Pure Appl. Chem. 81, 1555–1568. doi:10.1351/pac-con-08-09-05

CrossRef Full Text | Google Scholar

Ohtaki, H. (1967). Ionic equilibria in mixed solvents. I. Hydrolysis of beryllium ion in a 0.2 mole fraction dioxane-water mixture containing 3 M LiClO₄ as an ionic medium. Inorg. Chem. 6, 808–813. doi:10.1021/ic50050a033

CrossRef Full Text | Google Scholar

Ohtaki, H., and Kato, H. (1967). Ionic equilibria in mixed solvents. 2. Hydrolysis of beryllium ion in a 0.1 mole fraction dioxane-water mixture and in aqueous solution containing 3 M LiClO₄ as an ionic medium. Inorg. Chem. 6, 1935–1937. doi:10.1021/ic50056a045

CrossRef Full Text | Google Scholar

Pâris, M. R., and Gregoire, C. (1968). Application de la coulometrie à l'etude des complexes. I. Appareillage et application à l'hydrolyse de l'ion beryllium(II). Anal. Chim. Acta 42, 431–437. doi:10.1016/s0003-2670(01)80335-4

CrossRef Full Text | Google Scholar

Perera, L. C., Raymond, O., Henderson, W., Brothers, P. J., and Plieger, P. G. (2017). Advances in beryllium coordination chemistry. Coord. Chem. Rev. 352, 264–290. doi:10.1016/j.ccr.2017.09.009

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular-dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Rabung, T., Altmaier, M., Neck, V., and Fanghanel, T. (2008). A TRLFS study of Cm(III) hydroxide complexes in alkaline CaCl₂ solutions. Radiochim. Acta 96, 551–560. doi:10.1524/ract.2008.1536

CrossRef Full Text | Google Scholar

Schwarzenbach, G. (1962). Metastabile Protonierungs-und Deprotonierungsprodukte anorganischer Molekeln und Ionen. Pure Appl. Chem. 5, 377–402. doi:10.1351/pac196205030377

CrossRef Full Text | Google Scholar

Schindler, P., and Garett, A. B. (1960). Löslichkeitsprodukte Von Metalloxiden Und -Hydroxiden .5. Die Loslichkeit von -Be(OH)₂ in Verdunnten Säuren. Helv. Chim. Acta 43, 2176–2178. doi:10.1002/hlca.19600430740

CrossRef Full Text | Google Scholar

Schwarzenbach, G., and Wenger, H. (1969). Die protonierung von metall-aquaionen I.: be∙aq²⁺ solvatations-isomerie. Helv. Chim. Acta 52, 644–665. doi:10.1002/hlca.19690520313

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A32, 751–767. doi:10.1107/s0567739476001551

CrossRef Full Text | Google Scholar

Tsukuda, H., Kawai, T., Maeda, M., and Ohtaki, H. (1975). Ionic equilibria in mixed solvents. XI. A critical survey of hydroxo complexes of beryllium in aqueous and aqueous mixed solvents. Bull. Chem. Soc. Jpn. 48, 691–695. doi:10.1246/bcsj.48.691

CrossRef Full Text | Google Scholar

Vanni, A., Gennaro, M. C., and Ostacoli, G. (1975). Equilibrium studies of beryllium complexes. J. Inorg. Nucl. Chem. 37, 1443–1451. doi:10.1016/0022-1902(75)80788-3

CrossRef Full Text | Google Scholar

Vollpracht, A., Lothenbach, B., Snellings, R., and Haufe, J. (2016). The pore solution of blended cements: A review. Mater. Struct. 49, 3341–3367. doi:10.1617/s11527-015-0724-1

CrossRef Full Text | Google Scholar

Yalcintas, E., Gaona, X., Altmaier, M., Dardenne, K., Polly, R., and Geckeis, H. (2016). Thermodynamic description of Tc(IV) solubility and hydrolysis in dilute to concentrated NaCl, MgCl₂ and CaCl₂ solutions. Dalton Trans. 45, 8916–8936. doi:10.1039/c6dt00973e

PubMed Abstract | CrossRef Full Text | Google Scholar