A density functional theory analysis of the adsorption and surface chemistry of inorganic iodine species on graphitea

In the event of a nuclear accident, fission products may be released into the environment. The release of ¹³¹I is of particular concern to human health. Iodine can be captured using a number of materials and frequently, this is accomplished with activated carbon impregnated with organic bases. Previous studies have used DFT and the graphite (0001) surface as a surrogate for adsorption, those studies focus on the species I^•, I₂, and CH₃I. In this work we perform an ab initio study of the adsorption onto the surface of a graphite sheet of I₂, CH₃I, and inorganic acidic iodine species (HI, HOI, HIO₂, and HIO₃), which were selected to examine the possible effect of oxidation state on adsorption. The PBE exchange-correlation functional with D3 dispersion was employed. It was found that for molecular iodine, the iodine atoms tended to either situate above the center of a hexagonal site on the graphite or directly atop a carbon atom with the lighter components resting closer to the graphite. For each species the relative binding energies spanned the range of 21–33 kJ mol^-1 and graphite-iodine distance was in the range of 3.52–3.93 Å. In all cases we found no significant charge transfer between the iodine species and the graphite, thus we conclude that all the iodine species studied undergo strong physisorption to the graphite.

1 Introduction

Iodine is a common fission product resulting from the transmutation of uranium fuel in nuclear power reactors. The short-lived radioactive isotope, ¹³¹I, with a half-life of around 8 days, would be a particular health concern if released into the environment. Capture materials, such as activated carbon, are used routinely in nuclear power plants (Riley et al., 2016; Vellingiri et al., 2018) and medical isotope production facilities (Doll et al., 2014) to remove this hazard during normal operations to reduce emissions to acceptable levels. Iodine, unlike other common fission products such as noble gases, is challenging because of the wide range of molecular forms and oxidation states (from +7 in IF₇ to −1 in hydroiodic acid) that can be adopted. Iodine can change between oxidation states either by chemical reaction or disproportionation in both the gas and solution phases (Wren et al., 1986; Saiz-Lopez et al., 2012; Gómez Martín et al., 2022). In the atmosphere, a wide variety of chemical forms are observed due to radical pathways that can be initiated by interaction with light, whereas in the solution phase, iodide (I⁻), iodate (${\mathrm{I}\mathrm{O}}_3^{-}$) and molecular iodine (I₂) are the most common species (Pourbaix, 1974). In the event of a nuclear incident and subsequent release of radioactive iodine, such as the Fukushima accident, iodine-containing species could potentially interact with a number of surfaces causing further molecular interconversions. For example, the stainless steel reactor vessel, soil in the sub-surface and particulates in the atmosphere. Consequently, a detailed understanding of these complex chemical networks is required to design effective emergency response to contain the hazard to human health. The foundational science needed as a basis for this understanding begins with simple models of how iodine-containing molecules interact with surfaces such as pristine graphite surfaces as surrogates for one of the most important components in an activated carbon material.

The interaction of iodine-containing species with carbon-based capture materials has been studied extensively both experimentally and theoretically with a focus on molecular iodine, I₂. Measurements have been made to probe adsorption and desorption behavior on activated carbons (Reyerson and Cameron, 1936; Juhola, 1975; Liu et al., 1993; Bhatia et al., 2000; Park and Yang, 2005) and also other carbon materials such as graphite (Salzano, 1964; Iwamoto and Oishf, 1968), coal (Aronson et al., 1976) and carbon black (Kipling et al., 1964). Notably, Park and Yang (Park and Yang, 2005) determined the activation energy for desorption to be approximately 51 kJ mol^-1, which is a direct measure of the strength of interaction between iodine and the sorbent. Salzano measured both physisorption and chemisorption during adsorption of iodine on graphite (Salzano, 1964). Iwamoto and Oiski showed that both the heats of adsorption and activation energies for desorption varied with coverage for iodine on graphite (Iwamoto and Oishf, 1968). The heat of adsorption were reported as ranging from 50–79 kJ mol^-1, whereas for the activation energy of desorption distinction was made between physisorbed iodine (79–130 kJ mol^-1) and chemisorbed iodine (142–200 kJ mol^-1). Kipling and co-workers make conclusions regarding the packing structure of molecular iodine on the carbon surface based on the measured adsorption capacity (Kipling et al., 1964), and relate it to that observed in the molecular iodine crystal structure.

Although direct structural observation of iodine on the carbon surface are difficult, spectroscopic probes can provide useful information. Ghosh and co-workers performed measurement of shifts in Raman bands on adsorption of halogen molecules on nanotubes and graphene, and correlated the observations with density functional theory calculations (Ghosh et al., 2012). They observed that halogen-containing molecules have a greater degree of charge transfer between the molecule and the nanotube for halogens of higher electronegativity and of the halogens with stable isotopes iodine has the lowest electronegativity.

The majority of previous computational studies have focused on the behavior of molecular iodine bound to graphene surfaces. Gerber and co-workers studied the adsorption of both atomic and molecular iodine on graphene surfaces using a number of a density functional including non-local van der Waals corrections (Tristant et al., 2015). The calculated adsorption energy is strongly dependent on the binding site geometry and spans a range of 30–50 kJ mol^-1. Rudenko and co-workers investigated the binding of diatomic halogen molecules to graphene surfaces using a van der Waals density functional methods (Rudenko et al., 2010). They calculated binding energies ranging from 34–36 kJ mol^-1 for out-of-plane geometries and 48–50 kJ mol^-1 for in-plane geometries. They also predict the contribution of charge transfer to the binding energy. In the case of diatomic iodine, they showed that the binding energy was approximately five times greater when van der Waals interaction were included in the DFT functional than with no van der Waals interaction. This is evidence that some combination of physisorption and chemisorption is occurring but with physisorption being the larger contributor.

In this work, we present a comprehensive fundamental computational study addressing the interaction of a number of iodine-containing molecules with a graphite surface examining the effect of choice of modeling approach, system size and model representation to predict binding geometries and energetics. In particular, we probe the extent to which charge transfer may occur between the surface and the adsorbed molecule to understand the balance between physisorption and chemisorption effects. Our work examines the previously studied I₂ and CH₃I molecules (Connor et al., 1961; Salzano and Eshaya, 1961; Salzano, 1964; Iwamoto and Oishf, 1968; Osborne et al., 1976; Walton et al., 2014; González-García et al., 2011; Chun et al., 2016); HI and HOI which may arise from dissolution processes (Riley et al., 2016); and a sequence of iodine-containing inorganic acids (HIO₂ and HIO₃) to allow for a systematic investigation of higher iodine oxidation states.

2 Materials and methods

In order to properly study adsorption processes on the surface of graphite, it is necessary to validate the computational methodology (vide infra) for the bulk structure of the substrate. The hexagonal structure of graphite (Baskin and Meyer, 1955; Trucano and Chen, 1975) (space group P6₃/mmc, Figure 1A) was employed for this purpose. Specifically, lattice constants, phonon frequencies, elastic constants, and densities of states were used to evaluate whether specific methodologies were appropriate for this work.

FIGURE 1

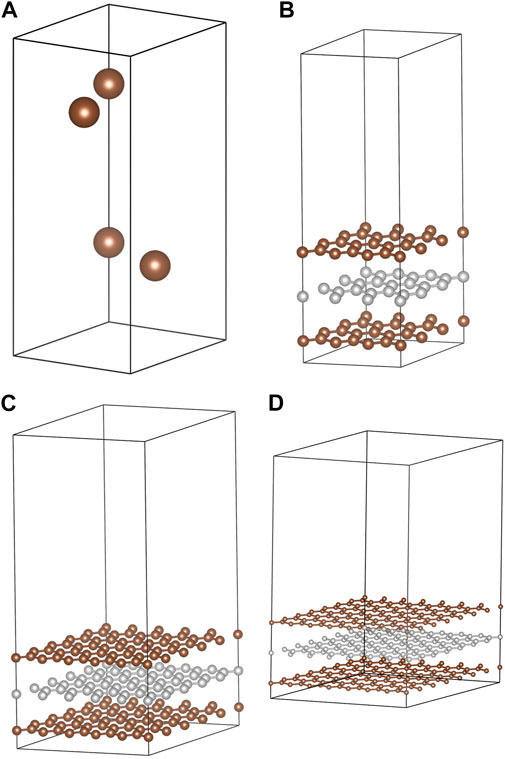
FIGURE 1. Structural models used in this study. These are (A) the 4-atom hexagonal unit cell of graphite, (B) the 3 × 3 hexagonal slab (54 atoms), (C) the 5 × 5 hexagonal slab (150 atoms), and (D) the 7 × 7 hexagonal slab (294 atoms).

Adsorption of I₂, HI, HOI, HIO₂, and HIO₃ molecules were modeled on the (0001) graphite surface using three-layer-thick slabs. Slabs were expanded laterally to have 3 × 3 unit cells (54 atoms, Figure 1B), 5 × 5 unit cells (150 atoms, Figure 1C) and 7 × 7 unit cells horizontally (294 atoms, Figure 1D). When one adsorbate molecule was placed on the surface, the surface coverages were 1/9, 1/25, and 1/49 where the denominator is the number of C₆ rings in the slab model. Alternatively, these coverages correspond to 0.021, 0.0076 and 0.0039 molecules per Ų, respectively. Activated carbon (AC) materials with CO₂ surface areas of 130–150 m²/g adsorb approximately 2 g of I₂ per Gram of AC (Bhatia and Shethna, 1994; Bhatia et al., 2000). The corresponding surface coverage is approximately 0.3 molecules per Ų, so attempts to exclude the influence of periodic images result in underestimating the surface coverage. Temperature programmed desorption (TPD) experiments on AX-21 activated carbon (a super-activated carbon) recorded a Brunauer–Emmett–Teller (Brunauer et al., 1938) (BET) surface area of 2,500–2,800 m²/g saturated at 3.25 g I₂ per g AX-21 (Park and Yang, 2005). The corresponding surface coverage is 0.03 molecules per Ų which is comparable to the highest coverage used in this study.

The three slab sizes were all tested when examining the I₂ adsorption. Subsequently, for the HI adsorption initial analysis was done using the 3 × 3 slab size. The 5 × 5 slab size was also tested for a subset of the adsorption sites. All other adsorptions were conducted using the 5 × 5 slab size.

Understanding how strongly iodine-containing molecules will stick to the graphite (0001) surface requires defining the adsorption energy. This is defined as the reaction of the isolated molecule with the surface slab resulting in the molecule adsorbed on the surface. The energy change for this process is given in Eq. 1.

$E_{\mathit{ads}}=E_{\mathit{slab+molecule}}-E_{\mathit{slab}}-E_{\mathit{molecule}}(1)$

E_ads is the adsorption energy, E_{slab+molecule} is the energy of the combined system, E_slab is the energy of the slab without the adsorbate, and E_molecule is the energy of the isolated molecule. Each energy term was calculated in a separate ab initio calculation with optimization of atomic positions with fixed cell dimensions. All atom positions were left unconstrained during each calculation, meaning our adsorption energy includes the effect of structural reorganization of the graphite by the adsorbed molecules. The implication of which is that our calculated E_ads includes the change in energy from the deformation of the slab and molecule. In this work, each energy is taken as the total energy of the corresponding electronic structure calculation. No zero-point energy (ZPE) contributions or thermal (enthalpic and/or entropic) contributions are included in this analysis. It is apparent that real adsorption behavior will include these thermal effects; however, the differences are expected to be small and the use of total energies suffices for the purpose of comparing the energetics of adsorption between different molecules. This was explicitly tested with the adsorption of I₂ and HOI onto the graphite sheet. The ZPE for I₂ was found to be 2.9 kJ/mol vs 2.8 kJ/mol after adsorption, and HOI was found to be 66.4 kJ/mol vs 65.2 kJ/mol after adsorption. These differences are much smaller than the expected adsorption energies of the molecules, therefore we conclude that they are unlikely to be a significant contributor to the other species studied.

Determining the most favorable adsorption geometry requires investigating multiple potential sites. We identified three high-symmetry sites for adsorption as shown in Figure 2. These sites are located on top of a surface carbon (top site), in the center of a C-C bond (bridge site), or in the center of a hexagonal carbon ring (hollow site). In principle, there are two forms of the top site depending on whether a subsurface carbon lies directly below the surface carbon. We do not employ this distinction as the two possible top sites showed similar behaviors.

FIGURE 2

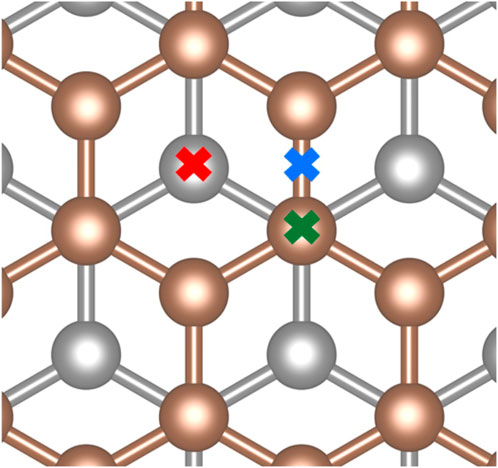
FIGURE 2. High-symmetry surface sites investigated for adsorption: top site (green), bridge site (blue), and hollow site (red).

Spin-polarized Kohn-Sham density functional theory (KS-DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) calculations were performed using the Vienna ab Initio Simulation Package (VASP) version 5.4.4 (Kresse and Hafner, 1993; Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b). The projector augmented-wave method (Blöchl, 1994) (PAW) was used to represent the interactions between nuclei and electrons. Standard (not soft) PAW potentials were taken from the VASP library (Kresse and Joubert, 1999) with the following valence electrons treated explicitly: ‘H’ (1s¹), ‘C’ (2s²2p²), ‘O’ (2s²2p⁴), and ‘I’ (5s²5p⁵). Electron exchange and correlation (XC) were treated within the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (Perdew et al., 1996) (PBE) and the strongly constrained and appropriately normed (SCAN) (Sun et al., 2015) meta-GGA functionals. The planewave kinetic energy cutoff was 900 eV. For the hexagonal graphite unit cell, a 15 × 15 × 9 Γ-centered mesh was used. Reduced k-point meshes were used for supercells in order to keep the k-point spacing approximately equal in all calculations. Gaussian smearing with a width of 0.1 eV was employed. This approach limits the entropic contribution to the total energy to less than 1 meV/atom. With these parameters, the total energy of the graphite unit cell (4 atoms) was converged to 1 meV/atom. Bulk system band structures were computed using the improved tetrahedron method of Blöchl, Jepsen, and Andersen (Blöchl et al., 1994). For slab calculations, only 1 k-point was used in the direction normal to the surface to minimize interactions between the slab and its periodic image. This gives 5 × 5 × 1, 3 × 3 × 1 and 3 × 3 × 1 Γ-centered k-point meshes for the 3 × 3, 5 × 5 and 7 × 7 slabs, respectively. At least 10 Å of vacuum was placed between the slab and its periodic image. All adsorption of molecules onto a the graphite slab was converged to less than 0.02 eV/Å, we found that this was sufficient to converge the adsorption energies to less that 1 kJ/mol. A dipole correction was applied to correct for the asymmetry of adsorption onto only one face of the graphite. Example INCAR and POSCAR files showing the computational settings and structures are provided in the supporting information.

Graphite contains carbon atoms covalently bonded in planes (Bučko et al., 2010). The layers are held together through dispersion (van der Waals) interactions. GGA functionals such as PBE poorly describe dispersion as evidenced by the extraordinarily large interlayer spacing predicted for graphite (Bučko et al., 2010). It is expected that meta-GGA functionals should incorporate some intermediate-range dispersion interactions (Peng et al., 2016). However, several methods have been proposed to improve the description of dispersion interactions in energies, geometries, and charge densities computed with DFT. These fall into two classes: a posteriori corrections that depend on an empirical potential (e.g., Grimme’s DFT-D family of corrections) (Grimme et al., 2010) and self-consistent corrections where an explicit dispersion term is added to the XC functional (e.g., the DFT-DF (Dion et al., 2004) approach). In the case of DFT-DF, non-spherical contributions to the gradient component of the XC functional are allowed inside the PAW spheres. This last choice reflects the tendency of DFT-DF dispersion models to produce favor aspherical densities when compared to standard GGA calculations (VASP Wiki: VdW-DF functional of Langreth and Lundqvist, 2020). To explore the effect of employing these functionals, we opted to utilize the vDW-DF tailored for the revPBE functional (Dion et al., 2004; Román-Pérez and Soler, 2009; Klimeš et al., 2011). We compare these approaches for the bulk structure of graphite (sec. 3.1) and the adsorption of the I₂ molecule (sec. 3.2).

3 Results and discussion

3.1 Graphite

Modeling adsorption of iodine-containing molecules on graphite requires validation that the chosen methods can properly describe the graphite bulk structure and electronic properties. Existing work has applied various XC functionals of LDA, GGA, and MetaGGA forms to graphite with mostly negative results. GGA calculations overestimate the interlayer spacing by 32% (Bučko et al., 2010). LDA calculations produce a bound structure; however, this is likely a fortuitous effect of the known tendency of LDA calculations to overestimate cohesive energies (van de Walle and Ceder, 1999). The fact that LDA and GGA functionals do not explicitly address dispersion (van der Waals) interactions causes this failure. MetaGGA functionals, such as the SCAN functional, are thought to describe dispersion interactions over intermediate distances. Different methods of accounting for the dispersion interactions in graphite (vide supra) are compared in Table 1.

TABLE 1

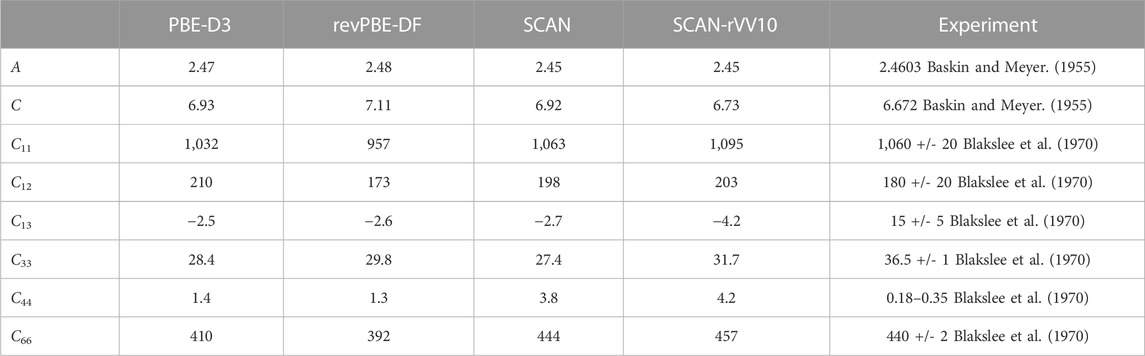
TABLE 1. A comparison of the structural and elastic properties of graphite computed with the PBE-D3, revPBE-DF, SCAN, and SCAN-rVV10 XC and dispersion approximations. C_ij values are reported in units GPa, a and c are given in units of Å.

Previous studies (Lebedeva et al., 2011; Peng et al., 2016; Lebedeva et al., 2017) have investigated a wide-range of methods for describing the inter-layer dispersion interactions in bilayer graphene and graphite. The results in Table 1 disagree with previously published values. The PBE-D3 was previously reported to predict elastic constants C₃₃ and C₄₄ of values 22.9 and 1.89 (Lebedeva et al., 2017), compared to our results of 28.4 and 1.4. Similarly, revPBE-DF was reported with elastic constants C₃₃ and C₄₄ of values 31.4 and 2.67 (Lebedeva et al., 2017), compared to our results of 29.8 and 1.3. In both cases the static elastic constants were calculated with a structure optimized with just PBE without vDW, we believe this along with differences in planewave cutoff and k-point mesh explains the difference. For SCAN we see closer agreement comparing the lattice constants a and c previously reported as 2.45Å and 6.86 Å (Peng et al., 2016) compared to our calculated values of 2.45 Å and 6.92 Å. For SCAN-rVV10 the lattice constants were previously reported as 2.45 Å and 6.54 Å (Peng et al., 2016) compared to our calculated 2.45 Å and 6.73 Å. In the case of SCAN the difference in the c lattice constant could be explained by the difference in the computational parameters: we employ a denser k-point mesh (15 × 15 × 9 vs. 12 × 12 × 6) and higher planewave energy cutoff (900 eV vs. 800 eV). However, it is unclear whether this is sufficient to explain the disagreement in the SCAN-rVV10 results. Despite this we do find that our SCAN-rVV10 results do the best at reproducing the experimental lattice parameters. Although, the SCAN-rVV10 approach offers the best structural performance, it is less clear which functional is superior in reproducing the elastic constants.

The question of the best method to achieve the correct electronic structure remains important. Figure 3 shows the densities of states (DOS) for bulk graphite computed with different methodologies. In all cases, the relaxed geometry obtained with that method is used to compute the DOS. The a posteriori nature of the D3 corrections make the resulting DOS (and charge density) identical to a PBE calculation at the same geometry. What Figure 3 reveals is a relative consistency between the methods in the calculated DOS; however, a clear distinction arises near the Fermi level. A small band gap (less than 42 meV) exists in the PBE-D3 and DFT-DF electronic structures. These values are consistent with the experimentally determined bandgap of approximately 40 meV (García et al., 2012). Both of these are based on GGA formulations of the XC functional, and the difference between a posteriori and self-consistent dispersion calculations has minimal effect on the computed densities of states. In contrast, the calculation using the SCAN Meta-GGA XC functional reveals a significant band gap of approximately 0.84 eV, whereas inclusion of self-consistent dispersion corrections (via the SCAN-RVV10 formulation) still yields a band gap of approximately 0.82 eV. Noting that DFT is a ground-state theory and typically underestimates the bandgap (Perdew, 1985), the Meta-GGA results do not reproduce the experimental band gap of graphite well. As our primary focus is on the adsorption of molecules onto the graphite surface the accuracy in electronic properties is more important than the accuracy in structural properties. For this reason we elected to use the PBE-D3 functional in subsequent calculations. To our knowledge, this is the first time that these methods have been compared for the electronic structure of graphite.

FIGURE 3

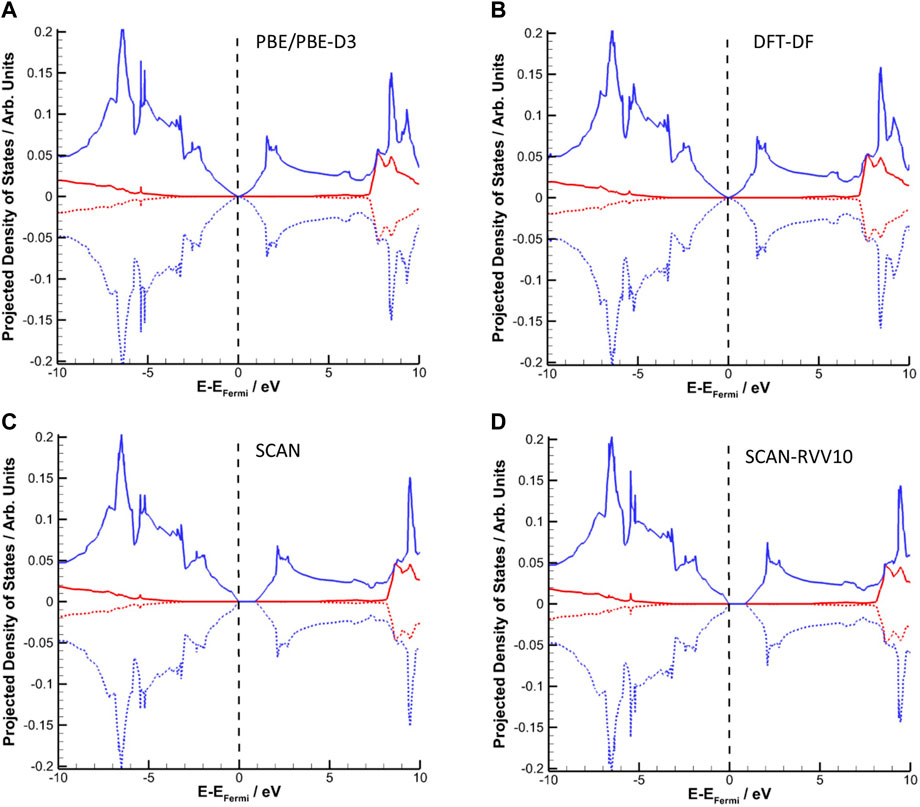
FIGURE 3. Projected densities of states (PDOS) for bulk graphite calculated with PBE-D3 (A), DFT-DF (B), SCAN (C), and SCAN-RVV10 (D) approaches. The s states are in red and the p states in blue. Positive values for the α-spin states and negative values for the β-spin states.

3.2 I₂ adsorption

An analysis of I₂ adsorption on graphite requires a structural model for the graphite (0001) surface. A 3 × 3 surface slab was used for an initial survey of the potential sites where molecular iodine could adsorb. High-symmetry sites were used to anchor the first iodine atom, and the second was placed either directly above the first atom or over another high symmetry site with the I₂ molecule angled upward from the first atom to the second atom. This initial geometry search revealed that the most favorable conformation was placing the I₂ parallel to the surface. When the surface was expanded to 5 × 5, two configurations (Figure 4) had the strongest adsorption energies.

FIGURE 4

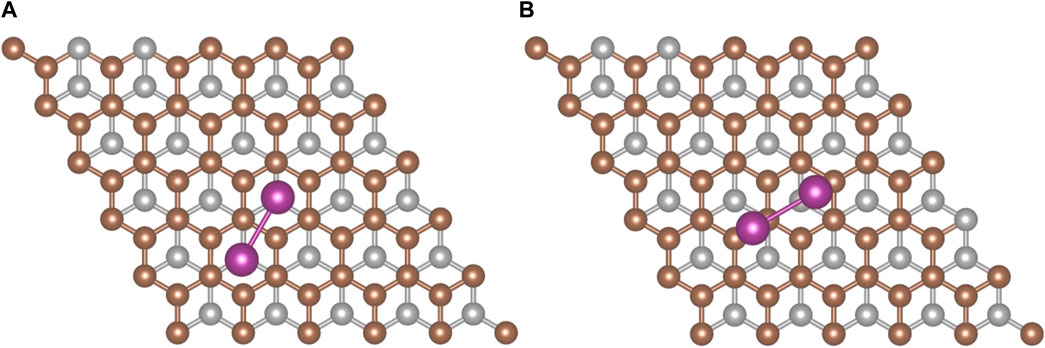
FIGURE 4. The two most favorable I₂ adsorption configurations on graphite. (A) hollow-hollow configuration and (B) offset configuration. Iodine (purple), surface carbon (brown), and subsurface carbon (silver) atoms are shown.

The first configuration (Figure 4A) involves the iodine atoms each sitting above a hollow site. The second configuration (Figure 4B) has one iodine displaced from the hollow site toward a top site while the second iodine resides on (or near) a bridge site. The adsorption energies computed with the PBE-D3 methodology for the hollow-hollow configuration are reported in Table 2. Standard PBE calculations for the hollow-hollow configuration on the 3 × 3 slab give a binding energy of less than 1 kJ/mol. This indicates that surface-I₂ interaction is almost all dispersive.

TABLE 2

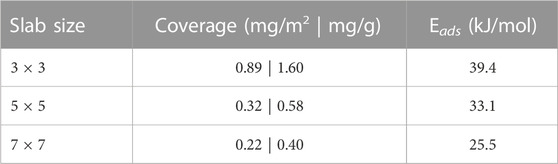
TABLE 2. I₂ Adsorption energies (E_ads) for the hollow-hollow configuration calculated with the PBE-D3 methodology for different slab sizes. The corresponding coverages are also provided in mg/m² and mg/g where the specific surface area was taken to be 1.8 m²/g (Iwamoto and Oishf, 1968).

The trend in Table 2 shows a decrease in the adsorption energy with decreasing surface coverage. By contrast, experimental studies (Iwamoto and Oishf, 1968) have found that lower coverages correspond to higher heats of adsorption for physisorbed iodine. The difference in the calculated and experimental observations are likely the result of the supercell model in the periodic calculations influencing the way that the dispersion energies are calculated. On the smallest slab, the PBE-D3 method yields the strongest interactions between periodic images of the adsorbate. As the distance between periodic images is increased, the r⁻⁶ and r⁻⁸ terms decrease in magnitude and the corresponding dispersion correction is reduced. At the same time, the adsorbate-slab dispersion interactions should be similar for all coverages since the slab-iodine distance is consistent (3.72–3.73 Å) in the 3 × 3 and 5 × 5 calculations. It is shorter (3.64 Å) in the 7 × 7 calculation. Furthermore, the dispersion energy in the slab calculations without the adsorbate is 0.070 eV/atom for all three slabs. The net result is that the PBE-D3 adsorption energies are expected to decrease as the coverage decreases. Iwamoto and Oishi (Iwamoto and Oishf, 1968) suggest that low coverage adsorption of I₂ occurs mainly at the edges of the basal plane instead of on its surface. Thus, the comparison between their experiments and our calculations should break down at coverages below 0.48 mg/g. Measuring adsorption energies (or desorption activation energies) as a function of iodine coverage on highly-oriented pyrolitic graphite would provide a way to validate the trend obtained from the periodic calculations.

3.3 HI adsorption

Being diatomic, the possible configurations for HI are nearly identical to I₂ from the previous section. However, due to the asymmetry of the molecule, we now have to consider cases in which the molecule aligns perpendicular to the graphite slab. When the hydrogen is located closer to the graphite than the iodine it will be referred to as H down, and when the hydrogen is located further it will be referred to as H up. Based on the small size of the molecule we used the 3 × 3 graphite slab size for the calculations. The adsorption energy for all configurations are summarized in Table 3. The hollow-hollow site requires a non-physical stretching of the HI bond, this is what leads to dissociation. This would not occur naturally due to the energy needed to stretch the bond to that degree.

TABLE 3

TABLE 3. Adsorption energies (E_ads) for all configuration of HI molecule on graphite surface.

Each site has a significant adsorption energy, however there is no clearly energetically preferred adsorption site. Given the number of configurations sampled, this suggests the HI could be mobile along the surface assuming the barrier to movement is small. When the hydrogen is placed between the iodine and the graphite (i.e., H down) there is a decrease in the adsorption energy. This is understandable as hydrogen position necessarily causes the iodine to be located further away from the surface. We also tested the convergence of the graphite slab size and found that increasing the slab size to 5 × 5 made a 1.1 kJ/mol difference for the top-vertical (H up) configuration). Overall, we observe little energetic change based on the position of the hydrogen atom, and therefore conclude that the binding is dominated by the dispersion interaction between the iodine atom and the graphite surface. This is further evidenced by the stronger adsorption energy of the I₂ molecule, having two iodine atoms contributing to the dispersion interactions.

3.4 HOI adsorption

Hypoiodous acid (with iodine in the +1 oxidation state), HOI, is frequently discussed in the context of molecular iodine dissolving into aqueous solutions (Wong, 1980). However, it is a likely species in a nuclear reactor effluent (Riley et al., 2016). The HOI molecule is bent which adds numerous potential adsorption configurations. For example, whether the molecule is flat or perpendicular to the surface and also which atom prefers to be closest to the surface.

To answer these questions, we start with three possible configurations of the HOI molecule (Figure 5) featuring the I-O bond parallel to the surface and the O-H bond directing the H atom toward the surface (down), parallel to the surface (flat), or away from the surface (up). These configurations are augmented by placing the iodine above the high-symmetry sites (hollow, top, bridge) and rotating the molecule such that the I-O bond is directed toward an adjacent high symmetry site though the O will not lie directly on top of that site. Optimization of the initial configurations using the PBE-D3 approach reveals that the flat configuration is not stable and results in the hydrogen rotating into the down configuration. We used the 5 × 5 graphite slab size for the calculations.

FIGURE 5

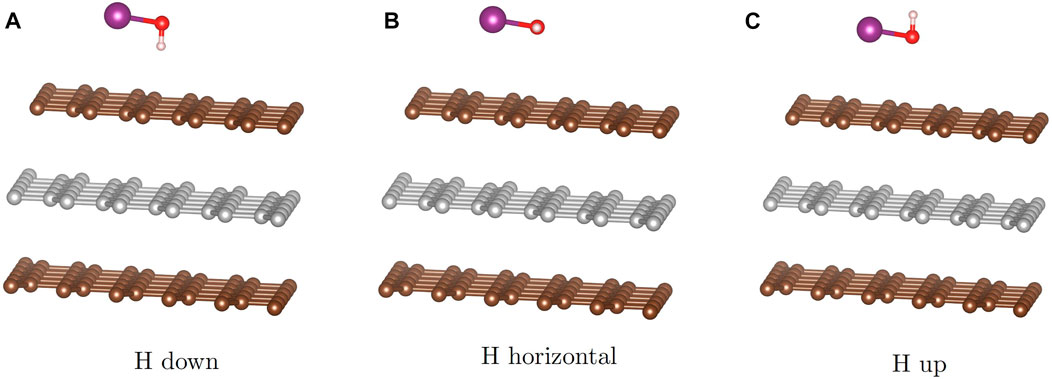
FIGURE 5. Starting configurations for the HOI molecule: with the hydrogen pointed toward the graphite (A), pointed in plane with the graphite (B) and pointed away from the graphite (C).

The strongest adsorption is found to occur with the iodine on a hollow site, the oxygen on a bridge site with the I-O bond crossing a top site and the hydrogen directed towards the surface (see Figure 6) resulting in a calculated adsorption energy of 30.8 kJ/mol. The iodine prefers the hollow site by approximately 6 kJ/mol and having the hydrogen oriented towards the surface is preferable by 5–6 kJ/mol. The preference for this configuration can be attributed in part due to the π-orbitals of the graphite which are known to extend perpendicular to the plane from each carbon atom, combined with the lone pair electrons of the oxygen. These would naturally result in the oxygen being repelled from the top sites and relaxing into either the bridge or hollow site.

FIGURE 6

FIGURE 6. Optimal configuration for HOI molecule adsorption onto graphite.

The surface-iodine distance is comparable to the adsorption of I₂ (vide supra) which results in sufficient space for the oxygen and the hydrogen to move toward the surface. This adds favorable dispersion interactions with the surface resulting in a lower adsorption energy. The most favorable configuration suggests that monolayer adsorption of HOI would involve one molecule per hollow site.

A Bader charge analysis of the HOI molecule shows that no charge transfer occurs upon adsorption. This is not unexpected, however, since the electron density arises from a DFT-PBE calculation which fails to property describe dispersion interactions. Thus, no significant perturbation occurs when the molecule adsorbs to the surface.

3.5 HIO₂ adsorption

Progressing to the next highest possible oxidation state of iodine (+3) leads to iodous acid (HIO₂). This molecule was recently detected in atmospheric experiments (Sipilä et al., 2016).

Unlike the preceding molecules, HIO₂ has the potential for non-planar behavior. The following considers on the most stable isomer, HOIO, as determined by high-quality computational chemistry calculations (Khanniche et al., 2017). Bond lengths, bond angles, and dihedral angles from this work agree reasonably well with the existing literature (addition detail is provided in the Supplementary Material). Of note, the dihedral angle is nearly 90 degrees indicating that the O-H bond lies perpendicular to the plane formed by the O-I=O backbone.

As discussed previously, the set of possible adsorption sites and molecular orientations is large. For HIO₂, the adsorption site was characterized by the initial position of the iodine atom relative to the surface carbons. The hollow, bridge, and top sites were chosen for this study. Furthermore, different orientations of the HIO₂ molecule were chosen: one where the I=O bond is perpendicular to the surface (with the O pointing upward) and another where the O=I-O backbone is nearly parallel to the surface. This leads to a total of six position/orientation combinations that were explored. We used the 5 × 5 graphite slab size for the calculations.

After optimizing the adsorption geometries described in the previous paragraph, the adsorption energies ranged from 9.6–23.1 kJ/mol. HIO₂ oriented with the I=O bond pointing upward were bound more strongly (by at least 8 kJ/mol) to the surface than the configurations where the O-I=O was oriented mostly parallel to the surface. The strongest adsorption occurred with the I=O bond pointing upward and the iodine atom sitting on a top site (see Figure 7). The optimizations also revealed certain preferences about the adsorption of HIO₂. Namely, regardless of the orientation of the rest of the molecule if the iodine is initially situated above a bridge site it will relax until it is either above a top site or hollow site.

FIGURE 7

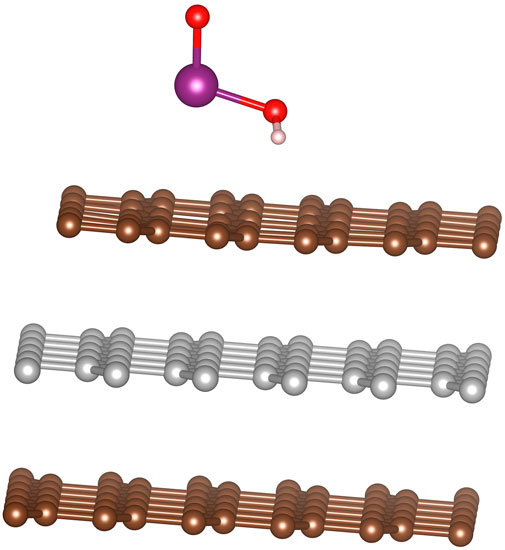
FIGURE 7. Optimal configuration for HIO₂ molecule adsorption onto graphite, with oxygens lying above the hollow graphite sites.

3.6 HIO₃ adsorption

The final acidic species of the series is iodic acid (with iodine in the +5 oxidation state), the geometry of which can be visualized as approximately trigonal pyramid with asymmetry caused by the hydrogen on one oxygen. The optimized configurations on the surface can be described with three common structural features: 1) the iodine corner of the pyramid pointing perpendicular to the graphite plane either towards or away from the surface, 2) the iodine lying at either a hollow or top site (the bridge is assumed to be not energetically favorable based on HIO₂ results), and 3) orienting the oxygens to, as closely as possible, occupy a hollow, top, or bridge site. This results in six configurations. We again used the 5 × 5 graphite slab size for these calculations. Overall, the most favorable adsorption sites have the iodine is pointing away from the plane of the graphite with the oxygens lying closer to the graphite plane. The exact locations of the oxygen atoms have little effect on the binding energy. When they are above the bridge sites the adsorption energy was 23.5 kJ/mol and when they lie above either the top or hollow sites the adsorption energy was 23.9 kJ/mol. A side view of the absorption site with the oxygens above the hollow site is shown in Figure 8.

FIGURE 8

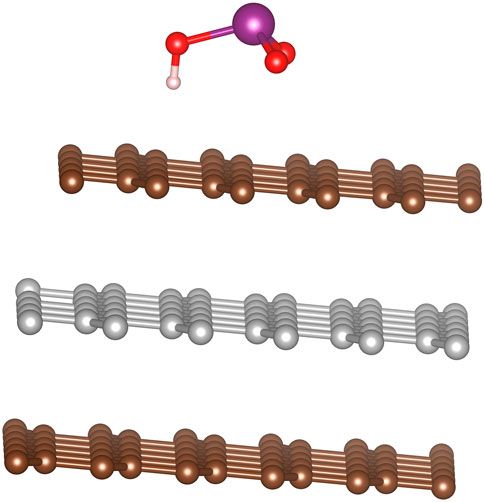
FIGURE 8. Optimal configuration for HIO₃ molecule adsorption onto graphite, with oxygens lying above the hollow graphite sites.

An additional Bader charge analysis of the iodic acid was performed both before and after adsorption. No significant charge transfer was found (≤0.05) therefore we conclude that the molecule is physisorbed.

3.7 CH₃I adsorption

The calculated binding sites for methyl iodide can similar to those for HI but with the methyl group replacing the proton. The free rotation about the C-I bond results in the exact position of the hydrogen having an negligible effect on the results. We used the 5 × 5 graphite slab size for the calculations. The adsorption energy for all configurations are summarized in Table 4.

TABLE 4

TABLE 4. Adsorption energies (E_ads) for all configuration of CH₃I molecule on graphite surface.

We observed that for when examining each site with the C-I bond orientation relative to the graphite was kept constant there was very little change in the absorption energy. Therefore, similar to the results from HI, we expect the uniformity of the in-plane adsorption energies could result in CH₃I possessing low barriers to translational motion across the graphite surface. When site location is held fixed and we look at the different orientations of the C-I bond relative to the graphite we find that adsorption energy is greatest when the C-I bond is oriented parallel to the surface. While we observed the perpendicular configurations to be stable, they are less energetically preferred. Based on this we expect that over time any CH₃I that binds perpendicular to the graphite will eventually relax into a configuration parallel to the graphite. The hollow-hollow configuration is shown in Figure 9.

FIGURE 9

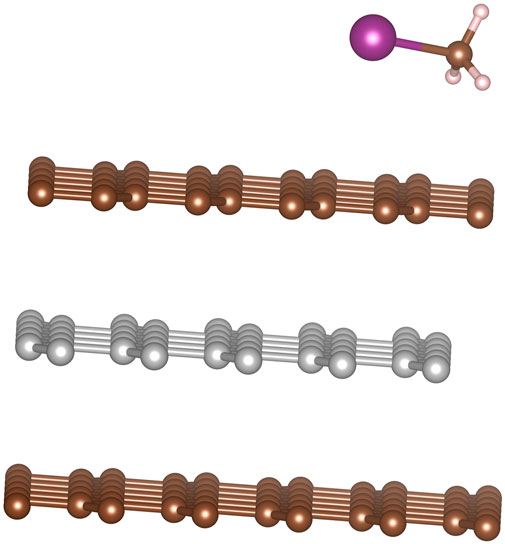
FIGURE 9. Optimal configuration for CH₃I molecule adsorption onto graphite. With Iodine and carbon lying above hollow sites.

3.8 Trends in adsorption energies and behaviors

Based on the Bader charge analysis performed on the molecules both before and after adsorption, we find that in all cases there was no significant charge transfer between the molecules and graphite surface and therefore all the molecules are predicted to be physisorbed to the surface. The adsorption energy is due entirely to the strength of the dispersion forces between the atoms of the molecular species and the graphite slab. To examine this further Table 5 summarized the adsorption energy and the graphite-iodine separation distances.

TABLE 5

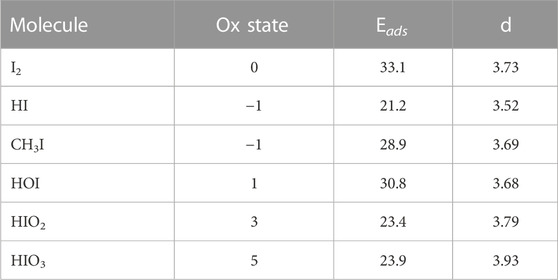
TABLE 5. Comparison of oxidation state of iodine, adsorption energies E_ads (kJ/mol), and surface-iodine distance d (Å) for all studied iodine compounds.

There is an apparent trend present between the oxidation state of the iodine and the distance between the iodine and the graphite sheet. As oxidation state increases we observe an increase in the iodine-graphite distance. To explore this further an addition set of calculations were performed for the series of molecules IF₃, IF₅, IF₇,ICl₃, ICl₅, and ICl₇ with iodine oxidation states (+3)-(+7). The trihalogenated molecules form a T-shape and were oriented such that the atom forming the bottom of the ‘T’ was between the iodine and the graphite. The pentahalogenated and heptahalogenated molecules can be thought of as spherical. All molecules were situated above a hollow site for simplicity. The 5 × 5 graphite slab size for the calculations. The results are summarized in Table 6. The results of this supplemental analysis show that it was not the oxidation state of the iodine that determined the distance from the graphite, but rather the physical size of the molecule.

TABLE 6

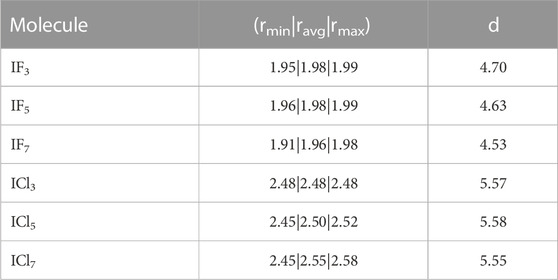
TABLE 6. Comparison of graphite surface–iodine distance d (Å) and bond length r (Å) for chlorine and fluorine bonded iodine compounds.

To explore whether or not the strength of adsorption could be explained by London dispersion (London, 1937), we performed a supplemental examination of the static polarizability of the molecules in a vacuum (Autschbach, 2007; Hammond et al., 2009; Autschbach, 2011; Mullin et al., 2012; Mullin and Schatz, 2012). This was performed using NWCHEM software (Aprà et al., 2020). For this supplemental study we opted to use the PBE functional, with the 6–311G** basis set (Krishnan et al., 1980; Glukhovtsev et al., 1995). To ensure consistency the geometries were allowed to relax before performing the polarizability calculation. The results of the calculation are the electric dipole μ), the isotropic static polarizability (α_iso), the anisotropic static polarizability (α_aniso) and the average static polarizability (α_avg). These are summarized in the Table 7 below:

TABLE 7

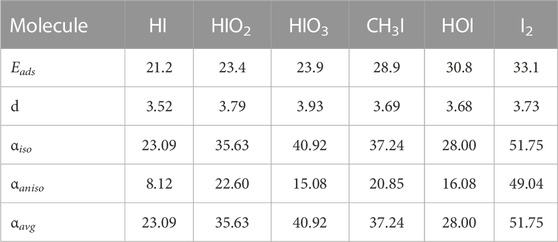
TABLE 7. Summary of results for the linear response calculation. Adsorption energy and graphite iodine distance are also displayed for reference. Adsorption energy is given in (kJ/mol), graphite iodine distance d in Å, and all other data is in atomic units.

The most promising trend we observe is that as the isotropic polarizability increases so does the adsorption energy. However, CH₃I and HOI, do not follow the trend. CH₃I can plausibly be said to have a higher adsorption energy by being able to adsorb closer to the graphite. However, this would not be enough to explain why HOI has a higher adsorption energy than CH₃I, despite having nearly identical surface to iodine distance and a smaller polarizability. The most likely hypothesis in our opinion is that the relative location and orientation of the HOI above the graphite leads to a greater London dispersion force than would be predicted by a simple comparisons of the magnitude of the static isotropic polararizability. Further calculations exploring this are beyond the focus of this work, but may be explored in future studies.

In summary, while we do observe an apparent qualitative trend between isotropic polarizability and the adsorption energy, other factors such as orientations and distance prevent us from concluding a definitive quantitative trend exists.

4 Conclusion

In the event of a nuclear accident various radioactive fission products can be released into the environment. ¹³¹Iodine in particular has a half-life on the order of days and presents a significant health risk. Low maintenance capture materials such as activated carbon are often employed to mitigate the release of fission products into the atmosphere. In this study, we sought to provide insight into the interaction of iodine-containing molecules and pristine graphite as a surrogate for activated carbon. The chemistry of iodine is complex and can include a wide range of properties. To investigate this we combined a set of common gaseous iodine-containing molecules (I₂, HI and CH₃I) and a set of molecules that sample much of the possible oxidation states of iodine (HOI, HIO₂, and HIO₃).

We systematically examined various methods of modeling the graphite to achieve a high degree accuracy and found that a 5 × 5 cell of graphite containing 3 vertical layers was sufficient to converge the adsorption energy to less than 1 kJ/mol. In addition, we found that of the XC functionals tested SCAN-rVV10 was most accurate in terms of structure, but overestimated the band gap. In comparison, PBE-D3 produced a band gap comparable to experiment, as such we chose to proceed using the PBE-D3 functional.

We proceeded to investigated the most favorable binding sites of our set of iodine-containing molecules. Our analysis found similar adsorption energies strengths for all species studied in the range of 21–33 kJ/mol. We also found that through Bader charge analysis that the adsorption was entirely due to physisorption with negligible charge transfer occurring between the molecules and graphite surface. As our results rule out any chemisorption between the iodine-containing molecules and the graphite surface, this suggests that any chemisorption measured experimentally is due to impurities or defects. Although there was an apparent trend between the iodine oxidation state and the proximity of the molecules to the graphite, a supplemental study using fluorinated and chlorinated iodine showed that the size and not the oxidation state was responsible for the apparent trend. An examination of the static polarizability of the molecules found a qualitative trend connecting increased polarizability to increased adsorption energy. These findings are consistent with the conclusion that the adsorption is entirely rationalized by the role of dispersion forces.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

In consulting with the fellow authors we believe ML and AR should share first authorship, NH should be assigned senior authorship, and that MS and AJ should be assigned last authorship.All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Laboratory Directed Research and Development (LDRD) and the Chemical Dynamics Initiative (CDi) at Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract DE-AC06-76RLO 1830. The research was performed using resources available through Research Computing at Pacific Northwest National Laboratory (PNNL). PNNL is operated by Battelle for the U.S. Department of Energy under Contract DE-AC05-76RL01830.

Acknowledgments

The authors would like to acknowledge DA, Scott Muller, and Amra Peles for their insights and guidance regarding this work. The release number for this work is TBD.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor DA declared a past collaboration with the authors NH and AR.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2023.1170424/full#supplementary-material

References

Aprà, E., Bylaska, E. J., de Jong, W. A., Govind, N., Kowalski, K., Straatsma, T. P., et al. (2020). NWChem: Past, present, and future. J. Chem. Phys. 152, 184102. doi:10.1063/5.0004997

PubMed Abstract | CrossRef Full Text | Google Scholar

Aronson, S., Schwebel, A., and Sinensky, G. (1976). Absorption of iodine by coal and lignite. Carbon 14, 93–95. doi:10.1016/0008-6223(76)90116-0

CrossRef Full Text | Google Scholar

Autschbach, J. (2007). Computation of optical rotation using time–dependent density functional theory. Comp. Lett. 3, 131–150. doi:10.1163/157404007782913327

CrossRef Full Text | Google Scholar

Autschbach, J. (2011). Time-dependent density functional theory for calculating origin-independent optical rotation and rotatory strength tensors. ChemPhysChem 12, 3224–3235. doi:10.1002/cphc.201100225

PubMed Abstract | CrossRef Full Text | Google Scholar

Baskin, Y., and Meyer, L. (1955). Lattice constants of graphite at low temperatures. Phys. Rev. 100, 544. doi:10.1103/physrev.100.544

CrossRef Full Text | Google Scholar

Bhatia, S. K., Liu, F., and Arvind, G. (2000). Effect of pore blockage on adsorption isotherms and dynamics: Anomalous adsorption of iodine on activated carbon. Langmuir 16, 4001–4008. doi:10.1021/la991418h

CrossRef Full Text | Google Scholar

Bhatia, S. K., and Shethna, H. K. (1994). A modified pore filling isotherm with application in determination of pore size distributions. Langmuir 10, 3230–3243. doi:10.1021/la00021a055

CrossRef Full Text | Google Scholar

Blakslee, O. L., Proctor, D. G., Seldin, E. J., Spence, G. B., and Weng, T. (1970). Elastic constants of compression-annealed pyrolytic graphite. J. Appl. Phys. 41, 3373–3382. doi:10.1063/1.1659428

CrossRef Full Text | Google Scholar

Blöchl, P. E., Jepsen, O., and Andersen, O. K. (1994). Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 49, 16223–16233. doi:10.1103/physrevb.49.16223

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

Brunauer, S., Emmett, P. H., and Teller, E. (1938). Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 60, 309–319. doi:10.1021/ja01269a023

CrossRef Full Text | Google Scholar

Bučko, T., Hafner, J., Lebègue, S., and Ángyán, J. G. (2010). Improved description of the structure of molecular and layered crystals: Ab initio DFT calculations with van der Waals corrections. J. Phys. Chem. A 114, 11814–11824. doi:10.1021/jp106469x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chun, H., Kang, J., and Han, B. (2016). First principles computational study on the adsorption mechanism of organic methyl iodide gas on triethylenediamine impregnated activated carbon. Phys. Chem. Chem. Phys. 18, 32050–32056. doi:10.1039/c6cp06483c

PubMed Abstract | CrossRef Full Text | Google Scholar

Connor, P., Lewis, J. B., and Thomas, W. J. (1961). Proc. Fifth Conf. Carbon 1, 120–124.

Dion, M., Rydberg, H., Schröder, E., Langreth, D. C., and Lundqvist, B. I. (2004). Van der Waals density functional for general geometries. Phys. Rev. Lett. 92, 246401. doi:10.1103/physrevlett.92.246401

PubMed Abstract | CrossRef Full Text | Google Scholar

Doll, C. G., Sorensen, C. M., Bowyer, T. W., Friese, J. I., Hayes, J. C., Hoffmann, E., et al. (2014). Abatement of xenon and iodine emissions from medical isotope production facilities. J. Environ. Radioact. 130, 33–43. doi:10.1016/j.jenvrad.2013.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

García, N., Esquinazi, P., Barzola-Quiquia, J., and Dusari, S. (2012). Evidence for semiconducting behavior with a narrow band gap of Bernal graphite. New J. Phys. 14, 053015. doi:10.1088/1367-2630/14/5/053015

CrossRef Full Text | Google Scholar

Ghosh, S., Yamijala Sharma, S. R. K. C., Swapan, K., and Rao, C. N. R. (2012). The interaction of halogen molecules with SWNTs and graphene. RSC Adv. 2, 1181–1188. doi:10.1039/c1ra00295c

CrossRef Full Text | Google Scholar

Glukhovtsev, M. N., Pross, A., McGrath, M. P., and Radom, L. (1995). Extension of Gaussian-2 (G2) theory to bromine- and iodine-containing molecules: Use of effective core potentials. J. Chem. Phys. 103, 1878–1885. doi:10.1063/1.469712

CrossRef Full Text | Google Scholar

Gómez Martín, J. C., Lewis, T. R., James, A. D., Saiz-Lopez, A., and Plane, J. M. C. (2022). Insights into the chemistry of iodine new particle formation: The role of iodine oxides and the source of iodic acid. J. Am. Chem. Soc. 144, 9240–9253. doi:10.1021/jacs.1c12957

PubMed Abstract | CrossRef Full Text | Google Scholar

González-García, C., González, J., and Román, S. (2011). Removal efficiency of radioactive methyl iodide on TEDA-impregnated activated carbons. Fuel Process. Technol. 92, 247–252. doi:10.1016/j.fuproc.2010.04.014

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammond, J. R., Govind, N., Kowalski, K., Autschbach, J., and Xantheas, S. S. (2009). Accurate dipole polarizabilities for water clusters n=2–12 at the coupled-cluster level of theory and benchmarking of various density functionals. J. Chem. Phys. 131, 214103. doi:10.1063/1.3263604

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864–B871. doi:10.1103/physrev.136.b864

CrossRef Full Text | Google Scholar

Iwamoto, K., and Oishf, J. (1968). The behavior of iodine in adsorption and desorption by graphite. J. Nucl. Sci. Technol. 5, 437–446. doi:10.1080/18811248.1968.9732491

CrossRef Full Text | Google Scholar

Juhola, A. (1975). Iodine adsorption and structure of activated carbons. Carbon 13, 437–442. doi:10.1016/0008-6223(75)90016-0

CrossRef Full Text | Google Scholar

Khanniche, S., Louis, F., Cantrel, L., and Černušák, I. (2017). Thermochemistry of HIO₂ species and reactivity of iodous acid with OH radical: A computational study. ACS Earth Space Chem. 1, 39–49. doi:10.1021/acsearthspacechem.6b00010

CrossRef Full Text | Google Scholar

Kipling, J. J., Sherwood, J. N., and Shooter, P. V. (1964). Adsorption of iodine from organic solvents by “graphitized” carbon blacks. Trans. Faraday Soc. 60, 401–411. doi:10.1039/tf9646000401

CrossRef Full Text | Google Scholar

Klimeš, J. C. V., Bowler, D. R., and Michaelides, A. (2011). Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131. doi:10.1103/physrevb.83.195131

CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/physrev.140.a1133

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mat. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Hafner, J. (1993). Ab initiomolecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118. doi:10.1103/physrevb.48.13115

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Krishnan, R., Binkley, J. S., Seeger, R., and Pople, J. A. (1980). Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 72, 650–654. doi:10.1063/1.438955

CrossRef Full Text | Google Scholar

Lebedeva, I. V., Knizhnik, A. A., Popov, A. M., Lozovik, Y. E., and Potapkin, B. V. (2011). Interlayer interaction and relative vibrations of bilayer graphene. Phys. Chem. Chem. Phys. 13, 5687–5695. doi:10.1039/c0cp02614j

PubMed Abstract | CrossRef Full Text | Google Scholar

Lebedeva, I. V., Lebedev, A. V., Popov, A. M., and Knizhnik, A. A. (2017). Comparison of performance of van der Waals-corrected exchange-correlation functionals for interlayer interaction in graphene and hexagonal boron nitride. Comp. Mat. Sci. 128, 45–58. doi:10.1016/j.commatsci.2016.11.011

CrossRef Full Text | Google Scholar

Liu, D., Zhao, J., Sung, C., and Zhang, L. (1993). The desorption isotherms of iodine from the catalyst of iodine-activated carbon. Carbon 31, 81–85. doi:10.1016/0008-6223(93)90159-8

CrossRef Full Text | Google Scholar

London, F. (1937). The general theory of molecular forces. Trans. Faraday Soc. 33, 8b. doi:10.1039/tf937330008b

CrossRef Full Text | Google Scholar

Mullin, J. M., Autschbach, J., and Schatz, G. C. (2012). Time-dependent density functional methods for surface enhanced Raman scattering (SERS) studies. Comput. Theor. Chem. 987, 32–41. doi:10.1016/j.comptc.2011.08.027

CrossRef Full Text | Google Scholar

Mullin, J., and Schatz, G. C. (2012). Combined linear response quantum mechanics and classical electrodynamics (QM/ED) method for the calculation of surface-enhanced Raman spectra. J. Phys. Chem. A 116, 1931–1938. doi:10.1021/jp2087829

PubMed Abstract | CrossRef Full Text | Google Scholar

Osborne, M., Compere, E. L., and De Nordwall, H. (1976). Studies of iodine adsorption and desorption on HTGR coolant circuit materials. Oak ridge national lab. technical report.

Google Scholar

Park, J.-H., and Yang, R. T. (2005). Predicting adsorption isotherms of low-volatile compounds by temperature programmed Desorption: iodine on carbon. Langmuir 21, 5055–5060. doi:10.1021/la046866q

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, H., Yang, Z.-H., Perdew, J. P., and Sun, J. (2016). Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 6, 041005. doi:10.1103/physrevx.6.041005

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P. (1985). Density functional theory and the band gap problem. Int. J. Quantum Chem. 28, 497–523. doi:10.1002/qua.560280846

CrossRef Full Text | Google Scholar

Pourbaix, M. (1974). Atlas of electrochemical equilibria in aqueous solutions/by Marcel Pourbaix. 2nd edn. Houston, Tex: National Association of Corrosion Engineers.

Google Scholar

Reyerson, L. H., and Cameron, A. E. (1936). The sorption of bromine and iodine by activated charcoal. J. Phys. Chem. 40, 233–237. doi:10.1021/j150371a009

CrossRef Full Text | Google Scholar

Riley, B. J., Vienna, J. D., Strachan, D. M., McCloy, J. S., and Jerden, J. L. (2016). Materials and processes for the effective capture and immobilization of radioiodine: A review. J. Nucl. Mat. 470, 307–326. doi:10.1016/j.jnucmat.2015.11.038

CrossRef Full Text | Google Scholar

Román-Pérez, G., and Soler, J. M. (2009). Efficient implementation of a van der Waals density functional: Application to double-wall carbon nanotubes. Phys. Rev. Lett. 103, 096102. doi:10.1103/physrevlett.103.096102

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudenko, A. N., Keil, F. J., Katsnelson, M. I., and Lichtenstein, A. I. (2010). Adsorption of diatomic halogen molecules on graphene: A van der Waals density functional study. Phys. Rev. B 82, 035427. doi:10.1103/physrevb.82.035427

CrossRef Full Text | Google Scholar

Saiz-Lopez, A., Plane, J. M. C., Baker, A. R., Carpenter, L. J., von Glasow, R., Martín, J. C. G., et al. (2012). Atmospheric chemistry of iodine. Chem. Rev. 112, 1773–1804. doi:10.1021/cr200029u

PubMed Abstract | CrossRef Full Text | Google Scholar

Salzano, F., and Eshaya, A. (1961).Adsorption of krypton and of mixed xenon and krypton on activated charcoa. New York: United States Atomic Energy Commission.

Google Scholar

Salzano, F. (1964). The behavior of iodine in graphite. Carbon 2, 73–81. doi:10.1016/0008-6223(64)90030-2

CrossRef Full Text | Google Scholar

Sipilä, M., Sarnela, N., Jokinen, T., Henschel, H., Junninen, H., Kontkanen, J., et al. (2016). Molecular-scale evidence of aerosol particle formation via sequential addition of HIO3. Nature 537, 532–534. doi:10.1038/nature19314

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J., Ruzsinszky, A., and Perdew, J. P. (2015). Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402. doi:10.1103/physrevlett.115.036402

PubMed Abstract | CrossRef Full Text | Google Scholar

Tristant, D., Puech, P., and Gerber, I. C. (2015). Theoretical study of graphene doping mechanism by iodine molecules. J. Phys. Chem. C 119, 12071–12078. doi:10.1021/acs.jpcc.5b03246

CrossRef Full Text | Google Scholar

Trucano, P., and Chen, R. (1975). Structure of graphite by neutron diffraction. Nature 258, 136–137. doi:10.1038/258136a0

CrossRef Full Text | Google Scholar

van de Walle, A., and Ceder, G. (1999). Correcting overbinding in local-density-approximation calculations. Phys. Rev. B 59, 14992–15001. doi:10.1103/physrevb.59.14992

CrossRef Full Text | Google Scholar

VASP Wiki: VdW-DF functional of Langreth and Lundqvist (2020). Functional_of_Langreth_and_Lu ndqvist. Avaliable At: https://www.vasp.at/wiki/index.php/VdW-DF_functional_of_Langreth_and_Lu ndqvist_et_al (Accessed 04 27, 2020).

Google Scholar

Vellingiri, K., Kim, K.-H., Pournara, A., and Deep, A. (2018). Towards high-efficiency sorptive capture of radionuclides in solution and gas. Prog. Mat. Sci. 94, 1–67. doi:10.1016/j.pmatsci.2018.01.002

CrossRef Full Text | Google Scholar

Walton, K. L., Ghosh, T. K., Viswanath, D. S., Loyalka, S. K., and Tompson, R. V. (2014). Adsorption of iodine on graphite in high temperature gas-cooled reactor systems: A review. Prog. Nucl. Energy 73, 21–50. doi:10.1016/j.pnucene.2014.01.005

CrossRef Full Text | Google Scholar

Wong, G. T. (1980). The stability of dissolved inorganic species of iodine in seawater. Mar. Chem. 9, 13–24. doi:10.1016/0304-4203(80)90003-1

CrossRef Full Text | Google Scholar

Wren, J. C., Paquette, J., Sunder, S., and Ford, B. L. (1986). Iodine chemistry in the +1 oxidation state. II. A Raman and uv–visible spectroscopic study of the disproportionation of hypoiodite in basic solutions. Can. J. Chem. 64, 2284–2296. doi:10.1139/v86-375

CrossRef Full Text | Google Scholar