A review of void and gas bubble superlattices self-organization under irradiation

Zhang, Yongfeng

doi:10.3389/fnuen.2023.1110549

REVIEW article

Front. Nucl. Eng., 19 January 2023

Sec. Nuclear Materials

Volume 2 - 2023 | https://doi.org/10.3389/fnuen.2023.1110549

This article is part of the Research Topic Rising Stars in Nuclear Materials: 2022 View all 7 articles

A review of void and gas bubble superlattices self-organization under irradiation

Yongfeng Zhang*

Department of Engineering Physics, University of Wisconsin Madison, Madison, WI, United States

Irradiation by high-energy particles has been well known as a destructive force that “damages” crystalline materials by creating lattice defects. One surprising outcome from irradiation is the self-organization of void superlattices and gas bubble superlattices in various materials under irradiation. While these superlattices exhibit crystal structures that mimic atomic lattices, their self-organization takes place in far-from-equilibrium environment. A thermodynamic driving force that entails ordering is either absent or yet to be identified. In the past few decades, extensive research efforts have been made to generate such superlattices and to discern their formation mechanisms. While a consensus is yet to reach, these studies have substantially enriched our understanding on defect evolution and self-organization under irradiation. Appending previous reviews that are mostly done two decades ago, this article presents a comprehensive review of new experimental, theoretical, and simulational studies of void and gas bubble superlattices in the past two decades. An in-depth discussion on the formation mechanisms and their implications on superlattice properties is provided for the purpose of encouraging future studies.

1 Introduction

Irradiation by high energy particles such as neutron, ion and electron has been widely known to damage materials by producing lattice defects and/or directly destructing the crystal lattice, e.g., amorphization. As a powerful tool to create far-from-equilibrium environments, it can also induce fascinating self-organized microstructural features in the target materials. Examples of irradiation induced self-organization include nanoscale compositional patterns in immiscible alloys (Enrique and Bellon, 2000), ordering of defect clusters and loops (Jäger et al., 1990; Zinkle and Snead, 1995; Kaoumi and Adamson, 2014), ordered nanodroplets (Wei et al., 2008) and formation of void and gas bubble superlattices (Evans, 1971). Following the first observation in 1971 by Evans (Evans, 1971), void superlattices (VSLs) and gas bubble superlattices (GBSLs) have attracted extensive research efforts, which have been focused on their structural properties, formation conditions, and self-organizing mechanisms. In particular, the fact that the superlattices adopt certain crystal structures suggests the possible existence of a thermodynamic driving force that entails their ordering, e.g., something similar to the interatomic interaction which determines the crystal structure of a given crystalline solid. However, such a thermodynamic interaction either does not exist or has yet to be identified. This makes it a challenging task to uncover the formation mechanism and has motivated a long list of hypotheses and theoretical studies. These studies have substantially enriched our understanding on defect evolution and self-organization in materials under irradiation. In addition to the scientific merits, studying the formation mechanisms of superlattices and their roles in defect evolution may help design materials with improved irradiation resistance. For instance, the nanoscale void or gas bubble superlattices may help mitigate gas swelling in neutron irradiated materials (Chen et al., 2017). It may also inspire strategies for engineering nanoscale patterns using irradiation as a tool for creating non-equilibrium conditions. Some of the theoretical formulations also have theoretical implications for pattern formation in diffusion reaction systems (Cross and Hohenberg, 1993).

Formation of superlattices under irradiation has been reviewed multiple times, e.g., by Krishan in 1982 (Krishan, 1982a), Evans in 1990 (Evans et al., 1990), Jager and Trinkaus in 1993 (Jager and Trinkaus, 1993), Johnson et al., in 1995 (Johnson and Mazey, 1995), and by Ghoniem et al., in 2001 (Ghoniem et al., 2001). Since then, many new observations have been made along with new theories proposed for the formation mechanisms. In particular, face-centered-cubic (fcc) superlattices have been observed in body-centered-cubic (bcc) UMo fuels (Gan et al., 2010), disrupting the previous conclusion that superlattices are always isomorphic with the host matrices. New theories based on thermodynamics-driven instability (Gao et al., 2018a; Noble et al., 2020) have also been proposed and demonstrated using computer simulations. The dependence of GBSL formation window and lattice parameters on the gas atomic-part-per-million (appm) to displacement-per-atom (dpa) ratio have been established (Harrison et al., 2017; Sun et al., 2019), suggesting the possibility of unifying VSL and GBSL. These new studies have substantially advanced our understanding on defect self-organization and are worth another comprehensive review. A brief review has recently been given by Sun (Sun, 2022), which focused on recent studies. Built on top of the previous reviews, this article serves three purposes. First, it serves as a comprehensive reference and a summary of new experimental data for the current and future researchers. Second, it provides an in-depth discussion of the proposed formation mechanisms and their implications of the superlattice properties. Third, several open questions are discussed for the purpose of motivating future studies.

The paper is organized as the following. We will first present the new experimental observations in Section II. The theoretical and simulational studies of formation mechanisms will be summarized in Section III. Several open questions will be discussed in Section IV, followed by the concluding remarks.

2 Experimental observations

In this Section, new experimental observations of superlattices under irradiation are summarized. To minimize the redundancy, only new experimental studies since the last comprehensive review by Ghoniem et al. (Ghoniem et al., 2001) in 2001 are included here. Following the previous reviews, VSLs and GBSLs are summarized separately as it is not yet fully clear whether they can be unified together.

2.1 Void superlattice–VSL

A few new observations of VSLs since 2001 are summarized in Table 1. The superlattice properties (structure and lattice parameter a_L) are summarized along with the irradiation conditions. For experimental results before 2001 please refer to Krishan (Krishan, 1982b), Evans (Evans et al., 1990), and Ghoniem et al. (Ghoniem et al., 2001). Several important findings summarized in the previous reviews are reiterated here:

1) There exists a temperature (T) window, 0.25T_m < T < 0.5T_m (Jager and Trinkaus, 1993), for VSL to form, although it is most easily to form at temperatures just below the peak swelling temperature (Ghoniem et al., 2001).

2) VSLs are partially or fully isomorphic with the host matrices. Self-organization of VSLs starts from random arrangement of voids, followed by planar ordering paralleling the close-packed planes of the host material. Fully developed VSLs are of fcc structure in fcc metals such as Ni and Cu and bcc structure in bcc metals such as Mo and Nb. The voids show planar ordering paralleling the basal plane in hcp metals such as Mg. Several examples of such isomorphic VSLs are shown in Figure 1.

3) The VSL lattice parameter a_L increases with irradiation temperature. It is less sensitive to and decreases slightly with dose rate. Usually, a_L varies in the range of tens to a couple of hundred nanometers, and is a few to about ten times of the void diameter r_d. Some studies suggested that a_L saturates over dose (Loomis et al., 1977).

4) Development of VSLs in fcc metals requires considerably higher damage levels (about 100–400 dpas) than in bcc metals; in the latter initial void ordering can occur at a few dpa, and fully developed VSLs form at tens to hundreds of dpa (Ghoniem et al., 2001).

5) VSLs in bcc metals exhibit a remarkably high-degree of ordering (see Figure 1A), although “defects” such as missing voids and dislocation-like features are commonly observed. The ordering is weaker in fcc and hcp metals (see Figures 1B, C) than in bcc metals.

TABLE 1

TABLE 1. Experimental observations of void superlattices since 2001.

FIGURE 1

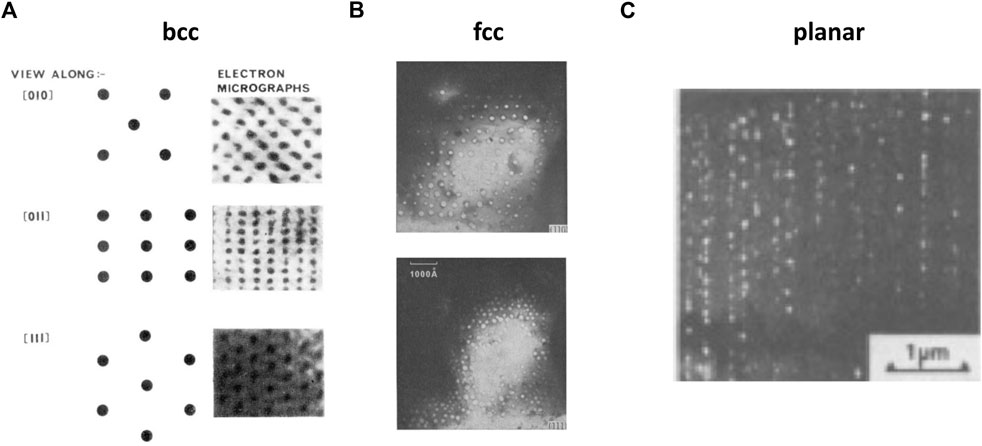
FIGURE 1. Experimental observations of (A) bcc VSL in bcc Mo (Evans, 1971), (B) fcc VSL in fcc Ni (Kulcinski et al., 1971), and (C) planar void ordering in the basal plane in Mg (Jostsons and Farrell, 1972). Voids are shown as black objects in (A) and white objects in (B) and (C).

A brief summary of the new findings is given here. In general, these new observations are consistent with previous understanding. The irradiation condition (dose and temperature) and superlattice properties (void diameter r_d, lattice parameter a_L, and structure) for the VSL in bcc W under neutron irradiation (Amino et al., 2016) are all within the ranges reported before (Ghoniem et al., 2001). The planar ordering of voids in Cr under 5 MeV Fe⁺ irradiation (Ryabikovskaya et al., 2021) is probably an early stage of superlattice formation. Samples irradiated in the same conditions were re-characterized by Sun et al. (Sun et al., 2022), and body-centered-tetragonal (bct) VSLs were identified, indicating that the VSLs were coherent but not isomorphic with the matrix. Furthermore, the VSLs were found to disappear upon additional Kr irradiation, followed by formation of Kr GBSLs. Using 3 MeV proton irradiation, Ipatova reported the formation of bcc VSL in Ta at 0.25 dpa along with dense dislocation loop tangles. While the voids were observed to grow in diameter, the VSL lattice parameter a_L kept decreasing over irradiation dose from 0.25 to 1.55 dpa, indicating that the VSL was yet to saturate (Ipatova et al., 2017). Adding W into Ta was found to delay loop evolution and suppress VSL formation.

The simple cubic (sc) VSL in CaF₂ observed by Ding et al. (Ding et al., 2005) created by in-situ electron irradiation with 200 keV electrons can be compared with those reported by Johnson et al. (Johnson and Chadderton, 1983) under 100keV, 200 keV and 1 MeV electron irradiation using in-situ transmission electron microscopy (TEM). The VSLs have been previously regarded as anion VSLs because with 100 keV electrons, the damage was believed to be purely radiolytic confined to the anion sublattice with the formation of anion vacancies (F centers) and anion interstitials (H centers), leaving the cation sublattice unaffected (Johnson and Chadderton, 1983). In contrast, in Ding et al. (Ding et al., 2005) the voids were characterized as cavities without Ca using Ca elemental mapping obtained by Energy Filtered TEM. This indicates that both anion and cation sublattices were damaged even with low energy electron irradiation. Further studies on the defect formation and migration mechanisms are then needed to explain the formation of VSLs in CaF₂.

2.2 Gas bubble superlattice–GBSL

Before reviewing the new observations, several key features of GBSL summarized in previous reviews (Jager and Trinkaus, 1993; Johnson and Mazey, 1995; Ghoniem et al., 2001) are reiterated in the below.

1) There exists a temperature window, 0.15T_m < T < 0.35T_m (Ghoniem et al., 2001), for GBSL to form. Note that this is slightly lower than the temperature window for VSL formation.

2) Similar to VSLs, GBSLs are also partially or fully isomorphic with the host materials. Examples of isomorphic bcc and fcc GBSLs and planar bubble ordering are shown in Figure 2.

3) The GBSL lattice parameters a_GBSL are smaller than that of VSL, and the bubble sizes are also smaller than the voids. No obvious temperature and dose rate dependence of a_GBSL have been identified (Johnson and Mazey, 1995).

4) In contrast to VSL, there is no obvious difference in the critical doses for GBSL to form in bcc and fcc metals.

5) GBSLs with various gases have been observed under ion irradiation, including H, He, Ne, and Kr. No GBSL formation has been observed under Xe ion irradiation, which is the largest inert gas.

FIGURE 2

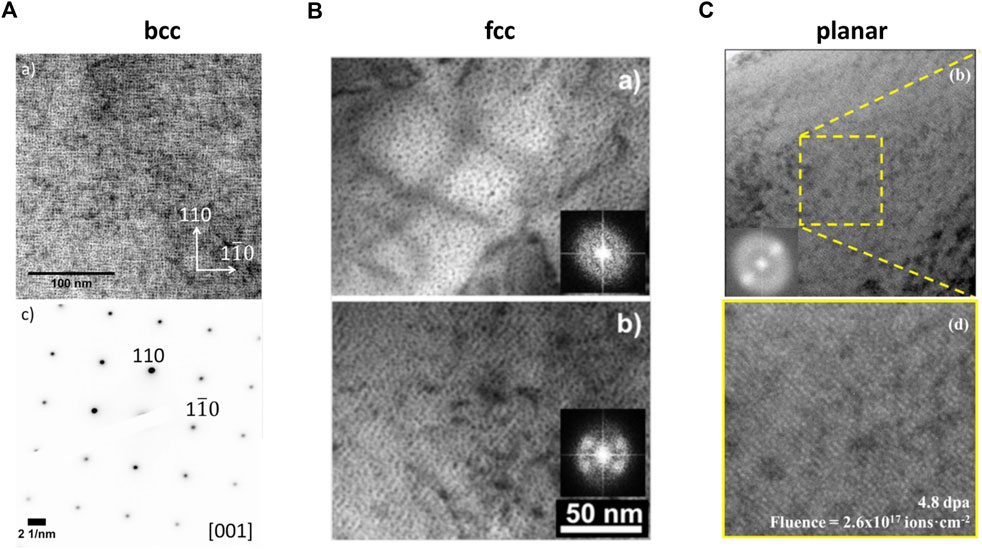
FIGURE 2. Experimental observations of (A) bcc GBSL in bcc W (Harrison et al., 2017), (B) fcc GBSL in fcc Cu (Robinson et al., 2017), and (C) planar bubble ordering in the basal plane in hcp Zr (Tunes et al., 2017). Bubbles are shown as white objects in black fields in (A) and (B) and white objects in (C).

The new observations of GBSL made after 2001 are summarized in Tables 2, 3. These observations have substantially extended the previous understanding. Several important findings from the new observations are summarized in the below.

TABLE 2

TABLE 2. Experimental observations of gas bubble superlattices since 2001.

TABLE 3

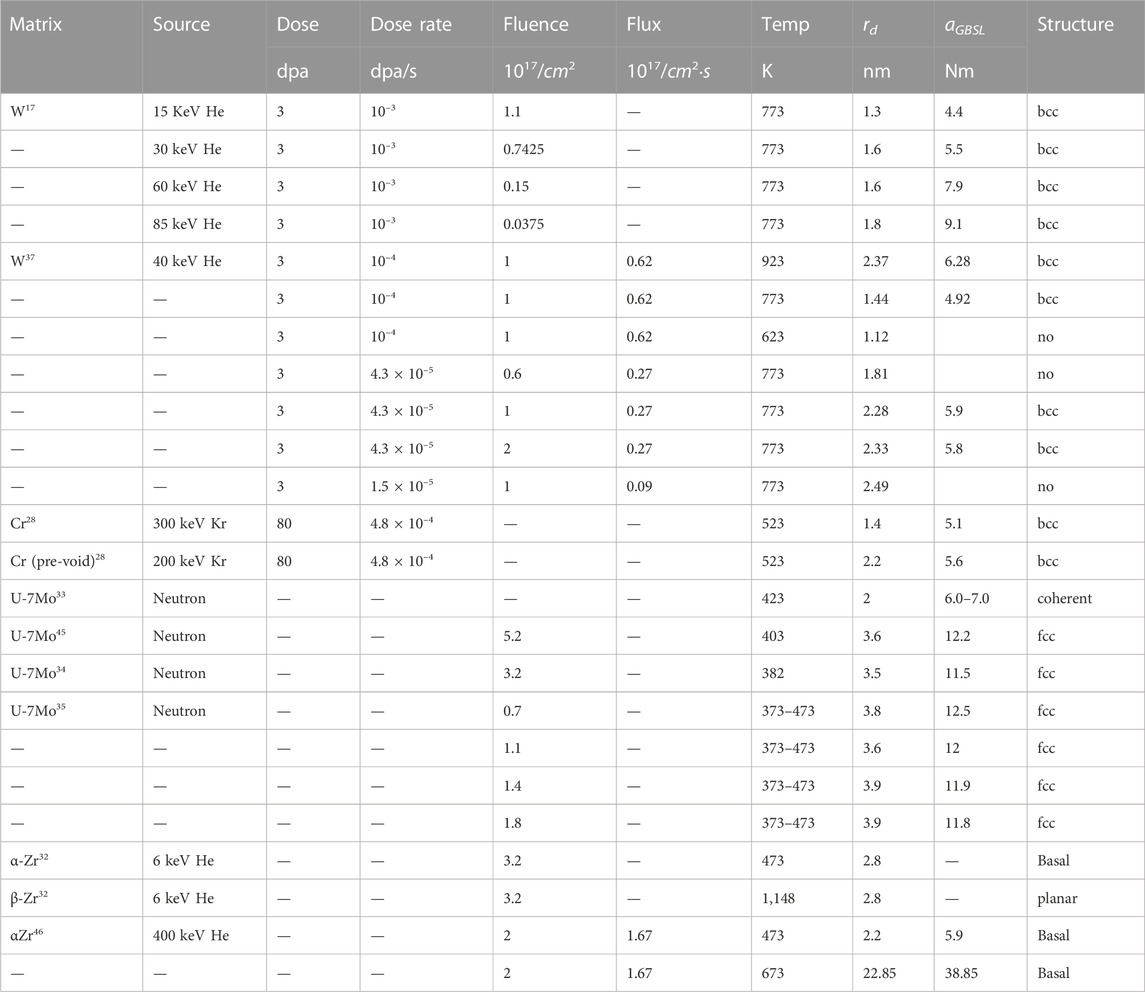
TABLE 3. Experimental observations of gas bubble superlattices since 2001. For fission neutron, the fission density is reported in the fluence column with a unit of 10²¹ fission/cm³.

First and most importantly, fcc Xe GBSLs have been observed in bcc U-7Mo fuels irradiated by fission neutron (see Figure 3A) by three different groups (Van den Berghe et al., 2008; Gan et al., 2010; Gan et al., 2014; Salvato et al., 2020), indicating that GBSLs are not necessarily isomorphic with the host materials. Although bct VSL and GBSL have been reported in bcc Cr (Sun et al., 2022) and Mo (Sun et al., 2018) (see Figure 3B), respectively, they were believed to be altered only slightly by lattice strain and would otherwise be isomorphic with the bcc host materials. For decades, the VSL and GBSL structures have been regarded the same as the host material structure, albeit a physical proof has never emerged. The disruption of this conclusion has motivated a list of studies searching for the actual factors determining the superlattice structure. It should also be mentioned that the Xe GBSL in U-7Mo has the highest degree of ordering among all VSLs and GBSLs observed so far. The Xe GBSL was found to form near grain boundaries first and then progressed into grain interiors upon increasing burnups (Salvato et al., 2020). Further analysis of Xe GBSL formed at low burnups suggested that the GBSL may have formed as VSL before a substantial amount of Xe was produced, giving a plausible explanation of its nearly perfect ordering compared to other GBSLs.

FIGURE 3

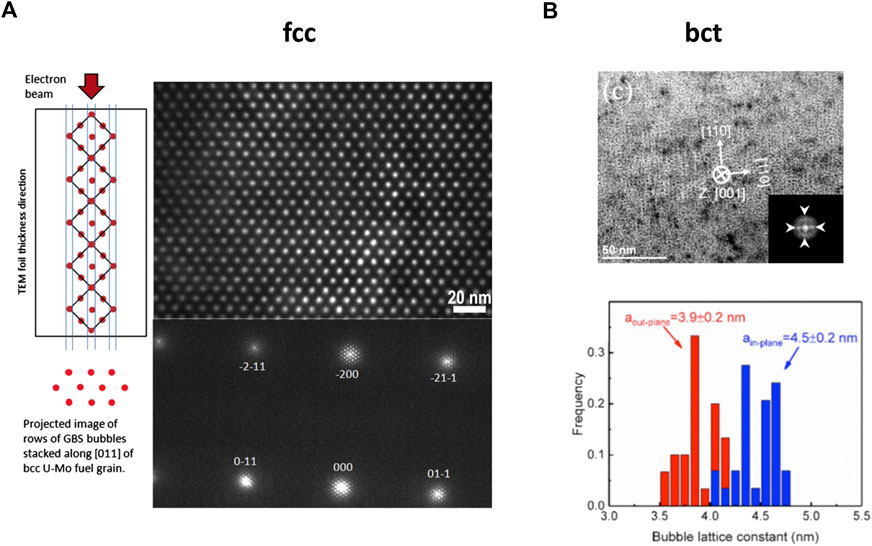
FIGURE 3. (Color online) Experimental observations of (A) fcc Xe GBSL in bcc UMo (Gan et al., 2014) and (B) bct He GBSL in bcc Mo (Sun et al., 2018). Bubbles are shown as white objects in black fields in (A) and black objects in bright field in (B).

In a series of experiments carried out by researchers from Idaho National Laboratory (INL) and Brookhaven National Laboratory (BNL) in the US, the dependence of GBSL lattice parameter a_GBSL on temperature, dose rate (He ion flux), and dose (He ion fluence) have been examined (Sprouster et al., 2019; Sun et al., 2019; Jossou et al., 2021), for the purpose of validating the prediction by a newly developed theory for superlattice formation (Gao et al., 2018a). For He GBSLs in both W (Sprouster et al, 2019) and Mo (Sun et al., 2019), a_GBSL was found to increase with temperature, decrease with dose rate, and saturate over dose. The dependence of a_GBSL on dose rate is weak but evident. These trends are similar to those exhibited by VSLs in bcc metals, suggesting the similarity between VSL and GBSL. In addition, these experiments demonstrated the unique strength of high energy X-ray for characterizing void/bubble ordering.

The temperature window for GBSL formation may be lower than previously thought. Using low energy He ion (12 keV), He GBSL was produced in Cu at −100 to 100°C, or 0.13 to 0.27 T_m taking a melting point of Cu at 1085°C. No GBSL formed at 200°C (0.35 T_m) with the same He ion energy and flux (Robinson et al., 2017). While the low homologous temperature boundary is only slightly lower than what’s observed before, 0.15T_m, this is the first time to observe GBSL well below room temperature. The author further showed that the bubble diameter and the GBSL lattice parameter increased with temperature, while the critical dose for bubble ordering decreased with temperature.

Motivated by the many similarities between VSL and GBSL, Harrison et al. (Harrison et al., 2017) designed a series of experiments to produce He GBSL in W with different gas-appm to dpa ratios, while the dose, dose rate, and temperature were fixed. They found that both the bubble size and the GBSL lattice parameter a_GBSL increased with decreasing gas-appm to dpa ratio. More interestingly, the trends can be extrapolated to VSLs formed in W under 1.54 dpa neutron irradiation at 1023 K²⁵ and another neutron irradiated W at 823 K³⁹. The clear dependence of a_GBSL on the gas-appm to dpa ratio led the authors to conclude on the significance of vacancy supply in determining the physical characteristics of GBSL.

In a separated article, Harrison et al. has studied the role of alloying chemistry on gas bubble size and a_GBSL using He irradiation in Ni, NiFe and FeCrNiCo (Harrison et al., 2019). This extended the studies of superlattices in simple metals and dilute alloys to the regime of complex concentrated alloys. Smaller a_GBSL and smaller bubble diameters were observed in NiFe and FeCrNiCo than in pure Ni, possibly due to sluggish diffusion, which is a characteristic of complex concentrated alloys.

The stability of GBSL under irradiation, thermal annealing, and mechanical deformation has also been studied. Sun et al. (Sun et al., 2022) showed that the VSLs formed in Cr disappeared upon further Kr irradiation, followed by formation of Kr GBSL. The voids were found to shrink at a higher rate with a lower Kr-appm to dpa ratio. Meanwhile, pre-existing voids led to larger bubble size and GBSL lattice parameter for the subsequent Kr GBSL. Upon thermal annealing, He GBSL formed in Mo at 300°C has been found to remain stable until 850°C for 30 min (Gan et al., 2018) but become unstable at 1000°C for 1 h (Sun et al., 2020). He GBSL in Mo produced in the same condition was found to disappear under up to 2.5 dpa Kr ion irradiation at 300°C. Complementary phase field simulations indicated that the order-disorder transformation of pre-existing He GBSL, which was imperfect, was likely caused by inhomogeneous growth and coarsening of bubbles (Sun et al., 2020). Pre-existing GBSLs may also be altered by mechanical deformation. Wang et al. (Wang et al., 2016) showed that He GBSL in Cu became disordered when the matrix was deformed by dislocation slip and underwent twinning when the matrix was deformed by twinning.

2.3 Summary of experimental findings on both VSL and GBSL

An updated summary of experimental findings on both VSL and GBSL since the first observation of superlattice is provided here. The focus is placed on several important superlattice characteristics: formation window, structure, lattice parameter, and critical dose of formation.

1) Both VSL and GBSL have been show to have a formation window in terms of temperature. The temperature formation window for VSL (0.25T_m < T < 0.5T_m) is slightly higher than that for GBSL (0.15T_m < T < 0.35T_m). As has been shown by Sun et al. (Sun et al., 2019), these two formation windows for He GBSL in Mo may be unified by the parameter gas-appm to dpa ratio. Increasing this ratio lowers both the high and low temperature boundaries and broadens the temperature window for GBSL formation, as shown in Figure 4A.

2) For both VSL and GBSL, the lattice parameter increases with temperature, decreases with dose rate (or ion flux), and saturates over dose (or ion fluence). While formed in the same host material and in similar irradiation conditions, GBSLs have smaller lattice parameters than VSLs. Again, it has been found by Harrison et al. (Harrison et al., 2017) that both the He bubble size and the GBSL lattice parameter decrease with the He-appm to dpa ratio and can be extrapolated to VSL by decreasing this ratio, as shown in Figure 4B.

3) The VSLs and GBSLs always share the same crystal structure when they form in the same host materials. For most VSLs and GBSLs, the lattice structure is the same as the host material, but this is not always true. A few exceptions are the fcc Xe GBSL in bcc U-7Mo nuclear fuel (Gan et al., 2014), the bct VSL in bcc Cr (Sun et al., 2022), and the bct He GBSL in bcc Mo (Sun et al., 2018). This indicates that the superlattice structure is not determined by the host material structure.

4) A few sets of experimental data show that the critical dose of formation depends on temperature. In Mo under 300 keV Kr irradiation, GBSL formed at 59 dpa at 773 K but not until 105 dpa at 673 K³⁷. In Cu under 12 keV He irradiation, the critical dose decreased from 5.48 dpa at 173 K to 2.09 dpa at 299 K and then increased to 2.69 dpa at 373 K (Robinson et al., 2017). These results imply that the critical dose may first decrease and then increase with temperature.

5) The experimentally observed VSLs show much higher degree of ordering than GBSLs formed under gas ion irradiation. Surprisingly, the Xe GBSLs in U-7Mo, which is the only GBSL observed so far under fission neutron irradiation, display the best ordering among all superlattices observed experimentally. The Xe GBSLs have been found to form at low fuel burnups before a significant amount of fission gas has been produced, suggesting that they may have formed as VSLs and become pressurized later (Salvato et al., 2020).

6) Both GBSL and VSL seem to form via a three stage process from randomly arranged voids/bubbles to planar ordering and then 3D lattice (Evans, 2006; Sun et al., 2019).

7) The formation of superlattice seems not limited by the crystal lattice and the bonding nature. So far, superlattice or void/bubble ordering have been observed in fcc, bcc and hcp metals and alloys and ionic ceramics with the fluoride (Johnson, 1979; Johnson and Chadderton, 1983) and the rock-salt (Vainshtein et al., 1997) structures. Furthermore, oxide particle superlattice (van Ommen et al., 1986) and order oxygen bubbles (Maszara, 1988) have been reported in silicon under oxygen implantation, which is a covalent semiconductor with the diamond structure.

8) Superlattice formation has been observed for all primary irradiation sources, namely, neutron, ion, and electron irradiation, although observations under electron irradiation are fewer than under ion and neutron irradiation. Most superlattices formed under electron irradiation are in ceramics (Johnson, 1979; Johnson and Chadderton, 1983; Vainshtein et al., 1997; Ding et al., 2005), with only one exception in stainless steels containing nitrogen impurities (Fisher and Williams, 1977). There have been observations of ordered vacancy defect clusters under electron irradiation in fcc Cu (Yoshida and Kiritani, 1975; Fujita et al., 1982; Jin et al., 1989) and Ni and Ag (Seeger et al., 1991).

Many of the above findings suggest the similarity between VSL and GBSL. This is not very surprising considering the fact that gas bubbles are voids filled with gases. The different properties of VSL and GBSL may come from the impacts of gas atoms on the stability of small voids and the diffusivity of vacancies (Sprouster et al., 2019). However, there have been no direct evidence that VSL and GBSL are formed via the same mechanisms, and theories that can unify them are yet to emerge. A good theory for superlattice formation will need to be able to explain the above characteristics and the transition from VSL to GBSL.

FIGURE 4

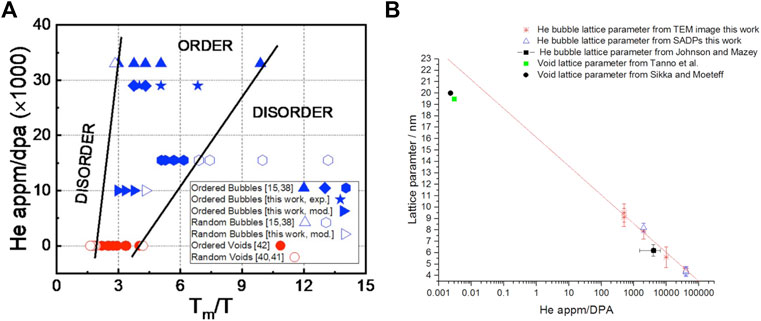
FIGURE 4. (Color online) (A) He GBSL formation window in bcc Mo with respect to He-appm to dpa ratio and inverse temperature. The figure is taken from Sun et al. (Sun et al., 2019). (B) He GBSL lattice parameter as a function of He-appm to dpa ratio in bcc W. The figure is taken from Harrison et al. (Harrison et al., 2017).

3 Theoretical and simulational studies of formation mechanisms

Various mechanisms have been proposed to explain the formation of superlattices under irradiation since its first observation. As a superlattice features both a crystal structure (symmetry) and a lattice parameter (characteristic length), a successful theory needs to be able to explain and predict both characteristics. Often, the theories are proposed for VSL and sometimes extended to GBSL without a clear distinction between them. For completeness and the purpose of cross comparison, all theories are briefly described here, although some of them have already been reviewed thoroughly in previous reviews (Krishan, 1982b; Evans et al., 1990; Ghoniem et al., 2001). A detailed review is given for the theory developed by the present author and coworkers for its success in predicting many of the VSL and GBSL properties.

The theories are divided into three main groups: the first that deals with the thermodynamic stability of superlattices based on elastic anisotropy, the second that explains the development of a characteristic length based on instability, and the third that focuses on symmetry development based on anisotropic self-interstitial-atom (SIA) diffusion. Note that theories from the second and third groups each focuses on one of the two superlattice characters and are often coupled together to fully explain superlattice formation. The simulational studies are presented along with the mechanisms on which they are based.

3.1 Thermodynamics-based theories

Given that the superlattices adopt crystal structures that mimic atomic lattices, it is logic to assume the existence of a thermodynamic interaction between voids or bubbles that stabilizes a superlattice. A natural candidate for such interaction is the elastic interaction between voids or bubbles. In some crystalline solids, the elastic moduli can be anisotropic along different crystal orientations. Accordingly, the strain energy in the host matrix is dependent on the arrangement of voids or bubbles, which are driven to adopt the arrangement that minimizes the total strain energy. This theory was initially proposed by Malen and Bullough (Malen and Bullough, 1971) and later followed by Stoneham, who showed that in bcc Mo a bcc void lattice with a a_L/R ratio of about 3.1 (Stoneham, 1971) is most stable; here, a_L is the VSL lattice parameter, and R is the void radius. This ratio is much smaller than that typically observed in experiments. Motivated by the fact that the anion VSL in CaF₂ is actually Ca colloids, Johnson and Chadderton made an analogy between voids and precipitates to explain the anion VSL formation (Johnson and Chadderton, 1983). Such elasticity induced ordering has also been demonstrated by 2D phase field simulation, although it is not clear whether such ordering would sustain in 3D simulations (Yu and Lu, 2005). As pointed out by Evans et al. (Evans et al., 1990), the elasticity based theories face several difficulties. First, it is difficult to explain superlattice formation in bcc W (Sikka and Moteff, 1972; Harrison et al., 2017; Sprouster et al., 2019), which is elastically isotropic. Second, the interaction needed to stabilize ordered voids was found much higher than what’s computed in molecular dynamics simulations (Finnis, 1987). Third, it ignores the strong dependence of superlattice characteristics on irradiation condition. Last, it does not explain the planar ordering of voids and bubbles in the early stage of superlattice formation. Recently, detailed analysis showed the elastic anisotropy in cubic crystals can lead to simple cubic (sc) or fcc, but not bcc superlattices (Gao et al., 2022), which in contrast have been commonly observed. These difficulties rule the elastic interaction between voids/bubbles unlikely the cause of superlattice formation.

3.2 Instability

Several theories based on instability have been proposed. These theories consider the instability of an initially homogeneous vacancy concentration field, which leads to the formation of concentration waves. Voids nucleated at the periodic wave peaks compose the superlattice. The corresponding wavelength is then related to the superlattice constant a_L. These models can be further separated into two categories: one which considers dynamics instability without explicitly considering the thermodynamic driving force for void formation, and the other which explicitly considers such thermodynamic driving force. An essential difference between these two categories of models is whether the dynamic evolution of defect clusters needs be considered. At lease one type of defect clusters must be considered for the dynamic instability theories to induce instability, while no explicit consideration of defect clusters is required in the thermodynamics-driven instability theories.

3.2.1 Dynamic instability

The theories based on dynamic instability describe the evolution of time and spatially dependent vacancy and SIA concentrations using the BEK rate equations derived by Bullough, Eyre and Krishan (Bullough et al., 1975). The diffusion of vacancy and SIA is considered using Fick diffusion. The vacancy and SIA evolution equations are often coupled with rate equations for defect clusters such as voids, stacking fault tetrahedrons (SFTs), and loops of either vacancy or SIA nature. Including these defect clusters is necessary for dynamic instability to occur. As has been reviewed in details previously (Krishan, 1982b; Ghoniem et al., 2001), theories in this category differ from each other by how the evolution of defect clusters are considered and the factors that cause the instability. For instances, the theory by Martin (Martin, 1983) considered the instability induced by mutual recombination, and the theory proposed by Krishan (Krishan, 1982a) focused on the instability induced by defect-sink interaction. In the theories proposed by Walgraef et al. (Walgraef et al., 1996), the instability was attribute to void growth when the contrition of SIAs to void growth exceeds that of vacancy. The models proposed by Krishan and Walgraef are briefly described in the below for completeness.

Krishan introduced a bifurcation analysis (Krishan, 1982a) to explain the development of a characteristic length. Using the rate theory equations for the evolution of vacancy, SIA, voids and vacancy loops, instability analysis showed that the homogeneous vacancy concentration field could lose stability to spatial fluctuations and bifurcate into concentration waves. Factors that may lead to the instability include production bias (differences in vacancy and SIA production rates), interaction bias (differences in capture rates by sinks) and couplings between sinks and point defects. The bifurcation was shown to eventually give a stable wavelength. This model has been reviewed in details by Krishan (Krishan, 1982b). Similar models have been proposed by Martin (Martin, 1983) and Imada (Imada, 1978) with different factors that contribute to the instability.

Walgraef and Ghoniem published a series of articles (Walgraef and Ghoniem, 1989; Evans et al., 1990; Walgraef et al., 1996; Walgraef and Ghoniem, 2003) proposing the reaction-diffusion models for nano- and microstructure formation. The models have been reviewed in details by Ghoniem et al. (Ghoniem et al., 2001). The theoretical models contained spatially dependent rate equations for migrating vacancies, SIAs, stationary voids, and vacancy and SIA loops. Non-linear instability analysis was carried out to predict pattern formation. Anisotropic interstitial diffusion has been introduced to induce the selection of patterns. Their theories have been applied to self-organization of vacancy loops, voids and SFTs. It was concluded that two general conditions, sink-absorption of point defects out-competing mutual recombination and a critical vacancy cluster density directly generated by displacement cascades, need to be satisfied for instability to occur. The predicted instability wavelength was found to be a few times larger than the experimentally observed ones, and this discrepancy was attributed to the non-linear interaction between defects in the post-bifurcation regime that determined the stable wavelength selection (Ghoniem et al., 2001).

3.2.2 Thermodynamics-driven instability

Two theories are recently proposed for superlattice formation taking into account the thermodynamic driving force for like defects to cluster, e.g., the vacancy and SIA formation energies. The theoretical models are analogous to a diffusion-reaction model that couples thermodynamics-driven phase separation, described by the Cahn-Hilliard dynamics (Cahn and Hillard, 1958), and reaction, including defect production, mutual recombination, and sink absorption, described by the BEK rate equations (Bullough et al., 1975). As such, the homogeneous vacancy concentration field will lose stability to form extended defects such as voids when the vacancy concentration exceeds a certain critical value that depends on the reaction terms, similar to a phase separation process. These two theories are reviewed in the below.

The Turing-instability based model proposed by Noble et al. (Noble et al., 2020) considers thermodynamics and evolution of both vacancy and SIAs. It was shown that voids with a uniform size and a uniform inter-void distance could emerge as a Turing instability in place of the more intuitive Ostwald ripening when the SIA mobility is much higher than that of vacancy, consistent with the observation from phase field simulations by Hu et al. (Hu and Henager, 2009). The formation of ordered voids was demonstrated using 2D phase field simulations with the ordering corresponding to bcc VSL. The authors pointed it out that the model can not predict fcc VSL because only one characteristic length results from the instability while the development of a fcc lattice needs two. No anisotropic SIA diffusion was taken into consideration in the model or the simulations.

At last, the instability model developed by the present author and coworkers (Gao et al., 2018a; Gao et al., 2018b; Zhang et al., 2020) is reviewed with more details for its capabilities of explaining the experimental findings summarized at the end of Section II. A notable outcome from this theory is an analytic expression for the void superlattice parameter a_L with explicit dependence on material properties and irradiation condition. The theoretical prediction can be quantitatively compared with a_L from experimental measurement and lattice kinetic Monte Carlo (LKMC) simulations without using any fitting parameters. Extending the prediction for GBSL by considering the dragging effect of gas atom on vacancy diffusion, the dependence of a_GBSL on temperature, dose rate, and dose have been validated by deliberately designed experiments (Sprouster et al., 2019; Sun et al., 2019; Jossou et al., 2021). Further, anisotropic SIA diffusion can be included into the analysis to predict the superlattice structure (Zhang et al., 2020).

The theory considers the evolution of vacancy and SIA using the rate theory, as.

\frac{\partial c_{v}}{\partial t} = P (1 - c_{v}) + ▿ \cdot M_{v} ▿ (\frac{δ F}{δ c_{v}}) - k_{i v} c_{i} c_{v} - k_{v s} D_{v} c_{v} (1)

\frac{\partial c_{i}}{\partial t} = P (1 - c_{v}) + ▿ \cdot D_{i} ▿ c_{i} - k_{i v} c_{i} c_{v} - k_{i s} D_{i} c_{i} (2)

Here, the rate theory is coupled with the Cahn-Hillard dynamics for chemical potential driving diffusion in place of Fick diffusion. The subscripts i, v, s denote SIA, vacancy and sink, respectively. P is the production rate (or dose rate). The term (1 − c_v) ensures mass conservation considering volumetric swelling. M and D are the atomic mobility and diffusivity; M = D/K_BT, with K_B being the Boltzmann constant. F is the total free energy of the system. In the theoretical analysis, F is formulated using a regular solution model for binary (vacancy and host material) systems, featuring a heat of mixing E_mix (i.e., the vacancy formation energy) and an interfacial energy κ. k_iv is the reaction rate for recombination, while k_vs and k_is are the rate coefficients for sink absorption of vacancy and SIA, respectively. And k_iv = 4πR_iv (D_i + D_v)/Ω; here R_iv is the instantaneous recombination radius and Ω is the atomic volume. Using Q = k_ivc_i + k_vsD_v + P for the production and reaction terms, the vacancy evolution equation in Equation 1 can be reduced to:

\frac{\partial c_{v}}{\partial t} = P + ▿ \cdot M_{v} ▿ (\frac{δ F}{δ c_{v}}) - Q c_{v} (3)

Or in its Fourier form,

\frac{\partial \tilde{c_{v}}}{\partial t} = P δ (k) - (M_{v} f^{''} k^{2} + M_{v} κ k^{4} + Q) \tilde{c_{v}} (4)

Considering a small perturbation wave with a wave vector k, its growth rate is given by R(k) = −(M_vf^″k² + M_vκk⁴ + Q) in the Fourier form evolution Equation 4 for vacancies. In certain irradiation conditions, the system may experience three different stages upon the accumulation of vacancies, as shown by the growth factors plotted in Figure 5A. In the first stage, when c_v is low, e.g., at low dose of irradiation, no perturbation waves are stable as the growth factor is negative for all k. Please note that this does not exclude the formation of vacancy clusters. Rather, unstable vacancy clusters can form as a result of perturbation or by direct production in displacement cascades. A likely scenario in reality is the constant formation and annihilation of random vacancy clusters. By time average a homogeneous vacancy concentration field is still maintained.

FIGURE 5

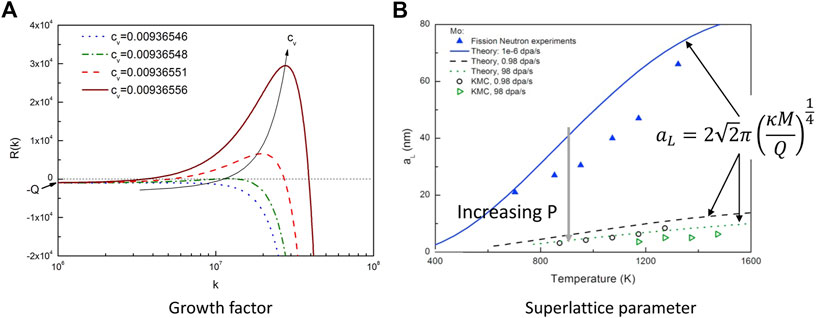
FIGURE 5. (Color online) (A) Growth factor R of perturbation waves k with increasing vacancy concentrations, c_v. (B) The VSL lattice parameter a_L as a function of temperature T in bcc Mo at different dose rate, P. The figures are taken from Gao et al. (Gao et al., 2018a).

In the second stage, when a critical c_v is reached, the growth factor transitions from negative to positive for a critical wave vector k_c, which can be determined by two mathematical conditions: R(k) reaches a maximum (i.e., dR(k)/dk = 0) and R(k) = 0 at k_c. As the stable perturbation wave grows exponentially about R(k), this critical wave k_c is expected to grow quickly. Collective formation of symmetrical waves lead to local nucleation of ordered voids at the intersections of wave peaks, forming a superlattice. This instability is driven thermodynamically by the separation of a “void phase” from the matrix. However, complete phase separation is impeded by the reaction terms, i.e., production, recombination, and sink absorption. Consequently, a finite critical wavelength is determined by the competition between phase separation kinetics, dictated by vacancy diffusion, and the reaction (Q in Equation 3). Such an instability is very similar to the onset of an inhomogeneous state in a non-equilibrium superconducting film (Scalapino and Huberman, 1977) and the chemical freezing of phase separation in immiscible binary mixtures (Carati and Lefever, 1997). An analytic expression for the critical can then be obtained from the critical wave number k_c, as

λ_{c} = \frac{2 π}{k_{c}} = 2 π {(\frac{κ M_{v}}{Q})}^{1 / 4} . (5)

Relating the vacancy concentration wave fronts to the close-packed planes, {110} in bcc crystals, a_L can be derived as $a_{L} = \sqrt{2} λ_{c} = 2 \sqrt{2} π {(\frac{κ M_{v}}{Q})}^{1 / 4}$ .

In the third stage, the ordered voids can continue to grow in size while the superlattice parameter a_L remain constant (as a change in a_L would require systematic migration of all voids). This implies that a_L is expected to saturate over irradiation dose until the superlattice becomes unstable, if it will.

The experimentally observed dependence of superlattice parameter on temperature, dose rate, and dose can be explained by Equation 5. First, a_L increases with temperature because of increasing vacancy mobility (i.e., diffusivity) with temperature. Although the reaction term Q also increases with temperature, the effect is secondary (Schneider et al., 2022). The prediction has been validated by both experiments and LKMC simulations, which were designed to be consistent with the theoretical formulation, as shown in Figure 5B. Second, a_L decreases with dose rate P because it contributes linearly to the term Q. Third, the saturation of a_L can be understood by the stability of the critical waves.

It should be emphasized that the second and third stages will be reached only in some certain irradiation conditions that favor superlattice formation. By using the conditions that the critical concentration is never reached or the predicted inter-void distance is too small, i.e., less than twice of the recombination radius, a low-temperature boundary can be predicted using the above theory, as shown in Figure 6. Remarkably, the low-temperature boundary is found to be nearly a linear line in the log(P) and T_m/T diagram, with a slope proportional to the vacancy migration barrier E_v, consistent with what has been shown previously (Ghoniem et al., 2001). Below the low-temperature boundary, random voids are expected to form and disappear without growing into large voids. However, theoretically predicting a high-temperature boundary is not possible in the proposed theory as thermal emission of vacancies from voids is not considered. As will be discussed later, it is expected that void ordering gradually vanishes until an ordered lattice can not be recognized.

FIGURE 6

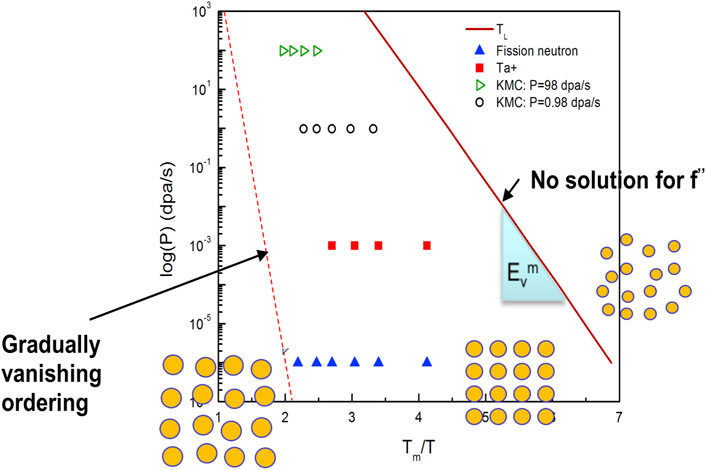
FIGURE 6. (Color online) Temperature - flux diagram for superlattice formation for bcc Mo. The figure is adapted from Gao et al. (Gao et al., 2018a).

Following the theoretical analysis, phase field simulations were carried out to further investigate the formation process in different irradiation conditions (Gao et al., 2018b). 1D SIA diffusion was considered in the simulations. It is found that the development of a characteristic length and void ordering are controlled by two different factors, the first by void formation driven by vacancy accumulation and the second by vacancy-SIA recombination via which anisotropic SIA diffusion affects pattern selection. Accordingly, three different formation processes may be observed depending on the irradiation condition. In ideal conditions for superlattice formation, the characteristic length and symmetry develop simultaneously, resulting in the highest degree of ordering. When vacancy accumulation is fast while recombination is slow, disordered voids form and become ordered gradually. When vacancy accumulation is slow while recombination is fast, ordering develops fast with ordered voids along the 1D SIA diffusion direction. Superlattice will form when more voids form. A fourth process was suggested by recent phase field simulation when thermal nucleation of voids is prevalent (Aagesen et al., 2022). In this case, random voids with a low density may form first, and ordering improves when more voids form until an ordered lattice emerges.

The newly proposed theory also implies an equivalency between logP and 1/T, similar to the case for void swelling (Mansur, 1994). Such an equivalency has been proven by LKMC simulations, which showed that both the superlattice parameter and the critical dose of formation remained invariant upon proportionally varying logP and 1/T (Schneider et al., 2022). A best condition for superlattice formation has been identified by correlating logP with 1/T for the highest degree of ordering. It was also found that the structural factor can be a very good parameter to quantify voids or gas bubble ordering.

3.3 Anisotropic SIA diffusion

The instability-based theories above focus on the development of a characteristic length (i.e., superlattice parameter) but are unable to predict the symmetry development (i.e., superlattice structure). There has been a general consensus that the symmetry development is caused by anisotropic SIA (or SIA clusters and loops) migration, which affects the selection of superlattice structure via the vacancy-SIA recombination. This idea is first proposed by Foreman (Foreman, 1972). It was speculated that with 1D SIA diffusion or 1D replacement sequence, voids aligned along the SIA diffusion or the replacement direction can shield each other from incoming SIA flux and will thereby grow preferentially over unaligned ones. As the 1D SIA diffusion or replacement sequence directions are likely the close-packed directions, voids aligned along those symmetrical crystal directions will form a 3D lattice coherent with the host matrix. This provides a plausible explanation of the observed isomorphic superlattices in various materials. Historically, two subgroups of theories were proposed based the dimensionality of SIA diffusion.

The first subgroup follows Foreman’s hypothesis of 1D SIA diffusion. Coupling this with the dynamic evolution equations for vacancy, dumbbells and crowdions in a two-interstitial model, Woo et al. showed that the effect of 1D crowdion diffusion on the selection of superlattice structure could be described by the so-called crowdion-supply-cylinder (CSC) (Woo and Frank, 1985; Semenov and Woo, 2006). The nucleation of superlattice was found to be an example of non-equilibrium phase separation process in a dissipative system, with the superlattice parameter a_L dictated by the 1D migration mean free path (MFP) of crowdions. It was further showed that the 1D crowdion MFP must be comparable to a_L (Semenov and Woo, 2006) for superlattices to form, in consistency with kinetic Monte Carlo (KMC) simulations (Heinisch and Singh, 2003). The 1D SIA diffusion mechanism has been supported by a series of phase field simulations by Hu and co-authors (Hu and Henager, 2009; Hu et al., 2016). Coupling 1D SIA random walk and Cahn-Hilliard dynamics for vacancy evolution, 2D phase field simulations showed that initially randomly arranged voids evolved into a 2D lattice when the SIA mobility is four orders of magnitude larger than the vacancy mobility (Hu and Henager, 2009). The model was further extended for GBSL by including Xe and elastic interaction between bubbles (Hu et al., 2016). The most remarkable finding from these simulations is that the lattice structure is dictated by the 1D SIA migration direction, not the matrix structure. 1D SIA migration along $< 110 >$ ( $< 11 >$ in the 2D simulations) was found to lead to a fcc GBSL (tilted square in 2D), allowing for explaining the formation of fcc Xe GBSL in bcc UMo. Albeit the success, the 1D SIA diffusion based theory “seems” to suggest that superlattice formation starts with 1D alignment of voids along the SIA migration direction. Such 1D alignment has not been observed in experiments, which often show 2D planar ordering in the early stage of superlattice formation. Such a discrepancy has led to some criticism of the 1D SIA diffusion mechanism (Evans, 2006; Robinson et al., 2017).

To explain the experimentally observed planar ordering in early stage superlattice formation, Evans proposed the 2D SIA migration mechanism and demonstrated it using KMC simulations in a series of articles (Evans, 1983; Evans and Mazey, 1986; Evans, 2006). It was shown that, 2D SIA diffusion in a single close-packed atomic plane could cause planar ordering of voids without necessarily a characteristic wavelength, consistent with the planar void ordering observed in the basal plane of hcp Mg (Jostsons and Farrell, 1972). When such 2D diffusion was activated simultaneously on symmetrical close-packed planes, sc, fcc, and bcc superlattices were successfully reproduced in KMC simulations depending on the 2D SIA migration planes. Such 2D SIA mechanism has been shown capable of explaining all types of void ordering that have been observed so far.

While implementation of anisotropic SIA diffusion has been done in various simulations, theoretically formulating how anisotropical SIA determines superlattice structure has been scarce. Following the thermodynamics-driven instability analysis described above, the present author computed the growth rate of perturbation waves along different wave directions considering both 1D and 2D SIA diffusion. Anisotropic SIA diffusion was found to result in direction-dependent growth rate of perturbation waves and thereby preferential growth of waves along favorable directions. 1D SIA diffusion along a single direction was found to cause 1D voids alignment, as shown in Figure 7A. In contrast, 1D SIA diffusion along two and more symmetrical directions was found to favor perturbation waves along specific directions, which implies plane waves and planar void alignment, as shown in Figures 7B, C. The theoretical predictions were confirmed by LKMC simulations in Figures 7D–F. A list of superlattice structures can then be predicted based on SIA diffusion anisotropy, as shown in Table 4. The most significant implication of the theoretical formulation is that 1D SIA diffusion does not necessarily lead to 1D alignment of voids or bubbles. Rather, it affects the selection of perturbation wave directions via the recombination term k_ivc_ic_v, which is a component of Q and the growth factor R in Equation 3. This means that even with 1D SIA diffusion superlattice formation is expected to start with planar ordering instead of 1D alignment of voids. The 3-stage formation process, from random voids to planar ordering and eventually 3D lattice was clearly demonstrated using LKMC simulations, as shown in Figure 8. This clears the criticism for 1D SIA diffusion that originate from the mistakenly assumed 1D alignment of voids. Another important finding from this theoretical analysis is that the same superlattice structure can actually be caused by either 1D or 2D SIA diffusion, consistent with Evans et al. (Evans et al., 1990). For instance, a bcc superlattice can result from 1D SIA diffusion along $< 111 >$ or 2D SIA diffusion in {110} plane. In either case, planar ordering precedes 3D lattice formation. It should be noted that all predictions in Table 4 are based on the assumption that SIA diffuses much faster than vacancy, which is true in most metals. When this assumption is reversed, it has been found that $< 111 >$ 1D SIA diffusion may lead to fcc superlattice instead of bcc (Gao et al., 2019).

FIGURE 7

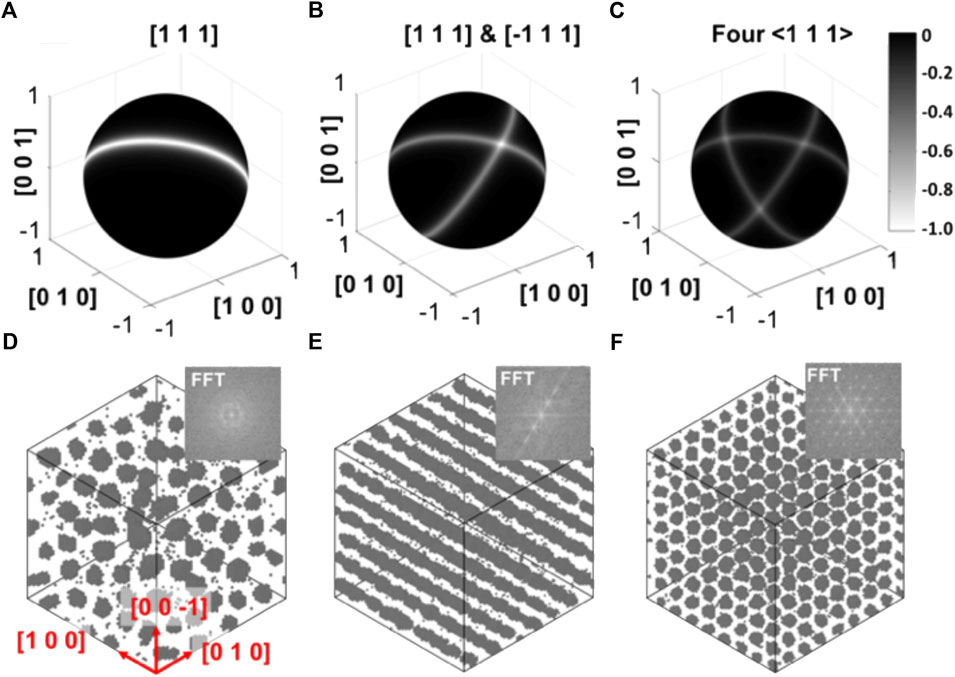
FIGURE 7. Normalized change in recombination with 1D SIA diffusion along (A) [1 1 1], (B) [1 1 1] & [-1 1 1], and (C) all $< 111 >$ directions. The minimums correspond to maximums in growth factors and are thereby obtained for preferential perturbation waves. (D–F) Void ordering predicted by LKMC simulations in bcc Mo with the SIA diffusion modes in (A–C). The simulation cell size is 80 × 80 × 80 $a_{0}^{3}$ . The figure is taken from Zhang et al. (Zhang et al., 2020).

TABLE 4

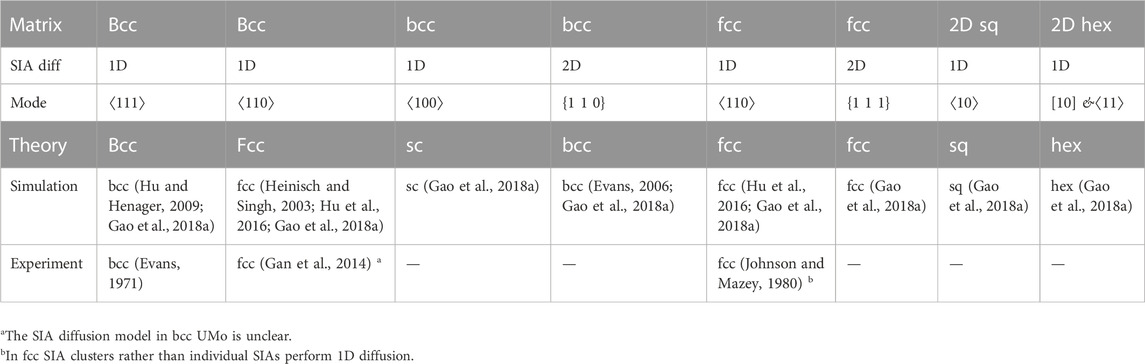
TABLE 4. Theoretical predictions of void/bubble ordering versus atomic kinetic Monte Carlo simulations and experimental observations.

FIGURE 8

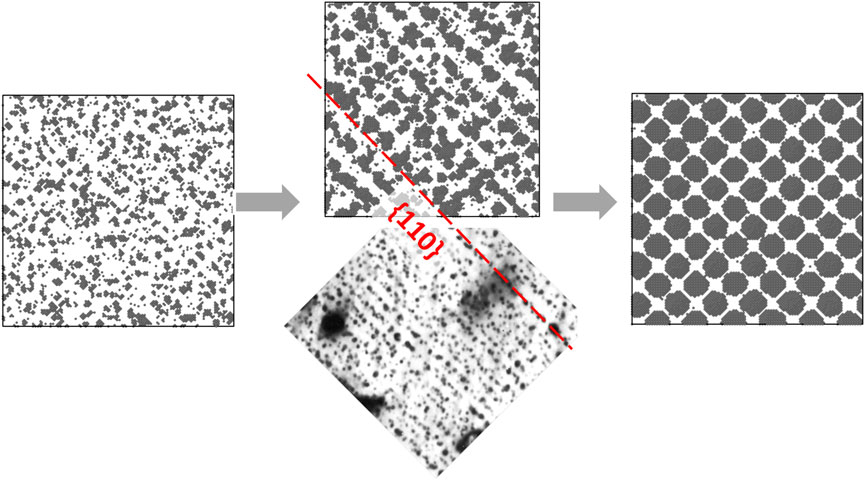
FIGURE 8. 3-stage formation process of void superlattice (VSL) in bcc Mo with 1D SIA diffusion demonstrated by LKMC simulations. The experimentally observed planar void ordering is taken from Evans (Evans, 2006).

Furthermore, the effectiveness of anisotropic SIA diffusion was found dependent on the ratio of 1D SIA diffusion MFP (l_i) relative to the perturbation wavelength (the inverse of the wave number k₀), which is related to the superlattice parameter a_L. A higher ratio implies better void ordering, as shown in Figures 9A,B,C. At high temperatures, the 1D SIA diffusion MFP is short due to frequent rotation, and a_L is large because of high vacancy diffusivity. Accordingly, the degree of void ordering will be weak. This implies that void ordering will gradually vanish over increasing temperature, until no recognizable superlattices due to poor ordering. Again, this suggests a gradually decreasing superlattice ordering instead of a clear high temperature boundary.

FIGURE 9

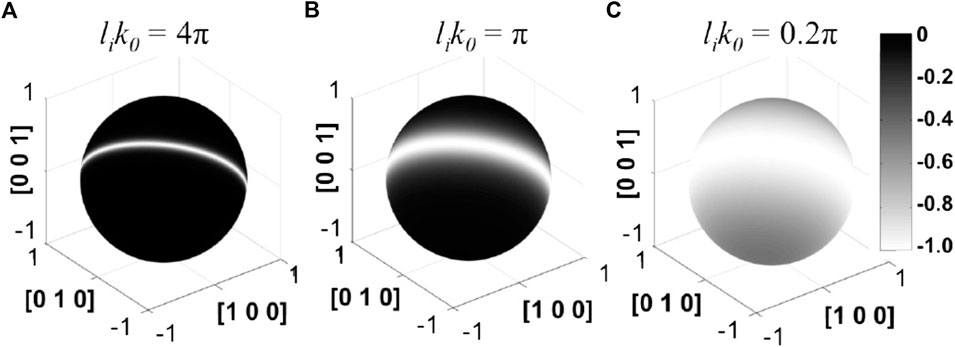
FIGURE 9. Normalized change in recombination caused by perturbation waves with 1D SIA diffusion along the [1 1 1] direction in a bcc crystal. The wavelength used in the calculation is (A) 0.5, (B) 2.0, and (C) 10.0 of SIA mean free path, l_i (Zhang et al., 2020).

The anisotropic SIA diffusion hypothesis has been extended to SIA clusters in the theory proposed by Dubinko (Dubinko et al., 1989), where 1D migration of SIA loops punched out from gas bubbles was used to explain GBSL ordering, and that of irradiation produced SIA loops to explain VSL formation. Such an extension has an important implication for superlattice formation in fcc metals and bcc Fe in which individual SIAs take the dumbbell configuration and are expected to perform 3D diffusion.

The anisotropic SIA diffusion theories were initially based on hypothesized SIA diffusion properties derived from crystal symmetry. Nowadays, a much better understanding on SIA and SIA cluster and loop diffusion has been achieved thanks to experimental observations and atomistic simulations. Although direct observation of individual SIA migration is yet to be realized, 1D migrations of $\frac{1}{2} < 111 >$ SIA loop and $\frac{1}{2} < 110 >$ vacancy loop have been directly observed using high-resolution TEM in bcc Fe (Arakawa et al., 2007) and fcc Au (Matsukawa and Zinkle, 2007), respectively. Combined experimental observations and KMC simulations have also suggested that individual SIA migration should be 1D rather than 3D in bcc W (Amino et al., 2016). More understanding on the configuration and diffusion of SIAs in bcc and fcc metals has been achieved via atomistic calculations, particularly density functional theory (DFT) calculations. The most stable SIA configuration in all non-magnetic bcc metals including V, Nb, Mo, Ta and W is predicted to be $< 111 >$ crowdion or dumbbell with a difference at the order of meV, in contrast to the $< 110 >$ and $< 11 ξ >$ dumbbells in magnetic Fe and Cr (Ma and Dudarev, 2019). The $< 111 >$ SIA configuration is expected to migration 1D along its axis direction, while the $< 110 >$ and $< 11 ξ >$ dumbbells are expected to migrate 3D by a translation-rotation mechanism. As such, superlattice formation in bcc Fe and Cr can not be explained by 1D SIA diffusion, but possibly by 1D SIA loop migration along its $< 111 >$ Burgers vector direction. In fcc Ni, the most preferred SIA configuration is $< 100 >$ dumbbell, which diffuses via a translation-rotation mechanism (Tucker et al., 2010; Lu et al., 2016). In contrast, 1D migration of SIA clusters and loops have been observed by molecular dynamics simulations in fcc Cu (Osetsky et al., 2010) and Ni (Lu et al., 2016). Again, this precludes explaining superlattice formation in fcc Ni using 1D SIA diffusion; instead, GBS formation has been attributed to 1D SIA cluster migration (Harrison et al., 2019).

4 Discussions

While the theory combining instability analysis and anisotropic SIA diffusion seems able to provide a plausible explanation of superlattice formation, there are still open questions to prove (or disprove) and accomplish the theory. Here, an in-depth discussion is given on several different aspects of superlattice formation combining the experimental observations and the proposed formation mechanisms. The purpose is to motivate future studies in this area.

4.1 Irradiation source

Superlattice formation has been observed under neutron, ion, and electron irradiation, implying that superlattice formation is not limited by the irradiation particle source. One crucial difference between electron and ion/neutron irradiation is that under ion/neutron irradiation defects are generated in isolated displacement cascades, in which substantial fractions of defects are generated in the form of clusters directly, while under electron irradiation Frenkel pairs (pairs of individual vacancy and SIAs) are generated. The theories based on dynamic instability consider direct generation of voids in displacement cascade as a necessary condition for instability to occur. This means that, electron irradiation may NOT be able to produce VSL. The critical role of directly produced voids by irradiation in VSL formation has also been highlighted by recent object KMC simulations (Li et al., 2021). It should be noted that, the few observations of VSL under electron irradiation (Fisher and Williams, 1977; Johnson and Chadderton, 1983; Vainshtein et al., 1997; Ding et al., 2005), although fewer than under ion and electron irradiation, actually indicate that direct generation of voids in displacement cascades is not necessary. Indeed, when a thermodynamic driving force for void formation is included, as in the thermodynamics-driven instability models (Gao et al., 2018a; Noble et al., 2020), no direct voids generation is required for instability to occur. Both LKMC and phase field simulations have shown that 3D VSLs can form with Frenkel pair production in the absence of preexisting voids (Gao et al., 2018a; Gao et al., 2018b). The rare observations of VSL under electron irradiation may possibly be caused by several reasons, for instances, the high voltage needed in a TEM to generate defects in heavy bcc metals and the thin-foil sample geometry used which bear a strong surface sink effect. Also, direct generation of voids in displacement cascades promotes the nucleation of stable voids and thereby VSL, possibly resulting in a lower critical dose for VSL formation under ion and neutron irradiation than under electron irradiation. Studies of the dependence of critical dose of formation on irradiation source (i.e., primary damage production) from both experiment and modeling sides may help elucidate this. Albeit the challenges, electron irradiation may be the best choice to directly prove the thermodynamics-based instability theories because of the consistency between electron irradiation and the rate theory description of defect dynamics. Non-magnetic bcc metals, in which SIAs perform 1D migration along $< 111 >$ , are suitable choice of material systems. Theoretical analysis and LKMC simulations can be used to help estimate the temperature, dose rate, and dose for superlattice formation. Further, in-situ observation of the onset of instability may be possible in this kind of experiments.

4.2 Necessary conditions for superlattice formation

The previous experimental, theoretical, and simulation studies suggest superlattice can form in a wide range of materials regardless of their crystal structures and bonding natures. There seem to be two necessary and sufficient conditions for VSL to form: i) an instability in the otherwise homogeneous defect concentration field and ii) an anisotropic factor that leads to void ordering. It should be noted that the anisotropic factor is only needed for void ordering and not necessary for instability to occur. The formation window established by experimental observations in terms of temperature, dose rate, and gas-appm to dpa ratio corresponds the irradiation condition for an instability to occur. On the other hand, anisotropic SIA and/or SIA cluster diffusion has been regarded as the factor responsible for void ordering. While 1D SIA diffusion has been shown able to cause void/bubble ordering in both theoretical formulations and computer simulations, the role of SIA cluster diffusion remains unclear because of the challenge of simulating SIA cluster migration in a timescale comparable to laboratory scale. Understanding the formation of superlattices in fcc metals and bcc Fe may require the consideration of anisotropic SIA cluster migration.

The above two conditions suggest that superlattice formation may be extended to material systems that have not been explored systematically, e.g., ceramics and semiconductors. The theoretical models reviewed in Section III can be used to guide the selection of irradiation condition. On the one hand, extending the studies to new materials can help testify the validity and generality of the proposed models. On the other hand, generating nanoscale superlattices in non-structural materials may lead to the discovery of novel functional properties.

The anisotropic diffusion properties of SIA and SIA cluster may also be tailored to tailor superlattice properties. For instance, 1D SIA diffusion may be altered by alloying, e.g., adding Re to W (Suzudo et al., 2014; Castin et al., 2020). Applying strain may also change the diffusion properties of SIAs, which has been used to explain bct VSL in bcc Cr (Sun et al., 2022) and bct He GBSL in bcc Mo (Sun et al., 2018).

4.3 Thermal and irradiation stability of superlattices

The searching for the formation mechanism depends critically on whether VSL or GBSL are thermodynamically stable (e.g., at temperatures below that for vacancy emission). As anisotropic elastic interaction has been shown unlikely the cause of superlattice formation, a thermodynamic interaction that stabilizes superlattices seems not to exist. As such, the large surface to volume ratio in a nanoscale VSL makes it energetically unfavorable compared to coarsened voids with the same total volume. For GBSL, the changes in bubble pressure and the resulting elastic strain energy caused by bubble coalescence have to be considered. As suggested by the proposed formation mechanisms, it is likely that both VSL and GBSL are not thermodynamically stable but stabilized by defect reactions. Following that, theoretically both VSL and GBSL are subject to coarsening under thermal annealing. The remarkable thermal stability of superlattice observed experimentally (Gan et al., 2018; Sun et al., 2020) may be attributed to the slow coarsening kinetics because of ordering. Coarsening of voids or bubbles may occur by two mechanisms: Ostwald ripening and coalescence by void/bubble migration. For relatively large voids and bubbles, migration is slow, particularly in the absence of a directional driving force. Ostwald ripening relies on the unbalanced emission and absorption flux of vacancy (and gas atoms) favoring the growth of large voids/bubbles along with shrinkage of small ones. When voids and bubbles are ordered with similar sizes, such unbalanced flux is negligible initially, resulting slow ripening kinetics. As has been shown by phase field simulations, ordered bubbles are much more resistant to coarsening than random ones (Sun et al., 2020).

Then what about the superlattice stability under irradiation? The instability based theories predict that the superlattice parameter is dependent on the irradiation condition, including temperature, flux, and gas-appm to dpa ratio. Following this, three scenarios may be expected. First, with continuous irradiation in the same conditions, superlattice will remain stable with possible improvement in ordering. However, formation of superlattice may slow down but does not fully stop defect accumulation. The superlattice is expected to collapse either due to internal pressure build up or by other microstructural processes, e.g., recrystallization in UMo fuel (Salvato et al., 2020). Second, when the irradiation condition is slightly changed, the superlattice may adapt to a new lattice parameter without a significant change. Third, with significant change in irradiation condition, the superlattice parameter that determined by the new condition can be significantly different from the existing one. In this case, the existing superlattice will collapse, followed by the establishment of a new one, as recently observed in Cr (Sun et al., 2022), or none if no superlattice is permitted by the new irradiation condition.

4.4 Are VSL and GBSL the same?

Another important question is whether VSL and GBSL are the same, or form by the same mechanism. This question is of interest for two different scenarios: i) in nuclear fuels where fission gases (e.g., Xe and Kr) are produced, and ii) in structural materials where He gas atoms are generated by transmutation reaction, e.g., in Ni-containing alloys proposed for fusion reactors. The answer may depend on the condition in which the superlattice start to form. Note that both void and bubbles are cavities, while the latter is filled with gas atoms. Under irradiation, the vacancy concentration increases linearly initially and plateaus at high dose, as shown in Figure 10. In contrast, the total gas concentration increases linearly with fluence (dose) because of mass conservation. In the case where superlattice form before a significant amount of gas is introduced, e.g., in the vacancy dominated regime, the growth in bubble size is dictated by vacancy flux, and VSL and GBSL may form by the same mechanism. Inert gas atoms bind strongly with vacancies with high binding energies, as shown by recent DFT calculations (Jiang et al., 2018). The strong binding will significantly reduce the diffusivity of both gas atoms and vacancies because diffusion requires their dissociation. In addition, the presence of gas in voids can substantially enhance their thermal stability, as indicated by object KMC simulations (Jiang et al., 2021), facilitating the nucleation of small voids. Both factors suggest a decreasing superlattice parameter with the gas-appm to dpa ratio. This gives a plausible explanation for the experimental observations in bcc W (Harrison et al., 2019; Sprouster et al., 2019). Recent characterization of Xe GBSL in UMo fuel along with bubble pressure analysis also indicated that the Xe GBSL may have formed as VSL and became pressurized over burnup (Salvato et al., 2020). In contrast, when superlattice forms after a substantial amount of gas has been introduced, e.g., in the gas dominated regime, nucleation and growth of bubble is dictated by SIA or SIA loop punching (Zhang et al., 2012; Jin et al., 2021). In this case, GBSL forms via a different mechanism (as proposed by Dubinko et al. (Dubinko et al., 1989) and may display different dependence on irradiation condition. In this scenario, GBSL may possibly form at low temperatures when vacancy mobility is not active. Simulations that are capable of considering concurrent gas production and irradiation, as well as SIA and loop punching, are needed to investigate whether there is a change in the superlattice formation mechanism because of the rate of production and/or type of the gas atoms.

FIGURE 10

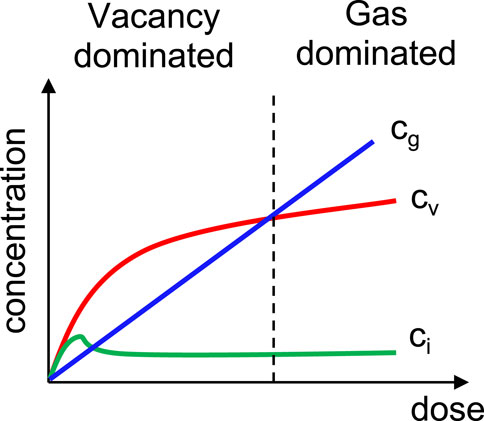
FIGURE 10. (Color online) Schematic plots showing the evolution of point defect (c_v and c_i) and gas (c_g) concentrations over irradiation dose.

4.5 Effect of initial microstructure

The initial microstructure of the host material may be controlled to tailor superlattice properties including lattice parameter a_L and critical dose of formation. Preexisting microstructural features such as grain size and dislocation density are sinks that absorb vacancy and SIAs. An appropriate sink strength is necessary for the instability to occur. Without sinks, mutual recombination dominates with no VSL formation. When the sinks strength is too high, the vacancy concentration may not reach the critical value for instability to occur either. As shown in the theoretical models by Walgraef et al. (Walgraef et al., 1996), a spatially organized defect microstructure is difficult to obtain in cold-worked Ni with a very high dislocation density. Within the formation window, varying the sink strengthen may result in a change in a_L. According to Equation 5, a higher sink strength corresponds to a smaller a_L. In addition, geometrical sinks such as grain boundaries may facilitate VSL nucleation, as has been shown by Xe GBSL formation near grain boundaries in U-7Mo (Salvato et al., 2020). Thereby, tuning grain size may provide another way to tailor superlattice formation. It is also of interest to see how the unique microstructure generated by additive manufacturing (Collins et al., 2016) may affect superlattice formation.

4.6 Functional properties of superlattices

It is of curiosity whether the nanoscale VSL and GBSL possess any superior functional properties. Studies on this are rare, probably because most studies of superlattices have focused on structural metals and alloys. For instances, nanoporous metals such as Au, Cu, and Ag have shown to have promising applications for fuel cells and CO₂ reduction (Kadja et al., 2022). Other than in bulk materials, VSL and GBSL may also be produced in nanoparticles under irradiation. Recent LKMC simulations from the present author’s group suggest that VSL can form in nanoparticles with sizes larger than a few times of the VSL lattice parameter. In addition, superlattices have been observed in ceramics such as CaF₂ and SrF₂ (Johnson, 1979; Johnson and Chadderton, 1983), and semiconductor like Si (van Ommen et al., 1986). It may be worth pursuing to investigate the functional properties of superlattices in these materials.

5 Conclusion

Built upon the perspectives shared in previous reviews, this articles provides a comprehensive review of studies of void superlattice (VSL) and gas bubble superlattice (GBSL) formed under irradiation since 2001. The new studies have advanced our understanding on VSL and GBSL self-organization in the below areas:

1) The observations of Xe GBSL in U-Mo fuel have disrupted the previous conclusion that VSL and GBSL are always isomorphic with the host material, excluding the host material structure as the decisive factor for superlattice structure selection.

2) The dependence of GBSL lattice parameter a_GBSL on temperature, dose rate, and dose have been established. Similar to VSL, a_GBSL of GBSL has been found to increase with temperature, decrease with dose rate, and saturate over dose.

3) Deliberately designed experiments have suggested the similarity between VSL and GBSL. In particular, it has been found that both the formation window and the superlattice parameter may be unified using the gas-appm to dpa ratio.

4) New theories based on thermodynamics-driven instability have been proposed for VSL formation. Compared to the previous theories based on dynamic instability, the new theories do not require direct vacancy cluster production in displacement cascade for instability to occur. Both the lattice parameter and the structure of VSL can be theoretically predicted without using any fitting parameters, with good agreements with both experiments and simulations.

These new findings have significantly advanced our current understanding on defect evolution and self-organization under irradiation. Still, answers are needed for a list of open questions to fully resolve the puzzle of superlattice formation.

Author contributions

The author YZ conducted the literature review and wrote the manuscript.

Funding

This work was partially sponsored by the U.S. Department of Energy, Office of Science, Basic Energy & Science (BES), Materials Sciences and Engineering Division under FWP #C000−14 − 003 at Idaho National Laboratory operated by Battelle Energy Alliance (BEA) under DOE−NE Idaho Operations Office Contract DE−AC07−05ID14517.

Acknowledgments

The author also acknowledges the support of the start-up funds by University of Wisconsin Madison. The author is very grateful for discussions with coworks, Drs. Jian Gan, Cheng Sun, Yipeng Gao, Chao Jiang, Larry Aagesen, Andrea Jokisaari, Anton Schneider, Lynne Ecker, David Sprouster, Simerjeet Gill, and Ericmoore Jossou.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aagesen, L. K., Jokisaari, A., Schwen, D., Jiang, C., Schneider, A., Zhang, Y., et al. (2022). A phase-field model for void and gas bubble superlattice formation in irradiated solids. Comput. Mater. Sci. 215, 111772. doi:10.1016/j.commatsci.2022.111772