Oxygen potential, oxygen diffusion, and defect equilibria in UO2±x

Since the oxygen potential and the oxygen diffusion coefficient of UO₂ have a significant impact on fuel performance, many experimental data have been obtained. However, experimental data of the oxygen potential and the oxygen diffusion coefficient in the high temperature region above 1673 K are very limited. In the present study, we aimed to obtain these data and analyze them by defect chemistry. the oxygen potentials and the oxygen chemical diffusion coefficient of UO2 were measured by the gas equilibrium method in the near stoichiometric region at temperatures ranging from 1673 to 1873 K. A data set of oxygen potentials was made together with literature data and analyzed by defect chemistry. The oxygen potential of UO₂ was determined as a function of O/U ratio and temperature, and an equation representing the relationship was derived. The oxygen chemical diffusion coefficient values obtained in this study were reasonably close to the literature values. The oxygen partial pressure dependence of the oxygen chemical diffusion coefficients was predicted from the evaluated results of the oxygen potential data, but no clear dependence was observed.

1 Introduction

It is well-known that UO₂, which has a fluorite structure, is a non-stoichiometric oxide that is stable in the hyper-stoichiometric composition range. It has also been shown that UO₂ can lose oxygen to form a hypo-stoichiometric phase at high temperatures and low oxygen potentials. Many researchers have investigated oxygen potentials to determine the oxygen-to-uranium (O/U) ratio and chemical stability (Aronson and Belle 1958; Markin TL. and Bones RJ. 1962; Aukrust, Forland, and Hagemark 1962; Markin TL. and Bones RJ. 1962; Aitken, Brassfield, and Fryxell 1966; Hagemark and Broli 1966; Markin, Wheeler, and Bones 1968; Tetenbaum and Hunt 1968; Ackermann, Rauh, and Chandrasekharaiah 1969; Wheeler 1971; Javed 1972; Wheeler and Jones 1972; Chilton and Edwards 1980; Ugajin 1983), because its stoichiometry significantly affects thermal properties and fuel performance. Ugajin (1983) investigated the near-stoichiometric region by thermogravimetry in a mixed-gas atmosphere of CO/CO₂. Oxygen partial pressure was determined in situ with a stabilized zirconia oxygen sensor. Aronson and Belle (1958) and Markin and Bones (1962) determined the oxygen potential for O/U ratios in the range of 2.01 to 2.53 by the electromotive force (EMF) method. The oxygen potential in UO_2−x was also measured at temperatures above 1873 K using H₂ and CO gases (Wheeler 1971; Javed 1972), and various methods were employed in the measurements. However, the data were scattered over a range larger than 200 kJ/mol, especially when located in the near-stoichiometric region because of difficulty in determining the O/U ratio and oxygen potential pressure. The relationship between the O/U ratio, the temperature, and the oxygen potential has been represented in previous works. Lindemer and Besmann (1985) derived the relationship from the literature data and the classical thermodynamic theory for a solid solution. Some studies represented the relationship by means of the thermodynamic database (Guéneau et al., 2002; Baichi et al., 2006).

The diffusion kinetics for the oxygen ions in oxide fuels are closely involved in diffusion-controlled phenomena such as oxidation and reduction, sintering, and irradiation behavior. For this reason, the oxygen diffusion coefficients of UO₂ have been measured since the 1960s (Auskern and Belle 1961; Belle 1969; Bittel, Sjodahl, and White 1969; Marin and Contamin 1969; Lay 1970; Murch, Bradhurst, and De Bruin 1975; Breitung 1978; Murch and Thorn 1978; Kim and Olander 1981; Bayoglu and Lorenzelli 1984; Ruello et al., 2004). The oxidation and reduction of oxide fuels rely on chemical diffusion in thermodynamically non-ideal systems where oxygen ions are the faster species. The oxygen chemical diffusion coefficient, $\stackrel{\sim }{D}$, is generally obtained by measuring weight changes or electrical conductivity changes during redox reactions (Bittel, Sjodahl, and White 1969; Lay 1970; Bayoglu and Lorenzelli 1984; Ruello et al., 2004) and has been measured over a wide temperature range; but there are very few reports above 1673 K.

In this work, the oxygen potentials of UO₂ were obtained in hyper-stoichiometric compositions by the gas equilibrium method, a Brouwer diagram was constructed, and correlations to represent the O/U ratio were derived as functions of temperature and oxygen partial pressure. In addition, the oxygen chemical diffusion coefficients of UO_2+x in the temperature range above 1673 K were measured and compared with literature data, and the dependence of oxygen chemical diffusion coefficients on oxygen partial pressure was discussed.

2 Experimental procedures

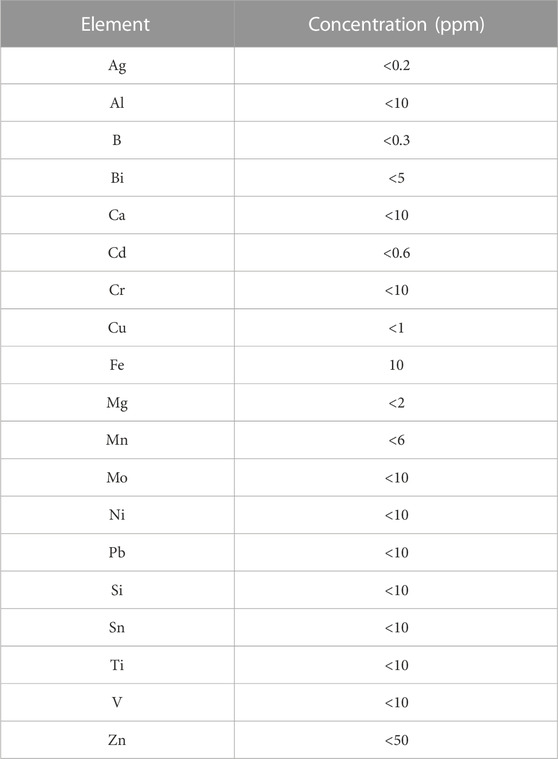
Samples of UO₂ were prepared by powder metallurgy, with UO₂ powder made by the ammonium diuranate (ADU) process used as the starting material. The main impurities contained in the raw powder are listed in Table 1. The powder was pressed into a disk-like sample and sintered at 1973 K for 2.5 h in a gas mixture of 4.5% H₂–Ar, with added moisture. The amount of moisture was adjusted by passing 4.5% H₂–Ar mixed gas through a water bath kept at a constant temperature. The sample weight was 331.91 mg, and the size was 4.253 mm in diameter by 2.275 mm in thickness.

TABLE 1

TABLE 1. Impurities in the UO₂ raw powder.

The oxygen potential and the oxygen chemical diffusion coefficient measurements were carried out at 1673 K, 1773 K, and 1873 K by the gas equilibrium method using a thermogravimeter (TG-DTA 2000SA, Bruker AXS). The uncertainty of the thermogravimeter was ±0.01 mg, which corresponds to ±0.0005 in the O/U ratio. In the measurements, it was observed that the sample weight was reduced by 60 μg/h. It was concluded that the high vapor pressure of the UO₃ species caused the large weight reduction. Due to the small sample volume and short time to reach equilibrium, the measurement of a data point was carried out in less than 30 min; therefore, the uncertainty in the O/U ratio determination was estimated to be ±0.00015.

The oxygen partial pressure in the atmosphere was controlled by the equilibrium reaction of H₂O = H₂ + 1/2O₂ and determined by oxygen sensors that measured the oxygen partial pressure at the equipment inlet and outlet. The gas phase equilibrium was related to the standard Gibbs free energy of formation of water, $\Delta G_f$ (J/mol), by the following equations (Kubaschewski and Alcock 1979)

$∆G_f=RT\ln \frac{P_{H_{2}O}}{P_{H_2}{P}_{O_2}^{1/2}},(1)$

$∆G_f=-246440+54.8T.(2)$

where R is the gas constant (8.3145 J/K/mol) and T is absolute temperature. Eq. 1 represents the value from 298 K to 2500 K. The ratio of $P_{H_{2}O}/P_{H_2}$ was calculated using $P_{O_2}$, which was monitored at 973 K using an oxygen sensor. The $P_{O_2}$ of the atmosphere in the thermogravimeter at higher temperature was calculated under the assumption that the $P_{H_{2}O}/P_{H_2}$ ratio had the same value at the oxygen sensor and the thermogravimeter. The $∆{\overline{G}}_{O_2}$ was described by the following equation

$\Delta {\overline{G}}_{O_2}=RT\ln P_{O_2}.(3)$

The uncertainty of $\Delta {\overline{G}}_{O_2}$ was estimated to be ±10 kJ/mol from the difference of $P_{O_2}$ between the inlet and outlet gas. In the measurements, the change in specimen weight was measured in response to changes in $P_{O_2}$ which were controlled by the ratio of $P_{H_{2}O}/P_{H_2}$. Equilibrium conditions were obtained in a relatively short time (∼15 min) because of the smallness and thinness of the specimen disk. An effect of vaporization of the specimen on measurement data was not observed.

3 Results

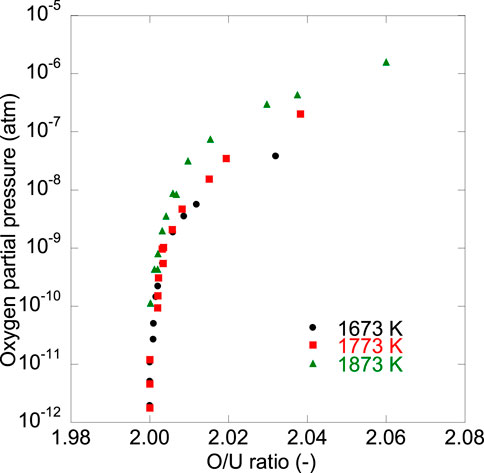
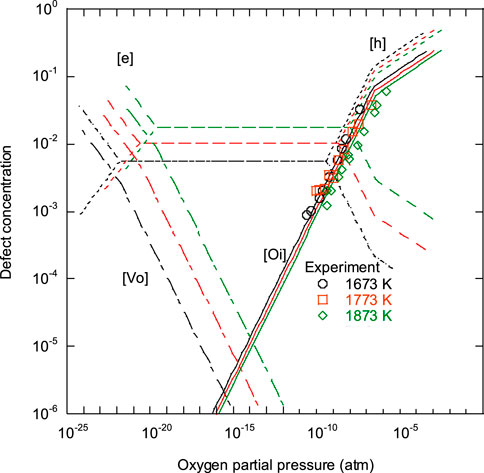
The oxygen potential was measured at temperatures of 1673 K, 1773 K, and 1873 K, and data are shown in Figure 1. The $P_{O_2}$ slightly increased with temperature, depending on the O/U ratio. The relationship between $P_{O_2}$ and x is plotted in Figure 2. In this figure, the well-known proportionality relationship between $P_{O_2}$ and deviation x from stoichiometry was observed:

$x\propto P_{O_2}^{1/n},(4)$

where n is a characteristic number identifying the type of point defect in agreement with literature data (Aronson and Belle 1958; Wheeler 1971; Javed 1972; Wheeler and Jones 1972). The figure shows that the present data changed in accordance with the relationship of n = +2. The literature data were also plotted in the figure and analyzed using the relationship of Eq. 4. In the higher $P_{O_2}$ region, the relationship was n = +6. In the hypo-stoichiometric region, it was observed to be n = −3, as previously reported (Tetenbaum and Hunt 1968; Javed 1972).

FIGURE 1

FIGURE 1. Oxygen potential measurement results at 1673 K, 1773 K, and 1873 K.

FIGURE 2

FIGURE 2. Relationships among oxygen partial pressures and deviations, x, in UO_2±x.

Since the specimen used in this work had the shape of a planar sheet, the diffusion equation was set up for planar sheet geometry with a thickness of 2L. If the sheet is initially at a uniform concentration, C₁, and the surface condition (Crank 1979) is such that

$-D{\left.\frac{\partial C}{\partial x}\right|}_{x=\pm l}=k\left(C_0-C_s\right),(5)$

where D is the diffusion coefficient, C is the concentration of diffusing substance in the planar sheet, k is the rate constant for surface reaction, C_s is the actual concentration just within the planar sheet, and C₀ is the concentration required to maintain equilibrium with the surrounding atmosphere. The obtained solution is

$\frac{C-C_1}{C_0-C_1}=1-{\displaystyle \sum }_{n=1}^{\infty }\frac{2L\cos \left({\beta }_{n}x/l\right)\exp \left(-{\beta }_n^{2}Dt/l^2\right)}{\left({\beta }_n^2+L^2+L\right)\cos {\beta }_n},(6)$

where the ${\beta }_n$ values are the positive roots of

$\beta \tan \beta =L.(7)$

and

$L=lk/D.(8)$

is a dimensionless parameter. The total amount of diffusing substance, $M_t$, entering or leaving the sheet up to time t is expressed as a fraction of $M_{\infty }$, the corresponding quantity after infinite time, by

$\frac{M_t}{M_{\infty }}=1-{\displaystyle \sum }_{n=1}^{\infty }\frac{2L^2\exp \left(-{\beta }_n^{2}Dt/l^2\right)}{{\beta }_n^2\left({\beta }_n^2+L^2+L\right)}.(9)$

The measured data were fitted by Eq. 9 using D and k as parameters. The experimental conditions and the fitting results are listed in Table 2, and Figure 3 shows the weight-change curve and the fitted curve at 1673 K. Good agreement can be seen between the experimental data and the fitted curve. The error in the oxygen chemical diffusion coefficient was calculated to be 84%. It is presumed that the periodic noise from the thermogravimeter degraded the fitting accuracy.

TABLE 2

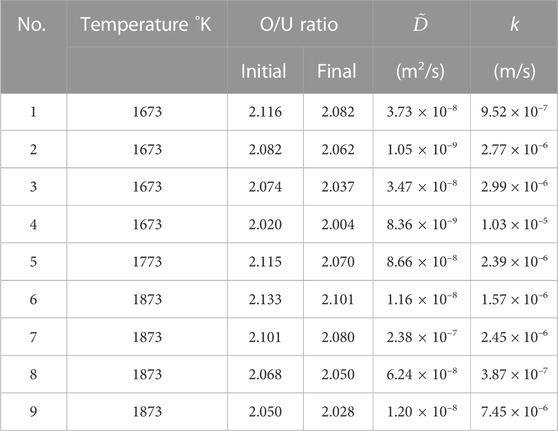
TABLE 2. Experimental conditions, oxygen chemical diffusion coefficient $\stackrel{\sim }{D}$, and surface reaction rate constant, k.

FIGURE 3

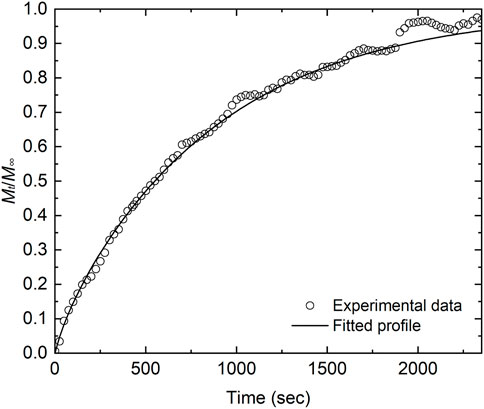
FIGURE 3. Experimental data and fitted curves after variation of the O/U ratio from 2.082 to 2.062 at 1673 K. The experimental data correspond to No. 2 in Table 2.

4 Discussion

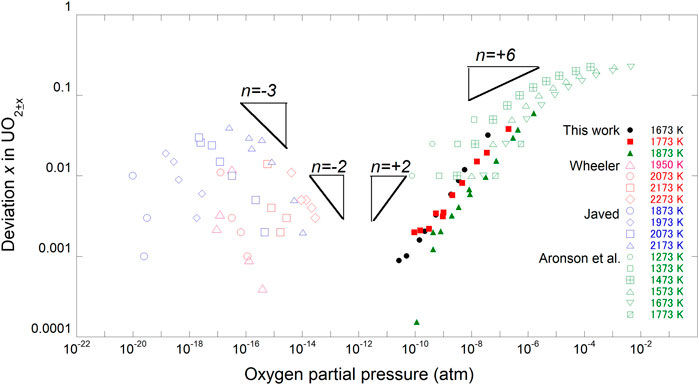
The relationships among n = +6, +2, and −3 are shown in Figure 2. Two types of Brouwer diagram are proposed depending on the kinds of dominant point defects: intrinsic defects and Frenkel defects. The reported electrical conductivity measurements showed that the electronic conduction mechanism was observed, therefore, it is assumed that intrinsic defects were dominant in the stoichiometric composition. Cooper et al. (2018) calculated a Brouwer diagram of UO₂ using an ab initio approach in which intrinsic defects were dominant. In the near stoichiometric region, defect equilibria were considered in reactions (10)–(13):

${\mathrm{O}}_{\mathrm{O}}^{\times }\to {\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }+{2\mathrm{e}}^{\prime }+\frac{1}{2}{\mathrm{O}}_2.(10)$

$\frac{1}{2}{\mathrm{O}}_2\to {\mathrm{O}}_{\mathrm{i}}^{″}+{2\mathrm{h}}^{\bullet }.(11)$

$\text{null}\to {\mathrm{e}}^{\prime }+{\mathrm{h}}^{\bullet }.(12)$

${\mathrm{O}}_{\mathrm{O}}^{\times }\to {\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }+{\mathrm{O}}_{\mathrm{i}}^{″}.(13)$

The equilibrium constants in the aforementioned defect reactions can be described by Eqs 14–17, respectively:

$K_V={\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]\left[{\mathrm{e}}^{\prime }\right]}^2{P}_{O_2}^{1/2},(14)$

$K_O={\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]\left[{\mathrm{h}}^{\bullet }\right]}^2{P}_{O_2}^{-1/2},(15)$

$K_i=\left[{\mathrm{e}}^{\prime }\right]\left[{\mathrm{h}}^{\bullet }\right],(16)$

$K_F=\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right].(17)$

In the case where intrinsic defects are dominant, the defect concentrations of ${\mathrm{e}}^{\prime }$ and ${\mathrm{h}}^{\bullet }$ dominate over those of ${\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }$ and ${\mathrm{O}}_{\mathrm{i}}^{″}$. Therefore, $\left[{\mathrm{e}}^{\prime }\right]=\left[{\mathrm{h}}^{\bullet }\right]$ near the stoichiometric region. The following Eqs 18–20 were obtained from 14–17:

$\left[{\mathrm{e}}^{\prime }\right]=\left[{\mathrm{h}}^{\bullet }\right]{=K_i}^{1/2},(18)$

$\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]=\left(\frac{K_O}{K_i}\right)\bullet P_{O_2}^{1/2}=K_{n=+2}\bullet P_{O_2}^{1/2},(19)$

$\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]=\left(\frac{K_V}{K_i}\right)\bullet P_{O_2}^{-1/2}=K_{n=-2}\bullet P_{O_2}^{-1/2}.(20)$

$K_F$ was obtained from experimental and literature data in the near-stoichiometric region as follows:

$K_F=K_{n=-2}\bullet K_{n=+2}=\frac{K_V{K}_O}{K_i^2}.(21)$

In the oxidation region where n = +2, the (2:2:2) Willis cluster (Willis 1987) was assumed as follows:

$2{\mathrm{O}}_{\mathrm{O}}^{\times }+{\mathrm{O}}_2\to {\left(2{\mathrm{O}}_{\mathrm{i}}^{\mathrm{a}}2{\mathrm{O}}_{\mathrm{i}}^{\mathrm{b}}2{\mathrm{V}}_{\mathrm{O}}\right)}^{\prime }+{\mathrm{h}}^{\bullet }\mathrm{f}\mathrm{o}\mathrm{r}n=+2.(22)$

The equilibrium constant in the aforementioned defect reaction can be described by the following equation:

$K_{ox}=\left[{\left(2{\mathrm{O}}_{\mathrm{i}}^{\mathrm{a}}2{\mathrm{O}}_{\mathrm{i}}^{\mathrm{b}}2{\mathrm{V}}_{\mathrm{O}}\right)}^{\prime }\right]\left[{\mathrm{h}}^{\bullet }\right]P_{O_2}^{-1}.(23)$

$\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]$ can be written as

$\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]=2\left[{\left(2{\mathrm{O}}_{\mathrm{i}}^{\mathrm{a}}2{\mathrm{O}}_{\mathrm{i}}^{\mathrm{b}}2{\mathrm{V}}_{\mathrm{O}}\right)}^{\prime }\right]=2K_{ox}^{1/2}{P}_{O_2}^{1/2}.(24)$

In the hypo-stoichiometric region, n = −3 has been reported by previous studies (Tetenbaum and Hunt 1968; Javed 1972). Kofstad proposed that interstitial uranium ions with two effective charges, ${\mathrm{M}}_{\mathrm{i}}^{\bullet \bullet }$, predominated in this region (Kofstad 1972). The following reaction was assumed:

$2{\mathrm{O}}_{\mathrm{O}}^{\times }+{\mathrm{M}}_{\mathrm{M}}^{\times }\to {\mathrm{M}}_{\mathrm{i}}^{\bullet \bullet }+2{\mathrm{e}}^{\prime }+{\mathrm{O}}_2\mathrm{f}\mathrm{o}\mathrm{r}n=-3,(25)$

$\left[{\mathrm{M}}_{\mathrm{i}}^{\bullet \bullet }\right]=\frac{1}{2}{\left(2K_{n=-3}\right)}^{1/3}{P}_{O_2}^{-1/3}.(26)$

In the oxidation region where n = +6, more complex defects were expected; however, there have been no reports describing this relationship. Defect reactions were not assumed in this region, and only the relationship of n = +6 was described by the following equation:

$\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]=K_{n=+6}{P}_{O_2}^{1/6}.(27)$

The relationships of n = +2 and −2 should be observed in the near-stoichiometric region because intrinsic ionization dominates. The relationships among n = −3, +2 and +6, are shown in Figure 2. The experimental data were fitted by Eqs. 26 and 19–27 assuming that x = $\left[{\mathrm{M}}_{\mathrm{i}}^{\bullet \bullet }\right]$, $\left[{\mathrm{V}}^{\bullet \bullet }\right]$, or $\left[{\mathrm{O}}^{″}\right]$, and the equilibrium constants were obtained for each temperature. The equilibrium constant, K, in the defect reactions can be written as

$K=\exp \left(\frac{\Delta S}{R}\right)\exp \left(-\frac{\Delta H}{RT}\right).(28)$

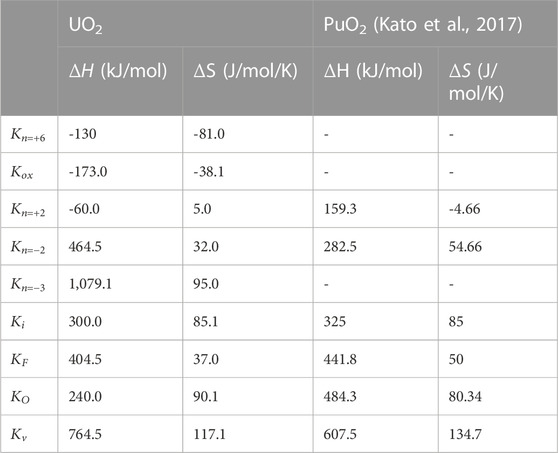
Enthalpy, $\Delta H$ (J/mol), and entropy, $\Delta S$ (J/mol/K), for the equilibrium constants were evaluated as follows:

$K_{n=-3}=\exp \left(\frac{95.0}{R}\right)\exp \left(-\frac{1079.1\times 10^3}{RT}\right).(29)$

$K_{ox}=\exp \left(\frac{-38.1}{R}\right)\exp \left(\frac{173.0\times 10^3}{RT}\right).(30)$

$K_{n=+6}=\exp \left(\frac{-81.0}{R}\right)\exp \left(\frac{130.0\times 10^3}{RT}\right).(31)$

In addition, it was assumed that Eq. 19 equals Eq. 24. The $\Delta H$ and $\Delta S$ in each region are shown in Table 3. Eqs 17–27 describe the Brouwer diagram as shown in Figure 4. The figure shows that the Brouwer diagrams at 1673, 1773, and 1873 K represented the experimental data very well. The Brouwer diagram can give the defect concentrations of $\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]$ and $\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]$. The O/U ratio can be described as Eq. 32, when the main defects are $\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]$ or $\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]$:

$\frac{\mathrm{O}}{\mathrm{U}}\hspace{0.33em}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}=2-\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]+\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right].(32)$

TABLE 3

TABLE 3. Defect formation energies of UO₂ and PuO₂.

FIGURE 4

FIGURE 4. Brouwer diagram of UO_2±x at 1673 K, 1773 K, and 1873 K.

$\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]$ and $\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]$ can be described in Eqs. 33 and 34 using Eqs. 19–27, respectively. The indices −5 and −1/5 are parameters that represent x near the boundary between each line:

$\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]={\left\{{\left(K_{n=-2}{P}_{O_2}^{-1/2}\right)}^{-5}+{\left({\left(2K_{n=-3}\right)}^{1/3}{P}_{O_2}^{-1/3}\right)}^{-5}\right\}}^{-1/5},(33)$

$\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]={\left\{{\left(K_{n=+2}{P}_{O_2}^{1/2}\right)}^{-5}+{\left({\left(K_{n=6}\right)}^{1/3}{P}_{O_2}^{-1/6}\right)}^{-5}\right\}}^{-1/5}.(34)$

Eq. 32 was rewritten as Eq. 35 using Eqs 33 and 34, which can represent the O/U ratio as functions of $P_{O_2}$ and T:

$\begin{array}{c}\frac{\mathrm{O}}{\mathrm{U}}\hspace{0.33em}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}=2-{\{{\left(\exp \left(\frac{32.0}{R}\right)\exp \left(-\frac{464500}{RT}\right)P_{O_2}^{-1/2}\right)}^{-5}+{\left({\left(2\exp \left(\frac{95.0}{R}\right)\exp \left(-\frac{1079100}{RT}\right)\right)}^{1/3}{P}_{O_2}^{-1/3}\right)}^{-5}\}}^{-1/5}\\ +{\left\{{{\left(\exp \left(\frac{5.0}{R}\right)\exp \left(\frac{60000}{RT}\right)P_{O_2}^{1/2}\right)}^{-5}+\left(\left({\left(\exp \left(\frac{-81.0}{R}\right)\exp \left(\frac{130000}{RT}\right)\right)}^{1/3}\right)P_{O_2}^{1/6}\right)}^{-5}\right\}}^{-1/5}.\end{array}(35)$

Eq. 35 gives the relationships between oxygen potential, temperature, and composition in UO_2±x. Figure 5 shows the relationships between x, T, and $P_{O_2}$ and literature data (Aronson and Belle 1958; Wheeler 1971; Javed 1972; Wheeler and Jones 1972).

FIGURE 5

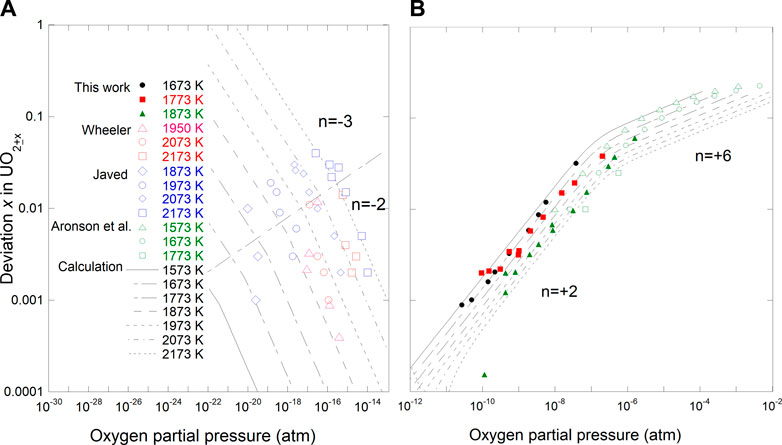
FIGURE 5. Comparison of deviation from stoichiometry vs temperature and oxygen partial pressure with calculated results using Eq. (35). (A) hypo-stoichiometric region; (B) hyper-stoichiometric region.

The $\Delta H$ and $\Delta S$ for the equilibrium constants were assessed as shown in Table 3. The formation energies of ${\mathrm{O}}_{\mathrm{i}}^{″}$, ${\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }$, $\left({\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }+{\mathrm{O}}_{\mathrm{i}}^{″}\right)$, and $\left({\mathrm{e}}^{\prime }+{\mathrm{h}}^{\bullet }\right)$ in UO₂ were -60.0 kJ/mol, 464.5 kJ/mol, 404.5 kJ/mol, and 300.0 kJ/mol, respectively. The Frenkel defect formation energy was compared with literature data (Catlow and Lidiard 1974; Catlow 1977; Clausen et al., 1984; Jackson et al., 1986; Matzke 1987; Murch and Catlow 1987; Petit et al., 1998; Crocombette et al., 2001; Freyss, Petit, and Crocombette 2005; Iwasawa et al., 2006; Gupta, Brillant, and Pasturel 2007; Terentyev 2007; Yun and Kim 2007; Nerikar et al., 2009; Tiwary, van de Walle, and Gronbech-Jensen 2009; Yu, Devanathan, and Weber 2009; Staicu et al., 2010; Andersson et al., 2011; Freyss et al., 2012; Konings and Benes 2013; Vathonne et al., 2014), as shown in Figure 6. The present data approximately corresponded to literature data, which were obtained by experiments and calculations. The Frenkel defect formation energies of UO₂were compared with those of PuO₂ (Kato et al., 2017) and they are almost the same (Table 3). The formation energy value for ${\mathrm{O}}_{\mathrm{i}}^{″}$ is lower in UO₂ than in PuO₂, -60.0 kJ/mol and 159.3 kJ/mol, respectively. Conversely, the formation energy value for ${\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }$ is lower in PuO₂ than in UO₂, 282.5 kJ/mol and 464.5 kJ/mol, respectively. These differences are caused by changing from M⁴⁺ to U⁵⁺ and Pu³⁺, respectively, in UO₂ and PuO₂.

FIGURE 6

FIGURE 6. Comparison of Frenkel defect formation energy in UO_2±x.

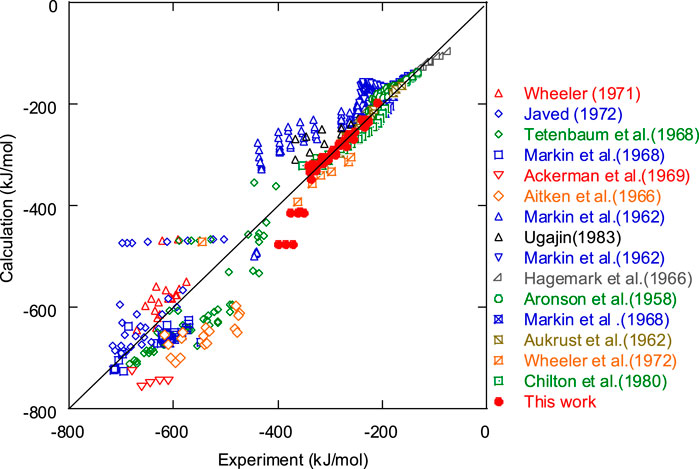
Figure 7 shows a comparison between the experimental data (Aronson and Belle 1958; Markin TL. and Bones RJ. 1962; Aukrust, Forland, and Hagemark 1962; Markin TL. and Bones RJ. 1962; Aitken, Brassfield, and Fryxell 1966; Hagemark and Broli 1966; Markin, Wheeler, and Bones 1968; Tetenbaum and Hunt 1968; Ackermann, Rauh, and Chandrasekharaiah 1969; Wheeler 1971; Javed 1972; Wheeler and Jones 1972; Chilton and Edwards 1980; Ugajin 1983) and the calculated results of the oxygen potential of UO₂. The results of the calculations represent the data within $\sigma$ = ±51 kJ/mol. It can be seen that there is no large discrepancy between the calculated values and the literature values in the hyper-stoichiometric composition range, but there is a large discrepancy in the near- and hypo-stoichiometric regions where there are few experimental data (Figure 7). Especially in the near-stoichiometric region, further expansion of experimental data is necessary, but it is greatly affected by impurities (Maillard et al., 2022); thus, it is necessary to reduce the impurities in the sample to obtain highly accurate data.

FIGURE 7

FIGURE 7. Comparison between measured and calculated data.

Figure 8 shows the comparison between the oxygen chemical diffusion coefficients measured in this study and the literature data (Bittel, Sjodahl, and White 1969; Lay 1970; Breitung 1978; Bayoglu and Lorenzelli 1979; Ruello et al., 2004; Berthinier et al., 2013). The data obtained in this study have larger values than those reported by Bittel et al. and Breitung, but smaller values than those in the near-stoichiometric composition proposed by Berthinier et al. (2013). The data reported by Bittel et al. are the only experimental data in the temperature range above 1673 K. They evaluated the oxygen chemical diffusion coefficients from the results of the steam oxidation of UO₂, but it was pointed out that the U₄O₉ phase was formed on the sample surface, which caused the evaluated oxygen chemical diffusion coefficients to be lower (Breitung 1978). According to the calculation results reported by Berthinier et al., the oxygen chemical diffusion coefficients had maximum values near the stoichiometric composition and decreased with increasing deviation from the stoichiometric composition (Berthinier et al., 2013). Thus, the oxygen chemical diffusion coefficients measured in this study can be considered reasonable, in general. The dependence of the measured diffusion coefficients on oxygen partial pressure is shown in Figure 9. The oxygen chemical diffusion coefficients and the oxygen self-diffusion coefficients ($D^{*}$) are related by Darken’s relationship as given by:

$\stackrel{\sim }{D}=\frac{2\pm x}{2x}{D}^{*}\left(\pm \frac{\partial \log P_{O_2}}{\partial \log x}\right),(36)$

where the positive and negative signs apply to the hyper- and hypo-stoichiometric ranges, respectively. The oxygen self-diffusion coefficient follows the equation of (Berthinier et al., 2013; Watanabe, Kato, and Sunaoshi 2020)

$D^{*}=D_{V_O}^0\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]\exp \left(-\frac{\Delta H_{V_O}^m}{RT}\right)+{2D}_{O_i}^0\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]\exp \left(-\frac{\Delta H_{O_i}^m}{RT}\right),(37)$

where $D_{V_O}^0$ is the pre-exponential term for the oxygen vacancy diffusion, $D_{O_i}^0$ is the pre-exponential term for oxygen interstitial diffusion, $\Delta H_{V_O}^m$ is the migration energy of the oxygen vacancy, and $\Delta H_{O_i}^m$ is the migration energy of the oxygen interstitial. The $\left[{\mathrm{V}}_{\mathrm{O}}^{\bullet \bullet }\right]$ and $\left[{\mathrm{O}}_{\mathrm{i}}^{″}\right]$ in Eq. 37 can be calculated by Eqs 33 and 34. The oxygen self-diffusion coefficient can be calculated by using the pre-exponential terms and the migration energies evaluated by Kato et al. The oxygen chemical diffusion coefficients can be derived from Eqs 36 and 37, and the calculation results are shown in Figure 9. Since the oxygen chemical diffusion coefficients were measured in the regions of n = +2 and n = +6, it is considered that the oxygen diffusion coefficients were dependent on the oxygen partial pressure; however, the oxygen partial pressure dependence was not clearly observed in this study.

FIGURE 8

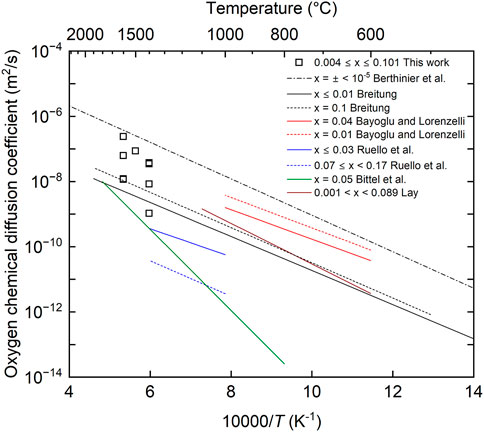
FIGURE 8. Comparison between oxygen chemical diffusion coefficients in this work and literature data.

FIGURE 9

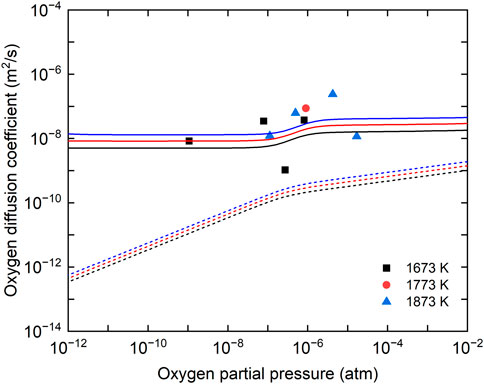
FIGURE 9. Dependence of measured oxygen chemical diffusion coefficients on oxygen partial pressure with calculation results. Solid lines show the calculation results of the oxygen chemical diffusion coefficients. Dashed lines show the calculation results of oxygen self-diffusion coefficients.

5 Conclusions

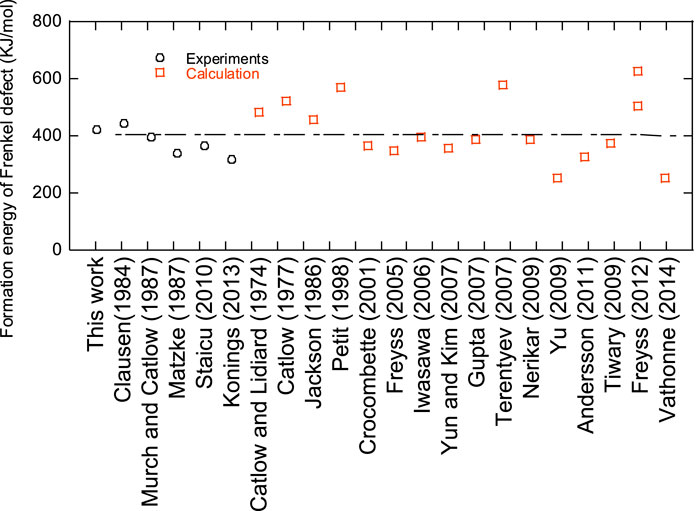
The oxygen potentials and oxygen chemical diffusion coefficients of UO₂ were measured by the gas equilibrium method. A data set of oxygen potential was made and analyzed based on defect chemistry. The relationships between deviation x from stoichiometric composition and the oxygen partial pressure were investigated. Defect equilibrium constants were evaluated by fitting the experimental data and defect formation energies were determined and used to construct a Brouwer diagram. The correlation with UO₂ oxygen potential was then derived. The correlation described the oxygen potential very well even in the near-stoichiometric composition range. The oxygen Frenkel formation energy was estimated to be 404.5 kJ/mol, which was in good agreement with literature values. As a result of comparison with the literature values, it was found that the values of the oxygen chemical diffusion coefficients obtained in this study were generally reasonable. The oxygen partial pressure dependence of the oxygen chemical diffusion coefficient was predicted from the evaluated results of the oxygen potential data, but no clear dependence was observed.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

MW: investigation, analysis, and writing the original draft; MK: conceptualization, analysis, and reviewing and editing the original draft.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ackermann, R. J., Rauh, E. G., and Chandrasekharaiah, M. S. (1969). 'Thermodynamics study of the urania-uranium system. J. Phys. Chem. 73, 762–769. doi:10.1021/j100724a002

CrossRef Full Text | Google Scholar

Aitken, E. A., Brassfield, H. C., and Fryxell, R. E. (1966). “Thermodynamic behaviour of hypostoichiometric UO₂,” in Conference: Symposium on thermodynamics with emphasis on nuclear materials and atomic transport in solids (Vienna (Austria), 435–453.

Google Scholar

Andersson, D. A., Uberuaga, B. P., Nerikar, P. V., Unal, C., and Stanek, C. R. (2011). U and Xe transport in UO2±x: Density functional theory calculations. Phys. Rev. B 84, 054105. doi:10.1103/physrevb.84.054105

CrossRef Full Text | Google Scholar

Aronson, S., and Belle, J. (1958). 'Nonstoichiometry in uranium dioxide. J. Chem. Phys. 29, 151–158. doi:10.1063/1.1744415

CrossRef Full Text | Google Scholar

Aukrust, E., Forland, T., and Hagemark, K. (1962). “Equilibrium measurements and interpretation of non-stoichiometry in UO_2+x,” in Thermodynamics of nuclear materials (Vienna: IAEA), 713–722.

Google Scholar

Auskern, A. B., and Belle, J. (1961). 'Oxygen ion self-diffusion in uranium dioxide. J. Nucl. Mater. 3, 267–276. doi:10.1016/0022-3115(61)90194-5

CrossRef Full Text | Google Scholar

Baichi, M., Chatillon, C., Ducros, G., and Froment, K. (2006). 'Thermodynamics of the O–U system. IV – critical assessment of chemical potentials in the U–UO_2.01 composition range. J. Nucl. Mater. 349, 17–56. doi:10.1016/j.jnucmat.2005.09.001

CrossRef Full Text | Google Scholar

Bayoglu, A., and Lorenzelli, R. (1984). 'Oxygen diffusion in fcc fluorite type nonstoichiometric nuclear oxides MO2±x☆', Solid State Ionics, 12, 53–66. doi:10.1016/0167-2738(84)90130-9

CrossRef Full Text | Google Scholar

Bayoglu, A. S., and Lorenzelli, R. (1979). 'Etude de la diffusion chimique de l'oxygene dans puo2−x par dilatometrie et thermogravimetrie. J. Nucl. Mater. 82, 403–410. doi:10.1016/0022-3115(79)90022-9

CrossRef Full Text | Google Scholar

Belle, J. (1969). 'Oxygen and uranium diffusion in uranium dioxide (a review). J. Nucl. Mater. 30, 3–15. doi:10.1016/0022-3115(69)90163-9

CrossRef Full Text | Google Scholar

Berthinier, C., Rado, C., Chatillon, C., and Hodaj, F. (2013). 'Thermodynamic assessment of oxygen diffusion in non-stoichiometric UO2±x from experimental data and Frenkel pair modeling. J. Nucl. Mater. 433, 265–286. doi:10.1016/j.jnucmat.2012.09.011

CrossRef Full Text | Google Scholar

Bittel, J. T., Sjodahl, L. H., and White, J. F. (1969). 'Steam oxidation kinetics and oxygen diffusion in UOz at high temperatures. J. Am. Ceram. Soc. 52, 446–451. doi:10.1111/j.1151-2916.1969.tb11976.x

CrossRef Full Text | Google Scholar

Breitung, W. (1978). Oxygen self and chemical diffusion coefficients in. J. Nucl. Mater. 74, 10–18. doi:10.1016/0022-3115(78)90527-5

CrossRef Full Text | Google Scholar

Catlow, C. R. A. (1977). 'Point-Defect and electronic properties of uranium-dioxide. Proc. R. Soc. Lond. Ser. a-Mathematical Phys. Eng. Sci. 353, 533–561.

Google Scholar

Catlow, C. R. A., and Lidiard, A. B. (1974). Symposium on the thermodynamics of nuclear materials, 27-42. Vienna, Austria: IAEA.Theoretical studies of point-defect properties of uranium dioxide.

Google Scholar

Chilton, G. R., and Edwards, J. (1980). Oxygen potentials of U_0.77Pu_0.23O_2+x in the temperature range 1523-1822 K." 17, United Kingdom Atomic Energy Authority, Northern DivisionIn.

Google Scholar

Clausen, K., Hayes, W., Macdonald, J. E., Osborn, R., and Hutchings, M. T. (1984). 'Observation of oxygen Frenkel disorder in uranium-dioxide above 2000-K by use of neutron-scattering techniques. Phys. Rev. Lett. 52, 1238–1241. doi:10.1103/physrevlett.52.1238

CrossRef Full Text | Google Scholar

Cooper, M. W. D., Murphy, S. T., and Andersson, D. A. (2018). 'The defect chemistry of UO_2±x from atomistic simulations. J. Nucl. Mater. 504, 251–260. doi:10.1016/j.jnucmat.2018.02.034

CrossRef Full Text | Google Scholar

Crank, J. (1979). The mathematics of diffusion. Oxford, United Kingdom, Oxford University Press.

Google Scholar

Crocombette, J. P., Jollet, F., Nga, L. N., and Petit, T. (2001). 'Plane-wave pseudopotential study of point defects in uranium dioxide. Phys. Rev. B 64, 104107. doi:10.1103/physrevb.64.104107

CrossRef Full Text | Google Scholar

Freyss, M., Dorado, B., Bertolus, M., Jomard, G., Vathonne, E., Garcia, P., et al. (2012). “First-principles DFT + U study of radiation damage in UO₂ : f electron correlations and the local energy minima issue,” in Psi-k newsletter, 35–61.

Google Scholar

Freyss, M., Petit, T., and Crocombette, J. P. (2005). 'Point defects in uranium dioxide: Ab initio pseudopotential approach in the generalized gradient approximation. J. Nucl. Mater. 347, 44–51. doi:10.1016/j.jnucmat.2005.07.003

CrossRef Full Text | Google Scholar

Guéneau, C., Baichi, M., Labroche, D., Chatillon, C., and Sundman, B. (2002). 'Thermodynamic assessment of the uranium–oxygen system. J. Nucl. Mater. 304, 161–175. doi:10.1016/s0022-3115(02)00878-4

CrossRef Full Text | Google Scholar

Gupta, F., Brillant, G., and Pasturel, A. (2007). 'Correlation effects and energetics of point defects in uranium dioxide: A first principle investigation. Philos. Mag. 87, 2561–2569. doi:10.1080/14786430701235814

CrossRef Full Text | Google Scholar

Hagemark, K., and Broli, M. (1966). 'Equilibrium oxygen pressures over the nonstoicheiometric uranium oxides UO_2+x and U₃O_8-z at higher temperatures. J. Inorg. Nucl. Chem. 28, 2837–2850. doi:10.1016/0022-1902(66)80010-6

CrossRef Full Text | Google Scholar

Iwasawa, M., Chen, Y., Kaneta, Y., Ohnuma, T., Geng, H. Y., and Kinoshita, M. (2006). 'First-principles calculation of point defects in uranium dioxide. Mater. Trans. 47, 2651–2657. doi:10.2320/matertrans.47.2651

CrossRef Full Text | Google Scholar

Jackson, R. A., Murray, A. D., Harding, J. H., and Catlow, C. R. A. (1986). The calculation of defect parameters in UO₂. Philosophical Mag. a-Physics Condens. Matter Struct. Defects Mech. Prop. 53, 27–50. doi:10.1080/01418618608242805

CrossRef Full Text | Google Scholar

Javed, N. A. (1972). 'Thermodynamic study of hypostoichiometric urania. J. Nucl. Mater. 43, 219–224. doi:10.1016/0022-3115(72)90053-0

CrossRef Full Text | Google Scholar

Kato, M., Nakamura, H., Watanabe, M., Matsumoto, T., and Machida, M. (2017). Defect chemistry and basic properties of non-stoichiometric PuO₂. Defect Diffusion Forum 375, 57–70. doi:10.4028/www.scientific.net/ddf.375.57

CrossRef Full Text | Google Scholar

Kato, M., Watanabe, M., Hirooka, S., and Vauchy, R. (In press 2023). Oxygen diffusion in flurotite-tyoe oxides, CeO₂, ThO₂, UO₂, PuO₂, and (U, Pu)O₂. Front. Nucl. Eng.

Google Scholar

Kim, K. C., and Olander, D. R. (1981). Oxygen diffusion in UO2−x. J. Nucl. Mater. 102, 192–199. doi:10.1016/0022-3115(81)90559-6

CrossRef Full Text | Google Scholar

Kofstad, P. (1972). Nonstoichiometry, diffusion, and electrical conductivity in binary metal oxides. Hoboken, New Jersey, United States, John Wiley & Sons.

Google Scholar

Konings, R. J. M., and Benes, O. (2013). 'The heat capacity of NpO2 at high temperatures: The effect of oxygen Frenkel pair formation. J. Phys. Chem. Solids 74, 653–655. doi:10.1016/j.jpcs.2012.12.018

CrossRef Full Text | Google Scholar

Kubaschewski, O., and Alcock, C. B. (1979). Metallurgical thermochemistry. Pergamon; 5th edition, Pergamon, Turkey.

Google Scholar

Lay, K. W. (1970). 'Oxygen chemical diffusion coefficient of uranium dioxide. J. Am. Ceram. Soc. 53, 369–373. doi:10.1111/j.1151-2916.1970.tb12134.x

CrossRef Full Text | Google Scholar

Lindemer, T. B., and Besmann, T. M. (1985). Chemical thermodynamic representation of UO_2±x. J. Nucl. Mater. 130, 473–488. doi:10.1016/0022-3115(85)90334-4

CrossRef Full Text | Google Scholar

Maillard, S., Andersson, D., Freyss, M., and Bruneval, F. (2022). 'Assessment of atomistic data for predicting the phase diagram and defect thermodynamics. The example of non-stoichiometric uranium dioxide. J. Nucl. Mater. 569, 153864. doi:10.1016/j.jnucmat.2022.153864

CrossRef Full Text | Google Scholar

Marin, J. F., and Contamin, P. (1969). Uranium and oxygen self-diffusion in UO2. J. Nucl. Mater. 30, 16–25. doi:10.1016/0022-3115(69)90164-0

CrossRef Full Text | Google Scholar

Markin, T. L., and Bones, R. J. (1962a). The determination of changes in free energy for uranium oxides using a high temperature galvanic cell Part 1.

Google Scholar

Markin, T. L., and Bones, R. J. (1962b). The determination of some thermodynamic properties of uranium oxides with O/U ratios between 2.00 and 2.03 using a high temperature galvanic cell Part 2.

Google Scholar

Markin, T. L., Wheeler, V. J., and Bones, R. J. (1968). High temperature thermodynamic data for UO_2±x. J. Inorg. Nucl. Chem. 30, 807–817. doi:10.1016/0022-1902(68)80441-5

CrossRef Full Text | Google Scholar

Matzke, H. (1987). Atomic transport properties in UO₂ and mixed oxides (U, Pu)O₂. J. Chem. Soc. Faraday Trans. 2, 1243. doi:10.1039/ft9908601243

CrossRef Full Text | Google Scholar

Murch, G. E., Bradhurst, D. H., and De Bruin, H. J. (1975). Oxygen self-diffusion in non-stoichiometric uranium dioxide. Philosophical Mag. A J. Theor. Exp. Appl. Phys. 32, 1141–1150. doi:10.1080/14786437508228095

CrossRef Full Text | Google Scholar

Murch, G. E., and Catlow, C. R. A. (1987). 'Oxygen diffusion in UO₂, ThO₂ and PuO₂ a review. J. Chem. Society-Faraday Trans. Ii 83, 1157–1169. doi:10.1039/f29878301157

CrossRef Full Text | Google Scholar

Murch, G. E., and Thorn, R. J. (1978). 'The mechanism of oxygen diffusion in near stoichiometric uranium dioxide. J. Nucl. Mater. 71, 219–226. doi:10.1016/0022-3115(78)90419-1

CrossRef Full Text | Google Scholar

Nerikar, P., Watanabe, T., Tulenko, J. S., Phillpot, S. R., and Sinnott, S. B. (2009). 'Energetics of intrinsic point defects in uranium dioxide from electronic-structure calculations. J. Nucl. Mater. 384, 61–69. doi:10.1016/j.jnucmat.2008.10.003

CrossRef Full Text | Google Scholar

Petit, T., Lemaignan, C., Jollet, F., Bigot, B., and Pasturel, A. (1998). 'Point defects in uranium dioxide. Philosophical Mag. B-Physics Condens. Matter Stat. Mech. Electron. Opt. Magnetic Prop. 77, 779–786. doi:10.1080/014186398259176

CrossRef Full Text | Google Scholar

Ruello, P., Chirlesan, G., Petot-Ervas, G., Petot, C., and Desgranges, L. (2004). 'Chemical diffusion in uranium dioxide – influence of defect interactions. J. Nucl. Mater. 325, 202–209. doi:10.1016/j.jnucmat.2003.12.007

CrossRef Full Text | Google Scholar

Staicu, D., Wiss, T., Rondinella, V. V., Hiernaut, J. P., Konings, R. J. M., and Ronchi, C. (2010). 'Impact of auto-irradiation on the thermophysical properties of oxide nuclear reactor fuels. J. Nucl. Mater. 397, 8–18. doi:10.1016/j.jnucmat.2009.11.024

CrossRef Full Text | Google Scholar

Terentyev, D. (2007). 'Molecular dynamics study of oxygen transport and thermal properties of mixed oxide fuels. Comput. Mater. Sci. 40, 319–326. doi:10.1016/j.commatsci.2007.01.002

CrossRef Full Text | Google Scholar

Tetenbaum, M., and Hunt, P. D. (1968). 'High-Temperature thermodynamic properties of oxygen-deficient urania. J. Chem. Phys. 49, 4739–4744. doi:10.1063/1.1669953

CrossRef Full Text | Google Scholar

Tiwary, P., van de Walle, A., and Gronbech-Jensen, N. (2009). 'ab initio construction of interatomic potentials for uranium dioxide across all interatomic distances. Phys. Rev. B 80, 174302. doi:10.1103/physrevb.80.174302

CrossRef Full Text | Google Scholar

Ugajin, M. (1983). 'Measurements of O/U ratio and oxygen potential for UO_2+x (0≤x≲0.1). J. Nucl. Sci. Technol. 20, 228–236. doi:10.1080/18811248.1983.9733384

CrossRef Full Text | Google Scholar

Vathonne, E., Wiktor, J., Freyss, M., Jomard, G., and Bertolus, M. (2014). 'DFT + U investigation of charged point defects and clusters in UO2. J. Phys. Condens Matter 26, 325501. doi:10.1088/0953-8984/26/32/325501

PubMed Abstract | CrossRef Full Text | Google Scholar

Watanabe, M., Kato, M., and Sunaoshi, T. (2020). Oxygen self-diffusion in near stoichiometric (U, Pu)O2 at high temperatures of 1673-1873 K. J. Nucl. Mater. 542, 152472. doi:10.1016/j.jnucmat.2020.152472

CrossRef Full Text | Google Scholar

Wheeler, V. J. (1971). High temperature thermodynamic data for UO2−x. J. Nucl. Mater. 39, 315–318. doi:10.1016/0022-3115(71)90151-6

CrossRef Full Text | Google Scholar

Wheeler, V. J., and Jones, I. G. (1972). Thermodynamic and composition changes in UO_2±x (x< 0.005) at 1950 K. J. Nucl. Mater. 42, 117–121. doi:10.1016/0022-3115(72)90018-9

CrossRef Full Text | Google Scholar

Willis, B. T. M. (1987). 'Crystallographic studies of anion-excess uranium-oxides. J. Chem. Society-Faraday Trans. Ii 83, 1073–1081. doi:10.1039/f29878301073

CrossRef Full Text | Google Scholar

Yu, J., Devanathan, R., and Weber, W. J. (2009). 'First-principles study of defects and phase transition in UO₂. J. Phys. Condens Matter 21, 435401. doi:10.1088/0953-8984/21/43/435401

PubMed Abstract | CrossRef Full Text | Google Scholar

Yun, Y. S., and Kim, W. W. (2007). “First principle studies on electronic and defect structures of UO₂, ThO₂, and PuO₂,” in Proceedings of the KNS spring meeting. Republic of Korea, daejeon, South Korea, (KNS).

Google Scholar